P. Kowalik, Laboratorium badań operacyjnych: zadanie optymalnej diety (wariant uproszczony)
1
3. Zadanie optymalnej diety (wariant uproszczony)
Zadanie to opisuje sytuację decyzyjną, w której trzeba dokonać wyboru najtańszej mieszanki produktów spo-
ż
ywczych zwanej dietą, spełniającej jednocześnie normy odnośnie spożycia składników odżywczych w pew-
nym ustalonym okresie (najczęściej jednego dnia). Choć nie ma to znaczenia z punktu widzenia obliczeń, z
praktycznego punktu widzenia ten model nadaje się raczej do układania planów żywienia dla zwierząt niż dla
ludzi (ze względu na pominięcie kwestii walorów smakowych oraz nieuchronną monotonię tak ułożonej diety).
Wyboru diety można dokonać spośród n różnych dostępnych produktów spożywczych. W rozważanym okresie
należy zapewnić spożycie co najmniej minimalnych wymaganych ilości m różnych składników odżywczych
(takich jak białko, węglowodany, tłuszcze, witaminy, sole mineralne itp. a także odpowiednią ilość kalorii) za-
wartych w produktach. Zakładamy, że koszty jednostkowe produktów są stałe i nie zależą od wielkości zakupu.
Dane są:
•
ij
a
,
i
= 1
,...,m, j
= 1
,...,n
- zawartość
i
-tego składnika odżywczego na jednostkę
j
-tego produktu (np. ilość g
białka na kg kiszonki w mieszance paszowej, g węglowodanów na kg dżemu, dag tłuszczu na kg mięsa, mg
witaminy C na litr soku itp.) ;
•
i
b
,
i
=1
,...,m
- minimalne wymagane spożycie
i
-tego składnika odżywczego w rozważanym okresie (liczone
np. w mg, g, kg, ml, l, cm
3
, kcal);
•
j
c
,
j
=
1,...,n -
cena jednostkowa dla
j
-tego produktu, liczona w PLN/l, PLN/kg, PLN/m
3
, PLN/t itp. – (za-
miast PLN może być dowolna inna waluta, ale dla wszystkich produktów jednakowa).
Należy zaplanować, które produkty spożywcze i w jakich ilościach należy
zakupić
aby zminimalizować łącz-
ne koszty ich zakupu
w rozważanym okresie, dostarczając przy tym co najmniej tyle składników odżyw-
czych, ile przewidują normy minimalnego wymaganego spożycia
. Zmiennymi decyzyjnymi w tym zagad-
nieniu są zatem ilości produktów spożywczych:
•
x
j
-
wielkość zakupu i spożycia
j
-ego produktu spożywczego,
a ogólny model zagadnienia można zapisać następująco:
min
...
2
2
1
1
→
+
+
+
n
n
x
c
x
c
x
c
- ł
ą
czny koszt zakupu produktów
przy ograniczeniach
rzeczywiste spo
ż
ycie
minimalne wymagane spo
ż
ycie
składników od
ż
ywczych
składników od
ż
ywczych
1
1
2
12
1
11
...
b
x
a
x
a
x
a
n
n
≥
+
+
+
2
2
2
22
1
21
...
b
x
a
x
a
x
a
n
n
≥
+
+
+
⋮ ⋮
m
n
mn
m
m
b
x
a
x
a
x
a
≥
+
+
+
...
2
2
1
1
0
1
≥
x
,
0
2
≥
x
,....,
0
≥
n
x
ilo
ś
ci produktów spo
ż
ywczych nie mog
ą
by
ć
ujemne
Je
ż
eli istniej
ą
górne normy spo
ż
ycia składników, to wtedy nale
ż
y doda
ć
nast
ę
puj
ą
c
ą
grup
ę
warunków ograni-
czaj
ą
cych
rzeczywiste spo
ż
ycie
maksymalne dopuszczalne spo
ż
ycie
składników od
ż
ywczych
składników od
ż
ywczych
1
1
2
12
1
11
...
d
x
a
x
a
x
a
n
n
≤
+
+
+
⋮
⋮
m
n
mn
m
m
d
x
a
x
a
x
a
≤
+
+
+
...
2
2
1
1
gdzie
i
d
- maksymalne dopuszczalne spo
ż
ycie i-tego składnika od
ż
ywczego w rozwa
ż
anym okresie (i=1,...,m),
(liczone np. w mg, g, kg, ml, l, cm
3
, kcal);
P. Kowalik, Laboratorium badań operacyjnych: zadanie optymalnej diety (wariant uproszczony)
2
Zadanie - optymalna dieta
1) Dla potrzeb tuczu
ś
wi
ń
nale
ż
y sporz
ą
dzi
ć
najta
ń
sz
ą
mieszank
ę
paszow
ą
składaj
ą
c
ą
si
ę
z (co najwy
ż
ej) sze-
ś
ciu dost
ę
pnych produktów (zbó
ż
, ro
ś
lin str
ą
czkowych oraz zielonki - li
ś
ci buraka pastewnego). Przy planowa-
niu mieszaki nale
ż
y uwzgl
ę
dni
ć
dzienne zapotrzebowanie na 4 składniki od
ż
ywcze oraz na kalorie. Dane licz-
bowe do zadania (z normami
ż
ywieniowymi dla 1
ś
wini) znajduj
ą
si
ę
w tabeli.
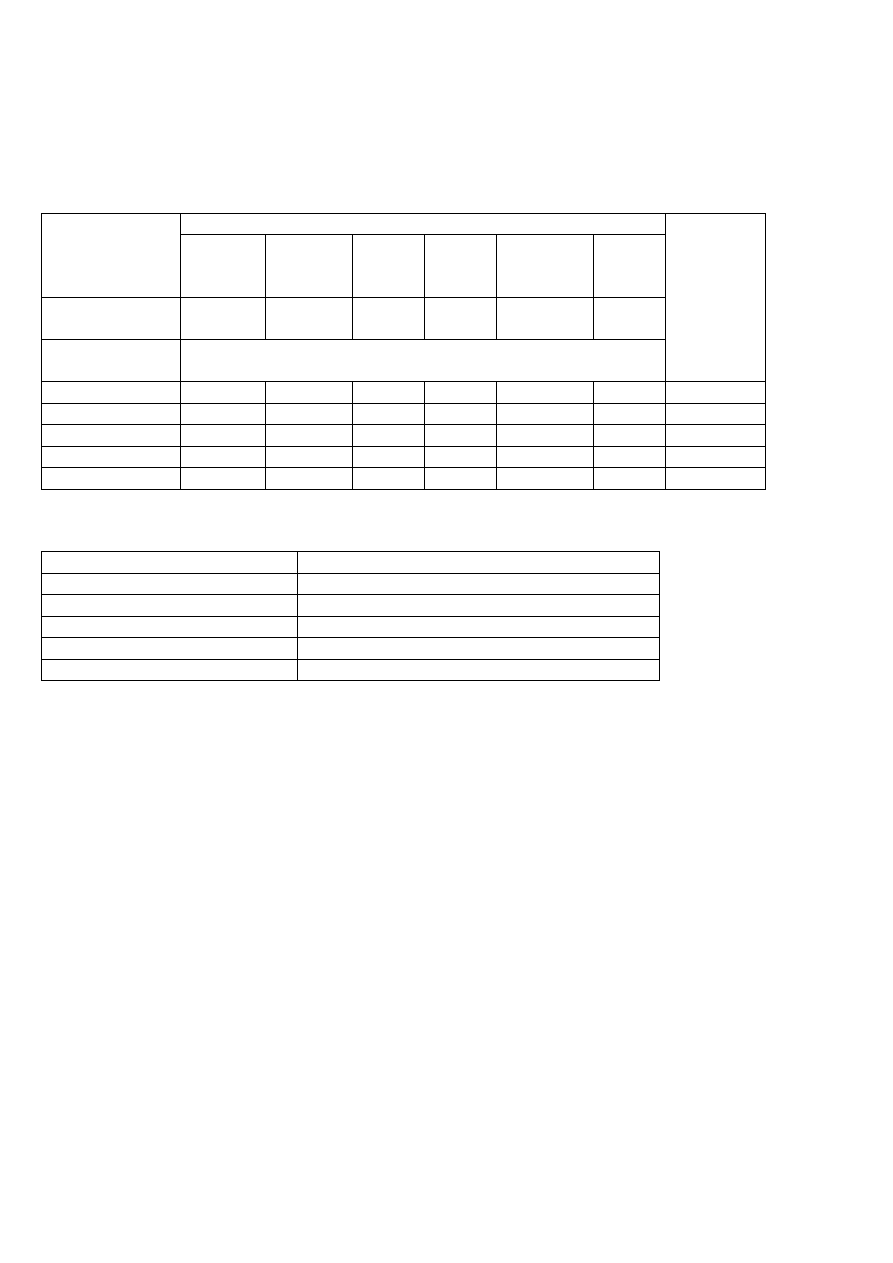
Produkty spożywcze
Minimalne
wymagane
ilości
składników
j
ę
czmie
ń
(kg)
kukurydza
(kg)
pszenica
(kg)
rzepak
(kg)
li
ś
cie
buraków
pastew.(kg)
soja
(kg)
ceny jednostkowe
(PLN/kg)
0,30
0,90
0,50
0,45
0,05
0,80
Składniki
odżywcze
Jednostkowe zawartości składników odżywczych
białko (g/kg)
110
95
121
330
19
400
450 g
tłuszcz (g/kg)
19
41
17
42
4
21
130 g
wap
ń
(g/kg)
0,7
0,5
1,2
3,7
1
3,6
25 g
fosfor (g/kg)
3,2
3
3,5
4,5
0,3
5,7
17 g
kalorie (kcal/kg)
2170
3420
3280
4530
90
3057
7300 kcal
2) Sprawdzi
ć
jak si
ę
zmieni wynik, je
ż
eli wprowadzimy normy maksymalnego dopuszczanego spo
ż
ycia skład-
ników dane poni
ż
ej.
Składniki odżywcze
Maksymalne dopuszczalne ilości składników
białko (g/kg)
780 g
tłuszcz (g/kg)
210 g
wap
ń
(g/kg)
40 g
fosfor (g/kg)
30 g
kalorie (kcal/kg)
10100 kcal
3) Sprawdzi
ć
jak zmieni si
ę
wynik, je
ż
eli górna norma spo
ż
ycia białka zostanie zmniejszona do 700g.
Wskazówka
: w punkcie 2) model nale
ż
y uzupełni
ć
o warunki ograniczaj
ą
ce typu „ ≤ ” jak podano we wzorach
ogólnych.
Model matematyczny do zadania
1
x
,
2
x
,
3
x
,
4
x
,
5
x
,
6
x
- ilo
ś
ci produktów spo
ż
ywczych (odpowiednio j
ę
czmienia, kukurydzy, rzepaku, li
ś
ci bu-
raków pastewnych i soi) wchodz
ą
cych w skład paszy.
min
8
,
0
05
,
0
45
,
0
5
,
0
9
,
0
3
,
0
6
5
4
3
2
1
→
+
+
+
+
+
x
x
x
x
x
x
(funkcja celu – ł
ą
czny koszt zakupu produktów)
przy ograniczeniach
rzeczywiste spo
ż
ycie składników od
ż
ywczych min. wymagane dzienne spo
ż
ycie składn. od
ż
ywczych
450
400
19
330
121
95
110
6
5
4
3
2
1
≥
+
+
+
+
+
x
x
x
x
x
x
130
21
4
41
17
41
19
6
5
4
3
2
1
≥
+
+
+
+
+
x
x
x
x
x
x
25
6
,
3
1
7
,
3
2
,
1
5
,
0
7
,
0
6
5
4
3
2
1
≥
+
+
+
+
+
x
x
x
x
x
x
17
7
,
5
3
,
0
5
,
4
5
,
3
3
2
,
3
6
5
4
3
2
1
≥
+
+
+
+
+
x
x
x
x
x
x
7300
3057
90
4530
3280
3420
2170
6
5
4
3
2
1
≥
+
+
+
+
+
x
x
x
x
x
x
0
1
≥
x
,
0
2
≥
x
,
0
3
≥
x
,
0
4
≥
x
,
0
5
≥
x
,
0
6
≥
x
- ilo
ś
ci produktów spo
ż
ywczych nie mog
ą
by
ć
ujemne
Funkcja celu i pierwszy z warunków ograniczaj
ą
cych „rozpisane” z jednostkami.
P. Kowalik, Laboratorium badań operacyjnych: zadanie optymalnej diety (wariant uproszczony)
3
Rozwiązywanie zadania: pierwszy etap – „klasyczne” zadanie optymalnej diety.
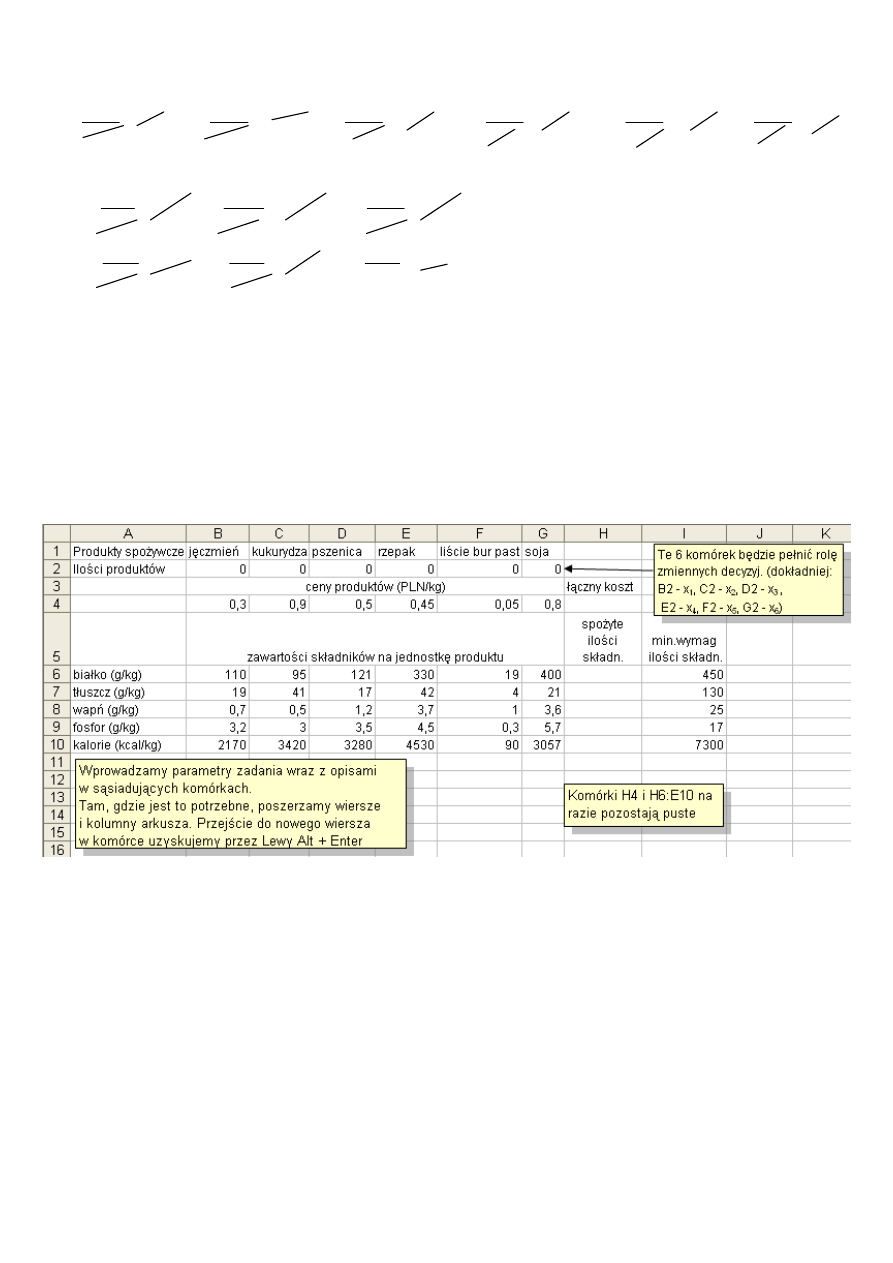
Wprowadzanie danych do komórek arkusza
Jak zwykle, u
ż
ytkownik
musi zdecydować, które komórki arkusza będą pełnić rolę zmiennych decyzyj-
nych
(„iksów”).
W rozwi
ą
zywanym wła
ś
nie zadaniu komórkami pełni
ą
cymi rol
ę
zmiennych decyzyjnych b
ę
d
ą
B2, C2, D2, E2,
F2, G2 czyli w skrócie zakres (tablica) B2:G2. Odpowiednio
ść
pomi
ę
dzy komórkami a zmiennymi jest nast
ę
-
puj
ą
ca:
B2 -
1
x
, C2 -
2
x
, D2 -
3
x
, E2 -
4
x
, F2 -
5
x
, G2 -
6
x
.
Rozmieszczenie danych dla zadania optymalnej diety
Poniewa
ż
współczynniki funkcji celu znajduj
ą
si
ę
w komórkach B4, C4, D4, E4, F4, G4, zatem odpowiedni-
kiem funkcji celu
6
5
4
3
2
1
8
,
0
05
,
0
45
,
0
5
,
0
9
,
0
3
,
0
x
x
x
x
x
x
+
+
+
+
+
b
ę
dzie formuła
=B4*B2+C4*C2+D4*D2+E4*E2+F4*F2+G4*G2
Zastosujemy jednak prostsz
ą
we wprowadzaniu (zwłaszcza, je
ż
eli u
ż
yty zostanie kreator funkcji z menu
Wstaw-Funkcja) równowa
ż
n
ą
formuł
ę
=SUMA.ILOCZYNÓW(B4:G4;B2:G2).
Analogicznie, jak na poprzednim laboratorium, funkcja celu jest podobna do lewych stron warunków ograni-
czaj
ą
cych (wszystkie s
ą
sumami iloczynów liczb i zmiennych). Dzi
ę
ki temu formuła reprezentuj
ą
ca w arkuszu
funkcj
ę
celu zostanie wykorzystana do stworzenia, przy pomocy kopiowania, formuł reprezentuj
ą
cych lewe
strony warunków ograniczaj
ą
cych W tym celu formuła ta musi by
ć
wpisana w postaci
=SUMA.ILOCZYNÓW(B4:G4;B$2:G$2)
b
g
S
kg
x
S
kg
b
g
L
kg
x
L
kg
b
g
R
kg
x
R
kg
b
g
P
kg
x
P
kg
b
g
K
kg
x
K
kg
b
g
J
kg
x
J
kg
b
g
450
400
19
330
121
95
110
6
5
4
3
2
1
≥
+
+
+
+
+
S
kg
x
S
kg
PLN
L
kg
x
L
kg
PLN
R
kg
x
R
kg
PLN
P
kg
x
P
kg
PLN
K
kg
x
K
kg
PLN
J
kg
x
J
kg
PLN
6
5
4
3
2
1
8
,
0
05
,
0
45
,
0
5
,
0
9
,
0
3
,
0
+
+
+
+
+
P. Kowalik, Laboratorium badań operacyjnych: zadanie optymalnej diety (wariant uproszczony)
4
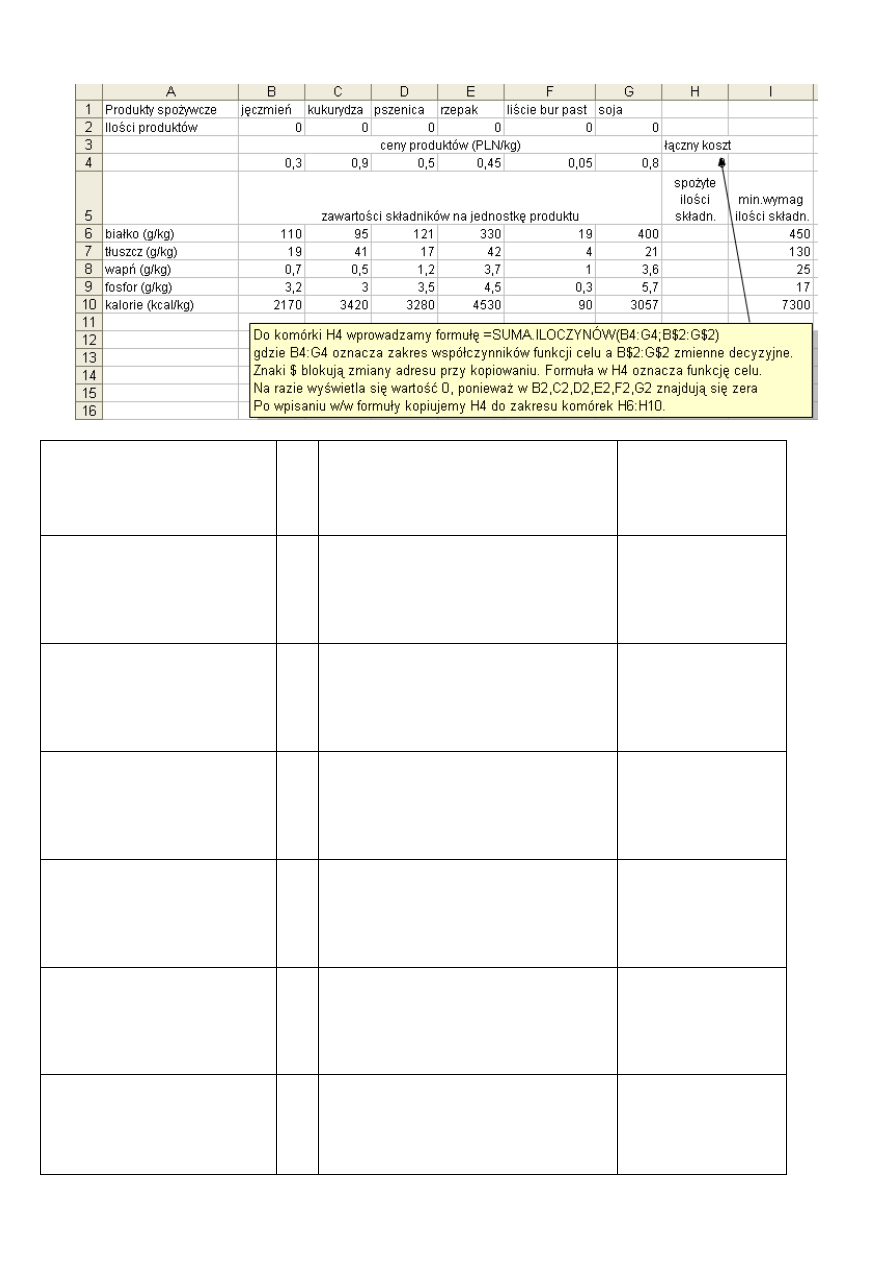
Informacja na temat formuł: wprowadzanej i kopiowanych
Zapis matematyczny
Formuły „dosłowne” tzn. takie które
należałoby wpisać przy literalnym
„przełożeniu” zapisu matematycznego
na składnię Excela
K
om
ór
ka
Formuły z SUMA.ILOCZYNÓW odpowiada-
jące formułom „dosłownym”
Uwagi
6
5
4
3
2
1
8
,
0
05
,
0
45
,
0
5
,
0
9
,
0
3
,
0
x
x
x
x
x
x
+
+
+
+
+
=B4*B2+C4*C2+D4*D2+
E4*E2+F4*F2+G4*G2
H4
=SUMA.ILOCZYNÓW(B4:G4;B$2:G$2)
Wprowadzona przez użyt-
kownika
6
5
4
3
2
1
400
19
330
121
95
110
x
x
x
x
x
x
+
+
+
+
+
=B6*B2+C6*C2+D6*D2+
E6*E2+F6*F2+G6*G2
H6
=SUMA.ILOCZYNÓW(B6:G6;B$2:G$2)
Otrzymana przez
kopiowanie z H4
6
5
4
3
2
1
21
4
41
17
41
19
x
x
x
x
x
x
+
+
+
+
+
=B7*B2+C7*C2+D7*D2+
E7*E2+F7*F2+G7*G2
H7
=SUMA.ILOCZYNÓW(B7:G7;B$2:G$2)
Otrzymana przez
kopiowanie z H4
6
5
4
3
2
1
6
,
3
1
7
,
3
2
,
1
5
,
0
7
,
0
x
x
x
x
x
x
+
+
+
+
+
=B8*B2+C8*C2+D8*D2+
E8*E2+F8*F2+G8*G2
H8
=SUMA.ILOCZYNÓW(B8:G8;B$2:G$2)
Otrzymana przez
kopiowanie z H4
6
5
4
3
2
1
7
,
5
3
,
0
5
,
4
5
,
3
3
2
,
3
x
x
x
x
x
x
+
+
+
+
+
=B9*B2+C9*C2+D9*D2+
E9*E2+F9*F2+G9*G2
H9
=SUMA.ILOCZYNÓW(B9:G9;B$2:G$2)
Otrzymana przez
kopiowanie z H4
6
5
4
3
2
1
400
19
4530
3280
3420
2170
x
x
x
x
x
x
+
+
+
+
+
=B10*B2+C10*C2+D10*D2+
E10*E2+F10*F2+G10*G2
H10
=SUMA.ILOCZYNÓW(B10:G10;B$2:G$2)
Otrzymana przez
kopiowanie z H4
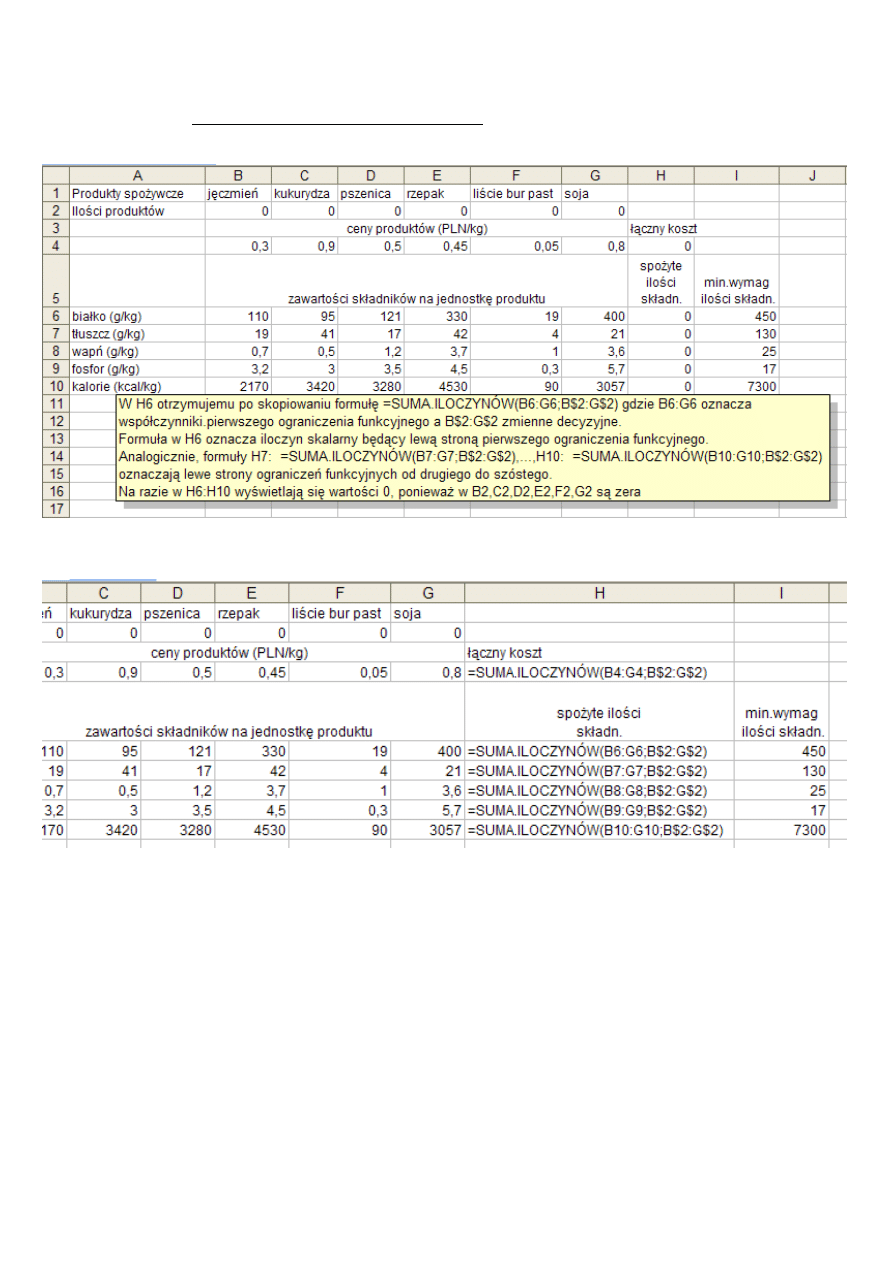
P. Kowalik, Laboratorium badań operacyjnych: zadanie optymalnej diety (wariant uproszczony)
5
Kopiowanie komórki H4
Kolejnym etapem jest skopiowanie komórki H4 na zakres H6:H10. Dzięki właściwościom kopiowania nie trzeba bowiem
wprowadzać 6 formuł (funkcja celu + 5 formuł na lewe strony warunków ograniczających). Wystarczy wpisać formułę
(odpowiadającą funkcji celu) jeden raz, a pozostałe formuły „wygenerować” poprzez kopiowanie.
Zrzut ekranu powy
ż
ej
nie ilustruje żadnych czynności
, a jedynie słu
ż
y do
kontroli poprawności
wprowadze-
nia danych!!!
To samo, co powy
ż
ej, ale
zamiast wyników formuł
(które to wyniki na tym etapie s
ą
zerami) s
ą
wy
ś
wietlone
same formuły
. Ze wzgl
ę
du na oszcz
ę
dno
ść
miejsca jest to tylko fragment arkusza.
Ustawienia Solvera
Na tym etapie zako
ń
czyło si
ę
wprowadzanie danych bezpo
ś
rednio do komórek arkusza.
Mamy nast
ę
puj
ą
ce zwi
ą
zki mi
ę
dzy zapisem matematycznym a zapisem w Excelu:
B2 C2 D2 E2 F2 G2
1
x
,
2
x
,
3
x
,
4
x
,
5
x
,
6
x
.
H4
min
8
,
0
05
,
0
45
,
0
5
,
0
9
,
0
3
,
0
6
5
4
3
2
1
→
+
+
+
+
+
x
x
x
x
x
x
(funkcja celu – łączny koszt zakupu produktów)
przy ograniczeniach
rzeczywiste spo
ż
ycie składników od
ż
ywczych min. dzienne wymagane spo
ż
ycie składn. od
ż
ywczych
H6
450
400
19
330
121
95
110
6
5
4
3
2
1
≥
+
+
+
+
+
x
x
x
x
x
x
I6
H7
130
21
4
41
17
41
19
6
5
4
3
2
1
≥
+
+
+
+
+
x
x
x
x
x
x
I7
P. Kowalik, Laboratorium badań operacyjnych: zadanie optymalnej diety (wariant uproszczony)
6
H8
25
6
,
3
1
7
,
3
2
,
1
5
,
0
7
,
0
6
5
4
3
2
1
≥
+
+
+
+
+
x
x
x
x
x
x
I8
H9
17
7
,
5
3
,
0
5
,
4
5
,
3
3
2
,
3
6
5
4
3
2
1
≥
+
+
+
+
+
x
x
x
x
x
x
I9
H10
7300
3057
90
4530
3280
3420
2170
6
5
4
3
2
1
≥
+
+
+
+
+
x
x
x
x
x
x
I10
0
1
≥
x
,
0
2
≥
x
,
0
3
≥
x
,
0
4
≥
x
,
0
5
≥
x
,
0
6
≥
x
- ilo
ś
ci produktów spo
ż
ywczych nie mog
ą
by
ć
ujemne
Nale
ż
y teraz z menu Narz
ę
dzia-Solver
(w Excelu 2007 Dane-Solver) otworzy
ć
okno Solver-Parametry a na-
st
ę
pnie zadeklarowa
ć
ustawienia:
Komórka celu:
H4
Równa: Min (poniewa
ż
funkcja celu jest minimalizowana; UWAGA trzeba ustawi
ć
r
ę
cznie – opcja domy
ś
lna
to Maks!)
Komórki zmieniane:
B2:G2
Warunki ograniczaj
ą
ce:
B2:G2>=0
H6:H10>=I6:I10
.
Uwaga
B2:G2>=0 jest skróconym zapisem dla B2>=0, C2>=0, D2>=0, E2>=0, F2>=0, G2>=0 (czyli
0
1
≥
x
,
0
2
≥
x
,
0
3
≥
x
,
0
4
≥
x
,
0
5
≥
x
,
0
6
≥
x
)
H6:H10>=I6:I10 jest skróconym zapisem dla H6>=I6, H7>=I7, H8>=I8, H9>=I9, H10>=I10 (warunki zwi
ą
za-
ne ze spo
ż
yciem składników od
ż
ywczych )
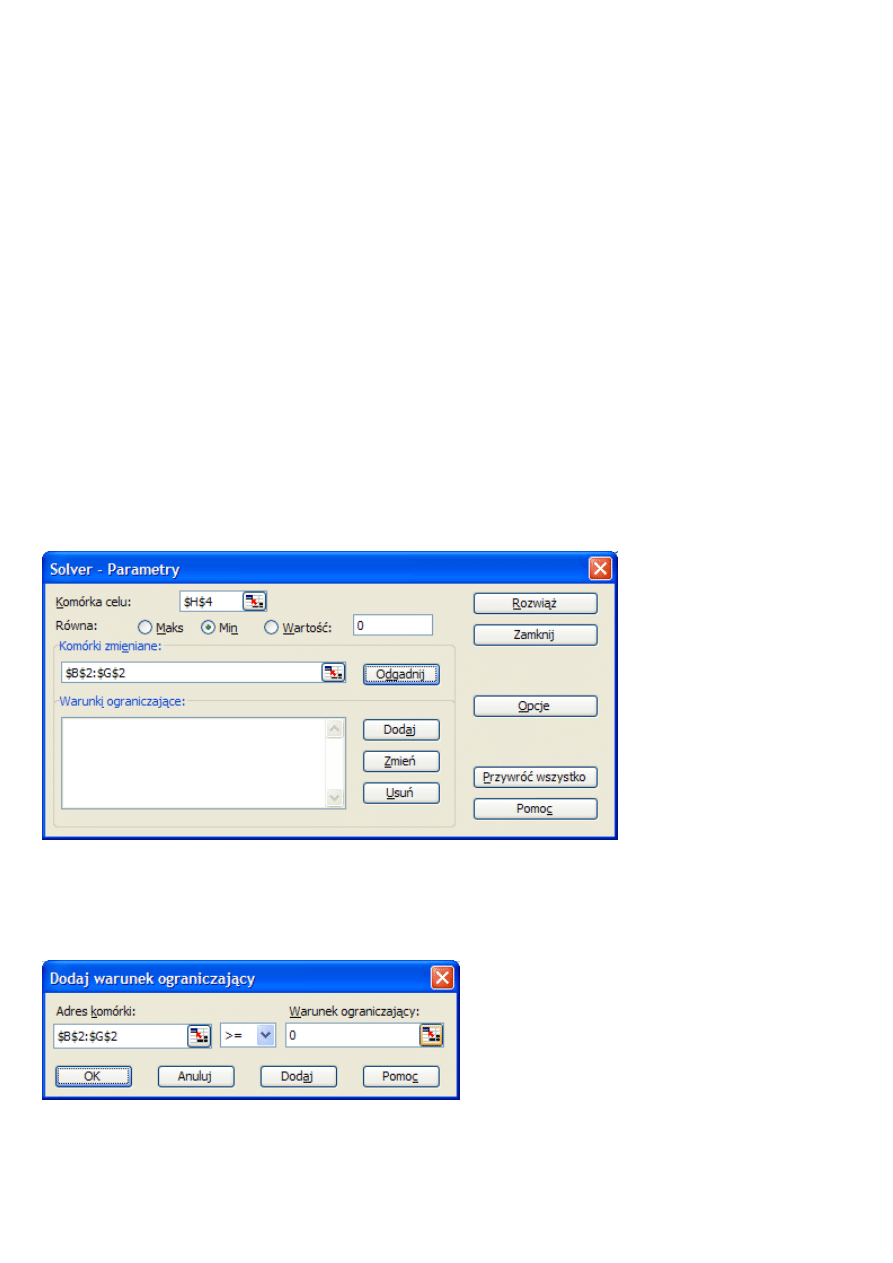
Główne okno Solvera (Solver - Parametry) – widok przed dodaniem warunków ograniczaj
ą
cych. W samym po-
lu Warunki ograniczaj
ą
ce
nic nie wpisujemy, poniewa
ż
jest to
NIEMOŻLIWE
. Aby doda
ć
warunki, klikamy
w Dodaj.
Otwiera si
ę
nowe okno Dodaj warunek ograniczaj
ą
cy
Wprowadzamy pierwsz
ą
grup
ę
warunków -warunki nieujemno
ś
ci zmiennych (B2:G2>=0) i klikamy Dodaj.
P. Kowalik, Laboratorium badań operacyjnych: zadanie optymalnej diety (wariant uproszczony)
7
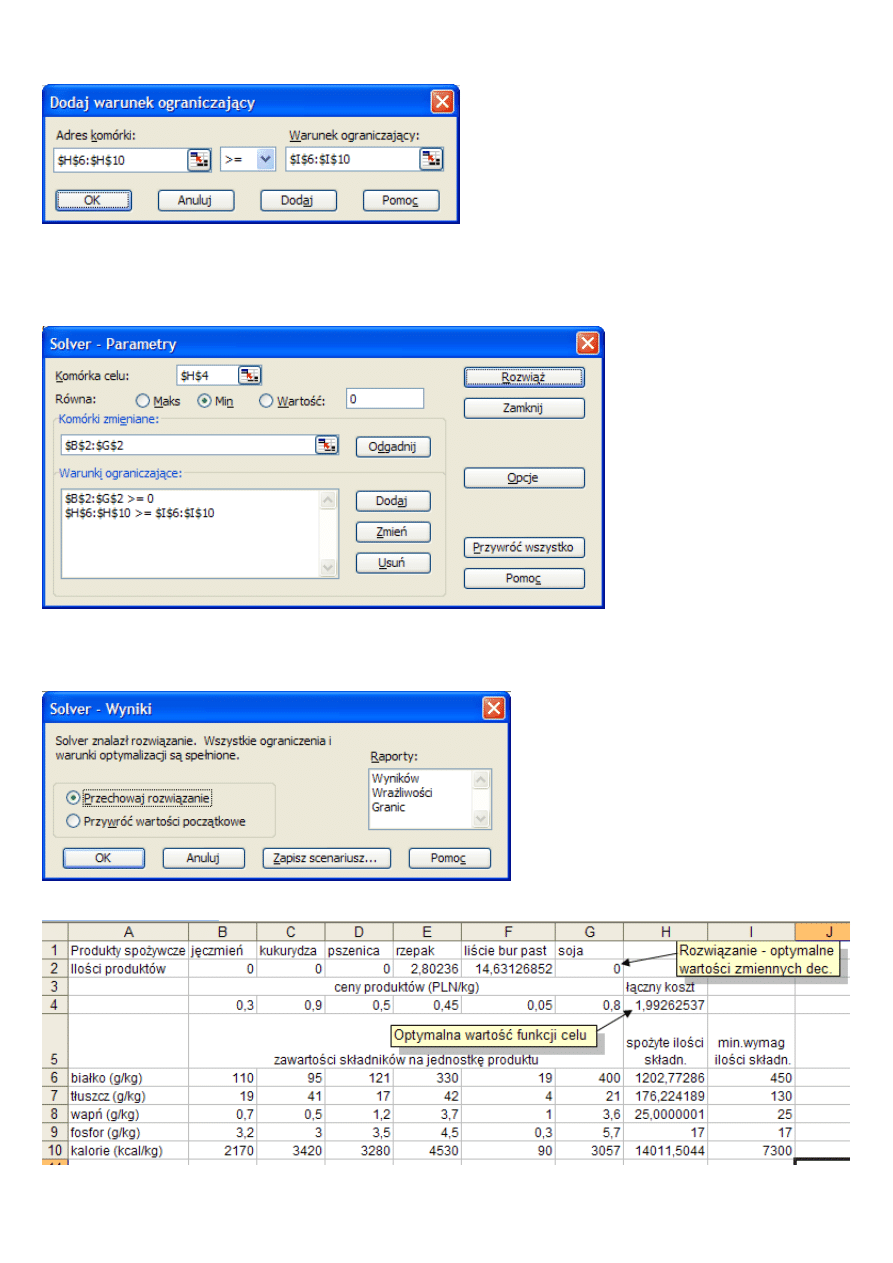
Pojawia si
ę
znowu okno Dodaj warunek ograniczaj
ą
cy.
Wprowadzamy analogicznie warunki ogranicze
ń
funk-
cyjnych (H6:H10>=I6:I10). Poniewa
ż
nie ma ju
ż
wi
ę
cej warunków do dodania, klikamy OK. Nast
ę
puje powrót
do okna Solver - Parametry
Po dodaniu warunków ograniczaj
ą
cych okno Solver – Parametry powinno wygl
ą
da
ć
jak ni
ż
ej
Ustawienia Solvera dla rozwiązywanego zadania
Teraz trzeba tylko klikn
ąć
w Rozwi
ąż
i zaczeka
ć
(bardzo krótko), a
ż
pojawi si
ę
nast
ę
puj
ą
ce okno:
Pozostaje ju
ż
tylko klikn
ąć
w OK aby zaakceptowa
ć
wynik.
P. Kowalik, Laboratorium badań operacyjnych: zadanie optymalnej diety (wariant uproszczony)
8
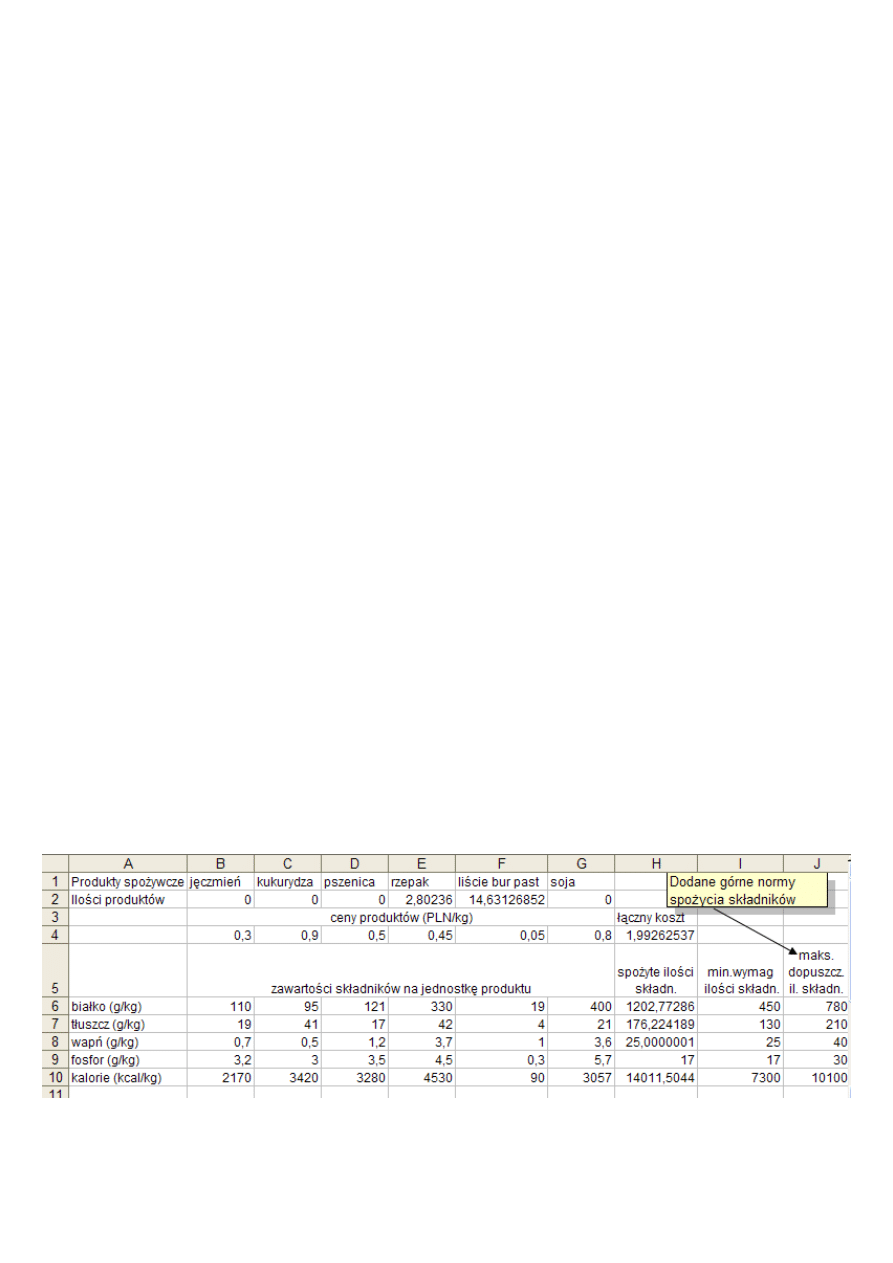
Rozwiązanie zadania
Odpowiedź „słowna”
Minimalny dzienny koszt diety wynosi 1,992625 PLN. Jest on osi
ą
gni
ę
ty dla nast
ę
puj
ą
cej diety (planu zaku-
pów i spo
ż
ycia):
0
*
1
=
x
kg j
ę
czmienia,
0
*
2
=
x
kg kukurydzy,
0
*
3
=
x
kg pszenicy,
802
,
2
*
4
=
x
kg rzepaku,
631
,
14
*
5
=
x
kg li
ś
ci buraków,
0
*
6
=
x
kg soi.
Poniewa
ż
spo
ż
ycie białka i kalorii bardzo przekracza wymagane minimalne spo
ż
ycie, zatem drugi etap rozwi
ą
-
zywania zadania uwzgl
ę
dnia górne limity spo
ż
ycia (uwzgl
ę
dnienie zasady „co za du
ż
o, to niezdrowo :-) ).
Drugi etap - rozszerzenie zadania o górne limity spożycia składników (górne) normy mak-
symalnego dopuszczalnego spożycia składników
Dodanie górnych limitów spo
ż
ycia poszerza model matematyczny o now
ą
grup
ę
warunków ograniczaj
ą
cych.
1
x
,
2
x
,
3
x
,
4
x
,
5
x
,
6
x
- ilo
ś
ci produktów spo
ż
ywczych (odpowiednio j
ę
czmienia, kukurydzy, rzepaku, li
ś
ci bu-
raków pastewnych i soji) wchodz
ą
cych w skład paszy.
min
8
,
0
05
,
0
45
,
0
5
,
0
9
,
0
3
,
0
6
5
4
3
2
1
→
+
+
+
+
+
x
x
x
x
x
x
(funkcja celu – ł
ą
czny koszt zakupu produktów)
przy ograniczeniach
rzeczywiste spo
ż
ycie składników od
ż
ywczych min. wymagane dzienne spo
ż
ycie składn. od
ż
ywczych
450
400
19
330
121
95
110
6
5
4
3
2
1
≥
+
+
+
+
+
x
x
x
x
x
x
130
21
4
41
17
41
19
6
5
4
3
2
1
≥
+
+
+
+
+
x
x
x
x
x
x
25
6
,
3
1
7
,
3
2
,
1
5
,
0
7
,
0
6
5
4
3
2
1
≥
+
+
+
+
+
x
x
x
x
x
x
17
7
,
5
3
,
0
5
,
4
5
,
3
3
2
,
3
6
5
4
3
2
1
≥
+
+
+
+
+
x
x
x
x
x
x
7300
400
19
4530
3280
3420
2170
6
5
4
3
2
1
≥
+
+
+
+
+
x
x
x
x
x
x
rzeczywiste spo
ż
ycie składników od
ż
ywczych maks. dopuszczalne dzienne spo
ż
ycie składn. od
ż
ywczych
780
400
19
330
121
95
110
6
5
4
3
2
1
≤
+
+
+
+
+
x
x
x
x
x
x
210
21
4
41
17
41
19
6
5
4
3
2
1
≤
+
+
+
+
+
x
x
x
x
x
x
40
6
,
3
1
7
,
3
2
,
1
5
,
0
7
,
0
6
5
4
3
2
1
≤
+
+
+
+
+
x
x
x
x
x
x
30
7
,
5
3
,
0
5
,
4
5
,
3
3
2
,
3
6
5
4
3
2
1
≤
+
+
+
+
+
x
x
x
x
x
x
10100
400
19
4530
3280
3420
2170
6
5
4
3
2
1
≤
+
+
+
+
+
x
x
x
x
x
x
0
1
≥
x
,
0
2
≥
x
,
0
3
≥
x
,
0
4
≥
x
,
0
5
≥
x
,
0
6
≥
x
- ilo
ś
ci produktów spo
ż
ywczych nie mog
ą
by
ć
ujemne
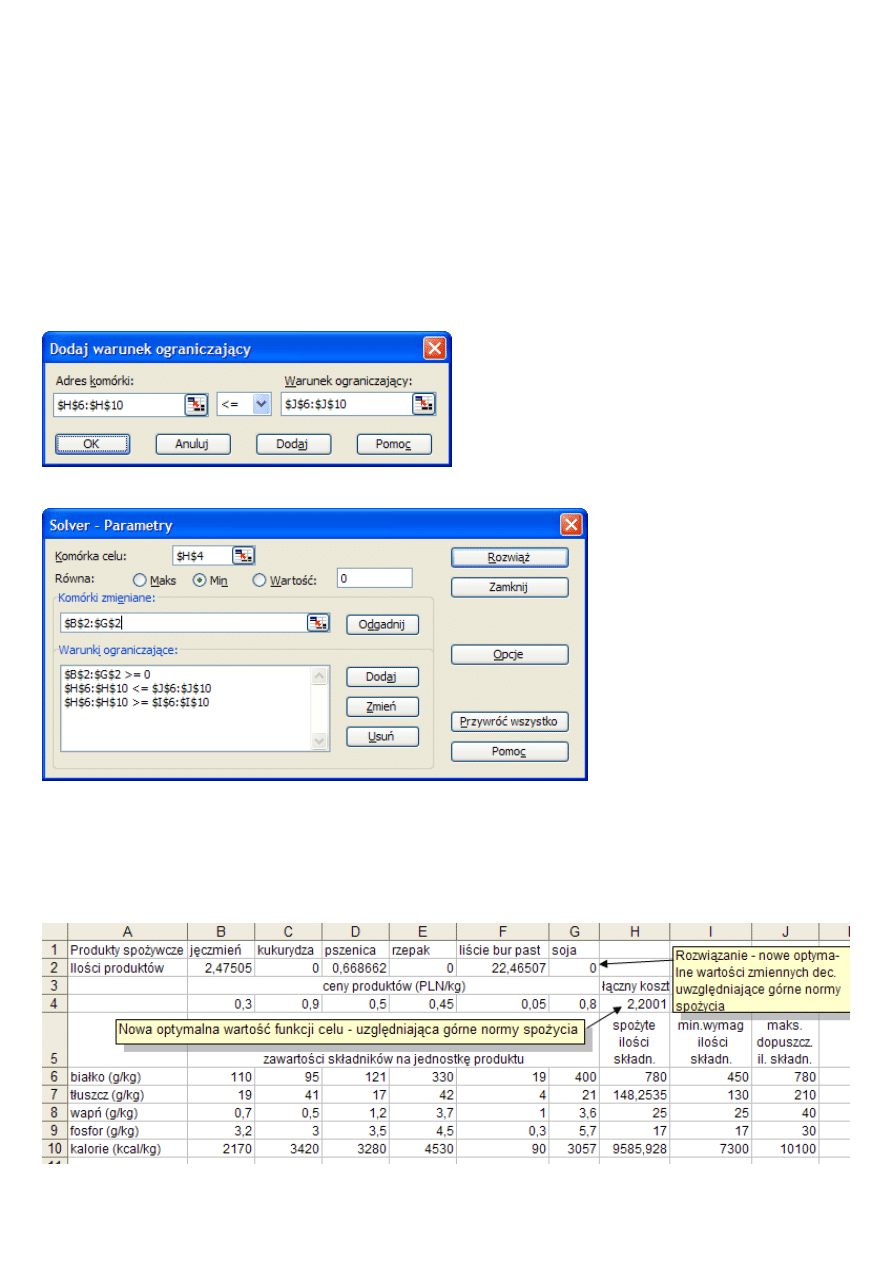
Przykładowe rozmieszczenie danych w arkuszu dla zadania optymalnej diety z dodatkowymi górnymi
normami spożycia składników
. Widoczne na zrzucie ekranu rozwi
ą
zanie odnosi si
ę
do zadania bez górnych
norm czyli otrzymanego w poprzednim etapie rozwi
ą
zywania. W kolumnie J dopisane s
ą
górne normy spo
ż
ycia
składników.
P. Kowalik, Laboratorium badań operacyjnych: zadanie optymalnej diety (wariant uproszczony)
9
Jak wida
ć
, nowe warunki ograniczaj
ą
ce „rozpisane” z adresami komórek wygl
ą
daj
ą
nast
ę
puj
ą
co
H6
780
400
19
330
121
95
110
6
5
4
3
2
1
≤
+
+
+
+
+
x
x
x
x
x
x
J6
H7
210
21
4
41
17
41
19
6
5
4
3
2
1
≤
+
+
+
+
+
x
x
x
x
x
x
J7
H8
40
6
,
3
1
7
,
3
2
,
1
5
,
0
7
,
0
6
5
4
3
2
1
≤
+
+
+
+
+
x
x
x
x
x
x
J8
H9
30
7
,
5
3
,
0
5
,
4
5
,
3
3
2
,
3
6
5
4
3
2
1
≤
+
+
+
+
+
x
x
x
x
x
x
J9
H10
10100
3057
90
4530
3280
3420
2170
6
5
4
3
2
1
≥
+
+
+
+
+
x
x
x
x
x
x
J10.
Teraz trzeba otworzy
ć
okno Solvera i doda
ć
te warunki „zbiorczo” jako H6:H10<=J6:J10.
Po klikni
ę
ciu „Dodaj” na oknie Solver-Parametry wpisujemy:
Okno Solvera z nowymi warunkami wygl
ą
da nast
ę
puj
ą
co.
Dodatkowe ograniczenia związane z górnymi normami spożycia
.
Grupa warunków z górnymi limitami spo
ż
ycia została dodana jako trzecia, ale jest wy
ś
wietlona jako druga. Co
prawda zgodnie z regułami sortowania alfabetycznego (J po I) grupa ta powinna by
ć
wy
ś
wietlona jako trzecia,
ale w sortowaniu warunków brana jest te
ż
pod uwag
ę
kolejno
ść
znaków równo
ś
ci i nierówno
ś
ci. Jest ona taka
jak na rozwijanej li
ś
cie w polu Dodaj warunek ograniczaj
ą
cy
czyli: <=,=,>=.
Pozostaje teraz tylko klikn
ąć
Rozwi
ąż
aby otrzyma
ć
nowe rozwi
ą
zanie.
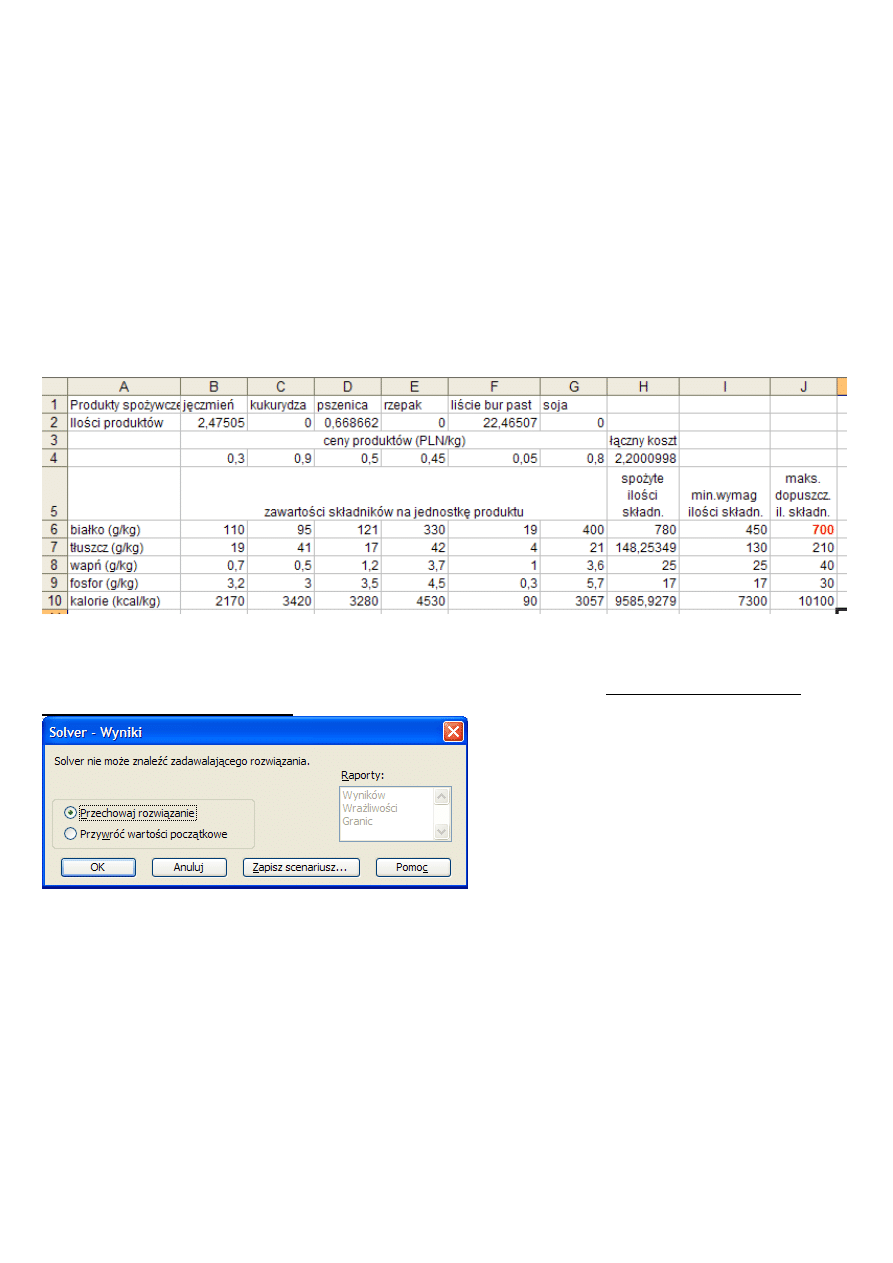
Rozwiązanie zadania z uwzględnieniem górnych norm spożycia.
P. Kowalik, Laboratorium badań operacyjnych: zadanie optymalnej diety (wariant uproszczony)
10
Rozwiązanie zadania
Odpowiedź „słowna”
Minimalny dzienny koszt diety z uwzgl
ę
dnieniem górnych norm spo
ż
ycia składników wynosi 2,200099 PLN
(na zrzucie ekranu jest wy
ś
wietlone zaokr
ą
glenie do 2,2001 ze wzgl
ę
du na oszcz
ę
dno
ść
miejsca). Jest on osi
ą
-
gni
ę
ty dla nast
ę
puj
ą
cej diety (planu zakupów i spo
ż
ycia):
475
,
2
*
1
=
x
kg j
ę
czmienia,
0
*
2
=
x
kg kukurydzy,
668
,
0
*
3
=
x
kg pszenicy,
0
*
4
=
x
kg rzepaku,
465
,
22
*
5
=
x
kg li
ś
ci buraków,
0
*
6
=
x
kg soi.
Trzeci etap - górna norma spożycia białka zmniejszona do 700g
.
Zmniejszenie górnego limitu spo
ż
ycia białka do 700 g oznacza,
ż
e warunek ograniczaj
ą
cy
780
400
19
330
121
95
110
6
5
4
3
2
1
≤
+
+
+
+
+
x
x
x
x
x
x
zmieni si
ę
na
700
400
19
330
121
95
110
6
5
4
3
2
1
≤
+
+
+
+
+
x
x
x
x
x
x
Nale
ż
y
poprawić
zawarto
ść
komórki
J16 z 780 na 700
i klikn
ąć
Rozwi
ąż
w oknie Solvera.
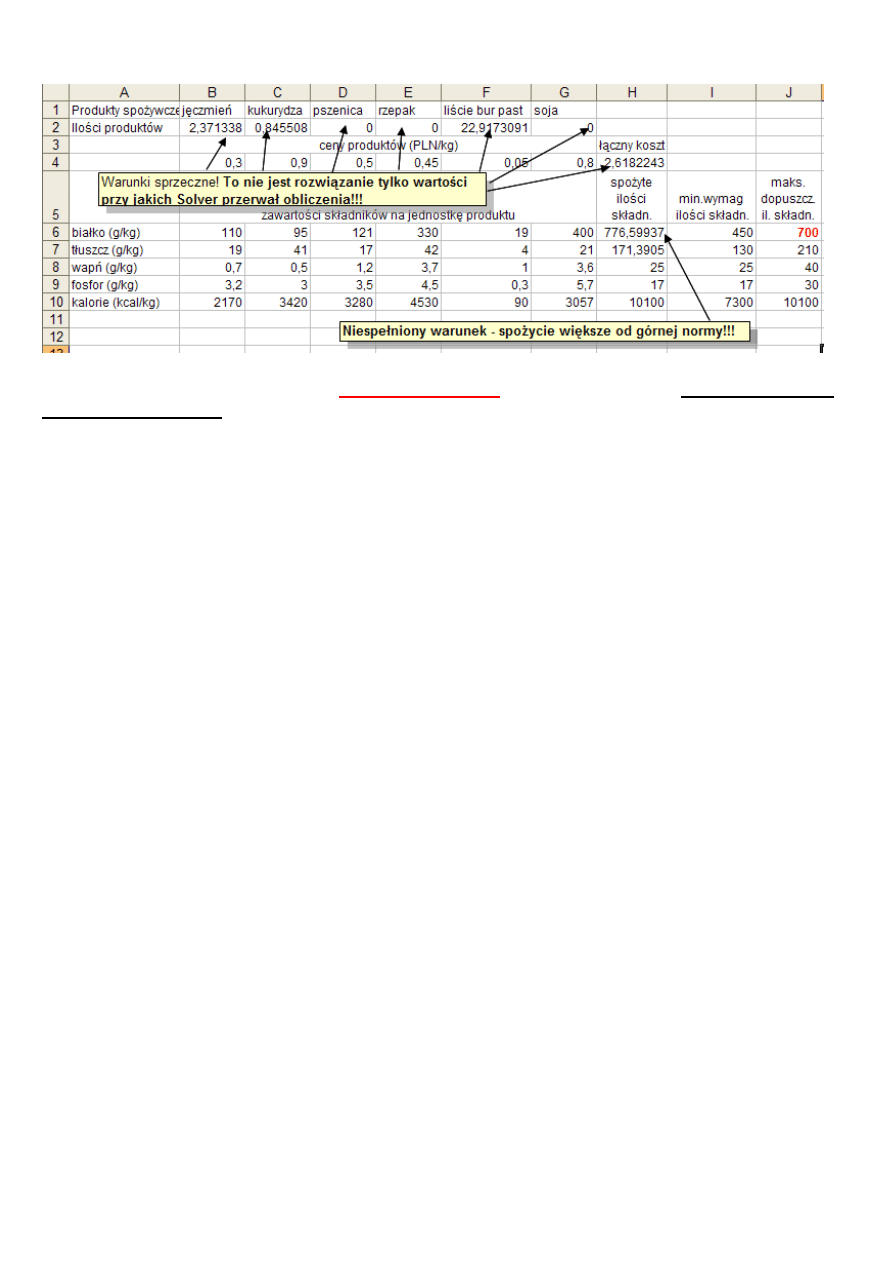
Nie ma
żadnych zmian w ustawieniach
Solvera!
Przy rozwi
ą
zywaniu Solver wy
ś
wietla komunikat jak ni
ż
ej, który oznacza,
ż
e
warunki ograniczające są
sprzeczne (nie ma rozwiązania!)
.
P. Kowalik, Laboratorium badań operacyjnych: zadanie optymalnej diety (wariant uproszczony)
11
Wartości komórek zmienianych
i zależnych od nich formuł modelu, które można odczytać w arkuszu po
wyświetleniu powyższego komunikatu
nie są rozwiązaniami
a jedynie wartościami, przy których Solver
wstrzymał obliczenia!!!
Wyszukiwarka
Podobne podstrony:
choroby wirus i bakter ukł odd Bo
1 bo
BO WYKLAD 03 2
BO W 4
chlamydiofiloza bo i ov
BO I WYKLAD 01 3 2011 02 21
bo mój skrypt zajebiaszczy
BO WYK2 Program liniowe optymalizacja
eksploracja lab03, Lista sprawozdaniowych bazy danych
2 BO 2 1 PP Przykłady Segregator [v1]
PB BO W1
Odp z BO
POLITECHNIKA BIAŁOSTOCKA, NAUKA, Politechnika Bialostocka - budownictwo, Semestr III od Karola, Budo
51 - BO Z DZIEWCZYNAMI, Teksty piosenek
egzamin Bo ena Koz owska - Praca z dzieckiem z Zespo, PWSZ Tarnów Filologia polska II rok, PWSZ Tran
więcej podobnych podstron