Plik:

 

MODEL_A_s_p_[v2].doc 

 

   

 

 

 

 

 

1 

/

 

10

 

A. KADZIŃSKI, 

 DETERMINISTYCZNY MODEL EKONOMICZNEJ WIELKOŚCI PARTII ZASOBU  W  WARUNKACH  NIEDOPUSZCZALNYCH  NIEDOBORÓW  ZASOBÓW  

 

 

 

B A D A N I A   O P E R A C Y J N E  

 

 
 
 
 

D

ETERMINISTYCZNY  MODEL  EKONOMICZNEJ  WIELKOŚCI  PARTII  

NABYWCZEJ  ZASOBU  W  WARUNKACH  NIEDOPUSZCZALNYCH

 

NIEDOBORÓW  ZASOBÓW

 

 
 

 

Materia

Materia

Materia

Materiały pomocnicze do wyk

y pomocnicze do wyk

y pomocnicze do wyk

y pomocnicze do wykładu

adu

adu

adu    

    

 

 

 
 

adam.kadzinski@put.poznan.pl

 

A 

 

 

 

Plik:

 

MODEL_A_s_p_[v2].doc 

 

   

 

 

 

 

            

2 

/

 

10

 

A. KADZIŃSKI,  

 

DETERMINISTYCZNY MODEL EKONOMICZNEJ WIELKOŚCI PARTII ZASOBU  W  WARUNKACH  NIEDOPUSZCZALNYCH  NIEDOBORÓW  ZASOBÓW 

 

 
 

Model  ten  jest  najprostszym  modelem  sterowania  zasobami.  Nazywa  się  go  także  modelem 

Wilsona.  Jest  to  model  ekonomicznej  (optymalnej)  wielkości  partii  nabywczej.  Zakłada  on  brak 
niedoboru  zasobu  tzn.  w  chwili  wyczerpania  się  zapasu  zasobu  jest  on  natychmiast  uzupełniany 
poprzez  dostarczenie  nowej  partii.  Zakłada  się  również,  że  zasób  jest  zużywany  ze  stałą 
intensywnością. Schemat ideowy modelu przedstawiono poniżej.  

 

 

 

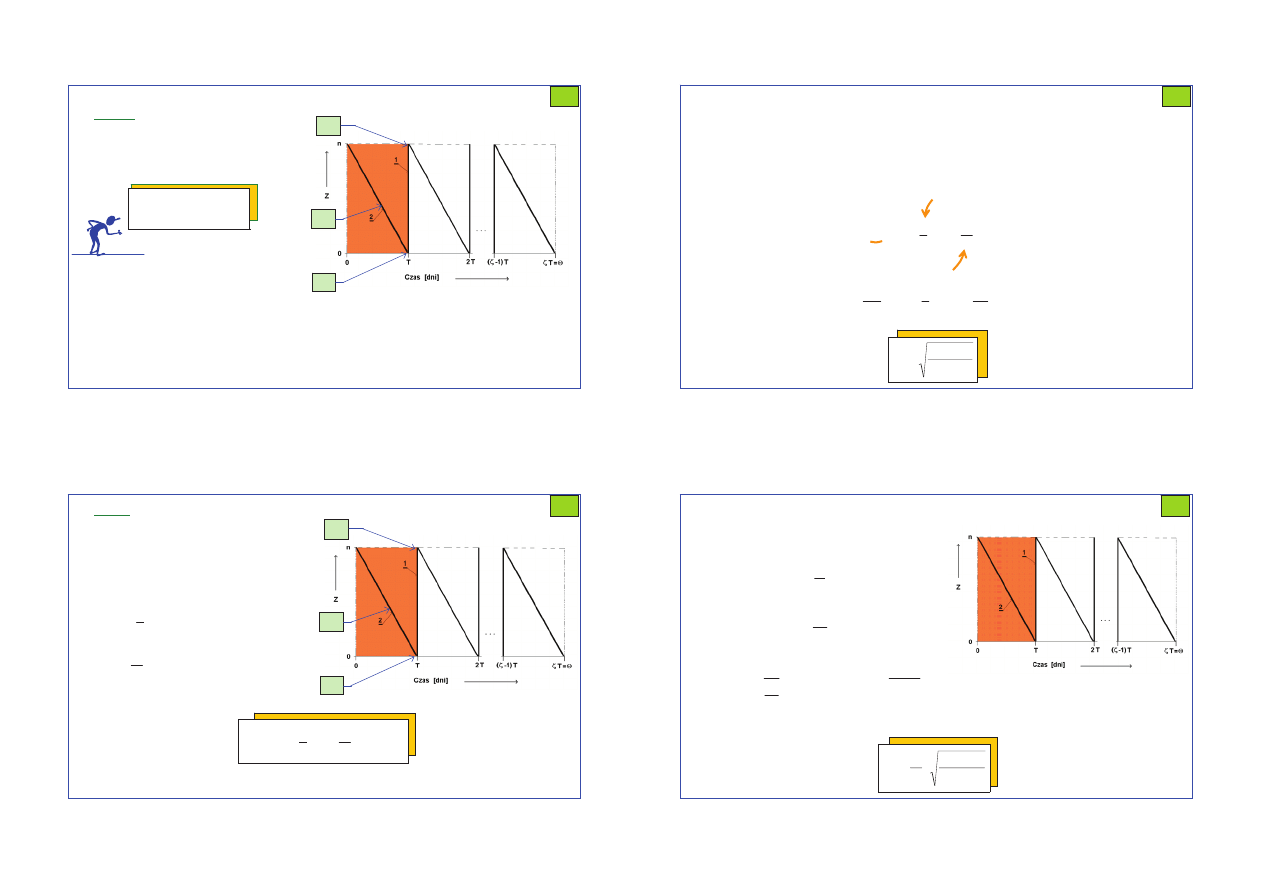
W  chwili 

0

  rozpoczyna  się  zużywanie  pierwszej 

partii  nabywczej  zasobu.  Zużywanie  to    trwa  do 
chwili 

T

  (

linia 

2

).  W  okresie  od 

0

  do 

T

  

realizowane  są  bieżące  zamówienia  na  zasoby. 
Maksymalny poziom zapasu w systemie zasobów 
osiąga 

się 

w 

chwili 

jego 

uzupełnienia. 

Uzupełnienia  zasobów  w  systemie  następuje 
w chwili 

T

 (

linia 

1

). 

 

 
 

 

Schemat ideowy modelu ekonomicznej wielkości partii 

nabywczej w warunkach niedopuszczalnych 

niedoborów zasobu 

A 

 

 

 

Plik:

 

MODEL_A_s_p_[v2].doc 

 

   

 

 

 

 

            

3 

/

 

10

 

A. KADZIŃSKI,  

 

DETERMINISTYCZNY MODEL EKONOMICZNEJ WIELKOŚCI PARTII ZASOBU  W  WARUNKACH  NIEDOPUSZCZALNYCH  NIEDOBORÓW  ZASOBÓW 

 

 

Założenia: 

 

 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 

 

5.  W  ciągu  okresu 

Θ

  jednostkowy  koszt  utrzymania 

k

m

   (magazynowania) zapasu  zasobu  nie ulega 

zmianie i nie zależy od wielkości zapasu. 

6.  W ciągu okresu 

Θ

 jednostkowy koszt realizacji zamówień 

k

r

  jest stały i nie zależy od wielkości 

partii nabywczej. 

7.  Zamówienia  składane  są  z  takim  czasem  wyprzedzenia  aby  dostawa  kolejnej  partii  zasobu 

następowała w momencie całkowitego zużycia partii poprzedniej. 

8.  Niedopuszczalny jest niedobór zasobu. 

1.  Zapotrzebowanie  na  zasób  w  okresie 

Θ

  jest 

znane i wynosi 

N

. 

2.  Zużycie  zasobu  jest  równomierne  w  czasie 

(

linia 

2

). 

3.  Zakupy zasobu w okresie 

Θ

 dokonywane są 

ζ

 

razy  w  jednakowych  odstępach  czasu 

T

 

w partiach  o  jednakowych  wielkościach 

n

  

(

linia 

1

). 

4.  W  ciągu  okresu 

Θ

  jednostkowa  cena  nabycia 

k

n

  zasobu  nie  ulega  zmianie  i  nie  zależy  od 

wielkości partii nabywczej. 

A 

 

 

 

Plik:

 

MODEL_A_s_p_[v2].doc 

 

   

 

 

 

 

            

4 

/

 

10

 

A. KADZIŃSKI,  

 

DETERMINISTYCZNY MODEL EKONOMICZNEJ WIELKOŚCI PARTII ZASOBU  W  WARUNKACH  NIEDOPUSZCZALNYCH  NIEDOBORÓW  ZASOBÓW 

 

 

Poszukiwane: 

 
 
 

 
 
 
 
 
 
 
 
 
 
 

1.  Optymalna 

wielkość 

partii 

nabywczej  

zasobu – 

∗

n

. 

2.  Optymalny 

czas 

między 

realizacjami 

zamówień na zasoby – 

∗

T

. 

3.  Optymalny  łączny  koszt  funkcjonowania 

systemu zasobów – 

∗

K . 

A 

 

 

 

Plik:

 

MODEL_A_s_p_[v2].doc 

 

   

 

 

 

 

            

5 

/

 

10

 

A. KADZIŃSKI,  

 

DETERMINISTYCZNY MODEL EKONOMICZNEJ WIELKOŚCI PARTII ZASOBU  W  WARUNKACH  NIEDOPUSZCZALNYCH  NIEDOBORÓW  ZASOBÓW 

 

 

Całkowity koszt funkcjonowania 
systemu zasobów 

 

 

n

r

m

K

K

K

K

+

+

=

 

 

 

Model: 

 

 

 

 

 

 

 

 

 

 

 
 

K  

– całkowity koszt funkcjonowania systemu zasobów,  

m

K

  – całkowity koszt magazynowania zasobów, 

r

K

  – całkowity koszt kolejnych uzupełnień zasobów, 

n

K

  – całkowity koszt nabycia zasobów.

 

m

K

 

r

K

 

n

K

 

A 

 

 

 

Plik:

 

MODEL_A_s_p_[v2].doc 

 

   

 

 

 

 

            

6 

/

 

10

 

A. KADZIŃSKI,  

 

DETERMINISTYCZNY MODEL EKONOMICZNEJ WIELKOŚCI PARTII ZASOBU  W  WARUNKACH  NIEDOPUSZCZALNYCH  NIEDOBORÓW  ZASOBÓW 

 

Model (cd.)

 

 
 

n

r

m

K

K

K

K

+

+

=

 

 

2

n

k

K

m

m

⋅

=

 

 

n

N

k

K

r

r

⋅

=

 

 

N

k

K

n

n

⋅

=

 

 

N

k

n

N

k

n

k

K

n

r

m

⋅

+

⋅

+

⋅

=

2

 

m

K

 

r

K

 

n

K

 

A 

 

 

 

Plik:

 

MODEL_A_s_p_[v2].doc 

 

   

 

 

 

 

            

7 

/

 

10

 

A. KADZIŃSKI,  

 

DETERMINISTYCZNY MODEL EKONOMICZNEJ WIELKOŚCI PARTII ZASOBU  W  WARUNKACH  NIEDOPUSZCZALNYCH  NIEDOBORÓW  ZASOBÓW 

 

 

SZCZEGÓŁOWE  ALGORYTMY  POZYSKIWANIA  ROZWIĄZAŃ 

 

1

.

  Optymalna wielkość partii nabywczej zasobu –

 

∗

n

 

 

Optymalna  wielkość  partii  nabywczej  zostanie  wyznaczona  przez  rozwiązanie  zadania  na  minimum 
bezwarunkowe funkcji przedstawionej zależnością: 
 

 

N

k

n

N

k

n

k

n

K

n

r

m

⋅

+

⋅

+

⋅

⋅

=

2

)

(

 

 

Zatem 

0

2

1

0

2

=

−

⇔

=

n

N

k

k

dn

dK

r

m

 

a stąd otrzymuje się: 

 

m

r

*

k

N

k

n

⋅

⋅

=

2

. 

(1) 

A 

 

 

 

Plik:

 

MODEL_A_s_p_[v2].doc 

 

   

 

 

 

 

            

8 

/

 

10

 

A. KADZIŃSKI,  

 

DETERMINISTYCZNY MODEL EKONOMICZNEJ WIELKOŚCI PARTII ZASOBU  W  WARUNKACH  NIEDOPUSZCZALNYCH  NIEDOBORÓW  ZASOBÓW 

 

2

.

  Optymalny czas między realizacjami zamówień na zasoby –

 

∗

T

 

 

 

Na podstawie założenia 

3

 wiadomo, że 

ς

Θ

=

T

  

ale 

*

n

N

=

ς

,  

zatem 

*

*

n

N

T

Θ

=

    i ostatecznie  

N

n

T

*

*

⋅

Θ

=

     

(2)

 

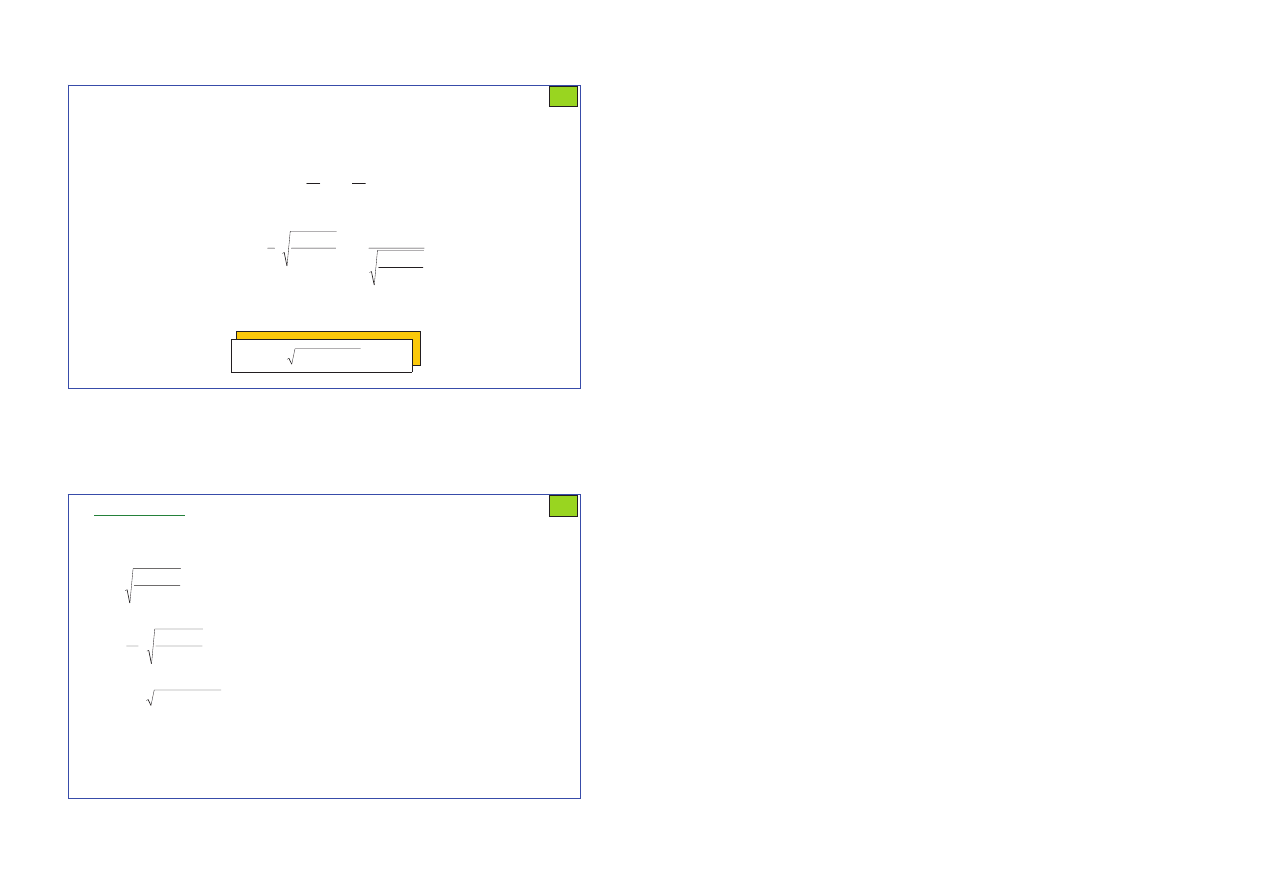
Wykorzystując zależność 

(1)

 otrzymuje się ostatecznie 

 

 

m

r

k

N

k

N

T

⋅

⋅

⋅

Θ

=

2

*

 

(3)

 

A 

 

 

 

Plik:

 

MODEL_A_s_p_[v2].doc 

 

   

 

 

 

 

            

9 

/

 

10

 

A. KADZIŃSKI,  

 

DETERMINISTYCZNY MODEL EKONOMICZNEJ WIELKOŚCI PARTII ZASOBU  W  WARUNKACH  NIEDOPUSZCZALNYCH  NIEDOBORÓW  ZASOBÓW 

 

 

3

.

  Optymalny łączny koszt funkcjonowania systemu zasobów –

 

∗

K

  

 

Na  podstawie  założeń  przyjętych  dla  niniejszego  modelu  oraz  na  podstawie  wcześniejszych  analiz 
można zapisać, że: 

N

k

n

N

k

n

k

n

K

n

r

m

⋅

+

⋅

+

⋅

=

*

*

*

2

)

(

 

Wykorzystując zależność 

(1)

 otrzymuje się  

N

k

k

N

k

N

k

k

N

k

k

n

K

n

m

r

r

m

r

m

⋅

+

⋅

⋅

⋅

+

⋅

⋅

⋅

⋅

=

2

2

2

1

)

(

*

 

a stąd ostatecznie można zapisać, że: 

 

 

N

k

N

k

k

n

K

n

r

m

⋅

+

⋅

⋅

⋅

=

2

)

(

*

 

(4) 

A 

 

 

 

Plik:

 MODEL_A_s_p_[v2].doc 

 

   

 

 

 

 

            

10 

/

 

10

 

A. KADZIŃSKI,  

 

DETERMINISTYCZNY MODEL EKONOMICZNEJ WIELKOŚCI PARTII ZASOBU  W  WARUNKACH  NIEDOPUSZCZALNYCH  NIEDOBORÓW  ZASOBÓW 

 

Podsumowanie: 

 
 
 
 

m

r

*

k

N

k

n

⋅

⋅

=

2

. 

 

(1) 

m

r

k

N

k

N

T

⋅

⋅

⋅

Θ

=

2

*

 

 

(3)

 

N

k

N

k

k

n

K

n

r

m

⋅

+

⋅

⋅

⋅

=

2

)

(

*

 

 

(4) 

 

 

A