P
li
k:
B
O
_
P
P
_
M
e
to
d
a
_
O
p
is
o
w
a
_
p
_
s
_
[v
1
].
d
o
c
1
/
1
A
.
K
A
D
ZI
ē
S
K
I,
M
O
D
E
L
O
W
A
N
IE
O
P
IS
O
W
E
P
R
A
C
Y
S
Y
S
T
E
M
U
M
A
S
O
W
E
J
O
B
Sà
U
G
I
B
A
D
A
N
I
A
O
P
E
R
A
C
Y
J
N
E
M
O
DE
L
O
W
ANI
E
O
P
IS
O
W
E
P
RAC
Y
S
Y
S
T
E
M
U
M
AS
O
W
E
J
O
BS
à
U
G
I
(
K
O
L
E
J
K
O
W
E
G
O
)
M
a
te
ri
a
áy
p
o
m
o
cn
ic
z
e
d
o
w
yk
áa
d
u
a
d
a
m
.k
a
d
z
in
s
k
i@
p
u
t.
p
o
z
n
a
n
.p
l
1
2
3
5
4
6
7
8
9
1
0
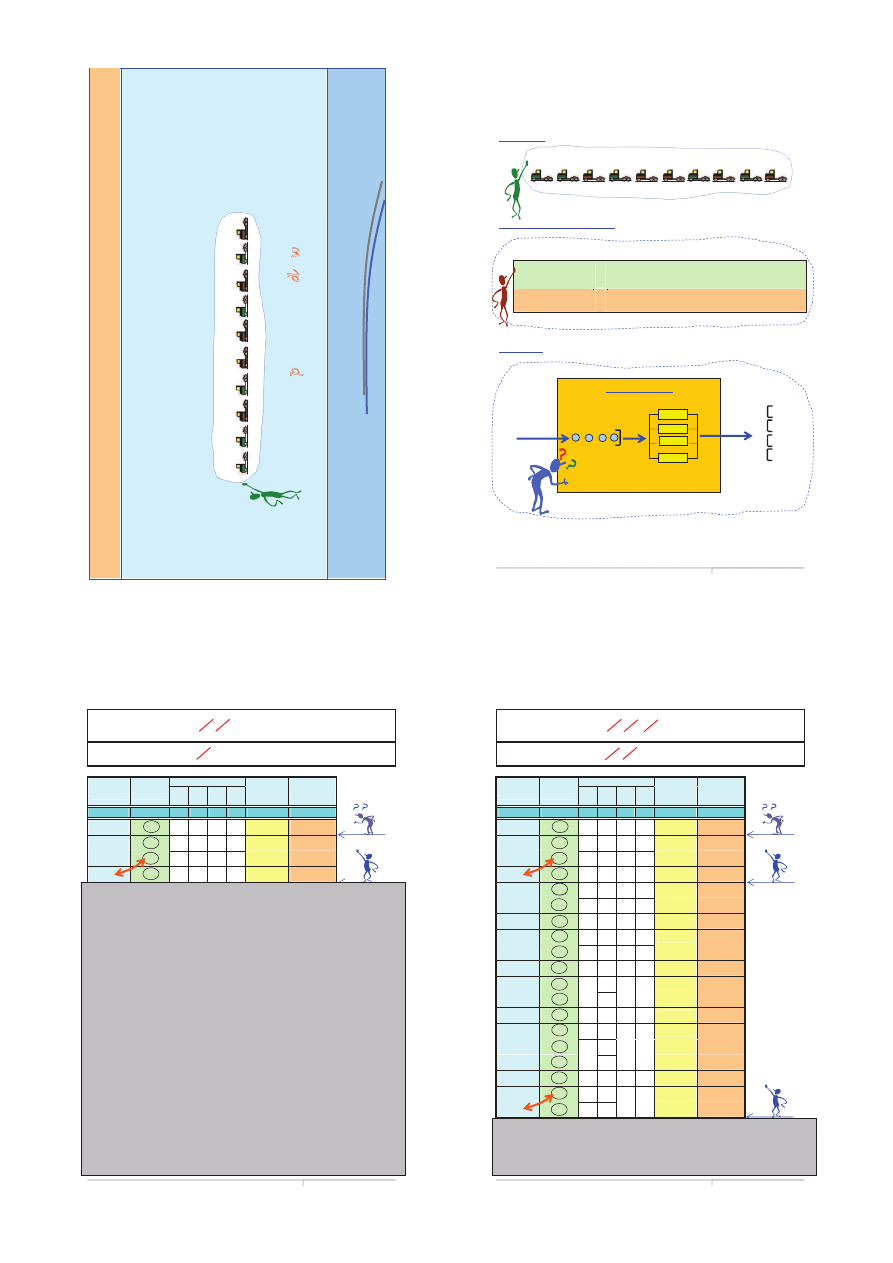
MODELOWANIE OPISOWE (HEURYSTYCZNE) PRACY
SYSTEMU KOLEJKOWEGO (MASOWEJ OBS
àUGI)
ZADANIE
5
4
6
1
2
3
10
7
8
9
Model opisowy;
Opracowa
á: Adam KadziĔski
PARAMETRY ZADANIA
1
2
3
5
4
6
7
8
9
10
Odst
Ċpy czasu miĊdzy
zg
áoszeniami
)
{ 3, 15, 4, 6, 2, 3, 19, 3, 13, 10}
Czasy obs
áugi zgáoszeĔ
)
{69, 20, 56, 41, 35, 11, 7, 3, 24, 20}
SYSTEM
wyj
Ğciowy
Strumie
Ĕ
wej
Ğciowy
(zg
áoszeĔ)
Strumie
Ĕ
SYSTEM OBS
àUGI
Kolejka
(poczekalnia)
Kana
áy
obs
áugi
2
4
3
?
?
?
S
?
K
Zasobniki
3
4
1
1
2
3
1
2
4
zg
áoszeĔ
obs
áuĪonych
Odst
Ċpy czasu miĊdzy
zg
áoszeniami
)
{ 3, 15, 4, 6, 2, 3, 19, 3, 13, 10}
Czasy obs
áugi zgáoszeĔ
)
{69, 20, 56, 41, 35, 11, 7, 3, 24, 20}
CHWILE
ZG
àO-
KONIEC OBS
àUGI DàUGOĝû
LICZBA
ZDARZE
ē SZENIE
S
1
S
2
S
3
S
4
KOLEJKI
K
ZAJ
ĉTYCH
KANA
àÓW
1
2
3
4
5
6
7
8
0
3
–
–
–
–
0
0
1
3
–
–
–
–
0
0
2
3
–
–
–
–
0
0
Model opisowy;
Opracowa
á: Adam KadziĔski
3
18
72
–
–
–
0
1
4
18
72
–
–
–
0
1
5
18
72
–
–
–
0
1
6
18
72
–
–
–
0
1
7
18
72
–
–
–
0
1
8
18
72
–
–
–
0
1
9
18
72
–
–
–
0
1
10
18
72
–
–
–
0
1
11
18
72
–
–
–
0
1
12
18
72
–
–
–
0
1
13
18
72
–
–
–
0
1
14
18
72
–
–
–
0
1
15
18
72
–
–
–
0
1
16
18
72
–
–
–
0
1
17
18
72
–
–
–
0
1
18
22
72 38
–
–
0
2
19
22
72 38
–
–
0
2
20
22
72 38
–
–
0
2
Odst
Ċpy czasu miĊdzy
zg
áoszeniami
)
{ 3, 15, 4, 6, 2, 3, 19, 3, 13, 10}
Czasy obs
áugi zgáoszeĔ
)
{69, 20, 56, 41, 35, 11, 7, 3, 24, 20}
CHWILE
ZG
àO-
KONIEC OBS
àUGI DàUGOĝû
LICZBA
ZDARZE
ē SZENIE
S
1
S
2
S
3
S
4
KOLEJKI
K
ZAJ
ĉTYCH
KANA
àÓW
1
2
3
4
5
6
7
8
0
3
–
–
–
–
0
0
1
3
–
–
–
–
0
0
2
3
–
–
–
–
0
0
3
18
72
–
–
–
0
1
4
18
72
–
–
–
0
1
5
18
72
–
–
–
0
1
6
18
72
–
–
–
0
1
7
18
72
–
–
–
0
1
8
18
72
–
–
–
0
1
9
18
72
–
–
–
0
1
10
18
72
–
–
–
0
1
11
18
72
–
–
–
0
1
12
18
72
–
–
–
0
1
13
18
72
–
–
–
0
1
14
18
72
–
–
–
0
1
15
18
72
–
–
–
0
1
16
18
72
–
–
–
0
1
17
18
72
–
–
–
0
1
18
22
72 38
–
–
0
2
19
22
72 38
–
–
0
2
20
22
72 38
–
–
0
2
Model opisowy;
Opracowa
á: Adam KadziĔski
O
d
stĊ
py
c
za
su m
i
Ċ
d
zy
z
g
áo
sz
en
ia
m
i
)
{ 3, 15, 4, 6, 2, 3, 19, 3, 13, 10}
C
za
sy
o
b
s
áu
g
i z
g
áo
sz
e
Ĕ
)
{69, 20, 56, 41, 35, 11, 7, 3, 24, 20}
C
H
W
IL
E
Z
G
à
O
-
K
O
N
IE
C
O
B
S
à
U
G
I
D
à
U
G
O
ĝû
L
IC
Z
B
A
Z
D
A
R
Z
E
ē
S
Z
EN
IE
S
1
S
2
S
3
S
4
K
O
L
E
J
K
I
K
Z
A
J
ĉ
T
Y
C
H
K
A
N
A
à
Ó
W
1
2
3
4
5
6
7
8
0
3
–
–
–
–
0
0
3
1
8
7
2
–
–
–
0
1
1
8
2
2
7
2
3
8
–
–
0
2
2
2
2
8
7
2
3
8
7
8
–
0
3
2
8
3
0
7
2
3
8
7
8
6
9
0
4
3
0
3
3
7
2
3
8
7
8
6
9
1
4
3
3
5
2
7
2
3
8
7
8
6
9
2
4
3
8
5
2
7
2
7
3
7
8
6
9
1
4
5
2
5
5
7
2
7
3
7
8
6
9
2
4
5
5
6
8
7
2
7
3
7
8
6
9
3
4
6
8
7
8
7
2
7
3
7
8
6
9
4
4
6
9
7
8
7
2
7
3
7
8
8
0
3
4
Mo
d
e
l o
p
is
o
w
y
;
O
p
ra
c
o
w
a
á:
A
d
a
m
K
a
d
z
i
Ĕ
s
k
i
7
2
7
8
7
9
7
3
7
8
8
0
2
4
7
3
7
8
7
9
7
6
7
8
8
0
1
4
7
6
7
8
7
9
1
0
0
7
8
8
0
0
4
7
8
7
9
1
0
0
–
8
0
0
3
7
8
7
8
–
7
9
1
0
0
9
8
8
0
0
4
7
9
–
–
1
0
0
9
8
8
0
0
3
8
0
–
–
1
0
0
9
8
–
0
2
9
8
–
–
1
0
0
–
–
0
1
1
0
0
–
–
–
–
–
0
0
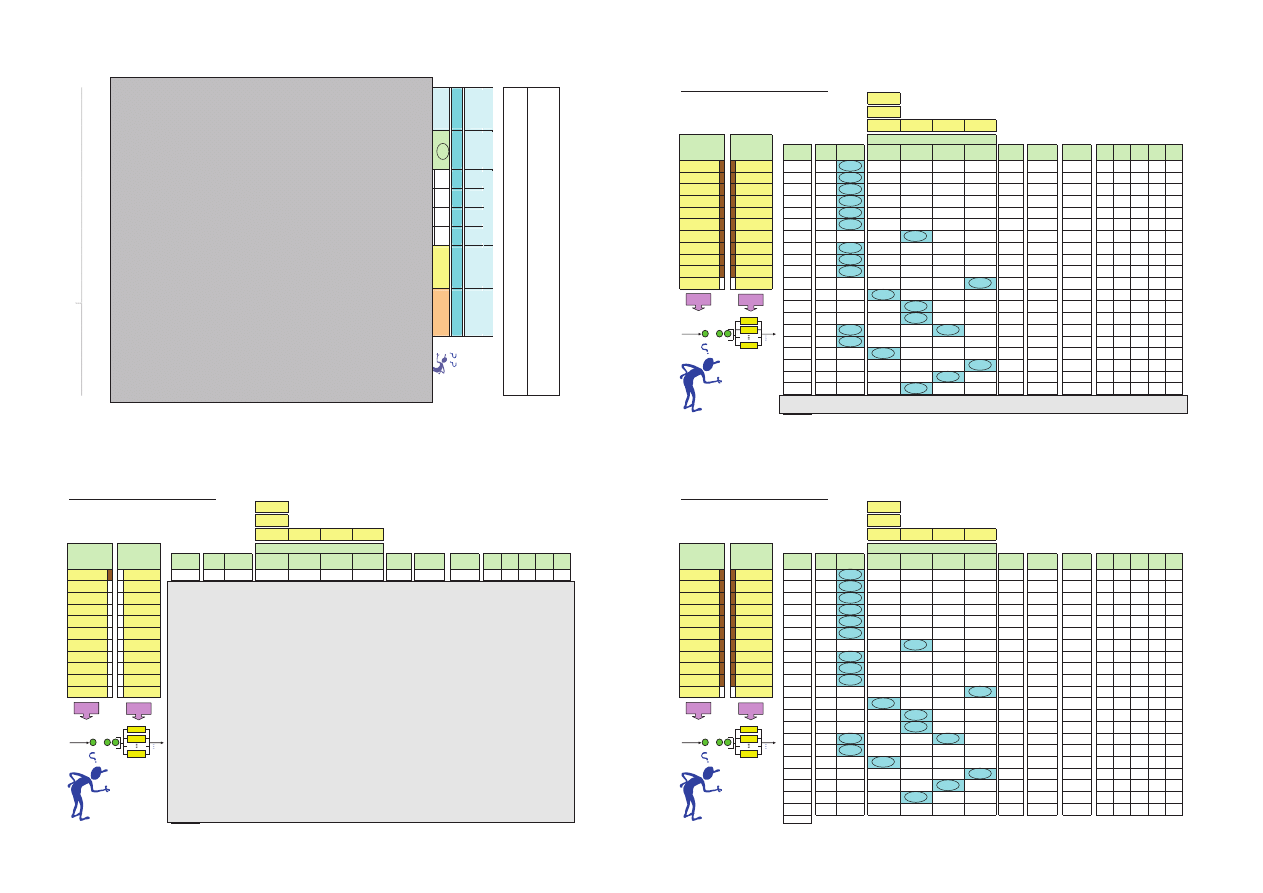
MODELOWANIE SYSTEMU ELEMENTARNEGO METOD
Ą OPISOWĄ
PRZYK
àAD - 4 KANAàY STANOWISKA
Liczba kana
á
á
ów stanowiska obs ugi . . . . . . . . . . .
4
Warto
Ğü
ą
pocz tkowa zegara symulacji . . . . . . . . .
0
Za ile chwil czasowych ko
Ĕ
Ċ
á
czy si obs uga . . . . .
-
-
-
-
Czasy
Czasy
Chwile zako
Ĕczenia obsáugi na kanaáach
Obiekty w kolejce
mi
Ċdzy
zg
áoszeniami
obs
áugi
zg
áoszeĔ
Zegar
symul.
Zdarz.
nast.
Chwila
zg
áosz.
1
2
3
4
Zaj
Ċte
kana
áy
D
áugoĞü
kolejki
Zegar
symul.
1
2
3
4
5
3
69
0
z
3
-
-
-
-
0
0
0
15
20
3
z
18
72
-
-
-
1
0
3
4
56
18
z
22
72
38
-
-
2
0
18
6
41
22
z
28
72
38
78
-
3
0
22
2
35
28
z
30
72
38
78
69
4
0
28
3
11
30
z
33
72
38
78
69
4
1
30
35
19
7
33
o
52
72
38
78
69
4
2
33
35 11
3
3
38
z
52
72
73
78
69
4
1
38
11
13
24
52
z
55
72
73
78
69
4
2
52
11
7
10
20
55
z
68
72
73
78
69
4
3
55
11
7
3
-
-
68
o
78
72
73
78
69
4
4
68
11
7
3
24
69
o
78
72
73
78
80
4
3
69
7
3
24
72
o
78
79
73
78
80
4
2
72
3
24
73
o
78
79
76
78
80
4
1
73
24
76
o
78
79
100
78
80
4
0
76
78
z
78
79
100
-
80
3
0
78
78
o
-
79
100
98
80
4
0
78
79
o
-
-
100
98
80
3
0
79
80
o
-
-
100
98
-
2
0
80
98
o
-
-
100
-
-
1
0
98
100
-
-
-
-
-
-
0
0
100
Koniec
F (t )
T
obs
...
1
2
1
2
n
...
T
zg
á
MODELOWANIE SYSTEMU ELEMENTARNEGO METOD
Ą OPISOWĄ
PRZYK
àAD - 4 KANAàY STANOWISKA
Liczba kana
á
á
ów stanowiska obs ugi . . . . . . . . . . .
4
Warto
Ğü
ą
pocz tkowa zegara symulacji . . . . . . . . .
0
Za ile chwil czasowych ko
Ĕ
Ċ
á
czy si obs uga . . . . .
-
-
-
-
Czasy
Czasy
Chwile zako
Ĕczenia obsáugi na kanaáach
Obiekty w kolejce
mi
Ċdzy
zg
áoszeniami
obs
áugi
zg
áoszeĔ
Zegar
symul.
Zdarz.
nast.
Chwila
zg
áosz.
1
2
3
4
Zaj
Ċte
kana
áy
D
áugoĞü
kolejki
Zegar
symul.
1
2
3
4
5
3
69
0
z
3
-
-
-
-
0
0
0
15
20
3
z
18
72
-
-
-
1
0
3
4
56
18
z
22
72
38
-
-
2
0
18
6
41
22
z
28
72
38
78
-
3
0
22
2
35
28
z
30
72
38
78
69
4
0
28
3
11
30
z
33
72
38
78
69
4
1
30
35
19
7
33
o
52
72
38
78
69
4
2
33
35 11
3
3
38
z
52
72
73
78
69
4
1
38
11
13
24
52
z
55
72
73
78
69
4
2
52
11
7
10
20
55
z
68
72
73
78
69
4
3
55
11
7
3
-
-
68
o
78
72
73
78
69
4
4
68
11
7
3
24
69
o
78
72
73
78
80
4
3
69
7
3
24
72
o
78
79
73
78
80
4
2
72
3
24
73
o
78
79
76
78
80
4
1
73
24
76
o
78
79
100
78
80
4
0
76
78
z
78
79
100
-
80
3
0
78
78
o
-
79
100
98
80
4
0
78
79
o
-
-
100
98
80
3
0
79
80
o
-
-
100
98
-
2
0
80
98
o
-
-
100
-
-
1
0
98
100
-
-
-
-
-
-
0
0
100
Koniec
F (t )
T
obs
...
1
2
1
2
n
...
T
zg
á
MODELOWANIE SYSTEMU ELEMENTARNEGO METOD
Ą OPISOWĄ
PRZYK
àAD - 4 KANAàY STANOWISKA
Liczba kana
á
á
ów stanowiska obs ugi . . . . . . . . . . .
4
Warto
Ğü
ą
pocz tkowa zegara symulacji . . . . . . . . .
0
Za ile chwil czasowych ko
Ĕ
Ċ
á
czy si obs uga . . . . .
-
-
-
-
Czasy
Czasy
Chwile zako
Ĕczenia obsáugi na kanaáach
Obiekty w kolejce
mi
Ċdzy
zg
áoszeniami
obs
áugi
zg
áoszeĔ
Zegar
symul.
Zdarz.
nast.
Chwila
zg
áosz.
1
2
3
4
Zaj
Ċte
kana
áy
D
áugoĞü
kolejki
Zegar
symul.
1
2
3
4
5
3
69
0
z
3
-
-
-
-
0
0
0
15
20
3
z
18
72
-
-
-
1
0
3
4
56
18
z
22
72
38
-
-
2
0
18
6
41
22
z
28
72
38
78
-
3
0
22
2
35
28
z
30
72
38
78
69
4
0
28
3
11
30
z
33
72
38
78
69
4
1
30
35
19
7
33
o
52
72
38
78
69
4
2
33
35 11
3
3
38
z
52
72
73
78
69
4
1
38
11
13
24
52
z
55
72
73
78
69
4
2
52
11
7
10
20
55
z
68
72
73
78
69
4
3
55
11
7
3
-
-
68
o
78
72
73
78
69
4
4
68
11
7
3
24
69
o
78
72
73
78
80
4
3
69
7
3
24
72
o
78
79
73
78
80
4
2
72
3
24
73
o
78
79
76
78
80
4
1
73
24
76
o
78
79
100
78
80
4
0
76
78
z
78
79
100
-
80
3
0
78
78
o
-
79
100
98
80
4
0
78
79
o
-
-
100
98
80
3
0
79
80
o
-
-
100
98
-
2
0
80
98
o
-
-
100
-
-
1
0
98
100
-
-
-
-
-
-
0
0
100
Koniec
F (t )
T
obs
...
1
2
1
2
n
...
T
zg
á
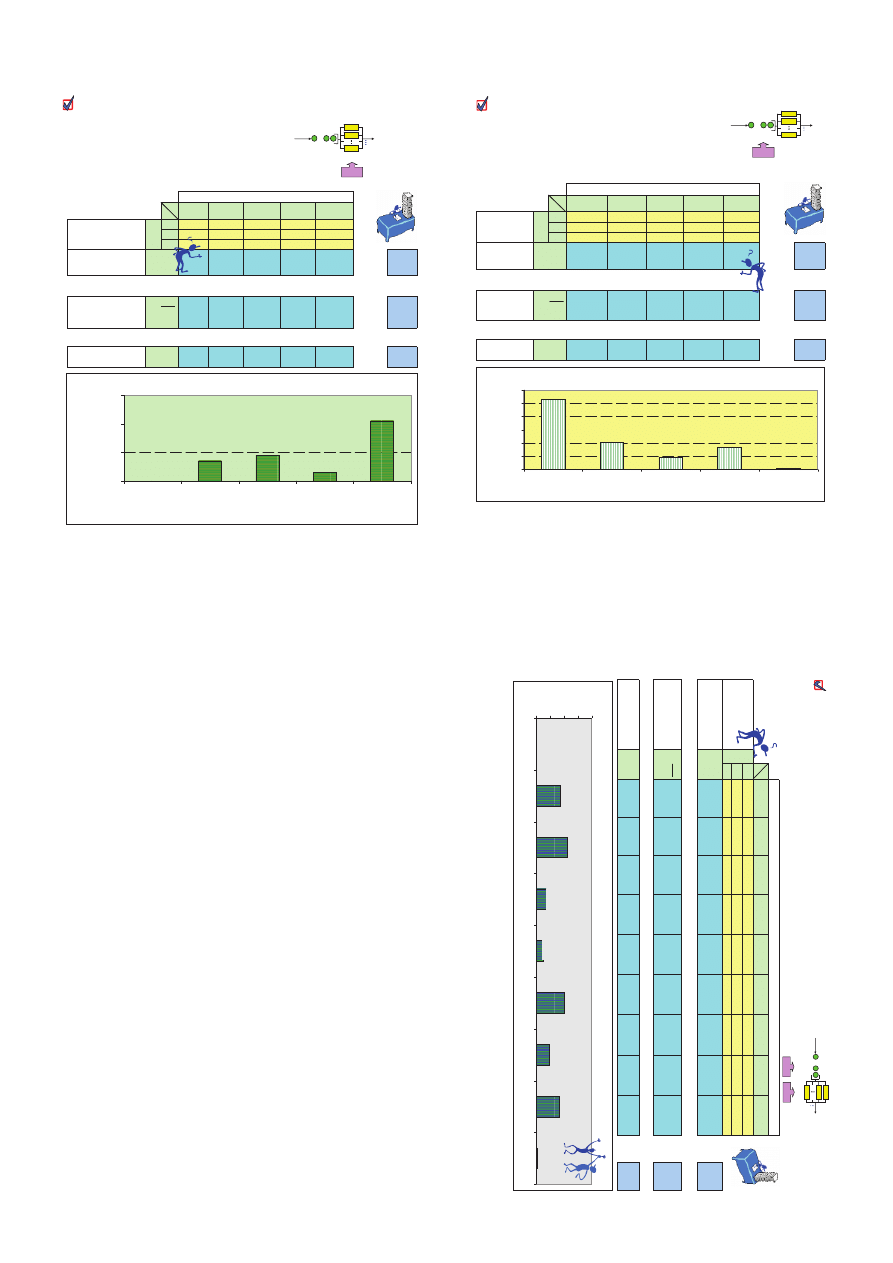
Charakterystyki wykorzytania kana
áów stanowiska
Obliczenia pomocnicze do wyznaczenia charakterystyk wykorzystania stanowiska
Liczba zaj
Ċtych kanaáów i
i
j
0
1
2
3
4
Sk
áadowe czasu,
w którym liczba zaj
Ċtych
kana
áów jest i
t
ij
1
18-3=15
22-18=4
28-22=6
78-28=50
2
100-98=2 98-80=18 78-78=0
79-78=1
3
80-79=1
àącznie czas,
w którym liczba zaj
Ċtych
kana
áów jest i
0
17
22
7
51
97
Wyznaczanie rozk
áadu liczby zajĊtych kanaáów stanowiska
Prawdopodobie
Ĕstwo,
Īe liczba zajĊtych
kana
áów jest i
0,000
0,175
0,227
0,072
0,526
1,000
Obliczenia
Ğredniej liczby zajĊtych kanaáów stanowiska
ĝrednia liczba zajĊtych
kana
áów
L
0,000
zaj
0,175
0,454
0,216
2,103
2,9485
Rozk
áad liczby zajĊtych kanaáów stanowiska
0,000
0,227
0,072
0,526
0,175
0,000
0,250
0,500
0,750
0
1
2
3
4
Liczba zaj
Ċtych kanaáów stanowiska i
p
i
¦
3
4
j
ij
i
t
t
¦
4
0
i
i
t
¦
4
0
i
i
p
¦
4
0
i
i
p
i
¦
4
0
i
i
i
i
t
t
p
F (t )
T
obs
...
1
2
1
2
n
...
T
zg
á
Plik: 2_Symul_i_Obl_d
áug_kol_i_zaj_kanaáów.xls
Opr. A. Kadzi
Ĕski
Charakterystyki oczekiwania zg
áoszeĔ
Obliczenia pomocnicze do wyznaczenia charakterystyk
oczekiwania zg
áoszeĔ
D
áugoĞü kolejki i
i
j
0
1
2
3
4
Sk
áadowe czasu,
w którym kolejka
ma d
áugoĞü i
t
ij
1
30-3= 27
33-30= 3
38-33= 5 68-55= 13 69-68= 1
2
100-76= 24 52-38= 14 55-52= 3 72-69= 3
3
76-73= 3
73-72= 1
àącznie czas,
w którym kolejka
ma d
áugoĞü i
51
20
9
16
1
97
Wyznaczanie rozk
áadu dáugoĞci kolejki
Prawdopodob.
Īe kolejka ma
d
áugoĞü i
0,5258
0,2062
0,0928
0,1649
0,0103
1,0000
Obliczenia
Ğredniej dáugoĞci kolejki
ĝrednia dáugoĞü
kolejki
L
0,0000
kol
0,2062
0,1856
0,4948
0,0412
0,9278
Rozk
áad dáugoĞci kolejki
0,0103
0,1649
0,0928
0,2062
0,5258
0,0000
0,1000
0,2000
0,3000
0,4000
0,5000
0,6000
0
1
2
3
4
D
áugoĞü kolejki i
p
i
¦
3
1
j
ij
i
t
t
¦
4
0
i
i
t
¦
4
0
i
i
p
¦
4
0
i
i
p
i
¦
4
0
i
i
i
i
t
t
p
F (t )
T
obs
...
1
2
1
2
n
...
T
zg
á
Plik: 2_Symul_i_Obl_d
áug_kol_i_zaj_kanaáów.xls
Opr. A. Kadzi
Ĕski
i
i
C
h
a
ra
k
te
ry
s
ty
k
i s
y
s
te
m
u
(k
o
le
jk
a
+
s
ta
n
o
w
is
k
o
)
O
b
lic
ze
n
ia
p
o
m
o
c
n
ic
ze
d
o
w
y
zn
a
c
ze
n
ia
c
h
a
ra
k
te
ry
s
ty
k
s
y
s
te
m
u
L
ic
zb
a
zg
áo
s
ze
Ĕ
w
s
y
s
te
m
ie
i
i
j
0
1
2
3
4
5
6
7
8
Sk
áa
d
o
w
e
c
za
s
u
,
w
k
tó
ry
m
li
c
zb
a
zg
áo
s
ze
Ĕ
w
s
y
s
te
m
ie
je
s
t
i
t
ij
1
1
8
-3
=
1
5
2
2
-1
8
=
4
2
8
-2
2
=
6
3
0
-2
8
=
2
3
3
-3
0
=
3
3
8
-3
3
=
5
6
8
-5
5
=
1
3
6
9
-6
8
=
1
2
1
0
0
-9
8
=
2
9
8
-8
0
=
1
8
7
8
-7
8
=
0
7
8
-7
6
=
2
5
2
-3
8
=
1
4
5
5
-5
2
=
3
7
2
-6
9
=
3
3
8
0
-7
9
=
1
7
9
-7
8
=
1
7
6
-7
3
=
3
7
3
-7
2
=
1
àą
c
zn
ie
c
za
s
,
w
k
tó
ry
m
li
c
zb
a
zg
áo
s
ze
Ĕ
je
s
t
0
1
7
2
2
7
5
2
0
9
1
6
1
9
7
W
y
zn
a
c
za
n
ie
r
o
zk
áa
d
u
l
ic
zb
y
zg
áo
s
ze
Ĕ
w
s
y
s
te
m
ie
Pr
a
w
d
o
p
o
d
o
b
ie
Ĕ
s
tw
o
,
Ī
e
li
c
zb
a
zg
áo
s
ze
Ĕ
je
s
t
0
,0
0
0
0
0
,1
7
5
3
0
,2
2
6
8
0
,0
7
2
2
0
,0
5
1
5
0
,2
0
6
2
0
,0
9
2
8
0
,1
6
4
9
0
,0
1
0
3
1
,0
0
0
0
O
b
lic
ze
n
ia
Ğ
re
d
n
ie
j
lic
zb
y
z
g
áo
s
ze
Ĕ
w
s
y
s
te
m
ie
ĝ
re
d
n
ia
li
c
zb
a
zg
áo
s
ze
Ĕ
w
s
y
s
te
m
ie
L
0
,0
0
0
0
sy
s
0
,1
7
5
3
0
,4
5
3
6
0
,2
1
6
5
0
,2
0
6
2
1
,0
3
0
9
0
,5
5
6
7
1
,1
5
4
6
0
,0
8
2
5
3
,8
7
6
3
R
o
zk
áa
d
li
c
zb
y
zg
áo
s
ze
Ĕ
w
s
y
s
te
m
ie
0
,2
0
6
2
0
,0
9
2
8
0
,1
6
4
9
0
,0
1
0
3
0
,0
5
1
5
0
,0
7
2
2
0
,2
2
6
8
0
,1
7
5
3
0
,0
0
0
0
0
,0
0
0
0
0
,1
0
0
0
0
,2
0
0
0
0
,3
0
0
0
0
,4
0
0
0
0
1
2
3
4
5
6
7
8
¦
3
1
j
ij
i
t
t
¦
8
0
i
i
i
i
t
t
p
¦
8
0
i
i
t
¦
8
0
i
i
p
¦
8
0
i
i
p
i
F
(t
)
T
o
b
s
...
1
2
1
2
n
...
T
zg
á
Pl
ik
:
2
_
Sy
m
u
l_
i_
O
b
l_
d
áu
g
_
k
o
l_
i_
za
j_
k
a
n
a
áó
w
.x
ls
O
p
r.
A
. K
a
d
zi
Ĕ
s
k
i
Wyszukiwarka
Podobne podstrony:
2 BO 2 1 PP Przykłady Segregator [v1]
2 BO 2 1 PP Przykłady Segregator [v1]
12 BO 2 1 PP Segregator Polityka Odnawiania Zasobów w Stacji Paliw s p [v2]
9 BO 2 1 PP MODEL A s p [v2]
8 BO 2 1 PP ZASOBY Wprowadzenie s p [v3]
0 BO 3 1 PP Dzienne 2014 AK&BK Plan cyklu wykładowego [v2]
4 BO 2 1 PP M M 1 oo Analityczne p s [v3]
13 BO 1 1 PP 1plus2 Paliwa 6000
14 BO 2 1 PP Generowanie Liczb Losowych 2008 s p [v9]
5 BO 2 1 PP M M n oo Analityczne p s [v3]
3 BO 2 1 PP Klasyfikacje systemów masowej obsługi s p
11 BO 2 1 PP MODEL D s p [v2]
10 BO 2 1 PP MODEL C s p [v3]
14 BO 2 1 PP Generowanie Liczb Losowych 2008 s p [v9]
6 BO 2 1 PP M M n r Analityczne p s [v2]
9 BO 2 1 PP MODEL A s p [v2]
więcej podobnych podstron