Specjalizowane metody modelowania 



Mgła jest zbiorem kropelek wody 



modelowanie każdej z nich nie wchodzi w grę 



co więcej 

percepcja

 mgły jest 

inna

 – rozmycie 

obrazu poprzez 

rozproszenie

 światła 



Liście drzew 



modelowanie 

każdego

 z nich jest 

nierealne 



istotny

 jest jedynie prawidłowy 

widok

 drzewa 

Specjalizowane metody modelowania 



Modele fraktalne 



śnieżynki von Kocha 



zbiór Julii-Fatou 



zbiór Mandelbrota 



Modele wykorzystujące gramatyki 



równoległe gramatyki grafowe 

Modele fraktalne 



Pojęcie oznacza obecnie wszystko co ma faktyczną 
miarę 

dokładnego

 lub 

statystycznego

 

samopodobieństwa

 dla wszystkich rozdzielczości 



Prawdziwe fraktale są generowane przez 

nieskończone

 procesy rekursywne 



W praktyce posługujemy się aproksymacjami ideału 
tzn. fraktalami generowanymi przez 

procesy 

skończone 

– pomijając nieistotne (praktycznie 

niezauważalne) szczegóły występujące po kilku 
pierwszych iteracjach 

Śnieżynki von Kocha 



Konstrukcja śnieżynki von Kocha 



 Każdy 

segment

 z rysunku a) jest 

zastępowany

 dokładną 

kopią

 

całej

 figury pomniejszoną 3 razy 



 Ten sam proces jest stosowany dla segmentów z rysunku 
b) do generowania obrazu z rysunku c) 

Definicja wymiaru fraktalnego 



Każda z części odcinka w przestrzeni 1D 
podzielonego na N części jest podobna do całości w 
skali N, tzn. N

1/1 



Kwadrat w przestrzeni 2D podzielony na N 
podobnych do oryginału części w skali N

1/2

. Np. 

podział na 9 podobnych kwadratów daje 
podobieństwo w skali 3 



Jeśli każdy z czterech odcinków śnieżynki Kocha 
zamienimy na kopię oryginału w skali 3, to ma on 

wymiar fraktalny d

, przy czym 4

1/d

 = 3. Stąd 

d = 

ln(4)/ln(3) = 1,26

…. 

Najbardziej znane zbiory fraktalne 



Zbiór generowany najprostszą i najbardziej znaną regułą x 



 x

2

 + c, gdzie x jest kolejnym, zespolonym elementem 

zbioru, a c również liczbą zespoloną 



Jeśli c = a + bi ma moduł < 1, to kolejne przetwarzanie 
regułą tworzy ciąg zbieżny do 0 



Jeśli c = a + bi ma moduł > 1, to kolejne przetwarzanie 
regułą tworzy ciąg rozbieżny do nieskończoności 



Jeśli c = a + bi ma moduł = 1, to kolejne przetwarzanie 
regułą tworzy ciąg o module 1 



część dąży do 0 



 część do nieskończoności 



część jest stała 

 
 

Zbiór Julia-Fatou 



Załóżmy, że 

wielokrotnie

 stosujemy przekształcenie 

zgodnie z regułą x 



 x

2

 + c do każdej liczby 

x

 o pewnej 

niezerowej

 wartości c (np. c = -0.12375 + 0.056805 

i)

 



Niektóre z liczb będą 

dążyć

 do 

0

, inne do 

nieskończoności

, a jeszcze inne 

nie

 będą podążać w 

żadnym z tych kierunków 



Rysując zbiór tych ostatnich uzyskamy wykres Julia-
Fatou 
 

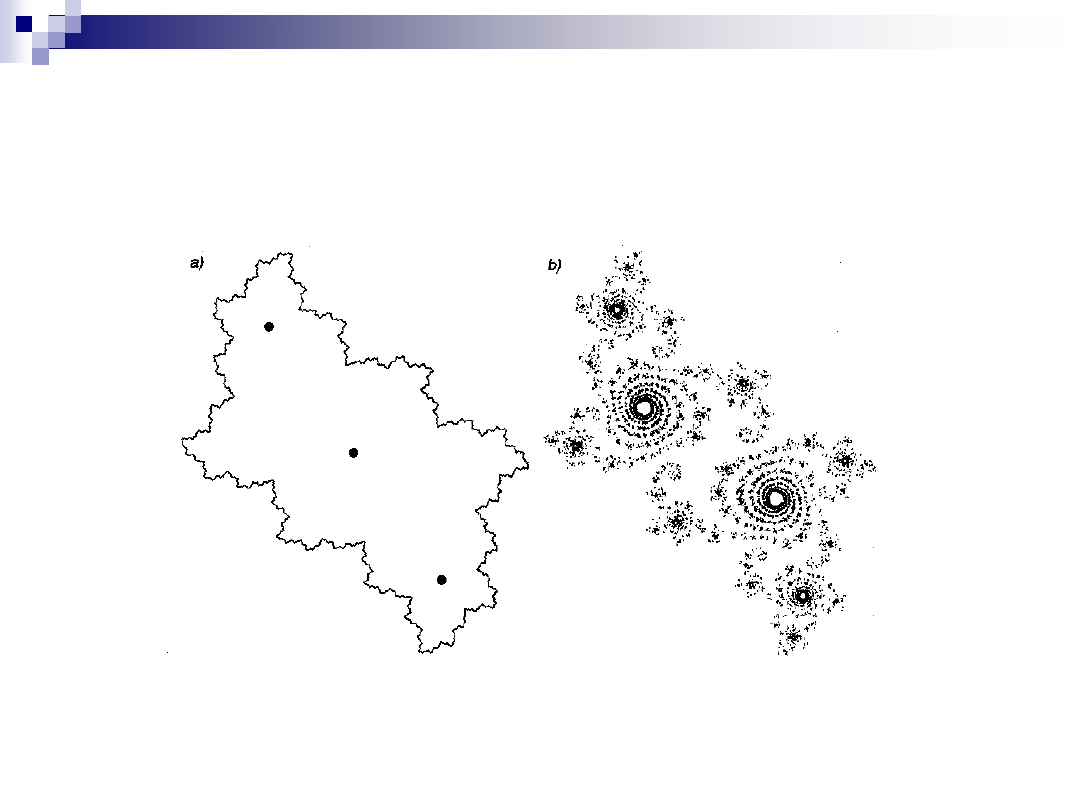
Zbiór Julia-Fatou - rysowane są tylko 
punkty o module 1 

a) c = -0.12375 + 0.056805 i 
b) c = -0.012 + 0.74 i 

Zbiór Mandelbrota 



Zbiór

 dla wszystkich możliwych 

punktów c

, przy czym 

zaznaczane są tylko punkty gdy zbiór Julia-Fatou jest 

spójny

, tzn. złożony z jednego kawałka 

niepodzielonego na rozłączne wyspy 



Łatwiejszy sposób generowania: 



dla każdej liczby c przyjmowana jest na początek liczba x 
równa 0 = 0 + 0i i reguła x= x

2

 + c stosowana jest skończoną 

liczbę razy (np. 1000)  



Jeśli po tych iteracjach punkt jest na zewnątrz dysku 
zdefiniowanego przez moduł < 100 to punkt c otrzymuje 
barwę białą 



w przeciwnym przypadku staje się czarny 

 

Zbiór Mandelbrota 

Zbiór Julii 



Zbiór tworzą te punkty 𝑝 ∈ 𝐶 dla których ciąg opisany równaniem rekurencyjnym: 

𝑧

0

= 𝑝 

𝑧

𝑛+1

= 𝑧

𝑛

2

+ 𝑐 

 



Nie dąży do nieskończoności: 

lim

𝑛→∞

𝑧

𝑛

≠ ∞ 



gdzie 𝑐 – liczba zespolona będąca parametrem zbioru.  



Można wykazać, że jest to równoważne z: 

∀

𝑛∈𝑁

𝑧

𝑛

< 2 



Podsumowując jednym zdaniem: 

𝐽 𝑐 = 𝑝 ∈ 𝐶: ∀

𝑛∈𝑁

𝑧

𝑛

< 2  



Dla różnych c otrzymuje się różne zbiory, stąd J jest rodziną zbiorów. 

Zbiór Julii 

Zbiór Julii dla z = z

2

 - 1 

Zbiór Julii – rzut trójwymiarowego 
przekroju zbioru czterowymiaroego – 
obliczenia kwaternionowe 

Zbiór Julia – po trójwymiarowym 
renderingu 

Modele fraktalne 



Wykresy fraktalne doskonale nadają się do 
modelowania wielu obiektów charakteryzujących się 
samopodobieństwem 



góry – szczyty, mniejsze szczyty, skały, skałki 



drzewa – konary, gałęzie, gałązki 



wybrzeże morskie – zatoki, zatoczki, ujścia rzek, 
strumyków, kanałów 



Generowanie fraktali prowadzi się w takiej liczbie 
rekursywnych iteracji, że dalsze zmiany są już na 
poziomie podpikselowym 

Modele fraktalne 



Fournier, Fussell i Carpenter zbudowali algorytm budowy gór 
fraktalnych 



Start następuje od odcinka 

leżącego

 na osi Ox 



Następnie odcinek jest 

dzielony

 na 

połowę

 i punkt 

środkowy

 

przesuwa się w 

górę

 na pewną wysokość 



Dalej następuje podział 

każdego

 z odcinków i oblicza się nową 

wysokość punktu środkowego z położenia (x

i

, y

i

) 

do położenia 

(x

i+1

, y

i+1

)

 wg reguły 

 
 
 
 



gdzie 

P() 

jest funkcją 

zakłócającą

, a 

R() 

jest liczbą 

losową

 z 

zakresu 0 do 1 na bazie 

x

new

.

 









)

(

)

(

2

1

;

2

1

1

1

1

new

i

i

i

i

new

i

i

new

x

R

x

x

P

y

y

y

x

x

x



















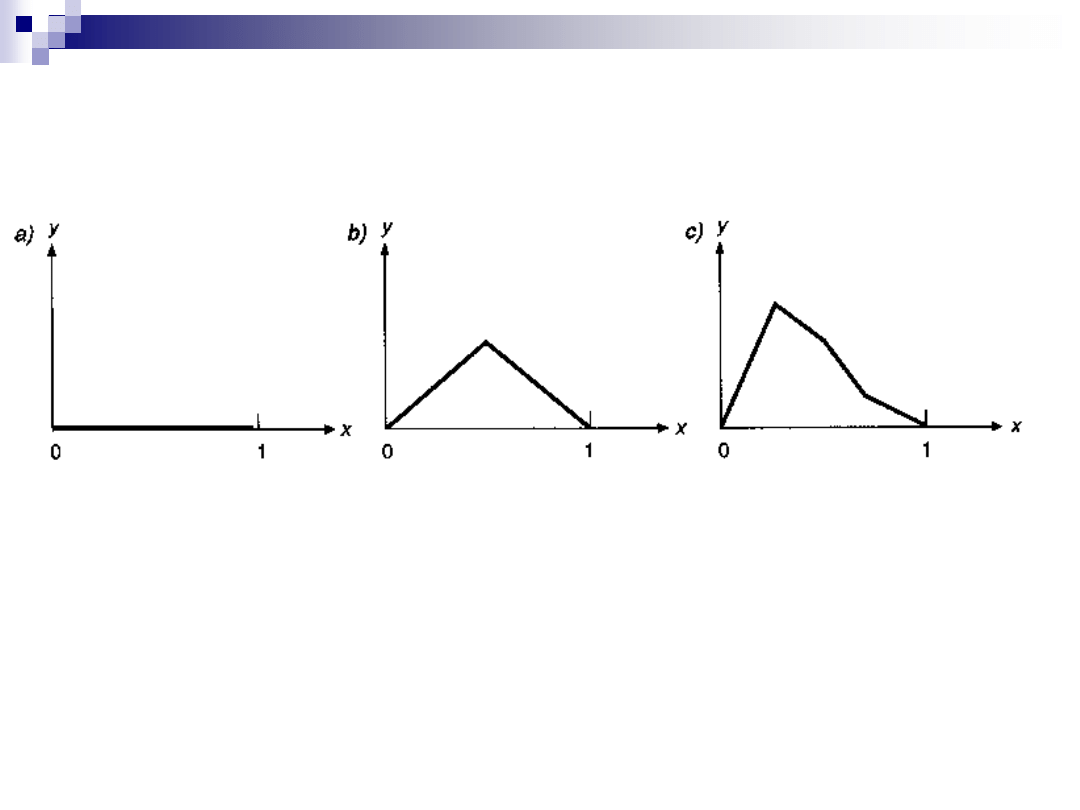
Klasy figur fraktalnych 



Odcinek a osi x (a) 



Punkt środkowy odcinka został przesunięty w 
kierunku y o wielkość losową (b) 



 Wynik kolejnej iteracji (c) 

Modele fraktalne 



Jeśli 

P(s) = s

, to pierwszy z punktów 

nie może 

być 

przesunięty o więcej niż 1, a każdy następny z dwóch punktów 
nie  może być przesunięty o więcej niż 1/2. 



Wszystkie punkty trafiają więc do 

jednostkowego kwadratu

. 



Dla

 P(s) = s

a

, kształt wyniku zależy od 

a

. 

Zakłócenia są 

odwrotnie proporcjonalne do

 

a

. 



Możliwe są inne postaci funkcji, np

. 

P(s) = 2

-s

 



Budowa obrazu gór wymaga modyfikacji kształtów 2D: 



początkową figurą jest trójkąt 



następnie łączy się jego punkty środkowe 



Współrzędna 

z

 każdego z punktów jest modyfikowana tak jak 

uprzednio współrzędna 

y

 w modelu 1D 

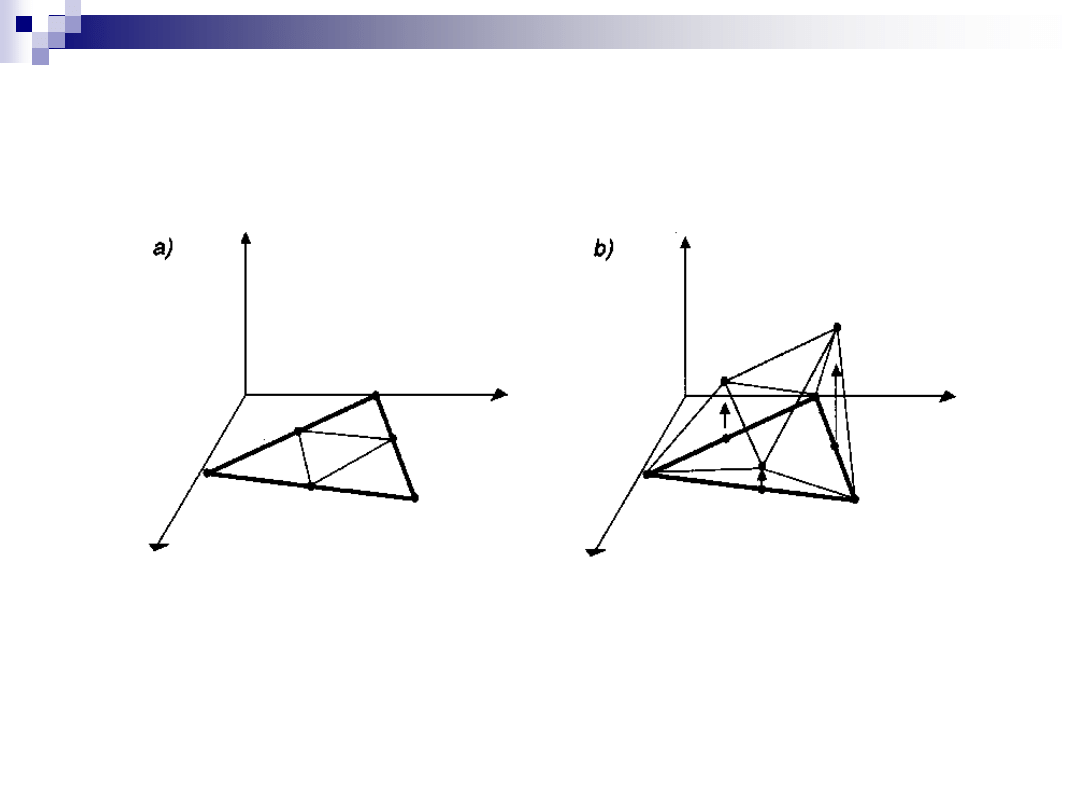
Klasy przestrzennych figur fraktalnych 



Podział trójkąta na cztery mniejsze trójkąty (a) 



Punkty środkowe oryginalnego trójkąta są przesuwane w 

kierunku y tak, że powstał kształt z rysunku (b). 



Proces powtarzany iteracyjnie tworzy obraz gór 

Góry fraktalne 

Modele oparte o gramatyki 
grafowe 



Lindenmayer opracował metodę opisu roślin w oparciu o 
metajęzyki równoległych gramatyk grafowych 



Smith nazwał je 

graftalami

. 



Typowym przykładem jest gramatyka z alfabetem: {A,B,[,]} i 
dwiema regułami:  

A 



AA 

B



A[B]AA[B] 



Poczynając od aksjomatu A pierwsze kilka generacji to: A,   
AA,   AAAA, itd. 



Poczynając od aksjomatu B pierwsze kilka generacji to: B,   
A[B]AA[B], AA[A[B]AA[B]]AAAA[A[B]AA[B]], itd. 
 

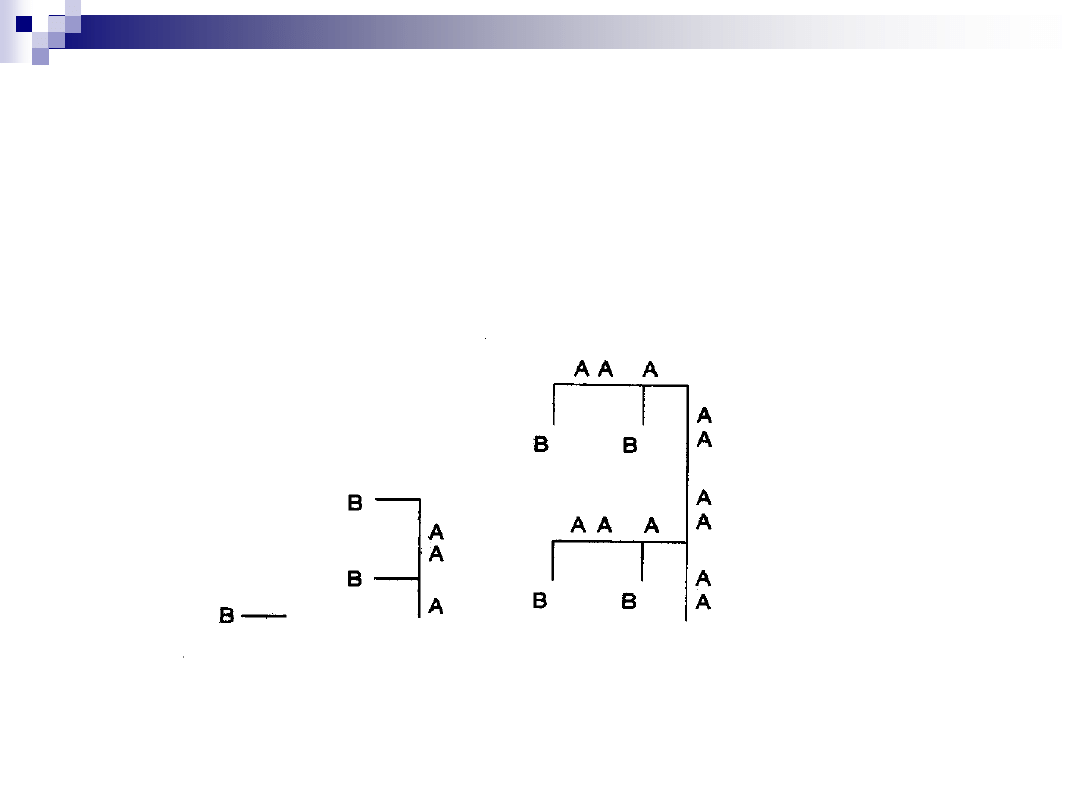
Modele oparte o gramatyki 



Jeśli teraz: 



słowo w metajęzyku reprezentuje sekwencję segmentów w strukturze grafu 
oraz 



części w nawiasach stanowią odgałęzienie, to uzyskamy strukturę 
 
 
 
 
 
 
 
 

 



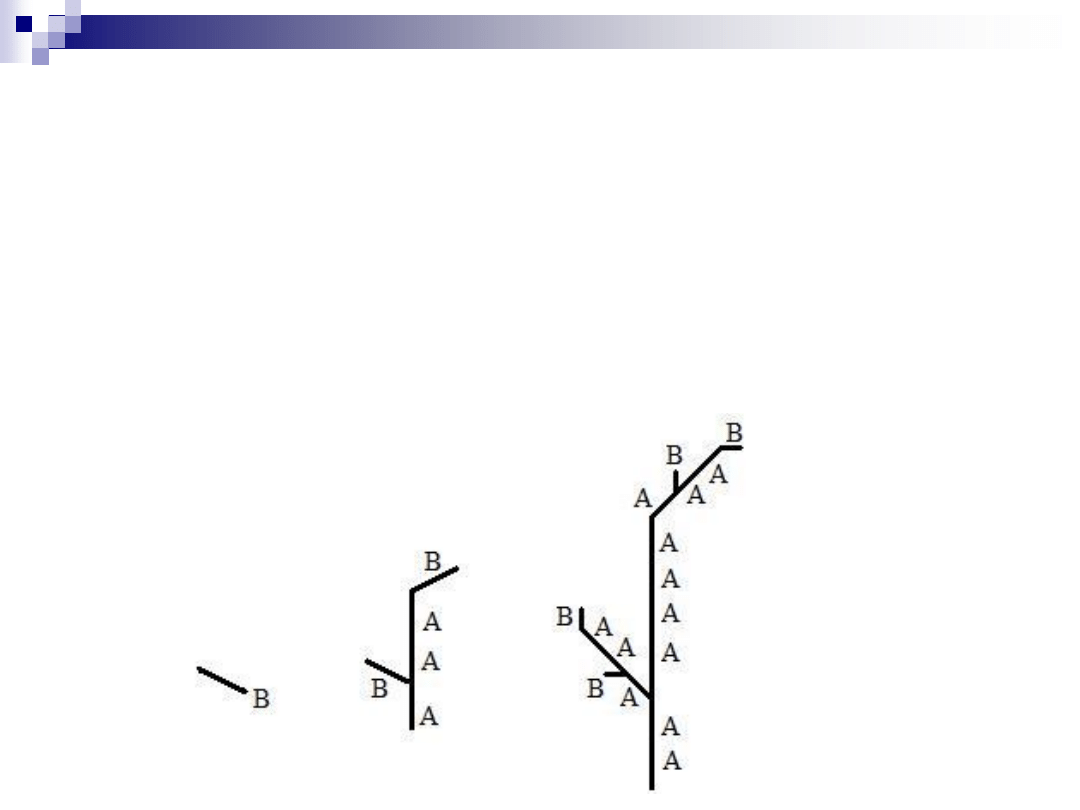
Drzewo reprezentujące trzy pierwsze słowa języka 



Wszystkie gałęzie są narysowane na lewo od bieżącej głównej osi 

B



A[B]AA[B]

 

Modele oparte o gramatyki 



Dla zrównoważenia rozgałęzień należy do języka wprowadzić 
nowe symbole „(„ oraz „)” i zmienić projekcję: B



A[B]AA[B] 

na B



A[B]AA(B) 



Jeśli teraz nawiasy kwadratowe oznaczają lewą gałąź, a 
okrągłe prawą, to otrzymamy obrazy: 

Modele oparte o gramatyki 



Kontynuując można uzyskać złożone struktury 



Samopodobieństwo w przypadku gramatyk grafowych polega na 

tym, iż wzór opisany przez meta-wyraz n–tej generacji jest zawarty 

(jedno, bądź wielokrotnie) w meta-wyrazie n+1–szej generacji 



 W kolejnych generacjach można zmieniać: 



długości linii 



grubości linii 



kąty nachylenia gałęzi 



W ten sposób uzyskuje się różne efekty rysując kwiatki czy liście w 

każdym węźle końcowym - 

ulepszając

 obraz w każdym węźle 

końcowym 



Korzystanie z gramatyk wymaga 

gramatycznej i geometrycznej

 

reprezentacji, które mogą być różne 



Stosuje się też 

rejestrację

 „

wieku

” poszczególnych symboli 

przypisując im 

różne

 

obiekty

 graficzne. 

Gramatyka Reffye’a 



Jest to narzędzie do opisu 

roślin 



Symulacja wzrostu jest opisywana za pomocą 

niewielkiego

 zbioru parametrów 



Parametry są 

kategoriami

 

biologicznymi

, które 

łatwo można dodać do algorytmu wzrostu 



Produkcje gramatyki są stosowane raczej 

losowo

, a nie deterministycznie 

Gramatyka Reffye’a 



Rozpoczynamy od 

jednej 

łodygi 



Na końcu łodygi jest 

pączek

, który może: 



umrzeć, 



zakwitnąć i umrzeć, 



być uśpiony przez 

pewien czas, 



stać się elementem 

międzywęzłowym – 

segmentem rośliny 

między pąkami. 

Gramatyka Reffye’a 



Proces stawania się elementem 

międzywęzłowym ma trzy etapy: 



oryginalny pączek może 

generować

 

jeden lub kilka 

specjalnych

 pączków 

(pączki z jednej strony połączenia 

między węzłami wewnętrznymi) – 

jest to 

rozgałęzienie 



dodawany jest element 

międzywęzłowy 



koniec odcinka międzywęzłowego 

staje się 

nowym

 

pączkiem

 

wierzchołkowym (początek jest 

oparty na końcu sekwencji 

elementów międzywęzłowych) 



Każdy z pączków w otrzymanym 

obiekcie może dalej podlegać 

podobnym przekształceniom 

 

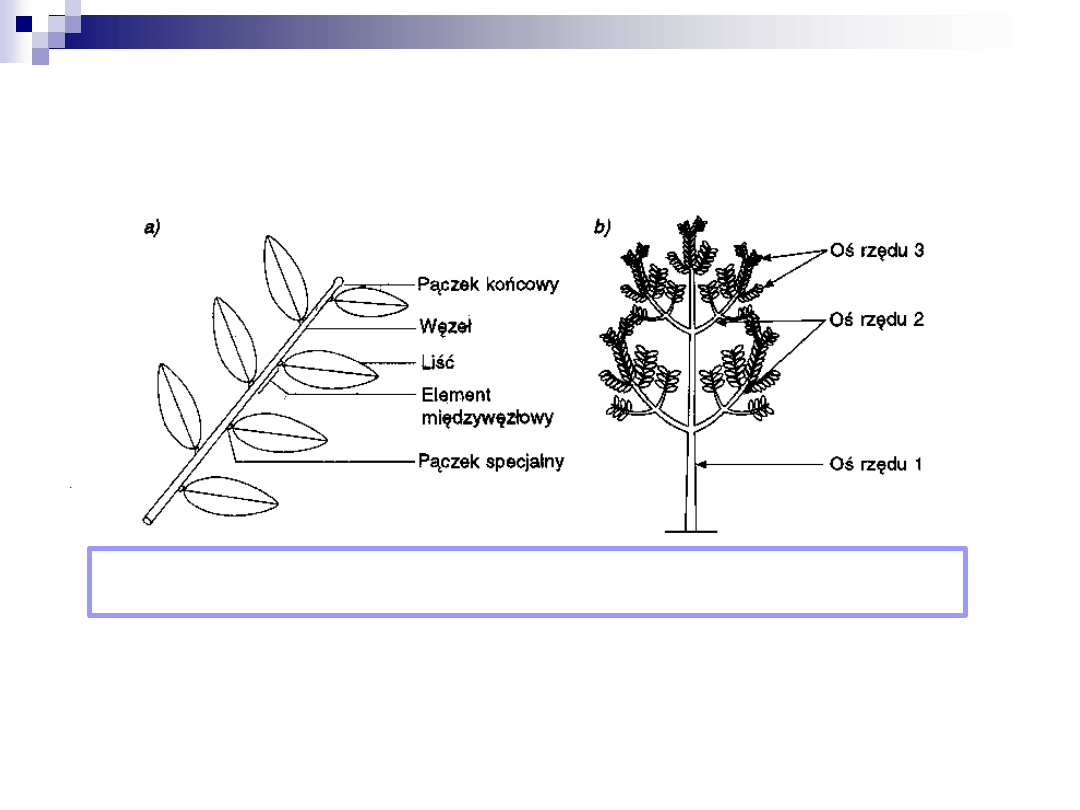
Gramatyka Reffye’a 



Początkowy segment drzewa jest rzędu 1 



Porządek wszystkich innych elementów 
miedzywęzłowych definiujemy indukcyjnie: 



odcinki międzywęzłowe generowane z 

węzłowego

 

pączka elementu rzędu 

i

 są również rzędu 

i

, 



odcinki międzywęzłowe generowane ze 

specjalnego

 pączka elementu rzędu 

i

 są rzędu 

i+1

, 



Pień drzewa jest zatem rzędu 1, konary rzędu 
2, gałęzie tych konarów rzędu 3, it. 

 

Gramatyki o parametrach 
biologicznych 



Konwersja opisu 

na aktualny 

obraz

 wymaga 

modelu kształtów 

różnych 

elementów: 



Element międzywęzłowy 

rzędu 1

 jest wysmukłym 

stożkiem

, podczas gdy ten sam 

element 

rzędu np. 7 

może być małym 

zielonym odcinkiem

. 



Przy każdym 

specjalnym pączku 

powinien znaleźć się 

liść

, który może później 

odpaść 

Gramatyka Reffye’a 



W celu symulacji wzrostu rośliny należy również 

określić „

informację biologiczną

” 



bieżący wiek modelu, 



szybkość wzrostu elementów międzywęzłowych 

poszczególnych rzędów 



ich prawdopodobieństwo zamierania, 



przerwy, 



rozgałęzienia, 



reiteracji. 



Jako funkcji 



wieku, 



rozmiaru i 



rzędu 
 
 

Gramatyka Reffye’a 



Należy ponadto określić „

informację geometryczną

”: 



kształt każdego elementu międzywęzłowego jako funkcja 

rzędu

 

i 

wieku 



kąty rozgałęzienia jako funkcja 

rzędu

 i 

wieku 



kształt każdego elementu międzywęzłowego jako funkcja 

rzędu

 

i 

wieku 



orientacja osi (element prosty, zakrzywiony w kierunku 

poziomym czy pionowym) jako funkcja 

rzędu

 i 

wieku 



Potrzebne są też dalsze informacje związane z renderingiem 

obiektów: 



barwa, 



tekstury,  



itp. 

  dla elementów międzywęzłowych 

każdego rzędu

, 

liści

 i 

kwiatów

 

w różnym wieku 

Gramatyki 
probabi-
listyczne