Wiązar płatwiowo-kleszczowy

ZUT, Katedra Budownictwa Ogólnego i Konstrukcji Drewnianych, EK

Wiązar płatwiowo-kleszczowy

ZUT, Katedra Budownictwa Ogólnego i Konstrukcji Drewnianych, EK

Wiązar płatwiowo-kleszczowy

ZUT, Katedra Budownictwa Ogólnego i Konstrukcji Drewnianych, EK

Słup 18/18 cm ściskany siłą osiową
P = 2S

2

.

cos (90

o

-45

o

)

– 2R

Az

= 2

.

47,4

.

cos45

o

– 2

.

1,73 = 63,6kN

𝑓

𝑐,0,𝑑

= 𝑘

𝑚𝑜𝑑

∙

𝑓

𝑐,0,𝑘

𝛾

𝑀

= 0,6 ∙

21

1,3

= 9,69 𝑀𝑃𝑎

A=18

.

18 = 324cm

2

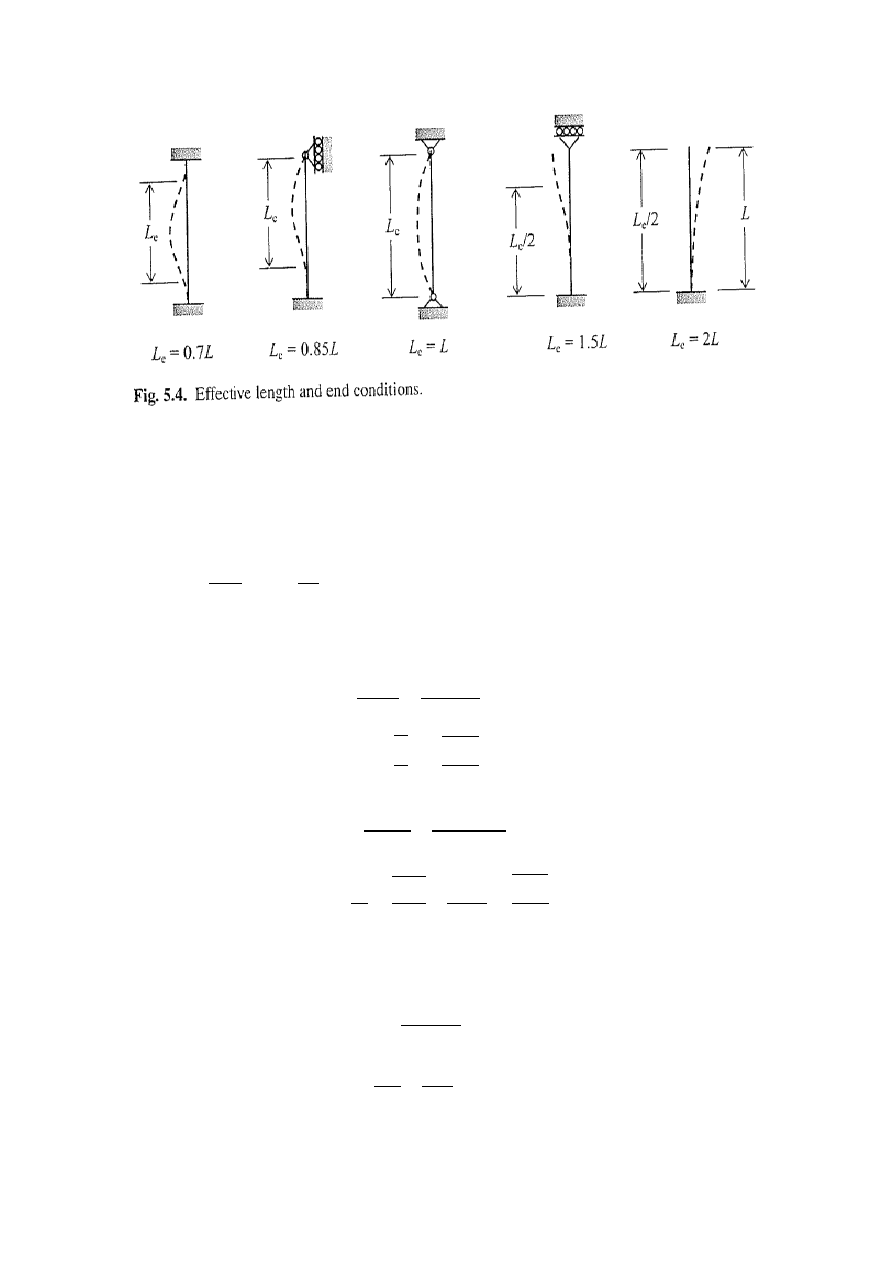
l

y

=278cm

l

z

=278-90cm=188cm < l

y

dlatego pomijamy w dalszych obliczeniach

𝐼

𝑦

=

𝑏 ∗ 𝑕

3

12

=

18 ∗ 18

3

12

= 8748 𝑐𝑚

4

𝑖

𝑦

=

𝐼

𝑦

𝐴

=

8748

324

= 5,2 𝑐𝑚

𝜆

𝑦

=

𝜇

𝑦

∗ 𝑙

𝑦

𝑖

𝑦

=

1,00 ∗ 278

5,2

= 53,46

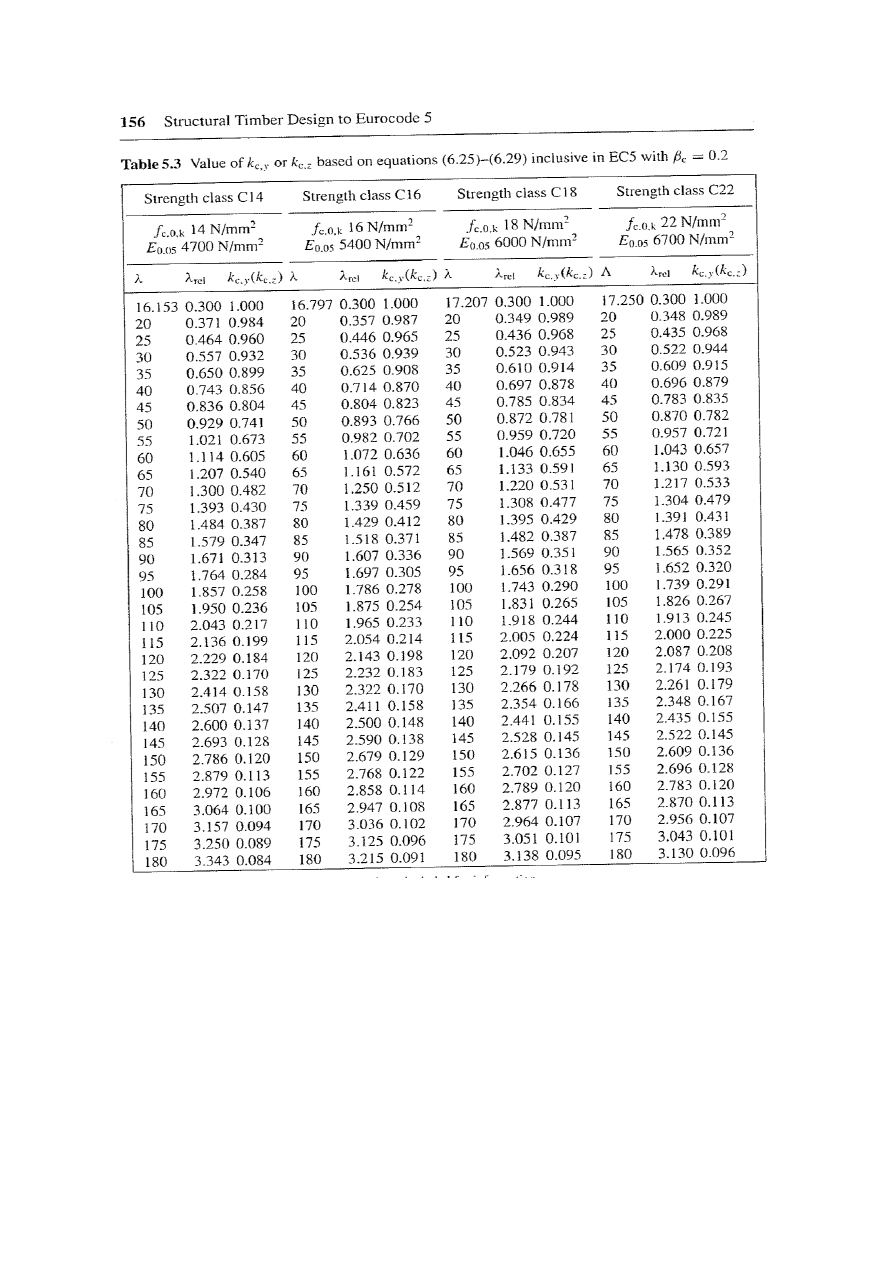
𝜆

𝑟𝑒𝑙 ,𝑦

=

𝜆

𝑦

𝜋

∙

𝑓

𝑐,0,𝑘

𝐸

0,05

=

53,46

𝜋

∙

21

7400

= 0,91

Ponieważ smukłości względem osi z i y > 0,3 obliczenia przeprowadza się po uproszczeniu
dla wzoru:

𝜎

𝑐,0,𝑑

𝑘

𝑐,𝑦

𝑓

𝑐,0,𝑑

< 1

𝜎

𝑐,0,𝑑

=

𝑁

𝐸𝑑

𝐴

=

63,6

324

∗ 10 = 1,96 𝑀𝑃𝑎

𝑓

𝑐,0,𝑑

= 9,69 𝑀𝑃𝑎

Wiązar płatwiowo-kleszczowy

ZUT, Katedra Budownictwa Ogólnego i Konstrukcji Drewnianych, EK

𝛽

𝑐

= 0,2 dla drewna litego

𝑘

𝑦

= 0,5 1 + 𝛽

𝑐

𝜆

𝑟𝑒𝑙 ,𝑦

− 0,3 + 𝜆

𝑟𝑒𝑙 ,𝑦

2

= 0,5 ∗ 1 + 0,2 0,91 − 0,3 + 0,91

2

= 0,98

𝑘

𝑐,𝑦

=

1

𝑘

𝑦

+ 𝑘

𝑦

2

− 𝜆

𝑟𝑒𝑙 ,𝑦

2

=

1

0,98 + 0,98

2

− 0,91

2

= 0,74

1,96

0,74 ∗ 9,69

+ 0 < 1

0,27 < 1

Warunek nośności został spełniony

Docisk słupa do podwaliny

Wg EN1995:

6.1.5 Ściskanie w poprzek włókien

(1)P Należy spełnid następujący warunek:

(6.3)

gdzie:

σ

c,90,d

- obliczeniowe naprężenie ściskające w poprzek włókien, w strefie docisku,

f

c,90,d

- obliczeniowa wytrzymałośd na ściskanie w poprzek włókien.

k

c,90

- współczynnik uwzględniający rozkład obciążenia, możliwośd powstania pęknięd oraz

stopieo odkształcenia przy ściskaniu.
(2) Wartośd współczynnika k

c,90

należy przyjmowad za równą 1,0, z wyjątkiem przypadków

określonych w poniższych punktach. W tych szczególnych przypadkach, współczynnik k

c,90

może

zostad zwiększony do wartości granicznej k

c,90

=

4,0.

d

c,90,

90

c

f

k

σ

,



d

c,90,

Wiązar płatwiowo-kleszczowy

ZUT, Katedra Budownictwa Ogólnego i Konstrukcji Drewnianych, EK

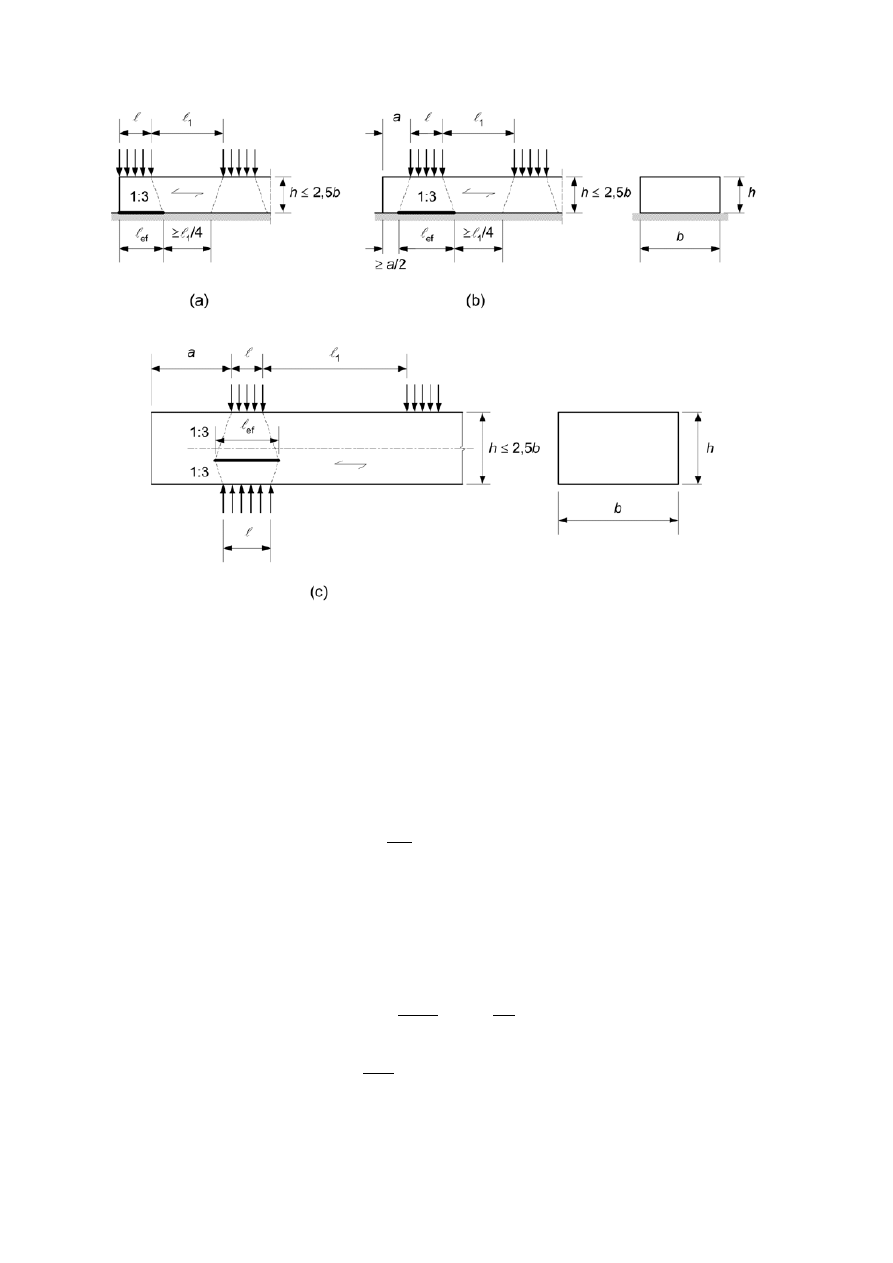
Powierzchnia docisku 18x18 zakładając połączenie przez kątowniki (bez czopu)

Przyjmuję podwalinę 18x6cm

P=63,6kN
f

c,90,k

=2,5MPa

𝑃

𝐴

𝑒𝑓

≤ 𝑘

𝑐,90

𝑓

𝑐,90,𝑑

𝑘

𝑐,90

= 1,25 𝑑𝑙𝑎 𝑒𝑙𝑒𝑚𝑒𝑛𝑡𝑢 𝑝𝑜𝑑𝑝𝑎𝑟𝑡𝑒𝑔𝑜 𝑤 𝑠𝑝𝑜𝑠ó𝑏 𝑐𝑖ą𝑔ł𝑦, 𝑑𝑟𝑒𝑤𝑛𝑜 𝑖𝑔𝑙𝑎𝑠𝑡𝑒 gdy l≥2h

L=18cm 2h=12cm stąd możemy zastosować wartość 1,25

A

ef

= 18 * (18+3+3)=432cm

2

𝑓

𝑐,90,𝑑

= 𝑘

𝑚𝑜𝑑

∙

𝑓

𝑐,90,𝑘

𝛾

𝑀

= 0,6 ∙

2,5
1,3

= 1,15 𝑀𝑃𝑎

63,6

432

∗ 10 ≤ 1,25 ∗ 1,15

1,47 > 1,44

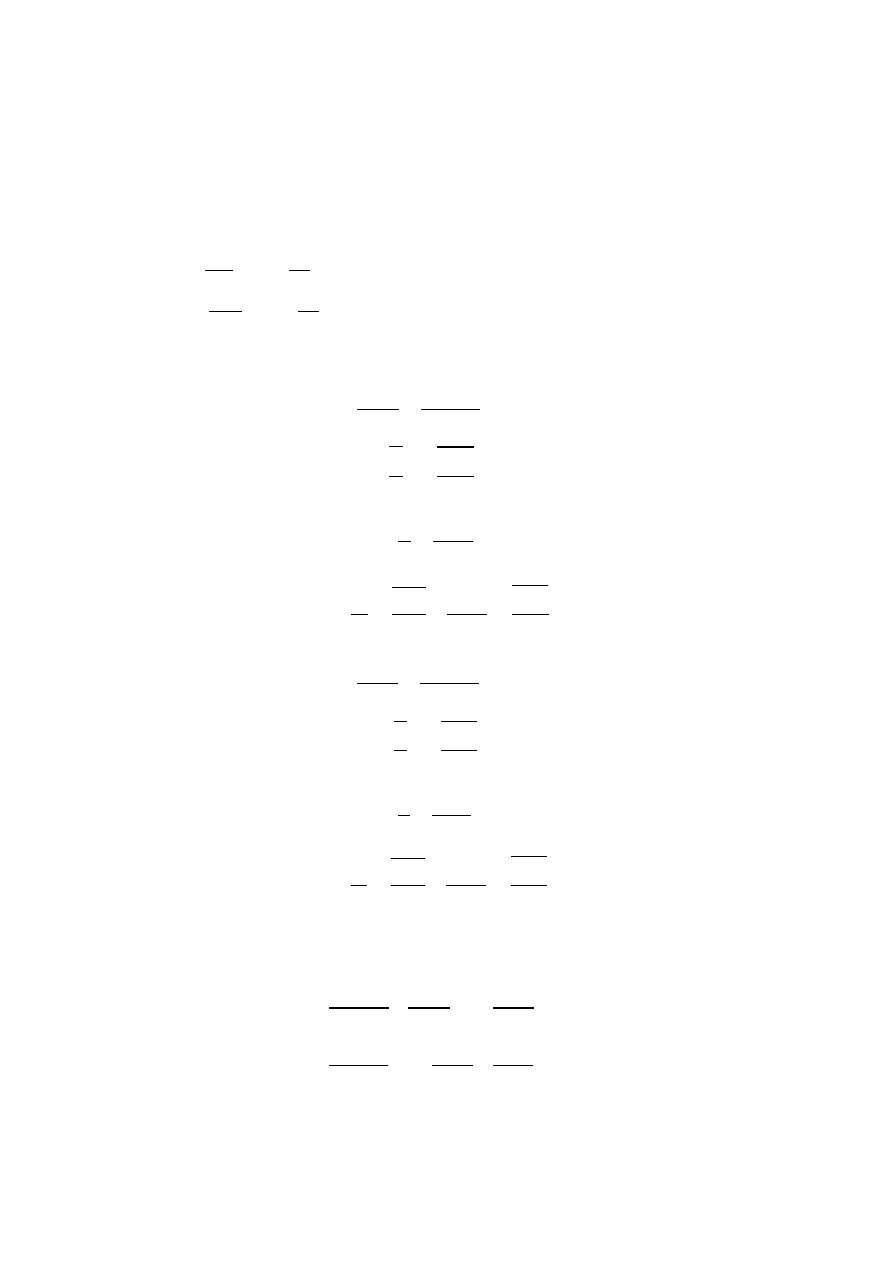
Wiązar płatwiowo-kleszczowy

ZUT, Katedra Budownictwa Ogólnego i Konstrukcji Drewnianych, EK

Warunek nie został spełniony (2%)

Miecz 18/14 cm o długości l=90cm *

√𝟐=127,3cm

Siła w mieczu S

2

=47,4kN

𝑓

𝑚,𝑑

= 𝑘

𝑚𝑜𝑑

∙

𝑓

𝑚,𝑘

𝛾

𝑀

= 0,6 ∙

24

1,3

= 11,08 𝑀𝑃𝑎

𝑓

𝑐,0,𝑑

= 𝑘

𝑚𝑜𝑑

∙

𝑓

𝑐,0,𝑘

𝛾

𝑀

= 0,6 ∙

21

1,3

= 9,69 𝑀𝑃𝑎

𝐴 = 𝑏𝑕 = 18 ∗ 14 = 252 𝑐𝑚

2

𝐼

𝑦

=

𝑏 ∗ 𝑕

3

12

=

18 ∗ 14

3

12

= 4116 𝑐𝑚

4

𝑖

𝑦

=

𝐼

𝑦

𝐴

=

4116

252

= 4,04 𝑐𝑚

𝜆

𝑦

=

𝑙

𝑦

𝑖

𝑦

=

127,3

4,04

= 31,51

𝜆

𝑟𝑒𝑙 ,𝑦

=

𝜆

𝑦

𝜋

∙

𝑓

𝑐,0,𝑘

𝐸

0,05

=

31,51

𝜋

∙

21

7400

= 0,53

𝐼

𝑧

=

𝑕 ∗ 𝑏

3

12

=

14 ∗ 18

3

12

= 6804 𝑐𝑚

4

𝑖

𝑧

=

𝐼

𝑧

𝐴

=

6804

252

= 5,2 𝑐𝑚

𝜆

𝑧

=

𝑙

𝑧

𝑖

𝑧

=

127.3

5,2

= 24,48

𝜆

𝑟𝑒𝑙 ,𝑧

=

𝜆

𝑧

𝜋

∙

𝑓

𝑐,0,𝑘

𝐸

0,05

=

24,48

𝜋

∙

21

7400

= 0,42

Ponieważ smukłości względem osi z i y > 0,3 obliczenia przeprowadza się dla wzorów
poniższych:

𝜎

𝑐,0,𝑑

𝑘

𝑐,𝑦

𝑓

𝑐,0,𝑑

+

𝜎

𝑚,𝑦,𝑑

𝑓

𝑚,𝑦,𝑑

+ 𝑘

𝑚

𝜎

𝑚,𝑧,𝑑

𝑓

𝑚,𝑧,𝑑

< 1

𝜎

𝑐,0,𝑑

𝑘

𝑐,𝑧

𝑓

𝑐,0,𝑑

+ 𝑘

𝑚

𝜎

𝑚,𝑦,𝑑

𝑓

𝑚,𝑦,𝑑

+

𝜎

𝑚,𝑧,𝑑

𝑓

𝑚,𝑧,𝑑

< 1

Wiązar płatwiowo-kleszczowy

ZUT, Katedra Budownictwa Ogólnego i Konstrukcji Drewnianych, EK

𝛽

𝑐

= 0,2 dla drewna litego

𝑘

𝑦

= 0,5 1 + 𝛽

𝑐

𝜆

𝑟𝑒𝑙 ,𝑦

− 0,3 + 𝜆

𝑟𝑒𝑙 ,𝑦

2

= 0,5 ∗ 1 + 0,2 0,53 − 0,3 + 0,53

2

= 0,66

𝑘

𝑐,𝑦

=

1

𝑘

𝑦

+ 𝑘

𝑦

2

− 𝜆

𝑟𝑒𝑙 ,𝑦

2

=

1

0,66 + 0,66

2

− 0,53

2

= 0,95

𝑘

𝑧

= 0,5 1 + 𝛽

𝑐

𝜆

𝑟𝑒𝑙 ,𝑧

− 0,3 + 𝜆

𝑟𝑒𝑙 ,𝑧

2

= 0,5 ∗ 1 + 0,2 0,42 − 0,3 + 0,42

2

= 0,6

𝑘

𝑐,𝑧

=

1

𝑘

𝑧

+ 𝑘

𝑧

2

− 𝜆

𝑟𝑒𝑙 ,𝑧

2

=

1

0,6 + 0,6

2

− 0,42

2

= 0,97

𝜎

𝑚,𝑦,𝑑

= 0

𝜎

𝑚,𝑧,𝑑

= 0

𝜎

𝑐,0,𝑑

=

𝑆

2

𝐴

=

47,4

18 ∗ 14

∗ 10 = 1,88𝑀𝑃𝑎

𝜎

𝑐,0,𝑑

𝑘

𝑐,𝑦

𝑓

𝑐,0,𝑑

+

𝜎

𝑚,𝑦,𝑑

𝑓

𝑚,𝑦,𝑑

+ 𝑘

𝑚

𝜎

𝑚,𝑧,𝑑

𝑓

𝑚,𝑧,𝑑

< 1

𝜎

𝑐,0,𝑑

𝑘

𝑐,𝑧

𝑓

𝑐,0,𝑑

+ 𝑘

𝑚

𝜎

𝑚,𝑦,𝑑

𝑓

𝑚,𝑦,𝑑

+

𝜎

𝑚,𝑧,𝑑

𝑓

𝑚,𝑧,𝑑

< 1

1,88

0,95 ∗ 9,69

< 1 0,2 < 1

1,88

0,97 ∗ 9,69

< 1 0,2 < 1

Warunek nośności został spełniony

Kleszcze 2x 6/18 cm

Siła ściskająca = reakcja pozioma od płatwi (wiązar pełny)
P

d1

= q

d2

.

l = 1,86

.

4,5 =8,37kN

Siła skupiona (człowiek) P

d2

=1,5kN

moment od siły skupionej M

P

=P

d2

l/4 = 1,5

.

3,45 /4 =1,29kNm

Obciążenie równomiernie rozłożone (ocieplenie) q

d3

= 0,55 kN/m

Moment od obc. równomiernie rozłożonego M

qd3

=q

d3

l

2

/8 = 0,55

.

3,45

2

/8 = 0,82kNm

Łączny moment M=1,29 + 0,82 =2,11kNm

Rozpiętość kleszczy 345cm,

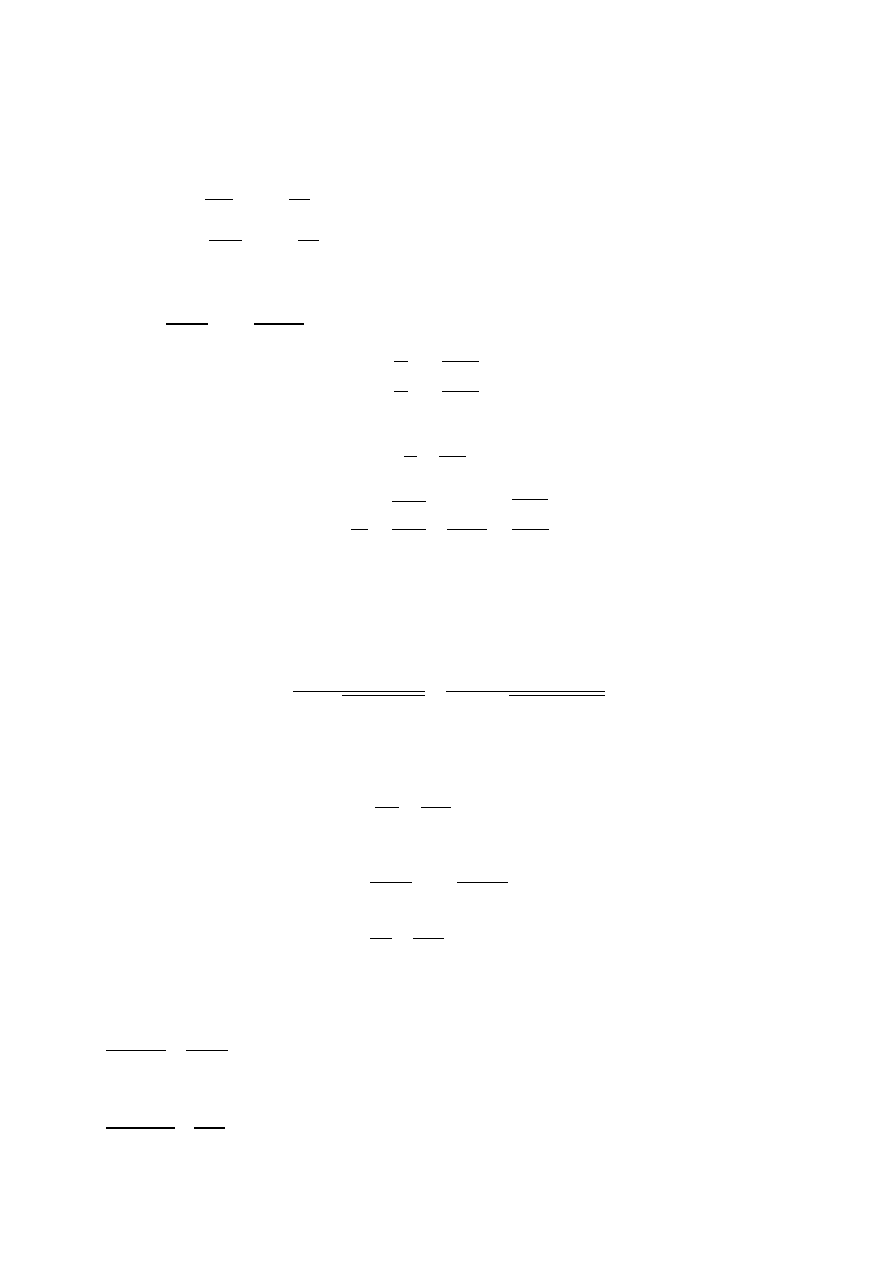
Wiązar płatwiowo-kleszczowy

ZUT, Katedra Budownictwa Ogólnego i Konstrukcji Drewnianych, EK

A = 2 *6*18 = 216cm

2

decydujące obciążenie chwilowe – człowiek stąd k

mod

=1,1

𝑓

𝑚,𝑑

= 𝑘

𝑚𝑜𝑑

∙

𝑓

𝑚,𝑘

𝛾

𝑀

= 1,1 ∙

24

1,3

= 20,3 𝑀𝑃𝑎

𝑓

𝑐,0,𝑑

= 𝑘

𝑚𝑜𝑑

∙

𝑓

𝑐,0,𝑘

𝛾

𝑀

= 1,1 ∙

21

1,3

= 17,77 𝑀𝑃𝑎

Sprawdzenie naprężeo z uwzględnieniem wyboczenia w płaszczyźnie z-x

𝐼

𝑦

= 2 ∗

𝑏 ∗ 𝑕

3

12

= 2 ∗

6 ∗ 18

3

12

= 5832 𝑐𝑚

4

𝑖

𝑦

=

𝐼

𝑦

𝐴

=

5832

216

= 5,2 𝑐𝑚

𝜆

𝑦

=

𝑙

𝑦

𝑖

𝑦

=

345

5,2

= 66,35

𝜆

𝑟𝑒𝑙 ,𝑦

=

𝜆

𝑦

𝜋

∙

𝑓

𝑐,0,𝑘

𝐸

0,05

=

66,35

𝜋

∙

21

7400

= 1,13

𝛽

𝑐

= 0,2 dla drewna litego

𝑘

𝑦

= 0,5 1 + 𝛽

𝑐

𝜆

𝑟𝑒𝑙 ,𝑦

− 0,3 + 𝜆

𝑟𝑒𝑙 ,𝑦

2

= 0,5 ∗ 1 + 0,2 1,13 − 0,3 + 1,13

2

= 1,22

𝑘

𝑐,𝑦

=

1

𝑘

𝑦

+ 𝑘

𝑦

2

− 𝜆

𝑟𝑒𝑙 ,𝑦

2

=

1

0,98 + 1,22

2

− 1,13

2

= 0,7

𝜎

𝑐,0,𝑑

=

𝑃

𝑑1

𝐴

=

8,37

216

∗ 10 = 0,39 𝑀𝑃𝑎

𝑊

𝑦

= 2 ∗

𝑏 ∗ 𝑕

2

6

= 2 ∗

6 ∗ 18

2

6

= 648 𝑐𝑚

3

𝜎

𝑚,𝑦,𝑑

=

𝑀

𝑦

𝑊

𝑦

=

2,11

648

∗ 1000 = 3,26 𝑀𝑃𝑎

𝜎

𝑐,0,𝑑

𝑘

𝑐,𝑦

𝑓

𝑐,0,𝑑

+

𝜎

𝑚,𝑦,𝑑

𝑓

𝑚,𝑦,𝑑

< 1

0,39

0,7 .17,77

+

3,26
20,3

< 1 0,19 < 1

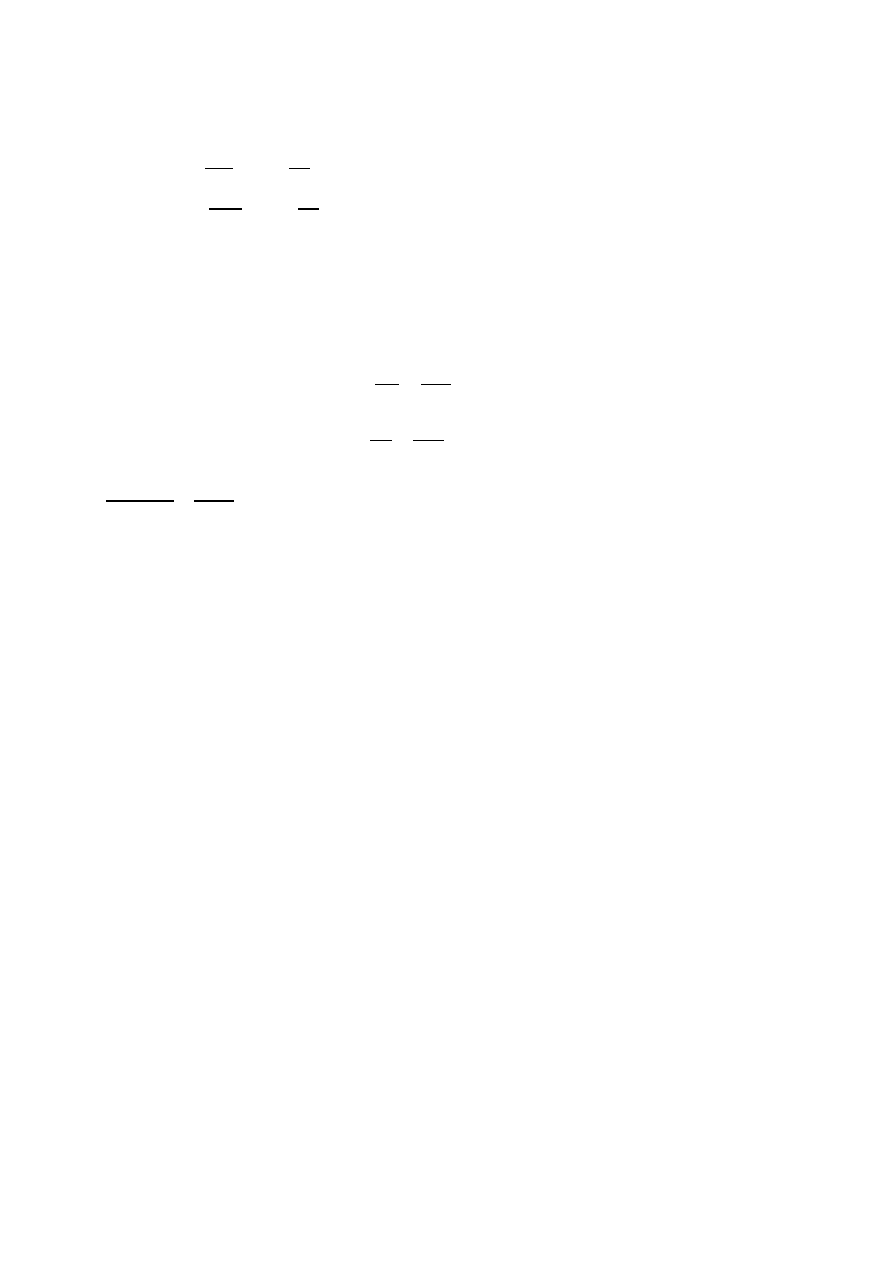
Wiązar płatwiowo-kleszczowy

ZUT, Katedra Budownictwa Ogólnego i Konstrukcji Drewnianych, EK

Dla przykładu i porównania– w przypadku sprawdzenia kombinacji występowania tylko obciążeo
stałych +i wiatr (decydujące stałe) k

mod

=0,6

𝑓

𝑚,𝑑

= 𝑘

𝑚𝑜𝑑

∙

𝑓

𝑚,𝑘

𝛾

𝑀

= 0,6 ∙

24

1,3

= 11,08 𝑀𝑃𝑎

𝑓

𝑐,0,𝑑

= 𝑘

𝑚𝑜𝑑

∙

𝑓

𝑐,0,𝑘

𝛾

𝑀

= 0,6 ∙

21

1,3

= 9,69 𝑀𝑃𝑎

Przyjmujemy tylko siłę osiową (wiatr) i moment od ocieplenia:

Siła ściskająca = reakcja pozioma od płatwi (wiązar pełny)
P

d1

= q

d2

.

l = 1,86

.

4,5 =8,37kN

Obciążenie równomiernie rozłożone (ocieplenie) q

d3

= 0,55 kN/m

Moment od obc. równomiernie rozłożonego M

qd3

=q

d3

l

2

/8 = 0,55

.

3,45

2

/8 = 0,82kNm

𝜎

𝑐,0,𝑑

=

𝑃

𝑑1

𝐴

=

8,37

216

∗ 10 = 0,39 𝑀𝑃𝑎

𝜎

𝑚,𝑦,𝑑

=

𝑀

𝑦

𝑊

𝑦

=

0,82

648

∗ 1000 = 1,27 𝑀𝑃𝑎

0,39

0,7 ∗ 9,96

+

1,27

11,08

< 1 0,17 < 1