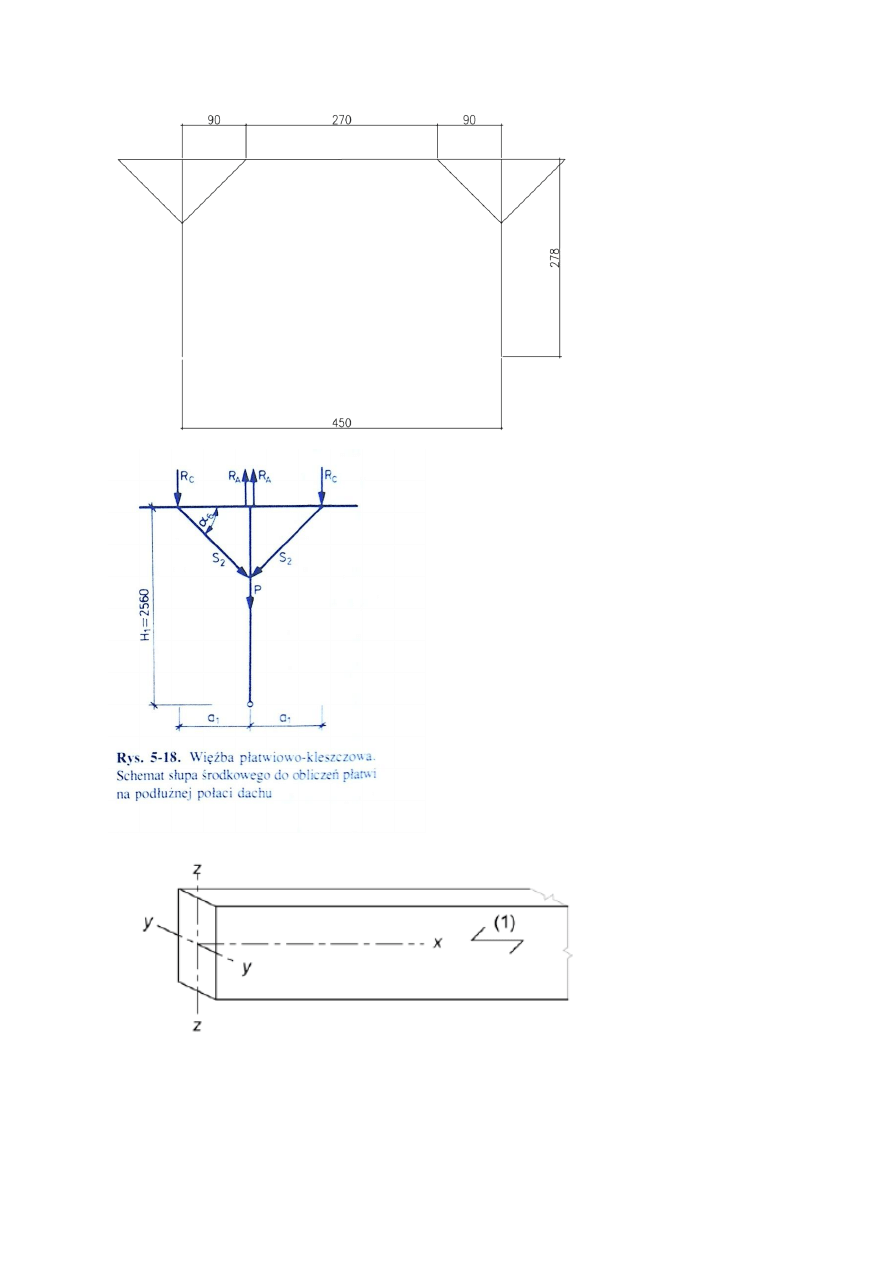
Wiązar płatwiowo-kleszczowy

ZUT, Katedra Budownictwa Ogólnego i Konstrukcji Drewnianych, EK

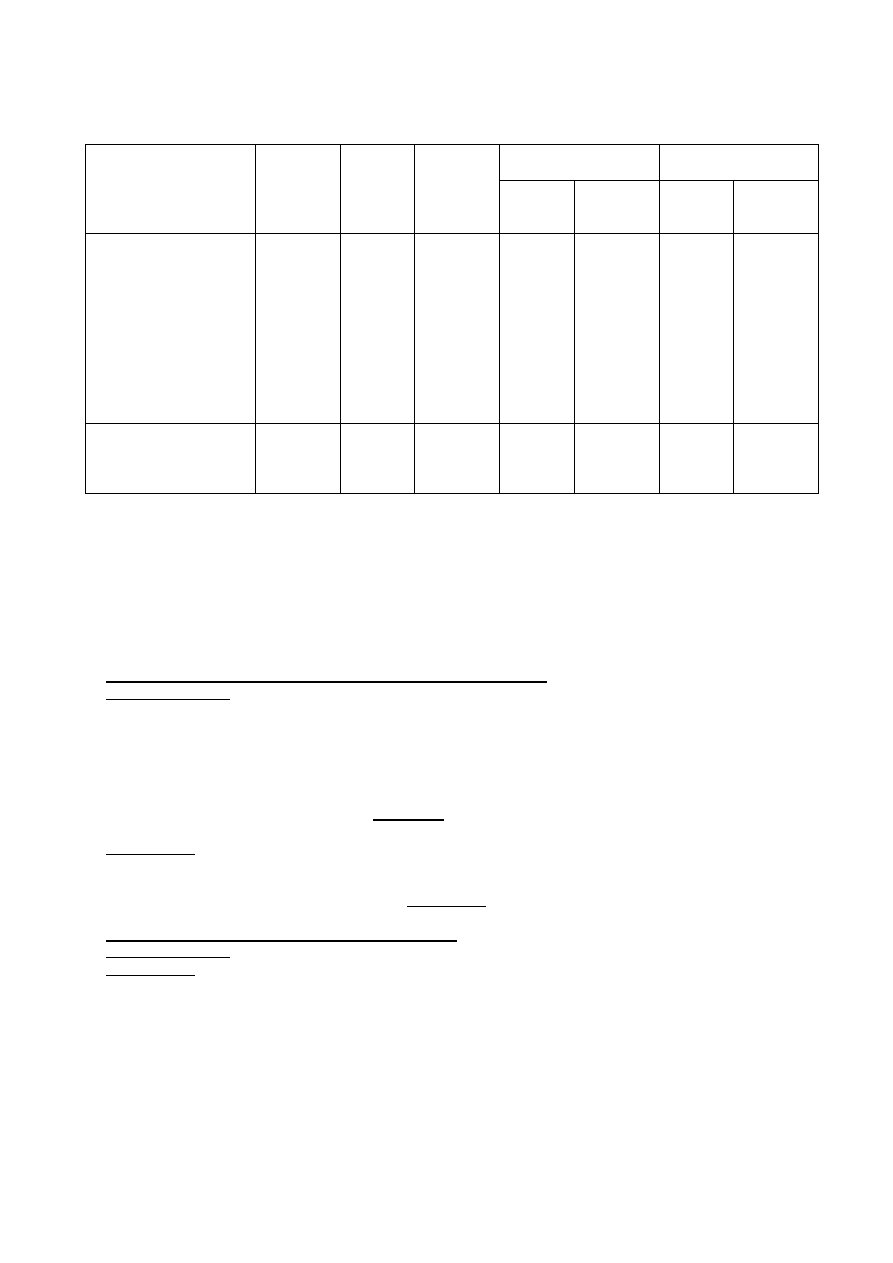
obciążenie

Wartość
charakte-
rystyczna
[kN/m

2

]

Współ-
czynnik
obciąże-
nia



f

Wartość
oblicze-
niowa
[kN/m

2

]

Składowe pionowe
obciążenia

Składowe poziome
obciążenia

Wartość
charakt.
[kN/m

2

]

Wartość
obl.
[kN/m

2

]

Wartość
charakt.
[kN/m

2

]

Wartość
obl.
[kN/m

2

]

Pokrycie 0,95

Ocieplenie i wyk.

Śnieg
Połać bardziej obc.

Wiatr
Połać nawietrzna

0,95

0,45


0,72


0,68

1,35

1,35


1,5


1,5

1,28

0,61


0,972


1,02

0,95

0,45


0,624


0,59

1,28

0,61


0,935


0,88

0,34

0,51

c. własny krokwi
c własny kleszczy

[kN/m]
0,06
0,091

1,35
1,35

[kN/m]
0,081
0,123

Wiatr

– składowa pionowa p

k

.

cos 30

o

= 0,68 x 0,866

Ciężar własny płatwi przy założeniu przekroju 180x240mm:
Charakterystyczny: 0,18x0,24 x 4,2kN/m

3

= 0,18kN/m

Obliczeniowy: 0,18 x 1,35 = 0,243kN/m

Obci

ążenie zbieramy na 1mb płatwi z całego odcinka górnego i 50% odcinka dolnego. [ q

d

(0,5l

d

+l

g

)] =

(0,5 x 3,12 + 2,08) = 3,64m oraz z połowy długości kleszczy przy ociepleniu na kleszczach 0,5

.

3,6 =

1,8m

Obciążenie pionowe maksymalne przypadające na 1mb płatwi
Charakterystyczne:
Stałe: =0,95 x (0,5 x 3,12 + 2,08) +0,45 x 0,5 x 3,12 +0,45 x 0,5 x 3,6 + 0.06 x (0,5 x 3,12 + 2,08)/0,9
+0,091 x 0,5 x 3,6/0,9 + 0,18=5,57
Śnieg =0,624 x (0,5 x 3,12 + 2,08)=2,27kN/m
Wiatr=0,59 x (0,5 x 3,12 + 2,08)=2,15kN/m
Razem maksymalne:
q

k1

=(0,95+0,624+0,59) x (0,5 x 3,12 + 2,08) +0,45 x 0,5 x 3,12 +0,45 x 0,5 x 3,6 + 0.06 x (0,5 x 3,12 +

2,08)/0,9 +0,091 x 0,5 x 3,6/0,9 + 0,18= 9,99 kN/m

Obliczeniowe:
Razem maksymalne
q

d1

=(1,28+0,935+0,88) x (0,5 x 3,12 + 2,08) +0,61 x 0,5 x 3,12 + 0,61 x 0,5 x 3,6 + 0.081 x (0,5 x 3,12

+ 2,08)/0,9 + 0,123 x 0,5 x 3,6 / 0,9 + 0,243= 14,13 kN/m

Obciążenia poziome maksymalne na 1 mb płatwi:
Charakterystyczne: q

k2

= 0,34 x (0,5 x 3,12 + 2,08) =1,24 kN/m

Obliczeniowe: q

d2

= 0,51 x (0,5 x 3,12 + 2,08) =1,86 kN/m

Wiązar płatwiowo-kleszczowy

ZUT, Katedra Budownictwa Ogólnego i Konstrukcji Drewnianych, EK

Przyjęto płatew 180x240mm, odległość podparcia mieczami a

1

= 90cm, stąd odległość między

punktami podparcia płatwi mieczami l

1

= 270cm.

Wiązar płatwiowo-kleszczowy

ZUT, Katedra Budownictwa Ogólnego i Konstrukcji Drewnianych, EK

Stosunek rozpiętości pomiędzy mieczami a odległością podparcia mieczem
m = l

1

/a

1

=270/90=3

Moment w punkcie C:
W płaszczyźnie x-z
M

Cy

=(-q

d1

.

a

1

2

/4)

.

[(1+m

3

)/(2+3m)]=(-14,13

.

0,9

2

/4)

.

[(1+3

3

) / (2+3

.

3)] = -7,28kNm

W płaszczyźnie x-y
R

y

= q

d2

.

l/2 = 1,86

.

4,5/2 = 4,19kN

M

Cz

= R

y

.

a

1

– q

d2

.

a

1

2

.

0,5 = 4,19

.

0,9

– 1,86

.

0,9

2

.

0,5 =3,02 kNm

Reakcja w pkt C:
R

Cz

= R + M

C

/a

1

= q

d1

(a

1

+l

1

)/2 +|M

C

|/a

1

=14,13 (0,9+2,7)/2 +7,28/0,9 =33,52kN

Reakcja podporowa nad słupem od obciążenia pionowego
R

Az

= (q

d1

.

a

1

/2)- lM

C

l / a

1

= (14,13

.

0,9/2 )

– 7,28 / 0,9 = -1,73kN

Siła ściskająca w mieczu
S

2

= R

C

/ sin 45

o

=33,52 / 0,7071 = 47,4kN

Siła w słupie
P = 2S

2

.

cos (90

o

-45

o

)

– 2R

Az

= 2

.

47,4

.

cos45

o

– 2

.

1,73 = 63,6kN

Siła ściskająca w płatwi między punktami podparcia mieczami (odcinek o dł 270 cm)
S

1

=S

2

cos 45

o

= R

C

ctg 45

o

=R

C

.

1 =33,52kN

Moment w przęśle l

1

bez uwzględnienia momentu od mimośrodowego działania siły S

1

.

M

y

= q

d1

.

l

2

/8

– R

Cz

.

a

1

= 14,13

.

4,5

2

/8

– 33,52

.

0,9 = 5,6kNm

M

z

= q

d2

.

l

2

/8 = 1,86

.

4,5

2

/8 = 4,71kNm

Sprawdzenie płatwi w przęśle
M

y

= 5,6 kNm, M

z

= 4,71 kNm S

1

= 33,52kN

𝑓

𝑚,𝑑

= 𝑘

𝑚𝑜𝑑

∙

𝑓

𝑚,𝑘

𝛾

𝑀

= 0,6 ∙

24

1,3

= 11,08 𝑀𝑃𝑎

𝑓

𝑐,0,𝑑

= 𝑘

𝑚𝑜𝑑

∙

𝑓

𝑐,0,𝑘

𝛾

𝑀

= 0,6 ∙

21

1,3

= 9,69 𝑀𝑃𝑎

𝑓

𝑡,0,𝑑

= 𝑘

𝑚𝑜𝑑

∙

𝑓

𝑡,0,𝑘

𝛾

𝑀

= 0,6 ∙

14

1,3

= 6,46 𝑀𝑃𝑎

A = bh = 18

.

24 = 432 cm

2

𝐼

𝑦

=

𝑏 ∗ ℎ

3

12

=

18 ∗ 24

3

12

= 20736 𝑐𝑚

4

𝑖

𝑦

=

𝐼

𝑦

𝐴

=

20736

432

= 6,93 𝑐𝑚

𝜆

𝑦

=

𝑙

𝑦

𝑖

𝑦

=

270

6,93

= 38,96

Wiązar płatwiowo-kleszczowy

ZUT, Katedra Budownictwa Ogólnego i Konstrukcji Drewnianych, EK

𝜆

𝑟𝑒𝑙 ,𝑦

=

𝜆

𝑦

𝜋

∙

𝑓

𝑐,0,𝑘

𝐸

0,05

=

38,96

𝜋

∙

21

7400

= 0,66

𝐼

𝑧

=

ℎ ∗ 𝑏

3

12

=

24 ∗ 18

3

12

= 11664 𝑐𝑚

4

𝑖

𝑧

=

𝐼

𝑧

𝐴

=

11664

432

= 5,2 𝑐𝑚

𝜆

𝑧

=

𝑙

𝑧

𝑖

𝑧

=

450

5,2

= 86,54

𝜆

𝑟𝑒𝑙 ,𝑧

=

𝜆

𝑧

𝜋

∙

𝑓

𝑐,0,𝑘

𝐸

0,05

=

86,54

𝜋

∙

21

7400

= 1,47

Ponieważ smukłości względem osi z i y > 0,3 obliczenia przeprowadza się dla wzorów poniższych:

𝜎

𝑐,0,𝑑

𝑘

𝑐,𝑦

𝑓

𝑐,0,𝑑

+

𝜎

𝑚,𝑦,𝑑

𝑓

𝑚,𝑦,𝑑

+ 𝑘

𝑚

𝜎

𝑚,𝑧,𝑑

𝑓

𝑚,𝑧,𝑑

< 1

𝜎

𝑐,0,𝑑

𝑘

𝑐,𝑧

𝑓

𝑐,0,𝑑

+ 𝑘

𝑚

𝜎

𝑚,𝑦,𝑑

𝑓

𝑚,𝑦,𝑑

+

𝜎

𝑚,𝑧,𝑑

𝑓

𝑚,𝑧,𝑑

< 1

𝛽

𝑐

= 0,2 dla drewna litego (współczynnik dotyczący prostoliniowości elementów -6.29)

𝑘

𝑦

= 0,5 1 + 𝛽

𝑐

𝜆

𝑟𝑒𝑙 ,𝑦

− 0,3 + 𝜆

𝑟𝑒𝑙 ,𝑦

2

= 0,5 ∗ 1 + 0,2 0,66 − 0,3 + 0.66

2

= 0,75

𝑘

𝑐,𝑦

=

1

𝑘

𝑦

+ 𝑘

𝑦

2

− 𝜆

𝑟𝑒𝑙 ,𝑦

2

=

1

0,75 + 0.75

2

− 0,66

2

= 0,9

𝑘

𝑧

= 0,5 1 + 𝛽

𝑐

𝜆

𝑟𝑒𝑙 ,𝑧

− 0,3 + 𝜆

𝑟𝑒𝑙 ,𝑧

2

= 0,5 ∗ 1 + 0,2 1,47 − 0,3 + 1.47

2

= 1,7

𝑘

𝑐𝑧,

=

1

𝑘

𝑧

+ 𝑘

𝑧

2

− 𝜆

𝑟𝑒𝑙 ,𝑧

2

=

1

1,7 + 1,7

2

− 1,47

2

= 0,39

Wg 6.1.6:
Dla elementów z drewna litego, drewna klejonego warstwowo oraz LVL:
- dla przekrojów prostokątnych: k

m

= 0,7,

- dla innych przekrojów:

k

m

= 1,0.

𝜎

𝑐,0,𝑑

=

𝑆

1

𝐴

=

33,52

432

∗ 10 = 0,78 𝑀𝑃𝑎

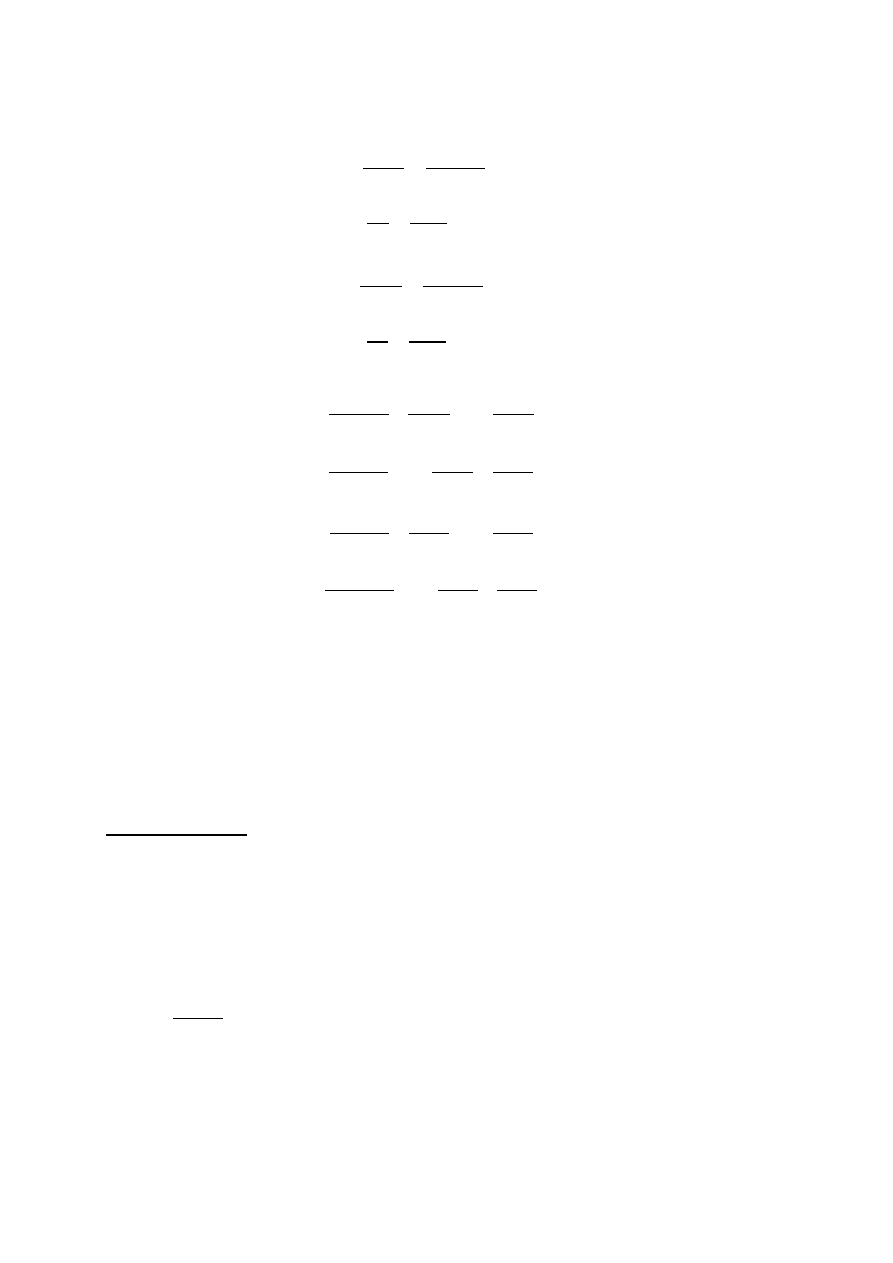
Wiązar płatwiowo-kleszczowy

ZUT, Katedra Budownictwa Ogólnego i Konstrukcji Drewnianych, EK

𝑊

𝑦

=

𝑏 ∗ ℎ

2

6

=

18 ∗ 24

2

6

= 1728𝑐𝑚

3

𝜎

𝑚,𝑦,𝑑

=

𝑀

𝑦

𝑊

𝑦

=

5,6

1728

∗ 1000 = 3,24 𝑀𝑃𝑎

𝑊

𝑧

=

ℎ ∗ 𝑏

2

6

=

24 ∗ 18

2

6

= 1296 𝑐𝑚

3

𝜎

𝑚,𝑧,𝑑

=

𝑀

𝑧

𝑊

𝑧

=

4,71

1296

∗ 1000 = 3,63 𝑀𝑃𝑎

𝜎

𝑐,0,𝑑

𝑘

𝑐,𝑦

𝑓

𝑐,0,𝑑

+

𝜎

𝑚,𝑦,𝑑

𝑓

𝑚,𝑦,𝑑

+ 𝑘

𝑚

𝜎

𝑚,𝑧,𝑑

𝑓

𝑚,𝑧,𝑑

< 1

𝜎

𝑐,0,𝑑

𝑘

𝑐,𝑧

𝑓

𝑐,0,𝑑

+ 𝑘

𝑚

𝜎

𝑚,𝑦,𝑑

𝑓

𝑚,𝑦,𝑑

+

𝜎

𝑚,𝑧,𝑑

𝑓

𝑚,𝑧,𝑑

< 1

0,78

0,9 .9,69

+

3,24

11,08

+ 0,7

3,63

11.08

< 1

0,78

0,39 .9,69

+ 0,7

3,24

11,08

+

3,63

11,08

< 1

0,61 < 1

0,74 < 1

Warunek nośności został spełniony

Zwichrzenie płatwi

W przypadku elementów z drewna iglastego o przekroju prostokątnym, σ

m,crit

należy obliczad ze

wzoru:

05

0

2

crit

m,

78

0

,

ef

E

h

b

,

σ





(6.32)

Wiązar płatwiowo-kleszczowy

ZUT, Katedra Budownictwa Ogólnego i Konstrukcji Drewnianych, EK

(3) W przypadku, gdy belka jest obciążona wyłącznie momentem M

y

(y

– oś przekroju,

względem której sztywność belki ma największą wartość), naprężenia powinny spełniać
następujący warunek:

d

m,

crit

d

m,

f

k

σ



(6.33)

gdzie:

σ

m,d

jest obliczeniowym naprężeniem zginającym,

f

m,d

jest obliczeniową wytrzymałością na zginanie,

k

crit

jest współczynnikiem uwzględniającym redukcję wytrzymałości ze względu na zwichrowanie

elementu.


L

ef

zgodnie z tablicą 6.1

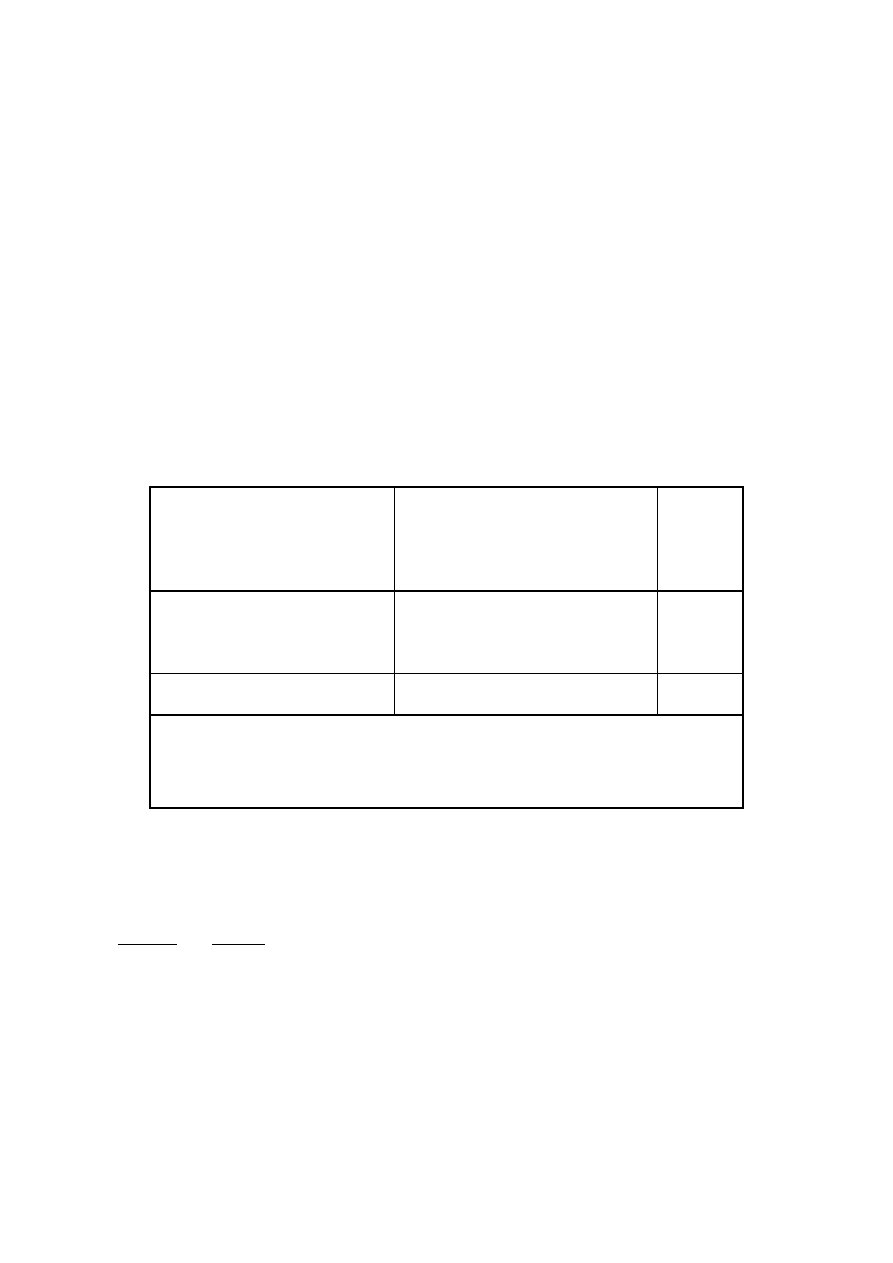
Tablica 6.1 – Długośd efektywna określona w stosunku do długości rzeczywistej

Rodzaj belki

Rodzaj obciążenia





/

ef

*

)

Swobodnie podparta

Stały moment zginający
Obciążenie równomiernie rozłożone
Obciążenie skupione w środku
rozpiętości

1,0
0,9

0,8

Wspornik

Obciążenie równomiernie rozłożone
Siła skupiona na koocu wspornika

0,5
0,8

*

)

Wartości stosunku długości efektywnej ℓ

ef

do długości rzeczywistej ℓ dotyczą belek podpartych w

sposób ograniczający możliwośd skręcania i obciążonych w osi środkowej belki. W przypadku obciążeo
przyłożonych do górnej powierzchni belki, obliczoną wartośd ℓ

ef

należy zwiększyd o 2h, a w przypadku

obciążeo przyłożonych do dolnej powierzchni belki – zmniejszyd o 0,5h, gdzie h - wysokośd belki.

(6) W przypadku obciążenia momentem zginającym M

y

(y – oś przekroju, względem której sztywnośd

belki ma największą wartośd), oraz siłą osiową Nc, naprężenia powinny spełniad następujący
warunek:

1

d

c,

d

c,

2

d

m,

crit

d

m,



















f

k

σ

f

k

σ

z

,

c

(6.35)

gdzie:

σ

m,d

jest obliczeniowym naprężeniem zginającym,

σ

c,d

jest obliczeniowym naprężeniem ściskającym,

f

m,d

jest obliczeniową wytrzymałością na zginanie,

f

c,0,d

jest obliczeniową wytrzymałością na ściskanie wzdłuż włókien,

k

c,z

jest współczynnikiem wyznaczanym ze wzoru (6.26).

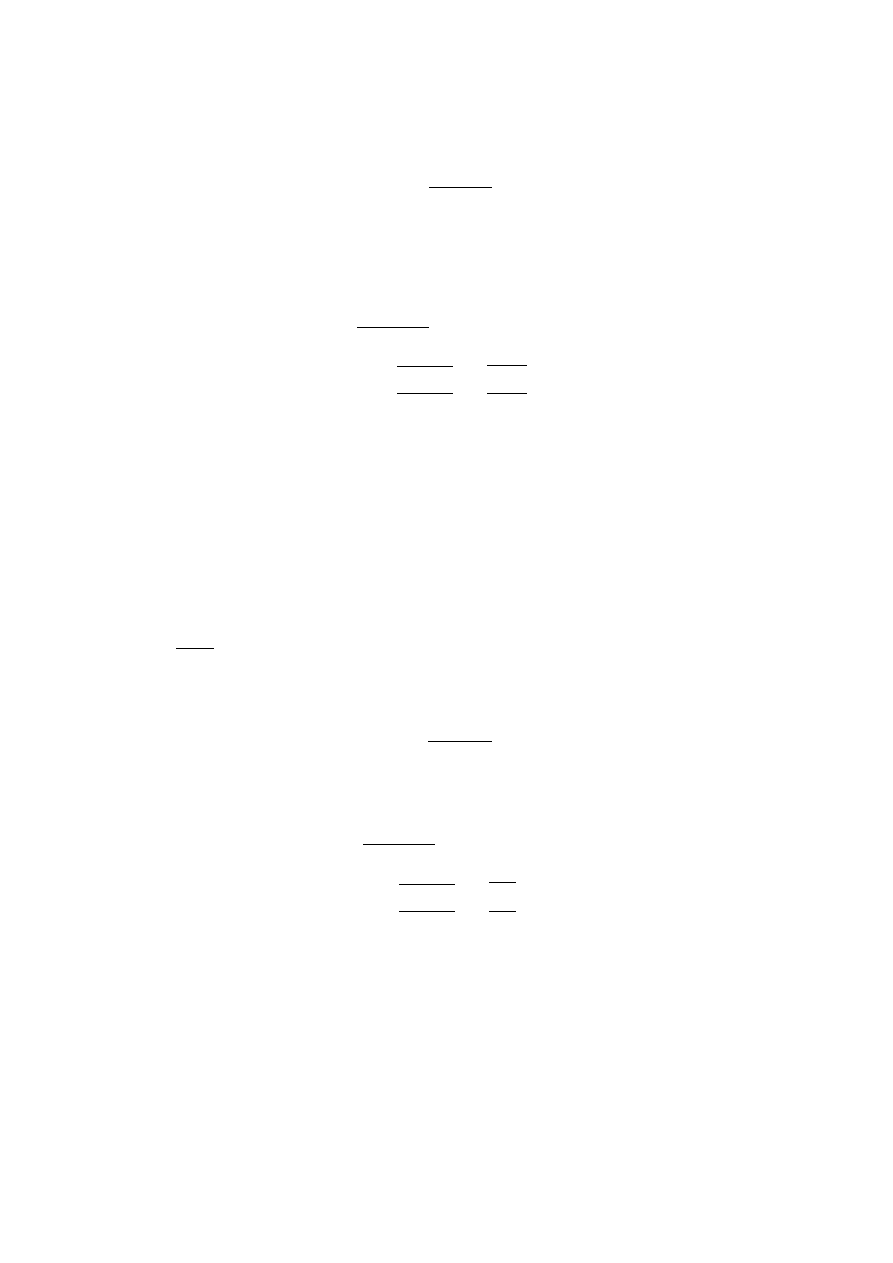
Wiązar płatwiowo-kleszczowy

ZUT, Katedra Budownictwa Ogólnego i Konstrukcji Drewnianych, EK

E

0,05

=7,4GPa

𝜎

𝑚,𝑐𝑟𝑖𝑡 ,𝑦

=

0,78 ∗ 𝑏

2

ℎ ∗ 𝑙

𝑒𝑓 ,𝑦

∗ 𝐸

0,05

𝑙

𝑒𝑓 ,𝑦

= 𝑙

𝑦

∗ 0,9 + 2 ∗ ℎ = 270 ∗ 0,9 + 2 ∗ 24 = 291𝑐𝑚

𝜎

𝑚,𝑐𝑟𝑖𝑡 ,𝑦

=

0,78 ∗ 18

2

24 ∗ 291

∗ 7,4 ∗ 1000 = 267,8𝑀𝑃𝑎

𝜆

𝑟𝑒𝑙 ,𝑚

=

𝑓

𝑚,𝑘

𝜎

𝑚,𝑐𝑟𝑖𝑡 ,𝑦

=

24

267,8

= 0,3

λ

rel,y

Smukłośd sprowadzona przy zginaniu względem osi y

Stąd zgodnie z 6.34 możemy przyjąd k

crity

= 1























2

m

rel,

m

rel,

m

crit,

1

75

0

56

1

1

λ

λ

,

,

k

𝜎

𝑚,𝑐𝑟𝑖𝑡 ,𝑧

=

0,78 ∗ ℎ

2

𝑏 ∗ 𝑙

𝑒𝑓

∗ 𝐸

0,05

𝑙

𝑒𝑓

= 𝑙

𝑧

∗ 0,9 + 2 ∗ 𝑏 = 450 ∗ 0,9 + 2 ∗ 18 = 441𝑐𝑚

𝜎

𝑚,𝑐𝑟𝑖𝑡 ,𝑧

=

0,78 ∗ 24

2

18 ∗ 441

∗ 7,4 ∗ 1000 = 418𝑀𝑃𝑎

𝜆

𝑟𝑒𝑙 ,𝑚

=

𝑓

𝑚,𝑘

𝜎

𝑚,𝑐𝑟𝑖𝑡 ,𝑦

=

24

418

= 0,24

𝑘

𝑐𝑟𝑖𝑡𝑧

= 1

dla

λ

rel,m

≤ 0,75

dla

0,75 < λ

rel,m

≤ 1,4

(6.34)

dla

λ

rel,m

> 1,4

Wiązar płatwiowo-kleszczowy

ZUT, Katedra Budownictwa Ogólnego i Konstrukcji Drewnianych, EK

Obliczenie ugięcia

k

def

= 0,8 dla klasy 2 użytkowania wg tablicy 3.2

E

0,mean

= 11,0 GPa = 1100

.

10

4

kN/m

2

I

y

=20736cm

4

= 2,0736 x10

-4

m

4

I

z

=11664cm

4

= 1,1664 x10

-4

m

4

𝑢

𝑖𝑛𝑠𝑡

=

5 ∗ 𝑞 ∗ 𝑙

𝑦

4

384 ∗ 𝐸

𝑚𝑒𝑎𝑛

∗ 𝐼

𝑦

𝑢

𝑖𝑛𝑠𝑡

=

5 ∗ 𝑞 ∗ 𝑙

𝑧

4

384 ∗ 𝐸

𝑚𝑒𝑎𝑛

∗ 𝐼

𝑧

stałe (pion)

𝑢

𝑖𝑛𝑠𝑡 ,1

= 1,7𝑚𝑚

𝑢

𝑓𝑖𝑛 ,1

= 𝑢

𝑖𝑛𝑠𝑡 ,1

∗ (1 + 𝑘

𝑑𝑒𝑓

) = 1,7 ∗ (1 + 0,8) = 3,06𝑚𝑚

śnieg (pion)

𝑢

𝑖𝑛𝑠𝑡 ,2

= 0,7𝑚𝑚

𝑢

𝑓𝑖𝑛 ,2

= 𝑢

𝑖𝑛𝑠𝑡 ,2

∗ (1 + 𝜓

2

∗ 𝑘

𝑑𝑒𝑓

) = 0,7 ∗ (1 + 0,2 ∗ 0,8) = 0,81𝑚𝑚

wiatr (pion)

𝑢

𝑖𝑛𝑠𝑡 ,3

= 0,7𝑚𝑚

𝑢

𝑓𝑖𝑛 ,3

= 𝑢

𝑖𝑛𝑠𝑡 ,3

∗ (𝜓

0

+ 𝜓

2

∗ 𝑘

𝑑𝑒𝑓

) = 0,7 ∗ (0,6 + 0,0 ∗ 0,8) = 0,42𝑚𝑚

wiatr (poziom)

𝑢

𝑖𝑛𝑠𝑡 ,4

= 5,2𝑚𝑚

𝑢

𝑓𝑖𝑛 ,4

= 𝑢

𝑖𝑛𝑠𝑡 ,4

∗ (𝜓

0

+ 𝜓

2

∗ 𝑘

𝑑𝑒𝑓

) = 5,2 ∗ (0,6 + 0,0 ∗ 0,8) = 3,12𝑚𝑚

Suma

𝑢

𝑓𝑖𝑛

= (𝑢

𝑓𝑖𝑛 ,1

+ 𝑢

𝑓𝑖𝑛 ,2

+ 𝑢

𝑓𝑖𝑛 ,3

)

2

+ 𝑢

𝑓𝑖𝑛 ,4

2

= (3.06 + 0,81 + 0,42)

2

+ 3,12

2

= 5,3𝑚𝑚

u

fin

= 5,3 mm < u

net,fin

= 2700 / 200 = 13,5 mm

Warunek ugięcia został spełniony