Błędy przypadkowe

To błędy zmieniające się w sposób nieprzewidziany zarówno co do wartości bezwzględnej, jak i
znaku przy wykonywaniu dużej liczby pomiarów tej samej wartości pewnej wielkości
w warunkach pozornie niezmiennych.

Rozproszenie wyników pomiarów powtarzanych w pozornie tych samych warunkach świadczy o
obecności błędów przypadkowych (tzw. losowych).
W praktyce założenie o niezmienności warunków fizycznych pomiaru, obiektu, narzędzi
pomiarowych nie jest spełnione.

Ź

ródła błędów są niestałe w czasie i w przestrzeni.

Wyeliminowanie błędu przypadkowego nie jest możliwe. Wartości tych błędów wyznacza się
korzystając z metod rachunku prawdopodobieństwa i statystyki matematycznej.
Zjawisk, które powodują rozproszenie wyników pomiarowych nie można opisać zależnością
„przyczyna

→ skutek”. Błędy przypadkowe modeluje się za pomocą

zmiennej losowej.

Zmienna losowa

zmienna, która przyjmuje wartości

z określonym prawdopodobieństwem

↓

↓

↓

↓

↓

↓

↓

↓

dyskretna

ciągła

Rozkład zmiennej losowej X

prawdopodobieństwo przyjmowania przez zmienną losową X wartości x

Parametry charakteryzujące rozkład zmiennej losowej X:

•

Dystrybuanta

•

Funkcja gęstości prawdopodobieństwa

•

Momenty centralne

Dystrybuanta F(x)

)

x

X

(

P

)

x

(

F

≤

=

Na podstawie dystrybuanty można wyznaczyć prawdopodobieństwo, że a

< X≤ b,

gdzie a

< b ; a, b - dowolne liczby rzeczywiste

)

a

(

F

)

b

(

F

)

b

X

a

(

P

−

=

≤

<

Funkcja gęstości prawdopodobieństwa f(x)

•

Mierzymy

n

– krotnie wartość pewnej wielkości

•

Uzyskujemy różne wyniki, które porządkujemy w ciąg liczb o charakterze rosnącym,
tj.

x

min

... x

max

•

Jeżeli niektóre z wyników występują wielokrotnie, to określamy częstość ich wystąpienia

częstość względna – informuje, jaka część spośród

n

pomiarów dała wynik

x

i

, tj.

n

n

i

•

Uzyskane wyniki można przedstawić w postaci wykresu słupkowego

•

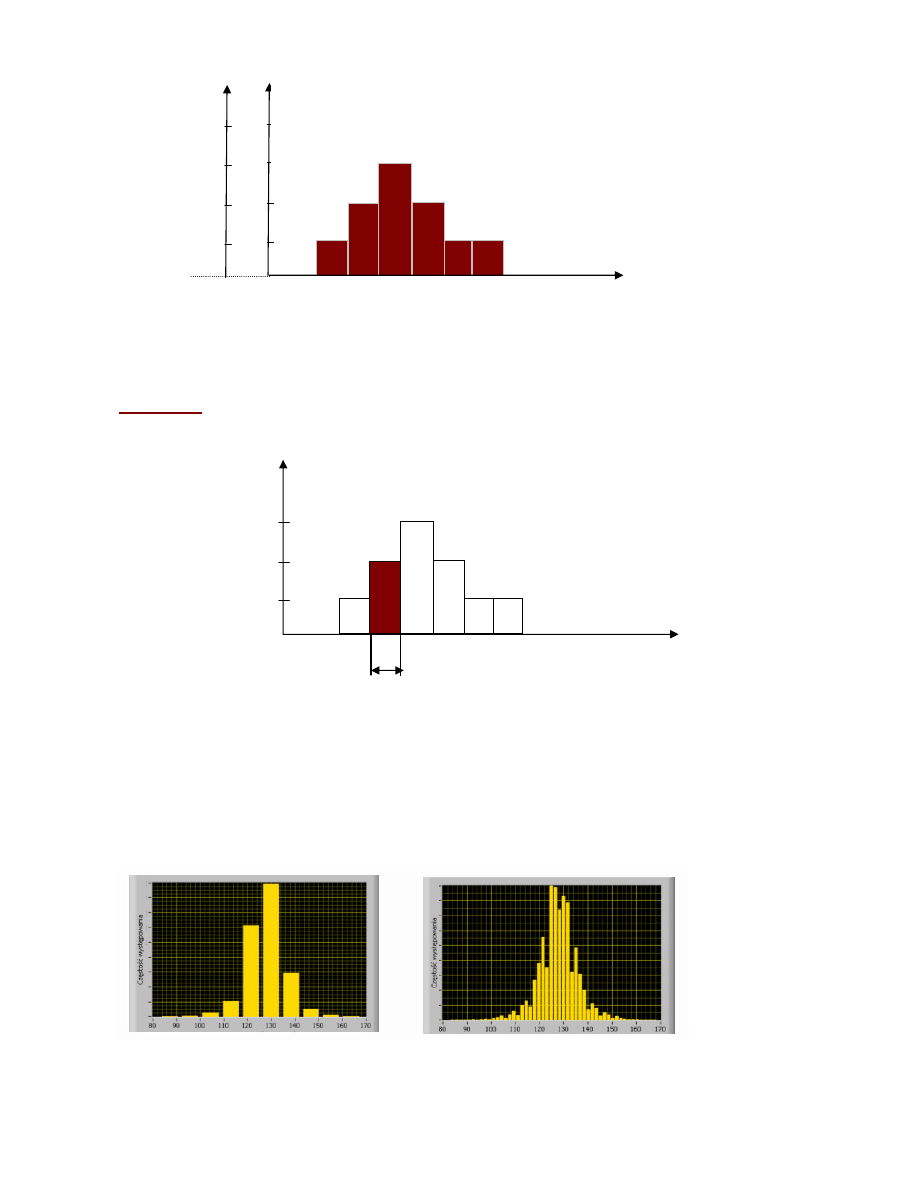
Uzyskane wyniki można zgrupować w

l

rozłącznych przedziałach (tj. komórkach, tzw.

klasach

)

o długości

∆

Xi

,

gdzie i=1, ... , l

n

i

– oznacza liczbę wyników, które trafiły do

i

-tego przedziału

Histogram

- graficzne przedstawienie rozkładu wyników pomiarów

(częstość występowania pomiarów w klasach)

∆

Xi

Pole prostokąta jest równe częstości względnej (n

i

/n)

Problem:

Jak dobrać szerokość przedziału

∆

Xi

= ?

Jeżeli liczba pomiarów jest mała, to przedziały ∆

Xi

powinny być relatywnie „szerokie”.

W miarę wzrostu liczby pomiarów należy zmniejszać ∆

Xi

.

n=10

1

2

3

n

i

n

i

/n

0,2

0,1

x

x

∆

Xi

(n

i

/n)

⋅⋅⋅⋅ (

1

/

∆

Xi

)

0,3

Gdy n

→ ∞ , to ∆

Xi

→ 0,

a

histogram

upodabnia się do gładkiej krzywej ciągłej, która jest

wykresem funkcji opisującej rozkład zmiennej losowej ciągłej, tj. funkcji gęstości
prawdopodobieństwa f(x)

Funkcja gęstości prawdopodobieństwa f(x)

x

x

0

∆

∆

)

∆

x

X

x

(

P

)

x

(

f

lim

x

+

<

<

=

→

∫

+∞

∞

−

=

=

dx

)

x

(

f

)

x

(

F

;

dx

)

x

(

dF

)

x

(

f

Momenty centralne

•

Wartość oczekiwana

zmiennej losowej X

∫

∑

∞

+

∞

−

=

⋅

=

⋅

=

=

dx

)

x

(

f

x

p

x

µ

)

X

(

E

i

n

1

i

i

Wartość oczekiwana jest miarą skupienia rozkładu

•

Wariancja

zmiennej losowej X

∫

∑

∞

+

∞

−

=

⋅

−

=

−

=

−

=

=

dx

)

x

(

f

]

µ

x

[

p

]

µ

x

[

)]

X

(

E

X

[

E

σ

)

X

(

D

2

i

2

n

1

i

i

2

2

2

Wariancja jest miarą rozproszenia rozkładu wokół wartości oczekiwanej

Odchylenie standardowe

(sigma σ)

)

X

(

D

σ

2

+

=

Rozkład normalny – rozkład Gaussa

Do rozkładu normalnego prowadzi taki proces kształtowania zjawiska, w ramach którego na dane
zjawisko oddziałowywuje duża liczba niezależnych czynników, których wpływ, traktowany
odrębnie, jest mało znaczący.

Zmienna losowa X ma rozkład normalny o parametrach

µ

i

σ

, co w skrócie zapisujemy jako

X:N(µ ,σ)

jeśli jej funkcja gęstości prawdopodobieństwa wyraża się wzorem

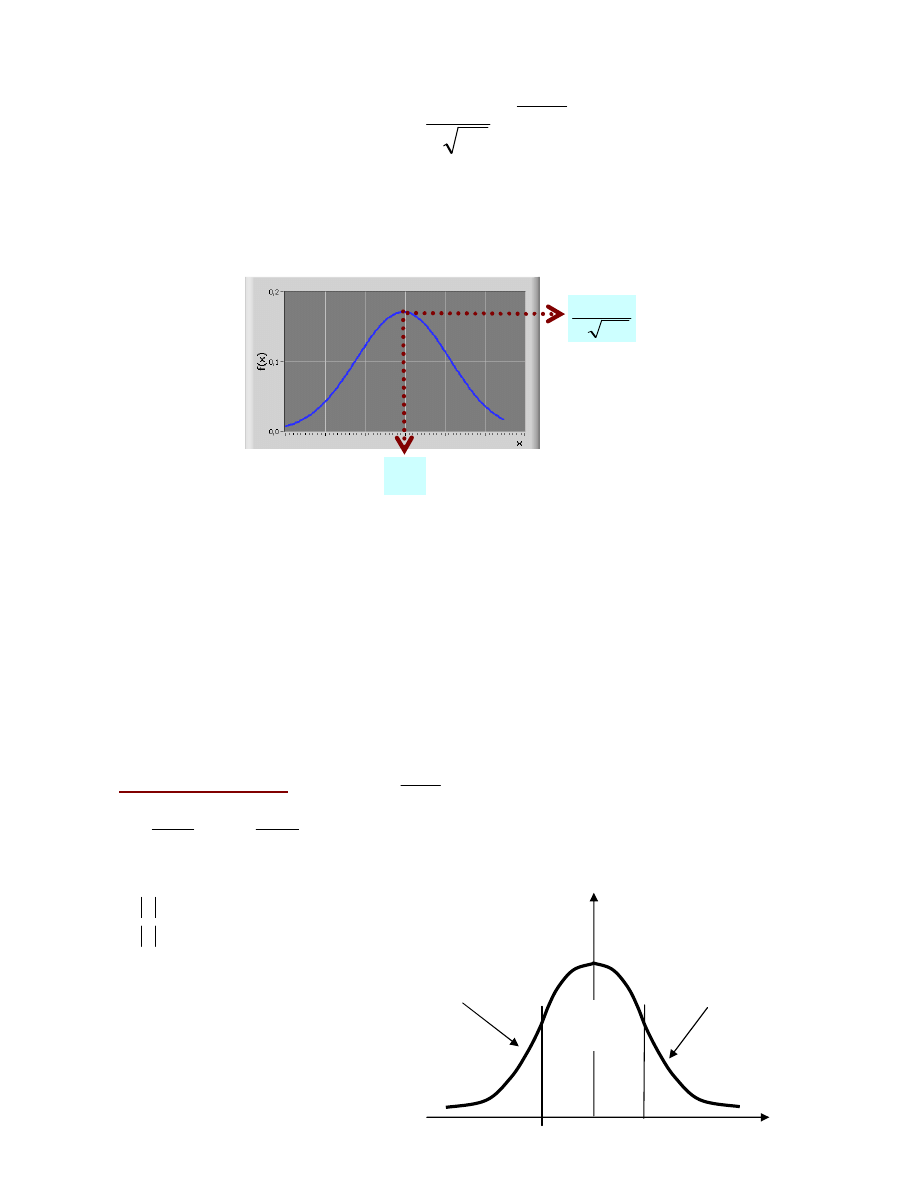
2

2

σ

2

)

µ

x

(

e

π

2

σ

1

)

x

(

f

−

−

=

gdzie -

∞< x <∞ , σ >0

W rozkładzie normalnym
-

wartość oczekiwana:

E(x) =

µ

-

wariancja

D

2

(X) =

σ

2

Rozkład normalny z

µ=0 oraz σ=1 nazywa się

standardowym rozkładem normalnym N(0,1)

Często zmienną losową mającą taki rozkład oznacza się jako Z (lub U).
Wartości funkcji gęstości

ϕ(z) – funkcji Gaussa

i wartości dystrybuanty

Φ(z) –funkcji Laplace’a

są

stabelaryzowane.

Problem:

Jak określić prawdopodobieństwo

P(x

1

< X ≤ x

2

) = ?

gdy

X: N(

µ,σ)

Prawdopodobieństwo, że wynik pomiaru wystąpi w przedziale (x

1

,x

2

) wynosi:

∫

=

≤

<

2

1

x

x

2

1

dx

)

x

(

f

)

x

X

x

(

P

f(x) - analitycznie niecałkowalna dla rozkładu normalnego

Operacja standaryzacji

:

σ

σσ

σ

µ

µµ

µ

−

−−

−

=

==

=

x

z

σ

µ

x

z

,

σ

µ

x

z

2

2

1

1

−

=

−

=

Po tej operacji zmienna losowa Z staje się zmienną standaryzowaną i ma rozkład N(0,1)

)

(

)

(

...

)

(

1

2

2

1

z

z

x

X

x

P

Φ

Φ

Φ

Φ

−

−−

−

Φ

Φ

Φ

Φ

=

==

=

=

==

=

≤

≤≤

≤

<

<<

<

γ

α

1

)

z

Z

(

P

α

)

z

Z

(

P

α

α

=

−

=

<

=

>

α

α

α

α

poziom istotności

1-

α

α

α

α

poziom ufności

f(z)

-z

α

α

α

α

z

α

α

α

α

z

1-

α

α

α

α

½

α

α

α

α

½

α

α

α

α

µ

µ

µ

µ

π

2

σ

1

Prawdopodobieństwo występowania zmiennej losowej X w przedziale:

9973

,

0

)

3

3

(

)

95

,

0

)

2

2

(

)

68

,

0

)

(

)

=

==

=

+

++

+

<

<<

<

<

<<

<

−

−−

−

=

==

=

+

++

+

<

<<

<

<

<<

<

−

−−

−

=

==

=

+

++

+

<

<<

<

<

<<

<

−

−−

−

σ

σσ

σ

µ

µµ

µ

σ

σσ

σ

µ

µµ

µ

σ

σσ

σ

µ

µµ

µ

σ

σσ

σ

µ

µµ

µ

σ

σσ

σ

µ

µµ

µ

σ

σσ

σ

µ

µµ

µ

X

P

c

X

P

b

X

P

a

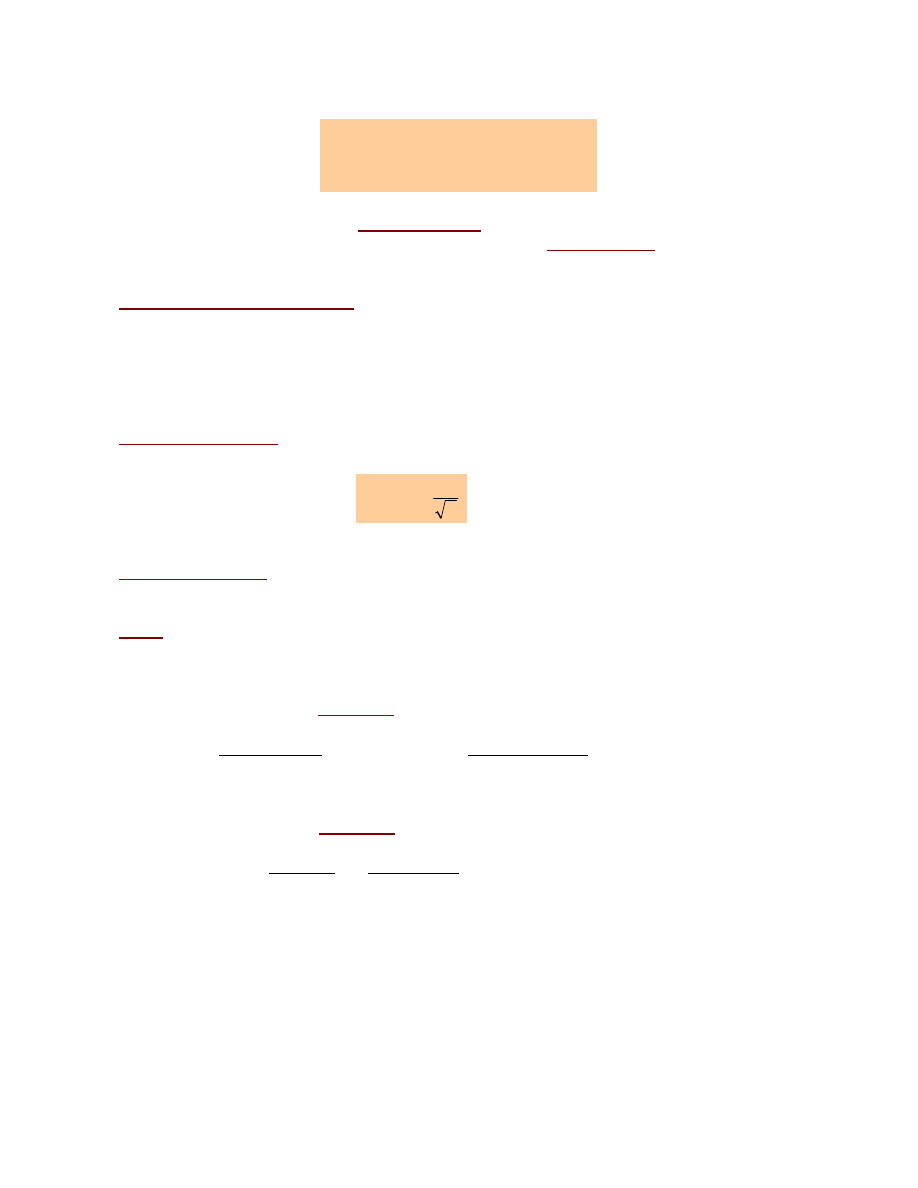
Przedział

(

µ

µµ

µ

- k

⋅⋅⋅⋅σ

σ

σ

σ

,

µ

µµ

µ

+ k

⋅⋅⋅⋅σ

σ

σ

σ

)

to tzw.

przedział ufności

Prawdopodobieństwo odpowiadające temu przedziałowi to

poziom ufności

Centralne twierdzenie graniczne

Suma dużej liczby zmiennych losowych niezależnych o dowolnych rozkładach ma rozkład normalny.

Jeżeli rozpatrywana wielkość jest wynikiem działania wielu czynników od siebie niezależnych, a
zmieniających się chaotycznie, to zmienna losowa o rozkładzie normalnym jest wiarygodnym
modelem tej wielkości.

Średnia arytmetyczna

serii losowo wybranych wartości zmiennej X o rozkładzie normalnym N

(

µ

x

,

σ

x

) jest zmienną losową o rozkładzie normalnym:

gdzie n – liczba pomiarów.

Populacja generalna

Zbiór wszystkich możliwych do uzyskania w danym pomiarze wartości x zmiennej losowej X

Próba

Zbiór wszystkich uzyskanych w danym pomiarze wartości x zmiennej losowej X
Próba – reprezentatywna, dostatecznie liczna

Estymacja

– ocena

↓

↓

parametryczna

nieparametryczna

postać funkcjonalna rozkładu - znana
parametry = ?

Estymacja

↓

↓

punktowa

przedziałowa

)

,

(

:

n

N

X

x

x

σ

σσ

σ

µ

µµ

µ

−

−−

−

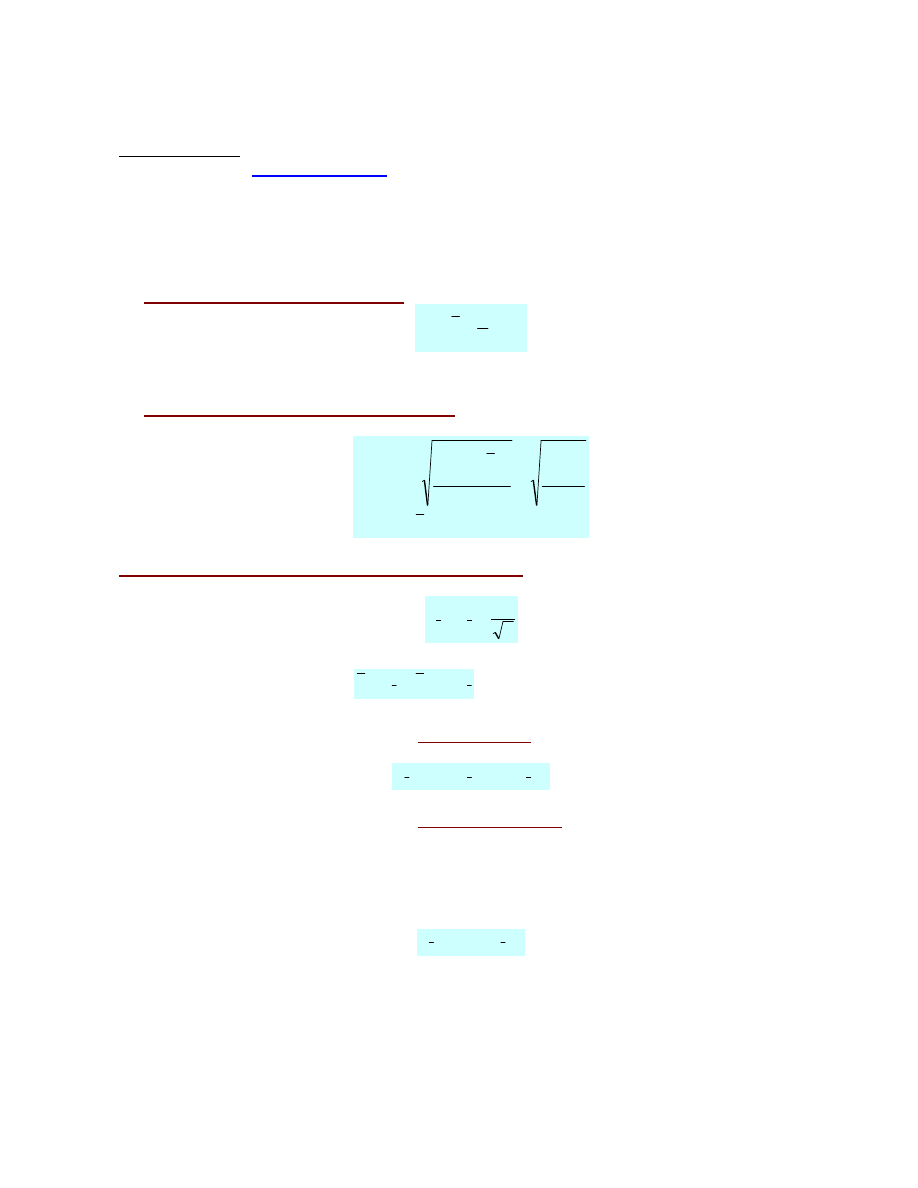
Opracowanie wyników pomiarów obarczonych błędami przypadkowymi

(błędy systematyczne zostały wyeliminowane)

Seria pomiarów:

x

1

, x

2

, x

3

, ..., x

n

Założenie:

Rozkład normalny

Wartość oczekiwana

µ

µµ

µ

x

= ?

Odchylenie standardowe

σ

σ

σ

σ

x

= ?

____________________________________________

µ

µµ

µ

x

,

σ

σ

σ

σ

x

należy oszacować na podstawie n pomiarów

Estymator wartości oczekiwanej

∑

=

=

≈

n

1

i

i

x

x

n

1

x

µ

wartość średnia

serii pomiarów jest optymalnym estymatorem wartości oczekiwanej

Estymator odchylenia standardowego -
odchylenie standardowe eksperymentalne

(

)

x

x

∆

1

n

∆

1

n

x

x

s

σ

i

i

n

1

i

2

i

n

1

i

2

i

x

x

−

=

−

=

−

−

=

≈

∑

∑

=

=

Estymator odchylenia standardowego dla średniej
odchylenie standardowe eksperymentalne średniej

n

s

s

σ

x

x

x

=

≈

Wynik końcowy pomiaru:

x

x

σ

3

x

∆

x

⋅

±

=

±

1)

liczba pomiarów

n > 20

rozkład Gaussa

dla przedziału 3-sigma, P=0,9973

x

x

x

s

3

σ

3

∆

⋅

±

≈

⋅

±

=

2)

liczba pomiarów

n < 20

rozkład t - Studenta

zmienna losowa t=f(P,n)

P - prawdopodobieństwo, n - liczba pomiarów

Odchylenie standardowe w tym rozkładzie jest większe niż

σ w rozkładzie Gaussa – w ten

sposób uwzględnia się małą liczbę pomiarów .
Gdy n > 30 rozkład Studenta

→ rozkład Gaussa

x

P

,

n

x

s

t

∆

⋅

±

≈

t

n,P

– liczba z tablic funkcji t-Studenta

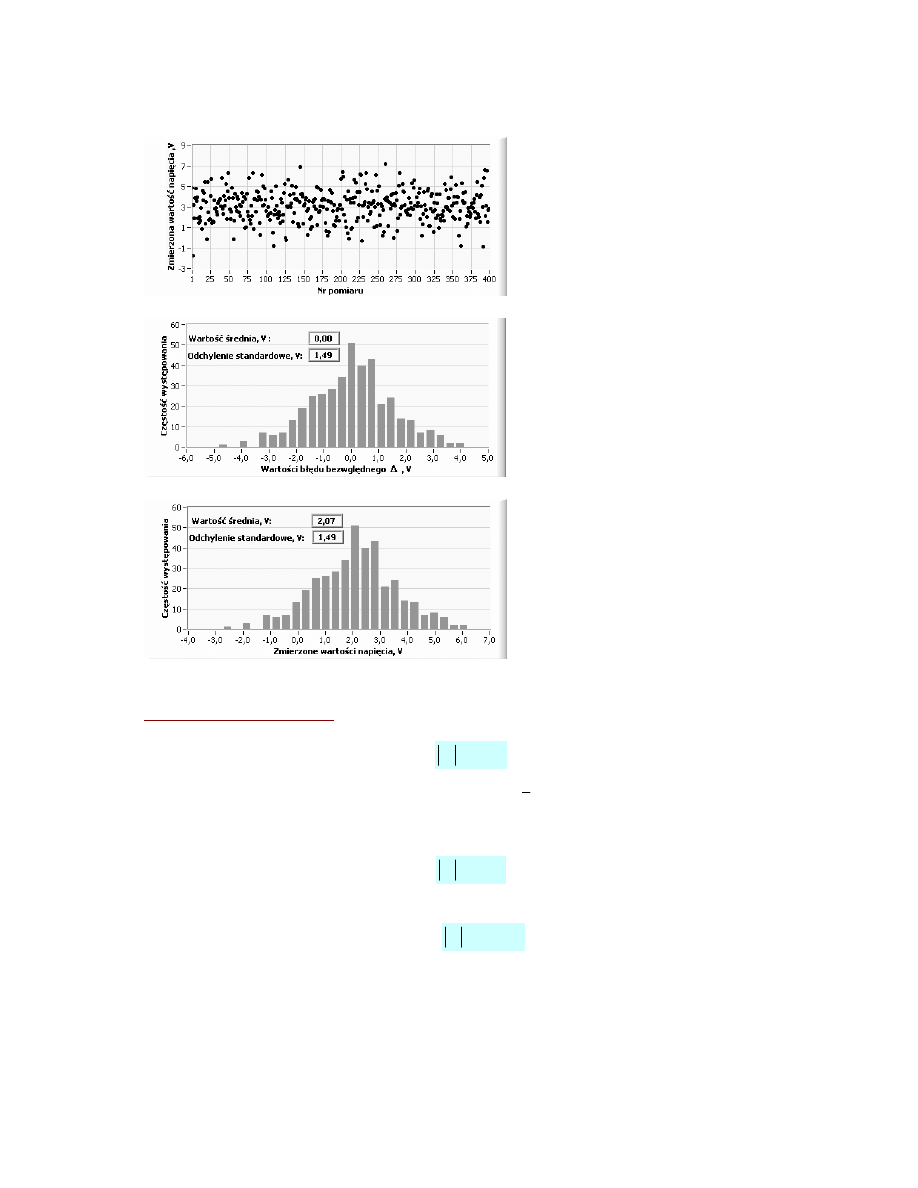
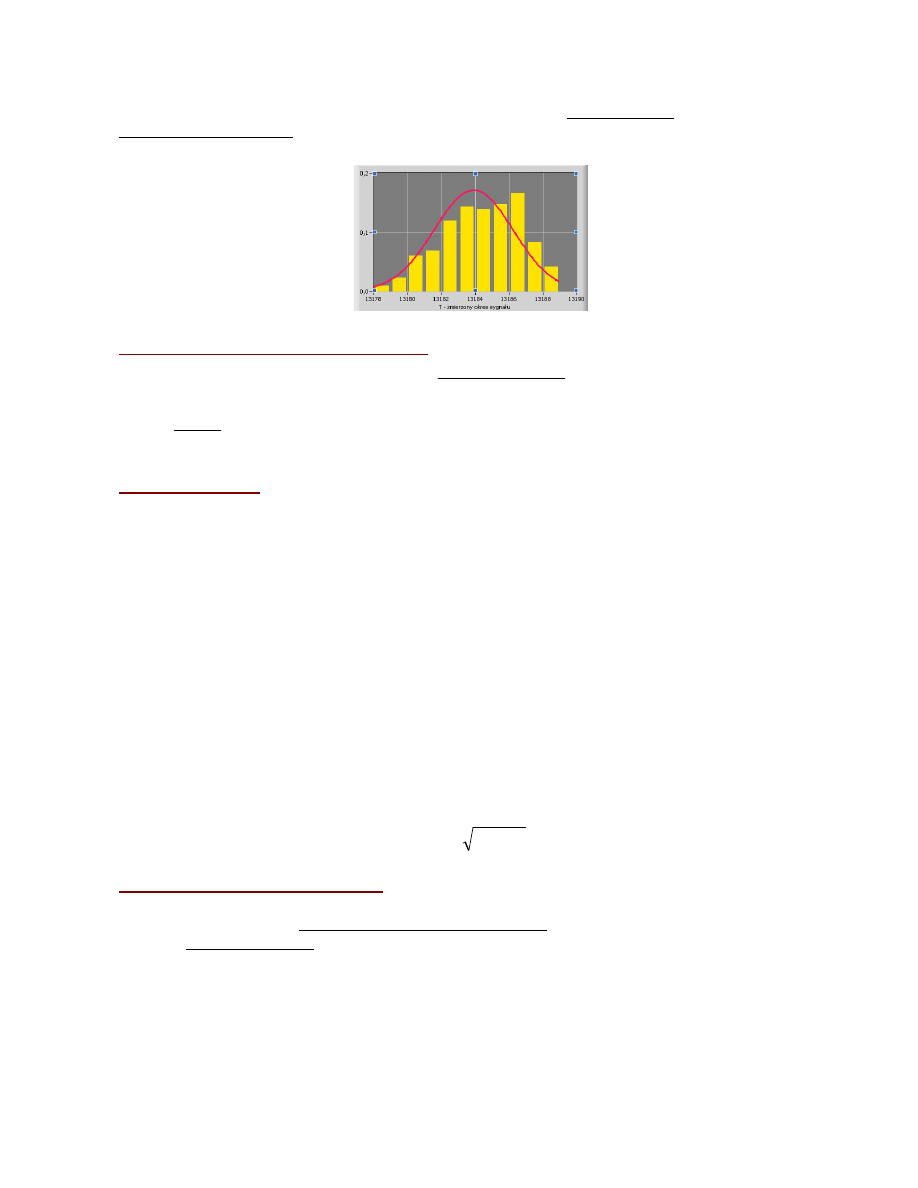
Przykład:
Pomiar wartości napięcia stałego w obecności zakłóceń losowych o rozkładzie normalnym

Wyniki pomiaru

Histogram - błędy losowe

Histogram – wyniki pomiaru

Błąd gruby (nadmierny)

Wynik pomiaru obarczony błędem grubym należy odrzucić, bo jest niewiarygodny

x

i

σ

3

∆

⋅

>

błąd przypadkowy dla i-tego pomiaru wynosi:

x

x

∆

i

i

−

=

1)

liczba pomiarów n > 20

x

i

s

3

∆

⋅

>

2)

liczba pomiarów n <20

x

P

,

n

i

s

t

∆

⋅

>