O
p
ty
k
a
f
a
lo
w
a
5
D
y
fr
ak
cj
a
Ñw
ia
t»
a
Dyfra
kcja
-
ze
sp
ó
»
z
ja
w
is
k
p
o
w
st
a
j
c
y
c
h
p
o
d
c
z
a
s
ro
zc
h
o
d
ze
n
ia
s
i
Ñw
ia
t»
a
w
o
Ñr
o
d
k
u
z
o
st
ry
m
i
niejedn
oro
Ñc
ia
m
i,
z
w
i
za
n
y
ch
z
o
d
ch
y
le
n
ia
m
i
o
d
p
ra
w
o
p
ty
k
i
g
eo
m
et
ry
cz
n
ej
.
W
sz
cz
eg
ó
ln
o
Ñc
i
d
y
fr
ak
cj
a
p
ro
w
a
d
zi
d
o
o
m
ij
an
ia
p
rz
ez
fa
le
Ñw
ie
tl
n
e
p
rz
es
zk
ó
d
i
w
n
ik
an
ia
Ñ
w
ia
t»
a
d
o
o
b
sz
ar
ó
w
c
ie
n
ia
g
eo
m
et
ry
cz
n
eg
o
.
D
y
fr
ak
cj
a
a
in
te
rf
er
en
cj
a
N
ie
ma
istotn
ych
ró
ón
ic
n
a
tu
ry
fizy
cznej.
Rozró
ón
ie
n
ie
m
a
p
o
d
»o
óe
h
is
to
ry
cz
n
e.
In
te
rf
er
en
cj
a
-
su
p
e
rp
o
zy
cj
a
fa
l
w
y
tw
a
rz
a
n
y
c
h
p
rz
e
z
sk
o
½
cz
o
n
i
lo
Ñ
d
y
sk
re
tn
y
ch
ï
ró
d
e»
s
p
ó
jn
y
ch
,
D
y
fr
ak
cj
a
-
su
p
e
rp
o
zy
c
ja
fa
l
w
y
tw
a
rz
a
n
y
c
h
p
rz
e
z
ï
ró
d
»a
s
p
ó
jn
e
ro
z
»o
óo
n
e
w
s
p
o
só
b
c
i
g
»y
.
D
w
a
ro
d
za
je
d
y
fr
ak
cj
i
a)
d
y
fr
ak
cj
a
fa
l
k
u
li
st
y
ch
(
d
y
fr
ak
cj
a
F
re
sn
el
a)
P
rz
y
d
u
óe
j
o
d
le
g
»o
Ñc
i
ïr
ó
d
»a
o
d
p
rz
y
s
»o
n
y
i
d
y
f
r
a
k
c
ja
F
r
e
s
n
e
la
je
s
t
r
ó
w
n
o
w
a
ó
n
a
d
y
f
r
a
k
c
j
i
F
ra
u
n
h
o
fe
ra
,
g
d
z
ie
a
-
w
ie
lk
o
Ñ
o
tw
o
ru
,
l
-
o
d
le
g
»o
Ñ
e
k
ra
n
u
o
d
p
rz
y
s»
o
n
y
.
b
)
d
y
fr
ak
cj
a
f
al
p
»a
sk
ic
h
(
d
y
fr
ak
cj
a
F
ra
u
n
h
o
fe
ra
)
R
e
al
iz
ac
ja
dyf
rakcji
Fraunh
ofera
w
warunkac
h
la
borato
ryj
ny
ch
.
O
p
ty
k
a
f
a
lo
w
a
6
D
y
fr
ak
cj
a
F
ra
u
n
h
o
fe
ra
n
a
p
o
je
d
y
n
cz
ej
s
zc
ze
li
n
ie
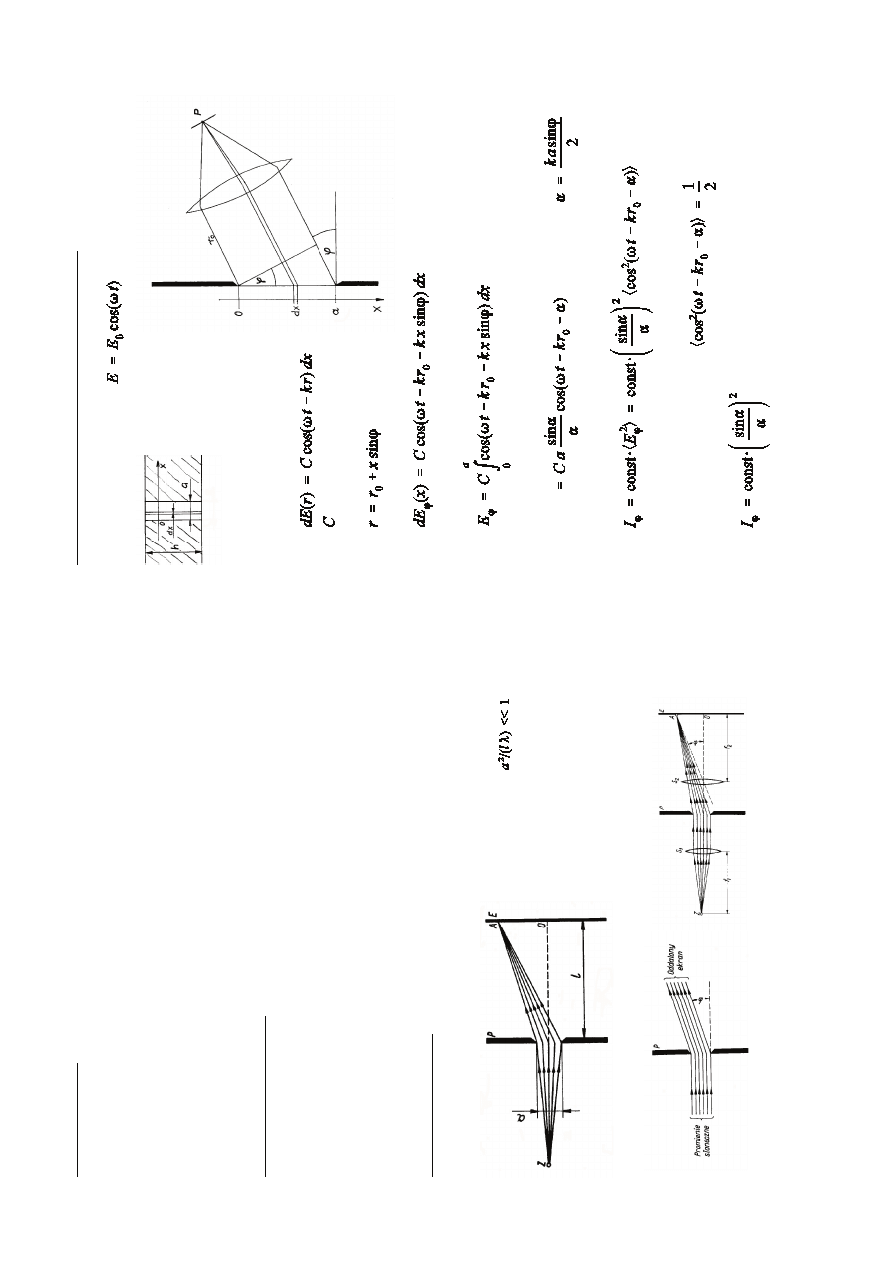
W
p
»a
sz
c
zy
ïn
ie
s
z
cz
el
in
y
P
rz
y
cz
y
n
ek
d
o
E
w
p
u
n
k
c
ie
P
o
d
e
le
m
en
tu
d
x
-
s
ta
»a
O
p
ty
k
a
f
a
lo
w
a
7
D
y
fr
ak
cj
a
F
ra
u
n
h
o
fe
ra
n
a
p
o
je
d
y
n
cz
ej
s
zc
ze
li
n
ie
,
cd
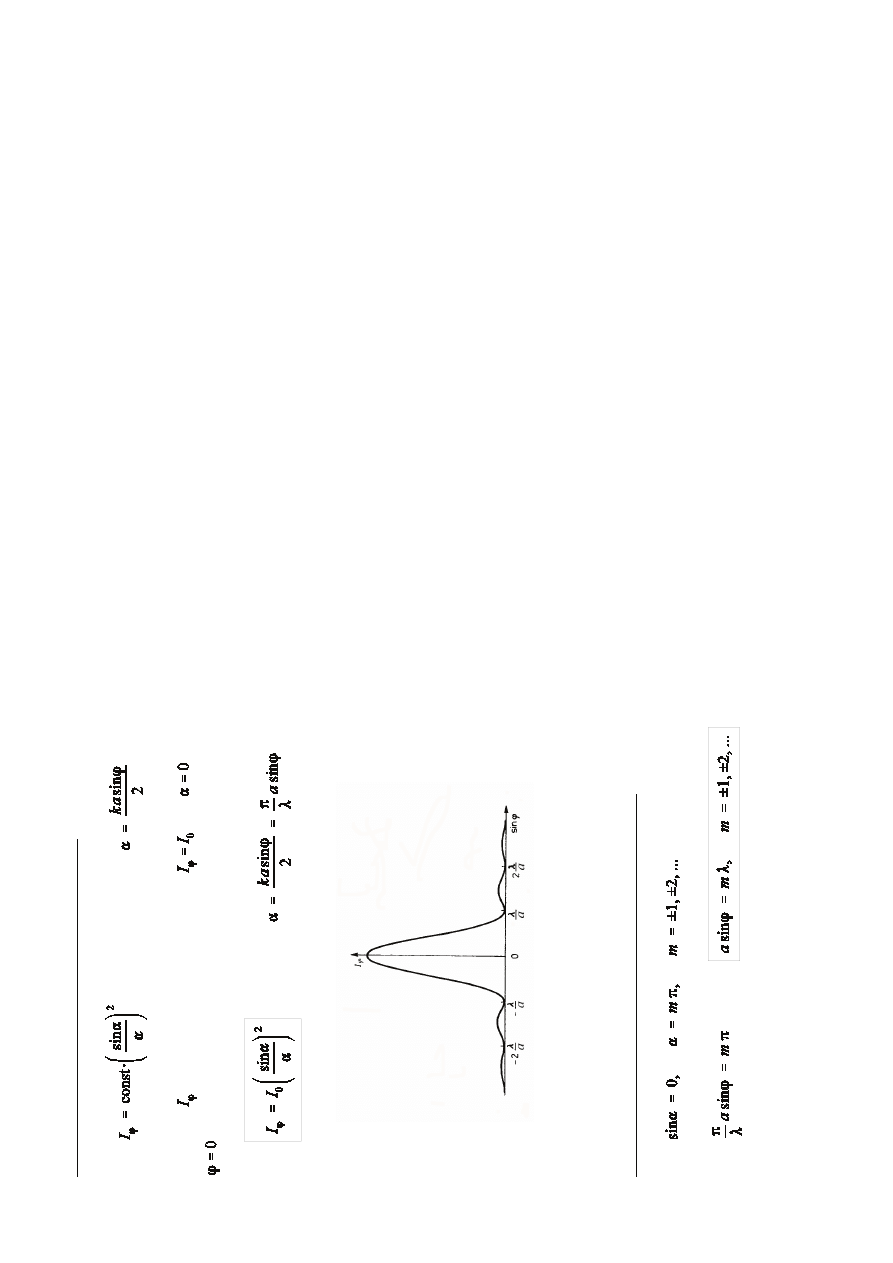
N
at
óe
n
ie
p
rz
y
jm
u
je
w
ar
to
Ñ
m
ak
sy
m
al
n
,
,
d
la
,
cz
y
li
d
la
.
S
t
d
P
o
»o
óe
n
ie
m
in
im
ó
w
d
y
fr
ak
cy
jn
y
ch
z
a
p
o
je
d
y
n
cz
sz
cz
el
in
6
Wyszukiwarka
Podobne podstrony:
Sprawozdanie 6 (Dyfrakcja Światła na Pojedyńczej Szczelinie) , Wydział
Konspekt na sprawdzenie szczelności masek NOWY, Chemia MON
E4A Dyfrakcja na podwójnej szczelinie
Pomiar rozkładu promieniowania w widmie dyfrakcyjnym światła pojedynczej szczeliny i szerokości t (2
Konspekt na sprawdzenie szczelności masek 3kł, Chemia MON
fotka, steroskopowe widzenie - sprawozdanie, Efektem przestrzennego widzenia jest zdjęcie do pomiaru
Ściągi, Obsługa 1, Kontrola szczelności cylindrów Na stan szczelności komory spalania mają wpływ: zu
Drukowanie wielu zdjęć na pojedynczym arkuszu
Pomiar rozkładu energii promieniowania w widmie dyfrakcyjnym światła pojedynczej szczeliny i szeroko
Lab 6, Dyfrakcja Światła na szczelinie pojedynczej i podwójnej Wykonanie
Lab 6 Dyfrakcja Światła na szczelinie pojedynczej i podwójnej, Wykonanie
Lab 6, Dyfrakcja Światła na szczelinie pojedynczej i podwójnej Opis
Lab 6 Dyfrakcja Światła na szczelinie pojedynczej i podwójnej, Opis
Wyprawa na polanę z 1000 letnim dębem, ZHP - przydatne dokumenty, Zbiórki pojedyncze
Działanie pojedynczego żołnierza na polu walki - konspekt, Konspekty, SZKOLENIE TAKTYCZNE
dyfrakcja swiatla na szczelinie
POJEDYNKI PRZEDBITEWNE NA PRZYKŁADZIE WALKI RUSINA Z PIECZYNGIEM
garry stix(pojedynek na fale uderzeniowe)
więcej podobnych podstron