Ć w i c z e n i e 44

WYZNACZANIE MOMENTU BEZWŁADNOŚCI BRYŁY

SZTYWNEJ WZGLĘDEM DOWOLNEJ OSI OBROTU

Z WYKORZYSTANIEM TWIERDZENIA STEINERA

44.1 Opis teoretyczny

W celu zastosowania twierdzenie Steinera, zwanego również twierdzeniem o osiach równoległych,
należy wyznaczyć położenie środka masy danej bryły sztywnej.

Dla układu dyskretnego składającego się z N mas o różnych wartościach

środek jego masy

wyznaczamy następująco (masa całego układu M jest sumą mas składowych

):

i

m

i

m

Obieramy dowolny punkt w przestrzeni, który będziemy traktować jako punkt odniesienia
względem, którego określimy położenie środka masy. Wektory

[

]

i

i

i

i

z

y

x

r

,

,

=

r

opiszą wówczas

położenia poszczególnych mas składowych

względem punktu odniesienia. Odległość środka

masy od punktu odniesienia określona wektorem

i

m

[

]

C

z

C

C

C

y

x

r

,

,

=

r

wyznacza się z definicyjnej

zależności:

∑

=

=

N

i

i

i

C

m

r

M

r

1

1

r

r

(44.1)

którą można rozłożyć na trzy następujące wyrażenia:

∑

=

=

N

i

i

i

C

m

x

M

x

1

1

(44.1a)

∑

=

=

N

i

i

i

C

m

y

M

y

1

1

(44.1b)

∑

=

=

N

i

i

i

C

m

z

M

z

1

1

(44.1c)

W przypadku ciała rozciągłego aby wyznaczyć jego środek masy należy rozłożyć go na
nieskończenie wiele małych mas dm , których położenia względem punktu odniesienia są określone
wektorem

. Wówczas w powyższych wzorach sumy przyjmują postać całek :

[

z

y

x

r

,

,

=

r

]

∫

=

dm

r

M

r

C

1

r

(44.2)

to znaczy

∫

=

dm

x

M

x

C

1

(44.2a)

∫

=

dm

y

M

y

C

1

(44.2b)

∫

=

dm

z

M

z

C

1

(44.2c)

Przy czym całkowanie musi się odbyć po wszystkich elementach dm to znaczy po całej objętości
ciała sztywnego. Należy zwrócić szczególną uwagę na przypadek gdy punkt odniesienia pokrywa
się ze środkiem masy. Wówczas

[

0

,

0

,

0

=

C

r

]

r

tzn.

0

;

0

;

0

=

=

=

∫

∫

∫

dm

z

dm

y

dm

x

(44.3)

Wielkość fizyczna zwana momentem bezwładności określa bezwładność ciała sztywnego, gdy
wykonuje ono ruch obrotowy. Została ona dokładnie opisana w części teoretycznej w ćwiczeniu
nr 36. Wartość momentu bezwładności zależy od osi, wokół której odbywa się obrót ciała. Jeżeli
znamy moment bezwładności ciała względem osi obrotu przechodzącej przez środek masy ciała, to
możemy za pomocą twierdzenia Steinera obliczyć momentem bezwładności tego ciała względem
innej osi równoległej do niej.

Z

*

Z

dm

Y

x

1

y

1

X

Y

*

d

x

C

x

2

y

C

X

*

y

2

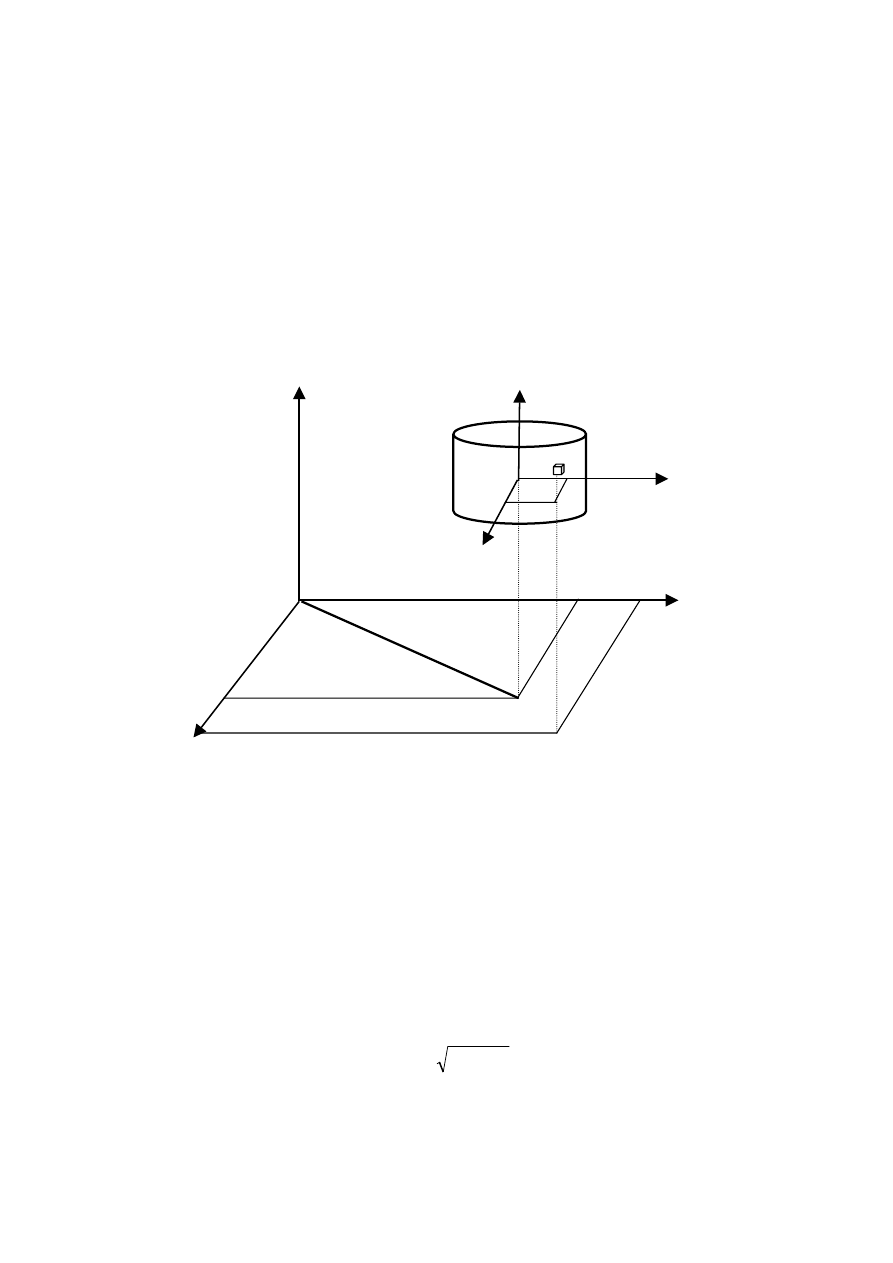
Rys.44.1. Rysunek do wyprowadzenia twierdzenia Steinera

Dla ciała przedstawionego na powyższym rysunku moment bezwładności względem osi obrotu
przechodzącej przez jego środek masy (jest to oś Z) wyraża się całką:

∫

+

=

dm

y

x

J

Z

)

(

2

1

2

1

(44.4)

Wyrażenie

określa odległość elementu dm od osi Z

2

1

2

1

y

x

+

Analogicznie możemy napisać wyrażenie na moment bezwładności względem osi obrotu Z

*

równoległej do osi Z i oddalonej od niej o

2

2

C

C

y

x

d

+

=

, gdzie współrzędne

określają

położenie środka masy rozpatrywanego ciała w nowym gwiazdkowanym układzie współrzędnych:

C

C

y

x i

∫

+

=

dm

y

x

J

Z

)

(

2

2

2

2

*

(44.5)

Wyrażenie

określa odległość elementu dm od nowej osi Z

*

przy czym:

2

2

2

2

y

x

+

1

2

x

x

x

C

+

=

;

1

2

y

y

y

C

+

=

(44.6)

Podstawiając wyrażenia 44.6 do 44.5 otrzymujemy:

(

) (

)

[

]

(

)

∫

∫

+

+

+

+

+

=

+

+

+

=

dm

y

y

y

y

x

x

x

x

dm

y

y

x

x

J

C

C

C

C

C

C

Z

2

1

1

2

2

1

1

2

2

1

2

1

*

2

2

(44.7)

dalej grupując wyrażenia

(

)

(

)

∫

∫

∫

∫

+

+

+

+

+

=

dm

y

y

dm

x

x

dm

y

x

dm

y

x

J

C

C

C

C

Z

1

1

2

2

2

1

2

1

*

2

2

Pierwsza całka (zgodnie z 44.4) odpowiada wyjściowemu momentowi bezwładności J

Z

.

Ponieważ jak zaznaczyliśmy wyżej

i

2

2

2

d

y

x

C

C

=

+

∫

= M

dm

druga całka przyjmuje postać:

(

)

M

d

dm

y

x

C

C

2

2

2

=

+

∫

Dwie ostatnie całki zerują się, gdyż spełniony jest warunek 44.3 tzn. położenie środka masy w
pierwotnym układzie odniesienia określa wektor zerowy

[

]

0

,

0

,

0

=

C

rr

.

Reasumując równanie (44.7) przyjmuje postać:

2

*

d

M

J

J

Z

Z

+

=

(44.8)

I to jest właśnie twierdzenie Steinera opisujące związek między momentami bezwładności

Z

Z

J

J i

*

44.2 Metoda pomiaru.

W ćwiczeniu wyznaczamy momenty bezwładności okrągłej tarczy metalowej o promieniu
R = 15 cm. Posiada ona 5 otworów rozmieszczonych co 3 cm. Umożliwia to równoległe
przesuwanie osi jej obrotu o znaną wartość d. Tarczę mocuje się na balansowym sprężynowym
mechanizmie obrotowym. Tarcza odchylona z położenia równowagi o nieduży kąt i puszczona
swobodnie wykonuje drgania harmoniczne jak wahadło torsyjne (patrz ćwiczenie nr 40).
Okres drgań tarczy wyraża się tym samym wzorem:

D

J

π

2

T

=

(44.9)

gdzie: J – moment bezwładności tarczy względem zadanej osi obrotu.

D – stała zwana modułem skręcenia lub momentem kierującym zależna od budowy

mechanizmu torsyjnego . W ćwiczeniu wynosi ona

0,0255 Nm

W ten sposób mierząc okres drgań T wyznacza się moment bezwładności J. Stanowisko
wyposażone jest w fotokomórkę, za pomocą której można automatycznie zmierzyć połowę okresu
drgań czyli T/2 .

44.3 Wykonanie pomiarów.

Kolejność pomiarów jest następująca:

1. Zapoznać się z budową zestawu pomiarowego.
2. Umocować tarczę na centralnym otworze.
3. Włączyć fotokomórkę.
4. Obrócić tarczę o kąt 90

o

, nacisnąć na fotokomórce przycisk SET i puścić tarczę. Po

wykonaniu przez układ pełnego drgania, odczytać na wyświetlaczu czas T/2. Czynność
powtórzyć dziesięciokrotnie, obracając tarczę po 5 razy w prawo i lewo.

5. Umocowywać tarczę na kolejnych otworach i powtarzając punkt 4 mierzyć kolejne okresy

drgań.

44.4 Opracowanie wyników pomiarów.

1. Obliczyć średnie arytmetyczne wyznaczonych okresów drgań i ich średnie błędy kwadratowe
2. Na podstawie zależności (44.9) obliczyć momenty bezwładności J dla 5 serii pomiarowych

oraz błędy pomiarów.

3. Wykonać wykres

.W eksperymencie

d przyjmuje kolejno wartości: 0, 3, 6,9, 12

[cm]. Nanieść punkty pomiarowe wraz z błędami i poprowadzić przez nie optymalną prostą
najlepiej stosując metodę najmniejszych kwadratów Gaussa. Reprezentuje ona twierdzenie
Steinera (wzór (44.8)). Wyciągnąć odpowiednie wnioski.

)

(

2

d

f

J

=

4. Z teoretycznego wzoru

2

2

1

MR

J

=

obliczyć moment bezwładności tarczy (R = 15 cm,

M = 0,4 kg) i porównać go z wynikiem eksperymentalnym (tzn. z miejscem przecięcia prostej
z punktu 3 z osią rzędnych). Wyciągnąć odpowiednie wnioski.

5. Obliczyć moment bezwładności tarczy względem osi stycznej i prostopadłej do niej.

44.5. Pytania kontrolne

1. Wyjaśnić pojęcie środka masy ciała.
2. Zdefiniować moment bezwładności bryły. Od czego on zależy?.
3. Wyprowadzić wzór na moment bezwładności walca o promieniu R względem osi obrotu.
4. Wyprowadzić wzór na okres wahadła torsyjnego.

L i t e r a t u r a

[1] Leyko J. :. :Mechanika ogólna . PWN W-wa 1995-r
[2] Kittel.C. , Knight W.D. , Ruderman M.A. : Mechanika. PWN W-wa 1973r.