1
Lista 1. do kursu Fizyka; rok. ak. 2013/14 sem. letni W. Inż. Środ.; kierunek Inż. Środowiska
Tabele
wzorów
matematycznych
(
http://www.if.pwr.wroc.pl/~wsalejda/mat-wzory.pdf
)
i
fizycznych
(
http://www.if.pwr.wroc.pl/~wsalejda/wzf1.pdf
;
http://www.if.pwr.wroc.pl/~wsalejda/wzf2.pdf
) są dostępne także na stro-
nach prowadzących ćwiczenia rachunkowe. Student jest zobowiązany do wydrukowania ww. tabel i przynoszenia na zajęcia.
Lista nr 1 ma za zadanie zdobycie/utrwalenie wiedzy z zakresu metodologii fizyki, podstaw rachunku wektorowego,
różniczkowo-całkowego.
1. Szacowanie wartości wielkości fizycznej. W wielu zagadnieniach interesuje nas przybliżona wartość wielkości fizycznej X.
Może to być spowodowane tym, że wyznaczenie dokładnej wartości trwałoby długo, wymagałoby dodatkowych informacji lub
danych, którymi nie dysponujemy albo są nam niepotrzebne. W innych przypadkach chcemy jedynie mieć grube oszacowanie
wartości wielkości fizycznej z dokładnością, jak mówimy, co do rzędu wielkości. Szacowanie prowadzimy w następujący
sposób: Liczbę x określającą miarę (liczbę jednostek) wielkości X w układzie SI zaokrąglamy do jednej cyfry znaczącej i
zapisujemy ją w systemie dziesiętnym w postaci wykładniczej (scientific notation): M·10
n
; gdzie M – liczba rzeczywista, n –
wykładnik. Np. jeśli znamy odległość 4243 m, to l
≅
4,2·10
3
m, a jeśli znamy liczbę sekund 3641 s, to t
≅
3,6·10
3
s.
Następnie na tak otrzymanych liczbach dokonujemy operacji algebraicznych i otrzymany wynik zapisujemy w postaci liczby
wykładniczej o podstawie dziesięć z jedną cyfrą znaczącą. Przykładowo, jeśli szacujemy rząd wartości prędkości v = l/t,
gdzie l = 2 160 128 m i t = 3 641 s, to w szacowaniu przyjmujemy kolejno l
≅
2·10
6
m, t
≅
4·10
3
s i otrzymujemy v
≅
(2·10
6
m)/(4·10
3
s) = 5·10
2
m/s.
A) Oszacuj grubość d kartki papieru książki, której grubość wynosi 4,4 cm a liczba stron 1515.
B) Średnia odległość Ziemi od Słońca wynosi 149 598 261 km, a prędkość światła 299 792 458 m/s. Oszacuj
w sekundach czas potrzebny światłu na przebycie odległości dzielącej Słońca od Ziemi.
C) Samodzielnie: Oszacuj liczbę: (a) swoich oddechów w ciągu godziny lekcyjnej, (b) uderzeń serca i od-
dechów w ciągu przeciętnego czasu życia Polki/Polaka, c) atomów miedzi w jednym metrze sześciennym tego
metalu, (d) atomów powietrza w pomieszczeniu, w którym aktualnie przebywasz, e) cząsteczek wody, liczbę
protonów i liczbę neutronów we własnym ciele, zakładając, że ciało składa się w 100% z wody. f) Oszacuj
powierzchnię i objętość swego ciała. Ws-ka: Niezbędne dane postaraj się określić/przyjąć/wyznaczyć
samodzielnie.
2. Podstawy analizy wymiarowej (patrz
http://www.foton.if.uj.edu.pl/documents/12579485/1b32a7ad-e4b5-4c58-
a5f0-eb6300fd742b
). Znak równości w fizyce oznacza równość wartości (liczby jednostek) i wymiarów (jednostek)
wielkości fizycznych znajdujących się po obu stronach znaku. Każda pochodna wielkość fizyczna ma wymiar, który wyraża
się za pomocą (wymiarów) wielkości podstawowych układu SI. Wymiarami podstawowych wielkości fizycznych w SI są na
podstawie definicji: długość – symbol L, czas – symbol T, masa – symbol M, temperatura – symbol K, natężenie prądu –
symbol I, światłość – symbol C. Wymiar wielkości pochodnej X – symbol dim X = [X], jest określany za pomocą definicji
tychże wielkości i jest wyrażany jest w postaci iloczynu lub ilorazu wielkości/wymiarów podstawowych w odpowiednich
potęgach (podniesionych do odpowiednich potęg), wykładniki potęgowe nazywa się wykładnikami wymiarowymi. Jeśli
pochodną wielkością fizyczna jest praca, to dim P = [P]= (dim F)·L=MLT
-2
L=
L
2
MT
-2
. Symbole pochodnych wielkości
fizycznych piszemy kursywą, a wymiar X oznaczamy zamiennie symbolami: dim X lub [X]. Analiza wymiarowa traktuje
wymiary jako wielkości algebraiczne, na których można wykonywać podstawowe działania algebraiczne (dodawanie,
odejmowanie, mnożenie, dzielenie, potęgowanie, pierwiastkowanie). Dwie podstawowe reguły analizy wymiarowej:
R1. Wielkości fizyczne mogą być dodawane lub odejmowane pod warunkiem, że mają ten sam wymiar.
R2. Wymiary strony lewej i prawej poprawnie sformułowanej równości wielkości fizycznych powinny być takie same.
Przykład 1. Czy poprawnym jest wzór s = const at
2
, określający zależność drogi od czasu w prostoliniowym ruchu
jednostajnie przyspieszonym?
Rozwiązanie: [s] = L, a wymiar prawej strony [at
2
] = [a][t
2
] = (LT
-2
)T
2
= L. Odpowiedz: Wzór jest poprawny z
dokładnością do bezwymiarowego czynnika const.
Zastosujemy analizę wymiarową do wyznaczenia postaci zależności funkcyjnej typu iloczynowego między kilkoma
wielkościami fizycznymi.
Przykład 2. Załóżmy, ze hipotetyczna zależność między przyspieszeniem a ciała wykonującego ruch po okręgu o promieniu R
ze stała prędkością v jest postaci a = v
a ·
R
b
. Jakie są wartości wykładników wymiarowych a i b?
Rozwiązanie: Skorzystamy z tego, że dim a =[a]= LT
-2
i że ten sam wymiar powinna mieć prawa strona wzoru, tj.
dim (v
a ·
R
b
)=[ v
a ·
R
b
] = (LT
-1
)
a
·L
b
= L
a+b
T
-a
. Aby więc wymiary obu stron wzoru były zgodne winny zachodzić równości a+b
= 1 i –a = –2. Zatem mamy odpowiedź: a = 2 i b = 1, jak powinno być. Uwaga: Powyższą analizę można przeprowadzić
posługując się w miejsce wymiarów jednostkami wielkości fizycznych.
Przypomnijmy wartości i wymiary uniwersalnych stałych przyrody:
–
stała grawitacji
:G = 6,67·10
-11
L
3
/(MT
2
), dim G = [G] = L
3
M
-1
T
-2
,
–
stała Diraca:
ℏ
= h/2
π
= 1,06·10
-34
kg· m
2
/s, więc dim
ℏ
= dim h = M
1
L
2
T
-1
,
–
predkość światła:
c = 3·10
8
m/s, dim c = M
1
T
-1
.
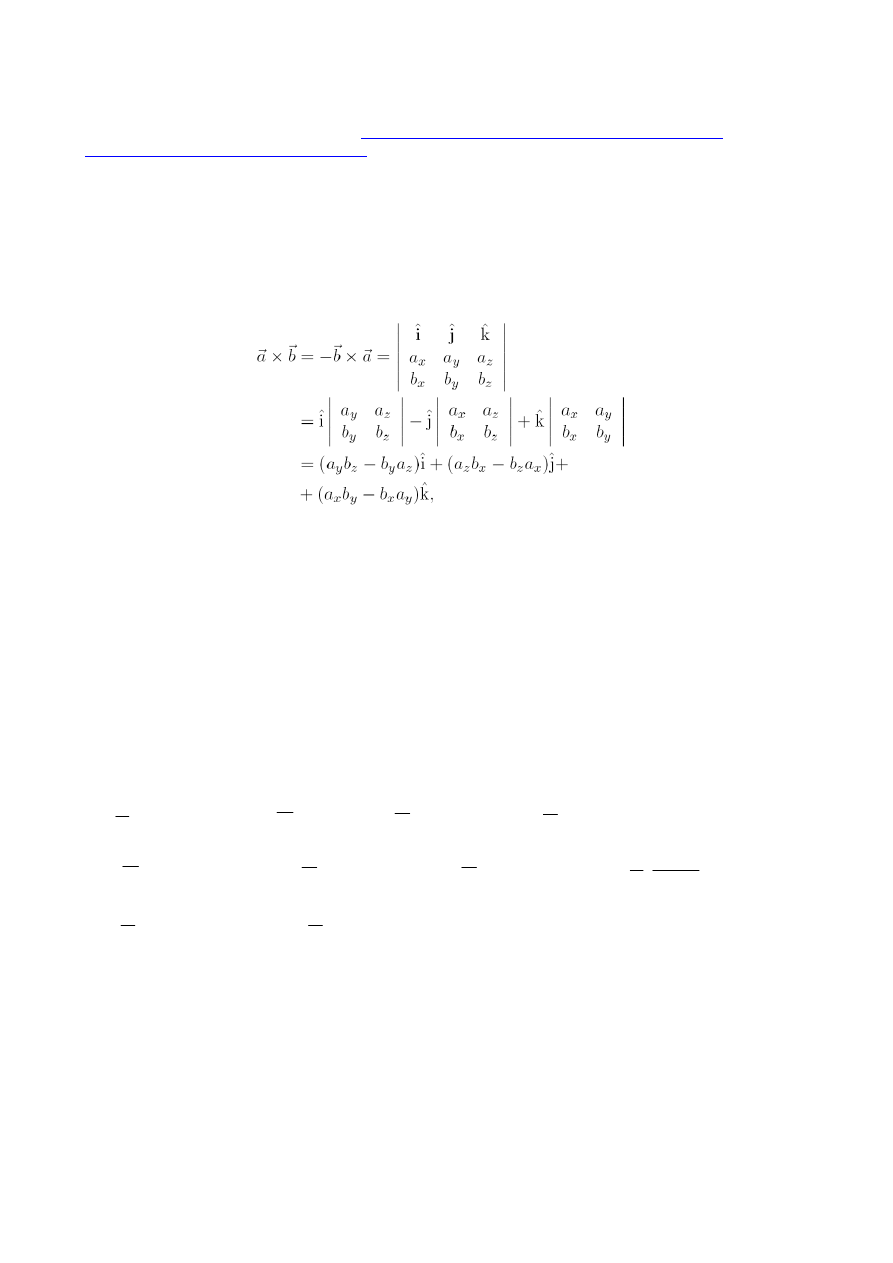
2
Korzystając z reguł analizy wymiarowej należy odtworzyć wielkości i obliczyć wartości:
(1)
t
P
=
ℏ
a
c
b
G
c
– czas (sekundę) Plancka, (2) l
P
=
ℏ
d
c
e
G
f
– długość (metr) Plancka).
O wielkościach i jednostkach Plancka czytaj:
http://www.if.pwr.wroc.pl/~wsalejda/metodologia_fizyki.pdf
lub
http://pl.wikipedia.org/wiki/Jednostki_Plancka
. Określają one najmniejszy okres czasu i najmniejszą długość akcepto-
walną fizycznie i są utożsamiane z czasem i rozmiarami niemowlęcego okresu ekspansji Wszechświat, który nastąpił po
Wielkim Wybuchu. Fizyka póki co nic wiarygodnego nie jest w stanie twierdzić o wcześniejszych etapach i mniejszych
rozmiarach rozszerzającego się Wszechświata.
3.
Pokaż z definicji, że iloczyn skalarny dwóch wektorów ma postać w kartezjańskim układzie współrzędnych
postać
.
x
x
y
y
z
z
a b
a b
a b
a b
⋅ =
+
+
4.
Pokaż z definicji, że iloczyn wektorowy dwóch wektorów danych w kartezjańskim układzie współrzędnych
ma postać:
5.
Samodzielnie zapoznaj się z uzasadnieniami zamieszczonymi na końcu listy, następujących równości:
a)
( )
(
)
( )
a
b c
b
c
a
c
a b
⋅ × = ⋅ × = ⋅ ×
, b)
( )
(
)
( )
a
b c
b c a
c a b
× × =
⋅ −
⋅
.
Zauważ, że cykliczne przestawianie symboli wektorów znacznie pomaga i ułatwia zapamiętywaniu powyższych wzorów.
6.
Dwa wektory
i
a
b mają składowe (w metrach): a
x
= 3,2; a
y
= 1,6; b
x
= 0,5; b
y
= 4,5.
Znajdź kąt między kierunkami wektorów
i
a
b . Na płaszczyźnie OXY można znaleźć dwa wektory, które są
prostopadłe do wektora a i mają długość równą 5 m. Jeden z nich c ma dodatnią składową x, a drugi d ma
składową x ujemną. Wyznacz składową x i składową y wektora c . Wyznacz składową x i składową y wektora
d .
7.
Samodzielnie: Wyznaczyć pochodne następujących funkcji, gdzie x
0
, A, w są stałymi:
( )
(
)
2
0
d
3
6
d
v t
x
t
t
t
=
+ −
,
( )
( )
( )
d
d
a t
v t
t
=
,
( )
( )
(
)
d
sin
d
v t
A
t
t
ω
=
⋅
,
( )
( )
(
)
2
d
sin
d
v t
A
t
t
ω
=
⋅
,
( )
( )
(
)
2
d
sin
,
d
v t
A
t
t
ω
=
⋅
( )
( )
(
)
2
d
sin
d
v t
A
t
t
ω
=
⋅
,
( )
( )
(
)
(
)
2
d
sin
,
d
v t
A
t
t
ω
=
⋅
( )
( )
( )
sin
d
d
cos
t
f t
t
t
ω
ω
=
,
( )
( )
( )
(
)
d
sin
cos
,
d
f t
t
t
t
ω
ω
=
⋅
( )
( )
d
d
n
f t
t
t
ω
=
, gdzie n jest liczbą całkowitą.
8.
Samodzielnie: Wyznaczyć całki nieoznaczone, gdzie v
0
, a, w są stałymi, n jest liczbą całkowitą
(
)
0
d
v
a t
t
± ⋅
∫
,
( )
d ,
a
t
±
∫
( )
sin
d
t
t
ω
∫
,
( )
cos
d ,
t
t
ω
∫
(
)
0
d
n
v
a t
t
± ⋅
∫
(rozpatrzyć różne przypadki n).
9.
Samodzielnie: Wyznaczyć całki oznaczone, gdzie v
0
, a,
ω
są stałymi, n jest liczbą całkowitą
(
)
2
1
0
d
t
t
v
a t
t
± ⋅
∫
,
( )
2
1
d ,
t
t
a
t
±
∫
( )
2
1
sin
d
t
t
t
t
ω
∫
,
( )
2
1
cos
d ,
t
t
t
t
ω
∫
(
)
1
2
0
d
t
n
t
v
a t
t
± ⋅
∫
,
gdzie n jest liczbą całkowitą; rozpatrzyć różne
wartości n.
Wrocław, 24 lutego 2014 W. Salejda
3
Pożyteczne materiały dostępne w Internecie
http://pl.wikibooks.org/wiki/Metody_matematyczne_fizyki
http://pl.wikibooks.org/wiki/Metody_matematyczne_fizyki/Działania_na_wektorach#Iloczyn_mieszany
Dowód ze strony:
http://pl.wikibooks.org/wiki/Metody_matematyczne_fizyki/Działania_na_wektorach#Iloczyn_mieszany
Iloczyn mieszany
Pierwsza równość w (1.23) jest iloczynem skalarnym wektorów
c
i
a b
×
. Tożsamości (1.24) są następstwem
właściwości wyznacznika z (1.23). Przestawiając pierwszy wiersz kolejno z drugim i trzecim otrzymujemy pierwszą równość
(1.24), tj.
x
y
c
x
y
z
x
y
c
a
a
a
b
b
b
c
c
c
.
Podobnie przestawiając ostatni wiersz kolejno z drugim i pierwszym dostajemy drugą równość w (1.24), tj.
x
y
c
x
y
z
x
y
c
b
b
b
c
c
c .
a
a
a
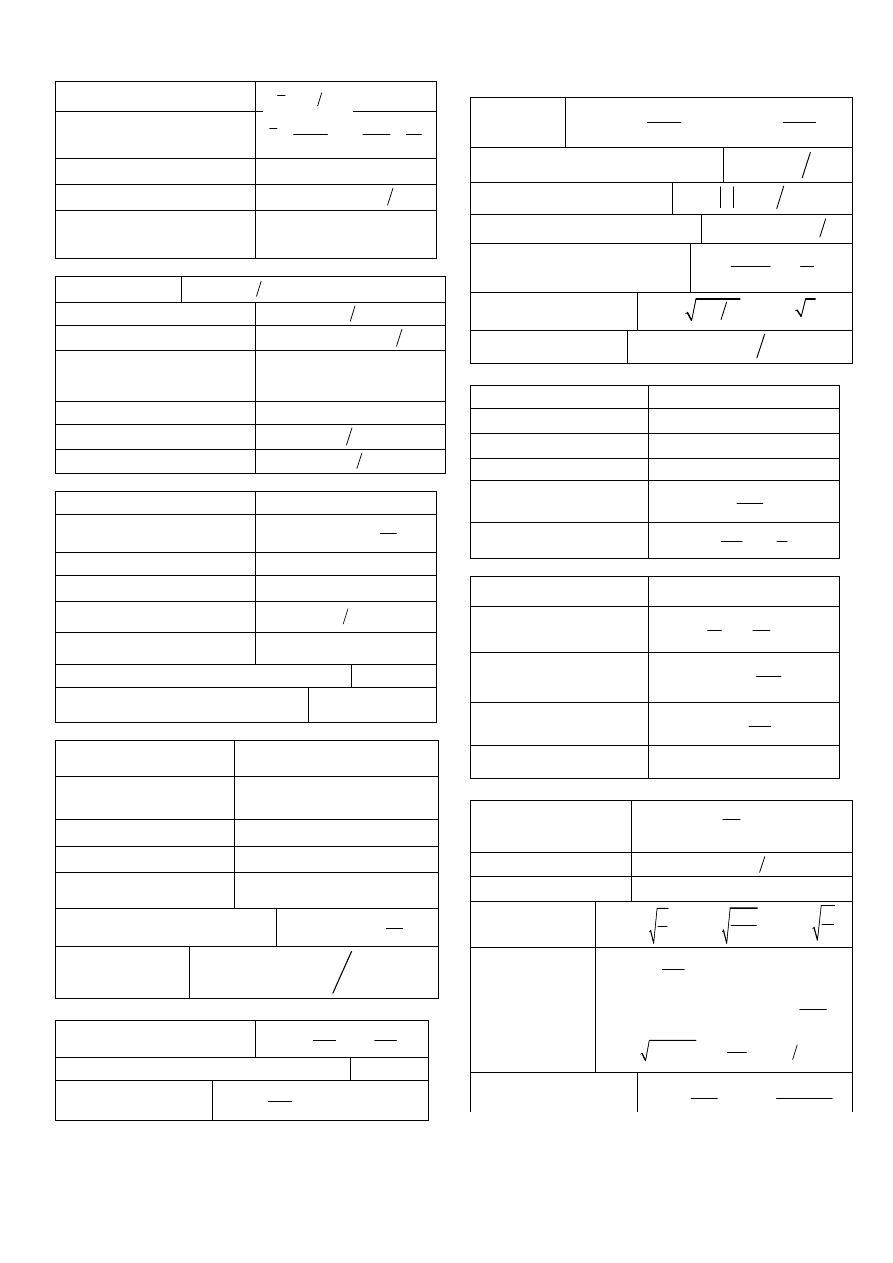
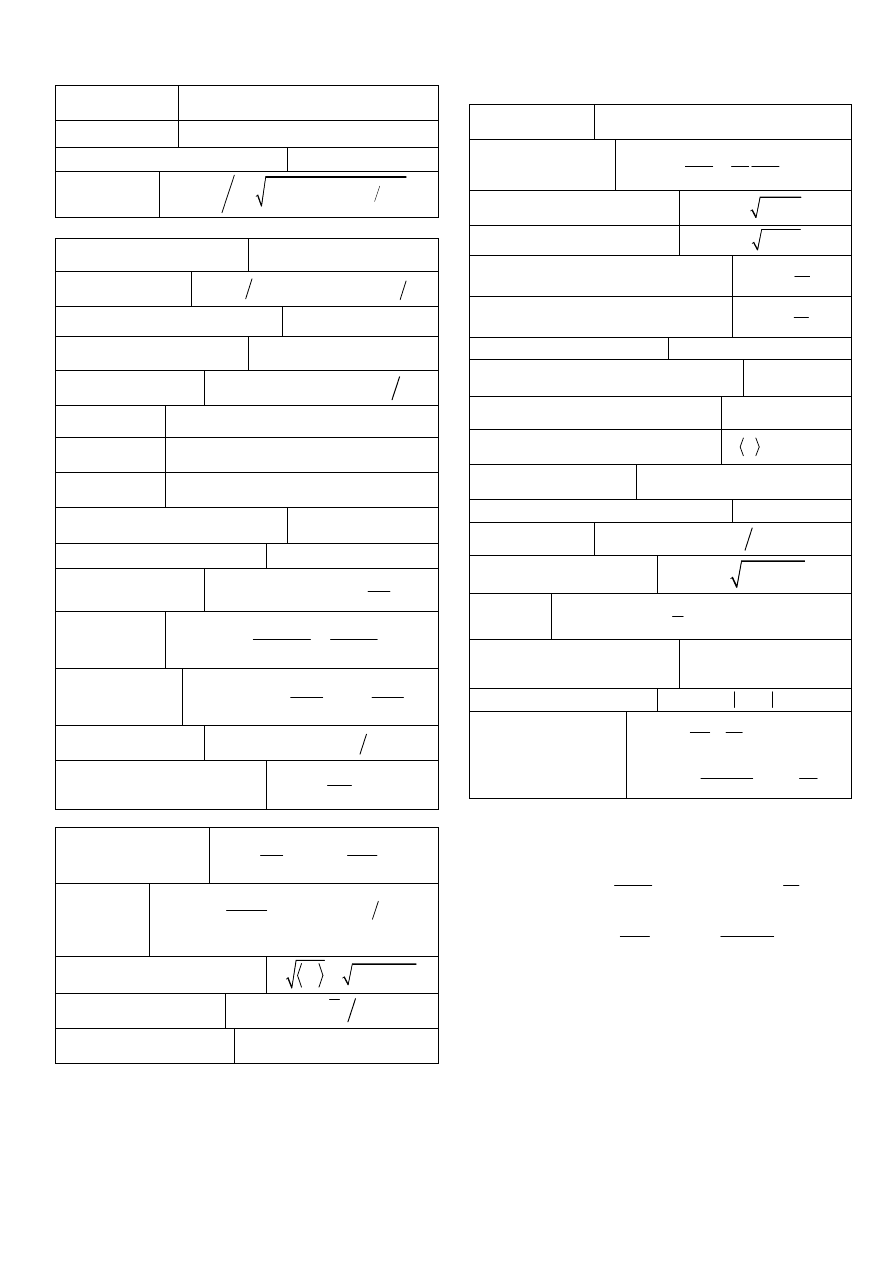
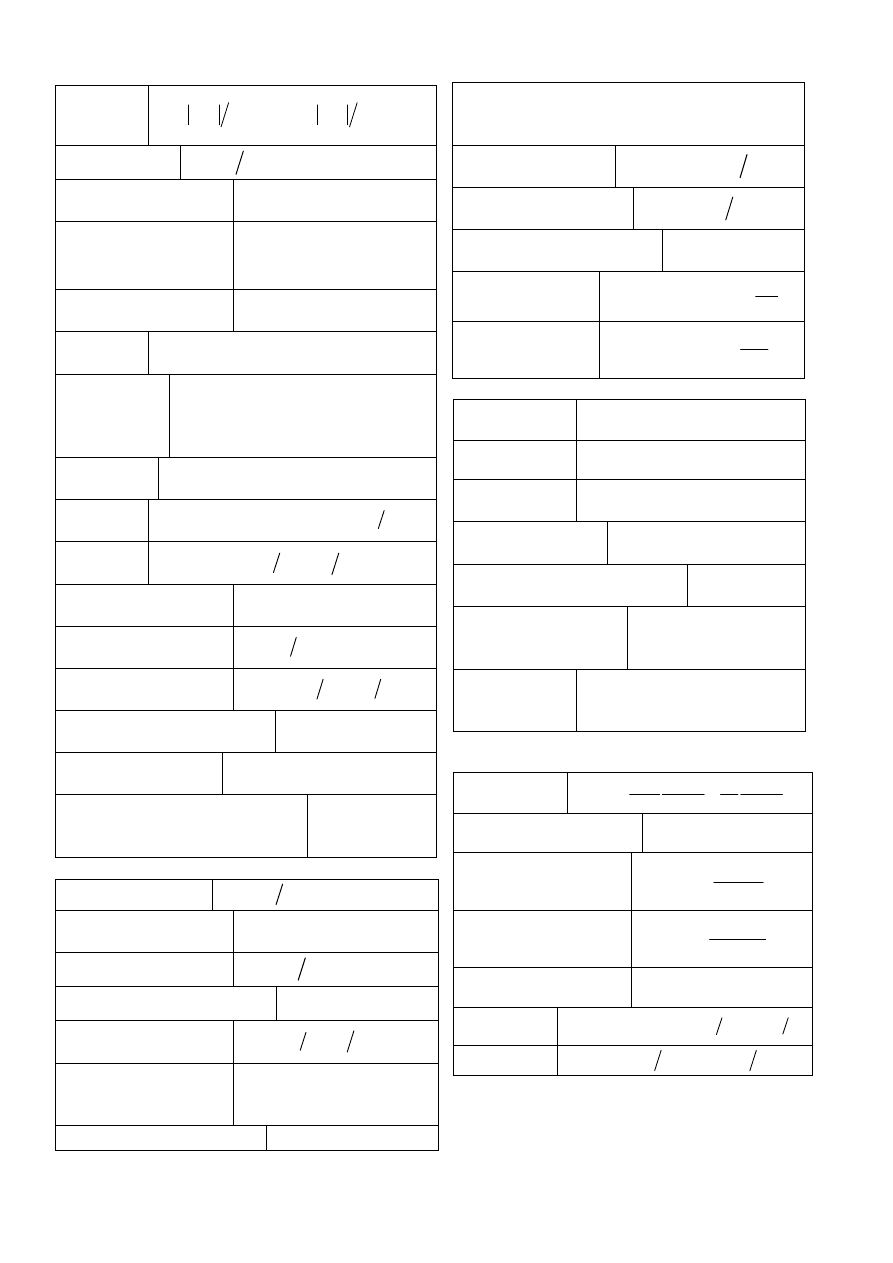
Poniżej tabele wzorów fizycznych i matematycznych
4
Ruch prostoliniowy (podano wartości)
Prędkość średnia
Przyspieszenia: średnie i
chwilowe
0
0
v v
a
t
t
−
=
−
;
( )
d
d
F t
v
a
m
t
=
=
Prędkość
0
k
v
v
a t
= + ⋅
Droga
2
0
0
2
s
s
v t
at
= +
+
Prędkość i droga w ruchu
jednostajnie zmiennym
(
)
2
2
0
0
2
k
k
v
v
a
s
s
= +
⋅
−
Ruch po okręg (podano wartości)
Prędkość kątowa
;
;
k
p
t v
R
t
ω
α
ω
ω
ω ε
= ∆ ∆
=
=
+
Przyspieszenie kątowe
t
ε
ω
= ∆ ∆
Droga kątowa
2
0
0
2
t
t
α α ω
ε
=
+
+
Prędkość i droga kątowa w
ruchu jednostajnie zmiennym
(
)
2
2
0
0
2
k
k
ω
ω
ε α α
=
+
⋅
−
Przyspieszenie styczne
st
a
R
ε
=
Przyspieszenie dośrodkowe
2
2
dos
a
v R
R
ω
=
=
Częstotliwość
1
f
T
=
Dynamika
Pęd
p
mv
=
Druga zasada dynamiki
;
p
F
ma
F
t
∆
=
=
∆
Wartość siły tarcia
T
N
F
F
µ
=
Ciężar ciała
Q
mg
=
Wartość siły dośrodkowej
2
2
v
dos
F
m
R
m
R
ω
=
=
Praca mechaniczna
( )
(
)
cos
,
W
FR
F R
=
⊲
Twierdzenie o pracy i energii kinetycznej
k
E
W
∆
=
Twierdzenie o pracy siły potencjalnej i
energii potencjalnej
p
E
W
−∆
=
Dynamika ruchu obrotowego
Wartość momentu siły
( )
(
)
sin
,
M
FR
F R
=
⊲
Moment bezwładności
2
1
n
i i
i
I
m r
=
=
∑
Twierdzenie Steinera
2
Ś
M
I
I
md
=
+
Moment pędu
;
L
r
p L
I
ω
= ×
=
Wartość momentu pędu
( )
(
)
sin
,
L
Rp
p R
=
⊲
II zas. dyn. dla ruchu obrotowego
;
L
M
I
M
t
ε
∆
=
=
∆
Ś
rodek masy
układu n punktów
materialnych
1
1
n
n
s r
i
i
i
i
i
r
m r
m
=
=
=
∑
∑
Praca, energia, moc
Energia kinetyczna ruchu
postępowego i obrotowego
2
2
;
2
2
k
k
mv
I
E
E
ω
=
=
Energia potencjalna (małe zmiany wysokości)
p
E
mgh
=
Moc
;
;
W
P
P
Fv P
M
t
ω
∆
=
=
=
∆
v
s
t
= ∆ ∆
Grawitacja
Wartość siły
grawitacji
2
11
1
2
2
2
Nm
;
6.67 10
kg
g
m m
F
G
G
R
−
=
=
⋅
Natężenie pola grawitacyjnego
g
F
m
γ
=
Wartość
γ
dla planety kulistej
2
Gm R
γ
=
Grawitacyjna energia potencjalna
1
2
pot
E
Gm m R
= −
Wartość przyspieszenia grawita-
cyjnego przy powierzchni Ziemi
Ziemi
Ziemi
0
2
2
m
10
s
Gm
g
R
=
=
I i II prędkość
kosmiczna
( )
I
II
I
;
2
v
Gm R v
v
=
=
III prawo Keplera
( )
2
2
3
4
T
r
Gm
π
=
Hydrostatyka
Siła parcia i ciśnienie
F
pS
=
Ciśnienie hydrostatyczne
p
gh
ρ
=
Wartość siły wyporu
W
F
gV
ρ
=
Równanie ciągłości
v
.
S
const
⋅ =
Prawo Bernoulliego
2
v
.
2
p
gh
const
ρ
ρ
+
+
=
Napięcie powierzchniowe
;
W
F
S
l
σ
σ
∆
=
=
∆
Sprężystość
Siła sprężystości
F
kx
= −
Prawo Hooke’a
F
l
E
E
S
l
σ
ε
∆
=
=
=
Naprężenia objętościowe
0
V
p
V
κ
∆
= −
Energia potencjalna
sprężystości
2
2
p
kx
E
=
Warunki równowagi
0;
0
wyp
wyp
F
M
=
=
Ruch drgający
Drgania nietłumione:
Równanie ruchu,
przemieszczenie
2
2
0
d
m
m
m
,
dt
( )
cos(
)
x
a
x
kx
x t
A
t
ω
φ
=
=
= −
=
+
ɺɺ
Częstość kołowa
0
2
T
ω
π
=
Wartość prędkości
0
0
v( )
sin(
)
t
A
t
ω
ω
φ
= −
+
Okresy wahadeł
2
l
T
g
π
=
;
2
;
I
T
mgd
π
=
2
m
T
k
π
=
Drgania
tłumione:
Równanie ruchu,
przemieszczenie,
log. dekrement
tłumienia
}
{
0
2
2
n
n+1
2
2
2
0
d
m
m
m
,
dt
A
( )
A
cos
;
ln
;
A
;
;
.
2
t
x
a
x
kx bv
x t
e
t
b
k m
m
β
ω φ
ω
ω
β β
ω
−
=
=
= − −
=
+
Λ =
=
−
=
=
ɺɺ
Energia tłumionych i
nietłumionych drgań
2
2
2
;
2
2
t
c
c
kA
kA e
E
E
β
−
=
≈
5
Drgania wymuszone
Siła
wymuszająca
0
( )
cos(
)
F t
F
t
ω
=
Równanie ruchu
0
cos(
)
ma
kx
bv
F
t
ω
= − −
+
Przemieszczenie drgań ustalonych
( )
sin(
)
x t
A
t
ω
φ
=
+
Amplituda
(
)
(
)
2
2
2
2
0
0
A
F
m
b
m
ω
ω
ω
=
−
+
Termodynamika fenomenologiczna
Rozszerzalność liniowa
0
l
l
T
α
∆ =
∆
Ciepło właściwe,
ciepło przemiany
(
)
;
c
Q m T
=
∆
przem.
przem.
c
Q
m
=
Równanie gazu doskonałego
pV
nRT
=
Równanie adiabaty
constans
pV
κ
=
Wzór Mayera,
wykładnik adiabaty
;
p
V
p
V
C
C
R
C
C
κ
−
=
=
Praca gazu
(stałe ciśnienie)
W
p V
∆ = ∆
Praca gazu
d ,
d
W
p V
W
p
V
=
∆ =
⋅
∫
δ
I zasada
termodynamiki
Q
U
W
δ
δ
= ∆ +
Energia wewnętrzna gazu
doskonałego
0
V
U
nC T
U
=
+
II zasada termodynamiki
0
S
∆ ≥
Zmiana entropii
d
/ ,
d
Q
S
Q T
S
T
T
=
∆ =
∫
δ
δ
Sprawność
silnika Carnot
użyteczne
1
0
calkowite
1
Q
T
T
Q
T
η
−
=
=
Zmiana entropii
gazu doskonałego
końc.
końc.
pocz.
pocz.
Rln
ln
V
V
T
S
n
C
V
T
∆ =
+
Praca w przemianie
izotermicznej
(
)
końc
pocz
R ln
W
n T
V
V
=
Ciepło molowe gazu idealnego
o i stopniach swobody
V
d
R / 2
d
U
C
i
T
=
= ⋅
Elementy termodynamiki statystycznej
Funkcja rozkładu
Boltzmanna
0
B
exp
k
j
j
N
E
N
T
=
−
Funkcja
rozkładu
Maxwella
(
)
3/ 2
2
2
0
0
B
B
( )
4π
exp
2k
2πk
m
f v
v
m v
T
T
=
−
Ś
rednia prędkość kwadratowa
2
B
0
3k
/
v
T m
=
Mikroskopowe równanie
gazu doskonałego
( )
2
3
k
p
NE
V
=
Entropia Boltzmanna-
Plancka; kwant entropii
B
k ln
;
S
=
Ω
B
k ln 2
Ruch falowy
Równanie fali
( )
(
)
0
,
sin
y x t
y
t
kx
ω
=
⋅
−
Równanie falowe
2
2
2
2
2
1
y
y
x
c
t
∂
∂
=
∂
∂
Prędkość fazowa fali
poprzecznej w strunie
/
L
c
N
ρ
=
Prędkość fali w cieczy
/
L
c
κ ρ
=
Odkształcenie względne ośrodka
wywołane ruchem falowym
y
x
ε
∂
=
∂
Prędkość cząsteczek ośrodka wywołana
ruchem falowym
y
v
t
∂
=
∂
Opór akustyczny ośrodka
c
ρ
Ś
rednia energia mechaniczna fali małego
fragmentu ośrodka o masie
m
∆
2
max
/ 2
m v
∆ ⋅
Ś
rednia moc energii fali sprężystej
2
max
/ 2
Scv
ρ
Ś
rednia intensywność fali sprężystej
(gęstość strumienia energii fali)
2
max
/ 2
J
cv
ρ
=
Ś
rednia gęstość energii
fali sprężystej
2
max
/ 2
v
ρ
Odległość miedzy węzłami fali stojącej
/ 2
λ
Efekt Dopplera
(
) (
)
ź
d
ź
f
f
v
v
v v
=
±
∓
Prędkość dźwięku
(
)
/
c
p
κ
ρ
=
Natężenie
dźwięku
12
2
0
0
10 log
;
10
W/m
J
J
J
β
−
=
=
Pole ciśnienia fali dźwiękowej
( )
(
)
max
,
cos
s x t
s
kx
t
ω
=
−
(
)
(
)
max
max
max
sin
;
p
p
kx
t
p
c
s
ω
ρω
∆ = ∆
−
∆
=
Częstotliwość dudnień
1
2
f
f
−
Prędkość grupowa fali
( )
( )
gr
d
d
d
d
d
d
d
d
v
c k
k
k
k
c k
c
c
k
c
k
ω
λ
λ
=
=
⋅
=
= +
= −
Wybrane stałe fizyczne
2
11
23
B
2
23
A
Nm
J
G
6, 67 10
; k
1, 38 10
;
K
kg
1
J
N
6, 02 10
; R
8, 31
mol
mol×K
−
−
=
⋅
=
⋅
=
⋅
=
6
Elektrostatyka
Prawo
Coulomba
(
)
(
)
2
2
1 2
r
0
1 2
4π
4π
F
q q
r
q q
r
ε ε
ε
=
=
Natężenie pola
0
q
=
E
F
Wektor indukcji pola
elektrycznego
r
0
ε ε
ε
=
=
D
Ε
Ε
Moment siły
działającej na dipol
p
qd
=
=
τ
p × E
Energia potencjalna
dipola
p
E
= − ⋅
p E
Prawo
Gaussa
r
0
wew
d
Q
ε ε
⋅
=
∫
E
S
Związek
pracy z
energią
potencjalną
k o ń c o w a
p o c z ą tk o w a
p
p
p
E
E
E
W
∆
=
−
=
= −
Energia
potencjalna
( )
p
r
E
r
W
∞→
= −
Różnica
potencjału
konćowy
początkowy
V
V
V
W q
∆ =
−
= −
Potencjał
w punkcie
( )
p
p
r
V r
W
q
E
q
∞→
= −
=
Związek energii z
potencjałem
V
= −
Ε
grad
Pojemność
elektryczna
C
Q U
=
Pojemność płaskiego
kondensatora
r
0
C
S d
S d
ε ε
ε
=
=
Energia potencjalna
kondensatora płaskiego
2
p
/ 2
E
CU
=
Gęstość energii pola
elektrostatycznego
2
E
r
0
/ 2
/ 2
u
E
ε ε
= ⋅
=
D E
Pojemność układu
kondensatorów połączonych
równoległe
i
C
C
=
∑
Stały prąd elektryczny
Natężenie prądu
d
d
I
q
t
=
Wektor gęstości
prądu
ne
=
d
j
v
Prawo Ohma
R
U I
=
Różniczkowe prawo Ohma
σ
=
j
E
Opór prostoliniowego
przewodnika
( )
R
L S
L
S
ρ
σ
=
=
Zależność oporu
właściwego od
temperatury
( )
[
]
0
0
1
(
)
T
T
T
ρ
ρ
α
=
+
−
Moc elektryczna
P
U I
= ⋅
Stały prąd elektryczny c.d.
Siła
elektromotoryczna
SEM
d
d
W
q
ε
=
Prawo Ohma dla
obwodu zamkniętego
(
)
SEM
+
R r
I
ε
=
Opór układu oporników
połączonych szeregowo
i
R
R
=
∑
Ładowanie
kondensatora
( )
SEM
1 exp
t
t
RC
q
C
ε
−
−
=
Rozładowywanie
kondensatora
( )
0
exp
t
t
RC
q
q
−
=
Magnetostatyka
Siła Lorentza
Q
= ⋅ ×
L
F
V B
Siła Lorentza
I
= ⋅
L
F
L × B
Prawo Gaussa
d
0
S
⋅
=
∫
B
Magnetyczny
moment dipolowy
I
= ⋅
µ
S
Moment siły działającej na
dipol
=
τ
µ × B
Energia potencjalna
dipola
magnetycznego
p
E
= − ⋅
µ B
Związek pracy
z energią
potencjalną
W
E
E
E
−
=
=
−
=
∆
początkowa
p
końcowa
p
p
Źródła pola magnetycznego
Prawo Biota-
Savarta
0
r
3
3
d
d
d
4π
4π
I
I
r
r
µ µ
µ
×
×
=
=
s r
s r
B
Wektor indukcji pola
magnetycznego
r
0
µ µ
=
B
H
Pole magnetycznego
prostoliniowego
przewodnika
0
r
2π
I
B
R
µ µ
=
Pole magnetycznego
przewodnika w
kształcie łuku okręgu
0
r
4π
I
B
R
µ µ φ
=
Prawo Ampere’a
0
r
p
d
I
µ µ
⋅
=
∫
B
L
Pole
solenoidu
0
r
0
r
B
n
I
IN L
IN L
µ µ
µ µ
µ
=
=
=
Pole toroidu
( )
( )
0
r
2π
2π
B
IN
r
IN
r
µ µ
µ
=
=
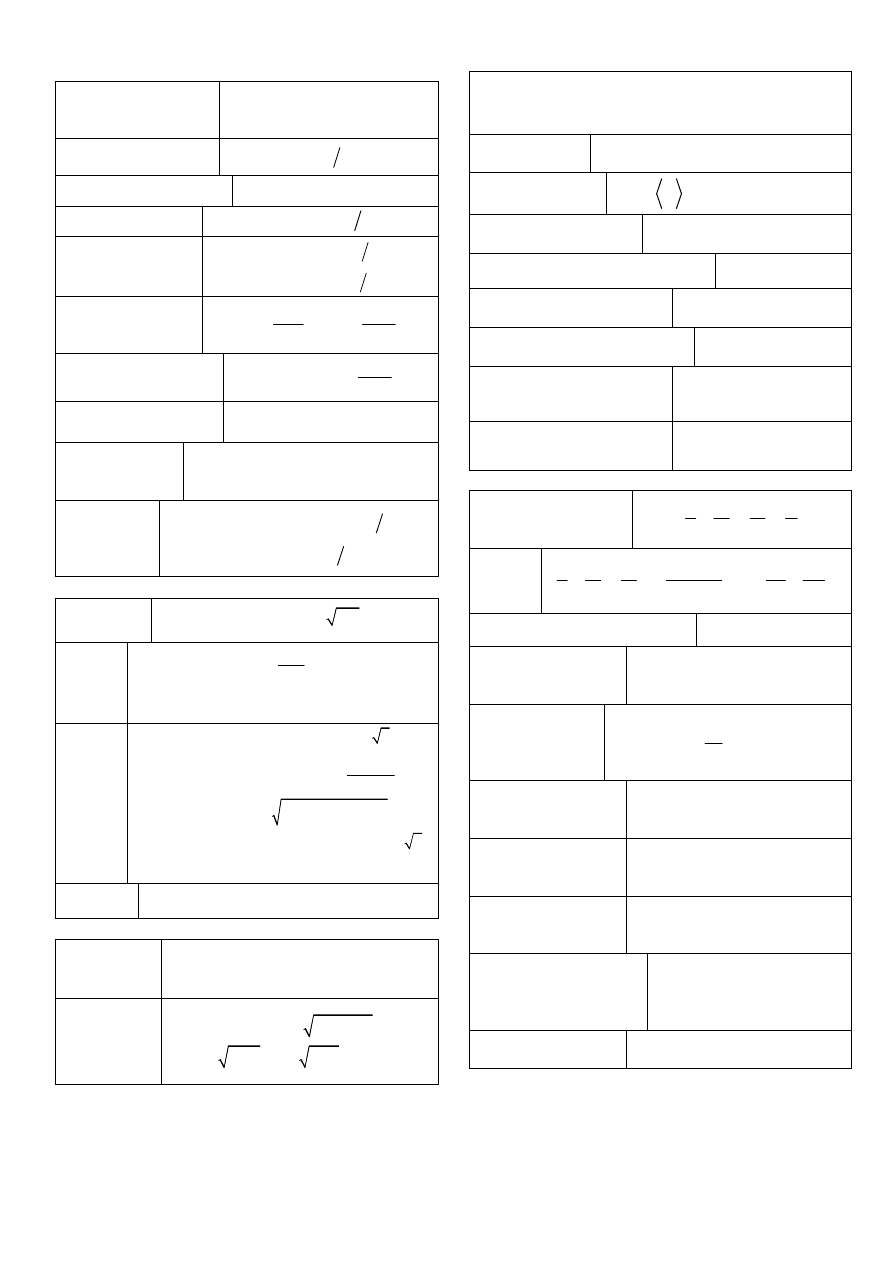
7
Indukcja elektromagnetyczna, magnetyzm materii
Strumień
magnetyczny
mag.
d
Φ
=
⋅
∫
B
S
Prawo Faradaya
SEM
mag.
d
d
d
t
ε
= − Φ
=
⋅
∫
E L
Indukcyjność cewki
mag.
/
L
N
I
= Φ
SEM samoindukcji
SEM
d d
L I
t
ε
= −
Indukcyjność
wzajemna
t
I
M
t
I
M
d
d
d
d
1
(2)
SEM
2
(1)
SEM
−
=
−
=
ε
ε
Szeregowy obwód
RL – włączanie
prądu
( )
SEM
1 exp
t R
t
R
L
I
ε
− ⋅
−
=
Szeregowy obwód RL
– wyłączanie prądu
( )
0
exp
t R
t
I
L
I
− ⋅
⋅
=
Energia pola
magnetycznego cewki
2
mag.
/ 2
E
LI
=
Gęstość energii
pola
magnetycznego
2
mag.
r
0
/ 2
/ 2
u
H
µ µ
= ⋅
=
B H
Uogólnione
prawo
Ampere’a-
Maxwella
0
r
0
r
elektr.
0
r
p
elektr.
p
d
d
d
d
d
t
I
t
I
µ µ ε ε
µ µ
µε
µ
⋅
=
Φ
+
+
=
Φ
+
∫
B
L
Drgania elektromagnetyczne i prąd zmienny
Obwód
LC
( )
( )
{
}
max
cos
/
t
t
LC
q
q
ϕ
⋅
+
=
Obwód
RLC
( )
(
)
(
)
( )
max
2
2
2
exp
cos
;
2
1/
/ 2
Rt
t
t
L
LC
R
L
q
q
ϕ
−
⋅
Ω +
Ω =
−
=
Obwód
RLC:
wymu-
szone
drgania
elektry
-czne
( )
(
)
( )
(
)
(
)
max
wym.
sk.
max
L
C
max
wym.
2
2
max
max
max
L
C
L
wym.
C
wym.
sk.
max
sk. sk.
sin
,
2,
sin
, tg
,
(
)
,
,
1
,
2,
cos .
/
/
/
/
/
t
t
R
R
I t
I
t
R
I
Z
R
R
R
R
L R
C I
I
P
I
ω
ω
ϕ
ϕ
ω
ω
ε
ϕ
ε
ε
ε
ε
ε
ε
⋅
⋅
−
=
⋅
⋅ −
=
=
=
+
−
=
⋅
=
⋅
=
=
=
=
Transfor-
matory
w
p
w
p
w
p
p
w
/
;
/
U
U N
N I
I N
N
=
=
Fale elektromagnetyczne
Pole fali
( )
( )
max
max
,
sin(
),
,
sin(
)
x t
kx
t
x t
kx
t
E
E
B
B
ω
ω
⋅
−
⋅
−
=
=
Prędkość
max
max
0
r
0 r
0
0
0 0
r
r
1
/ ,
1
,
/
/
/
c
n
c
n
c
E
B
µ µ ε ε
µ ε
µ ε
=
=
=
=
=
Fale elektromagnetyczne c.d.
Wektor
Poyntinga
(
)
(
)
0
r
/
µ µ
=
=
S
E × H
E × B
Natężenie średnie
fali
(
)
2
0
r
max
2
/
I
c
E
ε ε
=
=
S
Natężenie w odległości
r od źródła fali
( )
(
)
2
ź
ródla
/ 4π
I r
P
r
=
Ciśnienie fali – pełna absorpcja
/
p
I c
=
Ciśnienie fali – pełne
odbicie
2
/
p
I c
=
Natężenie światła
spolaryzowanego
spol.
niespol.
2
/
I
I
=
Prawo Malusa
( )
0
2
spol.
spol.
cos
I
I
=
Θ
Prawe załamania
1
1
2
2
sin
sin
n
n
Θ =
Θ
Zwierciadła i soczewki. Interferencja. Dyfrakcja
Zwierciadła sferyczne
,
1
1
1
2
s
f
r
s
+ = =
Cienkie
soczew
ki
soczewki
,
otoczenia
1
2
1
1
1
1
1
1
n
s
f
n
R
R
s
+ = =
−
−
Długość fali w ośrodku
0
/ n
λ λ
=
Doświadczenie
Younga – interfere- -
-ncja konstruktywna
sin
;
0, 1, 2,....
d
m
m
λ
⋅
Θ = ⋅
= ± ±
Interferencja
konstruktywna
w cienkich
warstwach
(
)
2
2
1
;
0, 1, 2,....
2
d
m
m
n
λ
=
+
= ± ±
Dyfrakcja na
pojedynczej
szczelinie - minima
sin
;
1, 2,....
a
m
m
λ
⋅
Θ = ⋅
= ± ±
Dyfrakcja na
okrągłej
szczelinie - minima
(
)
sin
1, 22
/ d
λ
Θ =
Dyfrakcja na siatce
dyfrakcyjnej -
maksima
sin
;
0, 1, 2,....
d
m
m
λ
⋅
Θ = ⋅
= ± ±
Dyfrakcja na siatce
krystalograficznej –
maksima, warunek
Bragga
(
)
o
cos 90
,
1, 2,....
d
m
m
λ
⋅
− Θ = ⋅
=
Kryterium Rayleigha
(
)
R
1, 22
/ D
λ
Θ =
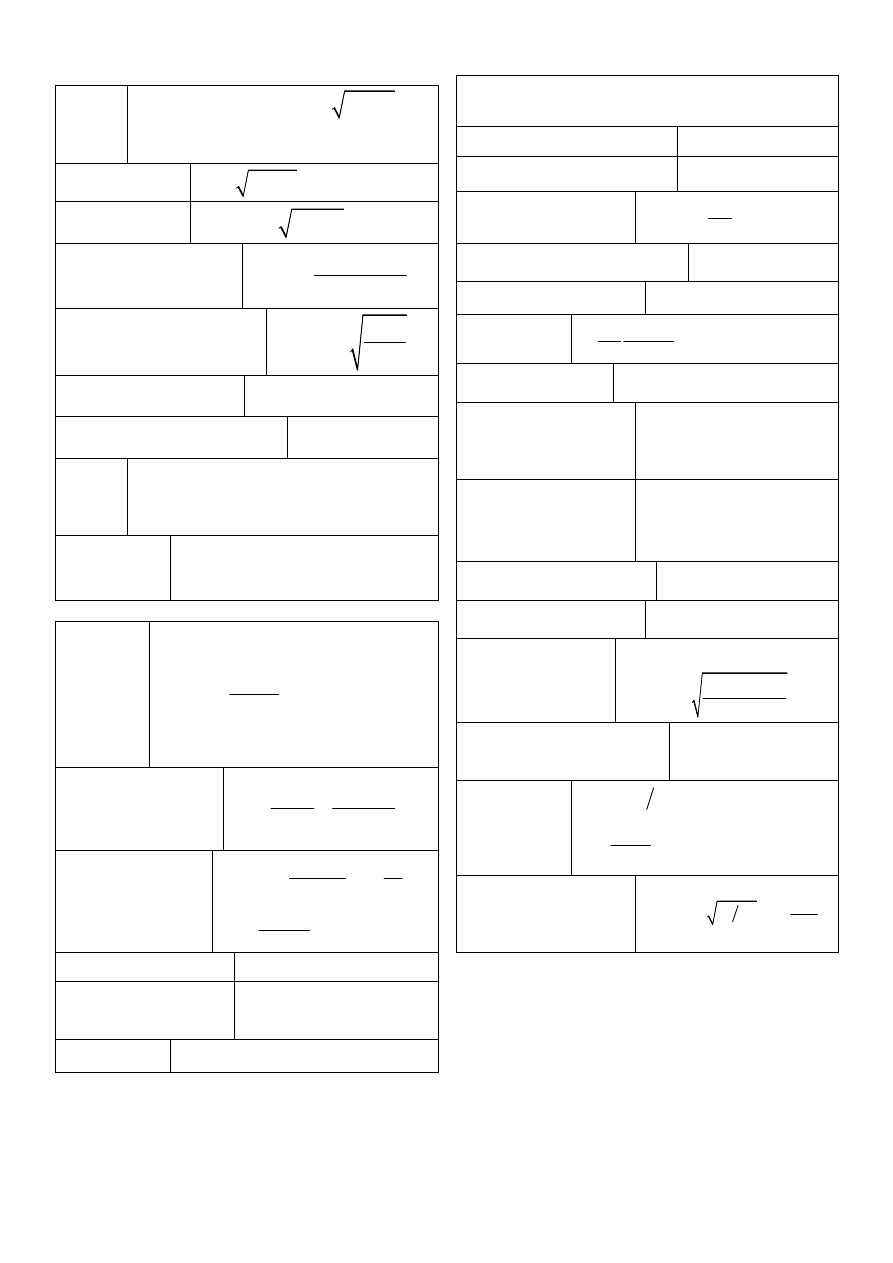
8
Szczególna teoria względności
Transfor
-macje
Lorentza
(
)
(
)
,
2
,
,
,
2
,
1/ 1
,
,
,
/
x
x Vt
y
y z
z t
t Vx c
γ
γ
β
γ
=
−
=
−
=
=
=
−
Dylatacja czasu
2
0
1
,
/
t
t
V c
β
β
∆ ⋅
−
= ∆
=
Skrócenie
długości
2
0
1
L
L
β
⋅
−
=
Transformacja
prędkości
'
'
2
1
/
x
x
x
V
V
V
V V c
+
=
+
Relatywistyczny efekt
Dopplera – źródło oddala
się
0
1
1
f
f
β
β
−
=
+
Pęd relatywistyczny
0
p
m
γ
=
V
Całkowita energia
relatywistyczna
calk.
2
rel.
0
E
m c
γ
=
Relatywi
styczna
energia i
pęd
(
)
( )
(
)
( )
(
)
2
2
2
calk.
2
rel.
0
2
2
kinetyczna
kinetyczna
2
rel.
rel.
0
,
2
E
pc
m c
pc
E
E
m c
=
+
=
+
Relatywistyc
zna energia
kinetyczna
(
)
kinetyczna
2
rel.
0
calk.
2
rel.
0
1
E
m c
E
m c
γ
=
−
=
=
−
Fotony i fale materii
Promień
n-tej
orbity
modelu
Bohra
atomu
wodoru
2
2
2
11
0
2
e
5,3 10
m
π
m
n
h
r
n
n
e
ε
−
=
=
⋅
⋅
Prędkość elektronu
na n-tej orbicie
modelu Bohra
atomu wodoru
2
6
0
2,19 10
m/s
2h
n
e
v
n
n
ε
⋅
=
=
Poziomy
energetyczne
elektronu w atomie
wodoru
4
1
2
2
2
2
0
2
8
13, 6eV
,
1, 2, 3,...
e
n
m e
E
E
h
n
n
n
n
ε
= −
= −
=
= −
=
Kwant energii (foton)
E
h
υ
=
Prawo Stefana-
Boltzmanna
4
8
2
4
;
6 10 W /(m K )
T
σ
σ
−
Φ =
≈ ⋅
Pęd fotonu
/
/
/
p
E c
h
c
h
υ
λ
=
=
=
Fotony i fale materii c.d.
Prawo Wiena
max .
const.
T
λ
⋅ =
Równanie Einsteina fotoefektu
kin
e
h
E
W
υ
=
+
Przesunięcie Comptona
(
)
1 cos
h
mc
λ
φ
∆ =
−
Minimalna energii kreacji
cząstka-antycząstka
2
min
0
2
E
m c
=
Hipoteza de Broglie’a
/
h p
λ
=
Równanie
Schrödingera
( )
( ) ( )
( )
2
2
2
d
2m
dx
x
U x
x
E
x
ψ
ψ
ψ
−
+
=
ℏ
Funkcja falowa
stanu stacjonarnego
( )
( ) (
)
exp
/
x
x
iEt
ψ
Ψ
=
−
ℏ
Zasada nieoznaczoności
dla pojedynczego
pomiaru
;
;
x
y
z
p
x
p
y
p
z
∆ ∆ ≥
∆ ∆ ≥
∆ ∆ ≥
ℏ
ℏ
ℏ
Zasada nieoznaczoności
dla serii pomiarów
( )
( )
( )
(
)
/ 4;
(
)
/ 4;
(
)
/ 4
x
y
y
p
x
p
y
p
y
σ
σ
σ
σ
σ
σ
≥
≥
≥
ℏ
ℏ
ℏ
Zasada nieoznaczoności
dla pojedynczego pomiaru
E t
∆ ∆ ≥
ℏ
Zasada nieoznaczoności
dla serii pomiarów
( ) ( )
/ 4
E
t
σ
σ
≥
ℏ
Tunelowanie
kwantowe
(
)
(
)
0
2
exp
2
,
2
T
kL
m U
E
k
≈
−
−
=
ℏ
Długości fal materii cząstki
kwantowej w bardzo
głębokiej studni potencjalnej
2 / ;
1, 2,3,...
n
L n
n
λ
=
=
Energia cząstki
kwantowej
w bardzo
głębokiej studni
potencjalnej
(
)
2
2
2
2
2
1
2
2
/
/ 2
,
1, 2,3,...
8
n
n
n
E
p
m
h
m
h
n
E n n
mL
λ
=
=
=
=
=
=
Funkcja falowa cząstki
kwantowej w bardzo
głębokiej studni
potencjalnej
( )
( )
π
2
sin
n
n x
x
L
L
ψ
=
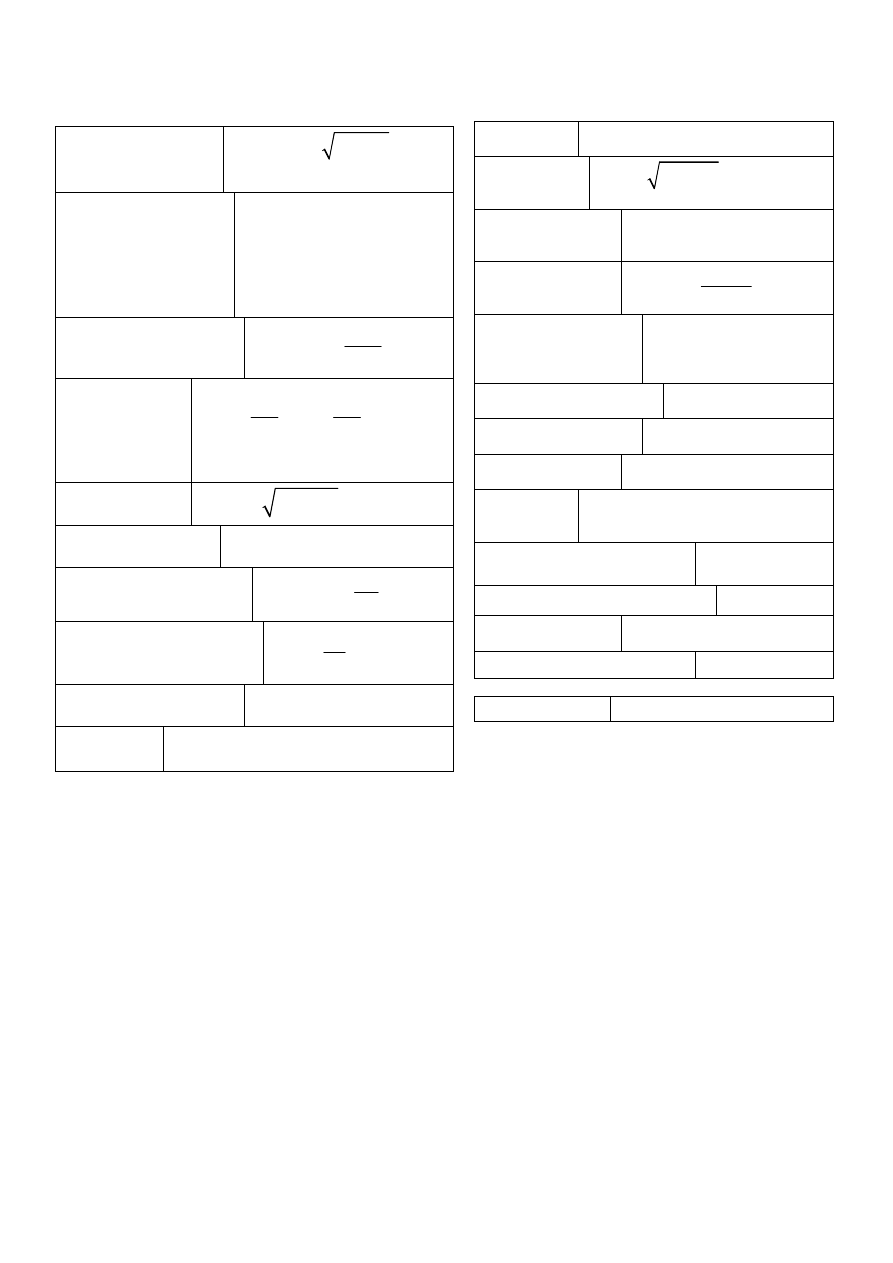
9
Atomy wieloelektronowe
Kwantowanie
orbitalnego moment
pędu L
o
elektronu
(
)
orb
1 ,
0,1,...,
1
L
l l
l
n
=
+
=
−
ℏ
Kwantowanie
przestrzenne orbi-
talnego moment pędu
L elektro
-nu - rzut L na
dowolną oś OZ
Z
orb
Z
Z
,
,
1,
,
1,
L
m
m
l
l
l
l
=
= − − +
−
ℏ
…
Orbitalny moment
magnetyczny elektronu
orb.
orb.
e
e
2m
L
µ
= −
⋅
Kwantowanie
orbitalnego
momentu
magnetycznego
elektronu
Z
Z
orb
orb
Z
B
Z
e
e
e
e
,
2m
2m
,
1,... 1, 0,1,...,
1,
z
L
m
m
m
l
l
l
l
µ
µ
= −
⋅
= −
= −
= − − +
−
−
ℏ
Spin S
elektronu
(
)
1 ,
1/ 2
S
s s
s
=
+
=
ℏ
Kwantowanie spinu
S elektronu
Z
S
S
;
1/ 2
S
m
m
=
= ±
ℏ
Spinowy moment
magnetyczny elektronu
s
e
e
m
= −
⋅
µ
S
Kwantowanie spinowego
momentu magnetycznego
elektronu
Z
S
Z
S
B
e
e
2
m
S
m
µ
µ
= −
⋅
= −
Granica krótkofalowa
promieniowania X
min
e
/
hc E
λ
=
Prawo
Moseleya
(
)
(
)
2
15
2, 48 10 Hz
1
f
Z
⋅
−
=
Włodzimierz Salejda
Fizyka jądrowa i energia jądrowa
Promień
jądra
1 / 3
0
0
,
1, 2 fm
r
r A
r
=
=
Spin S pro-
tonu/neutron
u
(
)
1 ,
1/ 2
S
s s
s
=
+
=
ℏ
Kwantowanie
spinu S
protonu/neutronu
Z
S
S
;
1/ 2
S
m
m
=
= ±
ℏ
Jądrowy magneton
J
proton
e
2m
µ
=
Kwantowanie
momentu
magnetycznego
protonu
Z
p
J
2, 7928
µ
µ
= ±
Kwantowanie momentu
magnetycznego neutronu
Z
n
J
1,9130
µ
µ
= ±
Prawo rozpadu promie-
niotwórczego
( )
( )
0
exp
t
t
N
N
λ
−
=
Aktywność
promieniotwórcza
( )
( )
R t
N t
λ
=
Energia wią-
zania jądra
atomowego
(
)
2
B
H
H
A
Z
E
Z M
N M
M c
=
⋅
+
⋅
−
Warunek kontrolowanej fuzji
izotopów wodoru
20
3
10 s/m
n
τ
>
Energia wiązania jednego nukleon
B
/
E
A
Defekt masy
reakcji jądrowej
początkowa
końcowa
M
M
M
∆ =
−
Energia reakcji jądrowej
(
)
2
Q
M c
= ∆
Rozszerzający się Wszechświat
Prawo Hubble’a
18
-1
0
0
;
~ 2, 3 10
s
v
H r H
−
=
≈
⋅
10
11
12
13