1

PODSTAWY STATYSTYKI I EKONOMETRII

CZ. 2

DR INŻ. TOMASZ BUDZYŃSKI

SPIS TREŚCI

Spis treści

1. Wstęp

2. Model ekonometryczny i jego elementy

2.1. Model regresji

2.2. Proces budowy modelu regresji

3. Przykłady budowy modelu ekonometrycznego (modelu regresji)

3.1. Budowa modelu ekonometrycznego (modelu regresji wielokrotnej) dla potrzeb

określenia wartości rynkowej nieruchomości gruntowej niezabudowanej

3.2. Budowa modelu ekonometrycznego (modelu regresji wielokrotnej) dla potrzeb

określenia wartości rynkowej nieruchomości lokalowej stanowiącej lokal mieszkalny

2

2

2

4

11

11

17

Załącznik

Rozkład t-Studenta

2

1. Wstęp

Niniejsze opracowanie zostało sporządzone dla potrzeb realizacji minimalnych wymogów
programowych na studiach podyplomowych w zakresie wyceny nieruchomości, określonych
przez Ministra Infrastruktury w rozporządzeniu z dnia 7 czerwca 2010 r. Zawiera ono
zgodnie z ww. wymogami jedynie podstawy ekonometrii niezbędne rzeczoznawcom
majątkowym w procesie wyceny nieruchomości.

2. Model ekonometryczny i jego elementy

Model ekonometryczny jest to formalny opis stochastycznej zależności zjawiska lub
przebiegu procesu ekonomicznego od czynników, które je kształtują, wyrażony w formie
pojedynczego równania bądź układu równań. W dalszej części konspektu będziemy używać
pojęcia używanego w statystyce tj. modelu regresji.

Można wyróżnić modele regresji:



wielokrotnej - dla przypadku dwóch i więcej zmiennych objaśniających,



prostej - dla przypadku jednej zmiennej objaśniającej.

Do budowy modeli regresji stosowana jest analiza regresji, pozwalająca na wykrywanie
zależności między zjawiskami, badanie siły zależności, wyjaśnianie ich oraz przewidywanie
wielkości jednego ze zjawisk na podstawie wielkości innych.

2.1. Model regresji

Stosując model regresji zakładamy, że istnieje zależność między co najmniej dwoma
zjawiskami oraz że wzrostowi jednej z badanych wielkości towarzyszy wzrost lub spadek
drugiej.

Model regresji w postaci addytywnej wyraża się wzorem:







)

(

i

x

f

Y

i=1,2, ..., k

(1)

a w postaci multiplikatywnej



)

(

i

x

f

Y



i=1,2, .., k

(2)

gdzie:

Y- zmienna zależna (objaśniana),

x

i

- zmienne niezależne (objaśniające)



-składnik losowy wyrażający tak zwany błąd w równaniu, czyli wpływ na Y czynników

nie uwzględnionych w modelu w sposób bezpośredni.

3

W modelu wartości nieruchomości zmienną objaśnianą jest cena transakcyjna a zmiennymi
objaśniającymi – cechy nieruchomości wpływające na zmienność cen a przez to na wartość.

Jeżeli założymy, że model jest liniowy i występuje w nim tylko jedna zmienna objaśniająca
wówczas model taki nazywamy liniowym modelem regresji prostej (dwuwymiarowej). Ma on
następującą postać













1

1

0

X

Y

(3)

gdzie:

Y- zmienna objaśniana

X

1

- zmienna objaśniająca



0,



1

- nieznane parametry strukturalne modelu



- składnik losowy

Jeżeli model (3) uogólnimy na dowolną liczbę zmiennych objaśniających to nazywany

jest on liniowym modelem regresji wielokrotnej (wielorakiej) i przyjmuje on następującą
postać:























n

n

X

X

X

Y

...

2

2

1

1

0

(4)

gdzie:

Y- zmienna objaśniana

X

1,

X

2

,,..., X

n

- zmienne objaśniające



0,



1

,...,



n

- nieznane parametry strukturalne modelu



- składnik losowy

Aby uwzględnić w jednym modelu wpływ wielu cech nieruchomości na jej wartość oprócz
przedstawionego wyżej modelu regresji wielokrotnej, można również zastosować model
zaproponowany przez Czaję – model wielu regresji prostych (dwuwymiarowych), opisujący
związek między ceną i cechami nieruchomości za pomocą kilku niezależnych modeli regresji
prostej. W metodzie tej wartość nieruchomości oblicza się jako średnią ważoną z wartości
nieruchomości uzyskanych z modelu regresji prostej. Wagi dla tych wartości stanowi
współczynnik r

2

(kwadrat wartości współczynnika korelacji liniowej Pearsona dla

poszczególnych zmiennych niezależnych (cech nieruchomości) i zmiennej zależnej (ceny
nieruchomości)) lub też współczynnik determinacji R

2

wyznaczony dla niezależnych modeli

regresji prostej.

4

2.2. Proces budowy modelu regresji

W celu stworzenia i zastosowania modelu regresji (w nazewnictwie ekonometrii zwanego
jednorównaniowym modelem ekonometrycznym) stosuje się 4-etapową procedurę
modelowania:

1. Merytoryczna analiza zjawiska i konstrukcja modelu;

2. Estymacja parametrów modelu;

3. Weryfikacja modelu;

4. Zastosowanie modelu.

2.2.1. Merytoryczna analiza zjawiska i konstrukcja modelu

Etap merytorycznej analizy zjawiska i konstrukcji modelu w procesie wyceny nieruchomości
obejmuje:

1. określenie zestawu cech zmiennych (cech rynkowych) i ich opis w przyjętej skali

liczbowej,

2. określenie postaci analitycznej modelu.

Określenie zestawu cech zmiennych wymaga wyodrębnienia grupy cech nieruchomości
wpływających na zmienność cen a przez to na wartość nieruchomości.

Kolejnym krokiem w I etapie modelowania jest opisanie w przyjętej skali liczbowej cech
mogących potencjalnie wpływać na wartość nieruchomości. Cechy te można podzielić na:
cechy ilościowe i cechy jakościowe lub odpowiednio mierzalne i niemierzalne. Dla cechy
ilościowej jej wartość może przyjmować bezwzględną wartość cechy np. powierzchnia
wyrażona w m

2

. Natomiast dla cechy jakościowej jej wartość przedstawia się na skali

interwałowej, na której mają znaczenie różnice między tymi wartościami np. cecha
lokalizacja wyrażona na skali porządkowej bardzo dobra – dobra - zła przyjmuje wartości na
skali interwałowej odpowiednio np. 4-2-1.

W przypadku budowy modelu regresji wielokrotnej ważnym zagadnieniem jest wybór
właściwych zmiennych objaśniających (cech nieruchomości). Dokonywany jest on ze zbioru
zmiennych potencjalnych, poprzez ich redukcję w podzbiór zmiennych dopuszczalnych.
Ogólną zasadą wyboru zmiennych jest preferowanie takich zmiennych objaśniających X

i

,

które są silnie (statystycznie istotnie) powiązane ze zmienną objaśnianą Y

i

i jednocześnie

słabo (nie są statystycznie istotnie) powiązane parami – to jest między sobą. Zasadę tę można
zrealizować opierając się na analizy macierzy współczynników korelacji par zmiennych
(macierzy współczynników korelacji zupełnej) i eliminacji tych zmiennych objaśniających,
których współczynniki korelacji:

 ze zmienną objaśniana są niskie lub nieistotne statystycznie,

5

 pomiędzy zmiennymi objaśniającymi są wysokie lub istotne statystycznie.

Przyjmuje się, że korelacja jest:

 słaba (niski współczynnik korelacji) gdy |r|<=0.3

 silna (wysoki współczynnik korelacji) gdy |r|>0.6

Kolejnym krokiem w tym etapie modelowania ekonometryczne jest określenie postaci
analitycznej modelu. Oznacza to konieczność określenia postaci funkcji, która będzie
opisywała zależność pomiędzy zmienną objaśnianą - wartością nieruchomości (ceną
transakcyjną) a zmiennymi objaśniającymi – cechami nieruchomości.

Modele regresji ze względu na postać analityczną zależności funkcyjnych modelu dzieli się
na:

 modele liniowe , w którym wszystkie zależności modelu są liniowe,

 modele nieliniowe, w których chociaż jedna zależność modelu jest nieliniowa.

Najczęściej w wycenie nieruchomości stosuje się modele liniowe lub modele nieliniowe
zawierające funkcje nieliniowe np. wielomianowe, które przed wyznaczeniem parametrów
modelu można doprowadzić do postaci liniowej. Popularność wspomnianych modeli wynika
z:

 prostoty rozwiązywania liniowych układów równań za pomocą wielu skutecznych

algorytmów algebry liniowej m.in. klasycznej metody najmniejszych kwadratów;

 łatwości w interpretacji wyników.

2.2.2. Estymacja parametrów modelu

Metody estymacji parametrów modelu można podzielić na:

 metody estymacji modeli liniowych,

 metody estymacji modeli nieliniowych.

Najczęściej stosowaną metodą estymacji parametrów modeli liniowych jest klasyczna metoda
najmniejszych kwadratów. Polega na spełnieniu warunku [vv]=min gdzie v stanowi różnicę
pomiędzy wartością nieruchomości wyliczoną z modelu a ceną transakcyjną.

Parametry strukturalne modelu oblicza się na podstawie wzoru:

A=(X

T

X)

-1

X

T

Y

(5)

gdzie:

A – wektor ocen nieznanych parametrów strukturalnych modelu

6

X – macierz wartości zmiennych objaśniających

Y – wektor wartości zmiennej objaśnianej

Metoda ta pozwala na oszacowanie dokładności wyznaczenia parametrów modelu.

Wymaga ona spełnienia kilku warunków:

1. Zmienne objaśniające są wielkościami nielosowymi i nie zachodzi między nimi

współliniowość;

2. Składnik losowy jest zmienną losową, której nadzieja matematyczna równa jest 0,

a wariancja stałą;

3. Obserwacje są niezależne;

4. Składnik losowy jest nieskorelowany ze zmiennymi objaśniającymi;

5. Liczba zmiennych objaśniających musi być mniejsza od liczby obserwacji;

6. Nie występują współzależności między składnikami losowymi poszczególnych równań

modelu (autokorelacja składnika losowego).

Estymacja parametrów modeli nieliniowych może odbywać się nieliniową metodą
najmniejszych kwadratów za pomocą m.in. następujących algorytmów:

 uogólniony proces Seidela,

 algorytm Centrum Quadricae,

 nieliniowy (kwadratowy) proces iteracyjny Newtona.

2.2.3. Weryfikacja modelu

Weryfikacja modelu składa się z dwóch części: weryfikacji merytorycznej oraz weryfikacji
statystycznej.

Podczas weryfikacji merytorycznej sprawdza się, czy zbudowany model jest zgodny z wiedzą
o badanym zjawisku i zdrowym rozsądkiem. Ocenia się zgodność znaków obliczonych
współczynników oraz wielkości oszacowanych współczynników. Negatywny wynik
weryfikacji merytorycznej np. niewłaściwe znaki współczynników w przypadku modelu
regresji wielokrotnej mogą świadczyć o: niewłaściwej postaci analitycznej modelu,
współliniowości zmiennych niezależnych, błędach przedstawienia zmiennych jakościowych
za pomocą liczb lub nieuwzględnieniu istotnej zmiennej niezależnej.

W ramach weryfikacji statystycznej sprawdza się, czy model spełnia postulaty statystyczne:
istotność zmiennych objaśniających, dopasowanie modelu do wyników obserwacji (cen
transakcyjnych) i pożądane właściwości składnika resztowego.

7

Weryfikacja statystyczna dotycząca dwóch pierwszych postulatów obejmuje:

 weryfikację hipotezy o nieistnieniu zależności między zbiorem zmiennych objaśniających

(cechami) a zmienną objaśnianą (ceną transakcyjną),

 weryfikację hipotezy o nieistotności parametrów regresji,

 ocenę współczynnika determinacji,

 ocenę błędu standardowego estymacji,

Weryfikacja hipotezy o nieistnieniu zależności między zbiorem zmiennych
objaśniających (cechami) a zmienną objaśnianą (ceną transakcyjną)

Hipotezę weryfikuje się za pomocą statystyki F, która przy spełnionym założeniu
o normalności rozkładu składnika losowego modelu (4) ma rozkład F-Snedecora.

Test F wykonuje się, testując hipotezę: H

0

:



1

, =



2

, = ... =



k

, = 0,

przy hipotezie alternatywnej H

1

: co najmniej jedno



1

różne od 0.

W celu weryfikacji hipotezy zerowej obliczoną wartość statystyki F porównuje się
z wartością krytyczną, odczytywaną z tabeli wartości krytycznych rozkładu F-Snedecora lub
obliczaną komputerowo za pomocą kalkulatora prawdopodobieństwa, dla przyjętego poziomu
istotności 0,05, określonej liczby zmiennych objaśniających i liczby stopni swobody równej
n-k-1 ( wg oznaczeń wzoru ( 6)).

Wartość statystyki F- Snedecora oblicza się ze wzoru:

F =

)

1

/(

]

1

2

)

ˆ

(

[

/

]

1

2

)

ˆ

(

[

















k

n

n

i

i

y

i

y

k

n

i

y

i

y

(6)

gdzie:

i

yˆ - kolejna cena estymowana

i

y

- średnia arytmetyczna obliczona z cen transakcyjnych

i

y

- kolejna cena transakcyjna

n - liczba obserwacji (cen transakcyjnych)

k - liczba zmiennych objaśniających (cech)

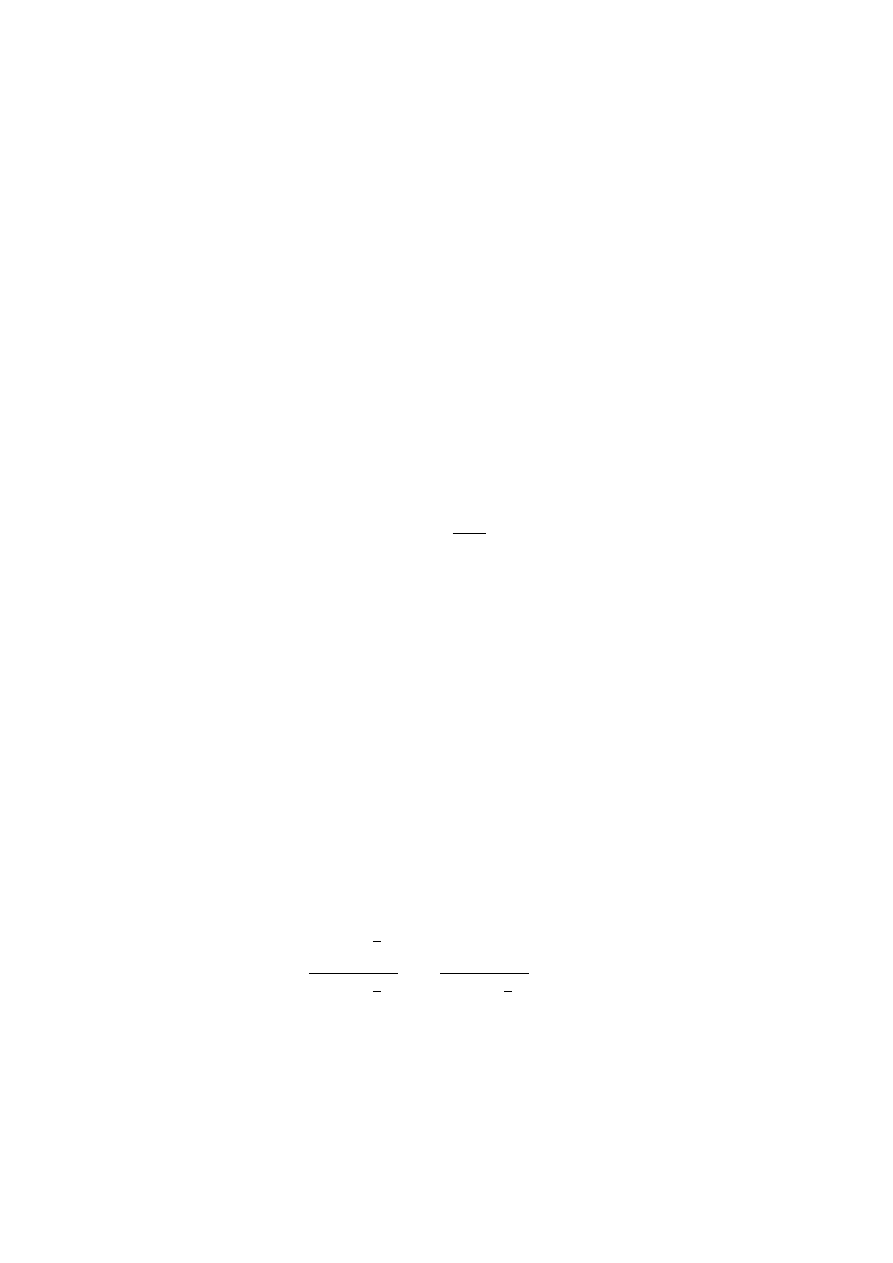
8

Jeżeli obliczona wartość statystyki F jest wyższa od wartości krytycznej to hipotezę zerową
o nieistnieniu zależności należy odrzucić. Oznacza to, że zależności opisane modelem nie
wystąpiły przypadkowo.

Weryfikacja hipotezy o nieistotności parametrów regresji

Hipotezę tę weryfikuje się, aby ocenić istotność poszczególnych zmiennych objaśniających.
W tym celu wykonuje się test t-Studenta, która przy spełnionym założeniu o normalności
rozkładu składnika losowego modelu (4) ma rozkład t-Studenta. Testem t-Studenta weryfikuje
się hipotezę zerową: H

0

:



i

= 0, przy hipotezie alternatywnej H

1

:



i

0



. W celu weryfikacji

hipotezy zerowej, oznaczającej brak wpływu zmiennej objaśniającej na zmienną objaśnianą,
obliczoną wartość statystyki t-Studenta porównuje się z wartością krytyczną, odczytywaną
z tabeli wartości krytycznych rozkładu t-Studenta lub obliczaną komputerowo za pomocą
kalkulatora prawdopodobieństwa, dla przyjętego poziomu istotności np. 0,05, określonej
liczby stopni swobody równej n-k-1 (wg oznaczeń wzoru (6)).

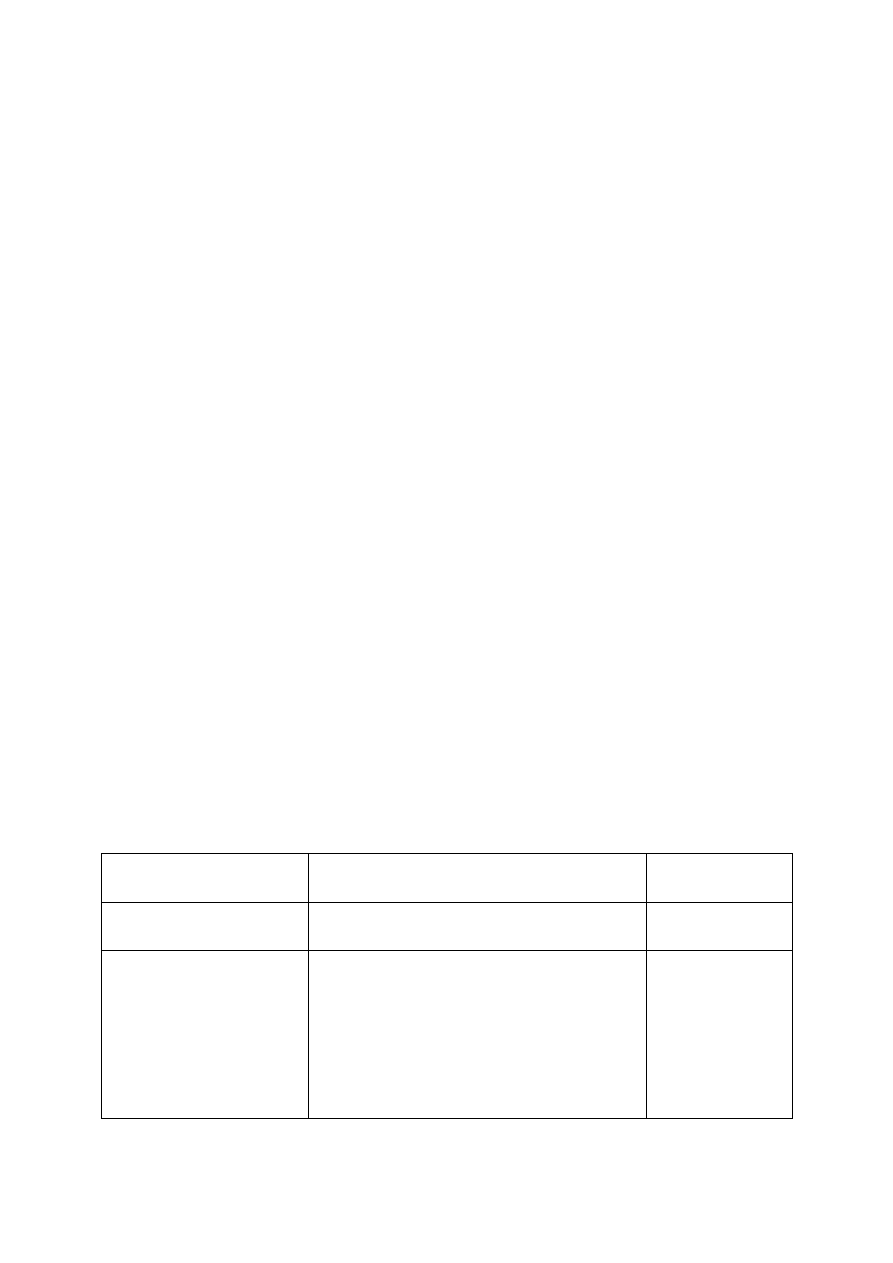
Wartość statystyki t-Studenta oblicza się ze wzoru:

i

S

i

t







(7)

gdzie:

i



- testowany parametr modelu regresji

i

S



- błąd standardowy parametru

i



Hipotezę zerową odrzuca się, jeżeli wartość bezwzględna statystyki t-Studenta jest wyższa od
wartości krytycznej. Jeśli tak jest, oznacza to, że przy wybranym poziomie istotności badana
zmienna objaśniająca (cecha) ma statystycznie istotny wpływ na zmienną objaśnianą (cenę).

Ocena współczynnika determinacji

Współczynnik determinacji R

2

jest miarą dopasowania modelu (4) do danych empirycznych.

Obliczany jest on na podstawie wzoru:































n

i

i

n

i

i

n

i

i

n

i

i

y

y

y

y

y

y

y

y

R

1

2

1

2

1

2

1

2

2

)

(

)

ˆ

(

1

)

(

)

ˆ

(

(8)

9

gdzie:

i

yˆ - kolejna cena estymowana

i

y

- średnia arytmetyczna obliczona z cen transakcyjnych,

i

y

- kolejna cena transakcyjna

Współczynnik determinacji R

2

wyrażony w procentach (100*R

2

) interpretowany jest jako

stopień wyjaśnienia całkowitej zmienności zmiennej objaśnianej (ceny) przez zmienność
zmiennych objaśniających (cech) występujących w modelu (4). Jest on liczbą z przedziału
<0,1>. Im wartość współczynnika determinacji bliższa jest jedności, tym lepiej model (4) jest
dopasowany do danego zbioru obserwacji (cen).

Niektórzy autorzy proponują zachowanie pewnej rezerwy przy stosowaniu współczynnika
determinacji R

2

ponieważ jego wysoka wartość wynika nie tylko z silnej korelacji między

zmiennymi objaśniającymi a zmienną objaśnianą, lecz również między zmiennymi
objaśniającymi. Uważają oni, że informacja jaką niesie o modelu współczynnik determinacji
może być fałszywa, jeśli w modelu występują zmienne objaśniające silnie skorelowane
z innymi zmiennymi objaśniającymi. Wówczas w modelu występuje zjawisko nazywane
efektem katalizy. Sprawdzenie występowania efektu katalizy można przeprowadzić za
pomocą miary zwanej natężeniem efektu katalizy określonej wzorem:

H

R





2



(9)

gdzie:

R

2

- współczynnik determinacji

H - integralna pojemność informacyjna zestawu zmiennych objaśniających modelu
obliczaną obliczana na podstawie wzoru:

,

1







k

i

i

h

H









i

ij

j

i

r

r

h

|

|

2

(10)

gdzie:

r

ij

- współczynniki korelacji liniowej Pearsona między zmiennymi objaśniającymi

r

j

- współczynniki korelacji liniowej Pearsona pomiędzy odpowiednią zmienną

objaśniającą a zmienną objaśnianą,

Ocena błędu standardowego estymacji

Błąd standardowy estymacji stanowi błąd, który jest możliwy do popełnienia w trakcie
określania wartości nieruchomości za pomocą modelu. Pokazuje on, o ile przeciętnie

10

odchylają się wartości obserwowane (ceny) od wartości teoretycznych obliczonych za
pomocą modelu.

Obliczany jest on na podstawie wzoru :

,

]

[

n

s





(11)

gdzie:

δ - odchylenie wartości obserwowanej (ceny) od wartości obliczonej z modelu

n – liczba obserwacji (cen)

Przy ocenie dokładności modelu można korzystać również z odchylenia przeciętnego
obliczanego na podstawie wzoru:

,

]

[

n

s





(12)

gdzie:

Δ = ((w-Wa)/w)*100%

w – cena transakcyjna

Wa – wartość wyliczona z modelu

Pożądane właściwości składnika resztowego

W celu weryfikacji statystycznej pożądanych właściwości składnika resztowego
przedmiotem analizy jest wektor reszt modelu (różnic między wartością empiryczną
a teoretyczną zmiennej objaśnianej), który uważa się za empiryczną realizację składnika
losowego modelu. Weryfikacja własności składnika losowego modelu składa z kilku kroków.
Obejmuje ona m.in. badanie losowości składnika losowego, badanie autokorelacji składnika
losowego, badanie normalności rozkładu składnika losowego.

Badanie losowości składnika losowego dokonuje się poprzez analizę losowego charakteru
reszt surowych lub standaryzowanych w drodze weryfikacji hipotezy zerowej

0

)

(

:

2

2

0





j

j

z

E

H



przy hipotezie alternatywnej

0

)

(

:

2

2

1





j

j

z

E

H



gdzie:

j



jest j-tym

składnikiem losowym a

j

z

jest j-tym składnikiem resztowym. W celu weryfikacji hipotezy

zerowej można zastosować test Walda-Wolfowitza.

W celu zbadania autokorelacji składnika losowego formułuje się hipotezę zerową H0: ρ = 0,
która oznacza nieskorelowanie składników losowych., przy hipotezie alternatywnej H1: ρ>0.
Do weryfikacji hipotezy zerowej najczęściej stosuje się test Durbina-Watsona.

11

Badanie normalności rozkładu składnika losowego wykonuje się porównując rozkładu
standaryzowanych reszt z standardowym rozkładem normalnym. Porównanie można
przeprowadzić: wizualnie z wykorzystaniem normalnego wykresu prawdopodobieństwa reszt
(gdy surowe reszty mają rozkład normalny to oczekiwane poziomy reszt standaryzowanych
mają przebieg liniowy) lub przy użyciu testów zgodności najczęściej testu chi-kwadrat.

2.2.4. Zastosowanie modelu

Uzyskany model stosuje się do określenia wartości jednostkowej nieruchomości poprzez
podstawienie do niego wartości cech opisujących szacowaną nieruchomość.

3. Przykłady budowy modelu ekonometrycznego (modelu regresji)

Poniżej przedstawiono proces budowy modelu ekonometrycznego ( modelu regresji
wielokrotnej) dla potrzeb:

1. określenia

wartości

rynkowej

nieruchomości

gruntowej

niezabudowanej

przeznaczonej pod zabudowę mieszkaniową jednorodzinną,

2. określenia wartości rynkowej nieruchomości lokalowej stanowiącej lokal mieszkalny.

3.1.

Budowa modelu ekonometrycznego (modelu regresji wielokrotnej) dla potrzeb

określenia wartości rynkowej nieruchomości gruntowej niezabudowanej

Proces budowy modelu ekonometrycznego obejmuje 4 etapy opisane w rozdziale 2.

3.1.1. Merytoryczna analiza zjawiska i konstrukcja modelu

1. Określenie zestawu cech zmiennych (cech rynkowych) i ich opis w przyjętej skali
liczbowej.

W celu zbadania, które cechy miały istotny wpływ na ceny tych nieruchomości, przyjęto
cechy (zmienne) i skale ocen (wartości zmiennej) podane w tabeli 1.

Tabela 1. Cechy nieruchomości i skale ocen

Cecha (zmienna)

(oznaczenie cechy)

Ocena

Wartości

zmiennej

Lokalizacja
(LOK)

centralna
peryferyjna

2
1

Powierzchnia działki
(POW)

od 5000 m2 (bardzo słaba)
od 2000 do 4999 m2 (słaba)
od 1000 do 1999 m2 (średnia)
od 500 do 999 m2 (dobra)
do 499 (bardzo dobra)

1
2
3
4
5

12

Uzbrojenie techniczne
(UZBR)

współczynniki określone (uzyskane z analizy
rynku) dla następujących mediów:

- energia elektryczna – 1,0
- gazociąg – 1,3
- wodociąg – 1,4

- kanalizacja – 1,0

Suma
współczynników
z kolumny Ocena

Dostęp komunikacyjny
(DK)

słaby
średni
dobry

1
2
3

Sąsiedztwo
(SĄS)

mało atrakcyjne
średnio atrakcyjne
atrakcyjne
bardzo atrakcyjne

1
2
3
4

Stan zagospodarowania i
ograniczenia w
użytkowaniu
(ZAG)

słaby
średni
dobry
bardzo dobry

1
2
3
4

Bazę sprzedanych nieruchomości gruntowych niezabudowanych przeznaczonych pod
zabudowę mieszkaniową jednorodzinną opisanych zgodnie z zasadami zawartymi
w powyższej tabeli 1 zawiera tabela 2.

Tabela 2. Baza danych transakcyjnych

Nr

CENA

[zł/m

2

]

LOK

POW

UZBR

DK

SĄS

ZAG

1

125,84

2

5

3,3

3

2

3

2

88,88

2

3

3,3

2

3

3

3

62,49

2

3

2

3

3

2

4

62,11

2

3

1

2

2

1

5

72,59

2

3

1

2

2

2

6

73,36

2

3

1

2

2

2

7

93,16

2

2

2,3

2

1

4

8

69,83

2

3

2,3

2

2

2

9

71,08

2

3

2

1

3

2

10

70,83

2

3

2

1

3

2

11

70,75

2

3

1

1

3

3

12

73,96

2

3

1

1

3

2

13

75,43

2

3

3,3

1

3

3

14

88,67

2

2

2,3

2

2

3

15

73,22

2

2

2

2

1

3

16

51,41

2

2

2

2

1

2

17

73,08

2

2

2

2

1

3

18

72,75

2

3

2

2

2

3

19

109,82

2

3

3,3

3

4

3

20

106,82

2

4

2,3

2

2

3

13

21

127,05

2

4

2,3

3

3

3

22

96,08

2

3

2,2

2

3

3

23

119,48

2

4

2,3

2

2

3

24

90,35

2

4

3,3

2

3

4

25

72,95

2

4

1

2

3

3

26

81,42

2

4

2,3

2

4

3

27

80,17

2

2

2,3

2

3

2

28

126,22

2

4

2,3

3

3

3

29

83,92

2

4

2,3

2

3

3

30

115,41

2

4

2,3

3

2

3

31

81,03

2

4

2,3

2

3

3

32

47,94

2

1

2

2

1

2

33

117,19

2

5

2,3

3

2

2

34

109,58

2

4

4,7

3

2

3

35

53,22

2

1

4,7

3

2

2

36

100,84

2

3

1

3

3

3

37

84,29

2

4

3,3

2

2

3

38

80,99

2

4

1

2

3

3

39

67,59

2

4

3,3

2

2

3

40

84,04

2

4

1

2

3

2

41

93,18

2

4

2,3

2

3

3

42

108,15

2

4

2,3

2

3

3

43

100,41

2

3

2,3

2

3

3

44

90,23

2

3

1

2

3

3

45

87,08

2

4

2,3

2

3

3

46

65,34

2

3

3,3

3

2

2

47

87,37

2

4

3,3

3

3

4

48

102,26

2

4

3,3

3

3

3

49

55,84

2

3

3,3

3

1

2

50

54,05

2

2

4,7

3

1

2

51

42,99

2

3

1

2

3

1

52

70,60

2

2

3,3

3

1

3

53

125,01

2

3

4,7

3

4

3

54

85,34

2

3

3,3

3

1

4

55

103,92

2

5

4,7

3

4

4

56

108,87

2

4

4,7

3

2

2

57

111,35

2

4

4,7

3

2

3

58

84,60

2

3

2

3

3

3

59

106,73

2

3

1

3

3

3

60

44,44

1

3

3,4

2

2

2

61

60,06

1

4

3,4

2

3

3

62

60,91

1

4

3,4

2

3

3

63

57,74

1

4

3,4

2

3

3

64

49,80

1

4

2,3

2

3

3

65

52,14

1

4

2,3

2

2

3

66

47,92

1

4

2,3

2

2

3

67

42,62

1

4

1

2

3

3

14

68

42,62

1

4

1

2

3

3

69

41,04

1

3

2,3

1

4

3

70

38,58

1

4

1

1

4

4

71

31,13

1

3

1

1

3

3

72

37,83

1

4

1

2

2

3

73

37,96

1

4

1

2

2

3

74

38,73

1

4

1

2

2

3

75

35,57

1

2

2,4

1

3

3

76

42,60

1

4

1,3

2

3

3

77

45,82

1

4

1,3

2

3

3

78

44,07

1

3

3,4

2

2

3

79

28,36

1

3

1

2

2

2

80

35,85

1

4

0

1

3

3

81

26,57

1

3

0

1

3

3

82

27,49

1

4

0

1

3

2

83

26,63

1

3

0

1

3

2

84

26,63

1

3

0

1

3

2

85

26,63

1

3

0

1

3

2

86

26,32

1

4

0

1

3

2

87

26,30

1

4

0

1

3

2

88

25,46

1

3

0

1

3

2

89

25,46

1

3

0

1

3

2

90

25,46

1

3

0

1

3

2

91

25,07

1

2

0

1

3

2

92

25,07

1

3

0

1

3

2

93

30,81

1

3

0

1

3

2

94

30,52

1

3

0

1

3

2

95

32,17

1

3

0

1

3

2

96

24,36

1

4

0

1

3

2

97

28,90

1

2

0

1

3

2

98

30,89

1

3

0

1

3

2

99

29,94

1

3

0

1

3

2

100

30,56

1

3

0

1

3

2

101

29,84

1

3

0

1

3

2

102

27,27

1

2

0

1

3

3

103

29,34

1

3

0

1

3

2

104

26,17

1

2

0

1

3

2

105

30,39

1

4

0

1

3

3

106

24,92

1

3

0

1

3

2

107

28,19

1

3

0

1

3

3

108

22,41

1

3

0

1

3

2

109

28,01

1

3

0

1

3

3

110

26,24

1

3

0

1

3

2

111

21,10

1

3

0

1

3

2

112

22,30

1

4

0

1

3

2

113

29,13

1

2

1

1

3

3

114

19,07

1

3

1

2

1

1

15

W celu doboru właściwych cech rynkowych – zmiennych niezależnych do modelu regresji
wielokrotnej, obliczono macierz współczynników korelacji liniowej (tabela 3) oraz
współczynniki korelacji cząstkowej (tabela 4) i dokonano ich analizy.

Tabela 3. Macierz współczynników korelacji liniowej

CENA LOK

POW

UZBR DK

SĄS

ZAG

CENA

1,00

0,85

0,30

0,69

0,75

-0,11

0,46

LOK

0,85

1,00

-0,00

0,62

0,67

-0,28

0,22

POW

0,30

-0,00

1,00

0,13

0,21

0,27

0,31

UZBR

0,69

0,62

0,13

1,00

0,76

-0,29

0,41

DK

0,75

0,67

0,21

0,76

1,00

-0,37

0,32

SĄS

-0,11

-0,28

0,27

-0,29

-0,37

1,00

0,09

ZAG

0,46

0,22

0,31

0,41

0,32

0,09

1,00

Tabela 4. Współczynniki korelacji cząstkowej

Cecha

Współczynniki

korelacji

cząstkowej

LOK

0,795723

POW

0,383905

UZBR

0,116524

DK

0,317048

SĄS

0,261611

ZAG

0,351292

Na podstawie analizy macierzy współczynników korelacji liniowej (tabela 3) oraz
współczynników korelacji cząstkowej (tabela 4) do budowy modelu regresji wielokrotnej
przyjęto następujące cechy: lokalizacja ogólna, powierzchnia działki, dostęp komunikacyjny,
sąsiedztwo i stan zagospodarowania.

2. Określenie postaci analitycznej modelu

Po analizie zależności cech rynkowych i ceny w oparciu o wykresy korelacyjne uznano, że
występujące zależności można przyjąć jako liniowe. Stąd budowany model będzie modelem
liniowej regresji wielokrotnej.

3.1.2. Estymacja parametrów modelu

Do estymacji parametrów modelu zastosowano metodę najmniejszych kwadratów,
wykorzystując program komputerowy STATISTICA.

Otrzymane wyniki prezentuje tabela 5.

16

Tabela 5. Podsumowanie regresji

Podsumowanie regresji zmiennej zależnej: CENA
R= ,93407490 R2= ,87249592 Popraw. R^2= ,86659295
F(5,108)=147,81 p<0,0000 Błąd std. estymacji: 11,475

Błąd st.

Błąd st.

BETA

BETA

B

B

t(108)

poziom p

W. wolny

-79,0020

7,288182

-10,8397

0,000000

LOK

0,670327

0,047380

41,9589

2,965744

14,1479

0,000000

POW

0,166734

0,039416

6,7243

1,589628

4,2301

0,000049

DK

0,252391

0,052861

10,6624

2,233152

4,7746

0,000006

SĄS

0,109895

0,040343

4,8204

1,769596

2,7240

0,007523

ZAG

0,169535

0,038129

8,3992

1,889033

4,4463

0,000021

Równanie modelu regresji wielokrotnej jest zatem następujące:

y=41,9589*x

LOK

+6,7243*x

POW

+10,6624*x

DK

+4,8204*x

SDZ

+8,3992*x

ZAG

-79,0020.

Dokładność modelu wyrażona poprzez błąd standardowy wynosi 11,48 zł/m

2

.

3.1.3. Weryfikacja modelu

Weryfikacja modelu składa się z dwóch części: weryfikacji merytorycznej oraz weryfikacji
statystycznej.

Weryfikacja merytoryczna modelu regresji

Wyniki analizy pod względem merytorycznym (wartości i znaki parametrów modelu)
ww. modelu nie odbiegają od tendencji obserwowanych na lokalnym rynku nieruchomości.

Weryfikacja statystyczna modelu regresji

Weryfikacja statystyczna modelu regresji następuje poprzez sprawdzenie postulatów
statystycznych:



istotność zmiennych objaśniających

Na poziomie istotności 0,05 odrzucono hipotezę o braku zależności pomiędzy
zmiennymi objaśniającymi a ceną transakcyjną jak również hipotezę o braku istotności
statystycznej parametrów regresji.



dopasowanie modelu do wyników obserwacji

Stwierdzono bardzo dobre dopasowanie modelu R

2

wyniosło 0, 87249592.



pożądane właściwości składnika resztowego m.in.:

-

autokorelacja składnika losowego

17

Wartość testu DW wynosząca 1,57 oznacza, że na poziomie istotności 0,05 została
odrzucona hipoteza zerowa o braku zjawiska autokorelacji reszt pierwszego rzędu.

-

normalność rozkładu składnika losowego

Oczekiwane poziomy reszt standaryzowanych miały przebieg liniowy co świadczyło
o spełnieniu założenia normalności rozkładu składnika losowego.

3.1.4. Zastosowanie modelu

Uzyskany model stosuje się do określenia wartości jednostkowej nieruchomości poprzez
podstawienie do niego wartości cech opisujących szacowaną nieruchomość.

3.2.

Budowa modelu ekonometrycznego (modelu regresji wielokrotnej) dla potrzeb

określenia wartości rynkowej nieruchomości lokalowej stanowiącej lokal mieszkalny

Proces budowy modelu ekonometrycznego obejmuje 4 etapy opisane w rozdziale 2.

3.2.1. Merytoryczna analiza zjawiska i konstrukcja modelu

1. Określenie zestawu cech zmiennych (cech rynkowych) i ich opis w przyjętej skali
liczbowej.

W celu zbadania, które cechy miały istotny wpływ na ceny tych nieruchomości, przyjęto
cechy (zmienne) i ich skale (wartości zmiennej) podane w poniższej tabeli 6.

Tabela 6. Cechy nieruchomości i skale ocen

Cecha (zmienna)
(oznaczenie cechy)

Opis

Ocena

Wartość

Lokalizacja
(LOK)

dzielnice:

Śródmieście,

Centrum,

Bolesława Prusa

dobra

3

dzielnica Bąki, osiedle Parkowe oraz
Lipowa Ostoja

przeciętna

2

osiedle Staszica cz. A oraz Staszica cz.
B, dzielnica: Gąsin i Żbików

słaba

1

Otoczenie
(OTOCZ)

budynek

otoczony

zabudową

jednorodzinną, oraz usytuowany w
bezpośrednim sąsiedztwie parku lub
otoczony w dużym stopniu zielenią

korzystne

3

budynek

charakteryzujący

się

przeciętnym otoczeniem

przeciętne

2

budynek

usytuowany

w

pobliżu

obiektów przemysłowych

niekorzystne

1

18

Dostępność
komunikacji i usług
(DKU)

bardzo dobry dostęp do komunikacji
publicznej, bezpośrednie sąsiedztwo
obiektów handlowo-usługowych oraz
obiektów użyteczności publicznej

bardzo
dobra

4

dobry

dostęp

do

komunikacji

publicznej, bliskie sąsiedztwo obiektów
handlowo-usługowych oraz łatwość w
dostępie do obiektów użyteczności
publicznej

dobra

3

słaby dostęp do komunikacji publicznej,
przeciętny

dostęp

do

obiektów

handlowo-usługowych oraz obiektów
użyteczności publicznej

przeciętna

2

utrudniony dostęp do komunikacji
publicznej, ograniczona ilość obiektów
handlowo-usługowych w sąsiedztwie
oraz trudność w dostępie do obiektów
użyteczności publicznej

słaba

1

Stan

techniczny

budynku
(STAN TECH)

budynek wykonany w nowoczesnej
technologii, wybudowany w 2000r.
i później

bardzo
dobry

4

budynek

wykonany

w

technologii

wielkiej płyty lub cegły, w którym
przeprowadzono gruntowne remonty,
niezależnie od roku budowy

dobry

3

budynek w technologii wielkiej płyty,
w którym przeprowadzono jedynie
drobne remonty, niezależnie od roku
budowy

przeciętny

2

budynek

z

cegły,

w

którym

przeprowadzono

jedynie

drobne

remonty, wybudowany do 1960r.

zły

1

Liczba izb (L IZB)

lokale jedno i dwuizbowe

bardzo
dobra

4

lokale trzy i czteroizbowe

dobra

2

lokale pięcioizbowe

słaba

1

W celu doboru właściwych cech rynkowych – zmiennych niezależnych do modelu regresji
wielokrotnej, obliczono macierz współczynników korelacji liniowej – tabela 7

19

Tabela 7. Macierz współczynników korelacji liniowej

LOK

OTOCZ

DKU

STAN
TECH

L IZB

CENA

LOK

1

0,2697

0,5529

0,3602

0,0856

0,4504

OTOCZ

0,2697

1

0,1498

0,2600

-0,0413

0,2864

DKU

0,5529

0,1498

1

-0,0820

-0,0438

0,2476

STAN
TECH

0,3602

0,2600

-0,0820

1

0,1442

0,4244

L IZB

0,0856

-0,0413

-0,0438

0,1442

1

0,1833

CENA

0,4504

0,2864

0,2476

0,4244

0,1833

1

Dokonując oceny współczynnika korelacji w parach cecha – cena można zauważyć, że
największa wartość współczynnika korelacji występuje dla atrybutów „lokalizacja” (0,4504)
oraz „stan techniczny” (0,4244), zatem mają one największy wpływ na zmienność cen.

Dokonując analizy, należy zauważyć, iż współczynnik korelacji pomiędzy cechą „dostępność
komunikacji i usług” oraz cechą „lokalizacja” charakteryzuje się wysoką wartością (0,5529).
Oznacza to, że atrybuty te są ze sobą ściśle skorelowane, więc opisują podobny zakres
zmienności cen transakcyjnych. Z tego powodu cechę „dostępność komunikacji i usług”
wyeliminowano z dalszych analiz.

Zatem ostatecznie do budowy modelu regresji wielokrotnej przyjęto następujące cechy:
lokalizacja, otoczenie, stan techniczny budynku, liczba izb.

2. Określenie postaci analitycznej modelu

Po analizie zależności cech rynkowych i ceny w oparciu o wykresy korelacyjne uznano, że
występujące zależności można przyjąć jako liniowe. Stąd budowany model będzie modelem
liniowej regresji wielokrotnej.

3.1.2. Estymacja parametrów modelu

Do estymacji parametrów modelu zastosowano metodę najmniejszych kwadratów,
wykorzystując program komputerowy STATISTICA.

Otrzymane wyniki prezentuje tabela 5.

20

Tabela 5. Podsumowanie regresji

Podsumowanie regresji zmiennej zależnej: CENA
R= , 55864469 R2= , 31208389 Popraw. R2= , 29752482
F(4,189)=21,436 p<0,0000 Błąd std. estymacji: 837,48

Błąd st.

Błąd st.

BETA

BETA

B

B

t(189)

poziom p

W. wolny

3431,666

315,1199

10,89003

0,000000

LOK

0,308509

0,066039

367,314

78,6269

4,67161

0,000006

OTOCZ

0,141234

0,063975

264,473

119,7994

2,20763

0,028474

STAN
TECH

0,258411

0,066385

260,268

66,8624

3,8926

0,000137

L IZB

0,125493

0,061264

126,517

61,7641

2,04839

0,041905

Równanie modelu regresji wielokrotnej jest zatem następujące:

y=367,314*x

LOK

+264,473*x

OTOCZ

+260,268*x

STAN TECH

+126,517*x

L IZB

+3431,67.

Dokładność modelu wyrażona poprzez błąd standardowy wynosi 837,48 zł/m

2

.

3.2.3. Weryfikacja modelu

Weryfikacja modelu składa się z dwóch części: weryfikacji merytorycznej oraz weryfikacji
statystycznej.

Weryfikacja merytoryczna modelu regresji

Dokonując oceny merytorycznej zbudowanego modelu, stwierdzono, że wartości
współczynników mają wartości dodatnie oraz pokazują prawdopodobny wpływ
poszczególnych cech nieruchomości na zmienność cen na lokalnym rynku nieruchomości.

Weryfikacja statystyczna modelu regresji

Weryfikacja statystyczna, polegająca na sprawdzeniu hipotez o braku zależności między
zmiennymi objaśniającymi a zmienna objaśnianą oraz o braku istotności statystycznej
parametrów regresji na poziomie istotności 0,05 w oparciu odpowiednio
o test F oraz test t-Studenta, przebiegła pomyślnie. Przeprowadzono także badanie
normalności składnika losowego, polegające na porównaniu rozkładu standaryzowanych reszt
modelu z rozkładem normalnym. Dokonano tego wizualnie, przy użyciu normalnego wykresu
prawdopodobieństwa reszt. Gdy surowe reszty mają rozkład normalny to oczekiwane
poziomy reszt standaryzowanych mają przebieg liniowy. Wykres nr 1 potwierdza
normalność rozkładu składnika losowego.

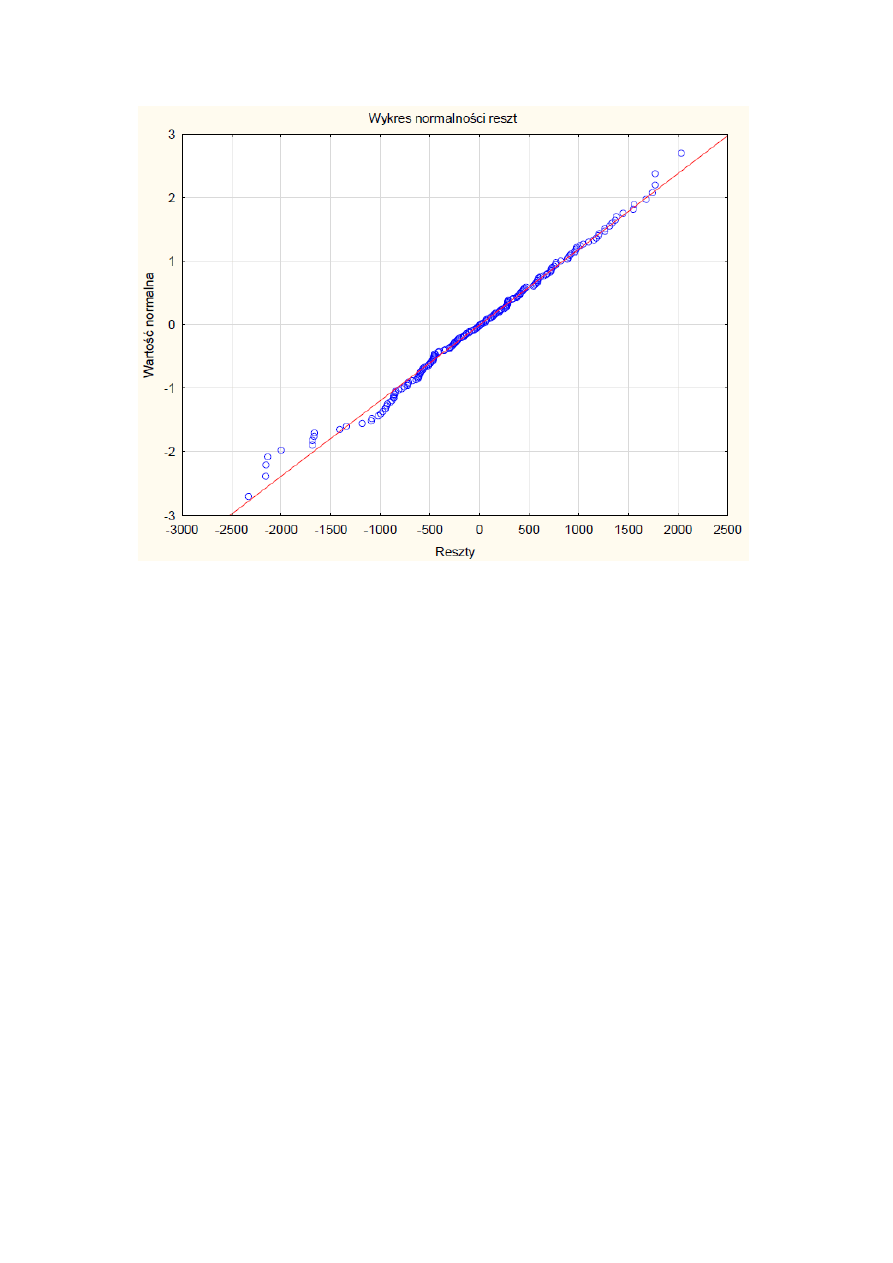
21

Wykres 1. Wykres normalności reszt.

Podsumowując, zbudowany model można uznać za statystycznie poprawny. Stwierdza się
jednak, na podstawie wartości współczynnika R

2

, że wyjaśnił on jedynie 31% zmienności cen

nieruchomości przyjętych do budowy modelu. Pozostała zmienność cen być może zależy od
innych czynników w tym czynników losowych. Dokładność modelu, wyrażona za pomocą
błędu standardowego wynosi 837,48zł/m2.

3.1.4. Zastosowanie modelu

Uzyskany model stosuje się do określenia wartości jednostkowej nieruchomości poprzez
podstawienie do niego wartości cech opisujących szacowaną nieruchomość.

Bibliografia

Adamczewski Z. 2002. Nieliniowe i nieklasyczne algorytmy w geodezji. Oficyna
Wydawnicza PW, Warszawa 2002

Adamczewski Z. 2011. Elementy modelowania matematycznego w wycenie nieruchomości.
Podejście porównawcze. Oficyna Wydawnicza PW, Warszawa 2011

Luszniewicz A. Słaby T. 2001. Statystyka z pakietem komputerowym STATISTICA PL.
Teoria i zastosowania. C.H. Beck. Warszawa 2001

Źróbek S. 2007. Metodyka określania wartości rynkowej nieruchomości. Educaterra 2007