1.1. Przedmiot ekonomii matematycznej

Przedmiotem ekonomii matematycznej są modeli realnych ekonomicznych procesów.

Model to jest obiekt, który zastępuje oryginał i odwzorowuje najistotniejsze dla danego badania cechy i właściwości oryginału.

Metoda ekonomii ekonomicznej to jest systemowa analiza ekonomiki jak skomplikowanego dynamicznego układu. Ekonomia Matematyczna tworze modele matematyczne w postaci założeń o powiązaniu zmiennych ekonomicznych. W skutek różnorodności podmiotów gospodarczych i zmienności warunków, Ekonomia Matematyczna dzieli się na szereg różnych modeli nie mających wartości uniwersalnej.

Główni podstawowe matematyczne modele mikro- i makroekonomii:

• Modele zachowania konsumenta

• Teoria produkcji

• Modele rynku

• Modele równowagi

• Modele wzrostu gospodarczego

• Modele cyklu koniunkturalnego

1.2. Modele zachowania konsumenta

Jednej z najistotniejszych pojęciem teorii ekonomicznej jest teoria konsumenta. Głównym pytaniem tu jest ustalenie konsumpcji dla danych cen na dobra i dochodzie.

Konkretna decyzja o zakupach określonego koszyka dóbr matematycznie może być pokazana jako wybór punktu w przestrzeni towarów. Niech
- jest ograniczona ilość dóbr, a
koszyk określonych dóbr w przestrzeni

Przestrzenią dóbr nazywa się zbiór wszystkich możliwych dóbr z dodatnimi współrzędnymi

.

W przestrzeni dóbr wprowadzimy normę

,

i odpowiednio metrykę (odległość pomiędzy elementami)

.

Przykład. 1.1 Narysować w przestrzeni dóbr wszystkie koszyki
, gdzie
są jajka,
męka. Obliczyć wielkość koszyka
i odległość pomiędzy koszykami
i
.

Rozwiązanie.

Wielkość koszyka:
.

Odległość:
.

Definicja 1.1. Zbiór
nazywa się
- otoczeniem.

Definicja 1.2. Zbiór
nazywa się otwarty, jeżeli każdy element x zbioru Y należy do niego razem z pewnym otoczeniem
.

Przykład. 1.2 Narysować w przestrzeni dóbr wszystkie koszyki należące do otoczenia
z przykładu 1.1.

Rozwiązanie.

Definicja 1.3. Punkt
nazywa się punktem brzegowym zboru A, gdy w dowolnym otoczeniu tego punktu znajdują się punkty należące i punkty nie należące do zbioru A.

Definicja 1.4. Zbiór
nazywa się domknięty, jeżeli Y jest sumą niektórego otwartego zbioru A i wszystkich brzegowych punktów A.

1.3. Ograniczenie budżetowe

Załóżmy, że możemy obserwować ceny wszystkich dóbr
, oraz budżet konsumenta
. Wtedy ograniczenie budżetowe może być zapisane jako

Zbiór punktów
, który spełniają ten warunek nazywa się zbiorem budżetowym lub zbiorem dopuszczalnych koszyków.

1.4. Własności zbioru budżetowego w
.

Definicja 1.5. Linią budżetu nazywamy zbiór koszyków
, który spełniają warunek

Równanie linię budżetu może być również zapisane w postaci

Jest to równanie prostej z nachyleniem
. Najprostszy sposób narysowania tej linii - to połączyć punkty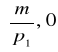
oraz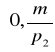
.

Nachylenie linii budżetu ma jasną interpretacje ekonomiczną: mierzy ono stopę według której konsument jest skłonny zamienić dobro 1 na dobro 2:

...

.

Występuje minus, ponieważ
zawsze mają znaki przeciwne.

Eliminacja jednego parametru.

1.5. Zmiany linii budżetu

Linia budżetu ma 3 parametry
, które mogą się zmienić. Z równania wynika, że wzrost dochodu (budżetu) przesunie równolegle do góry linię budżetu i nie zmieni kont nachylenia. Zmniejszenie ceny dobra 1 powoduje przesunięcie punktu przecięcia linii budżetu z poziomą osią na prawo. To znaczy, prosta staje się mniej stroma. Zmniejsza się kąt nachylenia.

Zmniejszenie ceny dobra 2 - bardziej stroma.

Zbiór budżetowy w przypadku racjonowania.

Rząd czasem nakłada ograniczenia w postaci racjonowania lub opodatkowania konsumpcji większej niektórego poziomu. Niech
- racjonowane dobro.

a) Kartki konsumpcyjne:
b)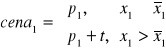
(t - podatek)

Później zobaczymy, że czasem sytuacji b) wynikają i w modelach bez racjonowania (konsumpcja międzyokresowa).

W teorii konsumpcji zakłada się, że każdy konsument ma własne preferencji na niektórym podzbiorze przestrzeni dóbr x. To oznacza, że dla dwóch dowolnych koszyków
i
konsument potrafi ich uszeregować według stopnia pożądania i zawsze mamy jedną z trzech relacji:

1. 
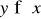
   , (mówimy y silnie preferowany nad x);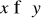

2. 
   , (mówimy x silnie preferowany nad y);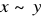

3. 
   , (koszyki x, y są obojętne (indyferentne)).

Wprowadzimy następujące relacji preferencji:

1. 
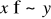
   , (mówimy x słabo preferowany nad y), co oznacza, że koszyk „y nie gorszy od koszyka x”.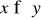

2. 
   
   , (mówimy x silnie preferowany nad y), co oznacza, że koszyk x jest z pewnością lepszy od koszyka y.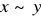

3. 
   , (koszyki x, y są obojętne (indyferentne)).

Pierwsza relacja nazywają się relacja słabej preferencji, druga relacja silnej preferencji, trzecia relacja indeferentności.

Podstawową relacją jest relacja słabej preferencji, na podstawie której możemy zdefiniować pozostałe relacji.

Definicja 1.5. Parę
nazywamy polem preferencji konsumenta.

Definicja 1.6. Niech
.

1. Mówimy, że koszyki x, y są indyferentne, jeżeli równocześnie
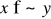
   i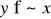
   .

2. Mówimy, że koszyk x jest silnie preferowany nad koszykiem y, jeżeli
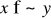
   i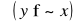
   

1.6. Właściwości preferencji.

Relacja słabej preferencji ma następujące właściwości:

1. Dla
   
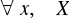
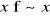
   (refleksyjność, zwrotność).

2. Dla
   
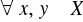
   (zupełność).

3. Jeżeli dla
   
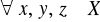
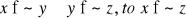
   (przechodniość, tranzytywność).

Aksjomat 3 wprowadza liniowy porządek w przestrzeni dóbr i daje możliwość konsumentowi zawsze dokonywać konkretnego wyboru i nie zamykać się w błędnym kole, natomiast aksjomat 2 wyklucza istnienie sytuacji, gdy konsument nie jest w stanie powiedzieć, który z koszyków jest lepszy.

Relacja indeferencji spełnia warunki ekwiwalentności:

1. Dla

(refleksyjność, zwrotność).

2. Dla


(symetryczność).

3. Jeżeli dla

(przechodniość, tranzytywność).

To znaczy, przestrzeń dóbr rozbija się na zbiory, które nie mają wspólnych punktów. Takie zbiory nazywają się obszary obojętności. Obszar obojętności w przypadku 2 dóbr nazywamy linią obojętności.

Własności relacji silnej preferencji.

1. Dla
   
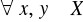
   (zupełność).

2. Jeżeli dla
   
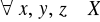
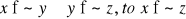
   (przechodniość, tranzytywność).

1.7. Dodatkowe założenia.

Definicja 1.7. Relację preferencji nazywamy ciągłą, jeżeli
zbiory
i
są zbiorami otwartymi w przestrzeni dóbr X.

Przykład. 1.3 Konsument kupuje bezpośrednio u rybaków skrzynie ze słabo słonymi śledziami. Relacja preferencji wygląda następująco: nie gorsze śledzie to takie, które są wcześniej wyłowione, ale nie wcześniej niż po 2 dobach i nie później niż po 5 dobach (tylko po takim terminie śledzie będą odpowiednio słone). Czy relacja preferencji jest relacją ekwiwalentności? Czy spełnia założenie zupełności? Czy relacja preferencji jest ciągła? Narysować na osi czasu wszystkie koszyki należące do otoczenia
i
.

Rozwiązanie.

Definicja 1.8. Niech M jest niepustym podzbiorem pola preferencji
.
nazywamy M - preferowanym koszykiem i oznaczamy

x=m.pref.M, jeżeli
jest słabo preferowany nad
.

Definicja 1.9. Zbiór M nazywa się wypukły, jeżeli dowolne dwa jego punkty można połączyć odcinkiem, należącym do zbioru M.

Definicja 1.10. Pole preferencji
nazywamy słabo wypukłe, jeżeli

1. Przestrzeń towarów jest zbiorem wypukłym

2. Dla
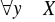
   zbiór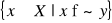
   jest zbiorem wypukłym w przestrzeni dóbr X.

Interpretacja w R²

Definicja 1.11. Pole preferencji
nazywamy silnie wypukłe, jeżeli

1. Przestrzeń towarów jest zbiorem wypukłym

2. Dla
   ,
   (
   ,
   )
   .
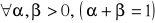
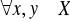
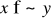
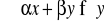
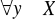
   zbiór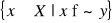
   jest zbiorem wypukłym w przestrzeni dóbr X.

W większości modeli przypuszczamy, że są spełnione 3 dodatkowe założenia:

Z1. Monotoniczność (zjawisko niedosytu): jeżeli x<y
.

Z2. Pole preferencji
- wypukłe.

Z3.
- relacja ciągła.

Twierdzenie 1.1. Jeżeli pole preferencji
jest słabo wypukłym, M jest niepustym, wypukłym podzbiorem X i istnieje M preferowany koszyk, to zbiór wszystkich M- preferowanych koszyków jest wypukły.

Twierdzenie 1.2. Jeżeli pole preferencji
jest silnie wypukłym, to w wypukłym zbiorze M istnieje nie więcej niż jeden M - preferowany koszyk.

1.8. Funkcja użyteczności.

Relację preferencji jest nie zbyt wygodna dla praktycznego zastosowania. Dla niektórych słabych założeniach

preferencji wygodnie przedstawiać w postaci liczbowego indykatora preferencji funkcji użyteczności, która dozwala zastąpić relację preferencji zwykłej relacją więcej.

Definicja 1.12. Określoną na przestrzeni dóbr funkcje
nazywamy funkcją użyteczności konsumenta związaną z relacją

, jeżeli
spełnia ona następujące warunki:

1.

2.

Twierdzenie. 1.3. (Debreu). Jeżeli relacja preferencji jest ciągła, to istnieje ciągła funkcja użyteczności, związana z tą relacją

Twierdzenie 1.4. Jeżeli U(x) - funkcja użyteczności,
- funkcja rosnąca, to superpozycja f(U(x)) jest funkcją użyteczności związaną z tą samą relacją.

Przykłady funkcji użyteczności w
:

multiplikatywna -
, dla
;

logarytmiczna -
, dla
;

addytywna -
, dla
;

1.9. Właściwości funkcji użyteczności.

W dalszych rozważaniach zakładamy, że spełnione warunki następnego twierdzenia

Twierdzenie 1.5. Niech relacja preferencji jest słabo wypukła i znajdujemy się w warunkach niedosytu, wtedy odpowiednia funkcja użyteczności jest quasi wklęsłą i rosnącą.

Więc funkcja użyteczności ma następujące właściwości:

1. 
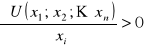
   - zjawisko niedosytu (większe koszyki zawsze lepszy).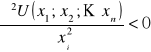

2. 
   - dla zwiększających się koszyków różnica w korzyści pomiędzy koszykami dla konsumenta maleje (prawo Gossena: macierz drugich pochodnych jest ujemne określona).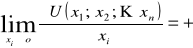

3. 
   - olbrzymie korzyści dla konsumenta od bardzo małych koszyków.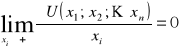

4. 
   - dla olbrzymich koszyków dalsze ich zwiększenie nie zwiększa ich przydatność.

Więc w przypadku dwuwymiarowych koszyków krzywa obojętności
jako funkcja uwikłana może być zapisana w postaci
, gdzie funkcja g ma poziomą i pionową asymptoty i jest wklęsła.

Nie ma sensu mówić o użyteczności, jako o liczbowej mierze zadowolenia. F.Uż. po prostu wprowadzają liczbową charakterystykę relacji preferencji.Przykład. U=x₁²x₂, U'=x₁^2/3x₂^1/3. Te same linii obojętności, różne wartości.

1.10. Stopa substytucji i elastyczność

Definicja 1.13. Krańcową użytecznością i-tego towaru nazywamy

.

Dla naszych założeń krańcowa użyteczność i-tego dobra maleje wraz z zrostem jego spożycia.

Definicja 1.14. Wyrażenie

=

nazywamy krańcową stopą substytucji i-tego dobra przez j-te dobro.

Definicja 1.15. Wyrażenie

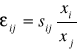
nazywamy elastycznością substytucji i-tego dobra przez j-te dobro.

MRS pokazuje o ile powinna zwiększyć się ilość j-tego dobra przy zmniejszeniu o jednostkę i-tego dobra, aby użyteczność koszyka nie zmieniła się.

Elastyczność mierzy to samo dla procentowych zmian. Elastyczność nie zależy od skali pomiaru dóbr.

1

10

20

X₂

X₁

7

6

5

6

5

4

3

2

4

3

2

1

20

X₂

X₁

7

6

5

4

3

2

1

7

Zmiany linii bud

t

żetu

1

x

2

x

1

p

m

2

p

m

x₂₀

x₁₀

---