1
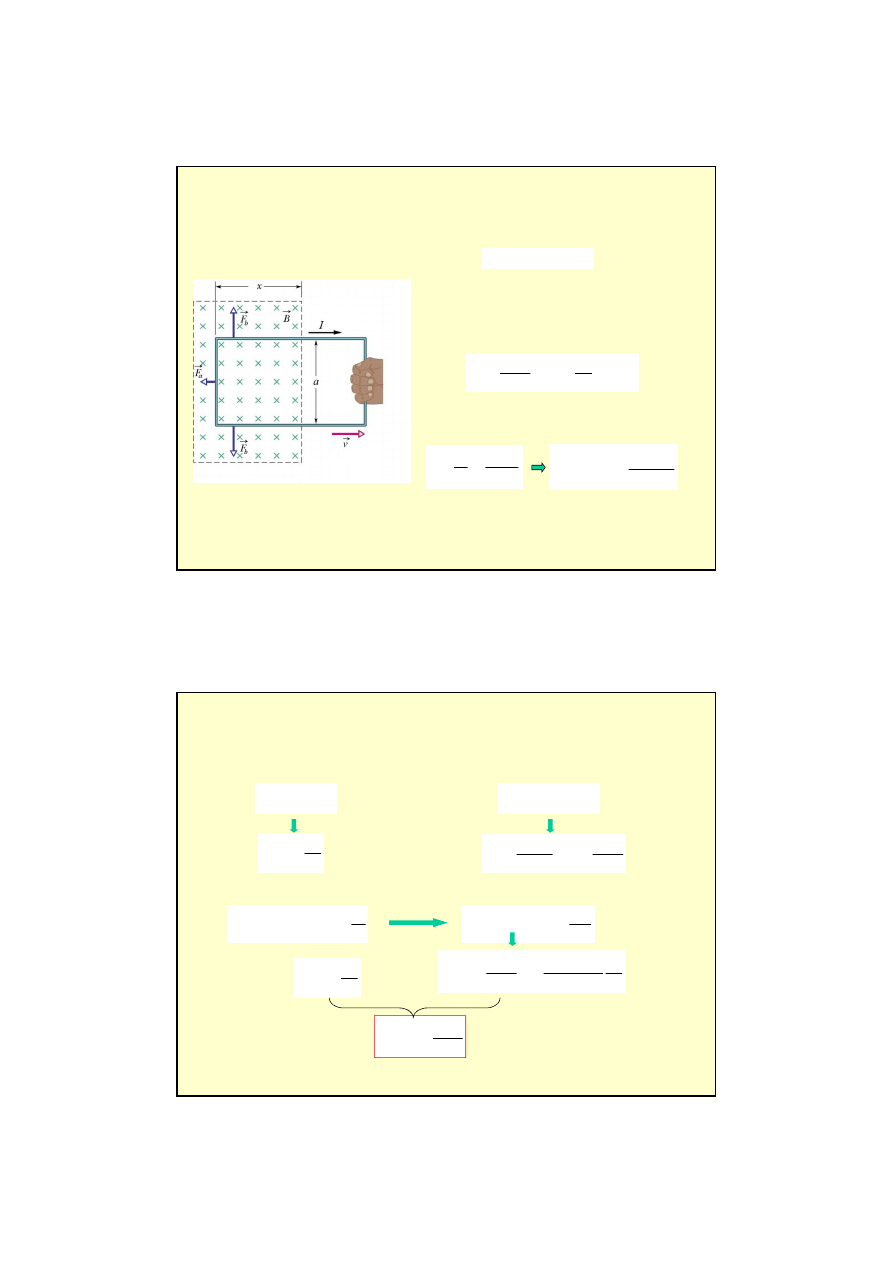
Przykład
Obwód w kształcie prostok
ą
tnej p
ę
tli jest wyci
ą
gany z obszaru stałego pola
magnetycznego (prostopadłego do p
ę
tli) ze stał
ą
pr
ę
dko
ś
ci
ą
v.
Je
ż
eli ramka przesuwa si
ę
o odcinek
dx
to
obszar ramki o powierzchni
dS
wysuwa si
ę
z
pola B i strumie
ń
przenikaj
ą
cy przez ramk
ę
maleje.
v
Ba
dt
dx
Ba
dt
d
ε
B
=
−
=
−
=
Φ
R
Ba
R
ε
I
v
=
=
ramka jest wykonana z przewodnika o oporze R
Siły (
F
b
) działaj
ą
ce na dłu
ż
sze boki ramki znosz
ą
si
ę
i pozostaje nieskompensowana
siła
F
a
, która działa przeciwnie do kierunku ruchu ramki i zgodnie z reguł
ą
Lenza,
przeciwdziała zmianom strumienia magnetycznego.
R
a
B
BIa
F
a
v
2
2
=
=
Bax
BS
=
=
Φ
Obliczamy indukcyjno
ść
cewki o długo
ś
ci
l
, przekroju poprzecznym
S
i
N
zwojach,
przez któr
ą
płynie pr
ą
d o nat
ęż
eniu
I
.
Indukcyjno
ść
mo
ż
na zwi
ę
kszy
ć
wprowadzaj
ą
c do cewki rdze
ń
z materiału o du
ż
ej
wzgl
ę
dnej przenikalno
ś
ci magnetycznej
µ
r
(np. z
ż
elaza).
Strumie
ń
magnetyczny przez ka
ż
dy zwój cewki wynosi:
l
N
I
nI
B
r
r
0
0
µ
µ
µ
µ
=
=
l
NS
I
BS
r
B
0
µ
µ
Φ
=
=
dt
dI
l
S
N
dt
d
N
ε
r
B
2
0
µ
µ
Φ
−
=
−
=
Indukcyjno
ść
L
(podobnie jak pojemno
ść
C
)
zale
ż
y tylko od geometrii układu i
przenikalno
ś
ci magnetycznej
µ
r
.
l
S
N
L
r
2
0
µ
µ
=
dt
dI
L
−
=
ε
dla cewki o N zwojach strumie
ń
jest N razy wi
ę
kszy ni
ż
dla pojedynczego zwoju (N
razy zwi
ę
ksza si
ę
pole przekroju)!
dt
dI
L
−
=
ε
LI
cał
=
Φ
dt
d
N
dt
d
ε
B
cał
Φ
Φ
−
=
−
=
B
cał
N
Φ
Φ
=
2
Zmiana pr
ą
du w obwodzie zawieraj
ą
cym cewk
ę
o indukcyjno
ś
ci L
powoduje powstanie na ko
ń
cach cewki ró
ż
nicy potencjałów U
L
(U
L
jest skierowane przeciwnie pradu o rosn
ą
cym nate
ż
eniu).
dt
dI
L
U
L
=
−
=
ε
Całkowita energia magnetyczna zgromadzona w
cewce podczas narastania pr
ą
du od zera do
I
2
0
1
d
d
2
I
B
W
W
LI I
LI
=
=
=
∫
∫
lS
W
w
B
B
=
lS
LI
w
B
2
2
1
=
g
ę
sto
ść
energii
l
- długo
ś
ci cewki
S
- powierzchnia
przekroju
l
S
N
L
r
2
0
µ
µ
=
l
N
I
nI
B
r
r
0
0
µ
µ
µ
µ
=
=
Energia pola magnetycznego
Je
ż
eli w jakim
ś
punkcie przestrzeni istnieje pole magnetyczne o indukcji B to mo
ż
emy
uwa
ż
a
ć
,
ż
e w tym punkcie jest zmagazynowana energia w ilo
ś
ci
na jednostk
ę
obj
ę
to
ś
ci.
r
B
µ
µ
0
2
2
0
2
2
1
µ
µ
r
B
B
w
=
dI
LI
t
d
q
d
dI
L
dq
t
d
dI
L
dq
U
W
L
=
=
=
=
δ
Do pokonania tej ró
ż
nicy
potencjałów przez ładunek
dq
potrzeba jest energia (praca) :
W
δ
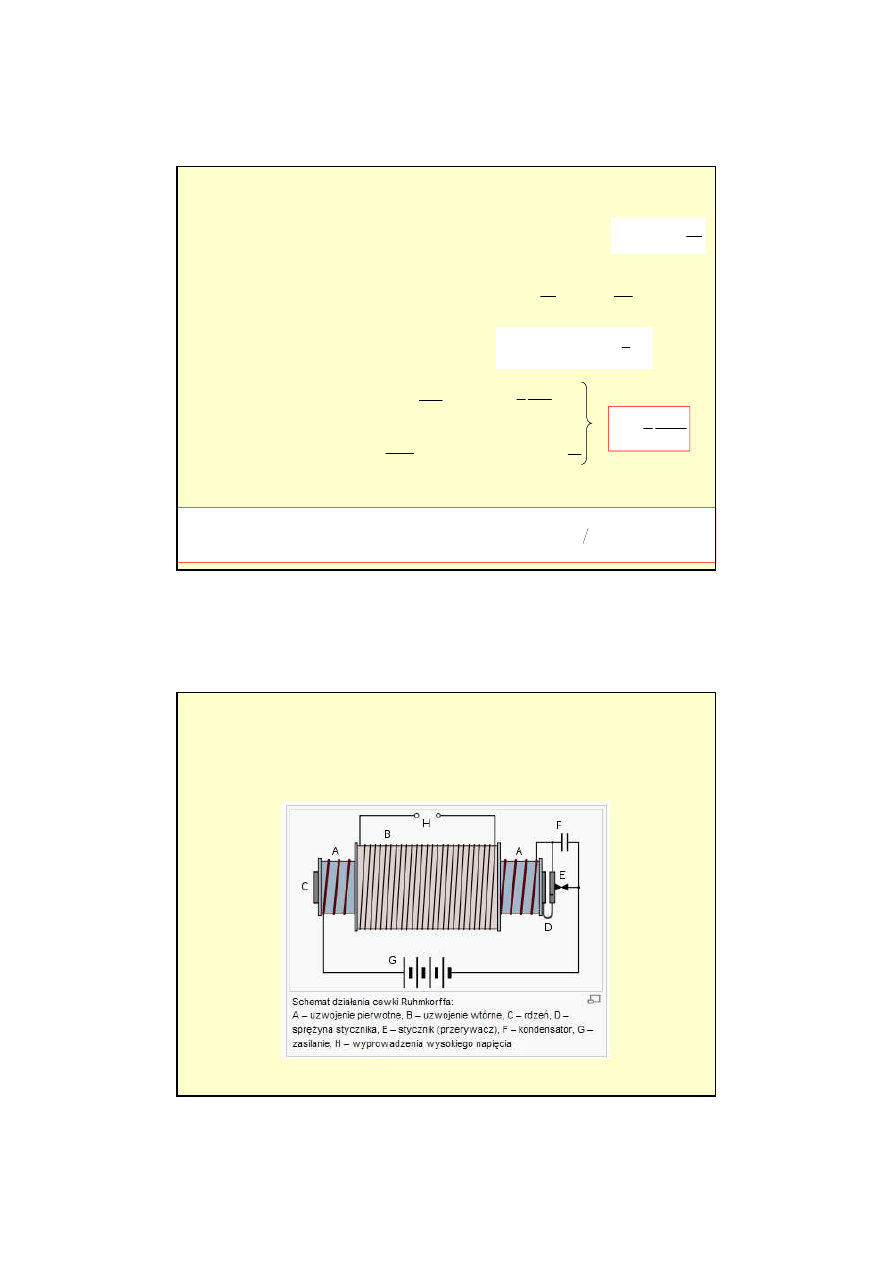
Cewka Ruhmkorffa
3
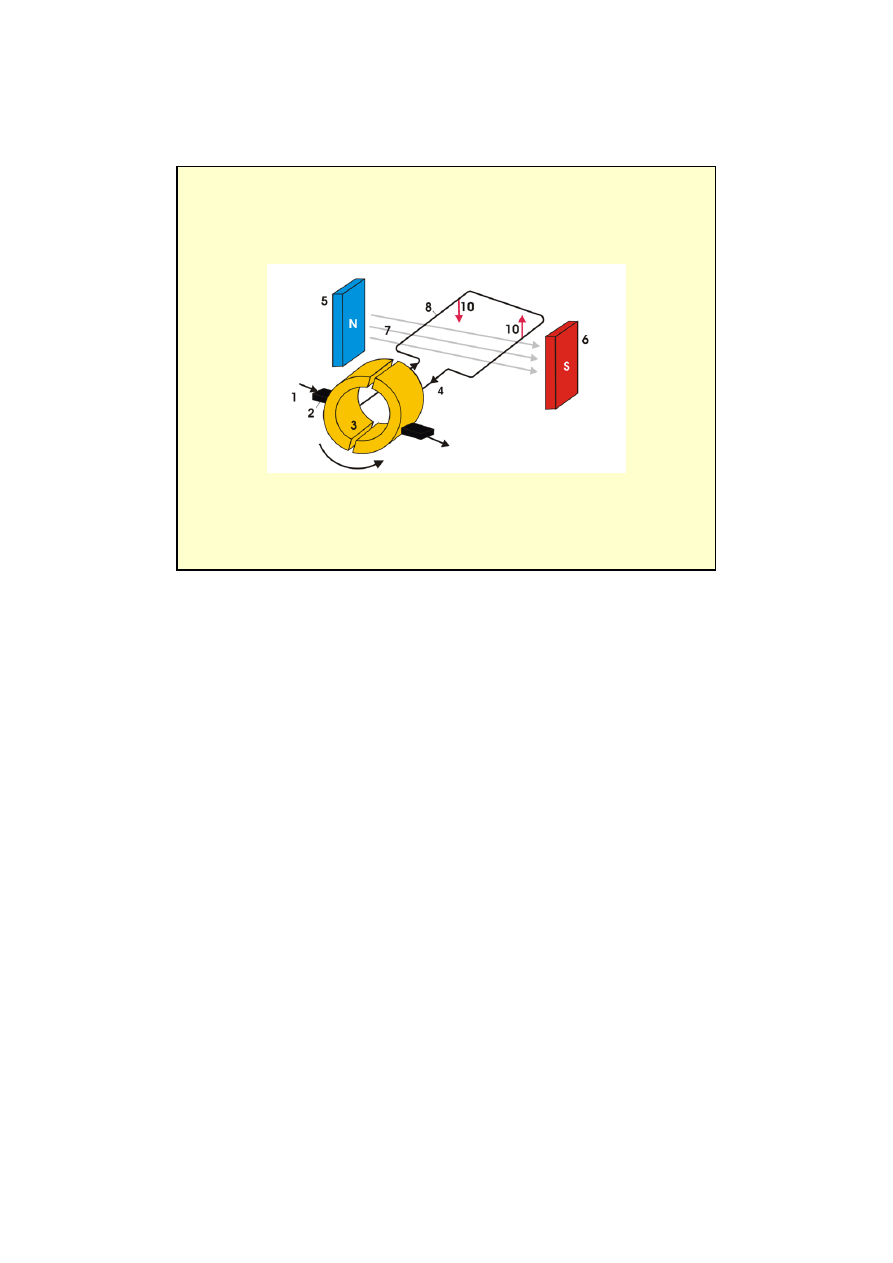
Silnik pr
ą
du stałego - generator
Wyszukiwarka
Podobne podstrony:
IMIR przykłady indukcja elektromagnetyczna
IMIR przykłady indukcja elektromagnetyczna
IMIC przykłady indukcja elektromagnetyczna
3IMIR przykłady indukcja elektromagnetyczna
IMIC przykłady indukcja elektromagnetyczna
IMIC przykłady indukcja elektromagnetyczna
9 IMIR przyklady elektrostatyka Nieznany (2)
IMIR przykłady elektrostatyka
2 IMIR przyklady dynamikaid 203 Nieznany (2)
IMIR przyklady praca energia id Nieznany
22 Pole magnetyczne, indukcja elektromagnetyczna
więcej podobnych podstron