1

1

dla N ładunków punktowych

i

i

i

i

i

r

r

Q

k

r

E

2

=

∑

=

=

N

i

i

1

E

E

r

l

E

E

=

1

3

3

2

1

r

p

k

r

Ql

k

r

Q

k

r

l

E

r

l

E

=

=













=

=

p = Q l

jest momentem dipolowym

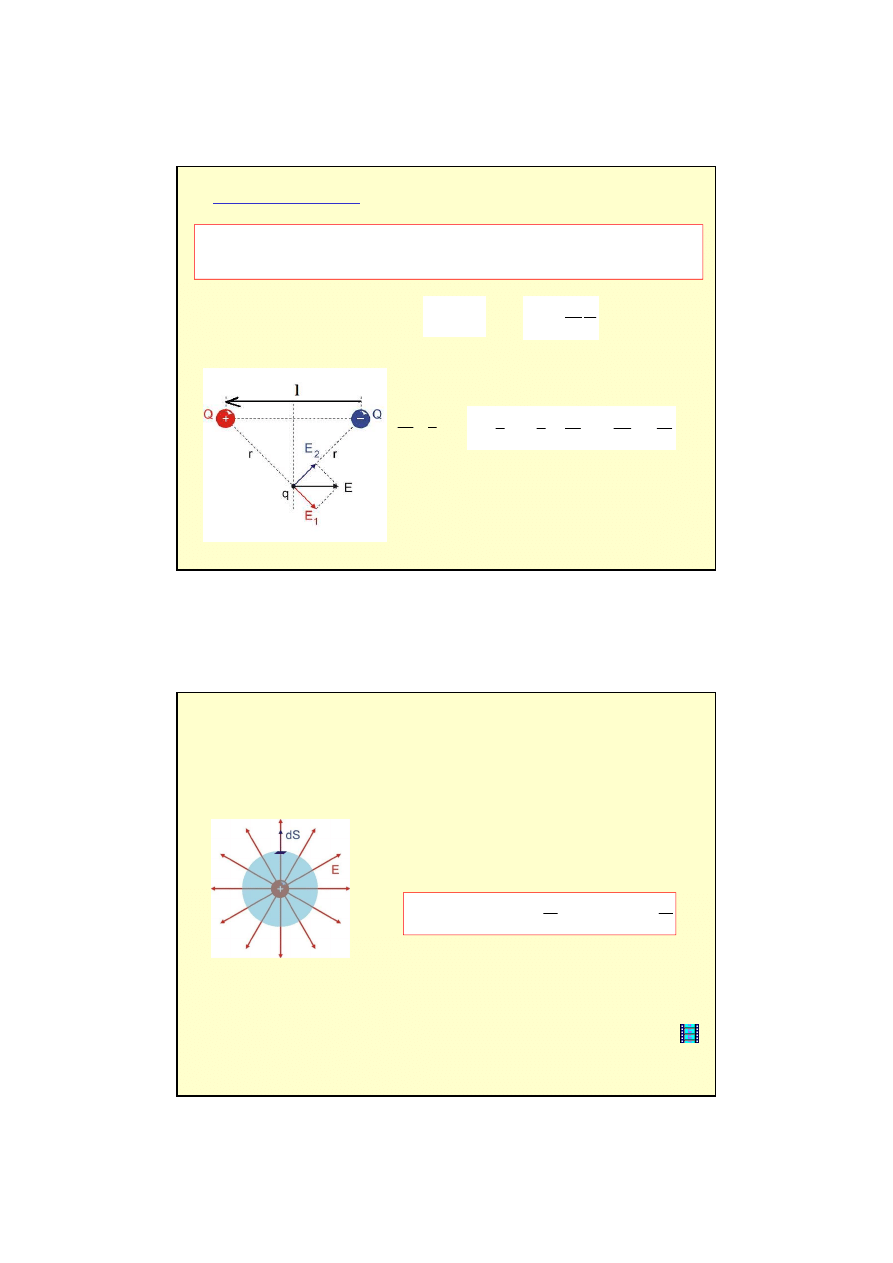
Zasada superpozycji

Gdy mamy do czynienia z kilkoma naładowanymi ciałami, wypadkowe nat

ęż

enie

pola (sił

ę

wypadkow

ą

), obliczamy dodaj

ą

c wektorowo nat

ęż

enia pól od

pojedynczych ładunków.

Przykład:

dipol elektryczny

2

Przykład:

strumie

ń

pola

E

od ładunku punktowego Q przez sfer

ę

otaczaj

ą

c

ą

ten ładunek

Rysujemy sfer

ę

o promieniu r wokół ładunku Q i liczymy strumie

ń

przechodz

ą

cych

przez t

ę

powierzchni

ę

.

Q

Pole E ma jednakow

ą

warto

ść

w ka

ż

dym punkcie

sfery i jest prostopadłe do powierzchni (

α

= 0)

0

2

2

2

4

)

4

(

)

4

(

ε

π

π

π

Q

kQ

r

r

Q

k

r

E

=

=













=

=

⋅

=

Φ

S

E

Otrzymany strumie

ń

nie zale

ż

y od r, a zatem strumie

ń

jest

jednakowy dla wszystkich r

2

3

0

2

2

2

0

0

0

0

1

1

cos

4

4

4

S

S

S

S

S

dS

Q

Q

r

Q

Q

d

d

d

dS

r r

r r

r

α

πε

πε

πε

ε

Φ =

Φ =

=

=

=

=

∫

∫

∫

∫

∫

r

E S

S

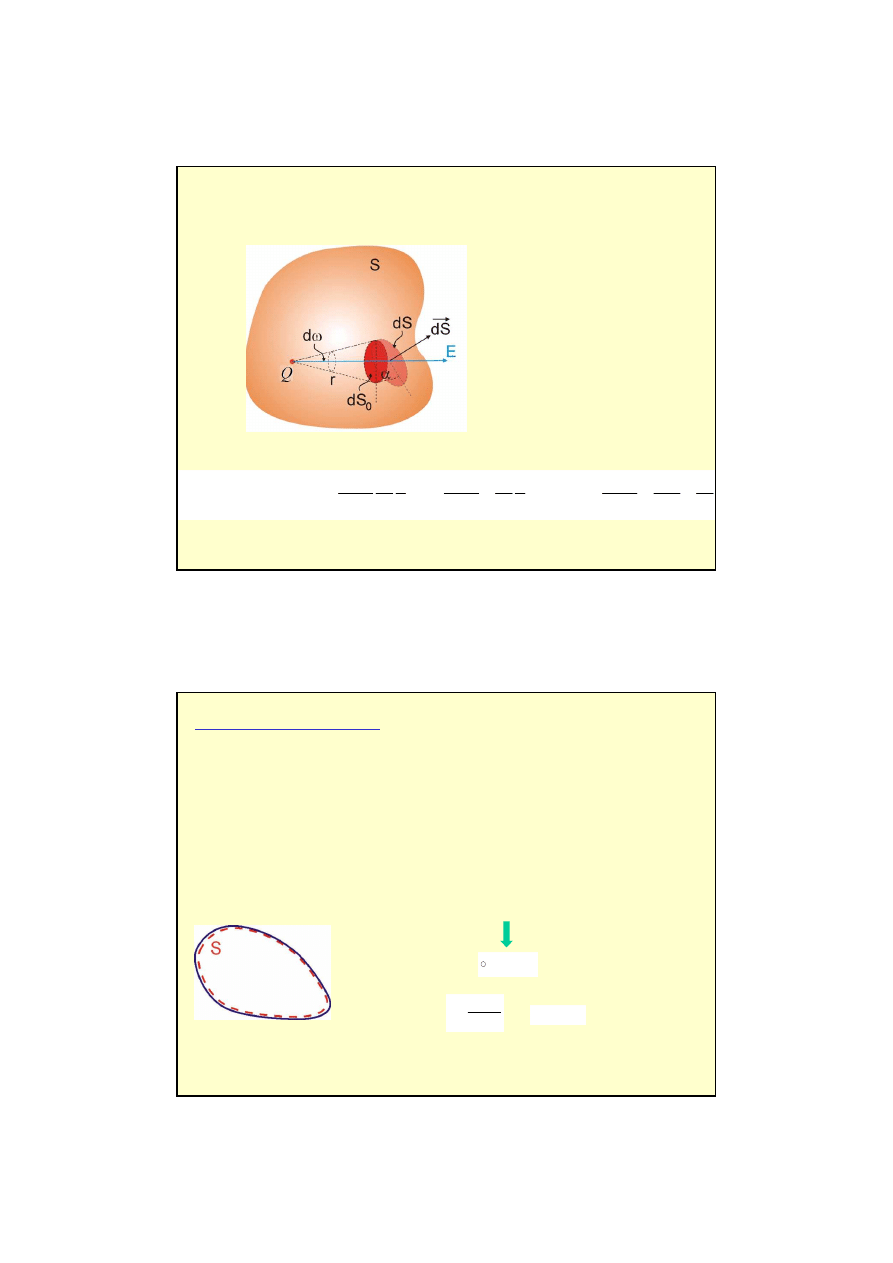
strumie

ń

pola

E

od ładunku punktowego przez dowoln

ą

powierzchni

ę

otaczaj

ą

c

ą

ten ładunek

4

Izolowany przewodnik

W izolatorze nadmiarowy ładunek mo

ż

e by

ć

rozmieszczony w całej jego obj

ę

to

ś

ci.

Ładunek rozmieszczony w przewodniku wytwarza pole elektryczne przemieszczaj

ą

ce

swobodne elektrony na powierzchni

ę

przewodnika dopóty, dopóki nie zniknie pole

wewn

ą

trz przewodnika.

Wtedy na ładunki nie działa ju

ż

siła i otrzymujemy statyczny rozkład ładunku.

0

d

=

∫

S

E

Wewn

ą

trz przewodnika

E

= 0

0

0

ε

.

wewn

Q

=

0

.

=

wewn

Q

Cały ładunek gromadzi si

ę

na powierzchni przewodnika

Prawo Gaussa - przykłady

3

5

Procedura obliczania pola

E

od symetrycznych rozkładów ładunków:

1. Trzeba okre

ś

li

ć

symetri

ę

pola

2. Wybra

ć

odpowiedni

ą

powierzchni

ę

Gaussa

3. Obliczy

ć

strumie

ń

przez t

ę

powierzchni

ę

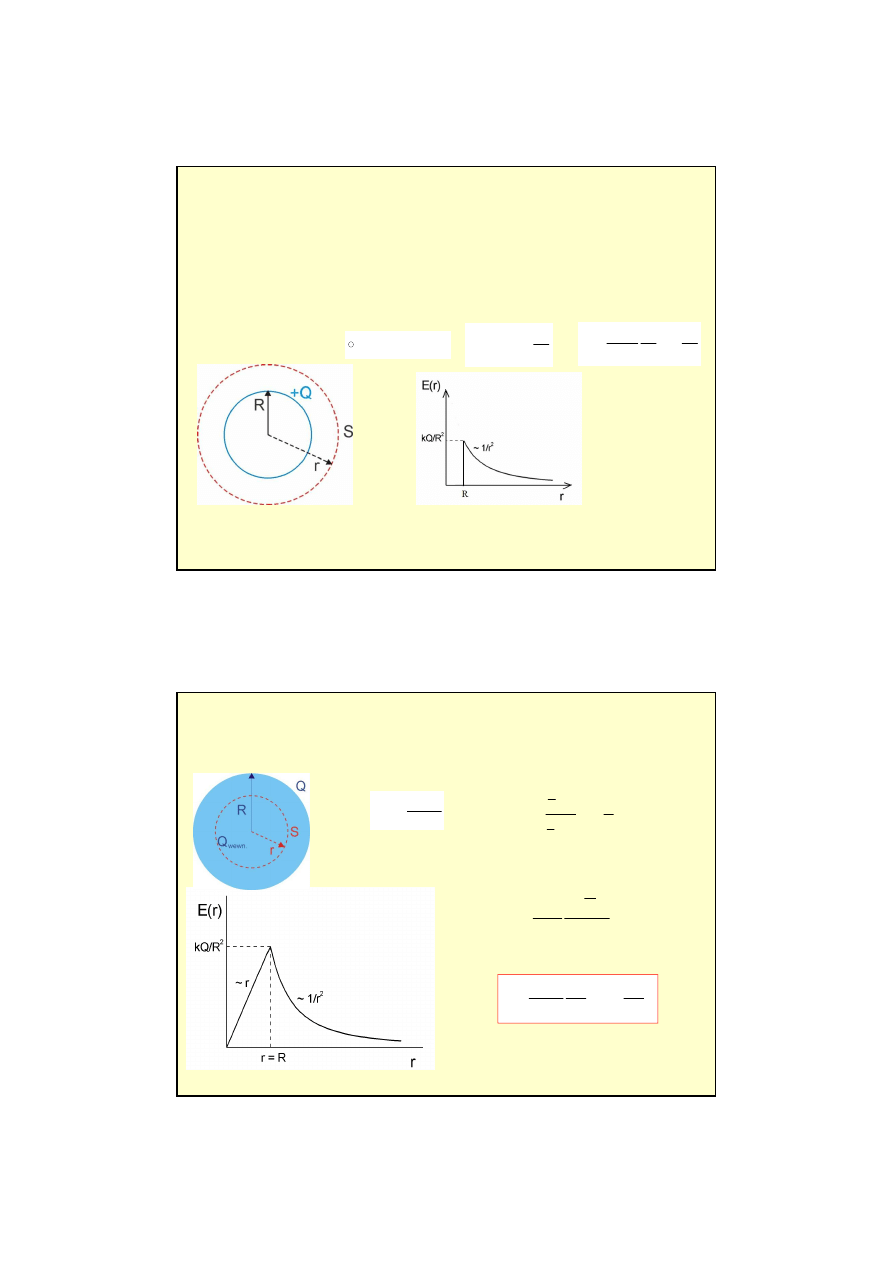
Kuliste rozkłady ładunków - jednorodnie naładowana sfera (lub kula z
przewodnika)

∫

=

)

πr

E(

EdS

2

4

0

2

)

4

(

ε

π

Q

r

E

=

2

2

0

4

1

r

Q

k

r

Q

E

=

=

πε

Na zewn

ą

trz sfery tj. dla r > R pole jest takie jakby cały ładunek skupiony był w

ś

rodku sfery. Natomiast wewn

ą

trz sfery (r < R) Q

wewn.

= 0 wi

ę

c E

wewn.

= 0.

6

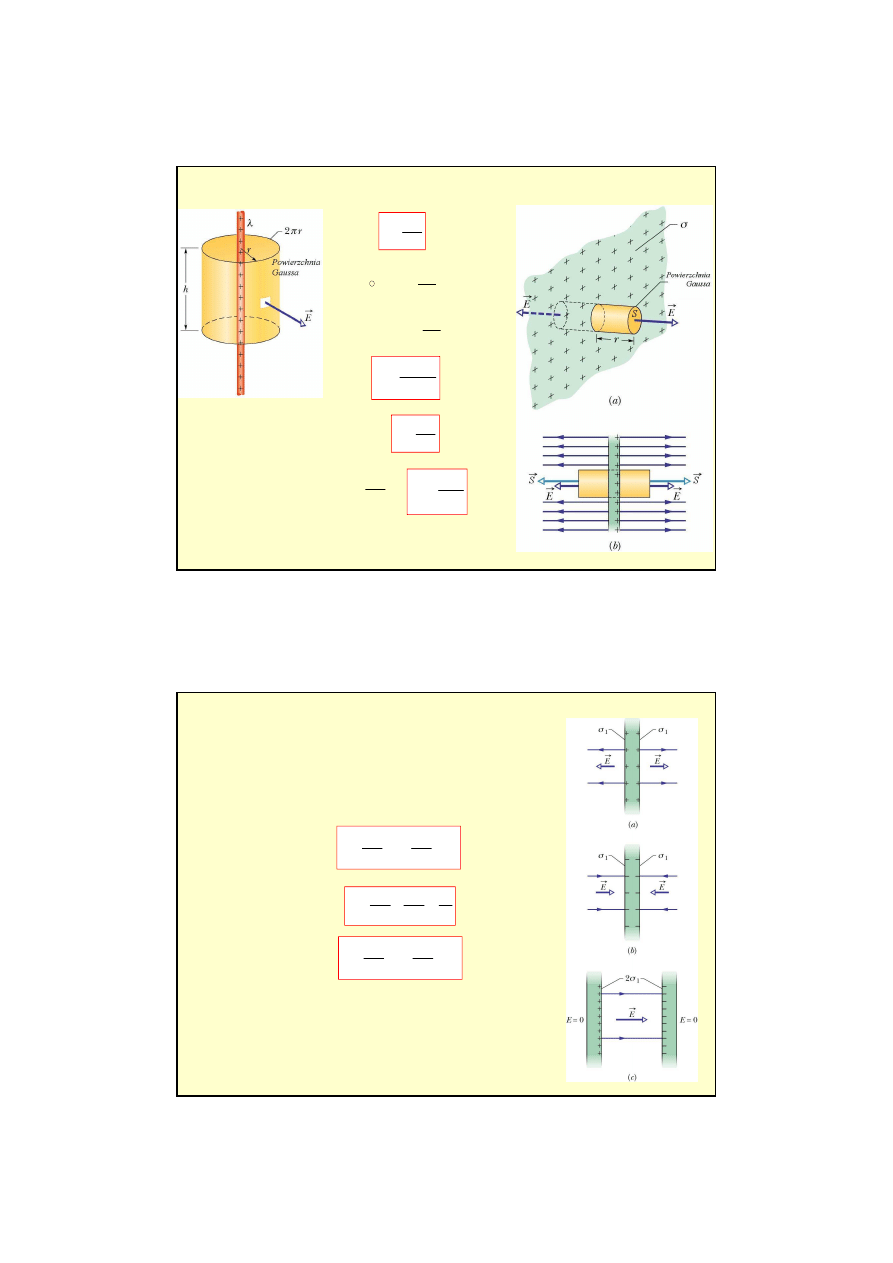
Kuliste rozkłady ładunków - jednorodnie naładowana kula (izolator)

2

.

r

Q

k

E

wewn

=

3

3

3

.

3

4

3

4













=

=

R

r

Q

R

r

Q

Q

wewn

π

π

2

3

0

4

1

r

R

r

Q

E













=

πε

r

R

Q

k

r

R

Q

E

3

3

0

4

1

=

=

πε

4

7

Liniowy rozkład ładunków

∫

=

0

ε

λ

h

dS

E

0

2

ε

λ

π

h

rh

E

=

r

E

0

2

πε

λ

=

0

2

ε

σ

S

S

E

=

0

2

ε

σ

=

E

Płaskie rozkłady ładunków

dS

dQ

σ

=

dl

dQ

λ

=

8

W praktyce stosuje si

ę

układ dwóch płaskich

równoległych płyt naładowanych ładunkami jednakowej
wielko

ś

ci ale o przeciwnych znakach (kondensator

płaski ).

0

0

0

2

2

ε

σ

ε

σ

ε

σ

=

+

=

E

0

2

2

0

0

=













−

+

=

ε

σ

ε

σ

E

0

2

2

0

0

=













−

+

=

ε

σ

ε

σ

E

po lewej stronie

po prawej stronie

pomi

ę

dzy płytami

Na zewn

ą

trz układu pole jest równe zeru a pomi

ę

dzy

płytami ma w ka

ż

dym punkcie stał

ą

warto

ść

σ

/

ε

0

.

Takie pole nazywamy polem jednorodnym.

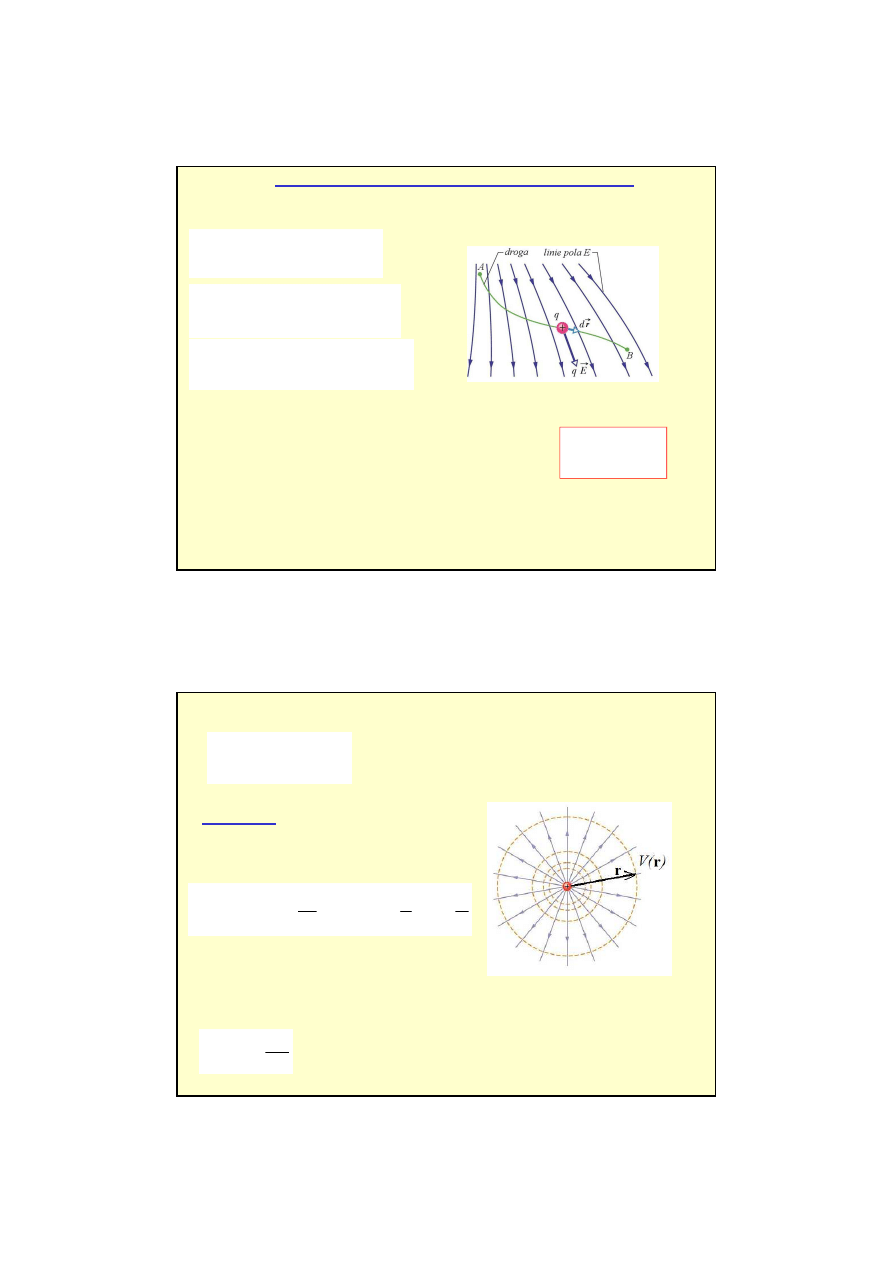
5

9

Energia potencjalna i potencjał pola elektrycznego

Pole elektryczne jest polem zachowawczym (potencjalnym), wi

ę

c warto

ść

pracy

nie zale

ż

y od wyboru drogi pomi

ę

dzy punktami A i B.

Potencjał elektryczny

Potencjał elektryczny to energia potencjalna
podzielona przez jednostkowy ładunek czyli

V = E

p

/q

:

∫

−

=

B

A

A

B

d

V

V

r

E

Jednostk

ą

potencjału elektrycznego jest wolt (V); 1 V = 1 J/C.

∫

−

=

−

=

−

B

A

AB

pA

pB

d

W

E

E

r

F

F

)

(

∫

∫

−

=

−

=

B

A

pA

B

A

pA

pB

d

q

E

d

E

E

r

E

r

F

∫

∑

=

∆

=

→

∆

B

A

i

i

AB

d

W

i

r

F

r

F

r

F

0

)

(

lim

10

W fizyce posługujemy si

ę

cz

ę

sto poj

ę

ciem ró

ż

nicy potencjałów czyli napi

ę

ciem

U

.

Znak minus odzwierciedla fakt,

ż

e

potencjał maleje w kierunku
wektora

E

.

∫

−

=

−

=

B

A

A

B

d

V

V

U

r

E

Czyli energia potencjalna dla ładunku punktowego

q

umieszczonego w polu

ładunku

Q

wynosi:

r

qQ

k

(r)

E

p

=

r

Q

k

r

kQ

dr

r

Q

k

V

V(r)

r

r

=









−

−

=

−

∞

=

∞

∞

∫

'

1

'

'

)

(

2

1) Potencjał pola ładunku punktowego

Q

:

przyjmujemu,

ż

e:

0

)

(

=

∞

V

Przykłady:

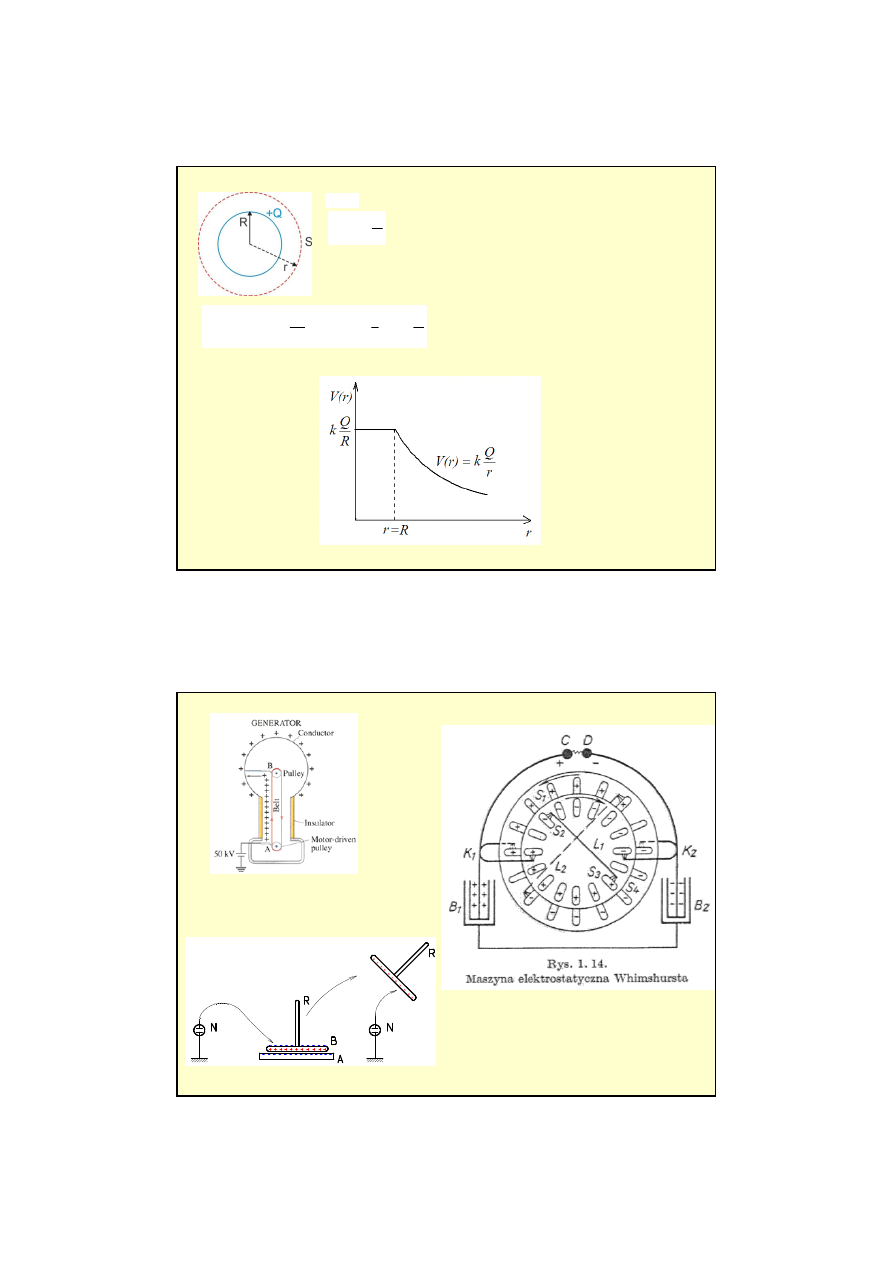
6

11

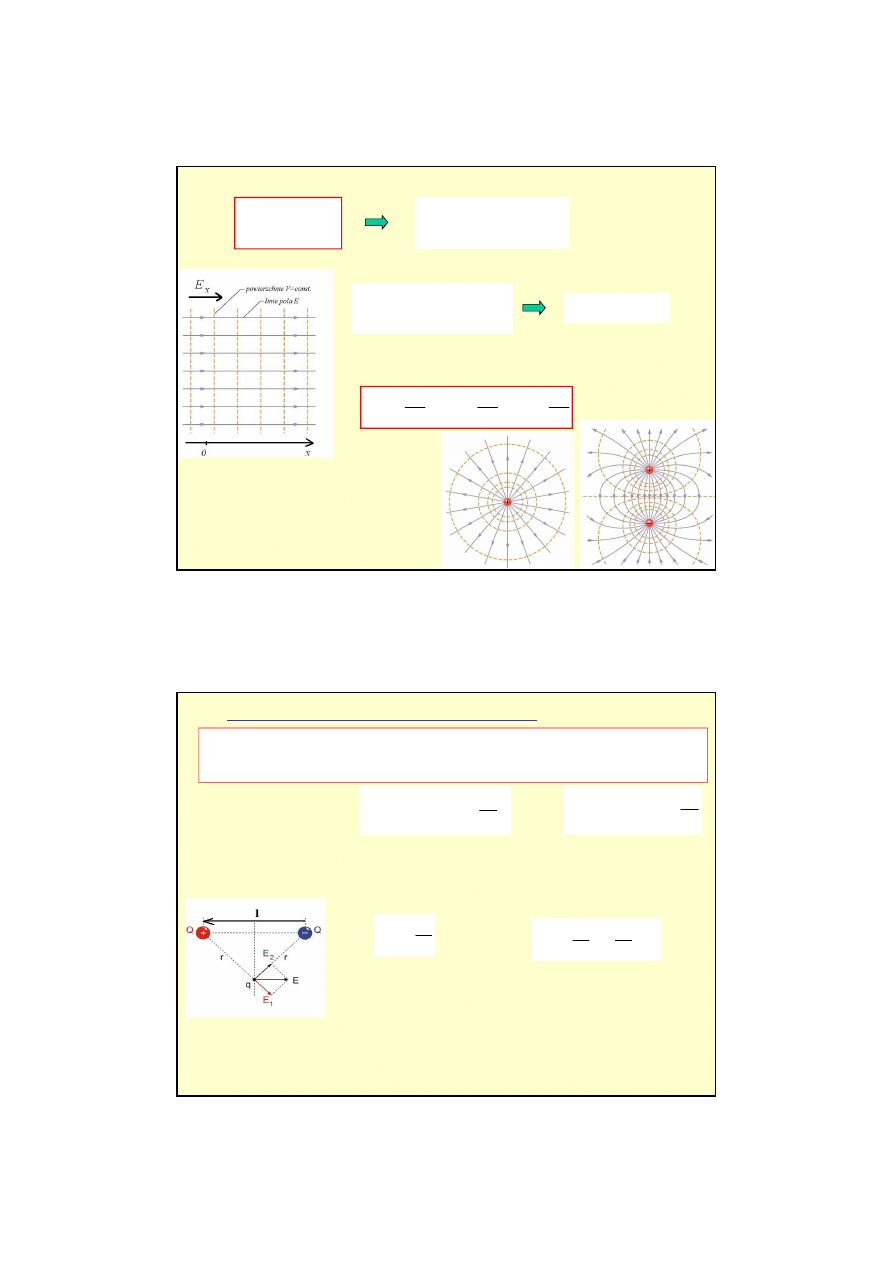
2) Jednorodnie naładowana sfera

R

Q

k

r

kQ

dr

r

Q

k

V

V(r)

R

R

=









−

−

=

−

∞

=

∞

∞

∫

1

'

'

)

(

2

R

r

≥

r

Q

k

V(r)

=

12

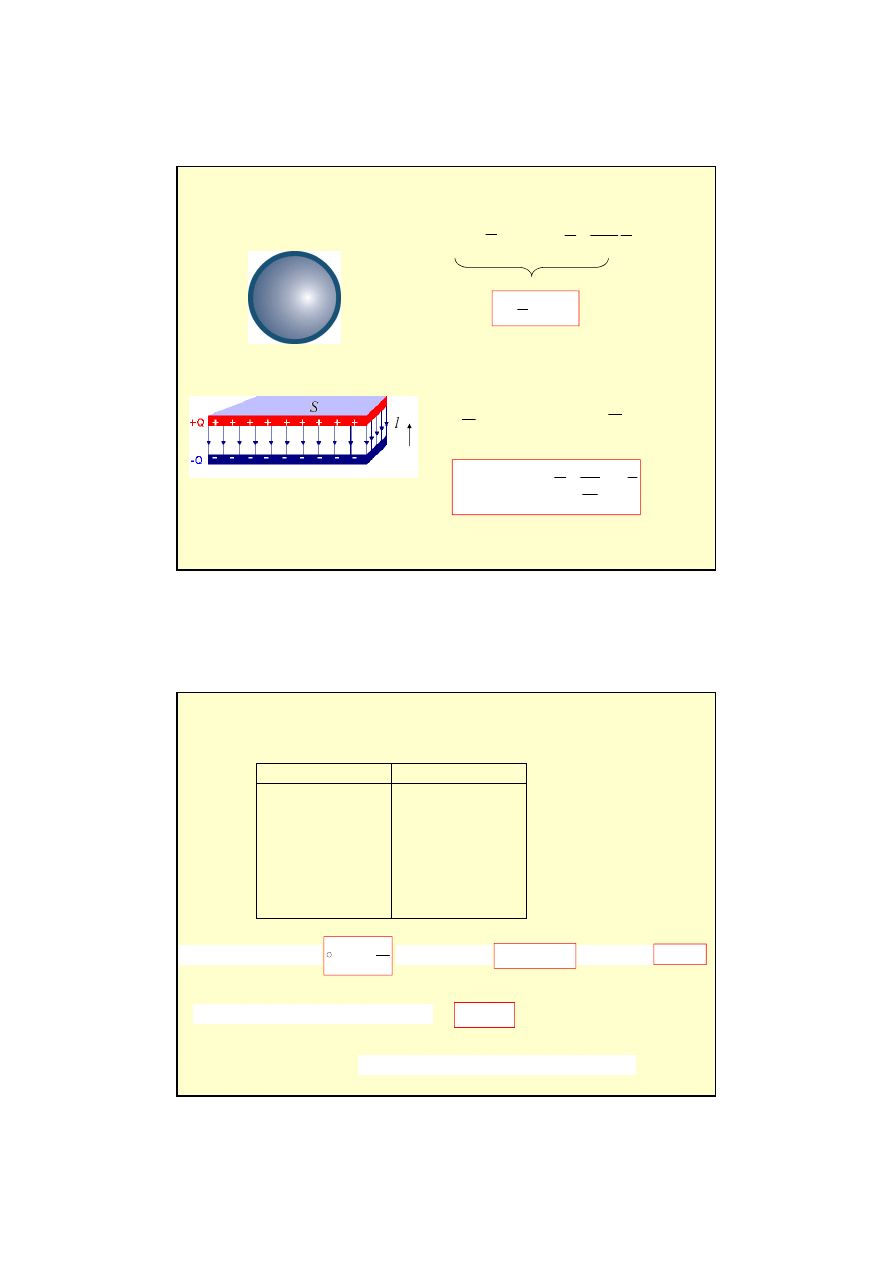
Generator elektrostatyczny Van de Graaffa.

Elektrofor

7

13

∫

−

=

B

A

A

B

d

V

V

r

E

∫

−

=

−

=

∆

B

A

A

B

d

V

V

V

r

E

dx

E

dV

x

−

=

Zwi

ą

zki pomi

ę

dzy

V

i

E

∫

−

=

−

=

∆

B

A

x

A

B

dx

E

V

V

V

Dla pola jednorodnego:

z

V

E

y

V

E

x

V

E

z

y

x

∂

∂

−

=

∂

∂

−

=

∂

∂

−

=

,

,

Gdy znamy rozkład potencjału elektrycznego
wytworzonego w każdym punkcie przestrzeni przez dany
układ ładunków to na podstawie wielkości zmiany
potencjału, przypadającej na jednostkę długości w danym
kierunku możemy określić natężenie pola elektrycznego

E

w tym kierunku.

Ogólnie dla pola elektrostatycznego wektor

E dany jest wzorami

:

14

dla N ładunków punktowych

∑

∑

=

∧

=

=

=

N

i

i

i

N

i

i

r

Q

k

1

2

1

r

E

E

Zasada superpozycji – potencjał i nat

ęż

enie

Gdy mamy do czynienia z kilkoma naładowanymi ciałami, wypadkowy potencjał
pola (energi

ę

potencjaln

ą

), obliczamy dodaj

ą

c skalarnie potencjały pól od

pojedynczych ładunków.

i

∑

∑

=

=

=

=

N

i

i

i

N

i

i

r

Q

k

V

V

1

1

3

r

p

k

E

=

Przykład 1:

dipol elektryczny

0

=

−

=

r

q

k

r

q

k

V

oraz

8

15

pojemno

ść

kuli o promieniu R

V

Q

C

=

R

Q

R

Q

k

V

0

4

1

πε

=

=

R

k

R

C

0

4

πε

=

=

Przykłady:

kondensator płaski

0

ε

σ

=

E

l

El

d

U

B

A

0

ε

σ

=

=

−

=

∫

r

E

l

S

l

S

U

Q

C

El

U

0

0

ε

ε

σ

σ

=

=

=

=

Pojemno

ść

zale

ż

y od kształtu okładek, ich rozmiaru i wzajemnego poło

ż

enia

A

B

r

16

ε

r

nazywamy wzgl

ę

dn

ą

przenikalno

ś

ci

ą

elektryczna lub stał

ą

dielektryczn

ą

Materiał

Stała dielektryczna

pró

ż

nia

powietrze

teflon

polietylen

papier

szkło

porcelana

woda

TiO

2

1.0000
1.0005

2.1
2.3
3.5
4.5
6.5

78

100

Prawo Gaussa dla dielektryka

0

r

ε

=

E

E

Prawo Gaussa w pró

ż

ni:

0

d

r

q

ε ε

=

∫

E S

0

0

d

ε

q

=

∫

S

E

dla dielektryka :

, poniewa

ż

:

Prawo Gaussa (niezale

ż

ne od materiału):

d

q

=

∫

D S

gdzie to wektor indukcji elektrycznej.

0

r

ε ε

=

D

E

9

17

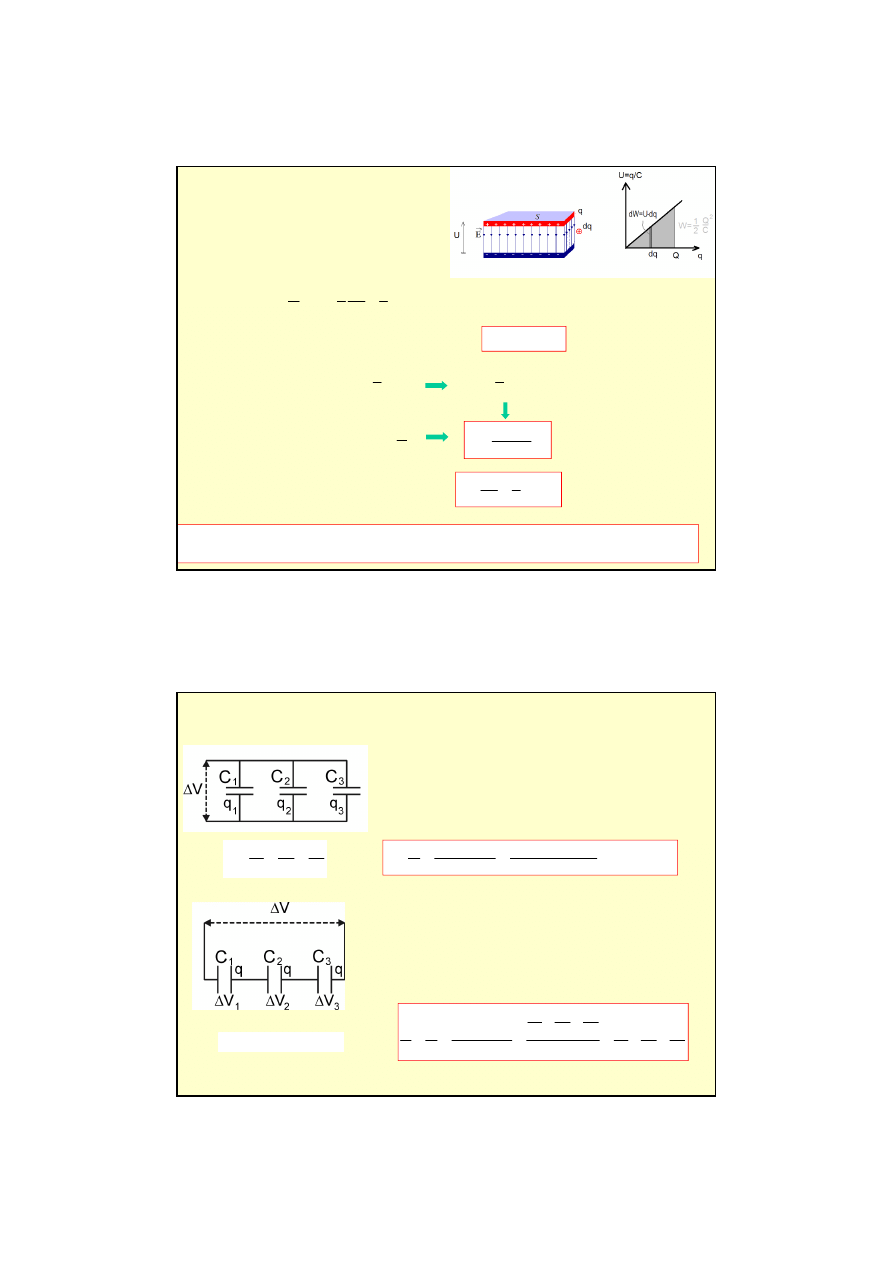
Praca zu

ż

yta na przeniesienie porcji ładunku

dq

pomi

ę

dzy okładkami przy panuj

ą

cej w

danej chwili ró

ż

nicy potencjałów

U=∆V.

Ładowanie kondensatora pró

ż

niowego.

Udq

dW

=

C

U

C

Q

q

C

q

q

U

W

Q

Q

2

2

0

0

2

1

2

1

d

d

=

=













=

=

∫

∫

Energia pola elektrycznego

2

0

2

1

E

Sd

W

w

r

ε

ε

=

=

G

ę

sto

ść

energii pola elektrycznego (energia

zawarta w jednostce obj

ę

to

ś

ci) wynosi:

Je

ż

eli w jakim

ś

punkcie przestrzeni istnieje pole elektryczne o nat

ęż

eniu

E

to mo

ż

emy uwa

ż

a

ć

,

ż

e w tym punkcie jest zmagazynowana energia w ilo

ś

ci ½

ε

0

ε

r

E

2

na jednostk

ę

obj

ę

to

ś

ci.

Prawo Gaussa dla o

ś

rodka o stałej dielektrycznej

ε

r

:

0

d

r

Q

ε ε

=

∫

E S

Sd

E

W

r

2

2

0

ε

ε

=

d

S

C

r

ε

ε

0

=

2

1

2

W

CU

=

2

2

1

2

W

CE d

=

dla kondensatora płaskiego:

18

Dla poł

ą

czenia równoległego ró

ż

nica potencjałów mi

ę

dzy

okładkami wszystkich kondensatorów jest taka sama
(poł

ą

czone okładki stanowi

ą

jeden przewodnik).

3

3

2

2

1

1

C

q

C

q

C

q

U

=

=

=

(

)

3

2

1

3

2

1

3

2

1

C

C

C

U

U

C

C

C

U

q

q

q

U

Q

C

+

+

=

+

+

=

+

+

=

=

Przy poł

ą

czeniu szeregowym ładunek wprowadzony na

okładki zewn

ę

trzne wywołuje równomierny rozkład

(rozdzielenie) ładunku pomi

ę

dzy okładkami wewn

ę

trznymi.

3

3

2

2

1

1

C

U

C

U

C

U

q

=

=

=

3

2

1

3

2

1

3

2

1

1

1

1

1

C

C

C

q

C

q

C

q

C

q

q

U

U

U

q

U

C

+

+

=

+

+

=

+

+

=

=

Baterie kondensatorów