1

Przykład 1:

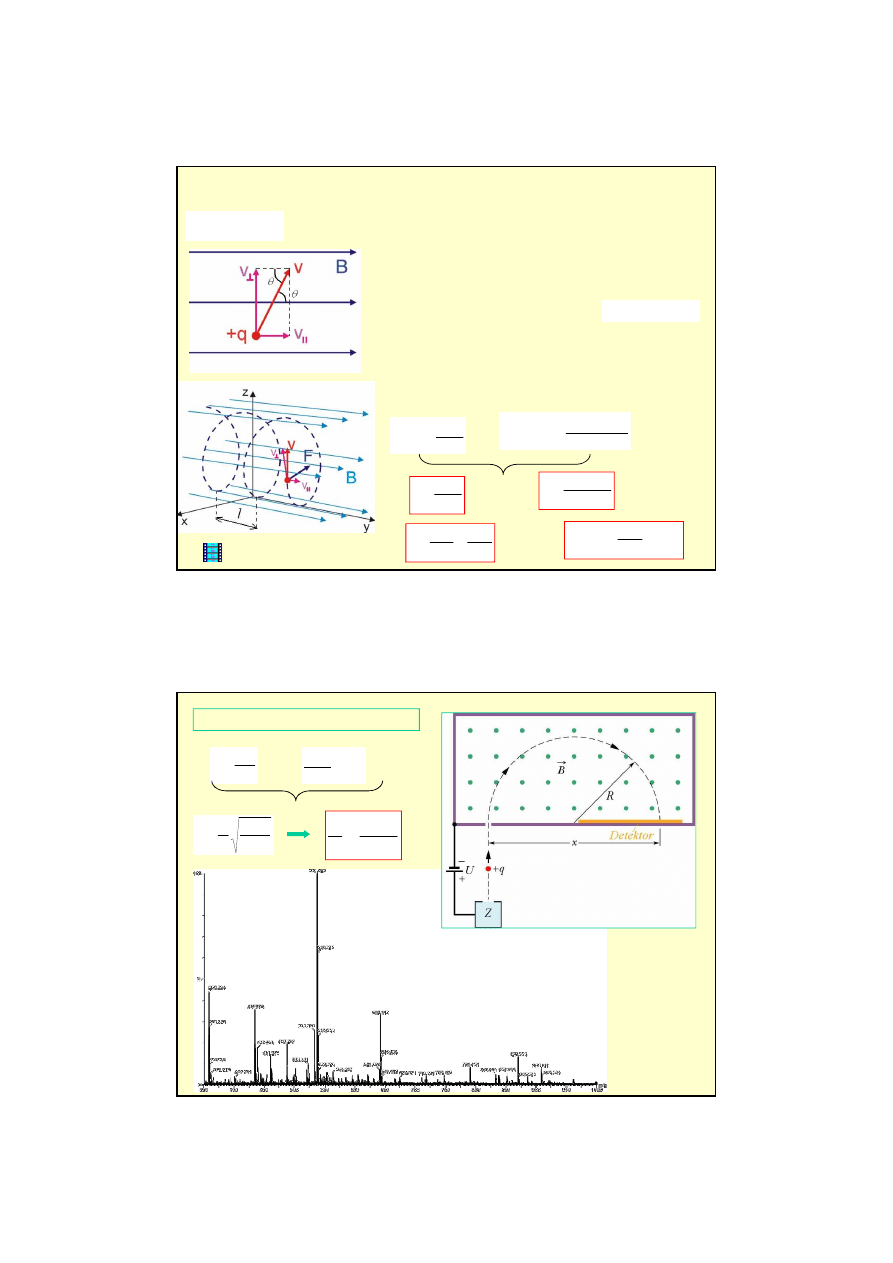
Ruch ładunku w jednorodnym polu magnetycznym

Wektor siły

F

jest prostopadły do wektora pr

ę

dko

ś

ci

v

i wektora

B

,

siła magnetyczna jest sił

ą

do

ś

rodkow

ą

.

B

v

F

×

=

q

Siła magnetyczna zmienia tylko składow

ą

pr

ę

dko

ś

ci

prostopadł

ą

do pola

B

(

θ

= 90º) natomiast nie zmienia

składowej równoległej do pola (

θ

= 0º)

θ

B

q

F

sin

v

=

R

m

B

q

2

⊥

⊥

=

v

v

R

m

qB

2

)

sin

(

sin

θ

θ

v

v

=

lub

qB

m

R

θ

sin

v

=

lub

qB

m

R

⊥

=

v

qB

m

R

T

π

π

2

2

=

=

⊥

v

θ

π

cos

2

||

v

v

qB

m

T

l

=

=

oraz

Cz

ą

stka przemieszcza si

ę

ze stał

ą

pr

ę

dko

ś

ci

ą

wzdłu

ż

pola

B

równocze

ś

nie zataczaj

ą

c pod wpływem siły

magnetycznej okr

ę

gi w płaszczy

ź

nie prostopadłej do pola.

Cz

ą

steczka porusza si

ę

po spirali.

qB

m

R

v

=

qU

m

=

2

2

v

q

mU

B

R

2

1

=

U

B

R

q

m

2

2

2

=

Przykład 3:

Spektrometr masowy

widmo masowe

2

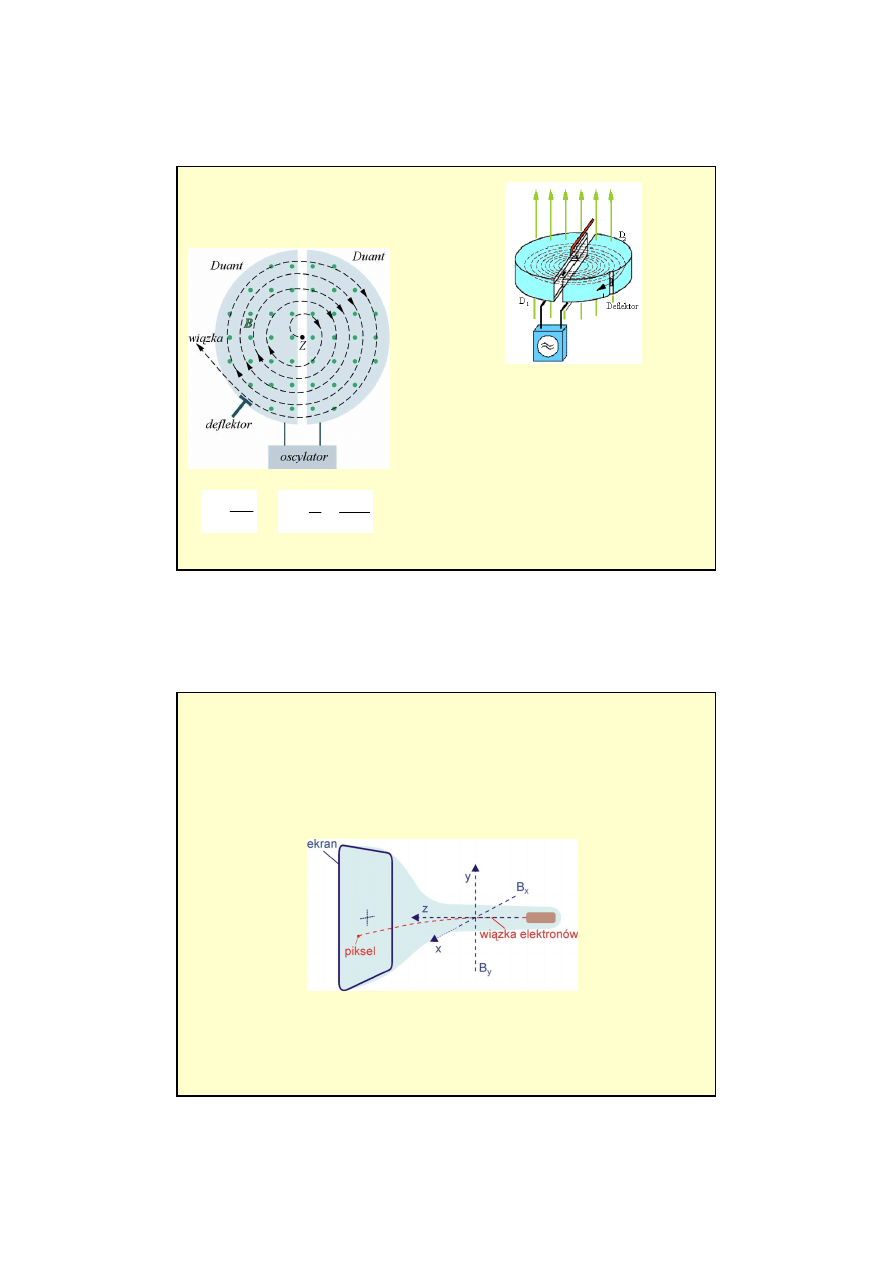
Przykładem akceleratora cyklicznego
jest

cyklotron

.

m

qB

T

f

π

2

=

=

1

qB

m

R

v

=

Generator cyklicznie zmienia kierunek pola
elektrycznego przyspieszaj

ą

cego ładunki

w szczelinie pomi

ę

dzy duantami.

Cz

ą

stki (w polu B) poruszaj

ą

si

ę

po spirali. Po

osi

ą

gni

ę

ciu maksymalnego promienia cz

ą

stki s

ą

wyprowadzane poza cyklotron za pomoc

ą

elektrody

nazywanej deflektorem.

Przykład 3:

Akceleratory

Przykład 4:

Odchylanie wi

ą

zki elektronów w lampie kineskopu

3

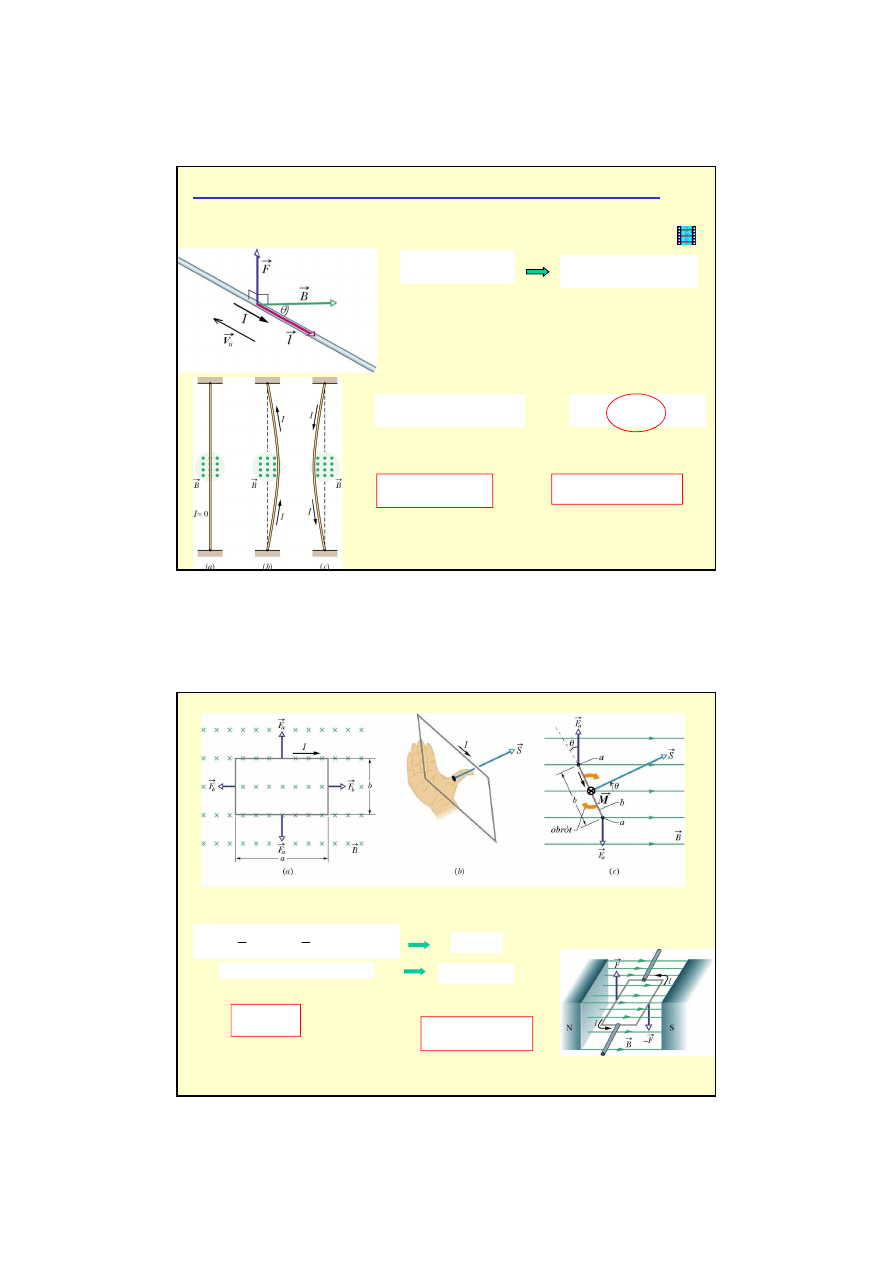
Działanie pola magnetycznego na przewodnik z pr

ą

dem

siła magnetyczna działa na ładunki w ruchu zatem działa na cały przewodnik z pr

ą

dem

PRZEWODNIKI Z PR

Ą

DEM W POLU MAGNETYCZNYM

B

v

F

×

−

=

e

e

B

v

F

×

−

=

u

Ne

N

jest liczb

ą

elektronów zawartych w danym przewodniku o

długo

ś

ci

l

i przekroju poprzecznym

S

, a

v

u

ich

ś

redni

ą

pr

ę

dko

ś

ci

ą

unoszenia.

nSl

N

=

B

v

F

×

−

=

u

nSle

lub

B

F

×

=

l

u

nSe

v

I

θ

B

l

I

F

sin

=

B

F

×

=

l

I

siła elektrodynamiczna

Obwód z pr

ą

dem

siły działaj

ą

ce na ramk

ę

znosz

ą

si

ę

wzajemnie

Siły

F

a

działaj

ą

ce na boki a tworz

ą

par

ę

sił daj

ą

c

ą

wypadkowy moment

siły obracaj

ą

cy ramk

ę

θ

θ

θ

sin

sin

2

sin

2

b

F

b

F

b

F

M

a

a

a

=

+

=

IaB

F

a

=

θ

θ

sin

sin

ISB

IabB

M

=

=

B

S

M

×

=

I

S

jest wektorem powierzchni

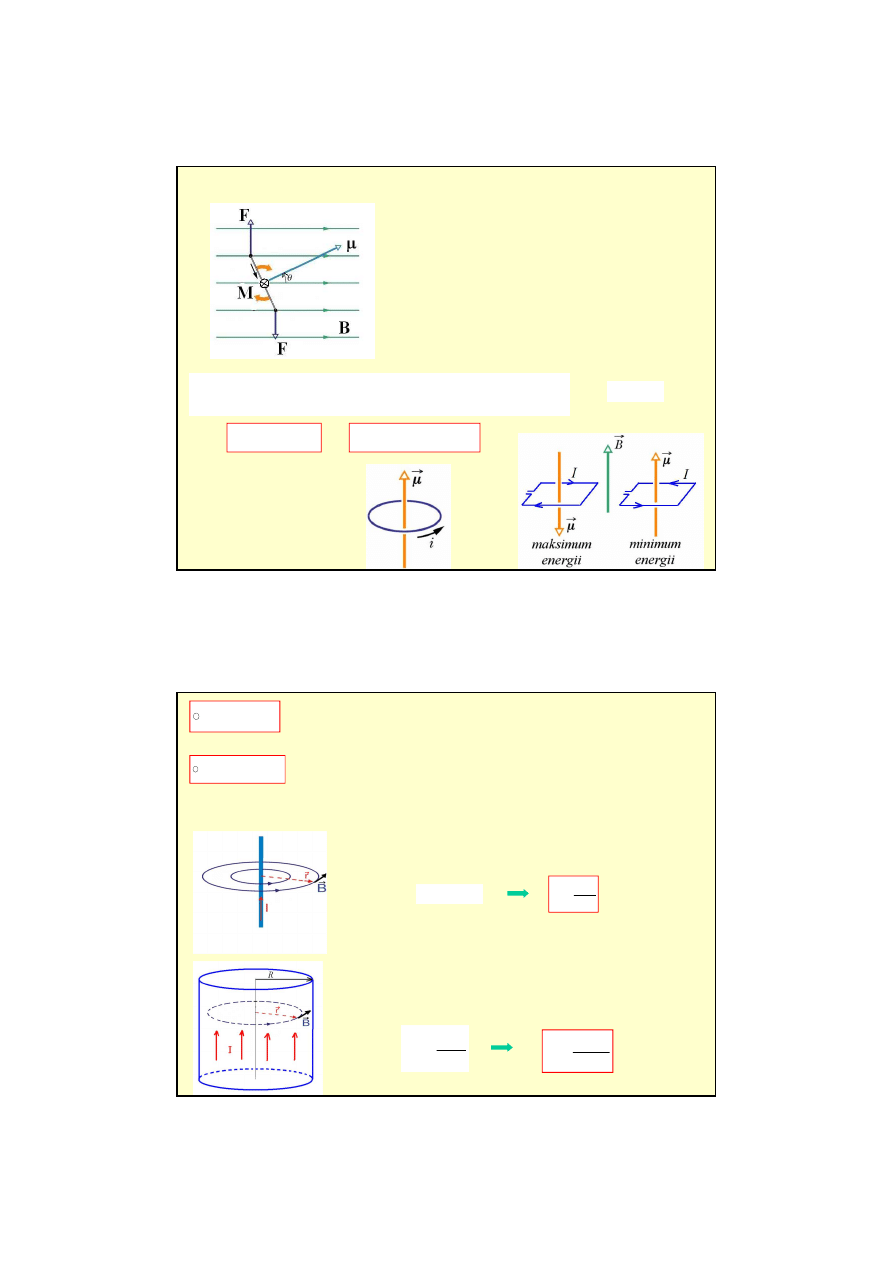
Pole magnetyczne działa na ramk

ę

z pr

ą

dem momentem skr

ę

caj

ą

cym obracaj

ą

c j

ą

tak jak

igł

ę

kompasu. Ramka zachowuje si

ę

wi

ę

c tak jak igła kompasu czyli dipol magnetyczny.

S

µ

I

=

B

µ

M

×

=

magnetyczny moment dipolowy

4

B

µ

⋅

−

=

E

Energia potencjalna ramki

Obracaj

ą

c dipol magnetyczny pole

magnetyczne wykonuje prac

ę

i wobec tego

dipol posiada energi

ę

potencjaln

ą

.

θ

θ

θ

θ

θ

θ

θ

cos

µ

'

'

sin

µ

)

'

(

0

0

0

0

0

0

B

d

B

E

Md

E

d

E

E

−

=

+

=

−

−

=

−

=

∫

∫

∫

θ

'

M

B

E

µ

0

−

=

θ

cos

µ

B

E

−

=

„Kołow

ą

ramk

ą

z pr

ą

dem" jest elektron

kr

ążą

cy po orbicie

w atomie.

∫

=

I

0

d

µ

l

B

Stała

µ

0

= 4

π

·10

-7

Tm/A, jest tzw.

przenikalno

ś

ci

ą

magnetyczn

ą

pró

ż

ni

∫

=

I

r

µ

µ

0

d l

B

Gdy pole magnetyczne jest wytworzone nie w pró

ż

ni ale w jakim

ś

o

ś

rodku to fakt ten uwzgl

ę

dniamy wprowadzaj

ą

c stał

ą

materiałow

ą

µ

r

zwan

ą

wzgl

ę

dn

ą

przenikalno

ś

ci

ą

magnetyczn

ą

o

ś

rodka

2

2

R

r

I

i

π

π

=

2

0

2 R

Ir

B

π

µ

=

Je

ż

eli chcemy obliczy

ć

pole wewn

ą

trz przewodnika to

wybieramy kontur kołowy o promieniu r < R, gdzie R jest
promieniem przewodnika.

Wewn

ą

trz konturu przepływa pr

ą

d i b

ę

d

ą

cy cz

ęś

ci

ą

całkowitego pr

ą

du I

Przykład 1

- prostoliniowy przewodnik

I

r

B

0

2

µ

π

=

W ka

ż

dym punkcie naszego konturu pole B jest do

niego styczne (równoległe do elementu konturu dl )

r

I

B

π

µ

2

0

=

5

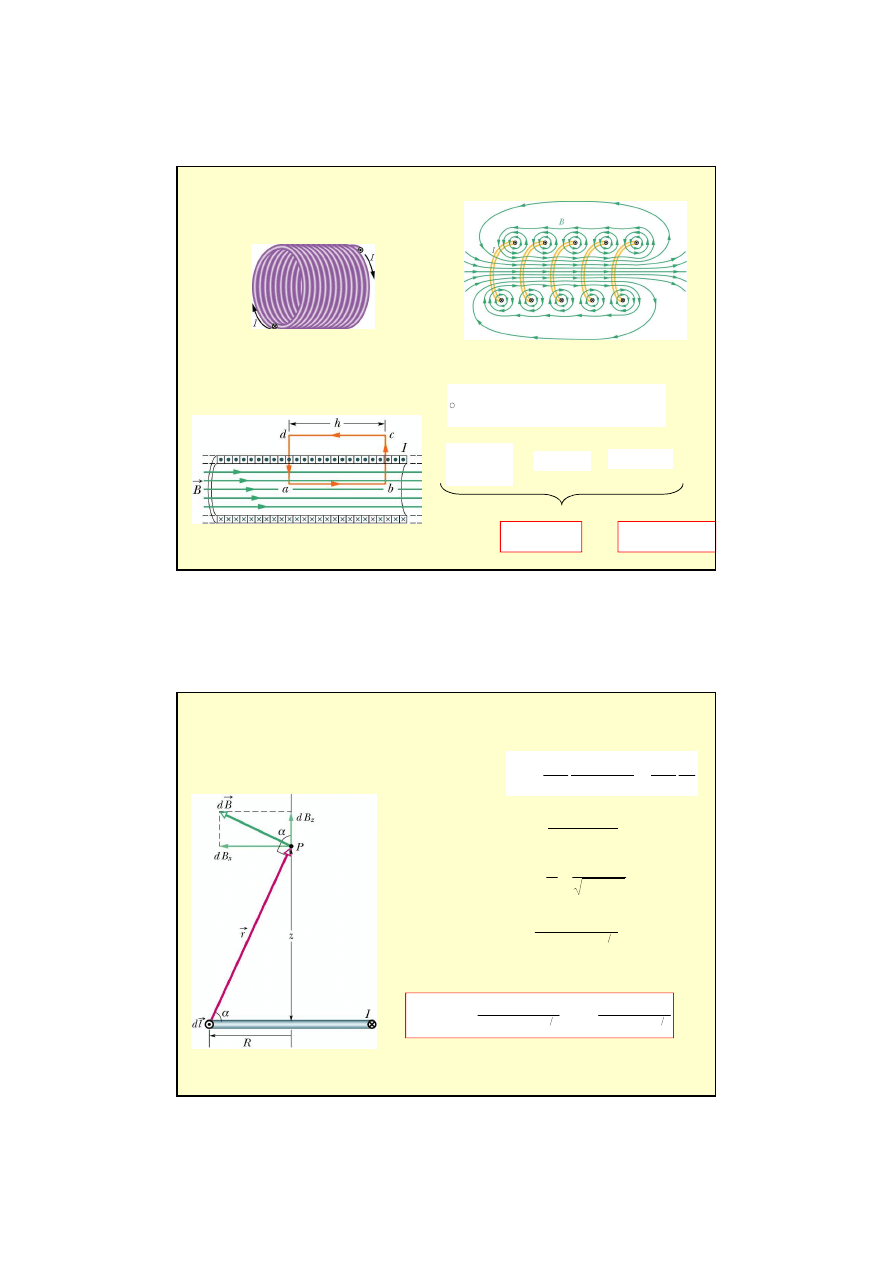
Przykład 3

-

Cewka (solenoid)

Je

ż

eli mamy do czynienia z solenoidem to pole magnetyczne wewn

ą

trz solenoidu jest

jednorodne, a na zewn

ą

trz równe zeru.

∫

∫

∫

∫

∫

+

+

+

=

a

d

d

c

c

b

b

a

l

B

l

B

l

B

l

B

l

B

d

d

d

d

d

∫

=

b

a

h

B

l

B d

Inh

I

całk

=

.

Inh

Bh

0

µ

=

n – g

ę

sto

ść

zwojów (ilo

ść

zwojów na jednostk

ę

długo

ś

ci)

nI

B

0

µ

=

nI

B

r

0

µ

µ

=

lub

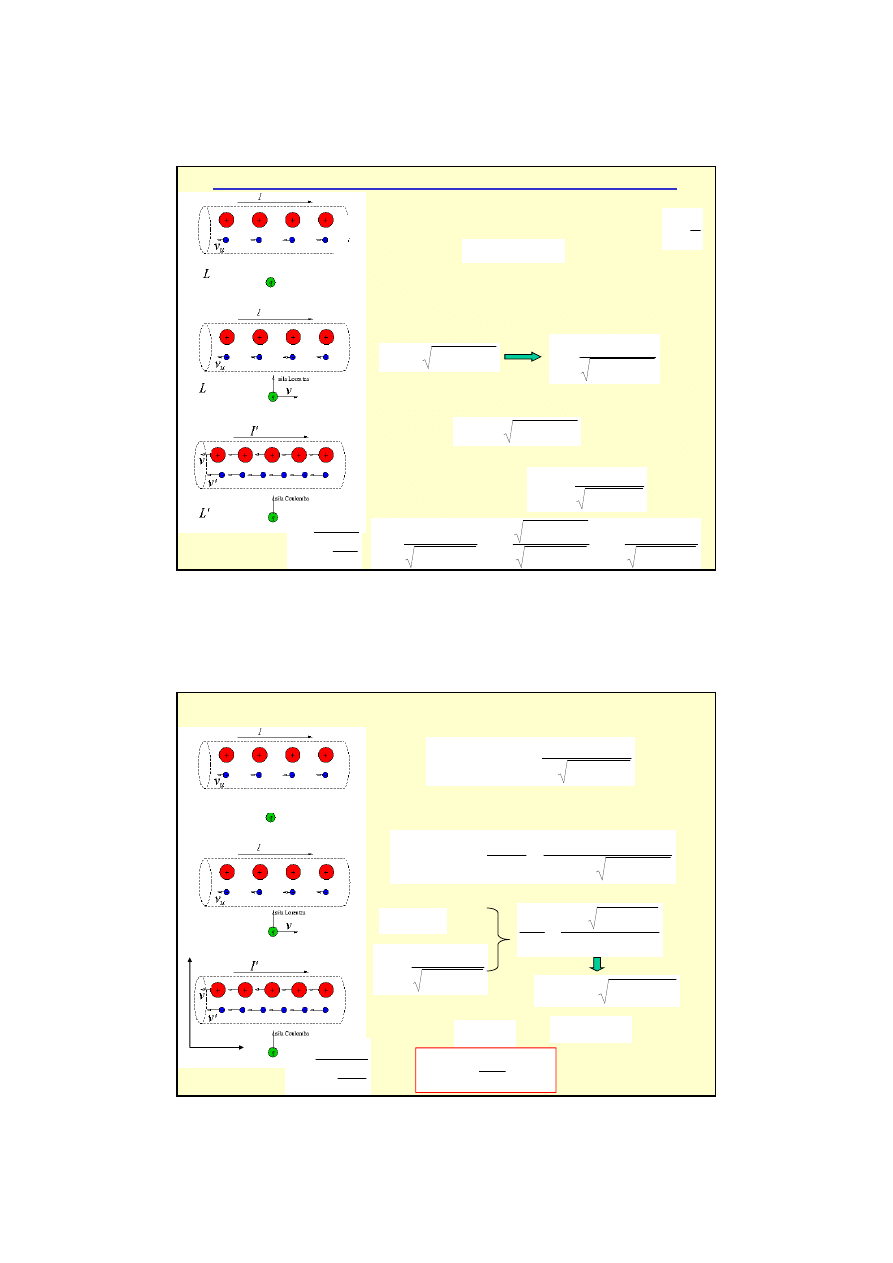
Przykład – przewodnik kołowy

α

dB

dB

z

cos

=

2

0

4

cos

πr

dl

α

I

µ

dB

z

=

2

2

cos

z

R

R

r

R

+

=

=

α

dl

)

z

(R

π

IR

µ

dB

z

2

3

2

2

0

4

+

=

2

0

2

0

4

90

sin

4

r

dl

π

I

µ

r

dl

π

I

µ

dB

o

=

=

prawo Biota-Savarta

2

3

2

2

2

0

2

0

2

3

2

2

0

)

(

2

)

(

4

d

z

R

IR

dl

z

R

IR

B

B

R

z

+

=

+

=

=

∫

∫

µ

π

µ

π

6

0

=

+

=

−

+

L

L

L

λ

λ

λ

WYJA

Ś

NIENIE POCHODZENIA SIŁ MAGNETYCZNYCH

W układzie laboratoryjnym (L) przewodnik z prądem
jest obojętny:

(

)

2

/

1

c

u

u

v

v

−

=

−

−

λ

λ

W układzie własnym elektronów gęstość ładunku „-” jest
mniejsza niż w układzie L:

−

λ

+

λ

l

q

=

λ

(

)

2

/

1

c

u

L

u

v

v

−

=

−

−

λ

λ

(

)

2

/

1

c

l

l

u

L

u

v

v

−

=

Transformacja z układu własnego elektronów (poruszającego
się wraz z elektronami z prędkością

v

u

) do układu

laboratoryjnego (L):

(

)

(

)

(

)

(

)

( )

2

2

2

2

2

'

/

1

/

1

/

'

1

/

1

/

'

1

c

c

c

c

c

u

L

u

L

L

u

v

v

v

v

v

v

v

−

+

=

−

−

=

−

=

−

−

−

−

λ

λ

λ

λ

( )

2

'

/

1

1

c

L

L

v

−

=

+

+

λ

λ

W układzie poruszającym się z prędkością

v

wraz z ładunkiem q (L’) :

2

1

'

c

u

u

v

v

v

v

v

+

+

=

(nieobowi

ą

zkowe)

2

1

'

c

u

u

v

v

v

v

v

+

+

=

0

=

+

=

−

+

λ

λ

λ

( )

2

2

'

'

'

/

1

c

c

u

L

L

L

L

v

v

v

−

=

+

=

−

−

+

−

λ

λ

λ

λ

Gęstość ładunków w przewodniku widziana w
układzie własnym poruszającego się ładunku q (L’) :

( )

2

2

0

0

'

'

'

/

1

2

2

c

c

r

v

r

q

E

q

F

L

u

L

L

L

v

v

−

=

=

=

−

−

ε

π

λ

ε

π

λ

Siła Coulomba w układzie własnym poruszającego się
ładunku q (L’):

−

=

λ

u

I

v

2

0

0

/

1

c

ε

µ

=

podstawmy:

y’

x’

Transformacja siły do układu laboratorujnego (L):

( )

2

'

/

1

c

dt

dt

L

L

v

−

=

'

L
y

L
y

dp

dp

=

( )

'

2

'

/

1

L

L
y

L

L
y

dt

c

dp

dt

dp

v

−

=

( )

2

'

/

1

c

F

F

L

L

v

−

=

B

q

r

I

q

F

L

v

v

=

=

π

µ

2

0

Siła Lorentza

7

TERMINY EGZAMINÓW

(sala A, D10)

• 0 termin – nie ustalony...

• I termin: 22 czerwca (12

00

-14

00

gr. 17,18,19

14

00

-16

00

gr. 20,21,22)

• II termin: 1 lipca (10

00

-12

00

gr. 17,18,19

14

00

-16

00

gr. 20,21,22)

• III termin: 24 września (10

00

-14

00

)