1

Całka nieoznaczona

∫

=

)

(

)

(

x

f

dx

x

g

Wynik operacji całkowania:
znaleziona funkcja pierwotna f(x) ma taką własność, że po zróżniczkowaniu
jej otrzymujemy funkcję podcałkową g(x):

C

x

f

dx

x

g

+

=

∫

)

(

)

(

ściślej:

Przykłady:

C

x

1

n

1

dx

x

1

n

n

+

+

=

+

∫

∫ e

x

dx = e

x

+ C

∫ (1/x) dx = ln x + C

∫ cos x dx = sin x + C

∫ sin x dx = - cos x + C

)

(

)

(

]

)

(

[

x

g

dx

x

df

dx

C

x

f

d

=

=

+

Całka oznaczona:

[

] [

]

∫

∫

=

=

+

−

+

=

−

b

a

b

a

dx

x

g

dx

x

g

C

a

f

C

b

f

a

f

b

f

)

(

)

(

)

(

)

(

)

(

)

(

C

x

f

dx

x

g

+

=

∫

)

(

)

(

Niech :

przyrost funkcji pierwotnej na przedziale [a,b]:

nazywamy całką oznaczoną.

)

(

)

(

)

(

a

f

b

f

dx

x

g

b

a

−

=

∫

CZYLI CAŁKA OZNACZONA TO:

C

x

f

dx

x

g

+

=

∫

)

(

)

(

gdzie:

)

(

)

(

]

)

(

[

x

g

dx

x

df

dx

C

x

f

d

=

=

+

2

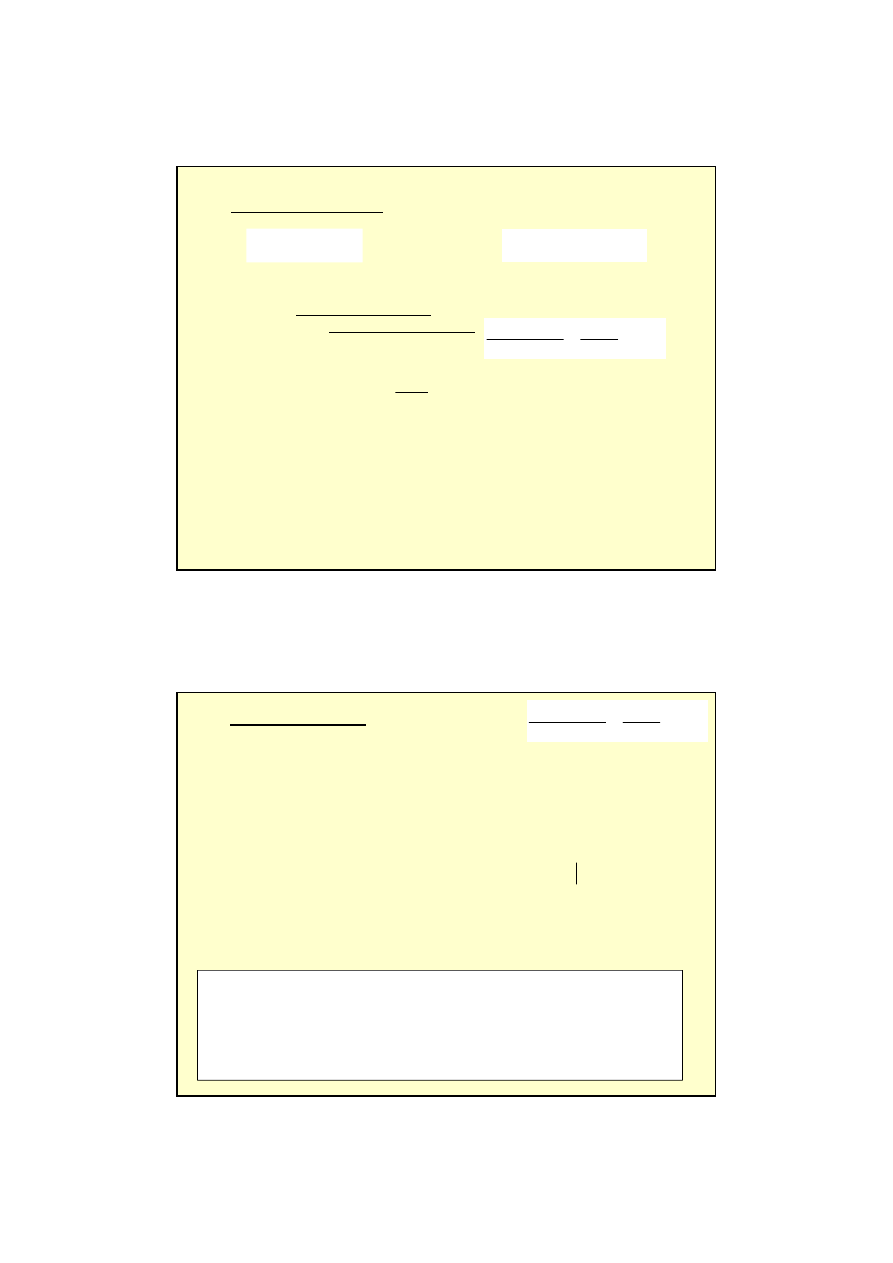
S

x

x

g

x

x

f

x

a

f

b

f

dx

x

g

i

N

i

i

i

N

i

i

i

b

a

=

∆

→

∆

=

∆

→

∆

=

−

=

∑

∑

∫

)

(

0

lim

)

(

0

lim

)

(

)

(

)

(

Znaczenie całki oznaczonej:

i

i

i

i

x

x

f

x

dx

x

df

x

g

∆

∆

→

∆

=

=

)

(

0

lim

)

(

)

(

i

i

i

x

x

g

x

f

∆

=

∆

)

(

)

(

∫

=

b

a

dx

x

g

S

)

(

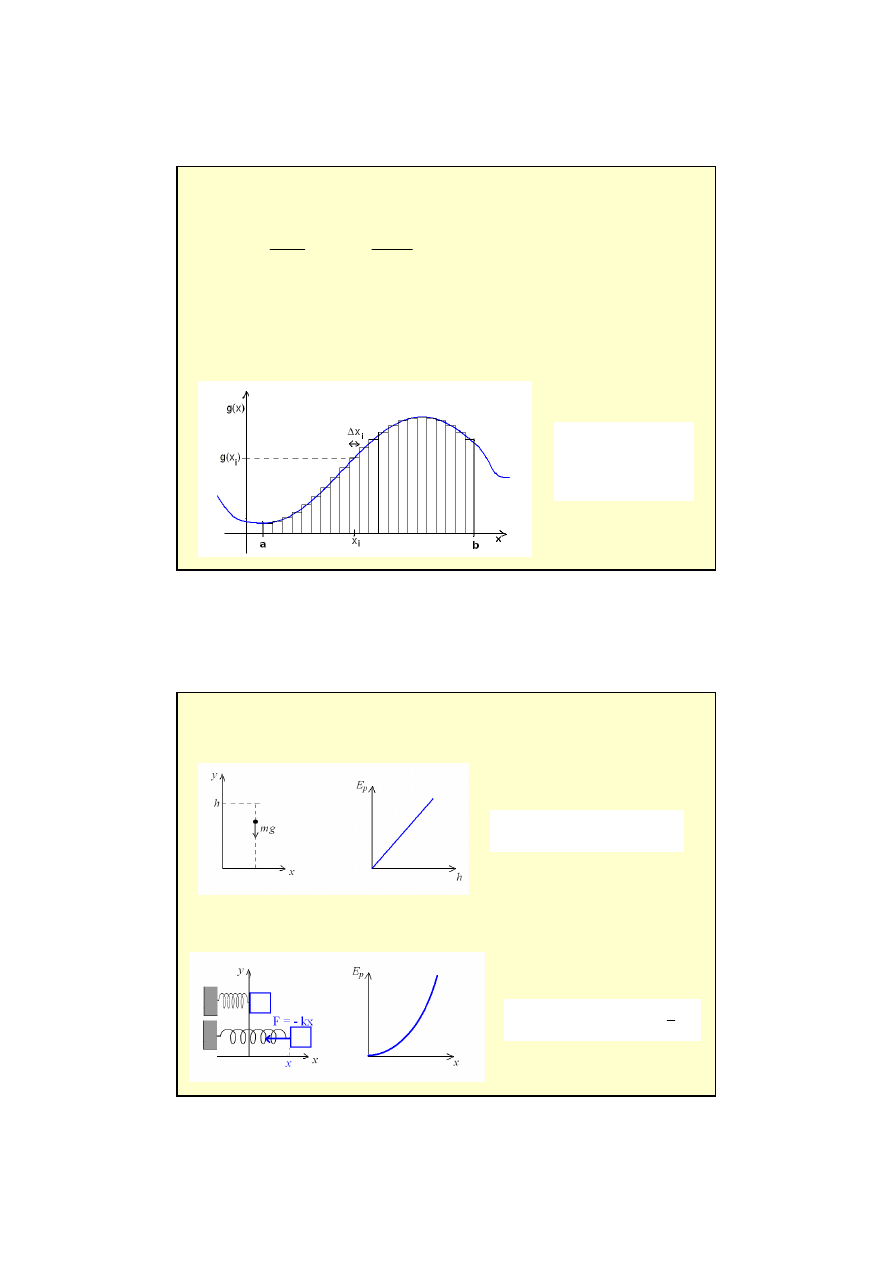
Przykłady liczenia energii potencjalnej

Energia potencjalna w pobliżu powierzchni Ziemi (punkt odniesienia na powierzchni Ziemi y

0

= 0)

mgy

y

mg

E

y

E

y

p

p

=

−

−

=

∫

'

d

)

(

)

0

(

)

(

0

0

)

0

(

=

p

E

dla:

Energia potencjalna idealnej nieważkiej sprężyny (punkt odniesienia x

0

= 0)

2

0

2

1

'

d

)

'

(

)

0

(

)

(

kx

x

kx

E

x

E

x

p

p

=

−

−

=

∫

0

)

0

(

=

p

E

dla:

3

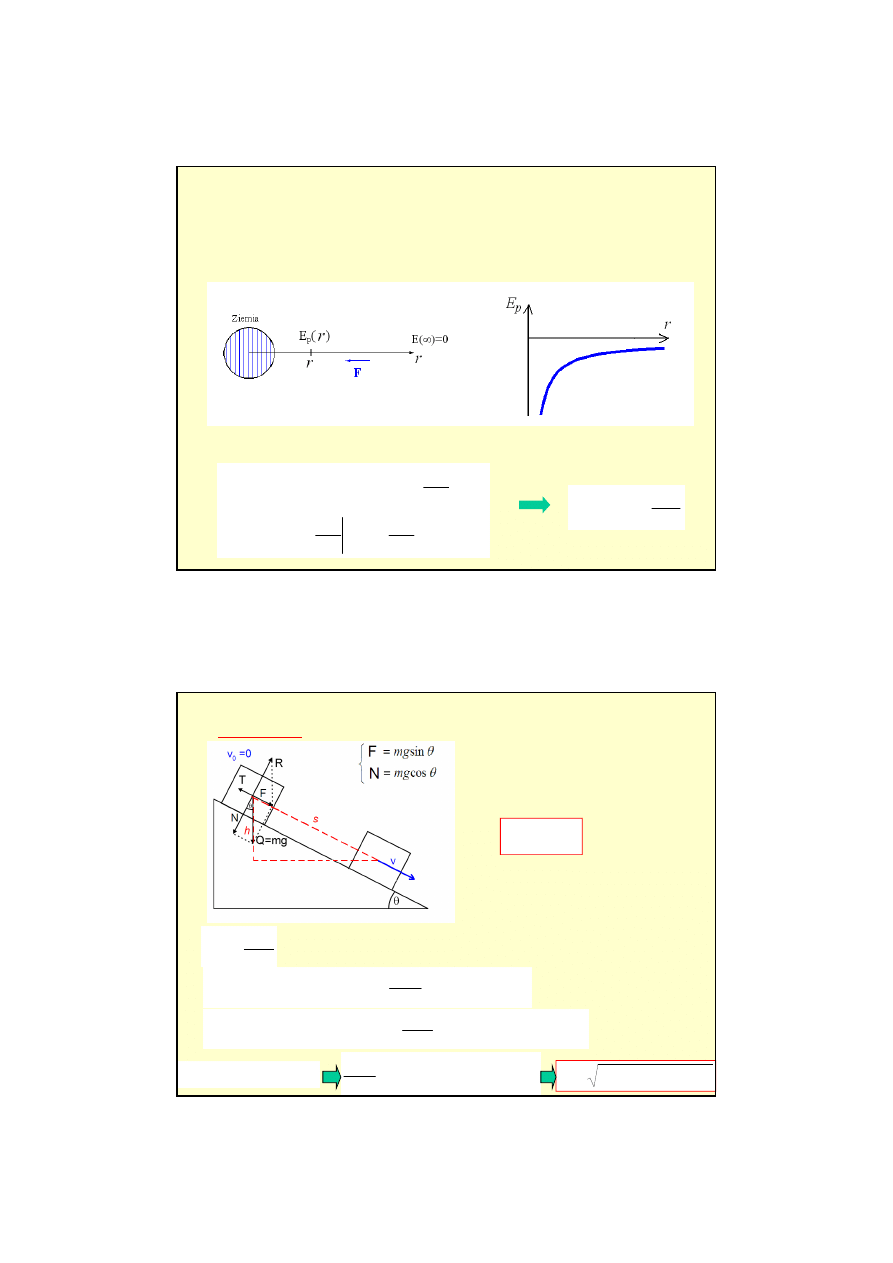
Energia potencjalna w dowolnym punkcie nad powierzchnią Ziemi, odległym o r od środka Ziemi
(zerową energię potencjalną przypisujemy punktowi odniesienia w nieskończoności r → ∞).

r

Mm

G

r

Mm

G

r

r

Mm

G

r

F

E

r

E

r

r

r

p

p

−

=

−

=













−

−

=

−

∞

=

∞

∞

∞

∫

∫

'

'

d

'

'

d

)

(

)

(

2

r

Mm

G

r

E

p

−

=

)

(

0

)

(

=

∞

p

E

dla:

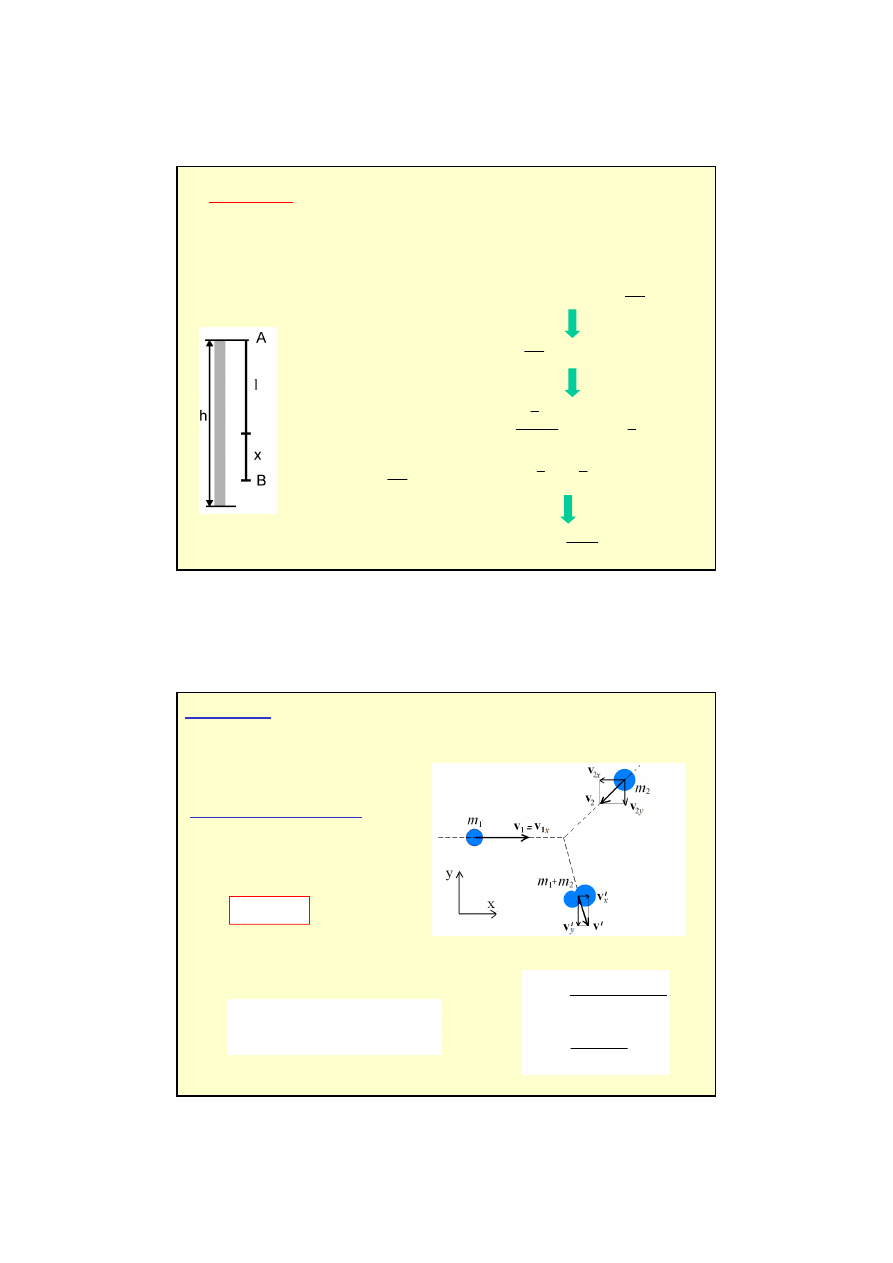
Przykład 1

s

f

>

θ

tg

θ

mg

f

θ

mg

θ

mg

f

N

f

T

T

F

s

s

s

cos

sin

cos

max

max

>

=

=

>

2

2

v

m

E

k

=

∆

mgh

mg

h

smg

W

E

F

p

−

=

−

=

−

=

−

=

∆

θ

θ

θ

sin

sin

sin

θ

θ

θ

θ

ctg

cos

sin

)

cos

(

k

k

k

T

f

mgh

mg

f

h

mg

f

s

W

U

=

=

−

−

=

−

=

∆

0

=

∆

+

∆

+

∆

U

E

E

p

k

0

ctg

2

2

=

−

+

mgh

f

mgh

m

k

θ

v

)

ctg

1

(

2

θ

k

f

gh

−

=

v

Przykłady dotycz

ą

ce prawa zachowania energii

4

Skoczek na linie "bungee" skacze z punktu A i osi

ą

ga najni

ż

szy punkt B. Obliczy

ć

współczynnik spr

ęż

ysto

ś

ci liny k (F = -kx) je

ś

li wiadomo,

ż

e miała ona długo

ść

poczatkow

ą

l i podczas skoku rozciagn

ę

ła si

ę

o x = 50% w stosunku do długo

ś

ci

pocz

ą

tkowej. Masa skoczka wynosi m.

mgh

E

A

=

2

)

(

2

kx

x

l

h

mg

E

B

+

−

−

=

Przykład 2

2

)

(

2

kx

x

l

h

mg

mgh

+

−

−

=

dla x = 0.5l :

0

2

2

=

−

−

mgx

mgl

kx

l

mg

k

12

=

0

2

1

2

2

1

2

=













−

−













l

mg

mgl

l

k

mgl

l

k

2

3

8

1

2

=

Przykłady dotycz

ą

ce prawa zachowania energii

Zderzenia:

-doskonale niesprężyste
-doskonale sprężyste
-inne

p

1

+p

2

=p’

doskonale niesprężyste:

-zas. zach. energii mechanicznej –

-niespełniona

- zas. zach. pędu -

spełniona













+

−

=

+

−

=

2

1

2

2

2

1

2

2

1

1

'

'

m

m

m

m

m

m

m

y

y

x

x

x

v

v

v

v

v







+

=

−

+

=

−

'

(

'

(

2

1

2

2

2

1

2

2

1

1

y

)v

v

)v

v

v

m

m

m

m

m

m

m

y

x

x

x

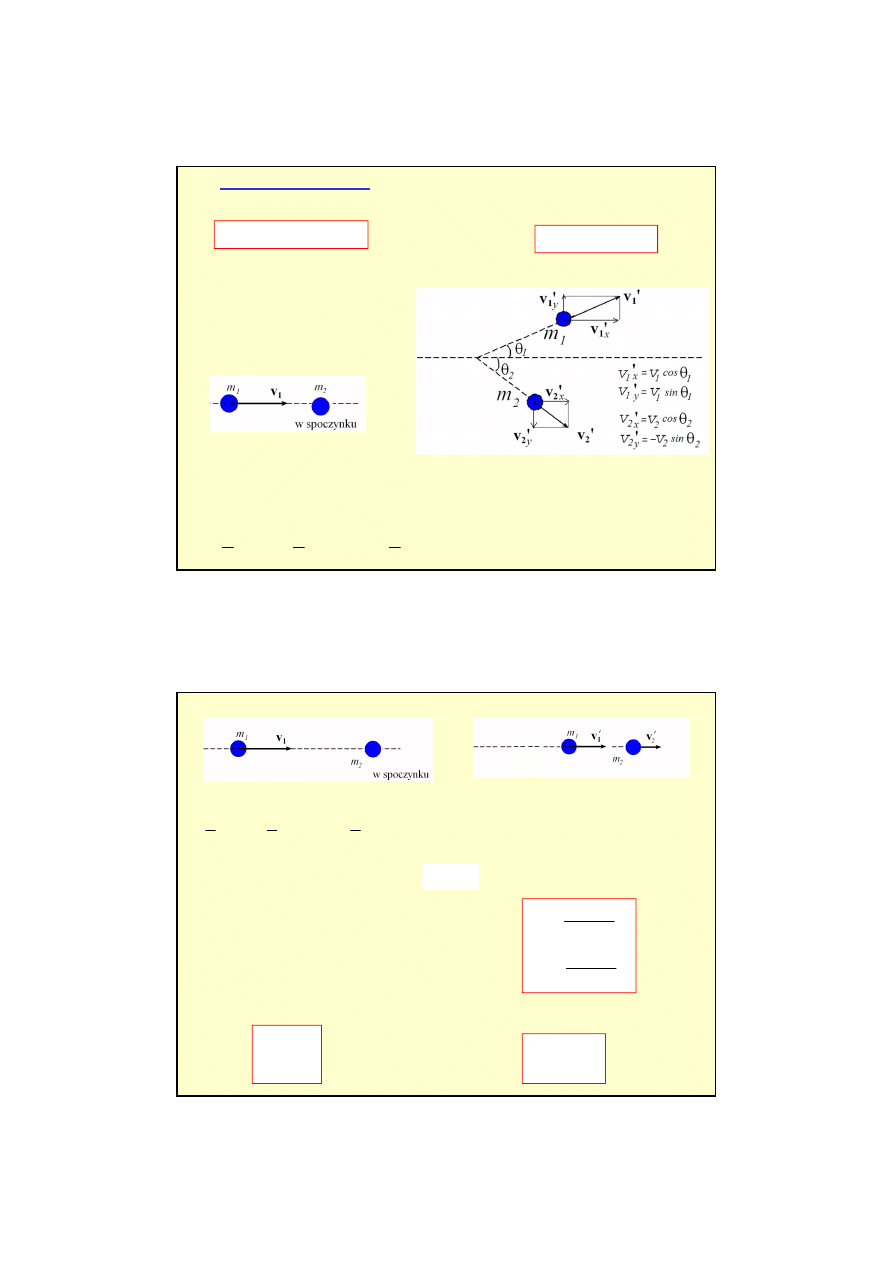
5

przykład zderzenia niecentralnego:







−

=

+

=

2

2

2

1

1

1

2

2

2

1

1

1

1

1

sin

'

sin

'

0

cos

'

cos

'

θ

θ

θ

θ

v

v

v

v

v

m

m

m

m

m

2

2

2

1

)

'

(

)

'

(

v

v

v

m

2

1

+

m

2

1

=

m

2

1

2

1

2
1

1

zas. zach. energii

zas. zach. pędu

p

1

+p

2

=p

1

’+ p

2

’

doskonale sprężyste:

- zas. zach. energii mechanicznej -

spełniona

- zas. zach. pędu -

spełniona

E

k1

+E

k2

=E

k1

’+ E

k2

’

przykład zderzenia centralnego (

θ

1

= θ

2

=0

)









+

=

2

2

2

1

2

2

1

1

1

1

)

'

(

)

'

(

'

'

v

v

v

v

v

v

m

2

1

+

m

2

1

=

m

2

1

m

m

m

2

1

2

1

1

zas. zach. energii

zas. zach. pędu







+

−

=

−

2

2

1

1

2

2

1

1

1

)

'

(

)

'

)(

'

(

'

)

'

(

v

v

v

v

v

v

v

v

m

=

m

m

m

2

1

1

1







+

=

−

'

)

'

(

'

)

'

(

2

1

2

2

1

1

1

v

v

v

v

v

v

=

m

m

1







+

+

=

−

'

)

'

(

)

'

(

)

'

(

2

1

1

2

1

1

1

v

v

v

v

v

v

v

=

m

m

1

1













+

=

+

−

=

v

v

v

v

1

1

m

m

m

m

m

m

m

1

2

1

2

1

2

2

1

1

2

'

'

przypadek szczególny gdy m

1

=m

2

=m:







=

=

1

2

1

'

0

'

v

v

v

1

1

'

v

v

≠







→

−

≈

0

'

'

2

1

1

v

v

v

przypadek szczególny gdy m

1

<<m

2:

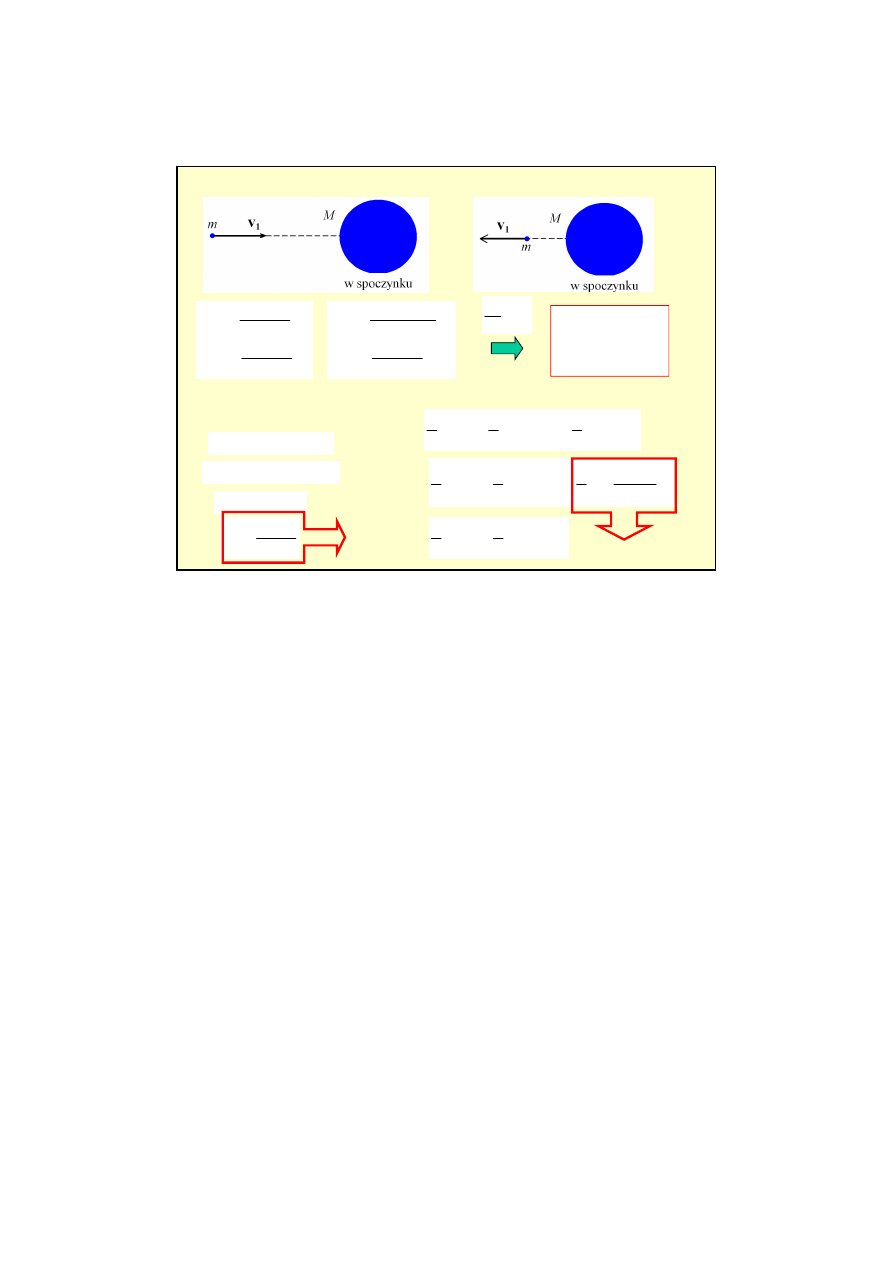
6

przypadek szczególny: odbicie od bardzo dużej masy tzn. M>>m













+

=

+

−

=

v

v

v

v

1

1

m

M

m

M

m

M

m

1

1

2

1

1

1

2

'

'













+

=

+

−

=

v

v

v

v

1

1

m

M

m

M

m

M

m

1

1

2

1

1

1

2

'

1

/

1

/

'







→

−

≈

0

'

'

2

1

1

v

v

v

0

1

→

M

m

zas. zach. energii

2

2

2

1

)

'

(

)

'

(

v

v

v

M

2

1

+

m

2

1

=

m

2

1

1

2

1

1

2

1

2

1

2

)

'

(













M

m

M

2

1

+

m

2

1

=

m

2

1

1

1

2

1

1

v

v

v

m

2

1

m

2

1

1

2

1

1

2

1

)

'

(

v

v

≈

0

'

2

1

1

1

1

v

v

v

M

m

m

+

−

≈

'

2

2

1

1

v

v

M

m

≈

M

m

1

1

2

2

'

v

v

≈

zas. zach. pędu

'

'

2

1

1

1

1

v

v

v

M

m

m

+

=

0