1. Aksjomaty mechaniki klasycznej.

a) Jeśli na punkt materialny nie działa żadna siła lub działa układ sił rownoważny zeru,

to punkt ten porusza się ruchem jednostajnym prostoliniowym.

b) Przyspieszenie punktu materialnego jest wprost proporcjonalne do siły działającej na

ten punkt, a wspołczynnikiem proporcjonalności jest odwrotność masy punktu.

c) Dwa punkty materialne oddziałują na siebie siłami o kierunku łączącym te punkty, o

tej samej wartości i przeciwnych zwrotach jako wektor przesuwny.

d) Oddziaływanie mechaniczne może być siłą traktowaną jako wektor przesuwny związany

z prostą lub momentem traktowanym jako wektor swobodny.

e) Przestrzeń, w ktorej ma miejsce ruch, traktowana jest jako przestrzeń euklidesowa

ogolnie trojwymiarowa.

2.

Moment wektora względem punktu

Moment wektora przesuwnego F wzgledem downolnego pukntu O nazywamy wektor bedący
nastepującym iloczynem wektorowym: M0=r x F gdzie r = OP [x0,y0,z0] jest wektorem
łączącym punkt 0 z początkiem P wektora F. moment wektora przesuwnego względem
dowolnego punktu 0 jest więc wektorem prostopadłym do płaszczyzny utworzonej przez ten
punkt i prostą działania wektora przesuwnego o zwrocie wynikającym z prawoskrętności
układu wektorów (r,F,M0) oraz wartości

3. Kiedy środek masy bryły pokrywa się z jej środkiem geometrycznym?

Dla ciała znajdującego się w jednorodnym polu grawitacyjnym środek ciężkości pokrywa się ze

środkiem masy.

4. Reguły Pappusa – Guldina

Pierwsza reguła Pappusa Guldina:
Pole powierzchni bocznej bryły obrotowej powstającej przez obrot krzywej płaskiej

wzglądem osi leżącej w jej płaszczyźnie i nieprzecinającej jej rowna się iloczynowi długości
krzywej przez długość okrągu, jaki zatacza przy obrocie jej środek masy.

Druga reguła Pappusa Guldina:
Objętość bryły obrotowej powstającej przez obrot figury płaskiej względem osi leżącej w

płaszczyźnie figury i nieprzecinającej jej rowna się iloczynowi pola powierzchni figury i
długości okręgu, jaki w czasie obrotu zatacza jej środek masy.

5. Twierdzenie Steinera dla momentów bezwładności

Moment bezwładności bryły względem dowolnej osi (O

x

, O

y

lub O

z

) rowna się sumie momentu

bezwładności względem osi rownoległej do danej osi i przechodzącej przez środek masy (

C

x

,

C

y

lub C

z

) oraz iloczynu masy bryły przez kwadrat odległości obu osi.

Otrzymujemy więc trzy następujące zależności:

I

x

=

I

X

+

m(b

2

+

c

2

)

I

y

=

I

Y

+

m(a

2

+

c

2

)

I

z

=

I

Z

+

m(a

2

+

b

2

)

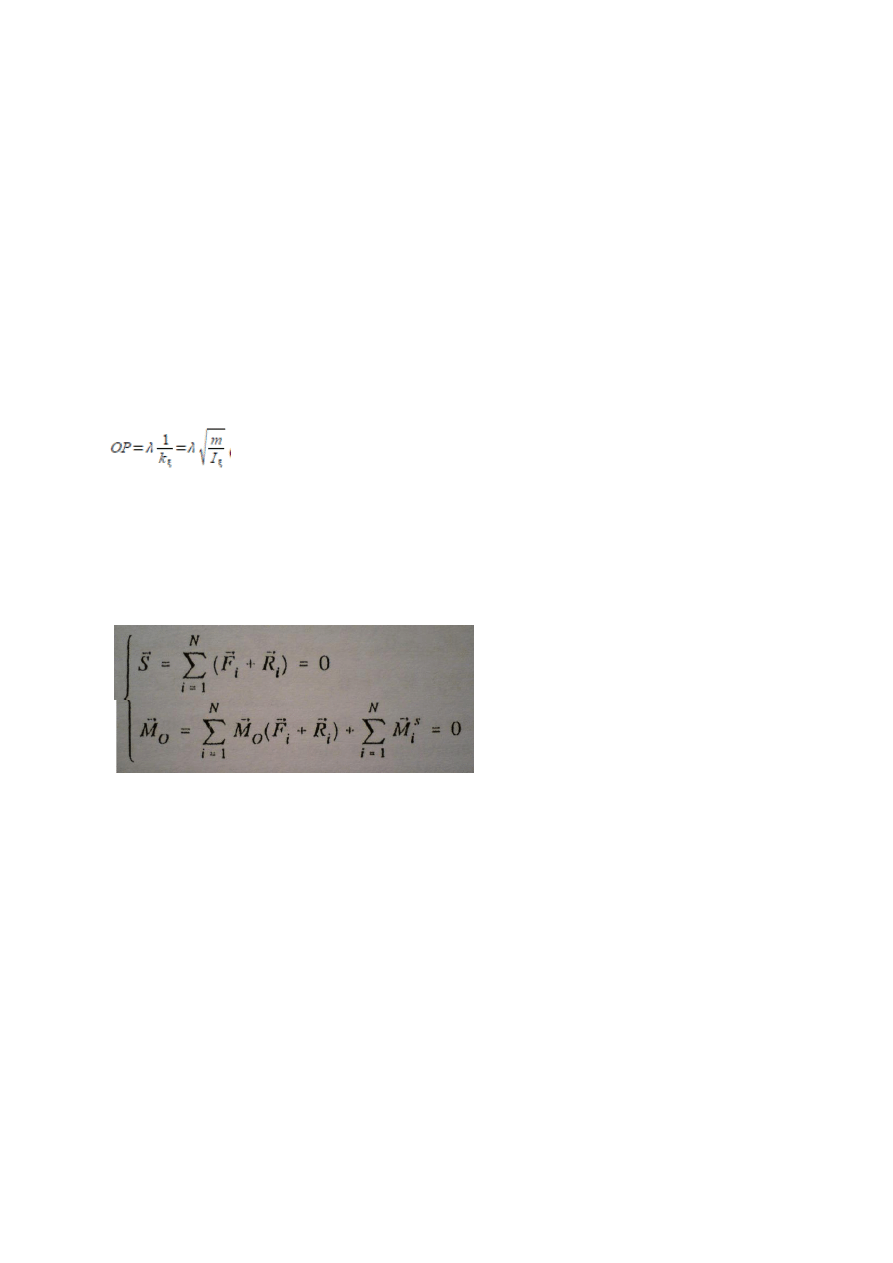
6. Twierdzenie Steinera dla momentów dewiacji

Moment dewiacji bryły względem dwu prostopadłych płaszczyzn rowna się sumie momentu

dewiacji względem dwu płaszczyzn rownoległych do danych płaszczyzn i zawierających
środek masy bryły oraz iloczynu masy tej bryły przez wspołrzędne określające położenie

obu płaszczyzn względem płaszczyzn centralnych. W układach C

XYZ

i O

xyz

mamy następujące

zależności:

I

xy

=

I

XY

+

mab

I

xz

=

I

XZ

+

mac

I

yz

=

I

YZ

+

mbc

7. Elipsoida bezwładności

Elipsoidą bezwładności nazywamy miejsce geometryczne punktów, których odległości od początku

układu są odwrotnie proporcjonalne do pierwiastka kwadratowego z momentu bezwładności względem
osi przechodzącej przez dany punkt i początek układu współrzędnych.

8. Co to jest skrętnik?

Jest to układ wektorów - sumy geometrycznej sił oraz sumy geometrycznej
momentów - mający tę właściwość, że obydwa wektory leżą na tej samej prostej,
która nazywa się skrętnikiem. Oś na której leży skrętnik nazywamy osią centralną.

9.

Geometryczne warunki równowagi

Aby dowolny układ sił był w równowadze, warunkiem koniecznym i wystarczającym jest, by suma sił i

suma ich momentów względem dowolnego punktu były równe zeru.

10. Redukcja płaskiego układu sił

Płaski układ sił można zredukować do układu równoważnego składającego się z jednej siły S

przyłożonej w dowolnie obranym biegunie redukcji O i pary sił o momencie M

0

.

Zatem płaski układ sił, redukuje się do:



wypadkowej, jeśli S =/= 0



momentu swobodnego, jeśli S = 0 i Mo =/= 0.

11. Kiedy dowolny układ sił redukuje się do siły wypadkowej?

Dla S =/= 0, MO =/= 0, ale MO prostopadłym do S => MS = 0.
Układ redukuje się do pojedynczego wektora siły W równoległego do S, nie leżącej jednak na prostej

przechodzącej przez punk O. Wypadkowa nie jest zatem geometryczną sumą sił F

i

.

Aby siła S była wypadkową, musi być umieszczona na jednej osi, która jest osią skrętnika.

12. Tarcie opasania

Jest to tarcie występujące w czasie opasania bębna przez cięgno. Kąt opasania jest to kąt

odpowiadający łukowi, wzdłuż którego cięgno przylega do bębna. Tarcie to zmienia stosunek między

siłami przyłożonymi do obu końców cięgna. Stosunek siły przyłożonej do cięgna i ciężaru

zawieszonego na drugim jej końcu wyraża się wzorem:

13. Samohamowność i zakleszczenie

Układ, w którym zachodzi przypadek szczególny (gdy Pmin. < lub = 0), nazywamy

samohamownym, a układ, w którym maksymalne obciążenie w stanie równowagi jest nieograniczone,
nazywamy układem zakleszczającym się.

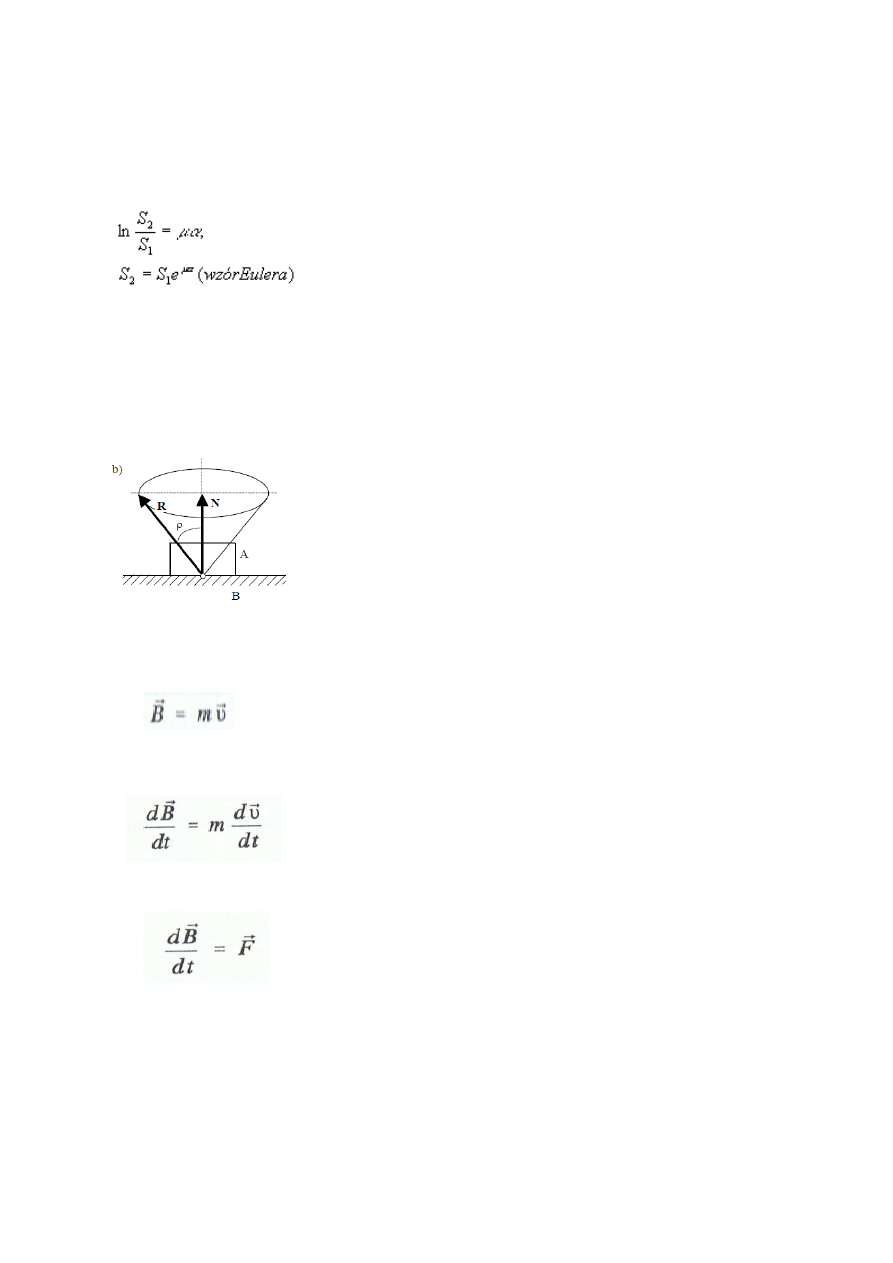
14. Stożek tarcia

Jeżeli siła styczna P będzie przyjmować wszystkie możliwe kierunki,

to reakcja R zakreśli stożek, którego osią jest prosta pokrywająca się

z reakcją normalną N.
Ten maksymalny kąt, o jaki może się odchylić reakcja całkowita R od

normalnej N, nazywamy

kątem tarcia

ρ

. Aby ciało znajdowało się w

spoczynku, reakcja całkowita R musi leżeć wewnątrz stożka tarcia, a

w przypadku tarcia całkowicie rozwiniętego na powierzchni tego
stożka.

15. Prawo zmienności pędu punktu materialnego
Pędem punktu materialnego nazywamy wektor będący iloczynem masy
punktu i jego prędkości:

Jeśli masa punktu nie zmienia się w czasie, to wektor pędu zmienia się

podczas ruchu, tak jak prędkość. Zmiany te odzwierciedla pochodna wektora
pędu względem czasu:

Wykorzystując II prawo Newtona, zapiszemy

prawo zmienności pędu

swobodnego

punktu materialnego, w postaci: