Strona 1

Dokument został pobrany z serwisu ZamKor.

Wszelkie prawa zastrzeżone.

Data utworzenia:

2011-06-15

Z

K

am or

Zadanie 2 z LX Olimpiady Fizycznej

Zawody III stopnia

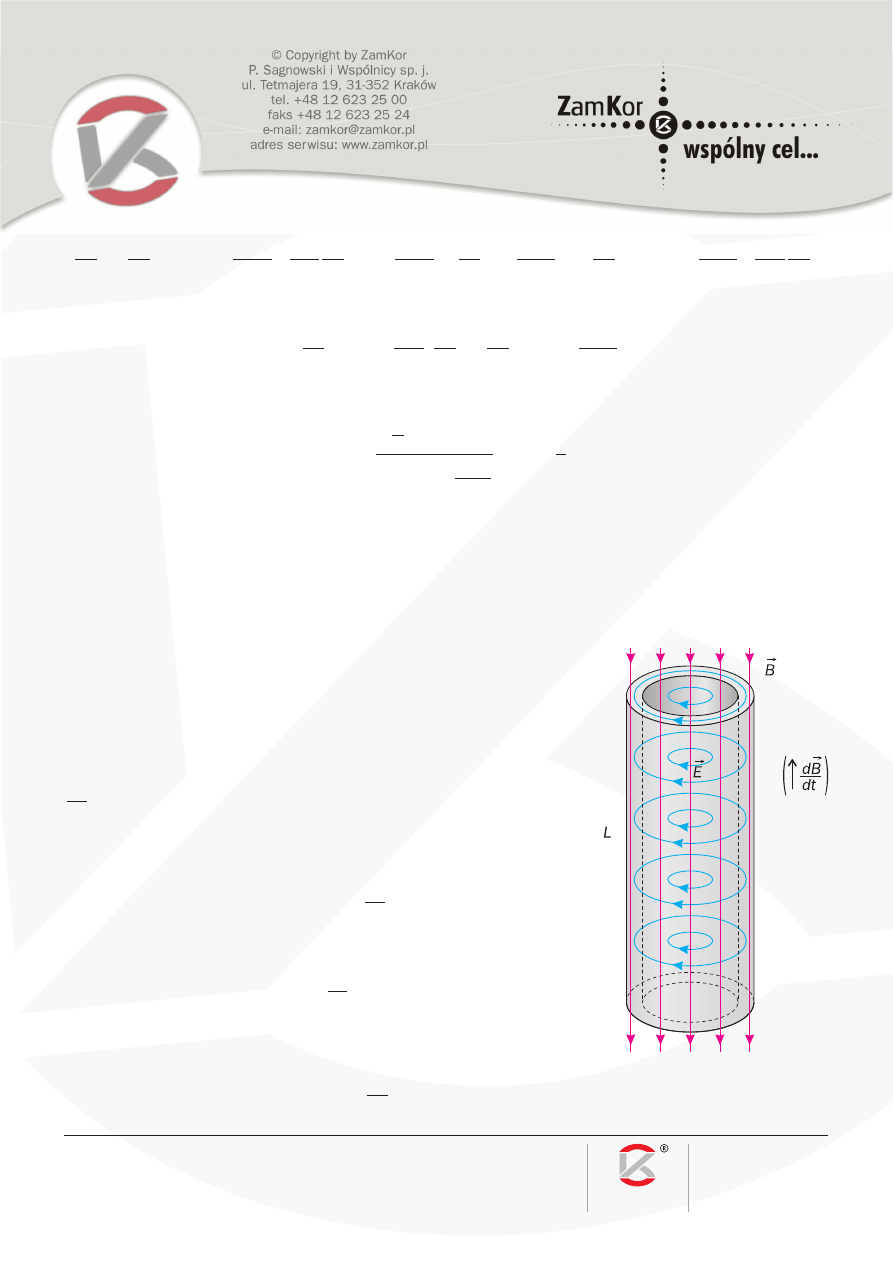
Jednorodna rura o momencie bezwładności I względem jej osi, długości L i promieniu wewnętrznym r

2

i ze-

wnętrznym r

1

(przy czym L r



1

) znajduje się w jednorodnym, równoległym do jej osi polu magnetycznym o in-

dukcji B

0

. Rura jest wykonana z nieprzewodzącego, niemagnetycznego materiału. Jej powierzchnia zewnętrzna

jest równomiernie naładowana ładunkiem o całkowitej wartości Q, a powierzchnia wewnętrzna jest równomier-

nie naładowana ładunkiem o całkowitej wartości –Q. Rura może się swobodnie obracać wokół swojej osi, ale

początkowo jest nieruchoma. Znajdź końcową prędkość kątową rury, jeśli wartość indukcji zewnętrznego pola

magnetycznego zmniejszono powoli od B

0

do zera.

Podaj wynik liczbowy dla L = 0,5 m, r

1

= 0,010 m, r

2

= 0,009 m, B

0

= 1 T, Q = 6 · 10

–5

C, I = 6 · 10

–9

kg · m

2

.

Przenikalność magnetyczna próżni m

0

= 4p · 10

–7

H/m.

Rozwiązanie Komitetu Głównego Olimpiady Fizycznej

Z prawa Ampere’a wynika, że gdy indukcja pola magnetycznego wynosi B

zew

a rura obraca się z prędkością

kątową w, przy czym kierunek i zwrot



B

zew

oraz  są takie same, to indukcja pola magnetycznego w odległości

r od osi jest równa:

B

B

r r

B

Q

L

r

r r

B

r r

zew

zew

zew







 

















dla

dla

dla

1

0

1

2

2

2

 



Jeśli pole magnetyczne ulega zmianie, to, zgodnie z prawem Faradaya, indukuje się pole elektryczne. Na

zewnętrznej powierzchni rury będzie ono wynosić:

E

r

d

dt

r

r

r

dB

dt

Q

L

d

dt

r

zew

1

1

1

1

1

2

2

2

0

1

2

1

2

2



































(

)

22

2

dB

dt

zew











natomiast na wewnętrznej będzie równe:

E

r

d

dt

r

r

dB

dt

zew

2

2

2

2

2

2

1

2

1

2























Pole elektryczne stara się obrócić naszą rurę. Moment siły wynosi:

M QE r

QE r





1 1

2 2

Po podstawieniu wzorów na E

1

i E

2

otrzymamy równanie ruchu obrotowego rury:

Strona 2

Dokument został pobrany z serwisu ZamKor.

Wszelkie prawa zastrzeżone.

Data utworzenia:

2011-06-15

Z

K

am or

I

d

dt

Q

r

r

dB

dt

Q

L

d

dt

r

dB

dt

zew

zew


































2

2

1

2

2

2

0

2

2

(

)
























Q

r

dB

dt

Q

r

r

dB

dt

Q

L

d

d

zew

zew

2

2

2

2

2

1

2

2

2

0















(

)

tt





















Przekształcając powyższy wzór, otrzymamy:

I

Q

r

r

Q

L

d

dt

Q

r

r

dB

dt

zew



















2

2

2

1

2

2

2

0

1

2

2

2















(

)

(

)

Skąd końcowa prędkość kątowa wynosi:







konc

Q

r

r B

I

r

r

Q

L











2

4

0 095

1

1

2

2

2

0

1

2

2

2

0

2

(

)

(

)

,

s

Znak + powyżej oznacza, że jeśli patrzymy zgodnie z



B

0

, to rura zacznie się obracać zgodnie z ruchem wska-

zówek zegara.

Rozwiązanie przedstawione przez dr Jadwigę Salach

1.

W pierwszej części rozwiązania nie uwzględnimy zjawiska samoinduk-

cji. Zrobimy to dopiero w części drugiej, aby wyraźnie zaznaczyć, który człon

otrzymanego wzoru na wartość końcowej prędkości rury stanowi poprawkę

na samoindukcję.

Z prawa indukcji Faradaya wynika, że w przestrzeni, w której zmienia się

pole magnetyczne, indukuje się wirowe pole elektryczne. W przypadku za-

nikającego pola magnetycznego o liniach zwróconych w dół (rys. 1), wektor

dB

dt



jest zwrócony w górę. Wynika z tego, że linie wirowego pola elektrycz-

nego są zwrócone zgodnie ze wskazówkami zegara (widok z góry).

Zakładamy, że B zewnętrznego pola magnetycznego zmniejsza się li-

niowo:

B B

At





0

dB

dt

A



gdzie A jest stałą dodatnią; całkowity czas, w którym pole zmaleje do zera,

będzie równy:

t

B

A

c



0

Korzystając z prawa Faradaya, obliczamy wartości natężenia pola elek-

trycznego na zewnętrznej i wewnętrznej powierzchni rury:

E

r

S

dB

dt

1

1

1

2



 



Rys. 1

Strona 3

Dokument został pobrany z serwisu ZamKor.

Wszelkie prawa zastrzeżone.

Data utworzenia:

2011-06-15

Z

K

am or

E

r

r

A

E

Ar

1

1

1

2

1

1

2

2





 









( )

Podobnie

E

r

S

dB

dt

2

2

2

2



 



E

r

r

A

E

Ar

2

2

2

2

2

2

2

2





 









( )

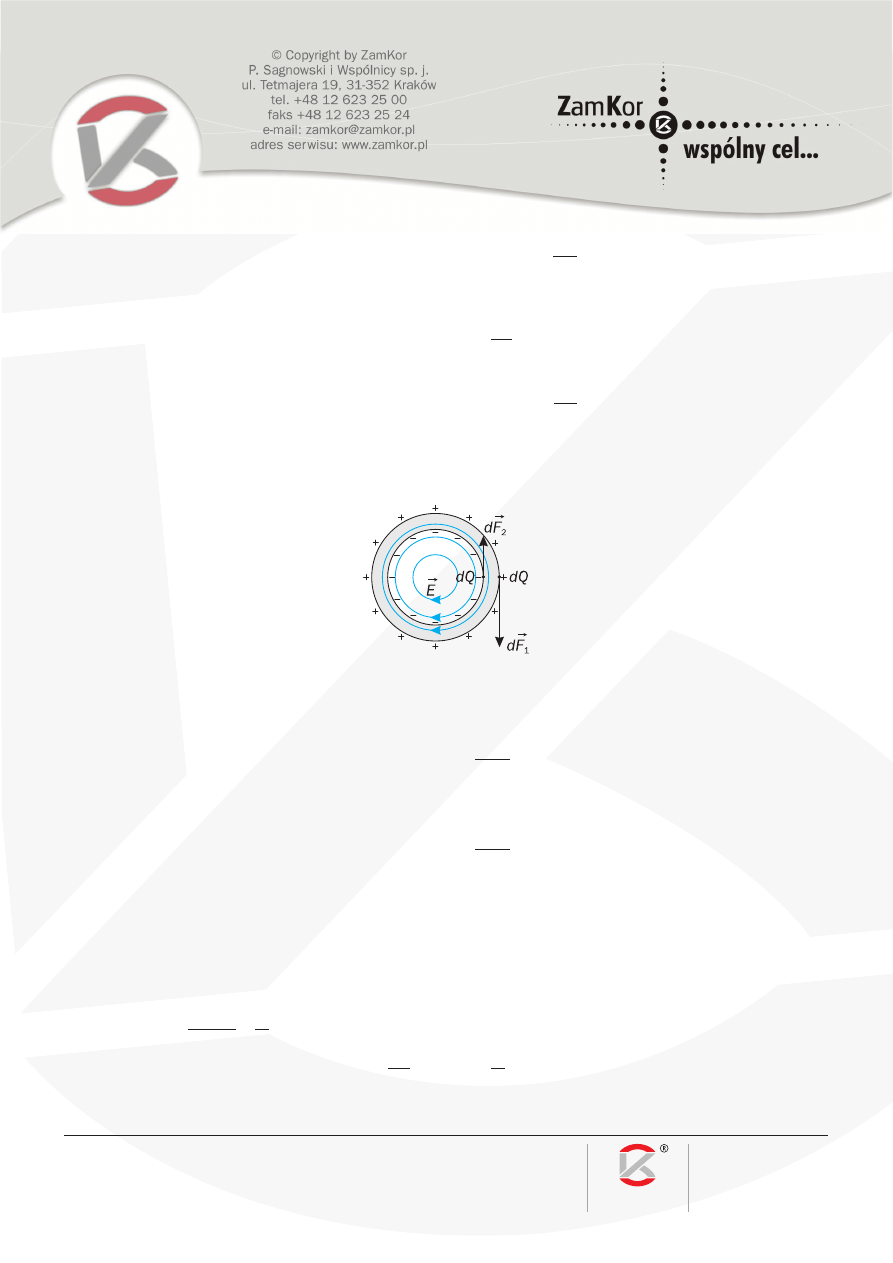
Pole elektryczne działa na ładunki rozmieszczone na zewnętrznej i wewnętrznej powierzchni rury. Na każdy

element ładunku dQ działa siła styczna do powierzchni, przy czym dF

2

< dF

1

, bo na okręgu o mniejszym promie-

niu wartość natężenia pola elektrycznego jest mniejsza (rys. 2).

Rys. 2

Całkowity moment siły elektrycznej działającej na zewnętrzną powierzchnię rury ma wartość:

M

QE r

Qr A

1

1 1

1

2

2





i zwrot zgodny z



B

0

, a na zewnętrzną powierzchnię rury ma wartość:

M

QE r

Qr A

2

2 2

2

2

2





i zwrot przeciwny do



B

0

. Moment siły wypadkowej



M jest stały, ma wartość M = M

1

– M

2

i jest zwrócony zgodnie

z



B

0

.

Stosujemy drugą zasadę dynamiki dla ruchu obrotowego rury:

M

1

– M

2

= I e

gdzie 

 











const

0

t

t

c

c

, bo w

0

= 0.

AQ

r

r

I

t

c

2

1

2

2

2

(

)







Strona 4

Dokument został pobrany z serwisu ZamKor.

Wszelkie prawa zastrzeżone.

Data utworzenia:

2011-06-15

Z

K

am or

skąd





AQt

I

r

r

c

2

1

2

2

2

(

)

At

c

= B

0

, więc





B Q

I

r

r

0

1

2

2

2

2

(

)

W chwili gdy zniknie pole magnetyczne, prędkość końcowa rury osiągnęłaby taką wartość, gdyby nie wystę-

powało zjawisko samoindukcji.

2.

Uwzględnienie zjawiska samoindukcji stanowi znacznie trudniejszą część rozwiązania.

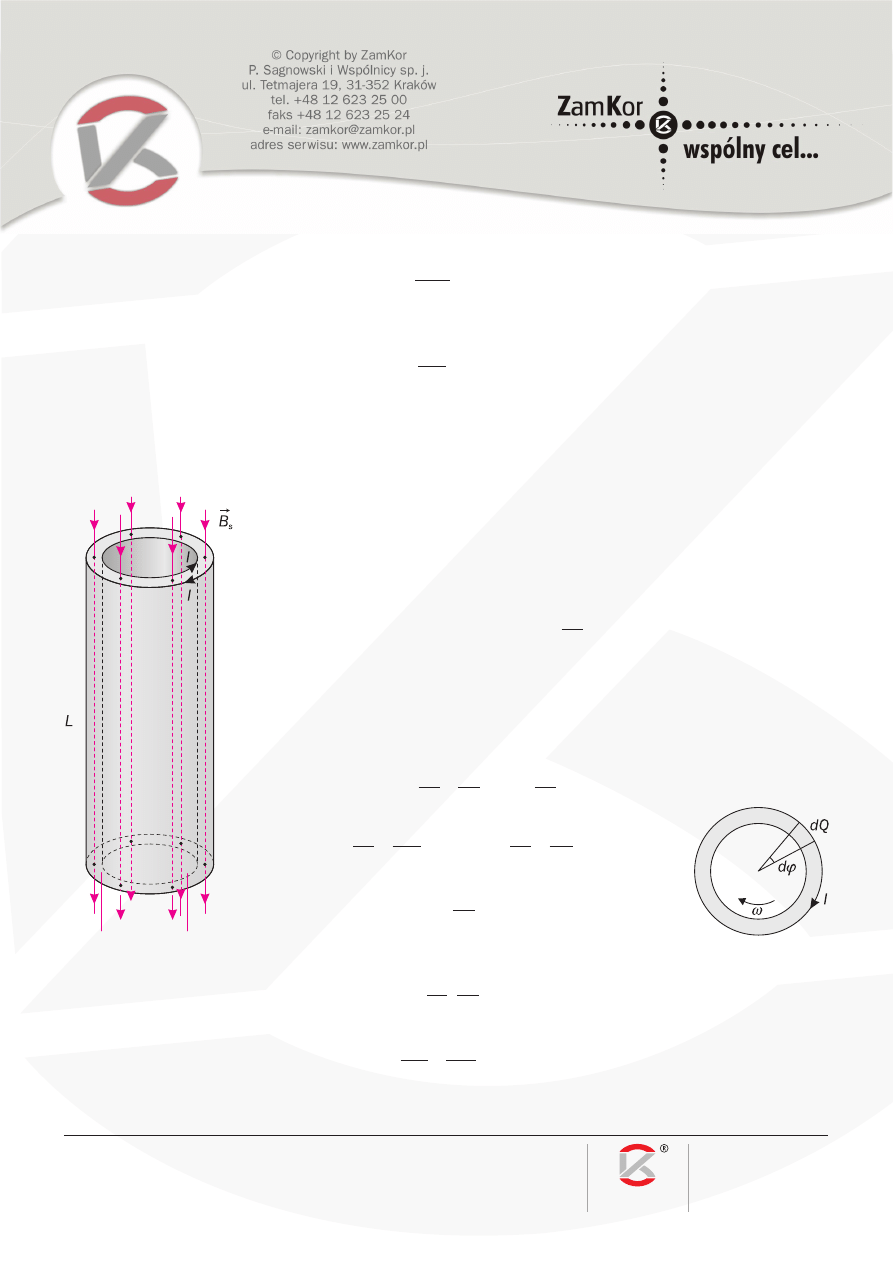
Obracająca się coraz szybciej naelektryzowana rura stanowi prąd o zmieniającym

się (rosnącym) natężeniu, który jest źródłem siły elektromotorycznej samoindukcji.

Powierzchnie rury możemy potraktować jako dwie współosiowe „zwojnice” z prą-

dem o jednakowym natężeniu I (t); kierunki tych prądów są przeciwne ze względu na

przeciwne znaki ładunków na zewnętrznej i wewnętrznej powierzchni rury. W każdej

„zwojnicy” powstaje jednorodne pole magnetyczne, którego indukcja ma wartość

B

I t

L

s







0

( )

gdzie I pełni rolę sumy natężeń prądów I

1

w poszczególnych „zwojach”, tzn. I = I

1

n.

Wewnątrz rury pola magnetyczne wytworzone przez te prądy znoszą się, pole ma-

gnetyczne pozostaje tylko między ściankami i pochodzi od „zwojnicy” zewnętrznej,
zatem



B

s

między ściankami jest zwrócone w dół, zgodnie z



B

0

(rys. 3).

Obliczamy I (t):
Zachodzi proporcja:

dQ

Q

d






2

, gdzie

d

dt







(rys. 4),

dQ

Q

dt







2

I

dQ

dt

Q








2

I t

Q

t

( )

( )





2



zatem

B t

L

Q

t

s

( )

( )













0

2

dB

dt

Q

L

s











0

2

Rys. 3

Rys. 4

Strona 5

Dokument został pobrany z serwisu ZamKor.

Wszelkie prawa zastrzeżone.

Data utworzenia:

2011-06-15

Z

K

am or

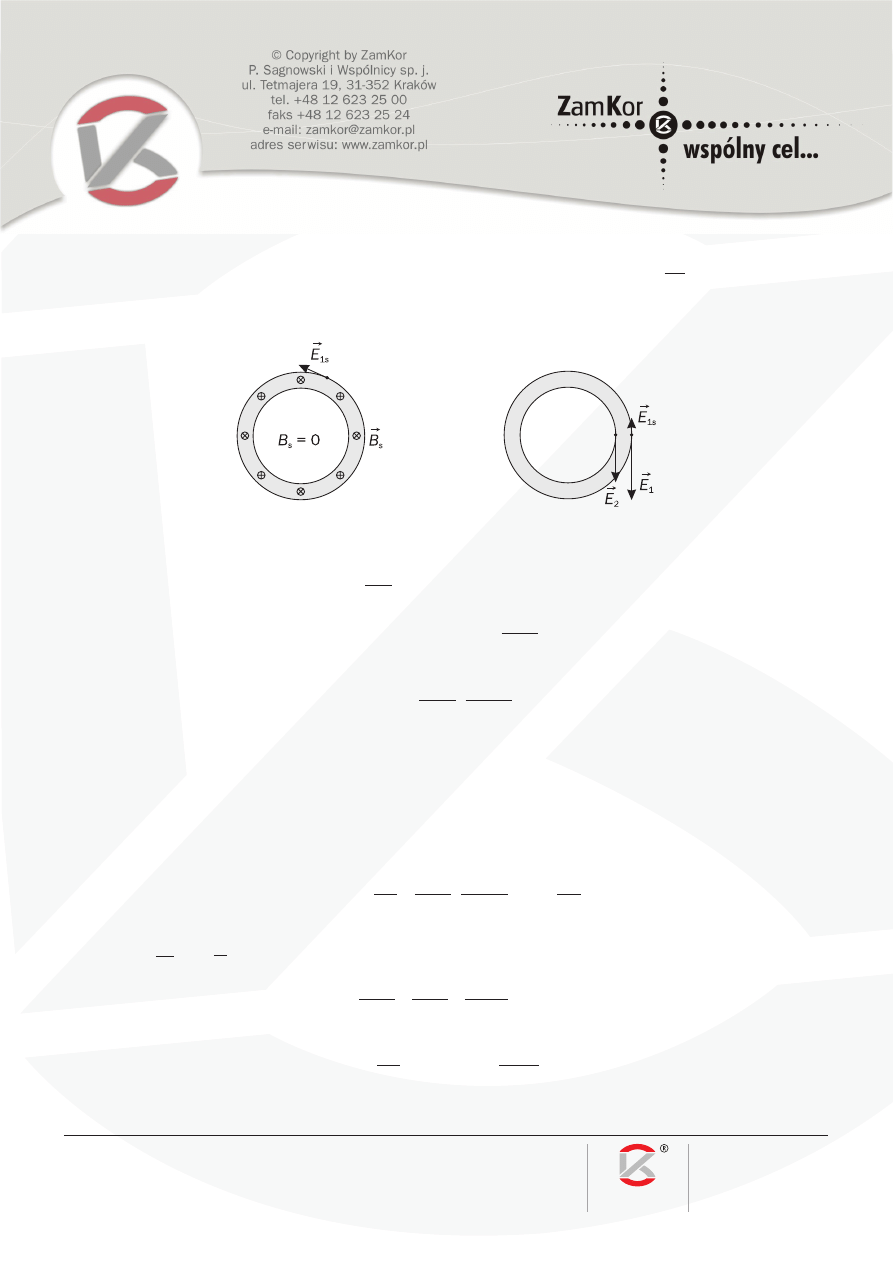
Korzystając znowu z prawa indukcji Faradaya, obliczamy wartość natężenia pola elektrycznego E

s

powstają-

cego wzdłuż konturów leżących na zewnętrznej i wewnętrznej powierzchni rury. Wektor

dB

dt



jest zwrócony w dół,

bo B

s

rośnie, więc natężenie pola elektrycznego



E

s

1

jest zwrócone przeciwnie do ruchu wskazówek zegara (wi-

dok z góry – rys. 5).

Rys. 5 Rys. 6





 

E

r

S

dB

dt

s

s

1

1

2

gdzie S

r

r







(

)

1

2

2

2

E

r

r

r

Q

L

s

1

1

1

2

2

2

0

2

2











 



(

)

E

Q

L

r

r

r

s

1

0

1

2

2

2

1

4







 



E

2s

wzdłuż konturu leżącego na wewnętrznej powierzchni rury jest równe zeru, bo kontur ten nie obejmuje

żadnego pola magnetycznego.

Tak więc poprzednio obliczona wartość E

1

zostaje zmniejszona o E

1s

, a E

2

nie ulega zmianie (rys. 6). Po

uwzględnieniu tego faktu, obliczenia będą następujące:

M Qr E

E

Qr E

s







1

1

1

2 2

(

)

M Qr

Ar

Q

L

r

r

r

Qr

Ar





















1

1

0

1

2

2

2

1

2

2

2

4

2

 



gdzie A

B

t

c



0

, 





t

c

.

M

QAr

QAr

Q

L

r

r









1

2

2

2

0

2

1

2

2

2

2

2

4







(

)

M

Q

t

r

r

B

Q

L

c

















2

2

1

2

2

2

0

0

(

)

 



Strona 6

Dokument został pobrany z serwisu ZamKor.

Wszelkie prawa zastrzeżone.

Data utworzenia:

2011-06-15

Z

K

am or

I

Q

t

r

r

B

Q

L

c



 



















2

2

1

2

2

2

0

0

(

)

Mnożymy obie strony wzoru przez t

c

:

I

Q

r

r B

Q

L

r

r

















2

4

1

2

2

2

0

0

2

1

2

2

2

(

)

(

)







I

Q

L

r

r

Q

r

r B



















0

2

1

2

2

2

1

2

2

2

0

4

2

(

)

(

)















Q

r

r B

I

Q r

r

L

2

4

1

2

2

2

0

0

2

1

2

2

2

(

)

(

)

lub 













Q r

r B

I

Q r

r

L

(

)

(

)

1

2

2

2

0

0

2

1

2

2

2

2

2

Porównując ten wynik z wynikiem otrzymanym w części 1. rozwiązania, widzimy, że drugi składnik sumy

w mianowniku pojawił się wskutek uwzględniania zjawiska indukcji własnej.

Podstawiamy dane liczbowe:











 



 

















6 0

1 0 01

0 009

2 6 10

4 0 6 10

2 0 5

5

2

2

9

7

5 2

[( , )

( ,

) ]

(

)

,

[[( , )

( ,

) ]

0 01

0 009

1

2

2



s

















114 10

12 0

2 7 10

1

11

9

20

,

s

 

0 095

1

,

s

Poprawka uwzględniająca zjawisko samoindukcji ma wartość o dziesięć rzędów wielkości mniejszą od pierw-

szego składnika sumy w mianowniku. Nie wpływa ona na wartość liczbową szybkości kątowej rury.