Laboratorium 

Komputerowego wspomagania podejmowania decyzji 

 

Procesy decyzyjne w postaci ekstensywnej  o sumie zerowej 

 

 

 

 

 

 

 

 

 

 

Autorzy(TI-1) 

Dawid Łapiński 

Kamil Wencel 

Data odbycia ćwiczenia: 22.05.2014 

1.  Rozwiązanie przykładowej gry. 

Stworzony przez nas problem wieloetapowy: 

[3 5 -1 6 7 0 2 6 12 13 -7 8 2 0 -8 4 9 11 23 -13 5 2 
-1 4 2 -3 1 -4 3 6 2 -1 0 1 -2 6 1 9 -5 0 8 4 0 5 -6 
8 -2 3 0 11 2 3 18 13 -2 0 1 0 2 6 12 4 10 13]; 
 

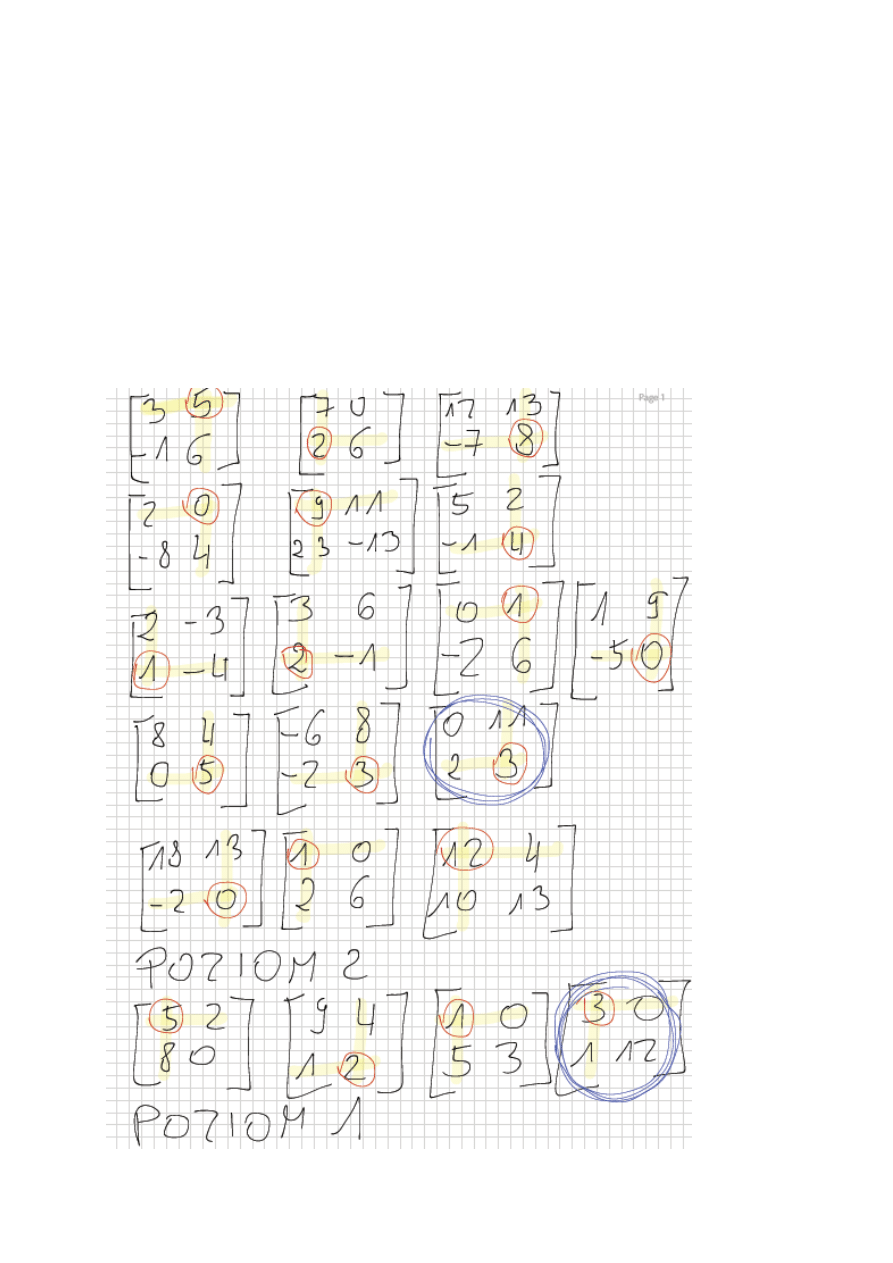
Rozwiązanie ręczne(wyniki obliczone metodą zamieszczoną w instrukcji-
zaznaczone strategie graczy, oraz wynik gry): 

 

 

2.  Wyniki działania programu w matlabie. 

 

 

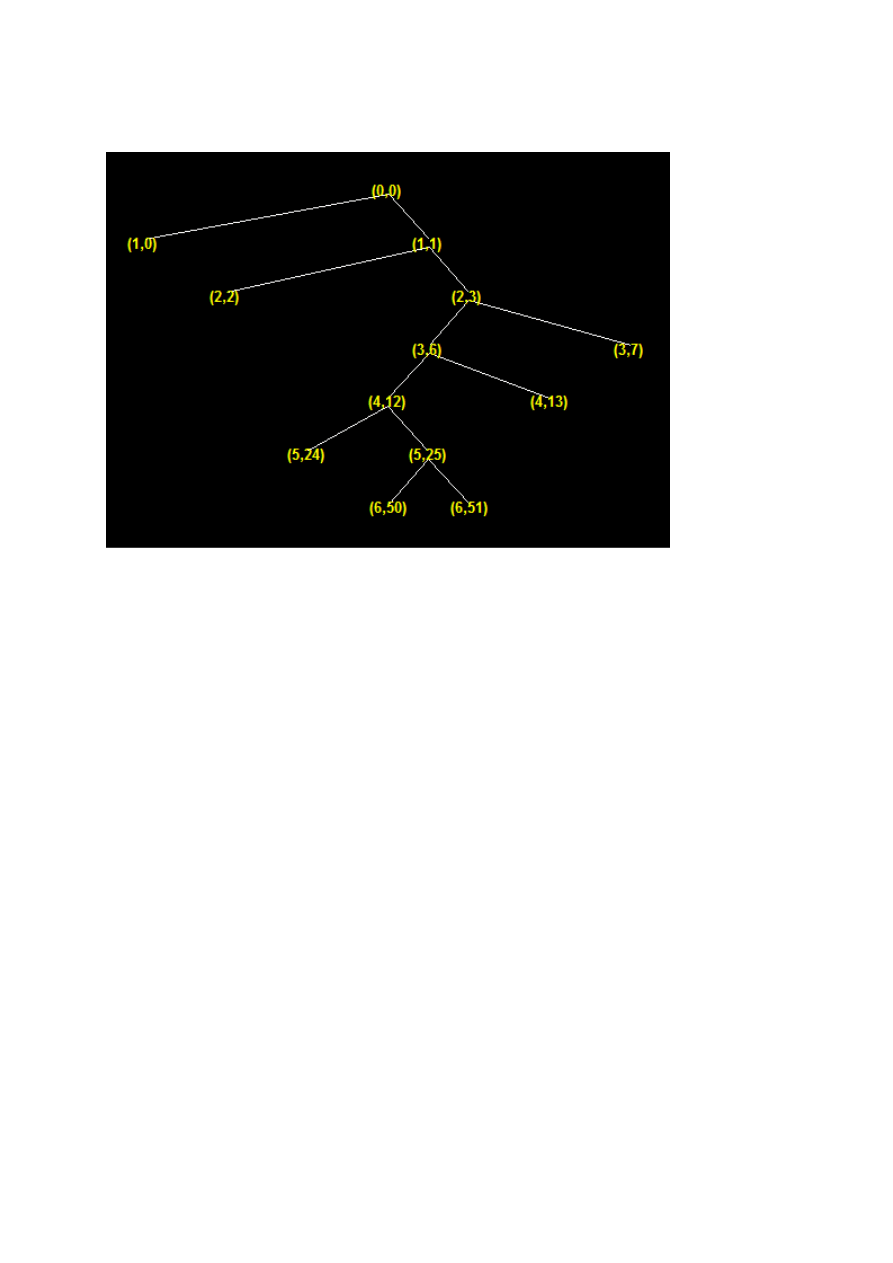
Oraz prosta interpretacja graficzna: 

 

3.  Zaimplementowany kod 

Kod matlaba wraz z odpowiednimi adnotacjami: 

4. 

clear 

all

 

5. 

clc

 

6. 

 

 

7. 

%wprowadzane dane- k oraz problem wieloetapowy

 

8. 

k=3;

 

9. 

dane(k,:,3)=[3 5 -1 6 7 0 2 6 12 13 -7 8 2 0 -8 4 9 11 23 -13 5 2 -1 4 2 -
3 1 -4 3 6 2 -1 0 1 -2 6 1 9 -5 0 8 4 0 5 -6 8 -2 3 0 11 2 3 18 13 -2 0 1 
0 2 6 12 4 10 13];

 

10. 

licznik=1;

 

11. 

 

 

12. 

for

 i=k:-1:2

 

13. 

    

for

 j=1:4:4^i

 

14. 

        

 

15. 

        

%fragment programu w tym forze rozwiązuje proces jednokrokowy 

i

 

16. 

        

%zapisuje do odpowiedniej macierzy wyniki (wybrane strategie 

oraz

 

17. 

        

%jej wynik)

 

18. 

        A=[dane(i,j,3) dane(i,j+1,3);dane(i,j+2,3) dane(i,j+3,3)];

 

19. 

        maxi=max(A');

 

20. 

        

for

 y=1:1:2

 

21. 

            

if

 min(max(A'))==maxi(y)

 

22. 

                dane(i-1,licznik,1)=y;

 

23. 

            

end

 

24. 

        

end

 

25. 

        

 

26. 

        mini=min(A);

 

27. 

        

for

 y=1:1:2

 

28. 

            

if

 max(min(A))==mini(y)

 

29. 

       

 

30. 

                dane(i-1,licznik,2)=y;

 

31. 

            

end

 

32. 

        

end

 

33. 

 

 

34. 

        dane(i-1,licznik,3)=A(dane(i-1,licznik,1),dane(i-

1,licznik,2));

 

35. 

        

 

36. 

        licznik=licznik+1;

 

37. 

    

end

 

38. 

    licznik=1;

 

39. 

end

 

40. 

 

 

41. 

%rozwiązanie macierzy dla poziomu pierwszego

 

42. 

A=[dane(1,1,3) dane(1,2,3);dane(1,3,3) dane(1,4,3)];

 

43. 

        maxi=max(A');

 

44. 

        

for

 y=1:1:2

 

45. 

            

if

 min(max(A'))==maxi(y);

 

46. 

                y1=y;

 

47. 

            

end

 

48. 

        

end

 

49. 

        

 

50. 

        mini=min(A);

 

51. 

        

for

 y=1:1:2

 

52. 

            

if

 max(min(A))==mini(y);

 

53. 

                y2=y;

 

54. 

            

end

 

55. 

        

end

 

56. 

        

%wynik gry

 

57. 

        A(y1,y2)

 

58. 

        

%decyzje graczy 1 i 2, poziomu pierwszego

 

59.   
60. 

        dzialania(1,1)=y1;

 

61. 

        dzialania(1,2)=y2;

 

62. 

        

 

63. 

        

%fragment kodu odpowiadający za "wyśledzenie", jakimi 

decyzjami

 

64. 

        

%doszło się do wyniku

 

65. 

        cosik=1;

 

66. 

        

for

 i=2:1:k

 

67. 

            cosik=(dzialania(i-1,1)-1)*2+dzialania(i-1,2)+(cosik-1)*4;

 

68. 

            dzialania(i,1)=dane(i-1,cosik,1);

 

69. 

            dzialania(i,2)=dane(i-1,cosik,2);

 

70. 

        

 

71. 

        

end

 

72. 

        

%wyświetlenie macierzy wynikowej, zawierającej poszczególne 

decyzje

 

73. 

        

%graczy (D1, D2)

 

74. 

        dzialania

 

75. 

        

 

76. 

        

%inicjalizacja drzewa decyzji

 

77. 

        T=ntree(2,0);

 

78. 

        

 

79. 

        licznik2=0;

 

80. 

        

for

 i = 1 : k 

 

81. 

            

%umiejscowienie rozgałęzień drzewa w odpowiednich 

miejscach

 

82. 

         T = nodesplt(T,licznik2); 

 

83. 

         licznik2 = licznik2*2 + dzialania(i,1); 

 

84. 

         T = nodesplt(T,licznik2); 

 

85. 

         licznik2 = licznik2*2 + dzialania(i,2); 

 

86. 

        

end

 

87. 

        

 

88. 

        plot(T)

 

89. 

        

 

 

Wyniki programu są zgodne z tymi wykonanymi ręcznie.