OBLICZENIA RÓWNOLEGŁE
I ROZPROSZONE
Temat 3:
Komunikacyjne aspekty obliczeń
równoległych
Prowadzący:
dr inż. Zbigniew TARAPATA
pok.225A, tel.: 83-95-04
e-mail:
Zbigniew.Tarapata@wat.edu.pl
http://
tarapata.
tarapata.
strefa
strefa
.pl
.pl
/
/
p_obliczenia_rownolegle_i_rozproszone
p_obliczenia_rownolegle_i_rozproszone
/
/
2
Z.Tarapata, Obliczenia równoległe i rozproszone, wykład nr 3,
http://tarapata.strefa.pl/p_obliczenia_rownolegle_i_rozproszone/
Plan wykładu
Składowe opóźnień komunikacyjnych w sieci
komunikacyjnej;
Miara opóźnień komunikacyjnych;
Czynniki wpływające na wielkość opóźnień
komunikacyjnych;
Algorytmy synchroniczne i asynchroniczne –
wprowadzenie;
Algorytmy synchroniczne – synchronizacja
globalna;
Algorytmy synchroniczne – synchronizacja
lokalna;
Algorytmy asynchroniczne;
3
Z.Tarapata, Obliczenia równoległe i rozproszone, wykład nr 3,
http://tarapata.strefa.pl/p_obliczenia_rownolegle_i_rozproszone/
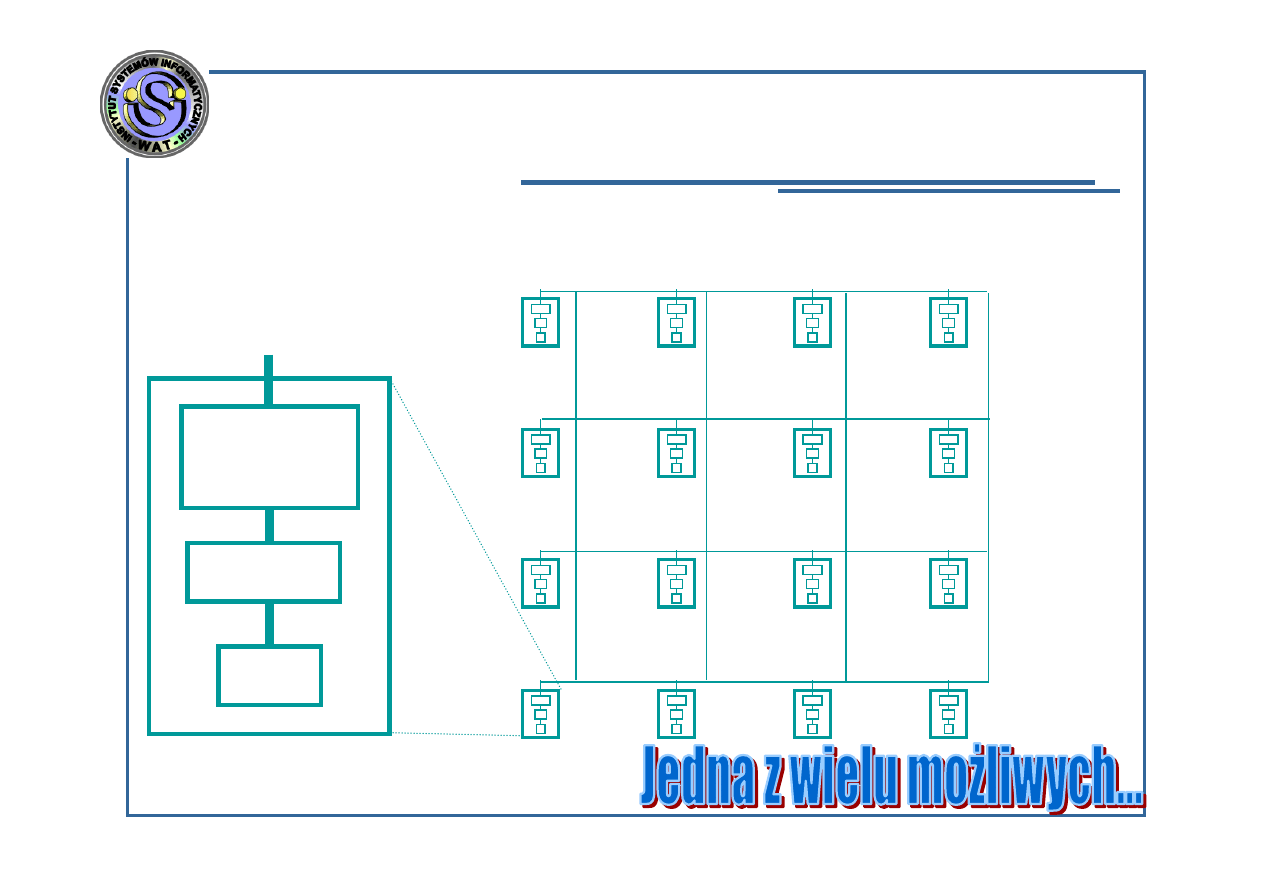
CPU
Pamięć
Interfejs
sieciowy
Struktura systemu obliczeń równoległych
4
Z.Tarapata, Obliczenia równoległe i rozproszone, wykład nr 3,
http://tarapata.strefa.pl/p_obliczenia_rownolegle_i_rozproszone/
Składowe opóźnień komunikacyjnych w sieci
komunikacyjnej
Czas przygotowywania informacji do transmisji
(
tworzenie pakietu, adresowanie, uzupełnianie
o informacje sterujące, wybór połączenia (kanału)
przesyłowego, przekazanie pakietu do bufora
);
Czas oczekiwania w kolejce (kolejkach) (
zajętość
połączenia (kanału), zajętość bufora u odbiorcy, błędy
transmisji
);
Czas transmisji;
Czas propagacji (
odstęp czasu między chwilą
transmisji ostatniego bitu pakietu u nadawcy, a chwilą
otrzymania ostatniego bitu przez odbiorcę
);
5
Z.Tarapata, Obliczenia równoległe i rozproszone, wykład nr 3,
http://tarapata.strefa.pl/p_obliczenia_rownolegle_i_rozproszone/
Miara opóźnienia komunikacyjnego
Przyjmuje się następującą miarę
τ
τ
d
d
opóźnienia
komunikacyjnego między dwoma ustalonymi
procesorami:
(1)
gdzie:
τ
p
– suma czasów: przygotowania informacji
oraz czasu propagacji;
R – czas transmisji 1 bitu informacji;
L – długość (w bitach) pakietu informacji;
Q – czas oczekiwania pakietu w kolejce
(kolejkach);
τ
d
=
τ
p
+ R
⋅L + Q
6
Z.Tarapata, Obliczenia równoległe i rozproszone, wykład nr 3,
http://tarapata.strefa.pl/p_obliczenia_rownolegle_i_rozproszone/
Czynniki wpływające na wielkość opóźnienia
komunikacyjnego
Na opóźnienie
τ
τ
d
d
wpływ mają następujące czynniki:
Algorytmy: sterowania siecią, detekcji i korekcji
błędów, wyboru tras przesyłania, sterowania
przepływem;
Topologia sieci oraz jakość połączeń między
procesorami (projektowanie niezawodnych
struktur sieci, np. grafy k-wierzchołkowo
rozłączne);
Struktura rozwiązywanego problemu oraz
związana z tym postać algorytmu
rozwiązującego ten problem (np. poziom
i zakres synchronizacji);
7
Z.Tarapata, Obliczenia równoległe i rozproszone, wykład nr 3,
http://tarapata.strefa.pl/p_obliczenia_rownolegle_i_rozproszone/
Algorytmy synchroniczne i asynchroniczne –
omówienie przykładu
Rozpatrzmy następujące zadanie obliczeniowe:
(2)
Założenia:
Dysponujemy systemem wieloprocesorowym
o co najmniej 3 procesorach;
Każdy procesor wylicza wartość tylko jednej,
przydzielonej zmiennej (
wed
wed
ł
ł
ug numer
ug numer
ó
ó
w procesora
w procesora
);
Obliczenie wartości jednej zmiennej w jednej iteracji
trwa
trwa
w każdym procesorze
jedn
jedn
ą
ą
jednostk
jednostk
ę
ę
czasu
czasu
.
x
1
=a
1
x
1
+a
2
x
2
x
2
=b
1
x
2
+b
2
x
3
x
3
=c
1
x
1
+c
2
x
3
8
Z.Tarapata, Obliczenia równoległe i rozproszone, wykład nr 3,
http://tarapata.strefa.pl/p_obliczenia_rownolegle_i_rozproszone/
Czas przesyłania informacji między procesorami
jest stały dla każdej iteracji i wynosi:
Na podstawie (2) skonstruujmy zbiory
A(i)
numerów tych procesorów,
do kt
do kt
ó
ó
rych
rych
informacja o uaktualnionych wartościach
zmiennej
x
i
będzie wysyłana z procesora
i
:
A(1)={1, 3}
A(2)={1, 2}
A(3)={2, 3}
Algorytmy synchroniczne i asynchroniczne –
omówienie przykładu
=
0
3
4
1
0
2
2
1
0
τ
x
1
=a
1
x
1
+a
2
x
2
x
2
=b
1
x
2
+b
2
x
3
x
3
=c
1
x
1
+c
2
x
3
9
Z.Tarapata, Obliczenia równoległe i rozproszone, wykład nr 3,
http://tarapata.strefa.pl/p_obliczenia_rownolegle_i_rozproszone/
Zadanie (2) możemy napisać w postaci
następującej formuły iteracyjnej:
(3)
Do zrealizowania jednej iteracji formuły (3)
potrzeba:
3
j.cz. dla x
1
(
2
j.cz. na przesłanie wartości x
2
(k)
z proc. 2 do proc. 1 oraz
1
j.cz. na obl. x
1
(k+1));
4
j.cz. dla x
2
(
3
j.cz. na przesłanie wartości x
3
(k)
z proc. 3 do proc. 2 oraz
1
j.cz. na obl. x
2
(k+1));
3
j.cz. dla x
3
(
2
j.cz. na przesłanie wartości x
1
(k)
z proc. 1 do proc. 3 oraz
1
j.cz. na obl. x
3
(k+1));
Algorytmy synchroniczne i asynchroniczne –
omówienie przykładu
x
1
(k+1) = a
1
x
1
(k) + a
2
x
2
(k)
x
2
(k+1) = b
1
x
2
(k) + b
2
x
3
(k)
x
3
(k+1) = c
1
x
1
(k) + c
2
x
3
(k)
A(1)={1, 3} ;
A(2)={1, 2} ;
A(3)={2, 3}
=
0
3
4
1
0
2
2
1
0
τ
10
Z.Tarapata, Obliczenia równoległe i rozproszone, wykład nr 3,
http://tarapata.strefa.pl/p_obliczenia_rownolegle_i_rozproszone/
W
synchronizacji globalnej
synchronizacji globalnej
obliczenia nowych wartości zmiennych
w kolejnej iteracji mogą rozpocząć się wtedy, gdy
wszystkie
wszystkie
procesory zgromadzą wszystkie potrzebne wartości zmiennych z
poprzedniej iteracji (zgodnie z zawartością zbiorów
A(i)
);
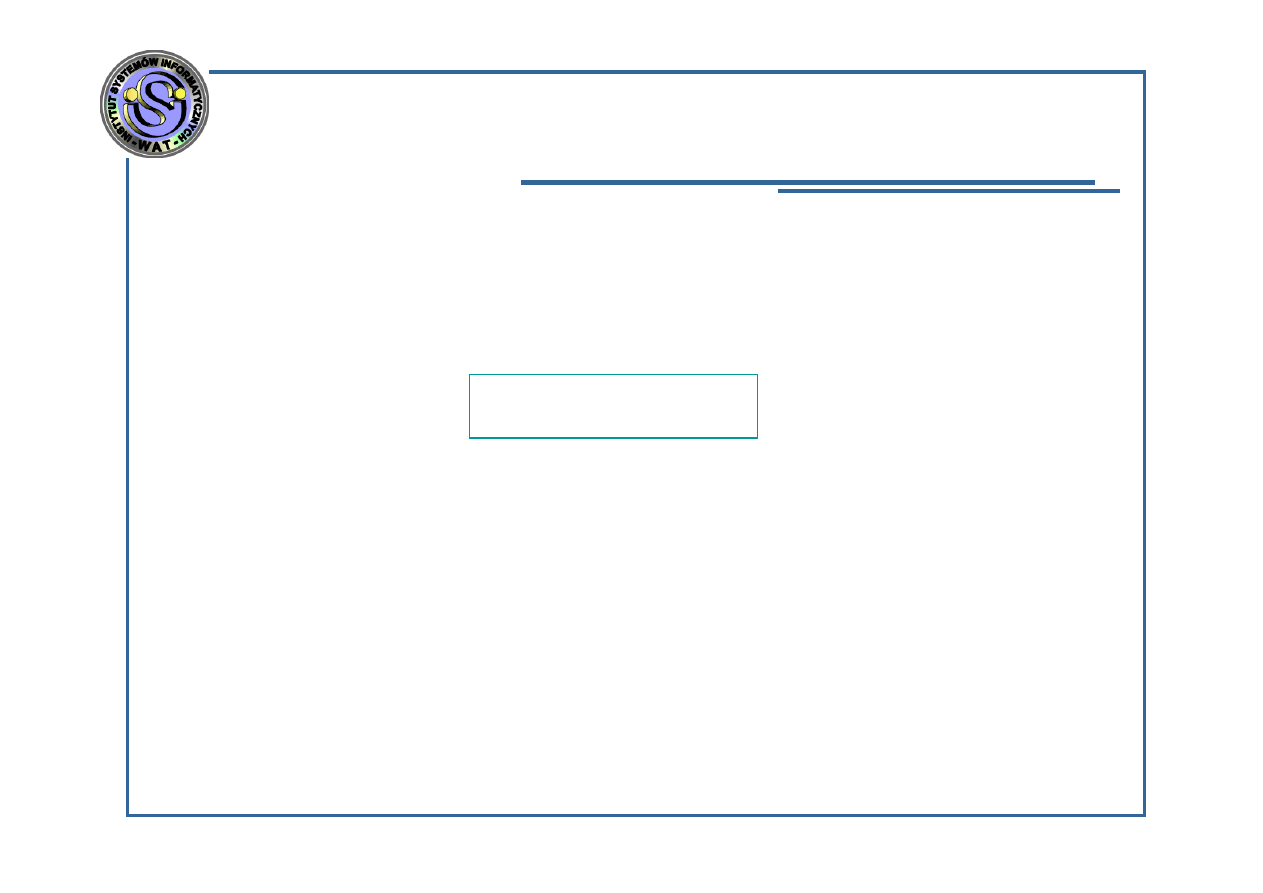
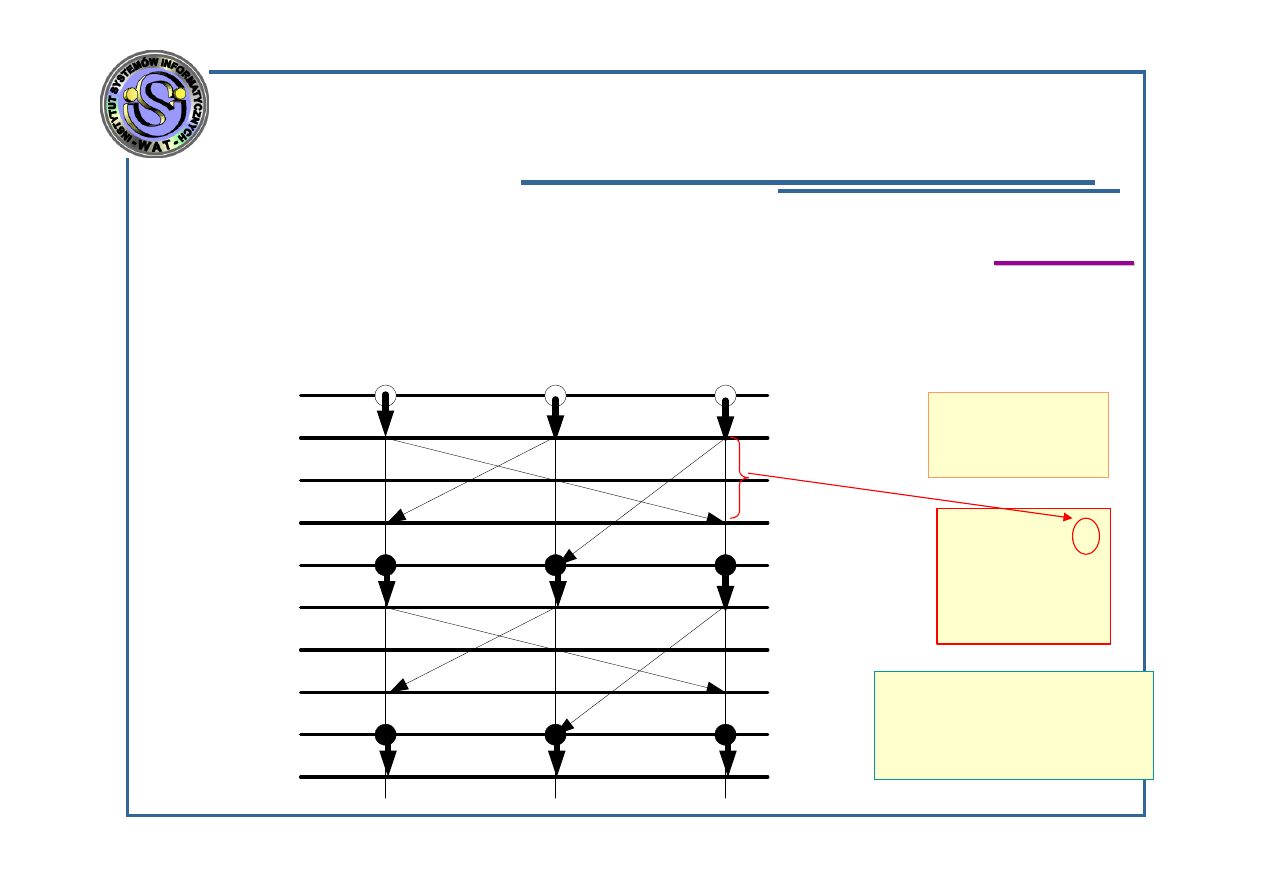
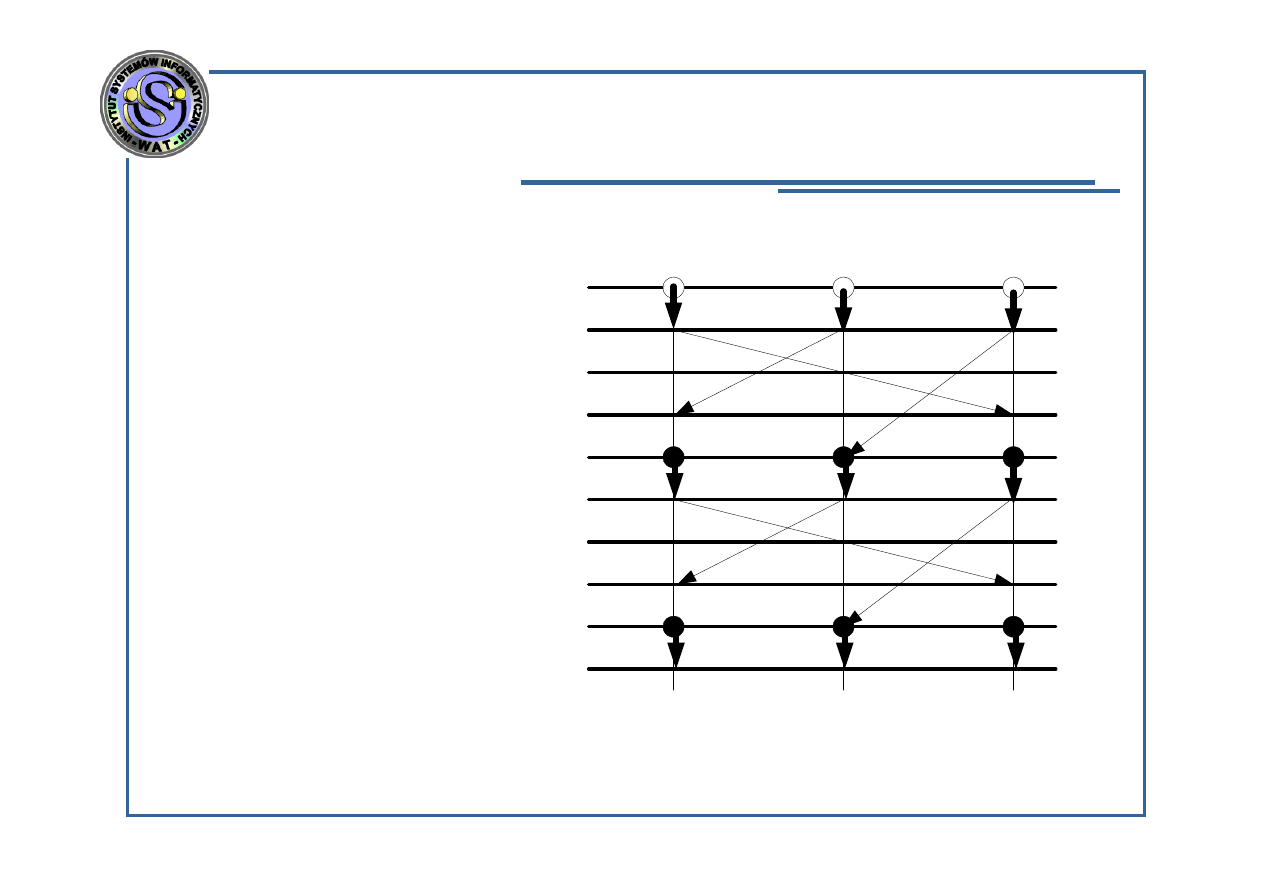
Algorytmy synchroniczne i asynchroniczne –
synchronizacja globalna
k=0
t=0
t=1
t=2
t=3
t=4
t=5
t=6
t=7
t=8
t=9
x
1
(0)
x
2
(0)
x
3
(0)
k=1
k=2
k=3
A(1)={1, 3} ;
A(2)={1, 2} ;
A(3)={2, 3}
=
0
3
4
1
0
2
2
1
0
τ
x
1
(k+1) = a
1
x
1
(k) + a
2
x
2
(k)
x
2
(k+1) = b
1
x
2
(k) + b
2
x
3
(k)
x
3
(k+1) = c
1
x
1
(k) + c
2
x
3
(k)
11
Z.Tarapata, Obliczenia równoległe i rozproszone, wykład nr 3,
http://tarapata.strefa.pl/p_obliczenia_rownolegle_i_rozproszone/
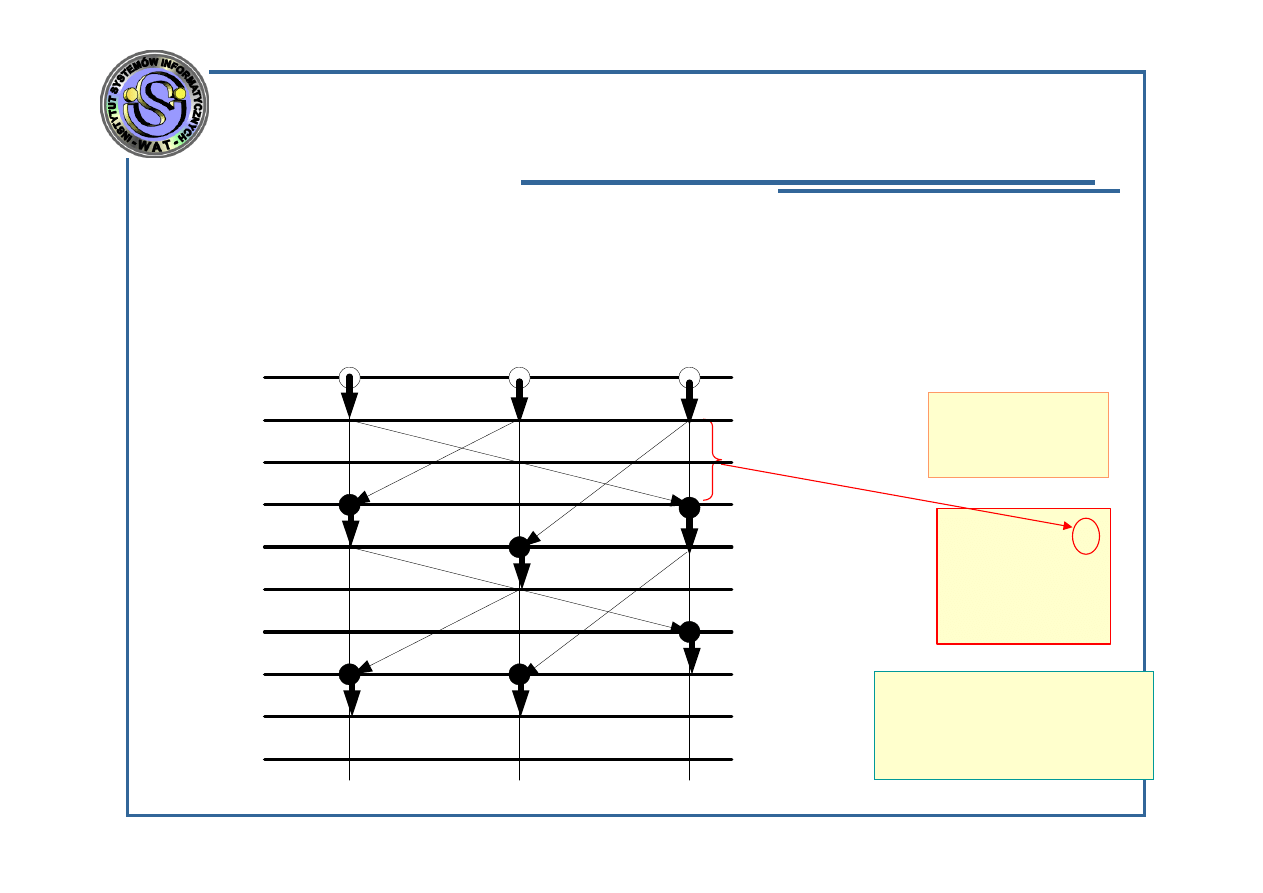
Wady:
Niektóre procesory
w pewnych
odcinkach czasu
czekają na inne
;
Np. procesory 1 , 3
mogłyby rozpocząć
wyznaczanie
wartości
zmiennych x
1
i x
3
dla iteracji k=3 w
chwili t=7, a
rozpoczynają – w
chwili t=8.
Algorytmy synchroniczne i asynchroniczne –
synchronizacja globalna
k=0
t=0
t=1
t=2
t=3
t=4
t=5
t=6
t=7
t=8
t=9
x
1
(0)
x
2
(0)
x
3
(0)
k=1
k=2
k=3
12
Z.Tarapata, Obliczenia równoległe i rozproszone, wykład nr 3,
http://tarapata.strefa.pl/p_obliczenia_rownolegle_i_rozproszone/
W
synchronizacji lokalnej
synchronizacji lokalnej
obliczenia nowych wartości zmiennych w
kolejnej iteracji mogą rozpocząć się już wtedy, gdy
i-ty
procesor
otrzyma wszystkie dane z poprzedniej iteracji (zgodnie z
zawartością zbiorów
A(i)
) (
nie czekając aż inne procesory otrzymają swoje dane);
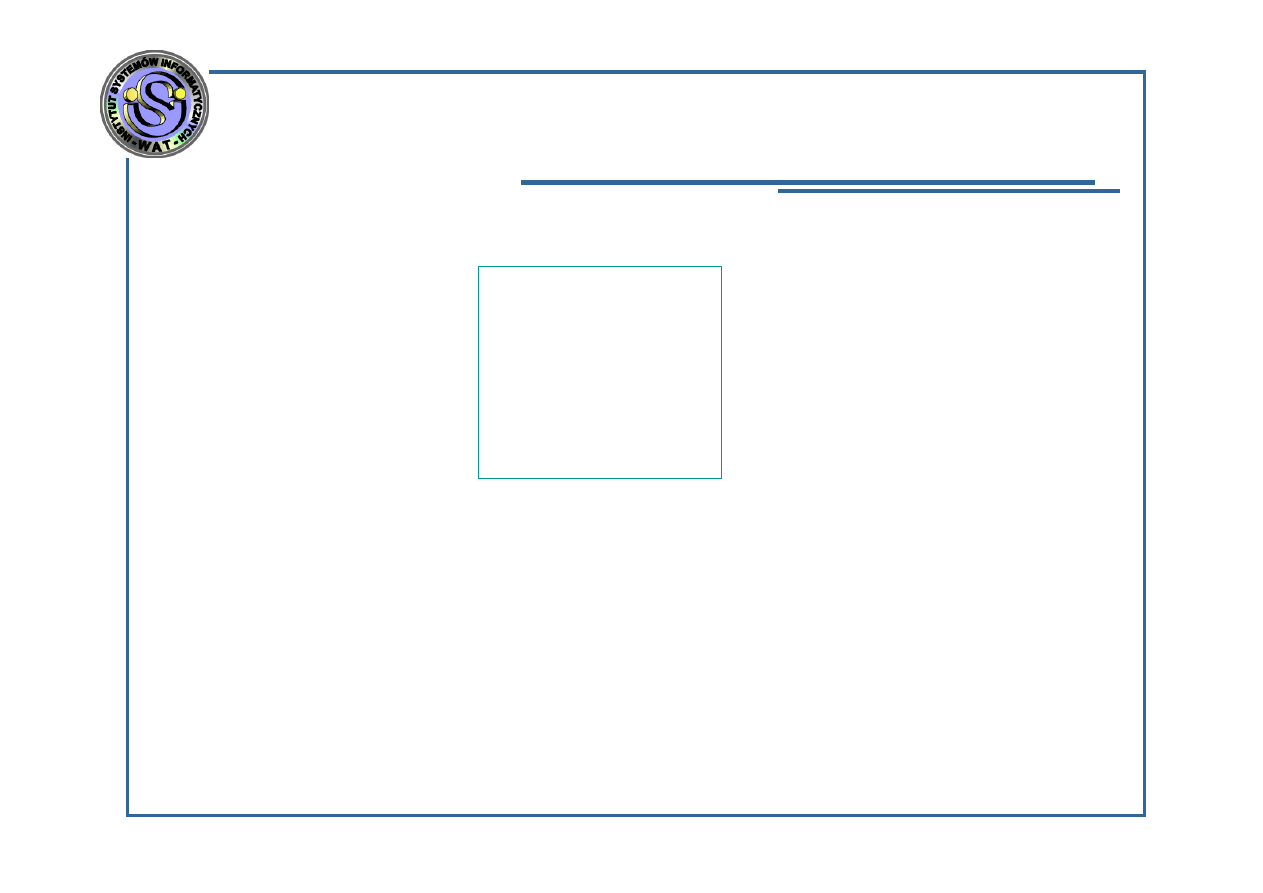
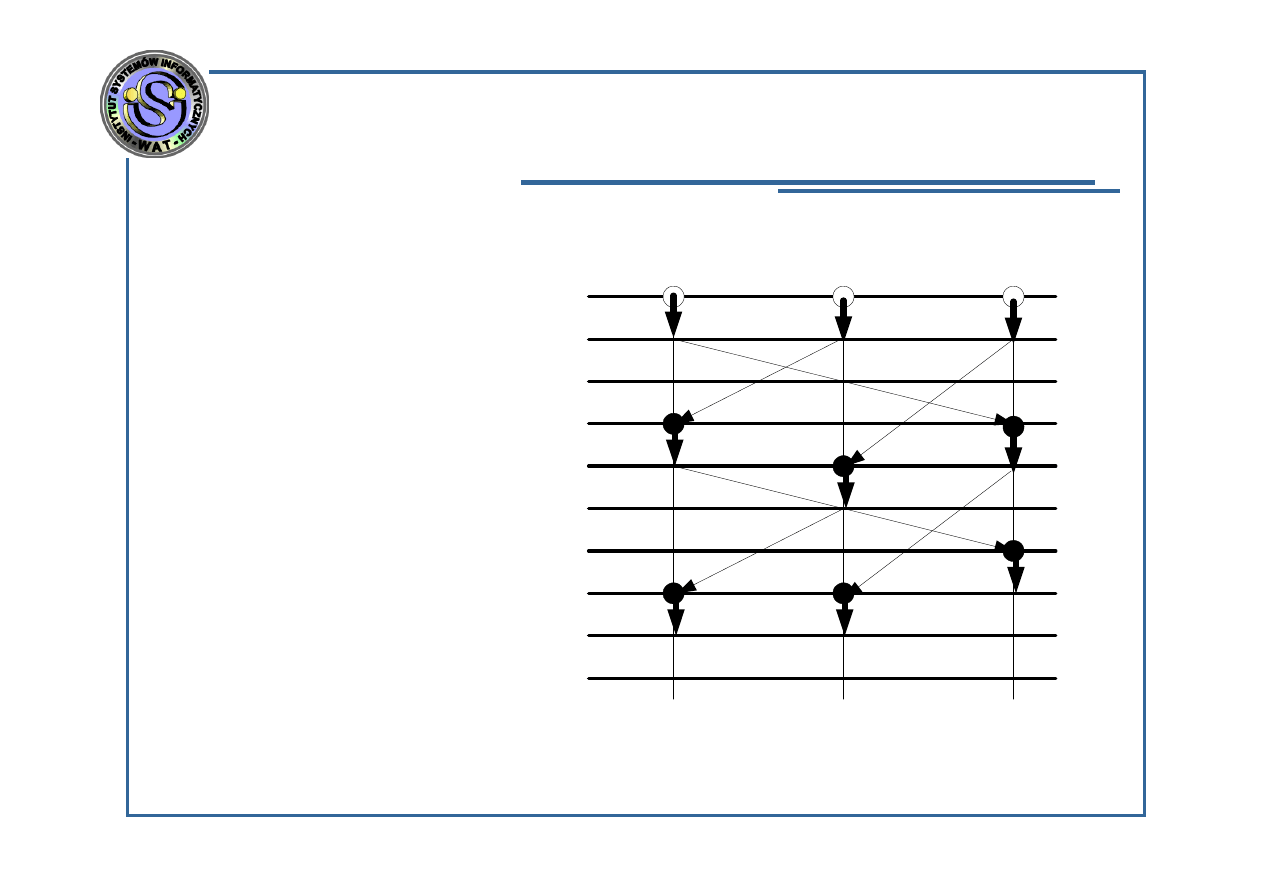
Algorytmy synchroniczne i asynchroniczne –
synchronizacja lokalna
A(1)={1, 3} ;
A(2)={1, 2} ;
A(3)={2, 3}
=
0
3
4
1
0
2
2
1
0
τ
x
1
(k+1) = a
1
x
1
(k) + a
2
x
2
(k)
x
2
(k+1) = b
1
x
2
(k) + b
2
x
3
(k)
x
3
(k+1) = c
1
x
1
(k) + c
2
x
3
(k)
k=0
t=0
t=1
t=2
t=3
t=4
t=5
t=6
t=7
t=8
t=9
x
1
(0)
x
2
(0)
x
3
(0)
k=1
k=2
k=3
k=2
k=2
k=3
13
Z.Tarapata, Obliczenia równoległe i rozproszone, wykład nr 3,
http://tarapata.strefa.pl/p_obliczenia_rownolegle_i_rozproszone/
Zalety (w stosunku
do synchronizacji
globalnej):
Redukcja czasu
obliczeń w
stosunku do
synchronizacji
globalnej;
Np. Dla iteracji k=3
wszystkie zmienne
zostały obliczone
do chwili t=8, a nie
jak poprzednio dla
t=9;
Algorytmy synchroniczne i asynchroniczne –
synchronizacja lokalna
k=0
t=0
t=1
t=2
t=3
t=4
t=5
t=6
t=7
t=8
t=9
x
1
(0)
x
2
(0)
x
3
(0)
k=1
k=2
k=3
k=2
k=2
k=3
14
Z.Tarapata, Obliczenia równoległe i rozproszone, wykład nr 3,
http://tarapata.strefa.pl/p_obliczenia_rownolegle_i_rozproszone/
W
obliczeniach asynchronicznych
obliczeniach asynchronicznych
obliczenia nowych wartości
zmiennych wykonywane są
natychmiast
, gdy co najmniej jeden ze
składników występujących w formule ma nową wartość i jest
dostępny procesorowi.
Obliczenia realizowane s
Obliczenia realizowane s
ą
ą
na tych danych,
na tych danych,
kt
kt
ó
ó
re aktualnie s
re aktualnie s
ą
ą
dost
dost
ę
ę
pne.
pne.
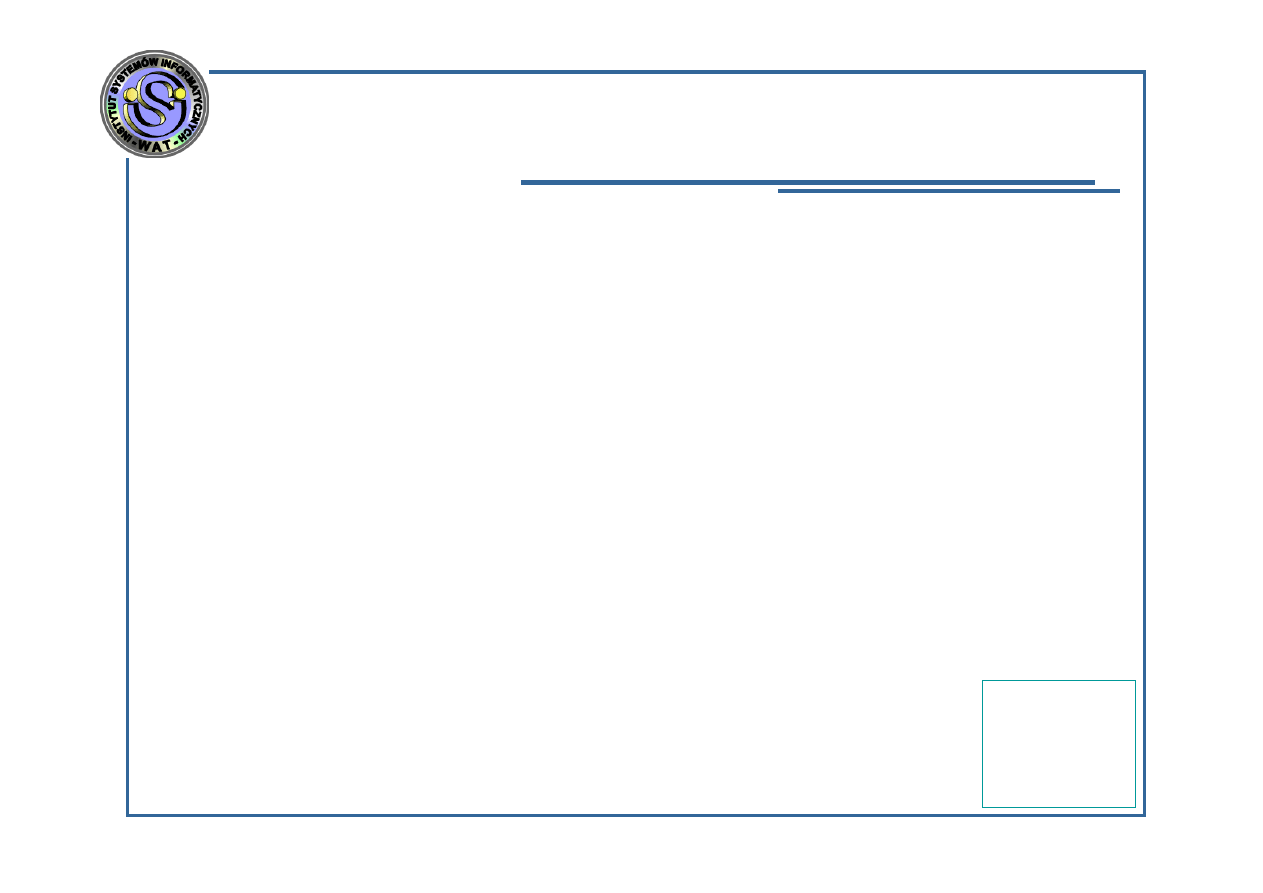
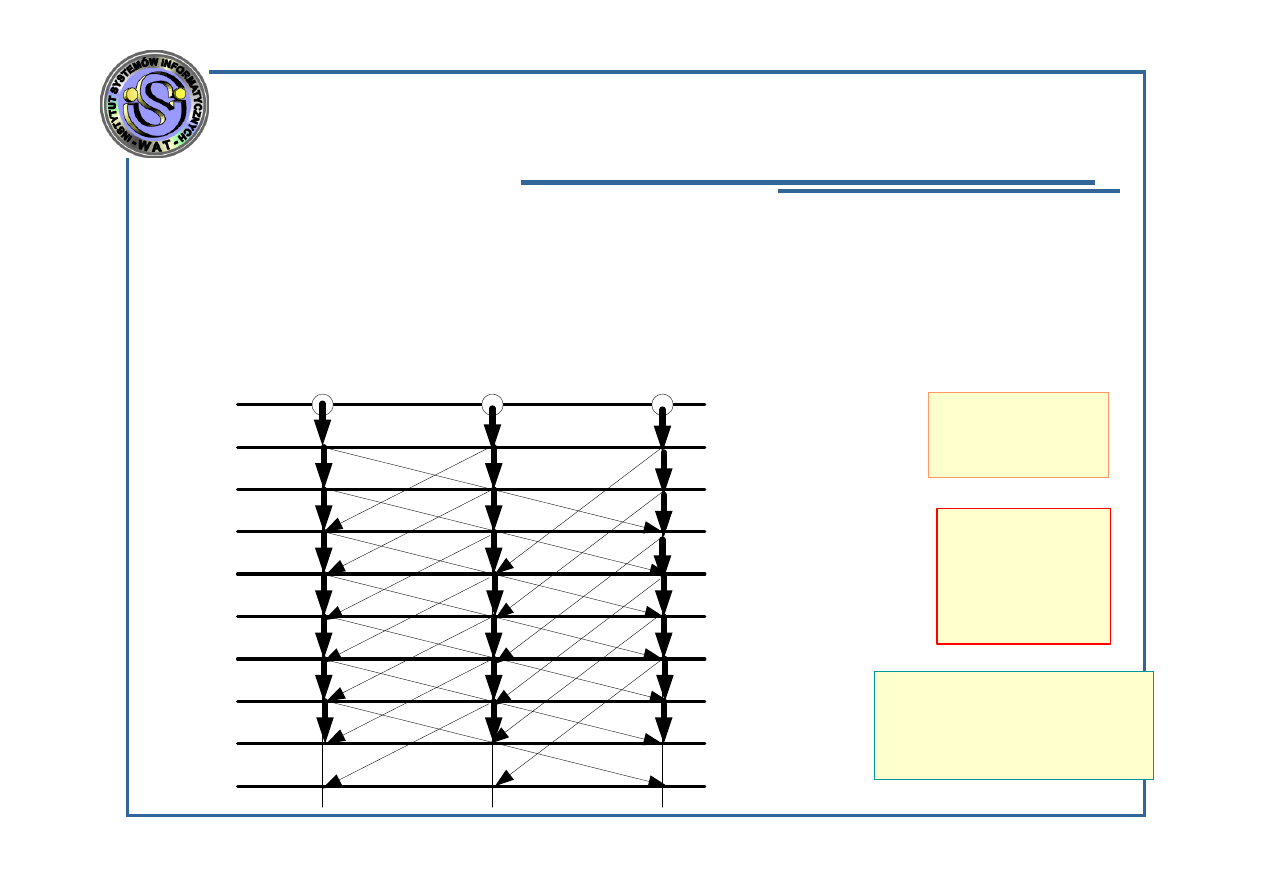
Algorytmy synchroniczne i asynchroniczne –
obliczenia asynchroniczne
A(1)={1, 3} ;
A(2)={1, 2} ;
A(3)={2, 3}
=
0
3
4
1
0
2
2
1
0
τ
x
1
(k+1) = a
1
x
1
(k) + a
2
x
2
(k)
x
2
(k+1) = b
1
x
2
(k) + b
2
x
3
(k)
x
3
(k+1) = c
1
x
1
(k) + c
2
x
3
(k)
k=0
t=0
t=1
t=2
t=3
t=4
t=5
t=6
t=7
t=8
t=9
x
1
(0)
x
2
(0)
x
3
(0)
k=1
k=2
k=8
k=3
k=4
k=5
k=6
k=7
15
Z.Tarapata, Obliczenia równoległe i rozproszone, wykład nr 3,
http://tarapata.strefa.pl/p_obliczenia_rownolegle_i_rozproszone/
Do podstawowej zasady obliczeń asynchronicznych
można dołożyć jeszcze następujące:
Przesyłanie uaktualnionych zmiennych do procesorów o
numerach należących do
A(i)
nie musi się odbywać po
każdej aktualizacji, a np. co kilka;
może ulec zmianie kolejność przesyłanych do innych
procesorów uaktualnień, np. wskutek awarii linii
komunikacyjnych;
Uaktualnienie w poszczególnych procesorach nie musi
trwać tyle samo jednostek czasu.
Zalety:
Znaczna redukcja czasu obliczeń w stosunku do synchronizacji;
Wady:
Zwiększenie częstotliwości przesyłania informacji między
procesorami;
Trudności w określeniu warunków zbieżności algorytmów.
Algorytmy synchroniczne i asynchroniczne –
obliczenia asynchroniczne
16
Z.Tarapata, Obliczenia równoległe i rozproszone, wykład nr 3,
http://tarapata.strefa.pl/p_obliczenia_rownolegle_i_rozproszone/
Dziękuję za uwagę