1. Przyspieszenie
Je

ż

eli dany wektor r

>

okre

ś

la poło

ż

enie punktu

materialnego a wektor v

>

okre

ś

la pr

ę

dko

ść

tego

punku, to przy

ś

pieszenie a

>

tego punktu jest

pochodn

ą

pr

ę

dko

ś

ci po czasie:

a

>

= dv

>

/ dt

>

poniewa

ż

pr

ę

dko

ść

jest pochodn

ą

poło

ż

enia po

czasie, to przyspieszenie mo

ż

na zapisa

ć

jako

druga pochodn

ą

poło

ż

enia po czasie:

a

>

= d

2

r

>

/ dt

2

Jednostk

ą

przyspieszenia w SI jest metr na

sekund

ę

do kwadratu.

[a

>

] = m/s

2

2. Praca wykonana przez stał

ą

sił

ę

:

A) (F=const)

Gdy na ciało działa siła F=const - ruch zachodzi po
linii prostej zgodnie z kierunkiem działania siły.
Praca W - wykonana przez sił

ę

przy

przemieszczeniu ciała
W= F s = |F| |s| cos

αααα

SI: [J=N m]

αααα

- k

ą

t pomi

ę

dzy F i s

s - przemieszczenie
W= F s (dla

αααα

=0) ********* W= F s= 0 (dla

αααα

=90)

Praca jest skalarem, dodatnia lub ujemna.
***ujemna - ciało ma składow

ą

ruchu przeciwn

ą

do

działaj

ą

cej siły F

***dodatnia - ciało ma składow

ą

ruchu zgodn

ą

z

kierunkiem działaj

ą

cej siły F (jak rys)

Działanie sił
B F

≠≠≠≠

const

Przyspieszenie cz

ą

stki a otrzymujemy z II zasady

dynamiki Newtona stosuj

ą

c rachunek całkowy.

Wzory v(t) i x(t) nie obowi

ą

zuj

ą

bo a

≠≠≠≠

const.

Siły (F=F(x)) zmieniaj

ą

ce si

ę

wraz z poło

ż

eniem

cz

ą

stki to np. siły grawitacyjne, spr

ęż

ysto

ś

ci.

Okre

ś

lenie ruchu cz

ą

steczek pod wpływem tych sił

prowadzi do poj

ę

cia pracy i energii kinetycznej

oraz poj

ę

cia energii.

Z energi

ą

, która odgrywa ogromna rol

ę

w rozwoju

fizyki zwi

ą

zana jest prawdopodobnie najwa

ż

niejsza

zasada: zachowania energii.
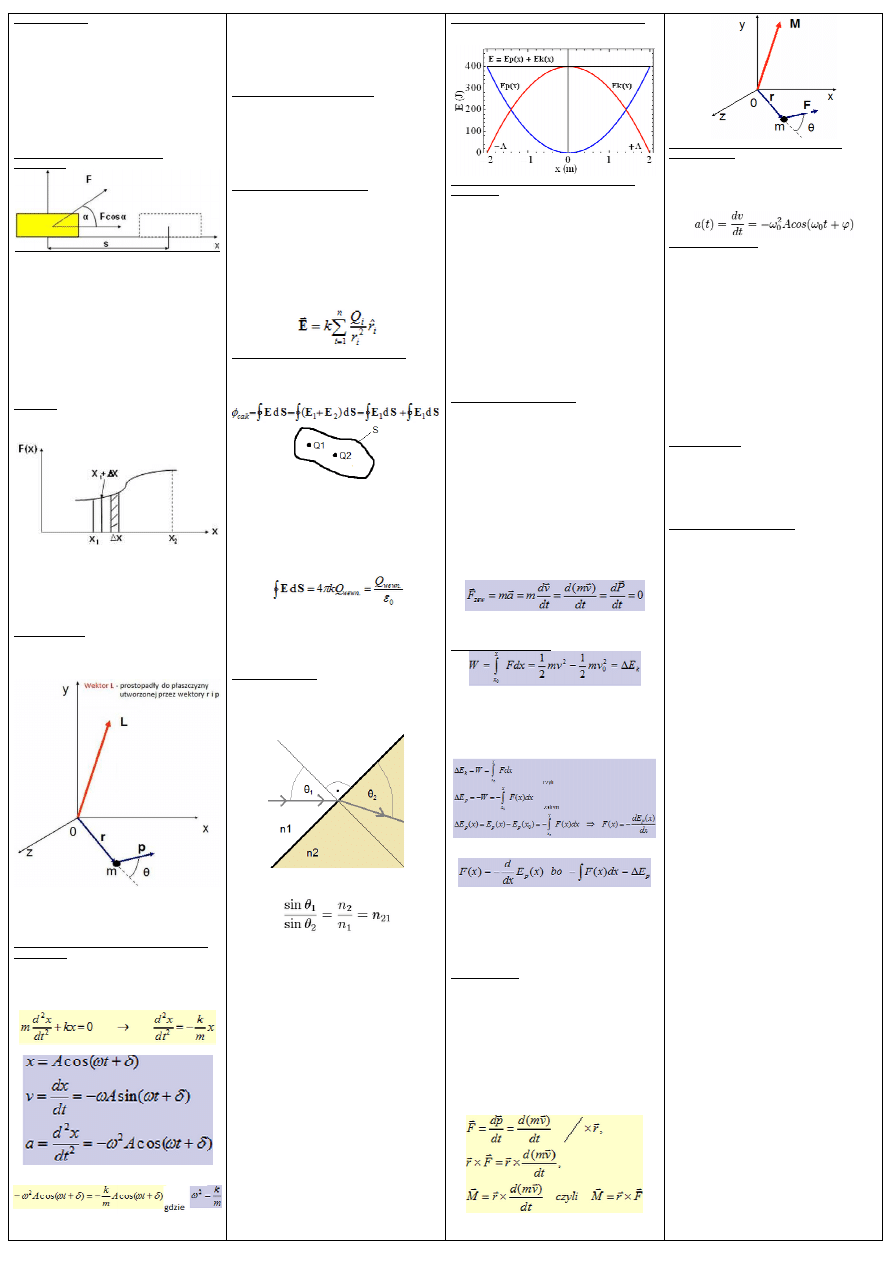
3. Moment p

ę

du.

Moment p

ę

du cz

ą

stki (taka sama rola jak p

ę

d)

p

>

=m v

>

a L

>

=I

ω

ωω

ω

>

Cz

ą

stka o masie m, p

ę

dzie p w odległo

ś

ci r od

pocz

ą

tku układu współrz

ę

dnych 0.

θ

- k

ą

t mi

ę

dzy r i p

r – poło

ż

enie cz

ą

stki wzgl. wybranego inercjalnego

układu odniesienia.

L

>

=r

>

p

>

L=r p sin

θ

4. Równanie ruchu oscylatora prostego i jego
rozwi

ą

zanie.

m(d

2

x / dt

2

) + kx = 0

Gdy znamy rozwi

ą

zanie równania - zale

ż

no

ść

:

x = x(t), to znamy ruch cz

ą

stki.

Znajdujemy rozwi

ą

zanie równania ruchu dla

oscylatora:

sprawd

ź

my, czy rozwi

ą

zaniem b

ę

dzie:

A,

ω

ωω

ω

, f - stałe

podstawiamy do równania oscylatora:

zatem: x=Acos(

ω

ωω

ω

t+

δδδδ

)

Rozwi

ą

zanie równania oscylatora

harmonicznego prostego:
Funkcja cos przyjmuje warto

ś

ci od -1 do 1, czyli

przemieszczenie x od poło

ż

enia równowagi (x=0)

osi

ą

ga warto

ść

maksymaln

ą

x

max

= A, czyli

A - amplituda ruchu
(

ω

ωω

ω

t+

δδδδ

) - faza ruchu,

δδδδ

- stała fazowa (faza pocz.)

5. Prawo powszechnego ci

ąż

enia

Stosuje si

ę

do wszystkich sił grawitacyjnych

(Newtona)
Dwa punkty materialne o masach M i m oddziałuja
na siebie (przyci

ą

gaj

ą

) wzajemnie sił

ą

F:

F = G(Mm) / r

2

lub: F

>

= [-G(Mm)/r

3

] r

>

gdzie:
r - odległo

ść

punktów materialnych

G - stała grawitacji
6. Nat

ęż

enie pola elektrycznego

N. pola el. definiujemy jako sił

ę

działaj

ą

c

ą

na

ładunek próbny q (umieszony w danym punkcie
przestrzeni) podzielon

ą

przez ten ładunek.

Analogicznie do nat

ęż

enia pola grawitacyjnego

(E=F/m):

E

>

=F

>

/q

ładunek próbny jest umownie dodatni, kierunek E

>

jest taki sam jak siły F

>

działaj

ą

cej na ładunek.

Pole elektryczne od n ładunków punktowych jest
równe sumie wektorowej pól elektrycznych
(zasada superpozycji):

7. Prawo Gaussa dla pola elektrycznego:
Niech zamkni

ę

ta powierzchnia obejmuje dwa

ładunki Q

1

i Q

2

. Całkowita liczba linii sił przecinaj

ą

ca

powierzchni

ę

zamkni

ę

t

ą

wokół ładunków Q

1

i Q

2

jest równa:

gdzie:
E

1

- jest wytwarzane przez Q

1

a E

2

przez Q

2

.

Powołuj

ą

c si

ę

na wcze

ś

niejszy wynik otrzymujemy:

φφφφ

całk

=(Q

1

/

εεεε

0

) + (Q

2

/

εεεε

0

) = (Q

1

+ Q

2

) /

εεεε

0

Całkowita liczba linii sił jest równa całkowitemu
ładunkowi podzielonemu przez

ε

0

.

Podobnie mo

ż

na pokaza

ć

dla dowolnej liczby n

ładunków:

Prawo Gaussa - strumie

ń

pola wychodz

ą

cy z

naładowanego ciała jest równy wypadkowemu
ładunkowi podzielonemu przez

ε

0

.

Je

ż

eli Q jest ujemne strumie

ń

pola wpływa do ciała.

Linie mog

ą

zaczyna

ć

si

ę

i ko

ń

czy

ć

tylko na

ładunkach, a wsz

ę

dzie poza tym s

ą

ci

ą

głe.

8. Prawo załamania.
Formułowane bazuj

ą

c na zało

ż

eniach optyki

geometrycznej. Promie

ń

padaj

ą

cy biegn

ą

cy w

o

ś

rodku pierwszym pada na granic

ę

o

ś

rodków po

czym zmienia kierunek (załamuje si

ę

) i jako

promie

ń

załamany biegnie w o

ś

rodku drugim.

Prawo Snelliusa mówi,

ż

e promie

ń

padaj

ą

cy i

załamany oraz prostopadła padania (normalna) le

żą

w jednej płaszczy

ź

nie, a k

ą

ty spełniaj

ą

zale

ż

no

ść

:

gdzie:
n

1

– współczynnik załamania

ś

wiatła o

ś

rodka

pierwszego,
n

2

– współczynnik załamania

ś

wiatła o

ś

rodka

drugiego,
n

21

– wzgl

ę

dny współczynnik załamania

ś

wiatła

o

ś

rodka drugiego wzgl

ę

dem pierwszego,

θ

1

– k

ą

t padania, k

ą

t mi

ę

dzy promieniem

padaj

ą

cym a normaln

ą

do powierzchni granicznej

o

ś

rodków,

θ

2

– k

ą

t załamania, k

ą

t mi

ę

dzy promieniem

załamanym a normaln

ą

.

Je

ż

eli

ś

wiatło przechodzi z o

ś

rodka o mniejszym

współczynniku załamania

ś

wiatła do o

ś

rodka o

współczynniku wi

ę

kszym (np. powietrze-woda), tak

jak na rysunku, to k

ą

t załamania jest mniejszy od

k

ą

ta padania. Je

ż

eli na odwrót (szkło-powietrze) –

k

ą

t załamania jest wi

ę

kszy.

Współczynnik załamania dla danego o

ś

rodka ro

ś

nie

wraz z g

ę

sto

ś

ci

ą

, np. w atmosferze maleje wraz z

wysoko

ś

ci

ą

. Dla ró

ż

nych o

ś

rodków tendencja ta jest

na ogół równie

ż

zachowana, ale nie jest reguł

ą

.

Przykładem mo

ż

e by

ć

etanol, który ma mniejsz

ą

g

ę

sto

ść

ni

ż

woda, ale wi

ę

kszy współczynnik

załamania.

9. Energia kinetyczna, potencjalna i całkowita

E

k

= mv

2

/2, E

p

= W = Fh = mgh, E=mc

2

10. Wyprowadzanie wzoru na I i II pr

ę

dko

ść

kosmiczn

ą

.

>>> I pr

ę

dko

ść

kosmiczna:

mv

2

/R = GMm/R

2

v

2

=GM/R

v

1

=

pierwiastek

(GM/R)

gdzie:
G -stała grawitacji
M -masa ciała niebieskiego
m -masa rozp

ę

dzonego ciała(kr

ążą

cego wokół ciała

niebieskiego)
R -promie

ń

orbity

>>> II pr

ę

dko

ść

kosmiczna:

E = -GMm/R + mv

2

/2

gdzie:
M -masa ciała niebieskiego
m -masa wystrzeliwanego ciała
v -pr

ę

dko

ść

pocz

ą

tkowa

R -promie

ń

ciała niebieskiego

St

ą

d:

v

2

=

pierwiastek

(2GM/R) = v

1

pierw

(2)

11. Zasada zachowania p

ę

du.

a) gdy mamy do czynienia z układem pkt.
materialnych o masach m

1

...m

n

i M=

Σ

m

i

b) P - całkowity p

ę

d układu pkt. - suma wektorowa

pojedynczych p

ę

dów

p =

ΣΣΣΣ

p

i

=

ΣΣΣΣ

m

i

v

i

= const.

p

>

= Mv

>

ś

rm

Całkowity p

ę

d układu punktów materialnych jest

równy iloczynowi całkowitej masy i pr

ę

dko

ś

ci

ś

rodka

jego masy.
Prawo zachowania p

ę

du - je

ż

eli wypadkowa sił

zewn

ę

trznych działaj

ą

cych na układ wynosi zero

(F

zew

=0) wtedy całkowity p

ę

d układu pozostaje

stały.
czyli,
całkowity p

ę

d układu odosobnionego jest wielko

ś

ci

ą

stał

ą

w ka

ż

dym czasie.

wtedy P

>

=const.

Układ odosobniony(zamkni

ę

ty lub izolowany) -

układ na który nie działaj

ą

ż

adne siły zewn

ę

trzne.

12. Energia potencjalna

Siły F(x) zale

ż

ne od poło

ż

enia x s

ą

siłami

zachowawczymi.
Spadek energii ruchu E

k

jest zwi

ą

zany ze wzrostem

energii potencjalnej (poło

ż

enia) E

p

czyli:

∆∆∆∆

E

k

= -

∆∆∆∆

E

p

bo

∆∆∆∆

E

p

+

∆∆∆∆

E

k

=const.

czyli ka

ż

da zmiana E

k

jest zwi

ą

zana z przeciwn

ą

zmian

ą

E

p

ale:

Zale

ż

no

ść

mi

ę

dzy sił

ą

F, a energi

ą

potencjaln

ą

E

p

mo

ż

na zapisa

ć

nast

ę

puj

ą

co:

Równanie to wyra

ż

a fizyczne znaczenie energii

potencjalnej:
Energia potencjalna jest funkcj

ą

poło

ż

enia, której

ujemna pochodna daje sił

ę

.

Energia E

p

przedstawia form

ę

nagromadzonej

energii, która mo

ż

e by

ć

całkowicie odzyskana i

zamieniona na E

k

. Nie mo

ż

na wi

ę

c wzi

ąć

E

p

z sił

ą

niezachowawcz

ą

.

13. Moment Siły
Moment siły cz

ą

stki - je

ż

eli siła F działa na cz

ą

stke

w punkcie P odległym o r wzgl

ę

dem pewnego

punktu odniesienia 0, to moment siły M wzgl

ę

dem

pocz

ą

tku układu definiujemy jako:

M

>

= r

>

F

>

M = r F sin

φφφφ

M

>

⊥

⊥⊥

⊥

F

>

, r

>

r -wektor wodz

ą

cy punktu przyło

ż

enia działaj

ą

cej

siły, okre

ś

la poło

ż

enie cz

ą

stki wzgl. wybranego

inercjalnego układu odniesienia (lub rami

ę

siły)

M -moment siły wzgl

ę

dem pkt. 0

φφφφ

-k

ą

t mi

ę

dzy r a F

Wiemy,

ż

e:

14. Wychylenie i przyspieszenie w ruchu
harmonicznym.

F

>

= -k x

>

gdzie:
F -siła
k -współcz. proporcjonalno

ś

ci

x -wychylenia z poło

ż

enia równowagi

15. Prawo Coulomba
Siła oddziaływania dwóch ładunków q1 i q2
(naładowanych ciał)
F = k q

1

q

2

/ r

2

gdzie stała k = 1 / 4

Π

Π

Π

Πεεεε

0

εεεε

0

= 8,854 x 10

-12

[C

2

/Nm

2

] - przenikalno

ść

elektryczna pró

ż

ni (stała dialektyczna).

Stała dialektyczna substancji lub wzgl

ę

dna

przenikalno

ść

elektryczna o

ś

rodka jest wielko

ś

ci

ą

charakterystyczn

ą

dla nowego o

ś

rodka, zawsze

wi

ę

ksza od 1.

Dla wody

ε

=81, pró

ż

ni

ε

=1, dla powietrza

ε

=1,0006.

Za pomoc

ą

prawa Coulomba mo

ż

na opisa

ć

:

--Oddziaływanie mi

ę

dzy poszczególnym

elektronami oraz pomi

ę

dzy elektronami a j

ą

drem

atomowym.
--Siły oddziaływania mi

ę

dzy atomami tworz

ą

cymi

cz

ą

steczk

ę

lub ciało stałe.

16. Siła Lorentza

F = q(E + v

x

B)

F -wektor siły [N]
q -ładunek elektryczny cz

ą

stki [C]

E -wektor nat

ęż

enia pola elektrycznego [V/m]

B -pseudowektor indukcji magnetycznej [T]
v -wektor pr

ę

dko

ś

ci cz

ą

stki [m/s]

x -iloczyn wektorowy.
18. Zjawisko fotoelektrzyczne
Zaproponowane przez Alberta Einsteina
wyja

ś

nienie zjawiska i jego opis matematyczny

oparte jest na zało

ż

eniu,

ż

e energia wi

ą

zki

ś

wiatła

pochłaniana jest w postaci porcji (kwantów).
Kwant promieniowania pochłaniany jest przy tym w
cało

ś

ci. Einstein zało

ż

ył dalej,

ż

e usuni

ę

cie

elektronu z powierzchni metalu (substancji)
wymaga pewnej pracy zwanej prac

ą

wyj

ś

cia, która

jest wielko

ś

ci

ą

charakteryzuj

ą

c

ą

dan

ą

substancj

ę

(stał

ą

materiałow

ą

). Pozostała energia unoszona

jest przez emitowany elektron. Z tych rozwa

ż

a

ń

wynika wzór:

hv = W + E

k

gdzie:

h -stała Plancka
v -cz

ę

stotliwo

ść

padaj

ą

cego fotonu

W -praca wyj

ś

cia

E

k

-maksymalna energia kinetyczna emintowanych

elektronów.