LABORATORIUM - ELEKTRONIKA

TECHNIKA CYFROWA: Układy kombinacyjne, multiplekser

1.

Cel ćwiczenia

Celem ćwiczenia jest praktyczna realizacja prostego układu kombinacyjnego na dwa sposoby: z wykorzystaniem

bramek NAND oraz z użyciem multipleksera, weryfikacja poprawności złożenia i działania obu wersji układu oraz nauka

oceny stopnia złożoności układu cyfrowego według różnych kryteriów. W trakcie ćwiczenia studenci zapoznają się też z

możliwościami konstruowania układów prototypowych z użyciem testera układów logicznych TTL typu PTC-1.

2.

Trochę podstaw

2.1.

Synteza układu kombinacyjnego na bramkach NAND - wersja pełna, czyli bez minimalizacji.

Załóżmy, że dany jest układ cyfrowy, opisany następującą tabelą stanów:

l.p.

A

B

C OUT

0

0

0

0

1

1

0

0

1

1

2

0

1

0

0

3

0

1

1

x

4

1

0

0

x

5

1

0

1

0

6

1

1

0

1

7

1

1

1

0



Znak X pojawiający się w tabeli oznacza iż określona kombinacja wejść nie ma prawa w układzie wystąpić lub że z

pewnych powodów nie interesuje nas wyjście układu dla danej kombinacji wejść.

Na podstawie danej tabeli stanów uzyskujemy opis kanoniczny projektowanego układu w postaci:

OUT =

∑

(

0,1,6

(

3,4

))

lub opis kanoniczny w zapisie Boola:

C

B

A

C

B

A

C

B

A

OUT



















,

z którego możemy bezpośrednio uzyskać schemat logiczny układu przy wykorzystaniu bramek NOT, AND i OR. Jednak

najczęściej realizuje się układy cyfrowe korzystając z jednego rodzaju bramek, najczęściej NAND i ewentualnie NOT. Aby

przekształcić powyższą postać funkcji do postaci bezpośrednio odwzorowywalnej przy użyciu bramek NAND, należy

uzyskaną wcześniej postać funkcji podwójnie zanegować i następnie skorzystać z praw de Morgana. Mają one postać:



2

1

2

1

a

a

a

a







,



2

1

2

1

a

a

a

a







.

W rozpatrywanym przypadku przekształcenie to wygląda następująco:

C

B

A

C

B

A

C

B

A

C

B

A

C

B

A

C

B

A

C

B

A

C

B

A

C

B

A

OUT























































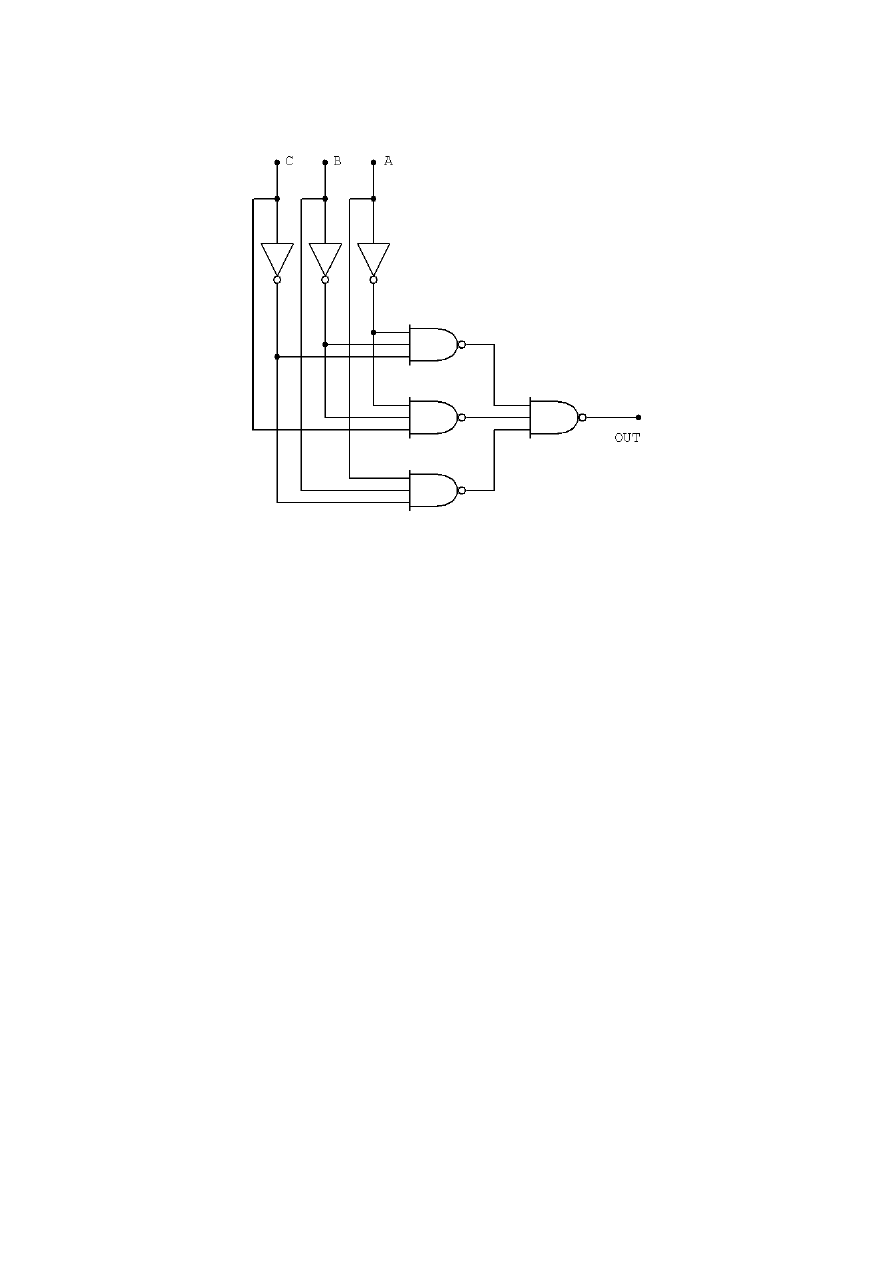
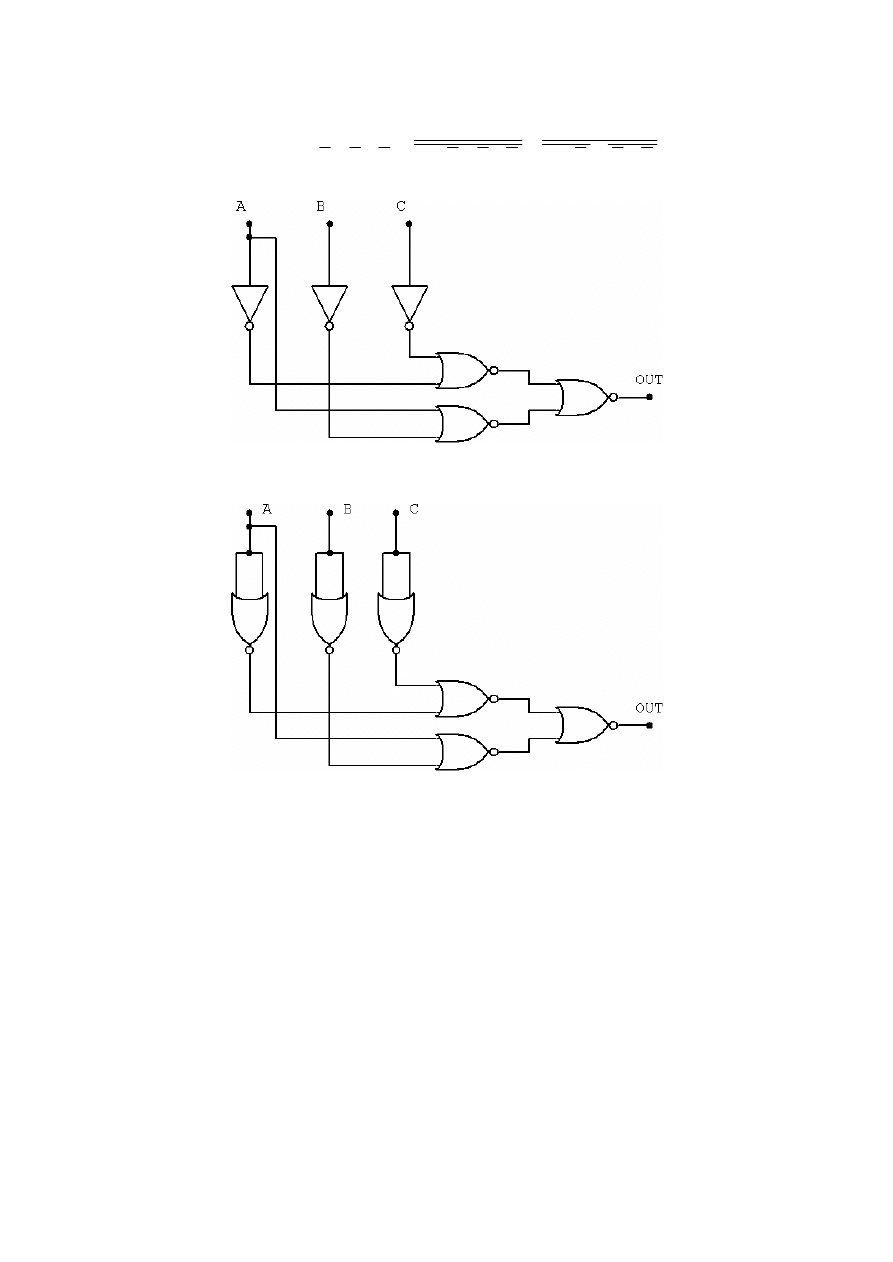
Jak widać, aby zrealizować powyższą postać funkcji potrzeba 4 bramek NAND 3-wejściowych i 3 bramek NOT (Rysunek 1).

Rysunek 1. Realizacja podstawowej funkcji opisującej układ przy użyciu bramek NAND (i NOT).

Należy pamiętać o tym, że układy scalone zawierające bramki NAND są produkowane w następujących konfiguracjach:



4 bramki NAND 2-wejściowe (np. US 7400 w technologii TTL lub 4011 w technologii CMOS),



3 bramki NAND 3-wejściowe (np. US 7410 w technologii TTL lub 4023 w technologii CMOS),



2 bramki NAND 4-wejściowe (np. US 7420 w technologii TTL lub 4012 w technologii CMOS),



1 bramka NAND 8-wejściowa (np. US 7430 w technologii TTL lub 4068 w technologii CMOS).

Bramki negujące można znaleźć w układzie scalonym zawierającym 6 bramek NOT (np. US 7404 w technologii TTL lub

4069 w technologii CMOS).

Warto zawsze sprawdzić tzw. złożoność układową zaprojektowanej postaci funkcji. Przez złożoność układową rozumie się:



LP - liczbę połączeń (liczba wejść wszystkich użytych elementów),



LB - liczbę użytych elementów (bramek logicznych),



LS - liczbę układów scalonych potrzebnych do realizacji układu.

Oczywistym jest, że dąży się do tego aby złożoność (jakkolwiek określona) była jak najmniejsza.

W powyższym przypadku:



LP = 15



LB = 7 (3 bramki NOT i 4 bramki NAND, razem 7)



LS = 3 (jeden układ 7400/4011 z którego wykorzystamy 3 (z 6 dostępnych) bramki NOT i np. dwa układy

7410/4023, z których weźmiemy 3-wejściowe bramki NAND)

Należy pamiętać, że mając do dyspozycji bramkę NAND o większej niż potrzebna liczbie wejść, można jej użyć jako bramki

o mniejszej ich ilości, do wejść nieużywanych należy wtedy podłączyć na stałe stan wysoki (logiczna jedynka). Dlatego też

np. realizując układ z Rysunku 1 można zamiast dwóch układów 7410, użyć dwa układy 7420, zawierające bramki 4-

wejściowe, lub też po jednym 7410 i 7420. Wybór sposobu realizacji zależy najczęściej od dostępności poszczególnych US.

2.2.

Synteza układu kombinacyjnego na bramkach NAND - wersja zminimalizowana

W celu uproszczenia układu należy go zminimalizować np. popularną metodą graficzną (metodą tablic Karnaugh), która dla

powyższego układu ma następujący wygląd:

A

BC

0

1

00

1

X

01

1

0

11

X

0

10

0

1

Tworzenie tablicy Karnaugh sprowadza się do przepisania do niej stanów wyjść z tabeli stanów układu.

Zasady tworzenia grup przy minimalizacji względem jedynek:



łączymy w grupy wszystkie jedynki (jedna jedynka to też grupa!),



X-y mogą być uznane za 1 lub 0, jak nam jest wygodniej, w przykładzie powyżej jeden X został

uznany za 1 i wykorzystany w minimalizacji, drugi za 0.



grupa powinna być ”zwarta”, ale może się symetrycznie „zawijać” (podobnie jak grupa złożona z 1 i

X w powyższym przykładzie),



grupę mogą stworzyć następujące ilości czynników: 1, 2, 4, 8, 16… (czyli potęgi dwójki), przy czym

pożądane jest by grupy były jak największe.

Minimalna (a także przekształcona do postaci realizowalnej na bramkach NAND) postać tej funkcji wygląda więc

następująco:

C

A

B

A

C

A

B

A

C

A

B

A

OUT

























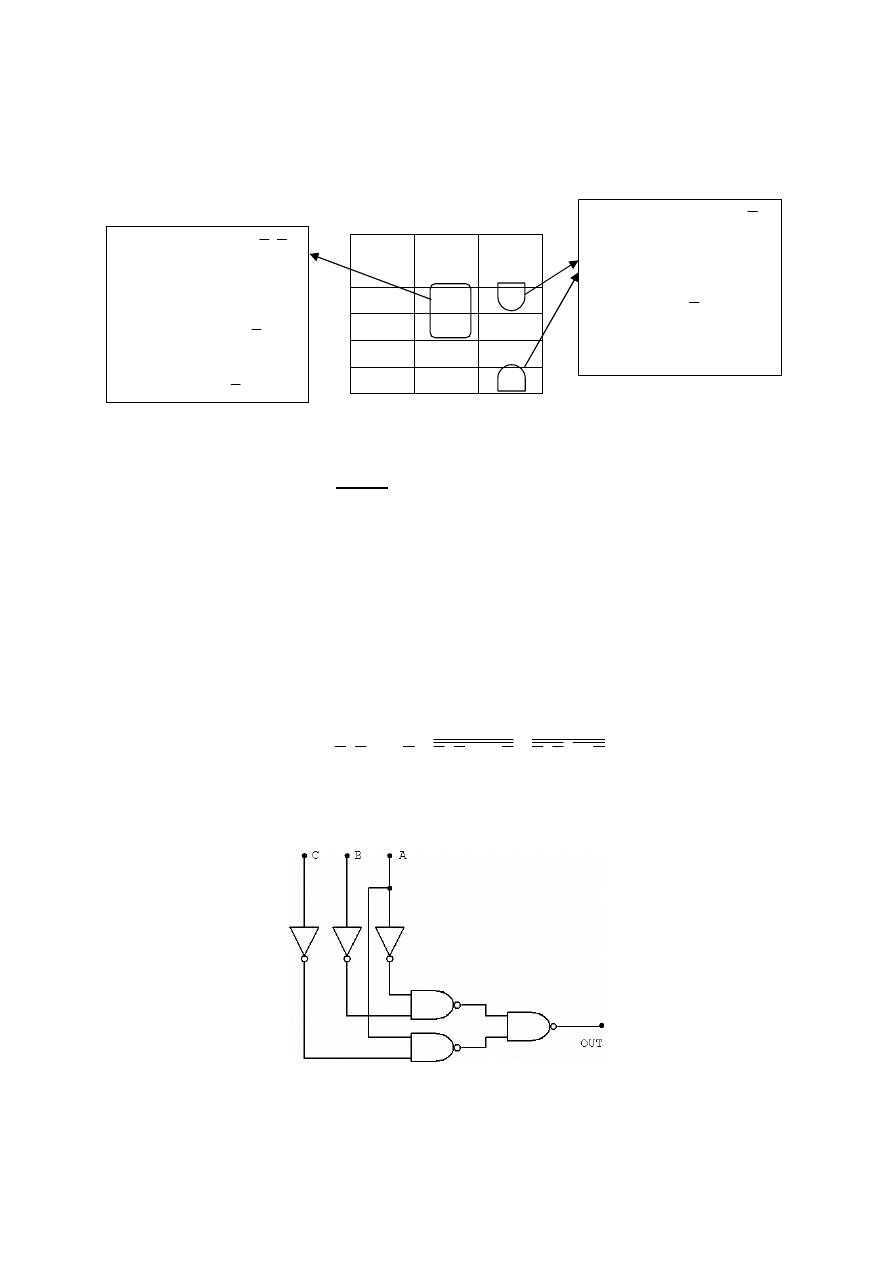
Jak widać, aby zrealizować powyższą postać funkcji potrzeba 3 bramek NAND 2-wejściowych i 3 bramek NOT (Rysunek 2).

Rysunek 2. Realizacja przykładowego układu w postaci zminimalizowanej przy użyciu bramek NAND (i NOT).

Zminimalizowany układ ma zdecydowanie mniejszą złożoność układową:

LP=9, LB=6, LS=2

(poprzedni układ: LP=15, LB=7, LS=3).

Ta grupa daje wyrażenie

B

A 

,

ponieważ:

- patrząc na nią w wierszach

(wiersze 1 i 2), B jest stałe i

równe 0, C się zmienia, stąd w

wyniku pojawia się

B

- patrząc na nią w kolumnach, A

jest stałe i równe 0, stąd w

wyniku jest

A

Ta grupa daje wyrażenie

C

A 

,

ponieważ:

- patrząc na nią w wierszach

(wiersze 1 i 4), C jest stałe i

równe 0, B się zmienia, stąd w

wyniku C

- patrząc na nią w kolumnach, A

jest stałe i równe 1, stąd w

wyniku A

2.3.

Realizacja funkcji z użyciem multipleksera

Jednym z zastosowań multiplekserów i demultiplekserów jest możliwość prostej realizacji przy ich pomocy układów

kombinacyjnych. W drugiej części ćwiczenia do realizacji układu kombinacyjnego wykorzystuje się multiplekser. Używając go

można zrealizować dowolny układ kombinacyjny o ilości wejść równej ilości wejść adresujących i jednym wyjściu. Minimalnie

rozbudowując układ można zrealizować także układ o ilości wejść większej o jeden niż ilość wejść adresujących. No ale

najpierw wersja (naj)prostsza.

Przeanalizujmy to na przykładzie multipleksera 74151. Multiplekser działa w taki sposób, że przekazuje na swoje

wyjście (Y) stan z tego wejścia danych (D0-D7) na które w danym momencie wskazuje stan wejść adresujących CBA. Czyli

np. jeżeli CBA = 000, to na wyjściu Y pojawia się stan z wejścia D0, a jeżeli CBA = 001, to na wyjściu Y pojawia się to samo

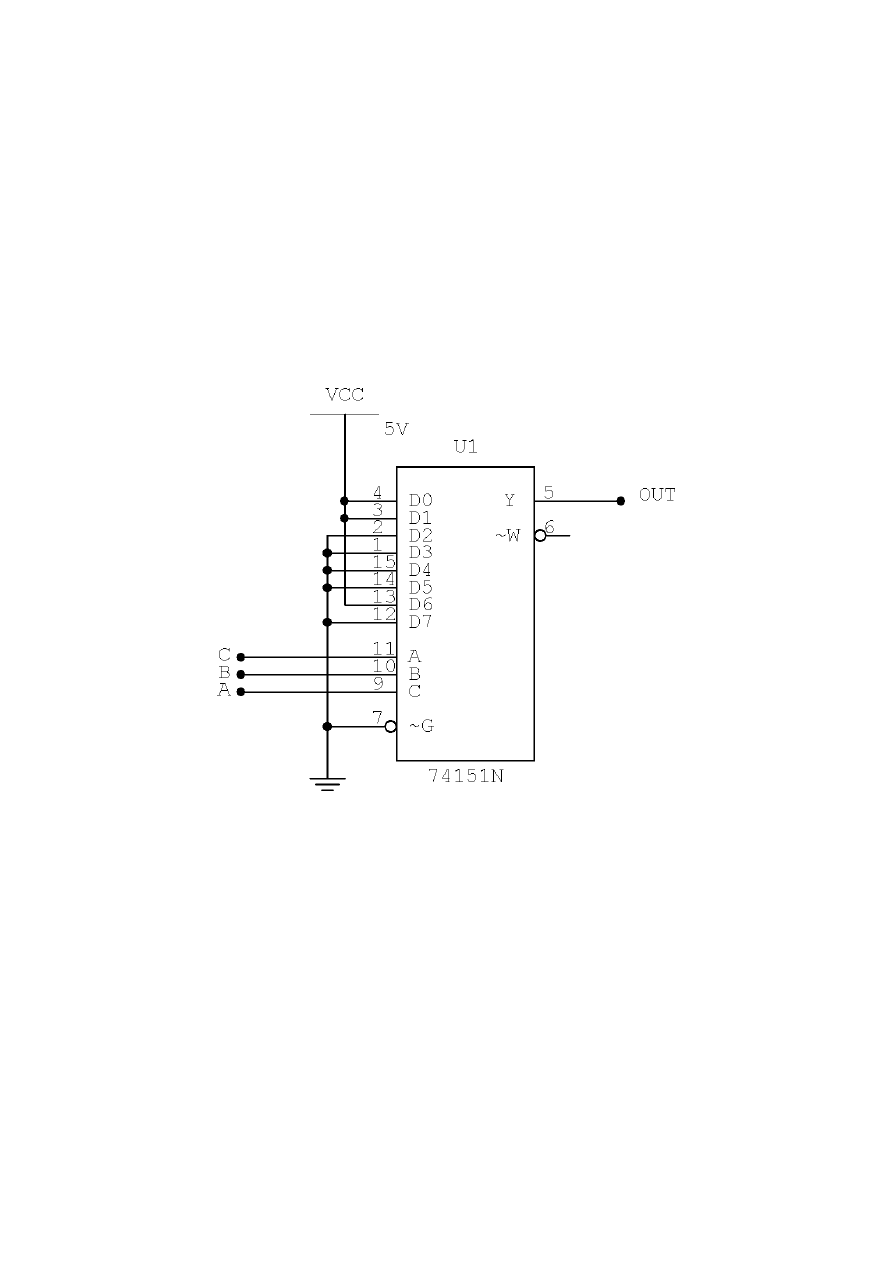
co na wejściu D1 itd. Czyli np. układ pokazany na rysunku:

realizuje funkcję









6

,

1

,

0

2

Z

OUT

, bo 5V (czyli jedynka) jest podłączone do wejść D0, D1 i D6, zatem jedynki

pojawią się na wyjściu Y gdy do wejść CBA podłączone zostaną słowa: 000 (dziesiętne 0), 001 (dziesiętne 1), 110

(dziesiętne 6), natomiast podanie na wejścia CBA innych kombinacji będzie skutkować zerem na wyjściu. Skoro tak, to

układ ten realizuje zadaną przykładową funkcję

 









4

,

3

6

,

1

,

0

2

Z

OUT

, przy czym stany nieokreślone (3 i 4) zostały

przyjęte za zero. Równie dobrze można było na te wejścia podać jedynki, wtedy realizowaną funkcją byłaby funkcja









6

,

4

,

3

,

1

,

0

2

Z

OUT

, co z punktu widzenia zadanej funkcji przykładowej nie ma znaczenia.

Należy także pamiętać o wejściu G, jest to wejście opisane jako „gate” lub „strobe”, czyli bramkujące albo

strobujące, mówiąc prościej – zezwalające. Dopóki nie podłączymy tam zera (o tym że wejście jest aktywne zerem mówi

nam „falka” przy oznaczeniu, ewentualnie negujące „kółko” na schemacie), układ nie zareaguje na nasze działania, jest to

coś w rodzaju „włącznika” dla tego multipleksera.

2.3.1.

Realizacja na multiplekserze układu kombinacyjnego o ilości wejść większej o jedno niż ilość wejść adresujących.

Korzystając z multipleksera można też zbudować układ kombinacyjny o ilości wejść większej niż liczba wejść

adresujących multipleksera. Budowa takiego układu jest niewiele bardziej skomplikowana. Załóżmy że mamy do zbudowania

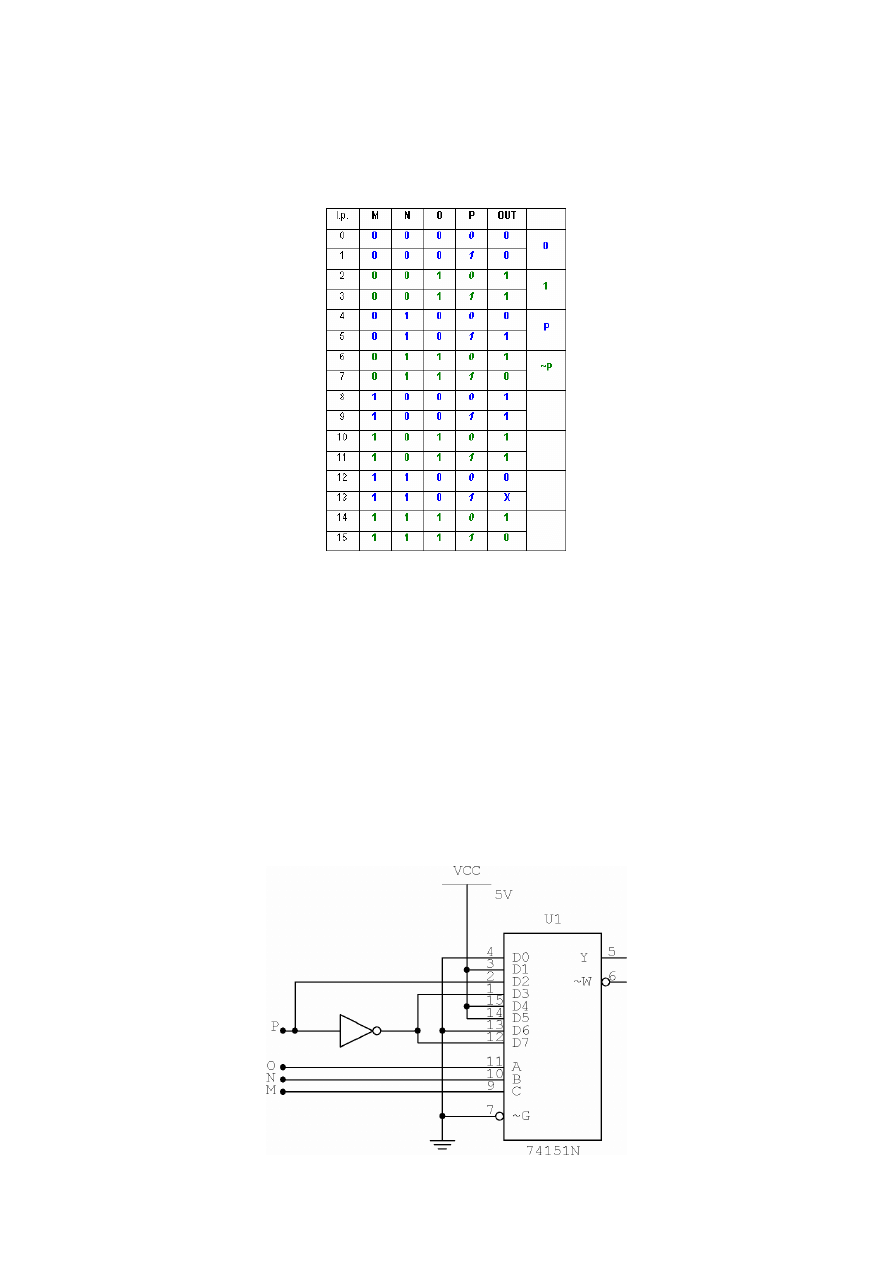
układ opisany tabelą jak niżej:

Jak widać układ ten ma 4 wejścia (M, N, O i P), natomiast my chcemy go zrealizować na multiplekserze 74151, czyli

dysponującym jedynie 3 wejściami adresujących. Co w tej sytuacji?

Algorytm postępowania jest następujący:

 Zaczynamy od podziału tabeli, co dwa wiersze, tak jak pokolorowano wyżej.

 I patrzymy na pierwszą parę wierszy. Kiedy wejścia MNO są równe 000, wyjście jest równe 0,

niezależnie od wejścia P.

 Drugi wiersz. Kiedy MNO=001, OUT=1,

niezależnie od P.

 Trzecia para wierszy. MNO=010, OUT jest równe ile? Tym razem nie jest to jednoznaczne, OUT się zmienia, nie możemy

powiedzieć że jest równe 0 lub 1 niezależnie od P. Więc może jest

zależne od P? No właśnie, OUT w tym przypadku jest takie

samo jak P. No to dalej…

 Trzecia para wierszy. Znów OUT zależy od P, tyle że jest odwrotnością P, czyli inaczej mówiąc

negacją P.

 I tak dalej… do końca tabeli.

Skoro tak, to układ realizujący tę funkcję wygląda tak jak na rysunku poniżej. Wejścia CBA są dla nas w tym momencie wejściami

MNO naszego układu, wejście P istnieje „obok”:

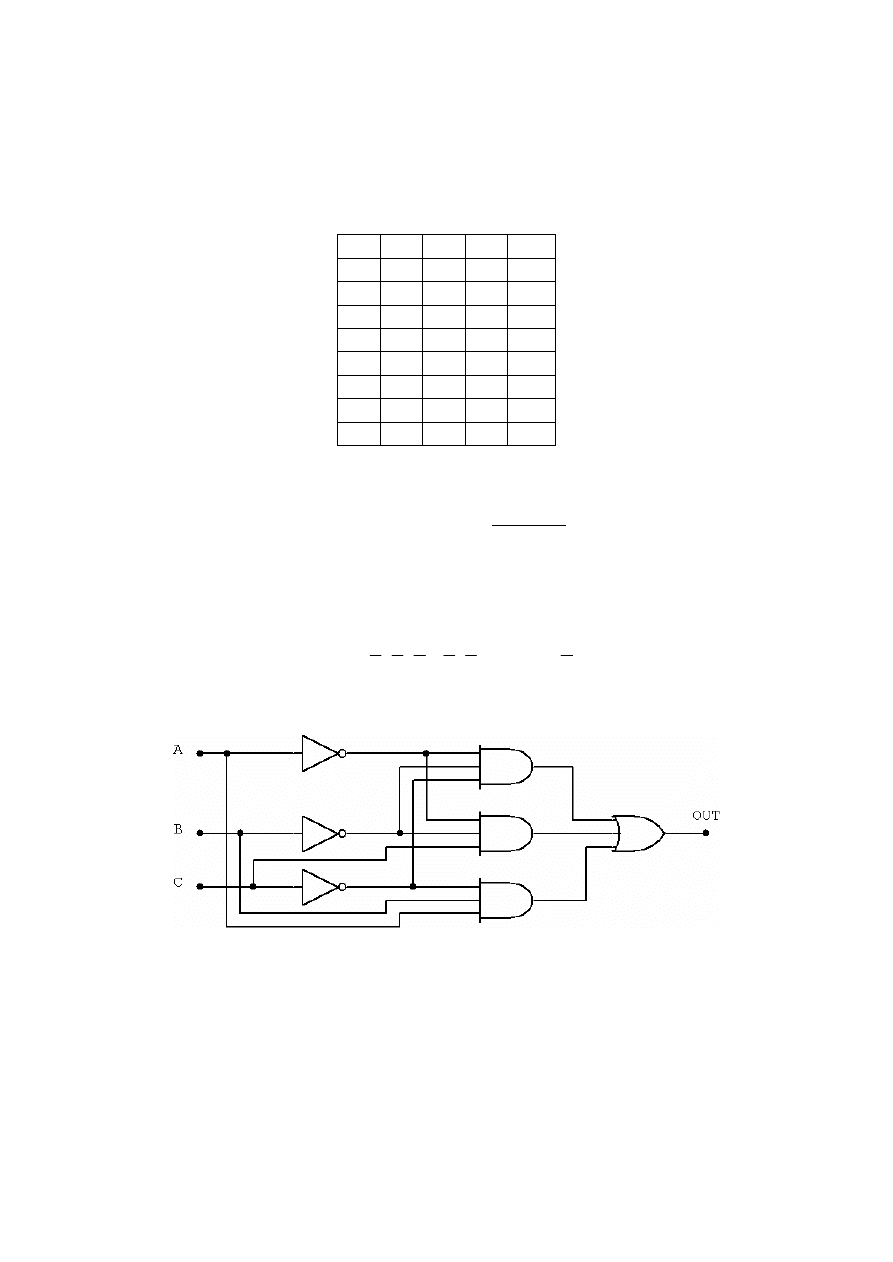
3.

DODATEK - Inne sposoby realizacji funkcji logicznych, warto się zapoznać, zwłaszcza przed kolokwium.

W kolejnych podpunktach zaprezentowano sposoby realizacji przykładowej funkcji (tej samej co w punkcie 2) w

innych wersjach.

Mamy zatem tabelę taką samą jak poprzednio:

l.p.

A

B

C OUT

0

0

0

0

1

1

0

0

1

1

2

0

1

0

0

3

0

1

1

x

4

1

0

0

x

5

1

0

1

0

6

1

1

0

1

7

1

1

1

0



Znak X pojawiający się w tabeli oznacza iż określona kombinacja wejść nie ma prawa w układzie wystąpić lub że z

pewnych powodów nie interesuje nas wyjście układu dla danej kombinacji wejść.

3.1.

Układ niezminimalizowany na bramkach AND i OR – trzy przykładowe sposoby realizacji

Na podstawie tabeli, tak jak we wstępie do ćwiczenia, uzyskujemy opis kanoniczny projektowanego układu w

postaci sumacyjnej:

OUT =

∑

(

0,1,6

(

3,4

))

i odpowiadający mu opis kanoniczny w zapisie Boola:

C

B

A

C

B

A

C

B

A

OUT



















.

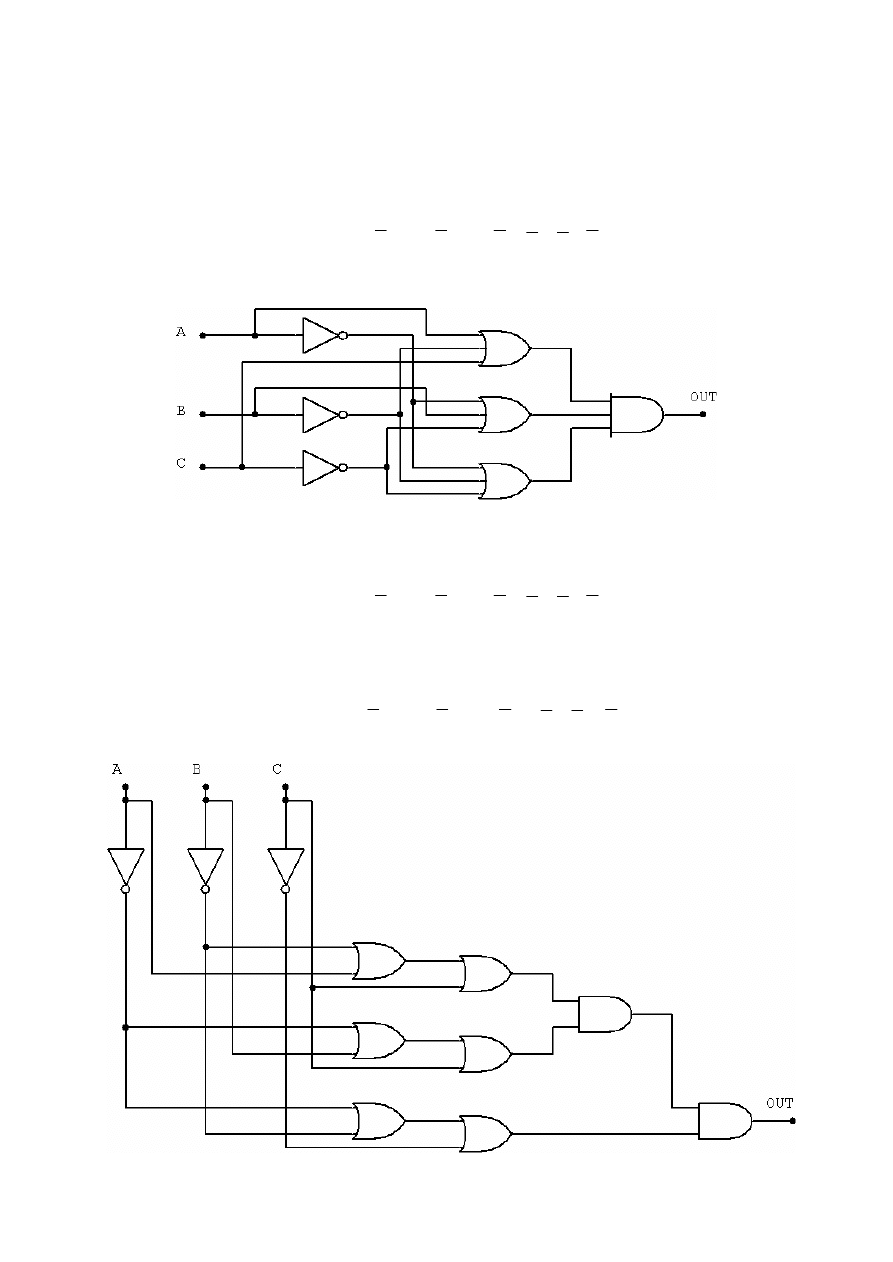
Na podstawie tego zapisu możemy wprost zrealizować funkcję logiczną, jak na rysunku:

Przy założeniu, że realizujemy układ w technologii CMOS, można do tego celu użyć jednego układu 4075 (trzy 3-

wejściowe bramki OR, z których wykorzystujemy jedną), jednego 4073 (trzy 3-wejściowe bramki AND) i jednego 4069 (sześć

inwerterów (bramek NOT), z których wykorzystujemy trzy).

Na podstawie tabeli można też pozyskać opis kanoniczny projektowanego układu w postaci iloczynowej:

OUT =

∏

(

2,5,7

(

3,4

)).

Pozyskuje się ją odwrotnie do sumacyjnej, tamta wynika z jedynek układu, ta z zer, stany dowolne się oczywiście

powtarzają. Opis kanoniczny w zapisie Boola w tym przypadku wygląda tak (zamiast sumy iloczynów mamy iloczyn sum):



 

 



C

B

A

C

B

A

C

B

A

OUT



















.

Układ taki można zrealizować z wykorzystaniem tych samych układów co poprzednio, tyle że tym razem

wykorzystane zostaną 3 bramki OR i jedna AND:

Czasem dysponujemy tylko określonym rodzajem bramek logicznych, należy wtedy (o ile to możliwe) doprowadzić

opis układu do takiej postaci by była możliwa realizacja założeń projektowych. Załóżmy np. że funkcję:



 

 



C

B

A

C

B

A

C

B

A

OUT



















.

musimy zrealizować korzystając tylko i wyłącznie z układów 7404, 7408 i 7432, czyli z bramek NOT i 2-wejściowych bramek

AND i OR. W realizacji powyżej korzystaliśmy z bramek 3-wejściowych, takiej jaka wynika bezpośrednio z postaci funkcji.

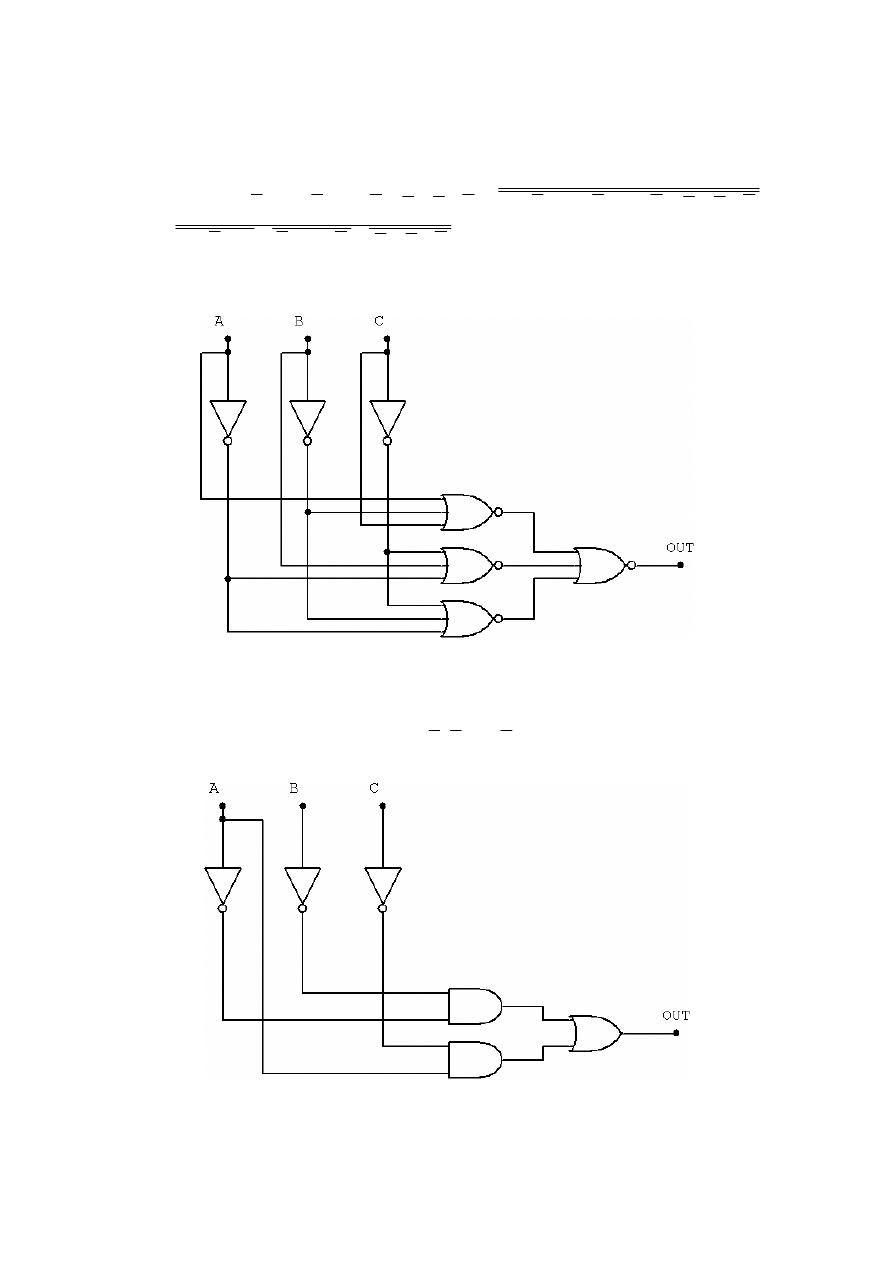
Jeżeli chcemy korzystać z bramek 2-wejściowych to funkcję tą musimy doprowadzić np. do postaci:







 



















C

B

A

C

B

A

C

B

A

OUT



















i wtedy da się ją zrealizować tak:

3.2.

Układ niezminimalizowany na bramkach NOR

Warto wspomnieć, że analogicznie jak w przypadku realizacji na bramkach NAND pokazanej we wstępie do

ćwiczenia, postać iloczynową funkcji można przekształcić z wykorzystaniem praw de Morgana do postaci:



 

 

 

 

 





 

 



C

B

A

C

B

A

C

B

A

C

B

A

C

B

A

C

B

A

C

B

A

C

B

A

C

B

A

OUT

























































,

dzięki czemu uzyskujemy postać do realizacji z wykorzystaniem 3-wejściowych bramek NOR (np. układów 4025 w

technologii CMOS lub 7427 w technologii TTL). Układ wygląda wtedy tak:

3.3.

Układ zminimalizowany na bramkach AND I OR – dwie wersje

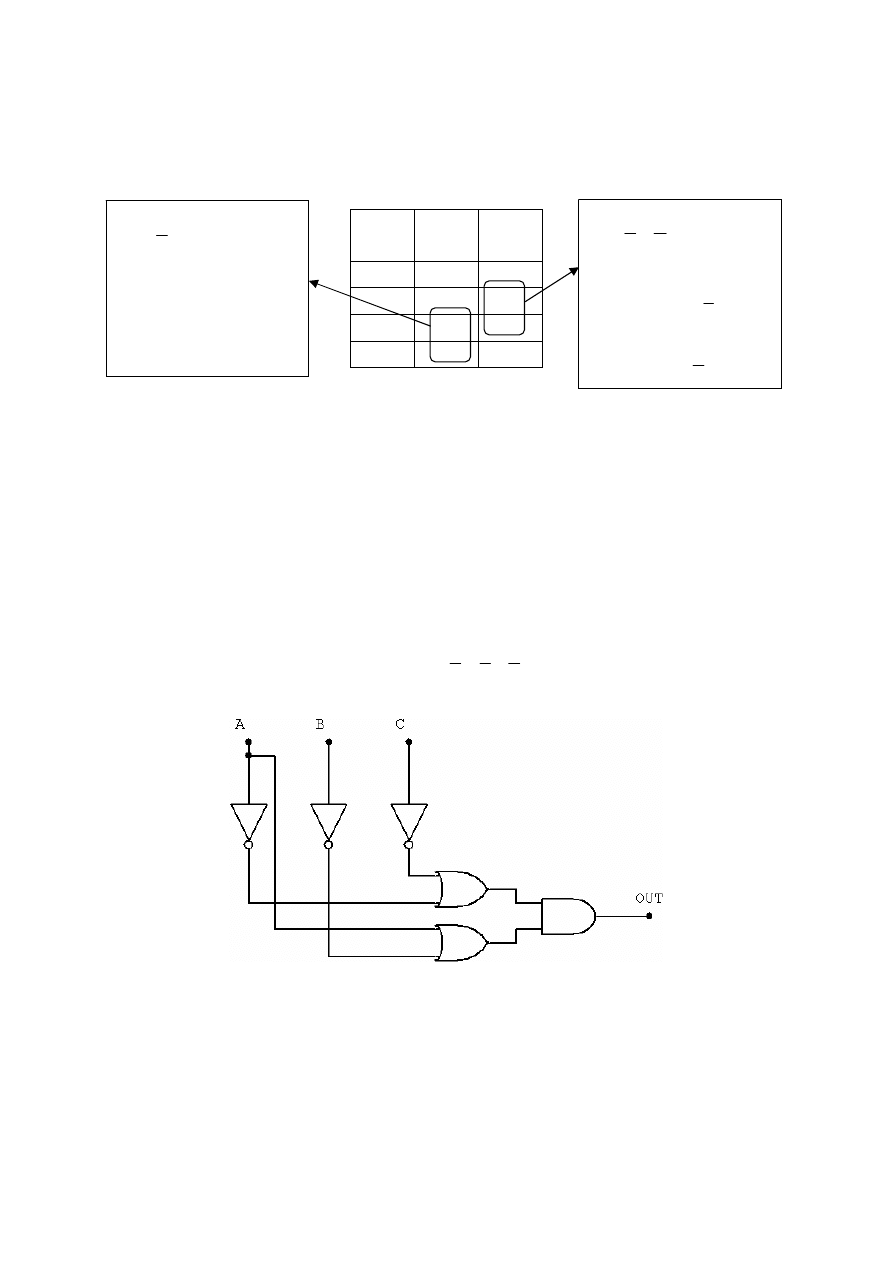
Funkcja zminimalizowana w punkcie 2.2 ma postać jak niżej:

C

A

B

A

OUT









zatem podobnie jak poprzednio można ją zrealizować na bramkach AND i OR, układ będzie wyglądał tak:

Niemniej podobnie jak postać nieminimalną funkcji można pozyskać tak z jedynek jak i z zer, tak samo

minimalizować układ można na dwa sposoby, względem jedynek lub zer. Jeżeli zadaną funkcję chcemy zminimalizować

korzystając z zer, to tablica Karnaugh będzie wyglądać tak samo, zmienią się grupy, tym razem łączymy zera:

A

BC

0

1

00

1

X

01

1

0

11

X

0

10

0

1

Zasady tworzenia grup przy minimalizacji względem zer:



łączymy w grupy wszystkie zera (jedno zero to też grupa!),



X-y mogą być uznane za 1 lub 0, jak nam jest wygodniej, w przykładzie powyżej jeden X został

uznany za 0 i wykorzystany w minimalizacji, drugi za 1 i niewykorzystany.



grupa powinna być ”zwarta”, ale może się symetrycznie „zawijać” (podobnie jak w minimalizacji

według 1 w poprzednim przykładzie),



grupę mogą stworzyć następujące ilości czynników: 1, 2, 4, 8, 16… (czyli potęgi dwójki), przy czym

pożądane jest by grupy były jak największe.

Postać minimalna iloczynowa wygląda więc tak:



 



C

A

B

A

OUT









natomiast jej realizacja tak:

Ta grupa daje wyrażenie

A

B 

, ponieważ:

- patrząc na nią w wierszach

(wiersze 3 i 4), B jest stałe i

równe 1, C się zmienia, stąd w

wyniku jest tylko B

- patrząc na nią w kolumnach, A

jest stałe i równe 0, stąd w

wyniku A

Ta grupa daje wyrażenie

C

A 

, ponieważ:

- patrząc na nią w wierszach

(wiersze 2 i 3), C jest stałe i

równe 1, B się zmienia, stąd w

wyniku tylko C

- patrząc na nią w kolumnach, A

jest stałe i równe 1, stąd w

wyniku

A

Opis minimalny można oczywiście przekształcić z pomocą praw de Morgana do postaci:



 

 

 

 

 



C

A

B

A

C

A

B

A

C

A

B

A

OUT

























,

która pozwala na realizację funkcji z wykorzystaniem wyłącznie bramek NOR:

a w przypadku gdy nawet bramki NOT chcemy zastąpić bramkami NOR:

3.4.

Podsumowanie

W dodatku pokazano 8 sposobów bramkowych realizacji przykładowej funkcji logicznej, kolejne 2 sposoby

pokazano we wstępie do ćwiczenia. Oczywiście nie są to wszystkie możliwości, ale w ogólności pokazują one jakie

możliwości ma projektujący tego typu układy.

4.

Przebieg ćwiczenia

4.1.

Układ na bramkach NAND (OBOWIĄZKOWO):

Na podstawie zadanej przez prowadzącego w postaci tabeli stanów funkcji logicznej (OUT

Z

) należy:

4.1.1.

Zdecydować jaki układ realizujemy – pełny czy minimalny. Lepiej minimalny, bo i prościej go zmontować i można

się wykazać umiejętnościami minimalizacji, ale wybór należy do Was.

4.1.2.

Zaprojektować (zgodnie z instrukcją) wybraną wersję układu na bramkach NAND.

4.1.3.

Wybrać układy scalone potrzebne do realizacji zaprojektowanego układu (noty katalogowe są załączone do

instrukcji). Wymagane układy scalone powinny być już umieszczone w podstawkach testera układów logicznych.

Przy pomocy dostępnych przewodów zbudować zaprojektowany układ. Jako wejścia układu posłużą wtyki opisane

jako „kombinacje wyjście”. Ich stan zmienia się zadając odpowiednie stany wejść przy pomocy rzędu przycisków

na dole testera stanów logicznych. Przycisk STAT powinien być wciśnięty. Logiczną 1 wymusza przycisk w stanie

OFF (wyciśnięty), logiczne zero w stanie ON (wciśnięty). Stan wyjścia można sprawdzić multimetrem lub

wskaźnikiem stanów logicznych.

Układy w podstawkach 14-nóżkowych są zasilane w układzie, nie trzeba zatem podłączać pinów Vcc i GND.

4.1.4.

Włączyć zasilanie.

4.1.5.

Sprawdzić poprawność działania układu (czyli czy działa on zgodnie z zadaną tabelą stanów).

4.1.6.

Zaprezentować prowadzącemu działanie układu, następnie rozmontować układ.

4.2.

Układ na multiplekserze (NADOBOWIĄZKOWO):

4.2.1.

Zaprojektować w protokole zadany przez prowadzącego układ kombinacyjny na multiplekserze 74151.

4.2.2.

Następnie projekt ten należy zrealizować korzystając z testera układów logicznych PTC-1, korzystając z wejść i

wyjść podobnie jak w punkcie 4.1.

Wykorzystywany w ćwiczeniu układ cyfrowy 8-wejściowego (3-bitowego) selektora/multipleksera 74151 jest

umieszczony w podstawce testera układów logicznych PTC-1.

Do instrukcji załączona jest odpowiednia nota katalogowa, na podstawie której należy zidentyfikować funkcje

poszczególnych nóżek układu scalonego, a następnie się do nich podłączyć dostępnymi przewodami zgodnie z

wcześniej wykonanym projektem.

Do układu scalonego należy najpierw podłączyć zasilanie (piny Vcc i GND), a następnie łączyć zaprojektowany

układ. Stany wysoki (1) i niski (0) można pozyskać podłączając się w dowolnym punkcie testera PTC-1

oznaczonym jako +5V (jedynka) lub masa (zero).

Nie zapomnieć o zasilaniu układu scalonego (piny V

cc

i GND) – układy w podstawkach 16-nóżkowych nie są

zasilane z układu!

4.2.3.

Sprawdzić poprawność działania układu w tej wersji.

4.2.4.

Zaprezentować prowadzącemu działanie układu, następnie rozmontować go.

5.

Opracowanie wyników

5.1.

Znaleźć opis zadanego w ćwiczeniu układu w postaci sumacyjnej i iloczynowej i zrealizować obie uzyskane

postacie funkcji z wykorzystaniem bramek AND i OR.

5.2.

Zminimalizować uzyskane funkcje względem zer i jedynek i zrealizować obie uzyskane postacie funkcji z

wykorzystaniem bramek AND i OR.

5.3.

Zadaną funkcję zrealizować też przy pomocy wyłącznie bramek NOR w dwóch wersjach:

zminimalizowanej i nie zminimalizowanej.

5.4.

Policzyć złożoność (LP, LB, LS) zbudowanego w trakcie ćwiczenia układu.

Jak ma się złożoność układu w wersji minimalnej do złożoności układu w wersji pełnej?

5.5.

Mile widziane dodatkowe wnioski i przemyślenia.

6.

Co trzeba umieć w kontekście zaliczenia?

6.1.

Jak zrealizować zadaną funkcję logiczną w postaci sumacyjnej lub iloczynowej z wykorzystaniem dowolnego lub

narzuconego rodzaju bramek (czyli AND i OR lub tylko NAND lub tylko NOR) w postaci pełnej lub minimalnej

(minimalizacja metodą tablic Karnaugh).

6.2.

Jak wykorzystać multiplekser cyfrowy do realizacji kombinacyjnych funkcji logicznych w dwóch wersjach:

 realizacja układu kombinacyjnego o ilości wejść równej ilości wejść adresujących multipleksera,

 realizacja układu kombinacyjnego o ilości wejść większej o jedno niż ilość wejść adresujących multipleksera.

7.

Literatura

[1] Ćwirko R., Rusek M., Marciniak W., „Układy scalone w pytaniach i odpowiedziach”, WN-T Warszawa 1987

[2] Filipkowski A., „Układy elektroniczne analogowe i cyfrowe”, Wydawnictwa Naukowo-Techniczne, Warszawa 1978

[3] Głocki W., Grabowski L., „Pracownia podstaw techniki cyfrowej”, WSiP, Warszawa 1998

[4] Górecki P., „Układy cyfrowe, pierwsze kroki”, Wydawnictwo BTC, Warszawa 2004

[5] Kalisz J., „Cyfrowe układy scalone w technice systemowej”, WMON, Warszawa 1997

[6] Pieńkos J., Turczyński J., „Układy scalone TTL w systemach cyfrowych”, WKiŁ, Warszawa 1986

[7] Sasal W., „Układy scalone serii UCA64/UCY74, parametry i zastosowania”, WKiŁ, Warszawa 1985

[8] www.datasheetcatalog.com

Opracowanie ćwiczenia: Seweryn Lipiński