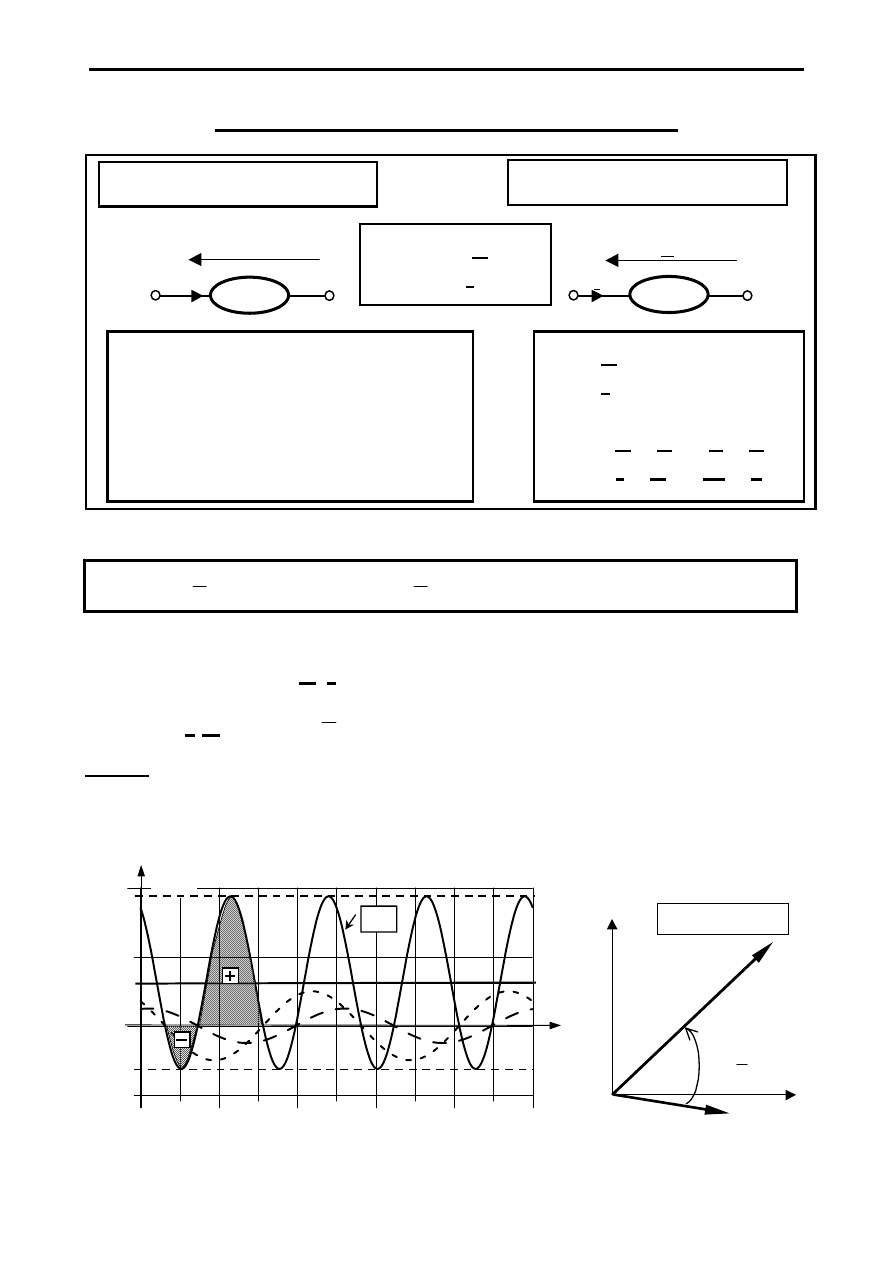
MOCE W OBWODACH SLS ZNAJDUJĄCYCH SIĘ W SUS
MOC CHWILOWA p(t) [W]
u
(t)
i
(t)
I
U
u(t) = U
m
cos(
ωt + α )
i(t) = I
m
cos(
ωt + α – ϕ )
PO: u(t) = A[i(t)] – [e
g
(t)
{ }
sin
cos
]
i(t) = A[u(t)] + [j
g
(t)
{ }
sin
cos
]
U = U
m
e
jα
I = I
m
e
j(α–ϕ)
PO: U = Z(
ω)⋅I – [E]
I = Y(
ω)⋅U – [J]
Dziedzina czasu „t”
Dziedzina pulsacji „
ω”
u(t) = Re[ U
⋅e
j
ωt
]
i(t) = Re[ I
⋅e
jωt
]
SLS
SLS
p(t) = u(t)
⋅i(t) = U
m
cos(
ωt + α )⋅I
m
cos(
ωt + α – ϕ )
p(t) =
2
1
U
m
I
m
cos
ϕ +
2
1
U
m
I
m
cos( 2
ωt + 2α – ϕ )
ω
p
= 2
ω
– pulsacja mocy chwilowej p(t) jest 2 razy większa od pulsacji
ω
sygnałów U, I
Jeśli
∠(I,U) = ϕ ≠ ±
2
π
, to moc chwilowa p(t) ma składową stałą.
Przykład
u(t) = 10
cos( 2
πt + π/4 ) V;
ω= 2π rad/s, α = π/4 rad
i(t) = 5cos( 2
πt + π/4 – π/3 ) A;
ϕ = π/3 rad
p(t) = 12,5 + 25cos[ 2(2
π)t + π/6 ] W;
ω
p
= 2
ω rad/s
0.00
0.40
0.80
1.20
1.60
2.00
-20.00
20.00
0.00
40.00
u(t) [V]
i(t) [A]
p(t) [W]
t [s]
p(t)
12,5
3
π
=
ϕ
U
I
im
re
Charakter „L”
Dr inż. Jacek Czosnowski
Katedra Elektrotechniki AGH Wydział EAIiE
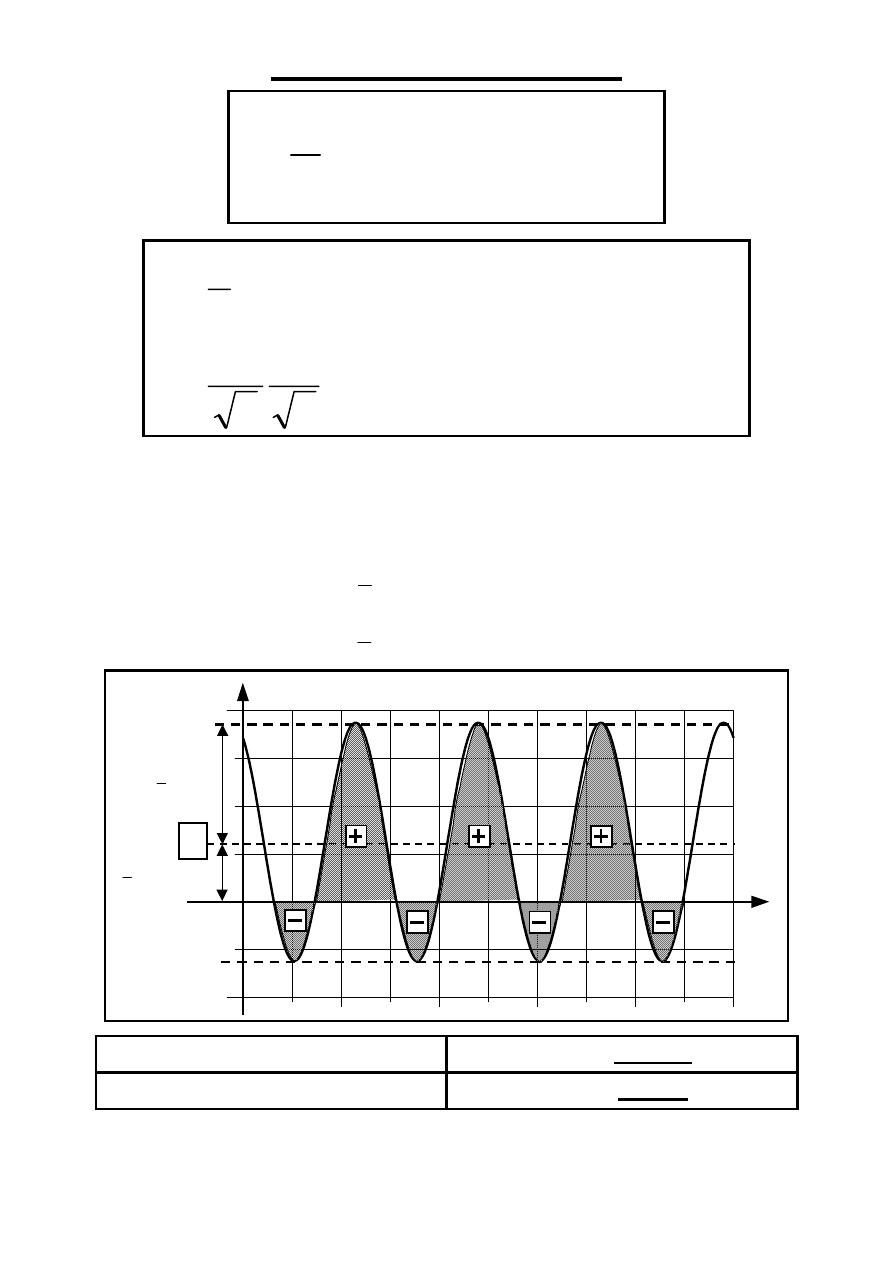
MOC CZYNNA P [W]
W]
[
d
)
(
T
1
P
T
t
t
0
0
ℜ
∈
=
∫
+
∆
τ
τ
p
[W]
cos
I
U
[W]
cos
2
I
2
U
P
[W]
cos
I
U
2
1
P
sk
sk
m
m
m
m
ϕ
ϕ
ϕ
=
=
=
gdzie: cos
ϕ – współczynnik mocy
p(t) = P + p
zm
(t)
p
max
=
2
1
U
m
I
m
( cos
ϕ + 1 )
p
min
=
2
1
U
m
I
m
( cos
ϕ – 1 )
p(t) [W]
t [s]
p
max
p
min
2
1
U
m
I
m
cos
ϕ
P
2
1
U
m
I
m
P > 0
( strzałkowanie odbiornikowe)
Dwójnik SLS pobiera energię
P < 0
( strzałkowanie odbiornikowe)
Dwójnik SLS oddaje energię
Dr inż. Jacek Czosnowski
Katedra Elektrotechniki AGH Wydział EAIiE
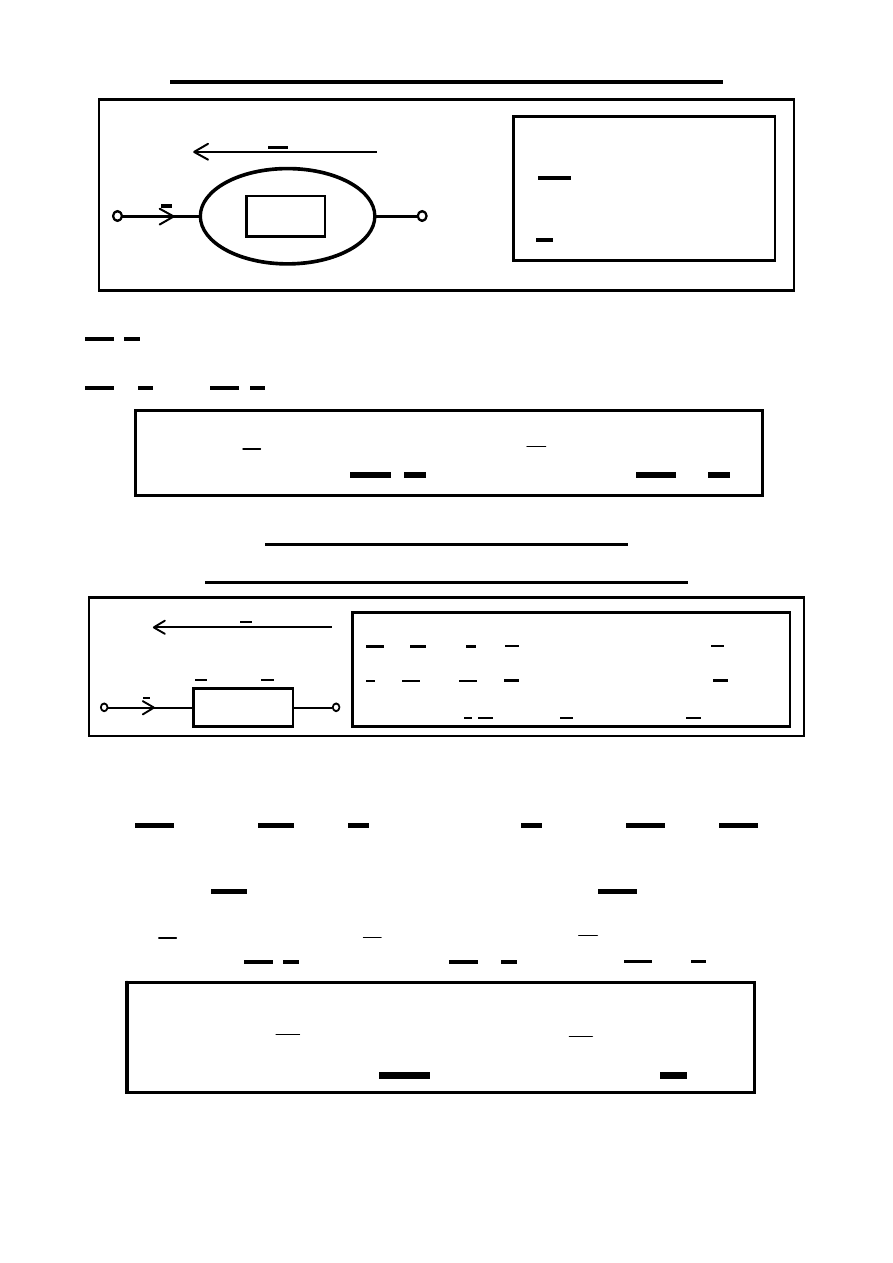
Moc czynna dowolnego dwójnika
U
I
SLS
U= U
m
e
j
α
I= I
m
e
j(
α – ϕ)
U
⋅I
*
= U
m
e
j
α
⋅I
m
e
–j(
α – ϕ)
= U
m
I
m
e
j
ϕ
U
*
⋅I = (U⋅I
*
)
*
= U
m
e
–j
α
⋅I
m
e
j(
α – ϕ)
= U
m
I
m
e
–j
ϕ
P =
2
1
Re[U
⋅I
*
] =
2
1
Re[U
*
⋅I]
Moc czynna z jaką w SUS
dwójnik SLSB przetwarza energię
Z(ω)
lub
Y(ω)
U
I
U = Z(
ω)⋅I;
Z(
ω)= r(ω) + j
x(
ω) = ⏐Z⏐e
j
ϕ
I = Y(
ω)⋅U;
Y(
ω)= g(ω) + j
b(
ω) = ⏐Y⏐e
–j
ϕ
ϕ = ∠(I,U) = arg[Z(ω)] = – arg[Y(ω)]
⎪U⎪=⎪Z⎪⎪I⎪; ⎪I⎪=⎪Y⎪⎪U⎪
r =
⎪Z⎪cos
ϕ; g =⎪Y⎪cos
ϕ
2
1
P =
2
1
Re[U
⋅I
*
] =
2
1
Re[U
*
⋅I] =
⎪U⎪⎪I⎪cos
ϕ
P =
2
1
g
⎪U⎪
2
=
2
1
r
⎪I⎪
2
Dr inż. Jacek Czosnowski
Katedra Elektrotechniki AGH Wydział EAIiE
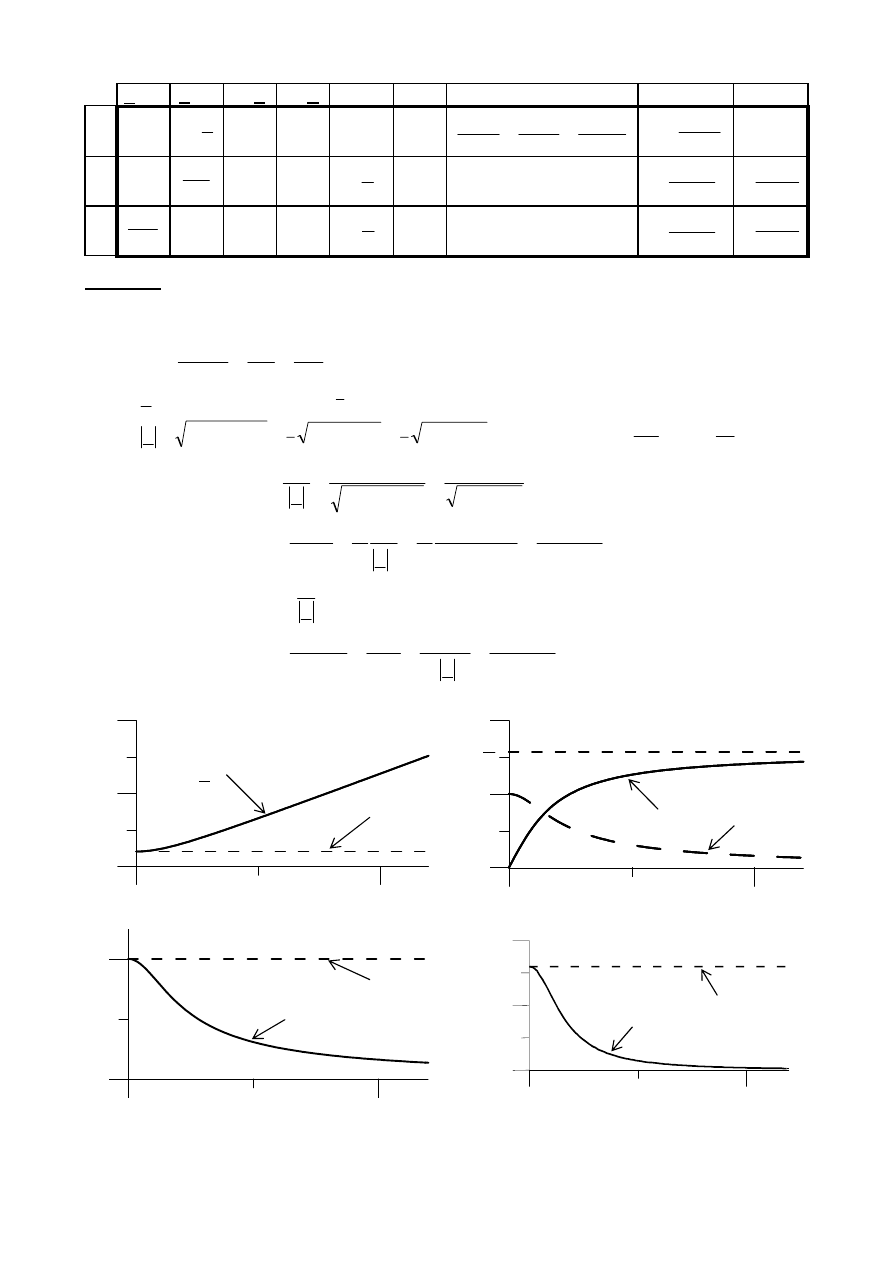
Moce podstawowych elementów biernych: R, L, C
Z [
Ω] Y [S] Re[Z] Re[Y] ϕ [rad] cos
ϕ
P [W]
p
max
[W]
p
min
[W]
R R
R
1
G
=
R G 0 1
2
U
G
2
I
R
2
I
U
2
m
2
m
m
m
⋅
=
⋅
=
2
I
U
P
m
m
=
0
L j
ωL
ωL
j
1
0 0
2
π
+
0 0
2
I
U
m
m
+
2
I
U
m
m
−
C
ωC
j
1
jωC 0 0
2
π
−
0 0
2
I
U
m
m
+
2
I
U
m
m
−
Przykład Dane: R = 8
Ω, L = 0,5 H, U
m
= 32 V.
Obliczyć
1). moc czynną P
R
z jaką energia wydziela się w rezystorze R;
2).
moc
czynną P
RL
z jaką energia wydziela się w dwójniku szeregowym R-L;
1).
W
64
8
2
32
2R
U
2
U
G
P
2
2
m
2
m
R
=
⋅
=
=
⋅
=
2).
(
)
]
[
jω
16
j0,5ω
8
L
jω
R
Z
2
1
Ω
+
=
+
=
+
=
( )
]
[
ω
256
ω
8
4
ωL
R
Z
2
2
1
2
2
2
1
2
2
Ω
+
=
+
⋅
=
+
=
[rad]
16
ω
arctg
R
ωL
arctg
=
=
ϕ
2a). PPK:
( )
[A]
ω
56
2
64
L
ω
R
U
Z
U
I
2
2
2
m
m
m
+
=
+
=
=
( )
[W]
ω
256
16384
L
ω
R
U
2
R
Z
U
2
R
2
I
R
P
2
2
2
2
m
2
2
m
2
m
RL
+
=
+
=
=
⋅
=
2b).
DN:
m
Rm
U
Z
R
U
=
[W]
ω
256
16384
Z
2
U
R
R
2
U
2
U
G
P
2
2
2
m
2
Rm
2
Rm
RL
+
=
⋅
=
=
⋅
=
0
100
0
40
80
|Z|
R
ω
0
100
0
40
80
0
100
0
1
2
0
100
0
1
2
cos
ϕ
ϕ
ω
0
100
0
1
2
2
π
0
100
0
4
ω
0
100
0
40
80
P
R
P
RL
I
mR
I
m
ω
Dr inż. Jacek Czosnowski
Katedra Elektrotechniki AGH Wydział EAIiE
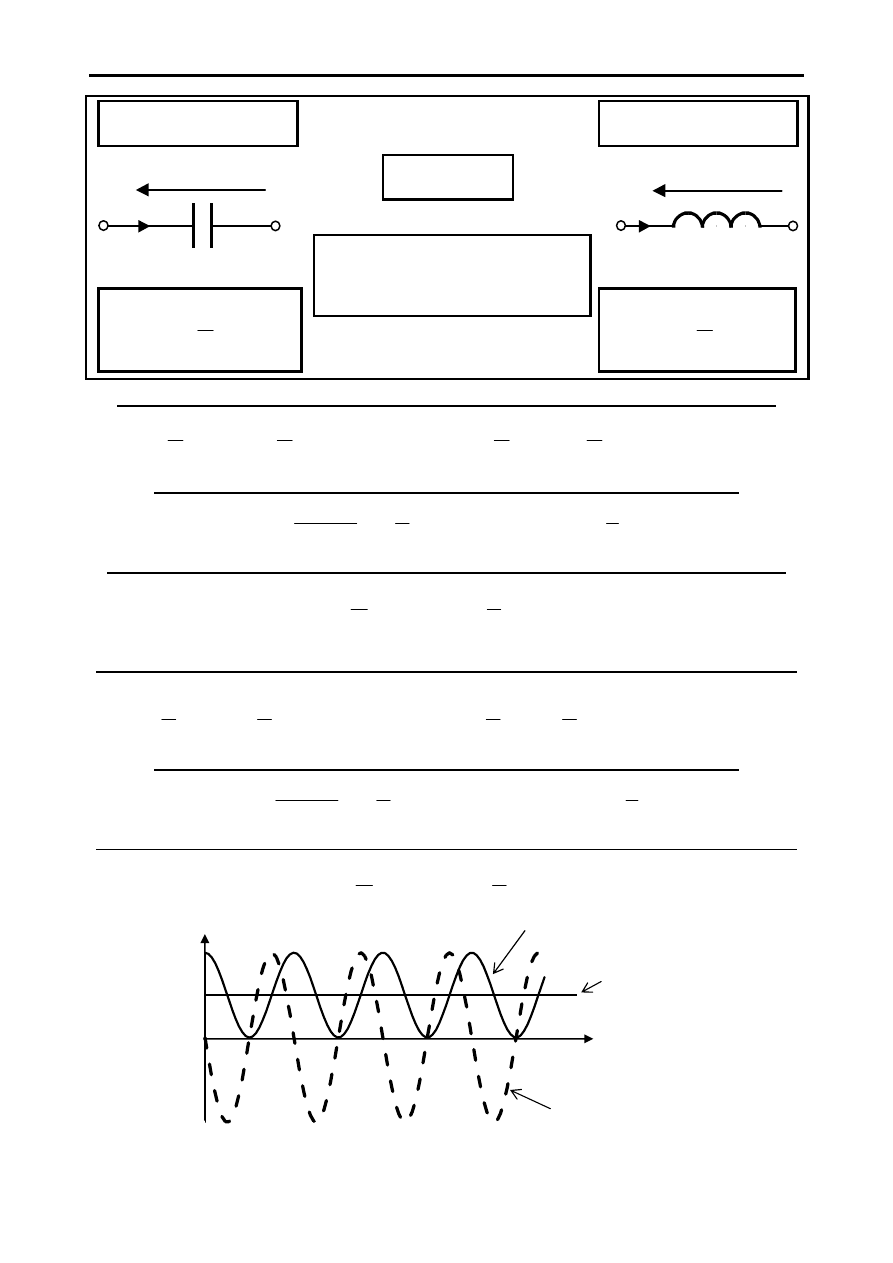
Energie gromadzone w pojemności i indukcyjności
u
(t)
i
(t)
u(t) = U
m
cos(
ωt + α )
i(t) = U
m
cos(
ωt + α – ϕ )
Pojemność
Indukcyjność
P = 0 [W]
u
(t)
i
(t)
)
(
C
2
1
)
(
2
C
t
u
t
w
=
)
(
L
2
1
)
(
2
L
t
i
t
w
=
Energia chwilowa gromadzona w polu elektrycznym pojemności
α)
2
ω
2
cos(
U
C
4
1
U
C
4
1
α)
ω
(
cos
U
C
2
1
)
(
C
2
1
)
(
2
m
2
m
2
2
m
2
C
+
+
=
+
=
=
t
t
t
u
t
w
Moc chwilowa przetwarzania energii pola elektrycznego w pojemności
W]
s
J
[
α)
2
ω
2
sin(
CU
2
1
d
)
(
d
)
(
2
m
C
C
=
+
−
=
=
t
t
t
w
t
p
Wartość średnia energii chwilowej gromadzonej w polu elektrycznym pojemności
( )
[J]
CU
4
1
dτ
τ
T
1
2
m
T
C
C
0
0
=
=
∫
+
∆
t
t
w
W
Energia chwilowa gromadzona w polu magnetycznym indukcyjności
)
2
α
2
ω
2
cos(
I
L
4
1
I
L
4
1
)
α
ω
(
cos
I
L
2
1
)
(
L
2
1
)
(
2
m
2
m
2
2
m
2
L
ϕ
ϕ
−
+
+
=
−
+
=
=
t
t
t
i
t
w
Moc chwilowa przetwarzania energii pola elektrycznego w pojemności
W]
s
J
[
)
2
α
2
ω
2
sin(
LI
2
1
d
)
(
d
)
(
2
m
L
L
=
−
+
−
=
=
ϕ
t
t
t
w
t
p
Wartość średnia energii chwilowej gromadzonej w polu elektrycznym indukcyjności
( )
[J]
LI
4
1
dτ
τ
T
1
2
m
T
L
L
0
0
=
=
∫
+
∆
t
t
w
W
w
C
(t)
lub
w
L
(t)
p
C
(t)
lub
p
L
(t)
ωt
W
C
lub
W
L
Dr inż. Jacek Czosnowski
Katedra Elektrotechniki AGH Wydział EAIiE
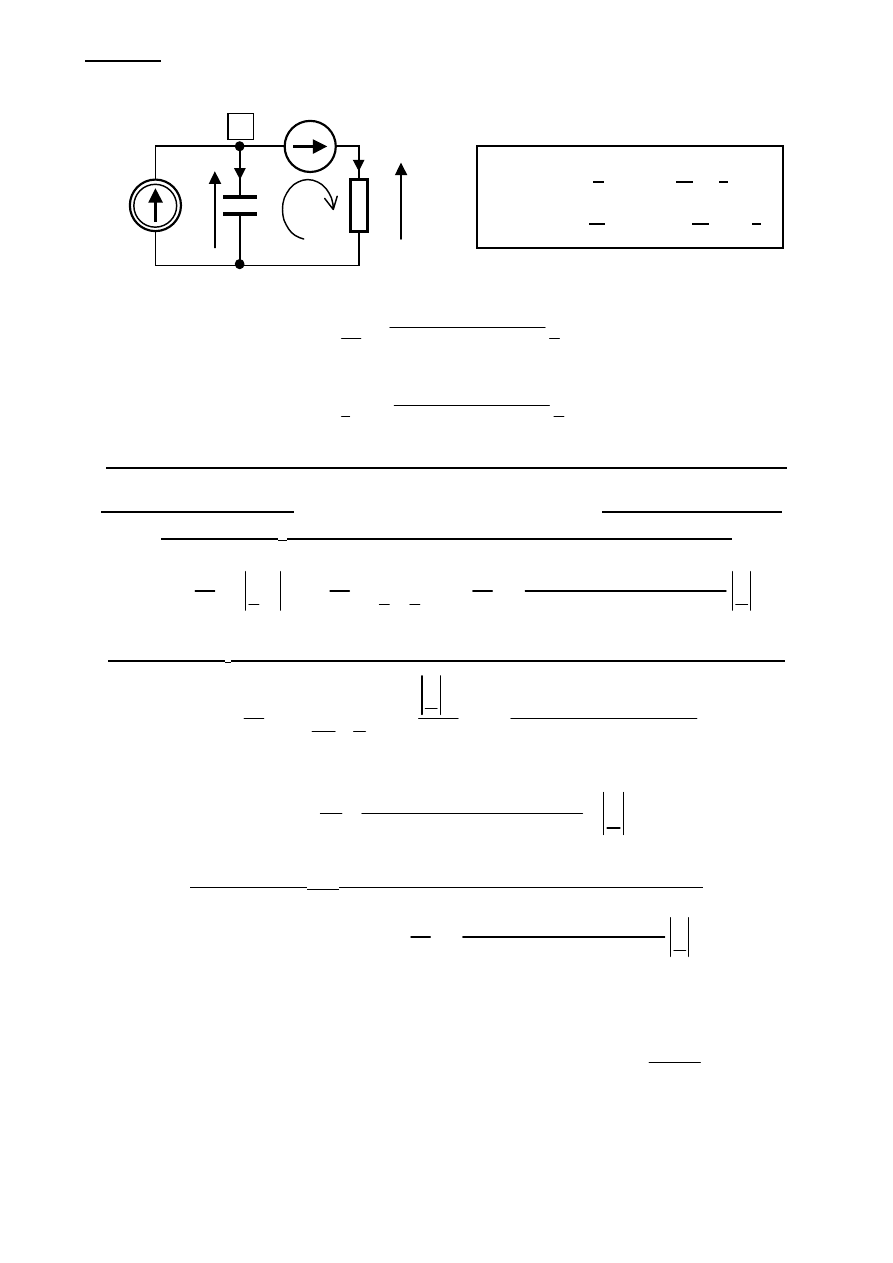
Przykład
W obwodzie SLS o schemacie pokazanym na rysunku dobrać parametr r ZNSP tak, aby
autonomiczne źródło prądu dostarczało do obwodu energię z taką samą mocą jak ZNSP.
j
R
r
⋅i
C
C
i
C
u
i
R
A
O
I
PPK w
A
: J = j
ωC
U + I
R
NPK O
I
: U + r
j
ωC
U =R I
R
⎪
⎪
⎩
⎪⎪
⎨
⎧
+
+
+
=
+
+
=
J
r)
C(R
jω
1
Cr
jω
1
I
J
r)
C(R
jω
1
R
U
R
Bilans mocy czynnych z jakimi w obwodzie przetwarzana jest energia elektryczna
(
dostarczanie energii )
P
J
+ P
ZNSP
= P
R
(
pobieranie energii )
Moc czynna P
R
z jaką opór R pobiera energię elektryczną z obwodu:
(
)
[
]
2
2
2
*
R
R
2
R
R
J
r)
C(R
ω
1
Cr
ω
1
R
2
1
I
I
R
2
1
I
R
2
1
P
+
+
+
=
=
=
Moc czynna P
J
z jaką autonomiczne źródło prądu j dostarcza energię do obwodu:
[ ]
]
r)
C(R
jω
1
R
Re[
2
J
J
U
Re
2
1
P
2
*
J
+
+
=
⋅
=
[
]
2
2
J
J
r)
C(R
ω
1
R
2
1
P
⋅
+
+
⋅
=
Moc czynna P
ZNSP
z jaką ZNSP dostarcza energię do obwodu:
(
)
[
]
2
2
2
J
R
ZNSP
J
r)
C(R
ω
1
Cr
ω
R
2
1
P
P
P
+
+
=
−
=
Rozwiązanie:
(
)
C
ω
1
r
:
1
Cr
ω
P
P
2
J
ZNSP
=
=
⇒
=
Dr inż. Jacek Czosnowski
Katedra Elektrotechniki AGH Wydział EAIiE
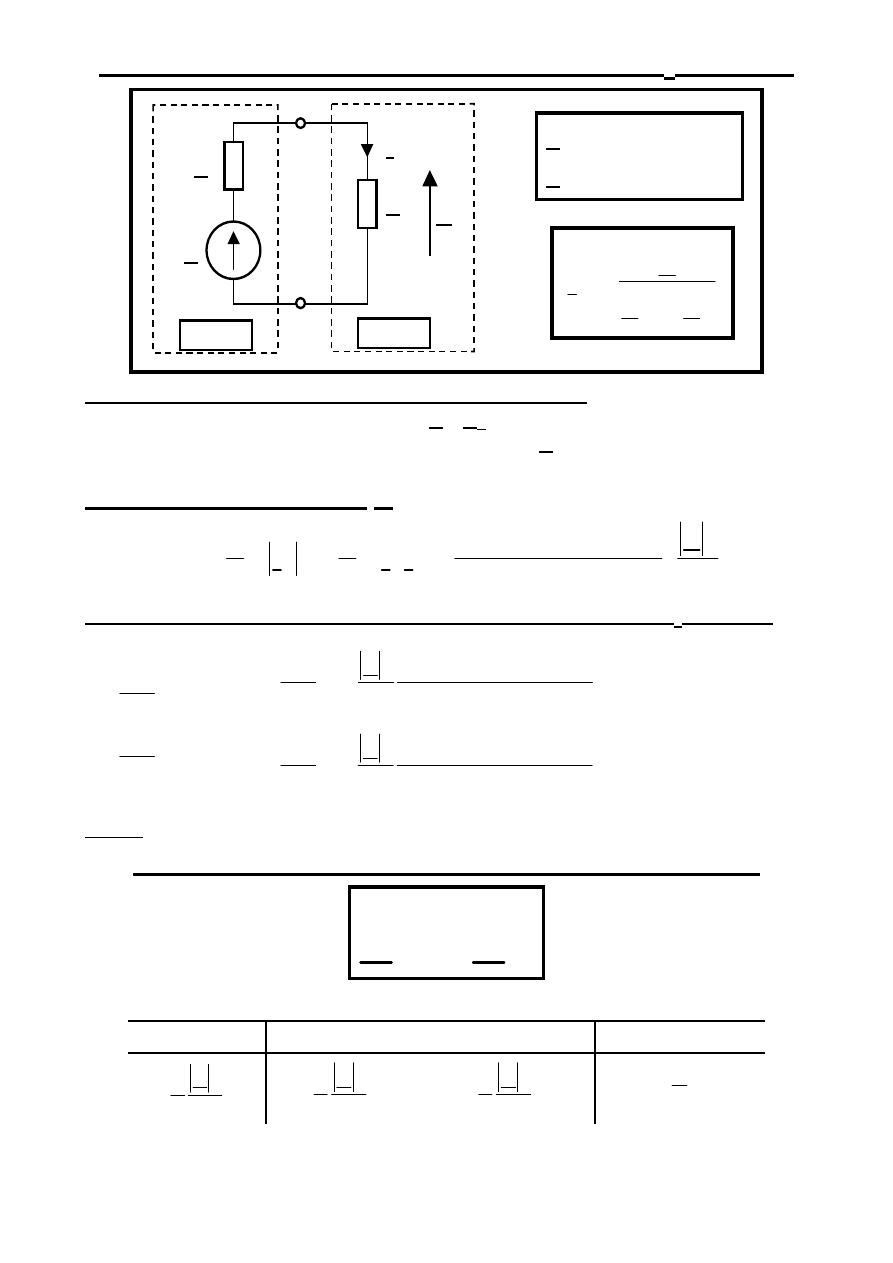
Dopasowanie energetyczne obciążenia Z
o
do NZE
NZE
OBC.
E
Z
w
Z
o
U
o
I
o
Z
w
= r + jx ; r > 0
Z
o
= R + jX ; R > 0
o
w
o
Z
Z
E
I
+
=
Problem dopasowania energetycznego NZE:
Dla znanych parametrów E, Z
w
= r + jx; r > 0, NZE
wyznaczyć taką impedancję obciążenia Z
o
= R + jX; R > 0,
aby pobierała ona energię z maksymalną mocą czynną P
o max
.
Moc czynna obciążenia Z
o
:
2
E
x)
(X
r)
(R
R
I
I
R
2
1
I
R
2
1
P
2
2
2
*
o
o
2
o
o
⋅
+
+
+
=
=
=
Warunki konieczne ekstremum funkcji dwu zmiennych P
o
= f(R,X):
(
)
(
)
(
) (
)
[
]
(
)
(
) (
)
[
]
⎩
⎨
⎧
−
=
=
⇒
⎪
⎪
⎩
⎪
⎪
⎨
⎧
=
+
+
+
+
−
=
∂
∂
=
+
+
+
+
+
−
+
=
∂
∂
⇒
⎪
⎪
⎩
⎪⎪
⎨
⎧
=
∂
∂
=
∂
∂
x
X
r
R
0
X
x
R
r
X
x
R
2
2
E
X
P
0
X
x
R
r
X
x
R
r
2
E
R
P
0
X
P
0
R
P
2
2
2
2
o
2
2
2
2
2
2
2
o
o
o
Zadanie
:
Sprawdzić czy w punkcie A(r,–x) funkcja P
o
= f(R,X) ma ekstremum i jeśli tak to jakie ?
Warunek dopasowania energetycznego NZE
*
o
Z
Z
w
=
Moce czynne w stanie dopasowania NZE
P
E
P
w
P
o max
= P
dysp NZE
η
E
= P
o max
/ P
E
R
E
4
1
2
R
E
8
1
2
R
E
8
1
2
2
1
Dr inż. Jacek Czosnowski
Katedra Elektrotechniki AGH Wydział EAIiE
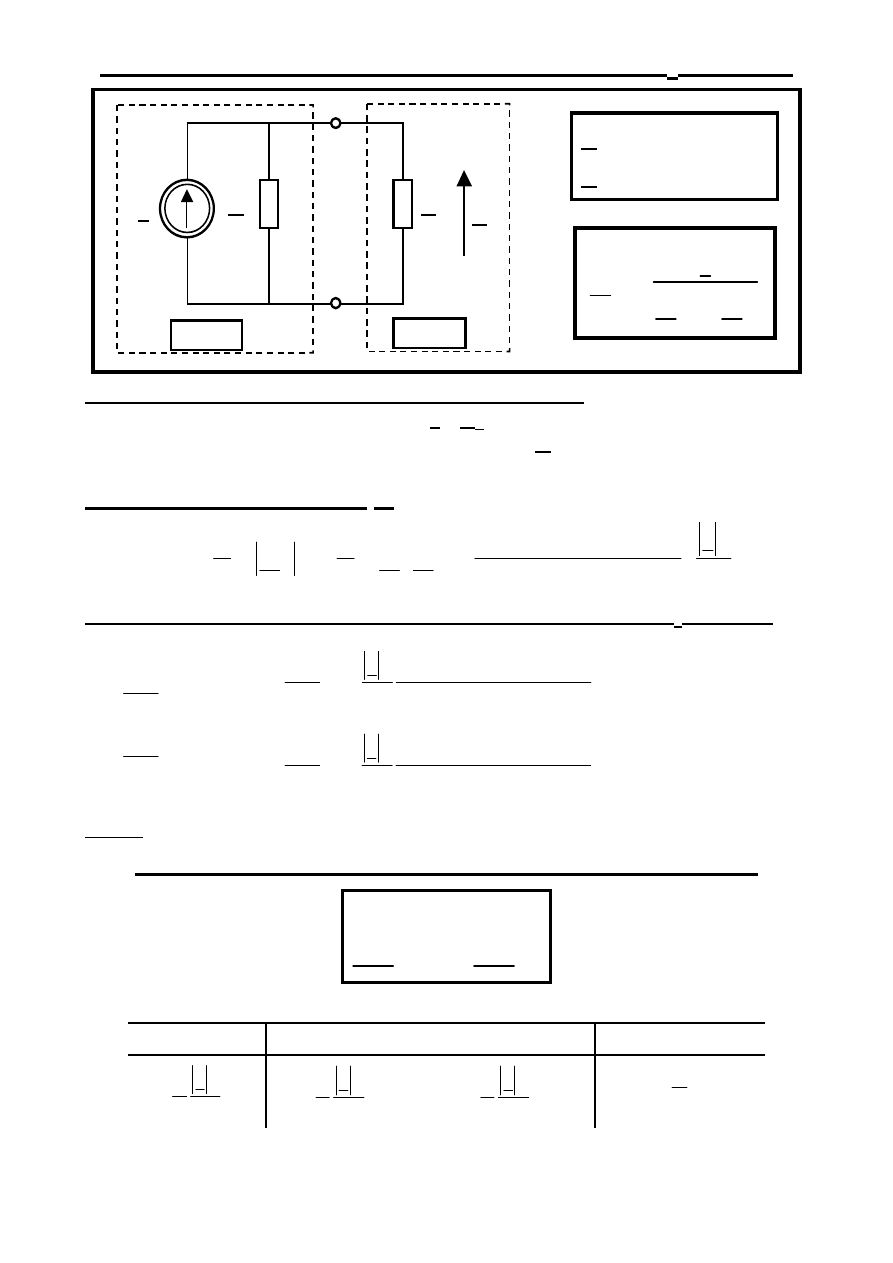
Dopasowanie energetyczne obciążenia Y
0
do PZE
PZE
OBC.
J
Y
w
Y
o
U
o
Y
w
= g + jb ; g > 0
Y
o
= G + jB ; G > 0
o
w
o
Y
Y
J
U
+
=
Problem dopasowania energetycznego PZE:
Dla znanych parametrów J, Y
w
= g + jb; g > 0, PZE
wyznaczyć taką admitancję obciążenia Y
o
= G + jB; G > 0,
aby pobierała ona energię z maksymalną mocą czynną P
o max
.
Moc czynna obciążenia Y
o
:
2
J
b)
(B
g)
(G
G
U
U
G
2
1
U
G
2
1
P
2
2
2
*
o
o
2
o
o
⋅
+
+
+
=
=
=
Warunki konieczne ekstremum funkcji dwu zmiennych P
o
= f(G,B):
(
)
(
)
(
) (
)
[
]
(
)
(
) (
)
[
]
⎩
⎨
⎧
−
=
=
⇒
⎪
⎪
⎩
⎪
⎪
⎨
⎧
=
+
+
+
+
−
=
∂
∂
=
+
+
+
+
+
−
+
=
∂
∂
⇒
⎪
⎪
⎩
⎪⎪
⎨
⎧
=
∂
∂
=
∂
∂
b
B
g
G
0
B
b
G
g
B
b
G
2
2
J
B
P
0
B
b
G
g
B
b
G
g
2
J
G
P
0
B
P
0
G
P
2
2
2
2
o
2
2
2
2
2
2
2
o
o
o
Zadanie
:
Sprawdzić czy w punkcie A(g,–b) funkcja P
o
= f(G,B) ma ekstremum i jeśli tak to jakie ?
Warunek dopasowania energetycznego PZE
*
o
Y
Y
w
=
Moce czynne w stanie dopasowania PZE
P
E
P
w
P
o max
= P
dysp PZE
η
E
=
P
o max
/ P
E
G
J
4
1
2
G
J
8
1
2
G
J
8
1
2
2
1
Dr inż. Jacek Czosnowski
Katedra Elektrotechniki AGH Wydział EAIiE
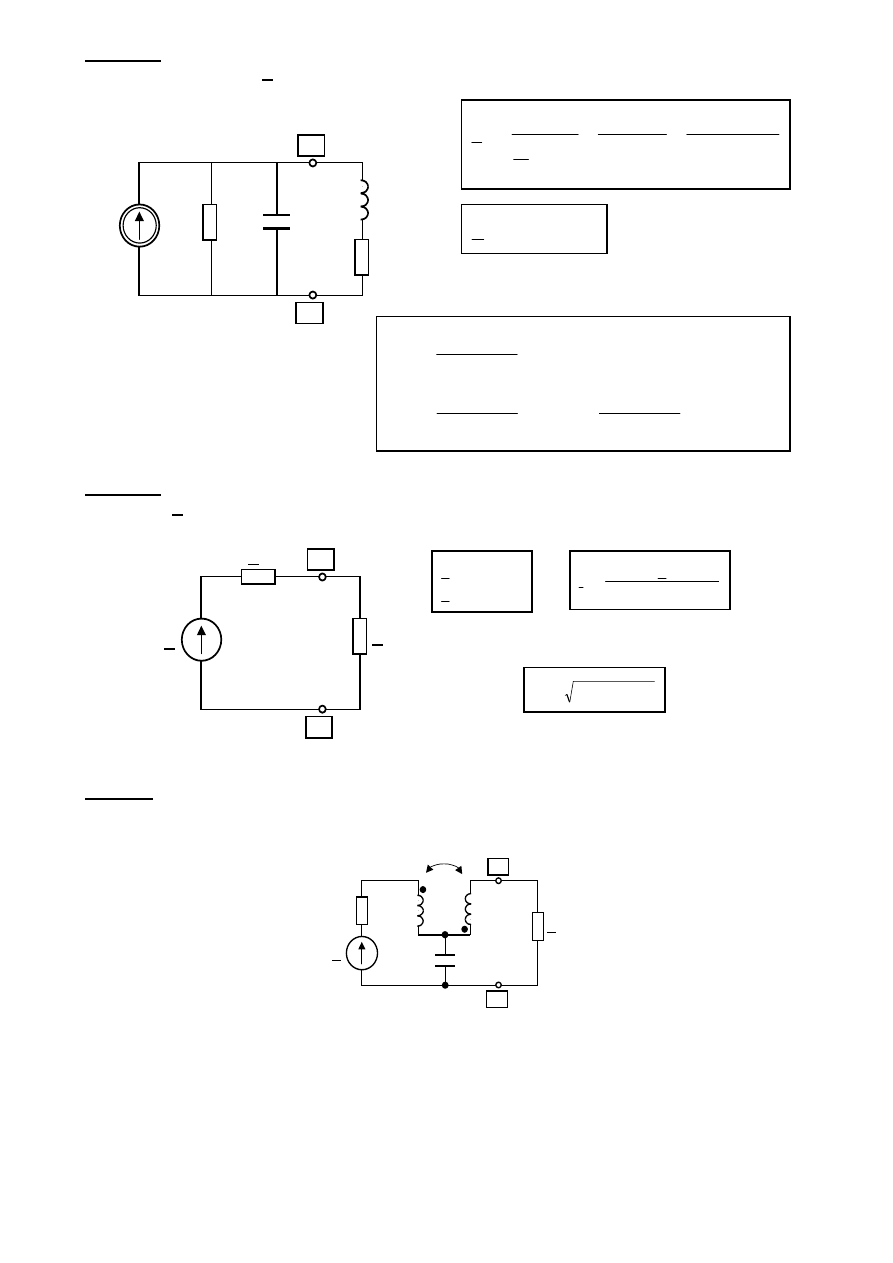
Przykład
W obwodzie SLS w SUS pokazanym na rysunku dobrać parametry R
o
, L
o
impedancji
obciążenia Z
o
tak, aby wystąpiło dopasowanie energetyczne.
j
R
C
R
o
L
o
A
B
(
)
(
)
2
RC
ω
1
RC
jω
1
R
RC
jω
1
R
C
jω
R
1
1
Z
+
−
=
+
=
+
=
w
L
jω
R
Z
o
o
+
=
(
)
(
)
(
)
⎪
⎪
⎩
⎪
⎪
⎨
⎧
=
⋅
+
=
⇒
+
=
+
=
RC
R
RC
RC
ω
1
R
L
RC
ω
1
C
R
ω
X
RC
ω
1
R
R
o
2
o
2
2
o
2
o
Przykład
W obwodzie SLS w SUS pokazanym na rysunku dobrać wartość R
o
impedancji obciążenia
Z
o
mającej określoną reaktancję X
o
≠ –X
w
tak, aby wystąpiło dopasowanie energetyczne.
E
Z
w
Z
o
A
B
o
o
o
jX
R
Z
jx
r
Z
+
=
+
=
w
)
j(X
)
r
(R
E
I
o
o
o
x
+
+
+
=
2
o
2
o
)
X
(
r
R
x
+
+
=
Zadanie
W obwodzie SLS w SUS pokazanym na rysunku dobrać impedancję obciążenia Z
o
tak, aby wystąpiło
dopasowanie energetyczne. Dane: R= 1 k
Ω, L
1
= 2 mH, L
2
= 3 mH, C= 1 nF, |M|= 1 mH,
ω= 10
6
[rad/s].
E
C
R
Z
o
A
B
L
2
L
1
M
Dr inż. Jacek Czosnowski
Katedra Elektrotechniki AGH Wydział EAIiE
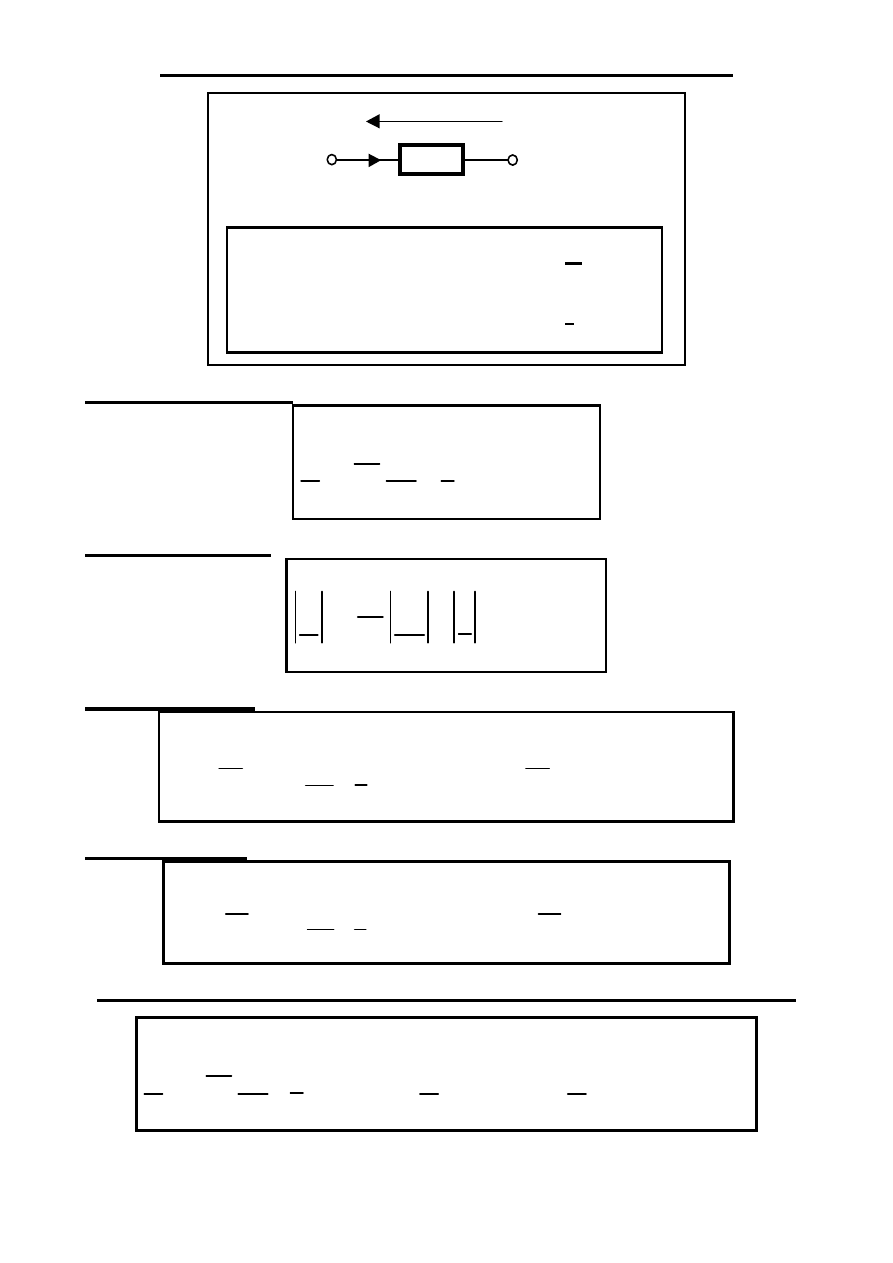
Moc zespolona, pozorna, czynna i bierna
u
(t)
i
(t)
u(t) = U
m
cos(
ωt + α ) = Re[ U⋅e
jωt
]
i(t) = U
m
cos(
ωt + α – ϕ ) = Re[ I⋅e
jωt
]
Moc zespolona
VA]
[
I
U
2
1
S
*
⋅
=
∆
Moc pozorna
VA]
[
I
U
2
1
S
⋅
=
∆
Moc czynna
ϕ
cos
I
U
2
1
W]
[
]
I
U
Re[
2
1
P
m
m
*
=
⋅
=
∆
Moc bierna
ϕ
sin
I
U
2
1
Var]
[
]
I
U
Im[
2
1
Q
m
m
*
=
⋅
=
∆
Związek między mocami w obwodach SLS w SUS
[ ]
[ ]
jQ
P
S
Im
j
S
Re
I
U
2
1
S
*
+
=
+
=
⋅
=
Dr inż. Jacek Czosnowski
Katedra Elektrotechniki AGH Wydział EAIiE
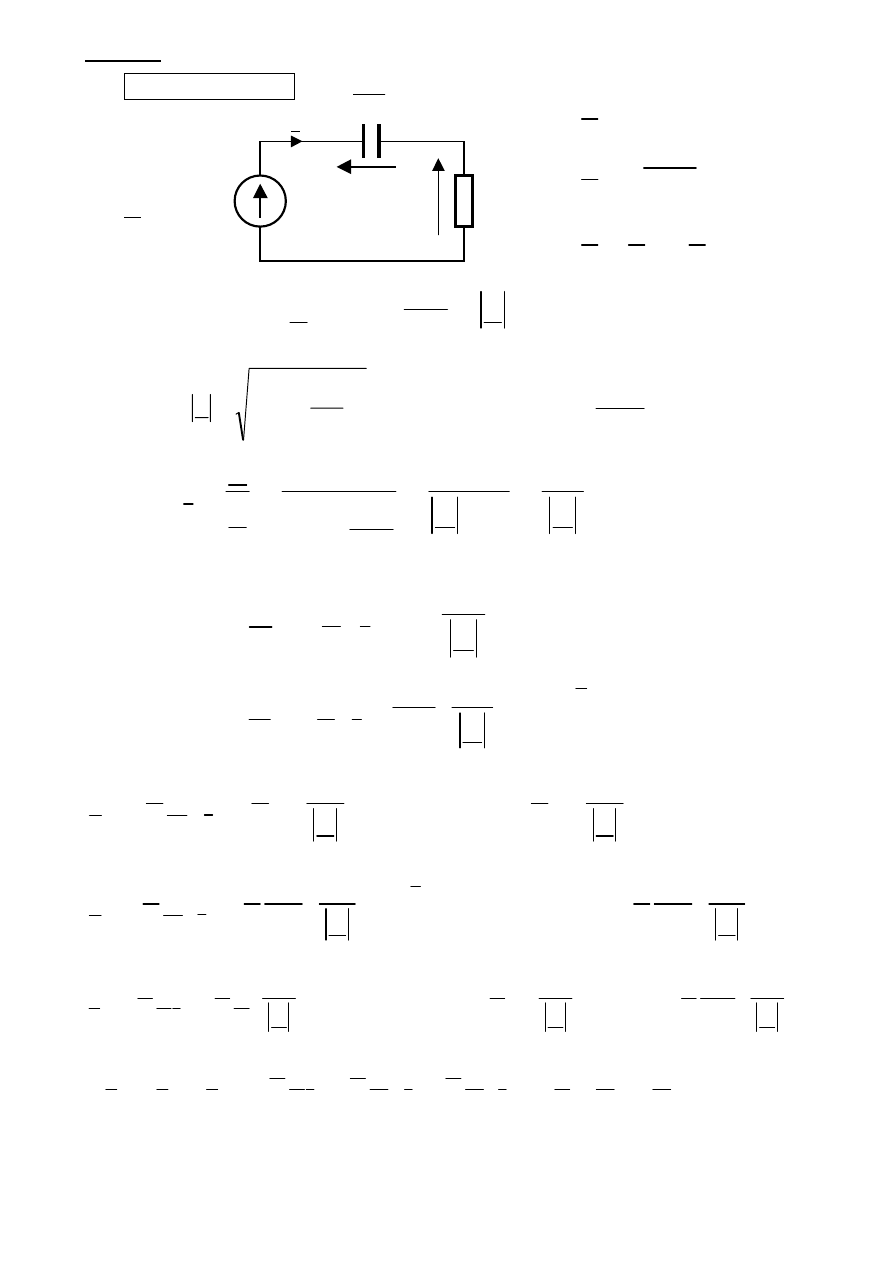
Przykład
Dla elementów tworzących obwód SLS w SUS pokazany na rysunku wyznaczyć wszystkie moce.
E= E
m
e
j
α
R
I
C
jω
1
[ ]
[ ]
C
R
C
R
Z
Z
Z
C
jω
1
Z
R
Z
+
=
Ω
=
Ω
=
Uwaga! Strzałkowanie !
[ ]
Ω
=
−
=
−
e
Z
C
ω
1
j
R
Z
j
ϕ
[ ]
[ ]
rad
RC
ω
1
arctg
;
C
ω
1
R
Z
2
2
−
=
Ω
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
+
=
ϕ
[ ]
A
e
E
e
e
E
C
ω
1
j
R
e
E
Z
E
I
)
j(α
m
j
jα
m
jα
m
ϕ
ϕ
+
−
=
=
−
=
=
Z
Z
[ ]
V
e
E
R
I
Z
U
)
j(α
m
R
R
ϕ
+
⋅
=
=
Z
[ ]
V
e
E
C
ω
1
I
Z
U
)
2
π
j(α
m
C
C
−
+
⋅
=
=
ϕ
Z
0
Q
,
E
R
2
1
P
E
R
2
1
I
U
2
1
S
R
2
m
R
2
m
*
R
R
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
=
⇒
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
=
=
Z
Z
2
m
C
C
2
π
j
2
m
*
C
C
E
C
ω
1
2
1
Q
,
0
P
e
E
C
ω
1
2
1
I
U
2
1
S
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
−
=
=
⇒
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
=
=
−
Z
Z
2
m
E
2
m
E
2
m
*
E
E
C
ω
1
2
1
Q
,
E
R
2
1
P
E
2
1
I
E
2
1
S
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
=
⇒
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
=
=
Z
Z
Z
Z
)
!
NPK
(
U
U
E
I
U
2
1
I
U
2
1
I
E
2
1
S
S
S
C
R
*
C
*
R
*
C
R
E
+
=
⇔
+
=
⇔
+
=
Dr inż. Jacek Czosnowski
Katedra Elektrotechniki AGH Wydział EAIiE
Document Outline