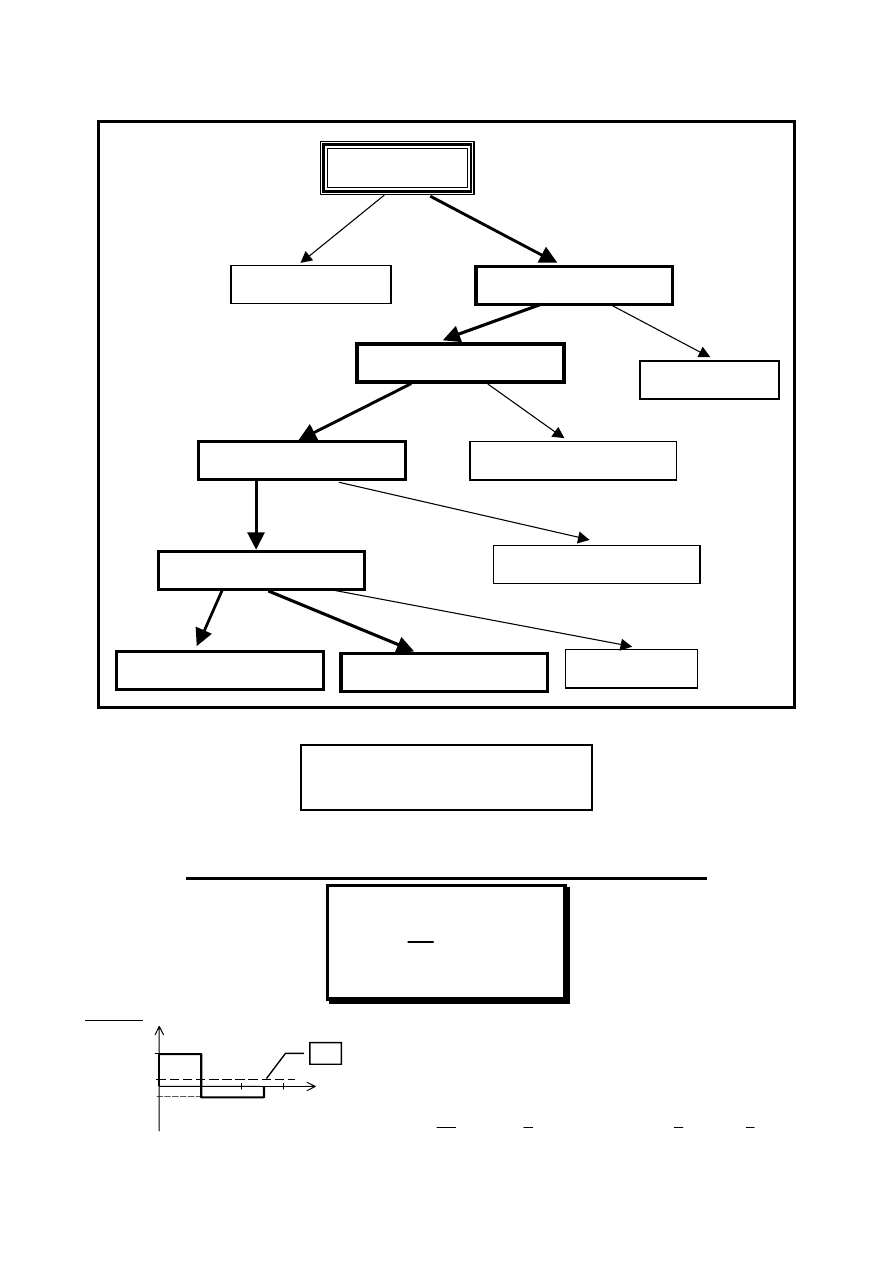
Sygnały
Sygnały f(t)
Stałe
Zmienne f(t)
≠ const
Okresowe
Nieokresowe
Pulsujące
Zachowujące znak
Zmieniające znak
Inne
Odkształcone
SINUSOIDALNE
Inne
Sygnał okresowy f(t)
)
(
)
(
0
T
t
f
t
f
t
T
+
=
∀
∃
>
Wartość średnia sygnału okresowego f(t)
∫
+
=
T
t
t
def
t
t
f
T
F
0
0
d
)
(
1
śr
Przykład Ob
liczyć wartość średnią nieskończonego ciągu impulsów o kształcie pokazanym na rysunku.
1
2,5
t [s]
f(t)
+3
–1
T= 2,5 [s]
0,6
F
śr
(
)
6
,
0
5
3
5
,
1
3
5
2
)d
1
(
3)d
5
,
2
0
,
1
=
=
−
=
⎟
⎟
⎠
⎞
−
+
∫
t
t
(
5
2
d
)
(
5
,
2
1
0
,
1
0
5
,
2
0
śr
⎜
⎜
⎝
⎛
+
=
=
∫
∫
t
t
f
F
Dr inż. Jacek Czosnowski
Katedra Elektrotechniki AGH Wydział EAIiE
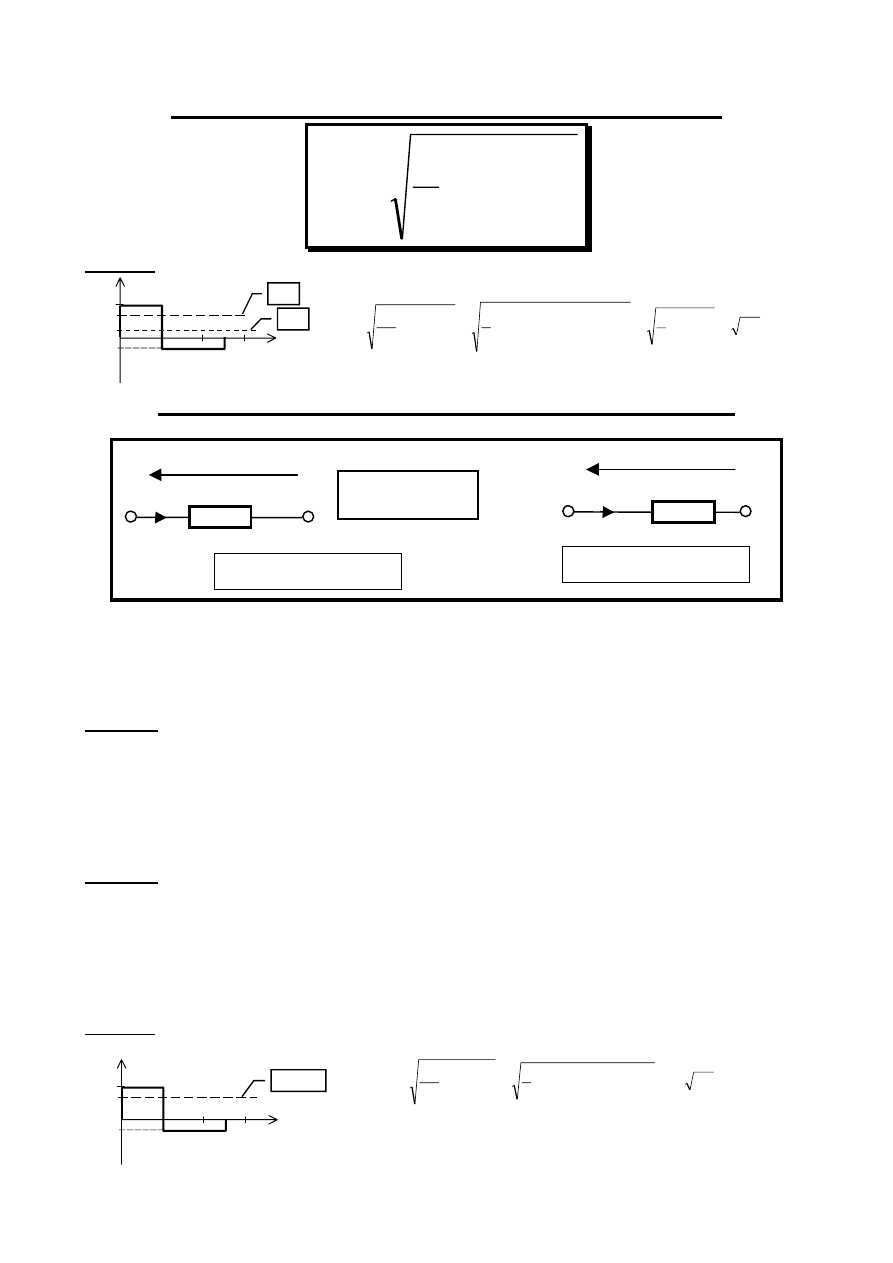
Wartość skuteczna sygnału okresowego f(t)
∫
+
=
T
t
t
def
t
t
f
T
F
0
0
d
)
(
1
2
sk
Przykład
Obliczyć wartość skuteczną nieskończonego ciągu impulsów o kształcie pokazanym na rysunku.
1
2,5
t [s]
f(t)
+3
–1
T= 2,5 [s]
0,6
F
sk
F
śr
2,05
Interpretacja energetyczna wartości skutecznej
i(t)
u(t)
R
i
(t)= i( t + T )
u
(t)= R
⋅i( t + T )
U= U
sk
R
I= I
sk
Prąd okresowy
Prąd stały
Energia wydzielona w oporze R w przedziale czasu t
0
≤ t
≤ t
0
+ T:
T
I
R
d
)
(
R
d
)
(
)
(
T)
,
(
2
sk
T
2
T
0
0
R
0
0
0
0
∫
∫
+
+
=
=
=
+
t
t
t
t
t
t
i
t
t
i
t
u
t
t
w
Wniosek: Energia wydzielona w oporze R w czasie jednego okresu T prądu
okresowego
i(t)= i( t + T ) jest równa energii, jaką w tym samym oporze i w tym samym
czasie wydzieli prąd stały o wartości I= I
sk
.
T
U
G
d
)
(
G
d
)
(
)
(
T)
,
(
2
sk
T
2
T
0
0
R
0
0
0
0
∫
∫
+
+
=
=
=
+
t
t
t
t
t
t
u
t
t
i
t
u
t
t
w
Wniosek: Energia wydzielona w oporze R w czasie jednego okresu T napięcia
okresowego u(t)= u( t + T ) jest równa energii, jaką w tym samym oporze i w
tym samym czasie wydzieli napięcie stałe o wartości U= U
sk
.
Przykład
Wyznaczyć wartość napięcia stałego dającego w rezystorze R taki sam skutek energetyczny jak napięcie
okresowe pokazane na rysunku
.
1
2,5
t [s]
u(t) [V]
+30
–10
T= 2,5 [s]
20,5
U= U
sk
(
)
05
,
2
2
,
4
5
,
1
9
5
2
d
)
1
(
d
3)
(
5
2
5
,
2
0
,
1
2
0
,
1
0
2
=
=
+
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
+
+
=
∫
∫
t
t
t
d
)
(
5
,
2
1
5
,
2
0
2
sk
=
∫
t
f
F
(
)
V
5
,
20
2
,
4
10
5
,
1
)
10
(
1
30
5
2
2
2
=
=
⋅
−
+
⋅
d
)
(
5
,
2
1
5
,
2
0
2
=
=
∫
t
t
u
U
sk
Dr inż. Jacek Czosnowski
Katedra Elektrotechniki AGH Wydział EAIiE
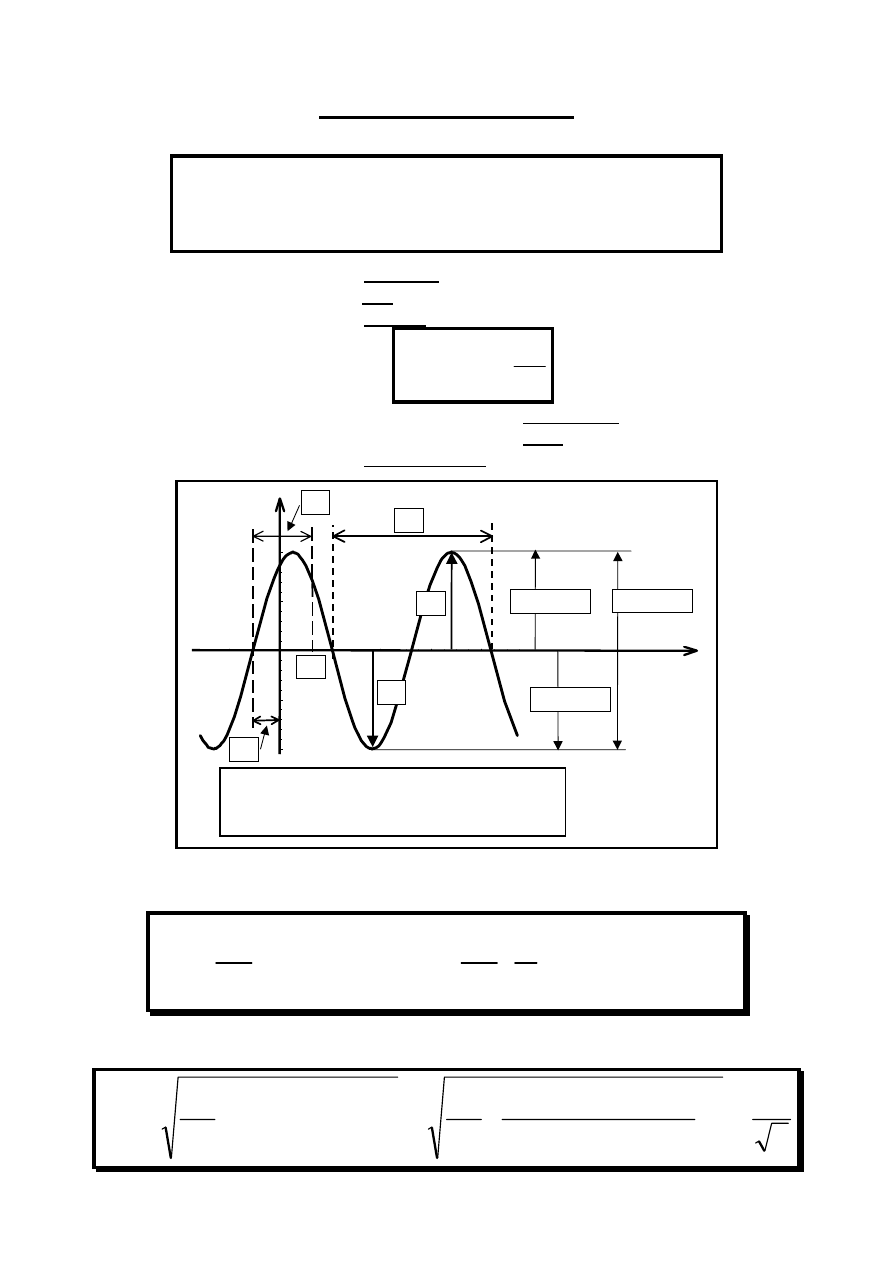
Sygnał sinusoidalny
Przemienny pulsujący ( zmienia znak ) okresowy określony dla t
∈ (–∞, +∞ ).
(
)
ϕ
ω
α
+
⋅
⎭
⎬
⎫
⎩
⎨
⎧
⋅
=
⎭
⎬
⎫
⎩
⎨
⎧
⋅
=
t
A
t
A
t
f
m
m
cos
sin
)
(
cos
sin
)
(
A
m
– amplituda sygnału;
α(t)= ω⋅t + ϕ – faza sygnału w [rad] lub [
o
];
ω
– pulsacja sygnału w [rad/s] lub [
o
/s] – przy czym:
T
π
2
f
π
2
ω
=
=
gdzie f [Hz] – częstotliwość sygnału,
T [s] – okres sygnału;
ϕ
– faza początkowa sygnału w [rad] lub [
o
];
-2
2
4
6
8
-2
-1
1
2
ϕ
A
m
A
m
ω
t [rad]
2π
f(t)
α
(t)
(
)
ϕ
ω
α
+
⋅
⎭
⎬
⎫
⎩
⎨
⎧
⋅
=
⎭
⎬
⎫
⎩
⎨
⎧
⋅
=
t
A
t
A
t
f
m
m
cos
sin
)
(
cos
sin
)
(
A
pp
= 2A
m
A
max
= +A
m
A
min
= – A
m
ω
t
Wartość średnia sygnału sinusoidalnego
0
)
ω
sin(
ω
1
T
d
)
ω
cos(
T
T
0
T
0
śr
=
⎥⎦
⎤
⎢⎣
⎡
+
=
+
=
∫
ϕ
ϕ
t
A
t
t
A
F
m
m
Wartość skuteczna sygnału sinusoidalnego
2
d
2
)
2
ω
2
cos(
1
T
d
)
ω
(
cos
T
T
0
T
0
2
sk
m
m
m
A
t
t
A
t
t
A
F
=
+
+
=
+
=
∫
∫
ϕ
ϕ
Dr inż. Jacek Czosnowski
Katedra Elektrotechniki AGH Wydział EAIiE
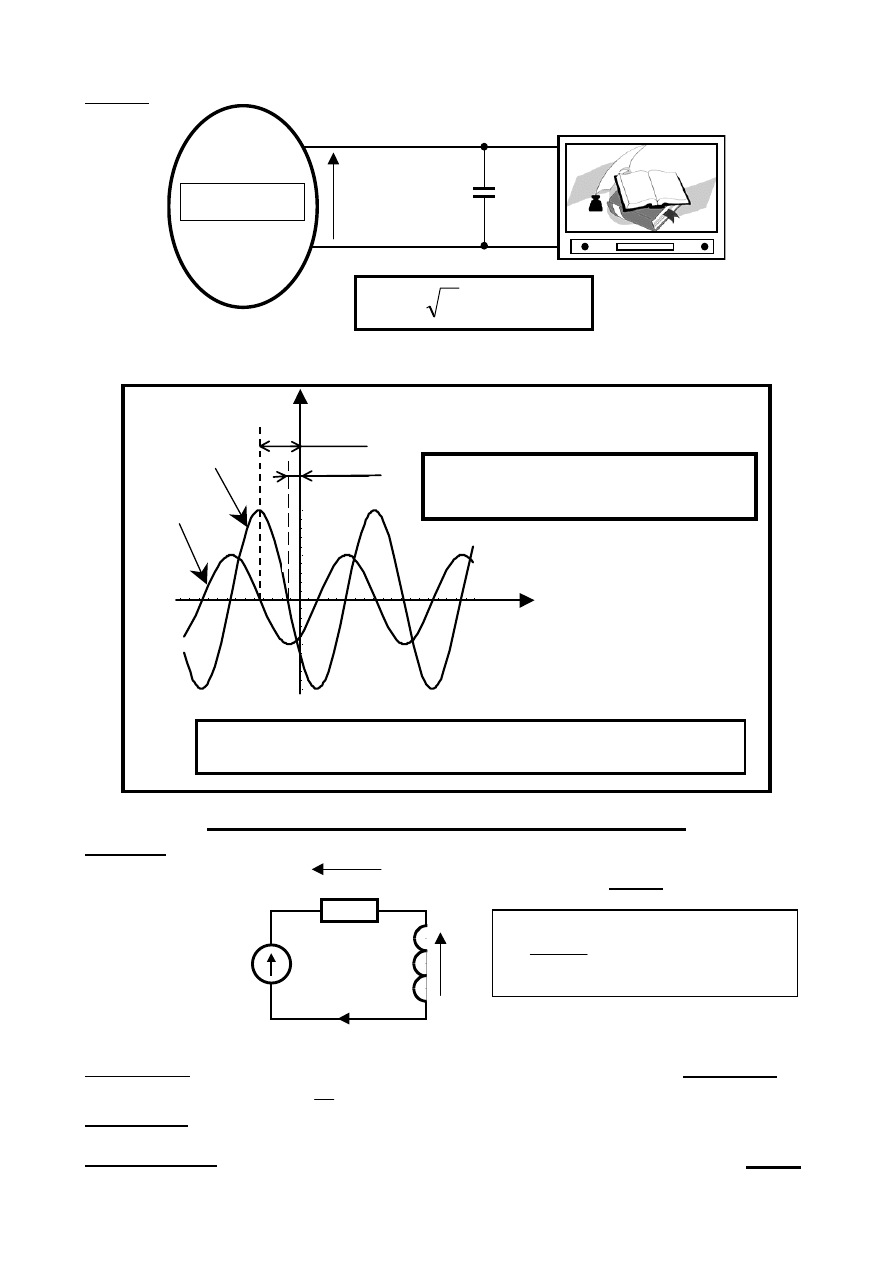
Przykład
Jakie napięci pracy powinien mieć kondensator filtrujący włączony równolegle do sieci zasilającej odbiornik TV
System
elektroenergetyczny
C
U
sk
= 230 V
V
U
U
sk
m
325
2
=
=
Czyli, 325 < U
C
= 400 V – minimalne napięcie pracy kondensatora C ( w praktyce, lepiej U
C
= 630 V ).
Przesunięcie fazowe sygnałów sinusoidalnych
-5
-2.5
2.5
5
7.5
-2
-1
1
2
ϕ
2
ω t
f
(
t)
∆α = α
2
(t) –
α
1
(t) = (
ω
t +
ϕ
2
) – (
ω
t +
ϕ
1
) =
ϕ
2
–
ϕ
1
f
1
(t)
f
2
(t)
ϕ
1
f
1
(t) = A
1
sin
α
1
(t) = A
1
sin(
ω
t + ϕ
1
)
f
2
(t) = A
1
sin
α
2
(t) = A
2
sin(
ω
t + ϕ
2
)
Stan Ustalony Sinusoidalny (SUS)
Przykład
Przyłączenie napięcia sinusoidalnego do dwójnika RL.
R
L
e(t)
= E
m
sin
ωt
i(t)
t
i
t
t
i
ω
sin
E
R
d
)
(
d
L
m
=
+
NPK
Rozwiązanie
i(t) = i
p
(t) + i
u
(t)
:
dla t
Æ
∞
całka ogólna:
t
e
t
i
GL
1
p
C
)
(
−
=
;
i
p
(t)
Æ
0
(
)
ϕ
+
=
+
=
t
t
t
t
i
ω
sin
K
ω
cos
K
ω
sin
K
)
(
2
1
u
;
i
u
(t)
Æ
SUS
całka szczególna:
Dr inż. Jacek Czosnowski
Katedra Elektrotechniki AGH Wydział EAIiE
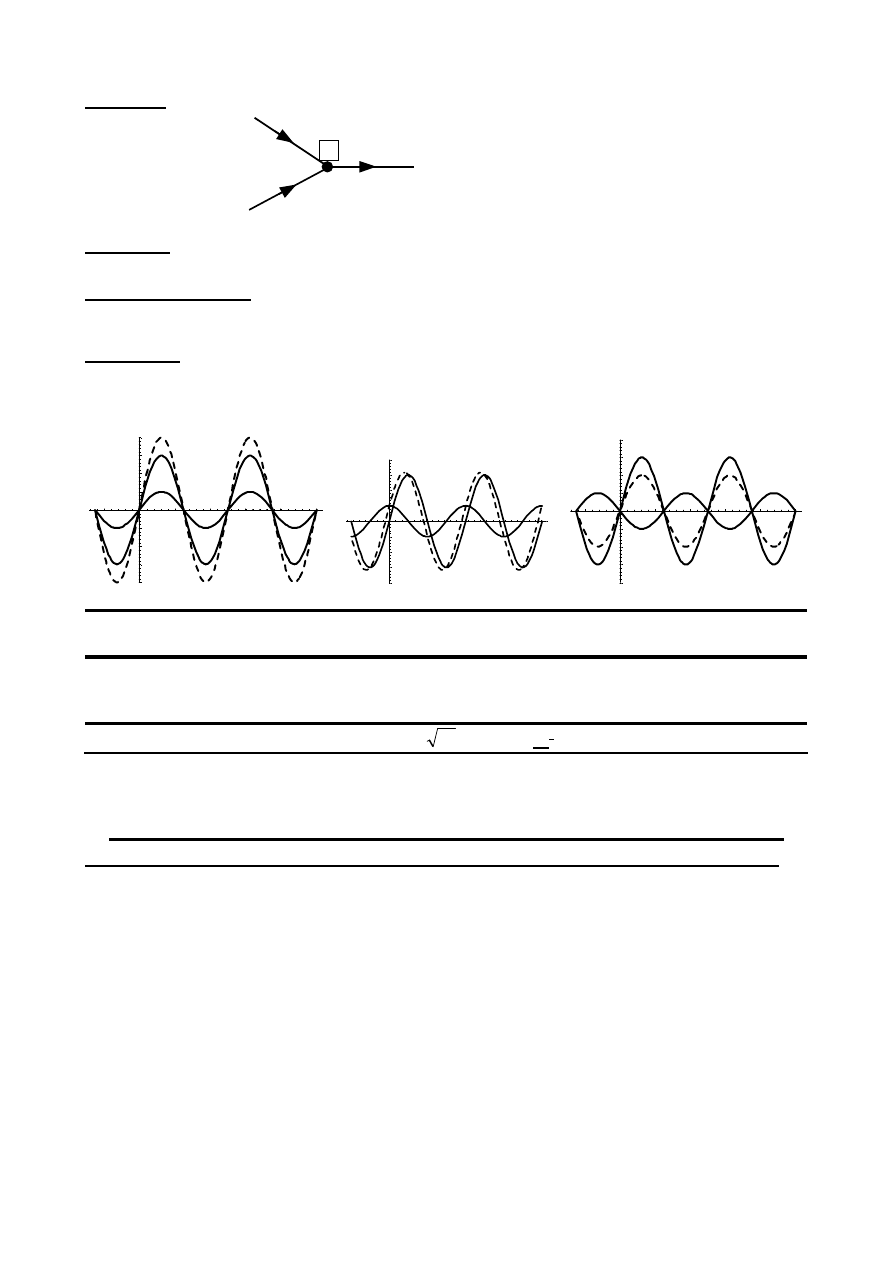
Przykład
Rozpływ prądów zgodnie z PPK
i
1
(t)
i
2
(t)
i
(t)
PPK w: i(t) = i
1
(t) + i
2
(t)
w
Prąd stały:
i
1
(t) = 3 A, i
2
(t) = 1 A
Æ
i(t) = i
1
(t) + i
2
(t) = 4 A.
( i po problemie ! )
Prądy sinusoidalne:
i
1
(t) = I
1m
sin
(
ωt + ϕ
1
),
i
2
(t) = I
2m
sin
(
ωt + ϕ
2
).
Dla danych:
I
1m
= 3 A,
I
2m
= 1 A,
można tylko stwierdzić, że dla przesunięcia fazy
∆α = 0: I
m
= +
4 A,
dla przesunięcia fazy
∆α = π: I
m
= +
2 A
i z tego:
+
2
≤ I
m
≤ +
4.
( i tu jest problem ! )
-2.5
2.5
5
7.5
10
12.5
-4
-3
-2
-1
1
2
3
4
-2.5
2.5
5
7.5
10
12.5
-2.5
2.5
5
7.5
10
12.5
-4
-3
-2
-1
1
2
3
4
-4
-3
-2
-1
1
2
3
4
Cały czas obowiązuje PPK dla węzła w:
i(t) = i
1
(t) + i
2
(t)
∆α = 0
∆α = 90
0
∆α = 180
0
sygnały w fazie
pośrednie przesunięcie fazowe
sygnały w przeciwfazie
i
1
(t) = 3 sin
(
ωt )
i
1
(t) = 3 sin
(
ωt )
i
1
(t) = 3 sin
(
ωt )
i
2
(t) = 1 sin
(
ωt )
i
2
(t) = 1 sin
(
ωt + π/2)
i
2
(t) = 1 sin
(
ωt + π)
i(t) = 4 sin
(
ωt )
i(t)
≈
10
sin
(
ωt +
18
0
)
i(t) = 2 sin
(
ωt )
Metoda bezpośredniej analizy obwodów znajdujących się w SUS jest „nieco” uciążliwa, aczkolwiek
wykonalna, i w związku z tym powstała metoda symboliczna oparta na liczbach zespolonych.
Kiedy w obwodzie jest „Stan Ustalony Sinusoidalny”
Obwód SLS znajduje się w stanie sinusoidalnym ustalonym ( SUS ) jeśli:
1. wszystkie obwodowe funkcje wymuszające ( napięcia e
n
(t) i prądy j
p
(t)
autonomicznych źródeł wymuszających ) mają przebieg sinusoidalny o
jednakowej pulsacji
ω;
2. autonomiczne źródła wymuszające działają w obwodzie nieskończenie długo – co
oznacza, że składowe przejściowe ( całki ogólne ), związane z zaistniałą w obwodzie
w chwili początkowej t
0
komutacją oraz początkowymi energiami w
C
(t
0
) i w
L
(t
0
)
zgromadzonymi w konserwatywnych elementach C i L, wszystkich obwodowych
funkcji gałęziowych zanikły do zera;
3. wszystkie obwodowe funkcje gałęziowe ( napięcia e
g
(t) i prądy j
g
(t) gałęzi ) mają
przebieg sinusoidalny o jednakowej pulsacji
ω – oznacza to brak w obwodzie
półdegeneracji w postaci przekrojów pojemnościowych ( złożonych z pojemności i
autonomicznych źródeł prądu ) i oczek indukcyjnych ( złożonych z indukcyjności i
autonomicznych źródeł napięcia )
Dr inż. Jacek Czosnowski
Katedra Elektrotechniki AGH Wydział EAIiE
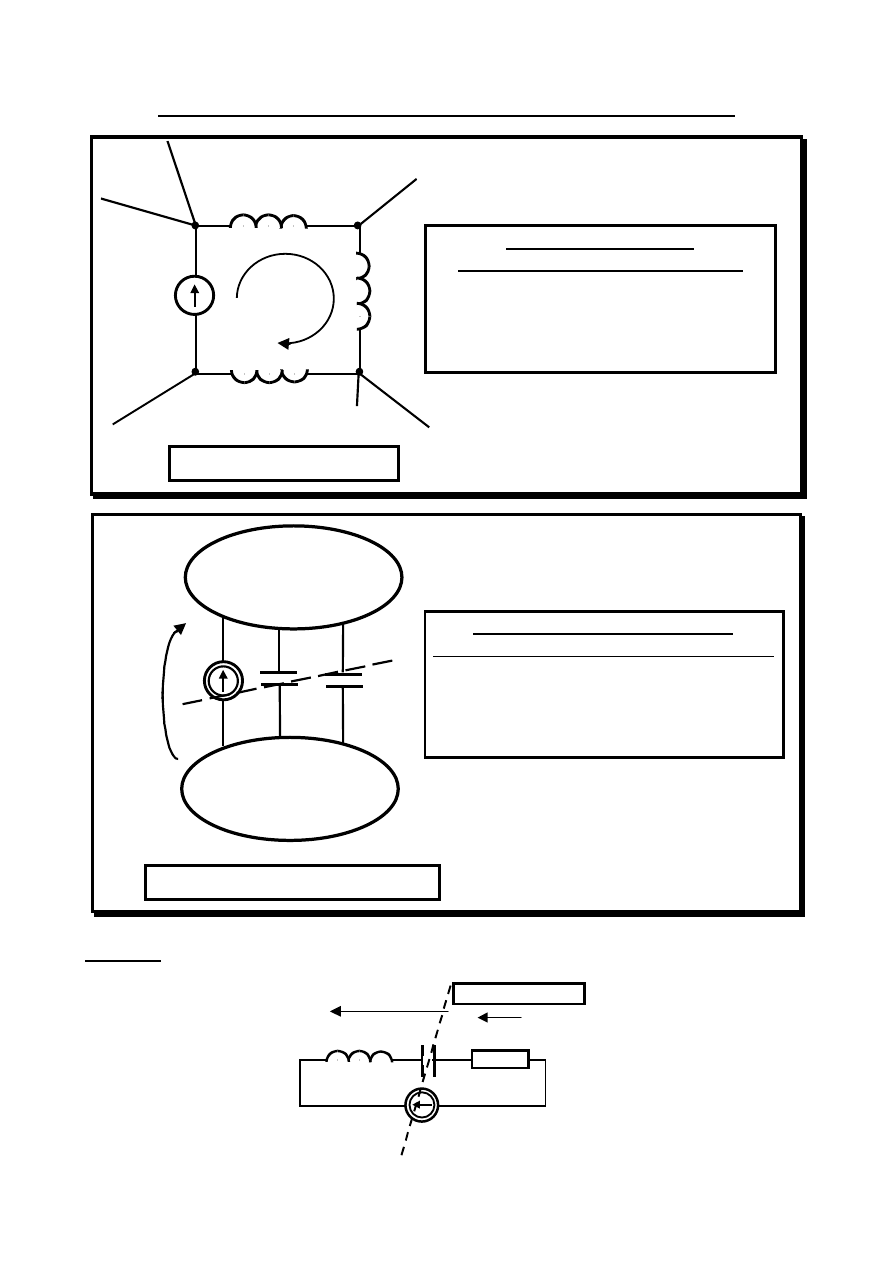
Półdegeneracje czyli przekroje „C” i oczka „L”
L
2
L
1
L
3
e(t)
I= ?
Oczko indukcyjne
W oczku indukcyjnym
może płynąć dowolny stały prąd I,
powodując, że prądy gałęziowe
nie będą miały przebiegu sinusoidalnego,
natomiast napięcia gałęziowe będą miały
przebieg sinusoidalny.
j(t)
U= ?
Przekrój pojemnościowy
C
1
C
2
Na przekroju pojemnościowym
może panować dowolne stałe napięcie U,
powodując, że napięcia gałęziowe
nie będą mały przebiegu sinusoidalnego,
natomiast prądy gałęziowe będą miały
przebieg sinusoidalny.
Obwód I
Obwód II
Przykład
W obwodzie pokazanym na rysunku, wyznaczyć przebieg napięcia u
LC
(
t
).
j(t)= J
sin(
ω
t)
⋅1(t)
C
R
L
u
LC
(t)=?
PRZEKRÓJ „C”
Dr inż. Jacek Czosnowski
Katedra Elektrotechniki AGH Wydział EAIiE
( )
(
)
)
(
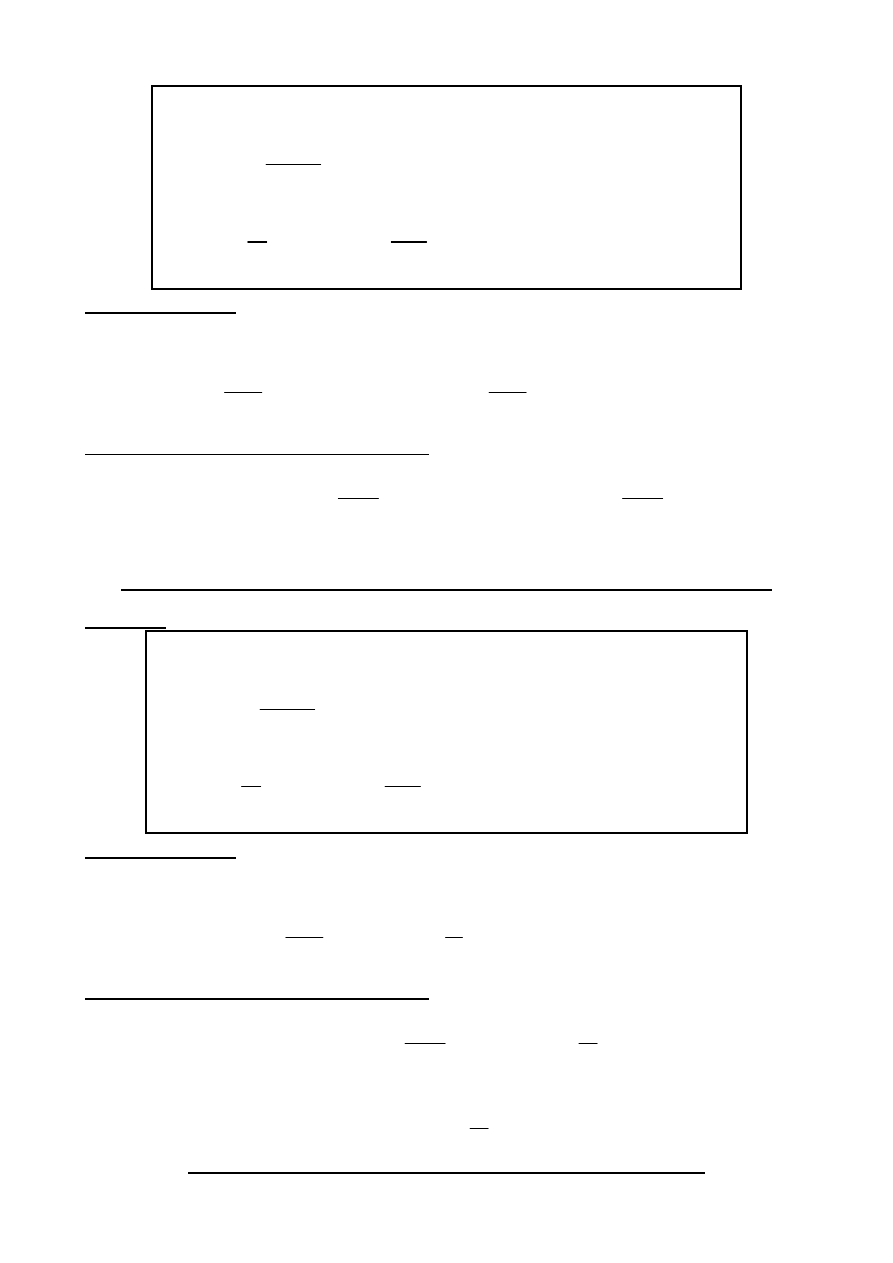
ω
cos
1
J
Cω
1
d
)
(
C
1
)
(
)
(
ω
sin
LJ
)
(
ω
cos
J
Lω
d
)
(
d
L
)
(
)
(
ω
sin
RJ
)
(
m
0
C
m
m
L
m
R
t
t
j
t
u
t
t
t
t
t
t
j
t
u
t
t
t
u
t
1
δ
1
1
⋅
−
⋅
⎟
⎠
⎞
⎜
⎝
⎛
=
=
⋅
+
⋅
⋅
=
=
⋅
⋅
=
∫
τ
τ
Pełna odpowiedź:
[
]
)
(
ω
sin
LJ
)
(
Cω
1
J
)
(
ω
cos
Cω
1
Lω
J
)
(
)
(
)
(
m
m
m
C
L
LC
t
t
t
t
t
t
u
t
u
t
u
δ
1
1
⋅
+
⎥
⎦
⎤
⎢
⎣
⎡
⋅
⎟
⎠
⎞
⎜
⎝
⎛
+
⎥
⎦
⎤
⎢
⎣
⎡
⋅
⋅
⎟
⎠
⎞
⎜
⎝
⎛
−
=
=
+
=
Odpowiedź w stanie ustalonym ( t
Æ
∞)
:
)
(
U
)
(
ω
cos
U
)
(
Cω
1
J
)
(
ω
cos
Cω
1
Lω
J
)
(
(LC)0
(LC)m
m
m
LC
t
t
t
t
t
t
t
u
1
1
1
1
⋅
+
⋅
=
=
⎥
⎦
⎤
⎢
⎣
⎡
⋅
⎟
⎠
⎞
⎜
⎝
⎛
+
⎥
⎦
⎤
⎢
⎣
⎡
⋅
⋅
⎟
⎠
⎞
⎜
⎝
⎛
−
=
Przykład
To samo co w poprzednim przykładzie ale dla wymuszenia j(t)= J
m
cos
ωt ⋅1(t)
( )
)
(
ω
sin
J
Cω
1
d
)
(
C
1
)
(
)
(
ω
cos
LJ
)
(
ω
sin
J
Lω
d
)
(
d
L
)
(
)
(
ω
cos
RJ
)
(
m
0
C
m
m
L
m
R
t
t
j
t
u
t
t
t
t
t
t
j
t
u
t
t
t
u
t
1
δ
1
1
⋅
⋅
⎟
⎠
⎞
⎜
⎝
⎛
=
=
⋅
+
⋅
⋅
−
=
=
⋅
⋅
=
∫
τ
τ
Pełna odpowiedź:
[
]
)
(
ω
cos
LJ
)
(
2
π
ω
cos
Cω
1
Lω
J
)
(
)
(
)
(
m
m
C
L
LC
t
t
t
t
t
u
t
u
t
u
δ
1
⋅
+
⎥
⎦
⎤
⎢
⎣
⎡
⋅
⎟
⎠
⎞
⎜
⎝
⎛
+
⋅
⎟
⎠
⎞
⎜
⎝
⎛
−
=
=
+
=
Odpowiedź w stanie ustalonym ( t
Æ
∞)
:
)
(
2
π
ω
cos
U
)
(
2
π
ω
cos
Cω
1
Lω
J
)
(
(LC)m
m
LC
t
t
t
t
t
u
1
1
⋅
⎟
⎠
⎞
⎜
⎝
⎛
+
=
=
⎥
⎦
⎤
⎢
⎣
⎡
⋅
⎟
⎠
⎞
⎜
⎝
⎛
+
⋅
⎟
⎠
⎞
⎜
⎝
⎛
−
=
Dr inż. Jacek Czosnowski
Katedra Elektrotechniki AGH Wydział EAIiE