Sygnał sinusoidalny, a liczby zespolone

Wzór Eulera: e

j

α

= cos

α + j

sin

α

gdzie:

1

j

−

=

∆

; jedno z dwu rozwiązań równania: j

2

+ 1 = 0.

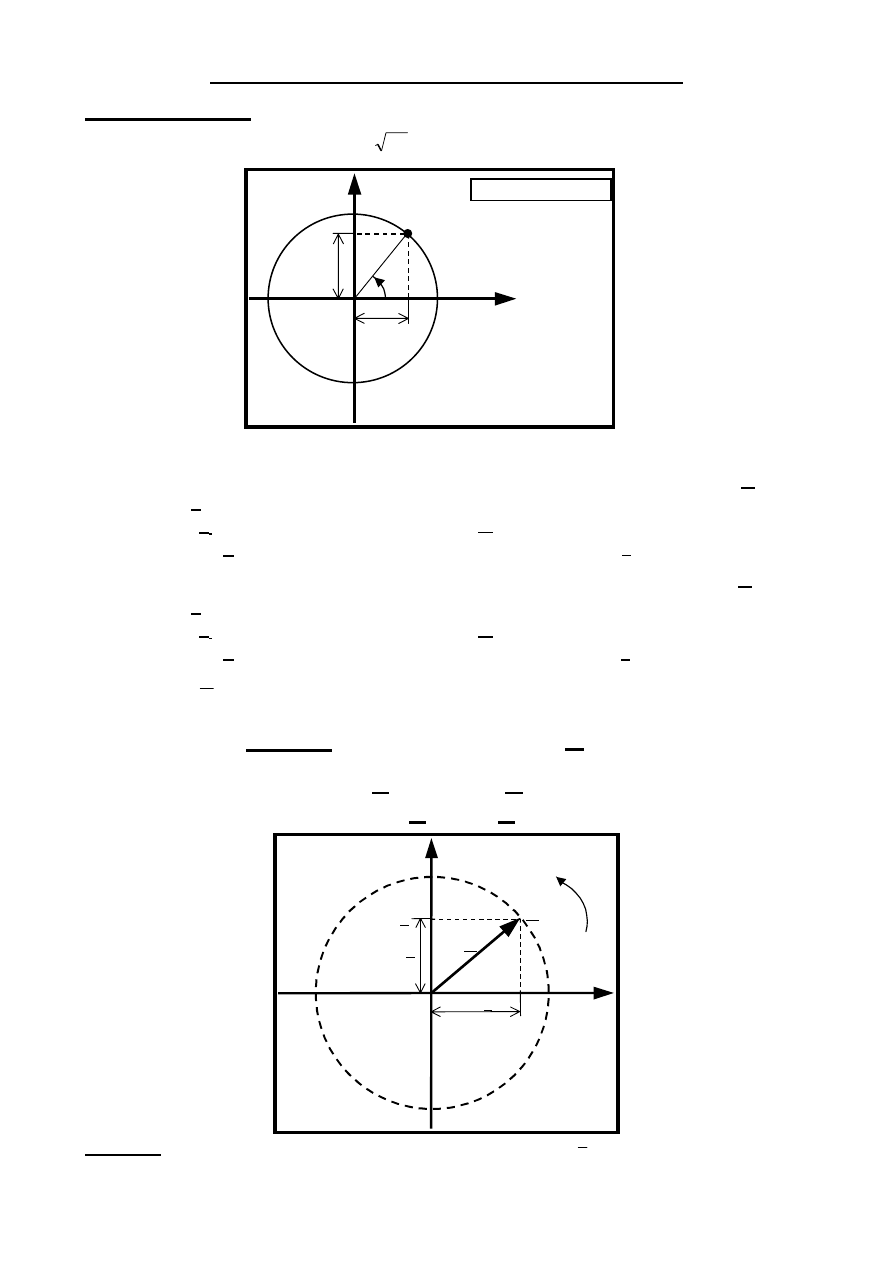
z

α

im

re

+1

–1

+j

–j

Płaszczyzna zespolona

Re z

Im

z

s(t) = S

m

cos(

ωt + α) = Re[ S

m

e

j(

ωt + α)

] = Re[ (S

m

e

j

α

) e

j

ωt

] = Re[Se

j

ωt

]

gdzie:

S = S

m

e

j

α

– amplituda zespolona sygnału sinusoidalnego S(t);

przy czym:

|

S

| = S

m

– moduł amplitudy zespolonej S;

arg

S =

α ∈(–π,+π)

– argument główny amplitudy zespolonej S.

s(t) = S

m

sin(

ωt + β) = Im[ S

m

e

j(

ωt + β)

] = Im[ (S

m

e

j

β

) e

j

ωt

] = Im[S e

j

ωt

]

gdzie:

S = S

m

e

j

β

– amplituda zespolona sygnału sinusoidalnego S(t);

przy czym:

|

S

| = S

m

– moduł amplitudy zespolonej S;

arg

S =

β ∈(–π,+π)

– argument główny amplitudy zespolonej S.

α

2

π

β

+

=

przy czym:

.

Fazor

– wektor wirujący: w = e

j

ωt

Moduł w:

w = |w| = 1;

Argument w: arg

w =

ωt

w

ωt

im

re

Re w

Im w

|w|

j Im w

+1

–1

+j

–j

Przykład: Napięcie sinusoidalne ma postać: u(t) = 10 cos(

ω

t +

6

π

) [V].

Dr inż. Jacek Czosnowski

Katedra Elektrotechniki AGH Wydział EAIiE

Amplituda zespolona:

U = 10 e

j

6

π

[V]

= 10 ( cos

6

π

+ j sin

6

π

) [V] = 5

( 3 + j ) [V];

Argument główny:

arg

U =

6

π

[rad].

Zmiana postaci amplitudy zespolonej S sygnału sinusoidalnego.

Postać wykładnicza (PW):

S = |S|

e

j

ϕ

Postać algebraiczna (PA):

S = a + j

b; a = Re

S, b = Im

S.

PW => PA

PA => PW

a =

|S|

cos

ϕ

2

2

b

a

+

=

S

b =

|S|

sin

ϕ

ϕ

ϕ

ϕ

⇒

⎪

⎪
⎭

⎪⎪

⎬

⎫

+

=

+

=

2

2

2

2

b

a

b

sin

b

a

a

cos

Wyliczanie kąta fazowego

0

a

>

⎟

⎠

⎞

⎜

⎝

⎛

+

<

<

−

2

π

2

π

ϕ

⇒

a

b

arctg

=

ϕ

0

a

=

⎟

⎠

⎞

⎜

⎝

⎛

+

=

∨

⎟

⎠

⎞

⎜

⎝

⎛

−

=

2

π

2

π

ϕ

ϕ

⇒

(

)

2

π

b

sgn

=

ϕ

0

a

<

π

2

π

2

π

π

⎟

⎠

⎞

⎜

⎝

⎛

<

<

∨

⎟

⎠

⎞

⎜

⎝

⎛

−

<

<

−

ϕ

ϕ

⇒

a

b

arctg

b

sgn

π

−

=

ϕ

Uwaga !

1). Każdemu sygnałowi sinusoidalnemu

można

(

ϕ

+

⎭

⎬

⎫

⎩

⎨

⎧

=

t

t

s

ω

cos

sin

S

)

(

m

)

jednoznacznie przyporządkować jego amplitudę zespoloną S = S

m

e

j

ϕ

.

2).

Każdej amplitudzie zespolonej S = S

m

e

j

ϕ

można przyporządkować dwa

sygnały sinusoidalne

różniące się fazą o

(

)

ϕ

+

⎭

⎬

⎫

⎩

⎨

⎧

=

t

t

s

ω

cos

sin

S

)

(

m

2

π

[rad].

W związku z tym należy przyjąć a priori umowę, że w roz-
patrywanym zagadnieniu wszystkie sygnały sinusoidalne
zapisujemy w postaci funkcji sinus albo funkcji cosinus.

Dr inż. Jacek Czosnowski

Katedra Elektrotechniki AGH Wydział EAIiE

Działania na sygnałach sinusoidalnych

1). Mnożenie sygnału sinusoidalnego przez liczbę rzeczywistą

Dane:
s

1

(t) = S

m1

cos(

ωt + α

1

) = Re[S

1

e

j

ωt

] Î S

1

= S

m1

e

j

α

1

s(t) = k s

1

(t) = S

m

cos(

ωt + α) = Re[S e

j

ωt

]

Î S

= S

m

e

j

α

s(t) = k

S

m1

cos(

ωt + α

1

) = Re[k

S

1

e

j

ωt

]

Î S

= (k

S

m1

)

e

j

α

1

S

= k

⋅S

1

przy czym:

k

∈ ℜ\{0}

Amplituda zespolona S iloczynu sygna-
łu sinusoidalnego przez stałą k

∈ ℜ\{0}

jest równa iloczynowi amplitudy zespo-
lonej tego sygnału przez tę stałą.

2). Suma sygnałów sinuso-

idalnych

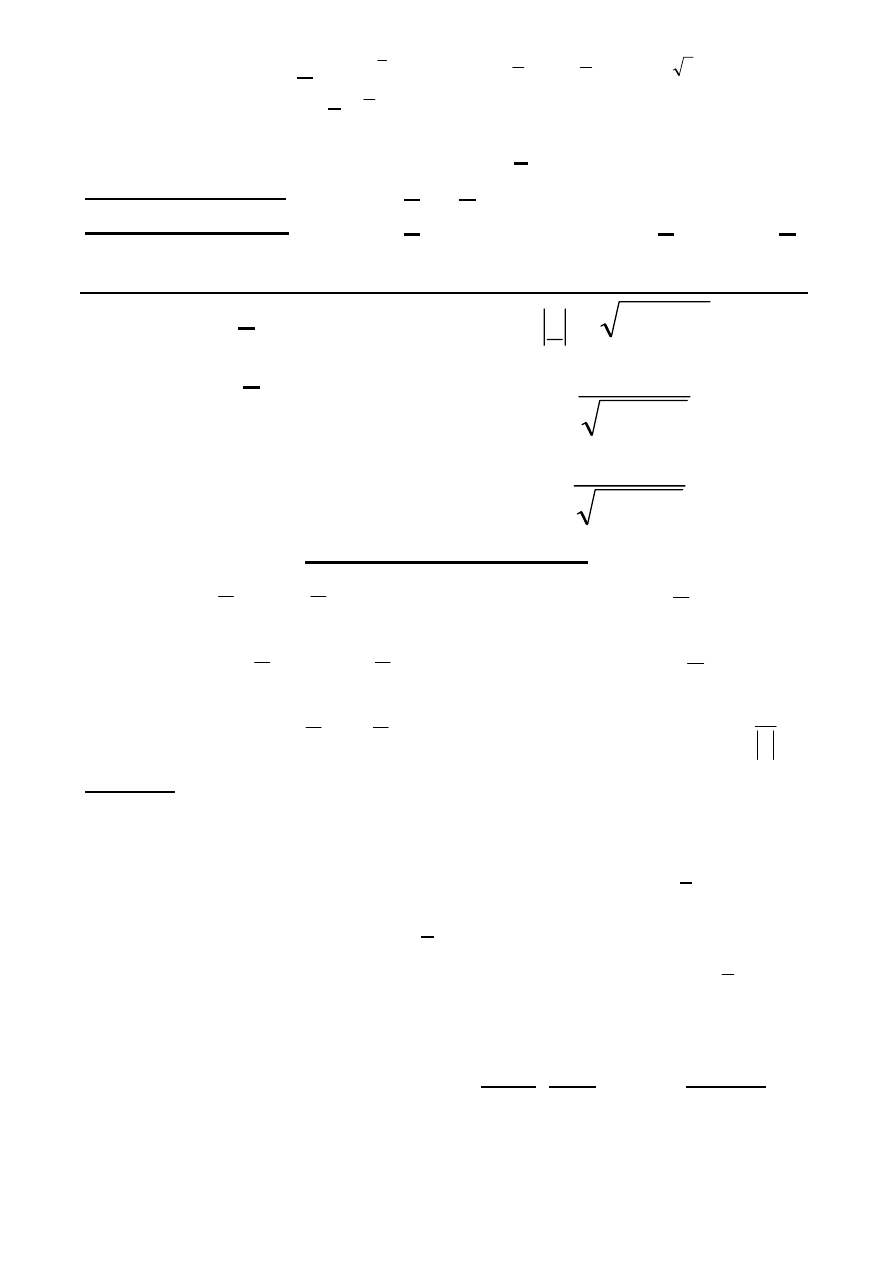
S

1

im

re

S = k S

1

ωt

α

1

k > 0

S

1

im

re

S = k S

1

ωt

α

1

k < 0

π

Dane:

s

1

(t) = S

m1

cos(

ωt + α

1

) = Re[S

1

e

j

ωt

] Î S

1

= S

m1

e

j

α

1

s

2

(t) = S

m2

cos(

ωt + α

2

) = Re[S

2

e

j

ωt

] Î S

2

= S

m2

e

j

α

2

Suma:

s(t) = s

1

(t) + s

2

(t) = S

m

cos(

ωt + α) = Re[S e

j

ωt

]

Î S

= S

m

e

j

α

s(t) = s

1

(t) + s

2

(t) = Re[S

1

e

j

ωt

] + Re[S

2

e

j

ωt

] = Re[(S

1

+ S

2

)e

j

ωt

]

Re[(S

1

+ S

2

)e

j

ωt

] = Re[S e

j

ωt

]

S

1

im

re

S

2

S

2

S = S

1

+ S

2

ωt

α

1

α

α

2

S = S

1

+ S

2

S = S

m1

e

j

α

1

+ S

m2

e

j

α

2

Amplituda zespolona S sumy sygnałów
sinusoidalnych o tej samej pulsacji

ω jest

równa sumie ich amplitud zespolonych

Dr inż. Jacek Czosnowski

Katedra Elektrotechniki AGH Wydział EAIiE

3). Różnica sygnałów sinusoidalnych

Dane:

s

1

(t) = S

m1

cos(

ωt + α

1

) = Re[S

1

e

j

ωt

] Î S

1

= S

m1

e

j

α

1

s

2

(t) = S

m2

cos(

ωt + α

2

) = Re[S

2

e

j

ωt

] Î S

2

= S

m2

e

j

α

2

Suma:

s(t) = s

1

(t) – s

2

(t) = S

m

cos(

ωt + α) = Re[S e

j

ωt

]

Î S

= S

m

e

j

α

s(t) = s

1

(t) – s

2

(t) = Re[S

1

e

j

ωt

] – Re[S

2

e

j

ωt

] = Re[(S

1

– S

2

)e

j

ωt

]

Re[(S

1

– S

2

)e

j

ωt

] = Re[S e

j

ωt

]

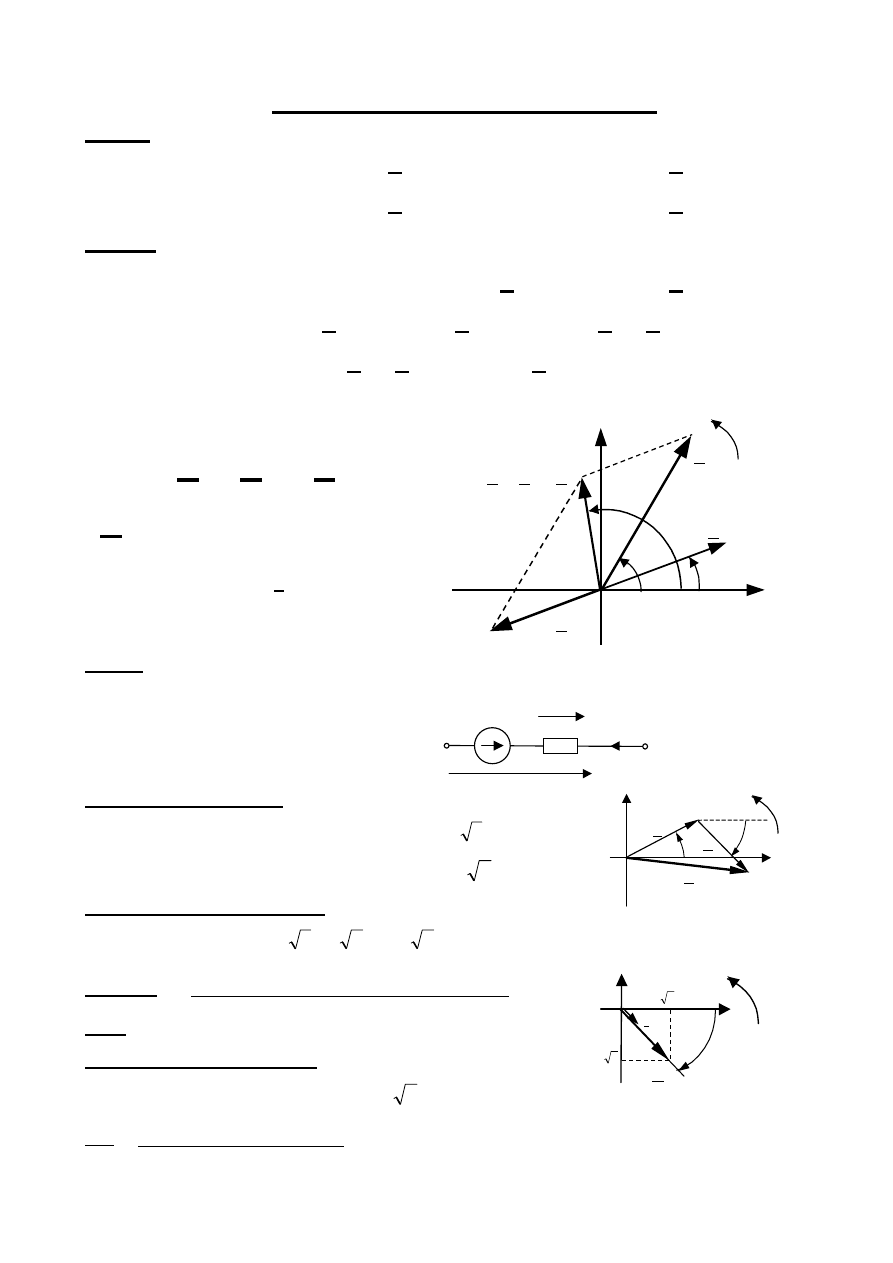
S

1

im

re

S

2

S = S

1

– S

2

–S

2

α

2

1

α

α

ωt

S = S

1

– S

2

S = S

m1

e

j

α

1

– S

m2

e

j

α

2

Amplituda zespolona S różnicy sygnałów
sinusoidalnych o tej samej pulsacji

ω jest

równa różnicy ich amplitud zespolonych

Przykład

Jakie jest napięcie u(t) oraz prąd i(t) gałęzi pokazanej na

rysunku, jeśli

R = 4

Ω,

e

1

(t)

u

1

(t)

R

u(t)

i(t)

e

1

(t) = 10 cos

(

ω

t +

π/6 ) [V]

u

1

(t) = 8 cos

(

ω

t –

π/4 ) [V]

Amplitudy zespolone napięć:

Im U [V]

Re U [V]

E

1

U

1

U

π/6

–

π/4

ωt

E

1

= 10

e

j

π/6

[V]

= 10( cos

π/6 + j sin

π/6 )

=

(

)

2

3

5

j

+

[V]

U

1

= 8

e

–j

π/4

[V]

= 8 [cos(–

π/4) + j sin(–

π/4)]

=

(

)

j

−

1

2

4

[V]

Amplituda zespolona sumy napięć:

U = E

1

+ U

1

=

(

) (

)

5

2

4

j

2

4

3

5

−

−

+

= 14,32 – j 0,66 = 14,76 e

-j2

°38′

Napięcie:

u(t) = 14,76

⋅cos( ωt –

2

°38′

) [V]

Im

Re

U

1

–

π/4

I

2

2

−

ωt

Prad:

i(t) = G u

1

(t) ( wg PO )

Amplituda zespolona prądu:

I = G U

1

= 0,25

⋅8

e

–j

π/4

[A] =

(

)

j

−

1

2

[A]

Prąd:

i(t) = 2,0

⋅cos( ωt –

π/4

) [A]

Dr inż. Jacek Czosnowski

Katedra Elektrotechniki AGH Wydział EAIiE

4). Różniczkowanie sygnałów sinusoidalnych

Dane:
s

1

(t) = S

m1

cos(

ωt + α

1

) = Re[S

1

e

j

ωt

] Î S

1

= S

m1

e

j

α

1

s(t) =

t

t

d

)

(

s

d

1

= S

m

cos(

ωt + α) = Re[S e

j

ωt

]

Î S

= S

m

e

j

α

s(t) =

(

)

]

e

S

jω

Re[

]

e

S

Re[

d

d

jω

1

jω

1

t

t

t

=

Î S

= j

ω

( S

m1

e

j

α

1

)

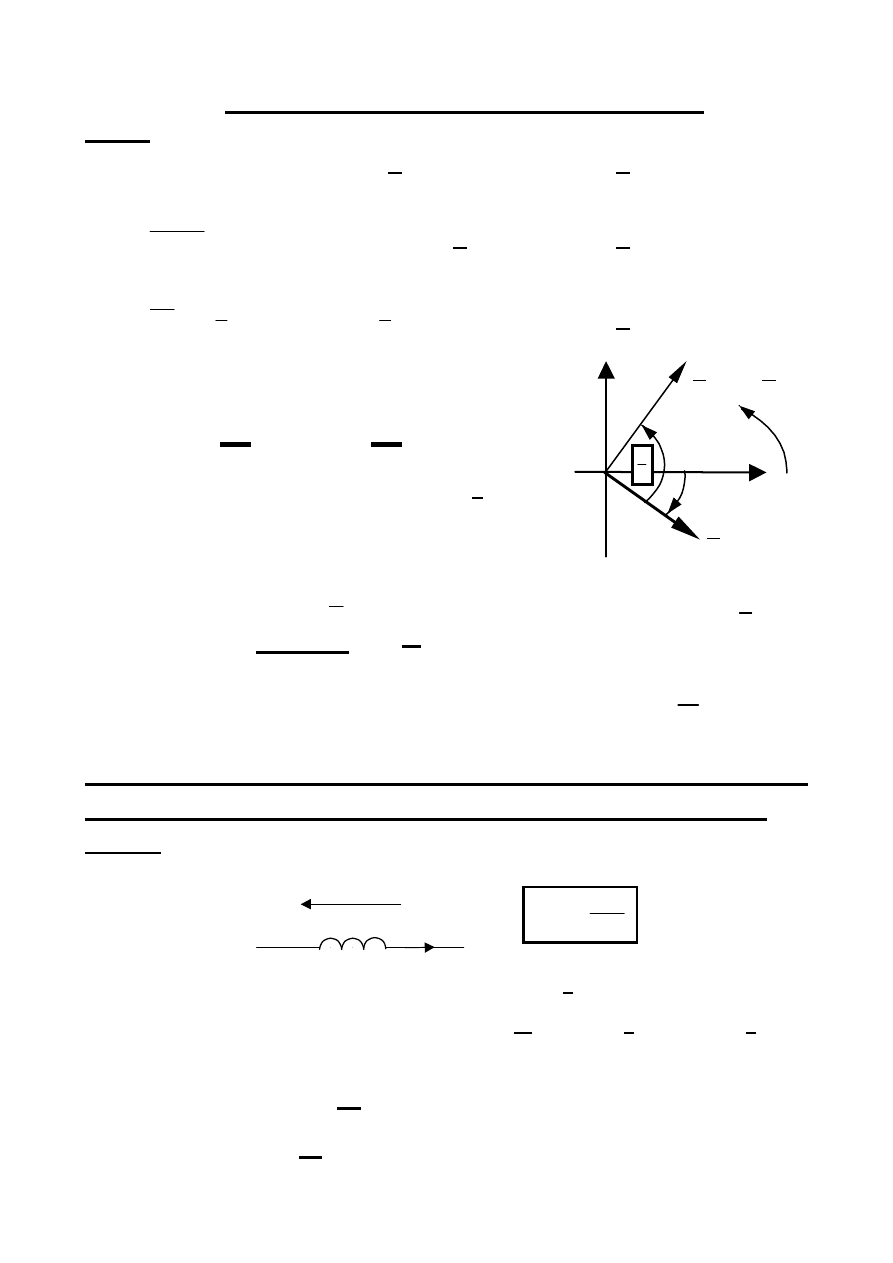
im

re

S

1

2

π

S = j

ω⋅S

1

α

1

S

1

S

ωt

S

= j

ω

S

1

Amplituda zespolona sygnału sinusoidalnego S powsta-
łego przez zróżniczkowanie względem czasu sygnału
sinusoidalnego o pulsacji

ω jest równa iloczynowi ampli-

tudy zespolonej tego sygnału przez j

ω.

Ponieważ:

2

j

e

j

π

=

, to

S = S

e

j

α

= [

ωS

1

]e

j(

α

1

+

2

π

)

,

z tego wynika:

S =

ω S

1

oraz

α = α

1

+

2

π

.

Sygnał sinusoidalny po zróżniczkowaniu względem czasu
wyprzedza w fazie sygnał różniczkowany o

π/2 radianów.

Przykład Jakie napięcie u(t) towarzyszy przepływowi prądu i(t) = 20 cos (

ωt + 15°) mA

o pulsacji

ω = 1 Mrad/s przez indukcyjność L = 3 mH

L

i(t)

u(t)

t

t

i

t

u

d

)

(

d

L

)

(

=

Amplituda zespolona prądu w indukcyjności:

I = 20 e

j15

°

[mA]

Amplituda zespolona napięcia na indukcyjności:

U = L

⋅( jωI ) = j

(

ωL) I [V]

(

ωL) = 10

6

3

⋅10

–

3

= 3 k

Ω;

U = 60 e

j105

°

[V]

u(t) = Re[U e

j

ωt

] = 60 cos(

ωt + 105

°

) [V]

Dr inż. Jacek Czosnowski

Katedra Elektrotechniki AGH Wydział EAIiE

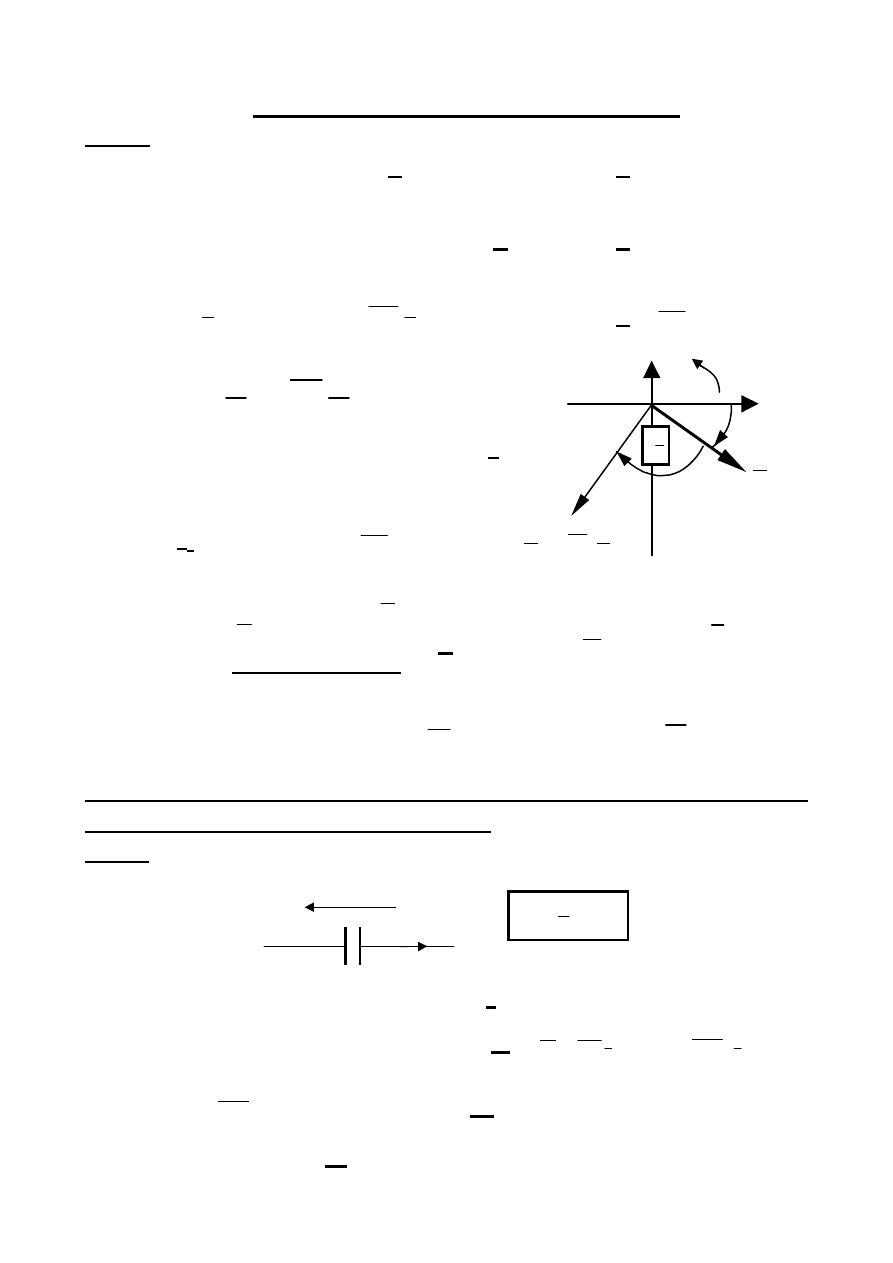
5). Całkowanie sygnałów sinusoidalnych

Dane:
s

1

(t) = S

m1

cos(

ωt + α

1

) = Re[S

1

e

j

ωt

] Î S

1

= S

m1

e

j

α

1

s(t) =

= S

m

cos(

ωt + α) = Re[S

τ

τ

d

)

(

s

1

∫

e

j

ωt

] Î S

= S

m

e

j

α

s(t) =

]

e

S

jω

1

Re[

d

]

e

S

Re[

jω

1

jω

1

t

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

=

∫

τ

τ

Î S

=

jω

1

( S

m1

e

j

α

1

)

im

re

S

1

ωt

2

π

−

S =

jω

1

⋅S

1

α

S

1

S

1

1

jω

1

S

S

=

Amplituda zespolona sygnału sinusoidalnego S,
będącego funkcją pierwotną sygnału sinusoidal-
nego o pulsacji

ω jest równa iloczynowi amplitudy

zespolonej S

1

tego sygnału przez

jω

1

.

Ponieważ:

2

j

e

j

j

1

π

−

=

−

=

, to

S = S

e

j

α

= [

ω

1

S

1

]e

j(

α

1

–

2

π

)

,

z tego wynika:

S =

ω

1

S

1

oraz

α = α

1

–

2

π

.

Sygnał sinusoidalny po scałkowaniu opóźnia się w fazie względem
sygnału całkowanego o

π/2 radianów.

Przykład Jakie napięcie u(t) towarzyszy przepływowi prądu i(t) = 20 cos (

ωt + 15°) mA

o pulsacji

ω = 1 Mrad/s przez pojemność C = 2 nF

C

i(t)

u(t)

t

t

i

t

u

d

)

(

C

1

)

(

∫

=

Amplituda zespolona prądu w pojemności:

I = 20 e

j15

°

[mA]

Amplituda zespolona napięcia na pojemności:

U =

⎟

⎠

⎞

⎜

⎝

⎛

⋅

I

jω

1

C

1

=

I

⎟

⎠

⎞

⎜

⎝

⎛

−

ωC

1

j

[V]

=

⎟

⎠

⎞

⎜

⎝

⎛

ωC

1

0,

5 k

Ω;

U = 10 e

–j75

°

[V]

u(t) = Re[U e

j

ωt

] = 10 cos(

ωt –75

°

) [V]

Dr inż. Jacek Czosnowski

Katedra Elektrotechniki AGH Wydział EAIiE

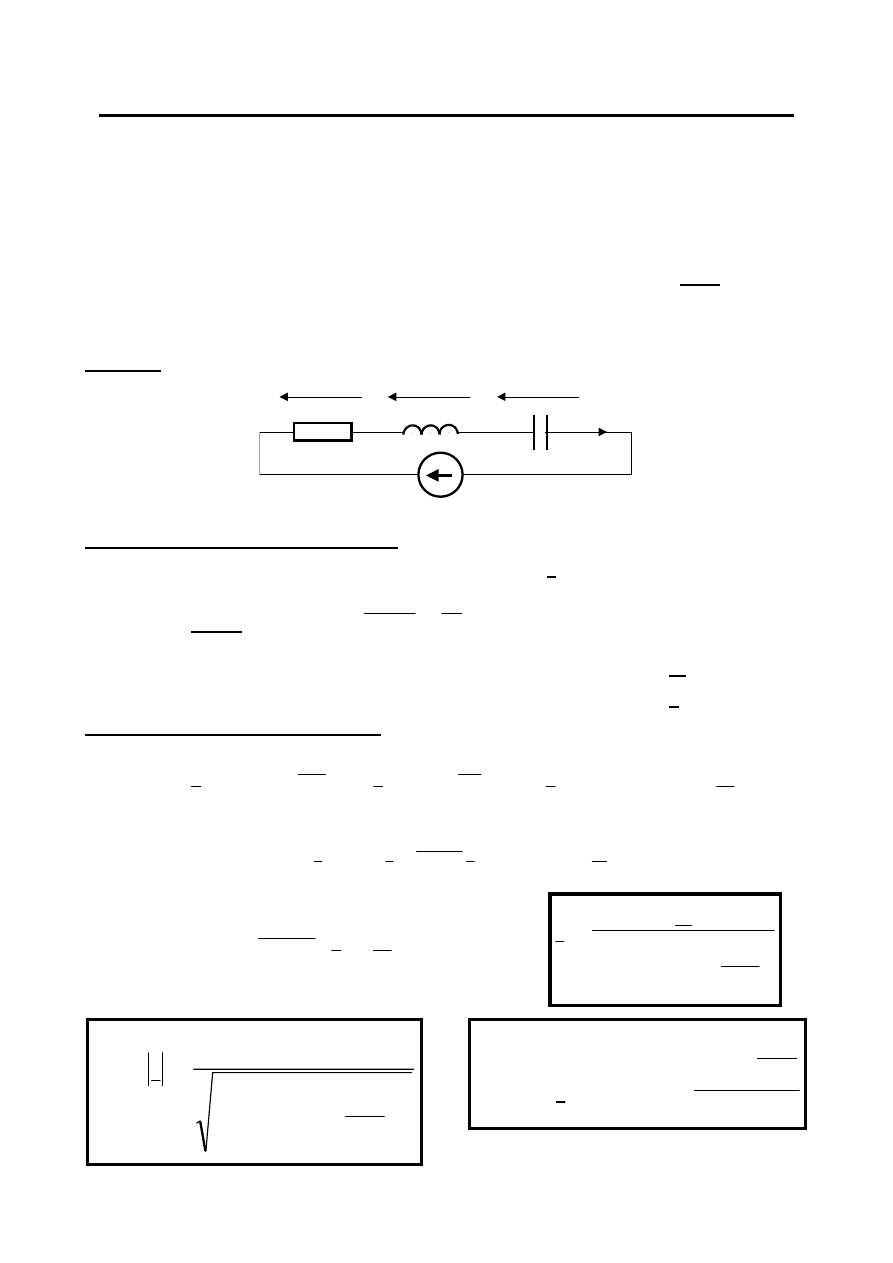
Analiza obwodów Metodą Amplitud Zespolonych (MAZ)

( metoda symboliczna ( MS ), metoda wskazowa ( MW ))

Jeśli obwód SLS znajduje się w stanie ustalonym sinusoidalnym (SUS), to
w celu dokonania analizy MAZ tego obwodu należy wszystkie występujące
w nim pobudzenia

( napięcia źródłowe e(t) oraz prądy źródłowe j(t))

przedstawić w

dziedzinie zespolonej jako odpowiednie amplitudy zespolone pobudzeń;
przy czym należy użyć jednolitej „konwencji” cos(

•) ↔ Re[•] albo sin(•) ↔

Im[

•]. Jednocześnie wszystkie szukane funkcje obwodowe należy zapisy-

wać zgodnie z przyjętą „konwencją”.

Przykład

Obwód pokazany na rysunku znajduje się w SUS. Wyznaczyć prąd i(t) płynący w tym obwodzie.

L

u

L

(t)

i(t)

u

C

(t)

u

R

(t)

R

e(t) = E

m

cos( ωt + α )

C

Szukamy rozwiązania w postaci:

i(t) = I

m

cos(

ωt + β) = Re[I e

j

ωt

]

)

(

d

)

(

C

1

d

)

(

d

L

)

(

R

t

e

i

t

t

i

t

i

=

+

+

∫

τ

τ

NPK:

Amplituda zespolona napięcia pobudzającego e(t):

E = E

m

e

j

α

Amplituda zespolona szukanego prądu i(t):

I = I

m

e

j

β

NPK w dziedzinie zespolonej:

]

e

E

Re[

d

]

e

I

Re[

C

1

]

e

I

Re[

d

d

L

]

e

I

Re[

R

jω

jω

jω

jω

t

t

t

t

=

+

+

⋅

∫

τ

τ

]

e

E

Re[

e

I

Cω

j

1

I

jLω

I

R

Re

jω

jω

t

t

=

⎥

⎦

⎤

⎢

⎣

⎡

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

+

+

E

I

Cω

j

1

jLω

R

=

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

+

+

Î

⎟

⎠

⎞

⎜

⎝

⎛

−

+

=

ωC

1

ωL

j

R

E

I

2

2

m

m

ωC

1

ωL

R

E

I

I

⎟

⎠

⎞

⎜

⎝

⎛

−

+

=

=

R

ωC

1

ωL

arctg

α

I

arg

β

−

−

=

=

Dr inż. Jacek Czosnowski

Katedra Elektrotechniki AGH Wydział EAIiE

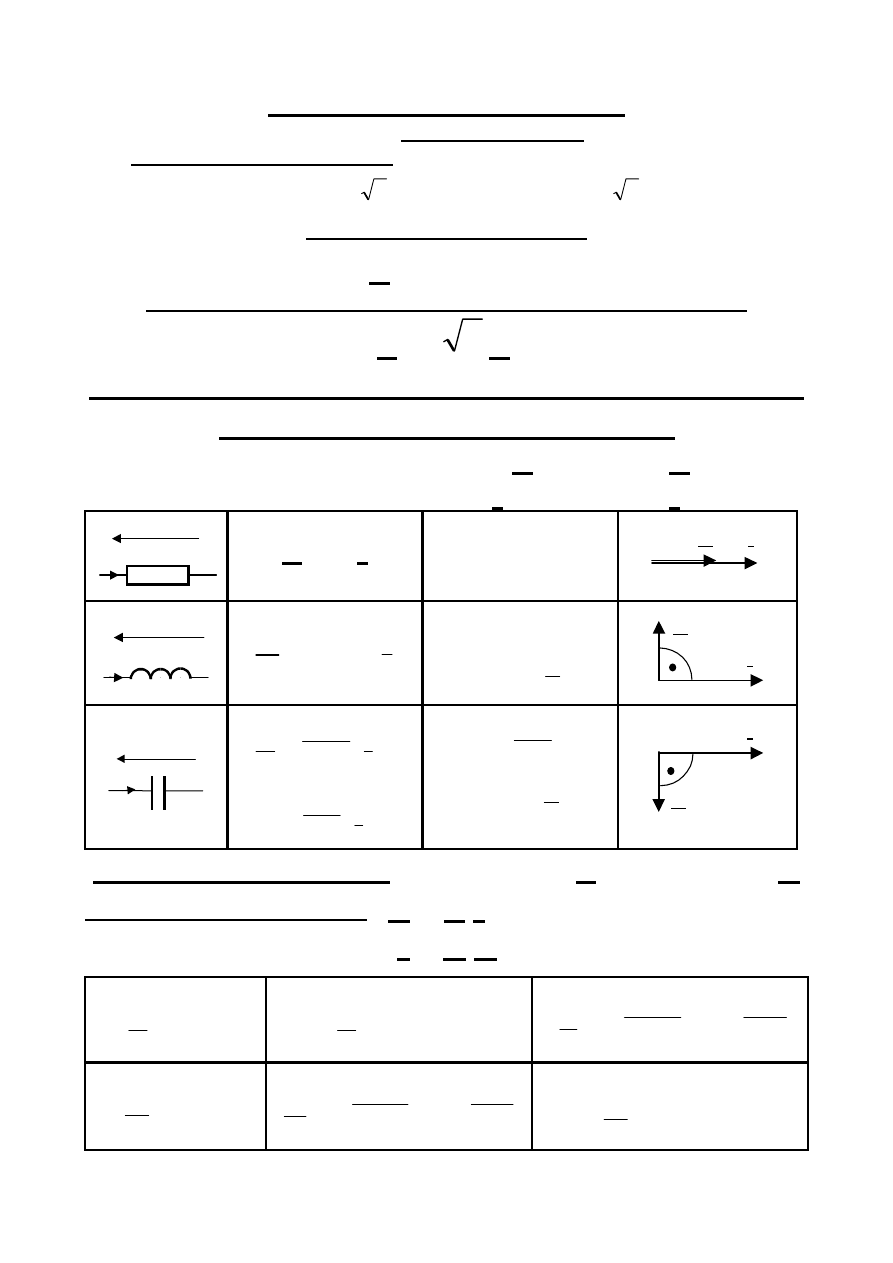
Wartość skuteczna zespolona

W metodzie MAZ zamiast pojęcia amplitudy zespolonej może być stosowane po-
jęcie wartości skutecznej zespolonej. (

Dotyczy to głównie energetyki. )

s(t) = S

m

cos(

ωt + α) =

2

S

sk

cos(

ωt + α) = Re[

2

(S

sk

e

j

α

) e

j

ωt

]

Wartość skuteczną zespolona

S

′

= S

sk

e

j

α

Związek amplitudy zespolonej i wartości skutecznej zespolonej

S =

2

S

′

Związki między amplitudami zespolonymi

(wskazami)

prądów i napięć na elementach

u(t) = U

m

cos(

ωt + α) = Re[U e

j

ωt

]

⇒ U = U

m

e

j

α

i(t) = I

m

cos(

ωt + β) = Re[I e

j

ωt

];

⇒ I = I

m

e

j

β

u(t)

R

i(t)

U = R

⋅I

U

m

= R

⋅I

m

β = α

U

I

L

u(t)

i(t)

I

jLω

U

⋅

=

m

m

I

Lω

U

⋅

=

2

π

α

β

−

=

U

I

u(t)

C

i(t)

I

Cω

1

j

I

jCω

1

U

⋅

−

=

=

⋅

=

m

m

I

Cω

1

U

⋅

=

2

π

α

β

+

=

U

I

Immitancje dwójników: Impedancja Z i Admitancja Y

PO dla amplitud zespolonych

:

U = Z

⋅I –

równanie impedancyjne

lub

I = Y

⋅U –

równanie admitancyjne

R

Z

R

=

Lω

j

Z

L

=

Cω

1

j

Cω

j

1

Z

C

−

=

=

G

Y

R

=

Lω

1

j

Lω

j

1

Y

L

−

=

=

Cω

j

Y

C

=

Dr inż. Jacek Czosnowski

Katedra Elektrotechniki AGH Wydział EAIiE

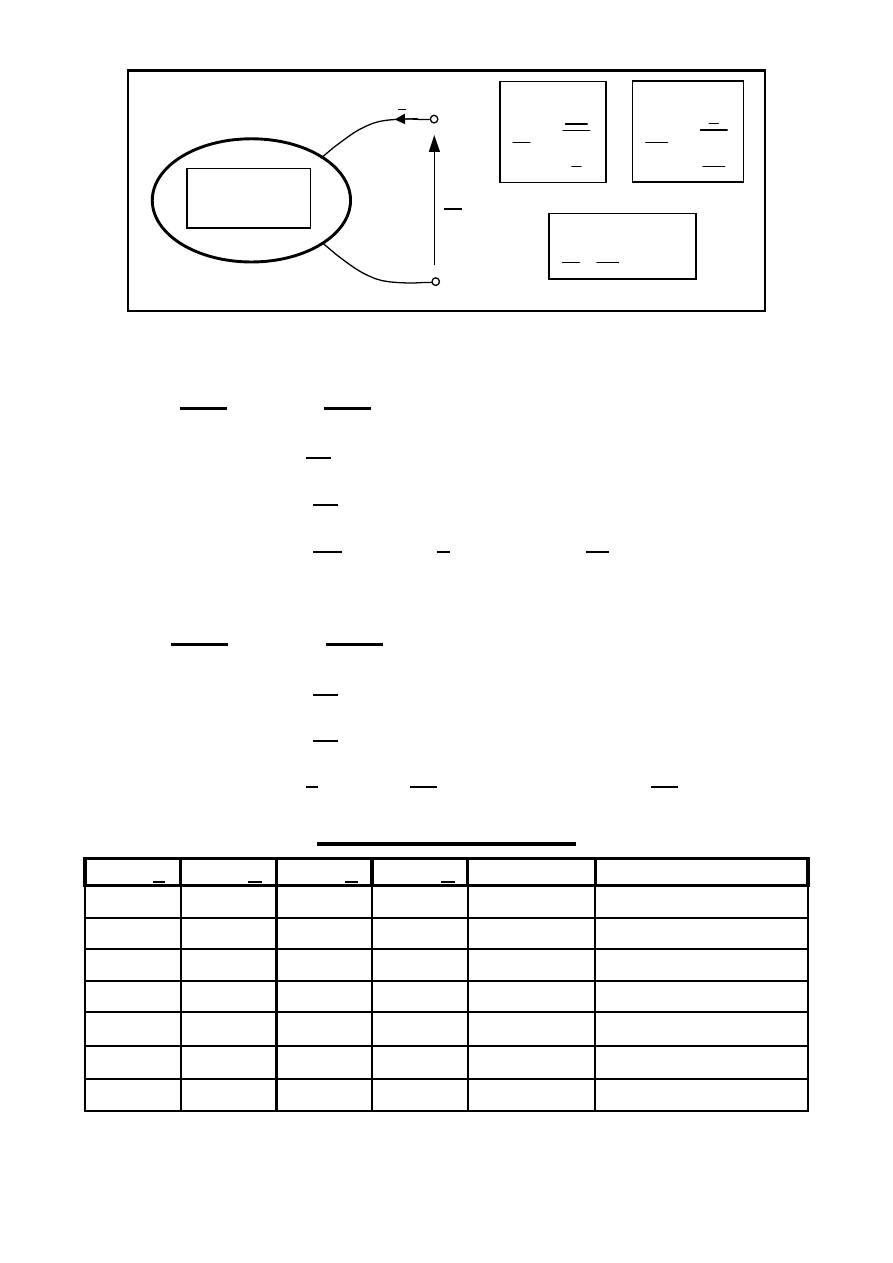
U

I

Dwójnik

SLS

I

U

ˆ

Z

=

1

Y

Z

1

=

⋅

−

U

I

ˆ

Y

=

Z = |Z|e

j

α

= r + jx

r = Re[Z] - rezystancja
x = Im[Z] - reaktancja

α = arg

U – arg

I - faza Z

Y = |Y|e

j

β

= g +jb

g = Re[Z] - konduktancja
b = Im[Z] - susceptancja

β = arg

I – arg

U = –

α - faza Y

Typy dwójników

r = Re[Z] g = Re[Y] x = Im[Z] b = Im[Y]

ϕ - faza

Typ

+ +

stratny pasywny

0 0

bezstratny pasywny

– –

Aktywny

+

– +

charakter indukcyjny

0

∞

0

Rezonans typu szeregowego

∞

0 0

Rezonans typu równoległego

–

+ –

Charakter pojemnościowy

Dr inż. Jacek Czosnowski

Katedra Elektrotechniki AGH Wydział EAIiE