
Praca Magisterska
Modelowanie oddziaływań ligandów
aromatycznych z kwasami nukleinowymi
Karol Langner
Wydział Podstawowych Problemów Techniki
Fizyka Ciała Stałego
Promotor: Prof. W.A. Sokalski
Politechnika Wrocławska
Wrocław 2005


Spis treści
1 Wstęp
1
1.1 Rola ligandów aromatycznych w procesach biologicznych . . . . . . . . . . . . .
1
1.2 Interkalacja kwasów nukleinowych . . . . . . . . . . . . . . . . . . . . . . . . . .
3
1.2.1
Energetyka interkalacji . . . . . . . . . . . . . . . . . . . . . . . . . . . .
5
1.2.2
Interkalatory jako cząsteczki hybrydowe . . . . . . . . . . . . . . . . . .
7
1.2.3
Kwantowochemiczne badania kompleksów interkalacyjnych . . . . . . . .
8
1.3 Natura oddziaływań miedzycząsteczkowych . . . . . . . . . . . . . . . . . . . . .
9
1.3.1
Składowe energii oddziaływania miedzycząsteczkowego i hierarchia modeli
teoretycznych . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
9
1.4 Przybliżone modele oddziaływań . . . . . . . . . . . . . . . . . . . . . . . . . . .
10
1.4.1
Oddziaływania elektrostatyczne . . . . . . . . . . . . . . . . . . . . . . .
10
1.4.2
Wielocentrowe rozwinięcia momentów multipolowych . . . . . . . . . . .
13
1.5 Cele pracy . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
15
2 Metody obliczeniowe
16
2.1 Przygotowywanie struktur i metodologia badań . . . . . . . . . . . . . . . . . .
16
2.2 Nieempiryczna analiza energii oddziaływań . . . . . . . . . . . . . . . . . . . . .
17
2.3 Kumulatywne Atomowe Momenty Multipolowe (CAMM) . . . . . . . . . . . . .
19
2.4 Oprogramowanie . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
21
3 Analiza oddziaływań w wybranych strukturach krystalograficznych
22
4 Badanie energii oddziaływania
w płaszczyźnie interkalacji
27
4.1 Powierzchnie oddziaływania multipolowego
w płaszczyźnie interkalacji . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
27
4.2 Analiza energii oddziaływania na wybranym odcinku w płaszczyźnie interkalacji
(położenie krystalograficzne - minimum A) . . . . . . . . . . . . . . . . . . . . .
37
5 Wnioski
40
6 Dodatki
vi
6.1 Używane skróty . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
vi
6.2 Wybrane wzory i fragmenty kodu źródłowego . . . . . . . . . . . . . . . . . . .
vii
6.2.1
Generowanie momentów multipolowych CAMM . . . . . . . . . . . . . .
vii
6.2.2
Obliczanie energii oddziaływań między momentami multipolowymi . . .
ix

1 Wstęp
1
1
Wstęp
Rozwój badań i kliniczne zastosowanie związków oddziałujących z kwasami nukleinowymi do
leczenia raka to jedno z najważniejszych osiągnięć nauk medycznych XX wieku. Jednocześnie,
wiele pytań na temat korelacji fizykochemicznych własności ligandów z ich aktywnością biolo-
giczną pozostaje bez odpowiedzi. Badania w tym kierunku doprowadziły do scharakteryzowania
dużej liczby kompleksów DNA-ligand pod względem strukturalnym i dynamicznym, co pozwo-
liło z kolei zaprojektować szereg bardziej efektywnych związków chemoterapeutycznych drugiej
i trzeciej generacji [1, 2]. Szczegółowa wiedza na temat mechanizmów działania takich leków,
zarówno na poziomie organizmu i w skali molekularnej, jest podstawą dalszego wzrostu ich war-
tości medycznej. Nowe leki zazwyczaj powstają w wyniku systematycznych badań dużej ilości
podobnych cząsteczek [3], ale w nielicznych przypadkach wprowadzane modyfikacje są celowe i
wynikają z odpowiedniej wiedzy i dobrze zdefiniowanej funkcji projektowanego związku [4].
Kluczowe dla zrozumienia działania takich ligandów jest rozpoznanie fizycznych własności
odpowiedzialnych za ich aktywność biologiczną - własności samych cząsteczek oraz ich komplek-
sów z kwasami nukleinowymi. Studia nad oddziaływaniami w takich kompleksach i analiza po-
szczególnych efektów zatem mogą uzupełnić wiedzę na temat ich natury fizycznej i zaproponować
zmiany, które mogą uczynić ich działanie jeszcze bardziej korzystne dla leczenia nowotworów.
1.1
Rola ligandów aromatycznych w procesach biologicznych
Oddziaływanie małych cząsteczek z kwasami nukleinowymi od kilku dekad pozostaje w centrum
uwagi. Pierwsza prezentacja podwójnie spiralnej struktury DNA [5] i późniejsze odkrycia powią-
zań jej cech strukturalnych i funkcyjnych [6,7], takich jak replikacja i transkrypcja, udowodniły
że ta makrocząsteczka jest ważnym celem dla środków zaburzających procesy biologiczne. Wy-
jątkowe cechy strukturalne - prawie płaskie i piętrowe ułożenie par zasad wzdłuż podwójnej
helisy - czynią ją obiecującym obiektem przy projektowaniu leków.
Funkcjonalnie, DNA stanowi magazyn informacji genetycznej w komórce. Liniowa sekwencja
zasad występująca wzdłuż fosforanowo-cukrowej nici definiuje tę informację i jest dobrze zacho-
wana podczas replikacji i transkrypcji, częściowo dzięki komplementarności tych zasad w parach.
Komplementarność jest też ważna w trakcie translacji, gdy kodon mRNA oddziałuje z antykodo-
nem tRNA. Zaburzenia sekwencji zasad lub zablokowanie możliwości odczytania jej przez inne,
trwale wiążące się makrocząsteczki, najczęściej białka, prowadzi do zmian w strukturze i funkcji
DNA. Jednym z czynników wywołujących takie zmiany to oddziaływanie z małymi cząsteczkami,
ligandami, a wynikłe zaburzenia w informacji genetycznej mogą mieć skutki mutageniczne lub
śmiertelne dla komórki (najczęściej poprzez apoptozę). Rozpoznanie cytotoksycznych własności
wielu ligandów doprowadziło do ich powszechnego stosowania w chemoterapeutycznym leczeniu
chorób, przede wszystkim raka [1, 2].
Rozważając znaczenie danego ligandu dla organizmów żywych i studiując jego relacje z DNA,
1 Wstęp
2
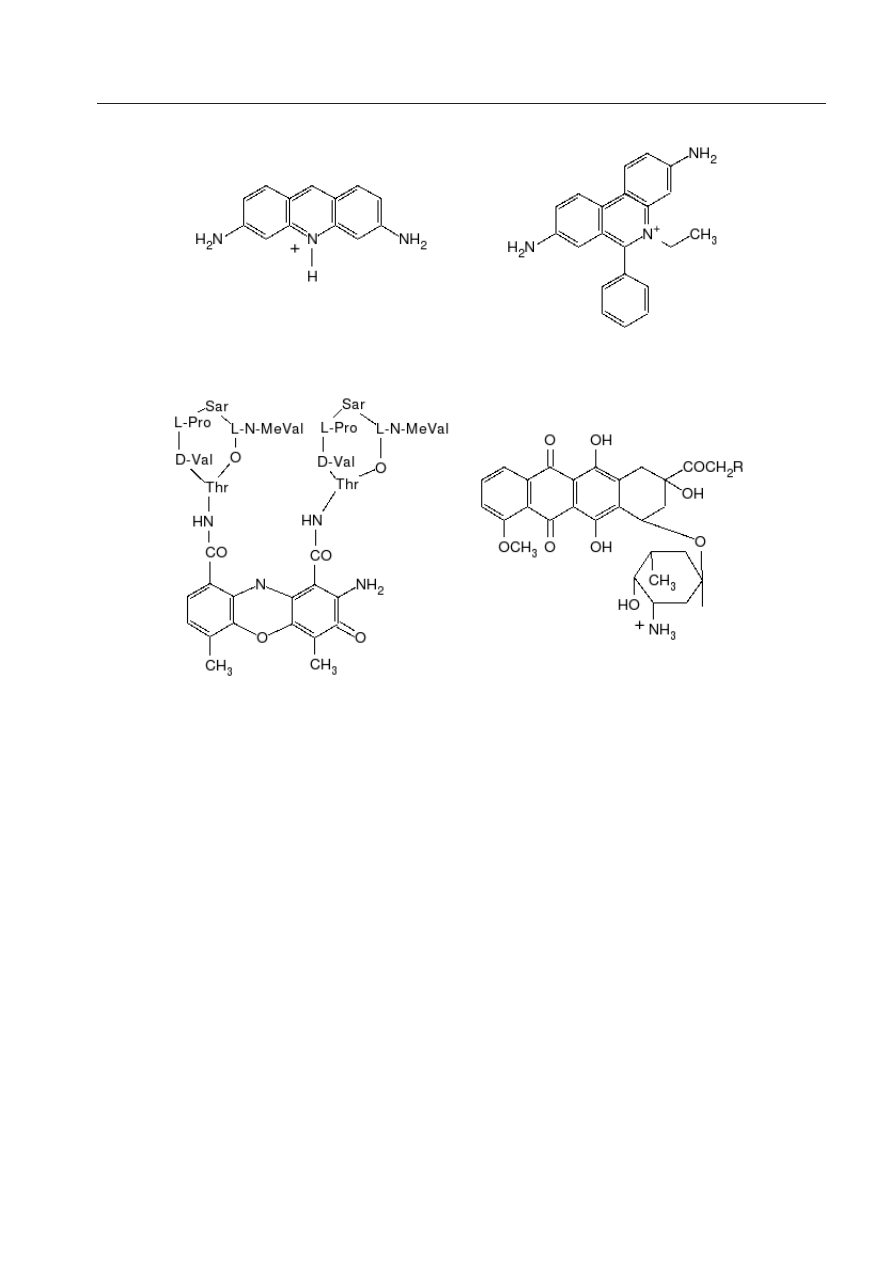
proflawina
ang. proflavine
etydyna
ang. ethidium
aktynomycyna D
ang. actinomycin D
R=H: daunomycyna
ang. duanomycin
R=OH: adriamycyna
ang. adriamycin
Rysunek 1:
Wzory strukturalne kilku wybranych interkalatorów.
należy pamiętać o złożoności kontekstu w układach biologicznych, ponieważ oddziaływanie li-
gandu z kwasami nukleinowymi to tylko jeden czynnik w jego aktywności biologicznej. Dwa-
dzieścia lat temu zidentyfikowano enzym, topoizomerazę II, jako jeden z głównych celów dla
wielu ligandów w komórkach. Ich działanie antyneoplastyczne polegało na tworzeniu potrój-
nych kompleksów, angażujących ligand, DNA, oraz enzym, a aktywność antyrakowa nie zawsze
bezpośrednio korelowała z siłą wiązania z kwasem nukleinowym [8, 9]. Zatem oddziaływanie
ligandów z DNA nie determinuje charakteru zaburzeń w procesach in vivo i nie decyduje o
śmierci komórki. Klasycznym przykładem ilustrującym ten fakt są konformery strukturalne
związku o nazwie AMSA, a w szczególności m-AMSA i o-AMSA [10]. Obydwa konformery
wiążą się z DNA, interkalując pomiędzy pary zasad [11], a powinowactwo o-AMSA jest około 4
razy większe od m-AMSA [12]. Z drugiej strony, m-AMSA stymuluje przerwanie nici zarówno w
ssDNA i dsDNA za pośrednictwem topoizomerazy II, podczas gdy o-AMSA nie indukuje takiego
efektu. Zatem w tym przypadku wiązanie się ligandu z DNA nie przekłada się bezpośrednio

1 Wstęp
3
na jego aktywność biologiczną, ponieważ istotne są oddziaływania w potrójnym kompleksie
ligand-DNA-enzym [13].
Badania również pokazują, że wiązanie się ligandów z DNA silnie zależy od warunków oto-
czenia. Dla DNA w roztworze, istotne są takie parametry jak siła jonowa, pH, oraz tempera-
tura [14, 15].
Ligandy mogą wiązać się z kwasami nukleinowymi na kilka sposobów, należą do nich:
-
interkalacja, która jest głównym tematem tej pracy,
-
niekowalencyjne wiązanie w dużym lub małym rowku DNA,
-
kowalencyjne wiązanie (ang. covalent binding/cross linking),
-
przerwanie nici DNA (ang. DNA cleavage),
-
włączanie analogów neukleotydowych (ang. nucleoside-analog incorporation).
Wszystkie powyższe sposoby wiązania zmieniają zarówno ligand i DNA tak, by mogło dojść
do utworzenia odpowiedniego kompleksu. Zmiany w strukturze DNA w wielu przypadkach
prowadzą do zmian w jej własnościach - innej stabilności termodynamicznej lub zmodyfikowanej
funkcji w komórce.
1.2
Interkalacja kwasów nukleinowych
Molekuły interkalujące w DNA tworzą liczną grupę leków, używanych od dekad do leczenia
raka [16]. Interkalacja polega na wejściu płaskiego, aromatycznego, i najczęściej policyklicznego
chromoforu interkalatora między sąsiadujące pary zasad nukleinowych DNA. Oprócz interkalacji,
dodatkowe podstawniki chemiczne na ligandzie mogą odgrywać istotną rolę w termodynamice
mechanizmu wiązania, mieć wpływ na geometrię kompleksu DNA-ligand, wreszcie powodować
selektywne wiązanie danego ligandu ze specyficzną sekwencją zasad [12].
Klasyfikacja interkalatorów zazwyczaj bazuje na strukturze ich chromoforów; wzory struk-
turalne kilku popularnych interkalatorów umieszczono na Rys.1. Etydyna i proflawina to przy-
kłady klasycznych interkalatorów, były to jedne z pierwszych związków badanych pod względem
ich powinowactwa z DNA. W swoich pionierskich badaniach z 1961 roku, Lerman zaobserwował
wyraźne zmiany w lepkości i współczynniku sedymentacji DNA w roztworze gdy dodał do niego
akrydynę lub proflawinę [17]. Z tych obserwacji wywnioskował, że leki te indukują następujące
zaburzenia strukturalne w podwójnej spirali DNA w miejscu wiązania interkalacyjnego (zobacz
schemat na Rys.2):
-
zwiększenie odległości między kolejnymi parami zasad w miejscu interkalacji,
-
lokalne wydłużenie nici DNA (stąd zmiany w sedymentacji),
-
lokalne rozwinięcie helisy DNA.
1 Wstęp
4
Pierwsze badania Lermana zwróciły uwagę na związek pomiędzy strukturalnymi zaburze-
niami w DNA i mutagenezą. Pierwszą biofizyczną charakterystykę kompleksu interkalacyjnego
przedstawił w 1965 Waring [14], opisując za pomocą spektroskopii UV i widzialnej oddziaływa-
nie etydyny z DNA w funkcji siły jonowej roztworu. W 1967 roku, LePecq i Paoletti wykorzy-
stali do tego samego celu spektroskopię fluorescencyjną [18] - fluorescencja etydyny związanej
z DNA okazała się ponad 21 razy większa od etydyny niezwiązanej, co pozwala wykorzystać
ten związek jako efektywny znacznik DNA [19,20]. W 1965, Gellert i współpracownicy pokazali
że aktynomycyna D (zobacz Rys.1), wówczas dobrze znany inhibitor transkrypcji, też tworzy
silne kompleksy z DNA [21]. Kolejne badania biofizyczne wskazały, że siła wiązania aktyno-
mycyny i innych małych aromatycznych ligandów może silnie zależeć od sekwencji zasad kwasu
nukleinowego [22, 23]. Po tych pierwszych badaniach, w podobnym duchu scharakteryzowano
kompleksy wielu heterocyklicznych płaskich kationów z DNA. W szczególności, zgromadzono
modele molekularne układów DNA-ligand, uzyskanych za pomocą dyfrakcji rentgenowskiej i
metod NMR [24–29].
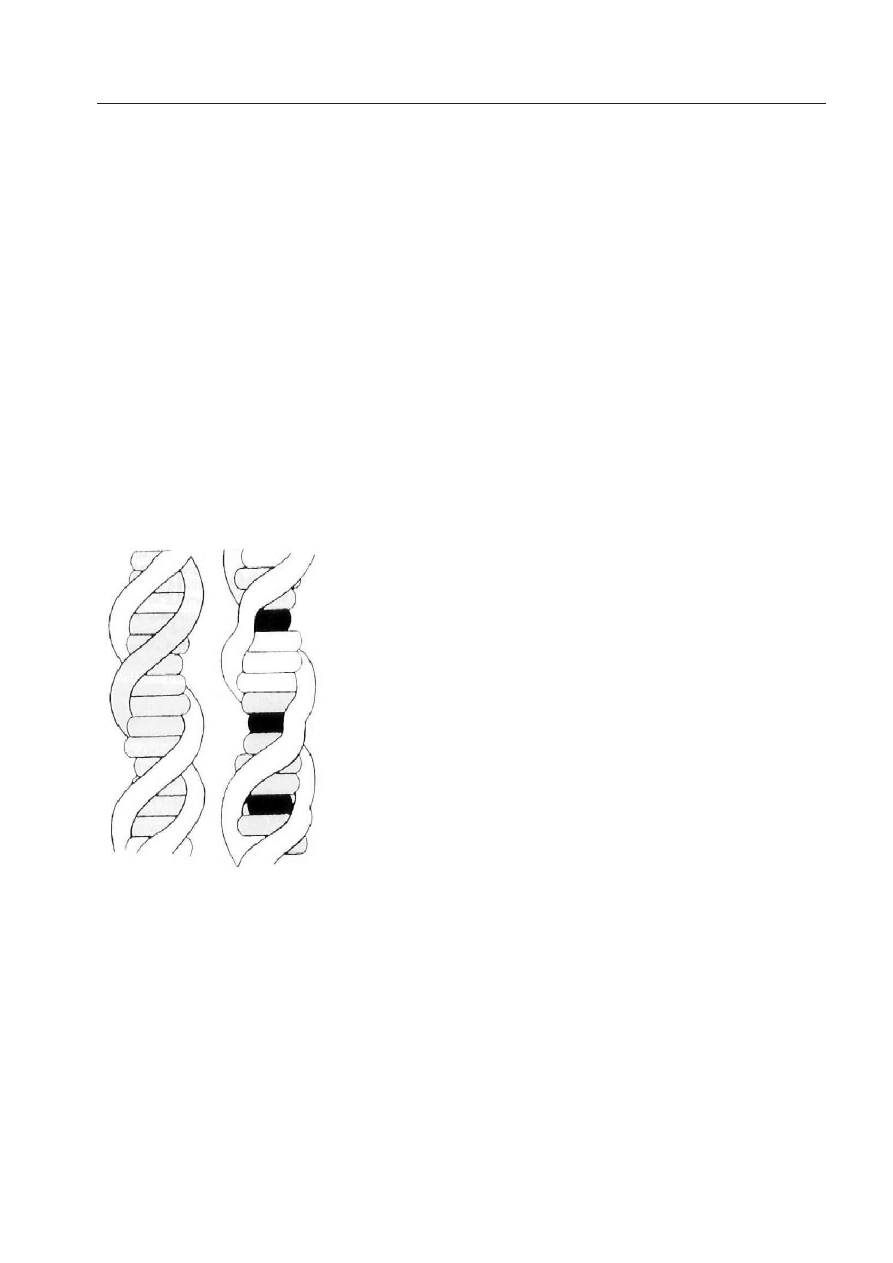
Rysunek 2:
Schemat interka-
lacji zaproponowany przez Ler-
mana w 1961 roku [17] - zwykła
podwójną nić DNA po lewej stro-
nie, oraz nić zaburzona zinter-
kalowanymi cząsteczkami (czarne
obszary) po prawej.
Z molekularnego punktu widzenia, utworzenie kompleksu
ligand-DNA wymaga rozsunięcia dwóch sąsiadujących par za-
sad nukleinowych o około 3.4˚
A, tak by chromofor interkalatora
mógł się zmieścić miedzy nimi. Jest to realizowane przez czę-
ściowe rozwinięcie spirali DNA wokół swojej osi, a stopień roz-
winięcia zależy od geometrii kompleksu DNA-ligand i rodzaju
cząsteczki interkalującej. Niezaburzone skręcenie helisy mię-
dzy kolejnymi parami zasad w B-DNA wynosi 36
o
. Wsunięcie
fenantradynowych pierścieni etydyny redukuje to skręcenie do
10
o
, czyli powoduje odkręcenie o kąt 26
o
. Dla porównania, in-
terkalacja proflawiny lub dzielącej ten sam chromofor akrydyny
powoduje odkręcenie o kąt około 17
o
[16]. Antracykliny, takie
jak daunorubicyna i adriamycina tworzą kompleksy interkala-
cyjne różniące się bardzo od poprzednich i indukują odkręcenie
jedynie o kąt 11
o
w miejscu wiązania. Lokalne odkręcenie helisy
DNA jest propagowane wzdłuż nici w obie strony, zaburzając
strukturę polimeru na dłuższych odcinkach. Zatem wiązanie się
ligandu w specyficznym miejscu wzdłuż DNA może indukować
dalekosiężne zmiany zarówno w jej strukturze DNA i funkcji.
Etydyna i proflawina (zobacz Rys.1), które są przedmiotem
badań niniejszej pracy, to dobrze opisane w literaturze interka-
latory, są wiec dobrym punktem wyjściowym dla nowych metod badania oddziaływań ligandów
aromatycznych z DNA. Etydyna jest powszechnie używana jako znacznik w biologii molekular-
nej [19, 20] i charakteryzuje się selektywnością dla poszczególnych sekwencji [23]. Proflawina i

1 Wstęp
5
jej pochodne akrydynowe są już od ponad pięćdziesięciu lat badane ze względu na swoje silne
działania antybakteryjne [30, 31], a ich działanie mutagenne było spośród pierwszych pozna-
nych [32]. Interkalacyjny charakter oddziaływania proflawiny oraz jej pochodnych akrydyno-
wych i hybrydów zawierających platynę jest nietrywialny, a jego kinetyka wskazuje na kilka
etapów w przebiegu procesu [33–36].
1.2.1
Energetyka interkalacji
Równie ważne z wiedzą na temat geometrii kompleksów tworzonych przez interkalujące czą-
steczki i DNA jest znajomość zmian termodynamicznych towarzyszących ich powstawaniu, po-
zwala ona bowiem zidentyfikować jakie składowe są odpowiedzialne i w jakim stopniu za powsta-
wanie kompleksu. Energetykę interkalacji policyklicznych, aromatycznych cząsteczek w DNA na-
leży rozważać w kontekście szerszych badań z ostatnich dziesięciu lat nad schematami podziału
energii swobodnej wiązania w molekularnych układach biologicznych [16, 37–40]. Wszystkie te
schematy zakładają addytywność pewnych wkładów do energii swobodnej i ich niezależność w
kierowaniu rozwojem termodynamicznym procesu jako całości.
Interkalacja składa się z kilku rozdzielnych mechanizmów, które wpływają na sumaryczny
rachunek energetyczny procesu do pewnego stopnia niezależnie. Właśnie addytywność tych
efektów składowych jest głównym założeniem podziału energii swobodnej reakcji powstawania
kompleksów interkalacyjnych [41]:
∆G
obs
= ∆G
konf
+ ∆G
t+r
+ ∆G
hyd
+ ∆G
poly
+ ∆G
mol
,
(1)
gdzie ∆G
obs
jest zaobserwowaną, eksperymentalną energią swobodną wiązania, odpowiadająca
tendencji do powstawania kompleksu ligand-DNA w roztworze. Jest ona powiązana z odpowied-
nią równowagową stałą wiązania K
int
równaniem Gibbsa:
∆G
obs
= −RT lnK
int
,
(2)
gdzie R jest stałą gazową i T jest temperaturą absolutną w kelwinach.
Składowym Równania 1 można przypisać kolejne mechanizmy zachodzące podczas reakcji
interkalacyjnej:
•
Niekorzystne zmiany konformacyjne, niezbędne dla utworzenia kompleksu ligand-DNA
(składowa ∆G
konf
). Są to przede wszystkim zaburzenia w lokalnej strukturze DNA, które,
jak opisano wcześniej, wynikają z rozsunięcia interkalowanych sąsiadujących par zasad o
około 3.4 ˚
A.
•
Utrata translacyjnych i rotacyjnych stopni swobody względem niezwiązanego ligandu (skła-
dowa ∆G
t+r
).

1 Wstęp
6
•
Zaburzenia zorganizowanej powłoki cząsteczek wody wokół interkalatora (przestrzeń mie-
dzy zasadami DNA jest hydrofobowa względem zewnętrznego roztworu), prowadzące do
korzystnych zmian entropowych (składowa ∆G
hyd
).
•
Efekt polielektrolityczny (ang. polyelectrolyte efekt), opisany składową ∆G
poly
i polegający
na uwolnieniu przeciwjonów związanych z interkalatorem kationowym. Ponadto, lokalne
wydłużenie i częściowe rozwinięcie się helisy DNA powoduje zwiększenie odległości po-
między kolejnymi grupami fosforowymi na fosforanowo-cukrowych nici DNA; to z kolei
prowadzi do redukcji zlokalizowanej gęstości elektronowej i przyczynia się do uwolnienia
dodatkowych przeciwjonów (na przykład Na
+
).
•
Utworzenie optymalnego kompleksu ligand-DNA, po wsunięciu się interkalatora między
docelowymi zasadami (składowa ∆G
mol
), poprzez oddziaływania niekowalencyjne.
Termodynamiczne badania Breslauera i współpracowników [42] pokazują, że wnioski oparte
wyłącznie na pomiarach zmiany energii swobodnej (∆G
obs
) mogą być mylące. Dwa kompleksy
mogą bowiem wykazywać niemal identyczne energie swobodne wiązania, które jednak mają
zupełne różne podłoża termodynamiczne, entropowe lub entalpowe. Energetyka oddziaływań
interkalującego ligandu z DNA należy zatem opisywać też kontekście zmian entalpii (∆H
obs
) i
entropii (∆S
obs
) jako odróżnialne wkłady do całkowitej energii swobodnej kompleksu:
∆G
obs
= ∆H
obs
− T ∆S
obs
(3)
Efektem w całości entropowym jest utrata stopni swobody podczas interkalacji, który może
być opisany składową ∆G
t+r
= T ∆S
t+r
w Równaniu 1. Średnia wartość strat entropowych pod-
czas interkalacji z powodu utraty stopni swobody szacuje się na ∆S
t+r
= 50±10 jednostek entro-
powych [37], co w temperaturze 25
o
C przekłada się na energię swobodną ∆G
t+r
= +14, 9(±3, 0)
kcal/mol. Ta niekorzystna energia musi zostać skompensowana przez inne, korzystne składowe
energii swobodnej aby interkalacja nastąpiła.
Kompleksy ligand-DNA są stabilizowane przez sumę energii swobodnych wszystkich wymie-
nionych efektów, co jest jednocześnie różnicą pomiędzy związanymi i niezwiązanymi stanami
ligandu i DNA. Do tej sumy wchodzą korzystne efekty - przede wszystkim zmiany hydrofobowe
(∆G
hyd
) i efekty polielektrolityczne (∆G
poly
). Równoważą one niekorzystne składowe, wynika-
jące ze zmian konformacyjnych (∆G
konf
) i utraty stopni swobody (∆G
t+r
). Sumaryczna energia
swobodna ∆G
obs
jest zazwyczaj bardzo mała w porównaniu do amplitudy poszczególnych skła-
dowych [43]. Wobec tego, niekowalencyjne oddziaływania molekularne, które zostały zbadane w
niniejszej pracy i są zawarte w członie ∆G
mol
, przyczyniają się do całkowitej energii wiązania w
stopniu, który nie zawsze można łatwo ocenić. W szczególności, w sytuacji gdy pozostałe człony
się w przybliżeniu równoważą, oddziaływania lokalne w miejscu interkalacji mogą decydować o
charakterze wiązania.
1 Wstęp
7
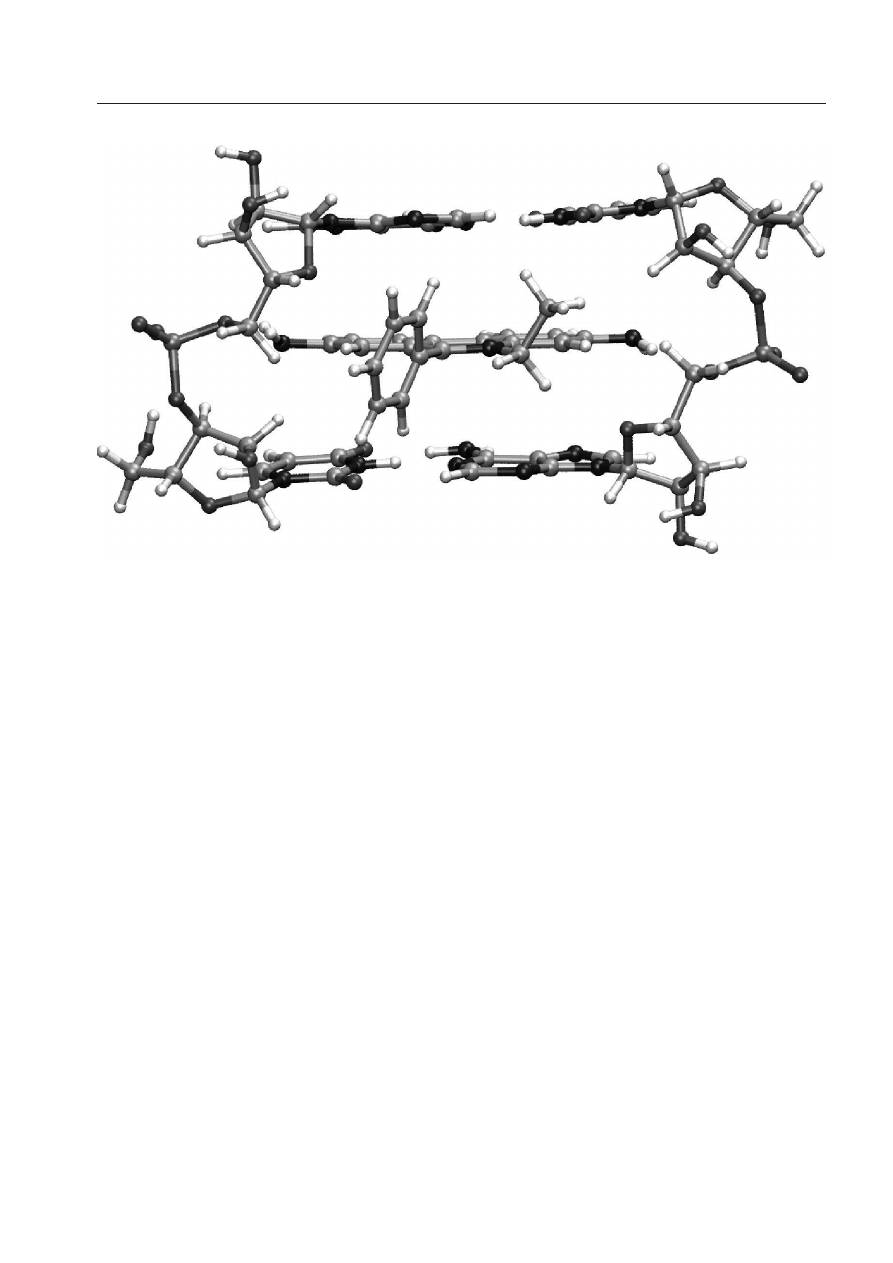
Rysunek 3:
Badany fragment kompleksu interkalacyjnego etydyny między parami zasad AU/UA,
wybrany z danych strukturalnych opublikowanych przez Jain and Sobell [24].
1.2.2
Interkalatory jako cząsteczki hybrydowe
Większość cząsteczek, które oddziałują z kwasami nukleinowymi mają struktury bardziej zło-
żone niż etydyna czy proflawina. Poza policyklicznym aromatycznym chromoforem, zawierają
dodatkowe podstawniki lub grupy boczne, które mają ogromny wpływ na energetykę wiązania,
często zmieniają charakter wiązania i definiują jego selektywność wobec sekwencji par zasad.
Takie podstawniki mogą mieć różną postać chemiczną, często spotykane rodzaje to grupa me-
tylowa, metoksylowa, ketylowa, hydroksylowa, różne grupy aminowe, lub bardziej rozbudowane
łańcuchy boczne w formie sperminy, spermadiny, cukrów, oligopeptydów, grup anilinowe lub
karboksamidowych. Obok interkalacji, te grupy wpływają na charakter wiązania oddziałując
elektrostatycznie lub hydrofobowo z grupami funkcjonalnymi DNA w małym i dużym rowka.
Niektóre takie grupy boczne oddziałują w rowkach bezpośrednio z fragmentami kilku następu-
jących po sobie par zasad, stąd ich oczywista rola w selektywności takich interkalatorów jak
adriamicyna, daunorubicyna, aktynomycyna D, nogalamycyna, i echinomycin.
Aktynomycyna D (zobacz Rys.1), silny lek antyrakowy, od dawna jest swoistym paradygma-
tem dla ligandów selektywnych na specyficzne sekwencje DNA. Wczesne badania hydrodyna-
micznych, kinetycznych, i termodynamicznych własności natywnych, heterogenicznych sekwencji
DNA i ich kompleksów z aktynomycyną D wykazały, że siła wiązania (K
int
od 1 do 5 x 10
6
M
−1
)
bezpośrednio koreluje z zawartością par zasad GC [21, 22].

1 Wstęp
8
1.2.3
Kwantowochemiczne badania kompleksów interkalacyjnych
Chemicznie rzecz biorąc, interkalację należy umieścić w rodzinie oddziaływań typu sandwiczo-
wych (ang. stacking), polegających na nakładaniu się aromatycznych fragmentów cząsteczek
tak, że ich płąskie strony są zwrócone ku sobie i równoległe. Ten niekowalencyjny tryb wią-
zania nie jest tak silny ani nie charakteryzuje się tak dobrze zdefiniowaną geometrią jak inne
oddziaływania między grupami funkcjonalnymi, na przykład punktowe wiązanie wodorowe. W
sandwiczowych oddziaływaniach mamy do czynienia z wielokrotnymi kontaktami miedzyczą-
steczkowymi pomiędzy nakładającymi się atomami w grupach aromatycznych i dużą różnorod-
nością możliwych grup funkcyjnych.
Oddziaływania grup aromatycznych typu stacking są ważne dla rozpoznawania molekular-
nego i samoorganizacji biocząsteczek i powszechnie występują w przyrodzie [44]. Przykładem
najbliższym tej pracy jest aromatyczne oddziaływanie sąsiadujących par zasad w DNA, zaob-
serwowane po raz pierwszy wraz z ogłoszeniem jego helikalnej struktury krystalograficznej [5].
Najczęściej stosowanym parametrem do określenia wpływu oddziaływania sąsiadujących par za-
sad jest temperatura topnienia T
M
, w której 50% podwójnej helisy jest zdysocjowana. T
m
rośnie
wraz z zawartością par GC, ale silnie zależy od konkretnej sekwencji i kompozycji kwasu nu-
kleinowego. Na podstawie teorii topnienia podwójnych łańcuchów helisowych, Zimm oszacował
tak zwaną energię swobodną stackingu, energię uzyskaną gdy zasady są nałożone na siebie w
konformacji helikalnej [45]. Oszacowana wartość wynosiła -29 kJ/mol na każdą parę zasad, co
stanowi główną część energii swobodnej stabilizującej helisę. Później zbadano eksperymental-
nie oddziaływania pojedynczych zasad i zmodyfikowanych zasad w roztworze [46], a ostatnio
wpływ zamiany końcowej zasady (ang. terminal base) na stabilizację całej helisy DNA [47, 48].
Ze wszystkich tych badań wynika, że stacking jest głównym czynnikiem stabilizującym struk-
turę spiralną DNA. Ponadto, zwiększanie rozmiarów powierzchni aromatycznej powoduje wzrost
temperatury topnienia helisy T
m
, czyli przycznia się do jej zwiększonej stabilizacji [47, 48].
Stosunkowo mało wyczerpujących badań teoretycznych zostało przeprowadzonych dla kom-
pleksów interkalacyjnych kwasów nukleinowych [49, 50], w porównaniu do dużej ilości prac do-
świadczalnych. Z drugiej strony, podobieństwo innych układów sandwiczowych pozwala je brać
jako punkt wyjścia, zwłaszcza stacking zasad nukleinowych [51–53]. Ze względu na wysoki
poziom technik obliczeniowych potrzebnych by dokładnie opisać interkalację DNA metodami
ab initio oraz wielkość tych układów, do niedawna nie było to możliwe, a dzisiaj kompleksy
aromatyczne pozostają jednym z najtrudniejszych problemów chemii obliczeniowej [50, 54].
Bazując na tym samym schemacie dekompozycji energii oddziaływania, który jest używany
w tej pracy, Hill i współpracownicy zauważyli, że dominujący człon korelacyjny w zasadach
DNA ułożonych w konformacji sandwiczowej jest w dużym stopniu równoważony przez inne
składowe energii oddziaływania, przede wszystkim przez efekty wymienne. Przez to elektro-
statyczna energia oddziaływania staje się bliska energii całkowitej i dobrze z nią koreluje dla

1 Wstęp
9
różnych zestawów ułożonych równolegle zasad. Medhi et al. niedawno zademonstrowali szcze-
gólną rolę oddziaływań elektrostatycznych w interkalacji dodatnio naładowanych chromoforów
między pary zasad [49]. W badaniach innych układów aromatycznych również położono nacisk
na ważną rolę elektrostatyki [55–57], lecz w innych z kolei zwracano uwagę na oddziaływania
nieelektrostatyczne [58].
1.3
Natura oddziaływań miedzycząsteczkowych
Oddziaływania miedzycząsteczkowe determinują większość własności gazowych, ciekłych, i sta-
łych substancji, są też odpowiedzialne za samoorganizację w zjawiskach supramolekularnych.
Według współczesnej teorii oddziaływań miedzycząsteczkowych [59,60], ich natura fizyczna jest
uniwersalna - taka sama dla klasycznie rozróżnianych typów niekowalencyjnych wiązań mię-
dzymolekularnych, czyli wiązania wodorowe, oddziaływania van der Waalsa, kompleksy z prze-
noszeniem ładunku, oraz inne. Te rodzaje wiązań międzycząsteczkowych różni tylko stosunek
odpowiednich, bardziej fundamentalnych komponentów w ich sumarycznej energii oddziaływa-
nia.
Do niedawna, nieempiryczne dekompozycje energii oddziaływania były ograniczone do ma-
łych układów, nie przekraczających 100-200 orbitali atomowych. Było to ograniczenie wyklu-
czające badania nad układami o znaczeniu biologicznym, i wynikało głównie z dużej liczby
transformowanych całek atomowych w konwencjonalnym rachunku wariacyjnym SCF [61]. Im-
plementacja bezpośredniej techniki SCF w wariacyjno-perturbacyjnej, hybrydowej dekompozycji
energii oddziaływania SCF ze zredukowanym błędem superpozycji bazy dla efektów wymien-
nych [62] pozwala znacznie powiększyć możliwości obliczeniowe po względem ilości uwzględnio-
nych orbitali atomowych (obecnie górna granica wynosi około 1700 orbitali atomowych).
1.3.1
Składowe energii oddziaływania miedzycząsteczkowego i hierarchia modeli
teoretycznych
Znajomość efektów fizycznych prowadzących do stabilizacji energii oddziaływania pomiędzy czą-
steczkami biologicznymi jest niezbędna do powiązania ich struktury i funkcji oraz do opracowania
przybliżonych metod, które mogłyby służyć do ich modelowania [59]. Według schematu dekom-
pozycji energii oddziaływania Morokumy-Zieglera [63], całkowitą międzycząsteczkowa energia
oddziaływania pomiędzy dwoma monomerami, ∆E
int
, można rozpisać jako:
∆E
int
= ∆E
el
+ ∆E
ex
+ ∆E
oi
,
(4)
gdzie ∆E
el
to elektrostatyczna energia oddziaływania, ∆E
ex
jest odpychającą energią wy-
miany, wynikającą z zasady Pauliego i odpowiedzialna za ograniczenia steryczne, oraz ∆E
oi
jest
energią oddziaływania orbitali elektronowych (ang. orbital interaction energy), która uwzględnia

1 Wstęp
10
ewentualne przenoszenie ładunku oraz efekty polaryzacyjne występujace skutek zrelaksowania
się gęstości elektronowych monomerów we wzajemnej obecności. Rozszerzeniem takiego sche-
matu dekompozycji energii oddziaływania jest analiza Kitaury-Morokumy [64], która wyraźnie
rozdziela ∆E
oi
dalej na wkłady pochodzące od efektów polaryzacyjnych i przenoszenia ładunku.
Niestety, schematy te obarczone są błędem superpozycji bazy [65, 66] (zobacz dyskusję i odno-
śniki w [61, 62, 67, 68]).
Oddziaływania międzycząsteczkowe zawsze wynikają z równowagi efektów wymienionych
wyżej. Równowaga ta się zmienia wraz z odległością i wzajemną orientacją rozważanych od-
działujących obiektów, a zmiany są największe gdy pomiędzy atomami występują odległości
kontaktowe. Dla niektórych sytuacji, niezbędne jest uwzględnienie wszystkich składowych od-
działywania [69], ale w innych przypadkach można, często na bardzo bliskich odległościach,
zaniedbać niektóre lub otrzymać wartościowe wyniki używając modeli przybliżonych albo czę-
ściowych [70]. Dlatego przydatne jest zbudowanie hierarchii modeli, która opisuje szereg skła-
dowych energii z dobrze zdefiniowanymy znaczenizmi fizycznymi i wymagających coraz większe
koszty obliczeniowe. Jednocześnie zostaje określone kilka poziomów teorii przez zaniedbanie
kolejnych składowych. Taką hierarchię stosowano w niniejszej pracy, a najwyższym poziomem
teorii użytym dla obliczania energii oddziaływania był rachunek Møllera-Plesseta drugiego rzędu
(MP2). Energię oddziaływania na poziomie MP2, ∆E
MP2
, podzielono w następujący sposób [61]:
∆E
MP2
= ∆E
(1)
el
+ ∆E
(1)
ex
+ ∆E
(R)
del
+ ∆E
(R)
corr
,
(5)
gdzie ∆E
(R)
del
zawiera wszystkie efekty wyższych rzędów wchodzące w skład energii oddziaływania
na poziomie SCF (∆E
SCF
) ze zrównoważoną korektą na BSSE [62], a ∆E
(R)
corr
reprezentuje efekty
korelacji elektronowej wewnątrz- i międzycząsteczkowej.
1.4
Przybliżone modele oddziaływań
1.4.1
Oddziaływania elektrostatyczne
Jedne z najbardziej popularnych składowych energii stabilizacji w układach o znaczeniu biolo-
gicznym to człon elektrostatyczny. Jest to naturalne, zważając na fakt że dużo cząsteczek w
nich jest naładowanych lub polarnych - chociażby DNA, które nosi periodyczny ujemny ładunek
wzdłuż podwójnej nici.
Swoją atrakcyjność oddziaływania elektrostatyczne zawdzięczają dużej anizotropii. Ta wy-
jątkowa cecha powoduje, że siły elektrostatyczne mogą być zarówno odpychające jak i przycią-
gające, zależnie od względnego usytuowania i orientacji molekuł. Nawet jeśli są mniejsze co do
wartości bezwzględnej niż inne rodzaje oddziaływań, potrafią decydować o wzajemnej geometrii
rozważanych monomerów. Tylko oddziaływania elektrostatyczna mogą zmienić swój znak po
odwróceniu jednej z cząsteczek o 180
o
, inne typy oddziaływań nie rozróżniają orientację molekuł

1 Wstęp
11
w tak wyraźny sposób.
W większości schematów dekompozycji typu Morokuma (Równania 4 i 5), elektrostatyczna
energia oddziaływania ∆E
el
reprezentuje klasyczne, kulombowskie oddziaływanie występujące
między rozkładami gestości elektronowej dwóch niezaburzonych monomerów (niezmodyfikowane
przez wzajemne oddziaływania), ρ
A
i ρ
B
, i może być zdefiniowane jako:
∆E
el
= −
Z Z
ρ
A
(r
A
)ρ
A
(r
B
)
|r
A
− r
B
|
dr
A
dr
B
(6)
Powyższe równanie jest wyrażeniem dokładnym, jednak niewygodnym do obliczeń ze względu
na skomplikowaną 6-wymiarową całkę i wymaganą wiedzę na temat rozkładu gęstości ładunków
w każdym punkcie przestrzeni. Stosuje się inne metody, na przykład ogólnione kwadratury
gaussowskie [71] lub bezpośrednie całkowanie numeryczne typu ’voxel-po-voxelu’ [72, 73].
Kiedy penetracja gęstości elektronowych rozważanych monomerów jest zaniedbywalna, czyli
gdy gęstości są oddalone lub szybko zanikają, wtedy Rrównanie 6 można przybliżyć rozwijając
|r
A
− r
B
| w szereg multipolowy. W wielu obszarach chemii i fizyki obliczeniowej (na przy-
kład dynamika molekularna) wykorzystuje się tylko pierwszy człon takich rozwinięć (monopol-
monopol). Dla wielu zagadnień chemii kwantowej i teorii potencjałów, konieczne jednak jest
uwzględnienie wyższych wyrazów żeby uzyskać zadowalającą dokładność.
Rozwinięcie |r
A
− r
B
| może mieć reprezentację w harmonikach sferycznych lub we współ-
rzędnych kartezjańskich jako szereg Taylora [74]. Obydwa rozwinięcia mają swoje zalety, a
wybór reprezentacji rozwinięcia jest często zależny od zagadnienia. W chemii fizycznej, forma-
lizm sferyczny ma długą tradycję, mimo że multipole kartezjańskie są naturalnym wyborem ze
względu na centralne miejsce kartezjańskich funkcji bazy typu gaussowskigo we współczesnych
programach kwantowo-mechaniznych. Szybkie metody obliczania przybliżonych oddziaływań
kulombowskich opartych na kartezjańskich rozwinięciach multipolowych [75, 76] lub teorii sfe-
rycznych tensorów [77–80] okazały się szczególnie przydatne do rozwiązywania chemicznych i
astrofizycznych zagadnień wielociałowych. Dla danego rzędu κ, multipole kartezjańskie zawie-
rają (κ+2)!/2!κ! elementów, podczas gdy sferyczne multipole mają tylko 2κ+1. Z drugiej strony,
obliczanie multipoli kartezjańskich i ich tensora oddziaływania jest ogólnie mniej kosztowne.
Po przekształceniu |r
A
− r
B
| w Równaniu 6 na szereg Taylora, można otrzymać następujące
asymptotyczne wyrażenie na energię oddziaływania elektrostatyczną [59] w zapisie tensorowym:
∆E
el
= T q
A
q
B
+ T
α
³
q
A
µ
B
α
− µ
A
α
q
B
´
+ T
αβ
³
1
3
q
A
Θ
B
αβ
+
1
3
Θ
B
αβ
q
B
− µ
A
α
µ
B
α
´
+
T
αβγ
³
1
15
q
A
Ω
B
αβγ
−
1
15
Ω
A
αβγ
q
B
−
1
3
µ
A
α
Θ
B
βγ
+
1
3
Θ
A
βγ
µ
B
α
´
+ ...
,
(7)
gdzie α, β, γ reprezentują współrzędne kartezjańskie sumowane po indeksach według kon-
wencji Einsteina i T
αβγ...
jest symetrycznym tensorem oddziaływania multipolowego postaci
∇
α
∇
β
∇
γ
...R
−1
(wektor R = r
A
− r
B
łączy środki ciężkości rozkładów A i B). Multipole q,
µ, Θ, Ω to odpowiednio ładunek, wektor dipolowy, macierz kwadrupolowa, i trójwymiarowa

1 Wstęp
12
macierz oktupolowa. Elementy multipoli są określone odpowiednimi całkami multipolowymi:
q =
R
ρ(r)dr
µ
α
=
R
ρ(r)αdr
(α = x, y, z)
Θ
αβ
=
R
ρ(r)αβdr
(αβ = x, y, z)
(8)
Ω
αβγ
=
R
ρ(r)αβγdr
(αβγ = x, y, z)
...
Ponieważ tensory momentów multipolowych charakteryzują sie dużą symetrią (na przykład
Θ
xxy
= Θ
xyx
= Θ
yxx
), Równanie 7 można zapisać prościej w postaci sum potrójnych po zesta-
wach rzędów współrzędnych dwóch oddziałujących rozwinięć momentów multipolowych:
∆E
el
=
∞
X
klm
∞
X
k
0
l
0
m
0
(−1)
k
0
+l
0
+m
0
M
A
klm
T
k+k
0
,l+l
0
,m+m
0
M
B
k
0
l
0
m
0
,
(9)
gdzie M
A
klm
jest kartezjańskim momentem multipolowym rozkładu gęstości ρ
A
(r) o rzędach
k, l, m, zdefiniowanym jako
M
A
klm
=
1
k!l!m!
Z
ρ
A
(r)x
k
y
l
z
m
dr.
(10)
W kontekście Równania 9, tensor oddziaływania ma postać:
T
klm
(R) =
∂
κ
∂R
k
x
∂R
l
y
∂R
m
z
1
R
,
(11)
gdzie κ = k + l + m.
Grupując momenty multipolowe określonych Równaniem 10 o tym samym sumarycznym
rzędzie κ można utworzyć κ-wymiarowy tensor multipolowy, którego składowe są indeksowane
tak jak w Równaniu 9, jako że ze względu na symetrię podanie współrzędnych dla wszystkich
wymiarów danego multipola jest równoważne z podaniem wykładników dla trzech współrzędnych
(na przykład, M
110
= Ω
xy
= Ω
yx
). Multipol o rzędzie κ ma κ
3
składowych, w tym (κ + 2)!/2!κ!
niezależnych. Kilka pierwszych multipoli można rozpisać jako:
κ = 0
q
i
= M
000,i
κ = 1
µ
i
= (M
100,i
, M
010.i
, M
001,i
)
(12)
κ = 2
Ω
i
=
M
200,i
M
110,i
M
101,i
M
110,i
M
020,i
M
011,i
M
101,i
M
011,i
M
002,i
,
gdzie q
i
, µ
i
, i Ω
i
są odpowiednio ładunkiem, dipolem, oraz kwadrupolem dla rozkłądu gęstości i.
Następne multipole to kwadrupol Θ
i
(κ = 3, 27 składowych, w tym 10 niezależnych), heksadeka-

1 Wstęp
13
pol Ψ
i
(κ = 4, 81 składowych, w tym 15 niezależnych), ditrentapol Γ
i
(κ = 5, 127 składowych, w
tym 21 niezależnych), i tak dalej. Tensory momentów multipolowych są symetryczne względem
zamian współrzędnych, czyli zawierają nadmiarową informację. Zatem implementacje oparte na
wzorach rozważających tylko ich elementy niezależne (takie jak Równanie 9 dla oddziaływania)
będą bardziej efektywne.
Wyrażenie na oddziaływanie momentów multipolowych w Równaniu 9 można podsumować
inaczej i wyrazić używając bezśladowych momentów multipolowych Buckinghama [74]:
¯
M
A
klm
= (−1)
κ
1
(κ)!
Z
drρ(r)|r|
2κ+1
∂
κ
∂x
k
∂y
l
∂z
m
1
|r|
,
(13)
które należy podstawić w wyrażeniu (9) ze współczynnikiem 2
κ
κ!/(2κ)! (tensor oddziaływa-
nia pozostaje ten sam).
Obszerne badania eksperymentalne i teoretyczne dla małych układów molekularnych wska-
zują, że energia oddziaływania multipolowego, nawet w obecności niezaniedbywalnego członu
penetracyjnego, ∆E
(1)
el,pen
, często determinuje uporządkowanie w polarnych i naładowanych kom-
pleksach [60], ponieważ jest ono bardziej wrażliwe na wzajemne położenie oddziałujących rozkła-
dów ładunku. Wówczas, jeśli oddziaływanie odpowiednich rozwinięć multipolowych jest zbieżne,
mamy do czynienia z dwoma addytywnymi częściami energii elektrostatycznej:
∆E
el
= ∆E
el,mtp
+ ∆E
el,pen
.
(14)
Zatem daleki zasięg członu multipolowego (w porównaniu z penetracyjnym, który zanika
dużo szybciej) oraz jego większa anizotropowość powodują, że to on determinuje optymalne
wzajemne położenia dwóch naładowanych monomerów.
1.4.2
Wielocentrowe rozwinięcia momentów multipolowych
W praktyce, opisywanie rozkładów gęstości elektronowej dużych obiektów, takich jak całe czą-
steczki, przez jedno rozwinięcie multipolowe nie jest efektywne. Zwłaszcza na bliskich odle-
głościach, multipole molekularne nie potrafią precyzyjnie odtworzyć kształt rozkładu gęstości
elektronowej i jej oddziaływań. Informację zawartą w rozwinięciu dla danego rozkładu gęstości
można zwiększyć rozważając rozwinięcia multipolowe wokół wielu centrów znajdujących sie w
danej cząsteczce. Najbardziej naturalnym wyborem położenia takich centrów są atomy - roz-
kład gęstości elektronowej w cząsteczce jest wtedy opisany zestawem rozwinięć multipolowych,
z jednym dla każdego atomu i = 1..N
A
. Niestety, momenty atomowe M
klm,i
nie mogą być jed-
noznacznie zdefiniowane, ponieważ nie ma jednego sposobu na rozdział funkcji falowej i gęstości
elektronowej pomiędzy atomami. Można przydzielić gęstość elektronową centrowi na podsta-
wie nakładania się funkcji falowych w różnych położeniach lub posługując się jednym z wielu
geometrycznych metod podziału końcowej gęstości elektronowej [81].

1 Wstęp
14
Przykładem geometrycznego rozdziału gęstości elektronowej jest teoria AIM (ang. atoms in
molecules) opracowana przez Badera [82]. Zdefiniowany jest w tej metodzie basen dla każdego
atomu, Ω
i
, jako dyskretny obszar w przestrzeni, ograniczony powierzchniami międzyatomowymi
(IAS), które spełniają warunek zerowego strumienia:
∇ρ(r) · n(r) = 0
∀r ∈ IAS,
(15)
gdzie ∇ρ(r) jest polem wektorowym gęstości elektronowej, a n(r) jest normalną do powierzchni
w punkcie r. Atomowe momenty M
i
dla odpowiednich basenów Ω
i
są następnie obliczane z
formy całkowej:
M
klm,i
=
Z
Ω
i
ˆ
M
klm
ρ(r)dr,
(16)
gdzie ˆ
M
klm
jest odpowiednim operatorem momentu. Ostatnio Popelier badał stosowalność mo-
delu AIM do obliczania elektrostatycznych energii oddziaływania dla różnych cząsteczek orga-
nicznych [83–86], w tym pary zasad DNA [87].
W tej pracy wykorzystany jest inny sposób, w którym atomom są przydzielane wkłady po-
chodzące od ich orbitali atomowych budujących całościową funkcję falową układu. Multipol dla
atomu i o rzędzie klm, czyli M
klm,i
, można wyrazić we współrzędnych kartezjańskich korzystając
ze znanej gęstości elektronowej na jego orbitalach:
M
klm,i
=
D
x
k
y
l
z
m
E
i
= Z
i
x
k
i
y
l
i
z
m
i
−
AO
X
I∈i
AO
X
J
P
IJ
D
I|x
k
y
l
z
m
|J
E
,
(17)
gdzie Z
i
jest ładunkiem jądrowym atomu i,
D
I|x
k
y
l
z
m
|J
E
jednoelektronową całką multipolową
rzędu klm dla orbitali atomowych I i J, a D
IJ
odpowiadającym im elementem macierzy gę-
stości. Tak zdefiniowane momenty atomowe sumują się do wartości oczekiwanej odpowiedniego
operatora momentu molekularnego,
D
x
k
y
l
z
m
E
=
P
i
D
x
k
y
l
z
m
E
i
.
Teoretycznie można posługiwać się zestawem rozwinięć wokół dowolnej ilości i dowolnie po-
łożonych centrów. Jednak naturalnym przedłużeniem multipoli atomowych obliczonych na pod-
stawie równania 17 są rozwinięcia multipolowe na wiązaniach łączących poszczególne atomy.
Całkowita energia oddziaływania pomiędzy dwoma wielocentrowymi zestawami rozwinięć mul-
tipolowych A i B będzie sumą przyczynków pochodzących od każdych dwóch par z tych zestawów
według równania 9:
∆E
el,mtp
=
X
i∈A
X
j∈B
Ã
∞
X
klm
∞
X
k
0
l
0
m
0
(−1)
k
0
+l
0
+m
0
M
A
klm,i
T
k+k
0
,l+l
0
,m+m
0
M
B
k
0
l
0
m
0
,j
!
.
(18)

1 Wstęp
15
1.5
Cele pracy
Głównym celem niniejszej pracy jest analiza oddziaływań w kompleksach interkalator-DNA,
opierająca się na fragmentach struktur krystalograficznych (zobacz Rys.3). Struktury chemiczne
popularnych interkalatorów można zobaczyć na Rys.1. Obecna analiza skupia się na oddziały-
waniach kluczowych dla pojęcia interkalacji, czyli oddziaływań występujących między chromo-
forem interkalatora i najbliższymi zasadami nukleinowymi. W niniejszej pracy wykorzystano
trzy krystalograficzne struktury kompleksów interkalacyjnych:
•
etydyna między parami zasad UA/AU (skrót Eth-UA/AU) [24],
•
etydyna między parami zasad CG/GC (skrót Eth-CG/GC) [25],
•
proflawina między parami zasad CG/AU (skrót Pf-CG/AU) [26].
Wszystkie trzy struktury podane wyżej zawierają interkalatory kationowe, o ładunku for-
malnym +1. Dla porównania, zbadano też zmodyfikowany kompleks Pf-CG/AU, w którym
proflawina była neutralna po usunięciu kationu wodorowego.
Punktowe oddziaływania w badanych strukturach zostały przeanalizowane przez ich podział
na składowe, które dają pełniejszy obraz charakteru oddziaływań i sił odpowiedzialnych za
stabilizację tego rodzaju kompleksów. Dyskusja skupia się na kompleksie Eth-AU/UA, dla
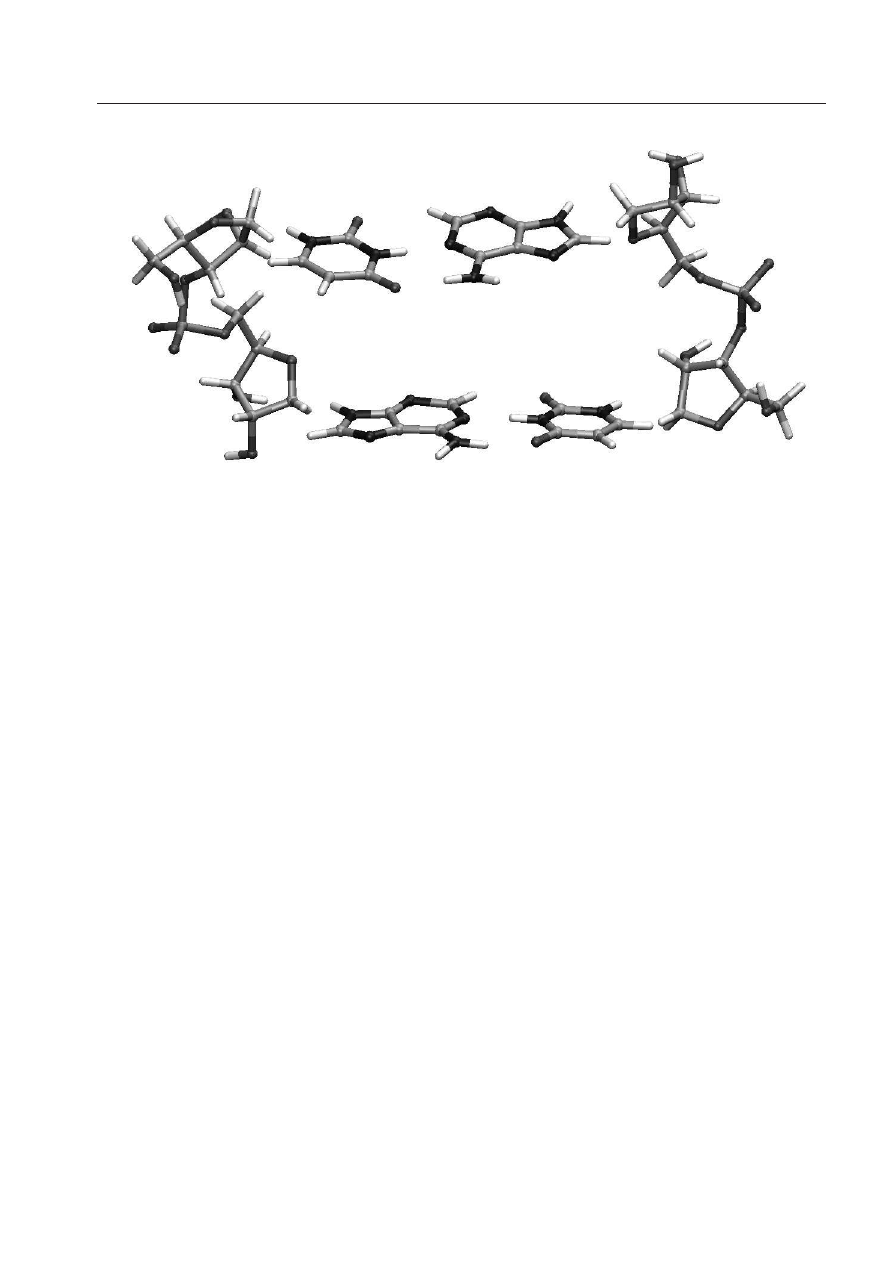
którego dokonano dodatkowe obliczenia. Fragment oryginalnej struktury, zawierający miejsce
interkalacyjne Eth-AU/UA, widać na Rys.3.
Ze względu na duże rozmiary badanych układów, zostały one podzielone na mniejsze części.
Fragmenty nici kwasu nukleinowego oddzielono od zasad (zobacz Rys.5). Etydyna z kolei została
podzielona na chromofor i podstawniki boczne (Rys.4), i ta praca skupia się przede wszystkim
na chromoforze. Cząsteczka proflawina nie ma podstawników bocznych, wobec czego rozważano
ją w całości. Takie podejście uznaje intuicyjną niezależność chromoforu i tych części bocznych
dla zjawiska interkalacji i zostało obrane wielokrotnie w przeszłości, między innymi w podobnym
badaniu przeprowadzonym przez Medhi et. al. [49]. Podobnie jak tam, w obecnej pracy zada-
wane jest pytanie czy ułożenie chromoforu interkalatora między zasadami kwasu nukleinowego
jest dyktowane wyłącznie przez oddziaływania lokalne (przede wszystkim elektrostatyczne) czy
też mają wpływ, i do jakiego stopnia, podstawniki boczne.
Chcąc scharakteryzować okolice miejsca wiązania interkalacyjnego, oddziaływanie elektro-
statyczne chromoforu z zasadami została zbadana w płaszczyźnie interkalacji używając atomo-
wych rozwinięć multipolowych CAMM. Dla wybranych punktów na tej płaszczyźnie przepro-
wadzono też analizę całkowitej energii oddziaływania. Pobudką dla takiego postępowania było
przypuszczcenie, że multipolowe oddziaływania elektrostatyczne mogą służyć do przynajmniej
jakościowego modelowania mechanizmu interkalacji, i w związku z tym są w stanie odtworzyć
miejsce wiązania interkalacyjnego chromoforu pomiędzy zasadami kwasu nukleinowego.
2 Metody Obliczeniowe
16
2
Metody obliczeniowe
2.1
Przygotowywanie struktur i metodologia badań
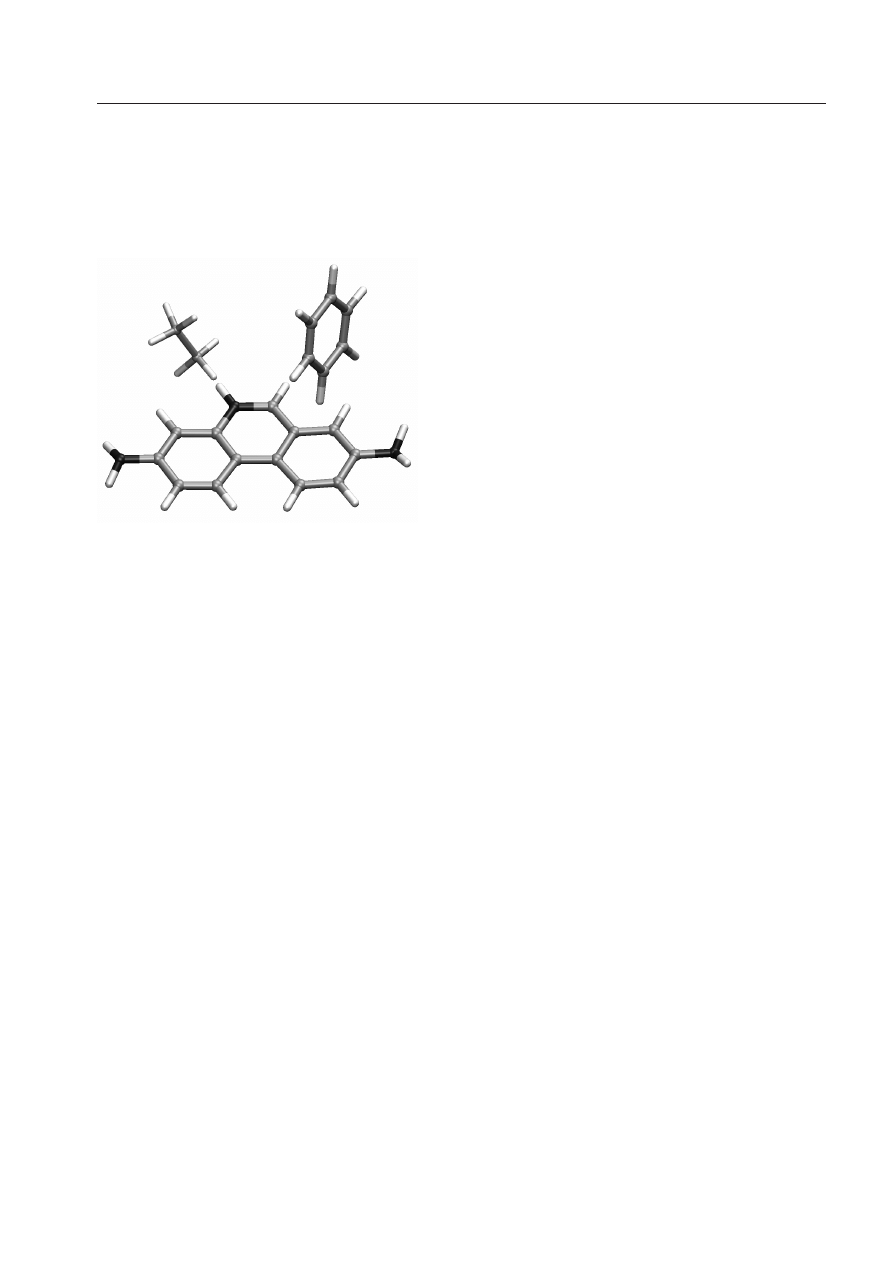
Rysunek 4:
Podział etydyny ze struktury
Eth-AU/UA (pokazanej na Rys.3) na czę-
ści: chromofor, łańcuch boczny, oraz pier-
ścień boczny.
Współrzędne atomów we wszystkich trzech bada-
nych kompleksach interkalacyjnych (Eth-AU/UA
[24], Eth-CG/GC [25], oraz Pf-CG/AU [26]) pocho-
dziły z krystalograficznych danych dyfrakcyjnych
promieniowania rentgenowskiego. Wobec tego, bra-
kuje w nich atomów wodoru. Po wycięciu z pierwot-
nych struktur fragmentów używanych w tej pracy
(dla Eth-AU/UA fragment ten jest widoczny na
Rys.3), atomy wodoru dodano za pomocą programu
Reduce [88]. Następnie współrzędne atomów wo-
doru zostały zoptymalizowane w programie GA-
MESS [89] używając hamiltonianu modelowego PM3
(współrzędne wszystkich ciężkich atomów zamro-
żono). Po optymalizacji, RMS zmian współrzędnych
atomów nigdy nie przekraczało 0,4 ˚
A.
Zoptymalizowane struktury poddano podzia-
łowi, żeby wyłonić te fragmenty najbardziej istotne dla oddziaływań aromatycznych w kom-
pleksie interkalacyjnym i jednocześnie zredukować potrzebny czas obliczeniowy najbardziej wy-
magających etapów analizy:
•
etydyna → chromofor + łańcuch boczny + pierścień boczny (patrz Rys.4),
•
proflawina: nie dzielona,
•
fragmenty kwasy nukleinowego → cztery zasady + nici boczne (patrz Rys.5),
Tak więc etydynę podzielono na chromofor, który znajduje się bezpośrednio pomiędzy za-
sadami, łańcuch boczny i pierścień boczny. Większość rozważań w obecnej pracy poświęcono
chromoforowi, jako że jest on centralnym elementem kompleksu interkalacyjnego. Proflawina
nie posiada podstawników bocznych, więc była rozważana w obliczeniach w całości. Frag-
menty kwasu nukleinowego podzielono na nici boczne i zasady. W analizie energii oddziaływań
uwzględniono jedynie te cztery najbliższe zasady, a z fragmentów nici bocznych skorzystano póź-
niej tylko dla rozważania efektów sterycznych. We wszystkich przypadkach, wiązania przecięte
podczas dzielenia kompleksu na części zakończono pojedynczymi wodorami. W ten sposób uzy-
skano współrzędne jednego chromoforu i czterech zasad dla każdego kompleksu interkalacyjnego,
które były używane bezpośrednio w dalszych obliczeniach.
Energie oddziaływania były we wszystkich przypadkach obliczane oddzielnie dla każdej pary
chromofor-zasada (cztery pary dla każdej struktury). Te energie sumowano do całkowitego od-
2 Metody Obliczeniowe
17
Rysunek 5:
Podział fragmentu kwasu nukleinowego struktury Eth-AU/UA (pokazanej na Rys.3) na
części: nici boczne i cztery zasady (dwie pary adeniny-uracylu).
działywania chromoforu z najbliższymi zasadami. Takie podejście do oddziaływań w badanych
układach można zapisać, symbolicznie, jako:
∆E =
X
4 zasady
∆E(chromof or − zasada)
(19)
Postępując w wyżej opisany sposób, zaniedbuje się oddziaływania wielociałowe, w szcze-
gólności polaryzację par zasad związanych wodorowo. Reha et al. [50], na podstawie rygory-
stycznych obliczeń ab initio, podkreślają że elektrostatyczne i jednoelektronowe własności pary
związanych zasad znacząco sie różnią od tych samych własności pojedynczych zasad, oraz że
najmniejszy zadowalajacy model interkalacji musi uwzględniająć kompleks chromofor-para za-
sad. W tym samym badaniu pokazali, dla kompleksu etydyna-AT/TA, że dalsze rozszerzenie
modelu do dwóch par zasad (górnej i dolnej) nie wprowadza dużej zmiany w oddziaływaniu
interkalatora. Nie zapominając o tych faktach, w tej pracy zbadano przydatność modelu po-
sługującego się pojedynczymi zasadami jako prostszy sposób oceniania energii stabilizujących
kompleksów interkalacyjnych i opisania ułożenia chromoforu interkalatora.
2.2
Nieempiryczna analiza energii oddziaływań
W hybrydowym podejściu dekompozycyjnym opartym na bezpośrednim rachunku SCF [62],
zrównoważona (ang. counterpoise corrected ) energia oddziaływania na poziomie SCF, ∆E
SCF
,
zostaje rozparcelowana na pierwszorzędową energię elektrostatyczną ∆E
(1)
el
, pierwszorzędową
energię wynikającą z oddziaływania wymiennego ∆E
(1)
ex
, oraz człon delokalizacyjny zawierający
przyczynki wyższych rzędów ∆E
(R)
del
. Wszystkie te energie są zdefiniowane konsekwentnie w bazie

2 Metody Obliczeniowe
18
dimeru (D), eliminując błąd superpozycji bazy (BSSE) przez zrównoważoną korektę [65, 66]:
∆E
SCF
= ∆E
(1)
el
+ ∆E
(1)
ex
+ ∆E
(R)
del
.
(20)
Składowa elektrostatyczna tutaj zostaje obliczona bezpośrednio z wyrażenia perturbacyj-
nego:
∆E
(1)
el
=
P
a
P
b
Z
a
Z
b
R
−1
ab
+
P
r
P
s
P
t
P
u
D
A
rs
(D)D
B
tu
(D) hrs|tui
−
P
t
P
u
P
a
D
A
tu
(D)
D
|Z
a
R
−1
1a
|u
E
−
P
r
P
s
P
b
D
B
rs
(D)
D
r|Z
b
R
−1
1b
|s
E
,
(21)
gdzie macierze gęstości monomerów, D
A
rs
(D) i D
B
tu
(D), uzyskano w bazie dimeru D = A + B.
Pozostałe oznaczenia w Równaniu 21 to: Z
a
, Z
b
- ładunki jądrowe atomów a i b; hrs|tui - całka
odpychania elektronowego (ang. electron repulsion integral);
D
r|Z
b
R
−1
b
|s
E
- całka potencjału
jądrowego (ang. nuclear attraction integral ). Sumowania po r, s, t, i u przebiegają bazę orbitali
atomowych dimeru, po a i b przebiegają tylko orbitale atomowe atomów A i B, odpowiednio.
Energia wynikająca z oddziaływania wymiennego w tym schemacie jest zdefiniowana jako:
∆E
(1)
ex
= ∆E
(1)
− ∆E
(1)
el
,
(22)
gdzie ∆E
(1)
jest energią dimeru obliczoną w bazie dimeru po pierwszej iteracji SCF z poprawką
na błąd superpozycji bazy (BSSE), zaczynając od zortogonalizowanej funkcji falowej Schmidta
dla monomerów.
Człon delokalizacyjny w Równaniu 20, ∆E
(R)
del
, zawiera przyczynki kilku oddziaływań wyż-
szego rzędu zdefiniowanych w teorii perturbacyjnej przystosowanej do symetrii (Symmetry
Adapted Perturbation Theory - SAPT) (patrz [61]): oddziaływanie indukcyjne, wymienno-
indukcyjne, sprzężone HF (coupled HF), i wymienno-deformacyjne:
∆E
(R)
del
= ∆E
SCF
− ∆E
(1)
(23)
Dalej, człon korelacyjny ∆E
(R)
corr
[90], zawierający przyczynki od dyspersji międzycząstecz-
kowej i korelacji wewnątrzcząsteczkowej (elektrostatyczna, wymienna, i indukcyjna), uzupełnia
wyżej zdefiniowany człon SCF, i może być zdefiniowany na poziomie MP2 jako:
∆E
(R)
corr
= ∆E
MP2
− ∆E
SCF
(24)
Zatem całkowita energia na poziomie MP2 można rozpisać tak jak w Równaniu 5. Jeśli ener-
gię elektrostatyczną się podzieli jeszcze na człon multipolowy ∆E
(1)
el,mtp
i penetracyjny ∆E
(1)
el,pen

2 Metody Obliczeniowe
19
(patrz Równanie 14, to cała energia na poziomie MP2 będzie następującą sumą:
∆E
MP2
= ∆E
(1)
el,mtp
+ ∆E
(1)
el,pen
+ ∆E
(1)
ex
+ ∆E
(R)
del
+ ∆E
(R)
corr
,
(25)
gdzie kolejno zdefiniowane człony w sposób naturalny odpowiadają hierarchii modeli teoretycz-
nych o stopniowo rosnącej złożoności, kosztowności, i dokładności: elektrostatyczny ∆E
(1)
el
,
pierwszego rzędu ∆E
(1)
, SCF ∆E
SCF
, i drugiego rzędu ∆E
MP2
. Człon ∆E
(1)
el,mtp
został obli-
czony na podstawie analizy DMA (uwzględniane są tutaj co najwyżej oktupole), a składowa
penetracyjna jako jego różnica względem całego oddziaływania elektrostatycznego, ∆E
(1)
el,pen
=
∆E
(1)
el
− ∆E
(1)
el,mtp
.
Ten schemat analizy energii oddziaływania jest używany do badań różnych układów, w tym
kryształów molekularnych [67, 68], miejsc aktywnych enzymów [69, 91–93], i DNA [53].
2.3
Kumulatywne Atomowe Momenty Multipolowe (CAMM)
Atomowe momenty multipolowe uzyskane za pomocą Równania 17 można przekształcić do lo-
kalnego układu współrzędnych każdego atomu, (x
i
y
i
z
i
), przez odpowiednią iteracyjną rekombi-
nację, uzyskując Kumulatywne Atomowe Momenty Multipolowe M
CAM M
klm,i
(Cumulative Atomic
Multipole Moments - CAMM) [94–96]:
M
CAM M
klm,i
= M
klm,i
−
k
X
k
0
≥0
l
X
l
0
≥0
m
X
m
0
≥0
k
0
l
0
m
0
6=klm
k
k
0
l
l
0
m
m
0
× x
k−k
0
i
y
l−l
0
i
z
m−m
0
i
M
CAM M
k
0
l
0
m
0
,i
.
(26)
Transformacja w Równaniu 26 powoduje, że wyrażone za jego pomocą momenty CAMM są
niezmiennicze względem każdego kartezjańskiego układu odniesienia dla pewnej transformacji
unitarnej. Jest to własność szczególnie przydatna gdy rozważa się dużą liczbę różnych położeń
danej cząsteczki reprezentowanej przez zestaw rozwinięć multipolowych. Translacja nie zmienia
multipoli CAMM, a inne przekształcenia multipola o rzędzie κ dokonuje się za pomocą zwykłej
macierzy rotacji:
˜
M
CAM M
klm,i
= (%
O→ ˜
O
)
κ
× M
CAM M
klm,i
,
(27)
gdzie %
O→ ˜
O
jest macierzą rotacji przekształcającą układ współrzędnych w wybrany sposób.
Ogólna postać energii oddziaływania pomiędzy poszczególnymi parami multipoli (ładunek-
ładunek, dipol-ładunek, dipol-dipol, kwadrupol-ładunek, i tak dalej) jest zawarta w sumarycz-
nym oddziaływaniu pojedynczych momentów multipolowych należących do rozwinięć multi-
polowych dwóch monomerów, M
klm,i
T
k+k
0
,l+l
0
,m+m
0
M
k
0
l
0
m
0
,j
(patrz Równanie 9). W 1982 roku
Cipriani i Silvi [97] wyprowadzili jawny wzór na elementy tensora oddziaływania multipolowego

2 Metody Obliczeniowe
20
wyrażone we współrzędnych kartezjańskich (σ = s + t + u i κ = k + l + m):
T
klm
(r) =
(−1)
κ
k!l!m!
2
κ
|r|
κ
[k/2]
X
s=0
[l/2]
X
t=0
[m/2]
X
u=0
"
(−1)
σ
(2κ − 2σ)!
s!t!u!(k − 2s)!(l − 2t)!(m − 2u)!(κ − σ)!
×
×
Ã
r
x
|r|
!
k−2s
Ã
r
y
|r|
!
l−2t
Ã
r
z
|r|
!
l−2m
(28)
Powyższy wzór jest nadal podstawowym wzorem używanym do obliczania składowych ten-
sora oddziaływania multipolowego. Można wyprowadzić dodatkowe, rekurencyjne zależności,
które pozwalają zredukować koszty obliczeniowe tych elementów [98].
Dla momentów bezśladowych, opisanych równaniem 13, energię oddziaływania pomiędzy
dwoma tensorami multipolowymi M
(κ),i
i M
(κ
0
),j
(M
(0),i
= q
i
, M
(1),i
= µ
α,i
, M
(2),i
= Ω
αβ,i
, itd.)
można napisać symbolicznie jako:
∆E
ij
(κκ
0
)
=
(−1)
κ+1
2
κ+κ
0
κ!κ
0
!
(2κ)!(2κ
0
)!
M
(κ),i
[κ]
(κ)
T
(κ
0
)
ij
[κ
0
]M
(κ
0
),j
,
(29)
gdzie operatory [κ] i [κ
0
] oznaczają kontrakcje rzędu κ i κ
0
, odpowiednio, pomiędzy dwoma ten-
sorami, a operator
(κ)
T
(κ
0
)
ij
jest symetrycznym tensorem oddziaływania rzędu (κ + κ
0
). Traktując
multipole jako wielowymiarowe wektory, operuje się wszystkimi ich elementami, których więk-
szość jest zależna dla wyższych rzędów. Dlatego, mimo zwięzłości zapisu tensorowego Równania
29, bardziej wydajna do zastosowań numerycznych jest implementacja algorytmów operującymi
wyłącznie elementami niezależnymi (tak jest w przypadku Równania 9).
Z wyrażeń na energię oddziaływania w Równaniach 9 i 29 wynika następująca, przydatna w
ich realizacji numerycznej relacja symetrii:
∆E
ij
κκ
0
= (−1)
κ+κ
0
∆E
ji
κ
0
κ
.
(30)
Całkowita energia oddziaływania dwóch rozwinięć multipolowych jest nieskończonym sze-
regiem oddziaływań pomiędzy parami momentów multipolowych (który często jest rozbieżny
asymptotycznie). W praktyce trzeba zakończyć ten szereg na jakimś możliwie najmniejszym
wyrazie. Zazwyczaj uwzględnia się człony oddziaływania pomiędzy multipolami o sumarycz-
nym rzędzie nie większym od wybranego rzędu oddziaływania K = κ + κ
0
. Przerywając energię
oddziaływania rozwinięć multipolowych w ten sposób, uzyskuje się gwarancję że wynik nie zależy
od jednakowych translacji obu rozważanych monomerów [99], czyli nie zależy też od przesunię-
cia układu współrzędnych. Zatem energia oddziaływania zerowego rzędu (K = 0) uwzględnia
tylko oddziaływania monopol-monopol, czyli pomiędzy ładunkami punktowymi. Kolejny rząd
odziaływania (K = 1) zawiera człony oddziaływania monopol-monopol oraz dipol-monopol.
Oddziaływania pomiędzy rozwinięciami multipolowymi różnych rodzajów używa się w wielu
badaniach do przybliżenia oddziaływań elektrostatycznych i wielociałowych [74–86], a przy-

2 Metody Obliczeniowe
21
datność multipoli typu CAMM została zilustrowana w pracach dotyczących miejsc aktywnych
enzymów [70,100], kwasów aminowych [101], polipeptydów [102], modeli solwatacji [103], i nawet
oddziaływań wewnątrzcząsteczkowych [104].
2.4
Oprogramowanie
Struktury krystalograficzne modyfikowano głównie za pomocą programu InsightII firmy Accelrys
i własnych narzędzi skryptowych. Do wizualizacji struktur używano ogólnodostępny program
VMD [105]. Wykresy generowano programem Gnuplot [106], a wyniki analizowano i przetwa-
rzano własnym narzędziami skryptowymi.
Energie oddziaływani pomiędzy wydzielonymi monomerami w kompleksach interkalacyjnych
(chromofor i cztery zasady) obliczono na poziomie MP2 z funkcją bazy 6-31G(1d,1p), i poddano
je procedurze dekompozycji według Równania 25 używając zmodyfikowanej wersji [67] kodu
GAMESS [89].
Kumulatywne atomowe momenty multipolowe typu CAMM otrzymano według Równania 26
używając własnego kodu sprzężonego z pakietem GAMESS [89]. Za pomocą tego kodu, uzyskano
momenty multipolowe do czwartego rzędu (heksadekapole) na podstawie skorelowanej macierzy
gęstości MP2 i bazy funkcyjnej 6-31G(1d,1p). Momenty multipolowe następnie modyfikowano
i ich energie oddziaływania obliczano według Równań 9 i 28 lub 29 (otrzymane wyniki są iden-
tyczne), korzystając z własnego kodu napisanego w języku FORTRAN oraz Python [107, 108].
W Dodatku 6.2 znajduje się listing wybranych fragmentów używanego kodu.

3 Analiza oddziaływań w wybranych strukturach krystalograficznych
22
3
Analiza oddziaływań w wybranych strukturach krysta-
lograficznych
Pierwszym etapem analizy trzech wybranych kompleksów interkalacyjnych było wyznaczenie
składowych energii oddziaływania na poziomie MP2, ∆E
MP2
, według opisanego wcześniej sche-
matu dekompozycyjnego (patrz Równanie 25). Tabela 1 przedstawia szczegółowe wartości tych
składowych i odpowiednich poziomów teorii dla oddziaływania chromoforu etydyny z najbliż-
szymi czterema zasadami w kompleksie Eth-AU/UA. Największe człony, mianowicie korelacyjny
∆E
(R)
corr
i wymienny ∆E
(1)
ex
, mają we wszystkich przypadkach podobne wartości i przeciwne znaki,
i przez to prawie się równoważą w energii całkowitej. Jest to prawdą zarówno dla wkładów pocho-
dzących od wszystkich poszczególnych zasad, jak i dla ich sumy, która stanowi miarę całkowitej
energii oddziaływania chromoforu w miejscu interkalacji według Równania 19. Metody, które
zaniedbują jeden z tych komponentów (rachunki Hartree-Fock i DFT nie uwzględniają efektów
korelacyjnych) wyraźnie nie nadają się do badania kompleksów interkalacyjnych. Obserwa-
cja ta zgadza się poprzednimi raportami dotyczących interkalacji [50] oraz układów równolegle
położonych zasad nukleinowych [53,54]. Należy jednak pamiętać, że używana baza funkcyjna, 6-
31G(1d,1p), jest bazą dosyć skromną dla opisywania efektów korelacyjnych, i w tym przypadku
prawdopodobnie daje dla nich zbyt niskie oszacowanie. Można więc spodziewać, że składowa
∆E
(R)
corr
będzie rosła w miarę zwiększania rozmiarów bazy lub liczby funkcji dyspersyjnych (d,p),
składowa ∆E
(1)
ex
z kolei już nie.
Ciekawe wydaje sie to, że podczas gdy energia oddziaływania ∆E
MP2
oraz jej składowe ko-
relacyjna i wymienna są około dwa większe w przypadku oddziaływania chromoforu etydyny z
adeniną niż z uracylem (co jest bezpośrednim wynikiem większej powierzchni nakładania, czyli
większej liczby kontaktów atomowych), nie widać tak mocno zarysowanej różnicy dla oddziały-
wania elektrostatycznego (jest to widoczne jednak dla jej członu penetracyjnego).
Oddziaływanie elektrostatyczne ∆E
(1)
el
jest najbliższe całkowitej energii ∆E
MP2
spośród po-
ziomów teorii zaprezentowanych w Tabeli 1: ∆E
(1)
el
∼ 0, 82∆E
MP2
. Nie jest to jednak regułą
dla czterech osobnych par chromofor-zasada, co odzwierciedla asymetrię badanej struktury. Ta
bliskość składowej elektrostatycznej zgadza się z wynikami uzyskanych dla innych układów aro-
matycznych [52, 53, 55, 57]. Względnie mała wartość członu delokalizacyjnego ∆E
(R)
del
w porów-
naniu do innych została też wcześniej zauważona [58]. Części multipolowa i penetracyjna mają
w tym kompleksie podobne wartości, więc przyczniają sie w tym samym stopniu do składowej
elektrostatycznej w Równaniu 14.
Tabela 2 z kolei ilustruje szacunki dla artefaktów zawartych w składowych energii oddzia-
ływania skutek izolowania chromoforu od łańcucha bocznego i zakończenia przeciętych wiązań
atomami wodoru. Suma oddziaływań ∆E
MP2
pomiędzy zasadami i chromofrem wraz z łańcu-
chem bocznych wynosi -32.74 kcal/mol, w porównaniu do -31.69 kcal/mol dla odosobnionego
chromoforu. Różnica pomiędzy tymi energiami jest mniejsza o tylko około 2,5% od energii
3 Analiza oddziaływań w wybranych strukturach krystalograficznych
23
adenina(A) uracyl(B) uracyl(A) adenina(B) suma
∆ε
IV
CAM M
-3.2
-3.0
-3.5
-3.2
-12.9
∆E
(1)
el,mtp
-2.8
-3.9
-3.9
-2.9
-13.5
∆E
(1)
el,pen
-5.0
-1.3
-1.6
-4.7
-12.5
∆E
(1)
ex
11.5
4.2
4.9
11.7
32.3
∆E
(R)
del
-1.7
-0.6
-0.8
-1.6
-4.7
∆E
(R)
corr
-12.0
-4.1
-4.2
-13.0
-33.3
∆E
(1)
el
-7.7
-5.2
-5.4
-7.7
-26.0
∆E
(1)
3.8
-1.0
-0.6
4.1
6.3
∆E
SCF
2.1
-1.6
-1.4
2.5
1.6
∆E
MP2
-10.0
-5.7
-5.5
-10.5
-31.7
Tablica 1:
Składowe i hierarchia modeli teoretycznych energii oddziaływania chromoforu etydyny z
czterema najbliższymi zasadami w strukturze Eth-AU/UA. Wszystkie wartości są podane w kcal/mol.
∆E
chain
∆E
chrom.+chain
∆E
chrom.+chain
∆E
ring
∆E
(1)
el,mtp
0.5
-13.5
0.5
-1.2
∆E
(1)
el,pen
-1.1
-13.7
0.1
-2.3
∆E
(1)
ex
3.4
35.3
0.4
5.9
∆E
(R)
del
-0.5
-5.1
-0.1
-1.2
∆E
(R)
corr
-2.5
-35.7
-0.1
-3.8
∆E
(1)
el
-0.6
-27.2
0.6
-3.5
∆E
(1)
2.8
8.0
1.0
2.4
∆E
SCF
2.3
3.0
1.0
1.2
∆E
MP2
-0.2
-32.7
0.8
-2.6
Tablica 2:
Składowe i hierarchia modeli teoretycznych energii oddziaływania w kompleksie Eth-
UA/AU. W kolumnach, od prawej strony do lewej, znajdują się sumy oddziaływań pomiędzy zasa-
dami oraz: łańcuchem bocznym etydyny (∆E
chain
), chromoforem etydyny wraz z łańcuchem bocznym
(∆E
chrom.+chain
), różnica pomiędzy chromoforem i łańcuchem bocznym policzonymi razem i osobno
(∆E
chrom.+chain
− ∆E
chrom.
− ∆E
chain
), i drugą grupą boczną będącą pierścieniem (∆E
ring
). Wszystkie
wartości są podane w kcal/mol.
oddziaływania pochodzącej od samego łańcucha bocznego.
Zbiorczy zestaw składowych energii oddziaływań dla wszystkich trzech badanych układów
znajduje się w Tabeli 3. Są w niej także wyniki dla wariantu kompleksu Pf-CG/AU, w którym
z proflawiny usunięto kation wodorowy, czyniąc z niej cząsteczkę neutralną. Ten sztuczny za-
bieg zmiany całkowitego ładunku proflawiny stanowi jednak skuteczny środek do ilustracji roli
ładunku na interkalatorze (wszystkie trzy badane interkalatory są kationami). W przypadku
etydyny między zasadami CG/GC, składowe energii oddziaływania ∆E
MP2
charakteryzują sie
podobnymi proporcjami co dla kompleksu Eth-AU/UA, z trochę większymi wartościami bez-
względnymi. To samo można zaobserwować dla profilu energetycznego kompleksu Pf-CG/AU w
Tabeli 3, dla którego bezwzględne wartości są jeszcze większe.
Wyniki dla kompleksu Pf-CG/AU z neutralną proflawiną są skrajnie różne. Składowa multi-

3 Analiza oddziaływań w wybranych strukturach krystalograficznych
24
Eth-AU/UA
(+1)
min.B
min.A
Eth-GC/CG
(+1)
Pf-CG/AU
(+1)
PF-AU/CG
(0)
∆ε
IV
CAM M
-12.9
-13.1
-11.4
-15.6
-16.5
0.1
∆E
(1)
el,mtp
-13.5
-15.6
-14.5
-16.8
-17.6
3.1
∆E
(1)
el,pen
-12.5
-12.5
-1.4
-12.3
-13.2
-14.9
∆E
(1)
ex
32.3
36.8
4.0
33.2
35.0
37.7
∆E
(R)
del
-4.7
-5.2
-4.2
6.5
-2.4
-5.3
∆E
(R)
corr
-33.3
-32.4
-3.5
-32.8
-34.5
-36.8
∆E
(1)
el
-26.0
-28.0
-15.9
-29.1
-30.8
-11.8
∆E
(1)
6.3
8.8
-11.8
4.2
4.2
25.9
∆E
SCF
1.6
3.6
-16.0
-2.4
-2.5
20.6
∆E
MP2
-31.7
-28.8
-19.4
-35.1
-37.0
-16.2
Tablica 3:
Składowe i hierarchia modeli teoretycznych energii oddziaływania w trzech badanych kom-
pleksach. Pierwsze trzy kolumny pokazują energie oddziaływania pomiędzy chromoforem etydyny i
zasadami w kompleksie Eth-AU/UA - w położeniu krystalograficznym, w minimum położonym najbli-
żej pozycji zerowej (B w Rys.10), oraz w minimum położonym w dużym rowku (A in Fig.10). Czwarta i
piąta kolumna prezentują analogiczne energie oddziaływania odpowiednio dla kompleksów Eth-CG/GC
i Pf-CG/AU. Ostatnia kolumna pokazuje składowe dla wariantu kompleksu Pf-CG/AU, w którym pro-
flawina jest neutralna. Wszystkie wartości są sumami wkładów pochodzących od czterech zasad i
są podane w kcal/mol. ∆ε
CAMM
oznacza energię oddziaływania multipolową obliczoną na podstawie
multipoli CAMM, ∆E z kolei wszędzie oznacza energie otrzymane z analizy dekompozycyjnej.
polowa zanika, przez co oddziaływanie elektrostatyczne ∆E
(1)
el
jest mniejsza o połowę. Całkowita
energia oddziaływania ∆E
MP2
jest również mniejsza, mimo jeszcze większego członu korelacyj-
nego. Podobnie jak w kompleksach kationowych, składowe korelacyjna i wymienna są tego
samego rzędu i mają przeciwne znaki.
Istnieje wysoka korelacja pomiędzy poszczególnymi składowymi energii oddziaływania dla
pozycji krystalicznych w trzech badanych kompleksach (Tabela 3). W szczególności, stosunek
∆E
(1)
el
/∆E
MP2
jest stały - dla Eth-AU/UA: 0.82, Eth-CG/GC: 0.82, Pf-CG/AU: 0.83. Podobnie
jest dla składowej multipolowej: ∆E
CAMM
/∆E
MP2
dla Eth-AU/UA: 0.41, Eth-CG/GC: 0.47,
Pf-CG/AU: 0.47. Ten sam trend stwierdzono ostatnio dla oddziaływań dimeru benzenu w
konfiguracji sandwiczowej [52], par zasad DNA [53], oraz innych układów aromatycznych [57].
Oprócz składowych budujących energię oddziaływania na poziomie MP2, w Tabelach 1 i 3 po-
kazano dla porównania najwyższy dostępny w tej pracy rząd energii oddziaływania obliczoną na
podstawie multipoli CAMM, czyli ∆ε
IV
CAM M
. Dla wszystkich kompleksów ma ono porównywalną
wartość z członem multipolowym ∆E
(1)
el,mtp
uzyskanym na podstawie analizy DMA (Distributed
Multipole Analysis), dla której uwzględnione są najwyżej oktupole. Te energie oddziaływania
multipolowego w przypadku kompleksu Eth-CG/GC można porównać z energią wiązania uzy-
skaną przez Medhi i współpracowników na podstawie analizy DMA [49] - bazowali oni na tej
samej strukturze krystalograficznej. Różnica między energią tamtych autorów (-7.9 kcal/mol)
a energią najwyższego rzędu oddziaływań w tej pracy (-12.9 kcal/mol, patrz Tabela 3) praw-
dopodobnie wynika głównie z wyidealizowanego, płaskiego modelu zasad zastosowanego przez

3 Analiza oddziaływań w wybranych strukturach krystalograficznych
25
Eth-AU/UA
(+1)
Eth-GC/CG
(+1)
PF-AU/CG
(+1)
∆ε
0
CAMM
-11.86
(91.8%)
-13.42
(85.8%)
-13.7 (83.0%)
∆ε
dip−q
CAMM
1.41
(-10.9%)
1.23
(-7.8%)
0.1 (-0,5%)
∆ε
I
CAMM
-10.45
(90.9%)
-12.19
(77.9%)
-13.6 (82.5%)
∆ε
dip−dip
CAMM
1.87
(-14.5%)
2.67
(-17.1%)
1.51 (-9.2%)
∆ε
quad−q
CAMM
-0.45
(3.5%)
-1.01
(6.4%)
-0.73 (4.5%)
∆ε
II
CAMM
-9.04
(69.9%)
-10.52
(67.3%)
-12.82 (77.8%)
∆ε
quad−dip
CAMM
-2.11
(16.4%)
-3.68
(23.5%)
-2.31 (14.0%)
∆ε
octup−q
CAMM
0.44
(-3.4%)
0.44
(-2.9%)
0.17 (-1.0%)
∆ε
III
CAMM
-10.71
(82.9%)
-13.75
(87.9%)
-14.95 (90.7%)
∆ε
quad−quad
CAMM
0.98
(-7.6%)
1.36
(-8.7%)
0.99 (-6.0%)
∆ε
octup−dip
CAMM
-3.11
(24.2%)
-3.20
(20.5%)
-2.33 (14.2%)
∆ε
hexdec−q
CAMM
-0.08
(0.6%)
-0.04
(0.3%)
-0.18 (1.1%)
∆ε
IV
CAMM
-12.92 (100.0%) -15.63 (100.0%) -16.48 (100.0%)
∆ε
octup−quad
CAMM
1.73
(-13.4%)
1.70
(10.9%)
1.30 (-7.9%)
∆ε
hexdec−dip
CAMM
0.59
(-4,6%)
0.68
(4.3%)
0.73 (4.4%)
Tablica 4:
Poszczególne wyrazy i rzędy elektrostatycznego oddziaływania multipolowego dla trzech
badanych kompleksów. W nawiasach obok energii są podane wzgledne wielkości poszczególnych czło-
nów w stosunku do energii na najwyższym obliczonym rzędzie, ∆ε
IV
CAMM
. Wszystkie energie zostały
obliczone używając multipoli CAMM na podstawie Równania 18 i są podane w kcal/mol.
Medhi et al.. Oryginalna geometria, zachowana w tej pracy, charakteryzuje sie pewną asymetrią
i niepłaskością par zasad oraz pewnym wykroczeniem chromoforu poza płaszczyznę interkalacji.
Bliższe kontakty i dodatkowe naprężenia związane z pozapłaszczyznowymi atomami zwiększają
oddziaływania, zwłaszcza pomiędzy rozkładami multipolowymi, które są wrażliwe na lokalną
anizotropię i nierówności. Dodatkowe różnice mogą wynikać z innej definicji stosowanych multi-
poli oraz ich różnego pochodzenia (macierz gęstości MP2 w przeciwieństwie do funkcji falowych
SCF).
Pełny profil oddziaływań multipolowych dla trzech badanych struktur można znaleźć w Ta-
beli 4 - pokazuje ona wszystkie obliczone w tej pracy oddziaływania między multipolami różnych
rzędów, ∆E
κ−κ
0
CAM M
, oraz odpowiednie rzędy oddziaływań, do których oddziaływania pomiędzy
poszczególnymi mulitpolami sie sumują. Maksymalna zmienność dla wszystkich rozważanych
rzędów oddziaływań wynosi ±15%. W szczególności, oddziaływania dipolowe mają duże bez-
względne wartości, systematycznie dla wszystkich struktur, w tym ∆ε
dip−dip
CAM M
i człony wyższego
rzędu ∆ε
quad−dip
CAM M
i ∆ε
octup−dip
CAM M
. Człon ∆ε
hexdec−dip
CAM M
(który wchodzi w skład energii oddziaływania
piatego rzędu) już ma stosunkowo mniejszą wartość bezwzględną. Jednak niezaniedbywalna war-
tość członu ∆ε
octup−quad
CAM M
potwierdza słabą zbieżność multipolowego oddziaływania w badanych
kompleksach. Naturalnym kolejnym krokiem jest zwiększenie uwzględnianego rzędu multipoli
lub wytwarzanie rozwinięć multipolowych na centrach pozaatomowych. Ze względu na bliskość
chromoforu i zasad w kompleksach interkalacyjnych (niewiele ponad 3 ˚
A), rozwinięcia te są naj-
prawdopodobniej rozbieżne asymptotycznie - energie oddziałyań wyższych rzędów będą miały

3 Analiza oddziaływań w wybranych strukturach krystalograficznych
26
coraz większe wartości. Zatem rozszerzenie zastosowanych rozwinięć multipolowych niekoniecz-
nie doprowadzi do lepszej zbieżności i lepsza opcją będzie generowanie większej liczby centrów.

4 Badanie energii oddziaływania w płaszczyźnie interkalacji
27
4
Badanie energii oddziaływania
w płaszczyźnie interkalacji
Na podstawie symetrii tkwiącej w kompleksach interkalacyjnych - równoległe ustawienie chro-
moforu względem dwóch prawie płaskich par zasad - można oczekiwać, że interkalator w miej-
scu wiązania (położenie krystalograficzne) będzie miał największą swobodę ruchu w kierunkach
zgodnych z tą symetrią, czyli równoległych do zasad. Te kierunki wyznaczają pewną abstrak-
cyjną płaszczyznę interkalacji, na której intuicyjnie znajduje się trajektoria interkalatora podczas
jego wejścia między pary zasad. Należy podkreślić, że jest to konstrukcja wyłącznie myślowa,
zakładająca niezmienność konformacji kwasu nukleinowego, co może być dobrym przybliżeniem
tylko dla małych odchyleń od położenia krystalograficznego. Im dalej interkalator się znajduje od
swojego miejsca wiązania, tym większe będą zmiany w konformacji zasad, z którymi oddziałuje,
ponieważ będą relaksowały pod jego nieobecnością w kierunku konformacji przedinterkalacyj-
nej. W tej pracy za płaszczyznę interkalacji przyjęto płaszczyznę chromoforu interkalatora - w
praktyce dopasowano równanie płaszczyzny do współrzędnych jego atomów.
4.1
Powierzchnie oddziaływania multipolowego
w płaszczyźnie interkalacji
Zamiast obliczać całkowitą energię oddziaływania ∆E
MP2
w wielu punktach na płaszczyźnie
interkalacji, co byłoby przedsięwzięciem skrajnie kosztownym, zbadano elektrostatyczną energię
oddziaływania rozkładów multipolowych na siatce w płaszczyźnie interkalacji. Energia oddziały-
wania pomiędzy rozwinięciami multipolowymi reprezentującymi interkalator i zasady angażuje
stosunkowo mały wysiłek obliczeniowy, nawet dla wyższych rzędów oddziaływania, i dlatego
można ją z łatwością rozważyć nawet dla bardzo dużej liczby punktów. Rysunek 6 pokazuje
powierzchnie takiej energii oddziaływania różnych rzędów na siatce punktów w płaszczyźnie in-
terkalacji dla kompleksu Eth-AU/UA. Każdy punkt siatki reprezentuje inne odchylenie środka
geometrycznego chromoforu względem położenia krystalograficznego (osie X i Y). Rys.7 i Rys.8
pokazują analogiczne powierzchnie czwartego rzędu, odpowiednio dla kompleksów Eth-CG/GC
oraz Pf-AU/GC. Energie na tych wykresach w położeniu krystalograficznym (zerowe przesunię-
cie) mają te same wartości co odpowiednie rzędy oddziaływań ∆ε
CAM M
w Tabeli 4.
Wszystkie powierzchnie przedstawione na Rysunku 6, dla pięciu kolejnych rzędów oddzia-
ływania ∆ε
0
CAM M
..∆ε
CAM M
IV , oraz powierzchnie dla pozostałych dwóch kompleksów krysta-
lograficznych (Rys.7 i Rys.8) mają wyraźne minima w pobliżu położenia zerowego (wyjątek
tu stanowi powierzchnia oddziaływania ∆ε
II
CAM M
dla kompleksu Eth-CG/GC, której tutaj nie
pokazano). Ta oczywista obserwacja jednak sugeruje, że część multipolowa oddziaływań elektro-
statycznych przynajmniej jakościowo opisuje rzeczywiste miejsce wiązania w zbadanych struk-
turach.
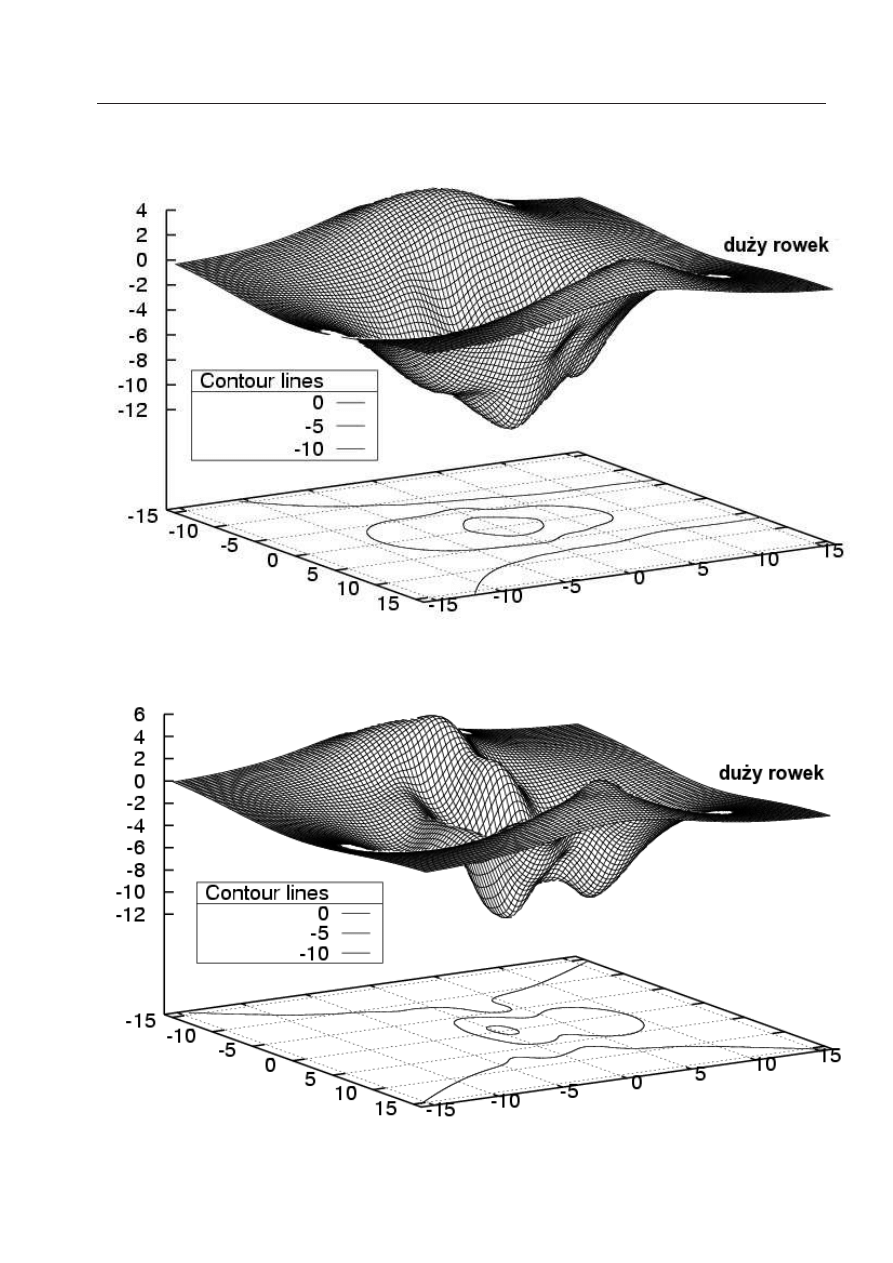
4 Badanie energii oddziaływania w płaszczyźnie interkalacji
28
(A) Powierzchnia energii oddziaływania zerowego rzędu, ∆ε
0
CAM M
.
(B) Powierzchnia energii oddziaływania pierwszego rzędu, ∆ε
I
CAM M
.
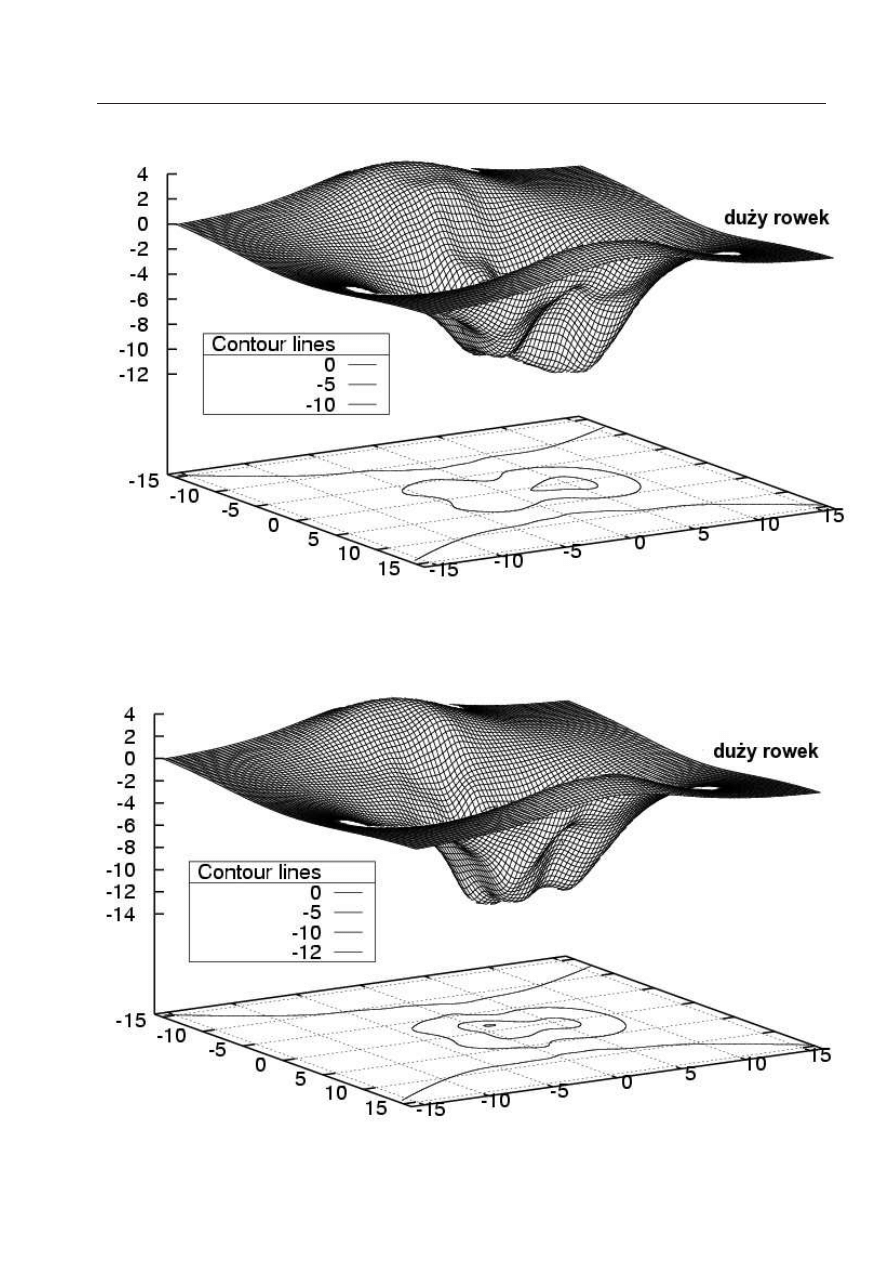
4 Badanie energii oddziaływania w płaszczyźnie interkalacji
29
(C) Powierzchnia energii oddziaływania drugiego rzędu, ∆ε
II
CAM M
.
(D) Powierzchnia energii oddziaływania trzeciego rzędu, ∆ε
III
CAM M
.
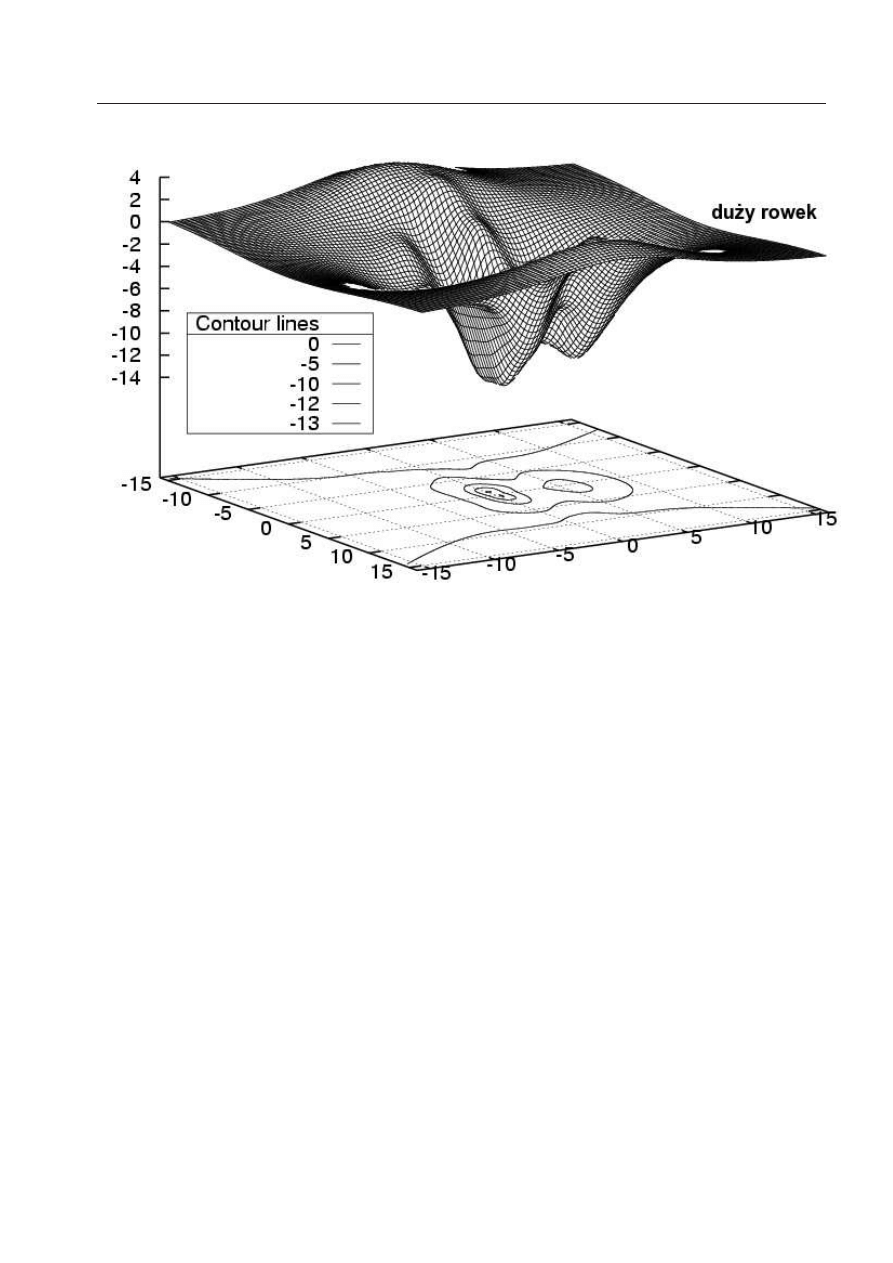
4 Badanie energii oddziaływania w płaszczyźnie interkalacji
30
(E) Powierzchnia energii oddziaływania czwartego rzędu, ∆ε
IV
CAM M
.
Rysunek 6: Powierzchnie sumarycznej energii oddziaływania chromoforu etydyny z czterema za-
sadami w płaszczyźnie interkalacji dla kompleksu Eth-AU/UA, obliczone na podstawie multipoli
CAMM. Kolejne wykresy (na poprzednich stronach) pokazują energie rzędu zerowego ∆ε
0
CAM M
(A), pierwszego ∆ε
I
CAM M
(B), drugiego ∆ε
II
CAM M
(C), trzeciego ∆ε
III
CAM M
(D), oraz czwartego
∆ε
IV
CAM M
(E). Na wszystkich wykresach energia jest przedstawiona w kcal/mol (oś pionowa), w
funkcji przesunięcia chromoforu względem położenia krystalograficznego w angstremach (osie X
i Y), z krokiem 0.3˚
A. Kierunek do dużego rowka opisano.
Powierzchnie energii oddziaływania różnych rzędów, pokazane dla przypadku kompleksu
Eth-AU/UA (Rys.6), są od siebie w sposób widoczny różne. Kształt powierzchni energetycz-
nej ∆ε
0
CAM M
, która wynika wyłącznie z ładunków punktowych na atomach, można opisać jako
łagodny, z jednym centralnym minimum o monotonicznych zboczach. Powierzchnie kolejnych
rzędów, opisujące oddziaływania między multipolami uwzględniającymi większą anizotropię roz-
kładu ładunku wokół atomów, charakteryzują się większą nierównością. Zaczynając od po-
wierzchni ∆ε
I
CAM M
, pojawia się drugie znaczące minimum w kierunku dużego rowka (kierunek
opisany na wykresach), które w przypadku oddziaływania drugiego rzędu (∆ε
II
CAM M
) jest nawet
głębsze niż minimum centralne. Różnice pomiędzy kształtem powierzchni oddziaływań trzeciego
(∆ε
III
CAM M
) i czwartego rzędu (∆ε
IV
CAM M
, najwyższy rząd rozważany w tej pracy) są mniejsze niż
zmiany między poprzednimi rzędami. Żeby uściślić to spostrzeżenie, Tabela 5 pokazuje średnie
względne zmiany energii na jednostkę powierzchni w płaszczyźnie interkalacji przy przejściu do
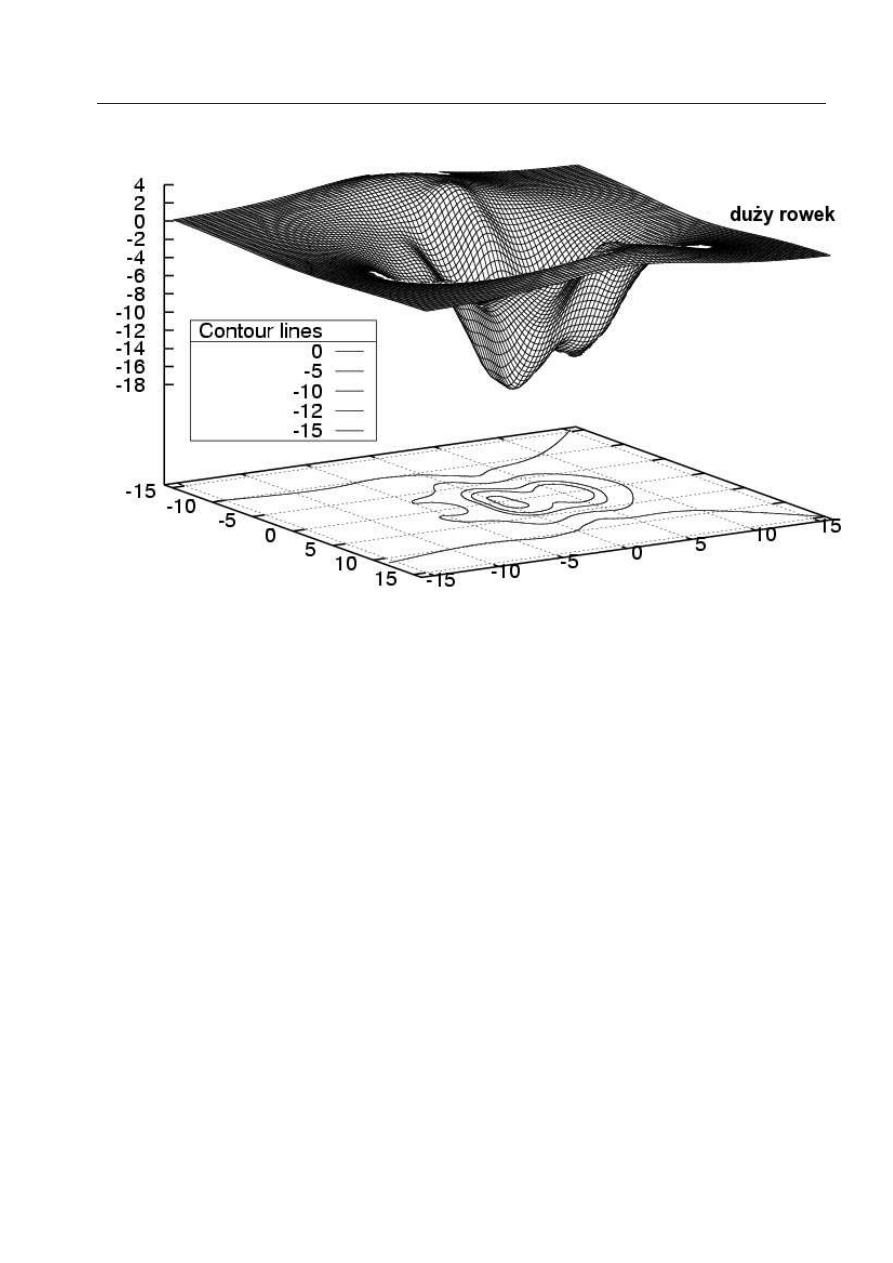
4 Badanie energii oddziaływania w płaszczyźnie interkalacji
31
Rysunek 7: Powierzchnia sumarycznej energii oddziaływania czwartego rzędu (∆ε
IV
CAM M
) mię-
dzy chromoforem etydyny i czterema zasadami w płaszczyźnie interkalacji dla kompleksu Eth-
CG/GC, obliczone na podstawie multipoli CAMM. Energia jest przedstawiona w kcal/mol (oś
pionowa), w funkcji przesunięcia chromoforu względem położenia krystalograficznego w angstre-
mach (osie X i Y), z krokiem 0.3˚
A. Kierunek do dużego rowka opisano.
kolejnych, wyższych rzędów oddziaływania multipolowego. Dla trzech struktur z kationowymi
interkalatorami (pierwsze trzy kolumny), zmiany te maleją o ponad cztery razy przechodząc do
wyższych rzędów, i przy powierzchni ∆ε
IV
CAM M
wynoszą poniżej 10%. Parametr ten ilustruje,
że dopiero na poziomach ∆ε
III
CAM M
i ∆ε
IV
CAM M
kształt tych powierzchni zaczyna się uzbieżniać,
co nie jest zaskoczeniem biorąc pod uwagę serię kolejnych rzędów oddziaływań dla położenia
krystalograficznego (Tabela 4. Wskazane byłoby wprowadzić kolejne poprawki i sprawdzić czy
energia oddziaływań rozwinięć multipolowych uwzględniających jeszcze wyższe rzędy oddziały-
wań, lub składające się z większej liczby centrów, potwierdzi ten trend.
W przeciwieństwie do proflawiny kationowej, powierzchnia energii oddziaływania dla kom-
pleksu z neutralną proflawiną (czwarta kolumna w Tabeli 5) nadal znacznie się zmienia przy
przejściu od ∆ε
III
CAM M
do ∆ε
IV
CAM M
. Powierzchnia ∆ε
IV
CAM M
dla tego układu jest pokazana na
Rysunku 9 - jest chaotyczna, wartości bezwzględne energii są dużo mniejsze niż dla komplek-
sów z kationowymi interkalatorami, i nie ma wyraźnego minimum które odtwarzałoby położenie
zerowe.
Rysunek 10 oferuje częściowy wykres konturowy powierzchni ∆ε
IV
CAM M
dla kompleksu Eth-
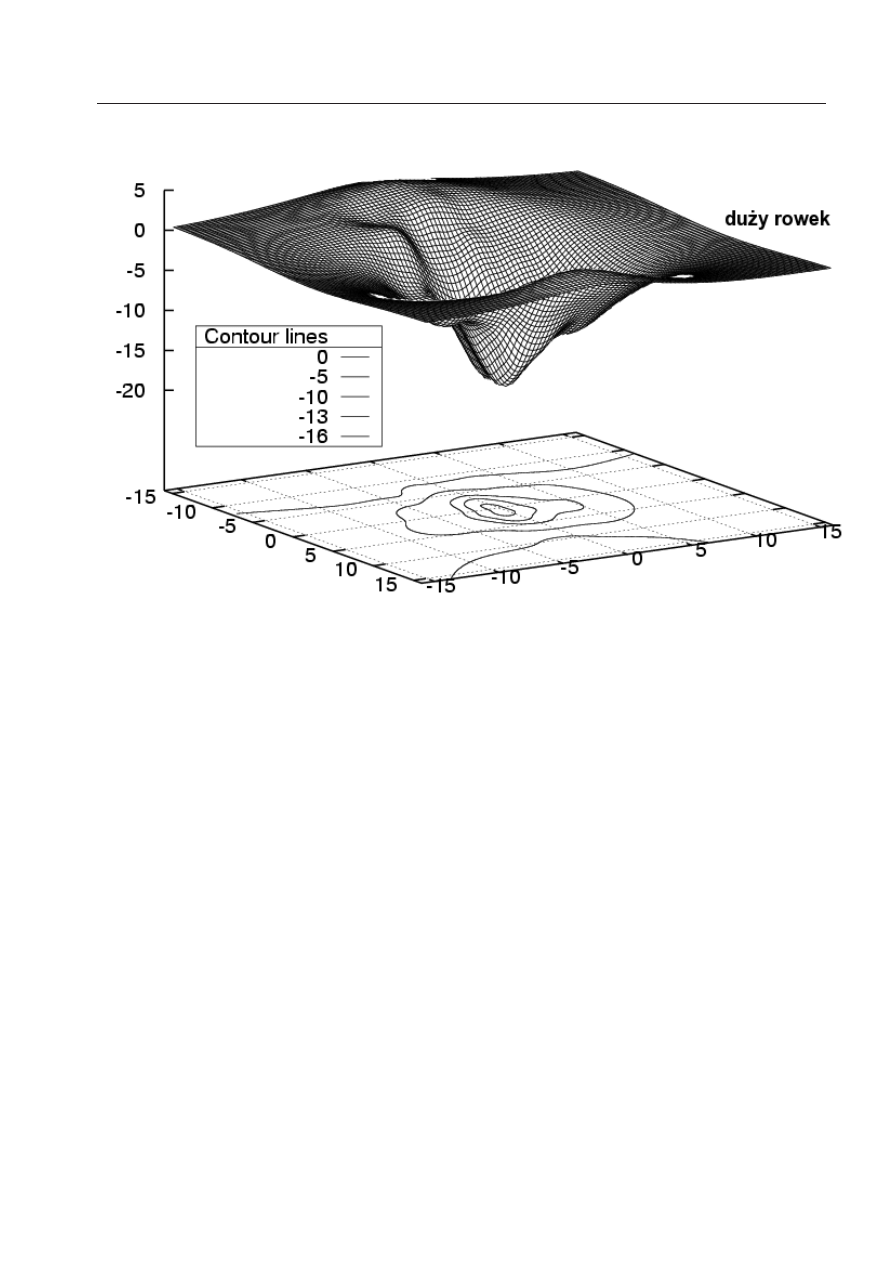
4 Badanie energii oddziaływania w płaszczyźnie interkalacji
32
Rysunek 8: Powierzchnia sumarycznej energii oddziaływania czwartego rzędu (∆ε
IV
CAM M
) między
chromoforem etydyny i czterema zasadami w płaszczyźnie interkalacji dla kompleksu Pf-AU/GC,
obliczone na podstawie multipoli CAMM. Energia jest przedstawiona w kcal/mol (oś pionowa),
w funkcji przesunięcia chromoforu względem położenia krystalograficznego w angstremach (osie
X i Y), z krokiem 0.3˚
A. Kierunek do ducego rowka opisano.
AU/UA (Rysunek 6E), na którym trzy główne minima zaznaczono czarnymi krzyżykami; jest
on osadzony na tych samych osiach co Rys.6E i zaznaczono na nim też kierunek do dużego
rowka. Centralny, szary kontur wokół minimów oznaczonych jako B i C reprezentuje on obszar,
w którym energia oddziaływania jest co najwyżej 2.0 kcal/mol powyżej najgłębszego minimum.
Ograniczenia steryczne związane z obecnością nici bocznych kwasu nukleinowego naniesiono za
pomocą zakreskowanego obszaru. Jego brzeg jest zdefiniowany przez międzycząsteczkowe kon-
takty promieni van der Waalsa atomów, przeskalowanych przez czynnik 0.8. W tej reprezentacji
widać, że zarówno położenie krystalograficzne jak i najbliższe minima (B i C) znajdują się na
granicy obszaru kontaktów sterycznych.
Wykresy podobne do tego na Rysunku 10 wygenerowano dla wszystkich trzech komplek-
sów interkalacyjnych i dla wszystkich rzędów oddziaływania multipolowego ∆ε
0
CAM M
..∆ε
IV
CAM M
.
Statystyki położeń minimów na tych powierzchniach i ich energie przedstawiono w Tabeli 6.
Poza współrzędnymi i odległością tych minimów od położenia zerowego, tabela ta pokazuje też
ich odległość energetyczną, która powinna być możliwie mała dla ewentualnych badań porów-
nawczych energii oddziaływania, na przykład dla dużej ilości sekwencji zasad w celu odtworzenia
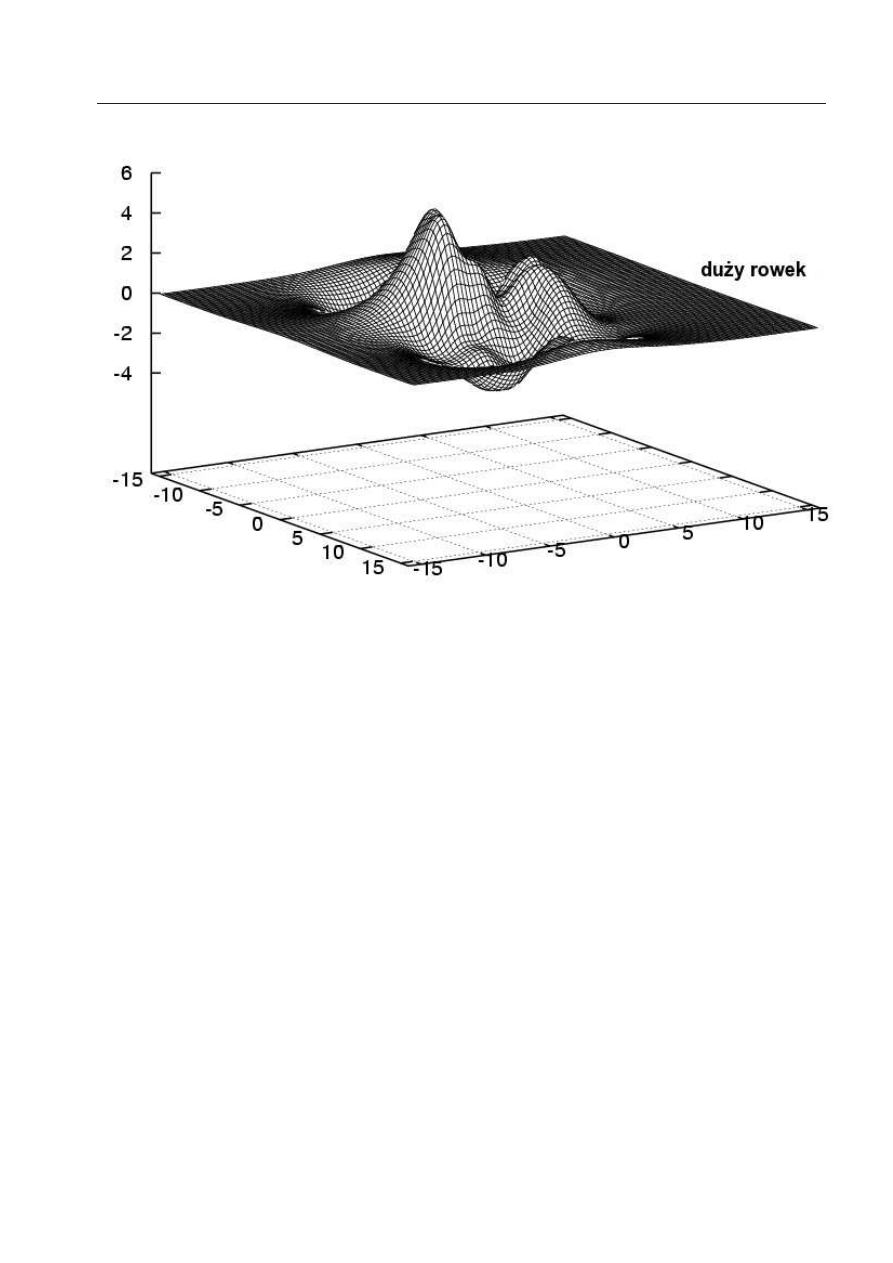
4 Badanie energii oddziaływania w płaszczyźnie interkalacji
33
Rysunek 9: Powierzchnia sumarycznej energii oddziaływania czwartego rzędu (∆ε
IV
CAM M
) mię-
dzy chromoforem etydyny i czterema zasadami w płaszczyźnie interkalacji dla kompleksu Pf
(0)
-
AU/GC (zmodyfikowany Pf-AU/GC, w którym proflawina jest neutralna), obliczone na podsta-
wie multipoli CAMM. Energia jest przedstawiona w kcal/mol (oś pionowa), w funkcji przesunię-
cia chromoforu względem położenia krystalograficznego w angstremach (osie X i Y) z krokiem
0,3˚
A. Kierunek do dużego rowka oznaczono.
lub przewidywania selektywności.
W przypadku, gdy dla danej powierzchni istnieją dwa lub więcej minima, a zazwyczaj są
to minima o porównywalnych energiach, obliczono też statystyki dla punktu znajdującego się
po środku nich. Dla przykładu, na powierzchni ∆ε
IV
CAM M
dla kompleksu Eth-AU/UA znajdują
się dwa minima, oba na głębokości -13.07 kcal/mol, a punkt leżący po środku nich jest jeszcze
bliższy położeniu zerowemu i ma bliższą energię do niego.
Charakterystyczne dla statystyk podanych w Tabeli 6 jest stosunkowo bliskie położenie mi-
nimów dla powierzchni ∆ε
0
CAM M
i ∆ε
I
CAM M
, ich oddalenie dla drugiego rzędu oddziaływania, i
ponownego zbliżenia do położenia krystalograficznego dla trzeciego i czwartego rzędu. Ogólnie,
najwyższy obliczany rząd oddziaływania multipolowego pozwala odtworzyć położenie krystalo-
graficzne w granicach około 1 ˚
A, co jest porównywalne z dokładnością używanych struktur kry-
stalograficznych. Ciekawe byłoby jednak zobaczyć czy równie centralne jest położone minimów
lepszych przybliżeń oddziaływania multipolowego - tak powinno być jeśli parametr przedsta-
wiony w Tabeli 5 pozostanie zbieżny.
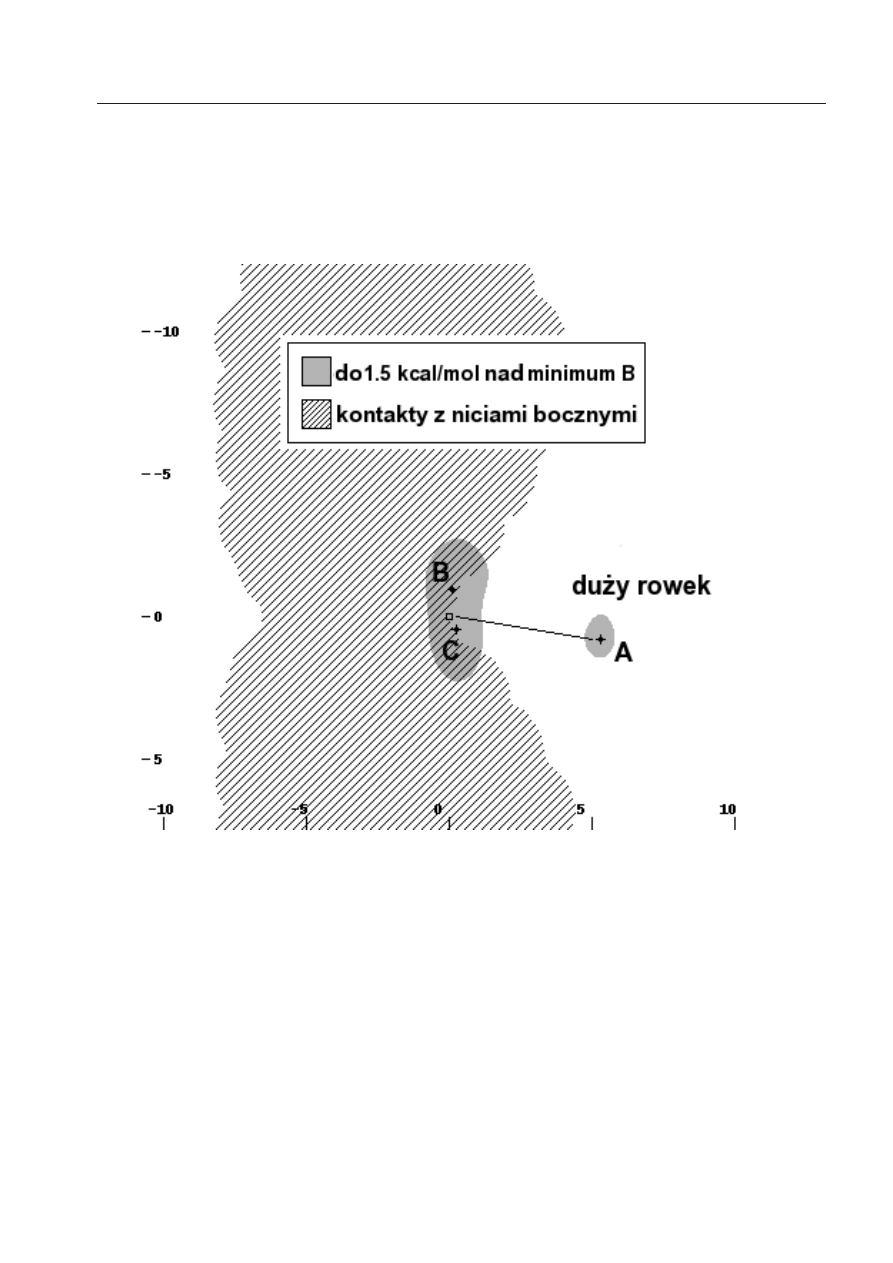
4 Badanie energii oddziaływania w płaszczyźnie interkalacji
34
Rysunek 10: Częściowy wykres konturowy multipolowej energii oddziaływania czwartego rzędu,
∆ε
IV
CAM M
, dla kompleksu Eth-AU/UA (Rys.6E), na którym zaznaczono trzy główne minima
czarnymi krzyżykami: A -10.9 kcal/mol (5.4 ˚
A., 0.7 ˚
A); B -12.1 kcal/mol (1.1 ˚
A, -1.5 ˚
A);
C -11.2 kcal/mol (1.2˚
A, 1.4˚
A). Ciemniejszy kontur przedstawia obszar, w którym energia od-
działywania jest co najwyżej 2.0 kcal/mol powyżej najgłębszego minimum B, z kolei obszar
zakreskowany przedstawia poglądowy obszar konfliktów sterycznych. Opisano też kierunek do
dużego rowka oraz osie odchylenia chromoforu (w ˚
A), identyczne z tymi na Rys.6. Profil ener-
getyczny oddziaływania na odcinku łączacym położenie krystalograficzne i minimum (A) jest
przedstawiony na Rys.11 i Rys.12.
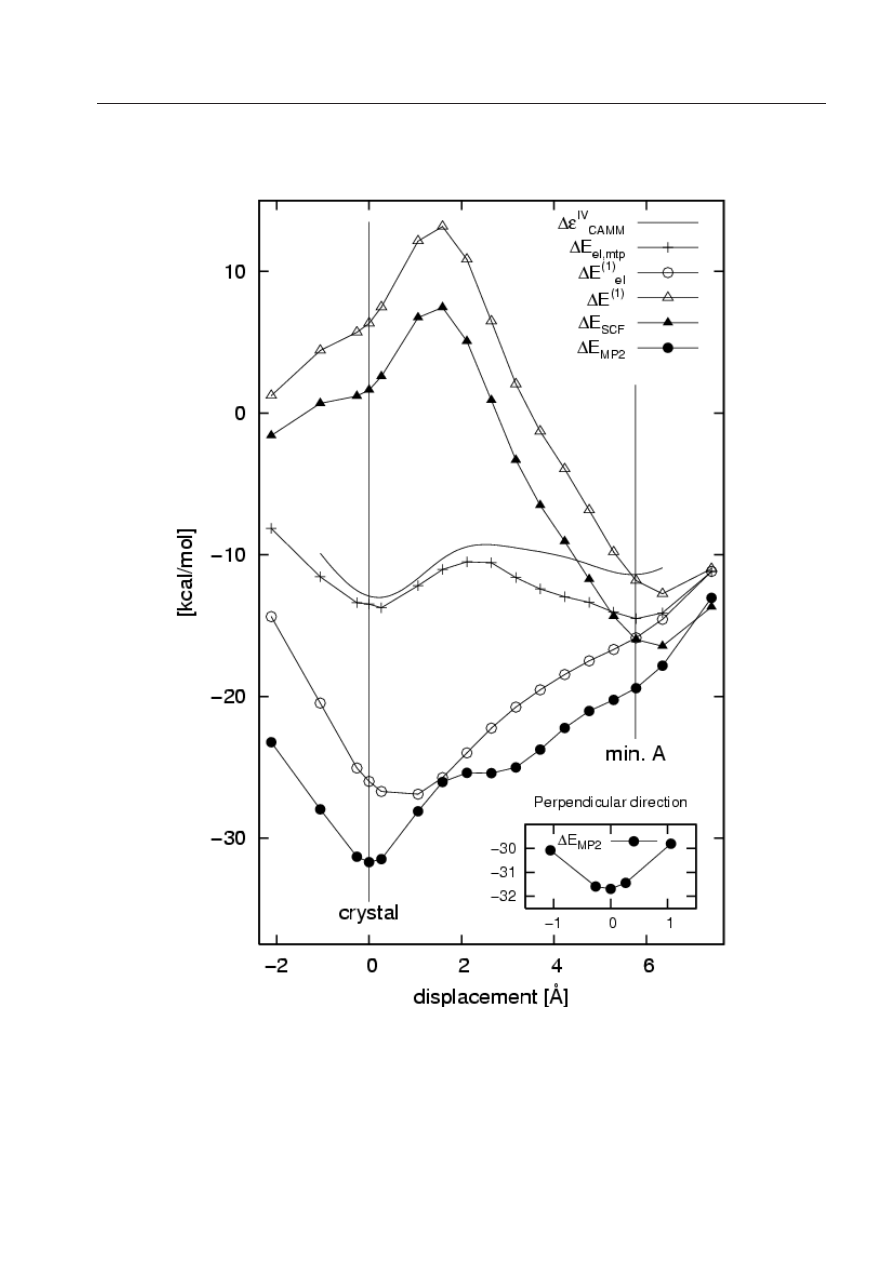
4 Badanie energii oddziaływania w płaszczyźnie interkalacji
35
Rysunek 11: Energia oddziaływania między chromoforem etydyny i czterema najbliższymi za-
sadami w kompleksie Eth-AU/UA na różnych poziomach teorii, na odcniku łączącym położenie
zerowe i minimum A w dużym rowku (patrz Rys.10). Mniejszy wykres wstawiony w prawym
dolnym rogu pokazuje najwyższy poziom teorii, ∆E
MP2
, w kierunku prostopadłym do zbadanej
ścieżki.
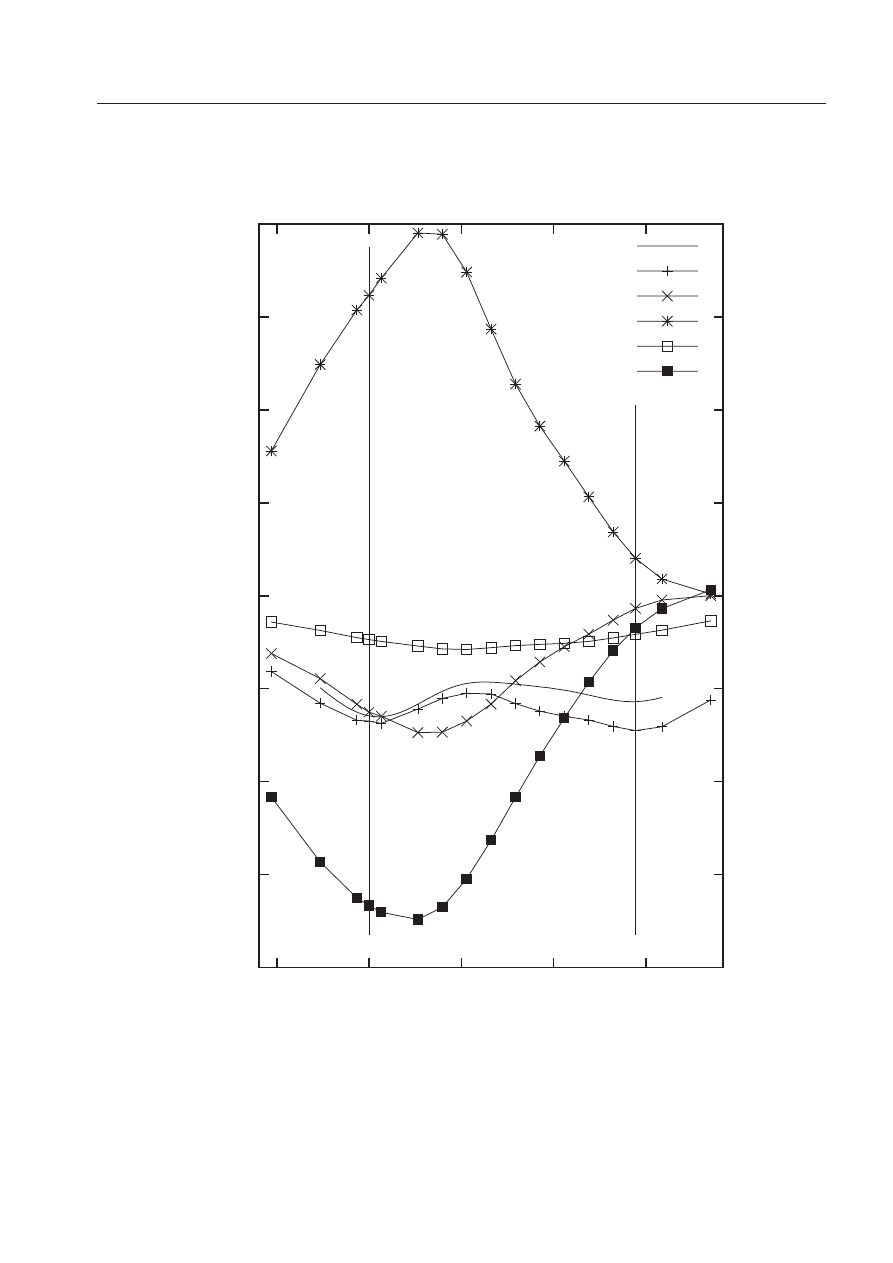
4 Badanie energii oddziaływania w płaszczyźnie interkalacji
36
−40
−30
−20
−10
0
10
20
30
40
−2
0
2
4
6
[kcal/mol]
displacement [Å]
crystal
min. A
∆ε
IV
CAMM
∆
E
el,mtp
∆
E
el,pen
∆
E
(1)
ex
∆
E
(R)
del
∆
E
(R)
corr
Rysunek 12: Składowe energii oddziaływania między chromoforem etydyny i czeterema najbliż-
szymi zasadami w kompleksie Eth-AU/UA na ścieżce łączącej położenie zerowe i minimum A
w dużym rowku (patrz Rys.10).
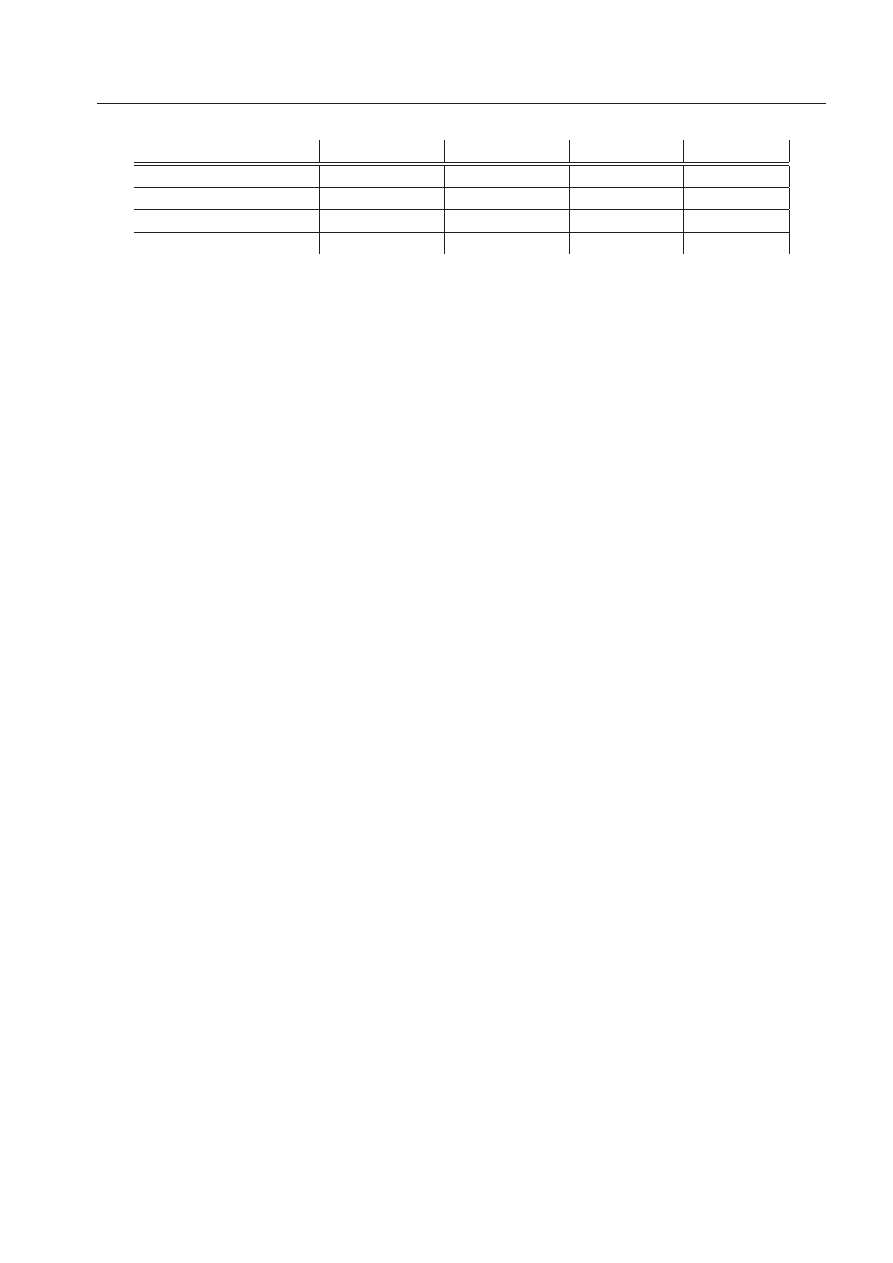
4 Badanie energii oddziaływania w płaszczyźnie interkalacji
37
Eth
(+1)
-AU/UA
Eth
(+1)
-CG/GC
Pf
(+1)
-CG/AU
Pf
(0)
-CG/AU
∆ε
0
CAM M
→ ∆ε
I
CAM M
49%
49%
47%
96%
∆ε
I
CAM M
→ ∆ε
II
CAM M
29%
30%
31%
100%
∆ε
II
CAM M
→ ∆ε
III
CAM M
12%
11%
13%
49%
∆ε
III
CAM M
→ ∆ε
IV
CAM M
7%
6%
6%
34%
Tablica 5: Średnia względna zmiana energii oddziaływania na jednostkę powierzchni w płasz-
czyźnie interkalacji przy przejściu do powierzchni oddziaływania wyższych rzędów, ∆ε
i
CAM M
→
∆ε
i+1
CAM M
.
4.2
Analiza energii oddziaływania na wybranym odcinku w płasz-
czyźnie interkalacji (położenie krystalograficzne - minimum A)
Żeby dokładniej opisać naturę oddziaływań w przynajmniej małym podzbiorze płaszczyzny in-
terkalacji, przeprowadzono analizę dekompozycyjną w kilku punktach wzdłuż odcinka łączącego
położenie krystalograficzne i minimum A (Rys.10) w płaszczyźnie interkalacji kompleksu Eth-
AU/UA, i dalej w tym kierunku do 8 ˚
A od położenia zerowego. Ruch chromoforu na tej ścieżce
w bardzo uproszczony sposób symuluje wchodzenie interkalatora między sąsiadujące pary za-
sad. Energia oddziaływań na różnych poziomach teorii oraz ich składowe wykreślono wzdłuż
tego odcinka odpowiednio na Rys.11 i Rys.12.
Najbardziej oczywista jest konsystentna z poprzednią obserwacja, że profile członów wy-
miennego ∆E
(1)
ex
i korelacyjnego ∆E
(R)
corr
mają podobne przebiegi a przeciwne znaki - mają jedno
minimum w odległości 1 ˚
A. Te dwie składowe, oraz część penetracyjna oddziaływania elektro-
statycznego (∆E
(1)
el,pen
), znikają na odległościach powyżej 5 ˚
A.
Z Rys.11 widać, że energia oddziaływania obliczona na poziomie MP2 dokładnie odtwarza
położenie krystalograficzne chromoforu etydyny wzdłuż tej ścieżki, z dokładnością przynajmniej
0.3 ˚
A (najmniejszy krok). To samo jest prawdą w kierunku prostopadłym (zobacz mały wykres
na Rys.11). Taka dokładność sugeruje, że czynniki inne niż oddziaływania lokalne - pomiędzy
chromoforem interkalatora i najbliższymi zasadami - nie są istotne dla ułożenia chromoforu
wewnątrz miejsca interkalacji, i uzasadnia podział zastosowany dla etydyny na potrzeby tej
pracy. Jednocześnie, warto zauważyć że oddziaływanie pierwszego rzędu, ∆E
(1)
, i na poziomie
SCF, ∆E
SCF
, nie odtwarzają położenia zerowego, a na większości zbadanej ścieżki są wręcz
destabilizujące (dodatnie).
Ponadto, wśród pozostałych poziomów teorii, człony multipolowe (zarówno obliczone na
podstawie momentów CAMM, ∆ε
IV
CAM M
, jak i uzyskane z analizy DMA, ∆E
(1)
el,mtp
) najlepiej od-
twarzają położenie zerowe na tym odcinku, dokładniej niż całe oddziałowanie elektrostatyczne
∆E
(1)
el
i człon korelacyjny ∆E
(R)
corr
. Należy jednak pamiętać, że wartość składowej multipolowej
jest znacznie mniejsza od całkowitego oddziaływania w położeniu zerowym, a staje się dominu-
jąca na większych odległościach.
O ile człon multipolowy energii oddziaływania zadowalająco odtwarza położenie krystalogra-
4 Badanie energii oddziaływania w płaszczyźnie interkalacji
38
∆ε
0
CAM M
∆ε
min
CAM M
∆(∆ε
CAM M
)
∆~r
|∆~r|
Eth-AU/UA
rząd 0
-11.86
-11.97
-0.11
(-0.74, -0.11)
0.75
rząd I
-10.45
-10.83
-0.38
(0.05, -0.48)
0.48
rząd II
-9.04
-9.32
-0.28
(1.53, 0.87)
1.75
rząd III
-10.71
-12.12
-1.41
(1.48, -1.11)
1.85
-11.15
-0.44
(-1.38, -1.22)
1.84
(średnia)
-11.39
-0.68
(0.05, -1.16)
1.16
rząd IV
-12.92
-13.07
-0.15
(1.01, -0.16)
1.01
-13.07
-0.15
(-0.53, -0.26)
0.59
(średnia)
-12.99
0.07
(0.24, 0.21)
0.44
Eth-CG/GC
rząd 0
-13.42
-13.90
-0.48
(-0.74, -0.58)
0.94
rząd I
-12.19
-13.19
-1.00
(-0.37, -0.85)
0.93
rząd II
—
rząd III
-13.75
-15.54
-1.79
(-1.75, -0.90)
1.96
-15.51
-1.76
(1.32, -0.85)
1.57
(średnia)
-14.58
-0.83
(-0.42, -0.87)
0.97
rząd IV
-15.63
-16.37
-0.74
(-0.90, -0.48)
1.02
Pf-AU/GC
rząd 0
-13.68
-13.86
-0.18
(0.95, 0.32)
1.01
-13.84
-0.16
(-1.22, 0.53)
1.34
(średnia)
-13.63
0.05
(-0.13, 0.42)
0.44
rząd I
-13.59
-13.71
-0.12
(0.32, 0.21)
0.38
rząd II
-12.82
-12.38
0.44
(-0.48, 1.69)
1.76
rząd III
-14.95
-16.56
-1.61
(-1.53, 0.79)
1.72
-15.62
-0.67
(1.38, 0.26)
1.40
(średnia)
-14.97
-0.02
(-0.08, 0.53)
0.53
rząd IV
-16.48
-16.75
-0.27
(-1.38, 0.48)
1.45
-16.66
-0.18
(1.45, 0.26)
0.47
(średnia)
-16.57
-0.09
(-0.48, 0.37)
0.60
Tablica 6: Szczegółowe dane dotyczące położenia głównych centralnych minimów w stosunku do
położenia zerowego dla powierzchni energetycznych obliczonych na podstawie multipoli CAMM.
Statystyki uwzględniają minima położone poniżej -5 kcal/mol i nie dalej niż 3 ˚
A od położenia
krystalograficznego i są podane dla pięciu rzędów oddziaływania. Kolumny od lewej strony:
oddziaływanie w położeniu zerowym, oddziaływanie w danym minimum, różnica między od-
działywaniem w minimum i położeniu zerowym, wektor położenia minimum w płaszczyźnie
interkalacji (dwie współrzędne w ˚
A), odległość do minimum w ˚
A. W przypadku gdy w obrę-
bie położenia krystalograficznego występowało więcej niż jedno minimum, przedstawiono także
dane dla punktu leżącego w połowie miedzy nimi.

4 Badanie energii oddziaływania w płaszczyźnie interkalacji
39
ficzne, mając blisko niego globalne minimum, ma również drugie minimum w kierunku dużego
rowka (co widać na powierzchniach energii ∆ε
CAM M
dla wszystkich kationowych kompleksów
interkalacyjnych - na Rys.6, Rys.7, oraz Rys.8), które dla wszystkich trzech badanych kom-
pleksów jest położone niewiele ponad 5 ˚
A od położenia zerowego. To minimum nie znajduje
odzwierciedlenia w całkowitej energii oddziaływania ∆E
MP2
na zbadanym odcinku i wskazuje
na ewentualne pułapki związane ze stosowaniem uproszczonego modelu do badania tego typu
układów.
Warto też zwrócić uwagę, że profil całkowitej energii oddziaływania ∆E
MP2
na wybranym
odcinku nie jest monotoniczny. Wykazuje bardzo płytkie minimum w odległości około 2.5 ˚
A
od położenia zerowego. Można więc przypuszczać, że w obrębie tego punktu, poza zbadanym
odcinkiem, znajduje się głębsze, bardziej wiążące minimum. Taka możliwość z kolei sugeruje, że
droga jaką interkalator pokonuje z otoczenia do miejsca wiązania krystalograficznego może być
nietrywialna i nawet przechodzić przez pośrednie miejsca wiązania wynikające z oddziaływań
aromatycznymi z docelowymi zasadami nukleinowymi.

5 Wnioski
40
5
Wnioski
Podsumowując wyniki przedstawione w tej pracy, można sformułować kilka wniosków, które, w
oparciu o badania przeprowadzone dla trzech wybranych kompleksów interkalacyjnych, należy
odnieść do doniesień na temat innych układów aromatycznych i do pewnego stopnia uogólnić
dla klasy wszystkich kompleksów interkalacyjnych.
1.
Energia oddziaływania obliczona na poziomie MP2, ∆E
MP2
, z dokładnością przynajmniej
0.3 ˚
A odtwarza położenie chromoforu etydyny w płaszczyźnie interkalacji kompleksu Eth-
AU/UA na zbadanym odcinku oraz w kierynku prostopadłym (Rys.11). Jest to silna
przesłanka, że oddziaływania lokalne (z najbliższymi zasadami) są wyłącznie odpowie-
dzialne za usytuowanie chromoforu w płaszczyźnie interkalacji. Jednocześnie, podkreśla
to pewną niezależność chromoforu i jego podstawników bocznych w kontekście oddziały-
wań w kompleksach interkalacyjnych i uzasadnia zastosowany podział etydyny w tej pracy
(Rys.4).
2.
Elektrostatyczna składowa energii oddziaływania, ∆E
(1)
el
, dla wszystkich trzech zbada-
nych kompleksów interkalacyjnych dobrze koreluje z całkowitą energią oddziaływania:
∆E
(1)
el
/∆E
MP2
∼ 0.82; podobnie jest dla członu multipolowego: ∆E
(1)
el,mtp
/∆E
MP2
∼ 0.45
(Tabela 3). W miarę oddalania się chromoforu od położenia krystalograficznego, inne
efekty maleją i człon multipolowy staje się dominujący (Rys.12).
3.
Bliskie odległości między interkalatorem (chromoforem etydyny lub proflawiną) i inter-
kalantami (cztery najbliższe zasady) oraz ich duże powierzchnie kontaktowe wzmacniają
efekty wymiany i korelacji w kompleksach interkalacyjnych. Uzyskane składowe wymiany
∆E
(1)
ex
i korelacyjne ∆E
(R)
corr
we wszystkich badanych układach miały duże wartości bez-
względne (porównywalne z całkowitą energią oddziaływania ∆E
MP2
) i przeciwne znaki
(Tabela 3). Ponadto, profile tych składowych wzdłuż zbadanego odcinka w płaszczyźnie
interkalacji mają podobne kształty (Rys.12). Podczas gdy we wszystkich obecnych wy-
nikach te dwie składowe w dużej mierze sie równoważą, skromna baza funkcyjna którą
zastosowano, 6-31G(1d,1p), najprawdopodobniej szacuje zbyt niskie wartości dla członów
korelacyjnych.
4.
W związku z dużym wkładem członów korelacyjnych i wymiennych, wszystkie metody
nie uwzględniające tylko jednej z tych składowych nie mogą doprowadzić do rozsądnych
wyników. Jest to widocznie zarówno w profilu energetycznym energii oddziaływania w
położeniu krystalograficznym (Tabela 3) i na wykresie energii oddziaływań na zbadanym
odcinku w płaszczyźnie interkalacji (Rys.11).
5.
Multipolowe energie oddziaływania obliczone na podstawie momentów multipolowych CAMM,
∆ε
CAM M
, wyraźnie odtwarzają krystalograficzne miejsce wiązania jednym lub więcej cen-

5 Wnioski
41
tralnymi minimam (Rys.6, Rys.7, i Rys.8). Dokładność predykcji nie rośnie jednoznacz-
nie wraz ze wzrostem rzędu oddziaływania multipolowego dla rzędów od zerowego do
czwartego, i jest najgorsza dla drugiego rzędu oddziaływania, ∆ε
II
CAM M
(Tabela 6). Dla
najwyższego rozważanego rzędu (∆ε
IV
CAM M
), dokładność ta jest rzędu 1 ˚
A.
6.
Oddziaływania występujące między multipolami wyższych rzędów (kwadrupole, oktupole)
są znaczące dla kompleksów interkalacyjnych (Tabela 4). Parametry opisujące średnią
zmianę kształtu powierzchni energii oddziaływania jako całości przy przejściu do wyższych
rzędów oddziaływania wskazują jednak na zdecydowaną zbieżność (Tabela 5). W tym
świetle, wskazane jest zwiększenie dokładności oddziaływania multipolowego - poprzez
zwiększenie rozważanego rzędu oddziaływania lub generowanie dodatkowych rozwinięć
multipolowych na centrach pozaatomowych.
7.
Wnioski dotyczące oddziaływań multipolowych, wysunietych na podstawie trzech zbada-
nych kompleksów interkalacyjnych, dotyczą tylko interkalatorów kationowych. Dla zmo-
dyfikowanego kompleksu, w którym interkalator miał zerowy ładunek formalny, człon mul-
tipolowy elektrostatycznej części oddziaływana zanikł (pozostałe składowe były porówny-
walne) i nie był w stanie odtworzyć miejsca wiązania.

Literatura
i
Literatura
[1]
Waring, M. J. Annu. Rev. Biochem. 1981, 50, 159–192.
[2]
Denny, W. A. Anti-cancer Drug Des. 1989, 4(4), 241–263.
[3]
Cashman, D. J.; Kellogg, G. E. J. Med. Chem. 2004, 47(6), 1360–1374.
[4]
Starcevic, K.; Karminski-zamola, G.; Piantanida, I.; Zinic, M.; Suman, L.; Kralji, M. J.
Am. Chem. Soc. 2005, 127(4), 1074–1075.
[5]
Watson, J. D.; Crick, F. H. C. Nature 1953, 171(4356), 737–738.
[6]
Hershey, A. D.; Chase, M. J. Gen. Physiol. 1952, 36(1), 39–56.
[7]
Meselson, M.; Stahl, F. W.; Vinograd, J. Proc. Natl. Acad. Sci. U. S. A. 1957, 43(7),
581–588.
[8]
Wang, J. C. Annu. Rev. Biochem. 1985, 54, 665–697.
[9]
Wang, J. C. Annu. Rev. Biochem. 1996, 65, 635–692.
[10]
Cain, B. F.; Atwell, G. J.; Denny, W. A. J. Med. Chem. 1975, 18(11), 1110–1117.
[11]
Wilson, W. R.; Baguley, B. C.; Wakelin, L. P. G.; Waring, M. J. Mol. Pharmacol. 1981,
20(2), 404–414.
[12]
Wadkins, R. M.; Graves, D. E. Biochemistry 1991, 30(17), 4277–4283.
[13]
Minford, J.; Pommier, Y.; Filipski, J.; Kohn, K. W.; Kerrigan, D.; Mattern, M.; Michaels,
S.; Schwartz, R.; Zwelling, L. A. Biochemistry 1986, 25(1), 9–16.
[14]
Waring, M. J. J. Mol. Biol. 1965, 13(1), 269–&.
[15]
Vardevanyan, P. O.; Antonyan, A. P.; Manukyan, G. A.; Karapetyan, A. T. Exp. Mol.
Med. 2001, 33(4), 205–208.
[16]
Graves, D. E.; Velea, L. M. Curr. Org. Chem. 2000, 4(9), 915–929.
[17]
Lerman, L. S. J. Mol. Biol. 1961, 3(1), 18–&.
[18]
Lepecq, J. B.; Paoletti, C. J. Mol. Biol. 1967, 27(1), 87–&.
[19]
Sharp, P. A.; Sugden, B.; Sambrook, J. Biochemistry 1973, 12(16), 3055–3063.
[20]
Lai, J. S.; Herr, W. Proc. Natl. Acad. Sci. U. S. A. 1992, 89(15), 6958–6962.
[21]
Gellert, M.; Smith, C. E.; Neville, D.; Felsenfeld, G. J. Mol. Biol. 1965, 11(3), 445–&.
[22]
Muller, W.; Crothers, D. M. J. Mol. Biol. 1968, 35(2), 251–&.
[23]
Krugh, T. R.; Reinhardt, C. G. J. Mol. Biol. 1975, 97(2), 133–162.
[24]
Jain, S. C.; Sobell, H. M. J. Biomol. Struct. Dyn. 1984, 1(5), 1161–1177.

Literatura
ii
[25]
Jain, S. C.; Sobell, H. M. J. Biomol. Struct. Dyn. 1984, 1(5), 1179–1194.
[26]
Aggarwal, A.; Islam, S. A.; Kuroda, R.; Neidle, S. Biopolymers 1984, 23(6), 1025–1041.
[27]
Wang, A. H. J.; Ughetto, G.; Quigley, G. J.; Rich, A. Biochemistry 1987, 26(4), 1152–
1163.
[28]
Krugh, T. R. Curr. Opin. Struct. Biol. 1994, 4(3), 351–364.
[29]
Berman, H. M.; Gelbin, A.; Westbrook, J. Prog. Biophys. Mol. Biol. 1996, 66(3), 255–&.
[30]
Foster, R. A. C. J. Bacteriol. 1948, 56(6), 795–809.
[31]
Kussovski, V. K.; Hristov, A. E.; Radoucheva, T. S. Microbios 2001, 105(411), 119–125.
[32]
Kohno, T.; Roth, J. R. J. Mol. Biol. 1974, 89(1), 17–&.
[33]
Schelhorn, T.; Kretz, S.; Zimmermann, H. W. Cell. Mol. Biol. 1992, 38(4), 345–365.
[34]
Davies, D. B.; Djimant, L. N.; Veselkov, A. N. Nucleosides Nucleotides 1994, 13(1-3),
657–671.
[35]
Ciatto, C.; D’amico, M. L.; Natile, G.; Secco, F.; Venturini, M. Biophys. J. 1999, 77(5),
2717–2724.
[36]
Shafirovich, V.; Dourandin, A.; Luneva, N. P.; Singh, C.; Kirigin, F.; Geacintov, N. E.
Photochem. Photobiol. 1999, 69(3), 265–274.
[37]
Spolar, R. S.; Record, M. T. Science 1994, 263(5148), 777–784.
[38]
Boresch, S.; Karplus, M. J. Mol. Biol. 1995, 254(5), 801–807.
[39]
Brady, G. P.; Sharp, K. A. J. Mol. Biol. 1995, 254(1), 77–85.
[40]
Chaires, J. B.; Satyanarayana, S.; Suh, D.; Fokt, I.; Przewloka, T.; Priebe, W. Biochemi-
stry 1996, 35(7), 2047–2053.
[41]
Chaires, J. B. Biopolymers 1997, 44(3), 201–215.
[42]
Breslauer, K. J.; Remeta, D. P.; Chou, W. Y.; Ferrante, R.; Curry, J.; Zaunczkowski, D.;
Snyder, J. G.; Marky, L. A. Proc. Natl. Acad. Sci. U. S. A. 1987, 84(24), 8922–8926.
[43]
Szwajkajzer, D.; Carey, J. Biopolymers 1997, 44(2), 181–198.
[44]
Hunter, C. A.; Lawson, K. R.; Perkins, J.; Urch, C. J. J. Chem. Soc.-perkin Trans. 2
2001, (5), 651–669.
[45]
Zimm, B. H. J. Chem. Phys. 1960, 33(5), 1349–1356.
[46]
Chan, S. I.; Schweizer, M. P.; Tso, P. O. P.; Helmkamp, G. K. J. Am. Chem. Soc. 1964,
86(19), 4182–&.
[47]
Guckian, K. M.; Schweitzer, B. A.; Ren, R. X. F.; Sheils, C. J.; Paris, P. L.; Tahmassebi,
D. C.; Kool, E. T. J. Am. Chem. Soc. 1996, 118(34), 8182–8183.

Literatura
iii
[48]
Guckian, K. M.; Schweitzer, B. A.; Ren, R. X. F.; Sheils, C. J.; Tahmassebi, D. C.; Kool,
E. T. J. Am. Chem. Soc. 2000, 122(10), 2213–2222.
[49]
Medhi, C.; Mitchell, J. B. O.; Price, S. L.; Tabor, A. B. Biopolymers 1999, 52(2), 84–93.
[50]
Reha, D.; Kabelac, M.; Ryjacek, F.; Sponer, J.; Sponer, J. E.; Elstner, M.; Suhai, S.;
Hobza, P. J. Am. Chem. Soc. 2002, 124(13), 3366–3376.
[51]
Sponer, J.; Leszczynski, J.; Hobza, P. Biopolymers 2001, 61(1), 3–31.
[52]
Tsuzuki, S.; Honda, K.; Uchimaru, T.; Mikami, M.; Tanabe, K. J. Am. Chem. Soc. 2002,
124(1), 104–112.
[53]
Hill, G.; Forde, G.; Hill, N.; Lester, W. A.; Sokalski, W. A.; Leszczynski, J. Chem. Phys.
Lett. 2003, 381(5-6), 729–732.
[54]
Hobza, P.; Sponer, J. J. Am. Chem. Soc. 2002, 124(39), 11802–11808.
[55]
Price, S. L.; Stone, A. J. J. Chem. Phys. 1987, 86(5), 2859–2868.
[56]
Newcomb, L. F.; Gellman, S. H. J. Am. Chem. Soc. 1994, 116(11), 4993–4994.
[57]
Perez-casas, S.; Hernandez-trujillo, J.; Costas, M. J. Phys. Chem. B 2003, 107(17), 4167–
4174.
[58]
Luo, R.; Gilson, H. S. R.; Potter, M. J.; Gilson, M. K. Biophys. J. 2001, 80(1), 140–148.
[59]
Stone, A. The Theory of Intermolecular Forces; Clarendon Press: Oxford, 1996.
[60]
Scheiner, S., Ed. Molecular Interactions, from van der Waals to Strongly Bound Comple-
xes; Wiley: Chchester, 1997.
[61]
Sokalski, W.; Kedzierski, P.; Grembecka, J.; Dziekonski, P.; Strasburger, K.; Elsevier-
Science: Amsterdam, 1999; chapter 10, pages 369–396; Computational Molecular Biology.
[62]
Sokalski, W. A.; Roszak, S.; Pecul, K. Chem. Phys. Lett. 1988, 153(2-3), 153–159.
[63]
Ziegler, T.; Rauk, A. Theor. Chim. Acta 1977, 46(1), 1–10.
[64]
Kitaura, K.; Morokuma, K. Int. J. Quantum Chem. 1976, 10(2), 325–340.
[65]
Boys, S. F.; Bernardi, F. Mol. Phys. 1970, 19(4), 553–&.
[66]
Schwenke, D. W.; Truhlar, D. G. J. Chem. Phys. 1985, 82(5), 2418–2426.
[67]
Gora, R. W.; Bartkowiak, W.; Roszak, S.; Leszczynski, J. J. Chem. Phys. 2002, 117(3),
1031–1039.
[68]
Gora, R. W.; Sokalski, W. A.; Leszczynski, J.; Pett, V. B. J. Phys. Chem. B 2005, 109(5),
2027–2033.
[69]
Kedzierski, P.; Sokalski, W. A.; Krauss, M. J. Comput. Chem. 2000, 21(6), 432–445.
[70]
Grembecka, J.; Kedzierski, P.; Sokalski, W. A.; Leszczynski, J. Int. J. Quantum Chem.
2001, 83(3-4), 180–192.

Literatura
iv
[71]
Cioslowski, J.; Liu, G. H. Chem. Phys. Lett. 1997, 277(4), 299–305.
[72]
Gavezzotti, A. J. Phys. Chem. B 2002, 106(16), 4145–4154.
[73]
Gavezzotti, A. J. Phys. Chem. B 2003, 107(10), 2344–2353.
[74]
Buckingham, A.; John Wiley and Sons: New York, 1987; pages 2–62.
[75]
Ding, H. Q.; Karasawa, N.; Goddard, W. A. J. Chem. Phys. 1992, 97(6), 4309–4315.
[76]
Salmon, J. K.; Warren, M. S.; Winckelmans, G. S. Int. J. Supercomput. Appl. High Per-
form. Comput. 1994, 8(2), 129–142.
[77]
White, C. A.; Headgordon, M. J. Chem. Phys. 1994, 101(8), 6593–6605.
[78]
White, C. A.; Johnson, B. G.; Gill, P. M. W.; Headgordon, M. Chem. Phys. Lett. 1994,
230(1-2), 8–16.
[79]
Cheng, H.; Greengard, L.; Rokhlin, V. J. Comput. Phys. 1999, 155(2), 468–498.
[80]
Mathias, G.; Egwolf, B.; Nonella, M.; Tavan, P. J. Chem. Phys. 2003, 118(24), 10847–
10860.
[81]
Volkov, A.; Coppens, P. J. Comput. Chem. 2004, 25(7), 921–934.
[82]
Bader, R. Atoms in Molecules: A Quantum Theory; Clarendon Press: Oxford, UK, 1990.
[83]
Popelier, P. L. A. Mol. Phys. 1996, 87(5), 1169–1187.
[84]
Popelier, P. L. A.; Joubert, L.; Kosov, D. S. J. Phys. Chem. a 2001, 105(35), 8254–8261.
[85]
Popelier, P. L. A.; Kosov, D. S. J. Chem. Phys. 2001, 114(15), 6539–6547.
[86]
Popelier, P. L. A.; Rafat, M. Chem. Phys. Lett. 2003, 376(1-2), 148–153.
[87]
Joubert, L.; Popelier, P. L. A. Phys. Chem. Chem. Phys. 2002, 4(18), 4353–4359.
[88]
Word, J. M.; Lovell, S. C.; Richardson, J. S.; Richardson, D. C. J. Mol. Biol. 1999, 285(4),
1735–1747.
[89]
Schmidt, M. W.; Baldridge, K. K.; Boatz, J. A.; Elbert, S. T.; Gordon, M. S.; Jensen,
J. H.; Koseki, S.; Matsunaga, N.; Nguyen, K. A.; Su, S. J.; Windus, T. L.; Dupuis, M.;
Montgomery, J. A. J. Comput. Chem. 1993, 14(11), 1347–1363.
[90]
Williams, H. L.; Mas, E. M.; Szalewicz, K.; Jeziorski, B. J. Chem. Phys. 1995, 103(17),
7374–7391.
[91]
Grembecka, J.; Kedzierski, P.; Sokalski, W. A. Chem. Phys. Lett. 1999, 313(1-2), 385–392.
[92]
Sokalski, W. A.; Kedzierski, P.; Grembecka, J. Phys. Chem. Chem. Phys. 2001, 3(5),
657–663.
[93]
Dyguda, E.; Grembecka, J.; Sokalski, W. A.; Leszczynski, J. J. Am. Chem. Soc. 2005,
127(6), 1658–1659.

Literatura
v
[94]
Sokalski, W. A.; Poirier, R. A. Chem. Phys. Lett. 1983, 98(1), 86–92.
[95]
Sokalski, W. A.; Sawaryn, A. J. Chem. Phys. 1987, 87(1), 526–534.
[96]
Sawaryn, A.; Sokalski, W. A. Comput. Phys. Commun. 1989, 52(3), 397–408.
[97]
Cipriani, J.; Silvi, B. Mol. Phys. 1982, 45(2), 259–272.
[98]
Challacombe, M.; Schwegler, E.; Almlof, J. Chem. Phys. Lett. 1995, 241(1-2), 67–72.
[99]
Stolarczyk, L. Z.; Piela, L. Int. J. Quantum Chem. 1979, 15(6), 701–711.
[100]
Kedzierski, P.; Wielgus, P.; Sikora, A.; Sokalski, W. A.; Leszczynski, J. Int. J. Mol. Sci.
2004, 5, 186–195.
[101]
Kedzierski, P.; Sokalski, W. A. J. Comput. Chem. 2001, 22(10), 1082–1097.
[102]
Gresh, N.; Kafafi, S. A.; Truchon, J. F.; Salahub, D. R. J. Comput. Chem. 2004, 25(6),
823–834.
[103]
Rinaldi, D.; Bouchy, A.; Rivail, J. L.; Dillet, V. J. Chem. Phys. 2004, 120(5), 2343–2350.
[104]
Strasburger, K.; Sokalski, W. A. Chem. Phys. Lett. 1994, 221(1-2), 129–135.
[105]
Humphrey, W.; Dalke, A.; Schulten, K. Journal of Molecular Graphics 1996, 14, 33–38.
[106]
Gnuplot 4.0. Thomas Williams.; Colin Kelley. Copyright 1986-1993, 1998, 2004.
[107]
van Rossum, G. Python Reference Manual CWI Report CS-R9524, 1995.
[108]
SciPy: Open source scientific tools for Python. Jones, E.; Oliphant, T.; Peterson, P.;
others. 2001–.

6 Dodatki
vi
6
Dodatki
6.1
Używane skróty
AIM
- atomy w cząsteczkach (atoms in molecules)
BSSE
- błąd superpozycji bazy (basis set superposition error )
CAMM
- kumulatywne atomowe momenty multipolowe (cumulative atomic multipole mo-
ments)
DNA
- kwas dezoksyrybonukleinowy (dezoxyribonucleic acid )
dsDNA
- dwuniciowe DNA (double-stranded DNA)
IAS
- powierzchnia międzyatomowa (interatomic surface)
MP2
- rachunek Møllera-Plesseta drugieg rzędu (second order Møller-Plesset)
mRNA
- kwas rybonukleinowy informacyjny (messenger ribonucleic acid )
NMR
- jądrowy rezonans magnetyczny (nuclear magnetic resonance)
ssDNA
- jednoniciowe DNA (single-stranded DNA)
RMS
- pierwiastek sumy kwadratów (root mean square)
RNA
- kwas rybonukleinowy (ribonucleic acid)
SCF
- pole samouzgodnione(self-consistent field )
tRNA
- kwas rybonukleinowy przenoszący (transport ribonucleic acid )
UV
- nadfioletowe (ultra-violet)

6 Dodatki
vii
6.2
Wybrane wzory i fragmenty kodu źródłowego
W celu zilustrowania najważniejszych własnych algorytmów używanych do zrealizowania badań
przedstawionych w tej pracy, w tym dodatku przedstawiono niektóre dłuższe wyprowadzenia i
fragmenty kodu źródłowego (w języku FORTRAN).
6.2.1
Generowanie momentów multipolowych CAMM
Jak już opisano w niniejszej pracy, multipole atomowe CAMM generowano wprowadzając własne
modyfikacje w odpowiednich miejscach ogólnodostępnego kodu programu GAMESS. W prak-
tyce, zrealizowano to poprzez jedną procedurę, wykonywaną przy okazji innej, wewnętrznej
macierzystego programu (dzieląc przy tym zarezerwowaną pamięć i zadeklarowane zmienne).
Pierwszy krok stanowił zliczanie wkładów do momentów atomowych pochodzących od gęstości
elektronowej i ładunku jądrowego według Równania 17. Fragment kodu używany do obliczania
wkładu elektronowego dla multipoli o indeksie M (M = 0 dla ładunku, M = 1, 2, 3 dla kolejnych
składowych dipoli, itd.) i gromadzący je w tablicy A dla kolejnych atomów, jest następujący:
C ----------------------------------------------------------
C Zero the array that will contain the multipoles, A.
do ia=1,NAT
A(M,ia)=0.0
enddo
k=0
C Loop over all atoms.
do ia=1,NAT
C Loop over the atomic orbitals of atom IA.
do io=LIMLOW(ia),LIMSUP(ia)
C Loop over all atomic orbitals with index <= io.
do jo=1,io
k=k+1
x=P(k)*AMI(k)
A(M,ia) = A(M,ia) - x
10
if (io.ne.jo) then
A(M,ITAB(jo)) = A(M,ITAB(jo)) - x
endif
enddo
enddo
enddo
C ----------------------------------------------------------
W powyższym fragmencie kodu NAT jest zmienną całkowitą zawierającą liczbę atomów,
LIMLOW i LIMSUP indeksują dolne i górne indeksy orbitali atomowych atomów, a ITAB przy-
porządkowuje orbitalom atomowym ich atomy. Tablice P i AMI zawierają elementy macierzy
gęstości i jednoelektronowe całki multipolowe, odpowiednio, w kolejności odpowiadającej używa-
nej pętli (iteracja po atomach, następnie po orbitalach danego atomu, i na końcu po wszystkich
orbitalach atomowych). Linia 10 uwzględnia symetrię pojedynczego wkładu, P
IJ
D
I|x
k
y
l
z
m
|J
E
,
i wlicza go w moment multipolowy atomu drugiego orbitala.
Kolejny fragment zlicza wkłady pochodzące od ładunków jądrowych do momentów poszcze-
gólnych atomów, Z
i
x
k
i
y
l
i
z
m
i
, do tej samej tablicy A (wkład elektronowy już w niej jest po wyko-
naniu poprzedniego fragmentu):

6 Dodatki
viii
C ----------------------------------------------------------
C Loop over all atoms
60 do ia=1,NAT
C ----------------------------------------------------------
C Center of mass is given by (XP,YP,ZP).
70 COOR(1) = C(1,ia) - XP
COOR(2) = C(2,ia) - YP
COOR(3) = C(3,ia) - ZP
C ----------------------------------------------------------
C Algorithm for adding nuclear contributions.
80 x=ZAN(ia)
do i=1,3
x=x*(COOR(i)**MAPCOOR(i,M))
enddo
85 A(M,ia)=A(M,ia)+x
C ----------------------------------------------------------
enddo
C ----------------------------------------------------------
Zmienne rzeczywiste XP, YP, ZP zawierają współrzędne środka masy cząsteczki, z kolei ZAN
zawiera ładunek jądrowy kolejnych atomów. Zmienna MAPCOOR jest tablicą pomocniczą, przypo-
rządkowującą wykładnik dla danej współrzędnej (x, y, z odpowiada ciagowi 1, 2, 3) i indeksu mo-
mentu multipolowego M. Tablica C zawiera współrzędne kartezjańskie (pierwszy indeks) wszyst-
kich atomów molekuły (drugi indeks).
Po wykonaniu poprzednich dwóch fragmentów kodu, tablica A zawiera zwykłę atomowe mo-
menty, które można wysumować do odpowiednich momentów molekularnych. Z nich uzyskano
momenty multipolowe CAMM transformując je do lokalnych układów współrzędnych według
rekombinacji opisanej Równaniem 26. Równanie to można rozpisać też ososbno dla momentów
multipolowych poszczególnych rzędów, używając indeksacji występujacej w Równaniu 9 [94] i
odejmując od momentów atomowych cyklicznie iloczyny momentów niższych rzędów i współ-
rzędnych. Dla kilka pierwszych multipoli:
µ
CAM M
s,i
= (M
CAM M
100,i
, M
CAM M
010,i
, M
CAM M
001,i
) = µ
s,i
− qs
i
(s = x, y, z),
Ω
CAM M
st,i
= Ω
st,i
− qs
i
t
i
− µ
s,i
t
i
− µ
t,i
s
i
(s, t = x, y, z),
Θ
CAM M
stu,i
= Θ
stu,i
− qs
i
t
i
u
i
− µ
s,i
t
i
u
i
− µ
t,i
u
i
s
i
− µ
u,i
s
i
t
i
−Ω
st,i
u
i
− Ω
tu,i
s
i
− Ω
us
t
i
(s, t, u = x, y, z),
(31)
Ψ
CAM M
stuv,i
= Ψ
stuv,i
− qs
i
t
i
u
i
v
i
− µ
s,i
t
i
u
i
v
i
− µ
t,i
u
i
v
i
s
i
− µ
u,i
v
i
s
i
t
i
− µ
v,i
s
i
t
i
u
i
−Ω
st,i
u
i
v
i
− Ω
su,i
t
i
v
i
− Ω
sv,i
t
i
u
i
− Ω
tu,i
s
i
v
i
− Ω
tv,i
s
i
u
i
− Ω
uv,i
s
i
t
i
−Θ
stu,i
v
i
− Θ
tuv,i
s
i
− Θ
uvs,i
t
i
− Θ
vst,i
u
i
(s, t, u, v = x, y, z).
Ta transormacja jest wykonana w poniższym fragmencie kodu źródłowego, na tej samej ta-
blicy A, która już zawiera nietransformowane momenty atomowe. Zmienna MAPCOOR jest ta sama
co wyżej, a MAPA jest inną tablicą pomocniczą, zawierającą odwrotne mapowanie - przyporząd-
kowuje ona więc danym wykładnikom k, l, m (tablica ta ma trzy wymiary) odpowiedni indeks
momentu multipolowego M. Fragment ten należy wykonywać dla rosnących indeksów M, tak by
zrealizować iteracyjny charakter Równania 26. Potrójna pętla (wykonana dla każdego atomu
osobno) odpowiada potrójnej sumie w Równaniu 26, a warunek na linii wyklucza możliwość
k
0
l
0
m
0
= klm. Funkcja BRACKET zwraca współczynnik dwumienny Newtona.

6 Dodatki
ix
C ----------------------------------------------------------
C Loop over all atoms
89 do ia=1,NAT
C ----------------------------------------------------------
C Recombination algorithm evaluates all cases intrinsically.
90 x = 0.0
ik = MAPCOOR(1,M)
il = MAPCOOR(2,M)
im = MAPCOOR(3,M)
do ikk = 0,ik
do ill = 0,il
do imm = 0,im
y = 1.0
n = MAPA(ikk+1,ill+1,imm+1)
92
if(n.ne.M)then
y = y*A(n,ia)
y = y*BRACKET(ik,ikk)
y = y*BRACKET(il,ill)
y = y*BRACKET(im,imm)
y = y*(COOR(1)**(ik-ikk))
y = y*(COOR(2)**(il-ill))
y = y*(COOR(3)**(im-imm))
x = x-y
endif
enddo
enddo
enddo
95 A(M,ia) = A(M,ia)+x
C ----------------------------------------------------------
enddo
C ----------------------------------------------------------
6.2.2
Obliczanie energii oddziaływań między momentami multipolowymi
Operując pełnymi bezśladowymi macierzami multipolowymi, można energię oddziaływania wy-
stępującą między nimi rozpisać za pomocą Równania 29. Dokonując pełną kontrakcę przez
symetryczny tensor oddziaływania
(κ)
T
(κ
0
)
ij
= −∇
κ+κ
0
³
1
r
ij
´
, można symbolicznie wyrazić oddzia-
ływania pomiędzy momentami multipolowymi kilku początkowych rzędów:
∆E
ij
(00)
=
q
i
q
j
r
ij
∆E
ij
(10)
= ~µ
j
[1]
(1)
T
(0)
q
i
= q
i
r
−3
ij
(r
ij
· ~µ
j
)
∆E
ij
(11)
= (~µ
i
· ~µ
j
) r
−3
ij
− 3 (~µ
i
· r
ij
) (r
ij
· ~µ
j
) r
−5
ij
(32)
∆E
ij
(20)
= (r
ij
· Ω
i
· r
ij
) q
j
r
−5
ij
∆E
ij
(21)
= 2 (~µ
j
· Ω
i
· r
ij
) r
−5
ij
− 5 (r
ij
· Ω
i
· r
ij
) (~µ
j
r
ij
) r
−7
Mając takie wyrażenia na energię oddziaływania multipoli, wystarczy zdefiniować odpowied-
nie iloczyny skalarne i kontrakcje tensorów i można w sposób rekurancyjny je zaprogramować.

6 Dodatki
x
Jednak znacznie wydajniej jest zaimplementować Równanie 9, które korzysta tylko z nieza-
leżnych momentów multipolowych i wymaga zatem innych współczynników przy sumowaniu
wkładów od poszczególnych momentów. Aby zrealizowac ten algorytm, należy wpierw zako-
dować wyrażenie na tensor oddziałwania multipolowego w Równaniu 28. Poniżej znajduje się
przkład takiego kodu:
function T(k,l,m,dr)
implicit real *8 (A-H,O-Z)
dimension dr(3)
integer F(11)
data F /1.0, 1.0, 2.0, 6.0, 24.0, 120.0,
*
720.0, 5040.0, 40320.0, 362880.0, 3628800.0 /
r = sqrt(dr(1)*dr(1) + dr(2)*dr(2) + dr(3)*dr(3))
xr = dr(1)/r
yr = dr(2)/r
zr = dr(3)/r
n = k+l+m
T = 0.0
do kk = 0,int(k/2)
do ll = 0,int(l/2)
do mm = 0,int(m/2)
nn = kk+ll+mm
kkk = k-2*kk
lll = l-2*ll
mmm = m-2*mm
x = (-1.0)**nn * F(2*n-2*nn+1) / F(n-nn+1)
x = x / (F(kk+1)*F(ll+1)*F(mm+1))
x = x / (F(kkk+1)*F(lll+1)*F(mmm+1))
T = T + x * (xr)**(kkk) * (yr)**(lll) * (zr)**(mmm)
enddo
enddo
enddo
x = (-1.0)**n * F(k+1) * F(l+1) * F(m+1) / (2.0**n)
T = T * x / (r**(n+1))
end function T
Tutaj, tablice F zawiera kolejne wartości silni dla liczb naturalnych. Należy dodać, że nie
jest to procedura zbyt wydajna dla niższych rzędów k, l, m, ale można ją przyspieszyć definiując
dodatkowe pomocnicze tablice.
Majać tak zdefiniowany tensor oddziaywania, można przystąpić do obliczania energii od-
działywania miedyz dowolnymi dwoma zestawami momentów multipolowych według Równania
9. Poniżzsy fragment kodu oblicza energie oddziaływania między wszystkimi octupolami w jed-
nym monomrze i dipolami w drugim. Momenty tych dwóch multipoli w tej imlementacji są
przekazane poprzez pełną macierz multipolową - na przykład w przypadku oktupola, trzywy-
miarową dla każdego atomu, czyli mającą 27 elementów. Procedura fill służy do wyznaczania
współrzędnych tych multipoli w odpowiednich wymiarach (wybór arbitralny w zmiennych ko1 i
kd2). Początkowe wartości x i y są czynnikami normalizacji dla momentów multipolowych we-
dług Równania 10. Gdyby sumować po współrzędnych multipoli raczej niz po ich wykłądnikach

6 Dodatki
xi
(2 ∗ (k + l + m) pętli zamiast 4), to współczynniki te można wyciagnąć przed sumowanie w Rów-
naniu 9 w zbiorczy czynnik (k + l + m)!. Kod ten można znacznie zoptymalizować organizując
momenty w sposób mniej ogólny, ale zgodny z iterowanymi zmiennymi - należałoby indeksować
multipole wykładnikami współrzędnych k, l, m (faktycznie przyspiesza ten fragment kodu nawet
o sto razy, zależnie od rzędu multipoli).
subroutine e31(coor1, coor2, octup1, dip2, N1, N2, E)
implicit real *8 (A-H,O-Z)
dimension coor1(N1,3), coor2(N2,3), octup1(N1,3,3,3), dip2(N2,3)
dimension F(9), dr(3), ko1(3), kd2(1)
data F /1.0,1.0,2.0,6.0,24.0,120.0,720.0,5040.0,40320.0/
do i = 1,N1
do j = 1,N2
do k = 1,3
dr(k) = coor1(i,k) - coor2(j,k)
enddo
nn1 = 3
nn2 = 1
do k1 = 0,nn1
do k2 = 0,nn2
do l1 = 0,nn1-k1
do l2 = 0,nn2-k2
m1 = nn1-k1-l1
m2 = nn2-k2-l2
call fill(ko1,nn1,k1,l1,m1)
call fill(kd2,nn2,k2,l2,m2)
x = F(k1+1)*F(l1+1)*F(m1+1)
y = F(k2+1)*F(l2+1)*F(m2+1)
x = octup1(i,ko1(1),ko1(2),ko1(3)) / x
y = dip2(j,kd2(1)) / y
E = E - x*T(k1+k2,l1+l2,m1+m2,dr)*y
enddo
enddo
enddo
enddo
enddo
enddo
end subroutine e31
Wyszukiwarka
Podobne podstrony:
W10 Oczyszczanie białek i badanie ich oddziaływań z kwasami nukleinowymi
Modelowanie, Szkoła - studia UAM, resocjalizacja semestr 2 (rok 1), Teoria wychowania, Teoria wychow
Cwiczenie6, Politechnika Wrocławska Energetyka, - MGR II semestr, Modelowanie matematyczne instalacj
Karol Sapieha mgr praca domowa modelowanie komputerowe w praktyce in ynierskiej
oddziaływanie pola ligandów
Inhibitory aromatazy w leczeniu uzupełniającym raka piersi
RK mgr W1sn
modelowanie systemow
modelowanie procesˇw transportowych
Prezentacja Składniki chemiczne kwasu nukleinowego
Oddziaływania międzypopulacyjne w biocenozie
Modelowanie biznesowe
MODELOWANIE DANYCH notatki
Seminaria mgr II
Tekst i dyskurs mgr
więcej podobnych podstron