XVII OGÓLNOPOLSKA KONFERENCJA WARSZTAT PRACY PROJEKTANTA KONSTRUKCJI

Ustroń, 20

÷

23 lutego 2002 r.

Kazimierz Flaga

ZBROJENIE PRZECIWSKURCZOWE, OBLICZENIA,

ZALECENIA KONSTRUKCYJNE W BUDOWNICTWIE

POWSZECHNYM

1. Uwagi ogólne

Problemy skurczu betonu, jego wpływ na pracę statyczno-wytrzymałościową konstrukcji

z betonu oraz na konieczne zbrojenie przeciwskurczowe w strefach przypowierzchniowych
elementów z betonu traktowane są przez kolejne polskie normy do obliczania konstrukcji
betonowych, żelbetowych i sprężonych - zupełnie marginalnie. Nic też dziwnego, że wiele z
tych elementów czy też konstrukcji ulega nieprzewidzianemu zarysowaniu, mimo że
projektant spełnił - w swoim przeświadczeniu - wszystkie wymagania polskich norm.

Autor spotkał się z tym problemem wielokrotnie przy ekspertyzach czy też ocenach stanu

technicznego konstrukcji z betonu, dochodząc do wniosku, że:
a) sposób nauczania tych problemów na polskich uczelniach technicznych jest

niewystarczający,

b) projektanci, za przykładem polskich norm przedkładają wzory i procedury obliczeniowe

nad fizyczne uwarunkowania pracy zaprojektowanych przez nich konstrukcji.
W odniesieniu do zagadnienia a) często uważa się, że problem skurczu betonu jest

zagadnieniem technologicznym i jako takie nie powinno być szerzej rozpatrywane przez
wysokiej klasy specjalistów od obliczeń, lubiących czyste schematy obciążeniowe,
materiałowe i obliczeniowe.

W zagadnieniu b) chodzi najczęściej o niewiedzę z zakresu oddziaływania środowiska na

beton, ciągłej wymiany masy i ciepła z otoczeniem, istnienia wewnątrz betonu
niestacjonarnych i nieliniowych pól wilgotności i temperatury, generujących w przekrojach
znaczne naprężenia własne. Wymiary przekrojów, cechy wytrzymałościowe materiałów,
obciążenia są widoczne, a przynajmniej można je sobie wyobrazić. Natomiast wymiana
masy czy ciepła, pola termiczne i wilgotnościowe, a także naprężenia własne są
niewidoczne, wręcz abstrakcyjne, i wyobrażenie ich sobie wymaga odpowiedniego
przygotowania z zakresu chemii fizycznej i fizyki ciał koloidalno - kapilarno - porowatych,
którego najczęściej absolwent wydziałów budownictwa polskich politechnik nie posiada.

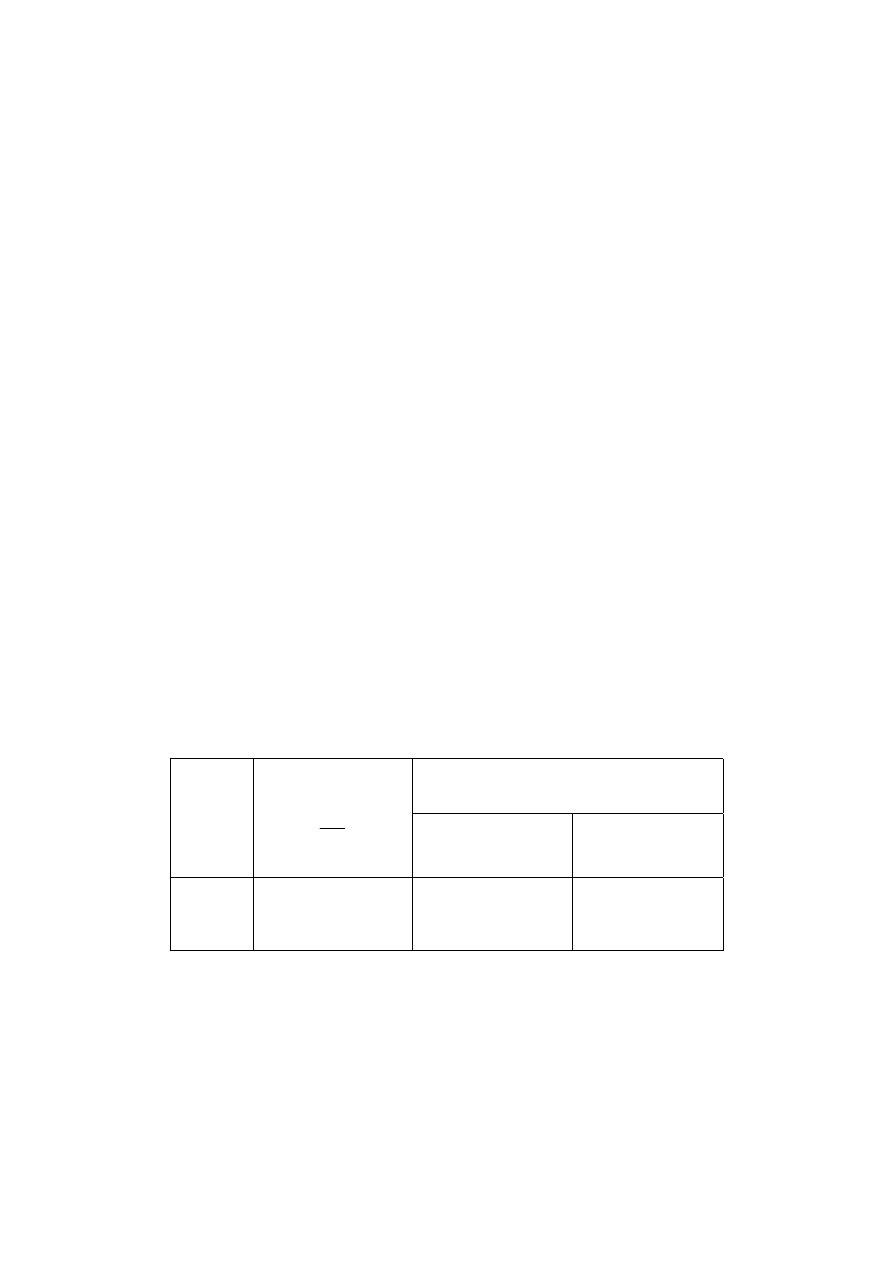
Efekty tego stanu rzeczy przejawiają się często w niedostatecznej jakości elementów i

konstrukcji z betonu, która rzutuje na ich trwałość, zwłaszcza w skażonym czy agresywnym
środowisku.

2 Przegląd polskich norm do obliczania konstrukcji z betonu w aspekcie

uwzględniania skurczu betonu

2.1 PN-56/B-03260 „Konstrukcje żelbetowe. Obliczenia statyczne i

projektowanie” [1]

W p. 6.2. „Temperatura i skurcz betonu” podano w 6.2.1, że: „Zabezpieczenie

budynków od ujemnego wpływu sił wywoływanego przez skurcz betonu i temperaturę może
nastąpić albo przez wykonanie odpowiednich przerw dylatacyjnych lub przez uwzględnienie
wpływu skurczu i temperatury w obliczeniu statycznym, albo wreszcie przez zastosowanie
obu sposobów jednocześnie”, zaś w 6.2.4., że: „Wpływ skurczu należy uważać za
równoważny z obniżeniem się temperatury o 15

o

C w zwykłych i o 20

o

C w lekkich

betonach”.

W p. 5.4.5.3.podano wymóg: „W belkach wyższych niż 1 m należy zaprojektować

wkładki przy powierzchniach bocznych o średnicy d

≥

8 mm, w odstępach nie większych niż

50 cm”.

2.2 PN-66/B-03320 „Konstrukcje z betonu sprężonego” [2]

W p. 4.3.3. „Pełzanie i skurcz betonu (metoda bardziej dokładna)” podano tablicę 2.1.

pt. „Wartości odkształcenia jednostkowego

ε

sk

w zależności od pielęgnacji betonu i wieku

betonu”, jak niżej:

Tablica 2.1 Wartości odkształcenia jednostkowego

sk

ε

w zależności od pielęgnacji

betonu i wieku betonu

Odkształcenie jednostkowe skurczowe

sk

ε

w

zależności od pielęgnacji betonu wykonanego przy

użyciu cementu portlandzkiego

Wiek betonu

w chwili

sprężenia

w dobach

Orientacyjny stosunek

wytrzymałości betonu do

wytrzymałości wymaganej

28

R

R

d

beton przechowywany w

powietrzu

o wilgotności względnej do

35 % (powietrze suche)

beton przechowywany w

powietrzu o wilgotności

względnej do 70 %

(powietrze wilgotne)

7

14
28
90

0,75
0,90
1,00
1,25

0,00032
0,00030
0,00026
0,00018

0,00026
0,00024
0,00020
0,00014

Dalej podano w tym punkcie, że: „W przypadku naparzania betonu można przyjąć

wartości odkształcenia jednostkowego skurczowego

ε

sk

... jak dla betonu o pełnej

wytrzymałości”.

W p. 10.2.6.2. występuje wymóg: „Pręty przeciwskurczowe i montażowe w kierunku

podłużnym belek i płyt należy przyjmować o średnicy co najmniej 4,5 mm w takiej liczbie,
aby ich łączny przekrój był równy co najmniej 0,2 % przekroju betonu i odstęp między
prętami nie przekraczał 33 cm. Zbrojenie podłużne można uwzględnić w obliczeniach
wytrzymałości, zarówno na ściskanie, jak i na rozciąganie”.

2.3 PN-76/B-03264 „Konstrukcje betonowe, żelbetowe i sprężone. Obliczenia

statyczne i projektowanie” [3]

W p. 2.2.2. „Odkształcenia skurczowe” podano, że: „Wartości odkształceń skurczowych

ε

s

betonu na jednostkę długości należy przyjmować:

- w konstrukcjach betonowych

ε

s

= 0,0003,

- w konstrukcjach żelbetowych

ε

s

= 0,0002,

- w konstrukcjach sprężonych - odpowiednio do wieku betonu w chwili sprężenia i
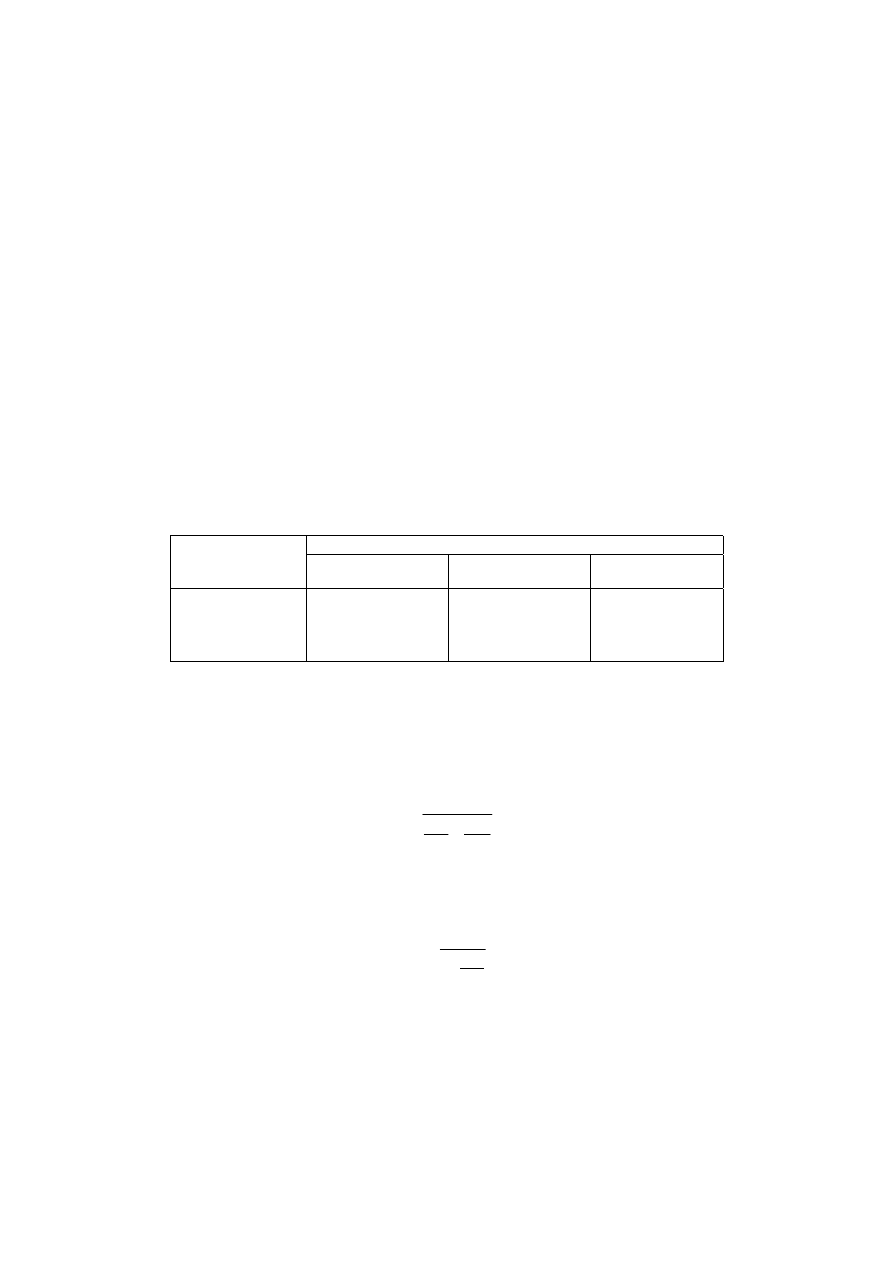
wilgotności środowiska - zgodnie z tabl. 2.2, jak niżej:

Tablica 2.2

Wartości odkształceń skurczowych

s

ε

Środowisko (wilgotność względna)

Wiek betonu w chwili
sprężenia w dobach

suche

(< 40 %)

zwykłe

(40-70 %)

wilgotne

(> 70 %)

7
14
28
90

0,00032
0,00028
0,00024
0,00017

0,00026
0,00023
0,00020
0,00014

0,00019
0,00017
0,00015
0,00010

Dalej podano, że: „W przypadku przyspieszenia twardnienia betonu przez naparzanie,

skurcz betonu należy przyjmować jak dla elementów sprężonych po 14 dniach twardnienia.
Dla konstrukcji znajdujących się w wodzie skurcz betonu

ε

s

= 0”.

W p. 6.1.1. zalecono sprawdzenie elementów żelbetowych osiowo i mimośrodowo

rozciąganych 1 kategorii rysoodporności na możliwość pojawienia się rys prostopadłych do
osi elementu, z warunku:

fp

fp

bs

bzk

W

e

F

R

N

+

−

≤

1

σ

(2.1)

gdzie:

bs

σ

oznacza naprężenie na sprawdzanej krawędzi przekroju wywołane skurczem

betonu (wartość bezwzględna). Wartości

bs

σ

dla przekroju symetrycznego, symetrycznie

zbrojonego należy obliczać wg wzoru:

µ

ε

σ

n

E

b

s

bs

1

1

+

=

(2.2)

Wzór na

bs

σ

nie uwzględniał relaksacji naprężeń skurczowych wywołanych pełzaniem

betonu, stąd b. często zachodziło, iż

bs

σ

> R

bzk

i siła rysująca wychodziła ujemna.

W p. 9.2.1.7. wprowadzono wymóg: „W belkach żelbetowych oraz w belkach

sprężonych 3 kategorii rysoodporności, jeżeli wysokość przekroju belki jest większa od
70 cm - przy powierzchniach bocznych należy umieszczać podłużne pręty konstrukcyjne w
rozstawie nie większym niż 40 cm. Sumaryczny przekrój tych prętów powinien być nie
mniejszy niż 0,1 % przekroju poprzecznego belki”.

W p. 9.5.1. „Odkształcenia konstrukcji od wpływu temperatury i skurczu betonu”

postanowiono, że: „Wpływ skurczu w konstrukcjach żelbetowych można przyjmować za
równoważny z obniżeniem się temperatury o 15

o

C”.

2.4 PN-84/B-03264 „Konstrukcje betonowe, żelbetowe i sprężone. Obliczenia

statyczne i projektowanie” [4]

W p. 2.2.2. „Odkształcenia skurczowe” podtrzymano ustalenia normy z 1976 r. z

wyjątkiem wartości

s

ε

dla konstrukcji żelbetowych, które można było przyjmować na

poziomie

s

ε

= 0,00015. Ponadto w tablicy 2.2 dotyczącej wartości jednostkowego

odkształcenia skurczowego

s

ε

w konstrukcjach sprężonych zmieniono granicę wilgotności

względnej środowiska z 70 % na 75 %.

W p. 6.1. przy sprawdzaniu stanu granicznego pojawienia się rys w elementach

rozciąganych przyjęto we wzorze (1) wartość

bs

σ

= 0, tzn. nie uwzględniono zmniejszenia

się siły rysującej w wyniku naprężeń rozciągających, wymuszonych w przekroju przez opór
wkładek zbrojeniowych.

W p. 9.2.1.5. zapisano, że: „W belkach żelbetowych i sprężonych 3 kategorii

rysoodporności, jeżeli wysokość przekroju belki jest większa niż 0,7

m, przy

powierzchniach bocznych należy umieszczać podłużne pręty konstrukcyjne o średnicy nie
mniejszej niż 8 mm w rozstawie nie większym niż 0,4 m”.

W p. 9.5.1. „Odkształcenia konstrukcji od wpływu temperatury i skurczu betonu”

postanowiono jak w normie z 1976 r.

2.5 PN-91/S-10042 „Obiekty mostowe. Konstrukcje betonowe, żelbetowe i

sprężone. Projektowanie” [5]

W roku 1991 ukazała się norma do projektowania betonowych konstrukcji mostowych,

bazująca na FIP Recommendations opartych na CEB-FIP Model Code (MC 78) z czerwca
1982 r., normie DIN 1045 z 1988 r., normie SIA 162 E z 1989 r. i normie BS 5400 z 1984 r.
Wprowadziła ona do polskiego mostownictwa szereg zmian i uściśleń w stosunku do
poprzedniej normy mostowej PN-58/B-03261.

W zakresie skurczu betonu postanawia ona w p. 3.6.1., że „wartości jednostkowe

odkształcenia skurczu

so

ε

należy przyjmować odpowiednio do wieku betonu w chwili

zmiany obciążenia (sprężenia) i wilgotności środowiska, w którym znajduje się konstrukcja
po tym obciążeniu (sprężeniu). Jeśli nie ma innych udokumentowanych źródeł wartość
odkształcenia skurczu

so

ε

należy przyjmować wg tablicy 2.3, jak niżej:

Tablica 2.3

Wartości odkształceń skurczu betonu zwykłego,

so

ε

, ‰

Grubość zastępcza

m

e

, mm

150

600

150

600

Wilgotność względna %

Wiek betonu w

chwili obciążenia

dni

50

80

7

28
90

0,43
0,32
0,19

0,31
0,30
0,28

0,26
0,23
0,16

0,21
0,21
0,20

„Podane w tablicy 2.3 wartości odkształceń skurczu .......... dotyczą typowych warunków

technologicznych i normalnych warunków dojrzewania dla określonych zakresów
wilgotności i grubości zastępczej. Wartości grubości zastępczej

m

e należy obliczać wg

wzoru:

u

A

e

b

m

2

=

(2.3)

w którym:

b

A

- pole przekroju betonu,

u

- obwód pola przekroju betonu, stykającego się z powietrzem, przynajmniej

okresowo.

Dla betonów znajdujących się stale pod wodą należy przyjmować

so

ε

= 0. W przypadku

stosowania przyspieszonego dojrzewania betonu przez podgrzewanie wartość

so

ε

należy

przyjmować jak dla betonu obciążonego po 7 dniach twardnienia”.

Norma podaje również sposób uwzględnienia wpływu składu mieszanki betonu, ilości

zbrojenia i czasu obciążenia na wartość odkształcenia

so

ε

.

W p. 12.4.9. „Minimalny procent zbrojenia w strefie rozciąganej ze względu na

rozwarcie rys” norma stanowi, że: „Dodatkowe zbrojenie przypowierzchniowe
(przeciwskurczowe) należy stosować do wszystkich powierzchni zewnętrznych i narażonych
na wpływy atmosferyczne. Ilość zbrojenia przypowierzchniowego siatkowego powinna
odpowiadać co najmniej 0,3 % objętości betonu strefy współpracującej, w obu kierunkach.
Ilość ta obejmuje łączne zbrojenie przypowierzchniowe przy obu przeciwległych
krawędziach przekroju poprzecznego elementu, stanowiące po 50 % każde”.

„Rolę tego zbrojenia mogą pełnić siatki zbrojenia głównego i rozdzielczego, dodatkowe

siatki przeciwskurczowe (np. przy powierzchniach zewnętrznych filarów i przyczółków
betonowych) lub kombinacja strzemion i podłużnych prętów przeciwskurczowych (przy
powierzchniach zewnętrznych belek)”.

„Przy wysokich belkach zaleca się stopniowanie podłużnych prętów umieszczonych przy

obu powierzchniach bocznych - gęściej od strony rozciąganych prętów głównych”.

„Dla części przekroju elementu masywnego o najmniejszym wymiarze co najmniej

400 mm należy określić taką ilość zbrojenia przypowierzchniowego jak dla przekroju
skrzynkowego o ściankach 200 mm grubości. Ilość tę należy umieścić w rozpatrywanej
części elementu masywnego”.

„Pręty zbrojenia siatkowego powinny być ułożone ortogonalnie i równomiernie. Jeśli nie

występuje zagrożenie skurczu (zarysowania skurczowego) należy zmniejszyć ilość zbrojenia
przypowierzchniowego do 60 % ilości minimalnych”.

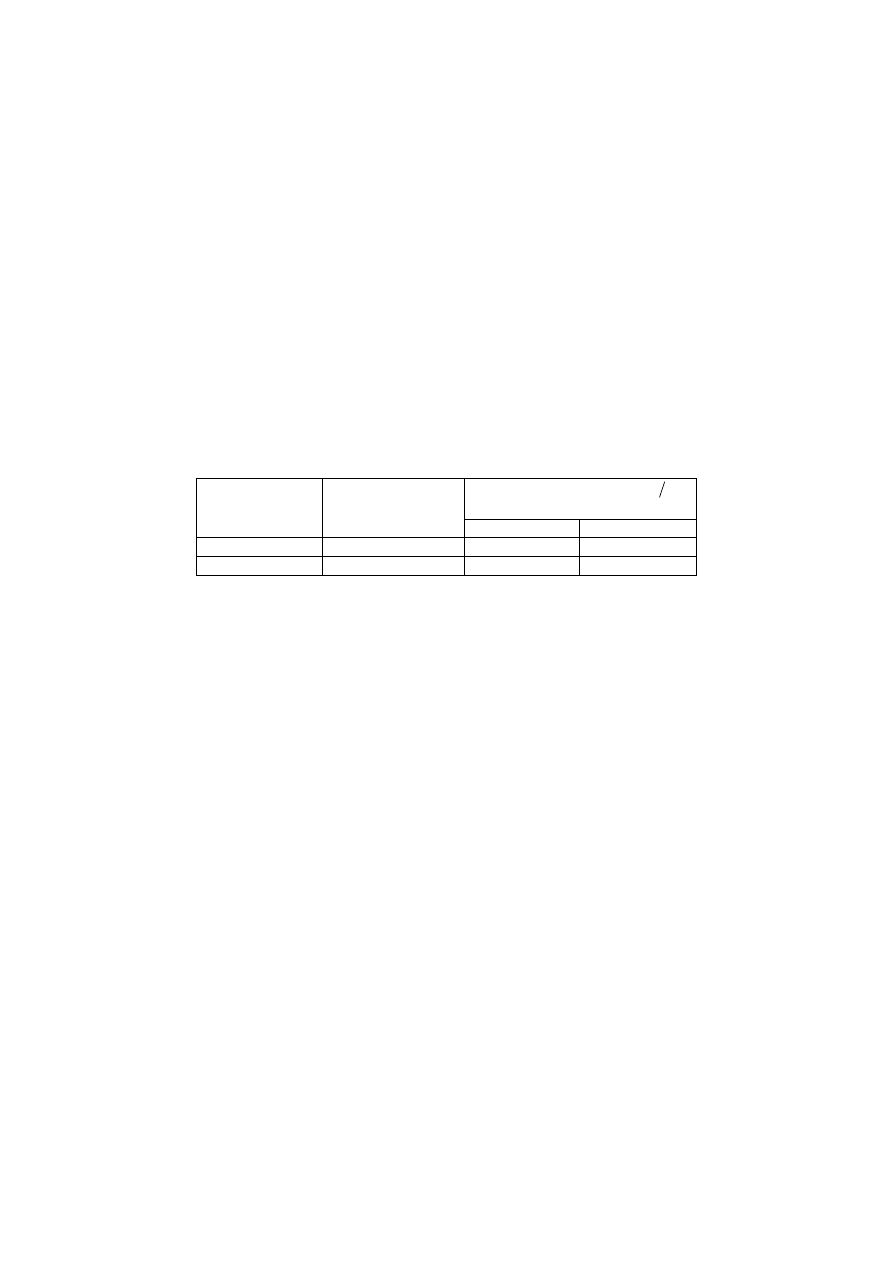
Jak z powyższego wynika norma mostowa PN-91/S-10042 po raz pierwszy w Polsce

wprowadziła obowiązek stosowania zbrojenia przypowierzchniowego (przeciw-
skurczowego) do wszystkich betonowych powierzchni zewnętrznych i narażonych na
wpływy atmosferyczne.

2.6 PrPN-B-03264 „Konstrukcje betonowe, żelbetowe i sprężone. Obliczenia

statyczne i projektowanie” [6]

Jest to najnowszy projekt normy PN-B-03264 będący nowelizacją PN-B-03264:1999,

uwzględniający kolejne uściślenia Eurocodu 2.

W projekcie tym, w p. 2.2.3. „Pełzanie i skurcz betonu” zapisano, że: „Wartości

końcowego ....... odkształcenia skurczowego

ε

cs

(

∞

, t

s

) – podano w tablicy 2.4”, jak niżej:

Tablica 2.4

Końcowe odkształcenie skurczowe

(

)

s

cs

t

,

∞

ε

(‰)

Miarodajny wymiar

o

h

=

u

A

c

2

(mm)

Miejsce elementu

Wilgotność względna

RH (%)

≤

150

600

wewnątrz

50

0,60

0,50

na zewnątrz

80

0,33

0,28

„W tablicy - A

c

oznacza pole przekroju elementu, u obwód tego pola. Dla wartości

pośrednich dopuszcza się interpolację liniową. Wartości ..... odkształceń skurczowych

ε

cs

(t, t

s

) w rozważanej chwili t - określać można wg załącznika B”. W załączniku B

(informacyjnym) podano sposób obliczania

ε

cs

(t, t

s

) wg ENV 1992-1-1:1991.

Punkt 6.2. projektu normy „Nominalne pole przekroju zbrojenia” podaje zasadę

obliczania minimalnego pola A

s

przekroju zbrojenia rozciąganego, wymaganego z uwagi na

ograniczenie szerokości rys spowodowanych naprężeniami wywołanymi przez odkształcenia
wymuszone przyczynami wewnętrznymi (skurcz) lub zewnętrznymi (osiadanie podpór).
Punkt ten wiąże się pośrednio z problemem zbrojenia przeciwskurczowego i będzie
omówiony w dalszej części niniejszej pracy.

Punkt 8.1.7. projektu normy poświęcony jest zbrojeniu przypowierzchniowemu. Nie ma

w nim jednak wzmianki o tym, że zbrojenie przypowierzchniowe może być także
zbrojeniem przeciwskurczowym. Punkt dotyczy zbrojenia przypowierzchniowego mającego
na celu ograniczenie szerokości rys w belkach o wysokości większej niż 1 m oraz zbrojenia
przypowierzchniowego przeciwdziałającego odłupywaniu się otuliny betonu w belkach
zbrojonych wiązkami prętów lub prętami o średnicy większej niż 25 mm.

W p. 9.3.1.5. „Zbrojenie belek” jest wymóg: „W belkach żelbetowych i sprężonych, w

których dopuszcza się zarysowanie, jeżeli wysokość przekroju belki jest większa niż
700 mm, przy powierzchniach bocznych należy umieszczać podłużne pręty konstrukcyjne o
średnicy nie mniejszej niż 8 mm w rozstawie nie większym niż 350 mm”.

W p. 9.7.1. „Odkształcenia konstrukcji od wpływu temperatury i skurczu betonu”

powtórzono za poprzednimi normami zapis, że: „Wpływ skurczu w konstrukcjach
żelbetowych można przyjmować za równoważny z obniżeniem się temperatury o 15

o

C”.

2.7. Podsumowanie

Jak wynika z powyższych zestawień polskich norm z lat 1956-2001 do projektowania

konstrukcji z betonu, w zakresie zagadnień związanych ze skurczem betonu, wpływem
skurczu na wartości sił wewnętrznych, zbrojeniem przeciwskurczowym - dochodziło na
przestrzeni lat do kolejnych uściśleń, ale niewystarczających. Problemy te wymagają
szerszego naświetlenia.

3. Skurcz betonu wg Eurokodu-2

Chcąc poczynić dalsze rozważania związane ze zbrojeniem przeciwskurczowym w

konstrukcjach betonowych w budownictwie powszechnym, należy przede wszystkim dość
precyzyjnie określić wartość skurczu betonu w tych konstrukcjach.

W roku 1991 ukazała się pierwsza wersja Eurokodu 2: „Projektowanie konstrukcji z

betonu - Część 1: Reguły generalne i reguły dla budynków”, opracowana przez European
Committee for Standarisation (CEN) i oznaczona jako ENV-1992-1-1: 1991. Dość szybko
bo już w 1992 r. Instytut Techniki Budowlanej w Warszawie wydał „Wersję polską
ENV 1992-1-1: 1991” [7] zaś w 1993 r., - „Postanowienia Krajowe do ENV 1992-1-
1: 1991” [8]. Oba te dokumenty stały się podstawą do prac nad znowelizowaniem PN-84/B-
03264 w duchu zaleceń europejskich, co związane było integralnie z dążeniami Polski do
wejścia w skład Unii Europejskiej.

W rezultacie w roku 1994 powstała pierwsza wersja znowelizowanej normy pod nazwą

PrPN-B-03264, która ostatecznie została wdrożona w roku 1999 jako PN-B-03264:1999 [9].

Równolegle Zespół Autorski pod patronatem Sekcji Konstrukcji Betonowych KILiW

PAN opracował w 1997 roku 3. tomowe dzieło pt. „Podstawy projektowania konstrukcji
żelbetowych i sprężonych według Eurokodu 2” [10], w ramach uzyskanego z KBN grantu.
Dzieło to miało stanowić komentarz do zmian wprowadzonych w PN-B-03264:1999.

Niestety w ostatnich 2. latach doszło do znacznego przyśpieszenia prac związanych z

przekształceniem Eurokodu 2 (ENV 1992) w normę europejską EN 1992 tak, iż w czerwcu
1999 r. ukazał się pierwszy Draft EN 1992-1 (1

st

draft) [11] wprowadzający zmiany do

ustaleń ENV 1992-1-1:1991. W ślad za tym PKN opracował kolejną nowelizację normy PN-
B-03264:1999 pod nazwą PrPN-B-03264 [6], która jednakże nie może być wersją
ostateczną, bo w październiku 2001 r. pojawił się Draft EN 1992-1-1-1:2001 [12],
wprowadzający dalsze zmiany.

Zmiany następują tak szybko, że trudno przedstawić stałą podstawę do dalszych

rozważań. Rozwiązania zaprezentowane przez ENV 1992-1-1-1:1991 zostały w polskiej
literaturze technicznej dokładnie przedyskutowane i wydaje się, że mogą one stanowić
podstawę do dalszej dyskusji, usankcjonowaną normą PN -B-03264:1999.

Zatem według ENV 1992-1-1-1:1991 [10], odkształcenia skurczu zależą od składu

betonu (przede wszystkim od rodzaju i zawartości cementu w 1 m

3

betonu oraz od wartości

współczynnika wodno-cementowego W/C, klasy wytrzymałości, wieku, wilgotności
środowiska oraz wymiarów elementu.

Odkształcenia spowodowane przez skurcz i pęcznienie betonu zwykłego klas C12/15 do

C 50/60 (wg normy PN-B-03264: 1999 - klas B15 do B60) wystawionego na oddziaływanie
średniej wilgotności względnej RH w przedziale od 40% do 100% i średniej temperatury T
w przedziale od 10

o

C do 20

o

C, można obliczać ze wzoru:

( )

(

)

s

s

cso

s

cs

t

t

t

t

−

=

β

ε

ε

,

(3.1)

w którym:

cso

ε

- podstawowe odkształcenie skurczowe,

s

β

- współczynnik określający postęp skurczu,

t

- wiek betonu w rozważanej chwili, w dniach,

s

t ,

- wiek betonu na początku rozpatrywanego procesu skurczu lub pęcznienia,

w dniach.

Podstawowe odkształcenie skurczowe można wyznaczyć ze wzoru:

( )

RH

β

ε

ε

cm

s

cso

f

=

(3.2)

w którym:

( )

(

)

[

]

6

10

90

160

−

−

+

=

cm

sc

cm

s

f

f

β

ε

(3.3)

( )

cm

s

f

ε

- współczynnik skurczu zależny od średniej wytrzymałości betonu po 28

dniach

cm

f

(MPa),









 −

=

ści

wytrzymao

wysokiej

cementów

ących

twardniej

szybko

dla

-

8

ących

twardniej

szybko

i

zwykych

cementów

dla

-

5

ących

twardniej

wolno

cementów

dla

4

sc

β







≥

+

≤

≤

=

wodzie)

w

wanie

(przechowy

%

99

RH

dla

0,25

powietrzu)

na

wanie

(przechowy

%

99

RH

%

40

dla

1,55

-

sRH

RH

β

β

W powyższych danych

RH

s

β

oznacza współczynnik określony wzorem:

(

)

3

RH

RH/100

1

−

=

s

β

(3.4)

a RH - względną wilgotność (w %) otaczającego beton powietrza.

Współczynnik

(

)

s

s

t

t

−

β

we wzorze (3.1), opisujący postęp skurczu w czasie, można

wyznaczyć z zależności:

(

)

5

,

0

2

035

,

0















−

+

−

=

−

s

o

s

s

s

t

t

h

t

t

t

t

β

(3.5)

w którym:

o

h oznacza miarodajny wymiar elementu, w mm, równy:

u

A

h

c

o

2

=

(3.6)

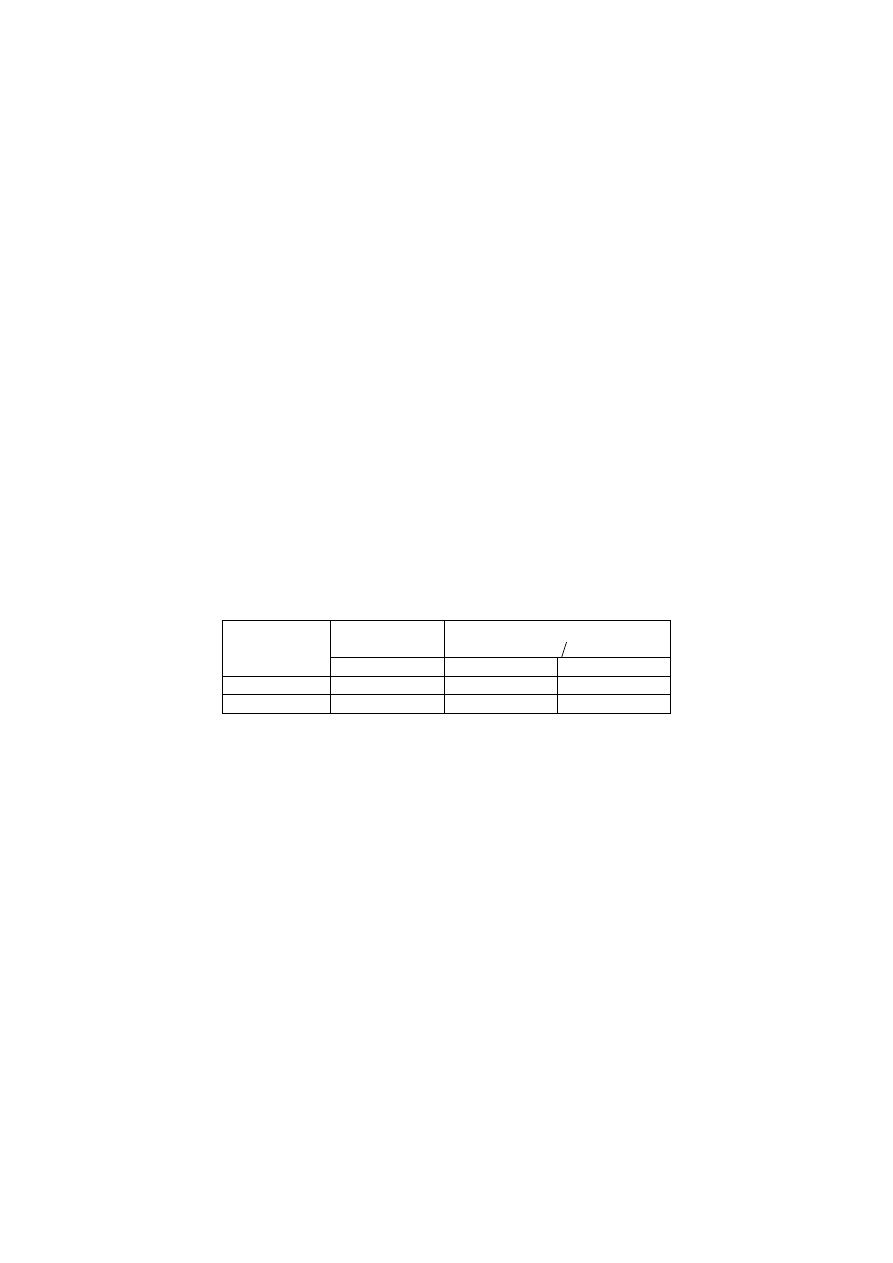
We wzorze (3.6):

c

A

- powierzchnia przekroju poprzecznego elementu,

u

- obwód przekroju wystawiony na działanie powietrza (czyli na wymianę

wilgoci zawartej w betonie, z otoczeniem).

Jak stwierdza się w [13], powyższy sposób obliczania wartości skurczu stosuje się wtedy,

gdy konieczne jest dokładne oszacowanie zmian skurczu w czasie, np. przy wyznaczaniu
efektów odkształceń reologicznych betonu.

Średni wskaźnik zmienności wyników powyższej prognozy dotyczącej skurczu, oceniony

na podstawie skomputeryzowanego banku danych z wyników badań laboratoryjnych, jest
rzędu 35 %.

Dokładność przyjętych metod obliczania wpływu skurczu (i pełzania) betonu powinna

odpowiadać wiarygodności danych, opisujących te zjawiska i znaczeniu ich wpływu na
rozważany stan graniczny. Zgodnie z EC2 efekty skurczu (i pełzania) betonu należy w
zasadzie uwzględniać tylko dla stanów granicznych użytkowalności oraz przy obliczaniu
efektów drugiego rzędu w stanach granicznych nośności, spowodowanych odkształceniami
konstrukcji. Konieczne jest ponadto uwzględnienie wpływu pełzania w wypadku, kiedy
może ono w sposób znaczący obniżać stateczność konstrukcji.

Jeżeli nie wymaga się dużej dokładności oceny to można za końcowe wartości

odkształceń skurczowych

∞

cs

ε

betonu zwykłego przyjąć dane zawarte w tabl. 3.1.

Tablica 3.1

Końcowe wartości odkształceń skurczowych

∞

cs

ε

(‰)

Wilgotność

względna

Miarodajny wymiar elementu

)

(

2

mm

u

A

h

c

o

=

Miejsce

elementu

RH (%)

≤

150

600

wewnątrz

30

-0,60

-0,50

na zewnątrz

80

-0,33

-0,28

Wartości podane w tabl. 3.1 dotyczą średniej temperatury betonu w przedziale 10

o

C do

20

o

C, co pozwala przyjąć, że uwzględniają one wahania temperatury w ciągu roku w

granicach od -10

o

C do + 40

o

C. Można je stosować przy zmianach wilgotności względnej

powietrza od RH = 20 % do RH = 100 %. Dla wartości pośrednich RH i

o

h dopuszcza się

interpolację liniową.

Wartości

∞

cs

ε

w tabl. 3.1 zostały określone dla betonu o konsystencji plastycznej klas

S2 i S3 (zgodnie z p. 7.2.1 ENV 206). Dla betonu o konsystencji wilgotnej S1 wartości te
należy pomnożyć przez współczynnik 0,70, a dla konsystencji półciekłej S4 - przez 1,20.

W przypadku betonów z superplastyfikatorami wartości skurczu

∞

cs

ε

w tabl. 3.1 odnoszą

się do konsystencji mieszanki przed dodaniem superplastyfikatorów.

Metoda obliczania odkształceń skurczowych betonu przedstawiona w EC2 jest

zaczerpnięta z CEB-FIP M.C.1990 [13]. Przy wskaźniku zmienności wynoszącym

ν

= 35 %,

dolne i górne wartości odkształceń skurczowych mogą się znacznie różnić od obliczonych
zgodnie z EC2, wartości średnich. I tak, kwantyle 5 i 10 % oraz 90 i 95 % zmiennych
losowych

( )

s

cs

t

t,

ε

wynoszą:

05

,

0

cs

ε

= 0,42

cs

ε

,

10

,

0

cs

ε

= 0,55

cs

ε

,

95

,

0

cs

ε

= 1,58

cs

ε

,

90

,

0

cs

ε

= 1,45

cs

ε

.

Co się tyczy wartości

s

t we wzorze (3.1), to CEB-FIP M.C.1990 [13] podaje tylko

informację, że dla

s

t < 14 dni przy dojrzewaniu w normalnej temperaturze, wpływ skurczu

na dodatkowe naprężenia i odkształcenia (duża wilgotność elementów, bardzo często jeszcze
zadeskowanych) jest mało istotny.

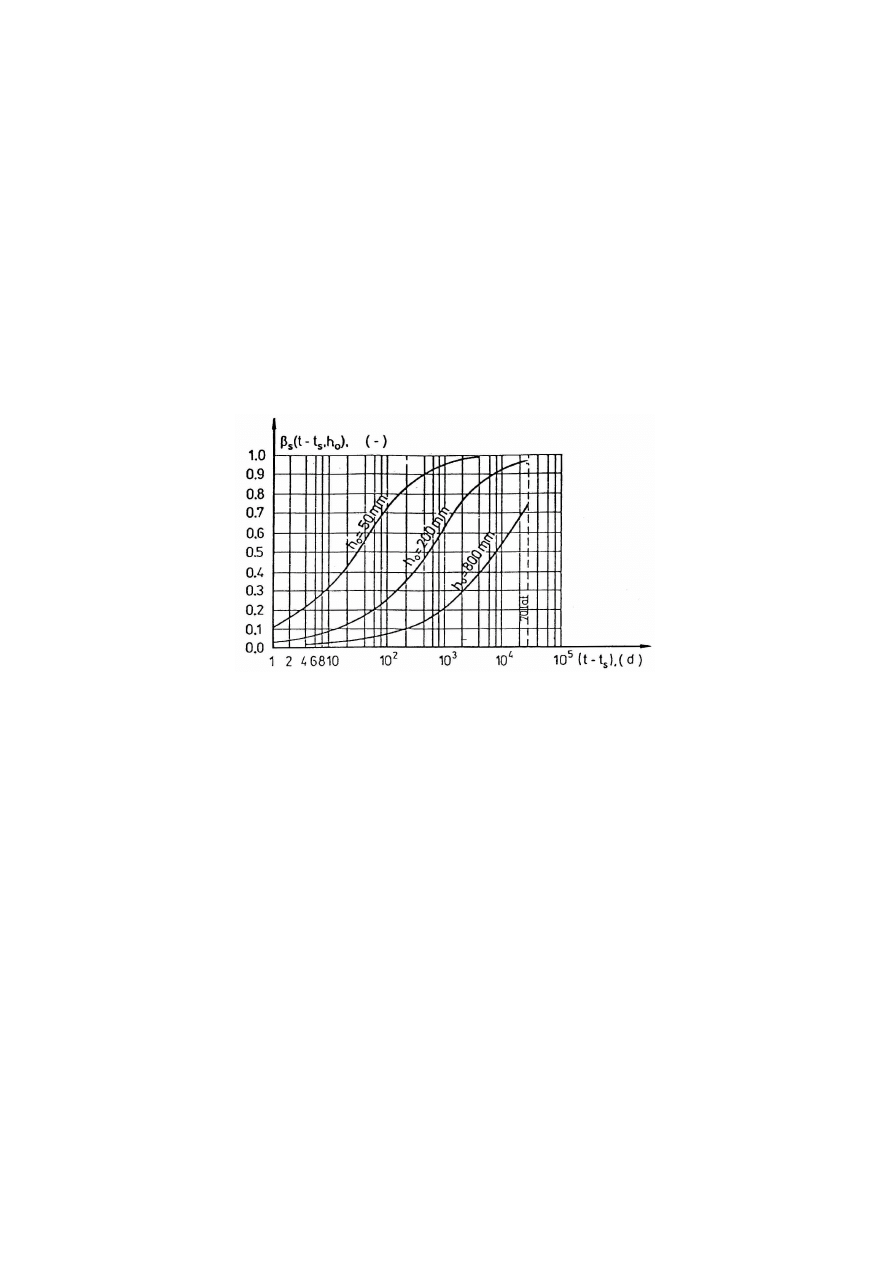
Na rys. 3.1 przedstawiono wykresy zależności współczynnika postępu skurczu w czasie

(

)

s

s

t

t

−

β

w funkcji miarodajnego wymiaru elementu

o

h , sporządzone na podstawie

wzorów (3.5) i (3.6).

Rys.3.1. Funkcje

(

)

s

s

t

t

−

β

przy różnych wartościach

o

h [14]

Wynika z nich wyraźnie, że skurcz rozwija się zupełnie inaczej w elementach o małej

(

o

h = 50 mm), średniej (

o

h = 200 mm) i dużej masywności (

o

h = 800 mm). Zjawisko to

jest związane głównie z szybkością odparowania nadmiaru wody zarobowej, znajdującej się
we wnętrzu elementu betonowego. W elementach o

o

h = 800 mm średni skurcz betonu

po 70 latach osiąga poziom skurczu 4-letniego dla elementów o

o

h = 200 mm i

3,5 miesięcznego dla elementów o

o

h = 50 mm.

W literaturze technicznej można znaleźć wiele metod obliczania odkształceń

skurczowych

( )

s

cs

t

t,

ε

. Wśród nich wyróżnić można [15] metodę CEP-FIP M.C. 1978 i

DIN-4227, metody Bažanta i Panuli ("BaP - Model") oraz przyjętą w EC2 metodę CEB-
FIP M.C. 1990. W metodach tych wyraźnie rozdzielono zależność odkształcenia
skurczowego od takich czynników jak wytrzymałość, konsystencja, rodzaj cementu,
wskaźnik C/W, współczynnik dyfuzji, względna wilgotności środowiska RH i miarodajny
wymiar elementu

o

h .

Na rys. 3.2. i 3.3 podano za H. Raszką [15] porównanie wyników obliczeń odkształceń

skurczowych

cs

ε

wg powyższych trzech metod dla betonu o

ck

f = 20 MPa i konsystencji

gęstoplastycznej, dla trzech wartości

o

h = 50 mm (krzywe "a"), 200 mm (krzywe "b") i

800 mm (krzywe "c"), dwóch wartości RH = 40 % (rys. 3.2) i RH = 80 % (rys. 3.3) oraz

temperatury środowiska T = 20 oC. Cyframi oznaczono: 1 - wartości wg "Model Code
1978", 2 - wg "BaP-Model", 3 - wg "Model Code 1990" oraz 4 - wg PN-84/B-03264 [4] dla
konstrukcji sprężonych.

Rys.3.2. Odkształcenia skurczowe

( )

s

cs

t

t,

ε

przy RH = 40 %

Wykresy na rys. 3.2 i 3.3 wyraźnie wskazują na:

- duże różnice w ocenie skurczu, zależne od zastosowanej teorii,
- silną zależność skurczu od wilgotności środowiska RH i sprowadzonego wymiaru

elementu

o

h ,

- znaczne różnice pomiędzy wartościami

( )

s

cs

t

t,

ε

przyjmowanymi w PN [4], a

wartościami wynikającymi z przeanalizowanych metod.
W polskich normach [3, 4] nie uwzględniano wpływu masywności elementu na skurcz

betonu. Stąd, przy RH = 40 %, dość dobra zgodność z wartościami EC2 dla

o

h = 200 mm i

(

)

s

t

t

−

= 0

÷

400 dni. Dla

(

)

s

t

t

−

= 70 lat niedoszacowanie

( )

s

cs

t

t,

ε

przez polskie normy

wynosi już około 40 %. Przy RH = 80 % występuje dość dobra zgodność z wartościami EC2
dla

o

h

≅

100 mm i

(

)

s

t

t

−

= 0

÷

400 dni, a dla

(

)

s

t

t

−

= 70 lat niedoszacowanie skurczu

wynosi około 20 %.

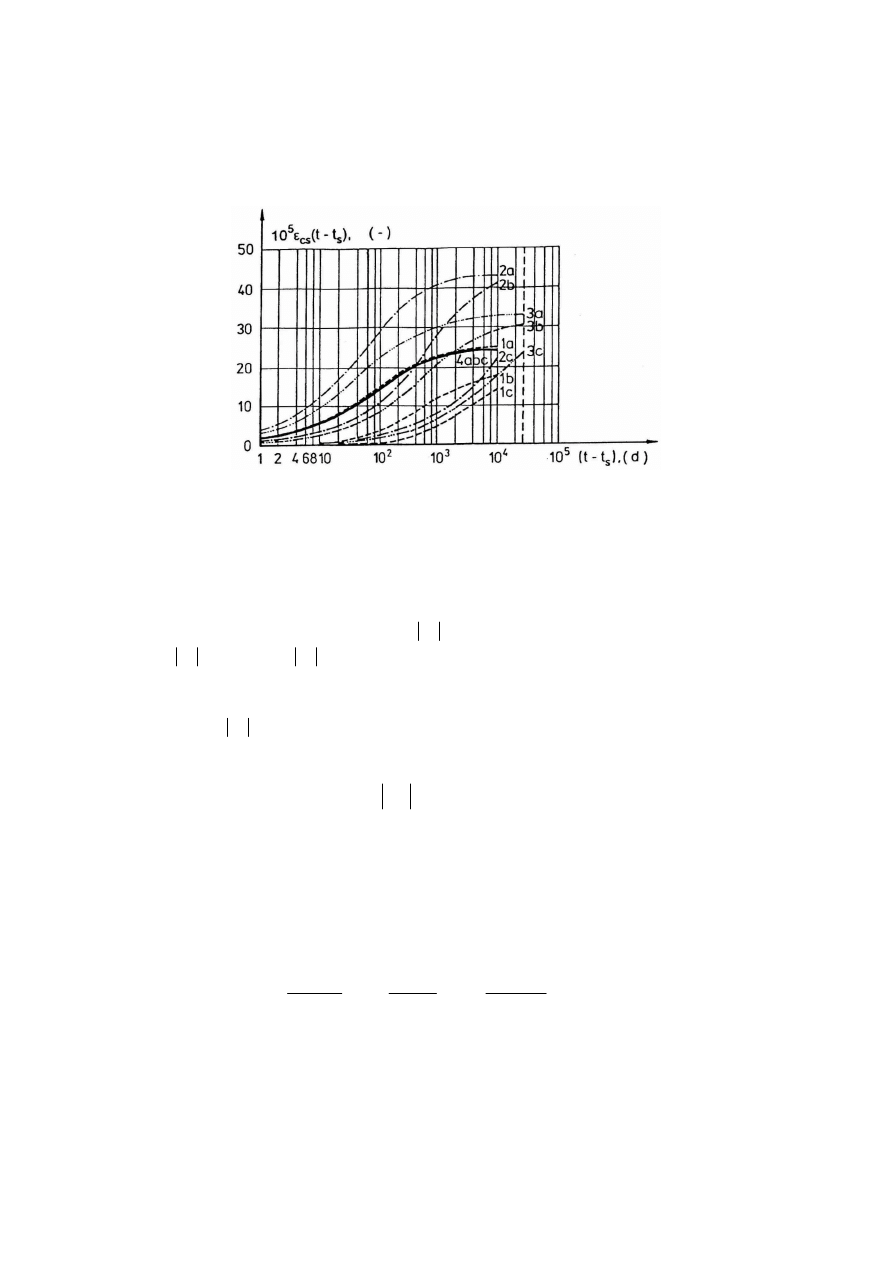
Rys.3.3. Odkształcenia skurczowe

( )

s

cs

t

t,

ε

przy RH = 80 %

Z powyższego wynika, że przy adaptacji EC2 dla warunków polskich, zagadnienie

odkształceń skurczowych powinno być potraktowane z dużo większą uwagą niż to czyniono
dotychczas. Dotyczy to zwłaszcza tych przypadków, gdy odkształcenia skurczowe mają
znaczny wpływ na siły wewnętrzne w konstrukcji (np. w ustrojach statycznie
niewyznaczalnych i w konstrukcjach sprężonych).

Należy również zwrócić uwagę na wartości odkształceń skurczowych zalecane przez

dawne PN dla konstrukcji betonowych (

cs

ε

= 0,0003 [3, 4]) oraz konstrukcji żelbetowych

(

cs

ε

= 0,0002 [3] i

cs

ε

= 0,00015 [4]).

Po pierwsze, w świetle powyższych wywodów wartość

cs

ε

zależy silnie od wymiaru

o

h elementu i wilgotności RH środowiska. Po drugie, nie powinno się podawać obniżonych

wartości

cs

ε

dla żelbetu, bez żadnego komentarza. Beton w konstrukcjach betonowych i

żelbetowych ma ten sam skurcz swobodny

cs

ε

.

W żelbecie skurcz ten jest hamowany przez opór wkładek zbrojeniowych, a więc w

badaniach obserwuje się wartości

RC

cs

ε

mniejsze niż

cs

ε

. Te dwie wielkości powinny się

różnić oznaczeniami.

Przybliżona zależność pomiędzy

RC

cs

ε

a

cs

ε

, wyprowadzona przez autora w pracy [16]

dla elementu pryzmatycznego o przekroju symetrycznym, symetrycznie zbrojonym, ma
postać:

(

)

3

3

RC

1

k

cs

cs

α

ε

ε

−

=

(3.7)

gdzie:

( )

2

1

2

1

3

,

,

1

ρ

ρ

µ

µ

µ

α

+

=

+

=

=

+

=

c

s

s

o

s

cm

s

o

o

o

o

o

A

A

A

t

E

E

n

n

n

k

3

- współczynnik relaksacji naprężeń skurczowych w wyniku pełzania betonu;

dla zmodyfikowanej teorii starzenia jest [17]:

(

)

o

t

Φ

k

,

1

1

3

3

∞

+

=

α

β

(3.8)

E

cm

(t

s

)- moduł sprężystości betonu na rozciąganie w momencie rozpoczęcia zjawiska

skurczu; można przyjąć E

cm

(t

s

) = E

cm

,

β

- funkcja starzenia; dla obciążenia skurczem

β

≅

0,8,

Φ

(

∞

, t

o

) - współczynnik pełzania.

Na przykład (Przykład I), dla belki o przekroju 300/600 mm (

o

h = 200 mm),

ρ

1

=

ρ

2

=

0,01 (

µ

o

= 0,02),

9

,

6

0

,

29

200

=

=

o

n

(beton klasy B20),

β

≅

0,8,

Φ

(

∞

, t

o

) = 2,4 (jak dla

obciążenia przyłożonego po 28 dniach przy RH = 50 %), otrzymuje się:

811

,

0

4

,

2

121

,

0

8

,

0

1

1

;

121

,

0

9

,

6

02

,

0

1

9

,

6

02

,

0

3

3

=

⋅

⋅

+

=

=

⋅

+

⋅

=

k

α

(

)

cs

cs

RC

cs

ε

ε

ε

713

,

0

811

,

0

121

,

0

1

=

−

=

czyli np. dla

cs

ε

= - 0,00030

→

RC

cs

ε

= - 0,000214.

Różnica w wartościach skurczu

RC

cs

ε

i

cs

ε

wywołuje wymuszone naprężenia ściskające

w stali

ss

σ

i rozciągające w betonie

cs

σ

.

Dla wyżej rozpatrzonego przekroju symetrycznego, symetrycznie zbrojonego:

(

)

3

3

1

k

E

s

cs

ss

α

ε

σ

−

=

(3.9)

3

3

k

E

cm

cs

cs

α

ε

σ

−

=

(3.10)

co dla

cs

ε

= - 0,00030, E

cm

= 29,0 GPa,

s

E = 200 GPa,

3

α

= 0,121,

3

k = 0,811 daje

wartości

ss

σ

= - 42,8 MPa (ściskanie) i

cs

σ

= 0,85 MPa (rozciąganie).

Naprężenie

cs

σ

= 0,85 MPa = 0,39

m

ct

f

= 0,57

ctk

f

jest naprężeniem znaczącym,

obniżającym siłę rysującą przekrój i powinno być w analizie stanów granicznych
użytkowalności uwzględnione.

4. Zmiany w ocenie wielkości skurczu betonu wprowadzone

przez Draft EN 1992-1-1:2001 [12]

Całkowite odkształcenie skurczowe

ε

cs

składa się z dwóch składników, odkształcenia

skurczowego na skutek wysychania

ε

cd

i samoczynnego odkształcenia skurczowego

ca

ε

.

Odkształcenie skurczowe na skutek wysychania rozwija się powoli, ponieważ jest funkcją
migracji wody przez twardniejący beton. Samoczynne odkształcenie skurczowe rozwija się

podczas twardnienia betonu: ważna jego część narasta we wczesnym okresie po
zaformowaniu. Skurcz samoczynny jest liniową funkcją wytrzymałości betonu. Powinien on
być brany pod uwagę gdy nowy beton jest formowany w zetknięciu z betonem stwardniałym.

Wartości całkowitego odkształcenia skurczowego

ε

cs

obliczamy z formuły:

ca

cd

cs

ε

ε

ε

+

=

(4.1)

Końcowa wartość odkształcenia skurczowego na skutek wypychania

ε

cd ,

∞

może być

wzięta z tablicy 4.1. Tablica ta podaje oczekiwane wartości średnie, przy współczynniku
zmienności na poziomie 30 %, obliczone na podstawie wzorów podanych w załączniku B do
Draftu.

Tablica 4.1

Końcowe wartości skurczu swobodnego na
skutek wysychania

ε

cd ,

∞

(w ‰) dla betonu

Względna wilgotność RH (w %)

cube

ck

ck

f

f

,

(MPa)

20

40

60

80

90

100

20/25

-0,75 -0,70 -0,59 -0,40 -0,20

0,12

40/50

-0,60 -0,56 -0,47 -0,29 -0,16

0,10

60/75

-0,48 -0,45 -0,38 -0,24 -0,13

0,08

80/95

-0,39 -0,36 -0,30 -0,19 -0,11

0,06

90/105

-0,35 -0,33 -0,27 -0,17

0,06

0,06

Rozwój w czasie odkształcenia skurczowego na skutek wysychania przebiega według

formuły:

( )

( )

ε

β

ε

cd

ds

s

cd

t

t t

=

−

⋅

∞

,

(4.2)

w której funkcja rozwoju skurczu w czasie jest zdefiniowana jako:

(

)

(

)

(

) (

)

5

,

0

2

1

350

















−

+

−

=

−

s

o

s

s

ds

t

t

h

h

t

t

t

t

β

(4.3)

gdzie:

t

- wiek betonu w rozpatrywanym momencie (dni),

t

s

- wiek betonu (dni) w momencie początku skurczu na skutek wysychania

(albo narastania). Normalnie odpowiada to końcowi pielęgnacji betonu,

h

o

=

2

A

c

/u - miarodajny wymiar (mm) przekroju elementu,

h

1

= 100 mm.

Samoczynne odkształcenie skurczowe wyraża się przez:

( )

( )

∞

⋅

=

,

ca

cc

ca

t

t

ε

β

ε

gdzie:

(

)

6

,

10

10

5

,

2

−

∞

−

−

=

ck

ca

f

ε

(4.4)

( )













































=

5

,

0

28

-

1

s

exp

t

t

cc

β

(4.5)

s

- współczynnik zależny od rodzaju cementu:

s

= 0,20 - dla szybko twardniejących cementów wysokiej wytrzymałości,
= 0,25 - dla normalnie i szybko twardniejących cementów,
= 0,38 - dla wolno twardniejących cementów.

Rozwój w czasie samoczynnego odkształcenia skurczowego określa formuła:

(

)

β

as

t

= −

1

0 5

exp - 0,2

,

(4.6)

Jak wynika z powyższych danych, Draft prEN 1992-1-1:2001 znacznie uściślił wielkości

odkształceń skurczowych betonu. Zmieniły się przy tym szczegółowe zasady obliczania
wartości skurczu końcowego wywołanego przez wysychanie betonu (tzw. skurcz fizyczny)

ε

cd ,

∞

. Należy go obliczać ze wzoru:

(

)

RH

6

ds2

1

,

10

-

exp

110

220

β

α

α

ε

⋅

⋅

























⋅

⋅

+

=

−

∞

cmo

cm

ds

cd

f

f

(4.7)

sl

o

β

β

⋅

<























−

−

=

%

99

RH

dla

RH

RH

1

55

,

1

3

RH

(4.8)

sl

β

β

⋅

≥

−

=

%

99

RH

dla

25

,

0

RH

(4.9)

1

,

0

5

,

3









=

cm

cmo

sl

f

f

β

(4.10)

gdzie:

f

cm

- średnia wytrzymałość betonu na ściskanie (MPa),

f

cmo

- 10 MPa,

α

ds1

- współczynnik zależny od rodzaju cementu:

α

ds1

= 3 - dla wolno twardniejących cementów (S),
= 4 - dla normalnie i wolno twardniejących cementów (N),
= 6 - dla szybko twardniejących wysoko wytrzymałych cementów (R),

α

ds2

- współczynnik zależny od rodzaju cementu:

α

ds2

= 0,13 – dla cementu S,

0,11 – dla cementu N,

0,12 – dla cementu R,

β

sl

- współczynnik uwzględniający niepełne wysychanie w betonach wysokiej

jakości (HSC),

RH

- względna wilgotność otoczenia (%),

RH

o

= 100 %.

Dla betonu o wytrzymałości f

ck

≤

50 MPa narastanie może zaistnieć w betonach

eksponowanych w środowisku o RH

≥

99 %.

Dla betonu o wytrzymałości f

ck

> 50 MPa narastanie może zaistnieć przy niższej

względnej wilgotności z powodu poprzedzającej redukcji wewnętrznej względnej
wilgotności spowodowanej niepełnym wysychaniem betonu.

5. Ustalenia co do wartości odkształceń skurczowych betonu

w warunkach polskich

W świetle wszystkich wyżej przytoczonych poglądów i zaleceń, wydaje się za konieczne

przyjąć następujące ustalenia:
1) Wartości odkształceń skurczowych przyjmowanych do obliczeń należy określać

dokładnie, w oparciu o dane rozdziału 4 niniejszej pracy.

2) Skurcz samoczynny (tzw. skurcz plastyczny)

ε

ca

powinien być uwzględniany w

obliczeniach konstrukcji zespolonych typu beton-beton, w odniesieniu do betonu
nowego, położonego na warstwie betonu starego (stwardniałego).

3) Skurcz wywołany przez wysychanie betonu (tzw. skurcz fizyczny

ε

cd

jest dla większości

przypadków skurczem wywołującym naprężenia skurczowe w konstrukcjach i
elementach z betonu i jego wielkości będą miarodajne do obliczeń.

4) Wartość odkształcenia skurczowego elementu czy konstrukcji żelbetowej różni się od

wartości swobodnego odkształcenia skurczowego betonu

ε

cs

, czy też

ε

cd

. Przyczyną

jest opór wkładek zbrojeniowych przeciw skurczowi. O ile opór ten jest niewielki w
początkowym okresie dojrzewania betonu, w czasie gdy ujawnia się skurcz samoczynny
(plastyczny) i gdy cechy sprężyste betonu są jeszcze mało rozwinięte, o tyle w
późniejszym okresie, gdy ujawnia się skurcz fizyczny, opór ten jest duży i wywołuje
zrównoważony stan naprężeń wymuszonych w przekroju elementu. Wówczas kosztem
zmniejszonego skurczu

RC

cs

ε

dochodzi w przekroju najczęściej do ściskania stali

zbrojeniowej i rozciągania betonu. Zagadnienie to zobrazowano w rozdziale 3. niniejszej
pracy. Podano tam sposób obliczania odkształcenia skurczowego elementu żelbetowego
symetrycznego, symetrycznie zbrojonego. W przedstawionym tam przykładzie, redukcja
odkształcenia skurczowego elementu żelbetowego, w stosunku do elementu betonowego,
wyniosła około 30 %. Redukcję na podobnym poziomie założyła norma PN-76/B-03264,
zaś na poziomie 50 % - norma PN-84/B-03264.

5) Wartość odkształcenia skurczowego elementu w konstrukcji żelbetowej zależy od

stopnia zbrojenia, miarodajnego wymiaru h

o

, wilgotności powietrza, klasy betonu. Może

być zatem różna w poszczególnych elementach konstrukcji. Przyjmowanie do obliczeń
statycznych skurczu jako równoważnego z obniżeniem się temperatury o 15

o

C jest

dużym przybliżeniem. Odpowiada ono odkształceniu skurczowemu elementów w
konstrukcji żelbetowej

00015

,

0

=

RC

cs

ε

= constans.

Przykładowo (Przykład II) w ramie portalowej z betonu klasy B25, pracującej w
środowisku o RH = 40 %, wartości

ε

cd

wyniosą po 10 latach (365 dniach), przy

założeniu, że t

s

= 7 dni:

- w słupach o przekroju 400/800 mm -

o

h

= 266,7 mm

(

)

(

)

(

) (

)

771

,

0

7

3650

100

/

7

,

266

350

7

3650

7

3650

5

,

0

2

=

















−

+

−

=

−

ds

β

cd

ε

(3650) = -0,771

⋅

0,70 = 0,540 ‰ = -0,00054

- w ryglu o przekroju 400/1500 mm

-

o

h

= 315,8 mm

(

)

(

)

(

) (

)

676

,

0

7

3650

100

/

8

,

315

350

7

3650

7

3650

2

=

















−

+

−

=

−

ds

β

cd

ε

(3650) = -0,676

⋅

0,70 = 0,473 ‰ = -0,00047.

Dopiero w stosunku do tych wartości należy przeprowadzić obliczenie

RC

cs

ε

.

Zakładając, że słupy i rygle są silnie obustronnie zbrojone o stopniu zbrojenia

(

)

04

,

0

02

,

0

2

1

=

=

=

o

µ

ρ

ρ

uzyskamy dla betonu klasy B25

(

)

GPa

0

,

30

=

cm

E

przy

β

= 0,8

i przyłożeniu obciążenia po 28 dniach:

- dla słupów:

(

)

o

t

,

∞

φ

= 2,51,

67

,

6

0

,

30

0

,

200

=

=

o

n

211

,

0

67

,

6

04

,

0

1

67

,

6

04

,

0

3

=

⋅

+

⋅

=

α

702

,

0

51

,

2

211

,

0

8

,

0

1

1

3

=

⋅

⋅

+

=

k

RC

cs

ε

= - 0,000540 (1 - 0,211)

⋅

0,702 = - 0,00030 (redukcja o 44 %)

- dla rygla:

(

)

o

t

,

∞

φ

= 2,46,

,

67

,

6

=

o

n

211

,

0

3

=

α

707

,

0

46

,

2

211

,

0

8

,

0

1

1

3

=

⋅

⋅

+

=

k

RC

cs

ε

= - 0,000473 (1 - 0,211)

⋅

0,707 = - 0,00026 (redukcja o 44 %)

Powyższe wartości

RC

cs

ε

są znacznie większe niż zakładały to dawne polskie normy, tzn.

RC

cs

ε

= 0,00015.

Gdyby w/w rama była wykonana z betonu klasy B50 (

cm

E = 35,0) i pracowała w

środowisku o RH = 80 %, wówczas uzyskalibyśmy:
- w słupach

cd

ε

(3650) = - 0,771

⋅

0,29 = 0,224 ‰,

(

)

o

t

,

∞

φ

= 1,94,

71

,

5

0

,

35

0

,

200

=

=

o

n

,

186

,

0

3

=

α

,

776

,

0

94

,

1

186

,

0

8

,

0

1

1

3

=

⋅

⋅

+

=

k

RC

cs

ε

= - 0,000224 (1 - 0,186)

⋅

0,776 = - 0,00014 (redukcja o 37 %)

- w ryglu

(

)

o

t

,

∞

φ

= 1,91,

,

71

,

5

=

o

n

186

,

0

3

=

α

,

779

,

0

91

,

1

186

,

0

8

,

0

1

1

3

=

⋅

⋅

+

=

k

RC

cs

ε

= - 0,000196 (1 - 0,186)

⋅

0,779 = - 0,00012 (redukcja o 37 %)

a więc mniej niż

RC

cs

ε

= 0,00015.

Przykład ten wskazuje na celowość wykonywania bardziej szczegółowych obliczeń

wartości

RC

cs

ε

dla analizy statyczno-wytrzymałościowej konstrukcji z betonu zbrojonego.

6. Naprężenia skurczowe w konstrukcji wymuszone przez więzy zewnętrzne

Najczęściej uwzględnianymi w obliczeniach statyczno-wytrzymałościowych konstrukcji

z betonu są siły uogólnione wywołane w ustroju przez więzy zewnętrzne. Więzy te mogą być
sztywne (np. w przypadku stropów połączonych z wzajemnie oddalonymi trzonami
komunikacyjnymi) lub podatne (np. w połączeniach rygli z podatnymi słupami w ramach).

W obu tych przypadkach należy zastosować dodatkowy schemat obliczeń statycznych,

uwzględniający wartość skurczu średniego w przekroju jak dla żelbetu, tzn.

RC

cs

ε

,

obliczonego wg zasad podanych w rozdziale 5.

W granicznych dwóch przypadkach (belka nieważka) mamy:

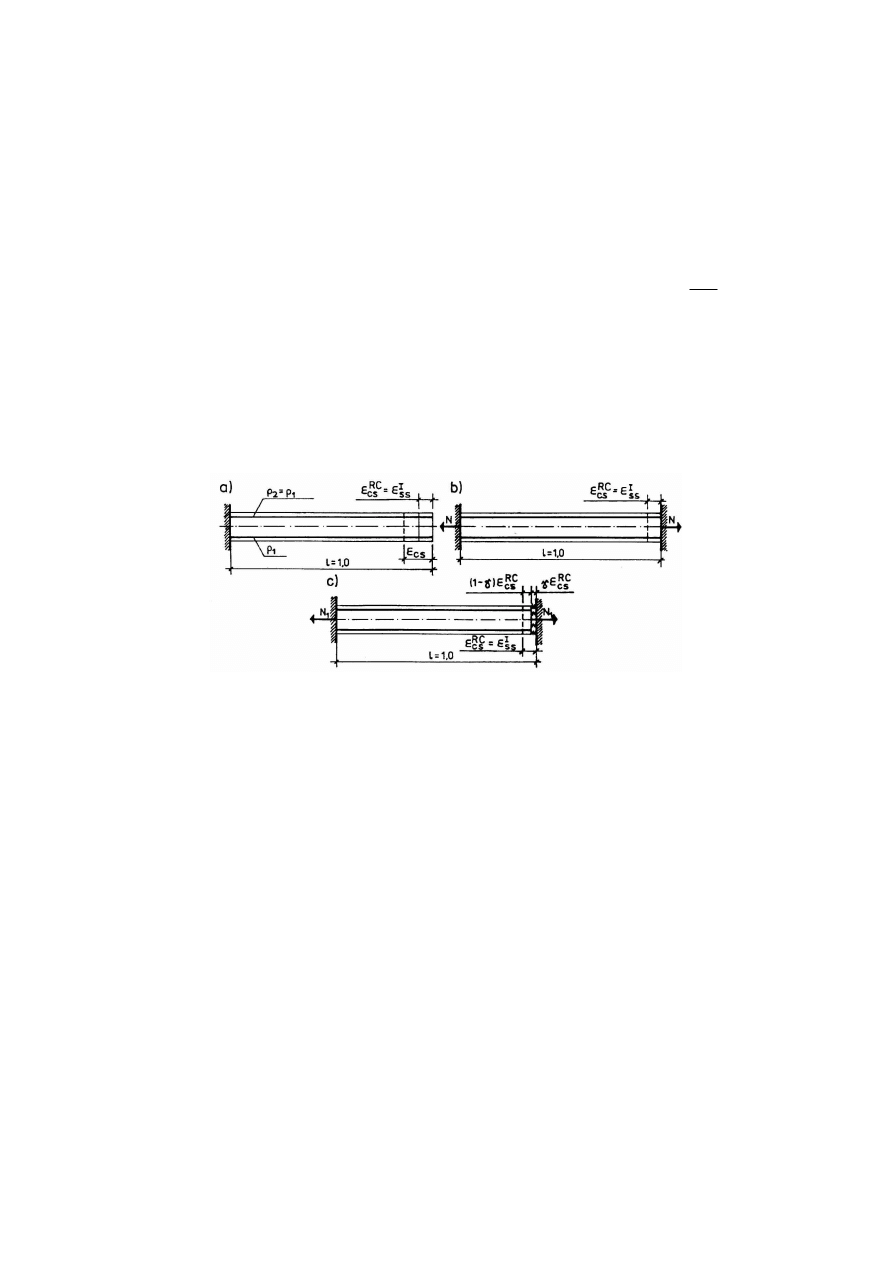
a) w przypadku braku więzów zewnętrznych (rys. 6.1.a) - tylko przemieszczenie swobodne

o wartości

RC

cs

ε

, bez dodatkowej siły rozciągającej N,

b) w przypadku więzów sztywnych (rys. 6.1.b) - rozciąganie w pręcie wywołane siłą

(

)

3

1

k

E

A

n

E

A

N

cm

c

cs

o

o

cm

c

RC

cs

ε

µ

ε

−

=

+

−

=

, bez przemieszczenia, gdzie

cm

s

o

E

E

n

=

,

2

1

ρ

ρ

µ

+

=

o

.

Dla przypadku pośredniego (rys. 6.1.c), z więzami podatnymi, odkształcenie skurczowe

RC

cs

ε

dzieli się na dwie części:

- beznaprężeniową

-

RC

cs

ε

γ

,

(

0

,

1

≤

γ

),

- naprężeniową

- (

γ

−

1

)

RC

cs

ε

, wywołującą rozciąganie siłą

N

1

= - (

γ

−

1

)

(

)

o

o

cm

c

RC

cs

n

E

A

µ

ε

+

1

.

Rys. 6.1.

W ustrojach np. mostowych wszędzie, gdzie jest to możliwe, dąży się do eliminowania

wpływu naprężeniowej części odkształcenia

(

)

RC

cs

ε

γ

−

1

na siły wewnętrzne w ustroju przez

stosowanie łożysk przesuwnych, przerw dylatacyjnych itp. Wówczas rola tej części
odkształcenia skurczowego może stać się zupełnie drugorzędna. Podobny przypadek może
zaistnieć dla żelbetowej płyty fundamentowej, jeżeli zapewnimy jej w miarę swobodne
przemieszczenia skurczowe po podłożu gruntowym lub izolacji na warstwie chudego betonu.

W przypadku więzów sztywnych, generowane w ustroju wewnętrzne siły rozciągające są

zazwyczaj tak duże, że powodują zarysowanie przekroju - skrośne przy przewadze siły
osiowej N (mimośrodowe rozciąganie z małym mimośrodem), lub jednostronne przy
współdziałaniu dużego momentu zginającego M (mimośrodowe rozciąganie z dużym
mimośrodem).

Zarysowanie skurczowe wywołane więzami zewnętrznymi nie zawsze musi być

szkodliwe dla konstrukcji. Powoduje ono bowiem rozładowanie niepożądanego stanu
naprężeń rozciągających w betonie i ściskających w stali (przy więzach podatnych).

Na przykład powstanie „n” rys skurczowych o szerokości „w

k

” w elemencie wg rys. 6.1.b

o odległości „l”, spowoduje spadek siły N o wartość:

(

)

o

o

cm

c

k

n

E

A

l

w

n

N

µ

+

⋅

=

∆

1

(6.1)

Odpowiada to wartości:

o

o

RC

cs

k

n

l

w

n

N

N

µ

ε

γ

+

⋅

⋅

⋅

=

∆

=

1

1

(6.2)

Średnie naprężenie rozciągające w betonie spadnie przy tym z wartości:

(

)

o

o

cm

RC

cs

c

I

cs

n

E

A

N

µ

ε

σ

+

−

=

=

1

(6.3)

do wartości:

(

)

(

)

(

)

o

o

cm

RC

cs

cs

I

cs

n

E

µ

γ

ε

σ

γ

σ

+

−

−

=

−

=

1

1

1

'

(6.4)

Przykładowo (Przykład III), dla n = 10, w

k

= 0,15 mm, l = 10

⋅

10

3

mm,

RC

cs

ε

= -

0,0002, E

cm

= 30,0 GPa (beton B25), n

o

= 0,04

γ

=

4

3

10

2

10

10

15

,

0

10

−

⋅

⋅

⋅

⋅

= 0,750

I

cs

σ

= 0,0002

⋅

30

⋅

10

3

(1 + 6,67

⋅

0,04) =

= 7,60 MPa »

ctm

f

= 2,20 MPa

I

cs'

σ

= (1 - 0,750

⋅

7,60 = 1,90 MPa <

ctm

f

= 2,20 MPa

Średnie naprężenie w stali na całym odcinku l,

σ

ss

= 0, przy czym lokalnie stal będzie

rozciągana (w rysach) i ściskana na środkowych odcinkach między rysami.

Omawiane naprężenia

I

cs

σ

nie są jedynym efektem oddziaływania skurczu na

konstrukcje z betonu. Efekt ten uwzględnia się w obliczeniach statyczno-
wytrzymałościowych konstrukcji poprzez wpływ na siły uogólnione w konstrukcji, a tym
samym jej stany graniczne nośności i użytkowalności.

7. Naprężenia skurczowe w konstrukcji wymuszone przez więzy wewnętrzne

(opór zbrojenia)

Drugą część oddziaływania skurczu na konstrukcje z betonu stanowią naprężenia

wymuszone w przekrojach poszczególnych jej elementach przez więzy wewnętrzne w
postaci oporu prętów zbrojenia przeciw skurczowi swobodnemu

ε

cs

. Więzy te wywołują

zazwyczaj naprężenia rozciągające w betonie i ściskające w stali zbrojeniowej. Dzięki

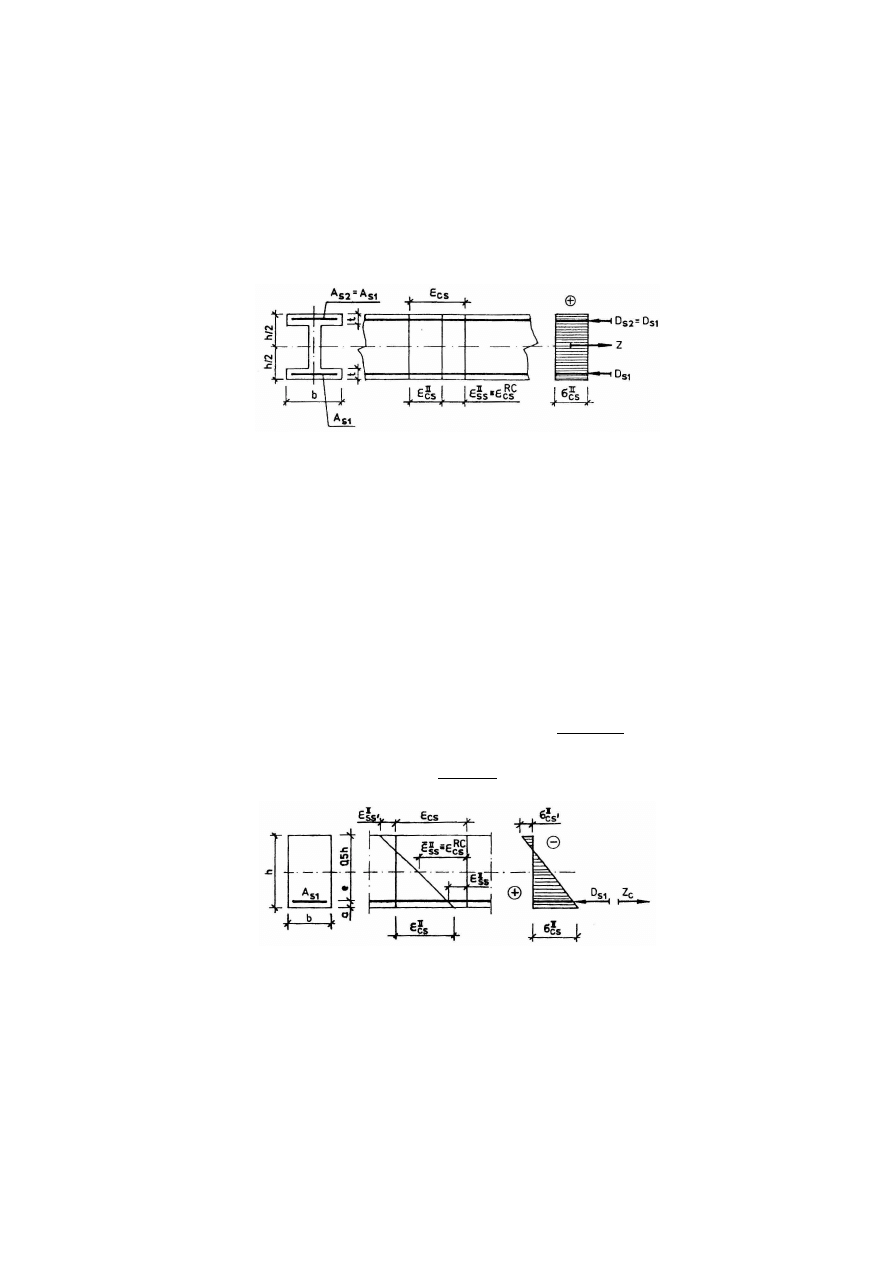
istnieniu tych więzów odkształcenia skurczowe w elementach żelbetowych

ε

cs

RC

są mniejsze

niż w betonowych

ε

cs

, ale w przekroju każdego z elementów pojawia się dodatkowe pole

naprężeń

σ

cs

II

, które zazwyczaj jest pomijane w analizach wytrzymałościowych.

Rys. 7.1.

W symetrycznym, symetrycznie zbrojonym przekroju żelbetowym oraz skurczu liniowym i
jednorodnym w przekroju (rys. 7.1.), wartości tych naprężeń wynoszą [16, 18]:

(

)

3

3

1

k

a

E

s

cs

II

ss

−

=

ε

σ

; ściskanie

(7.1a)

σ

ε

cs

II

cs

cm

E

a k

= −

3

3

; rozciąganie

(7.1b)

Na przykład (Przykład IV), dla elementu z betonu klasy B20,

ρ

1

=

ρ

2

= 0,01 (

µ

o

= 0,02),

n

o

= 6,9 otrzymamy:

E

cm

= 29,0,

ε

cs

= - 0,00030, a = 0,121, k

3

= 0,811 (jak w

przykładzie I).

σ

ss

II

= - 3,0

⋅

10

-4

⋅

200

⋅

10

3

(1 - 0,121)

⋅

0,811 = - 42,8 MPa ,

σ

cs

II

= 3,0

⋅

10

-4

⋅

29,0

⋅

0,121

⋅

0,811 = 0,85 MPa = 0,45

f

f

ctm

ctk

<

= 1,30 MPa

Rys. 7.2.

W rozważonym schemacie otrzymuje się najmniejsze wartości naprężeń rozciągających

σ

cs

II

. Wartości największe na krawędzi rozciąganej otrzymuje się w przypadku belki teowej

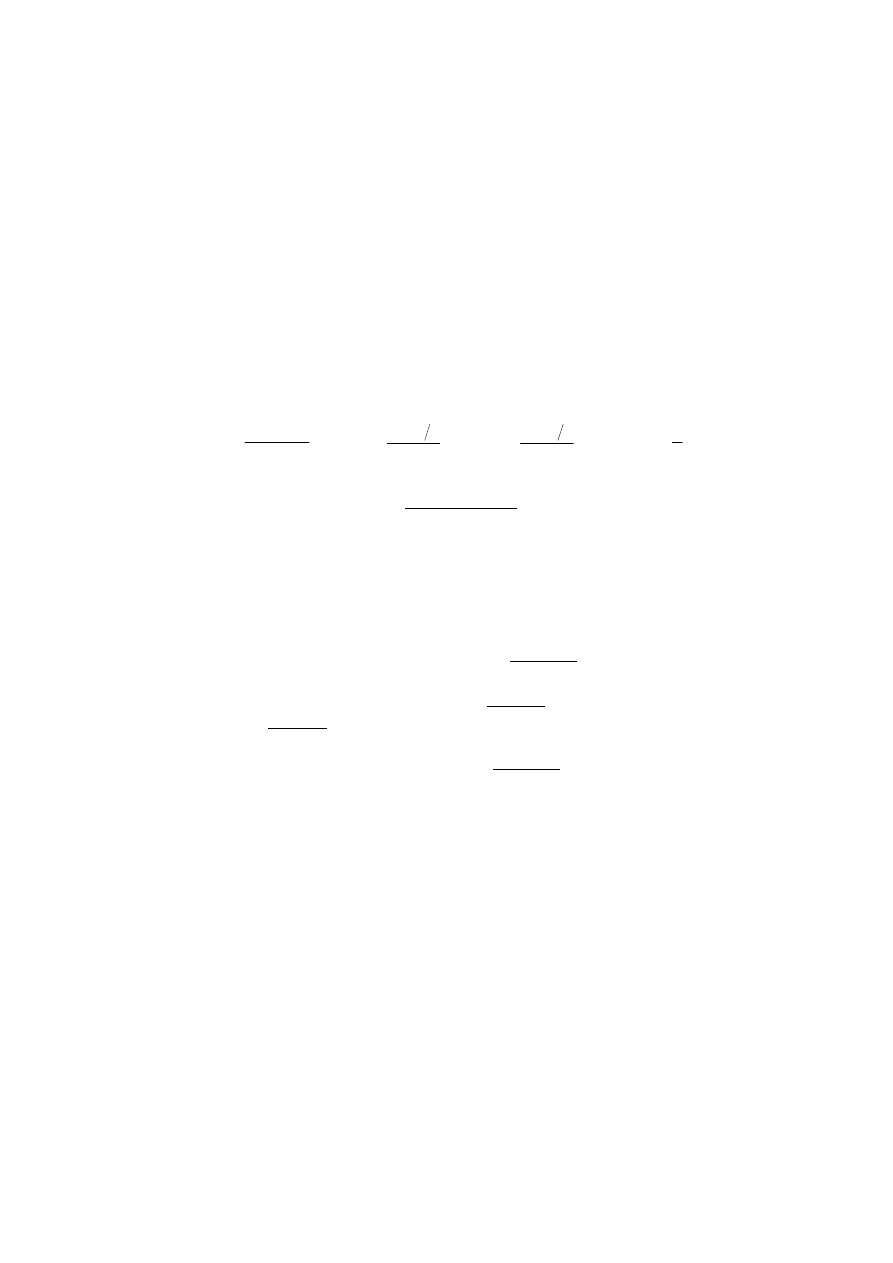
pojedynczo zbrojonej. Dla belki prostokątnej pojedynczo zbrojonej (rys.7.2.) uzyskuje się
następujące wyrażenia [16, 18]:

( )

3

'

1

k

a

E

s

cs

II

ss

−

=

ε

σ

,

(7.2a)

σ

ε

cs

II

cs

cm

E

a k

= −

''

3

,

(7.2b)

σ

ε

cs

II

cs

cm

E

a k

'

'''

= −

3

,

(7.2c)

gdzie:

a

n

n

o o

o o

'

=

+

µ η

µ η

1

;

a

a

e h

''

'

= ⋅ +

1 6

η

;

a

a

e h

'''

'

= ⋅ −

1 6

η

;

η = +









1 12

2

e
h

;

(

)

k

a

t

o

3

1

1

=

+

∞

β φ

'

,

(7.3)

Na przykład (Przykład V), dla elementu z betonu klasy B25,

s

E = 200 GPa,

E

cm

= 30 GPa,

n

o

= 6,67,

µ

ρ

o

=

1

= 0,015,

ε

cs

= - 3,0

⋅

10

-4

,

β

= 0,8,

(

)

φ ∞

, t

s

= 2,4,

e/h = 0,4,

η

= 2,92,

a

'

= 0,226,

a

''

= 0,263,

a

'''

= - 0,108, k

3

= 0,697, otrzymamy:

σ

ss

II

= - 3,0

⋅

10

-4

⋅

200

⋅

10

3

(1 - 0,226)

⋅

0,697 = - 32,4 MPa ,

σ

cs

II

= 3,0

⋅

10

-4

⋅

30,0

⋅

10

3

⋅

0,263

⋅

0,697 = 1,65 MPa = 0,75

f

f

ctm

ctk

>

=

= 1,50 MPa ,

σ

cs

II

'

= - 3,0

⋅

10

-4

⋅

30,0

⋅

10

3

⋅

0,108

⋅

0,697 = - 0,68 MPa ,

Z powyższych przykładów wynika, że naprężenia wymuszone

σ

cs

II

mogą osiągać

znaczne wartości. Szczególnie duże są te naprężenia w wysokich przekrojach teowych,
powszechnie stosowanych w mostownictwie. W pracach [17, 19] oszacowano, że naprężenia
te w dwóch konkretnych obiektach mostowych wyniosły (rys. 7.3):

1)

σ

cs

II

= 1,31 MPa = 0,82

f

f

ctm

ctk

>

= 1,10 MPa

2)

σ

cs

II

= 1,25 MPa = 0,66

f

f

ctm

ctk

<

= 1,30 MPa

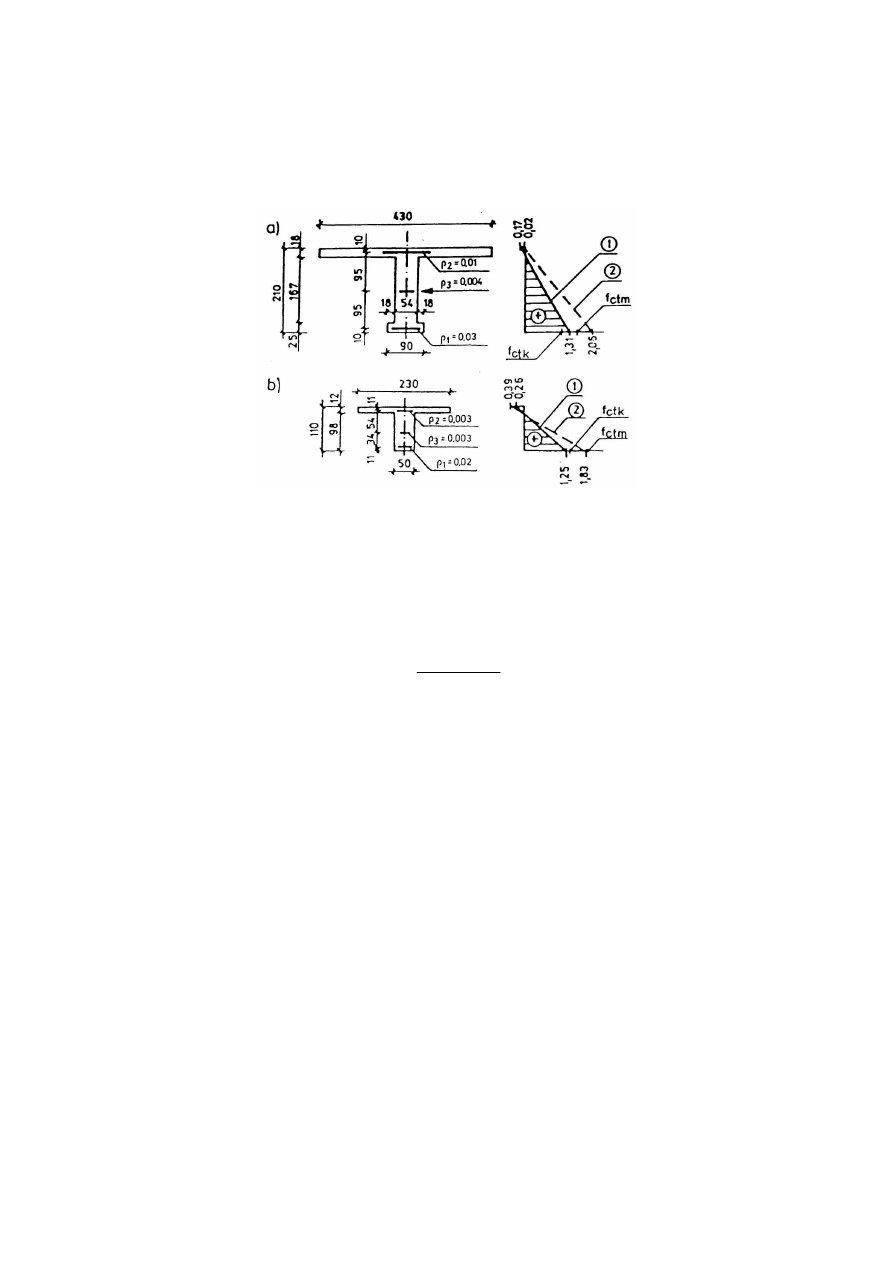
Rys. 7.3. Wykresy naprężeń skurczowych

σ

cs

II

(w MPa) spowodowane oporem zbrojenia w

rozpatrywanych belkach

Naprężenia skurczowe

σ

cs

II

zwiększają swe wartości ze wzrostem skurczu betonu w

czasie, podobnie jak naprężenia

σ

cs

I

. Miarą relaksacji tych naprężeń w wyniku pełzania

betonu jest wartość współczynnika k

3

, którą w odniesieniu do betonu zbrojonego można

obliczyć z formuł (3.8) lub (7.3), a także z przybliżonej zależności wg [20]:

( )

s

t

k

,

2

,

0

1

1

3

∞

+

=

φ

(7.4)

Jeżeli

(

)

φ ∞

, t

s

= 2,4 to

k

3

= 0,68. W omawianych przykładach wartość tego

współczynnika obliczona z formuł (3.8) lub (7.3) wyniosła odpowiednio: 0,81, 0,71, 0,78,
0,70.

Naprężenia rozciągające w betonie

σ

cs

II

, o tak dużych wartościach jak to wykazano

powyżej, są bardzo niekorzystne. Zmniejszają one bowiem wyraźnie moment rysujący M

cr

czy też siłę rysującą N

cr

w elemencie, przyśpieszając proces jego zarysowania. Z kolei

rzutuje to na mniejszą sztywność elementu oraz jego obniżoną odporność korozyjną.

Natomiast korzyści wynikające ze ściskających naprężeń

σ

ss

II

w stali zbrojeniowej są

iluzoryczne, gdyż w momencie zarysowania skurczowego elementu naprężenia te zanikają i
ich wpływ na podwyższenie nośności przekroju jest niewielki.

8. Naprężenia skurczowe własne w przekroju

Opisane w p. 6 i 7 dwie składowe naprężeń skurczowych

σ

cs

w przekroju elementu

żelbetowego są w pewnym stopniu niezależne od konstruktora, determinowanego
schematem statycznym konstrukcji czy też rozkładem zbrojenia w elementach. Powinien on

jednakże mieć wpływ na obniżenie wartości

σ

cs

w zastosowanym betonie przez

odpowiednią technologię użytej mieszanki betonowej. Wchodzą tu w grę takie czynniki jak
zastosowanie niskiego W/C, niskiego zużycia cementu i superplastyfikatorów, zastosowanie
odpowiedniej technologii zagęszczania jak np. odpowietrzanie betonu itp.

Istnieje natomiast jeszcze trzecia składowa odkształceń i naprężeń skurczowych w

przekroju elementów z betonu, która powinna być koniecznie poddana kontroli konstruktora.
Są to naprężenia skurczowe własne, wywołane w przekroju przez nieliniowe i równocześnie
niestacjonarne pola wilgotności w elemencie.

Współczynnik W/C w mieszance betonowej wynosi zazwyczaj 0,4

÷

0,6, podczas gdy do

pełnej hydratacji cementu potrzeba około W

h

/C = 0,25. Nadmiar wody zarobowej ponad tę

wartość wyparowuje z betonu przez powierzchnie zewnętrzne elementu. Pod wpływem
zaistniałego gradientu stężenia powstają w przekroju nieliniowe i niestacjonarne pola
wilgotności (rys. 8.1), które są przyczyną powstawania pewnego dodatku naprężeń
skurczowych

σ

cs

III

, rozciągających włókna przypowierzchniowe elementu i ściskających

włókna w głębi przekroju. Naprężenia te, samorównoważące się w przekroju, wywołane są
przez opór jednych warstw betonu w stosunku do innych pod wpływem ich tendencji do
nierównomiernych przemieszczeń skurczowych.

Rys. 8.1.

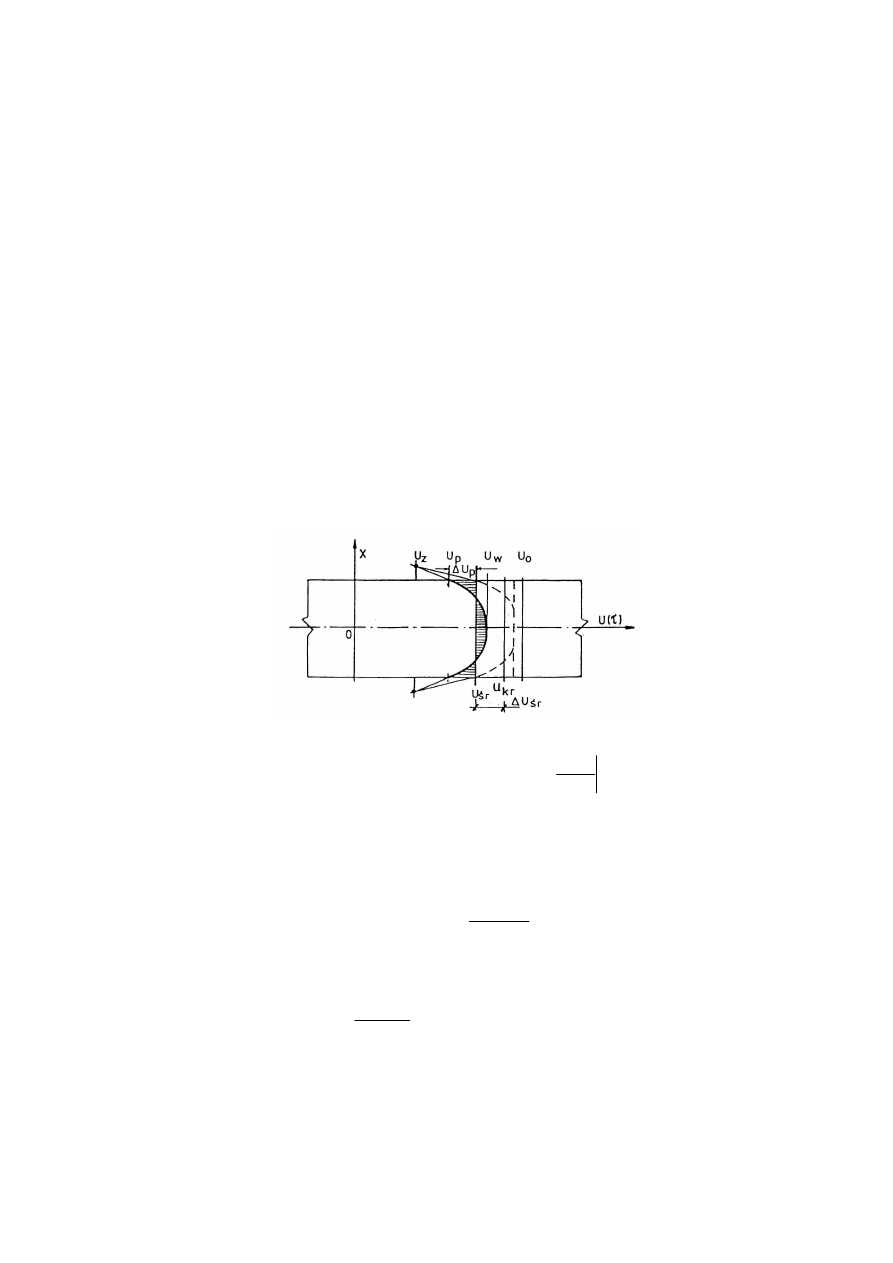
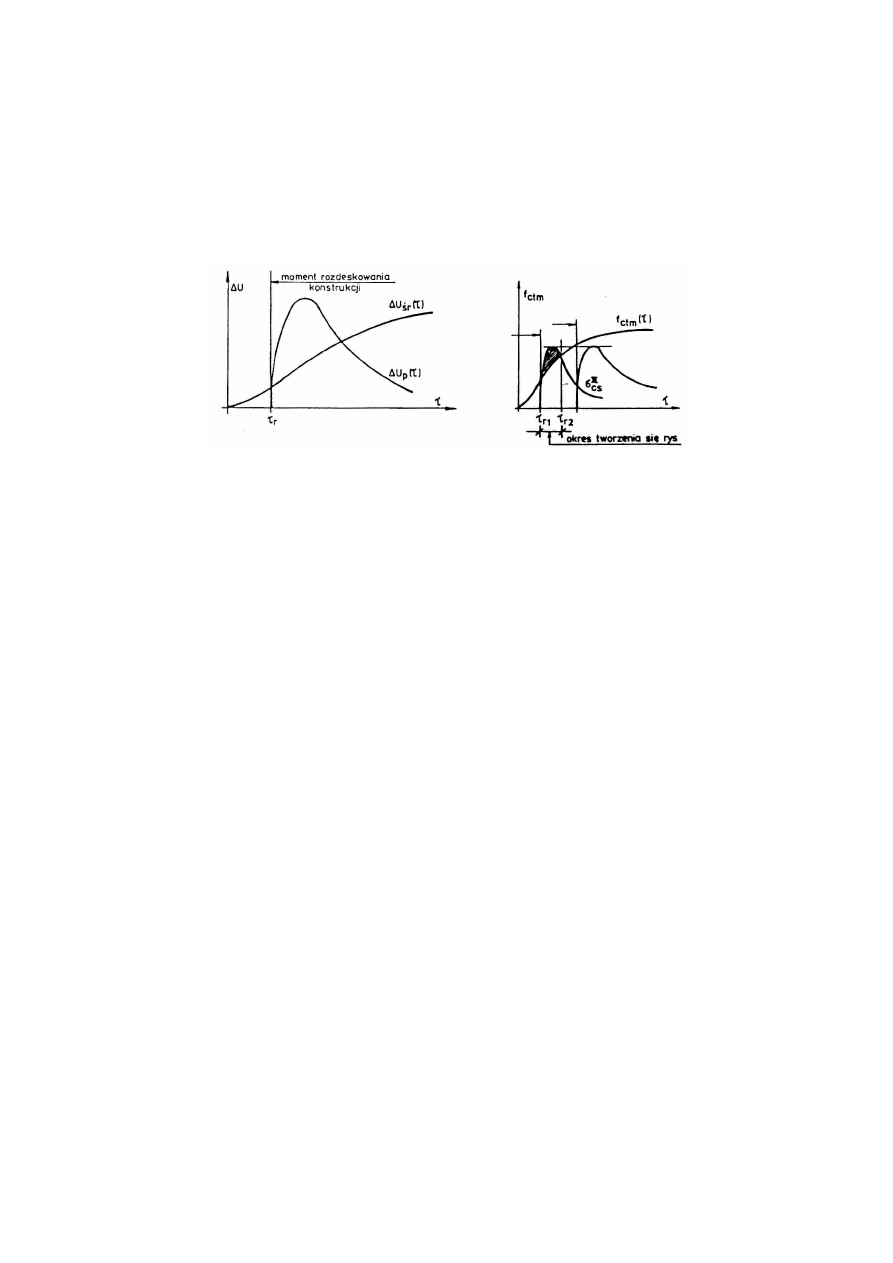
Gradient przypowierzchniowy omawianych pól wilgotności

( )

p

dx

dU

τ

jest największy po

rozdeskowaniu konstrukcji; z biegiem czasu wilgotność wnętrza elementu dąży do
wyrównania się i stabilizuje się na poziomie równowagi higrometrycznej z otaczającą
atmosferą.

Naprężenia własne

III

cs

σ

mogą być obliczone ze wzoru:

( )

( )

τ

τ

τ

τ

β

σ

τ

d

d

U

d

E

k

p

ct

w

III

cs

∆

∫

=

∞

1

3

(8.1)

gdzie:

β

w

- współczynnik liniowy odkształcalności wilgotnościowej betonu dla

jednostkowej zmiany wilgotności wagowej; można wg [21] przyjmować

β

w

= 3,0

⋅

10

-2

g

g

mm

mm

/

/

,

E

ct

(

τ

) - współczynnik sprężystości betonu na rozciąganie; zazwyczaj przyjmuje się

E

ct

(

τ

) = E

cm

(

τ

).

Rys. 8.2.

Rys. 8.3.

Odkształcenia skurczowe

cs

ε

odpowiadające za naprężenia skurczowe

I

cs

σ

i

II

cs

σ

są

funkcją średniej zmiany wilgotności U (

τ

) w przekroju (rys. 8.2):

( )

[

]

( )

τ

β

τ

β

ε

ε

śr

w

śr

kr

w

II

cs

I

cs

U

U

U

∆

=

−

=

≡

,

(8.2)

natomiast:

( )

( )

[

]

( )

τ

β

τ

τ

β

ε

p

w

p

śr

w

III

cs

U

U

U

∆

=

−

=

,

(8.3)

Zależności

( )

τ

śr

U

∆

i

( )

τ

p

U

∆

przedstawiono na rys. 8.2. Widać na ich podstawie

wyraźnie, że o ile odkształcenia skurczowe

II

I

cs

,

ε

z biegiem czasu mają tendencję rosnącą , o

tyle odkształcenia skurczowe

III

cs

ε

, odpowiadające za naprężenia

III

cs

σ

, po osiągnięciu

maksimum w krótkim czasie po rozdeskowaniu konstrukcji, mają później tendencję
malejącą.

Szacowanie wartości naprężeń

III

cs

σ

nastręcza wiele trudności. Zazwyczaj

konstruktorowi nie znany jest termin rozdeskowania konstrukcji, pogoda panująca podczas
dojrzewania betonu, zastosowane sposoby pielęgnacji powierzchni. Ważnym jest takie
sterowanie procesem rozdeskowania, aby ekstremum wartości

III

cs

σ

było poniżej krzywej

wytrzymałości betonu na rozciąganie

( )

τ

ctm

f

- por. rys. 8.3. W przeciwnym razie dojdzie

do zarysowania stref przypowierzchniowych elementu we wczesnym okresie jego "„życia".
Z jednej strony spowoduje to „rozładowanie” niepożądanego stanu naprężeń własnych, z
drugiej strony jednak rysy te pozostaną w elemencie w sposób trwały, co oznacza częściową
degradację przekroju z punktu widzenia jego wytrzymałości i sztywności, a w dalszej
konsekwencji - jego trwałości.

Próbę oszacowania naprężeń

III

cs

σ

podjęto w pracach [19, 22], a odkształceń

III

cs

ε

w

pracy [23]. Obliczone na podstawie pracy [22] największe naprężenia

III

cs

σ

, przy założeniu

betonu klasy B25 i k

3

= 0,7, wyniosłoby 1,28 MPa = 0,58

ctk

ctm

f

f

<

= 1,50 MPa, a na

podstawie pracy [23] - przy założeniu betonu klasy B20 i k

3

= 0,7 -

III

cs

σ

= 1,87 MPa = 0,98

ctk

ctm

f

f

>

= 1,30 MPa. Wskazuje to na duże znaczenie omawianych naprężeń, zwłaszcza,

że naprężenia te sumują się zazwyczaj z naprężeniami skurczowymi

I

cs

σ

i

II

cs

σ

(por. rys. 8.4), tak iż prawdopodobieństwo zaistnienia

Σ

(

)

( )

τ

σ

ctm

III

II

I

cs

f

≥

,

,

jest bardzo

duże. Należy tu jednakże zaznaczyć, że ekstrema poszczególnych składników

( )

τ

ctm

f

tej

sumy nie występują jednocześnie, co łagodzi ostrość powyższego zapisu.

Rys. 8.4.

Naprężenia

III

cs

σ

maleją tym szybciej, im mniejsza jest grubość zastępcza elementu.

Zachodzi tu zatem zjawisko odwrotne niż w odniesieniu do naprężeń

II

cs

σ

, które rosną tym

szybciej im mniejsza jest grubość zastępcza elementu. W elementach niemasywnych
dominującą rolę odgrywają naprężenia

II

cs

σ

, podczas gdy w masywnych -

III

cs

σ

.

Relaksacja naprężeń

III

cs

σ

w wyniku pełzania betonu zachodzi dużo wyraźniej w

elementach masywnych, niż w elementach o małej masywności. Według [20] współczynnik
relaksacji k

3

dla naprężeń skurczowych własnych może być określony z zależności

przybliżonej:

( )

s

t

k

,

2

1

3

∞

=

φ

+ 0,2

(8.4)

Tak więc przy

( )

s

t,

∞

φ

= 2,0 (długotrwałe oddziaływanie naprężeń

III

cs

σ

w elemencie

masywnym) k

3

= 0,45, przy

( )

s

t,

∞

φ

= 1,0 (zanikające w czasie oddziaływanie naprężeń

III

cs

σ

w elemencie o małej masywności k

3

= 0,70.

9. Obliczanie ilości przypowierzchniowego zbrojenia przeciwskurczowego

Największe wartości sumaryczne rozciągające naprężenia skurczowe

Σ

(

)

III

II

I

cs

,

,

σ

=

I

cs

σ

+

II

cs

σ

+

III

cs

σ

osiągają w skrajnych, przypowierzchniowych strefach przekroju i strefy

te wymagają przede wszystkim zabezpieczenia przed zarysowaniem skurczowym.

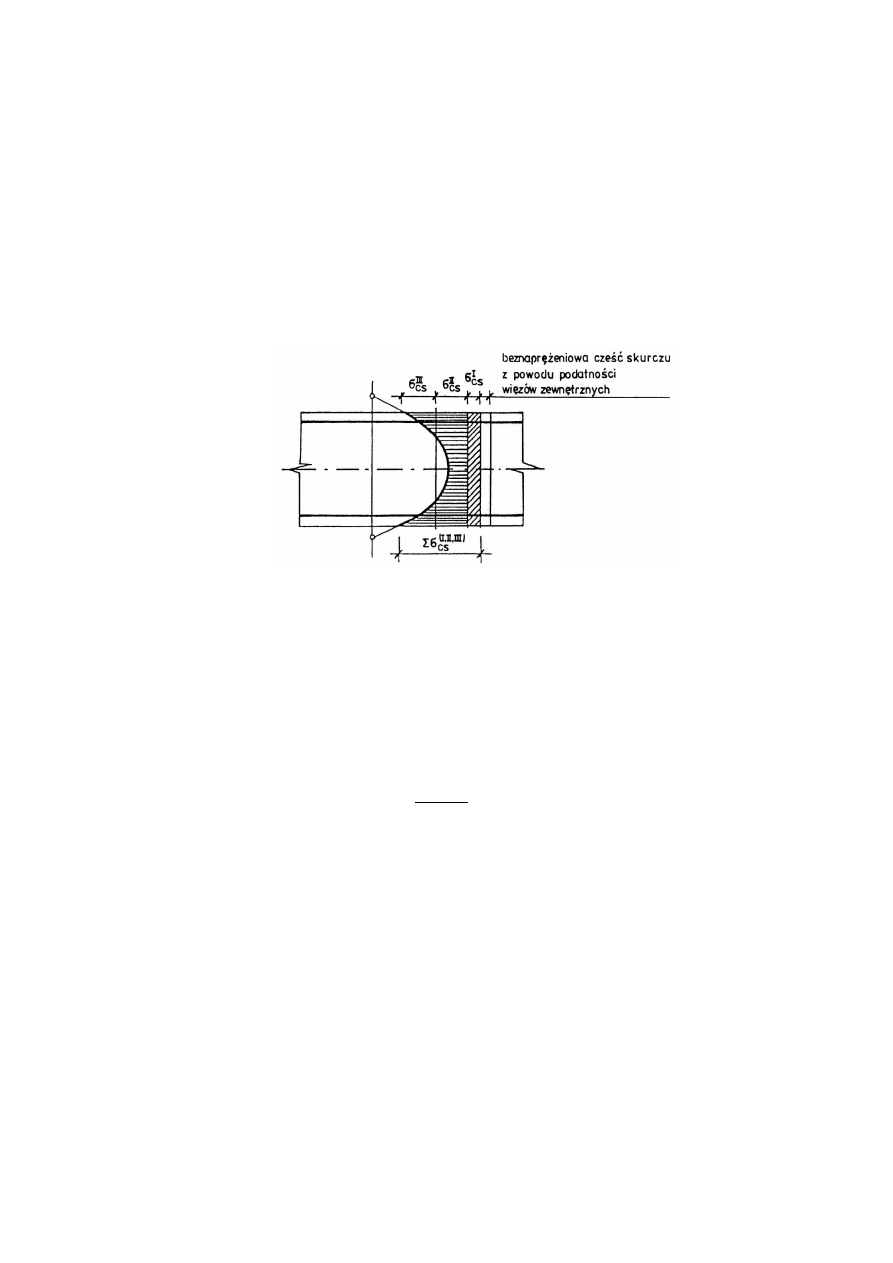
W przypadku elementów żelbetowych nasyconych zbrojeniem problem dodatkowego

przypowierzchniowego zbrojenia przeciwskurczowego jest najczęściej nieistotny, gdyż
istniejące wkładki zbrojenia zabezpieczają te strefy przed zarysowaniem lub też ograniczają
szerokość rozwarcia powstających rys skurczowych; z rozciąganiem betonu od skurczu
najczęściej sumują się naprężenia rozciągające od pracy elementu na obciążenia zewnętrzne
i morfologia powstających rys pochodzi od obu tych zjawisk łącznie.

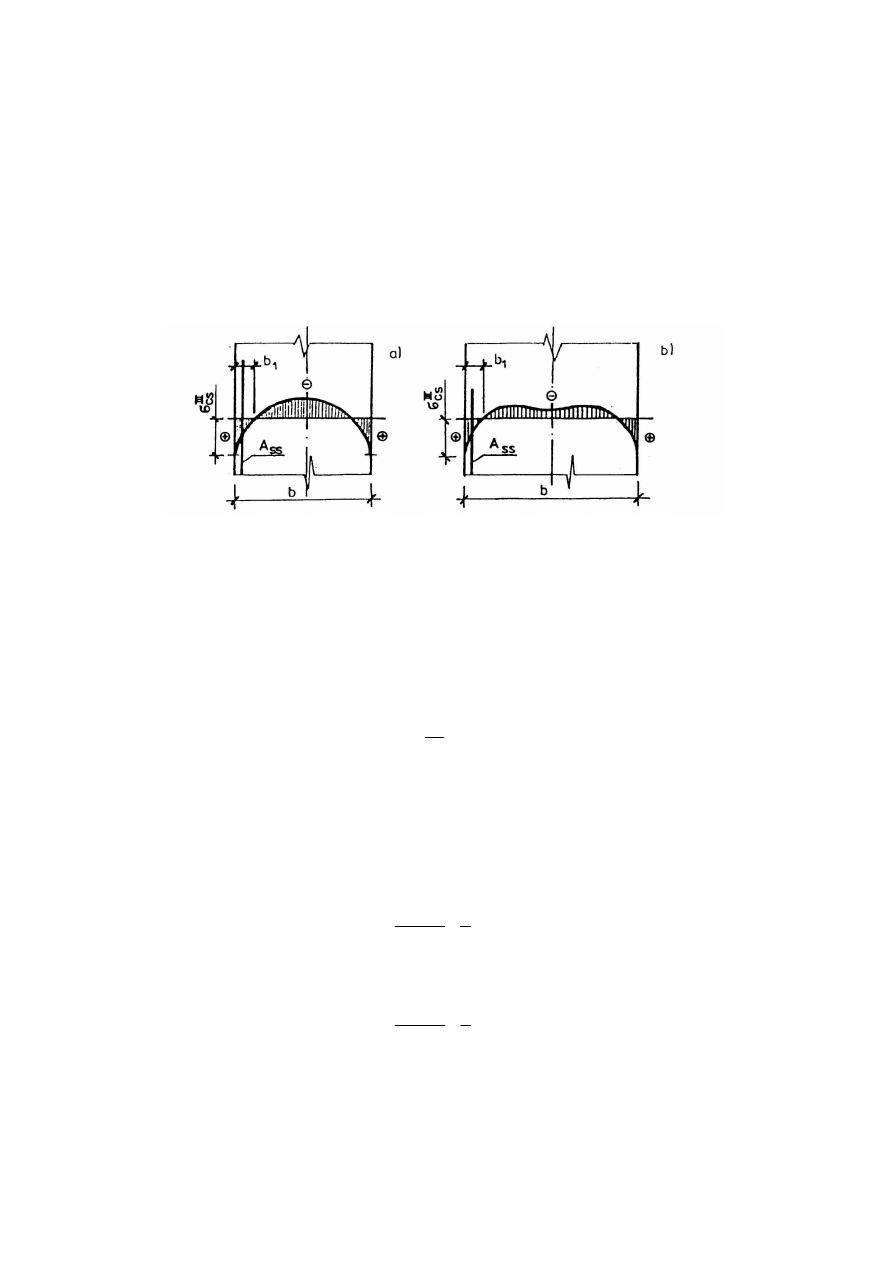
Rys. 9.1. Obliczeniowy rozkład naprężeń własnych

III

cs

σ

w przekrojach betonowych

Największy problem stwarzają przypowierzchniowe strefy elementów masywnych

(m

≤

2 m

-1

- rys. 9.1b) i o średniej masywności (2 < m < 15 m

-1

- rys. 9.1a), w których

zbrojenie ze względów obliczeniowych nie jest potrzebne. Należą do nich m.in. boczne
powierzchnie podpór mostowych, wysokich belek żelbetowych, górne powierzchnie grubych
płyt żelbetowych. Oddziaływujące na nie naprężenia skurczowe

III

cs

σ

powodują bardzo

często zarysowania ich powierzchni we wczesnym okresie po rozdeskowaniu.

Przez moduł powierzchniowy elementu [21, 24] rozumie się tu wyrażenie:

c

c

u

m

v

=

, [m

-1

]

(9.1)

gdzie:

u

c

- powierzchnia elementu wystawiona na wymianę wilgoci zawartej w betonie

z otoczeniem [m

2

],

v

c

- objętość betonu w elemencie [m

3

].

Dla płyty lub ściany o dominującym wymiarze „h” (grubość), w przypadku obustronnej

wymiany wilgoci, moduł powierzchniowy wynosi:

h

h

l

l

l

l

m

2

2

2

1

2

1

=

⋅

⋅

⋅

⋅

=

, [m

-1

].

(9.2)

Przy jednostronnej wymianie wilgoci (np. płyta fundamentowa na zaizolowanym podłożu):

h

h

l

l

l

l

m

1

2

1

2

1

=

⋅

⋅

⋅

=

, [m

-1

].

(9.3)

Dla pręta pryzmatycznego o długości

l

» a lub

l

» d

c

(gdzie a - wymiar boku pręta o

przekroju kwadratowym, d

c

- średnica pręta o przekroju kołowym), z wymianą wilgoci przez

całą powierzchnię zewnętrzną, zachodzi:

d

a

m

4

4

=

=

, [m

-1

].

(9.4)

Dla bloku sześciennego o boku a z wymianą wilgoci przez wszystkie powierzchnie

zewnętrzne, mamy:

a

m

6

=

, [m

-1

].

(9.5)

Płyta stropowa o grubości h = 0,10 m ma

20

10

,

0

2

=

=

m

m

-1

> 15,0 m

-1

i jest

niemasywna, podczas gdy płytowy ustrój nośny w moście o grubości h = 1,20 m ma

m =

20

,

1

2

= 1,67 < 2,0 m

-1

, co oznacza, że jest masywny. Masywną będzie również płyta

fundamentowa z jednostronną wymianą wilgoci, przy grubości h wynoszącej:

=

=

≥

0

,

2

1

1

m

h

0,50 m.

Typowe belki żelbetowe i sprężone stosowane w budownictwie powszechnym mają

moduł powierzchniowy m = 7÷14 m

-1

, zaś belki stosowane w budownictwie - m = 3÷7 m

-1

.

Są to zatem elementy o średniej masywności, w pierwszym przypadku bardziej zbliżone do
elementów niemasywnych, w drugim - do elementów masywnych.

W elementach niemasywnych dominują wymuszone naprężenia skurczowe

II

cs

I

cs

σ

σ +

, w

elementach masywnych - własne naprężenia skurczowe

III

cs

σ

. Elementy niemasywne

(m

≥

15,0 m

-1

) nie wymagają dodatkowego zbrojenia przeciwskurczowego

(przypowierzchniowego), dla przeniesienia naprężeń

III

cs

σ

. Mogą one wymagać takiego

zbrojenia dla przeniesienia naprężeń wymuszonych

II

cs

I

cs

σ

σ +

.

Między modułem powierzchniowym elementu „m”, a jego miarodajnym wymiarem „h

o

”

istnieje dla elementów płytowych i pryzmatycznych następująca zależność:

m =

o

c

o

c

c

c

c

h

A

h

A

A

u

u

2

2

0

,

1

0

,

1

v

=

⋅

=

⋅

⋅

=

, [m

-1

]

(9.6)

Jak wykazano w p. 8 już same naprężenia skurczowe własne

III

cs

σ

mogą osiągać wartości

zbliżone lub przekraczające wartość wytrzymałości średniej betonu na rozciąganie f

ctm

. Jeśli

weźmiemy pod uwagę fakt sumowania się w rzeczywistych konstrukcjach z betonu naprężeń

III

cs

σ

z naprężeniami

I

cs

II

cs

σ

σ +

, wówczas prawdopodobieństwo przekroczenia przez

sumaryczne naprężenia

(

)

∑

+

+

III

cs

II

cs

I

cs

σ

σ

σ

wytrzymałości f

ctm

znacznie się powiększa. Z

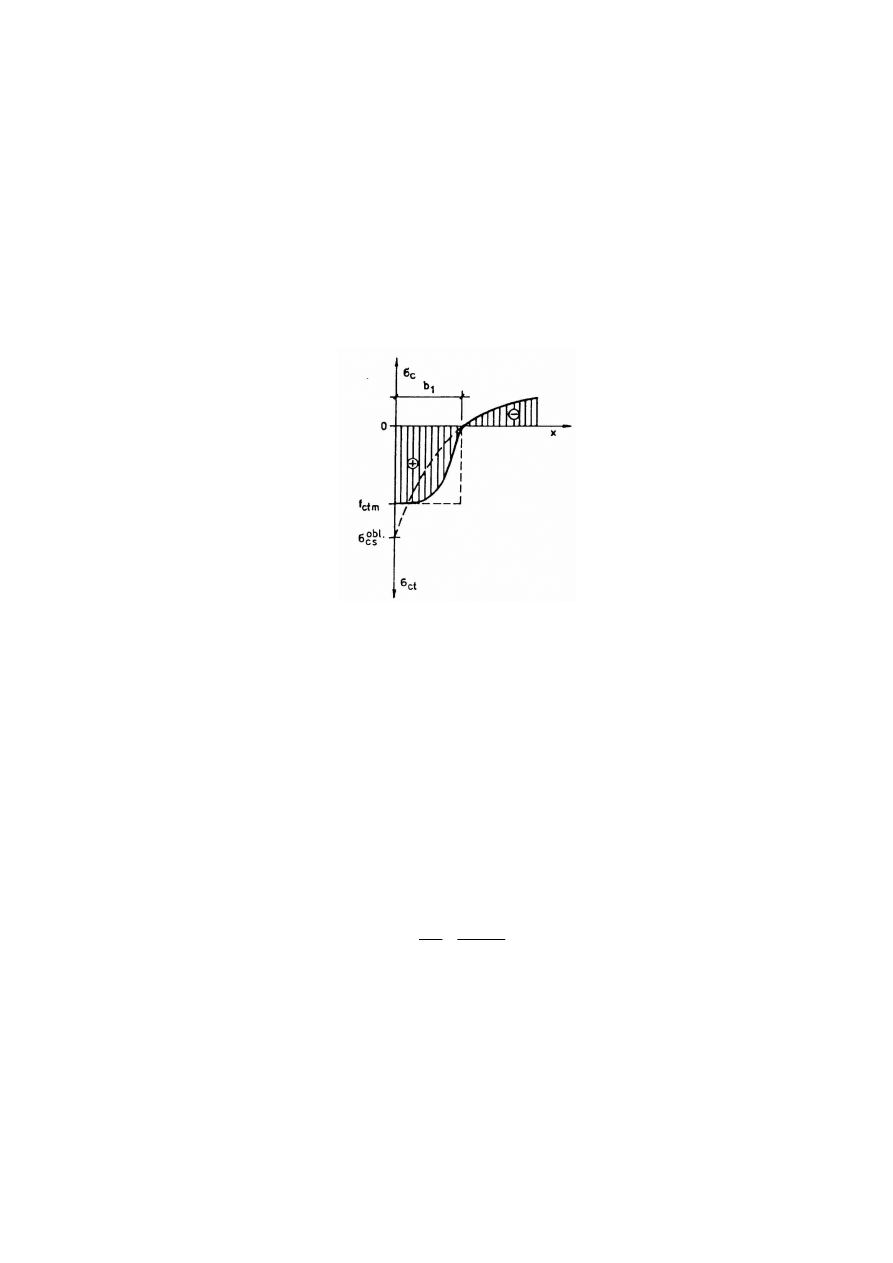
rys. 8.4 wynika, że naprężenia te są największe na krawędzi elementu, przez który odbywa
się wymiana masy (wilgoci) z otoczeniem i - przesuwając się w głąb elementu - szybko
spadają.

Najbardziej narażona zatem na rozciągające naprężenia skurczowe jest

przypowierzchniowa strefa elementów konstrukcyjnych z betonu. Dokładne oszacowanie
grubości tej strefy jest praktycznie niemożliwe. Zależy ona od podatności konstrukcji na
obciążenie skurczem, stopnia zbrojenia elementów, cech fizycznych mieszanki betonowej,
pielęgnacji betonu i warunków dojrzewania, wilgotności i temperatury środowiska
zewnętrznego, masywności elementu, itp.

Stąd też oszacowanie grubości tej strefy „b

1

”, może być tylko przybliżone. Najczęściej

przyjmuje się, że grubość „b

1

” wynika z rozkładu w przekroju naprężeń własnych

III

cs

σ

.

Grubość ta w stosunku do grubości elementu ”b” jest zdecydowanie inna w elementach o
średniej masywności i masywnych. W elementach o średniej masywności kształt pola
naprężeń własnych

III

cs

σ

w przekroju (w przybliżeniu podobny do kształtu pola wilgotności)

zbliżony jest do paraboli stopnia trzeciego i wówczas b

1

≅

0,185 b.

W elementach masywnych wykres pola wilgotności zbliża się do parabol wyższych

stopni, a nawet - w elementach bardzo grubych z uwagi na bezwładność wilgotnościową
środkowej części elementu oraz bardziej zaawansowaną dojrzałość z uwagi na
samoocieplenie pod wpływem ciepła hydratacji cementu - przyjmuje charakter jak na rys.
9.1b [24]. Wówczas grubość „b

1

” można przyjąć w przybliżeniu na podstawie doświadczeń.

Wynosi ona około (0,05

÷

0,15) b, więcej w elementach o współczynniku masywności

zbliżonym do m = 2,0 m

-1

, mniej w elementach o dużej grubości (m «2,0 m

-1

).

Kolejne założenie jakie należy przyjąć, to kształt wykresu naprężeń w rozciąganej,

przypowierzchniowej strefie elementu. Wykazany w p. 6, 7 i 8 sposób obliczania naprężeń
skurczowych

III

cs

II

cs

I

cs

σ

σ

σ

i

,

bazował na teorii sprężystości. Podane w tych rozdziałach

wzory uwzględniały tylko cechy sprężyste betonu (E

cm

= constans) oraz lepkie - przez

wprowadzenie współczynnika relaksacji naprężeń skurczowych na skutek pełzania - k

3

. Nie

uwzględniały one jednak cech plastycznych betonu, których udział jest tym większy im
naprężenie skurczowe jest bliższe wartości f

ctm

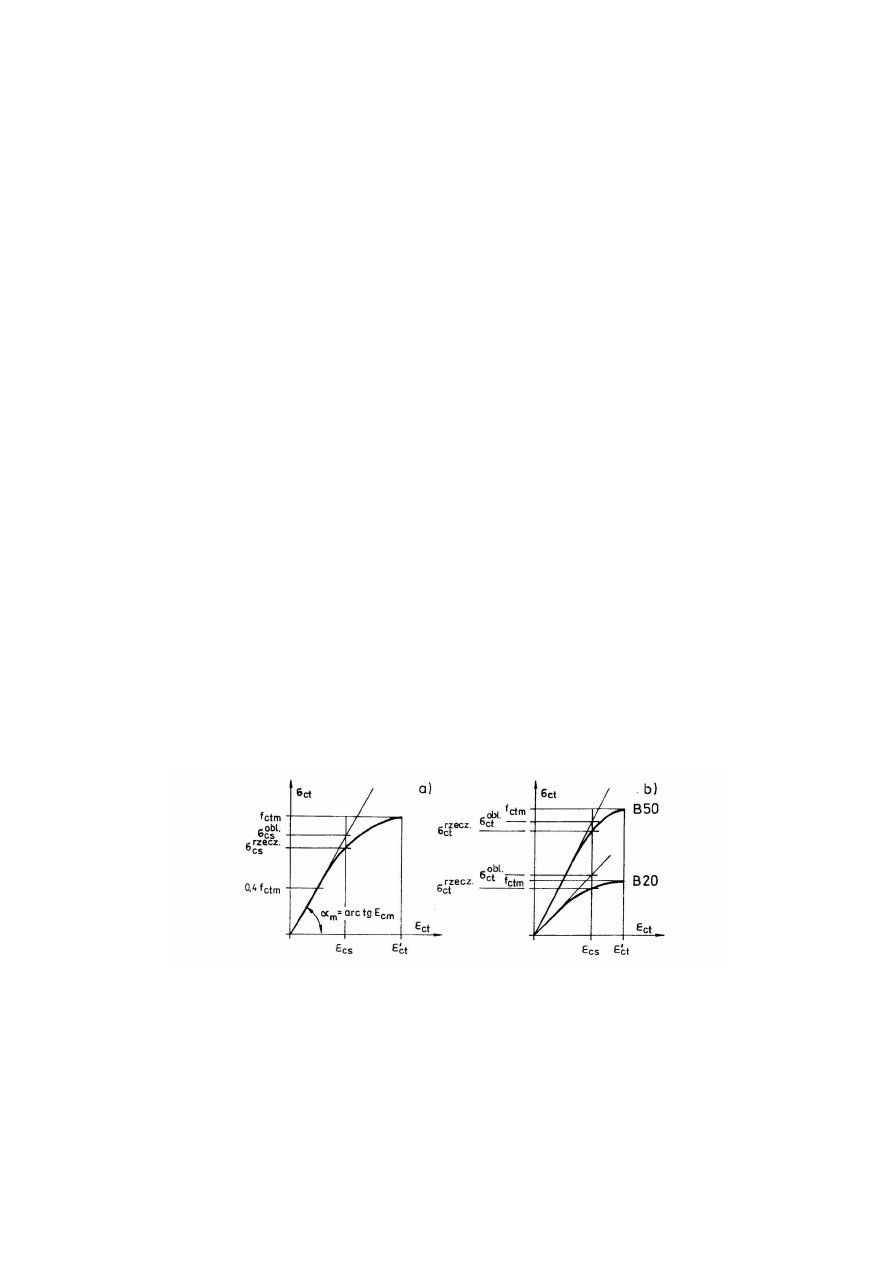
(por. rys. 9.2).

Rys. 9.2.

Udział cech plastycznych jest ponadto bardziej znaczący w betonach niższych klas (np.

B20), mniej w betonach klas wysokich (np. B50) - por. rys. 9.2b.

Obciążenie skurczem jest obciążeniem dystorsyjnym, o charakterze kinematycznym, tzn.

wiodącym jest odkształcenie skurczowe

ε

cs

, a pochodną wielkością jest naprężenie

skurczowe

σ

cs

. Stąd do zarysowania skurczowego dochodzi, gdy suma

(

)

[

]

III

cs

II

cs

I

cs

ε

ε

ε

γ

+

+

−

∑

1

osiągnie wartość większą od wydłużalności granicznej betonu na

rozciąganie

'

ct

ε

. Wówczas naprężenie rozciągające w betonie wynosi f

ctm

. Sytuację tę

przedstawia rys. 9.3.

Rys. 9.3. Diagram naprężeń rozciągających w przypowierzchniowej strefie betonu

Większość autorów potrzebną ilość zbrojenia przeciwskurczowego w strefie o szerokości

„b

1

” oblicza wychodząc z diagramu naprężeń, przedstawionego na rys. 9.3. Różnice dotyczą

tego, jaką wartość naprężenia f

ct

przyjmuje się za graniczną. Czy f

ctm

, czy f

ctk

. czy też jeszcze

inną. Następnie, czy rzeczywisty diagram naprężeń rozciągających

rzecz

ct

σ

aproksymuje się

prostokątem o wymiarach f

ct

⋅

b

1

⋅

(1,0 m), czy też prostokątem o uśrednionej szerokości

δ

⋅

b

1

(

δ

≤

1,0), czy też trójkątem o szerokości podstawy „b

1

” i wysokości f

ct

. I wreszcie, czy

uwzględnia się współpracę betonu przy rozciąganiu ze stalą zbrojenia przeciwskurczowego,
czy też nie.

Zakłada się przy tym, że w momencie pojawienia się rysy skurczowej całą bryłę

naprężeń rozciągających w strefie o szerokości „b

1

” przenosi stal zbrojenia

przypowierzchniowego. Naprężenie w tej stali nie może przekroczyć granicy plastyczności
f

yk

, tak aby możliwa była kontrola szerokości rys skurczowych. Poniżej zestawiono kilka

możliwych podejść do rozpatrywanego zagadnienia.

F. Leonhardt [26] wymaga, aby spełniony był warunek:

yk

ctk

ct

ss

ss

f

f

A

A

95

,

0

,

≥

=

ρ

(9.7)

gdzie:

ρ

ss

- stopień zbrojenia przeciwskurczowego w strefie o szerokości b

1

,

f

ctk,0,95

- kwantyl 95 % wytrzymałości losowej betonu na rozciąganie (MPa),

f

yk

- wytrzymałość charakterystyczna stali zbrojeniowej (MPa).

We wzorze tym przyjęto wytrzymałość graniczną w momencie zarysowania betonu na

wysokim poziomie, równym f

ctk,0,95

oraz prostokątny wykres naprężeń w strefie rozciąganej.

H. Rüsch i D. Jungwirth [20] proponują obliczać

ρ

ss

z wzoru:

(

)

yk

ctm

yk

ct

ss

f

f

f

f

n

05

,

1

1

≅

+

≥

µ

ρ

(9.8)

gdzie f

ct

jest wytrzymałością betonu na rozciąganie, szacowaną w przybliżeniu jako wartość

średnia z f

ctk,0,05

i f

ctm

, z uwzględnieniem wpływu wieku betonu na wzrost wytrzymałości na

rozciąganie. Wzór zakłada prostokątny wykres naprężeń rozciągających oraz sprężystą
współpracę betonu z wkładkami zbrojenia przeciwskurczowego [(1 + n

µ

) = (1 + n

o

ρ

ss

)], tuż

przed zarysowaniem.

Według SIA 162 [27] ilość minimalnego zbrojenia zabezpieczającego przed powstaniem

rys oblicza się z wzoru:

yk

ct

ss

f

f

α

ρ

≥

(9.9)

gdzie

α

jest współczynnikiem zależnym od rozstawu prętów przypowierzchniowych i

wynosi

α

= 1,0 dla e

p

= 10 cm oraz

α

= 1,4 dla e

p

= e

pmax

= 30 cm. f

ct

jest wytrzymałością

betonu na rozciąganie przyjmowaną w wysokości 2,00 MPa dla betonów klas niższych od
B 35/25 (oznaczenia według [27]) oraz 2,50 MPa dla pozostałych klas betonu.

W pracach [18, 28] K. Flaga zaproponował zależność:

0,55

yk

ctk

ss

yk

ctk

f

f

f

f

10

,

1

≤

≤

ρ

(9.10)

później skorygowaną [29] do postaci:

0,55

yk

ctm

ss

yk

ctm

f

f

f

f

10

,

1

≤

≤

ρ

(9.11)

Dolna granica odpowiada osiągnięciu przez naprężenia

obl

cs

σ

wartości f

ctm

tylko we włóknach

skrajnych rozciąganej strefy przypowierzchniowej (w przybliżeniu trójkątny wykres
naprężeń rozciągających), natomiast górna granica odpowiada założeniu uplastycznienia
całej tej strefy (prostokątny wykres naprężeń rozciągających). Wzory (9.10) i (9.11)
uwzględniają również plastyczną współpracę betonu z wkładkami zbrojenia
przeciwskurczowego, tuż przed zarysowaniem (1,10

≅

1 + 2 n

o

ρ

ss

).

I wreszcie Eurokod 2 [7, 8], a w ślad za nim norma PrPN-B-03264 [6] w p. 6.2 podaje

wzór, ważny dla minimalnego pola A

s

przekroju zbrojenia rozciąganego, wymaganego z

uwagi na ograniczenie szerokości rys spowodowanych naprężeniami wywołanymi przez
odkształcenia wymuszone przyczynami wewnętrznymi (skurcz) lub zewnętrznymi (osiadanie
podpór), w postaci:

A

s

= k

c

⋅

k

⋅

f

ct,eff

⋅

s

ct

A

σ

(9.12)

gdzie:

k

c

- współczynnik uwzględniający rozkład naprężeń w przekroju w chwili

poprzedzającej zarysowanie,

k

- współczynnik uwzględniający wpływ nierównomiernych naprężeń

samorównoważących się w ustroju,

f

ct,eff

- średnia wytrzymałość betonu na rozciąganie w chwili spodziewanego

zarysowania,

A

ct

- pole przekroju strefy rozciąganej elementu w chwili poprzedzającej

zarysowanie,

σ

s

- maksymalne naprężenie przyjęte w zbrojeniu rozciąganym natychmiast po

zarysowaniu, zależne od średnicy prętów.

Wzór (9.12) można łatwo adaptować do obliczenia zbrojenia przeciwskurczowego w

przypowierzchniowych strefach elementów konstrukcyjnych z betonu, przyjmując:
- k

c

= 1,0 (jak przy rozciąganiu osiowym),

- k = 0,8 (z uwagi na niepełne „wypełnienie” prostokąta o szerokości b

1

przez pole

naprężeń rozciągających),

- A

ct

= b

1

⋅

1,0 m.

Wówczas:

s

eff

ct

ss

f

σ

ρ

,

8

,

0

⋅

≥

(9.13)

Wartość f

ct,eff

zależy od terminu spodziewanego zarysowania skurczowego. W przypadku

braku ściślejszych informacji zaleca się przyjmować f

ct,eff

= f

ctm

odpowiednio do

projektowanej klasy betonu, lub do klasy betonu w momencie spodziewanego zarysowania.

Eurokod 2 sugeruje [7, 8, 11], że jeżeli zarysowanie nie nastąpi wcześniej niż po 28

dniach wówczas jako minimalną należy przyjmować f

ct,eff

= 3,0 MPa.

K. Flaga dyskutuje z tą sugestią w pracy [30], proponując przyjąć f

ct,eff

= 2,0 MPa dla

betonów klas do B20, 2,5 MPa - dla betonów klas do B30 i 3,0 MPa - dla betonów klas
wyższych.

Wartość

σ

s

naprężeń w zbrojeniu rozciąganym można przyjąć równą f

yk

z tym, że z

uwagi na nieprzekroczenie granicznej szerokości rys - może być potrzebne obniżenie tego
naprężenia. Stosowny przykład będzie przytoczony w dalszej części niniejszej pracy.

W tablicy 9.1 podano wyniki analizy porównawczej stopnia zbrojenia

przeciwskurczowego

ρ

ss

, obliczonego z wzorów (9.7), (9.8), (9.9), (9.11) i (9.13), dla 2 klas

betonu (B20 i B50) i 2 klas stali (A-I i A-III). Do obliczeń przyjęto f

ctm

= 1,9 MPa i

3,5 MPa, f

ctk

,

0,95

= 2,5 MPa i 4,6 MPa, f

ctk

= 1,3 MPa i 2,5 MPa, f

ct,eff

= f

ctm

≥

3,0 MPa,

f

yk

= 240 MPa i 410 MPa,

α

= 1,2.

Tablica 9.1. Wartości minimalnego stopnia zbrojenia przeciwskurczowego

ρ

ss

min

ss

ρ

według wzoru

Stal

f

yk

[MPa]

Klasa

betonu

(9.7)

(9.8)

(9.9)

(9.11)

*

(9.13)

Wartość

średnia

B20

0,0104 0,0070 0,0100 0,0087 0,0100

0,0092

240

B50

0,0192 0,0131 0,0125 0,0160 0,0117

0,0145

B20

0,0070 0,0041 0,0055 0,0051 0,0059

0,0055

410

B50

0,0112 0,0077 0,0073 0,0094 0,0068

0,0085

* wartości obliczone ze wzoru

ρ

ss

= 1,10 f

ctm

/f

yk

.

Jak wynika z powyższej tablicy, różnice między wartościami

min

ss

ρ

obliczone z

przytoczonych wzorów są dość znaczne, rzędu

±

25 % w stosunku do wartości średnich.

Wartości

min

ss

ρ

zbliżone do powyższych wartości średnich można uzyskać jako średnią

arytmetyczną z wartości obliczonych według wzorów (9.11) i (9.13).

Reasumując można stwierdzić, że stopień zbrojenia przeciwskurczowego w

przypowierzchniowych strefach elementów konstrukcyjnych z betonu powinien wynosić dla
stali o f

yk

= 240 MPa - od 0,90 do 1,45 % dla betonu klas od B20 do B50 oraz dla stali o

f

yk

= 410 MPa - 0,55 do 0,85 % dla betonu klas jak wyżej.

Przykład VI. Belka mostowa o przekroju 600/3000 mm wykonana jest z betonu klasy

B30 o f

ctm

= 2,6 MPa i zbrojona prętami ze stali 18G2 o f

yk

= 355 MPa. Należy określić ilość

zbrojenia przeciwskurczowego przy powierzchniach bocznych belki.

Moduł powierzchniowy:

m =

(

)

00

,

3

60

,

0

00

,

3

60

,

0

2

c

c

⋅

+

=

v

u

= 4,0 m

-1

> 2,0 m

-1

< 15,0 m

-1

.

Jest to zatem element o średniej masywności wymagający zbrojenia przypowierzchniowego.
Grubość strefy rozciąganej: b

1

= 0,185

⋅

600 = 111 mm. Konieczny stopień zbrojenia

przeciwskurczowego:
- z wzoru (9.5)

0081

,

0

355

60

,

2

10

,

1

=

≥

ss

ρ

- z wzoru (9.7)

0068

,

0

355

00

,

3

8

,

0

=

≥

ss

ρ

.

Wartość średnia

ρ

ss

= 0,0075.

Konieczne pole przekroju zbrojenia przeciwskurczowego:

A

ss

=

ρ

ss

⋅

b

1

⋅

1,0

⋅

10

3

= 0,0075

⋅

111

⋅

1,0

⋅

10

3

= 832,5 mm

2

= 8,33 cm

2

/1 mb konturu

a więc na przykład

φ

14 co 185 mm o A

ss

= 8,32 cm

2

/1 mb.

Zbrojenie to powinno być umieszczone w pobliżu środka ciężkości bryły naprężeń

rozciągających w betonie i rozmieszczone równomiernie zarówno poziomo jak i pionowo, z
uwagi na podobny rozwój odkształceń i naprężeń skurczowych. Dużo większe
prawdopodobieństwo przekroczenia przez naprężenia

σ

cs

wartości f

ctm

zachodzi dla kierunku

poziomego, gdyż sumują się tu naprężenia skurczowe wymuszone przez zbrojenie główne

II

ct

σ

z naprężeniami własnymi

III

ct

σ

- por. rys. 9.4. W kierunku pionowym występują tylko

naprężenia

III

ct

σ

, gdyż naprężenia wymuszone przez opór strzemion

II

ct

σ

są stosunkowo

małe.

Stąd też obliczone powyżej zbrojenie A

ss

należy w pełni zastosować jako pręty podłużne

przy obu bocznych powierzchniach belki. W kierunku pionowym ilość tego zbrojenia może
być zredukowana maksimum do połowy (por. wzór 9.11), a według normy [5] (por. p. 2.5)
do 60 % ilości minimalnych. Ostatecznie przyjęto dla kierunku pionowego:

pion

ss

A

= 0,6

⋅

8,33 = 5,00 cm

2

/1 mb

a więc na przykład

φ

14 co 300 mm, na całej długości belki. Na odcinkach ścinania powinny

to być pręty dodatkowe, w postaci np. dodatkowych strzemion [31]. Poza odcinkami
ścinania, rolę tę mogą pełnić pionowe ramiona strzemion stosowanych ze względów
konstrukcyjnych.

Przykład VII. Belka żelbetowa o przekroju 300/800 mm wykonana z analogicznych

materiałów jak w przykładzie VI.

m =

(

)

80

,

0

30

,

0

80

,

0

30

,

0

2

⋅

+

= 12,2 m

-1

> 2,0 m

-1

< 15,0 m

-1

b

1

= 0,185

⋅

300 = 55,5 mm.

Element o średniej masywności, bliskiej elementów niemasywnych; małe
prawdopodobieństwo osiągnięcia przez naprężenia

obl

cs

σ

wartości porównywalnych z

wytrzymałością f

ctm

.

0040

,

0

355

60

,

2

55

,

0

=

≥

ss

ρ

A

ss

= 0,0040

⋅

55,5

⋅

1,0

⋅

10

3

= 222 mm

2

= 2,22 cm

2

/1 mb konturu

a więc na przykład

φ

10 co 350 mm o A

ss

= 2,26 cm

2

/1 mb.

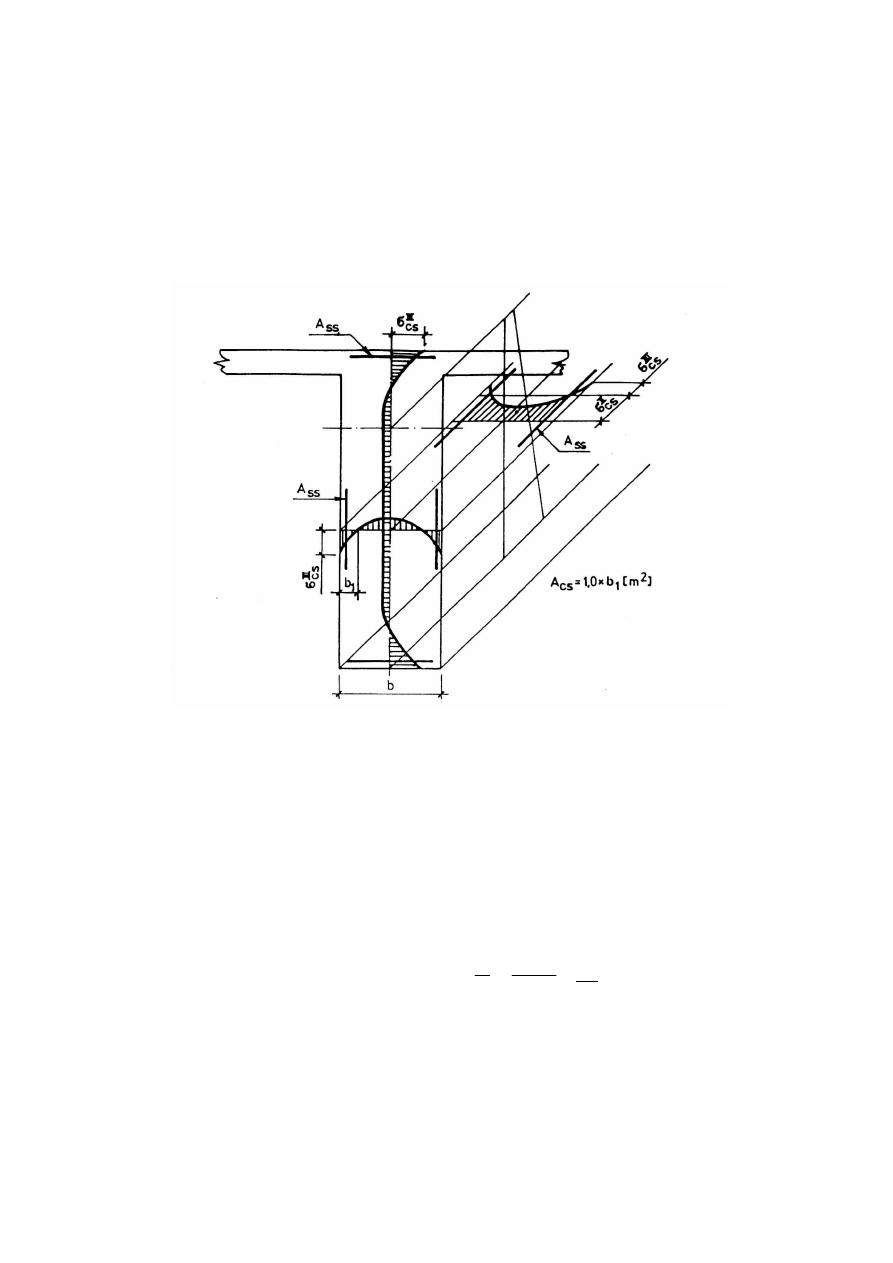
Zbrojenie powyższe jest zgodne z wymogami Pr PN-B-03264 [6] w zakresie dodatkowego
zbrojenia podłużnego. Powinno być ono również uwzględnione w tej ilości przy
konstruowaniu pionowych ramion strzemion w tej belce.

Rys. 9.4. Zmienność naprężeń skurczowych

II

cs

σ

i

III

cs

σ

, w przekroju belki mostowej o dużej

wysokości (żelbetowej lub sprężonej)

W pracy [29] autorzy zestawili ilości przypowierzchniowego zbrojenia podłużnego,

wymaganego przez różne normy w belkach wysokich z betonu. Stopień tego zbrojenia
odniesiony do pola przekroju poprzecznego b

⋅

h, przy każdej z powierzchni belek o

szerokości b = 400 mm wyniósł:
0,025 % (wg PN-56/B-03260), 0,031 % (wg PN-84/B-03264), 0,050 % (wg PN-76/B-
03264), 0,066 % (wg ACI), 0,100 % (wg SIA oraz DIN), 0,150 % (wg PN-91/S-10042).
Stosunek między wartościami skrajnymi wynosi tu 6 i dotyczy 2. polskich norm, starej z
1956 r. i nowej z 1991 r.

Dane te świadczą o wzrastającym w Polsce zrozumieniu dla przypowierzchniowego

zbrojenia przeciwskurczowego. Aby przeliczyć powyższe dane na wartości porównywalne z

tablicą 9.1, należy je pomnożyć przez czynnik

κ

=

1

b

b

=

b

b

185

,

0

= 5,4.

Otrzymany wówczas

ρ

ss

= 0,00135 (dla PN-56/B-03260),

ρ

ss

= 0,0054 (dla SIA i DIN) i

ρ

ss

= 0,0081 (dla PN-91/S-10042). Dopiero wartości

ρ

ss

wg norm SIA 162 [27], DIN 1075

[32] i PN-91/S-10042 [5] są porównywalne z wartościami

min

ss

ρ

z tablicy 9.1.

Aktualny projekt Pr PN-B-03264 [6] wymaga w analizowanym przypadku tylko:

0019

,

0

4

,

5

1000

400

1

10

50

,

0

350

1000

1

2

1

=

⋅

⋅

⋅

⋅

⋅

=

⋅

⋅

⋅

=

κ

ρ

h

b

A

n

s

ss

«

min

ss

ρ

z tablicy 9.1, a więc stanowczo za mało.

10. Średnica i rozstaw zbrojenia przeciwskurczowego

Zastosowanie zbrojenia przeciwskurczowego w ilości obliczonej według zasad podanych

w p. 9 nie wyczerpuje zagadnienia. Zapewnia ono jedynie to, że nieciągłość powstała w
strefie przypowierzchniowej na skutek zarysowania skurczowego zostaje „zszyta” przez
zbrojenie przeciwskurczowe, w którym w momencie powstania rysy nie zostaje
przekroczona granica plastyczności f

yk

. Pozwala to na kontrolę szerokości powstałych rys

skurczowych w

k

. Szerokość ta przy naprężeniu w stali równym f

yk

może być za duża z

punktu widzenia trwałości elementu. Powstaje zatem kolejny problem, a to średnicy i
rozstawu zbrojenia przeciwskurczowego w ilości A

ss

, zapewniających odpowiednią

dopuszczalną morfologię rys skurczowych w strefach przypowierzchniowych elementu.
Według H.

Rüscha i D.

Jungwirtha [20] zapewnienie warunku w

k

< w

lim

wymaga

zastosowania zbrojenia o średnicy

φ

s

spełniającej warunek:

2

lim

1

3

yk

s

s

f

E

w

⋅

⋅

≤

τ

φ

(10.1)

gdzie:

τ

1

- wytrzymałość na przyczepność betonu do stali zbrojeniowej; w przypadku

prętów zabetonowanych w pozycji poziomej można przyjąć

τ

1

= 0,15 f

cm

,

f

cm

- średnia wytrzymałość betonu na ściskanie.

Dla rozpatrzonego w p. 9 przykładu VI otrzymalibyśmy, przy w

lim

= 0,3 mm i

f

cm

= 33 MPa:

2

3

355

10

200

3

,

0

33

,

0

15

,

0

3

⋅

⋅

⋅

⋅

⋅

≤

s

φ

= 7,1 mm.

Dla większej średnicy zastosowanego zbrojenia przeciwskurczowego

φ

należy zmniejszyć

naprężenie w stali do wartości:

3

φ

φ

σ

s

yk

s

f

=

(10.2)

oraz stosownie podnieść stopień zbrojenia przeciwskurczowego, z wartości

ρ

ss

do wartości

ρ

1ss

.

W rozpatrywanym przykładzie VI prowadzi to do wartości:

3

14

1

,

7

355

=

s

σ

= 283,1 MPa

1

,

283

355

1

=

ss

ρ

⋅

0,0075 = 0,0094

0075

,

0

0094

,

0

1

=

ss

A

⋅

8,33 = 10,45 cm

2

/1 mb konturu,

a więc należy zastosować

φ

14 co 150 mm o A

1ss

= 10,27 cm

2

/1 mb.

Gdyby zastosować pręty o średnicy

φ

= 18 mm, wówczas

3

18

1

,

7

355

=

s

σ

= 260,3 MPa

3

,

260

355

1

=

ss

ρ

⋅

0,0075 = 0,0102

0075

,

0

0102

,

0

1

=

ss

A

⋅

8,33 = 11,36 cm

2

/1 mb konturu,

a więc pręty

φ

18 co 225 mm o A

1ss

= 11,29 cm

2

/1 mb.

Ważnym zagadnieniem jest nie tylko właściwa średnica zbrojenia przeciwskurczowego,

ale również jego rozstaw. Rozstaw powinien być taki, aby korzystne oddziaływanie prętów
przeciwskurczowych obejmowało całą przypowierzchniową strefę rozciąganą betonu, a nie
tylko najbliższe okolice tych prętów.

Pręty przeciwskurczowe zwiększają wydłużalność graniczną betonu do wartości

"

ct

ε

,

określonej np. przez G.D. Ciskreliego [32] wzorem:









+

=

φ

ρ

ε

ε

1

'

"

ct

ct

(10.3)

gdzie:

ρ

- stopień zbrojenia; w przypadku zbrojenia przeciwskurczowego

ρ

=

ρ

ss

lub

ρ

=

ρ

1ss

,

φ

- średnica zbrojenia (w m),

'

ct

ε

- wydłużalność graniczna betonu niezbrojonego, przyjmowana najczęściej na

poziomie 1

⋅

10

-4

.

Odnosząc się do przykładu VI zastosowanie zbrojenia przeciwskurczowego z prętów

φ

14 mm co 150 mm spowodowało wzrost wydłużalności granicznej betonu w rozciąganej

strefie przypowierzchniowej do wartości:







 +

⋅

=

−

014

,

0

0094

,

0

1

10

1

4

"

ct

ε

= 1,67

⋅

10

-4

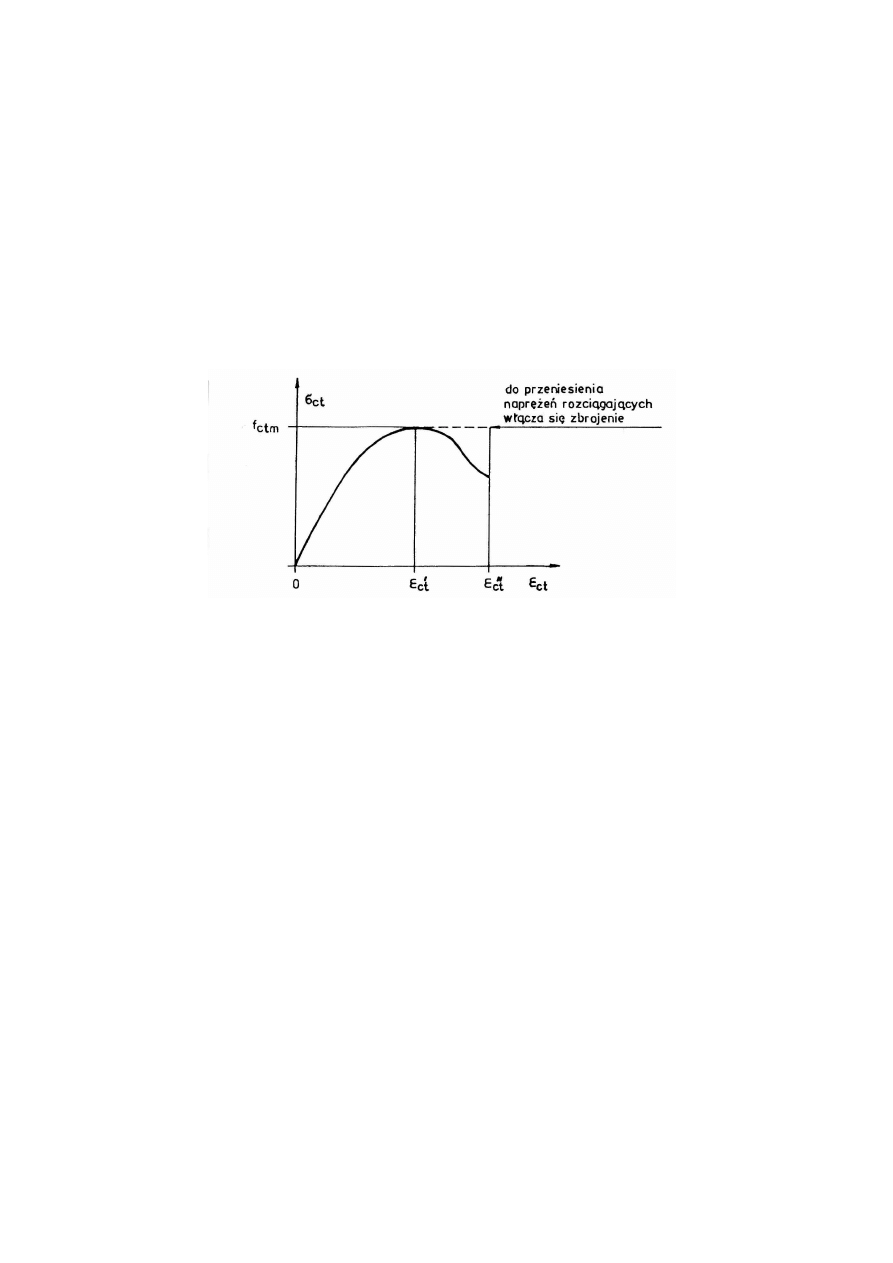
a więc o 67 %. Wzrost ten dotyczy najbliższej okolicy prętów przeciwskurczowych, w
dalszej od nich odległości maleje do zera.

Wzrost

'

ct

ε

do wartości

"

ct

ε

oznacza, że w okolicy prętów przeciwskurczowych nie

dochodzi z chwilą osiągnięcia przez naprężenia skurczowe wartości

σ

cs

= f

ctm

do nagłego

zarysowania, ale - z uwagi na kinematyczny charakter obciążenia - dochodzi do dekompresji
w betonie spowodowanej degradacją struktury betonu na skutek mikrozarysowań. Struktura
ta jest jednak „zszyta” przez zbrojenie i ujawnienie się rys skurczowych zachodzi dopiero po
osiągnięciu przez odkształcenie skurczowe wartości

ε

cs

≥

"

ct

ε

(rys. 10.1).

Rys. 10.1. Diagram

σ

ct

-

ε

ct

betonu rozciąganego przy obciążeniu typu kinematycznego

(np. skurczem betonu)

Według G.D. Ciskreliego [33], oddziaływanie prętów zbrojeniowych na rozciągany

beton sięga na odległość e = 6

φ

przy

φ

≤

3 mm i e = 3

φ

przy średnicach większych,

według F. Leonhardta [26] - na odległość e = 7

φ

poza lico pręta, według normy [5] - na

odległość e = 7,5

φ

od osi pręta. Wariant najbardziej optymistyczny e = 7,5

φ

od osi pręta

wskazuje, że osiowa odległość prętów zbrojenia przeciwskurczowego nie powinna być
większa niż s = 2e = 15

φ

. Rozstawy prętów z przykładu VI odpowiadają temu warunkowi,

podczas gdy rozstaw s = 350 mm dla prętów

φ

10 z przykładu VII warunku tego nie spełnia

i zbrojenie to nie będzie efektywne.

Na zakończenie należy zwrócić uwagę na fakt, że naprężenia skurczowe są zmienne w

czasie, jedne

(

)

II

cs

I

cs

σ

σ

,

rosną z czasem, inne

( )

III

ct

σ

z czasem maleją. Stąd też jeżeli ilość

zbrojenia przeciwskurczowego w strefach przypowierzchniowych jest podyktowana
naprężeniami własnymi

III

ct

σ

, wówczas należy spodziewać się z biegiem czasu zamykania

się rys skurczowych (o ile powstaną) i zmniejszenia się naprężeń

III

ss

σ

w zbrojeniu

przeciwskurczowym. Pręty tego zbrojenia mogą być wówczas przydatne do innych celów,
jak np. do współpracy z betonem przy przenoszeniu obciążeń zewnętrznych i innych
oddziaływań (np. termicznych).

Jeśli natomiast ilość zbrojenia przeciwskurczowego jest podyktowana sumowaniem się

naprężeń

III

cs

σ

z naprężeniami

II

cs

I

cs

σ

σ

i

(rys. 8.4), wówczas powstałe rysy skurczowe mogą

w czasie nawet się rozszerzyć, i stąd należy dużą wagę przywiązać zarówno do ilości jak i
średnicy oraz rozstawu prętów zbrojenia przypowierzchniowego. Dotyczy to np. dolnych

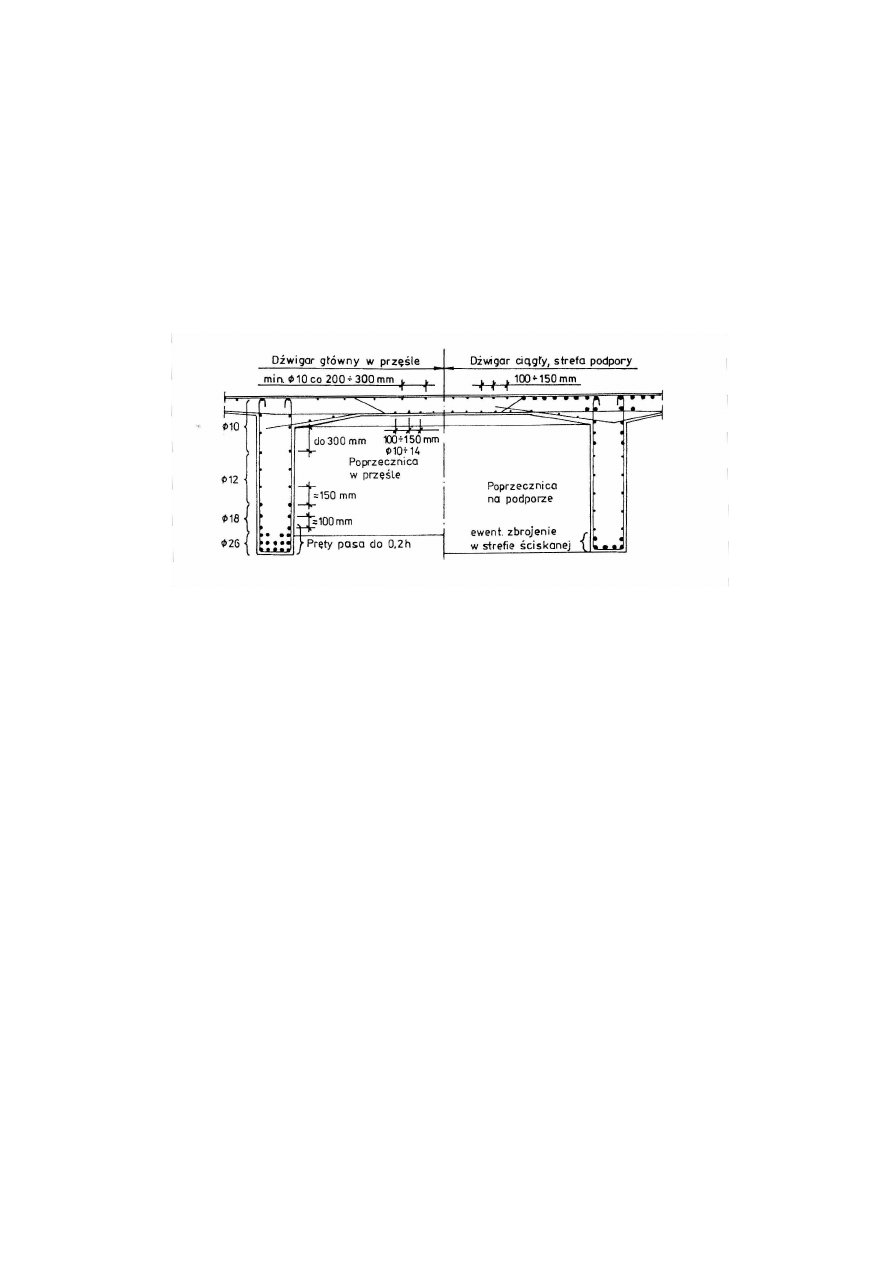
stref ścian bocznych wysokich belek żelbetowych i sprężonych, gdzie naprężenia skurczowe

II

bs

σ

i

III

bs

σ

sumują się w przęsłach z naprężeniami rozciągającymi od pracy belek na

zginanie. W takich przypadkach np. norma [5] zaleca stopniowanie podłużnych prętów przy
obu powierzchniach bocznych - gęściej od strony rozciąganych prętów głównych.

F. Leonhardt [34] wręcz zaleca stopniowanie tych prętów wg rysunku 10.2.

Rys. 10.2. Rozkład poziomych prętów przypowierzchniowych dla wysokiej belki mostowej

11. Uwagi końcowe

Praca niniejsza, mimo swojej obszerności, nie wyczerpuje całości zagadnienia. Nie

można bowiem zagadnienia naprężeń skurczowych rozpatrywać w oderwaniu od naprężeń
termicznych [35], wywołanych w konstrukcji bądź przez wpływy wewnętrzne (ciepło
hydratacji cementu) bądź przez wpływy zewnętrzne (zmiany temperatury otoczenia,
insolacja itp.). W elementach niemasywnych i o średniej masywności rzędu m

≥

10 m

-1

dominują naprężenia skurczowe wymuszone, w elementach masywnych i o średniej
masywności m < 10 m

-1

- naprężenia skurczowe plus naprężenia termiczne, własne i

wymuszone. I tu, każdy przypadek należy rozpatrywać oddzielnie.

Oddziaływanie naprężeń termicznych i skurczowych jest w zasadzie podobne, z tym, że

odkształcenia skurczowe są ujemne, termiczne mogą być dodatnie (np. podczas rozgrzewu
elementu przez ciepło hydratacji cementu) lub ujemne (np. podczas stygnięcia tego
elementu). Ponadto ekstremalne wartości odkształceń termicznych i skurczowych mogą
występować w różnym czasie. Stąd też podanie ogólnych reguł postępowania nastręcza
duże trudności.

Klasycznym przykładem mogą tu być zagadnienia związane z połączeniem ścian z

fundamentami, np. bardzo dużych trzonów z płytami fundamentowymi znacznej grubości,
ścian zbiorników i basenów z fundamentami. Zazwyczaj jest tak, że ściany te wykonujemy z
dużym opóźnieniem w stosunku do realizacji płyt fundamentowych. W płytach tych doszło
już do stabilizacji termicznej oraz w dużym stopniu zaistniały już odkształcenia skurczowe.

Nowo zabetonowana ściana (najczęściej o średniej masywności, np. dla h = 0,4 m,

m = 5,0 m

-1

) najpierw rozszerza się termicznie pod wpływem ciepła hydratacji cementu.

Tzw. szok termiczny zachodzi w pierwszych 50-80 godzinach dojrzewania [25], gdy beton

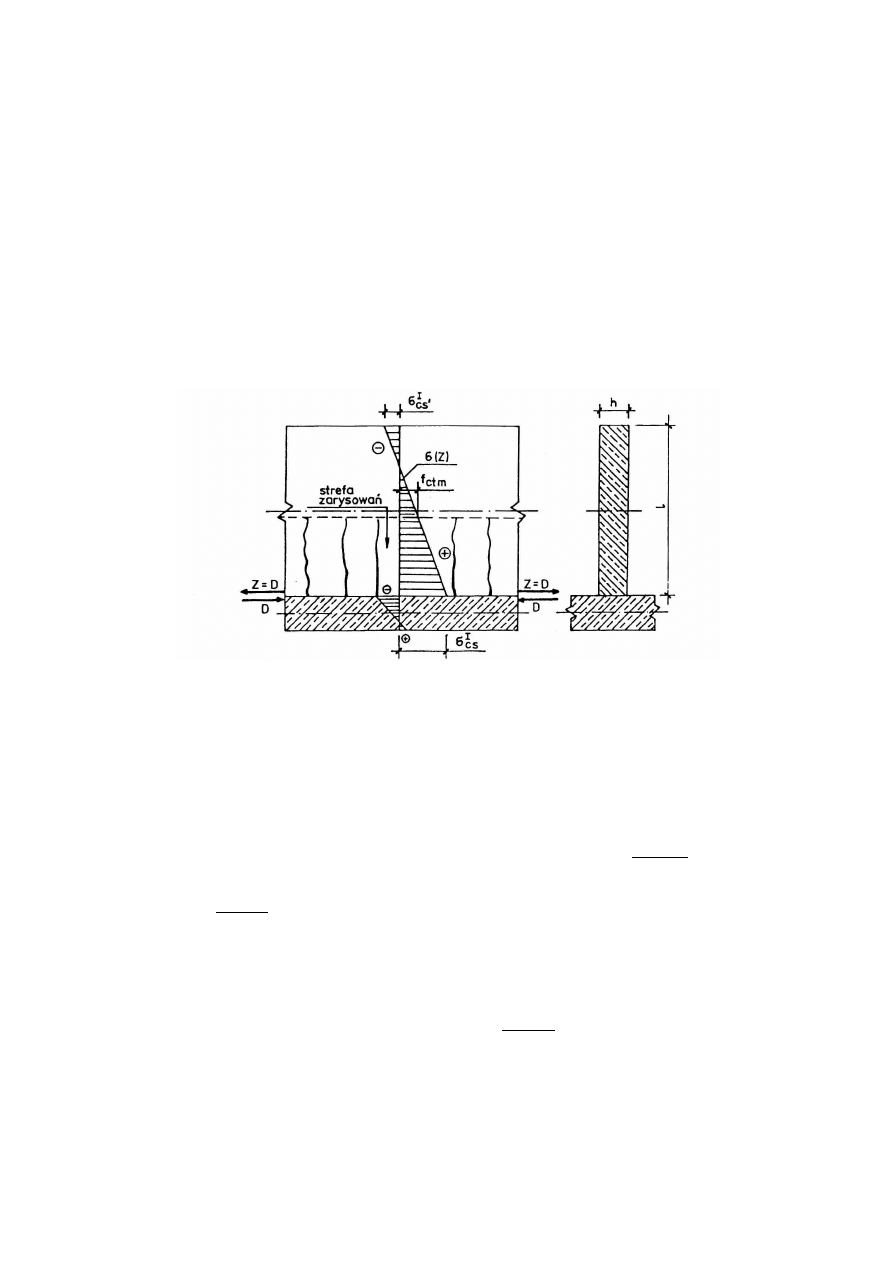
jest najpierw ciałem o cechach cieczy lepkiej, a później ciałem pseudo stałym, o małym
zaawansowaniu cech sprężystych. Z biegiem czasu beton w ścianie twardnieje i zaczyna się
wychładzać, kurcząc się termicznie. Do skurczu tego dodaje się skurcz fizyczny. Temu
łącznemu odkształceniu termiczno-skurczowemu stawia opór wcześniej wykonany
fundament, który dla rozpatrywanej ściany jest więzem zewnętrznym o dużej sztywności.

Na skutek istnienia tego więzu dochodzi do zaistnienia dużych sił w strefie stykowej tych

dwóch elementów; ściana jest mimośrodowo rozciągana, a fundament mimośrodowo
ściskany. Prowadzi to najczęściej do znaczących zarysowań skrośnych w dolnej części
ściany (rys. 11.1).

Rys. 11.1.

Zapobiec im można układając w ścianie dodatkowe zbrojenie poziome obliczone przy

założeniu, że ściana jest rozciągana na całej grubości „h”, tzn. A

cs

= h

⋅

1,0 m, na podstawie

analogicznych wzorów, jak przypowierzchniowe zbrojenie przeciwskurczowe (por. pkt 9).

Na przykład (przykład VIII) dodatkowe zbrojenie poziome ściany dla przeniesienia

rozciągających naprężeń termiczno-skurczowych, dla betonu klasy B20, stali 34GS o
f

yk

= 410 MPa i grubości ściany h = 400 mm, zgodnie z tablicą 9.1 powinno wynosić:

ρ

ss

= 0,0055

A

ss

=

ρ

ss

⋅

h

⋅

1,0

⋅

10

3

= 0,0055

⋅

400

⋅

1,0

⋅

10

3

= 2200 mm

2

= 22,0 cm

2

/1 mb

wysokości.

Dano zbrojenie poziome w 3 warstwach na grubości ściany z prętów

φ

14 co 150 mm o

A

1ss

= 30,8 m

2

/» A

ss

= 22,0 cm

2

/1 mb, z uwagi na ograniczenie szerokości rys do

w

k

≤

w

lim

= 0,3 mm.

W kierunku pionowym należy, z uwagi na skurczowe naprężenia własne, zastosować

zbrojenie:
- w 2. warstwach zewnętrznych

ρ

ss

= 0,0055

A

ss

= 0,0055

⋅

0,185

⋅

400

⋅

1,0

⋅

10

3

= 407,0 mm

2

= 4,07 cm

2

/1 mb szerokości,

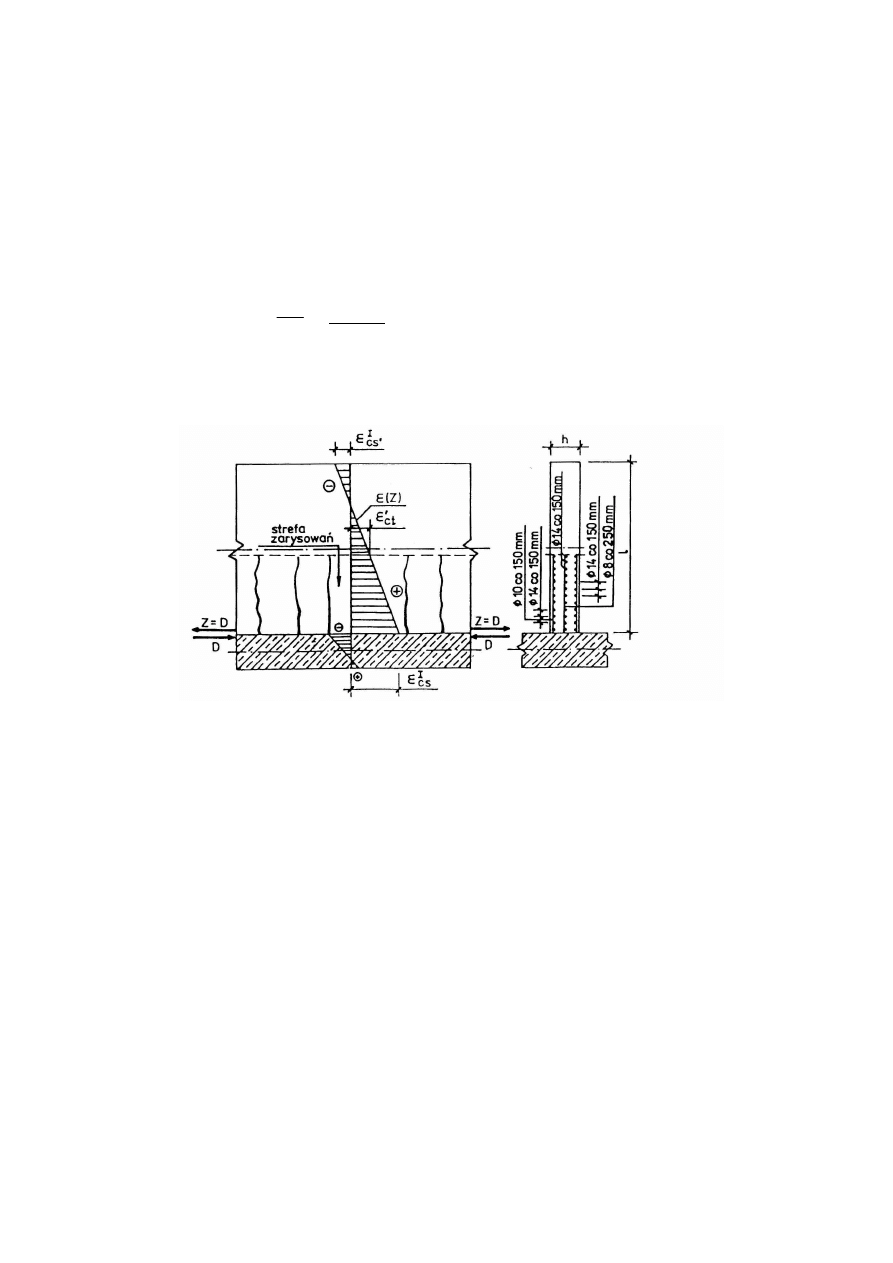
a więc np. pręty

φ

10 co 150 mm o A

1ss

= 5,27 cm

2

/1 mb z uwagi na ograniczenie

szerokości rys do w

k

≤

w

lim

= 0,3 mm.

- w warstwie wewnętrznej

zbrojenie konstrukcyjne w ilości 20 % zbrojenia poziomego:

A

1ss

= 0,20

⋅

3

8

,

30

= 2,05 cm

2

/1 mb szerokości, a więc np. pręty

φ

8 co 250 mm o

A

1ss

= 2,00 cm

2

na 1 mb.

Sposób zbrojenia przedmiotowej ściany dla zabezpieczenia przed skutkami naprężeń

termiczno-skurczowych przedstawiono na rys. 11.2.

Rys. 11.2.

Piśmiennictwo

[1] PN-56/B-03260. Konstrukcje żelbetowe. Obliczenia statyczne i projektowanie.
[2] PN-66/B-03320.

Konstrukcje z betonu sprężonego. Obliczenia statyczne i

projektowanie.

[3] PN-76/B-03264. Konstrukcje betonowe, żelbetowe i sprężone. Obliczenia statyczne i

projektowanie.

[4] PN-84/B-03264. Konstrukcje betonowe, żelbetowe i sprężone. Obliczenia statyczne i

projektowanie.

[5] PN-914/S-10042. Obiekty mostowe. Konstrukcje betonowe, żelbetowe i sprężone.

Projektowanie.

[6] Pr PN-B-03264. Konstrukcje betonowe, żelbetowe i sprężone. Obliczenia statyczne i

projektowanie.

[7] Eurokod 2. Projektowanie konstrukcji z betonu.

Część 1. Reguły ogólne i reguły dla budynków.
Tom I. Wersja polska ENV 1992-1-1:1991, ITB Warszawa 1992.

[8] Eurokod 2. Projektowanie konstrukcji z betonu.

Część 1. Reguły ogólne i reguły dla budynków.
Tom II. Postanowienia krajowe do ENV 1992-1-1:1991. 2-ga wersja. ITB Warszawa
1993.

[9] PN-B-03264:1999: Konstrukcje betonowe, żelbetowe i sprężone. Obliczenia statyczne i

projektowanie.

[10] Praca zbiorowa: Podstawy projektowania konstrukcji żelbetowych i sprężonych według

Eurokodu 2.Trzy tomowe opracowanie dla KBN, Warszawa 1997.

[11] Eurokode 2: Design of concrete structures - Part 1: General rules and rules for

buildings. Wersja angielska EN 1992-1 (1

st

draft), July 1999.

[12] Eurokode 2: Design of concrete structures - Part 1-1: General rules and rules for

buildings. Wersja angielska EN 1992-1-1 (1

st

draft), October 2001.

[13] Comité Euro - International du Beton: CEB-FIP Model Code 1990. Design Code. CEB

Bulletin No 213/214. Thomas Telford Services Ltd. London 1993.

[14] Raszka H.: Skurcz betonu - geneza, objawy i przebieg w czasie. Inżynieria i

Budownictwo, nr 2/1995.

[15] Raszka H.: Uogólnione metody obliczania przewidywanych odkształceń skurczowych

elementów betonowych. Inżynieria i Budownictwo, nr 1/1990.

[16] Flaga K.: Wpływ pól wilgotnościowych na zarysowanie i nośność konstrukcji

żelbetowych. Księga Referatów I Ogólnopolskiego Sympozjum „Wpływy środowiskowe
na budowle i ludzi”. Lublin, XII. 1994.

[17] Flaga K., Furtak K., Jargiełło J.: Zastosowanie zmodyfikowanej teorii starzenia do

oceny relaksacji naprężeń skurczowych w elementach żelbetowych. Archiwum Inżynierii
Lądowej, tom XXX, z. 4/1984.

[18] Flaga K.: Skurcz betonu a trwałość mostów betonowych. Inżynieria i Budownictwo, nr

7-8/1988.

[19] Flaga K.: Praca zbrojenia przeciwskurczowego w wysokich belkach żelbetowych.

Księga Referatów XXVIII Konferencji Naukowej KILiW PAN i KN PZITB. Warszawa-
Krynica, IX. 1982.

[20] Rüsch, Jungwirth D.: Skurcz i pełzanie w konstrukcjach betonowych. Arkady,

Warszawa 1979.

[21] Aleksandrowskij S.W.: Rascziot bietonnych i żelezobietonnych konstrukcij na

temperaturnyje i włażnostnyje wozdiejstwia. Strojizdat, Moskwa 1966.

[22] Flaga K., Andreasik M.: Naprężenia termiczno-skurczowe w masywnych elementach

betonowych. Księga Referatów XXXIII Konferencji Naukowej KILiW PAN i KN
PZITB. Gliwice-Krynica, IX. 1987.

[23] Flaga K., Wilczyński T.: Odkształcenia skurczowe w pryzmatycznych elementach

betonowych obciążonych niejednorodnym polem wilgoci. Zeszyt Naukowy Komisji
Budownictwa O/K PAN. Ossolineum, Wrocław 1982.

[24] Flaga K.: Wpływ czasu na mosty żelbetowe i z betonu sprężonego. Inżynieria i

Budownictwo, nr 6/1997.

[25] Flaga K.: Naprężenia własne termiczne „makro” w elementach i konstrukcjach z

betonu. Cement, Wapno, Gips, nr 4-5/1991.

[26] Leonhardt F.: Cracks and Crack Control at Concrete Structures. IABSE Periodica, nr

1/1987.

[27] SIA Norme 162. Ouvrages en béton. Societe Suisse des Ingenieurs et des Architectes.

Zürich 1989.

[28] Flaga K., Wilczyński T.: O obliczaniu przypowierzchniowego zbrojenia

przeciwskurczowego w elementach z betonu. Inżynieria i Budownictwo, nr 11-12/1983.

[29] Flaga K., Furtak K.: Projektowanie konstrukcyjnego zbrojenia przeciwskurczowego w

elementach żelbetowych. Księga Referatów XXXVIII Konferencji Naukowej KILiW
PAN i KN PZITB, Łódź-Krynica, IX.1992.

[30] Flaga K. Minimalne zbrojenie ze względu na stan graniczny zarysowania. Inżynieria i

Budownictwo, nr 2/1995.

[31] Holst K.H.: Brücken aus Stahlbeton und Spannbeton. Ernst und Sohn, Berlin 1985.
[32] DIN 1075: Betonbrücken, Bemessung und Ausführung.
[33] Ciskreli G.D.: O rastiażimosti armirowanych bietonow. Bieton i Żelezobieton, nr

19/1964.

[34] Leonhardt F.: Podstawy budowy mostów betonowych. Przekład z niemieckiego Józef

Głomb i Feliks Lipski. WKiŁ, Warszawa 1982.

[35] Andreasik M.: Naprężenia termiczno-skurczowe w masywach betonowych. Praca

doktorska, Kraków 1982.