1

Wykład 4

Energia kinetyczna i praca.

Energia kinetyczna i praca.

Energia potencjalna

Energia potencjalna

Wrocław University of Technology

5-XI-2011

2

Praca

Kto wykonał wi

ę

ksz

ą

prac

ę

?

ENERGIA KINETYCZNA I PRACA

5.XI.2011

Hossein Rezazadeh

Olimpiada w Atenach 2004 WR

Podrzut 263 kg

Paul Anderson

Rekord Guinnessa 1957

Ci

ęż

ar 27900N (2850kg)

3

Energia

Energia – wielko

ść

skalarna opisuj

ą

ca stan w jakim si

ę

w danym

momencie znajduje jedno lub wiele ciał.

ENERGIA KINETYCZNA I PRACA

5.XI.2011

Termin energia pochodzi od greckiego słowa „energeia” u

ż

ywanego

ju

ż

przez Arystotelesa i w ró

ż

nych tłumaczeniach oznacza

działanie, przyczyn

ę

ruchu, moc.

A jak nale

ż

y rozumie

ć

słowo energia w j

ę

zyku fizyki?

Słownik wyrazów obcych PWN: „… wielko

ść

fizyczna okre

ś

laj

ą

ca

zdolno

ść

ciała lub układu ciał do wykonywania pracy przy

przej

ś

ciu z jednego stanu do drugiego”

4

Energia kinetyczna

ENERGIA KINETYCZNA I PRACA

5.XI.2011

Energię kinetyczną E

k

ciała o masie m, poruszającego się z prędkością

o wartości v, znacznie mniejszej od prędkości światła, definiujemy
jako:

2

2

1

mv

E

k

=

Jednostką energii kinetycznej (i każdego innego
rodzaju energii) w układzie SI jest dżul (J).
Nazwa ta pochodzi od nazwiska XIX-wiecznego
uczonego angielskiego, Jamesa Prescotta Joule'a.

James Prescott Joule

2

2

1

s

m

kg

J

⋅

=

5

Energia kinetyczna

ENERGIA KINETYCZNA I PRACA

5.XI.2011

W 1896 roku w Waco, w Teksasie William Crush na oczach 30000 widzów
ustawił dwie lokomotywy naprzeciwko siebie, na końcach toru o długości
6.4km. Zablokował dźwignie w położeniu pełnego gazu i pozwolił
rozpędzonym lokomotywom zderzyć się ze sobą czołowo. Wyznacz łączną
energię kinetyczną lokomotyw tuż przed zderzeniem zakładając, że każda z
nich miała ciężar równy 1.2

.

10

6

N, a przyspieszenia obydwu lokomotyw

wzdłuż toru były stałe i wynosiły 0.26 m/s

2

.

przed

po

6

Energia kinetyczna

ENERGIA KINETYCZNA I PRACA

5.XI.2011

Przyspieszenie każdej z lokomotyw było stałe, więc do obliczenia

jej prędkości v tuż przed zderzeniem możemy zastosować wzór:

(

)

s

m

v

x

x

a

v

v

/

8

.

40

2

0

2

0

2

=

−

+

=

(

)

(

)

J

s

m

kg

mv

E

k

8

5

2

10

2

/

8

.

40

10

22

.

1

2

1

2

⋅

=

⋅

⋅

=













=

Energia wybuchu trotylu:

E

zderzenia lokomotyw

≈

51kg trotylu

kg

J

E

WT

/

10

9

.

3

6

⋅

=

7

Praca

ENERGIA KINETYCZNA I PRACA

5.XI.2011

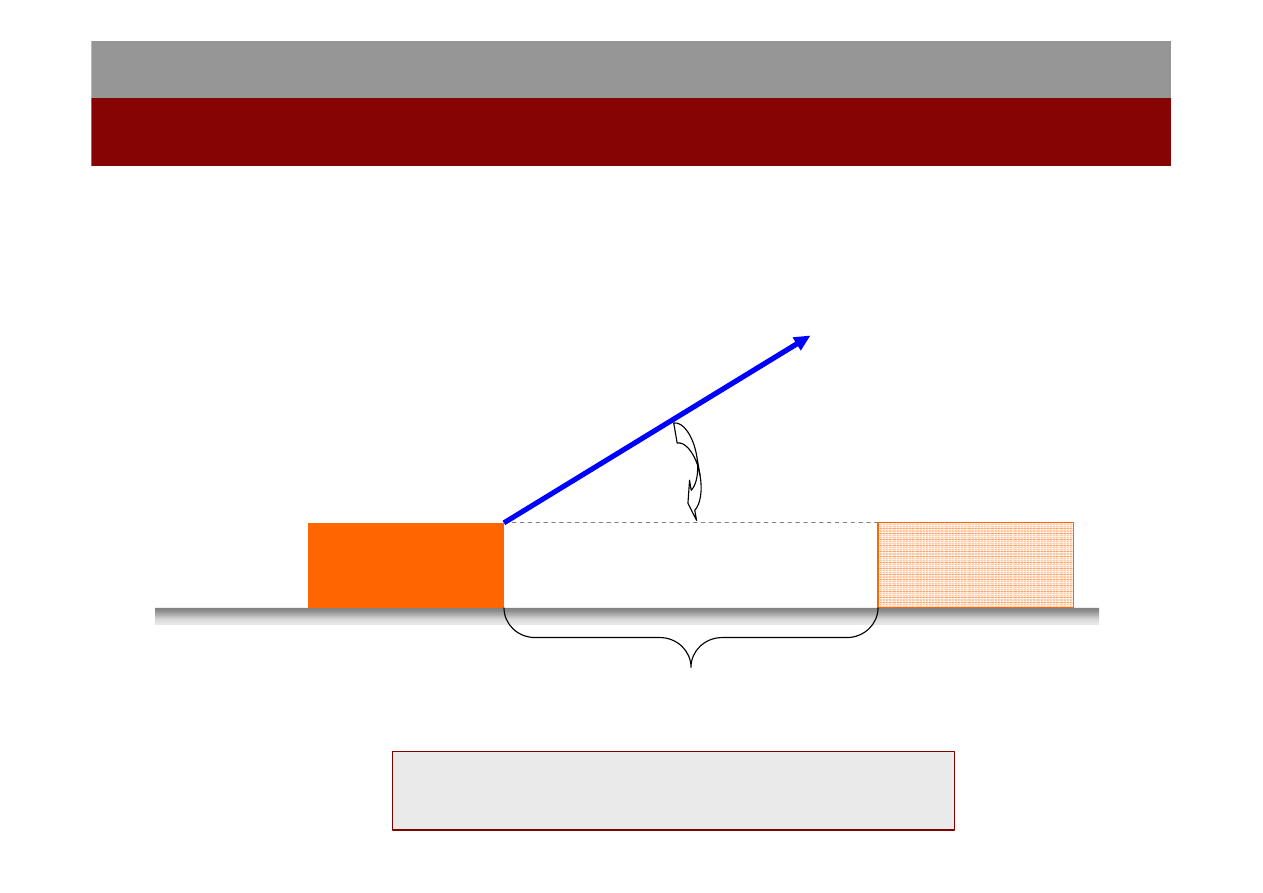
Praca W jest to energia przekazana ciału lub od niego odebrana na
drodze działania na ciało sił

ą

. Gdy energia jest przekazana ciału,

praca jest dodatnia, a gdy energia jest ciału odebrana, praca jest
ujemna.

F

r

α

r

∆

α

cos

r

F

r

F

W

∆

⋅

=

∆

=

r

o

r

8

Praca

ENERGIA KINETYCZNA I PRACA

5.XI.2011

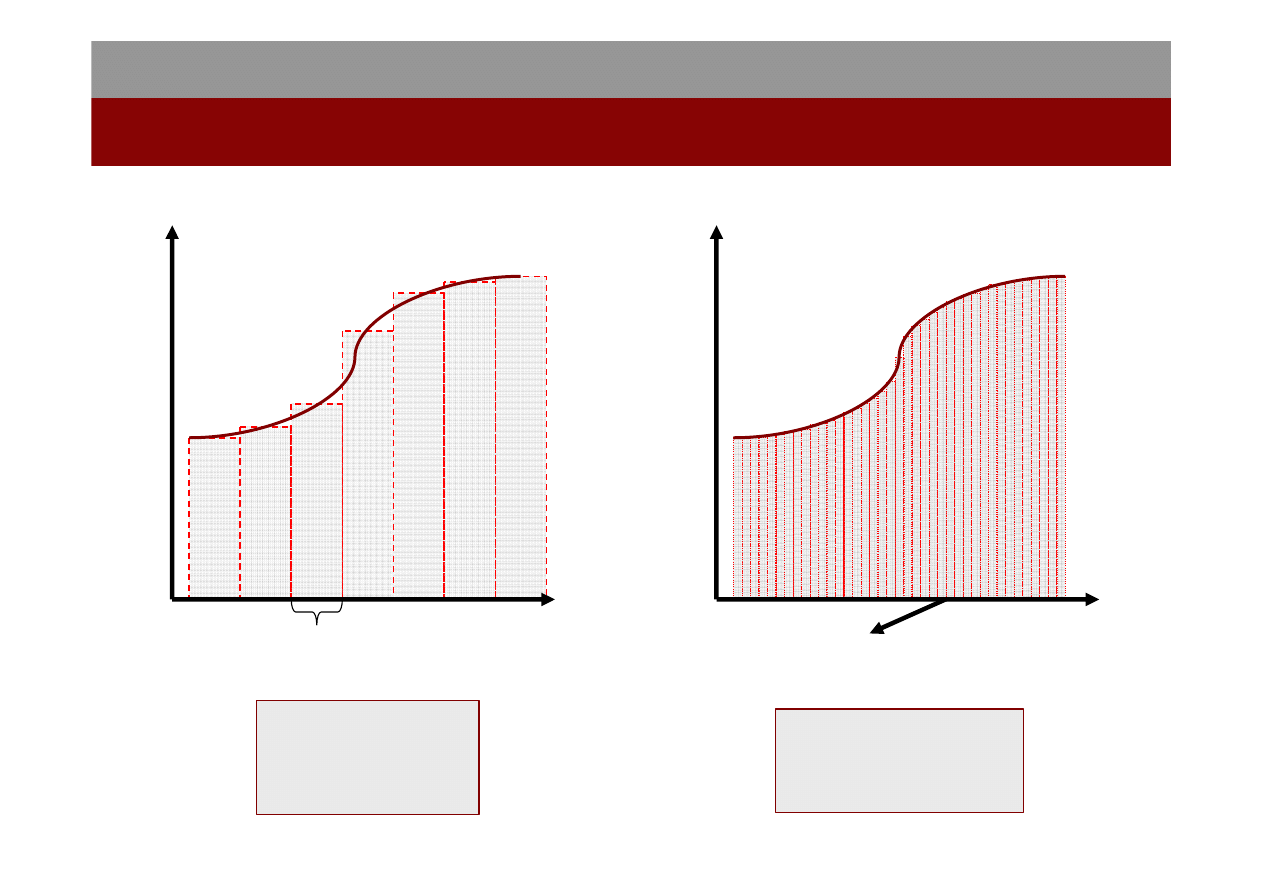
Jeśli siła jest funkcją położenia, tzn. F = F(r) to całkowite przemieszczenie
ciała rozkładamy na n odcinków, tak aby w każdym z nich siłę można
uważać za stałą. Wówczas praca całkowita wykonana przez siłę F(r) przy
przesunięciu ciała z punktu 1 do punktu 2, których położenia są dane przez
promienie wodzące r

1

i r

2

, wynosi:

( )

( )

( )

( )

∫

∑

∫

∑

⋅

=

⋅

=

∆

⋅

=

∆

⋅

=

→

=

→

∆

=

2

1

2

1

1

0

1

lim

)

2

1

(

r

r

n

i

r

r

i

i

r

i

n

i

i

r

d

r

F

W

r

d

r

F

r

r

F

r

r

F

W

i

r

r

r

r

r

r

r

r

r

r

r

9

Praca

∑

∆

⋅

=

n

r

F

W

r

r

ENERGIA KINETYCZNA I PRACA

5.XI.2011

F

r

r

r

r

r

F

r

r

∆

dr

∫

=

r

d

F

W

r

r

10

Praca

ENERGIA KINETYCZNA I PRACA

5.XI.2011

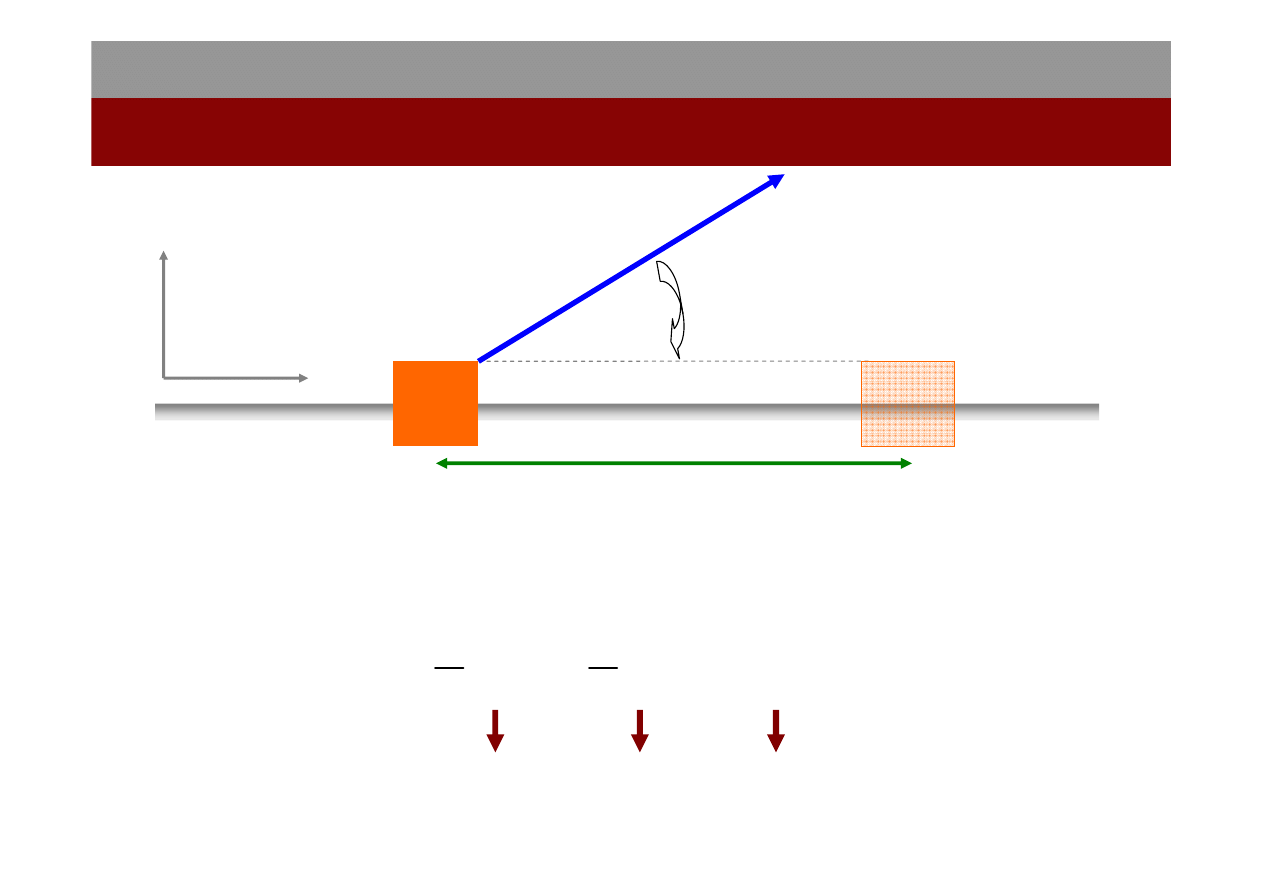
Jeśli , tzn. kąt między kierunkiem F i dr jest mniejszy od
90

o

, to wówczas W>0, czyli praca wykonana przez siłę F jest dodatnia.

Przykładem takiej sytuacji jest praca wykonana przez siły grawitacji
podczas swobodnego spadku ciała. Jeśli natomiast , tzn.
kąt między F i dr jest większy od 90

o

, to praca siły F jest ujemna.

Przykładem takich sił są siły oporu ruchu.

Jednostka pracy: dżul.

0

)

,

cos(

>

r

d

F

r

r

0

)

,

cos(

<

r

d

F

r

r

m

N

s

m

kg

J

1

1

1

1

1

2

2

⋅

=

⋅

=

11

Praca

ENERGIA KINETYCZNA I PRACA

5.XI.2011

Gdy na ciało działa wektor siły

k

F

j

F

i

F

F

z

y

x

ˆ

ˆ

ˆ

+

+

=

r

w wyniku której cząstka doznaje niewielkiego przesunięcia

k

dz

j

dy

i

dx

r

d

ˆ

ˆ

ˆ

+

+

=

r

praca wynosi

dz

F

dy

F

dx

F

r

d

F

W

z

y

x

+

+

=

⋅

=

r

r

Całkowita praca z punktu pocz do punktu kon

∫

∫

∫

∫

+

+

=

⋅

=

kon

pocz

kon

pocz

kon

pocz

kon

pocz

r

r

z

r

r

y

r

r

x

r

r

dz

F

dy

F

dx

F

r

d

F

W

r

r

12

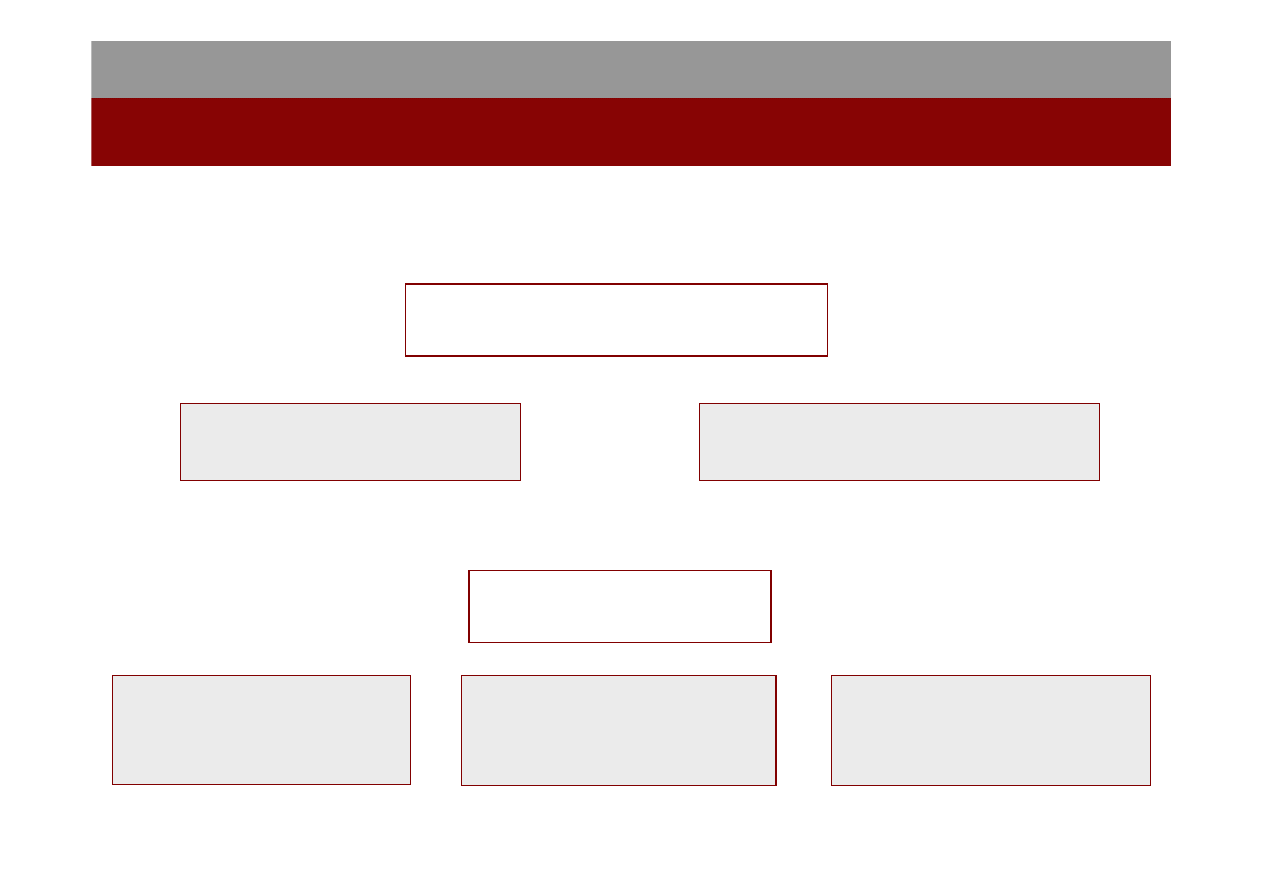
Praca a energia kinetyczna

ENERGIA KINETYCZNA I PRACA

5.XI.2011

d

ma

mv

mv

x

⋅

=

−

2

0

2

2

1

2

1

F

r

α

0

v

r

v

r

d

r

d

a

v

v

x

r

r

⋅

+

=

2

2

0

2

x

y

d

F

E

E

x

K

K

pocz

kon

⋅

=

−

13

Praca a energia kinetyczna

ENERGIA KINETYCZNA I PRACA

5.XI.2011

Ponieważ

więc

dt

v

r

d

r

r

=

( )

( )

∫

∫

⋅

=

⋅

=

2

1

2

1

t

t

r

r

dt

v

r

F

r

d

r

F

W

r

r

r

r

r

r

Jeśli założymy, że masa ciała jest stała, to wtedy

dt

v

d

m

a

m

F

r

r

r

=

⋅

=

2

2

2

2

1

2

2

2

2

1

2

1

v

m

v

m

v

m

v

d

v

m

W

v

v

v

v

−

=













=

⋅

=

∫

v

v

r

r

Gdzie v

1

i v

2

są prędkościami ciała odpowiednio w punkcie 1 i 2.

14

Praca a energia kinetyczna

ENERGIA KINETYCZNA I PRACA

5.XI.2011

Zmiana energii kinetycznej ciała jest równa pracy wykonanej nad tym
ciałem:

W

E

E

E

pocz

kon

K

K

K

=

−

=

∆

ZMIANA ENERGII

KINETYCZNEJ CZĄSTKI

CAŁKOWITA PRACA

WYKONANA NAD CZĄSTKĄ

=

Związek ten można zapisać inaczej

W

E

E

pocz

kon

K

K

+

=

ENERGIA

KINETYCZNEJ PO

WYKONANIU PRACY

=

ENERGIA

KINETYCZNEJ PRZED

WYKONANIEM PRACY

CAŁKOWITA PRACA

WYKONANA NAD

CZĄSTKĄ

+

15

Moc

ENERGIA KINETYCZNA I PRACA

5.XI.2011

Jeżeli w przedziale czasu ∆t została wykonana praca ∆W, to średnia
moc P jest określana

t

W

P

∆

∆

=

Mocą chwilową nazywamy granicę do jakiej zmierza moc średnia
gdy ∆t = 0

dt

dW

t

W

P

t

=

∆

∆

=

→

∆

0

lim

Moc chwilowa jest więc pochodną pracy względem czasu.

16

Moc

ENERGIA KINETYCZNA I PRACA

5.XI.2011

v

F

dt

dr

F

dt

dW

P

⋅

=

⋅

=

=

W zapisie wektorowym

v

F

P

r

r

⋅

=

Moc danej siły F jest proporcjonalna do prędkości v.

Jednostką mocy w układzie SI jest wat [W]. Moc jest równa
jednemu watowi, jeżeli stała siła wykonuje pracę jednego dżula w
czasie jednej sekundy.

s

J

J

1

1

1

=

17

Energia potencjalna

ENERGIA POTENCJALNA

5.XI.2011

W

E

p

−

=

∆

Definicja energii potencjalnej E

p

: jest to energia związana z

konfiguracją (czyli ustawieniem) układu ciał, działających na
siebie siłami. Gdy zmienia się konfiguracja tych ciał, może się
również zmieniać energia potencjalna układu.

Zmianę grawitacyjnej energii potencjalnej ∆E

p

definiujemy —

zarówno dla wznoszenia, jak i dla spadku ciała — jako pracę
wykonaną nad ciałem przez siłę ciężkości, wziętą z przeciwnym
znakiem. Oznaczając pracę — jak zwykle — symbolem W,
zapisujemy to stwierdzenie w postaci:

18

Siły zachowawcze i niezachowawcze

ENERGIA POTENCJALNA

5.XI.2011

W sytuacji, gdy zawsze spełniony jest związek W

1

= — W

2

,

energia kinetyczna zamieniana jest na energię potencjalną, a siłę
nazywamy siłą zachowawczą. Siła ciężkości i siła sprężystości są
siłami zachowawczymi (gdyby tak nie było. nie moglibyśmy mówić
o grawitacyjnej energii potencjalnej i energii potencjalnej
sprężystości).

Siłę, która nie jest zachowawcza, nazywamy siłą niezachowawczą.
Siła tarcia kinetycznego i siła oporu są niezachowawcze.

19

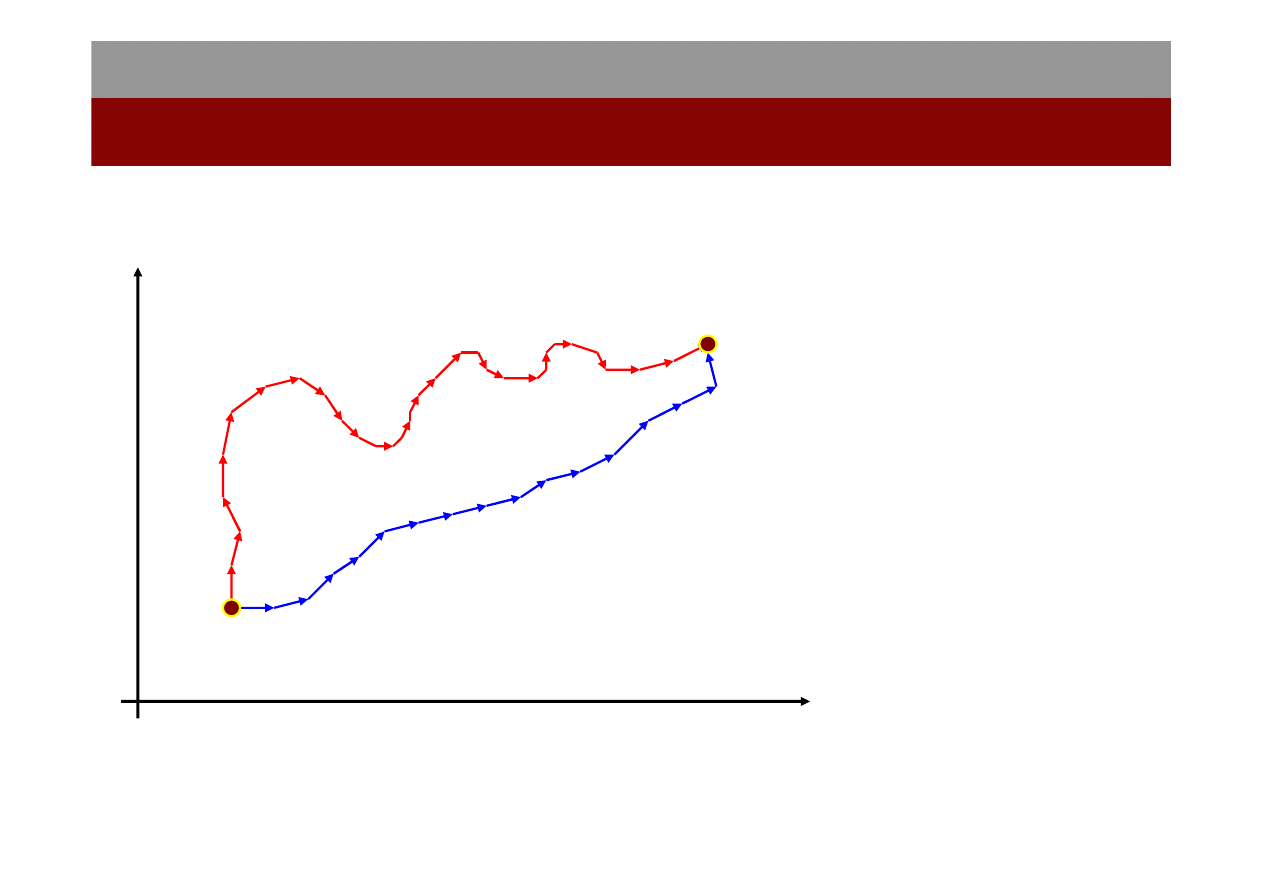
Siły zachowawcze i niezachowawcze

5.XI.2011

Ile wynosi praca przesunięcia masy m pod działaniem siły F(x,y) z punktu 1 do
2 po drodze A oraz B?

B

A

2

1

Jeśli praca przemieszczenia
masy m między punktami A i B
nie zależy od drogi po której
nastąpiło przemieszczenie to
mówimy, że siła jest
zachowawcza, albo potencjalna.

Praca przemieszczenia masy m z punktu A po drodze 1 do punktu B i potem z
punktu B po drodze 2 do punktu A wynosi zero.

20

Energia potencjalna

ENERGIA POTENCJALNA

5.XI.2011

Jeżeli praca przemieszczenia masy m po drodze (krzywej) zamkniętej wynosi
zero to mówimy, że siła jest zachowawcza, albo potencjalna.

Możemy zapisać pracę siły F(x,y) na drodze elementarnego przemieszczenia dr
jako:

dW = F

o

dr

Ponieważ praca siły F(x,y) nie zależy od drogi, a tylko od punktu startu i końca
przemieszczenia to można określić funkcję skalarną, zależną tylko od
współrzędnych (x,y). Nazywamy ją energią potencjalną i określamy jej
nieskończenie mały przyrost:

dU = - F

o

dr

Minus został wybrany ze względu na to, że ubytek energii potencjalnej jest
równy wykonanej elementarnej pracy.

21

Gradient energii potencjalnej

ENERGIA POTENCJALNA

5.XI.2011

Przyrost funkcji U(x,y) można wyrazić jako sumę przyrostów funkcji względem
obydwu zmiennych niezależnych x i y jako:

dy

y

U

dx

x

U

dU

∂

∂

+

∂

∂

=

Pochodne U względem x i y nazywają się pochodnymi cząstkowymi i liczymy
je tak, jakby druga zmienna była stałą przy liczeniu pochodnej cząstkowej po
pierwszej zmiennej.

Z drugiej strony:

Grupując wyrazy z odpowiednimi przyrostami dx i dy otrzymamy:

(

)

dy

y

U

dx

x

U

dy

F

dx

F

r

d

F

dU

y

x

∂

∂

+

∂

∂

=

⋅

+

⋅

−

=

−

=

r

o

r

0

dy

y

U

F

dx

x

U

F

y

x

=













∂

∂

+

+













∂

∂

+

22

Gradient energii potencjalnej

ENERGIA POTENCJALNA

5.XI.2011

W przestrzeni trójwymiarowej równanie to obowiązuje dla dowolnych przyrostów
dx, dy i dz stąd muszą znikać tożsamościowo wyrażenia w nawiasach:

Siła równa jest ujemnemu gradientowi energii potencjalnej:

z

∂

∂

−

=

∂

∂

−

=

∂

∂

−

=

U

F

y

U

F

x

U

F

z

y

x













∂

∂

+

∂

∂

+

∂

∂

−

=













∂

∂

∂

∂

∂

∂

−

=

∇

=

k

z

E

j

y

E

i

x

E

z

E

;

y

E

;

x

E

E

-

F

p

p

p

p

p

p

p

)

)

)

∫

−

=

kon

pocz

r

r

r

d

F

r

r

p

E

Stąd:

Grawitacyjna energia potencjalna

Energia potencjalna sprężystości

mgy

(y)

E

p

=

2

p

kx

2

1

(x)

E

=

23

Zasada zachowania energii mechanicznej

Z.Z.E.

5.XI.2011

Energia mechaniczna E

mech

układu jest sumą jego energii potencjalnej E

p

oraz

energii kinetycznej E

k

wszystkich jego składników:

Gdy siła zachowawcza wykonuje pracę W w układzie izolowanym nad jednym
z ciał układu, zachodzi zamiana energii kinetycznej E

k

ciała w energię

potencjalną E

p

układu. Zmiana energii kinetycznej ∆E

k

jest równa:

Z drugiej strony wiadomo, że zmiana energii potencjalnej wynosi:

Stąd otrzymujemy, że

k

p

mech

E

E

E

+

=

W

∆

E

k

=

W

∆

E

p

−

=

p

k

∆

E

∆

E

−

=

24

Zasada zachowania energii mechanicznej

Z.Z.E.

5.XI.2011

przy czym wskaźniki 1 i 2 odnoszą się do dwóch różnych chwil, a zatem dwóch
różnych konfiguracji składników układu.
Przekształcając otrzymujemy zasadę zachowania energii mechanicznej:

p2

p1

k1

k2

p

k

E

E

E

E

∆

E

∆

E

−

=

−

−

=

p2

k2

p1

k1

E

E

E

E

+

=

+

SUMA E

k

i E

p

DLA

DOWOLNEGO STANU UKŁADU

SUMA E

k

i E

p

DLA

KAśDEGO INNEGO STANU UKŁADU

=

W układzie izolowanym, w którym zamiana energii pochodzi jedynie od sił
zachowawczych energia kinetyczna i energia potencjalna mogą się zmieniać, lecz
ich suma czyli energia mechaniczna E

mech

nie może ulegać zmianie.

25

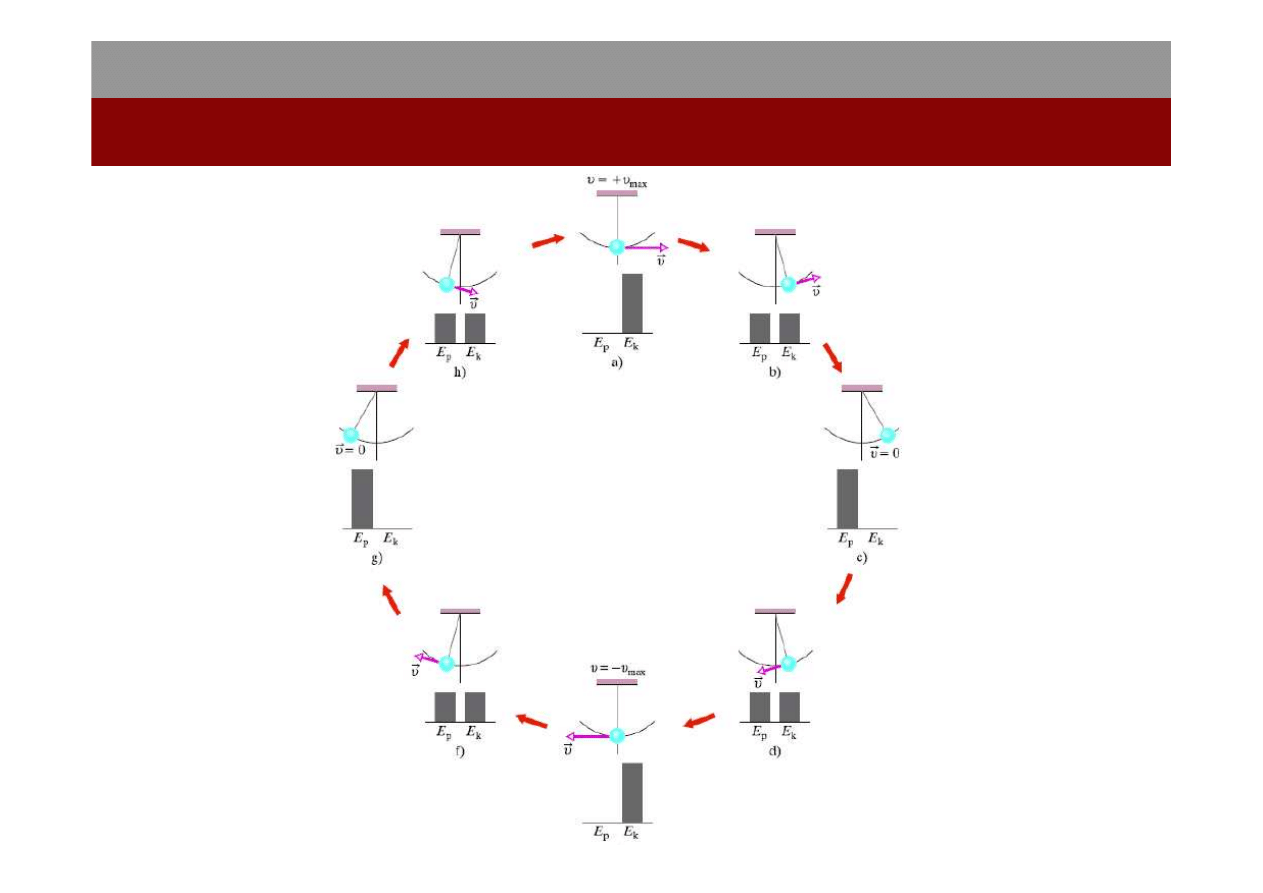
Zasada zachowania energii mechanicznej

Z.Z.E.

5.XI.2011

26

Zasada zachowania energii

Z.Z.E.

5.XI.2011

• Zmiana całkowitej energii E układu jest równa energii dostarczonej do układu
lub od niego odebranej.

przy czyni ∆E

mech

jest dowolną zmianą energii mechanicznej układu. ∆E

term

—

dowolną zmianą jego energii termicznej, a ∆E

wewn

— dowolną zmianą innych

postaci jego energii wewnętrznej. Zmiana energii mechanicznej ∆E

mech

zawiera

w sobie zmianę energii kinetycznej ∆E

k

oraz zmianę energii potencjalnej ∆E

p

układu (sprężystości, grawitacyjnej lub jakiejkolwiek innej).

• Całkowita energia E układu izolowanego nie może się zmieniać.

wewn

term

mech

∆

E

∆

E

∆

E

∆

E

W

+

+

=

=

0

∆

E

∆

E

∆

E

wewn

term

mech

=

+

+