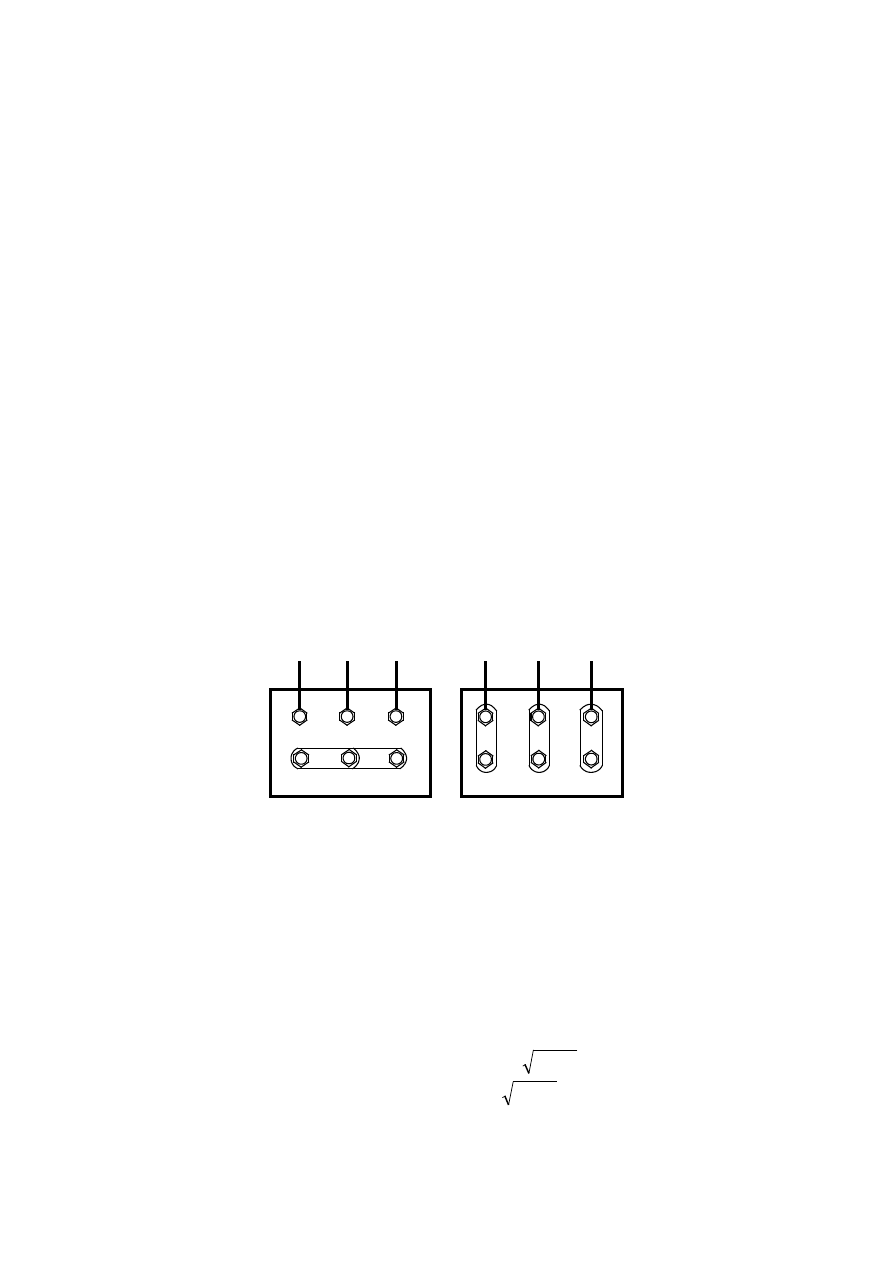
SI-1

Wydział Inżynierii Elektrycznej i Komputerowej
Katedra Maszyn Elektrycznych
Laboratorium Maszyn Elektrycznych

Ćwiczenie SI - Silniki indukcyjne

Badania wstępne
Do badań wstępnych zalicza się:

•

rozeznanie budowy i rodzaju uzwojeń badanego silnika,

•

badanie stanu izolacji za pomocą megaomomierza,

•

badanie ciągłości uzwojeń,

•

identyfikację zacisków tabliczki zaciskowej,

•

zaznajomienie się z danymi znamionowymi silnika.

Pomiar rezystancji izolacji
Przed przystąpieniem do pomiaru należy za pomocą omomierza dobrać parami zaciski
odpowiadające poszczególnym fazom oraz określić ewentualne przerwy w uzwojeniach.
Następnie megaomomierzem induktorowym o napięciu stałym przeprowadzić kolejno pomiar
rezystancji między poszczególnymi uzwojeniami oraz między uzwojeniami a korpusem.
Pozostałe uzwojenia powinny być w czasie pomiarów zwarte z masą. Rezystancja izolacji nie
może być mniejsza niż 1k

Ω

na 1V napięcia znamionowego. Odczytu dokonuje się po 15 i 60

sekundach od chwili przyłożenia napięcia. Iloraz R

60

/R

15

świadczy o stopniu zawilgocenia

uzwojeń. Dla suchej maszyny powinien być on większy od 1,5.

Identyfikacja zacisków na tabliczce zaciskowej
Trójfazowe uzwojenie stojana jest zwykle wyprowadzone na tabliczkę z sześcioma zaciskami,
umożliwiającą połączenie uzwojeń w gwiazdę lub trójkąt za pomocą blaszek zwierających.

Y

∆

1

U

2

U

1

V

2

V

1

W

2

W

2

W

2

U

2

V

1

U

1

V

1

W

1

L

1

L

2

L

2

L

3

L

3

L

Silnik indukcyjny pierścieniowy
1. Dane znamionowe badanego silnika

N

P = 3kW,

N

U = 220/380V (

∆/

Υ

),

N

I = 11.4/6.6A,

N

ϕ

cos

= 0.81,

N

n = 1420/min.

2. Pomiary rezystancji uzwojeń
Pomiaru rezystancji fazowych uzwojeń stojana

s

R i wirnika

r

R

przeprowadza się metodą

techniczną przy zasilaniu prądem stałym lub mostkiem technicznym. Należy zwrócić uwagę,
aby rezystancja uzwojonego wirnika była mierzona bezpośrednio na pierścieniach
ś

lizgowych.

W zależności od oczekiwanej wartości rezystancji pomiar wykonujemy:

•

metodą techniczną z łącznią napięciową, gdy

V

A

R

R

R

>

•

metodą techniczną z łącznią prądową, gdy

V

A

R

R

R

<

R

A

, R

V

– rezystancja wewnętrzna amperomierza i woltomierza.

W obu przypadkach prąd pomiarowy nie może przekroczyć 0,2I

N

, by nie nagrzać uzwojeń.

SI-2

•

mostkiem Wheatstone’a, gdy

Ω

>

1

R

•

mostkiem Thomsona, gdy

Ω

<

1

R

Zmierzoną w temperaturze

0

t wartość rezystancji

0

R przelicza się na temperaturę

t (75

0

C dla

izolacji uzwojeń klasy A, B, E lub 115

0

C dla uzwojeń z izolacją klasy F i H) według

zależności obowiązującej dla uzwojeń miedzianych:

0

0

235

235

t

t

R

R

t

+

+

=

.

Tu: zmierzona wartość rezystancji fazy uzwojenia stojana -

s

R =1.12

Ω

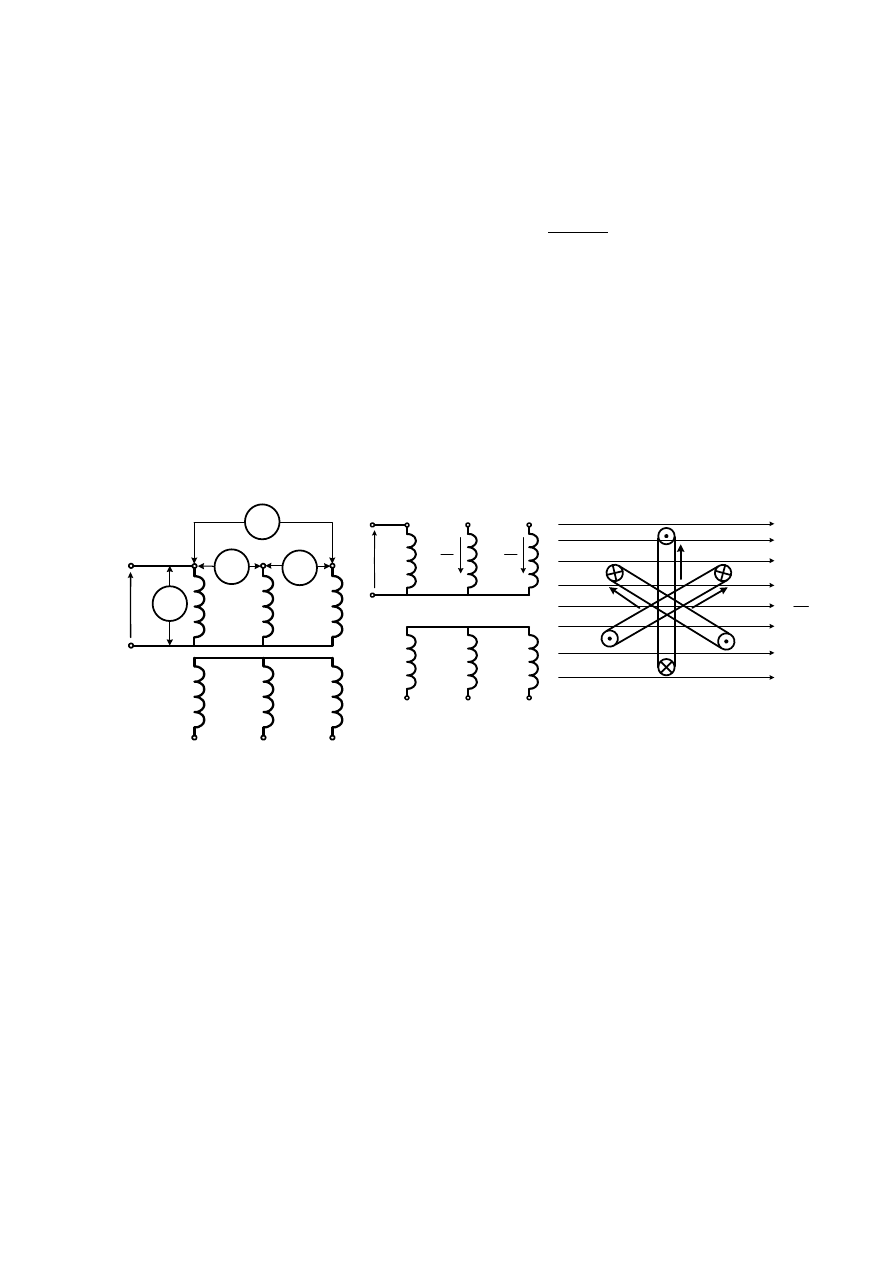
3. Wyznaczania początków i końców uzwojeń metodą woltomierzową
Uzwojenie wirnika jest na stałe połączone w gwiazdę i podczas pomiaru pozostaje rozwarte.
Łączymy ze sobą po jednym zacisku każdej fazy uzwojenia stojana i jedną z faz zasilamy
obniżonym napięciem przemiennym

1

U

(rysunek poniżej). Jeżeli każde z napięć

2

U

pomiędzy wolnym końcem fazy zasilanej i nie zasilanej będzie większe ok. 1,5 razy od
napięcia

1

U

, a wartość napięcia pomiędzy wolnymi końcami faz nie zasilanych

3

U wyniesie

0, to zwarte zostały zaciski jednoimienne faz (wszystkie początki lub końce faz uzwojenia).
W innym przypadku zostały zwarte zaciski różnoimienne.

V

V

V

V

1

U

2

U

2

U

3

U

2

U

2

U

U

1

U

1

V

1

W

2

U

2

V

2

W

1

U

1

V

1

W

2

U

2

V

2

W

2

/

U

2

/

U

U

2

Φ











Φ





















Uzasadnienie metody pomiaru: Wytworzony przez zasilaną fazę zmienny strumień magne-
tyczny tylko w części równej

Φ

=

Φ

5

,

0

120

cos

0

sprzęga się z innymi fazami stojana, co

wynika z wzajemnego geometrycznego przesunięcia osi faz. Zgodnie z regułą Lenza napięcia
indukowane w nie zasilanych fazach mają przeciwny zwrot, niż w fazie zasilanej.
Metoda nie nadaje się do silnika klatkowego, gdyż wytworzone wtedy w zwartym uzwojeniu
wirnika prądy i strumienie zniekształca wartości napięć w fazach stojana.

4. Pomiar przekładni napięciowej silnika pierścieniowego
Pomiar przeprowadzamy przy połączeniu uzwojeń stojana i wirnika w gwiazdę i przy
rozwartym obwodzie nie zahamowanego wirnika. Dowolne dwie fazy stojana zasilamy z
regulatora indukcyjnego napięciem

s

U i kręcimy wałem wirnika, znajdując położenie, przy

którym woltomierz wpięty między dwie fazy wirnika pokaże największe napięcie

0

r

U (wtedy

osie faz uzwojeń pokryją się). Następnie, przy rozwartym uzwojeniu stojana, zasilamy te fazy
wirnika, napięciem

r

U

o wartości zbliżonej do

0

r

U (zmierzonej uprzednio) i obracając wirnik

wyznaczamy największą wartość napięcia

0

s

U - indukowanego między dwiema fazami

uzwojenia stojana. Mierzymy napięcia międzyfazowe, lecz ich stosunek jest taki sam jak
napięć fazowych, które z definicji wyznaczają przekładnię napięciową (ten sam układ

SI-3

połączeń obu uzwojeń). Wartość przekładni napięciowej (która odnosi się do relacji napięć
fazowych) wyznaczamy jako średnią arytmetyczną napięć przy zasilaniu stojana i wirnika ze
wzoru:

(

)













+

=

+

=

0

0

0

2

1

2

1

2

1

r

s

r

s

U

U

U

U

U

K

K

K

Uzasadnienie metody pomiaru, przy prowadzeniu analizy dla układu „faza stojana – faza
wirnika” na podstawie poniższych schematów zastępczych:

- dla

1

K

s

I

s

jX

σ

s

U

s

R

0

r

U

r

R

r

jX

σ

s

E

r

E

0

r

r

U

E

=

- dla

2

K

0

s

U

r

I

s

jX

σ

s

R

0

r

U

r

R

r

jX

σ

0

s

E

0

r

E

0

0

s

s

U

E

=

Rzeczywista przekładnia napięciowa K jest równa stosunkowi fazowych sił elektro-

motorycznych:

0

0

r

s

r

s

E

E

E

E

K

=

=

. W obu przypadkach pomiaru wyznaczamy przekładnię jako

stosunek napięcia fazy zasilanej do siły elektromotorycznej indukowanej w niezasilanej fazie
Napięcie zasilania jest wyższe niż siła elektromotoryczna w tej fazie o spadek napięcia na
rezystancji i reaktancji rozproszenia fazy.
W przypadku zasilania stojana:

0

)

(

)

(

)

(

r

s

s

s

r

s

s

s

s

s

s

s

s

U

K

I

jX

R

E

K

I

jX

R

E

I

jX

R

U

+

+

=

+

+

=

+

+

=

σ

σ

σ

W przypadku zasilania wirnika:

0

0

0

0

1

)

(

1

)

(

)

(

s

r

r

r

s

r

r

r

r

r

r

r

r

U

K

I

jX

R

E

K

I

jX

R

E

I

jX

R

U

+

+

=

+

+

=

+

+

=

σ

σ

σ

Dalej zakładamy równość względnych spadków napięcia na impedancjach gałęzi podłużnych,
(odniesionych do wartości sił elektromotorycznych):

δ

σ

σ

=

+

=

+

0

)

(

)

(

r

r

s

s

s

s

s

s

E

I

jX

R

E

I

jX

R

Stąd:

0

)

1

(

r

r

s

s

U

K

E

K

E

U

+

=

+

=

δ

δ

oraz

0

0

0

0

0

0

)

1

(

1

1

1

s

s

s

r

r

r

U

K

E

K

E

K

E

E

U

+

=

+

=

+

=

δ

δ

δ

i dalej

1

0

0

+

=

δ

r

s

U

K

U

Zatem zmierzona średnia wartość przekładni wyniesie:

)

)

1

(

2

1

(

)

1

(

2

1

)

1

(

2

1

1

)

1

(

2

1

)

1

(

2

2

2

0

0

0

0

0

+

+

=

+

+

+

=

+

+

+

=

+

+

+

=

+

=

δ

δ

δ

δ

δ

δ

δ

δ

K

K

K

U

U

K

U

K

U

U

U

K

r

r

r

r

s

s

U

Jeśli uwzględnić, że

1

<<

δ

można przyjąć tak wyznaczoną wartość przekładni napięciowej

za prawidłową -

K

K

U

=

(dla pojedynczego pomiaru przekładnia wyniesie:

)

1

(

δ

+

=

K

K

U

).

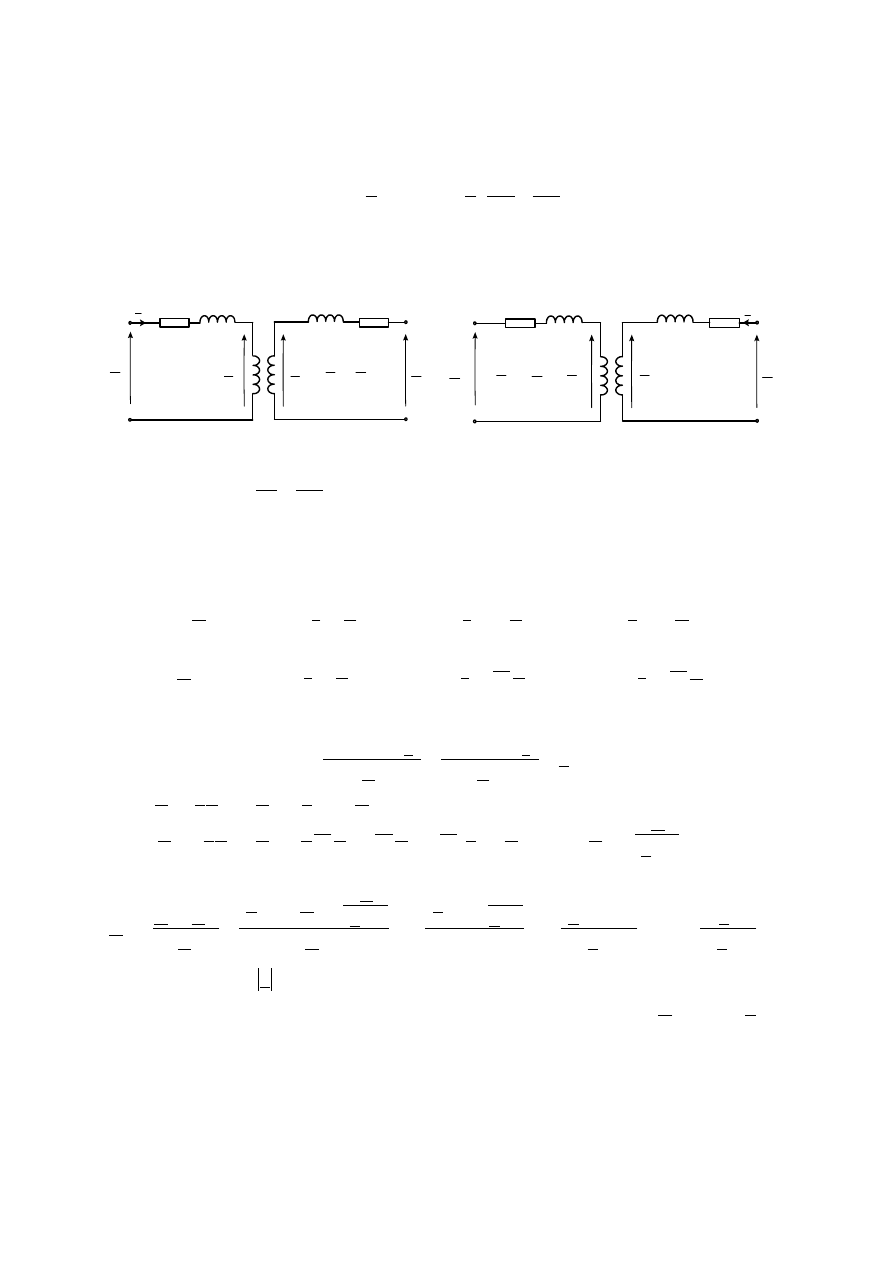
5. Pomiary biegu jałowego
Łączymy układ według poniższego schematu, przy zamkniętym wyłączniku W (zwarte
pierścienie ślizgowe). Wykonujemy rozruch napięciowy nieobciążonego silnika. Uzwojenie
wirnika jest zwarte na pierścieniach, a silnik nie jest obciążony momentem zewnętrznym,
Wirnik obraca się z prędkością bliską synchronicznej -

0

≈

s

, wytwarzając moment

równoważący moment strat mechanicznych.

SI-4

V

W

W

A

Regulator indukcyjny

Stojan

Wirnik

W

L1

L2

L3

s

U

1

P

2

P

∗

∗

∗

∗

Schemat układu pomiarowego do badania biegu jałowego i zwarcia silnika

Pomiary przeprowadzamy obniżając napięcie stojana od

sN

U

05

,

1

do wartości, przy której

zacznie wyraźnie maleć prędkość obrotowa (ok.

sN

U

3

,

0

). W stanie pracy jałowej

współczynnik mocy silnika jest niewielki (

0

60

>

ϕ

), stąd jeden z watomierzy w układzie

Arona wychyla się w stronę przeciwną.

Przed pomiarem należy zatem przełączyć jego

cewkę prądową i przy sumowaniu mocy uwzględnić ujemny znak mocy wskazywanej przez
watomierz.
Wyniki pomiarów zapisujemy w tabeli:

s

U

[V]

0

s

I

[A]

1

P

[W]

2

P

[W]

2

1

0

P

P

P

+

=

[W]

0

ϕ

cos

Wyniki pomiarów są podstawą do wykreślenia charakterystyk biegu jałowego

)

(

cos

,

,

s

s

U

f

P

I

=

0

0

0

ϕ

, gdzie:

0

0

0

3

s

s

I

U

P

=

ϕ

cos

.

0

P

0

s

I

0

cos

ϕ

sN

U

0

s

U

0

P

0

s

I

0

cos

ϕ

Charakterystyki biegu jałowego.

6. Pomiary stanu zwarcia
Łączymy układ według schematu jak w punkcie5, przy zamkniętym wyłączniku W i
zahamowanym wirniku (blokada mechaniczna wału) -

1

=

s

. Przed pomiarem nagrzewamy

silnik prądem znamionowym, a w celu utrzymania ustalonej temperatury uzwojeń
rozpoczynamy pomiary od zasilenia stojana napięciem, przy którym zwarciowy prąd stojana
jest równy

sN

sk

I

I

1

,

1

=

. Następnie dokonujemy odczytów, przy napięciu zasilania

zmniejszanym do ok.

N

U

3

,

0

.

Wyniki pomiarów zapisujemy w tabeli:

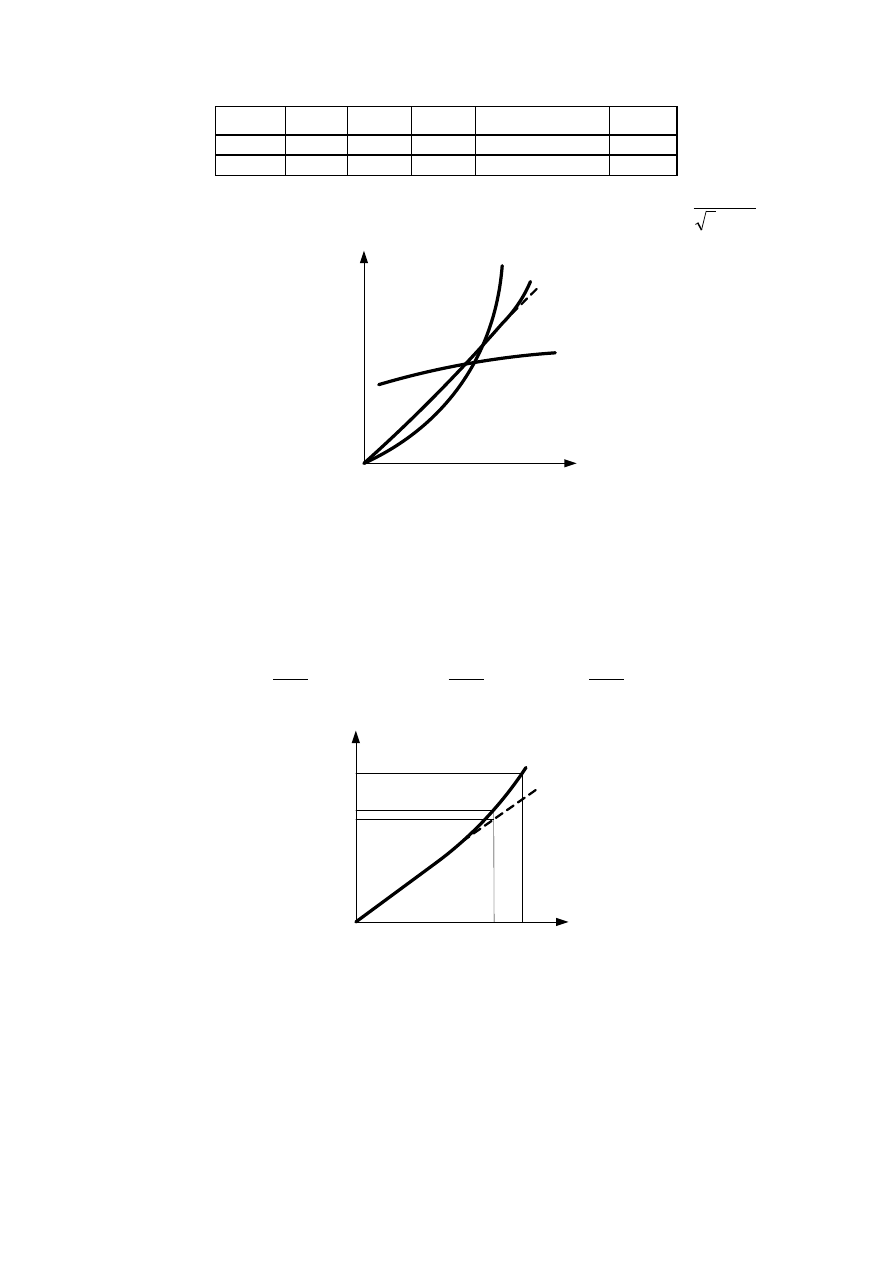
SI-5

s

U

[V]

sk

I

[A]

1

P

[W]

2

P

[W]

2

1

P

P

P

k

+

=

[W]

k

ϕ

cos

Należy wykreślić charakterystyki zwarcia

)

(

cos

,

,

s

k

k

sk

U

f

P

I

=

ϕ

, gdzie:

sk

s

k

k

I

U

P

3

=

ϕ

cos

.

k

P

k

ϕ

cos

sk

U

sk

I

k

ϕ

cos

sk

I

k

P

Charakterystyki zwarcia

Następnie wyznacza się wartości prądu stojana

skN

I

oraz mocy zwarciowej

kN

P dla napięcia

znamionowego stojana -

sN

s

U

U

=

, korzystając z poniższych uwag. Prąd zwarcia rośnie

początkowo liniowo z napięciem, a w miarę nasycania się obwodu magnetycznego strumieni
rozproszenia reaktancje

s

X

σ

i

r

X

σ

′

maleją, co pociąga za sobą szybszy wzrost prądu. Z tego

powodu rośnie współczynnik mocy silnika w stanie zwarcia

k

ϕ

cos

. Wartości

skN

I

i

kN

P

przybliżają poniższe wzory:

5

.

1

0

1

0

)

(













⋅

−

+

⋅

≅

skN

sN

k

k

sN

skN

k

skN

U

U

I

I

U

U

I

I

,

k

skN

sN

kN

P

U

U

P

⋅













=

2

s

U

sk

I

0

k

I

1

k

I

skN

U

sN

U

skN

I

Charakterystyka

)

(

s

sk

U

f

I

=

7. Pomiary przy obciążeniu
W ćwiczeniu wykonuje się rozruch oporowy silnika indukcyjnego za pomocą zwieranego
rozrusznika, przy połączeniu uzwojenia stojana w trójkąt i zasileniu stojana napięciem
znamionowym

sN

U

. Następnie poprzez zmianę prądu wzbudzenia sprzężonej z badanym

silnikiem prądnicy obcowzbudnej prądu stałego zmienia się obciążenie i odczytuje: moc
pobraną z sieci P , prąd przewodowy stojana

s

I , moment obciążenia T , obroty silnika

n

,

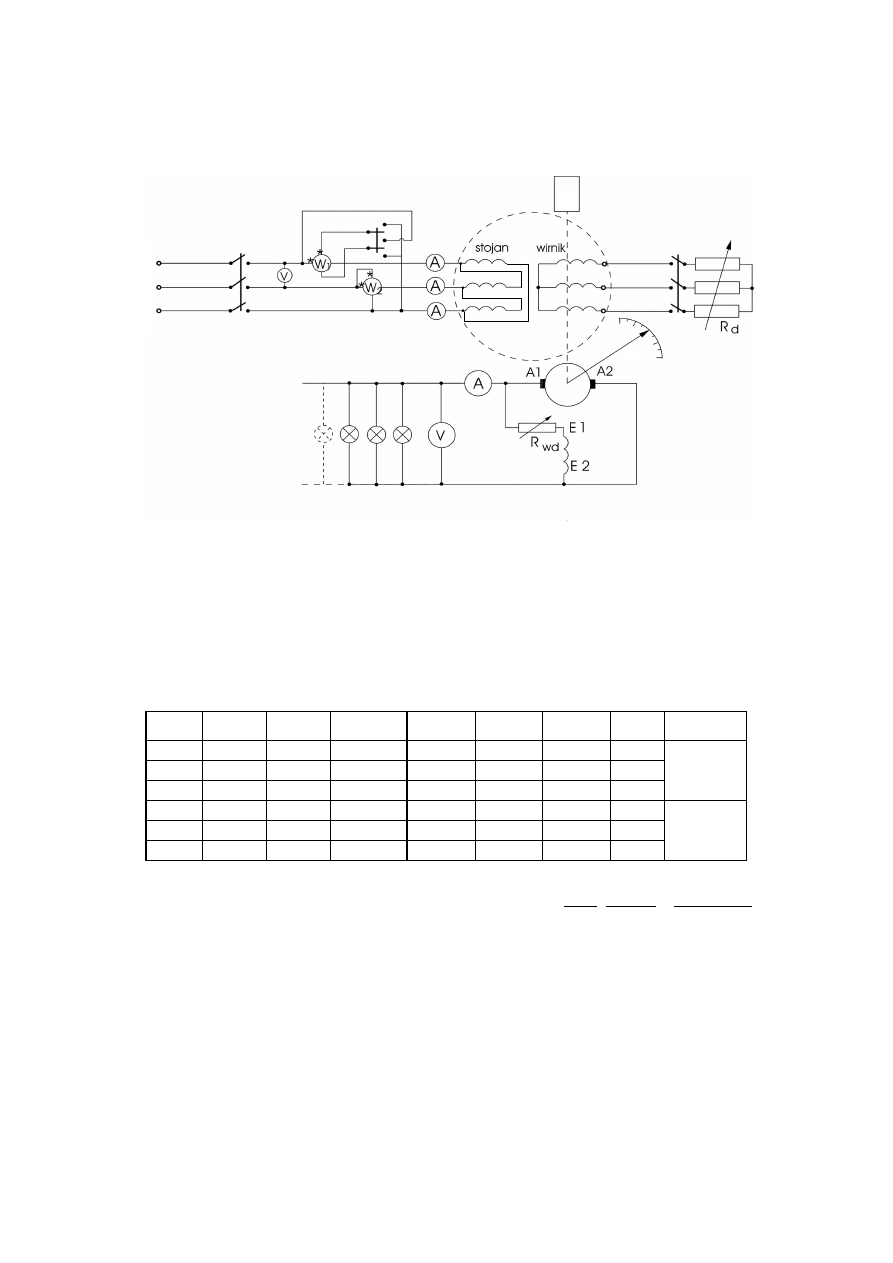
SI-6

napięcie

L

U

i prąd obciążenia prądnicy grzałkami -

L

I

. Moment rozwijany przez silnik jest

proporcjonalny do nacisku na wagę elektroniczną łap ruchomego stojana prądnicy.

n

T

U

V

W

Schemat układu pomiarowego do badania silnika indukcyjnego pierścieniowego

Pomiar wykonujemy dla dwóch przypadków: przy zwartych pierścieniach wirnika i przy
dołączonych do wirnika dodatkowych rezystancjach o wartości fazowej -

d

R , w zakresie

prądu stojana od prądu biegu jałowego do wartości

sN

I

2

1.

. Aby uniknąć obliczeń związanych

z przeliczaniem wyników na temperaturę pracy, pomiary należy wykonać na maszynie
nagrzanej.
Wyniki pomiarów zapisujemy w tabeli:

s

I

[A]

1

P

[W]

2

P

[W]

n

[min

-1

]

T

[Nm]

L

U

[V]

L

I

[A]

η

0

=

d

R

[

Ω

/fazę]

=

d

R

0.58

[

Ω

/fazę]

Sprawność wyznaczona metodą bezpośrednią jest równa:

2

1

2

1

105

0

30

P

P

n

T

P

P

T

n

+

⋅

⋅

=

+

⋅

⋅

=

,

π

η

Na podstawie pomiarów należy wykreślić charakterystyki mechaniczne i zewnętrzne

)

(

,

n

f

I

T

s

=

dla

0

=

d

R

i

0

≠

d

R

.

Opracowanie sprawozdania:
W sprawozdaniu powinny być zawarte:

-

dane znamionowe badanego silnika,

-

opis kolejnych pomiarów, schematy układów pomiarowych,

-

wyniki pomiarów w postaci tabel i wykresów,

-

obliczenia parametrów schematu zastępczego silnika i narysowanie schematu
zastępczego,

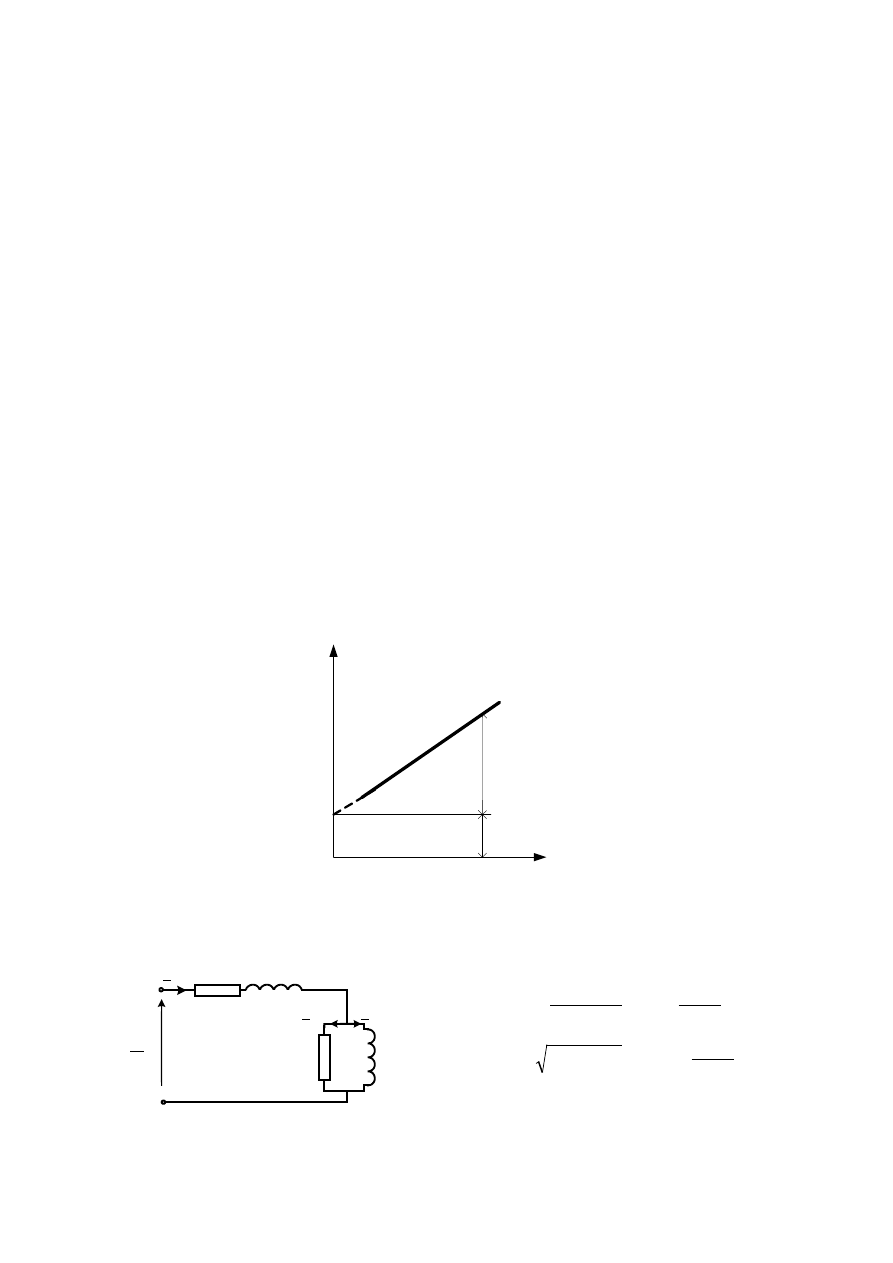
SI-7

-

wyznaczone straty poszczególne mocy, niezbędne do wyznaczenia sprawności metodą
strat poszczególnych i obliczenie sprawności znamionowej,

-

obliczenia teoretyczne charakterystyki momentu w funkcji obrotów, porównane we
wspólnym zakresie poślizgów z wynikami pomiarów,

-

wnioski

Pomocne procedury, schematy i wzory:

Wyznaczanie parametrów fazowego schematu zastępczego

•

Obliczenia w stanie jałowym:

Moc czynna

0

P (zmierzona jako suma algebraiczna wskazań watomierzy w układzie Arona -

2

1

0

P

P

P

+

=

) pobierana w czasie biegu jałowego jest sumą strat mocy w żelazie stojana

Fe

P

∆

,

strat mechanicznych

m

P

∆

i niewielkich strat w uzwojeniu stojana

ws

P

∆

:

ws

m

Fe

P

P

P

P

∆

+

∆

+

∆

=

0

, gdzie:

2

0

0

3

sph

s

ws

I

R

P

=

∆

.

Rozdział strat w rdzeniu

Fe

P

∆

i strat mechanicznych

m

P

∆

, przy biegu jałowym silnika

przeprowadza się metodą graficzną dla znamionowego napięcia zasilania stojana. Ponieważ w
trakcie pomiaru biegu jałowego obroty silnika są praktycznie stałe, straty mechaniczne też
mają stałą wartość i nie zależą od zmiany napięcia zasilania. Straty w rdzeniu, głównie
stojana (z racji niewielkiej wartości poślizgu), zależą od kwadratu napięcia zasilania.
Rysując zależność zmian sumy obu strat względem kwadratu napięcia:

( )

2

0

0

0

0

U

f

P

P

P

P

P

m

Fe

ws

=

∆

+

∆

=

∆

−

=

∆

otrzymuje się w przybliżeniu linię prostą.
Punkt przecięcia tej prostej z osią rzędnych wyznacza wartość strat mechanicznych silnika

m

P

∆

. Straty mechaniczne zwykle przyjmuje się jako równe (0,6

÷

1,5)%

N

P

2

s

U

m

Fe

P

P

P

∆

+

∆

=

∆

0

m

P

∆

Fe

P

∆

sN

U

Wyznaczenie

Fe

P

∆

i

m

P

∆

Parametry gałęzi poprzecznej schematu zastępczego wyznaczamy ze wzorów:

0

sph

I

s

R

s

jX

σ

sph

U

Fe

R

m

jX

Fe

I

m

I

Fe

sphN

Fe

P

U

R

∆

=

2

)

(

3

;

Fe

sphN

Fe

R

U

I

=

;

2

2

0

Fe

sph

m

I

I

I

−

=

;

m

sphN

m

I

U

X

=

SI-8

Znajomość przekładni napięciowej K i napięcia fazowego

0

rph

U

indukowanego w uzwojeniu

wirnika w stanie pracy transformatorowej, przy zasilaniu stojana napięciem znamionowym

sphN

U

, umożliwia dokładniejsze wyznaczenie parametrów gałęzi poprzecznej schematu.

Wtedy na wyniki nie ma wpływu spadek napięcia na rezystancji i reaktancji rozproszenia
uzwojenia stojana.

(

)

Fe

rph

Fe

P

K

U

R

∆

⋅

=

2

0

3

,

Fe

rph

Fe

R

K

U

I

⋅

=

0

,

2

2

0

Fe

sph

m

I

I

I

−

=

,

m

rph

m

I

K

U

X

⋅

=

0

.

•

Obliczenia w stanie zwarcia

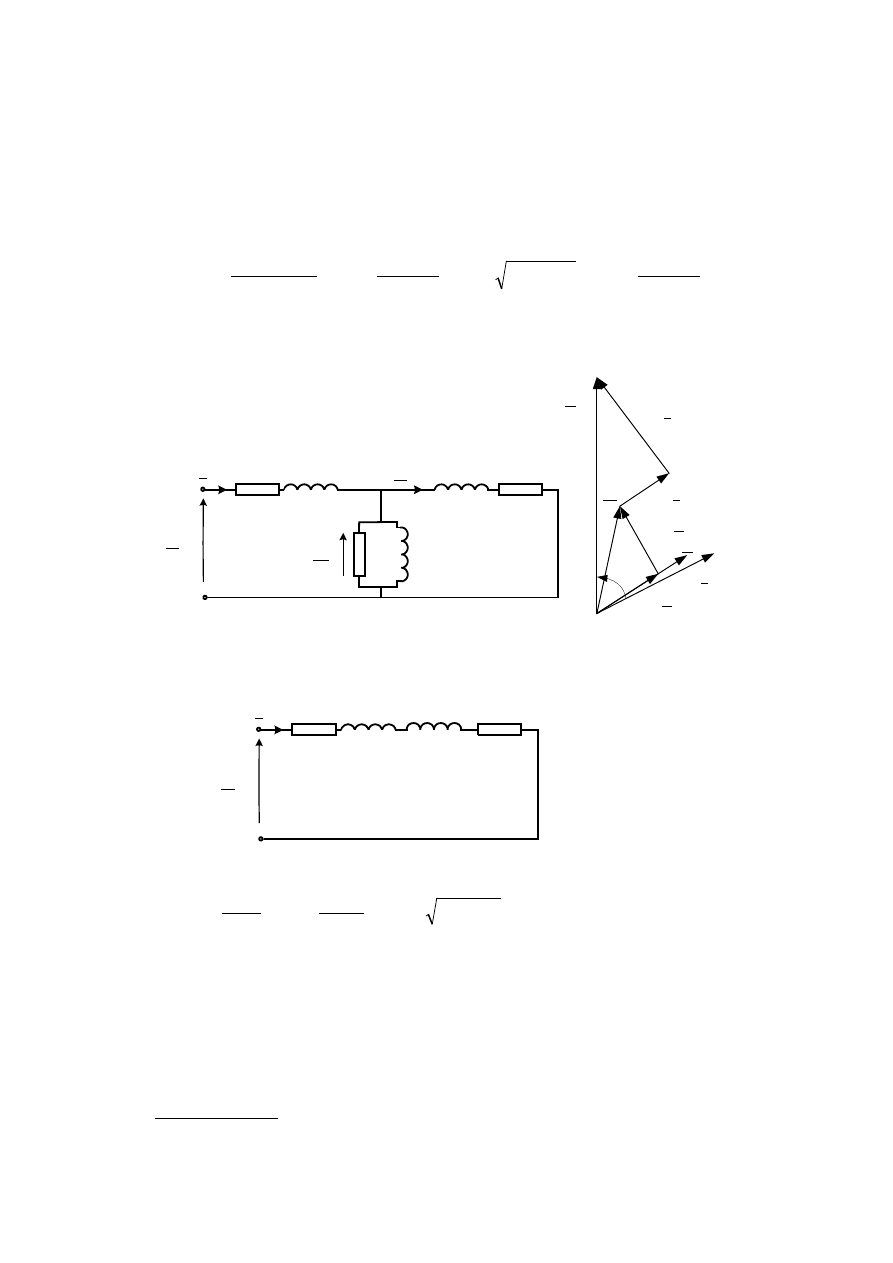
Poniżej przedstawiono schemat zastępczy i wykres wskazowy dla stanu zwarcia silnika.

sphk

I

s

R

s

jX

σ

r

X

j

σ

′

rphk

I

′

r

R

′

sphk

U

Fe

R

m

jX

0

r

E

′

0

r

E

′

sphk

I

rphk

r

I

R

′

′

rphk

I

′

sphk

s

I

jX

σ

sphk

s

I

R

rphk

r

I

X

j

′

′

0

σ

sphk

U

k

ϕ

W obliczeniach przybliżonych dla stanu zwarcia silnika pierścieniowego można pominąć
gałąź poprzeczną schematu zastępczego maszyny, z uwagi na relatywnie znaczną wartość jej
impedancji, w porównaniu z impedancją gałęzi podłużnej.

sphk

I

s

R

s

jX

σ

r

X

j

σ

′

r

R

′

sphk

U

Parametry wyznaczamy dla prądu zwarcia równego prądowi znamionowego stojana.

sphN

sphk

k

I

U

Z

=

,

2

3

sphN

k

k

I

P

R

=

,

2

2

k

k

k

R

Z

X

−

=

,

2

K

R

R

R

R

R

r

s

r

s

k

⋅

+

=

′

+

=

Rzeczywistą wartość rezystancji fazowej wirnika można oszacować jako:

2

/

)

(

K

R

R

R

s

k

r

−

=

.

Na podstawie pomiaru biegu jałowego i zwarcia, przy znajomości napięcia indukowanego w
wirniku przy pomiarze przekładni napięciowej (stan pracy transformatorowej silnika) można
oszacować reaktancje rozproszeń stojana i wirnika:

0

0

sph

rph

sphN

s

I

U

K

U

X

⋅

−

=

σ

- jeśli przyjąć, że

s

s

R

X

>>

σ

oraz

s

k

r

r

X

X

K

X

X

σ

σ

σ

−

=

⋅

=

′

2

.

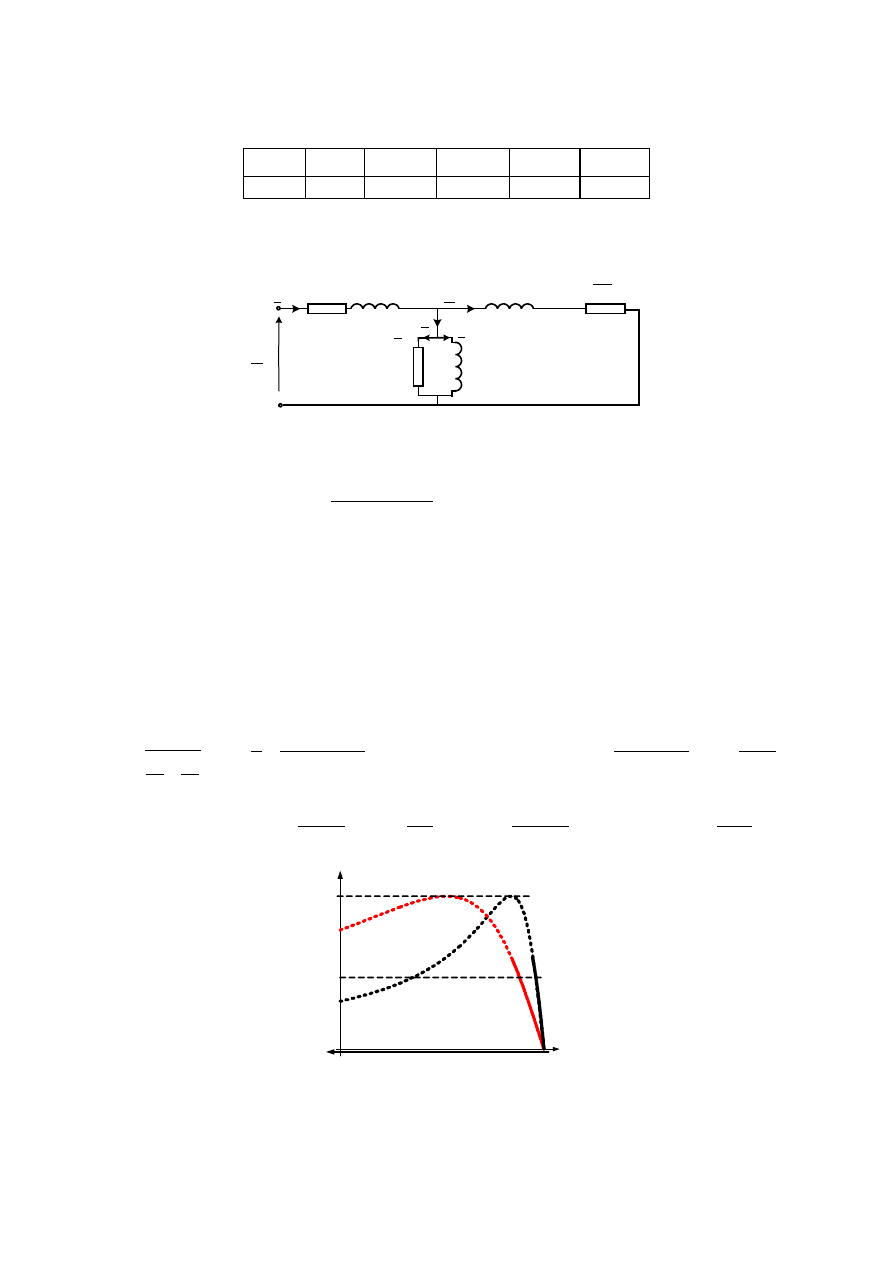
SI-9

Parametry fazowego schematu zastępczego zapisujemy w tabeli:

s

R

[

Ω

]

r

R

′

[

Ω

]

s

X

σ

[

Ω

]

r

X

σ

′

[

Ω

]

Fe

R [

Ω

]

m

X [

Ω

]

W sprawozdaniu należy zamieścić układ zastępczy silnika z wartościami poszczególnych
parametrów.

sph

I

s

R

s

jX

σ

r

X

j

σ

′

rph

I

′

s

R

r

′

sph

U

Fe

R

m

jX

0

I

Fe

I

m

I

Wyznaczanie sprawności znamionowej metodą strat poszczególnych

pN

N

pN

N

P

P

P

∑

∆

−

=

η

,

N

sphN

sphN

pN

I

U

P

ϕ

cos

3

=

,

∑

∆

+

∆

+

∆

+

∆

+

∆

=

∆

dod

m

wrN

Fe

wsN

N

P

P

P

P

P

P

,

2

3

sphN

s

wsN

I

R

P

=

∆

,

(

)

s

P

P

P

P

Fe

wsN

pN

wrN

⋅

∆

−

∆

−

=

∆

,

N

dod

P

P

⋅

=

∆

%

5

,

0

.

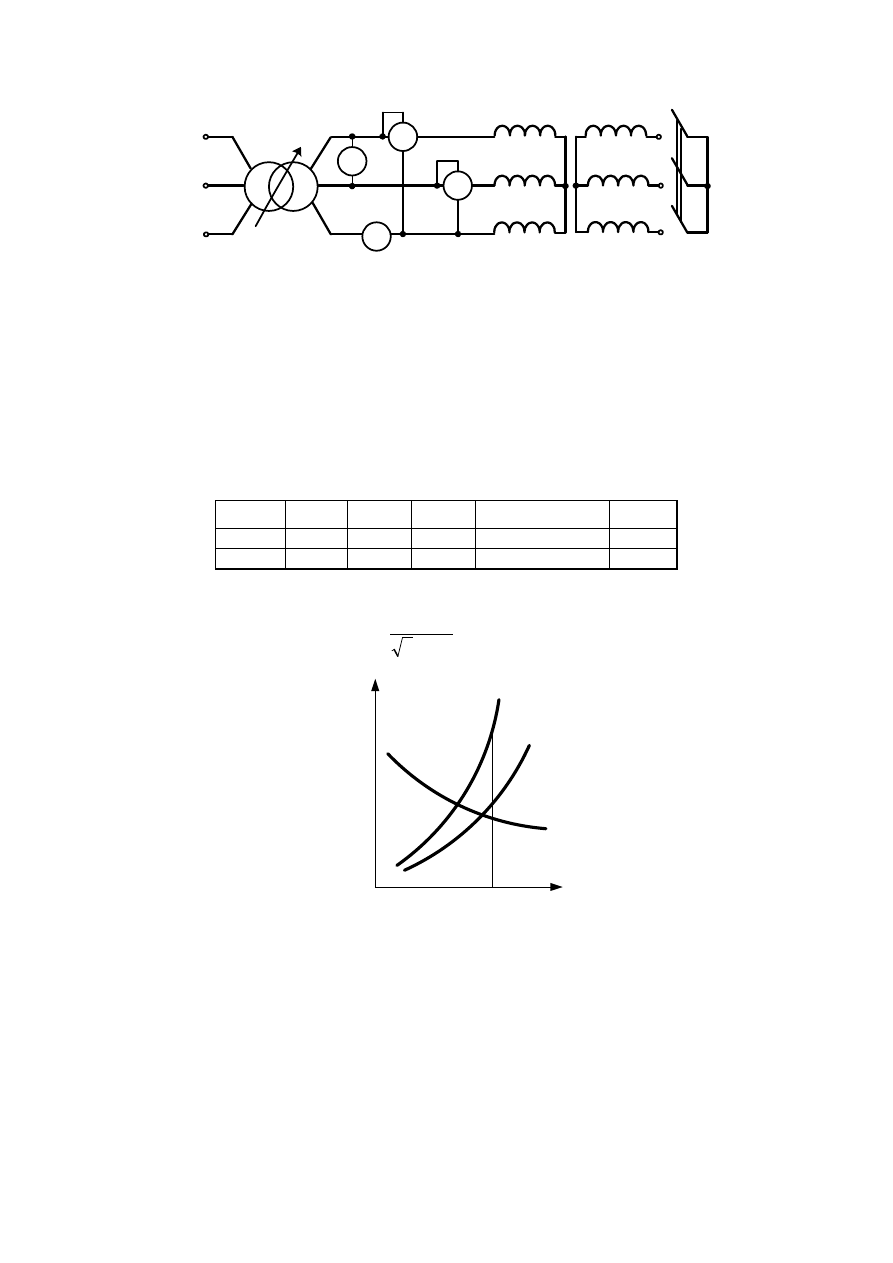
Wyznaczanie teoretycznej charakterystyki mechanicznej silnika (wzór Klossa)

Obliczyć charakterystyki momentu w funkcji poślizgu s od 0 do 1 i wrysować na nią
charakterystyki zmierzone przy braku i przy obecności w obwodzie wirnika dodatkowej
rezystancji. Przyjąć do wzorów parametry wyznaczonego schematu zastępczego silnika.

s

s

s

s

T

T

b

b

b

+

=

2

,

k

sphN

S

b

X

U

C

p

T

0

2

)

(

2

3

ω

=

,

2

=

p

,

π

π

ω

100

2

0

=

=

s

f

,

m

s

m

S

X

X

X

C

+

=

σ

,

p

f

n

s

60

0

=

r

s

s

k

X

X

C

X

σ

σ

′

+

=

,

0

0

n

n

n

s

−

=

,

k

r

b

X

R

s

′

=

albo

k

d

r

b

X

R

R

s

′

+

′

=

,

d

d

R

K

R

2

=

′

,

30

n

⋅

=

Ω

π

0

=

d

R

0

>

d

R

0

1

b

T

s

0

n

s

n

N

T

T

Przebieg teoretyczny charakterystyki mechanicznej silnika indukcyjnego przy zmianie
rezystancji w wirniku, z zaznaczeniem zakresu odpowiadającego wykonanym pomiarom

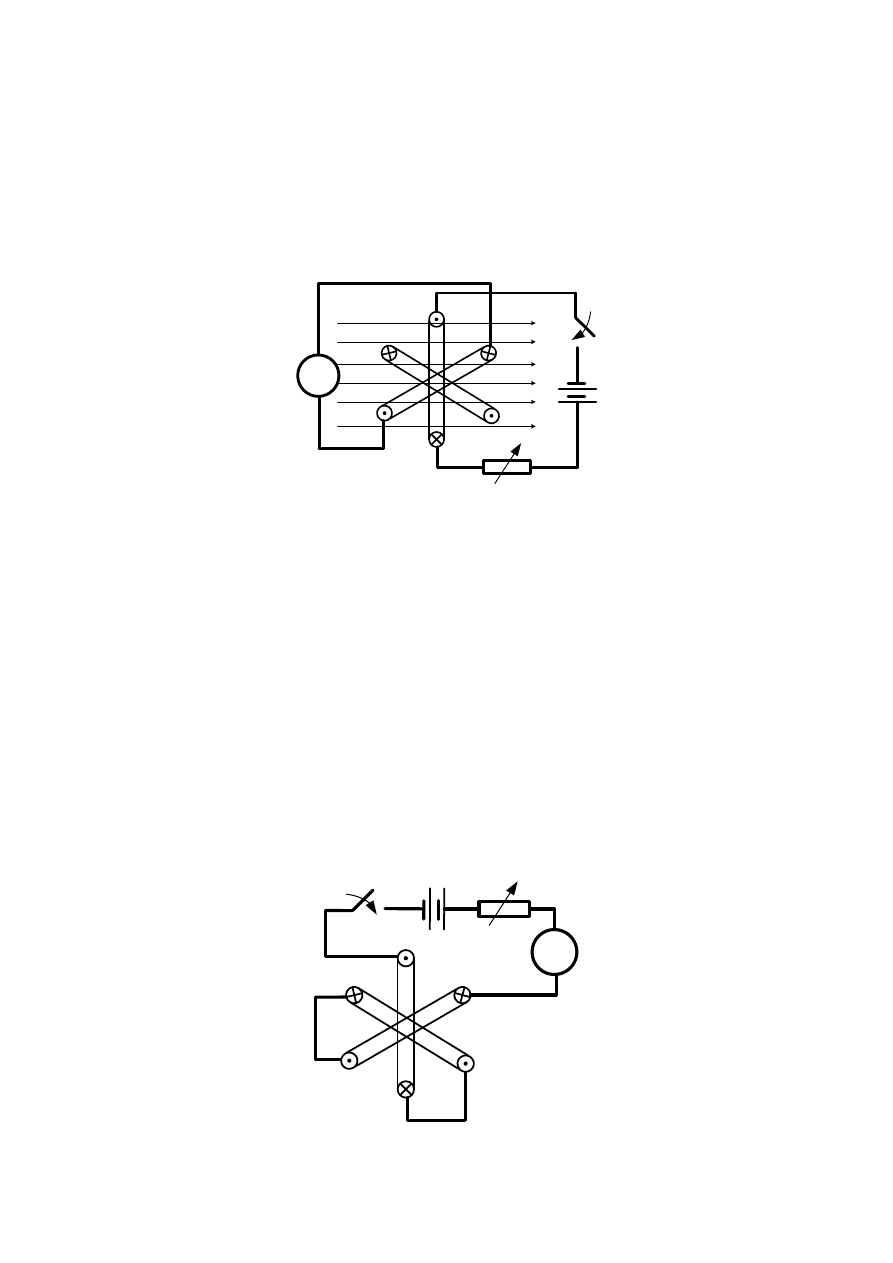
SI-10

Silnik indukcyjny klatkowy

Wyznaczanie początków i końców uzwojeń stojana
Przeprowadza się w przypadku nie oznaczonej tabliczki zaciskowej jedną z poniższych
metod:
1. Metoda impulsów prądu stałego
Przed przystąpieniem do pomiaru należy za pomocą omomierza dobrać parami zaciski
odpowiadające poszczególnym fazom. Łączymy układ według poniższego schematu.

1

U

1

V

1

W

2

U

2

V

2

W

Φ

V

+

+

−

−

Początek i koniec jednej z faz przyjmuje się dowolnie, a następnie zasila się tą fazę
niewielkim napięciem stałym, uzyskanym np. z prostownika jednofazowego zasilanego z
autotransformatora. Do innej fazy uzwojenia stojana przyłącza się woltomierz
i obserwuje się jego wychylenie przy załączaniu napięcia. Jeżeli ujemny biegun źródła został
przyłączony do zacisku przyjętego za początek danej fazy a dodatni do końca tej fazy, to przy
impulsowym załączeniu napięcia plus woltomierza wskazuje na początek drugiej fazy, jeśli
woltomierz wychyla się prawidłowo.

2. Metoda zasilania prądem stałym
Uzwojenie trójfazowe łączy się szeregowo i zasila prądem stałym. Jeżeli kierunek płynięcia
prądu we wszystkich uzwojeniach jest jednakowy (od początku do końca lub odwrotnie), to
wypadkowy strumień w maszynie, będący sumą trzech strumieni przesuniętych w przestrzeni
co 120

0

, jest bliski zeru. Obracając zwarty wirnik, nie odczuwa się wtedy oporu, gdyż w

klatce nie indukują się prądy i nie wytworzą momentu hamującego. Gdy jedno z uzwojeń
połączymy przeciwnie (np. zacisk

2

U z zaciskiem 2

V i dalej zacisk 1

V z zaciskiem

1

W ), to

wypadkowy strumień będzie różny od zera. Przy obracaniu wirnika prądy indukowane w
klatce wytworzą wyczuwalny ręką moment hamujący.

+

−

1

U

1

V

1

W

2

U

2

V

2

W

A

SI-11

Rozruch silnika za pomocą przełącznika „gwiazda – trójkąt”

Po wyznaczeniu początków i końców faz uzwojenia stojana, łączymy je zgodnie z poniższym
schematem.

A

1

L

2

L

3

L

∆

Y

1

U

1

V

1

W

2

U

2

V

2

W

Wykonując rozruch nieobciążonego silnika z użyciem przełącznika „gwiazda – trójkąt”
obserwujemy na amperomierzu zmiany prądu przewodowego stojana i pracę silnika, w obu
pozycjach przełącznika.


W sprawozdaniu należy przedstawić: schematy układów pomiarowych, opis stosowanych
metod pomiarowych i przeprowadzonych badań, objaśnienie przyczyn obserwowanych
zjawisk.



Literatura podstawowa:
1. J.K. Markielowski i in.: Laboratorium maszyn elektrycznych, PK, Kraków 1982
2. J. Skwarczyński i in.: Laboratoryjne pomiary maszyn elektrycznych, AGH, Kraków 1985.


Opracował: dr inż. Konrad Weinreb
Kraków, grudzień 2010