1
6.Ruch punktu materialnego polu centralnym. Prawo powszechnego ciążenia. Prawa Keplera.
Wyznaczanie stałej grawitacji.
Ciało obdarzone masą modyfikuje w pewien sposób otaczającą przestrzeń tworząc tzw. pole
grawitacyjne. Pole to działa następnie na każde inne znajdujące się w nim ciało obdarzone masą
wywierając nań siłę przyciągania grawitacyjnego.
Siłę F działającą na daną masę m można przedstawić:
g
m
F
=
gdzie
g
jest natężeniem pola grawitacyjnego, charakteryzującym siły pola grawitacyjnego.
Pole nazywamy jednorodnym, jeśli natężenie we wszystkich jego punktach jest jednakowe.
Pole nazywamy centralnym, jeżeli we wszystkich jego punktach wektory natężenia skierowane są
wzdłuż prostych, przecinających się w jednym punkcie, nieruchomym względem dowolnego układu
inercjalnego (punkt ten nazywamy środkiem sił).
Pole centralne jest zachowawcze. Pole zachowawcze jest to pole w którym praca potrzebna do
przeprowadzenia ciała z punktu 1 do 2 po torze krzywoliniowym nie zależy od kształtu krzywej.
Pole centralne nazywamy kulisto-symetrycznym, jeśli liczbowa wartość wektora natężenia pola
zależy tylko od odległości od środka sił.
Zasada superpozycji pól (nakładania się pól): przy nałożeniu się kilku pól (np. ciążenia), natężenie
pola wypadkowego równa się sumie wektorowej natężeń wszystkich tych pól.
Pola charakteryzuje się również pewną wielkością skalarną, zwaną potencjałem pola. Równy jest on
stosunkowi energii potencjalnej punktu materialnego do jego masy:
m
E
V
p
≡
W przypadku pola grawitacyjnego pojedynczego punktu materialnego o masie
m
, potencjał tego
pola wyraża się wzorem:
r
Gm
V
g
−
=
Związek pomiędzy natężeniem pola i jego potencjałem:
( )
g
V
grad
g
−
=
Wzajemne przyciąganie się ciał jest źródłem jednej z podstawowych sił w fizyce – sił przyciągania,
które podlegają prawu powszechnego ciążenia (grawitacji). Prawo to podał Isaac Newton (1687;
pierwsze obserwacje już od 1655)
2
2
1
r
m
m
G
F
=
w postaci wektorowej :
12
3
12
2
1
12
r
r
m
m
G
F
−
=
Między każdymi dwoma punktami materialnymi działa siła wzajemnego przyciągania, wprost
proporcjonalna do iloczynu mas tych punktów (m
1
i m
2
) a odwrotnie proporcjonalna do kwadratu
odległości r między nimi.
Współczynnik
2
2
11
10
672
,
6
kg
Nm
G
−
⋅
=
to stała grawitacji, wyznaczona po raz
pierwszy doświadczalnie w 1797 r. przez Henry`ego Cavendisha przy użycie tzw. wagi skręceń.
2
Johannes Kepler (korzystając z obserwacji Tycho de Brache) podał wyprowadzone empirycznie
prawa ruchu planet – prawa te można wyprowadzić z prawa powszechnego ciążenia Newtona.
Pierwsze prawo Keplera:
Każda planeta krąży po orbicie eliptycznej, ze Słońcem w jednym z ognisk tej elipsy.
Drugie prawo Keplera (prawo równych pól):
Linia łącząca Słońce i planetę zakreśla równe pola w równych odstępach czasu.
Trzecie prawo Keplera:
Sześciany półosi wielkich orbit jakichkolwiek dwóch planet maja się tak do siebie, jak kwadraty ich
okresów obiegu:
2
2
2
1
3
2
3
1
T
T
R
R =
Rozpatrzmy ruch ciała w polu sił centralnych:
r
r
F
F
r
=
Moment siły
F
względem środka pola jest równy zeru:
0
=
⎟
⎠
⎞
⎜
⎝
⎛
×
=
×
=
r
r
F
r
F
r
M
r
,
dlatego moment pędu tego ciała względem środka pola jest zachowany:
( )
const
v
m
r
K
=
×
=
Stąd z kolei wynika, że w centralnym polu sił tor ruchu tego ciała jest krzywą płaską
(płaszczyzna, zawierająca wektory położenia
r
i prędkości
v
nie zmienia swej orientacji względem
środka pola).
Skoro krzywa ruchu jest krzywą płaską, położenie punktu w przestrzeni określimy we współrzędnych
biegunowych
r
i
ϕ
, a prędkość rozłożymy na prostopadłe składowe: radialną
r
v
i
transwersalną (poprzeczną)
ϕ
v
:
3
ϕ
v
v
v
r
+
=
gdzie:
dt
dr
v
r
=
i
dt
d
r
v
ϕ
ϕ
=
Moment pędu układu zależy tylko od prędkości poprzecznej:
( )
const
v
m
r
K
=
×
=
ϕ
Wartość momentu pędu jest równa:
const
dt
d
mr
K
=
=
ϕ
2
Promień wodzący
r
zakreśla przy swoim obrocie o mały kąt
ϕ
d
w czasie
dt
wycinek kołowy,
którego pole
dS
jest równe:
ϕ
d
r
dS
2
2
1
=
stąd wielkość
p
v
:
dt
d
r
dt
dS
v
p
ϕ
2
2
1
=
≡
nazywamy prędkością polową (wycinkową).
Biorąc pod uwagę powyższą definicję i zasadę zachowania momentu pędu, otrzymujemy:
const
m
K
v
p
=
=
2
przy ruchu ciała w polu siły centralnej jego prędkość polowa (rozumiana jako pole zakreślane
przez promień wodzący w jednostce czasu) jest stała. (II prawo Keplera)
Aby wyprowadzić I i III prawo Keplera, skorzystajmy z zasady zachowania momentu pędu i zasady
zachowania energii:
const
E
E
E
p
k
=
+
=
⎥
⎦
⎤
⎢
⎣
⎡
⎟
⎠
⎞
⎜
⎝
⎛
+
⎟
⎠
⎞
⎜
⎝
⎛
=
⎥
⎦
⎤
⎢
⎣
⎡
⎟
⎠
⎞
⎜
⎝
⎛
+
⎟
⎠
⎞
⎜
⎝
⎛
=
=
2
2
2
2
2
2
2
2
mr
K
dt
dr
m
dt
d
r
dt
dr
m
mv
E
k
ϕ
skąd otrzymujemy:
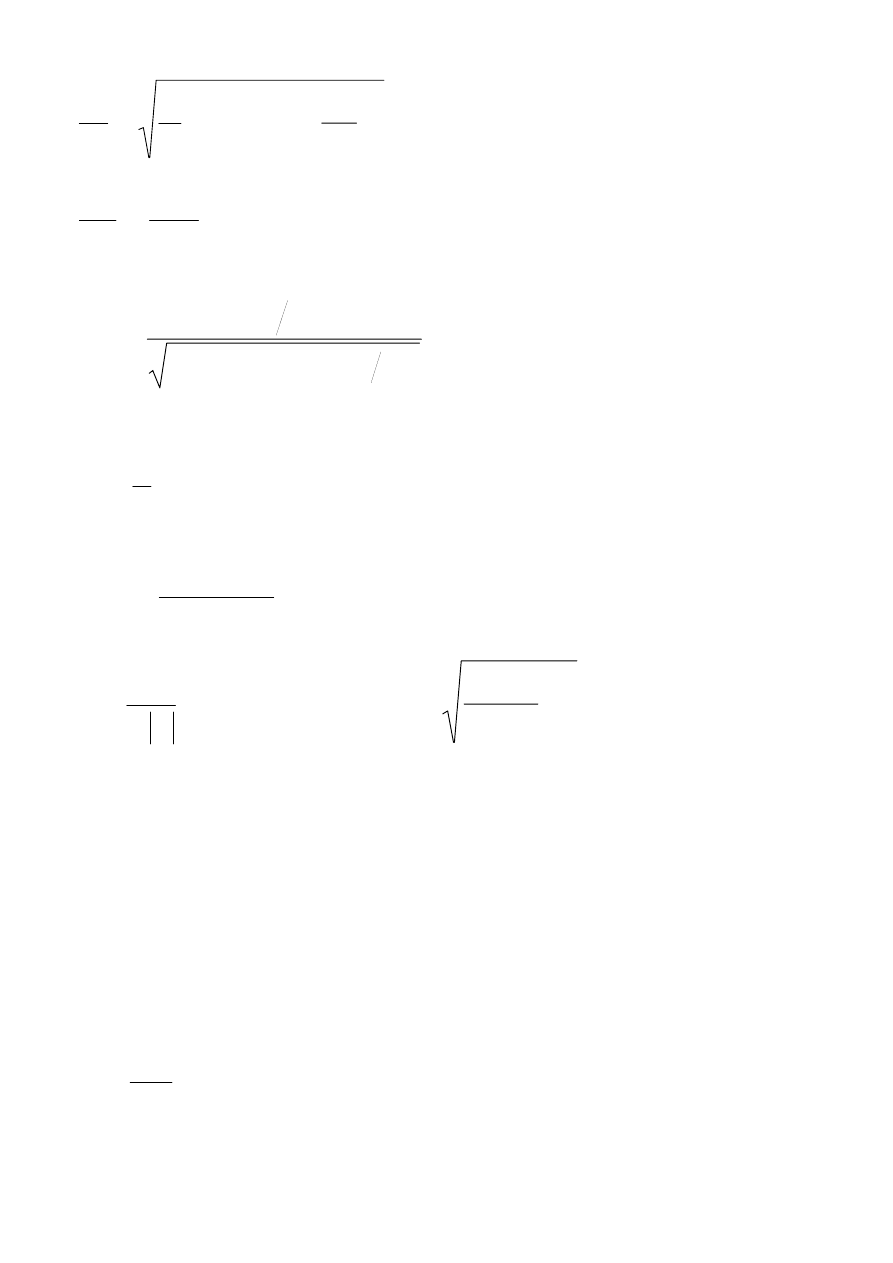
4
(
)
2
2
⎟
⎠
⎞
⎜
⎝
⎛
−
−
=
mr
K
E
E
m
dt
dr
p
a ponieważ:
2
mr
K
dt
d
=
ϕ
więc ostatecznie:
(
)
(
)
dr
r
K
E
E
m
r
K
d
p
2
2
2
−
−
=
ϕ
Aby rozwiązać podane równanie trajektorii ruchu, musimy podstawić konkretne wyrażenie na energię
potencjalną, która w przypadku pola grawitacyjnego ma postać:
r
E
p
β
=
gdzie:
GMm
β
= −
Ostateczne rozwiązanie można przedstawić w postaci:
( )
ϕ
ϕ
cos
1 e
p
r
+
=
gdzie:
β
m
K
p
2
=
i
1
2
2
2
+
=
β
m
EK
e
Tor ruchu (orbita), jest więc krzywą drugiego stopnia, przy czym
p
jest jej parametrem
ogniskowym a
e
- mimośrodem;
W zależności od tego, jaka jest energia całkowita
E
ciała, możliwe są następujące rozwiązania
równania toru (trajektorii):
-
dla E<0 (czyli e<1) jest to orbita eliptyczna;
-
dla E=0 (e=1) jest to orbita paraboliczna;
-
dla E>0 (e>1) jest to orbita hiperboliczna;
-
dla K=0 (e=1, p=0) jest to tor prostoliniowy, przechodzący przez środek pola.
Dla planet, poruszających się w polu grawitacyjnym Słońca:
0
<
E
a więc torami ruchu planet są elipsy (I prawo Keplera).
Wtedy również można wyprowadzić wzór na okres
T
obiegu planety po tej elipsie:
3
2
2
4
a
GM
T
π
=
gdzie
a
jest dużą osią elipsy. Stąd otrzymujemy III prawo Keplera.
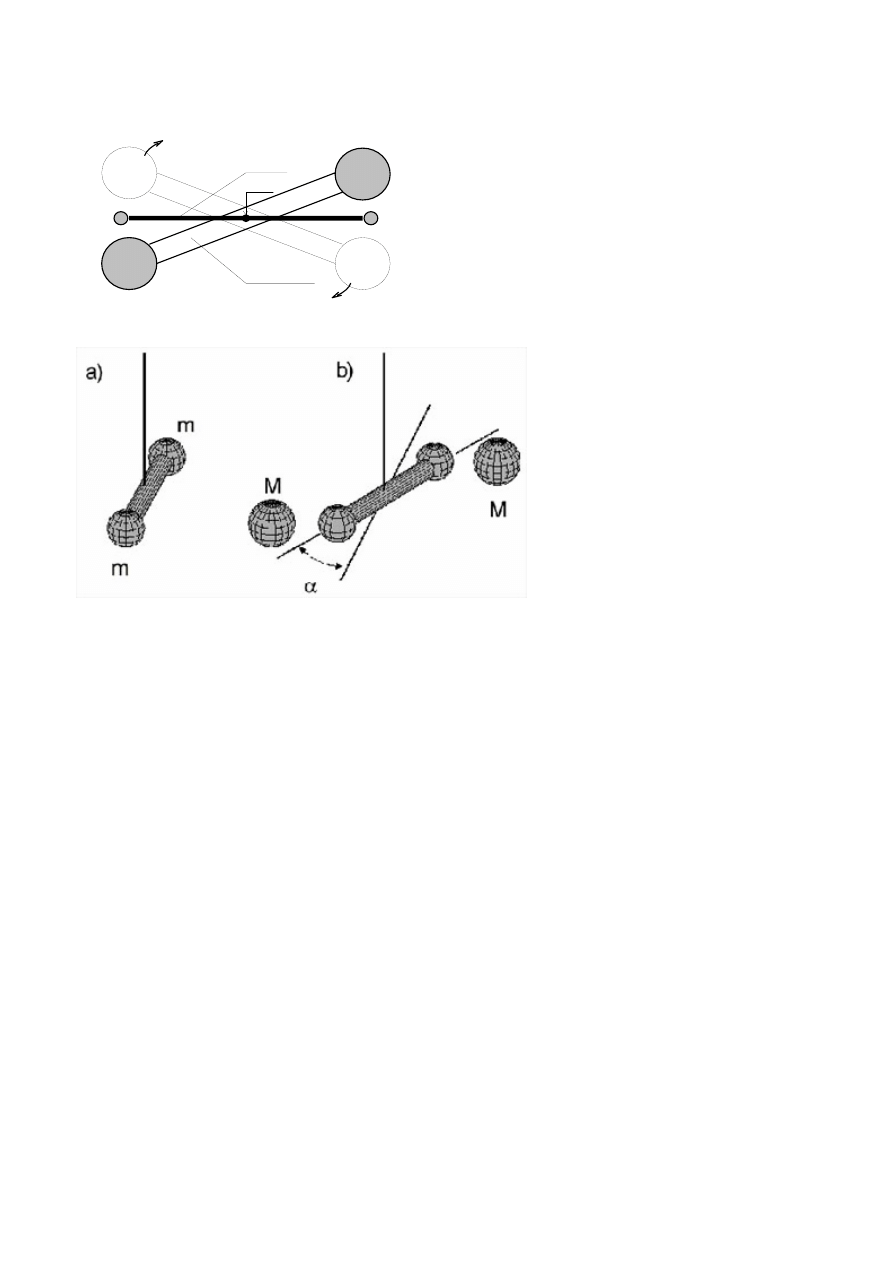
Eksperyment Cavendisha, wyznaczenie stałej grawitacji G za pomocą wagi skręceń.
5
Na cienkiej, sprężystej nici, będącej osią obrotu, zawieszono poziomo lekki pręt P, obciążony
na obu końcach kulkami o jednakowych masach m, tak że może on obracać się w płaszczyźnie
poziomej (tu w płaszczyźnie rysunku). W pobliżu tych kulek, na podstawie, którą można obrócić,
umieszcza się symetrycznie, dwie duże kule o masach M, tak by każda przyciągała „swoją” masę m z
taką samą siłą. Pod wpływem przyciągania grawitacyjnego będzie następował obrót pręta i skręcanie
nici, na której jest on zawieszony. W zależności od tego, z której strony mas m zbliżymy masy M
(patrz Rys. 1., linie ciągłe, lub przerywane) kierunek obrotu pręta będzie różny. Skręcenie nici
spowoduje powstanie sił sprężystych, przeciwdziałających obrotowi.Warunkiem równowagi
statycznej takiego układu jest warunek, aby moment pary sił przyciągania grawitacyjnego obu par
kulek , i moment sił sprężystości były sobie równe. Do nici może być przymocowane lusterko na
które kierujemy wiązkę światła. Po odbiciu światło pada na skalę dzięki temu można wyznaczyć kąt
skrętu.
M
M
M
M
m
m
oś
pręt
Podstawa
dużych kul
Widok z góry
P
Rys. 1. Schemat wagi skręceń Cavendisha