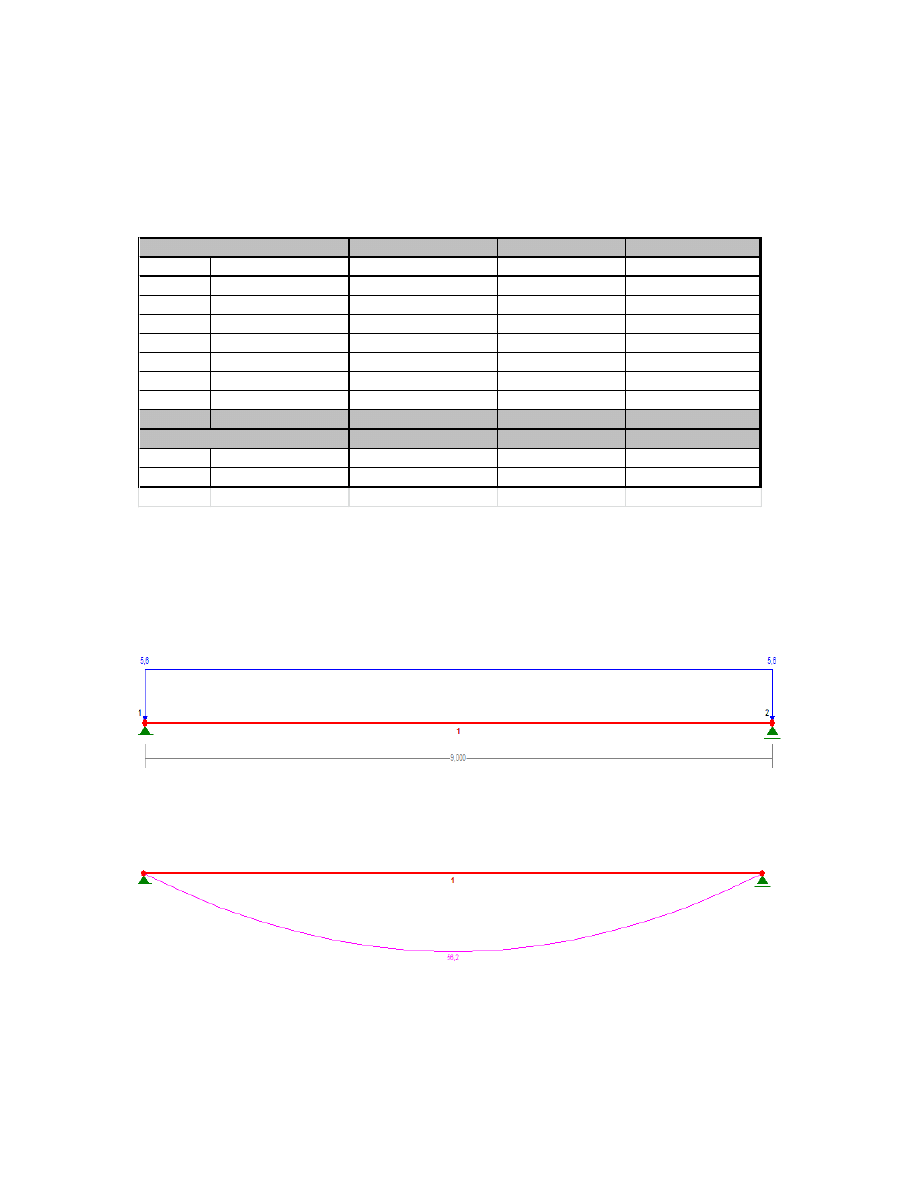
1. Wymiarowanie belki pomostu technologicznego

1.1 Zestawienie obciążeń na powierzchni pomostu

Obciążenia stałe
1.1.

lastryko
22kN/m3*0,05m

1,10

1,35

1,49

1.2.

gładź cementowa

1,35

0,03m*21kN/m3

0,63

1,35

0,85

1.3.

Płyta żelbetowa

1,35

0,08m*25kN/m3

2,00

1,35

2,70

1.4.

Tynk wapienny

1,35

0,02m*19kN/m3

0,38

1,35

0,51

SUMA

4,11

5,55

Obciążęnie zmienne
2.1.

Obciążenia tech.

1,20

1,50

1,80

SUMA

1,20

1,80

1.2 Sprawdzenie stanów granicznnych belki zabezpieczonej
przed zwichrzeniem

Wykres momentów zginających

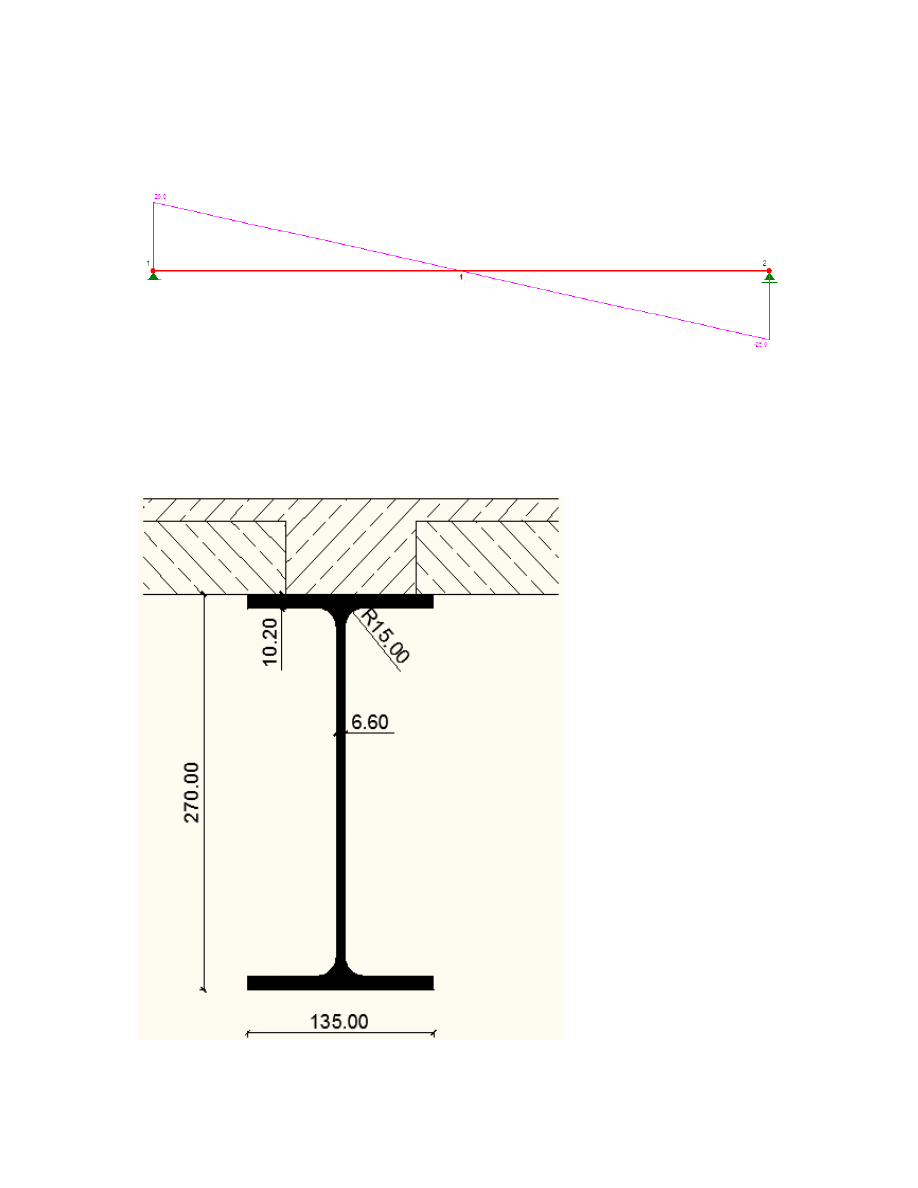
Wykres sił poprzecznych

Belka wykonana jest z dwuteownika walcowanego IPE 270 ze stali gatungu S355. Obciązenie
ciągłe o wartości obliczeniowej q

d

=5,55 kN/m powoduje powstanie obliczeniowej momentów

zginających o maksymalnej wartości obliczeniowej M

max,Ed

=56,2 kN*m w środku belki i sił

poprzecznych o maksymalnej wartości obliczeniowej V

max,Ed

=22 kN przy podporach. wartość

chrakterystyczna obciążenia ciągłego belki wynosi q

k

=4,11 kN/m.

Na pasie górnnym belki oparta
jest płyta żelbetowa stropowa
która uniemożliwia poprzeczne
przemieszczenia. Tak więc
belka jest zabezpieczona
przez zwichrzeniem.

1.3 Charakterystyka materiałowa i geometryczna belki

Przyjęto IPE 270 - stal klasy S355

wysokość

h

270mm



szerokość

b

135mm



grubość środnika

tw

6.6mm



tf

10.2mm



grubość półki

R

15mm



promień wyokrągleń

mIPE

36.1

kg

m



masa

pole przekroju

A

45.9cm

2



Iz

420cm

4



moment bezwładności względem osi x

moment bezwładności względem osi y

Iy

5790cm

4



wskażnik wytrzymałości względem osi x

Wel.z

62.2cm

3



wskaźnik wytrzymałości względem osi y

Wel.y

429cm

3



promień bezwładności względem osi x

iz

3.02cm



iy

11.2cm



promień bezwładności względem osi y

plastyczny wskaźnik wytrzymałości względem osi x

Wpl.z

97cm

3



plastyczny wskażnik wytrzymałości względem osi y

Wpl.y

484cm

3



Iw

70580cm

6



wycinkowy moment bezwładności przekroju płatwi

It

16.4cm

4



moment bezwładności na skręcanie przekroju płatwi

Iz 420 cm

4





moment bezwładności względem mniejszej osi bezwładności

L

9 m





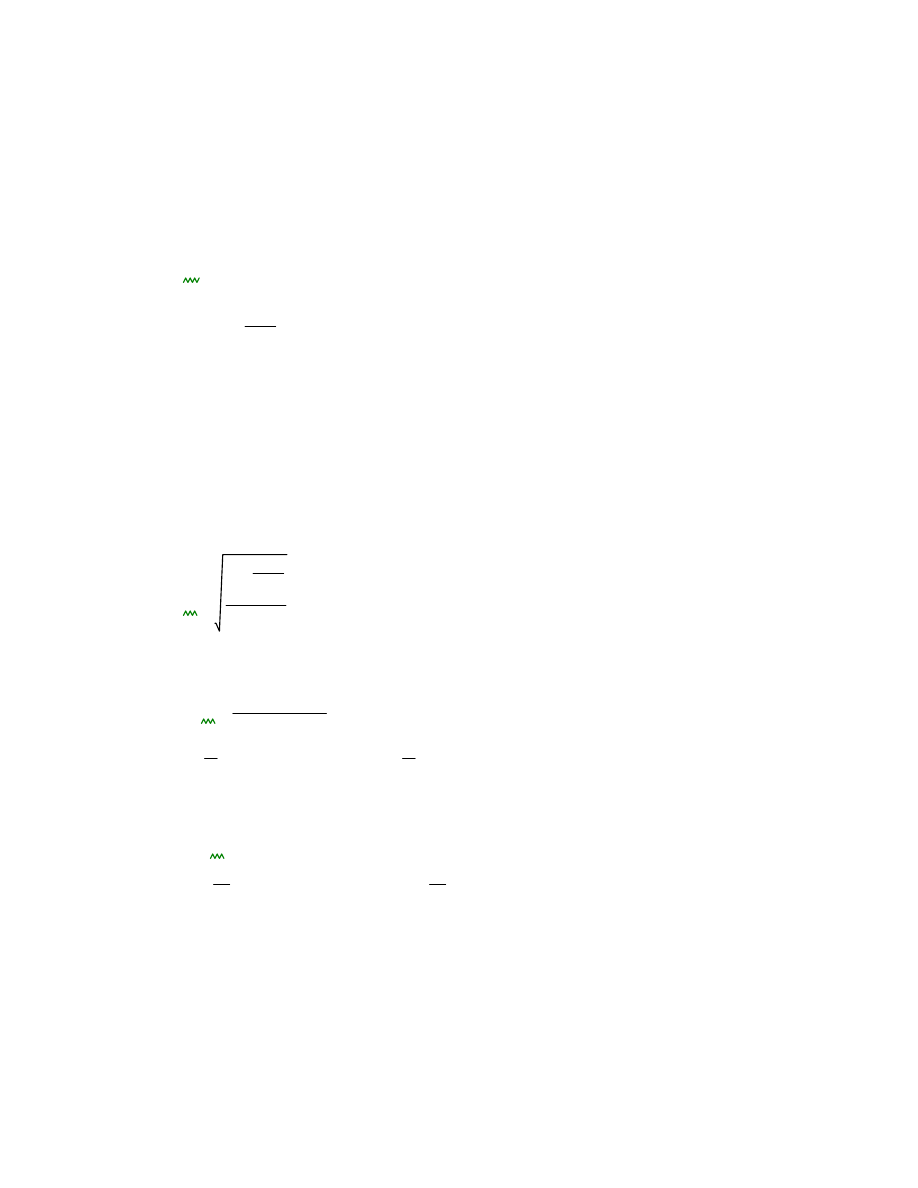
1.4 Sprawdzenie klasy przekroju

Właściwości stali gatunku S355:

E

210 GPa





moduł Younga dla stali

G

81 GPa





moduł sprężystości poprzecznej

fy

355

N

mm

2



gatunek stali S355

Częściowe wspólczynniki bezpieczeństwa

γM0

1.00



współczynnik częściowy dla nośności przekroju poprzecznego
wg PN-EN 1993-1-1 NA.14

γM1

1.00



współczynnik częściowy dla nośności elementów
wg PN-EN 1993-1-1 NA.14

Parametr ε zależy od granicy plastyczności dwuteownika

ε

235

N

mm

2

fy



ε

0.814



półka górna - poddana równomiernemu ściskaniu

c

b

tw



2 R









2

49.2 mm







c

tf

4.824



9 ε



7.323



c

tf

9 ε





1 klasa przekroju

środnik poddany zginaniu

c

h

2 tf





2 R





219.6 mm







1 klasa przekroju

c

tw

33.273



72 ε



58.58



c

tw

72 ε





Klasa przekroju poprzeczengo to najbardziej niekorzystna klasa sprawdzanego elementu
przekroju, w tym wypadku mamy doczynienia z Klasą 1. Sprawdzenie Stanu Granicznego
Nośności powinno być oparte na plastycznej analizie przekroju poprzecznego.

1.5 Sprawdzenie możliwości utraty stateczności miejscowej
przekroju belki spowodowanej oddziaływaniem siły
poprzecznej.

hw

tw

72

ε

η





η

1.2



hw

tw

h

2 tf





2 R





tw

33.273





hw

tw

72

ε

η



48.817



hw

tw

72

ε

η





stateczność zapewniona

Analizowany schemat statyczny dla belki

Maksymalne siły przekrojowe belki

qk

4.11

kN

m













qd

5.55

kN

m













My.Ed.b

qd L

2



8

56.194 kN m









maksymalny moment dla belki

Vy.Ed.b

qd L



2

24.975 kN







maksymalna siła ścinająca dla belki

1.6 Stan graniczny nośności dla belki drugorzędnej (SGN)

Sprawdzenie nośności przekroju w którym występuje maksymalny moment zginający

Mmax.Ed

56.2 kN



m





Mpl.Rd

Wpl.y fy



γM0

171.82 kN m









Mc.Rd

Mpl.Rd 171.82 kN m









My.Ed

Mmax.Ed 5.62 10

4



J





My.Ed.b

Mc.Rd

0.327



My.Ed.b

Mc.Rd

1



warunek spełniony

Sprawdzenie nośności przekroju w którym występuje maksymalna siła poprzeczna:

Vmax.Ed

25 kN





Pole przekroju czynnego belki przy ścinaniu

Av.z

A

2 b

 t

f





tw 2 R









tf





22.093 cm

2







hw

h

2 tf





0.25 m





lecz nie mniej niż:

η hw



tw



1.977

10

3





m

2



Przy projektowaniu plasttycznym przyjmuje się

Vc.Rd

Vpl.Rd



Vpl.Rd

Obliczeniowa nośnoścć plastyczna przy ścinaniu

Vpl.Rd

Av.z fy



3 γM0



452.821 kN







Warunek nośności przekroju przy obciążeniu siłą poprzeczną:

Vmax.Ed

Vpl.Rd

0.055



VEd

Vpl.Rd

1



warunek spełniony

1.7 Sprawdzenie nośności belki nad podporą:

Przyjęto: c

1

30 mm





długość strefy docisku s

s

70mm



kF

2

6

ss c1



hw

















6





kf

2

6

ss c1



hw

















4.404





< 6

Fcr

0.9 kF



E



tw

3

hw



2.177

10

5



N





Fcr

242.8 kN





m1

fy b



fy tw



20.455





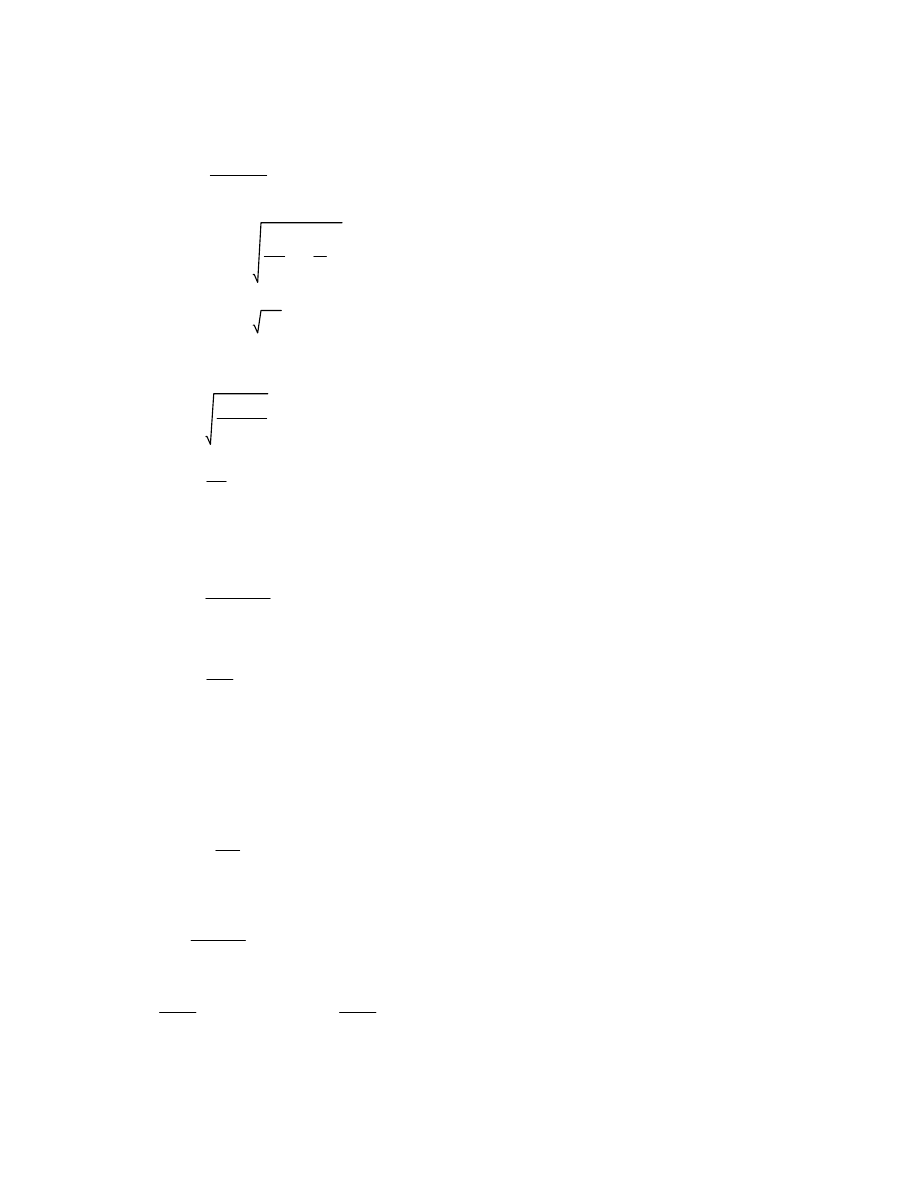
le

kF E

 t

w

2



2 fy

 h

w



0.052 m





ss c1



0.1 m



ly1

le tf

m1

2

le
tf













2







0.113 m





ly2

le tf m1





0.098 m





ly

min ly1 ly2







0.098 m





λF

ly tw



fy



Fcr

0.971





χF

0.5

λF

0.515





< 1

Leff

χF ly



0.05 m





FRd

fy Leff



tw



γM1

1.179

10

5



N





FEd

Vmax.Ed



η2

FEd
FRd

0.212





< 1

Warunek nośności belki nad podporą jest spełniony,

1.8 Stan graniczny użytkowalności dla belki drugorzędnej (SGU)

Wyliczenie ugięć

wmax

L

250

36 mm







w

5 qk



L

4



384 E

 I

y



28.877 mm







w

wmax

0.802



w

wmax

1



warunek spełniony

2. Wymiarowanie podciągu pomostu technologicznego

2.1 Zestawienie kombinacji obciażeń

Podciąg projektownay jest jako belka ciągła wykonana z dwuteownika walcowanego IPE 270
Obciązenie podciagu traktujemy jako równomiernie rozłożone.

Zestawienie obciążeń

L.p.

Rodzaj obciążenia

wartość char. [kN/m2] wspł. obciążeniowy wartość obl.[kN/m2]

Obciążenia stałe
1.1.

lastryko
22kN/m3*0,05m

1,10

1,35

1,49

1.2.

gładź cementowa

1,35

0,03m*21kN/m3

0,63

1,35

0,85

1.3.

Płyta żelbetowa

1,35

0,08m*25kN/m3

2,00

1,35

2,70

1.4.

Tynk wapienny

1,35

0,02m*19kN/m3

0,38

1,35

0,51

SUMA

4,11

5,55

Obciążęnie zmienne
2.1.

Obciążenia tech.

1,20

1,50

1,80

SUMA

1,20

1,80

qk

4.11

kN

m

2



qd

5.55

kN

m

2



gk

1.2

kN

m

2





gd

1.8

kN

m

2





2.2 Sprawdzanie stanów granicznych trójprzęsłowego podciągu
ciągłego

Podciąg wykonany jest z dwuteownika walcowanego IPE 500 ze stali gatunku S355

Maksymalny moment zginający występuje nad podporą 2:

Mmax.Ed

74.4 kN



m





Maksymalna siła poprzeczna również występuje nad podporą 2: V

max.Ed

41.38kN



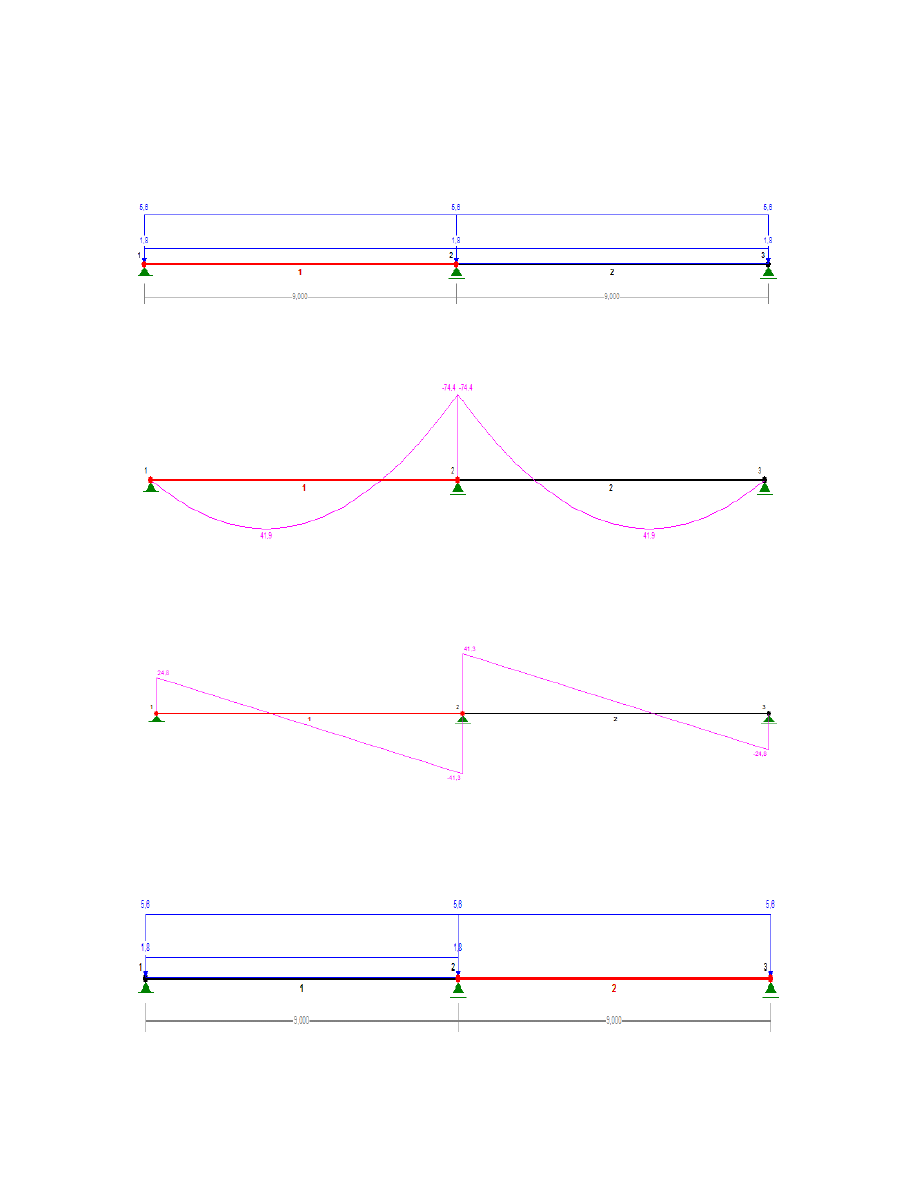
Schemat obciążenia, przy którym uzyskuje sie maksymalny moment podporowy

Wykres momentów zginających

Wykres sił tnących

Schemat obciążenia, przy którym występuje maksymalny moment w przęśle 1-2

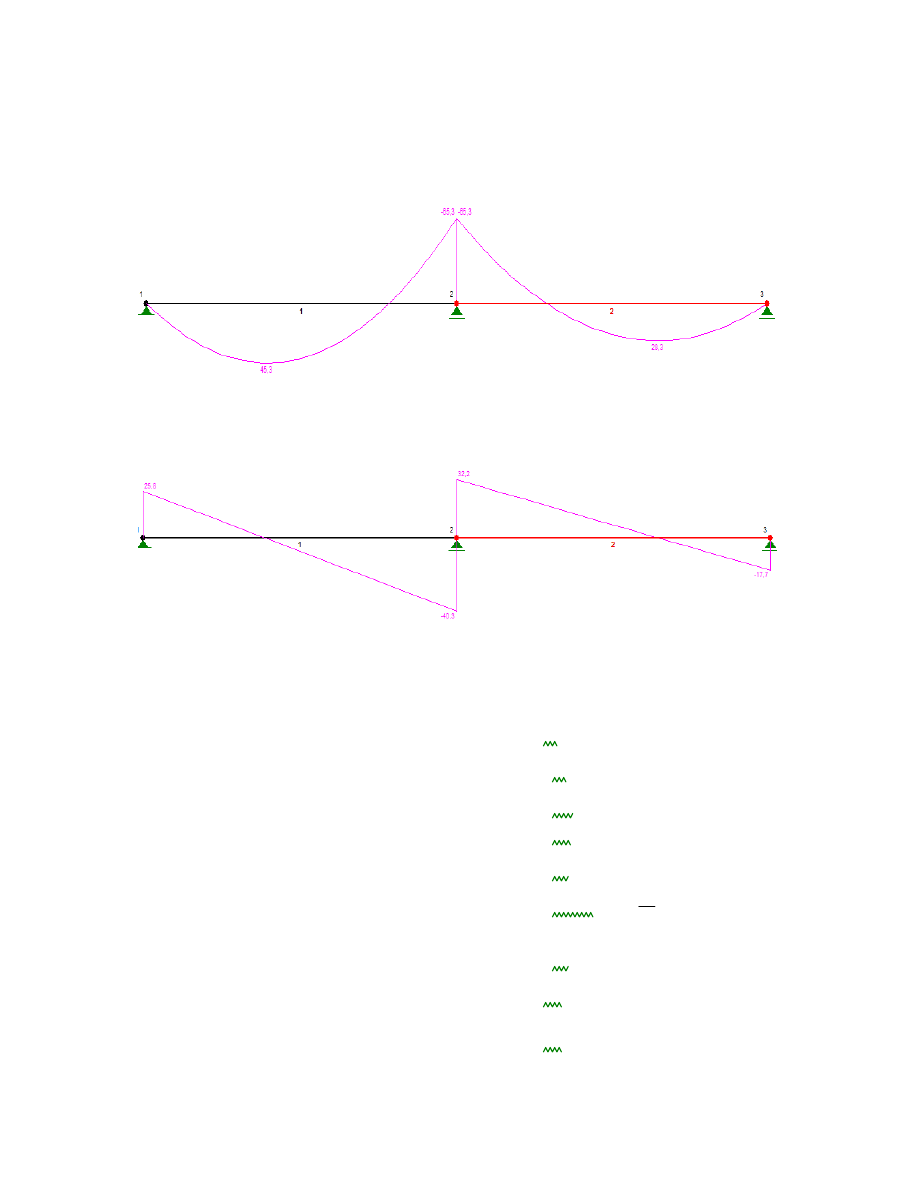
Wykres momentów zginających

Wykres sił tnących

2.3 Podstawowe dane projektowe podciągu:

wysokość

h

270mm



szerokość

b

135mm



grubość środnika

tw

6.6mm



tf

10.2mm



grubość półki

R

15mm



promień wyokrągleń

mIPE

36.1

kg

m



masa

pole przekroju

A

45.9cm

2



Iz

420cm

4



moment bezwładności względem osi x

moment bezwładności względem osi y

Iy

5790cm

4



wskażnik wytrzymałości względem osi x

Wel.z

62.2cm

3



wskaźnik wytrzymałości względem osi y

Wel.y

429cm

3



promień bezwładności względem osi x

iz

3.02cm



iy

11.2cm



promień bezwładności względem osi y

plastyczny wskaźnik wytrzymałości względem osi x

Wpl.z

97cm

3



plastyczny wskażnik wytrzymałości względem osi y

Wpl.y

484cm

3



Iw

70580cm

6



wycinkowy moment bezwładności przekroju płatwi

It

16.4cm

4



moment bezwładności na skręcanie przekroju płatwi

Iz 420 cm

4





moment bezwładności względem mniejszej osi bezwładności

Właściwości stali gatunku S355:

moduł Younga dla stali

E

210 GPa





moduł sprężystości poprzecznej

G

81 GPa





gatunek stali S355

fy

355

N

mm

2



Częściowe współczynniki bezbieczeństwa:

γM0 1



γM1 1



2.4 Sprawdzenie klasy przekroju

Sprawdzenie warunku stateczności nieużebrowanego ściananego środnika przekroju
dwuteowego. Sprawdzany przekrój znajduje się w klasie 1.

ε

235

N

mm

2

fy

0.814





η

1



Środnik jest poddany zginaniu. Smukłość środnika:

c

h

2 tf





2 R





0.22 m





t

tw



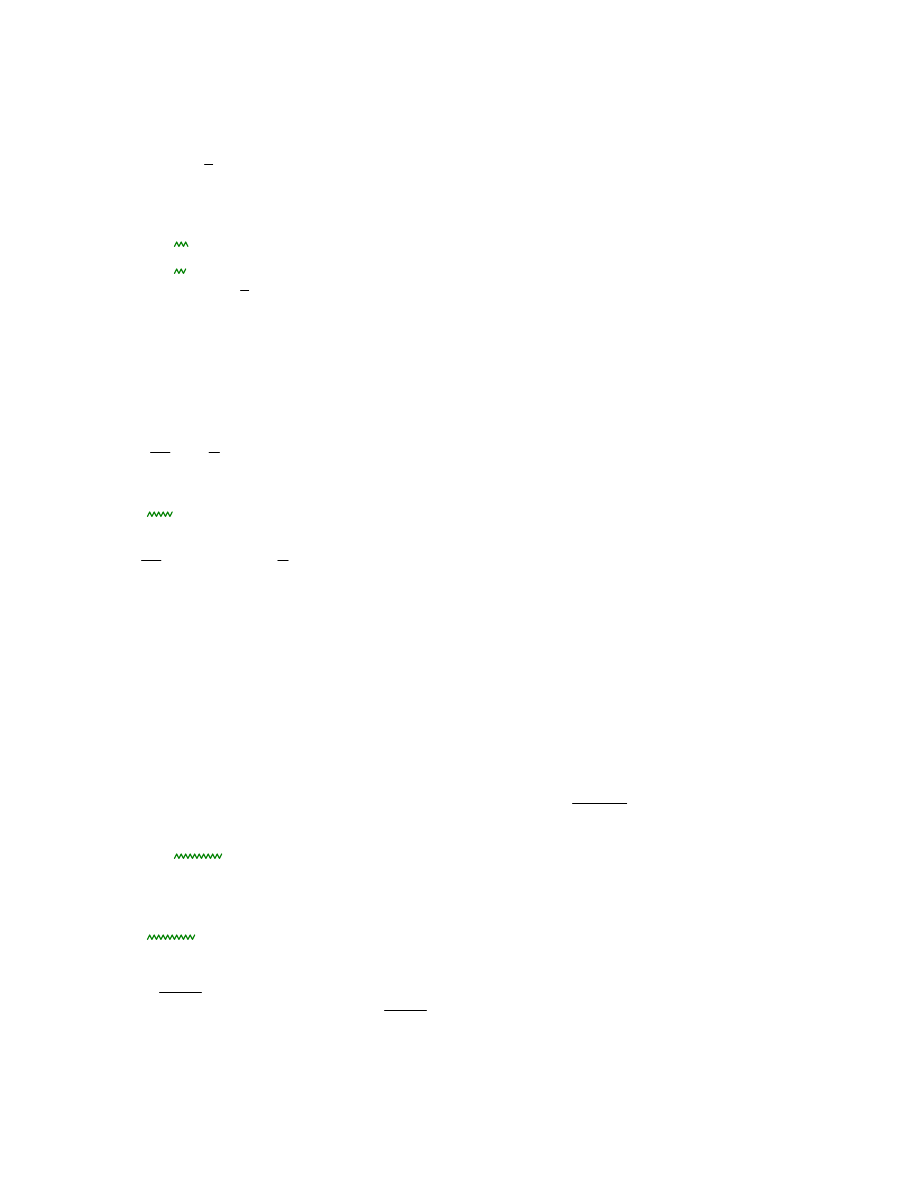
c

t

33.273



<

72 ε



58.58



Pas jest poddany ściskaniu. Smukłość pasa

c

0.5 b

tw



2 R











0.049 m





t

tf



c

t

4.824



<

9 ε



7.323



Kształtownik spełnia warunki przekroju klasy 1

2.5 Sprawdzenie możliwości utraty stateczności miejscowej przekroju
podciągu spowodowanej oddziaływaniem siły poprzecznej

hw

tw

72

ε

η





hw

h

2 R

tf











0.22 m





hw

tw

33.273



<

72

ε

η



58.58



Stateczność środnika belki poddanego ściskaniu jest zapewniona

2.6 Sprawdzenie nośności na zginanie przekroju nad podporą 2, w której
występuje największy moment zginający:

Ze względu na współpracę płyty z podciagiem:

χLT

1



Nośność dla przekroju klasy 1 :

Mc.Rd.

χLT

Wpl.y fy



γM0



1.718

10

5



J





Mc.Rd

778.9 kN



m





Warunek nośności przekroju przy obciążeniu momentem zginającym

My.Ed

Mmax.Ed 7.44 10

4



J





My.Ed
Mc.Rd

0.096



My.Ed
Mc.Rd

1



warunek został spełniony

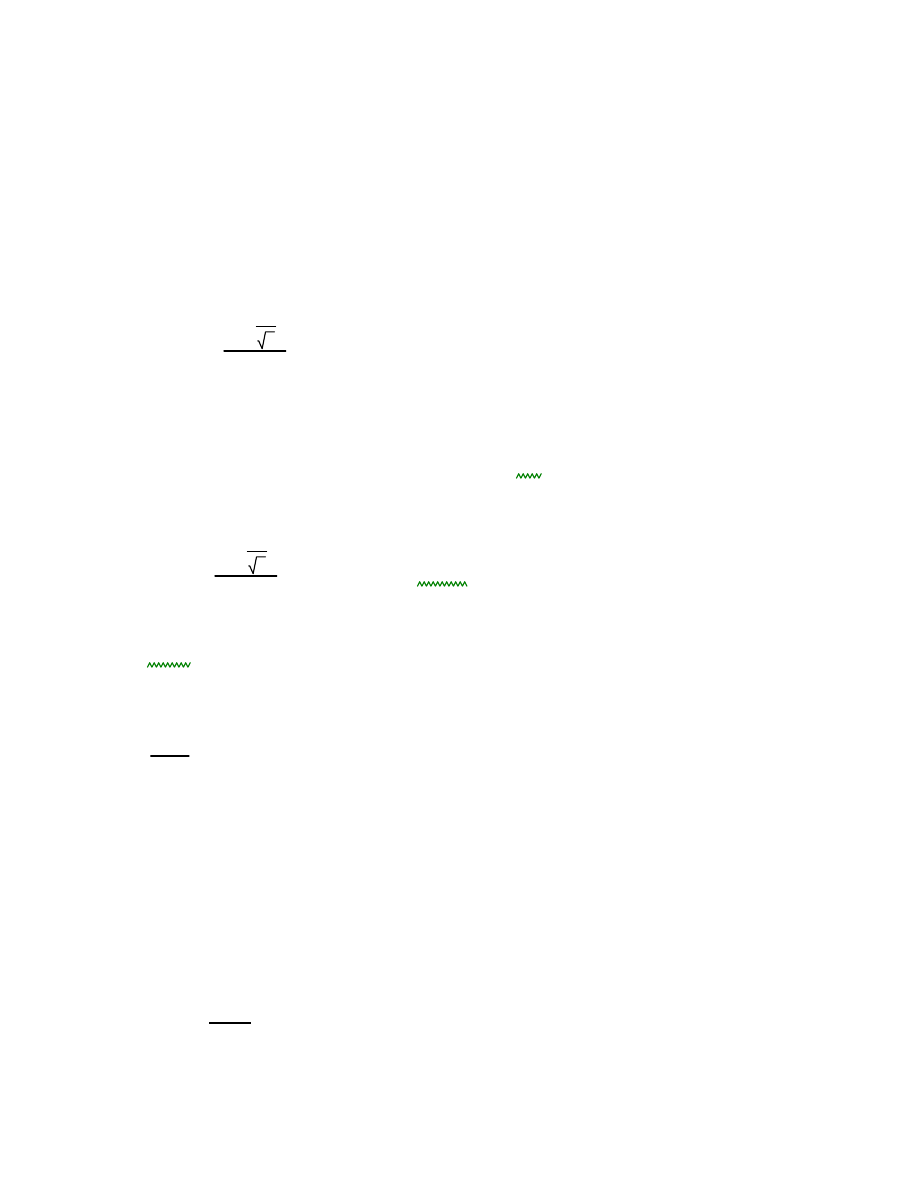
2.7 Sprawdzenie nośności na ścinanie przekroju nad podporą 2
w której wystepuje największa siła poprzeczna

Vc.Rd

Vpl.Rd



Przy projektowaniu plastyczności przyjmuje się

Obliczeniowa nośność plastyczna V

pl.Rd

przy ścinaniu:

Vpl.Rd

Av

fy

3















γM0



Av

Pole przekroju czynnego przy ścinaniu A

v

dwuteownika walcowanego, ścinanego prostopadle

do osi y-y:

Av

A

2 b

 t

f





tw 2R







tf





2.209

10

3





m

2





Av

6032 mm

2





lecz nie mniej niż:

η hw



tw



4260 mm

2





η hw



tw



Vpl.Rd

Av

fy

3















γM0

1.236

10

6



N





Vpl.Rd

1236 kN





Warunek nośności przekroju przy obciążeniu siłą poprzeczną:

Vc.Rd

Vpl.Rd



VEd

Vmax.Ed 4.138 10

4



N





VEd

Vc.Rd

0.033



< 1

warunek spełniony

2.8 Sprawdzenie przekroju nad podporą na jednoczesne
oddziaływanie momentu zginającego i siły poprzecznej.

Wpływ ścinania na nośność przy zgninaniu można pominąć, jeśli nośność przekroju nie ulega
redukcji w skutek wyboczenia przy ściananiu, a siła poprzeczna nie przekracza 50% nośności
plastycznej przekroju.

0.5 Vpl.Rd



618 kN





>

VEd 41.38 kN





Warunek został spełniony zatem przekrój nie jest narażony na wyboczenie z powodu ścinania,
dlatego siła poprzeczna nie ma istotnego wpływu na nośność przy zginaniu.

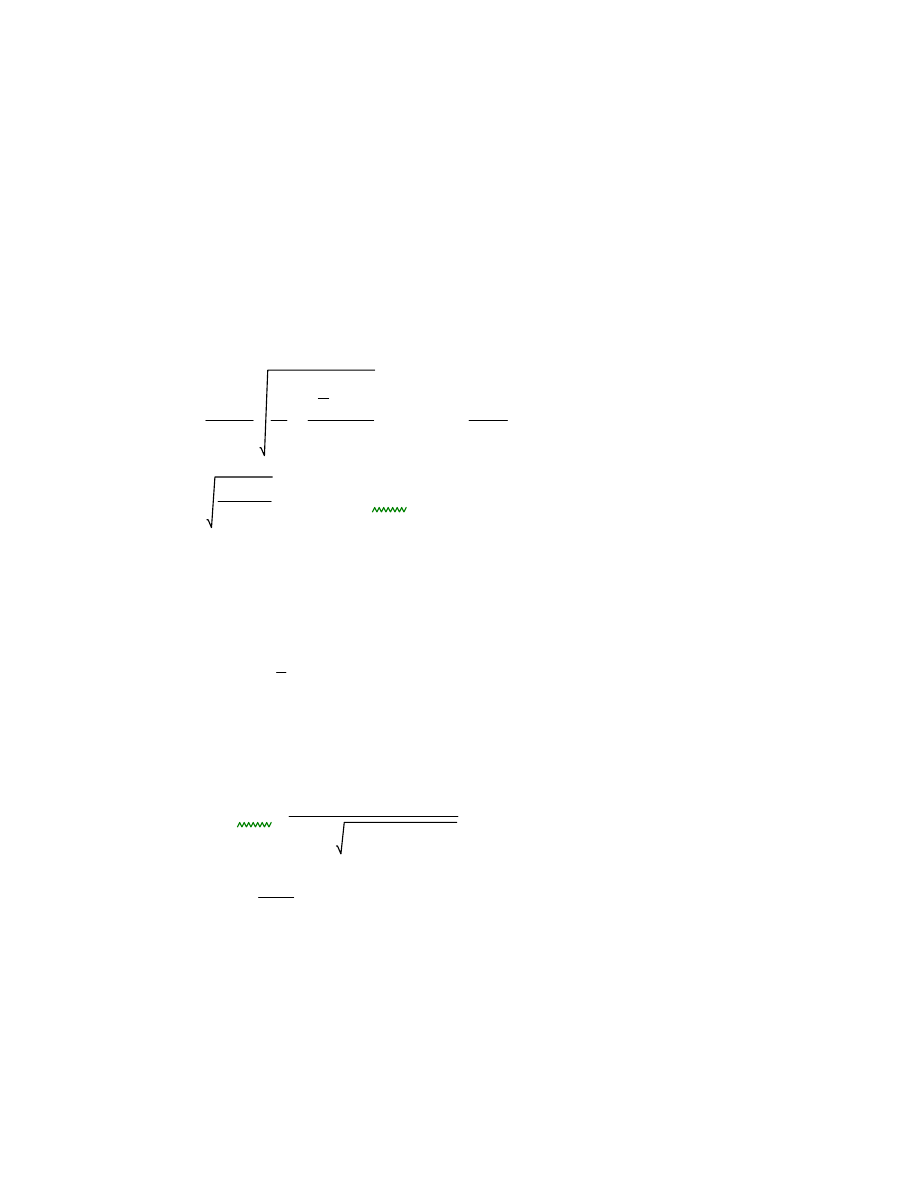
2.9 Sprawdzenie stateczności odcinka między podparciem
środkowym, a pierwszym żebrem podciągu - nośność przy
zwichrzeniu.

Przyjęto stałą wartość momentu zginającego na tym odcinku równą masymalnemu momentowi
przęsłowemu

MEd.ab

65.3 kN



m





Długość analitycznego odcinka belki

L1

2



Sprężysty moment krytyczny przy zwichrzeniu belki:

Mcr

π

2

E

 I

z



L1

2

Iw

Iz

L

4









2

G

 I

t



π

2

E

 I

z







3.408

10

5



m

4

kg



s

2





λLT

Wel.y fy



Mcr



λLT

0.668



λLT.0

0.4



dla profili walcowanych

β

0.75



Zgodnie z PN-EN 1993-1-1 Tablica 6.3 oraz Tablica 6.5 przyjmujemy zalecaną wartość parametru
imperfekcji przy zwichrzeniu:

h

b

2



stąd krzywa a

αLT

0.21



zatem

ϕLT

0.5 1

αLT λLT λLT.0











β λLT

2















0.695





współczynnik zwichrzenia

χLT

1

ϕLT

ϕLT

2

β λLT







2





0.849





< 1

1

λLT

2

2.241



> 1

Warunki spełnione

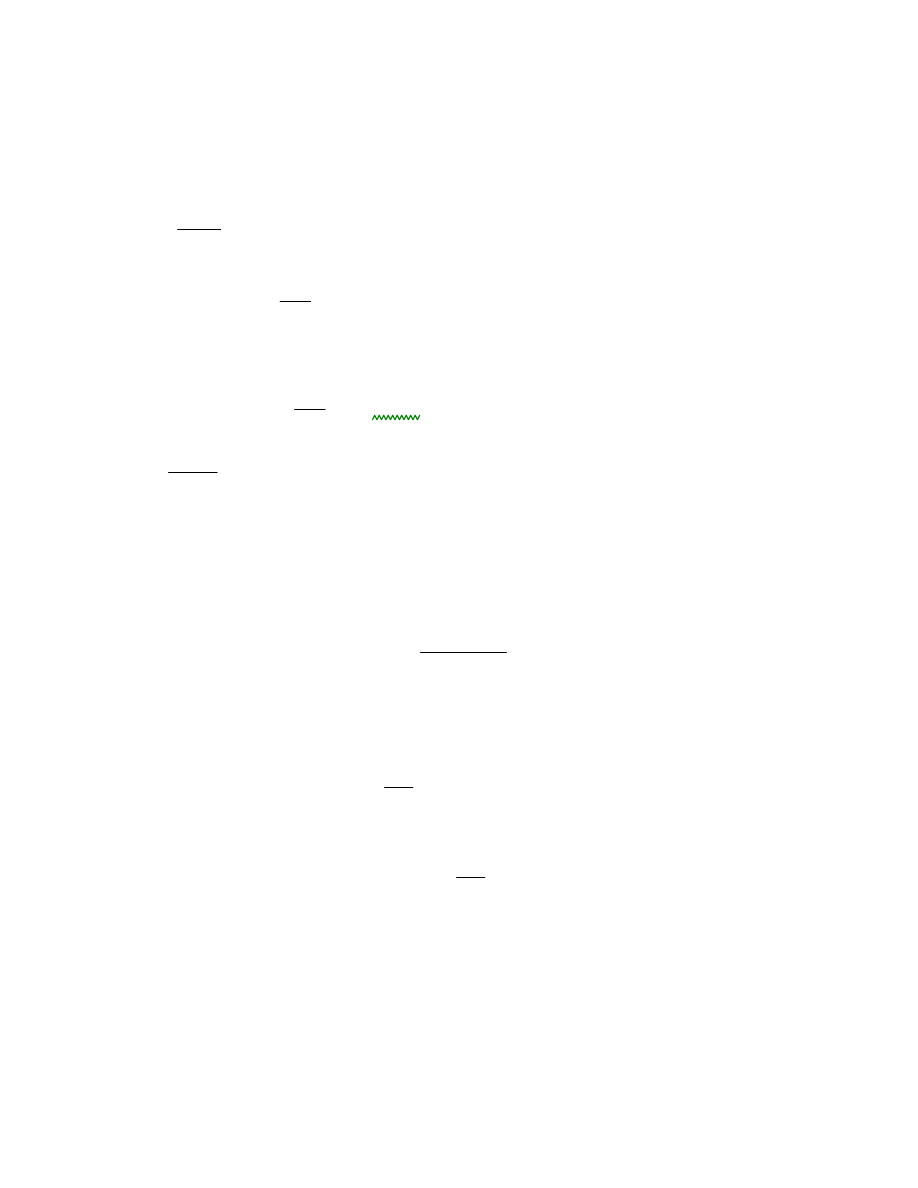
2.10 Nośność elementu na zwichrzenie

Warunek nośności elementu przy zginaniu względem osi y-y ze względu na zwichrzenie

MEd

Mb.Rd

1



Mb.Rd

χLT Wy



fy

γM1





Wy

Przekrój klasy 1.: W

y

Wpl.y 0.484 L





Mb.Rd

χLT Wpl.y



fy

γM1



1.459

10

5



J





Mb.Rd

768 kN



m





MEd.ab

Mb.Rd

0.085



< 1

Warunek spełniony

Sprawdzenie stateczności odcinka belki 1-2 - nośność na zwichrzenie

Rozkład momentów zginających bliski trójkątnemu:

ψ

0



Współczynnik poprawkowy:

kc

1

1.33

0.33 ψ





0.752





Współczynnik f:

f

1

0.5 1

kc









1

2 λLT 0.8







2

















0.88





f

1



warunek spełniony

χLT

f

0.964



Zatem zmodyfikowany współczynnik zwichrzenia:

χLT.mod

min

χLT

f

1















0.964





Tak więc na rozpatrywanym odcinku belki zwichrzenie nie nastąpi, o nośności decyduje
wyłącznie nośność przekroju.

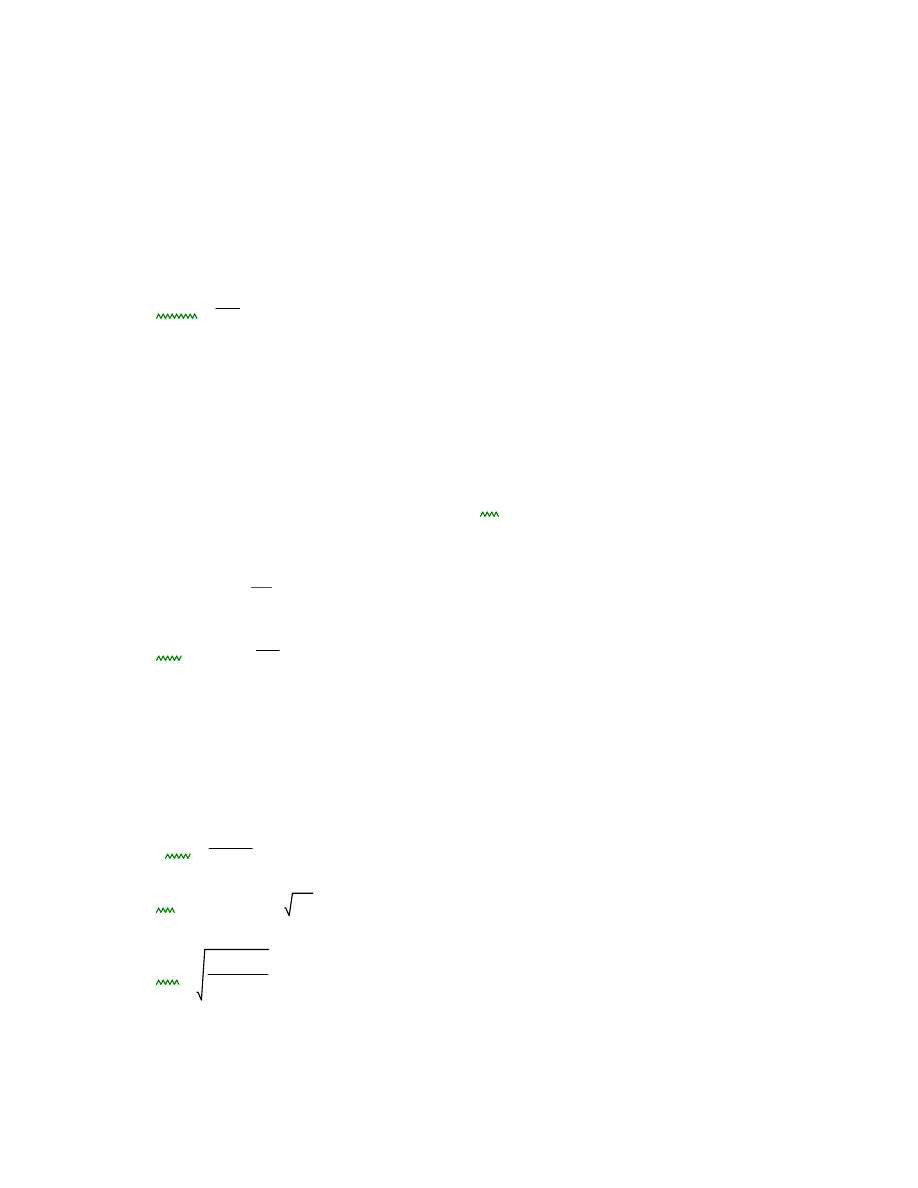
2.11 Sprawdzenie stanu granicznego użytkowalności:

Aby spełnić wymagania stany granicznego użytkowalności, należy sprawdzić ugięcie podciągu.
Maksymalne ugięcie wywołane obciążeniami charakterystycznymi wynosi

Wyliczenie ugięć dopuszczalnych

wmax

L

300

0.03 m





w

0.029 m



wmax w



warunek jest spełniony

2.12 Sprawdzenie nośności belki w obszerze przyłożenia
obciążenia skupionego

Przyjęto długość strefy przyłożenia obciążenia s

s

5mm



Ze względu na brak żeber usztywniających przyjęto a=∞

kF

6

2

hw

∞













2







2

hw

∞













2



kF

6



Fcr

0.9 kF



E



tw

3

hw



1.485

10

6



N





fyf

fy 3.55 10

8



Pa





fyw

fy 3.55 10

8



Pa





bf

b

0.135 m





m1

fyf bf



fyw tw



20.455





ly

.ss 2 tf



1

m1











0.113 m





λF

ly tw



fyw



Fcr

0.422





χF

0.5

λF

1.186





Warunek dodatkowy:

χF

1.0



Leff

χF ly



0.113 m





Obliczeniowa nośność środnika ze wzgledu na niestateczność pod siłą skupioną;

FRd

fyw Leff



tw



γM1

2.64

10

5



N





Warunek nośności:

η2

FEd
FRd

0.095





< 1

Warunek nośności środnika przy obciażeniu poprzeczną siłą skupioną jest spełniony

Interakcja obciążenia skupionego i momentu zginjącego: dodatkowo powinien być spełniony
warunek:

η2 0.8 η1





1.4



η1

Mmax.Ed

Mpl.Rd

0.433





η2 0.8 η1





0.441



0.441

1.4



Warunek jest spełniony