Automaty abstrakcyjne

maszyna Turinga

Wykład nr 3 z Podstaw Informatyki

Maszyna Turinga

●

Abstrakcyjna maszyna zdolna wykonywać
algorytmy (Alan Mathison Turing – On Com-
putable Numbers, 1936)

●

Obecnie stosowana głównie do udowadnia-
nia nierozstrzygalności problemów matema-
tycznych

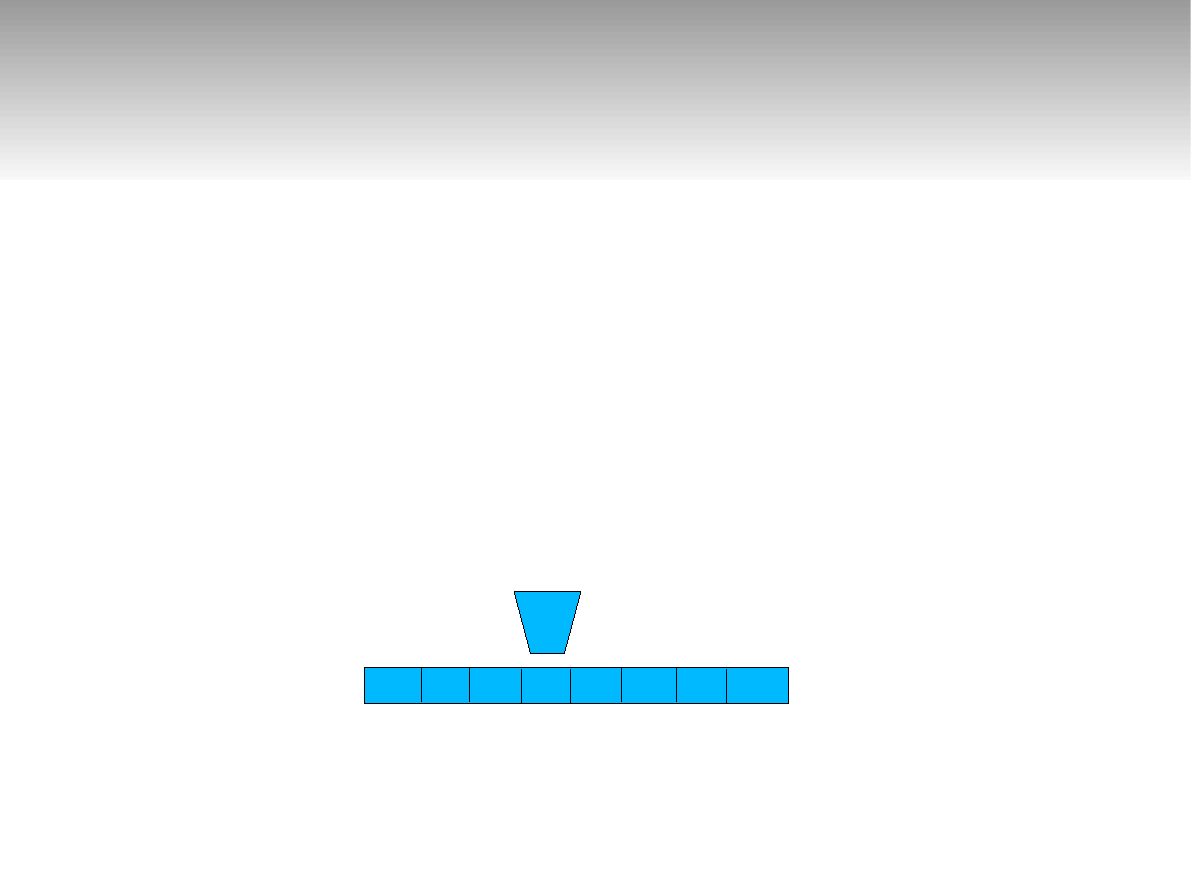
Elementy tworzące

maszynę Turinga

●

Nieskończenie długa taśma podzielona na
pola (z zapisanymi w nich symbolami)

●

Ruchoma głowica czytająco-pisząca znajdu-
jąca się w jednym z m możliwych stanów
wewnętrznych

Φ Φ b a b Φ Φ Φ

G

Program dla maszyny Turinga

●

Aktualny stan maszyny S

ij

= ( s

i

, q

j

)

●

s

i

symbol na taśmie pod głowicą

●

q

j

wewnętrzny stan głowicy

●

Ruch maszyny R

ij

= ( s

k

, K, q

l

)

●

s

k

nowy symbol zapisany na taśmie

●

K kierunek ruchu głowicy

●

q

l

nowy wewnętrzny stan głowicy

●

Program to zbiór reguł (rozkazów) postaci
R

ij

 = T( S

ij

) zwany tablicą charakterystyczną

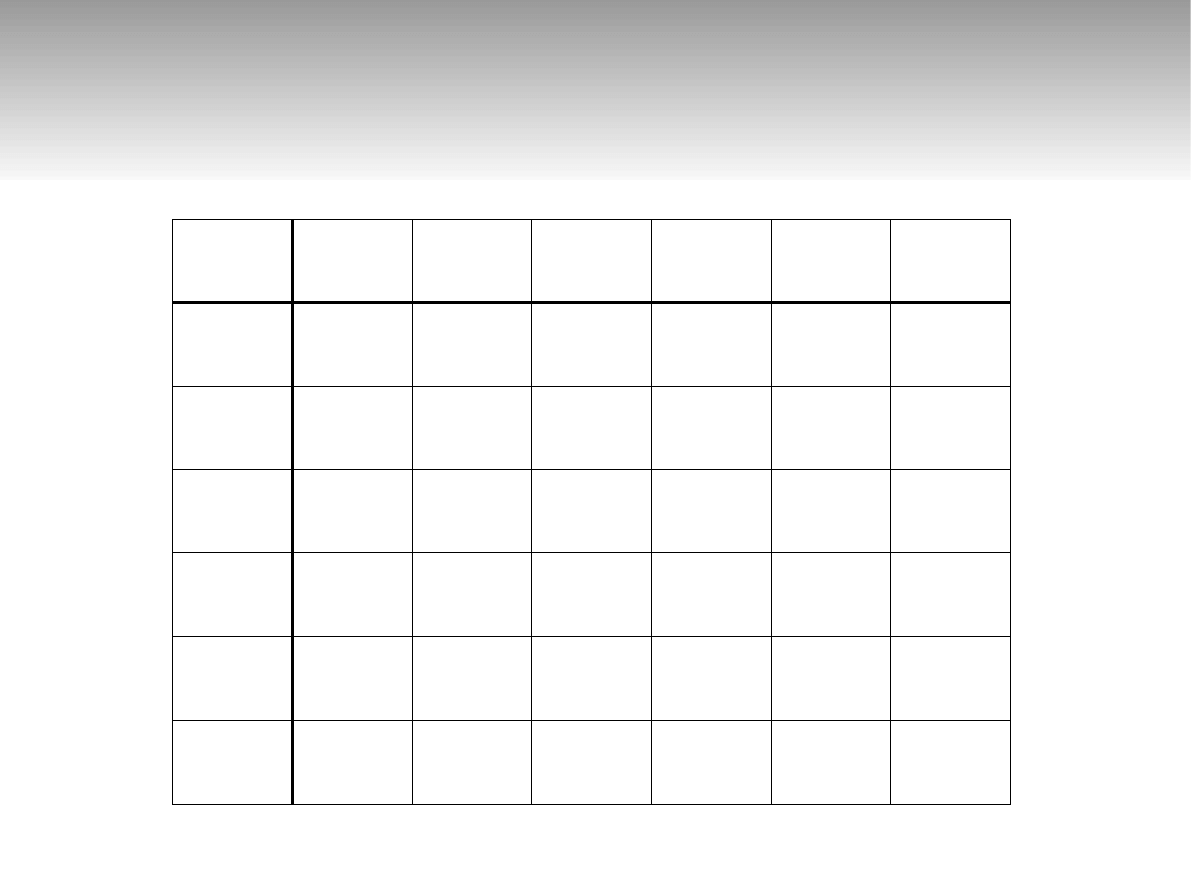
Tablica charakterystyczna

T

...

...

...

...

...

...

...

...

...

...

...

...

...

...

...

...

...

...

...

...

...

...

...

...

q

1

q

2

q

j

q

m

s

1

R

11

R

12

R

1j

R

1m

s

2

R

21

R

22

R

2j

R

2m

s

i

R

i1

R

i2

R

ij

R

im

s

n

R

n1

R

n2

R

nj

R

nm

Twierdzenie Turinga

●

Każdy algorytm może być realizowany przez
odpowiednio zaprogramowaną maszynę Tu-
ringa

Przykład 1

●

Na taśmie zapisano 3-literowy ciąg złożony
z symboli: a, b i c.

●

Tylko napis abc jest poprawny

●

Podać algorytm rozpoznawania tego napisu

Przykład 1 – algorytm

1. Pobierz symbol. Jeżeli jest nim a to przejdź

do 2, w przeciwnym przypadku przejdź do 4.

2. Przesuń głowicę w prawo, pobierz symbol,

jeżeli jest nim b to przejdź do 3, jeśli nie
– przejdź do 4.

3. Przesuń głowicę w prawo, pobierz symbol,

jeżeli jest nim c to przejdź do 5, jeśli nie
– przejdź do 4.

4. Sygnalizuj nieprawidłowy napis. Koniec.
5. Sygnalizuj napis prawidłowy. Koniec.

Przykład 1 – tablica charaktery-

styczna

a

b

c

q

1

q

2

q

3

q

4

q

5

aPq

2

aNq

4

aNq

4

aNq

4

aNq

5

bNq

4

bPq

3

bNq

4

bNq

4

bNq

5

cNq

4

cNq

4

cNq

5

cNq

4

cNq

5

Przykład 1 – algorytm

a

b

c

q

1

q

2

q

3

q

4

q

5

aPq

2

aNq

4

aNq

4

aNq

4

aNq

5

bNq

4

bPq

3

bNq

4

bNq

4

bNq

5

cNq

4

cNq

4

cNq

5

cNq

4

cNq

5

↓
a a c

Przykład 1 – algorytm

a

b

c

q

1

q

2

q

3

q

4

q

5

aPq

2

aNq

4

aNq

4

aNq

4

aNq

5

bNq

4

bPq

3

bNq

4

bNq

4

bNq

5

cNq

4

cNq

4

cNq

5

cNq

4

cNq

5

↓
a a c

Przykład 1 – algorytm

a

b

c

q

1

q

2

q

3

q

4

q

5

aPq

2

aNq

4

aNq

4

aNq

4

aNq

5

bNq

4

bPq

3

bNq

4

bNq

4

bNq

5

cNq

4

cNq

4

cNq

5

cNq

4

cNq

5

↓

a a c

Przykład 1 – algorytm

a

b

c

q

1

q

2

q

3

q

4

q

5

aPq

2

aNq

4

aNq

4

aNq

4

aNq

5

bNq

4

bPq

3

bNq

4

bNq

4

bNq

5

cNq

4

cNq

4

cNq

5

cNq

4

cNq

5

↓

a a c

Przykład 1 – algorytm

a

b

c

q

1

q

2

q

3

q

4

q

5

aPq

2

aNq

4

aNq

4

aNq

4

aNq

5

bNq

4

bPq

3

bNq

4

bNq

4

bNq

5

cNq

4

cNq

4

cNq

5

cNq

4

cNq

5

↓

a a c

Automat kończy pracę w stanie q

4

.

Napis niepoprawny

Przykład 1 – algorytm

a

b

c

q

1

q

2

q

3

q

4

q

5

aPq

2

aNq

4

aNq

4

aNq

4

aNq

5

bNq

4

bPq

3

bNq

4

bNq

4

bNq

5

cNq

4

cNq

4

cNq

5

cNq

4

cNq

5

Przykład 1 – algorytm

a

b

c

q

1

q

2

q

3

q

4

q

5

aPq

2

aNq

4

aNq

4

aNq

4

aNq

5

bNq

4

bPq

3

bNq

4

bNq

4

bNq

5

cNq

4

cNq

4

cNq

5

cNq

4

cNq

5

↓
a b c

Przykład 1 – algorytm

a

b

c

q

1

q

2

q

3

q

4

q

5

aPq

2

aNq

4

aNq

4

aNq

4

aNq

5

bNq

4

bPq

3

bNq

4

bNq

4

bNq

5

cNq

4

cNq

4

cNq

5

cNq

4

cNq

5

↓
a b c

Przykład 1 – algorytm

a

b

c

q

1

q

2

q

3

q

4

q

5

aPq

2

aNq

4

aNq

4

aNq

4

aNq

5

bNq

4

bPq

3

bNq

4

bNq

4

bNq

5

cNq

4

cNq

4

cNq

5

cNq

4

cNq

5

↓

a b c

Przykład 1 – algorytm

a

b

c

q

1

q

2

q

3

q

4

q

5

aPq

2

aNq

4

aNq

4

aNq

4

aNq

5

bNq

4

bPq

3

bNq

4

bNq

4

bNq

5

cNq

4

cNq

4

cNq

5

cNq

4

cNq

5

↓

a b c

Przykład 1 – algorytm

a

b

c

q

1

q

2

q

3

q

4

q

5

aPq

2

aNq

4

aNq

4

aNq

4

aNq

5

bNq

4

bPq

3

bNq

4

bNq

4

bNq

5

cNq

4

cNq

4

cNq

5

cNq

4

cNq

5

↓

a b c

Przykład 1 – algorytm

a

b

c

q

1

q

2

q

3

q

4

q

5

aPq

2

aNq

4

aNq

4

aNq

4

aNq

5

bNq

4

bPq

3

bNq

4

bNq

4

bNq

5

cNq

4

cNq

4

cNq

5

cNq

4

cNq

5

↓

a b c

Przykład 1 – algorytm

a

b

c

q

1

q

2

q

3

q

4

q

5

aPq

2

aNq

4

aNq

4

aNq

4

aNq

5

bNq

4

bPq

3

bNq

4

bNq

4

bNq

5

cNq

4

cNq

4

cNq

5

cNq

4

cNq

5

↓

a b c

Przykład 1 – algorytm

a

b

c

q

1

q

2

q

3

q

4

q

5

aPq

2

aNq

4

aNq

4

aNq

4

aNq

5

bNq

4

bPq

3

bNq

4

bNq

4

bNq

5

cNq

4

cNq

4

cNq

5

cNq

4

cNq

5

Automat kończy pracę w stanie q

5

.

Napis poprawny

Przykład 2 – inkrementacja liczby

●

Na taśmie umieszczono liczbę całkowitą ze
znakiem zapisaną w zapisie uzupełnienio-
wym do 2

●

W miejsce tej liczby wpisać liczbę o 1 więk-
szą (dodać jedynkę)

●

Głowica znajduje się na prawo od liczby na
symbolu pustym Φ

●

Binarna reprezentacja liczby całkowitej bez
znaku:

a

6

∙2

6

+a

5

∙2

5

+a

4

∙2

4

+a

3

∙2

3

+a

2

∙2

2

+a

1

∙2

1

+a

0

∙2

0

a

6

∙64+a

5

∙32+a

4

∙16+a

3

∙8+a

2

∙4+a

1

∙2+a

0

∙1

Binarna reprezentacja liczby

●

Binarna reprezentacja liczby całkowitej bez
znaku:

a

6

∙2

6

+a

5

∙2

5

+a

4

∙2

4

+a

3

∙2

3

+a

2

∙2

2

+a

1

∙2

1

+a

0

∙2

0

a

6

∙64+a

5

∙32+a

4

∙16+a

3

∙8+a

2

∙4+a

1

∙2+a

0

∙1

Np. 23

23 = 16 + 4 + 2 + 1

23 = 0∙64+0∙32+1∙16+0∙8+1∙4+1∙2+1∙1

Binarna reprezentacja liczby

●

Binarna reprezentacja liczby całkowitej bez
znaku:

a

6

∙2

6

+a

5

∙2

5

+a

4

∙2

4

+a

3

∙2

3

+a

2

∙2

2

+a

1

∙2

1

+a

0

∙2

0

a

6

∙64+a

5

∙32+a

4

∙16+a

3

∙8+a

2

∙4+a

1

∙2+a

0

∙1

Np. 23

23 = 16 + 4 + 2 + 1

23 = 0∙64+0∙32+1∙16+0∙8+1∙4+1∙2+1∙1

23 ≡ 0010111

Binarna reprezentacja liczby

●

Znak reprezentowany w postaci dodatkowe-
go bitu zwanego bitem znaku

●

Liczba dodatnia – 0, liczba ujemna – 1

●

3 formy zapisu:

●

znak moduł

●

uzupełnieniowy do 1

●

uzupełnieniowy do 2

Co zrobić ze znakiem ?

●

Z lewej strony liczby binarnej umieścić bit
znaku

●

Np. 23

Liczba dodatnia w zapisie U2

●

Z lewej strony liczby binarnej umieścić bit
znaku

●

Np. 23

0 0 1 0 1 1 1

Liczba dodatnia w zapisie U2

●

Z lewej strony liczby binarnej umieścić bit
znaku

●

Np.

+

23

0

0 0 1 0 1 1 1

Liczba dodatnia w zapisie U2

●

Znaleźć reprezentację liczby przeciwnej

●

Zanegować wszystkie bity

●

Dodać jedynkę

Liczba ujemna w zapisie U2

●

Znaleźć reprezentację liczby przeciwnej

●

Zanegować wszystkie bity

●

Dodać jedynkę

●

Np.

-

23

0

0 0 1 0 1 1 1 (+23)

Liczba ujemna w zapisie U2

●

Znaleźć reprezentację liczby przeciwnej

●

Zanegować wszystkie bity

●

Dodać jedynkę

●

Np.

-

23

0

0 0 1 0 1 1 1 (+23)

1

1 1 0 1 0 0 0

Liczba ujemna w zapisie U2

●

Znaleźć reprezentację liczby przeciwnej

●

Zanegować wszystkie bity

●

Dodać jedynkę

●

Np.

-

23

0

0 0 1 0 1 1 1 (+23)

1

1 1 0 1 0 0 0

+ 1

Liczba ujemna w zapisie U2

●

Znaleźć reprezentację liczby przeciwnej

●

Zanegować wszystkie bity

●

Dodać jedynkę

●

Np.

-

23

0

0 0 1 0 1 1 1 (+23)

1

1 1 0 1 0 0 0

+ 1

1

1 1 0 1 0 0 1 (-23)

Liczba ujemna w zapisie U2

●

Dodawanie jedynki do liczby parzystej

0 1 1 0 1 1 0 0 (+108)

+ 1

0 1 1 0 1 1 0 1 (+109)

Inkrementacja liczb binarnych

●

Dodawanie jedynki do liczby parzystej

0 1 1 0 1 1 0 0 (+108)

+ 1

0 1 1 0 1 1 0 1 (+109)

1 1 1 1 0 1 1 0 (-10)

+ 1

1 1 1 1 0 1 1 1 (-9)

Inkrementacja liczb binarnych

●

Dodawanie jedynki do liczby parzystej

●

Inkrementacja liczby nieparzystej

0 0 0 0 1 0 1 1 (+11)

+ 1

0 0 0 0 1 1 0 0 (+12)

Inkrementacja liczb binarnych

●

Dodawanie jedynki do liczby parzystej

●

Inkrementacja liczby nieparzystej

●

Sytuacje szczególne

1 1 1 1 1 1 1 1 (-1)

+ 1

0 0 0 0 0 0 0 0 (0)

Inkrementacja liczb binarnych

●

Dodawanie jedynki do liczby parzystej

●

Inkrementacja liczby nieparzystej

●

Sytuacje szczególne

0 1 1 1 1 1 1 1 (+127)

+ 1

1 0 0 0 0 0 0 0 (-128)

Inkrementacja liczb binarnych

●

Dodawanie jedynki do liczby parzystej

●

Inkrementacja liczby nieparzystej

●

Sytuacje szczególne

0 1 1 1 1 1 1 1 (+127)

+ 1

1 0 0 0 0 0 0 0 (-128)

Inkrementacja liczb binarnych

●

Dodawanie jedynki do liczby parzystej

●

Inkrementacja liczby nieparzystej

●

Sytuacje szczególne

0 1 1 1 1 1 1 1 (+127)

+ 1

0 1 0 0 0 0 0 0 0 (-128)

Inkrementacja liczb binarnych

●

Przesuwaj się od prawej do lewej i zamieniaj
wszystkie jedynki na zera aż do napotkania
zera, które należy zamienić na jedynkę

●

Dodatkowo sprawdzaj czy zamienione na
jedynkę zero nie było bitem znaku. Jeśli tak
rozszerz liczbę o nowy bit znaku.

Algorytm inkrementacji liczb binar-

nych

Stan q

1

– poszukiwanie najmniej znaczącego

bitu liczby

Przykład 2 – tablica charaktery-

styczna

Φ

0

1

q

1

q

2

q

3

q

4

ΦLq

1

1Nq

4

0Lq

2

Przykład 2 – tablica charaktery-

styczna

Φ

0

1

q

1

q

2

q

3

q

4

ΦLq

1

ΦNq

4

1Nq

4

1Lq

3

0Lq

2

0Lq

2

Stan q

2

– zamiana jedynek na zera aż do napo-

tkania zera i zamiana go na jedynkę

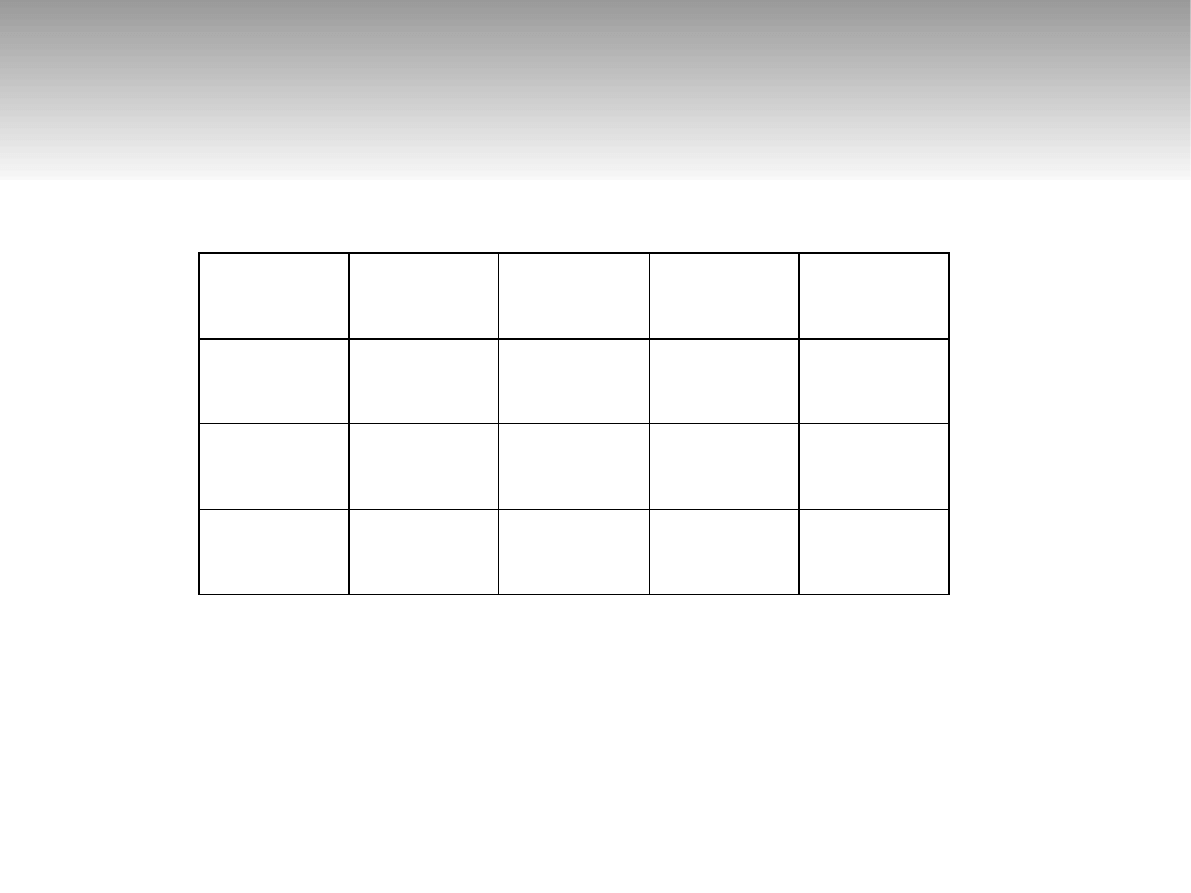
Przykład 2 – tablica charaktery-

styczna

Φ

0

1

q

1

q

2

q

3

q

4

ΦLq

1

ΦNq

4

0Nq

4

1Nq

4

1Lq

3

0Nq

4

0Lq

2

0Lq

2

1Nq

4

Stan q

3

– sprawdzenie czy nie zmieniono zna-

ku liczby

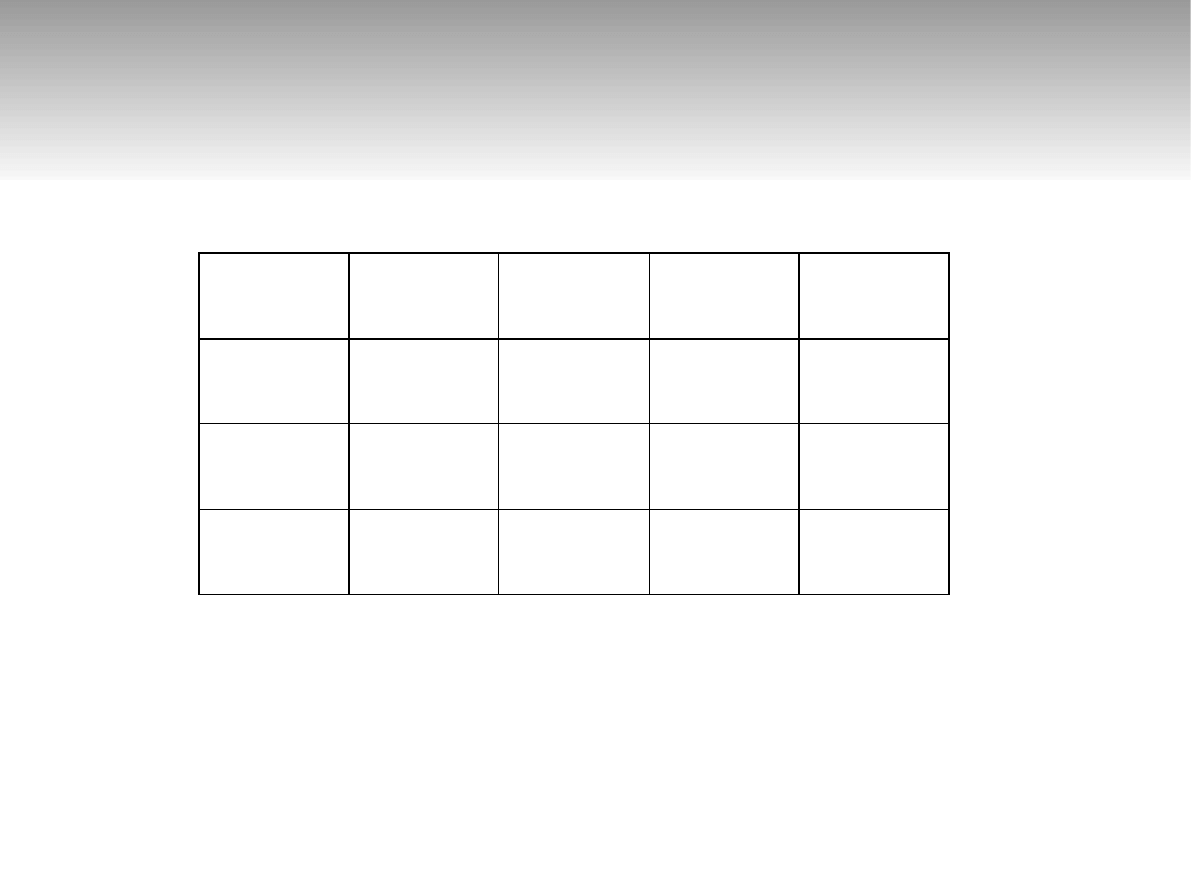
Przykład 2 – tablica charaktery-

styczna

Φ

0

1

q

1

q

2

q

3

q

4

ΦLq

1

ΦNq

4

0Nq

4

ΦNq

4

1Nq

4

1Lq

3

0Nq

4

0Nq

4

0Lq

2

0Lq

2

1Nq

4

1Nq

4

Stan q

4

– stan końcowy

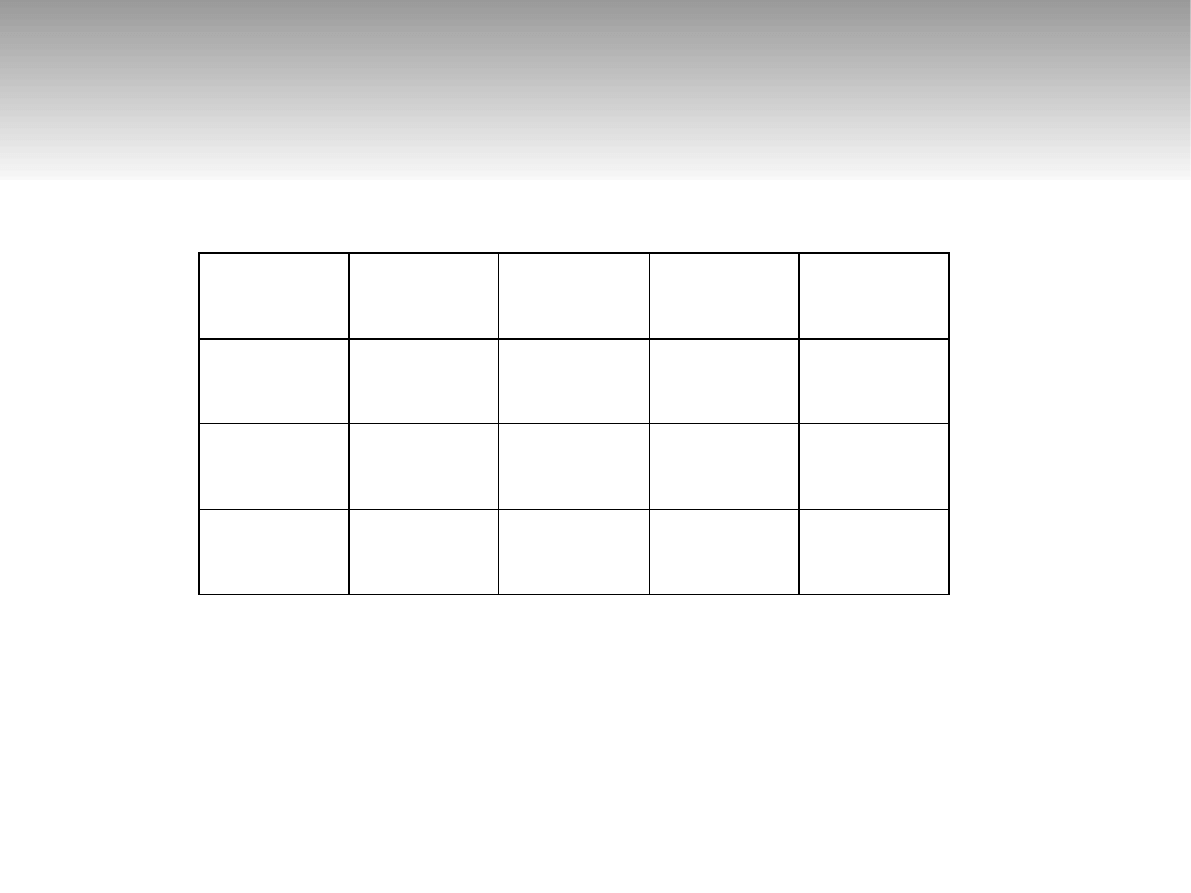
Przykład 2 – tablica charaktery-

styczna

Φ

0

1

q

1

q

2

q

3

q

4

ΦLq

1

ΦNq

4

0Nq

4

ΦNq

4

1Nq

4

1Lq

3

0Nq

4

0Nq

4

0Lq

2

0Lq

2

1Nq

4

1Nq

4

↓

Φ Φ 0 0 1 0 1 1 1 1 Φ Φ

47

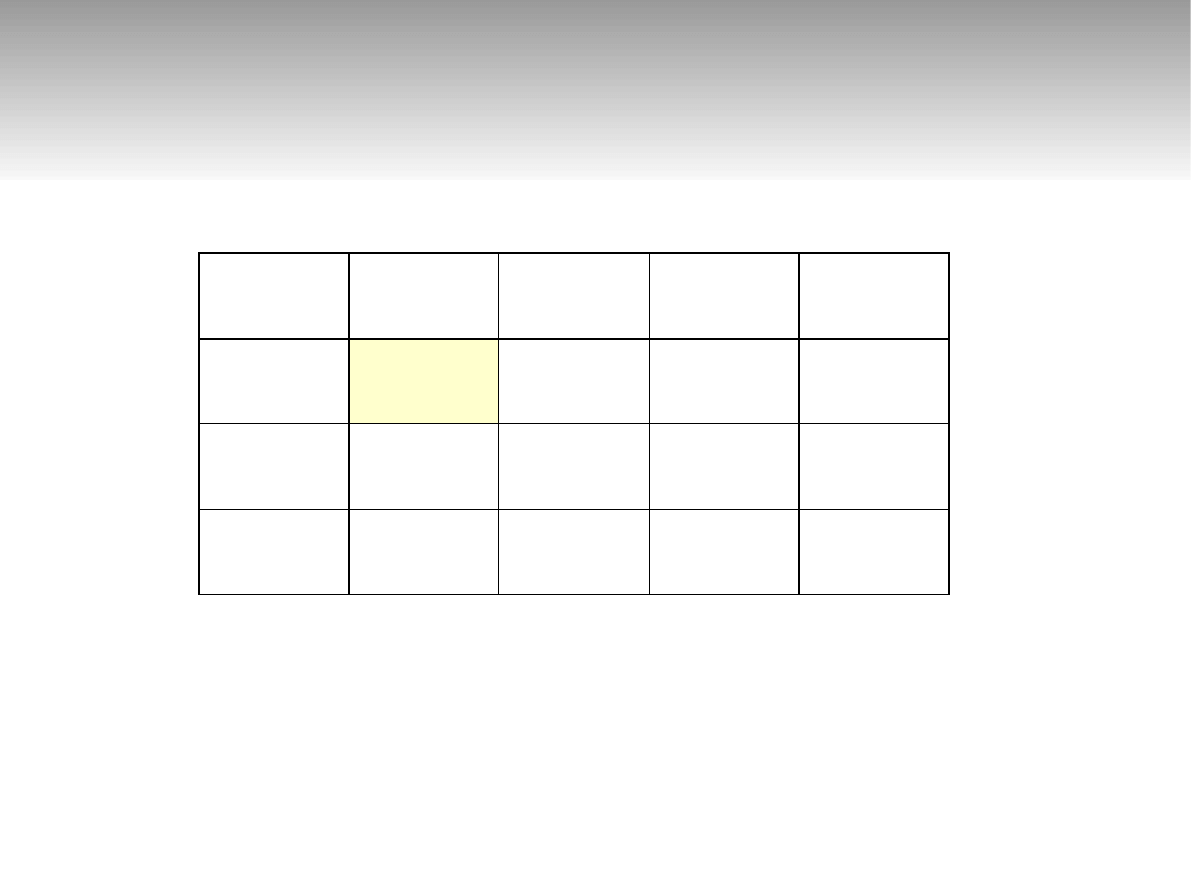
Przykład 2 – tablica charaktery-

styczna

Φ

0

1

q

1

q

2

q

3

q

4

ΦLq

1

ΦNq

4

0Nq

4

ΦNq

4

1Nq

4

1Lq

3

0Nq

4

0Nq

4

0Lq

2

0Lq

2

1Nq

4

1Nq

4

↓

Φ Φ 0 0 1 0 1 1 1 1 Φ Φ

Przykład 2 – tablica charaktery-

styczna

Φ

0

1

q

1

q

2

q

3

q

4

ΦLq

1

ΦNq

4

0Nq

4

ΦNq

4

1Nq

4

1Lq

3

0Nq

4

0Nq

4

0Lq

2

0Lq

2

1Nq

4

1Nq

4

↓

Φ Φ 0 0 1 0 1 1 1 1 Φ Φ

Przykład 2 – tablica charaktery-

styczna

Φ

0

1

q

1

q

2

q

3

q

4

ΦLq

1

ΦNq

4

0Nq

4

ΦNq

4

1Nq

4

1Lq

3

0Nq

4

0Nq

4

0Lq

2

0Lq

2

1Nq

4

1Nq

4

↓

Φ Φ 0 0 1 0 1 1 1 1 Φ Φ

Przykład 2 – tablica charaktery-

styczna

Φ

0

1

q

1

q

2

q

3

q

4

ΦLq

1

ΦNq

4

0Nq

4

ΦNq

4

1Nq

4

1Lq

3

0Nq

4

0Nq

4

0Lq

2

0Lq

2

1Nq

4

1Nq

4

↓

Φ Φ 0 0 1 0 1 1 1 0 Φ Φ

Przykład 2 – tablica charaktery-

styczna

Φ

0

1

q

1

q

2

q

3

q

4

ΦLq

1

ΦNq

4

0Nq

4

ΦNq

4

1Nq

4

1Lq

3

0Nq

4

0Nq

4

0Lq

2

0Lq

2

1Nq

4

1Nq

4

↓

Φ Φ 0 0 1 0 1 1 0 0 Φ Φ

Przykład 2 – tablica charaktery-

styczna

Φ

0

1

q

1

q

2

q

3

q

4

ΦLq

1

ΦNq

4

0Nq

4

ΦNq

4

1Nq

4

1Lq

3

0Nq

4

0Nq

4

0Lq

2

0Lq

2

1Nq

4

1Nq

4

↓

Φ Φ 0 0 1 0 1 0 0 0 Φ Φ

Przykład 2 – tablica charaktery-

styczna

Φ

0

1

q

1

q

2

q

3

q

4

ΦLq

1

ΦNq

4

0Nq

4

ΦNq

4

1Nq

4

1Lq

3

0Nq

4

0Nq

4

0Lq

2

0Lq

2

1Nq

4

1Nq

4

↓

Φ Φ 0 0 1 0 0 0 0 0 Φ Φ

Przykład 2 – tablica charaktery-

styczna

Φ

0

1

q

1

q

2

q

3

q

4

ΦLq

1

ΦNq

4

0Nq

4

ΦNq

4

1Nq

4

1Lq

3

0Nq

4

0Nq

4

0Lq

2

0Lq

2

1Nq

4

1Nq

4

↓

Φ Φ 0 0 1 1 0 0 0 0 Φ Φ

Przykład 2 – tablica charaktery-

styczna

Φ

0

1

q

1

q

2

q

3

q

4

ΦLq

1

ΦNq

4

0Nq

4

ΦNq

4

1Nq

4

1Lq

3

0Nq

4

0Nq

4

0Lq

2

0Lq

2

1Nq

4

1Nq

4

↓

Φ Φ 0 0 1 1 0 0 0 0 Φ Φ

48

Przykład 2 – tablica charaktery-

styczna

Φ

0

1

q

1

q

2

q

3

q

4

ΦLq

1

ΦNq

4

0Nq

4

ΦNq

4

1Nq

4

1Lq

3

0Nq

4

0Nq

4

0Lq

2

0Lq

2

1Nq

4

1Nq

4

Przykład 2 – tablica charaktery-

styczna

Φ

0

1

q

1

q

2

q

3

q

4

ΦLq

1

ΦNq

4

0Nq

4

ΦNq

4

1Nq

4

1Lq

3

0Nq

4

0Nq

4

0Lq

2

0Lq

2

1Nq

4

1Nq

4

↓

Φ Φ 0 1 1 1 1 Φ Φ

15

Przykład 2 – tablica charaktery-

styczna

Φ

0

1

q

1

q

2

q

3

q

4

ΦLq

1

ΦNq

4

0Nq

4

ΦNq

4

1Nq

4

1Lq

3

0Nq

4

0Nq

4

0Lq

2

0Lq

2

1Nq

4

1Nq

4

↓

Φ Φ 0 1 1 1 1 Φ Φ

Przykład 2 – tablica charaktery-

styczna

Φ

0

1

q

1

q

2

q

3

q

4

ΦLq

1

ΦNq

4

0Nq

4

ΦNq

4

1Nq

4

1Lq

3

0Nq

4

0Nq

4

0Lq

2

0Lq

2

1Nq

4

1Nq

4

↓

Φ Φ 0 1 1 1 0 Φ Φ

Przykład 2 – tablica charaktery-

styczna

Φ

0

1

q

1

q

2

q

3

q

4

ΦLq

1

ΦNq

4

0Nq

4

ΦNq

4

1Nq

4

1Lq

3

0Nq

4

0Nq

4

0Lq

2

0Lq

2

1Nq

4

1Nq

4

↓

Φ Φ 0 1 1 0 0 Φ Φ

Przykład 2 – tablica charaktery-

styczna

Φ

0

1

q

1

q

2

q

3

q

4

ΦLq

1

ΦNq

4

0Nq

4

ΦNq

4

1Nq

4

1Lq

3

0Nq

4

0Nq

4

0Lq

2

0Lq

2

1Nq

4

1Nq

4

↓

Φ Φ 0 1 0 0 0 Φ Φ

Przykład 2 – tablica charaktery-

styczna

Φ

0

1

q

1

q

2

q

3

q

4

ΦLq

1

ΦNq

4

0Nq

4

ΦNq

4

1Nq

4

1Lq

3

0Nq

4

0Nq

4

0Lq

2

0Lq

2

1Nq

4

1Nq

4

↓

Φ Φ 0 0 0 0 0 Φ Φ

Przykład 2 – tablica charaktery-

styczna

Φ

0

1

q

1

q

2

q

3

q

4

ΦLq

1

ΦNq

4

0Nq

4

ΦNq

4

1Nq

4

1Lq

3

0Nq

4

0Nq

4

0Lq

2

0Lq

2

1Nq

4

1Nq

4

↓

Φ Φ 1 0 0 0 0 Φ Φ

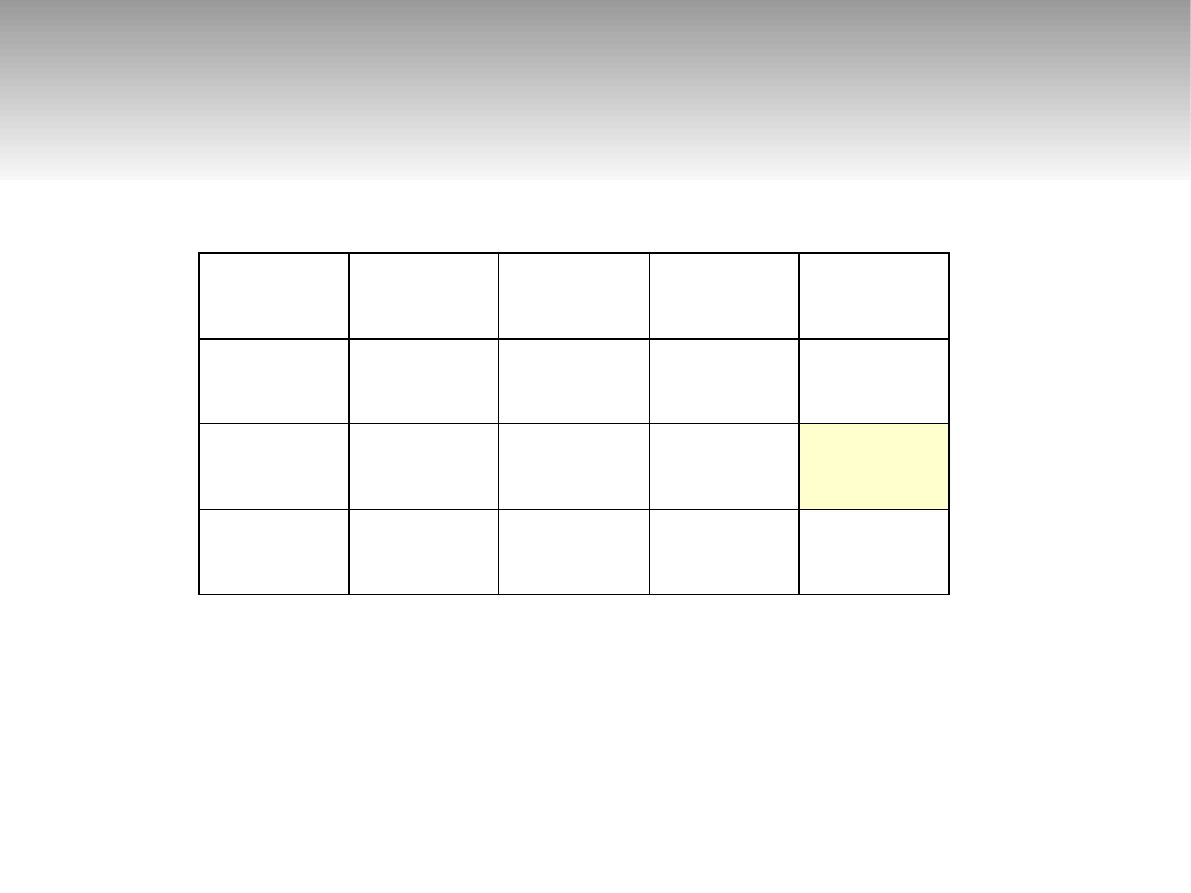
Przykład 2 – tablica charaktery-

styczna

Φ

0

1

q

1

q

2

q

3

q

4

ΦLq

1

ΦNq

4

0Nq

4

ΦNq

4

1Nq

4

1Lq

3

0Nq

4

0Nq

4

0Lq

2

0Lq

2

1Nq

4

1Nq

4

↓

Φ 0 1 0 0 0 0 Φ Φ

16

Przykład 3 – obliczanie wartości

bezwzględnej liczby

●

Na taśmie umieszczono liczbę całkowitą ze
znakiem zapisaną w zapisie uzupełnienio-
wym do 2

●

W miejsce tej liczby wpisać jej wartość bez-
względną

●

Głowica znajduje się na lewo od liczby na
symbolu pustym Φ

Przykład 3 – algorytm

1. Czy liczba na taśmie jest liczbą nieujemną ?

Jeżeli tak – STOP, jeśli nie – idź do 2

2. Oblicz liczbę przeciwną:

1. Zaneguj wszystkie bity liczby

2. Dodaj jedynkę

Przykład 3 – algorytm

1. Czy liczba na taśmie jest liczbą nieujemną ?

Jeżeli tak – STOP, jeśli nie – idź do 2

2. Oblicz liczbę przeciwną:

1. Zaneguj wszystkie bity liczby

2. Dodaj jedynkę

Np. + 11

Przykład 3 – algorytm

1.

Czy liczba na taśmie jest liczbą nieujemną ?
Jeżeli tak – STOP, jeśli nie – idź do 2

2. Oblicz liczbę przeciwną:

1. Zaneguj wszystkie bity liczby

2. Dodaj jedynkę

Np. + 11

0

0 0 0 1 0 1 1

Przykład 3 – algorytm

1.

Czy liczba na taśmie jest liczbą nieujemną ?
Jeżeli tak – STOP, jeśli nie – idź do 2

2. Oblicz liczbę przeciwną:

1. Zaneguj wszystkie bity liczby

2. Dodaj jedynkę

Np. - 11

1

1 1 1 0 1 0 1

Przykład 3 – algorytm

1. Czy liczba na taśmie jest liczbą nieujemną ?

Jeżeli tak – STOP, jeśli nie – idź do 2

2. Oblicz liczbę przeciwną:

1.

Zaneguj wszystkie bity liczby

2. Dodaj jedynkę

Np. - 11
1 1 1 1 0 1 0 1

Przykład 3 – algorytm

1. Czy liczba na taśmie jest liczbą nieujemną ?

Jeżeli tak – STOP, jeśli nie – idź do 2

2. Oblicz liczbę przeciwną:

1.

Zaneguj wszystkie bity liczby

2. Dodaj jedynkę

Np. - 11

0

1 1 1 0 1 0 1

Przykład 3 – algorytm

1. Czy liczba na taśmie jest liczbą nieujemną ?

Jeżeli tak – STOP, jeśli nie – idź do 2

2. Oblicz liczbę przeciwną:

1.

Zaneguj wszystkie bity liczby

2. Dodaj jedynkę

Np. - 11

0

0

1 1 0 1 0 1

Przykład 3 – algorytm

1. Czy liczba na taśmie jest liczbą nieujemną ?

Jeżeli tak – STOP, jeśli nie – idź do 2

2. Oblicz liczbę przeciwną:

1.

Zaneguj wszystkie bity liczby

2. Dodaj jedynkę

Np. - 11

0

0

0

1 0 1 0 1

Przykład 3 – algorytm

1. Czy liczba na taśmie jest liczbą nieujemną ?

Jeżeli tak – STOP, jeśli nie – idź do 2

2. Oblicz liczbę przeciwną:

1.

Zaneguj wszystkie bity liczby

2. Dodaj jedynkę

Np. - 11

0

0

0

0

0 1 0 1

Przykład 3 – algorytm

1. Czy liczba na taśmie jest liczbą nieujemną ?

Jeżeli tak – STOP, jeśli nie – idź do 2

2. Oblicz liczbę przeciwną:

1.

Zaneguj wszystkie bity liczby

2. Dodaj jedynkę

Np. - 11

0

0

0

0

1

1 0 1

Przykład 3 – algorytm

1. Czy liczba na taśmie jest liczbą nieujemną ?

Jeżeli tak – STOP, jeśli nie – idź do 2

2. Oblicz liczbę przeciwną:

1.

Zaneguj wszystkie bity liczby

2. Dodaj jedynkę

Np. - 11

0

0

0

0

1

0

0 1

Przykład 3 – algorytm

1. Czy liczba na taśmie jest liczbą nieujemną ?

Jeżeli tak – STOP, jeśli nie – idź do 2

2. Oblicz liczbę przeciwną:

1.

Zaneguj wszystkie bity liczby

2. Dodaj jedynkę

Np. - 11

0

0

0

0

1

0

1

1

Przykład 3 – algorytm

1. Czy liczba na taśmie jest liczbą nieujemną ?

Jeżeli tak – STOP, jeśli nie – idź do 2

2. Oblicz liczbę przeciwną:

1.

Zaneguj wszystkie bity liczby

2. Dodaj jedynkę

Np. - 11

0

0

0

0

1

0

1

0

Przykład 3 – algorytm

1. Czy liczba na taśmie jest liczbą nieujemną ?

Jeżeli tak – STOP, jeśli nie – idź do 2

2. Oblicz liczbę przeciwną:

1. Zaneguj wszystkie bity liczby

2.

Dodaj jedynkę

Np. - 11
0 0 0 0 1 0 1 0
+ 1

Przykład 3 – algorytm

1. Czy liczba na taśmie jest liczbą nieujemną ?

Jeżeli tak – STOP, jeśli nie – idź do 2

2. Oblicz liczbę przeciwną:

1. Zaneguj wszystkie bity liczby

2.

Dodaj jedynkę

Np. - 11
0 0 0 0 1 0 1

1

Przykład 3 – algorytm

1. Czy liczba na taśmie jest liczbą nieujemną ?

Jeżeli tak – STOP, jeśli nie – idź do 2

2. Oblicz liczbę przeciwną:

1. Zaneguj wszystkie bity liczby

2. Dodaj jedynkę

Każdy fragment algorytmu można zrealizować
niezależnie a potem połączyć uzyskane roz-
wiązania w jedno.
Założenie: głowica z lewej strony liczby

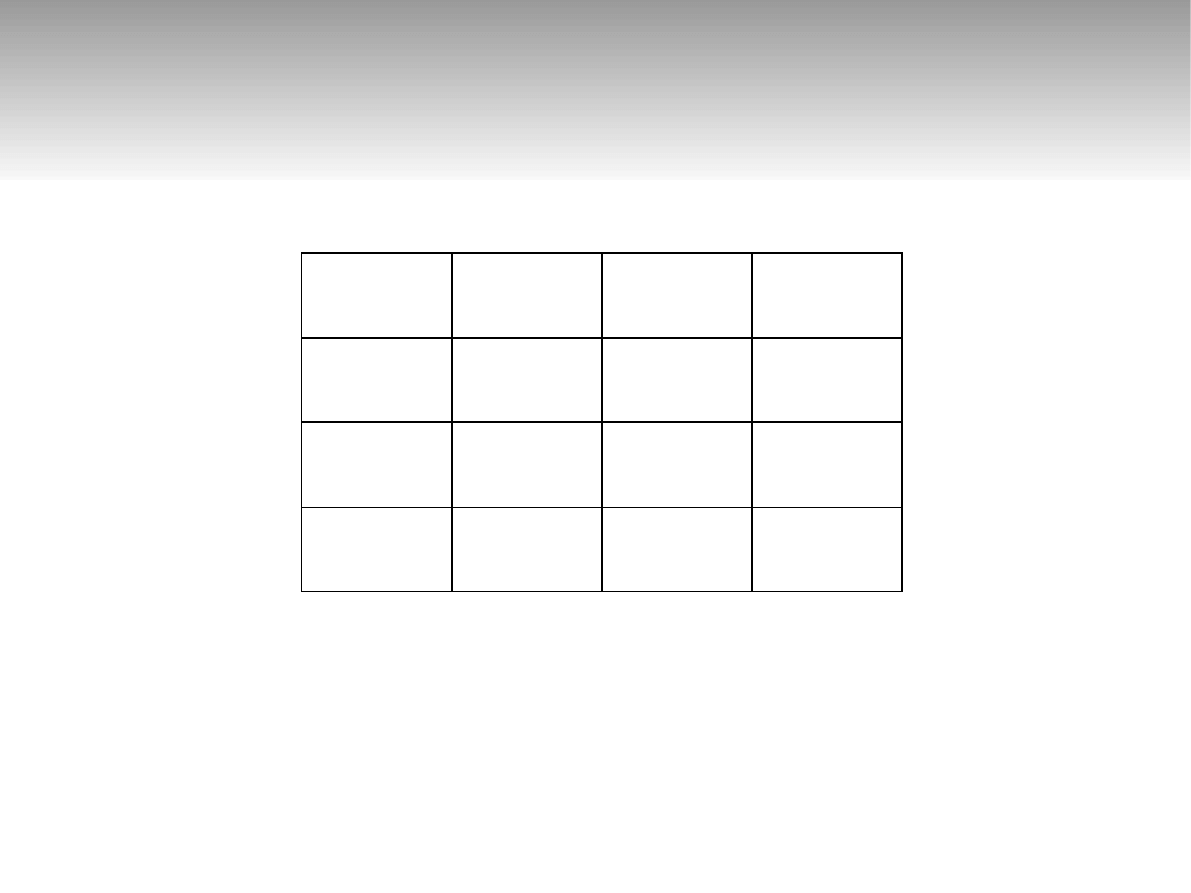
q

1

– szukanie bitu znaku

q

2

– stan końcowy, liczba dodatnia

q

3

– stan końcowy liczba ujemna

Przykład 3 – testowanie bitu znaku

Φ

-

-

0

-

1

-

q

1

q

2

q

3

ΦPq

1

0Nq

2

0Nq

2

1Nq

3

1Nq

3

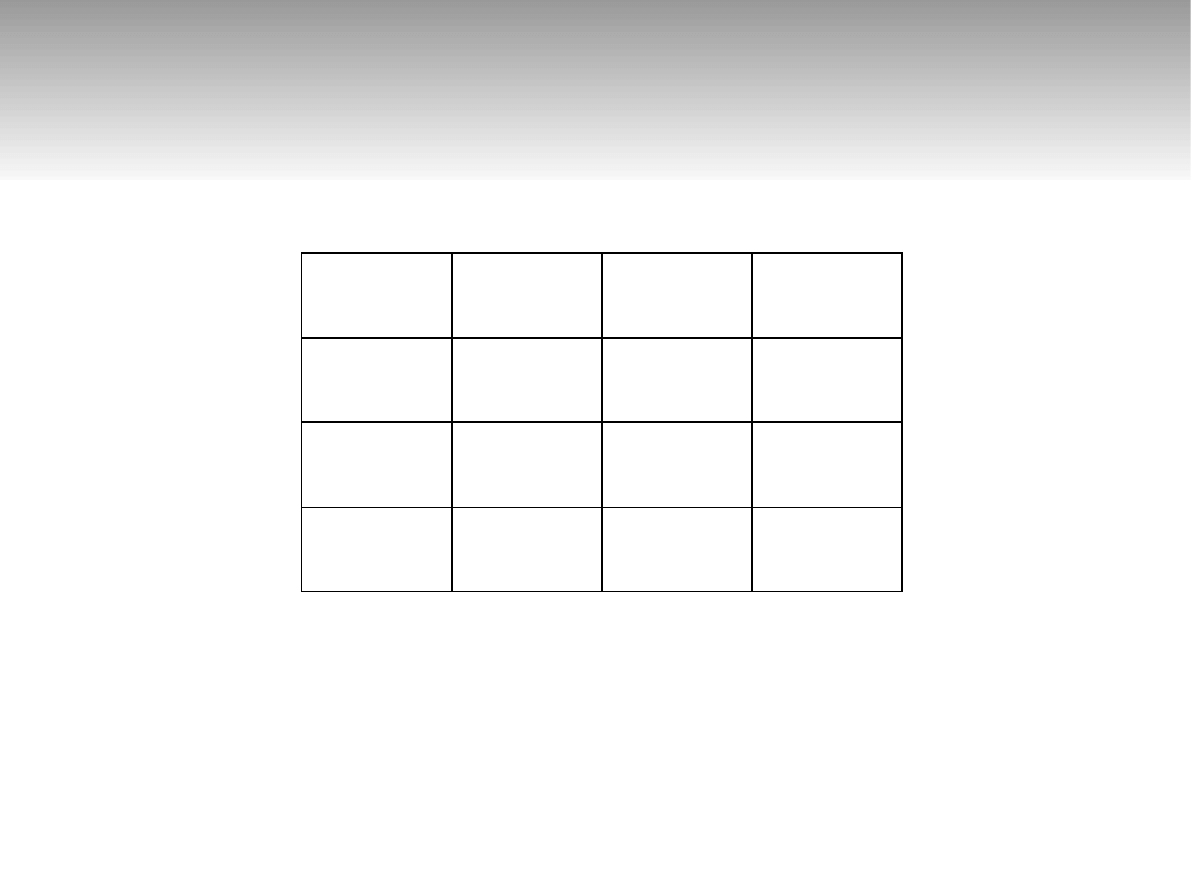
q

1

– szukanie początku liczby

q

2

– zamiana bitów

q

3

– stan końcowy

Przykład 3 – negowanie bitów

Φ

0

-

1

-

q

1

q

2

q

3

ΦPq

1

ΦNq

3

ΦNq

3

1Pq

2

1Pq

2

0Pq

2

0Pq

2

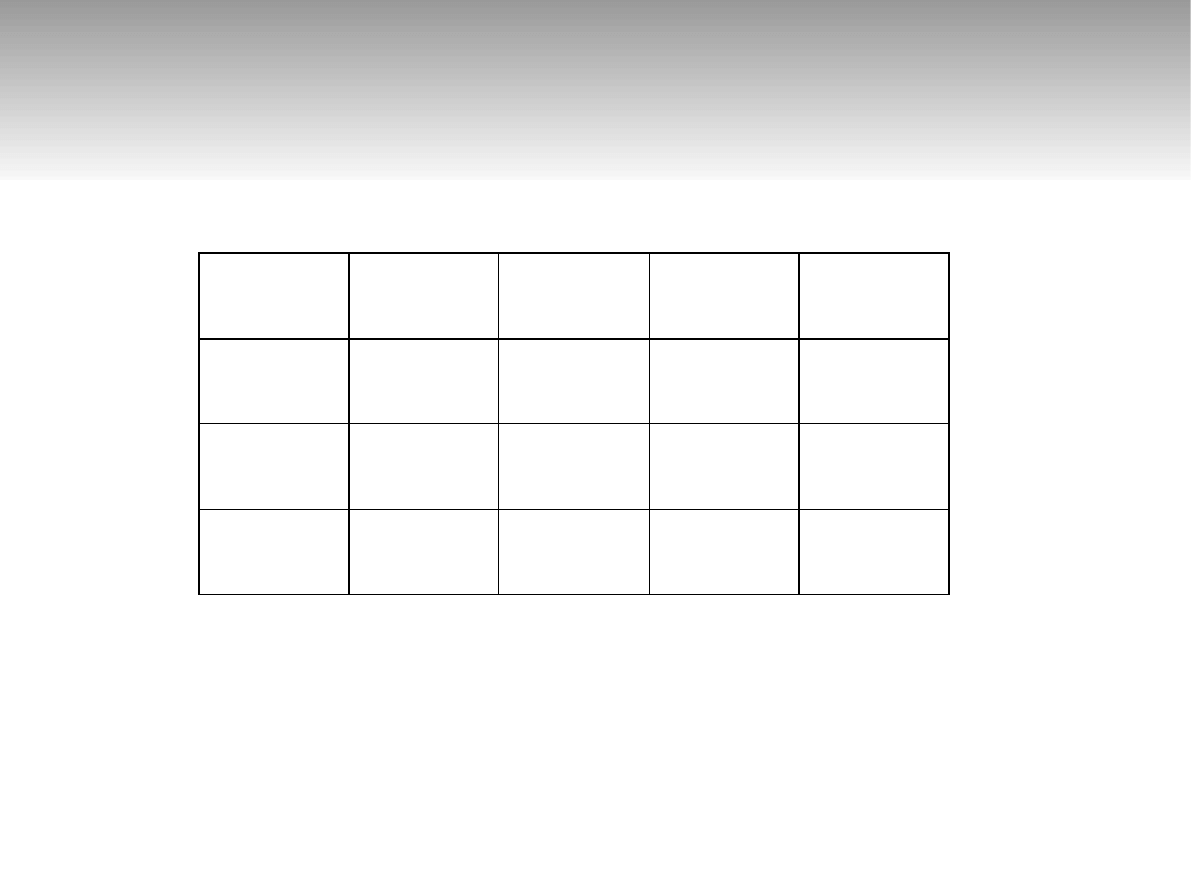
Przykład 3 – inkrementacja

Φ

0

1

q

1

q

2

q

3

q

4

ΦLq

1

ΦNq

4

0Nq

4

ΦNq

4

1Nq

4

1Lq

3

0Nq

4

0Nq

4

0Lq

2

0Lq

2

1Nq

4

1Nq

4

Przykład 3 – całe zadanie

Φ

-

-

0

-

1

-

q

1

q

2

q

3

ΦPq

1

0Nq

2

0Nq

2

1Nq

3

0Nq

3

Badanie znaku liczby

Przykład 3 – całe zadanie

Φ

-

-

0

-

1

-

q

1

q

2

q

3

ΦPq

1

0Nq

2

0Nq

2

1Nq

3

0Nq

3

2 stany końcowe:

●

q

2

– liczba dodatnia

●

q

3

– liczba ujemna

Przykład 3 – całe zadanie

Φ

-

-

0

-

1

-

q

1

q

2

q

3

ΦPq

1

0Nq

2

0Nq

2

1Nq

3

0Nq

3

W miejsce stanu q

3

wstawiamy tablicę z nega-

cją bitów

Przykład 3 – całe zadanie

Φ

-

0

1

-

q

1

q

2

q

3

q

4

q

5

ΦPq

1

ΦPq

3

ΦNq

5

ΦNq

5

0Nq

2

0Nq

2

1Pq

4

1Pq

4

0Nq

5

1Nq

3

0Pq

4

0Pq

4

1Nq

5

Negowanie bitów

W miejsce stanu końcowego q

5

wstawiamy ta-

blicę inkrementującą.

Przykład 3 – całe zadanie

Φ

-

0

1

-

q

1

q

2

q

3

q

4

q

5

ΦPq

1

ΦPq

3

ΦNq

5

ΦNq

5

0Nq

2

0Nq

2

1Pq

4

1Pq

4

0Nq

5

1Nq

3

0Pq

4

0Pq

4

1Nq

5

Przykład 3 – całe zadanie

Φ

-

0

1

-

q

1

q

2

q

3

q

4

q

5

q

6

q

7

q

8

ΦPq

1

ΦPq

3

ΦNq

5

ΦLq

5

ΦLq

8

0Lq

8

ΦLq

8

0Nq

2

0Nq

2

1Pq

4

1Pq

4

1Lq

8

1Lq

7

0Lq

8

0Lq

8

1Nq

3

0Pq

4

0Pq

4

0Lq

6

0Lq

6

1Lq

8

1Lq

8

Inkrementacja liczby

Przykład 3 – całe zadanie

Φ

-

0

1

-

q

1

q

2

q

3

q

4

q

5

q

6

q

7

q

8

ΦPq

1

ΦPq

3

ΦNq

5

ΦLq

5

ΦLq

8

0Lq

8

ΦLq

8

0Nq

2

0Nq

2

1Pq

4

1Pq

4

1Lq

8

1Lq

7

0Lq

8

0Lq

8

1Nq

3

0Pq

4

0Pq

4

0Lq

6

0Lq

6

1Lq

8

1Lq

8

Dwa stany końcowe:

●

q

2

– gdy liczba była nieujemną

●

q

8

– gdy była liczba ujemna

Podsumowanie

●

Elementy tworzące maszynę Turinga

●

Tablica charakterystyczna jako zapis pro-
gramu dla maszyny Turinga

●

Przykłady algorytmów i zaprogramowania
ich na maszynie Turinga

●

Twierdzenie Turinga o realizowalności algo-
rytmów