Maszyna Turinga

Alan Mathison Turing (ur. 23 czerwca 1912 w Londynie –

zm. 7 czerwca 1954 w Wilmslow) –

angielski matematyk, twórca maszyny Turinga

i jeden z twórców informatyki.

Budowa maszyny Turinga

Alan Turing pod koniec lat trzydziestych
ubiegłego wieku na potrzeby swoich bada

ń

nad

problemami

obliczalno

ś

ci

opracował

model maszyny, który mo

ż

na zrealizowa

ć

nawet na kartce papieru.

Był

to automat abstrakcyjny, słu

żą

cy do

analizy algorytmów.

Maszyna Turinga zbudowana jest z trzech

głównych elementów:

1. Niesko

ń

czonej ta

ś

my zawieraj

ą

cej komórki

z przetwarzanymi symbolami.

2. Ruchomej głowicy zapisuj

ą

co-odczytuj

ą

cej.

3. Układu sterowania głowic

ą

.

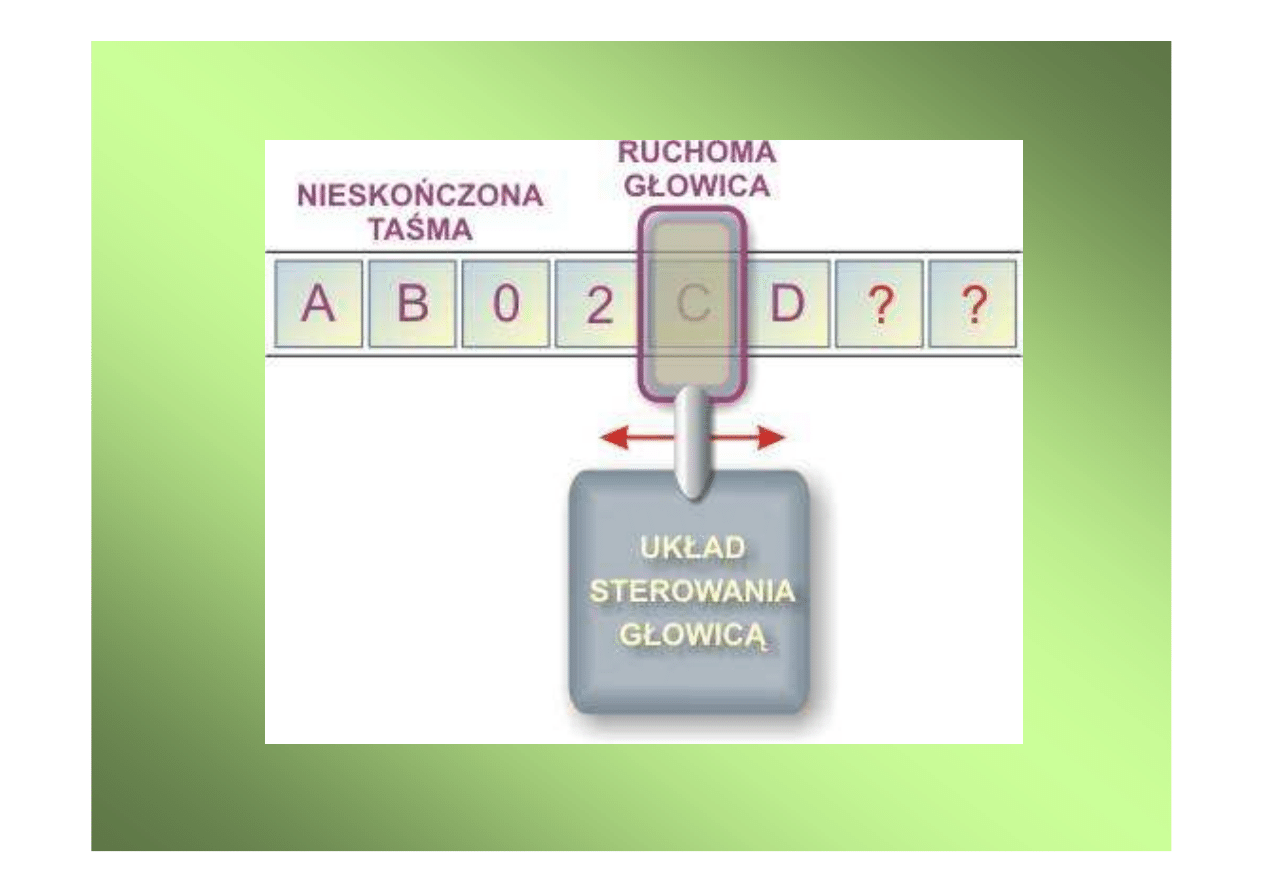
Niesko

ń

czona ta

ś

ma

jest odpowiednikiem

współczesnej pami

ę

ci komputera. Ta

ś

ma dzieli

si

ę

na komórki, w których umieszczone zostały

symbole, czyli po prostu znaki przetwarzane
przez maszyn

ę

Turinga. Symbole te stanowi

ą

odpowiednik danych wej

ś

ciowych. Maszyna

Turinga odczytuje te dane z kolejnych komórek
i przetwarza na inne symbole, czyli dane
wyj

ś

ciowe.

Wyniki

oblicze

ń

równie

ż

s

ą

zapisywane w komórkach ta

ś

my.

... A A C C D D 0 1 2 3 E F G Z ? ? ...

Głowica zapisuj

ą

co – odczytuj

ą

ca

Głowica

ta

odpowiada

funkcjonalnie

urz

ą

dzeniom wej

ś

cia/wyj

ś

cia współczesnych

komputerów lub układom odczytu i zapisu
pami

ę

ci.

Głowica zawsze znajduje si

ę

nad jedn

ą

z komórek ta

ś

my. Mo

ż

e ona odczytywa

ć

zawarto

ść

tej komórki oraz zapisywa

ć

do niej

inny symbol - na tej zasadzie odbywa si

ę

przetwarzanie danych - z jednych symboli
otrzymujemy

inne.

Oprócz

odczytywania

i zapisywania symboli w komórkach głowica
wykonuje ruchy w prawo i w lewo do s

ą

siednich

komórek na ta

ś

mie. W ten sposób mo

ż

e si

ę

ona

przemie

ś

ci

ć

do dowolnie wybranej komórki

ta

ś

my.

Układ sterowania

Układ

sterowania

głowic

ą

zarz

ą

dza

przetwarzaniem informacji. Jego współczesnym
odpowiednikiem jest procesor komputera. Układ
ten odczytuje za pomoc

ą

głowicy symbole

z komórek ta

ś

my oraz przesyła do głowicy

symbole do zapisu w komórkach. Dodatkowo
nakazuje on głowicy przemie

ś

ci

ć

si

ę

do

s

ą

siedniej komórki w lewo lub w prawo.

Podstaw

ą

działania maszyny Turinga s

ą

stany

układu sterowania. Stan układu sterowania
okre

ś

la jednoznacznie jak

ą

operacj

ę

wykona,

oraz jak zareaguje maszyna Turinga, gdy
odczyta z ta

ś

my okre

ś

lony symbol.

Zatem operacje wykonywane przez układ
sterowania zale

żą

od dwóch czynników:

1. Symbolu odczytanego z komórki na ta

ś

mie.

2. Bie

żą

cego stanu układu steruj

ą

cego.

Stany zostały okre

ś

lone kolejnymi nazwami:

q0, q1, q2, ... ,qn, gdzie q0 jest stanem
pocz

ą

tkowym, w którym znajduje si

ę

maszyna

Turinga przed rozpocz

ę

ciem przetwarzania

symboli na ta

ś

mie.

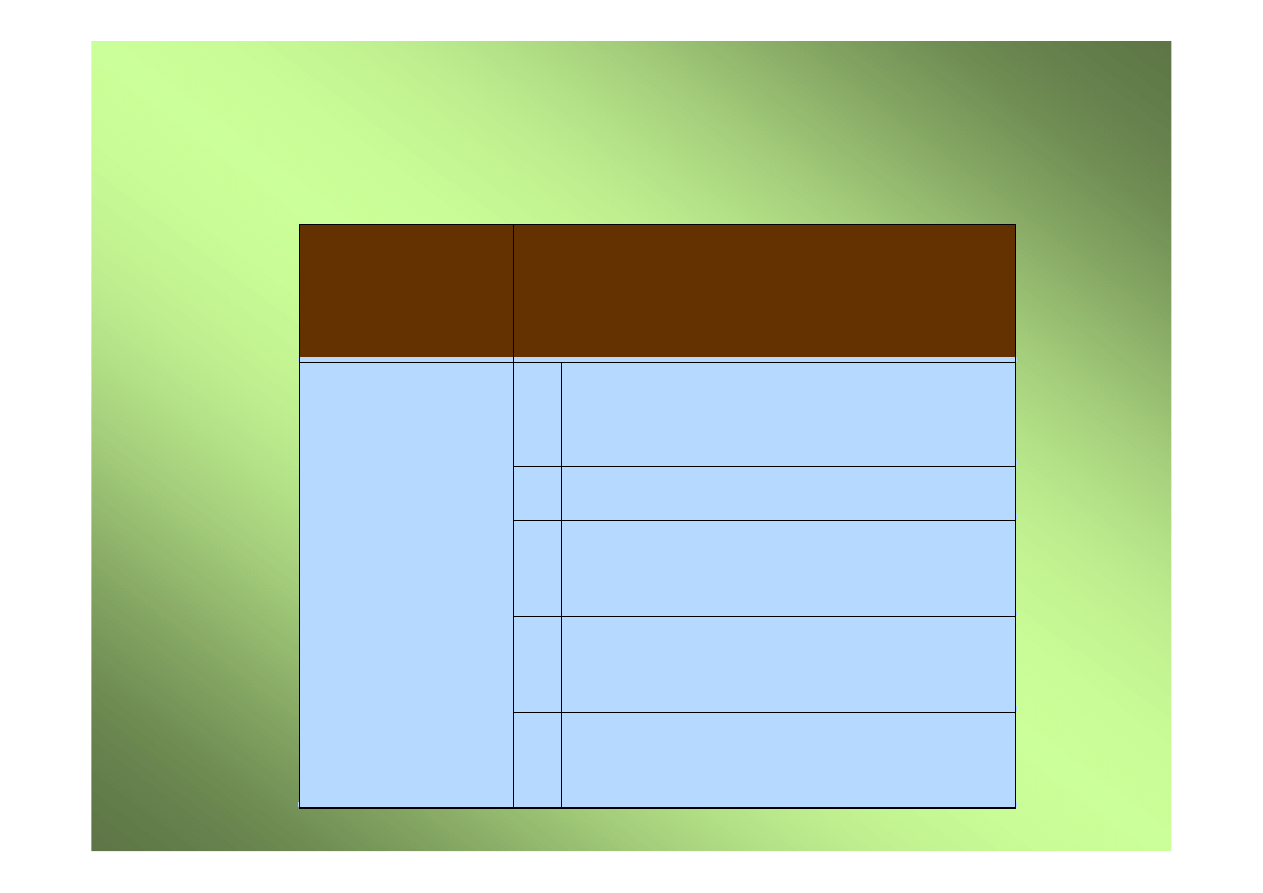
Przyjmijmy nast

ę

puj

ą

c

ą

składni

ę

instrukcji

dla maszyny Turinga:

Instrukcja

maszyny

Turinga

Znaczenia symboli

S

o

- symbol odczytany przez głowic

ę

z

bie

żą

cej komórki na ta

ś

mie

q

i

- bie

żą

cy stan układu sterowania

S

z

- symbol, jaki zostanie zapisany w

bie

żą

cej komórce na ta

ś

mie

q

j

- nowy stan, w który przejdzie układ

sterowania po wykonaniu tej operacji

(S

o

,q

i

,S

z

,q

j

,L/R)

L/R

- ruch głowicy o jedn

ą

komórk

ę

w lewo

(L) lub w prawo (R)

S

0

i q

i

s

ą

tzw. cz

ęś

ci

ą

identyfikacyjn

ą

instrukcji. Maszyna Turinga wykonuje tyle
ró

ż

nych instrukcji, ile zdefiniujemy cz

ęś

ci

identyfikacyjnych - w programie nie mo

ż

e by

ć

dwóch ró

ż

nych instrukcji o identycznej cz

ęś

ci

identyfikacyjnej.

Powód jest oczywisty -

któr

ą

instrukcj

ę

nale

ż

ałoby w takim wypadku wykona

ć

?

S

z

, q

j

i L/R s

ą

tzw. cz

ęś

ci

ą

operacyjn

ą

, która

okre

ś

la

jakie

działanie

podejmuje

dana

instrukcja. Cz

ęś

ci operacyjne ró

ż

nych instrukcji

mog

ą

by

ć

takie same - oznacza to jedynie, i

ż

instrukcje te wykonuj

ą

dokładnie to samo

działanie.

Program dla maszyny Turinga

Aby lepiej zrozumie

ć

działanie maszyny

Turinga, rozwa

ż

my nast

ę

puj

ą

cy program

zło

ż

ony z dwóch instrukcji:

Program

0,q0,1,q0,L bit

0 zamień na 1

1,q0,0,q0,L bit

1 zamień na 0

Przyjmijmy równie

ż

,

ż

e fragment niesko

ń

czonej

ta

ś

my zwiera nast

ę

puj

ą

cy ci

ą

g symboli:

... ? 1 0 1 1 0 ? ...

Symbolem pustym jest znak pytajnika. Dane do
przetworzenia przez program zawarte s

ą

w kolejnych

5 komórkach - 10110.
Załó

ż

my, i

ż

jest to jaka

ś

warto

ść

binarna.

Przed rozpocz

ę

ciem wykonywania programu

ustawiamy głowic

ę

na okre

ś

lonej komórce ta

ś

my.

W tym przypadku niech b

ę

dzie to ostatni symbol

0:

Po uruchomieniu maszyny Turinga obserwujemy
co si

ę

stanie:

... ? 1 0 1 1 0 ? ...

Ta

ś

ma z

głowic

ą

Odczytany

znak

Stan

bie

żą

cy

Wykonywana operacja

? 1 0 1 1

0

?

0

q0

Kombinacja odczytanego znaku i stanu q0
wyznacza instrukcję 0,q0,1,q0,L. Zatem
znak w bieżącej komórce maszyna
Turinga umieści symbol 1, stanu nie
zmieni (

wciąż pozostanie w q0

) i

przemieści głowicę do sąsiedniej komórki
po lewej stronie.

? 1 0 1

1

1 ?

1

q0

Teraz kombinacja odczytanego znaku i
stanu wewnętrznego wyznacza instrukcję
1,q0,0,q0,L. Znak w bieżącej komórce
taśmy zostanie zastąpiony znakiem 0, stan
wewnętrzny nie zmieni się i głowica
będzie przesunięta w lewo do następnej
komórki.

? 1 0

1

0 1 ?

1

q0

To samo, co powy

ż

ej, instrukcja

1,q0,0,q0,L.

? 1

0

0 0 1 ?

0

q0

Instrukcja 0,q0,1,q0,L.

?

1

1 0 0 1 ?

1

q0

Instrukcja 1,q0,0,q0,L

?

0 1 0 0 1 ?

?

q0

Ta instrukcja nie została zdefiniowana,

zatem program zako

ń

czy swoj

ą

prac

ę

Maszyna Turinga,

a współczesny komputer

Odpowiednikiem procesora jest tu głowica,
pami

ę

ci - ta

ś

ma, natomiast diagram przej

ść

mi

ę

dzy

stanami

odpowiada

BIOS-owi,

Windowsowi lub innemu oprogramowaniu.

Przykład:

maszyna realizuj

ą

ca algorytm Euklidesa wyznaczania

NWD (Najwi

ę

kszy Wspólny Dzielnik) dwóch liczb:

function NWD (x0= 24, x1= 9: Word): Word

;

repeat

x

2

:= x

0

mod x

1

;

x

0

:= x

1

;

x

1

:= x

2

;

until (x

2

= 0);

NWD:= x

0

1. x

2

:= 6; x

0

:=9; x

1

:=6;

2. x

2

:= 3; x

0

:=6; x

1

:=3

3. x

2

:= 0; x

0

:=3; x

1

:=0;

4. NWD=3;

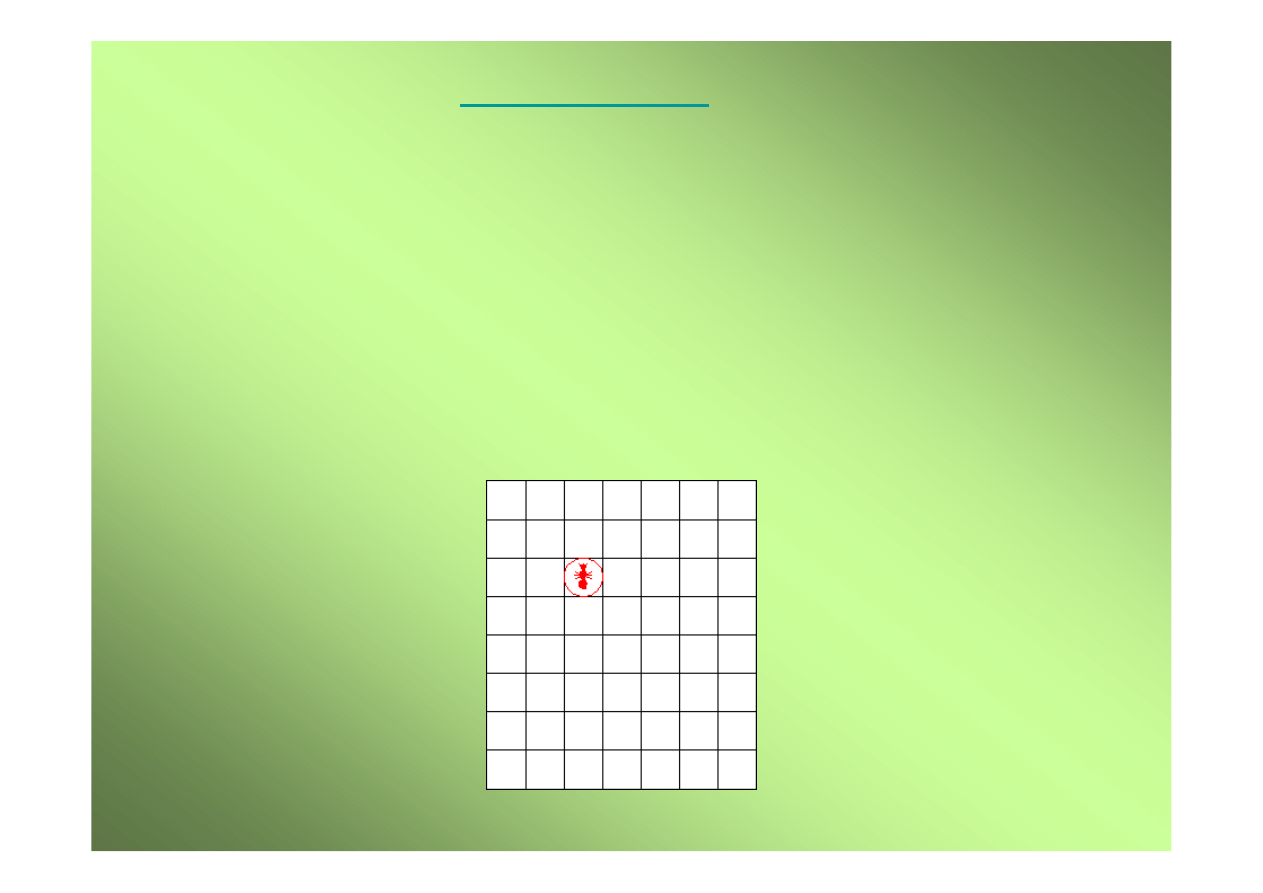
2-wymiarow

ą

Turing machine

opracowano w latach

80-tych. Mrówka porusza si

ę

po siatce zawieraj

ą

cej

białe i czarne pola według nast

ę

puj

ą

cych reguł:

1.

Kiedy mrówka znajdzie si

ę

na polu czarnym obraca si

ę

w prawo i przesuwa o jedno pole do przodu.

2.

Kiedy mrówka jest na polu białym, obraca si

ę

w lewo

i przesuwa do przodu o jedno pole.

3.

Kiedy mrówka opuszcza pole zmienia ono kolor.

Test Turinga

Test Turinga to sposób okre

ś

lania zdolno

ś

ci

maszyny

do

posługiwania

si

ę

j

ę

zykiem

naturalnym i po

ś

rednio maj

ą

cym dowodzi

ć

opanowania przez ni

ą

umiej

ę

tno

ś

ci my

ś

lenia

w sposób podobny do ludzkiego. Test ten został
zaproponowany w 1950 roku przez Alana
Turinga. Turing zaproponował ten test w celu
zamiany pełnego emocji i w jego poj

ę

ciu

bezsensownego pytania "Czy maszyny my

ś

l

ą

?"

na pytanie lepiej zdefiniowane, w ramach bada

ń

nad stworzeniem sztucznej inteligencji.

Test Turinga

Test wygl

ą

da nast

ę

puj

ą

co: s

ę

dzia - człowiek -

prowadzi

rozmow

ę

w

j

ę

zyku

naturalnym

z pozostałymi stronami. Je

ś

li s

ę

dzia nie jest

w stanie wiarygodnie okre

ś

li

ć

, czy która

ś

ze

stron jest maszyn

ą

czy człowiekiem, wtedy mówi

si

ę

,

ż

e maszyna przeszła test. Zakłada si

ę

,

ż

e

zarówno człowiek jak i maszyna próbuj

ą

przej

ść

test zachowuj

ą

c si

ę

w sposób mo

ż

liwie zbli

ż

ony

do ludzkiego.

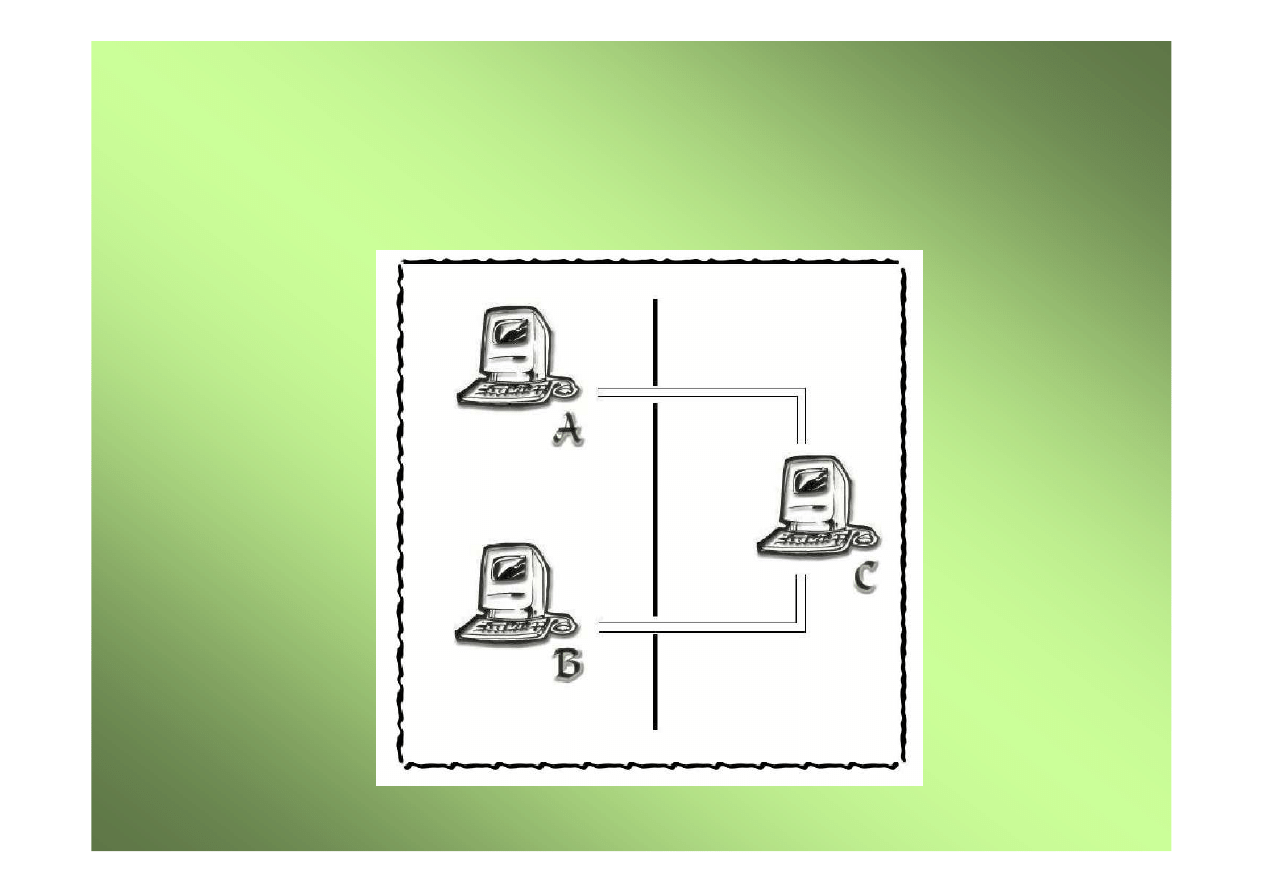
SCHEMAT TESTU TURINGA

Test pochodzi od zabaw polegaj

ą

cych na

zgadywaniu

płci

osoby

znajduj

ą

cej

si

ę

w innym pokoju przy pomocy serii pyta

ń

i odpowiedzi pisanych na kartkach papieru.
W pierwotnym pomy

ś

le Turinga człowiek musiał

udawa

ć

przeciwn

ą

płe

ć

, a test był ograniczony

do pi

ę

ciominutowej rozmowy. Dzi

ś

nie uwa

ż

a si

ę

tych cech za podstawowe i zasadniczo nie
umieszcza w specyfikacji testu Turinga.

Turing oczekiwał,

ż

e maszyny w ko

ń

cu b

ę

d

ą

w stanie przej

ść

ten test. Ocenił,

ż

e około roku

2000 maszyny z pami

ę

ci

ą

o pojemno

ś

ci 109

bitów (około 119 MB) b

ę

d

ą

w stanie oszuka

ć

30% s

ę

dziów w czasie pi

ę

ciominutowego testu.

Przewidywał

równie

ż

,

ż

e ludzie przestan

ą

uwa

ż

a

ć

zdanie

"my

ś

l

ą

ca

maszyna"

za

wewn

ę

trznie sprzeczne. Oceniał,

ż

e uczenie

maszynowe

nabierze

du

ż

ego

znaczenia

w budowaniu wydajnych maszyn. To twierdzenie
jest przez dzisiejszych badaczy sztucznej
inteligencji oceniane jako zasadne.

Spory o to, czy test Turinga we wła

ś

ciwy sposób

definiuje inteligencj

ę

maszynow

ą

(lub "my

ś

lenie

maszynowe") dotyczyły głównie trzech punktów:

1. Maszyna, która przejdzie test Turinga mo

ż

e by

ć

w stanie symulowa

ć

ludzkie zachowanie

konwersacyjne, lecz mo

ż

e to by

ć

znacznie mniej

ni

ż

prawdziwa inteligencja. Maszyna mo

ż

e

zwyczajnie u

ż

ywa

ć

sprytnie wymy

ś

lonych reguł.

Cz

ę

st

ą

ripost

ą

w społeczno

ś

ci zajmuj

ą

cej si

ę

badaniami nad sztuczn

ą

inteligencj

ą

jest

zadanie pytania "A sk

ą

d wiemy czy ludzie sami

po prostu nie posługuj

ą

si

ę

jakimi

ś

sprytnie

wymy

ś

lonymi regułami?".

2. Maszyna mo

ż

e by

ć

inteligentna nie posiadaj

ą

c

ludzkiej umiej

ę

tno

ś

ci prowadzenia rozmowy.

3. Wielu ludzi mogłoby nie by

ć

w stanie zaliczy

ć

takiego testu. Z drugiej strony, inteligencj

ę

innych ludzi oceniamy zazwyczaj wył

ą

cznie na

podstawie tego co i jak mówi

ą

.

Jak dot

ą

d,

ż

aden komputer

nie zaliczył testu Turinga.

Co roku wyznaczana jest Nagroda Loebnera dla
najlepszych zawodników w te

ś

cie Turinga.

Po raz pierwszy ograniczony test Turinga odbył
si

ę

w 1991 roku, w Bosto

ń

skim Muzeum

Komputerów. Sze

ść

komputerów miało udawa

ć

ludzi, a dwie osoby komputery. Wszystkie
terminale poł

ą

czona ze sob

ą

za pomoc

ą

modemów i sieci telefonicznej. Dziesi

ę

ciu

s

ę

dziów podchodziło kolejno do ka

ż

dego

terminala

i

brało

udział

w

konwersacji

z niewiadomym partnerem. Wynik eksperymentu
był zaskoczeniem.

Zwyci

ę

zc

ą

został

program

komputerowy

autorstwa Josepha Weintrauba, który jako temat
rozmów zadeklarował pogaduszki. A

ż

pi

ę

cioro

s

ę

dziów było przekonanych,

ż

e rozmawiało

z człowiekiem. Z kolei specjalista zajmuj

ą

cy si

ę

twórczo

ś

ci

ą

Shakespeara został uznany przez

troje s

ę

dziów za program komputerowy, gdy

ż

zbyt szybko i dokładnie cytował jego dzieła
z pami

ę

ci. Zostało to odebrane jako odczyt

z pami

ę

ci masowej, w której zmagazynowane

zostały teksty utworów.

Maszyna

von Neumana

W roku 1946 John von Neuman (1903-1957),
genialny ameryka

ń

ski uczony w

ę

gierskiego

pochodzenia (przede wszystkim matematyk, ale
tak

ż

e

chemik,

fizjolog,

biolog,

fizyk

i filozof) okre

ś

lił zasady, według których powinno

si

ę

konstruowa

ć

komputery. Zasady te wytyczyły

nowy kierunek w historii komputerów i s

ą

stosowane do dnia dzisiejszego.

John von Neumann

Zasady von Neumana mo

ż

na zawrze

ć

w trzech

punktach:

1.

instrukcje

i

dane

maj

ą

by

ć

identycznie

reprezentowane w maszynie;

2.

program i dane musz

ą

mie

ś

ci

ć

si

ę

w tej samej

wewn

ę

trznej pami

ę

ci (operacyjnej) komputera;

3.

dzi

ę

ki jednakowej reprezentacji danych i instrukcji

maszyna powinna móc wykonywa

ć

operacje na

instrukcjach i całym programie.
Tak

ą

architektur

ę

komputera nazywano sterowan

ą

programem. Wobec tak sformułowanej definicji
komputera ENIAC wszystkie poprzedzaj

ą

ce go

maszyny nie były komputerami.

Maszyna von Neumanna była komputerem w pełni
automatycznym,

cyfrowym

i

uniwersalnym,

z

wczytywanym

programem.

Jej

wewn

ę

trzna

architektura stała si

ę

wzorem dla komercyjnych maszyn

nast

ę

pnej generacji. Komputer posłu

ż

ył do wykonania

wielu oblicze

ń

z dziedziny abstrakcyjnej matematyki,

fizyki i

meteorologii. Pomógł

zbada

ć

wewn

ę

trzn

ą

struktur

ę

gwiazd

i

stabilno

ść

orbit

cz

ą

stek

w

akceleratorach.

Był

naprawd

ę

uniwersalny.

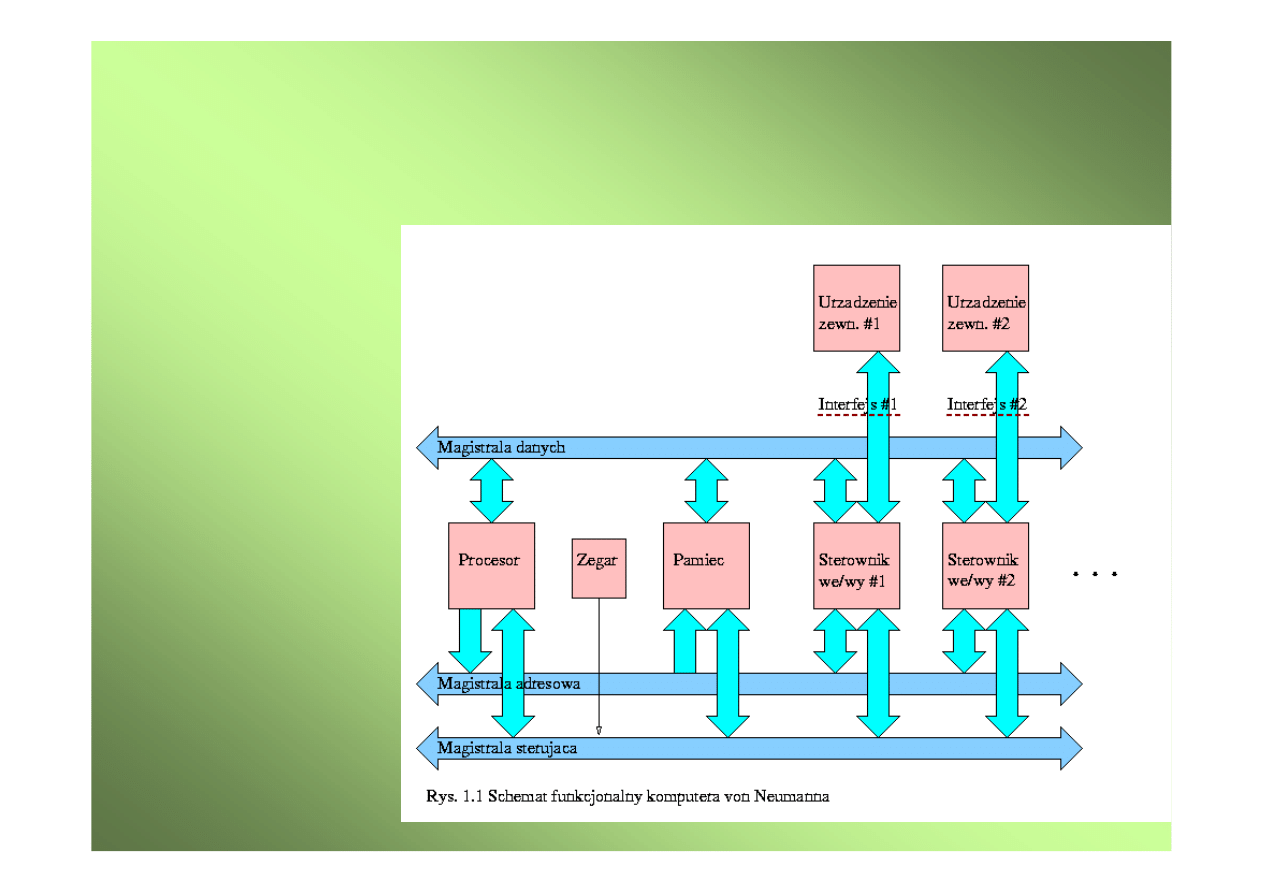
Schemat funkcjonalny komputera

von Neumanna

idea komputera sterowanego programem

Opis schematu maszyny

von Neumanna

• Procesor

• Pami

ęć

• Zegar

• Magistrale

• Wej

ś

cie/Wyj

ś

cie

Procesor (ang. processor) -

układ

dokonuj

ą

cy

operacji

na

danych

zgromadzonych w pami

ę

ci lub płyn

ą

cych z/do

urz

ą

dze

ń

wej

ś

cie/wyj

ś

cie,

sterowany

programem, którego kod znajduje si

ę

w pami

ę

ci.

Do przechowywania swojego wewn

ę

trznego

stanu procesor wyposa

ż

ony jest w pewn

ą

ilo

ść

rejestrów.

Do najwa

ż

niejszych rejestrów procesora nale

żą

:

•

Wska

ź

nik instrukcji (ang. instruction pointer)

-

wskazuje komórk

ę

pami

ę

ci, z której pobrany b

ę

dzie

nast

ę

pna instrukcja do wykonania.

•

Rejestr flag stanu (ang. flag register, flags) - składaj

ą

si

ę

na niego jednobitowe flagi przechowuj

ą

ce

informacje o stanie procesora (np. dopuszczalno

ś

ci

przerwa

ń

) lub rezultacie ostatnio wykonanej instrukcji.

• Wska

ź

nik stosu (ang. stack pointer) - wskazuje

pierwsz

ą

woln

ą

komórk

ę

pami

ę

ci na stosie

procesora - strukturze danych typu FILO (ang.
first in last out - pierwszy przyszedł, ostatni
wyszedł) wykorzystywanej przy skokach do
podprogramów dla przechowywania adresu
powrotu i zmiennych lokalnych.

• Akumulator (ang. accumulator) - słu

ż

y jako

argument a zarazem miejsce umieszczania
rezultatów operacji arytmetycznych.

Pami

ęć

(pami

ęć

operacyjna,

ang. memory) -

przechowuje dane i kod prgramu. Je

ż

eli jej

konstrukcja

umo

ż

liwia

oprócz

odczytu

dokonywanie w niej modyfikacji nazywamy j

ą

RAM (ang. random access memory), je

ś

li jej

konstrukcja

pozwala

jedynie

na

odczyt

nazywana jest ROM (ang. read only memory).

Pami

ęć

dzieli si

ę

na komórki, z których

ka

ż

da jest w stanie przechowa

ć

liczb

ę

całkowit

ą

z ustalonego dla danej architektury zakresu.
Najcz

ęś

ciej jest to 0, 1,...,255. Do zakodowania

takich liczb potrzeba 8 bitów tj. 1 bajt. Ka

ż

da

komórka pami

ę

ci posiada unikalny numer zwany

adresem fizycznym, który słu

ż

y procesorowi do

odwoływania si

ę

do niej.

Zegar

odmierza cykle wykonywania instrukcji
programu.

Magistrale (ang. buses) -

słu

żą

do przesyłania danych i synchronizacji elementów

komputera:

1. Magistrala danych (ang. data bus) słu

ż

y do przesyłania

danych

mi

ę

dzy

pami

ę

ci

ą

,

układami

we/wy,

a procesorem. Ilo

ść

u

ż

ytych tutaj linii (szeroko

ść

szyny)

jest równa długo

ś

ci słowa maszynowego i jest równa

rozmiarowi

komórki

pami

ę

ci,

lub

jest

jego

wielokrotno

ś

ci

ą

.

2. Magistrala

adresów

(ang.

address

bus)

słu

ż

y

procesorowi do wysyłania numerów komórek pami

ę

ci

lub rejestrów we/wy na których b

ę

dzie dokonane

nast

ę

pne przesłanie danych. Ilo

ść

u

ż

ytych tutaj linii

decyduje o ilo

ś

ci pami

ę

ci jak

ą

mo

ż

na zaadresowa

ć

.

3. Magistrala steruj

ą

ca

(ang. control bus) słu

ż

y do

wzajemnej

synchronizacji

oraz

przekazywania

i potwierdzania przyj

ę

cia/wykonania zlece

ń

.

Wej

ś

cie/Wyj

ś

cie

Pozwala

komputerowi

kontaktowa

ć

si

ę

z zewn

ę

trznym

ś

wiatem (klawiatura, monitor,

czytniki,

adaptery

sieciowe

itp)

lub

przechowywa

ć

dane poza pami

ę

ci

ą

operacyjn

ą

(dyski).

Na wej

ś

cie/wyj

ś

cie składaj

ą

si

ę

nast

ę

puj

ą

ce

układy i urz

ą

dzenia

:

1. Sprz

ę

towe sterowniki wej

ś

cia - wyj

ś

cia.

Układy te potrafi

ą

si

ę

porozumiewa

ć

z

procesorem

poprzez

rejestry

we/wy,

przerwania, kanały DMA i własn

ą

adresowaln

ą

przez procesor pami

ęć

układu. Wykonuj

ą

c

zlecenia

procesora

steruj

ą

urz

ą

dzeniami

wej

ś

cia

wyj

ś

cia.

W

technologii

mikrokomputerowej s

ą

montowane jako karty

rozszerzaj

ą

ce wewn

ą

trz obudowy komputera.

2. Urz

ą

dzenia zewn

ę

trzne - zapewniaj

ą

kontakt

komputera

ze

ś

wiatem.

Mog

ą

to

by

ć

klawiatury, monitory, dyski, drukarki, modemy
ale tak

ż

e czujniki i ramiona robotów w procesie

produkcyjnym.

3. Interfejsy. Interfejs jest to specyfikacja sposobu

przesyłania

danych

mi

ę

dzy

dwoma

urz

ą

dzeniami.

Poj

ę

cie

to

bywa

cz

ę

sto

przenoszone na realizacj

ę

sprz

ę

tow

ą

interfejsu

w postaci gniazd, wtyków i kabli. Bywa te

ż

rozszerzane

na

komunikacj

ę

człowiek-

maszyna,

mówimy

wtedy

o

interfejsie

u

ż

ytkownika.

Pierwsze pokolenie komputerów

•

przeznaczone do rozwi

ą

zywania jednego zadania w trybie

pasywnym

•

algorytm posiada stał

ą

struktur

ę

i jest wykonywany

sekwencyjnie

•

funkcjonowanie okre

ś

lone zostaje na etapie projektowania

•

brak systemu operacyjnego

•

budowane w oparciu o lampy elektronowe

•

funkcjonowały w latach 1945-1954

jednostka arytmetyczno-logiczna

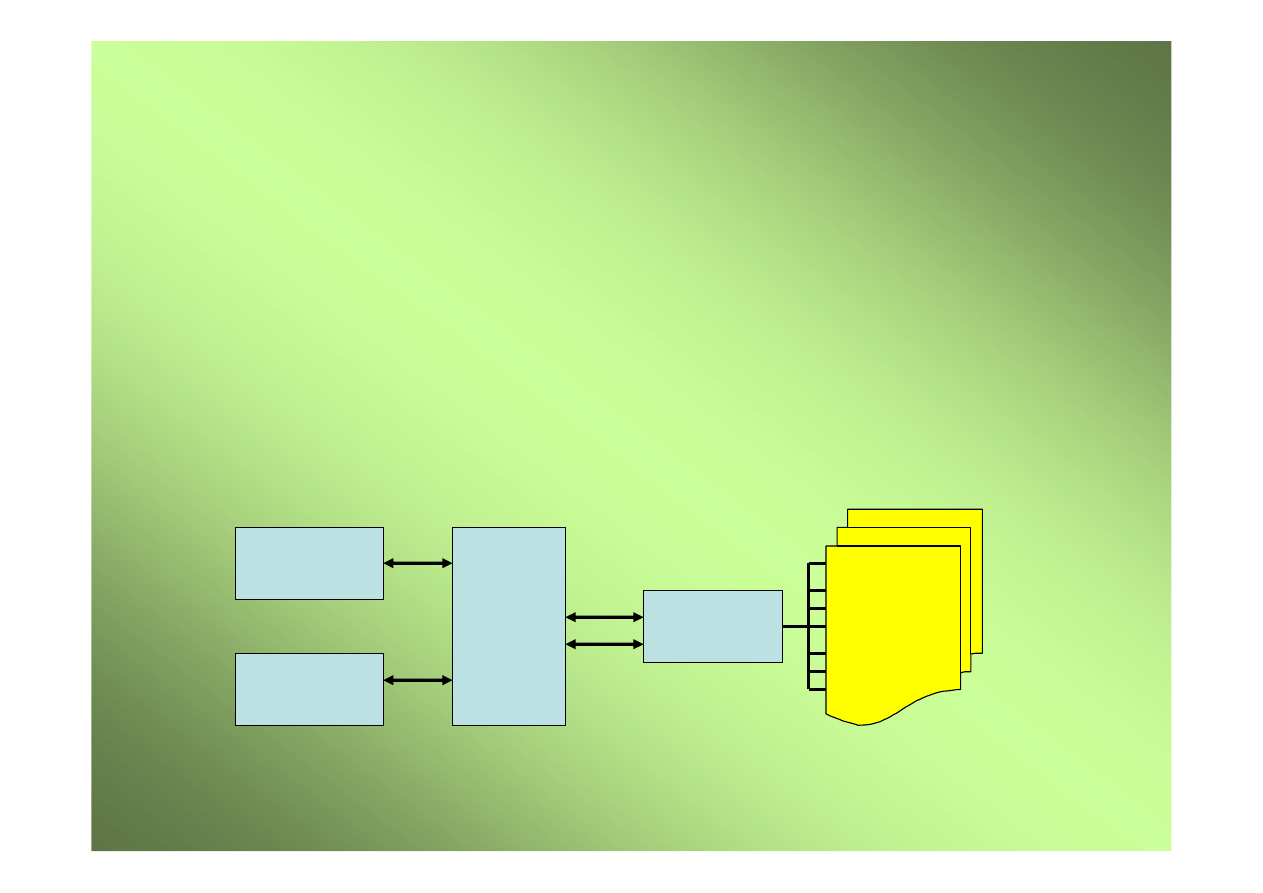
Struktura komputerów pierwszego pokolenia

Pami

ęć

główna

Urz

ą

dzenia

wej

ś

cia-wyj

ś

cia

ALU

Jednostka steruj

ą

ca

Drugie pokolenie komputerów

•

przeznaczone do rozwi

ą

zywania wielu zada

ń

w trybie pasywnym

•

zastosowano algorytm szeregowo-równoległy (elementy
współbie

ż

no

ś

ci)

•

zastosowano prosty system operacyjny (tzw. monitor)

•

wykorzystanie pierwszych j

ę

zyków programowania

•

po raz pierwszy zastosowano pami

ęć

wirtualn

ą

•

budowane w oparciu o tranzystory

•

funkcjonowały w latach 1955-1964

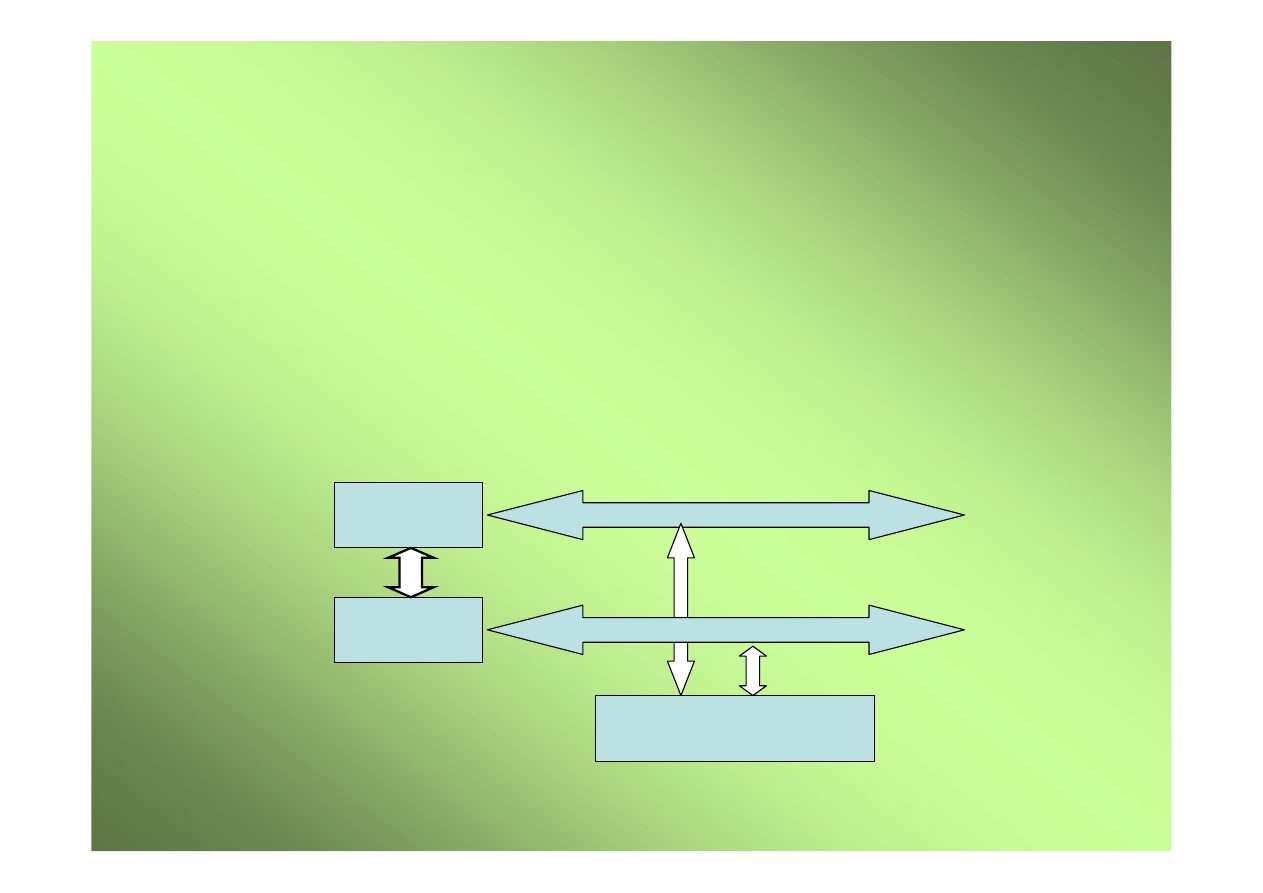
Struktura komputerów drugiego pokolenia

Procesor

centralny

Pami

ęć

Multi-

plekser

Kanały

danych

Urz

ą

dzenia

peryferyjne

Trzecie pokolenie komputerów

•

wykorzystywały algorytm sterowania, pozwalaj

ą

cy r

ę

cznie

zmienia

ć

struktur

ę

maszyny

•

rozwini

ę

to wieloprogramowalno

ść

i zastosowano podział czasu

•

zastosowano tryb interakcyjny

•

wykorzystanie j

ę

zyków wysokiego poziomu

•

do budowy wykorzystywano układy scalone małego i

ś

redniego

stopnia scalania

•

funkcjonowały w latach 1955-1964

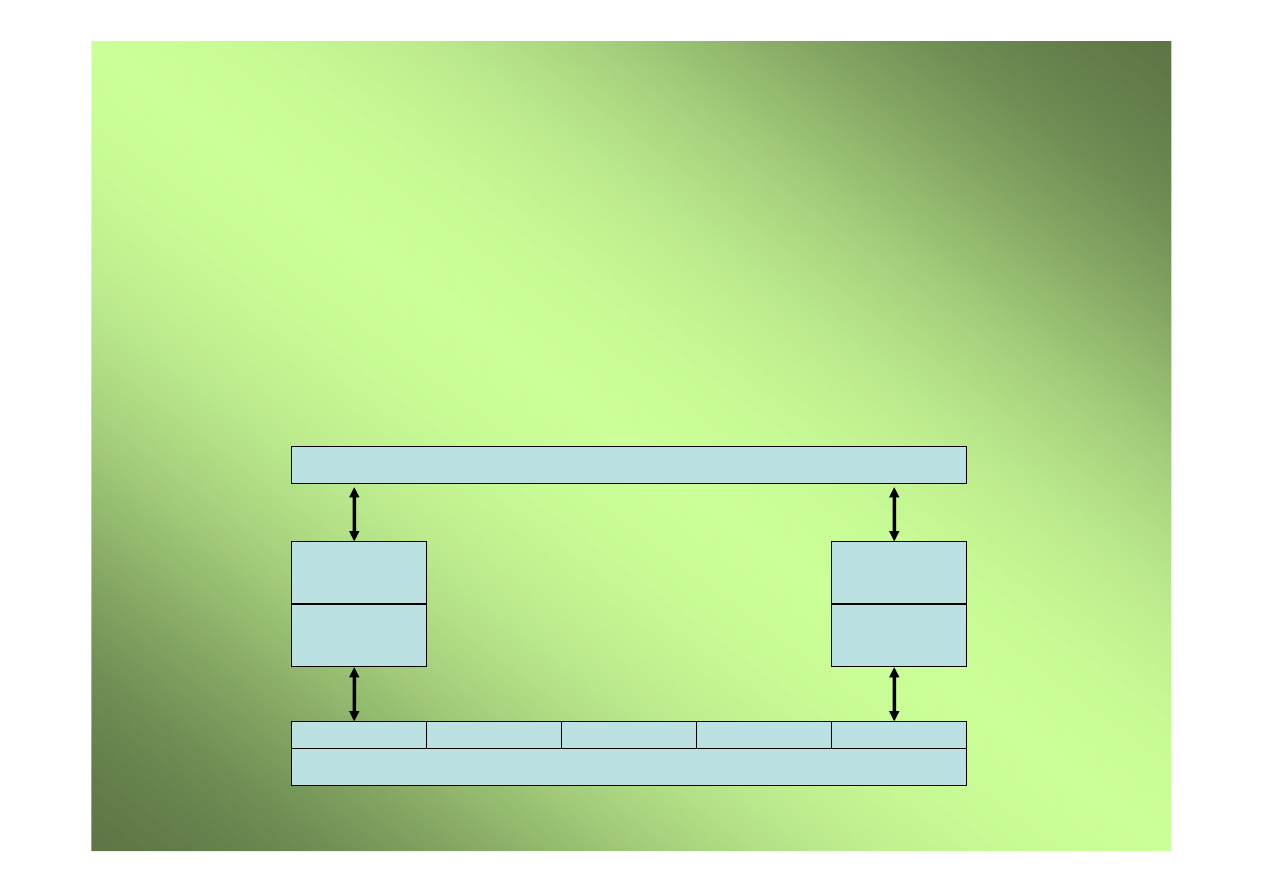
Struktura komputerów trzeciego pokolenia

Procesor

centralny

Pami

ęć

operacyjna

Interfejs pami

ę

ci

Kanały

danych

Interfejs procesora

Czwarte pokolenie komputerów

•

Algorytm sterowania procesem obliczeniowym pozwala na równoległe
rozwi

ą

zywanie szeregu problemów

•

Struktura systemu automatycznie dostosowuje si

ę

do struktury

rozwi

ą

zywanego zadania

•

W celu zwi

ę

kszenia szybko

ś

ci szerzej zastosowano sprz

ę

towe metody

rozwi

ą

zywania niektórych problemów

•

Budowane w oparciu o układy scalone o du

ż

ym stopniu integracji

•

U

ż

ywane w latach 1970-1990

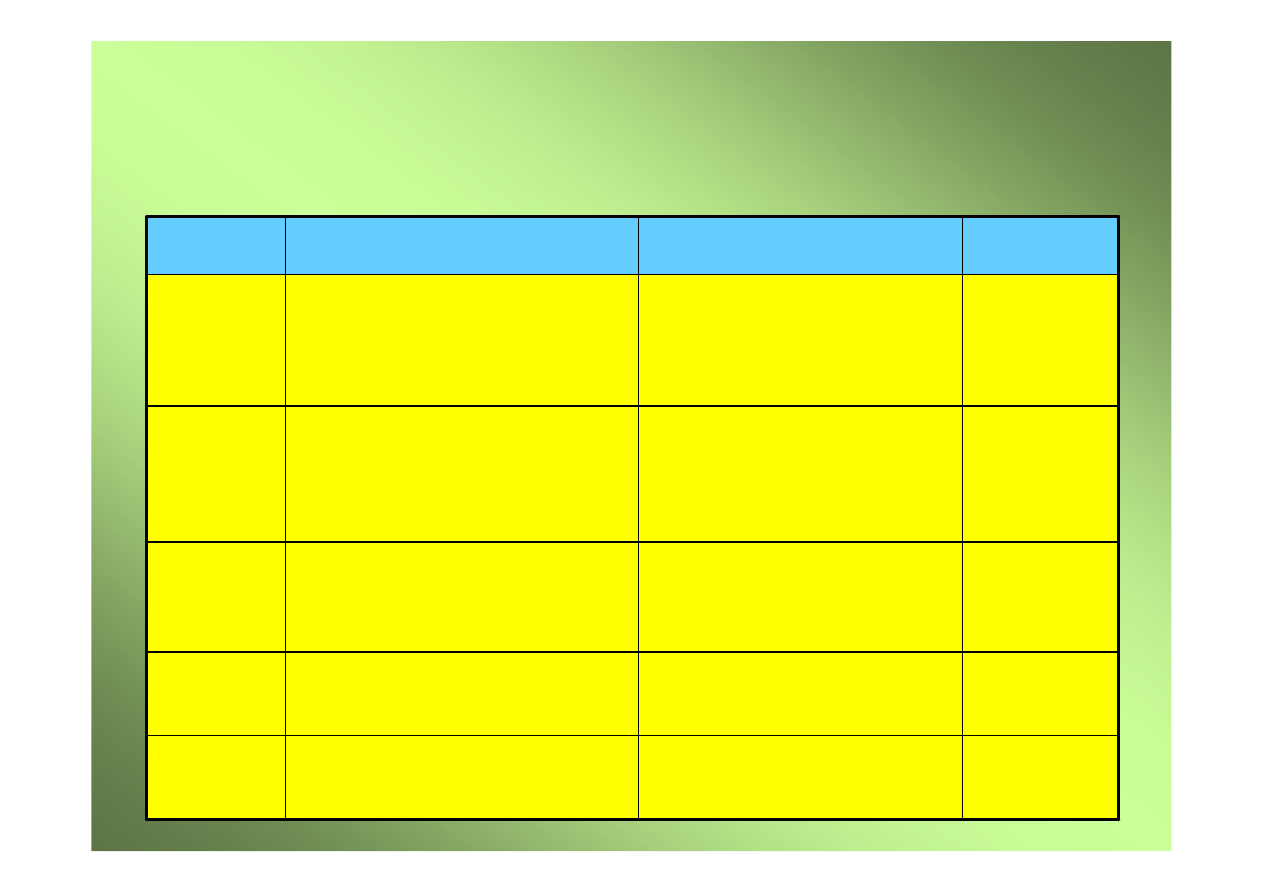
Pami

ęć

operacyjna

Sie

ć

poł

ą

cze

ń

Procesor n

Procesor 1

Procesor 2

.......

Piąte pokolenie komputerów

•

Pozwala rozwi

ą

zywa

ć

bardzo skomplikowane zadania

•

Algorytm sterowania dopuszcza zmian

ę

struktury systemu

obliczeniowego w trakcie rozwi

ą

zywania zadania

•

U

ż

ywane j

ę

zyki programowania coraz bardziej zbli

ż

aj

ą

si

ę

do

j

ę

zyka naturalnego

•

Wybrane funkcje realizuje si

ę

sprz

ę

towo

Sie

ć

poł

ą

cze

ń

Procesor

skalarny

Pami

ęć

operacyjna

Układy wej

ś

cia wyj

ś

cia

Procesor

wektorowy

Pami

ęć

operacyjna

..........

Architektura komputera pi

ą

tego pokolenia

Pięć pokoleń komputerów - zestawienie

Cray MPP

Intel Paragan

VPP500

J

ę

zyk Java. WWW.

Przetwarzanie równoległe

Układy scalone (ULSI)

Architektura skalowalna

Pi

ą

te

1991-.....

VAX 9000

Cray X-MP

IBM 3090

Wieloprocesorowo

ść

J

ę

zyki Ada, Modula

Ś

rodowisko dla pracy równoległej

Układy scalone (LSI oraz VLSI)

Pami

ę

ci półprzewodnikowe

Superkomputery wektorowe

Czwarte

1975-1990

IBM 360/370

CDC 6600

TI-ASC

PDP-8

Wieloprogramowo

ść

i podział czasu

J

ę

zyki PL/I, C, Cobol

Rozbudowany SO

Praca interaktywna

Układy scalone (SSI oraz MSI)

Pami

ęć

cache

Mikroprogramowanie, potokowanie

Trzecie

1965-1974

IBM 7090

CDC 1604

Univac LARC

Elementy wieloprogramowo

ś

ci

J

ę

zyki Algol, Fortran – kompilatory

Monitory (protoplasta SO)

Tranzystory

Dyskretne pami

ę

ci rdzeniowe

Arytmetyka zmiennopozycyjna

Procesory we/wyj

Dzielony dost

ę

p do pami

ę

ci

Drugie

1955-1964

ENIAC

Pronceton IAS

IBM 701

Tryb jednou

ż

ytkownikowy wsadowy

J

ę

zyki maszynowe

Brak podprogramów

We/wy obsługiwane przez procesor
centralny

Lampy elektronowe,

Pami

ęć

na liniach opó

ź

niaj

ą

cych,

Procesor centralny sterowany przez
licznik rozkazów i akumulator

Arytmetyka stałopozycyjna

Pierwsze

1945-1954

Przykłady

Oprogramowanie

I aplikacje

Technologia

i architektura

Pokolenie

Ź

ródło: M. Hajder i inni „Informatyka.Wirtualna podró

ż

w

ś

wiat systemów i sieci komputerowych

Cechy współczesnych systemów

komputerowych

Systemem komputerowym nazywamy zbiór wzajemnie

powi

ą

zanych wzajemnie elementów (komputer,

urz

ą

dzenia peryferyjne, oprogramowanie) których

współdziałanie pozwala osi

ą

gn

ąć

zadany cel

• Wielofunkcyjno

ść

– przystosowanie do realizacji

ró

ż

norodnych zada

ń

(uniwersalno

ść

)

• Zło

ż

ono

ść

– wysoki stopie

ń

skomplikowania sprz

ę

tu i

oprogramowania

• Hierarchiczno

ść

– podział na etapy, umo

ż

liwia rozbicie

przetwarzania

• Spójno

ść

– systemu nie da si

ę

rozbi

ć

na niezale

ż

ne

funkcjonalne elementy

• Rozproszenie – informacja przetwarzana w ró

ż

nych

miejscach (tam gdzie powstaje)

Cechy współczesnych systemów

komputerowych

• Zmienno

ść

struktury – mo

ż

liwo

ść

dostosowania

systemu do zadania

• Niezawodno

ść

– bezawaryjno

ść

, mo

ż

liwo

ść

odtworzenia danych w razie uszkodzenia

• Kontrola i diagnostyka – dost

ę

pno

ść

narz

ę

dzi

diagnostycznych

• Niejednorodno

ść

– ró

ż

norodno

ść

w działaniu

(nie przeszkadzaj

ą

ca we współpracy)

• Równoległo

ść

– mo

ż

liwo

ść

jednoczesnej pracy

wielu elementów przetwarzaj

ą

cych

• Otwarto

ść

systemu – mo

ż

liwo

ść

jego rozbudowy

• Moc obliczeniowa