Maszyna Turinga

W roku 1937 angielski matematyk,

Alan Turing

,pracuj c nad koncepcj

obliczalno ci funkcji matematycznych opisuje bardzo prost maszyn
logiczn , która dzi nosi nazw Maszyny Turinga.
.

Pomimo swej prostoty Maszyna Turinga
posiada obecnie olbrzymie
znaczenie teoretyczne, poniewa
wszystkie współczesne komputery daj
si do niej sprowadzi , zatem dany

problem jest rozwi zalny na komputerze,

je li da si zdefiniowa rozwi zuj c
go maszyn Turinga

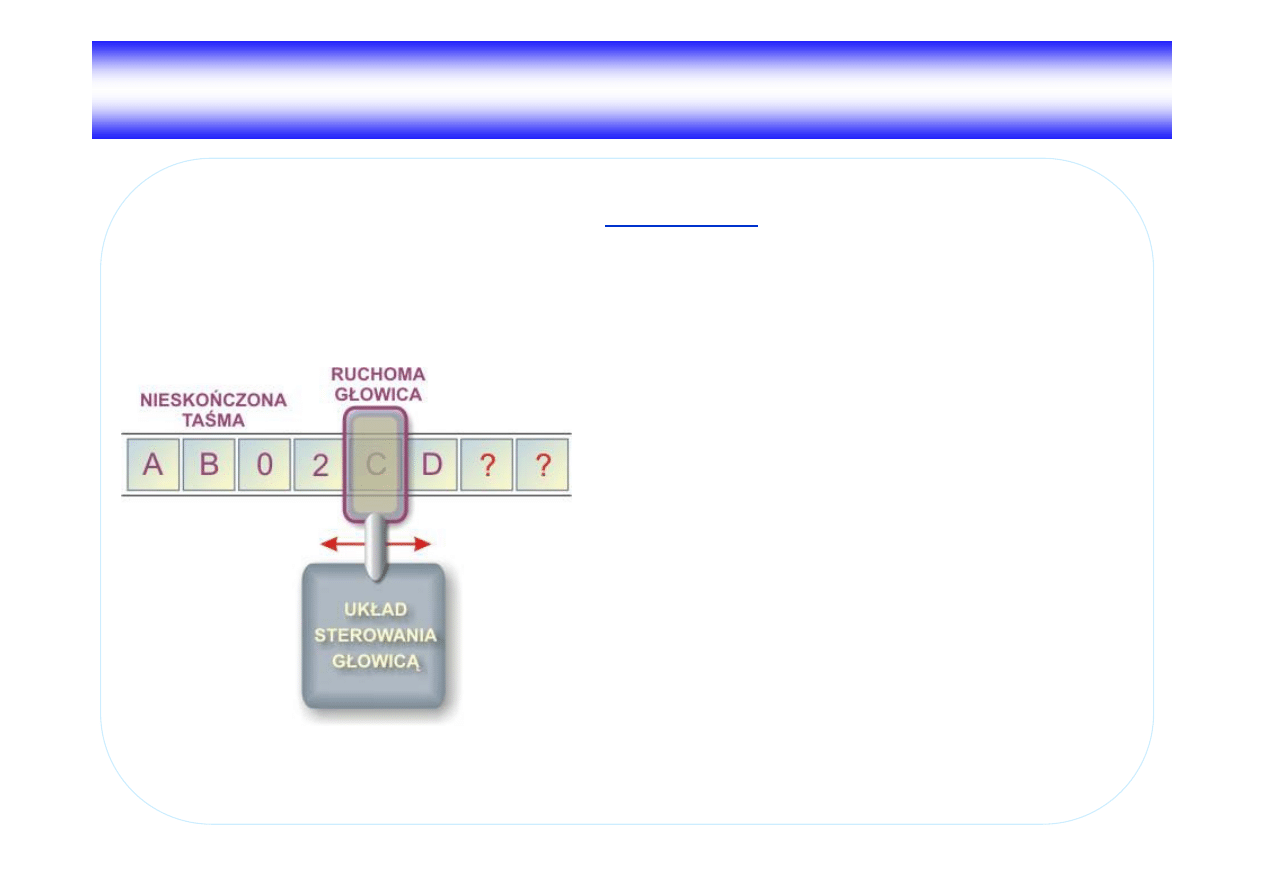
Ta ma

Niesko czona

ta ma

jest

odpowiednikiem

współczesnej

pami ci komputera

. Ta ma dzieli si

na komórki, w których umieszczone zostały symbole,

czyli po prostu znaki przetwarzane przez maszyn

Turinga. Symbole te stanowi odpowiednik danych

wej ciowych. Maszyna Turinga odczytuje te dane z

kolejnych komórek i przetwarza na inne symbole,

czyli dane wyj ciowe. Wyniki oblicze równie s

zapisywane w komórkach ta my.

Głowica zapisuj co-odczytuj ca

Aby przetwarza

dane, maszyna Turinga musi potrafi

je

odczytywa

z ta my i zapisywa

na ta m . Do tego celu

przeznaczona jest wła nie głowica zapisuj co-odczytuj ca, która

odpowiada

funkcjonalnie

urz dzeniom

wej cia/wyj cia

współczesnych komputerów lub

układom odczytu i zapisu pami ci

.

Głowica zawsze znajduje si nad jedn z komórek ta my. Mo e

ona odczytywa zawarto

tej komórki oraz zapisywa do niej inny

symbol - na tej zasadzie odbywa si przetwarzanie danych - z

jednych symboli otrzymujemy inne. Oprócz odczytywania i

zapisywania symboli w komórkach głowica wykonuje ruchy w

prawo i w lewo do s siednich komórek na ta mie. W ten sposób
mo e si ona przemie ci do dowolnie wybranej komórki ta my.

Układ sterowania

Przetwarzaniem informacji zarz dza układ sterowania

głowic . Jego współczesnym odpowiednikiem jest

procesor

komputera

. Układ ten odczytuje za pomoc

głowicy

symbole z komórek ta my oraz przesyła do głowicy

symbole do zapisu w komórkach. Dodatkowo nakazuje on

głowicy przemie ci si do s siedniej komórki w lewo lub w

prawo.

Zbiór symboli S = {s

i

} - zbiór symboli, które b d przetwarzane przez maszyn

Turinga, nazwany alfabetem S

Stan maszyny - okre la jednoznacznie stan głowicy q

j

i odczytany przez ni

symbol alfabetu s

i

:

S

ij

= (s

i

,q

j

)

Ruch maszyny - opisuje akcj , jak ma wykona MT. Ruch maszyny jest reakcj

maszyny na stan maszyny S

ij

. Opisywany jest jako trójka:

R

ij

= (s

k

, q

l

, p

m

),

Gdzie:
s

k

– symbol zapisany przez głowic ,

q

l

– nowy stan wewn trzny głowicy,

p

m

–przesuni cie głowicy {P, N, L},

q

1

q

2

...

q

j

...

q

m

s

1

s

2

...

...

s

n

•

Ka dy ruch R

ij

jest zwi zany jednoznacznie ze stanem maszyny S

ij

.

Zatem: R

ij

= T (S

ij

), gdzie T – to tablica charakterystyczna maszyny Turinga

R

ij

= (s

k

, q

l

, p

m

)

Je li b d c w stanie q

j

głowica

odczytała symbol s

i

, to nale y

zapisa na ta mie symbol s

k

,

zmieni stan wewn trzny głowicy

na q

l

i dokona przesuni cia

głowicy p

m

,

Twierdzenie:

Ka dy algorytm mo e by realizowany
przez odpowiednio zaprogramowan (za

pomoc tablicy charakterystycznej)
Maszyn Turinga

Zadanie 1

Maszyna Turinga odejmuj ca 1 od liczby binarnej

Liczba parzysta

Liczba nieparzysta

10

100

1010

1

-

1

-1

10011

10100

Negacja wszystkich cyfr od prawej a do pierwszej jedynki wł cznie

Uwagi:
•

Alfabet składa si ze znaków: {

φ, 0, 1}.

•

Głowica na pocz tku umieszczona jest z prawej strony ta my.

Po wykonaniu przetwarzania głowica pozostaje po lewej stronie liczby

binarnej.

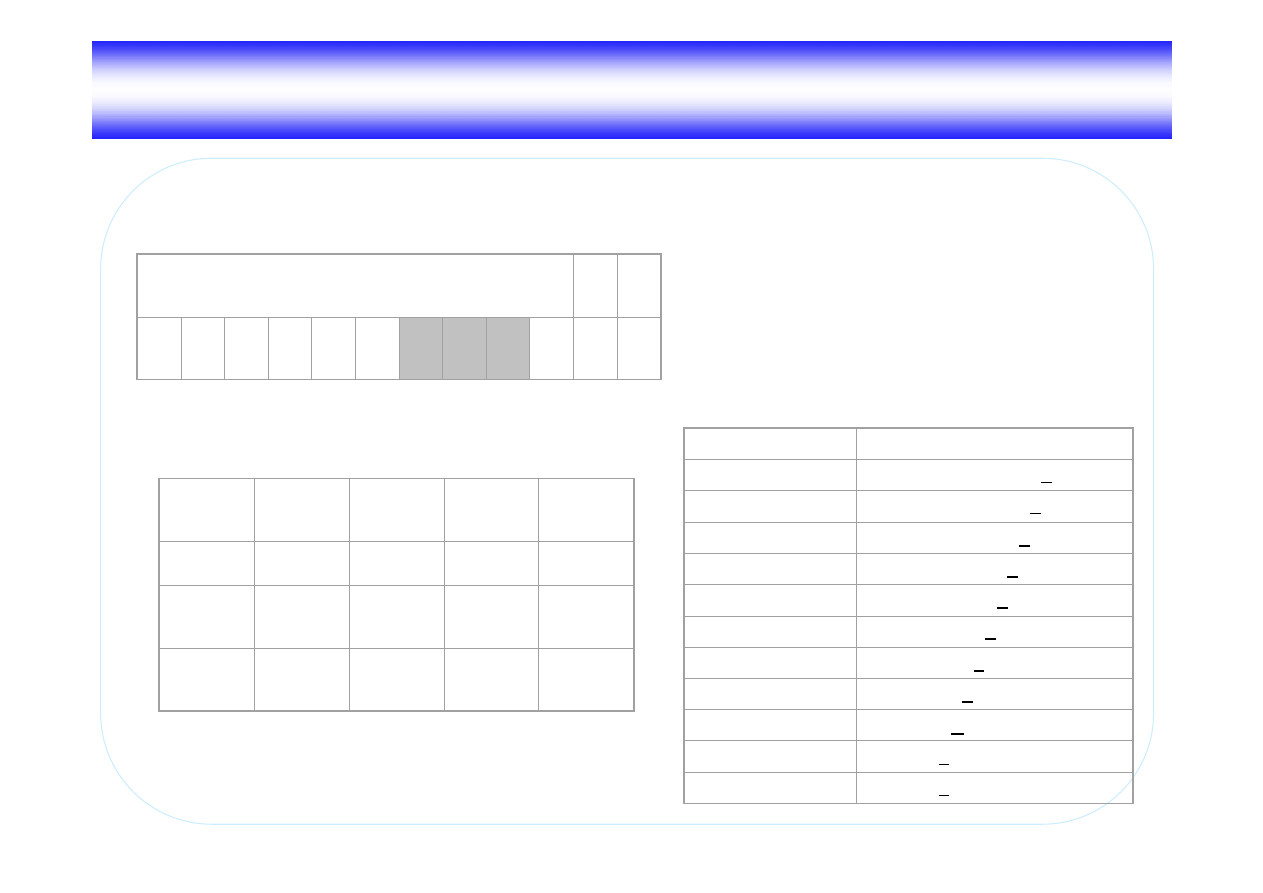
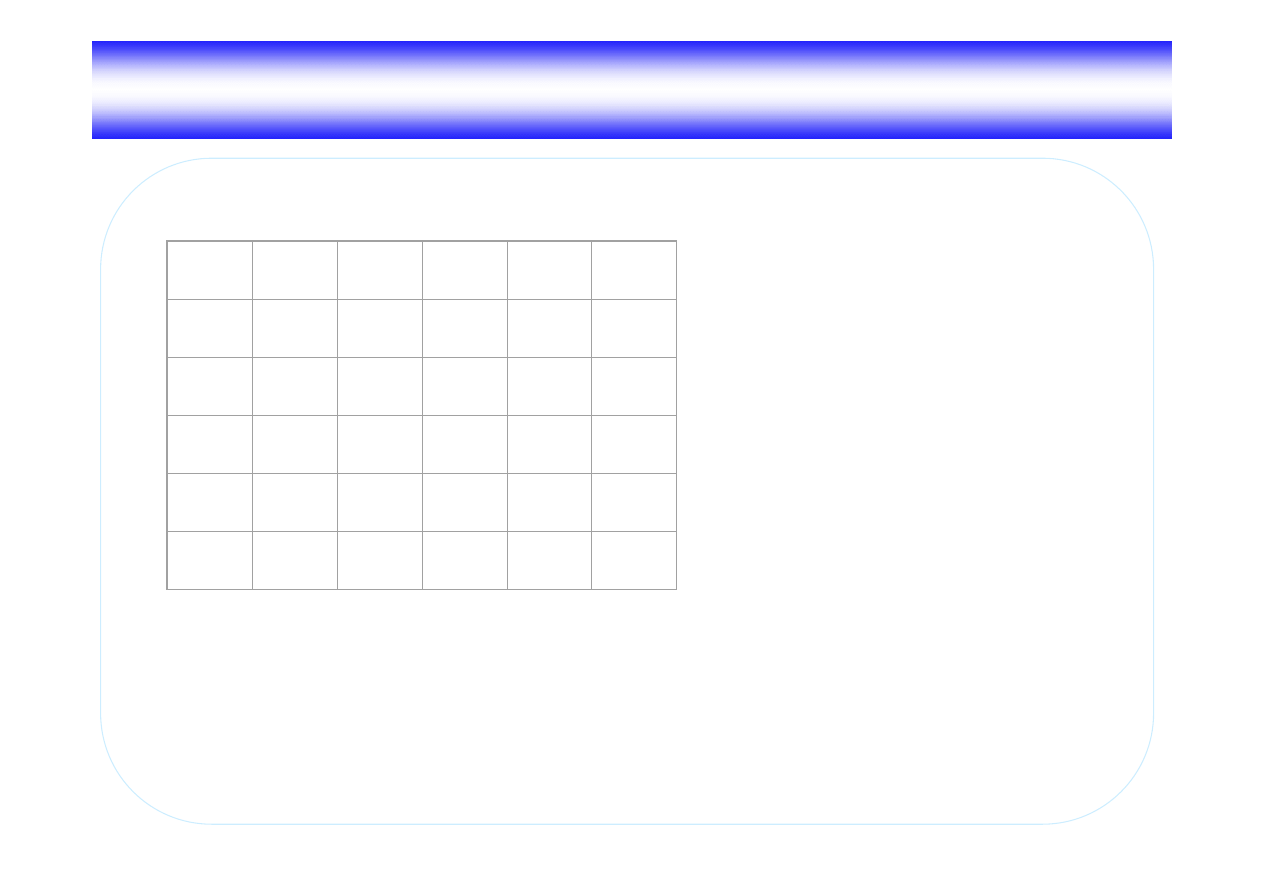
q

0

q

1

q

2

q

3

φ

φq

0

L

φq

3

L

φq

3

L

φq

3

N

0

1q

1

L

1q

1

L

0q

2

L

0q

3

N

1

0q

2

L

0q

2

L

1q

2

L

1q

3

N

Stany wewn trzne głowicy
q

0

– stan pocz tkowy, szukanie liczby,

q

1

– stan inwersji,

q

2

– stan przepisywania,

Q

3

– stan ko cowy.

Pocz tkowy napis i poło enie głowicy

↓

φ

1

0

0

0

1

0

0

φ

φ

Stan głowicy

Napis na ta mie

q

0

φ

φφφφφ

q

0

φ

φφφφφ

q

0

φ

0φφ

q

1

φ

01φφ

q

1

φ

111φφ

q

2

φ

0011φφ

q

2

φ 00011φφ

q

2

φ 000011φφ

q

2

φ 000011φφ

q

2

φφφφ

φφ

q

3

φφφφ

φφ

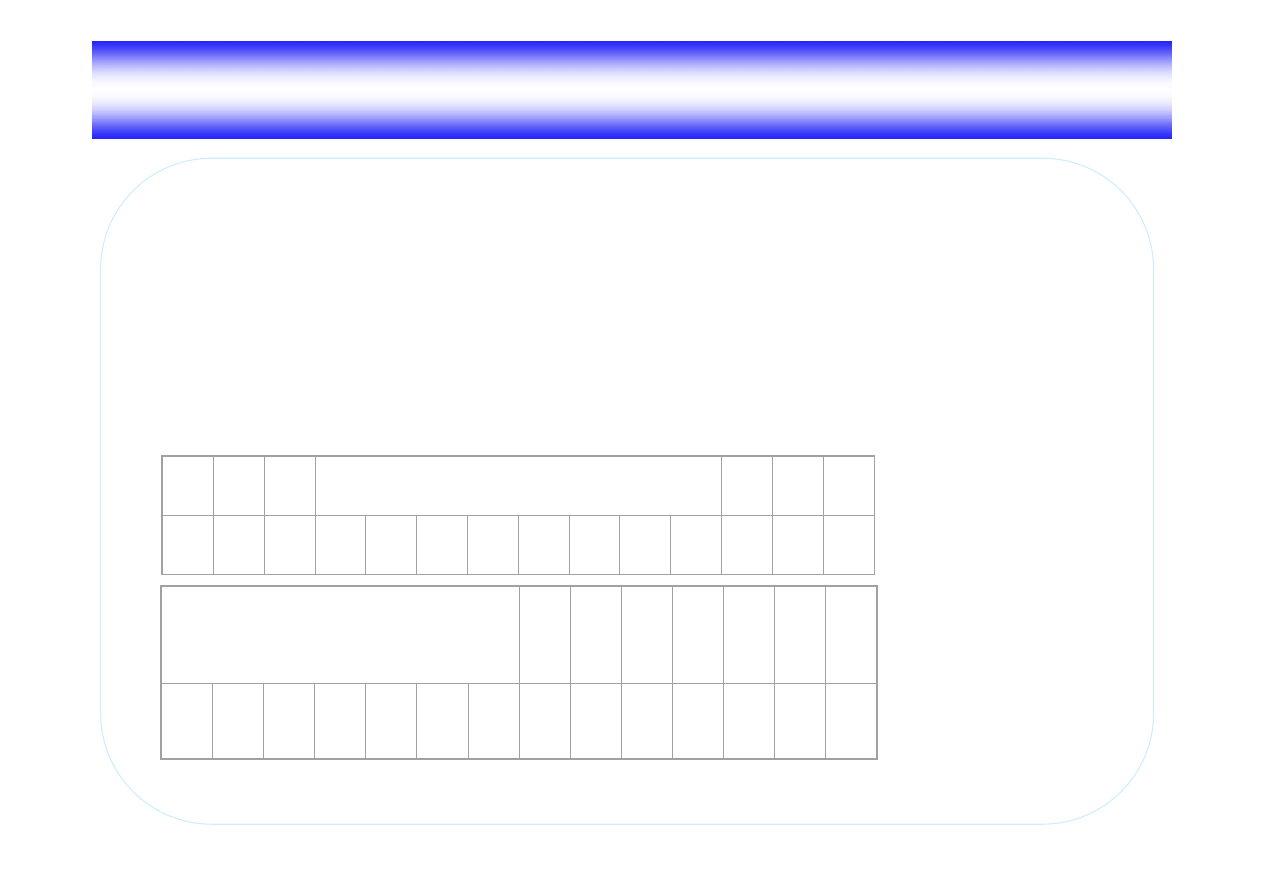
Zaprojektowa maszyn Turinga eliminuj c nieznacz ce zera liczb ułamkowych

w zapisz trójkowym (zarówno na pocz tku jak i na ko cu liczby).

Mo liwe symbole:

∅

∅

∅

∅, 0, 1, 2, .

Stan pocz tkowy głowicy:

z lewej strony liczby

Zało enia:

Liczby s tylko w poprawnej postaci: <ci g cyfr>.<ci g cyfr>

↓

Pocz tkowy napis i poło enie głowicy

φ

φ

0

0

1

.

0

1

0

0

0

φ

φ

Ko cowy napis i poło enie głowicy

↓

φ

φ

φ

φ

1

.

0

1

φ

φ

φ

φ

φ

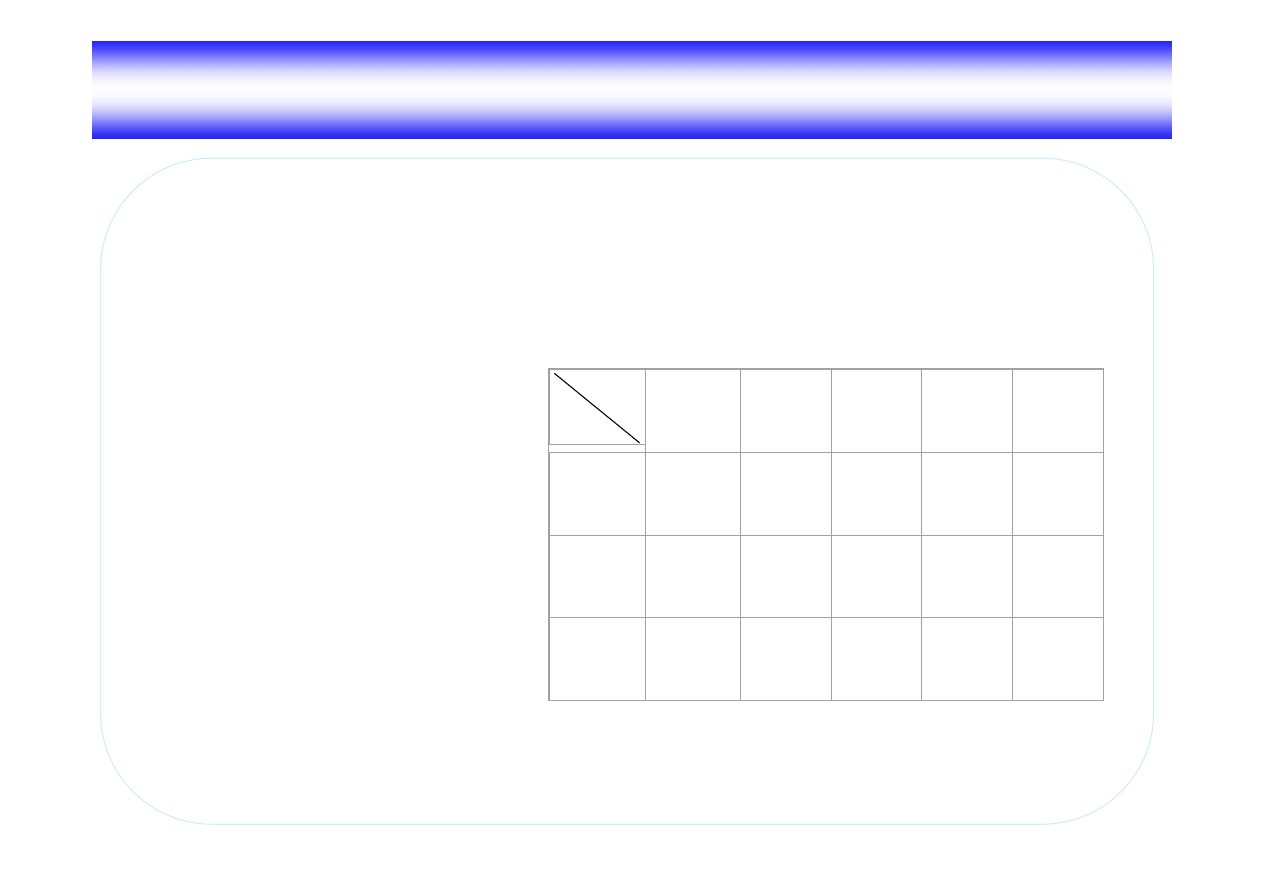
q

0

q

1

q

2

q

3

q

4

φ

φq

0

P

φq

2

L

φq

4

N

φq

3

N

φq

4

N

0

φq

0

P

0q

1

P

φq

2

L

0q

3

N

1

1q

1

P

1q

1

P

1q

3

N

1q

3

N

2

2q

1

P

2q

1

P

2q

3

N

2q

3

N

.

.q

1

P

.q

1

P

.q

3

N

.q

3

N

Stany wewn trzne głowicy
q

0

– przesuwanie w prawo i pomijanie

zer pocz tkowych,

q

1

– przej cie na prawy koniec liczby,

q

2

– eliminowanie zer ko cowych,

q

3

– poprawny stan ko cowy,

q

4

– bł dny stan ko cowy.

Ogólny opis zło enia dwóch maszyn Turinga

Dane maszyny: T1, T2
Alfabet wspólny:

S = {s

0

, s

1

, .. , s

l

}

Zbiory stanów wewn trznych:

Q

1

= {q

01

, q

11

, q

21

, .. , q

n1

}

Q

2

= {q

02

, q

12

, q

22

, .. , q

m2

}

Zło enie (iloczyn) maszyn Turinga jest maszyn Turinga o tym samym

alfabecie oraz zbiorze stanów wewn trznych Q:

Q = {q

0

, q

1

, q

2

, .. , q

m+n

},

w którym kolejne stany odpowiadaj stanom maszyn T1, T2 w nast puj cy

sposób:

q

0

≡ q

01

q

1

≡ q

11

q

2

≡ q

21

...

q

n-1

≡ q

n-1,1

q

n

≡ q

n1

≡ q

02

q

n+1

≡ q

12

q

n+2

≡ q

22

...

q

n+m

≡ q

m,2

Zakłada si , e q

n1

jest stanem poprawnego zako czenia pracy maszyny T1 i pocz tkowym

stanem dla maszyny T2.

Zadanie

Zaprojektowa maszyn Turinga dodaj c 1 do liczby binarnej, je li jest ona ujemna albo

odejmuj ca 1, je li liczba jest dodatnia.

Uwagi:

·

Symbole alfabetu: {

φ, 0, 1}.

·

Pierwszy znak z lewej strony napisu jest bitem znaku.

·

Głowica na pocz tku znajduje si z lewej strony liczby binarnej,

Po wykonaniu przetwarzania głowica z prawej stronie liczby.

T1 –

maszyna testuj ca znak liczby i szukaj ca jej prawego ko ca (stan pocz tkowy

głowica z lewej)

T2 –

maszyna dodaj ca 1 (stan pocz tkowy głowica z prawej)

T3 –

maszyna odejmuj ca 1 (stan pocz tkowy głowica z prawej)

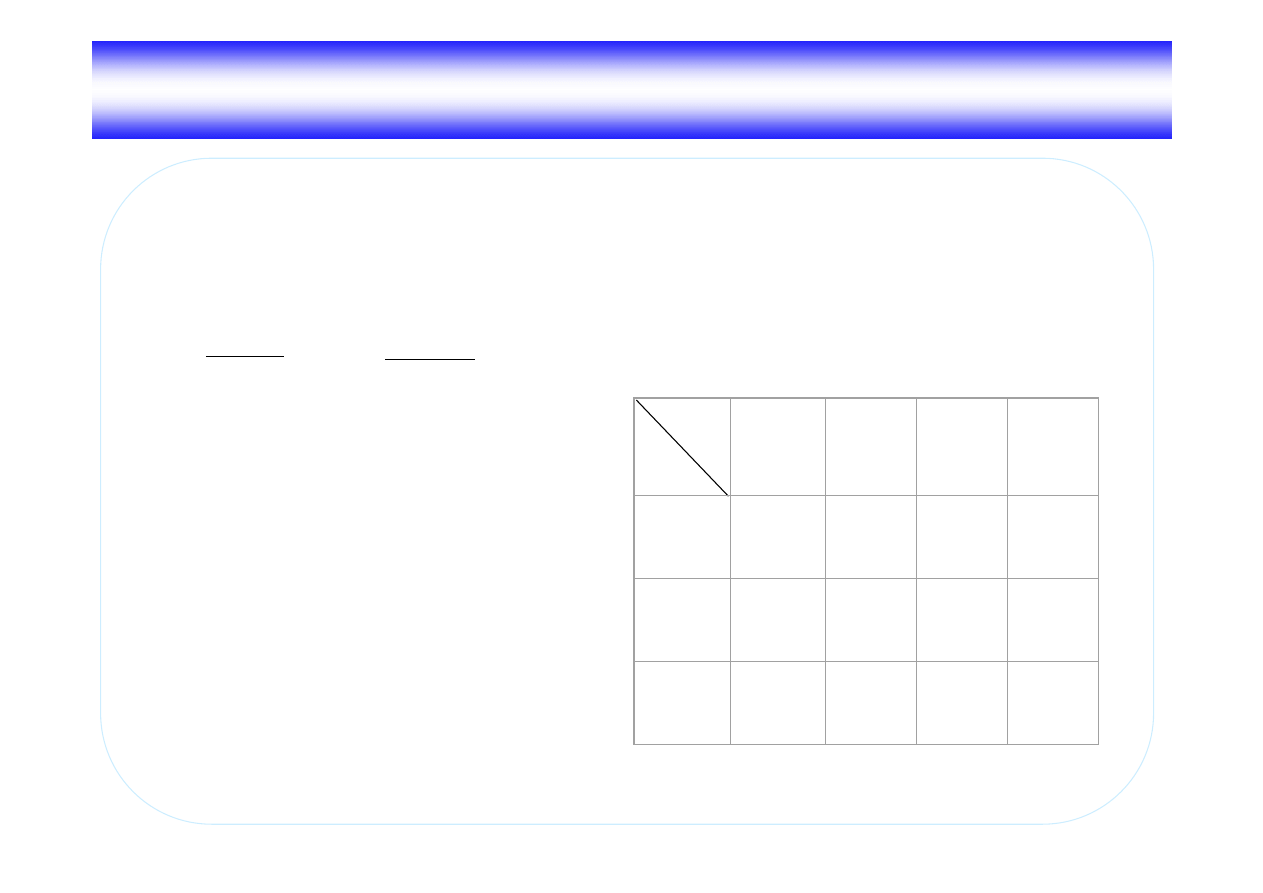
Maszyna T1

maszyna testuj ca znak liczby i szukaj ca jej prawego ko ca

Stany wewn trzne głowicy
q

0

– stan pocz tkowy,

q

1

– bit znaku ‘0’,

q

2

– bit znaku ‘1’,

q

3

– liczba ujemna,

q

4

– liczba dodatnia.

Tablica charakterystyczna

q

0

q

1

q

2

q

3

q

4

φφφφ

φq

0

P

φq

4

N

φq

3

N

q

3

N

q

4

N

0

0q

1

P

0q

1

P

0q

2

P

q

3

N

q

4

N

1

1q

2

P

1q

1

P

1q

2

P

q

3

N

q

4

N

q

s

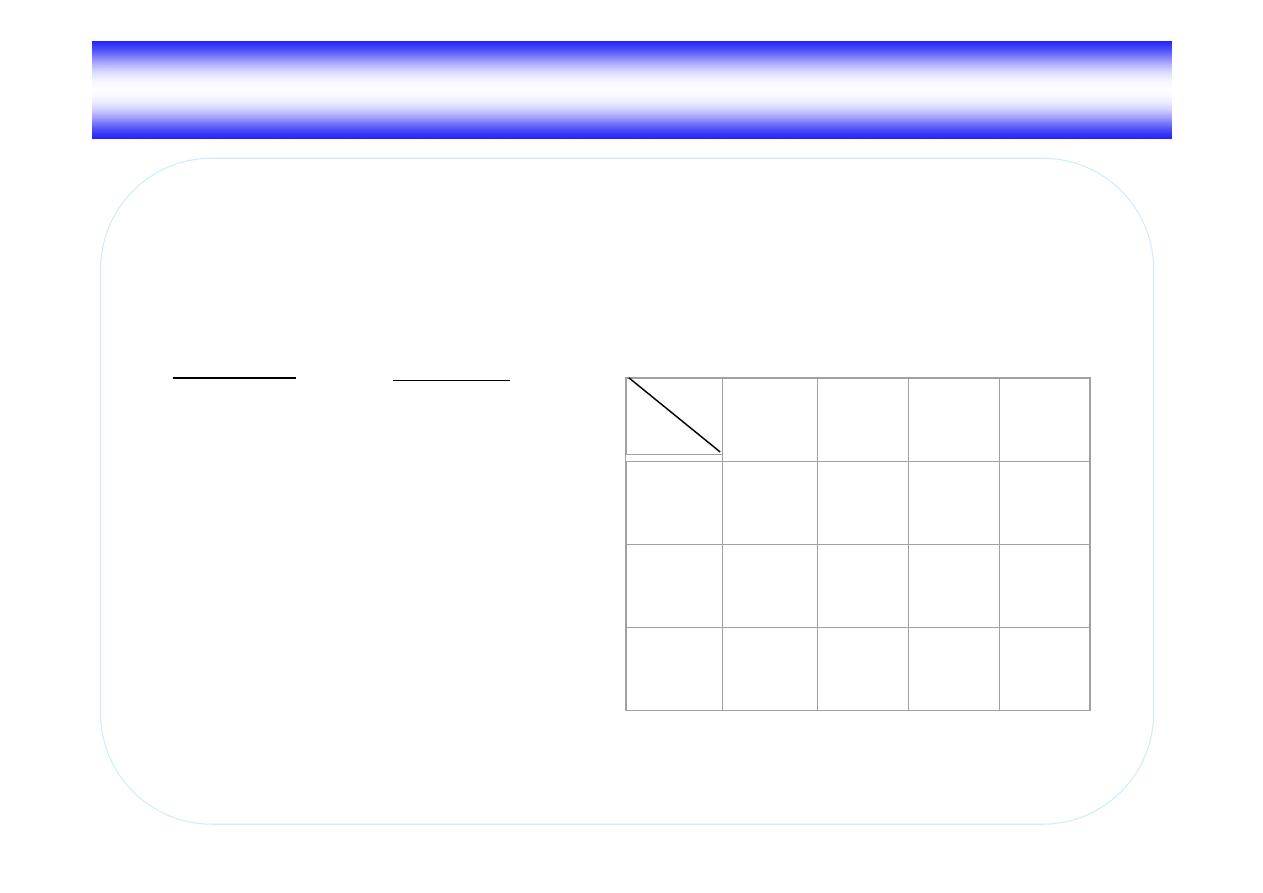
Maszyna T2 - dodaj ca 1

(głowica z prawej)

1010

0

00

011

10101

00100

+ 1

+ 1

Stany wewn trzne głowicy

q

0

– stan pocz tkowy, głowica z prawej,

q

1

– inwersja,

q

2

– przepisywanie,

q

3

– stan ko cowy.

S

Q

q

0

q

1

q

2

q

3

φφφφ

φq

0

L

φq

3

N

φq

3

N

q

3

N

0

1q

2

L

1q

2

L

0q

2

L

q

3

N

1

0q

1

L

0q

1

L

1q

2

L

q

3

N

Tablica charakterystyczna

T3 – maszyna odejmuj ca 1 (głowica z prawej)

10

100

0001

1

10011

00010

– 1

– 1

Stany wewn trzne głowicy
q

0

– stan pocz tkowy, głowica z prawej,

q

1

– inwersja,

q

2

– przepisywanie,

q

3

– stan ko cowy.

q

0

q

1

q

2

q

3

φφφφ

φq

0

L

φq

3

N

φq

3

N

q

3

N

0

1q

1

L

1q

1

L

0q

2

L

q

3

N

1

0q

2

L

0q

2

L

1q

2

L

q

3

N

s

q

Tablica charakterystyczna

T1

q

0

q

1

q

2

q

3

q

4

T2

q

0

q

1

q

2

q

3

T3

q

0

q

1

q

2

q

3

T

q

0

q

1

q

2

q

3

q

4

q

5

q

6

q

7

q

8

q

9

φφφφ

φq

0

P

φq

6

N

φq

3

N

φq

3

L

φq

9

N

φq

9

N

φq

6

L

φq

9

N

φq

9

N

φq

9

N

0

0q

1

P

0q

1

P

0q

2

P

1q

5

L

1q

5

L

0q

5

L

1q

7

L

1q

7

L

0q

8

L

φq

9

N

1

1q

2

P

1q

1

P

1q

2

P

0q

4

L

0q

4

L

1q

5

L

0q

8

L

0q

8

L

1q

8

L

φq

9

N