Jerzy Peja : Algorytmy i struktury danych

- 1 -

ALGORYTMICZNA

UNIWERSALNO

Maszyna Turinga

Jerzy Peja : Algorytmy i struktury danych

- 2 -

UPRASZCZZANIE ZŁO ONO CI

Co to jest i co ma na celu?

Upraszczanie zło ono ci ma na celu budowanie urz dze

(algorytmicznych) tak prostych jak tylko jest to mo liwe, wr cz

prymitywne z obecnymi komputerami i j zykami programowania,

a jednak na tyle silnych, e pozwalaj one na wykonywanie nawet

najbardziej zło onych algorytmów.
Dzi ki upraszczaniu zło óno ci chcemy osi gn trzy cele:

•

odkry obiekty (m.in. struktury danych), które s tak proste, jak

to tylko mo liwe, a mimo to tak silne, jak adne inne tego typu,

•

pokaza , czy okre lony tzw. trudno obliczeniowo problem nie

posiada teraz i w przyszło ci adnych rozs dnych rozwi za ,

•

przeprowadzenie cisłych dowodów pokazuj cych, czy dany

problem jest rozstrzygalny, czy te nie.

Upraszczanie danych

Ka dy element danych mo na traktowa jako ci g symboli. Z tego

powodu ka dy obiekt mo na zakodowa , traktuj c go jako zawsze

jako ci g symboli, np. ci g cyfr, liter lub słów.
Liczba ró nych symboli w takich kodach jest sko czona i tworzy
tzw.

alfabet. Ka d jednostk danych mo na wi c zapisa na

jednowymiarowej

ta mie, składaj cej si z ci gu kwadratów, z

których ka dy zawiera pojedynczy symbol ze sko czonego

alfabetu.
Dzi ki za wszystko i takiemu podej ciu ka d , nawet najbardziej

zło on struktur danych mo na zlinearyzowa .

Przykład 1: Uproszczenie (linearyzacja) tablicy dwuwymiarowej
Je li przyj , e ka dy element tablicy znajduj cy si w tym samym

wierszu b dziemy oddziela od siebie znakiem *, za całe wiersze

znakiem **, wówczas dowolna tablic mo na łatwo rozci gn na

jednowymiarowej ta mie.

Jerzy Peja : Algorytmy i struktury danych

- 3 -

MASZYNA TURINGA

Przykład 1: Uproszczenie tablicy dwuwymiarowej (c.d.)
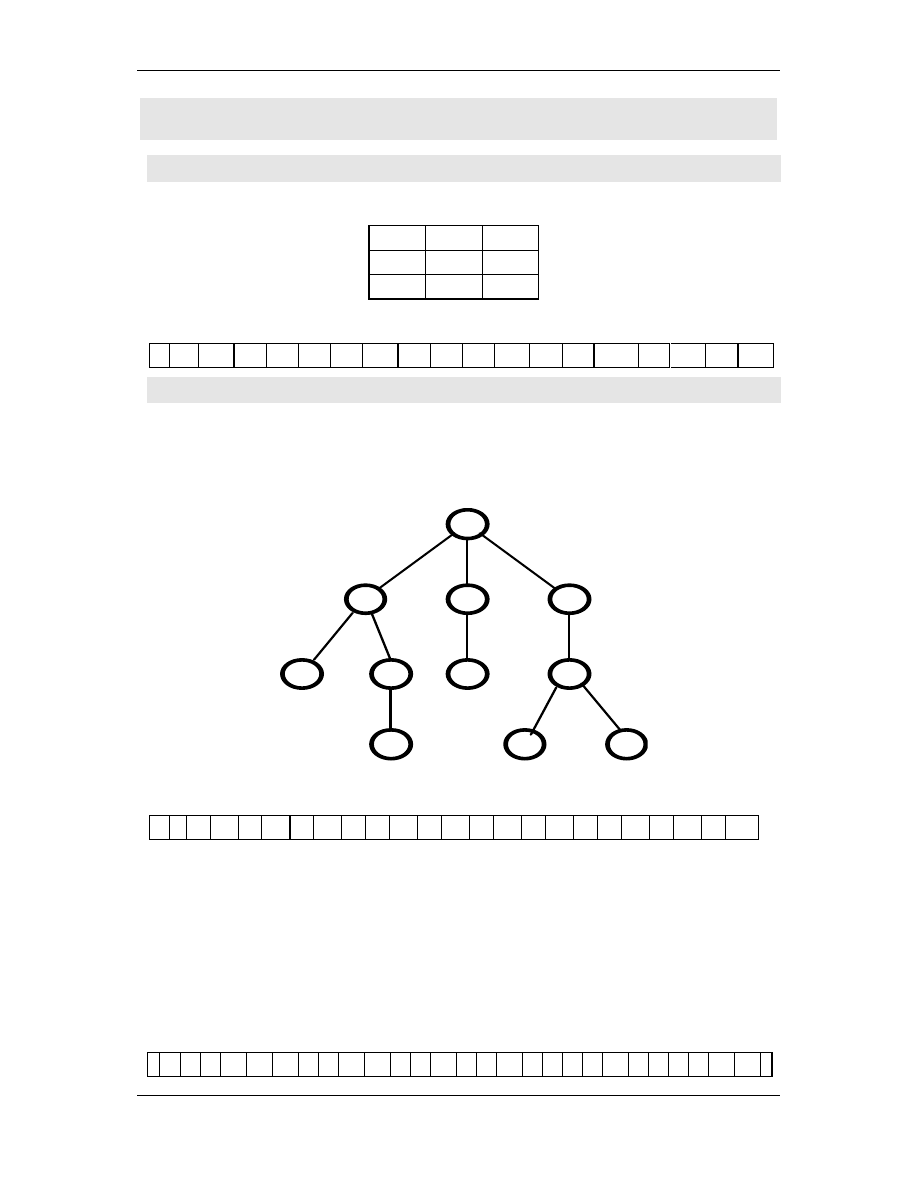
Dla tablicy o postaci:

7

45

-3

91

0

12

-15

11

17

Otrzymamy nast puj ca ta m jednowymiarow :

7 * 45 * -3 * * 91 * 0 * 12 * * -15 * 11 * 17

Przykład 2: Linearyzacja drzewa
Drzewo mo emy linearyzowa poziom po poziomie, oddzielaj c

poziomy znakiem **, za w zły drzewa z tego samego poziomu przy

pomocy *. Wówczas dla drzewa o postaci:

N

R

M

Y

F

A

O

I

T

K

A

za ta ma:

I * * N * F * O * * R * M * A * T * * Y * K * A

Koduj c w powy szy sposób trudno jest dowiedzie si np. czy A

jest potomkiem w zła N, F, czy te mo e O.
Linearyzuj c drzewo musimy wzi wi c pod uwag konieczno

zachowania jego dotychczasowej struktury. Jeden ze sposobów mo e

polega na zaznaczeniu pocz wszy od lewej strony drzewa grup

bezpo rednich potomków poziom po poziomie.. Dla omawianego

drzewa mo e ona mie posta :

( I ) ( N F O ) ( R M ) ( A ) ( T ) ( ) ( Y ) ( ) ( K A )

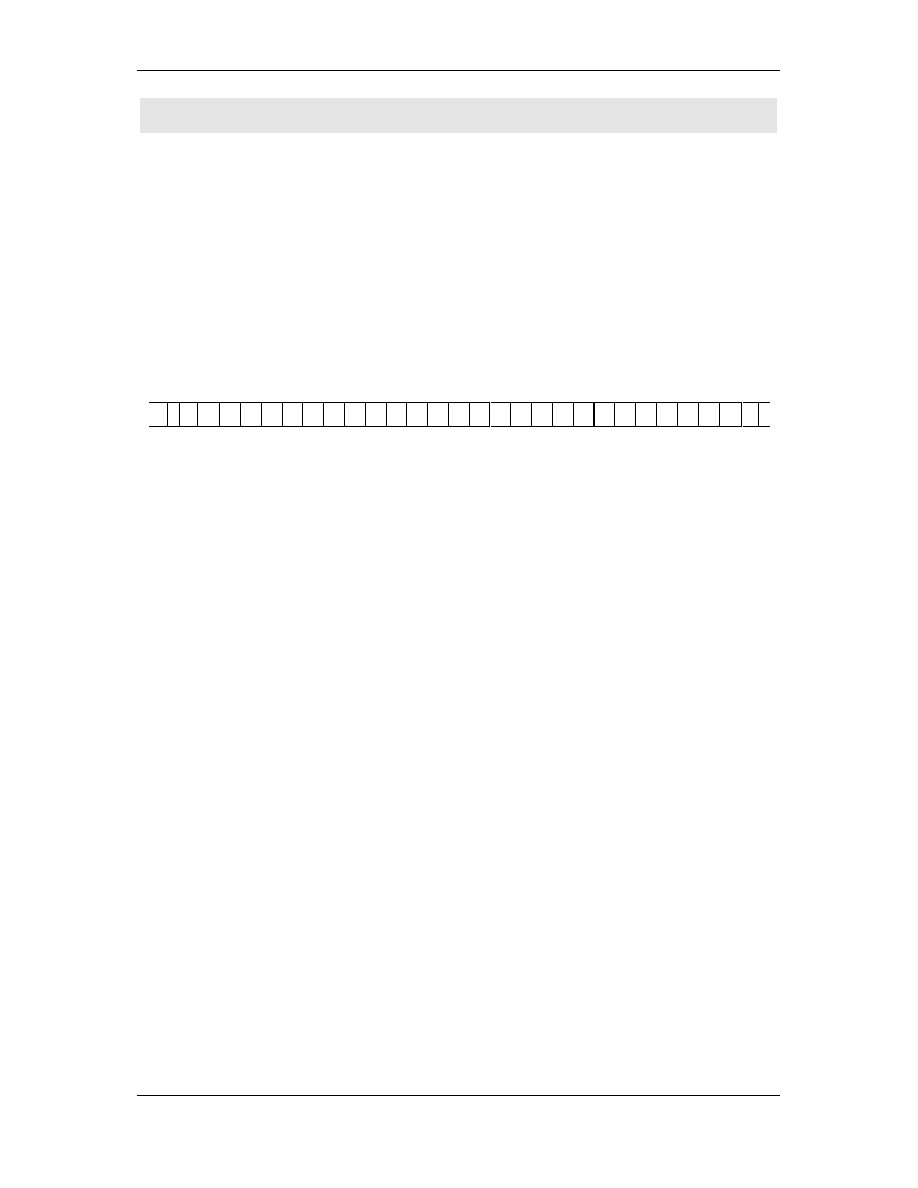
Jerzy Peja : Algorytmy i struktury danych

- 4 -

MASZYNA TURING

Konkluzje

Dowolne dane (wej ciowe, wyj ciowe, po rednie) na których

działa algorytm, mo na zapisa w postaci jednowymiarowej ta my,

by mo e o nieograniczonej długo ci.
Algorytm w danej chwili przetwarza tylko sko czona liczb
danych, zwanych

znacz c porcj danych otoczonych z ka dej

strony ci giem symboli pustych (oznaczanych dalej przez

#).

Ta ma ma wi c zawsze posta :

# # # #

Odpowiada ona nast puj cemu modelowi pami ci:

• niesko czona jednowymiarowa ta ma

• dopuszczalny zestaw symboli (alfabet), które mog by

zapisywane w komórkach ta my

• pusta komórka oznaczana symbolem #

Upraszczanie struktur steruj cych

Znajdowanie si procesora w okre lonym miejscu algorytmu
(programu, dokładniej procesu) nazywamy jego

stanem. Je li wi c

stan procesora b dziemy u ywa do kodowania miejsc w

algorytmie, to poruszanie si po algorytmie mo emy modelowa

jako zmiany stanu wzgl dem stanu aktualnego. Ze wzgl du na

sko czono liczby akcji podstawowych algorytmu liczba stanów

jest tak e sko czona.
Przej cie do innego miejsca algorytmu (stanu) zale y od stanu

aktualnego i od warto ci pewnych jednostek danych, które

stosuje si w wielu strukturach steruj cych (np.

if-then-else lub

do-while) w celu sprawdzenia, do jakiego miejsca algorytmu

nale y przekaza sterowanie.
Dane w naszym przypadku tworz jednowymiarow ta m .

Załó my wi c, e przyszły stan procesora, b d cego w okre lonym

stanie aktualnym, b dzie zale ał od nast pnego symbolu

odczytanego z ta my.

Jerzy Peja : Algorytmy i struktury danych

- 5 -

MASZYNA TURINGA

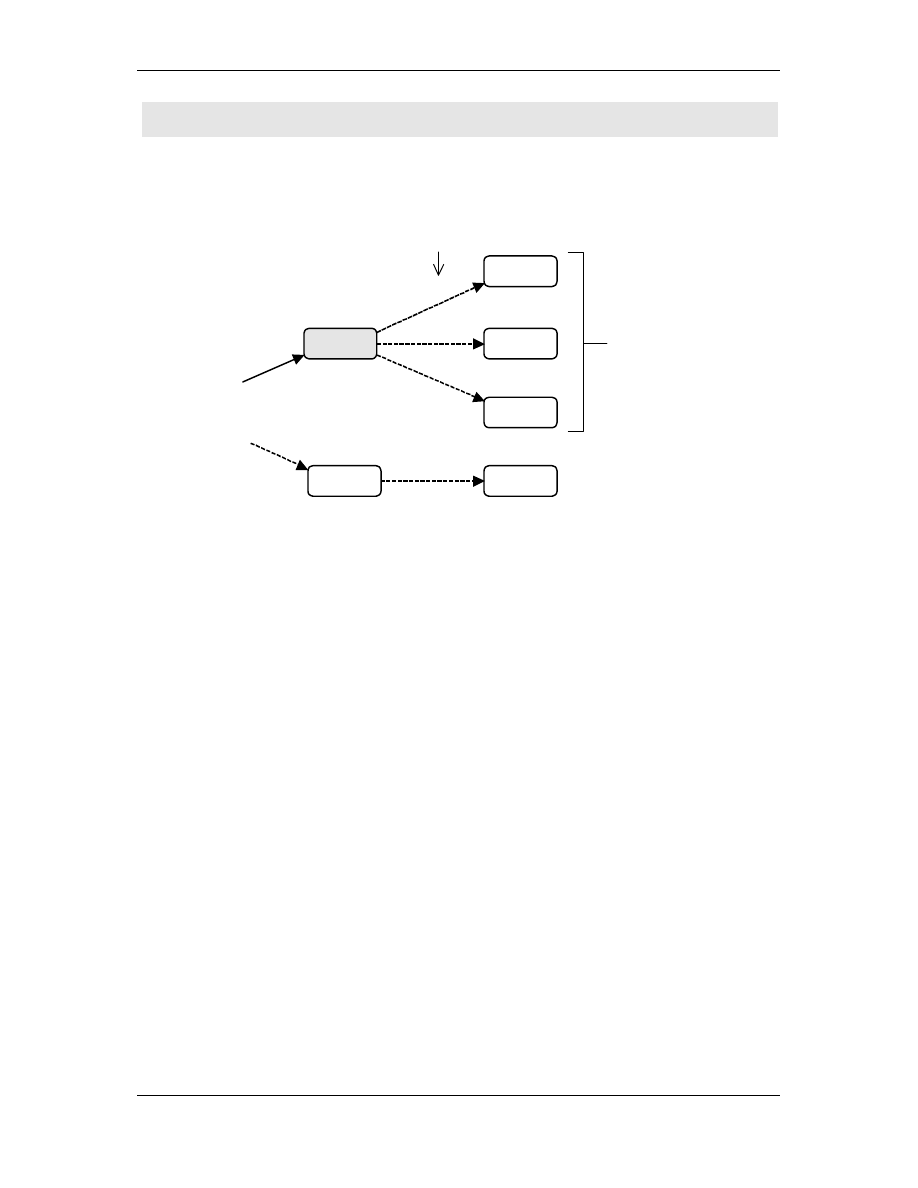
Upraszczanie struktur steruj cych (c.d.)

stan

aktualny

symbole

alfabetu

mo liwe

stany

nast pne

a

b

c

Stan procesora

Konkluzje

Procesor mo e odczytywa w danej chwili tylko jeden symbol z

ta my.
Procesor mo e w danej chwili zapisywa do komórki (kwadratu)

ta my tylko jeden symbol nale cy do przyj tego alfabetu.
Procesor mo e przemieszcza si wzdłu ta my, ale w danej chwili

mo e posun si tylko o jedn komórk ta my (w lewo lub

prawo). Kierunek ruch b dzie zale ał od bie cego stanu procesora

skrzyni biegów i od symbolu

Upraszczanie operacji podstawowych

Na podstawie rozwa a o upraszczaniu struktur steruj cych

wyposa my mechanizm naszego procesora w nast puj ce

podstawowe (pierwotne) operacje:

•

zmie stan,

•

przesu si o jedn komórk ta my w lewo lub w prawo,

•

przekształ widoczny (odczytany) symbol w inny symbol z

dost pnego alfabetu.

Jerzy Peja : Algorytmy i struktury danych

- 6 -

MASZYNA TURING

Maszyna Turinga

Mechanizm powstały w wyniku uproszczenia struktur danych,

struktur steruj cych oraz operacji podstawowych nazywa si

maszyn Turinga. Wymy lił j w roku 1936 brytyjski matematyk

Alan M.Turing.

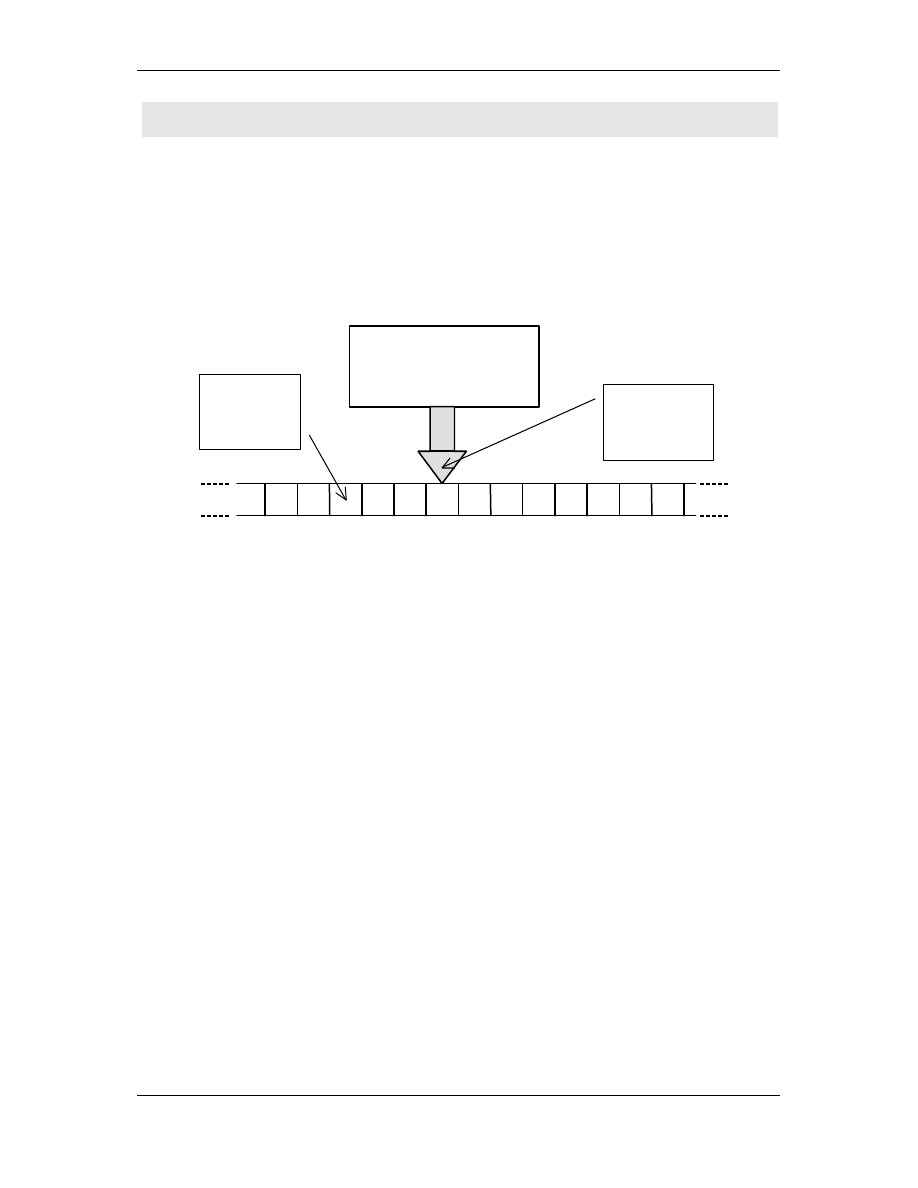
STEROWANIE

(diagram przej

pomi dzy stanami)

niesko czona ta ma

#

#

pojedynczy

symbol

alfabetu

głowica

odczytuj co

-zapisuj ca

#

#

Maszyna Turinga składa si z nast puj cych elementów:
• sko czonego alfabetu symboli,

• sko czonego zbioru stanów,

• niesko czonej ta my podzielona na komórki przechowuj ce

pojedyncze symbole alfabetu,

• krokowo poruszaj cej si głowica odcztuj co-zapisuj ca;

głowica mo e przesuwa sie na raz tylko o jedn komórk ,

• diagram przej miedzy stanami, który steruje (w oparciu o

instrukcj ) głowic tak, e zmiany nast puj po ka dym jej

zatrzymaniu,

• stan pocz tkowy i stany ko cowe (elementy uzupełniaj ce).
Diagram przej jest

grafem skierowanym, którego wierzchołki

(w postaci zaokr glonych czworok tów) reprezentuj stany,

kraw dzie nazywa si przej ciem, za ich wagi przyjmuj posta

<

a/b, kierunek>, gdzie a i b s symbolami z alfabetu, a kierunek

oznacza albo w prawo albo w lewo. Cz

a wagi jest

wyzwalaczem (pobudzeniem) przej cia, a cz <b, kierunek> -

akcj .

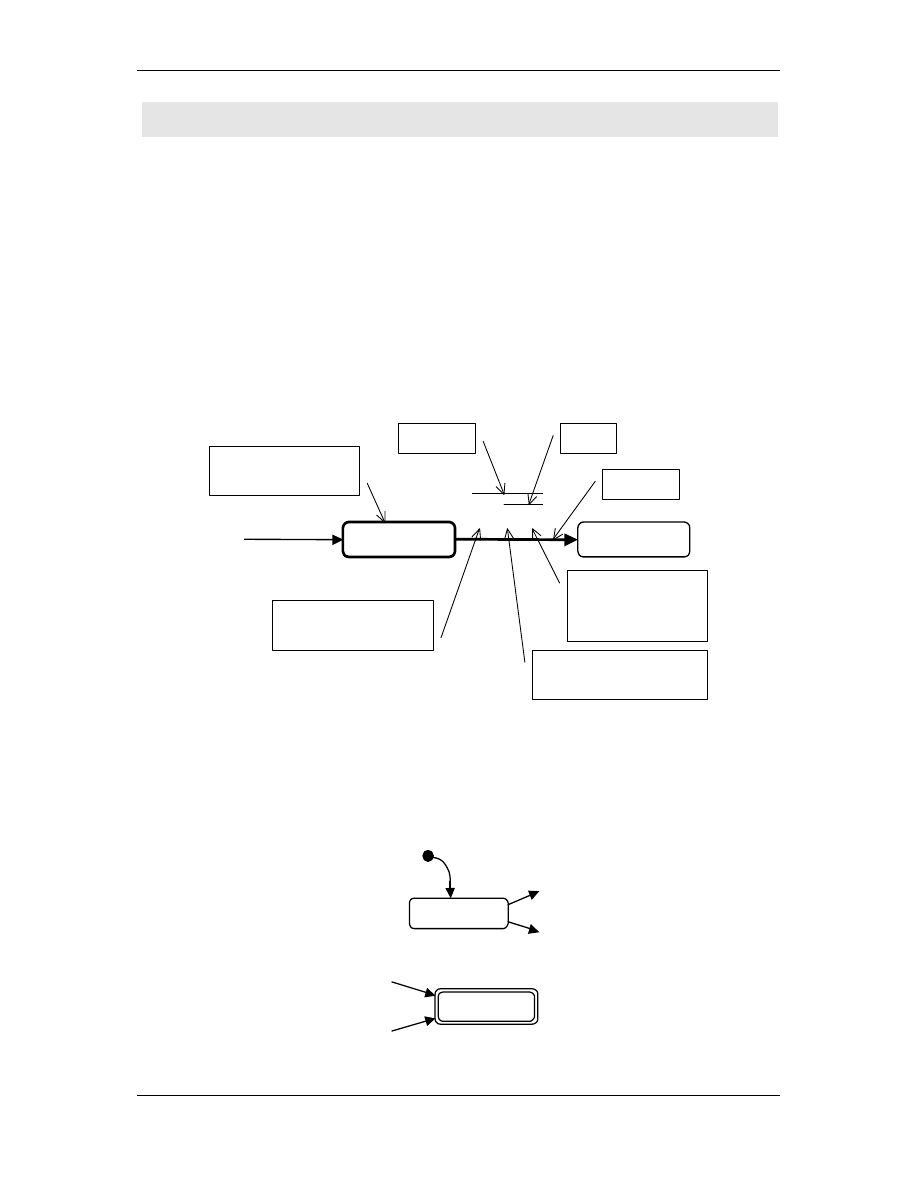
Jerzy Peja : Algorytmy i struktury danych

- 7 -

MASZYNA TURINGA

Maszyna Turinga (c.d.)

Przej cie ze stanu s do stanu t opisanego wag <

a/b, kierunek>

interpretuje si nast puj co:

Je li tylko maszyna Turinga znajdzie si w stanie s, a

a jest

symbolem odczytywanym przez głowic w danej chwili, to

symbol

a jest wymazywany z komórki ta my i zast powany

przez (wpisywany) symbol

b, głowica przesuwa si o jeden

kwadrat w kierunku kierunek i na ko cu nast puje przej cie

do stanu t.

nazwa stanu

a / b L

stan

(wierzchołek grafu)

etykieta

przej cie

symbol alfabetu -

wyzwalacz przej cia

symbol alfabetu

zapisywany w komórce

kierunek

przesuni cia

głowicy (L lub P)

akcja

Przyjmijmy na razie, e maszyna Turinga jest automatem

sko czonym deterministycznym. Oznacza to, e

• maszyna jest deterministyczna je li z adnego stanu nie wychodzi

wi cej ni jedno przej cie z tym samym wyzwalaczem

• jeden ze stanów jest wyró niony jako stan pocz tkowy:

nazwa stanu

• stany, z których nie wychodz adne przej cia, nazywane s stanami

ko cowymi

nazwa stanu

• w stanie pocz tkowym głowica jest ustawiona na pierwszej od lewej

niepustej komórce ta my.

Jerzy Peja : Algorytmy i struktury danych

- 8 -

MASZYNA TURINGA

Maszyna Turinga (c.d.)

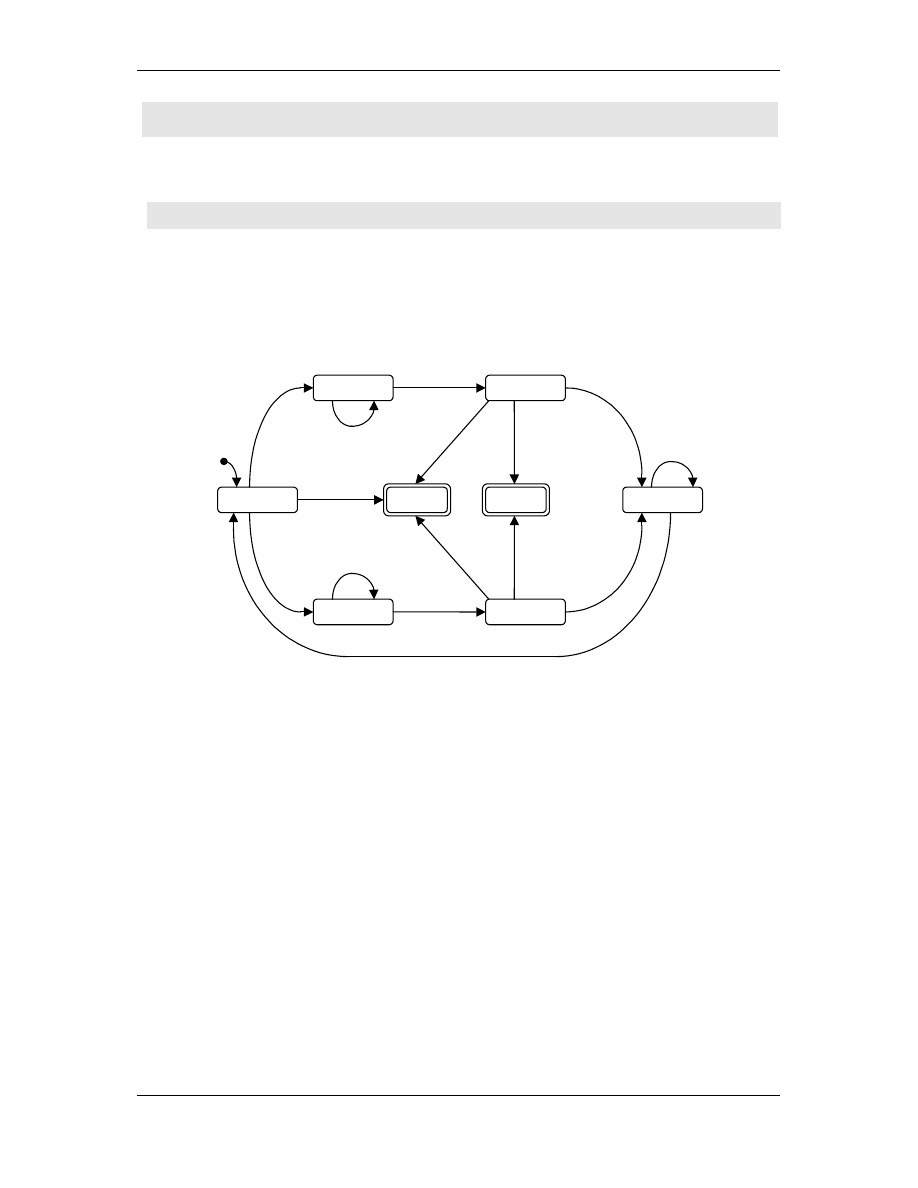
Przykład 3: Wykrywanie palindromów

Palindrom jest słowem, które czyta si tak samo z obu stron, np.

abba, ababa, kok, itp. Diagram stanów, który realizuje zadanie

weryfikacji, czy słowo abba jest palindromem ma posta

przedstawion na rysunku poni ej.

zaznacz

TAK

NIE

powrót

ruch dla a

ruch dla b

test dla a

test dla b

# / # P

# / # L

b / # L

a / # L

a / a L

b / b L

b / b L

a / a L

# / # L

# / # L

# / # L

# / # L

b / # P

a / # P

a / a P

b / b P

a / a P

b / b P

Diagram stanów maszyny Turinga

Maszyna pami ta pierwszy przeczytany symbol (przechodz c do

stanów ruch

a

lub ruch

b

), po czym wymazuje go zast puj c

symbolem pustym i przechodzi w prawo, a do osi gni cia

symbolu pustego (etap 5, patrz rysunek nast pny).
Teraz przesuwa si o jeden symbol w lewo i zatrzymuje si na

najbardziej na lewo poło onym symbolu (osi ga stan test

a

lub

test

b

). Je li oczytany symbol byłby ró ny od pami tanego,

wówczas maszyna zatrzymałaby si w stanie NIE. W naszym

przypadku zarówno pami tany, jak i wczytany jest symbol a, st d

praca maszyny jest kontynuowana: symbol a jest wymazywany i

maszyna przechodzi do stanu powrót. Doprowadza to do

pierwszego na lewo poło onego symbolu pustego. Cykl zaczyna

si od pocz tku.

Jerzy Peja : Algorytmy i struktury danych

- 9 -

MASZYNA TURINGA

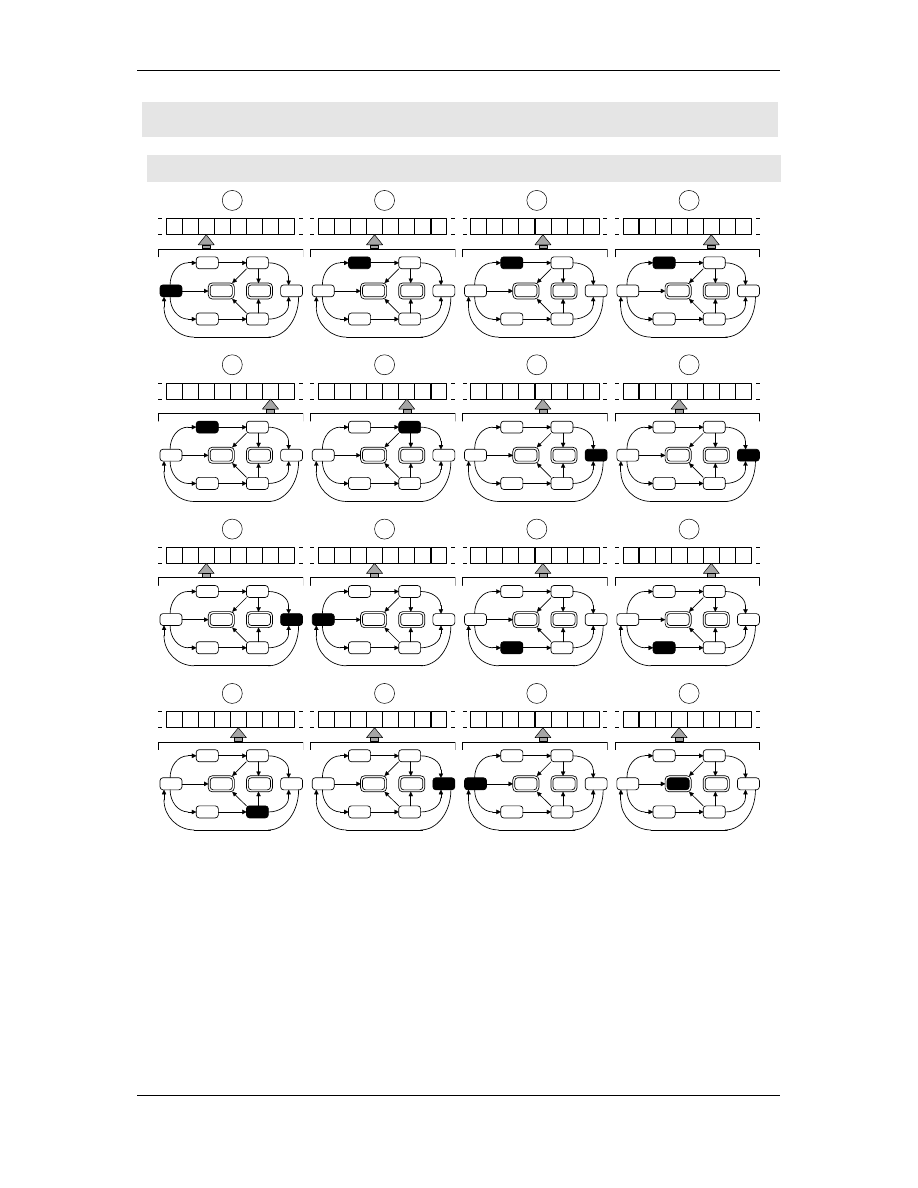
Przykład 3: Wykrywanie palindromów (c.d.)

a b b a

#

# #

#

1

# b b a

#

# #

#

2

# b b a

#

# #

#

3

# b b a

#

# #

#

4

# b b a

#

# #

#

5

# b b a

#

# #

#

6

# b b #

#

# #

#

7

# b b #

#

# #

#

8

# b b #

#

# #

#

9

# b b #

#

# #

#

10

# # b #

#

# #

#

11

# # b #

#

# #

#

12

# # b #

#

# #

#

13

# # # #

#

# #

#

14

# # # #

#

# #

#

15

# # # #

#

# #

#

16

TAK !

Realizacja diagramu stanów dla wykrywania palindromów

Diagramy stanu maszyny Turinga nazywane s czasami

programem, a sam proces ich przygotowania – programowaniem.
Przy pomocy maszyny Turinga mo na zapisywa wyniki

przetwarzania danych. W tym celu przyjmijmy, e w momencie

maszyna Turinga zatrzymuje si , wówczas wynikiem jest napis na

ta mie zawarty pomi dzy dwoma znakami ! (wykrzykmik).

Jerzy Peja : Algorytmy i struktury danych

- 10 -

MASZYNA TURINGA

Przykład 5: Dodawanie dwóch liczb całkowitych (dziesi tnych) X i Y

Maszyna przechodzi do najbardziej prawej cyfry liczby X

(dochodz c do symbolu * oddzielaj cego obie liczby, maszyna

cofa si o jeden symbol w lewo). Wymazuje ja i zapami tuje ja w

swoim stanie. Jak łatwo zauwa y , w tym celu maszyna b dzie

potrzebowała 10 stanów; oznaczmy je przez cyfra

0

do cyfra

9

.

Nast pnie maszyna przechodzi do skrajnie prawej cyfry liczby Y i

wymazuje j , po czym przechodzi do stanu, w którym jest

zapami tana suma cyfr obu liczb oraz informacja o znaku

przeniesienia.
Maszyna przesuwa si teraz na lewo od pozostało ci po liczbie X i

zapisuje cyfr sumy, nast puj ca po znaku ! jako ogranicznika.
Dalsze kroki wykonywane s podobnie, przy jednoczesnym

uwzgl dnieniu znaku przeniesienia.

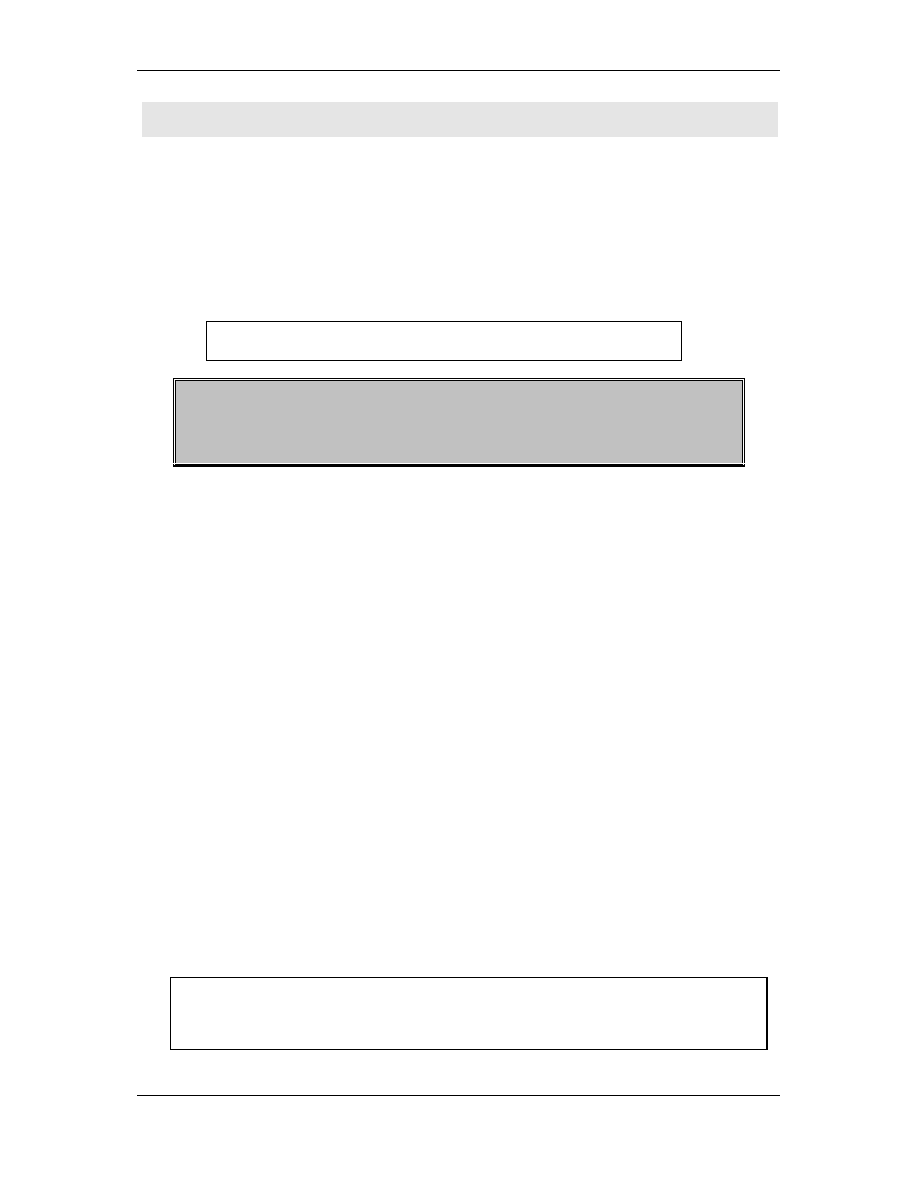
... # # # # # # # # 7 3 6 + 6 3 5 1 9 # ...

... # # # # # # 5 ! 7 3 # + 6 3 5 1 # # ...

... # # # # # 5 5 ! 7 # # + 6 3 5 # # # ...

... # # # # 2 5 5 ! # # # + 6 3 # # # # ...

... # # # 4 2 5 5 ! # # # + 6 # # # # # ...

... # # 6 4 2 5 5 ! # # # + # # # # # # ...

... # ! 6 4 2 5 5 ! # # # + # # # # # # ...

Tabela powy ej zawiera stan ta my podczas realizacji kolejnych

etapów dodawania cyfr tworz cych liczby 736 i 63519.

Ka dy kto spróbuje zaprogramowa maszyn Turinga, która

dodaje dwie liczby, szybko przekona si , e nawet w tym prostym

przypadku nie jest to zadanie proste.

Jerzy Peja : Algorytmy i struktury danych

- 11 -

MASZYNA TURINGA

Teza Churcha-Turinga

Jak poprzednio pokazano maszyna Turinga:
• ma sko czenie wiele stanów

• zapisuje po jednym symbolu na liniowej ta mie

• umo liwia programowanie, chocia mo e by nu ce.

Co mo na zrobi za pomoc maszyny Turinga?

Wszystko!

Maszyna Turinga potrafi rozwi za ka dy efektywnie

rozwi zywalny problem algorytmiczny!

Pow sze stwierdzenie jest jedn z wersji tezy Church-Turinga.

Oznacza ona, e ka dy problem algorytmiczny, dla którego mo na

znale algorytm (nawet taki, który wymaga nieograniczonej ilo ci

czasu i pami ci) i oprogramowa w dowolnym j zyku, i wykona

na dowolnym komputerze (istniej cym lub mo liwym do

zbudowania), jest tak e rozwi zywalny przy pomocy maszyny

Turinga.
Teza ta znana jest tak e pod nazw CT (sktór pochodzi zarówno od

Churcha-Turinga, jak i od Computability Theory).
Teza Churcha-Turinga jest efektem prac prowadzonych w latach

trzydziestych nad opracowaniem idei komputera uniwersalnego.

Wtedy to stworzono modele :
• prymitywnej maszyny Turinga,

• rachunek lambda (Church), b d cy podstaw j zyka Lisp,

• system produkcji dla symboli (Post),

• klasa funkcji rekurencyjnych (Kleen),

• ... i wiele innych.

Wszystkie modele s

równowa ne w sensie problemów

algorytmicznych, które rozwi zuj !

Jerzy Peja : Algorytmy i struktury danych

- 12 -

MASZYNA TURINGA

Odmiany maszyny Turinga

Wszystkie wymienione poni ej odmiany maszyn Turinga mog

rozwi zywa dokładnie te same problemy co podstawowy model

maszyny Turinga i w my l tezy Churcha-Turinga nie s od niego

słabsze.

Maszyna z ta m jednostronnie niesko czon – ta ma mo e by

niesko czona np. tylko z prawej strony, a dane zapisywane s na

ta mie od lewego skraju, przy czym maszyna nie mo e przesuwa

si na lewo od skrajnie lewej komórki.
Maszyny z wieloma ta mami i głowicami – ka da ta ma

wyposa ona jest głowic czytaj co-pisz c , działaj c w ten

sposób, e przej cia zale od całego zbioru symboli widzianych

jednocze nie przez głowice, a akcje okre laj kierunki ruchu dla

ka dej głowicy i nowy symbol, który ma by napisany na ka dej

ta mie.
Maszyny z ta mami dwuwymiarowymi – w tym przypadku

uzyskuje si mo liwo zwi kszenia kierunków ruchu do czterech.
Maszyny niedeterministyczne – w jednym stanie mo e istnie

wiele przej dla tego samego wyzwalacza. Ka dy wybór

pozostawia si maszynie, zakładaj c, e maszyna zrobi to najlepiej.

Przykład 6: Symulacja jednej maszyny na drugiej – składanie ta my

niesko czone

Z tezy Churcha-Turinga wynika, e aden efektywny model

oblicze nie jest silniejszy od podstawowej maszyny Turinga,

wł czaj c w to tak e jej rozszerzenia.
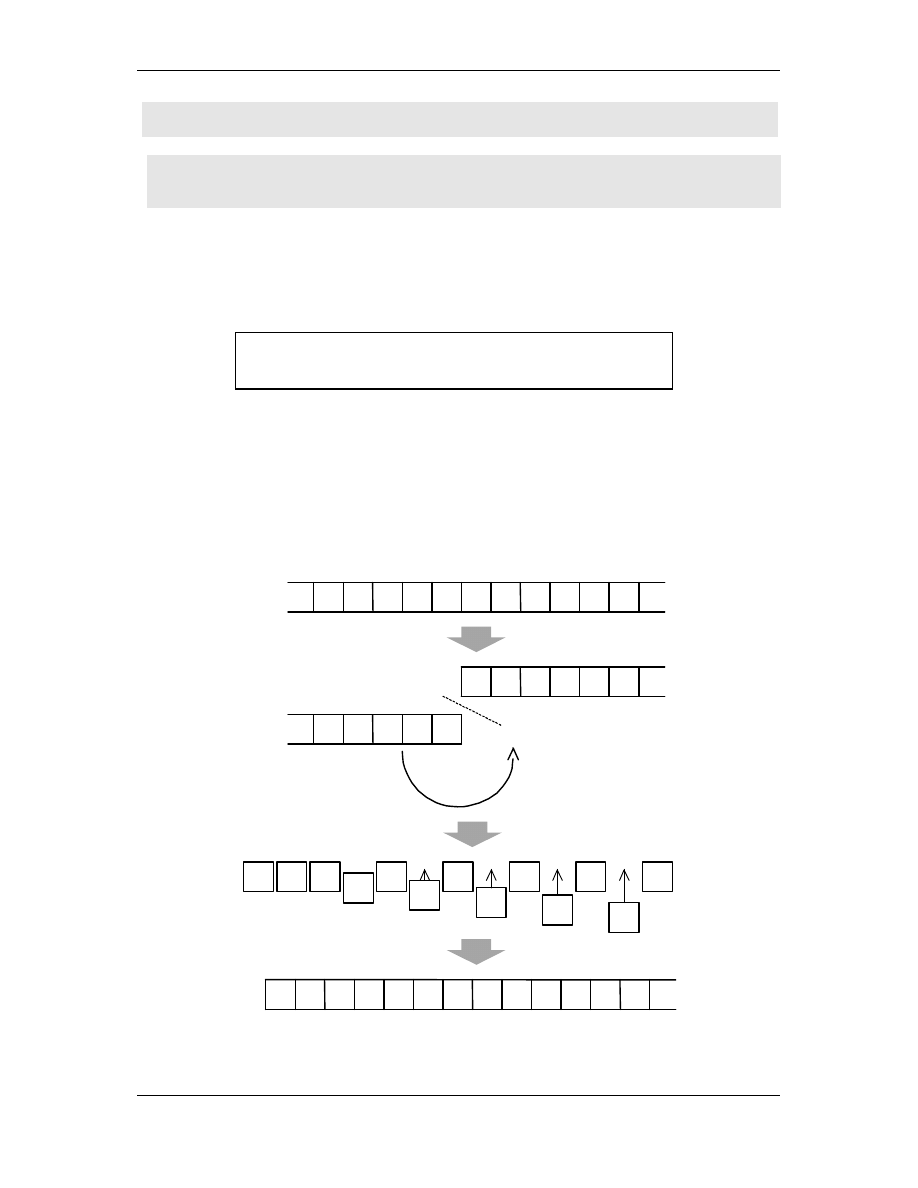
Równowa no ci modeli ustala si na podstawie symulacji, któr

wykorzystuje si do pokazania, e dla ka dej maszyny M

1

jednego

typu istnieje odpowiadaj ca jej maszyna M

2

(pokazuje si wi c jak

symulowa jeden typ maszyny przy pomocy drugiego.

Jerzy Peja : Algorytmy i struktury danych

- 13 -

MASZYNA TURINGA

Przykład 6: Symulacja jednej maszyny na drugiej – składanie ta my

niesko czone (c.d.)

Załó my, e dana jest maszyna M z ta ma niesko czon z obu

stron. Poka emy, e mo na skonstruowa równowa na maszyn

M

1

z ta m niesko czon tylko z prawej strony, a zatem chcemy

wykaza , e:

MASZYNA M NIE JEST SILNIEJSZA OD

MASZYNY M

1

Aby tego dowie , wystarczy pokaza , e na maszynie M

1

mo na

symulowa działanie maszyny M.
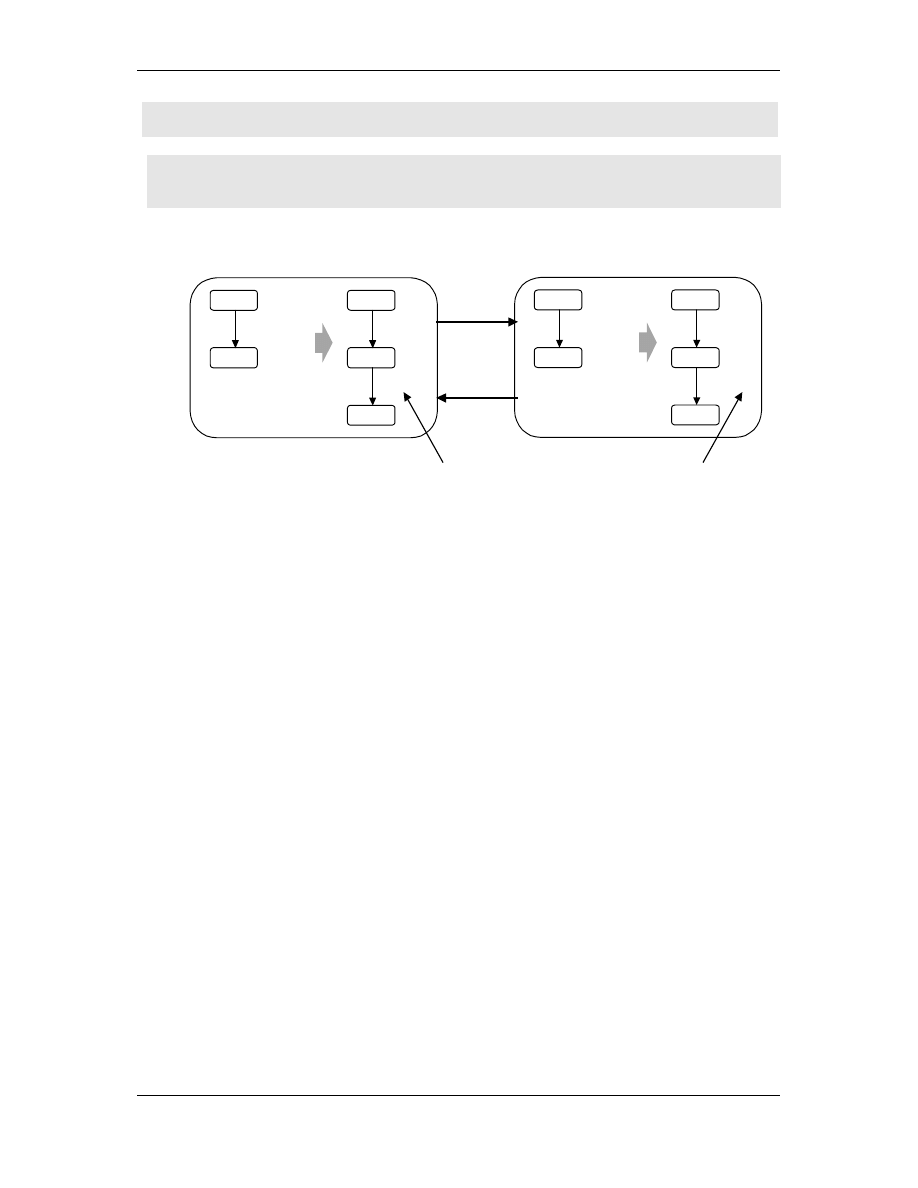
• Jest oczywiste, e ta ma jednokierunkowa maszyny M

1

widziana

jest jako ta ma dwukierunkowa zło ona w pół i scalona (patrz

rysunek poni ej).

# b

#

∗∗∗∗ a 5 b 7 a c a

. . .

. . .

ta ma maszyny

M

# b

#

∗∗∗∗ a 5

b 7 a c a

. . .

. . .

#

b

7

a

c

a

. . .

$ $

#

b

∗∗∗∗

a

5

#

b

7

a

c

a

. . .

$ $

#

b

∗∗∗∗

a

5

ta ma maszyny

M

1

Jerzy Peja : Algorytmy i struktury danych

- 14 -

MASZYNA TURINGA

Przykład 6: Symulacja jednej maszyny na drugiej – składanie ta my

niesko czone (c.d.)

• Zmodyfikujmy przej cia mi dzystanowe w nowym diagramie,

który składa si z dwóch diagramów maszyny M.

a / b, P

s

t

a / b, P

s

t

s

′

<# / #, P>, <a / a, P>, <b / b, P>, ...

symuluj maszyn M

poruszaj c si po dwie

komórki na raz

a / b, L

s

t

a / b, P

s

t

s

′

L

symuluj maszyn M

poruszaj c si po dwie

komórki na raz w

kierunku przeciwnym

$ / $ PPP

$ / $ P

P

<# / #, L>, <a / a, L>, <b / b, L>, ...

Załó my, e maszyna rozwi zuje problem decyzyjny (nie zapisuje

wyników na ta mie) i e K danych X jest umieszczonych w

kolejnych komórkach od 1 do K, licz c od lewej strony ta my.
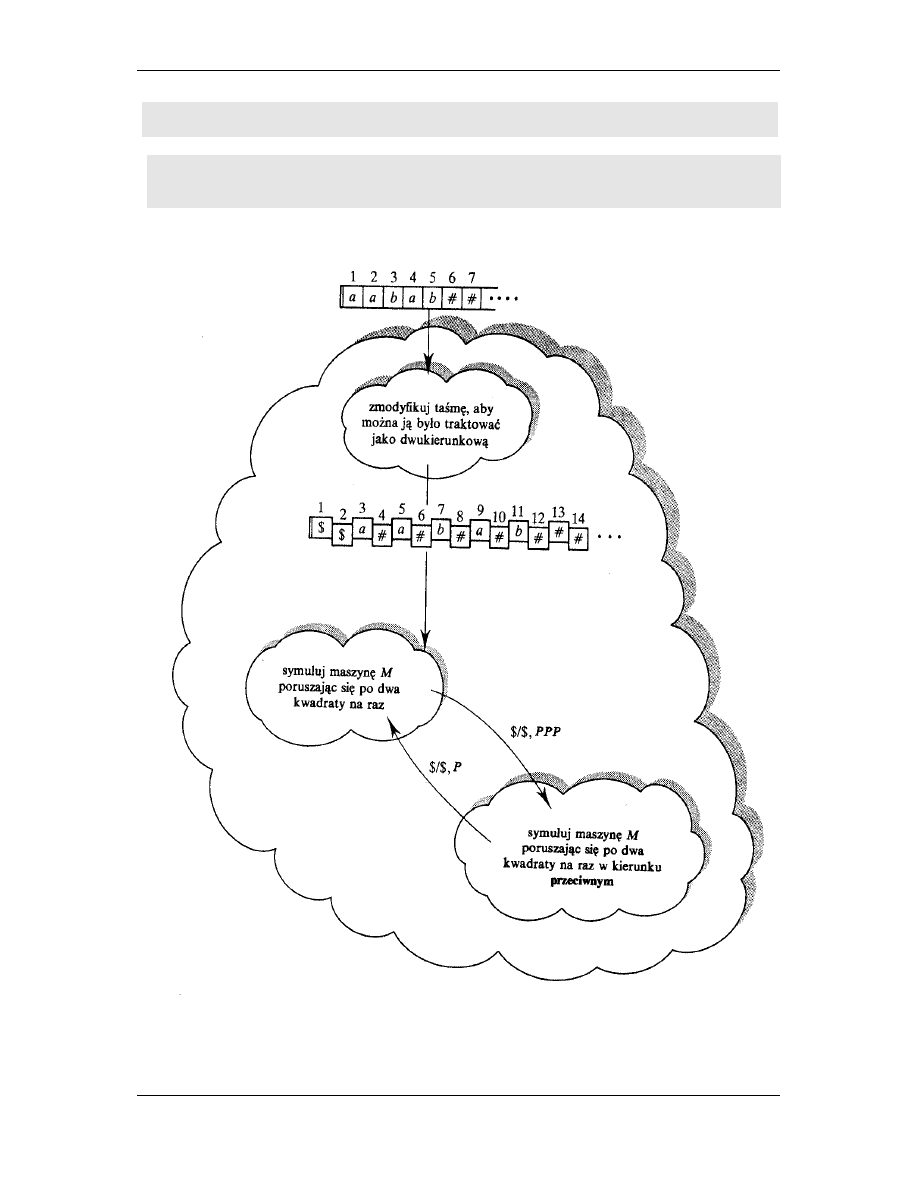
W pierwszym kroku maszyna rozci ga dane X tak aby zajmowały

komórki 3, 5, 7, ..., 2K +1, wstawiaj c w komórkach 1 i 2 znaki $,

a symbole # w pozostałych (patrz rysunek na nast pnej stronie).
Po rozci gni ciu ta my maszyna M

1

przechodzi do kwadratu 3 i

zaczyna symulowa maszyn M, wykonuj c dwa kroki w

dowolnym kierunku. P oznacza wi c dwa kroki w prawo, za L –

dwa kroki w lewo. Uzyskuje si to modyfikuj c diagram maszyny

M za pomoc transformacji przedstawionych powy ej.
Praca maszyny M

1

na nieparzystych komórkach ta my odpowiada

pracy maszyny M na prawostronnej cz ci ta my (niesko czonej).
Napotykaj c w czasie symulacji na znak $ (przy poruszaniu si po

nieparzystych komórkach ta my musi to by znak $ w pierwszej

komórce) maszyn M

1

przesuwa si o trzy kwadraty w prawo i

osi ga pierwszy znak pusty # i kontynuuje symulowanie maszyny

M

poruszaj c si po dwa kroki na raz do tyłu (z zamienionymi

ruchami: w prawo – to w lewo, w lewo – to w prawo).

Jerzy Peja : Algorytmy i struktury danych

- 15 -

MASZYNA TURINGA

Przykład 6: Symulacja jednej maszyny na drugiej – składanie ta my

niesko czone (c.d.)

Jerzy Peja : Algorytmy i struktury danych

- 16 -

MASZYNA TURINGA

Przykład 6: Symulacja jednej maszyny na drugiej – składanie ta my

niesko czone (c.d.)

Teraz maszyna M

1

na parzy cie ponumerowanych kwadratach, co

symuluje prac maszyny M na lewostronnej cz ci ta my, ale ze

zmienionymi kierunkami.
Po ponownym osi gni ciu znaku $ (w drugiej komórce ta my),

nast puje zmiana trybu i maszyna przesuwa si o jeden kwadrat w

prawo (do komórki numer 3) i wraca do pierwszego trybu

symulacji.

Maszyna M

1

działa dokładnie tak samo jak maszyna M

wtedy,

gdy zachodzi jeden z przypadków: (1) zarówno maszyna M

jak i maszyna M

1

zatrzymuj si w tym samym stanie TAK,

(2) obie zatrzymuj si w stanie NIE lub (3) obie wchodz w

p tl niesko czon

Programy licznikowe

Program licznikowy mo e operowa na nieujemnych liczbach
całkowitych pami tanych w zmiennych (tzw.

licznikach). W

modelu dopuszcza si tylko trzy typy elementarnych operacji na

zmiennych interpretowanych w nast puj co (przyjmuje si , e Y-1

jest 0, je li Y było równe 0):
• X ← 0,

X

← Y + 1, X ← Y - 1

Struktury steruj ce składaj si jedynie z instrukcji bezpo redniego

nast pstwa oraz instrukcji skoku warunkowego

skocz-do:

• je li X = 0 skocz-do L (L jest etykiet pewnej instrukcji)
Program licznikowy zatrzymuje si wtedy, gdy:
• wyst puje próba wykonania nieistniej cej instrukcji
• wyst puje próba przej cia do nieistniej cej etykiety
• wyczerpana zostaje lista instrukcji.

Jerzy Peja : Algorytmy i struktury danych

- 17 -

MASZYNA TURINGA

Programy licznikowe (c.d.)

Przykład 7: Przykład programu licznikowego – mno enie dwóch liczb

Wynik mno enia dóch liczb X i Y znajduje si w Z:

U

←

←

←

←

0

Z

←

←

←

←

0

A

:

je li

X

= 0

skocz-do

L

X

←

←

←

←

X

- 1

V

←

←

←

←

Y

+ 1

V

←

←

←

←

V

- 1

B

:

je li

V

= 0

skocz-do

A

V

←

←

←

←

V

- 1

Z

←

←

←

←

Z

+ 1

je li

U

= 0

skocz-do

B

W powy szym programie licznikowym zastosowano dwa triki:
• V ← Y + 1 oraz V ← V - 1 zast puj V ← Y
• U ← 0 oraz je li U = 0 skocz-do B zast puj skocz-do B

W powy szym programie licznikowym wyst puj dwie p tle:
• wewn trzna (od B: do skocz-do B) - zwi ksza Z o Y
• zewn trzna (od A: do skocz-do A) - wykonuje p tl wewn trzn

X razy
Programy licznikowe s równowa ne maszynom Turinga w

sensie problemów algorytmicznych, które rozwi zuj

Przykład 8: Przy pomocy programu licznikowego mo na symulowa

dowoln maszyn Turinga

Ta m i poło enie głowicy maszyny Turinga mo na zakodowa za

pomoc dwóch liczb, a ka de przej cie w diagramie reprezentowa

odpowiednim „bloczkiem” programu licznikowego. Na przykład
dla alfabetu

#, !,

∗∗∗∗

, a, b, c, d, e, f, g przyjmijmy nast puj ce kody,

odpowiadaj ce symbolom:

# - 0

∗ - 2 b - 4 d - 6 f - 8

! - 1 a - 3 c - 5 e - 7 g - 9

Jerzy Peja : Algorytmy i struktury danych

- 18 -

MASZYNA TURINGA

Programy licznikowe (c.d.)

Przykład 8: Przy pomocy programu licznikowego mo na symulowa

dowoln maszyn Turinga (c.d.)

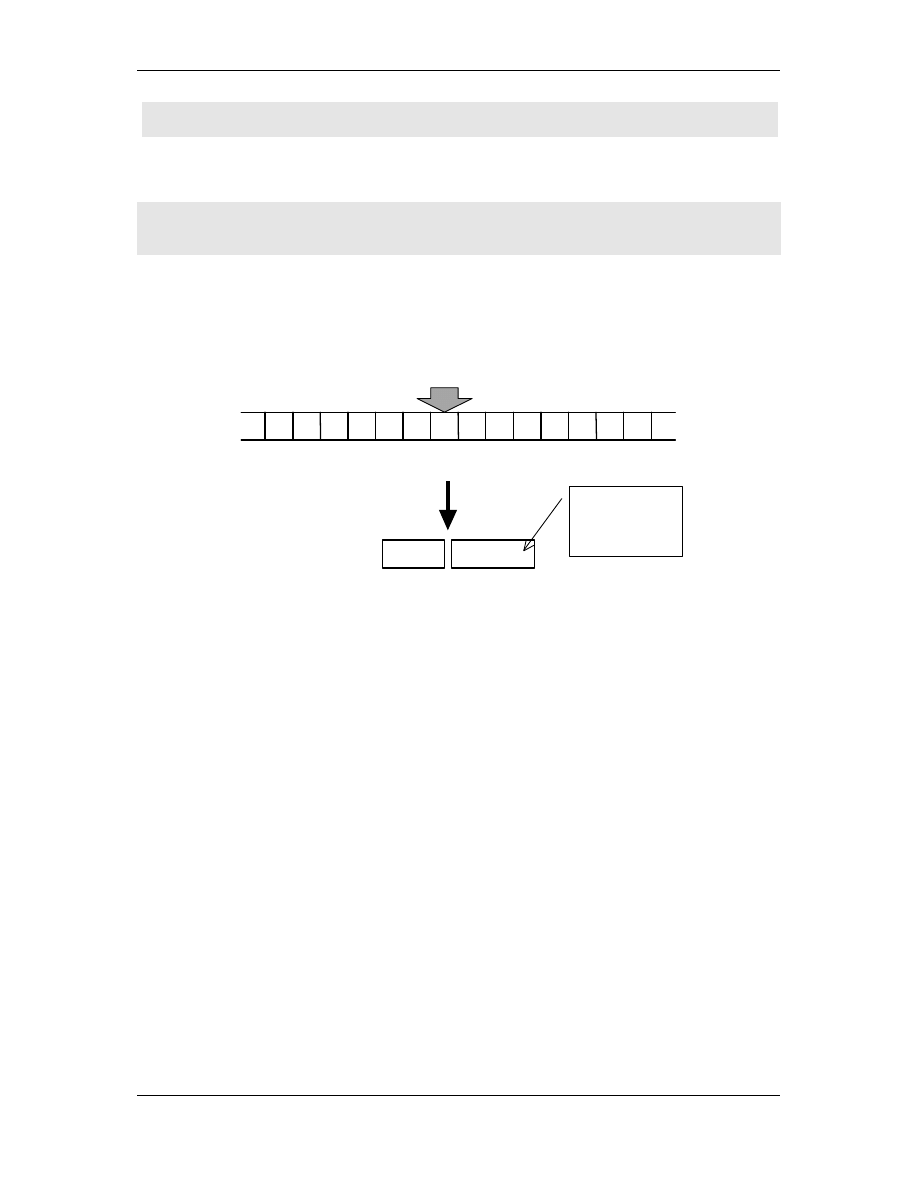
Obie liczby koduj cz ci ta my po obu stronach głowicy, przy

czym prawa strona ta my reprezentowana jest na odwrót. Dzi ki

temu najmniej znacz ce cyfry obu liczb le blisko głowicy.

# #

#

a b ∗∗∗∗ e b ! # a

. . .

. . .

ta ma maszyny

3427

g a #

poło enie głowicy

393014

kod symbolu

widzianego
przez

głowic

Maszyny Turinga i programy licznikowe stały si uniwersalnymi

modelami dzi ki wykorzystaniu niesko czonej ilo ci pami ci:
• w maszynach Turinga ilo informacji w pojedynczej komórce

jest sko czona i ograniczona, ale liczba komórek jest

potencjalnie niesko czona,

• w programach licznikowych liczba zmiennych-liczników jest

sko czona, ale w ka dej mo na przechowa dowolnie du

liczb , za pomoc której mo na zakodowa potencjalnie

niesko czon ilo informacji.

Algorytmy uniwersalne

Konsekwencj tezy CT jest istnienie

algorytmów uniwersalnych.

Algorytm uniwersalny mo e działa jak jakikolwiek dowolny

algorytm. Jako dane akceptuje on opis dowolnego algorytmu A i

dowolnych dopuszczalnych jego danych X i wykonuje (symuluje)

algorytm A na danych X zatrzymuj si tylko wtedy, gdy

rzeczywi cie był wykonany na danych X.

Jerzy Peja : Algorytmy i struktury danych

- 19 -

MASZYNA TURINGA

Algorytmy uniwersalne

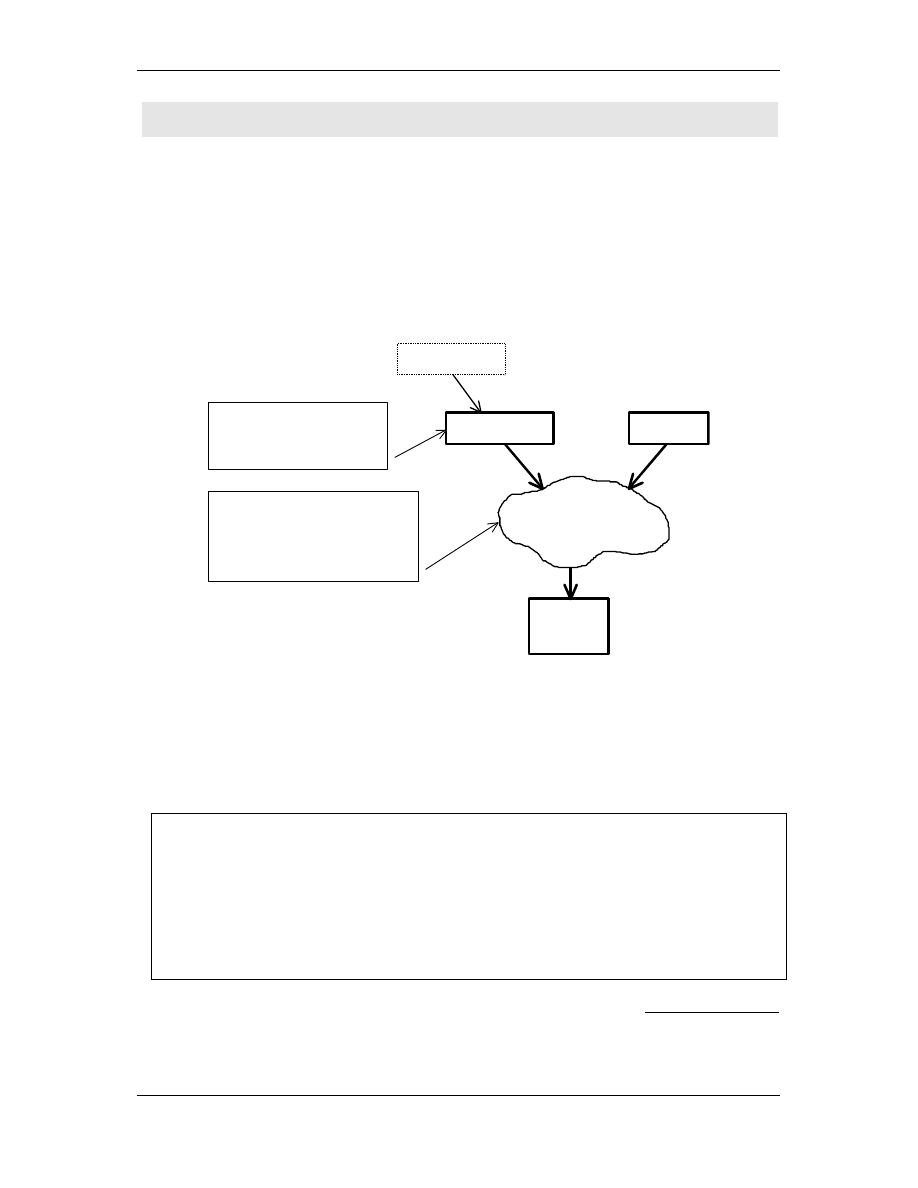
Aby otrzyma algorytm uniwersalny musimy jedynie u y

pewnego j zyka L

1

, napisa efektywnie wykonywalny program U,

który akceptuje jako dane ka dy program napisany w j zyku L

2

oraz ka de dane do tego programu i symuluje jego wykonanie na

tych danych.

program P

dane X

wyniki

(je li s )

algorytm A

program P realizuj cy

algorytm A napisany w

uniwersalnym j zyku L

2

wykonaj program P

na danych X

uniwersalny program U

napisany w j zyku L

1

-

symuluje wynik programu w

j zyku L

2

na jego danych

Program U mo na uwa a za niezale ny od j zyka i maszyny,

poniewa na podstawie tezy CT, (1) mógłby by napisany w

ka dym uniwersalnym j zyku i wykonywany na ka dej maszynie,

(2) mo e symulowa ka dy efektywnie wykonywalny algorytm

napisany w ka dym j zyku.

• Mo na zbudowa uniwersaln maszyn Turinga, która mo e

symulowa działanie dowolnej maszyny Turinga na dowolnych

danych (trzeba opisa na ta mie zlinearyzowany diagram przej ,

reprezentuj c ka de przej cie jako par stanów z podan etykiet

przej cia)

• Mo na tak e skonstruowa uniwersalny program licznikowy

Maszyny Turinga i programy licznikowe s wielomianowo

równowa ne, tzn. klasa problemów łatwo rozwi zywalnych jest

taka sama dla obu modeli

Jerzy Peja : Algorytmy i struktury danych

- 20 -

POPRAWNO

ALGORYTMÓW

Automaty sko czone stanowe (automaty sko czone)

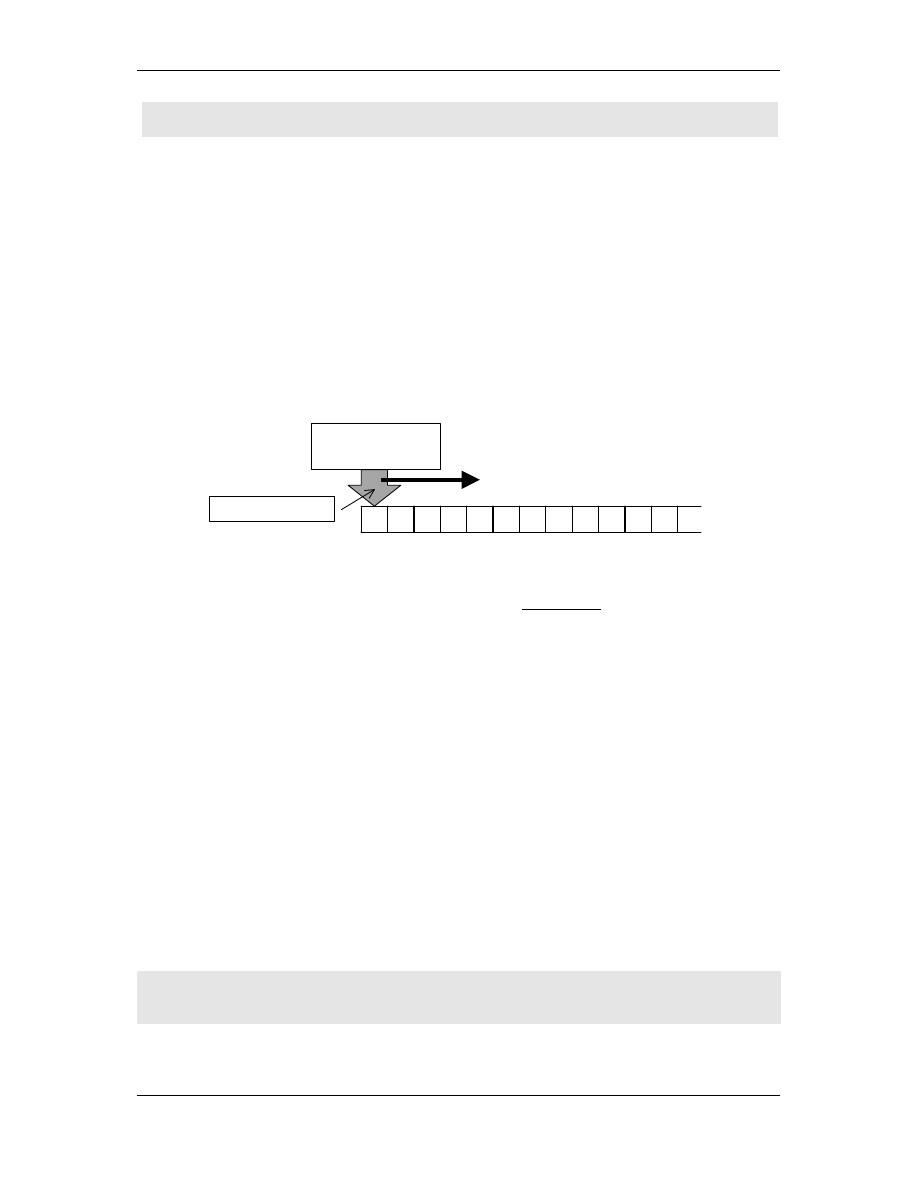
Ograniczaj c poruszanie si maszyny Turinga na ta mie tylko do

ustalonego kierunku, np. w prawo otrzymujemy wtedy urz dzenie

zwane

automatem sko czenie stanowym lub krócej automatem

sko czonym.
Poruszanie si tylko w jednym kierunku sugeruje, e mechanizm

nie mo e niczego zapisywa na ta mie, poniewa nie jest w stanie

tego pó niej odczyta .

#

a b ∗∗∗∗ e b ! c a

. . .

g a #

głowica czytaj ca

diagram przej

Automat sko czony ma wi c nast puj ce cechy:
• ka da komórka mo e by odczytana tylko raz
• nie mo na wróci do zapisywanych komórek, czyli w

problemach decyzyjnych nie jest potrzebna dla głowicy funkcja

zapisu

• poza dan sekwencj automat zawiera na ta mie tylko symbole

puste, czyli mo e zatrzymywa si po osi gni ciu ko ca danych

wej ciowych

• wystarcz stany ko cowe tylko z odpowiedzi na TAK, gdy

zatrzymanie si automatu na ko cu danych w ka dym innym

stanie mo na interpretowa jako odpowied na NIE

• etykieta przej cia zawiera zatem tylko symbol-wyzwalacz (nie

jest potrzebny człon akcji, bo jest ona tylko jedna - przejd do

nast pnej komórki)

Przykład 9: Automat sko czony – parzysto znaku

a w dowolnej

sekwencji znaków

Zdefiniujmy automat sko czony nad alfabetem {a, b} i badaj cy

parzysto wyst pie symbolu a.

Jerzy Peja : Algorytmy i struktury danych

- 21 -

MASZYNA TURINGA

Automaty sko czone stanowe (c.d.)

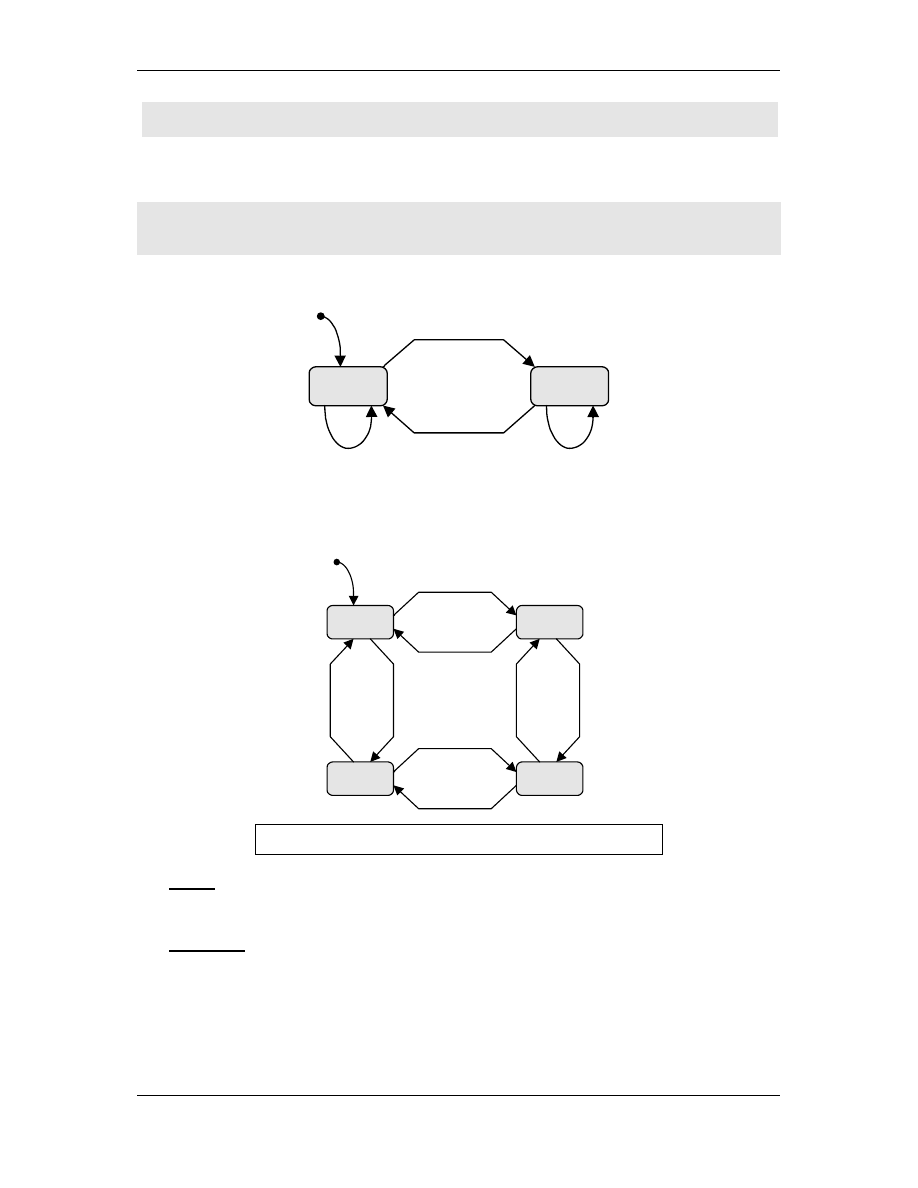
Przykład 9: Automat sko czony – parzysto znaku

a w dowolnej

sekwencji znaków

Automat realizuj cy to zadanie ma posta :

TAK

a

a

b

b

Ten automat nie liczy, ale o parzysto ci potrafi rozstrzyga .

Co

wi c potrafi ten automat?

TAK

a

a

b

a

a

b

b

b

Automat sko czony nie potrafi liczy !

Teza: aden automat sko czony nie potrafi rozstrzygn , czy dana

sekwencja wej ciowa zawiera tak sam liczb symboli a i b.
Dowód: (nie wprost)
Załó my, e pewien automat

F potrafi rozstrzygn podany

problem decyzyjny. Niech liczba stanów automatu

F wynosi N.

Rozwa my sekwencj wej ciow

X, która zawiera najpierw

dokładnie

N + 1 symboli a, a potem N + 1 symboli b.

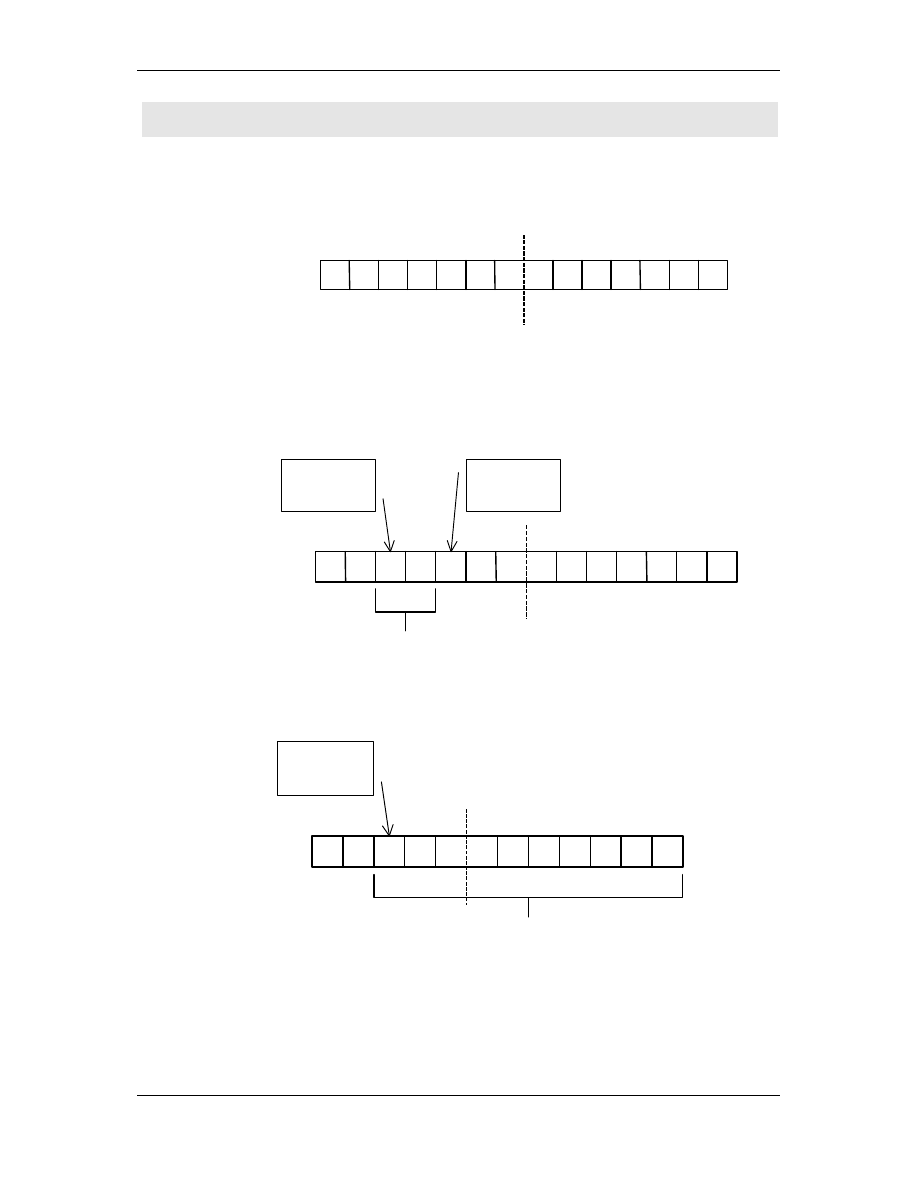
Jerzy Peja : Algorytmy i struktury danych

- 22 -

MASZYNA TURINGA

Automaty sko czone stanowe (c.d.)

b

a a a a a a a b b b b

b

b

sekwencja X :

N = 6

odpowied TAK

5

1 2 3 4 5 6 7 1 2 3 4

7

6

W trakcie przesuwania si głowicy wzdłu ta my musz pojawi

si dwie komórki, w których automat b dzie w tym samym stanie

s, gdy liczba komórek z tym samym symbolem jest wi ksza od

liczby stanów.

b

a a a a a a a b b b b

automat

w stanie s

b

b

sekwencja X :

N = 6

automat

w stanie s

odpowied TAK

5

1 2 3 4 5 6 7 1 2 3 4

7

6

usuwamy

W nowej sekwencji

Y usu my komórki, tak aby stan s był osi gany

tylko raz przy trzeciej komórce.

b

a a a a a b b b b

automat

w stanie s

b

b

sekwencja Y :

N = 6

odpowied wci TAK

5

1 2 3 4 5 1 2 3 4

7

6

automat działa dokładnie tak jak dla sekwencji X

Zatem istnieje sekwencja zawieraj ca ró n liczb symboli

a i b,

dla której automat daje odpowied TAK. Przeczy to zało eniu, e

automat daje tak odpowied tylko dla sekwencji z tak sama

liczb symboli

a i b !

Jerzy Peja : Algorytmy i struktury danych

- 23 -

MASZYNA TURINGA

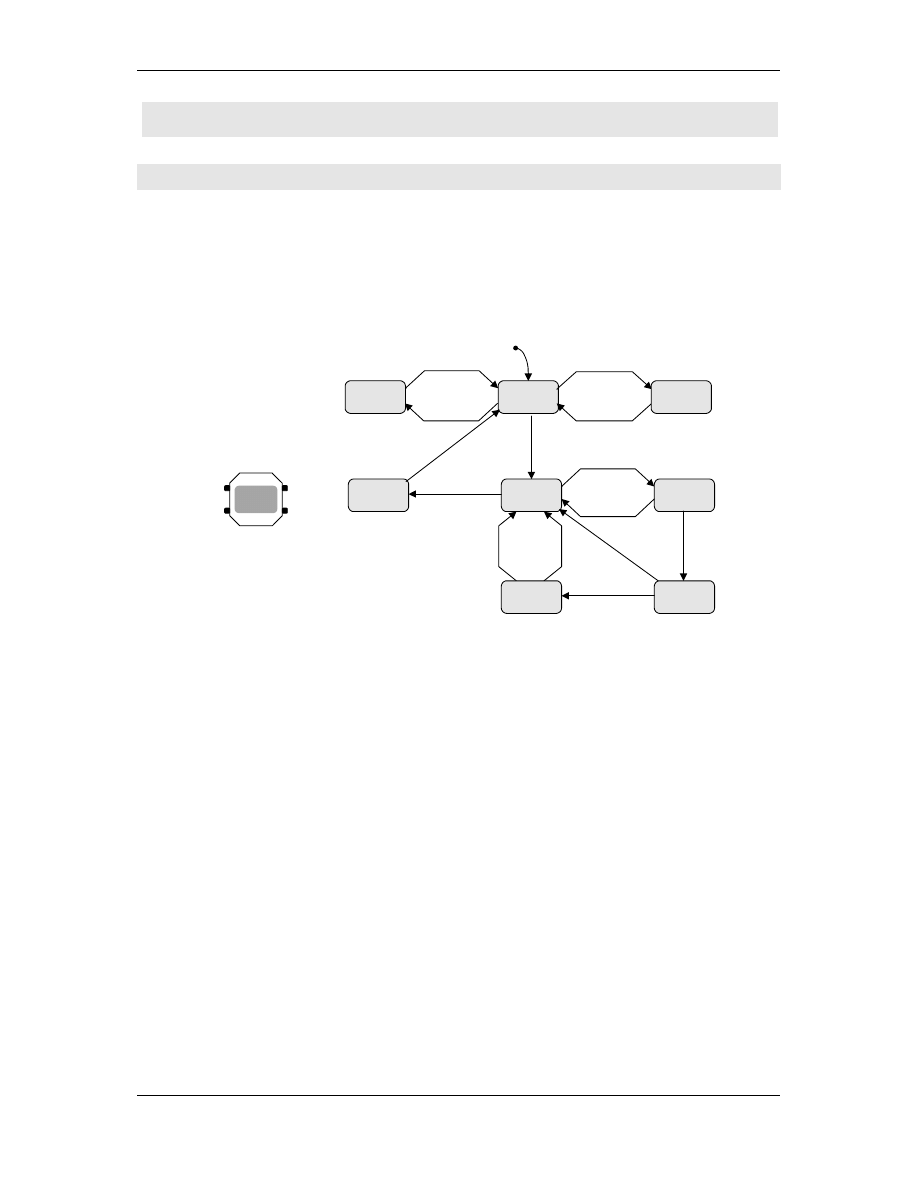
Przykład 10: Automat sko czony – zegarek cyfrowy

Automat przedstawiony poni ej opisuje cz

zachowania si

prostego zegarka cyfrowego z czterema przyciskami a, b, c i d.

Danymi wej ciowymi s sygnały lub zdarzenia, które docieraj do

automatu z otoczenia- w tym przypadku w wyniku wci ni cia

przez u ytkownika którego z przycisków.

d

d

b

a

c

a

a

b

d

c

a

b

wy wietl

czas

wy wietl

dat

wy wietl

stoper

c

c

nastaw

czas

nastaw

budzik

nastaw

godziny

nastaw

minuty

nastaw

10 min.

c

c

b

c

Rola abstrakcyjnych modeli oblicze

Badania nad zło ono ci obliczeniow i nierozstrzygalno ci

Teoria automatów

Teoria j zyków formalnych

Automaty ze stosem w lingwistyce strukturalnej i w konstruowaniu

kompilatorów

Badanie siły niedeterminizmu np. niedeterministyczny automat ze stosem

Badania nierozstrzygalno ci problemów decyzyjnych dotycz cych samych

modeli oblicze :

•

równowa no

algorytmiczna

dwóch

maszyn

Turinga

jest

nierozstrzygalna,

•

równowa no algorytmiczna dwóch automatów sko czonych jest

rozstrzygalna,

•

o rozstrzygalno ci problemu równowa no ci algorytmicznej dwóch

automatów ze stosem nic nie wiadomo (a problem ma istotne znaczenie

dla budowy j zyków programowania i kompilatorów)

Zagadnienie „obliczalnego” zapytania do bazy danych - jak powinny

wygl da „maszyny Turinga” dla baz danych lub baz wiedzy.