W

W

Y

Y

K

K

Ł

Ł

A

A

D

D

 

 

1

1

3

3

 

 

O

O

B

B

L

L

I

I

C

C

Z

Z

E

E

N

N

I

I

A

A

 

 

R

R

U

U

R

R

O

O

C

C

I

I

Ą

Ą

G

G

Ó

Ó

W

W

,

,

 

 

R

R

U

U

C

C

H

H

 

 

L

L

A

A

M

M

I

I

N

N

A

A

R

R

N

N

Y

Y

 

 

I

I

 

 

T

T

U

U

R

R

B

B

U

U

L

L

E

E

N

N

T

T

N

N

Y

Y

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

“Gallery of Fluid Motion”-M. Samimy, K.S. Breuer

 

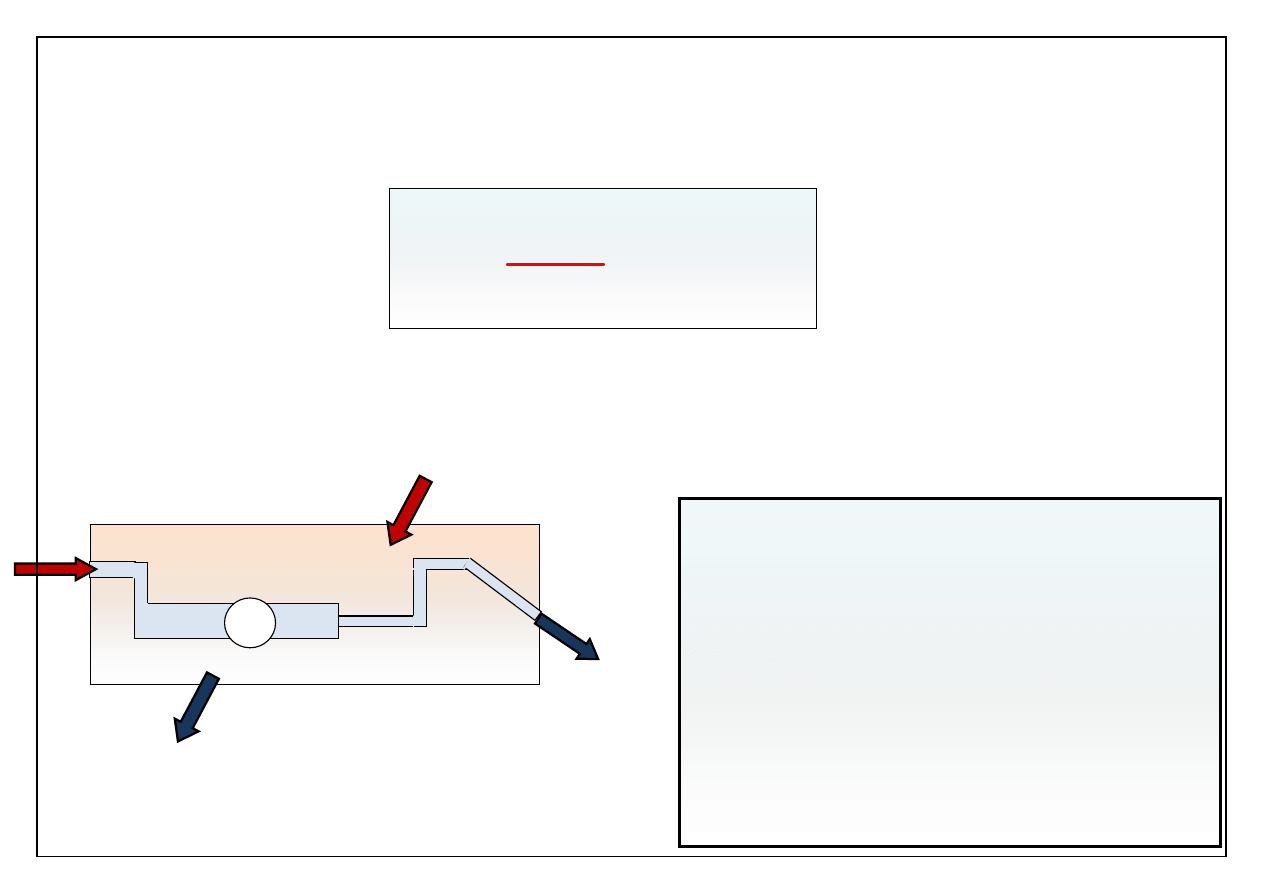
Spadek ciienia  

Δp

 

określa ubytek energii mechanicznej. Energia 

mechaniczna to suma energii kinetycznej, potencjalnej i ciśnienia.  
Dla cieczy 

– na mocy równania Bernoulliego otrzymamy: 

 
 
 
 
 
 

U

 

- oznacza 

prędkość średnią w przekroju przewodu. 

 

 
 
 
 
 
 
 
 

2

m

U

e

gz

p

2











 

 

P 

e

m2 

e

m1 

Δe

p 

Δe

s 

Bilans energii mechanicznej 

 

dla dowolnego rurociągu: 

 

 

m1

p

m 2

s

e

e

e

e

  

 

 

 

Δe

p

 

– energia dostarczana przez pompę

 

 

Δe

s 

– energia wynikająca ze strat

 

 

 
Oznaczmy                          i                     .  
 
Podstawmy też odpowiednie zależności za  

Δe

m1 

i

 

 

Δe

m2

 .  

 
Dostaniemy 

bilans energii

 w postaci: 

 

 
 

 

 

 

 
 
 
 
 
 
 
 

p

p

e

p

  

 

s

s

e

p

  

 

2

2

1

2

1

1

p

2

2

s

U

U

gz

p

p

gz

p

p

2

2











   





 

 

Korzystając z powyższego związku możemy wyznaczyć np. różnicę 
ciśnień, różnicę poziomów,

 

Δp

p  

lub

 

 

Δp

s

 

gdy zadany jest wydatek 

płynący przewodem. 

 

Możemy też szukać wydatku, gdy znane są ciśnienia oraz poziomy – 
początkowy i końcowy. 
 

W obu przypadkach geometria rurociągu, masa właściwa cieczy i 
lepkość są znane.   

 
Schematy postępowania: 
 

1. 

Znamy wydatek Q

         

określamy  prędkość  w każdym  

 

odcinku rury        liczymy 

Re

         wyznaczamy 

λ

     

 

liczymy

 

Δp

s 

 

2. 

Szukamy wydatku Q 

– nie możemy bezpośrednio  

 

wyznaczyć liczbowych wartości współczynników 

λ

. 

 

Q występuje w równaniu bilansowym za pośrednictwem 

λ

. 

 

Musimy zastosować metodę kolejnych przybliżeń. 

 
 
 
 

 

  

Przypomina to równanie 

x = f(x) 

które rozwiązujemy 

tak:   

 





1

2

Q

f

,

(Q),

(Q),







 

n 1

n

x

f (x )





 

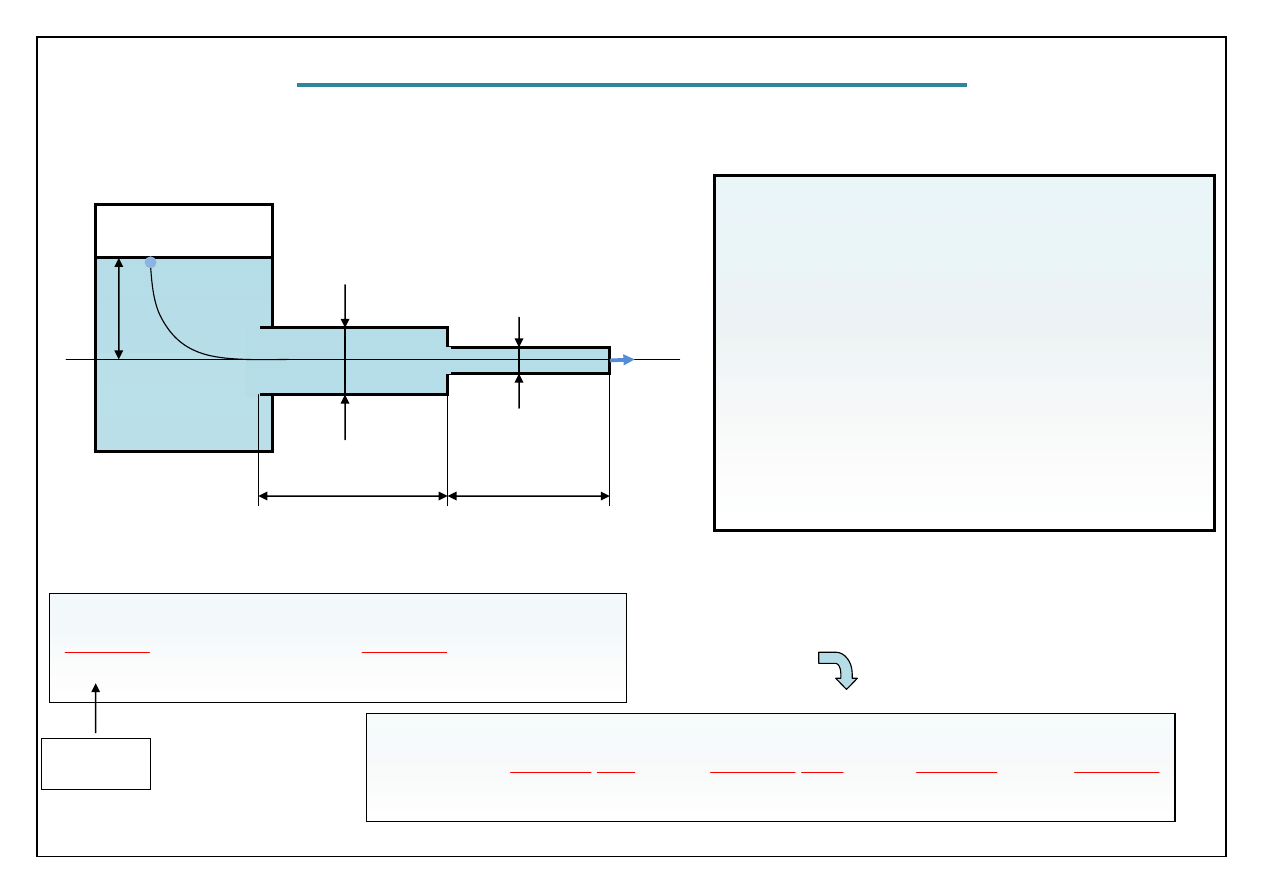
Przykład ilustrujący 2 –gi przypadek 

 
 
 
 
 
 
 

 

 

 

 

 

 

 

 

 

   

 

 

 

gdzie 

Δp

s

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

p

1 

0 

H 

ζ

1

=1 

L

1 

L

2 

p

A 

2 

D 

d 

ζ

2

=0.5 

Dane: 

p

1 

= 2 bary, p

2 

= p

A

= 1bar, H = 10m 

 
L

1 

= 100m,  L2 = 50m, 

 
D = 10cm,   d = 2cm, 
 
ρ = 10

3 

kg/m

3

,  ν=5∙10

-6

 m

2

/s 

 

2

2

0

2

1

A

s

U

U

gH

p

p

p

2

2















 

 

2

2

2

2

1

1

2

2

1

2

s

1

2

1

2

U L

U

L

U

U

p

2

D

2

d

2

2

















 







 

0

U

0



 

 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 

Podstawiamy: 
 
 
 
 
I otrzymujemy w rezultacie: 
 
 
 
 
  
 
 

 

Liczby Reynoldsa dla poszczególnych odcinków rur:

 

1

2

2

2

4Q

4Q

U

,

U

D

d









 





1

A

2

4

1

2

2

1

1

p

p

2 gH

d

Q

4

L

L

d

1

d

D

D































 









 

 

 

1

1

U D

4

Re

Q

D



 





 

2

2

U d

4

Re

Q

d



 





 

 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 

Obliczamy wydatek: 
 

 

 

 

 

 

 

 
 
 
 
 
 
 
 
i liczby Reynoldsa 
 
 
 
 
 
Wykorzystamy związek                              i policzymy     

 

 

 
 
 





4

2

1

62.83 10

Q

1.5 2500

0.0016 1 1000

















 

6

1

Re

2.54 10 Q





 

6

2

Re

12.7 10 Q





 

1 4

0.316

Re





 

1

2

,

 

 

 
 

 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 

 

 

Wykonujemy kolejne przybliżenia zakładając wyjściowo 

Q=0.01 m

3

/s

. 

 
 
 
 

 

 

 

 

 

 

 
 
 
 
Dla tych 

wartości wydatek 

Q=0.00097 m

3

/s

 

i jest on wyjściem do kolejnego 

przybliżenia. 
   

 

 

 

 
 
 
 
 
 
Dla tych wartości 

Q=0.095∙10

-2

 m

3

/s 

co kończy obliczenia. 

4

1

1

Re

2.5 10

0.025









 

4

2

2

Re

12.7 10

0.0167









 

1

1

Re

2425

64 Re 0.026









 

4

2

2

Re

12.1 10

0.017









 

P

P

O

O

D

D

S

S

U

U

M

M

O

O

W

W

A

A

N

N

I

I

E

E

 

 

 

 

-

-

 

 

R

R

U

U

C

C

H

H

 

 

L

L

A

A

M

M

I

I

N

N

A

A

R

R

N

N

Y

Y

,

,

 

 

R

R

U

U

C

C

H

H

 

 

T

T

U

U

R

R

B

B

U

U

L

L

E

E

N

N

T

T

N

N

Y

Y

 

 

 

 

 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 

 

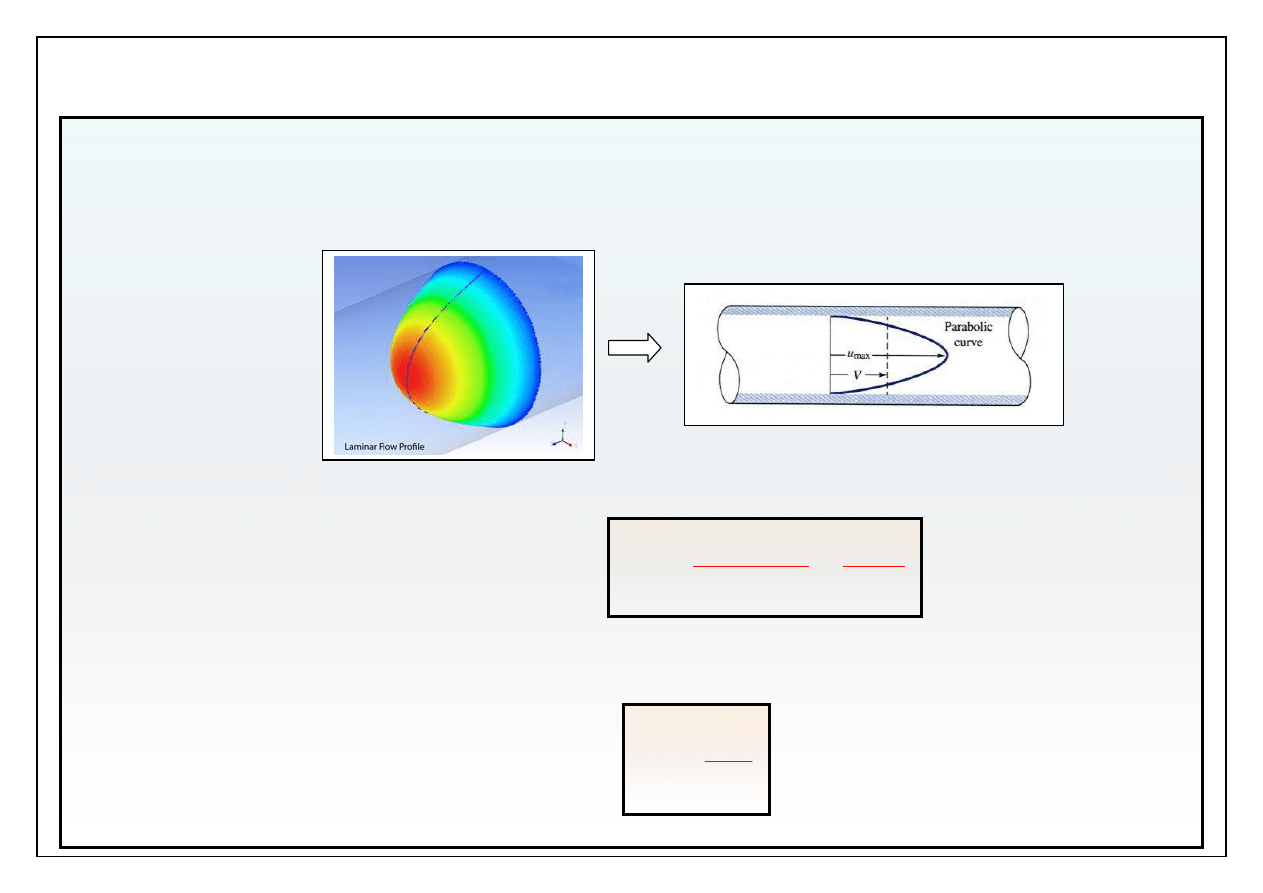
Ruch cieczy w okrągłym przewodzie może być zgodny z 

wyznaczonym rozwiązaniem równań Naviera - Stokesa, opisującym 
niezmienny z długością, niezależny od czasu, paraboloidalny rozkład 
prędkości.  
 
 
 
 
 
 
 
Jest tak, gdy liczba Reynoldsa 
 
ma stosunkowo niewielką wartość. 
 
 
Dla takiego ruchu wsp

ółczynnik 

 
 
 
 

sr

U

d

4Q

Re

d







 

 





 

64

Re





 

 

 

http://me.queensu.ca/People/Sellens/images/Profiles.jpg 

http://www2.emersonprocess.com/en-

US/brands/daniel/Documents/Newsletters/0610/DanielMatters-0610-index.html 

 
 
 
 
 
 
 
 
 
 
 
 

Przykłady przepływów laminarnych 

 
 
 
 

 

 
 
 
 
 
 

Ruch o paraboloidalnym profilu prędkości, niezależny od czasu i dla którego 
prędkość nie ma składowych poprzecznych obserwujemy dla liczb Reynoldsa 
mniejszych od krytycznej. 

 
Dla rury okrągłej  

Re

kr 

= 2300 

 

G

dy zachodzi nierówność 

Re < 2300 

to ruch jest laminarny 

– pomiędzy 

sąsiednimi warstwami cieczy zachodzi jedynie molekularna wymiana masy, 
pędu i energii. 
 

 
 

 

 

 

 

http://my-woodcarving.blogspot.com/2011/06/updates-on-laminar-flow-nozzle.html

 

http://www.waterartsconsulting.com/waterfall_weirs 

http://www.geol.umd.edu/~jmerck/geol342/lectures/04.html 

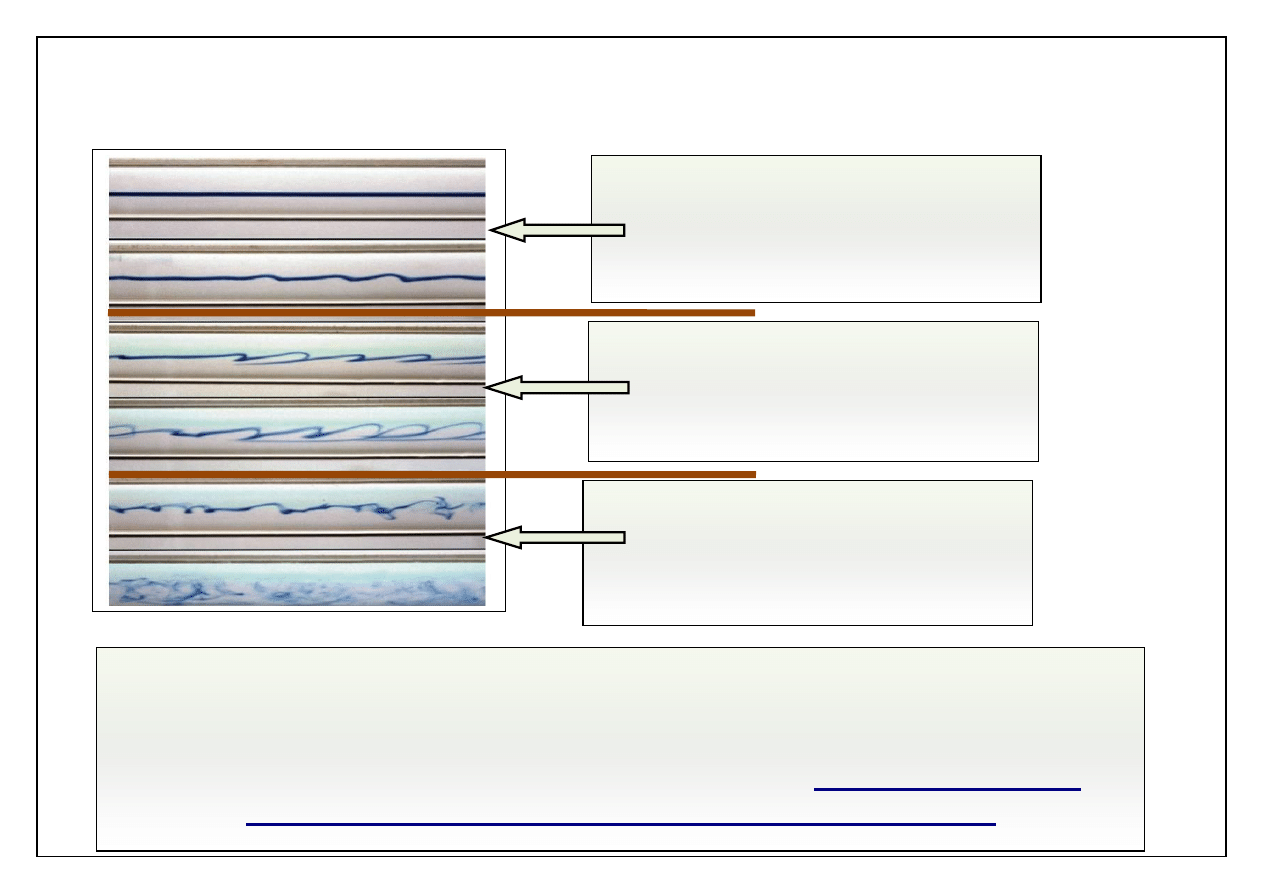
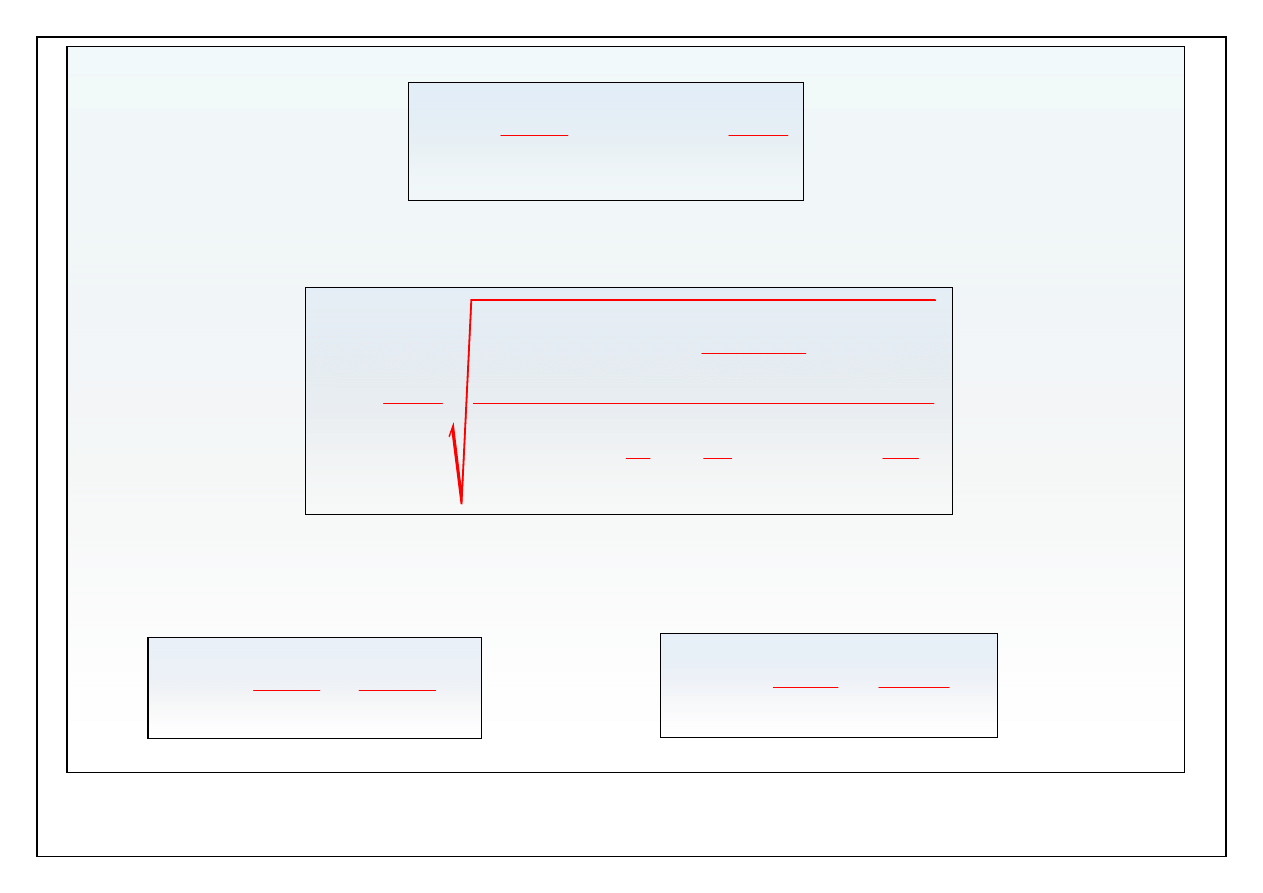
Przepływ w rurze 

 

 
 
 
 
 
 
 

 

 
 
 
 
 
 
 
 
 
 
 
 
 

 

laminarny 

 

przejściowy 

turbulentny 

Dla 

większych liczb Reynoldsa pole prędkości zależy od czasu i 

zmiennej wzdłużnej. Obserwuje się składowe poprzeczne prędkości. 

 

Gdy liczba Reynolds

a jest dostatecznie duża, większa od drugiej 

krytycznej liczby Reynoldsa to ruch jest turbulentny.

 

http://www.azimuthproject.org/azimuth/show/Blog+-+eddy+who%3F

 

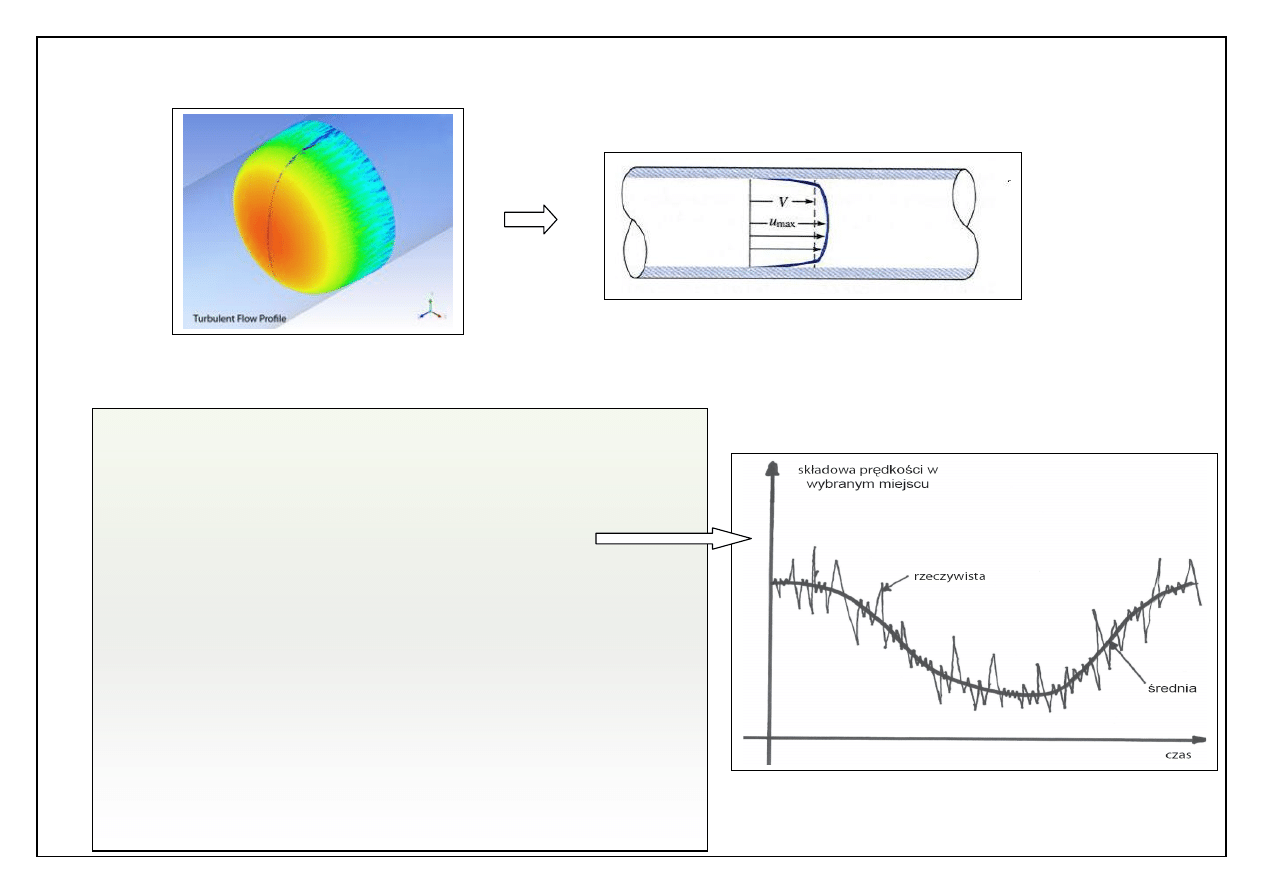
Profil prędkości dla ruchu turbulentnego w rurze 

 

 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 

 

 

Dla ruchu turbulentnego : 



 

pole prędkości ma przebieg losowy 

(losowe oscylacje wokół 
wolnozmiennej średniej) 

 

 



 

pomiędzy sąsiednimi warstwami 

płynu oprócz wymiany molekularnej, 
masa, pęd i energia zastają 
wymieniane makroskopowo

 

 

http://me.queensu.ca/People/Sellens/images/Profiles.jpg 

http://www2.emersonprocess.com/en-

US/brands/daniel/Documents/Newsletters/0610/DanielMatters-0610-index.html 

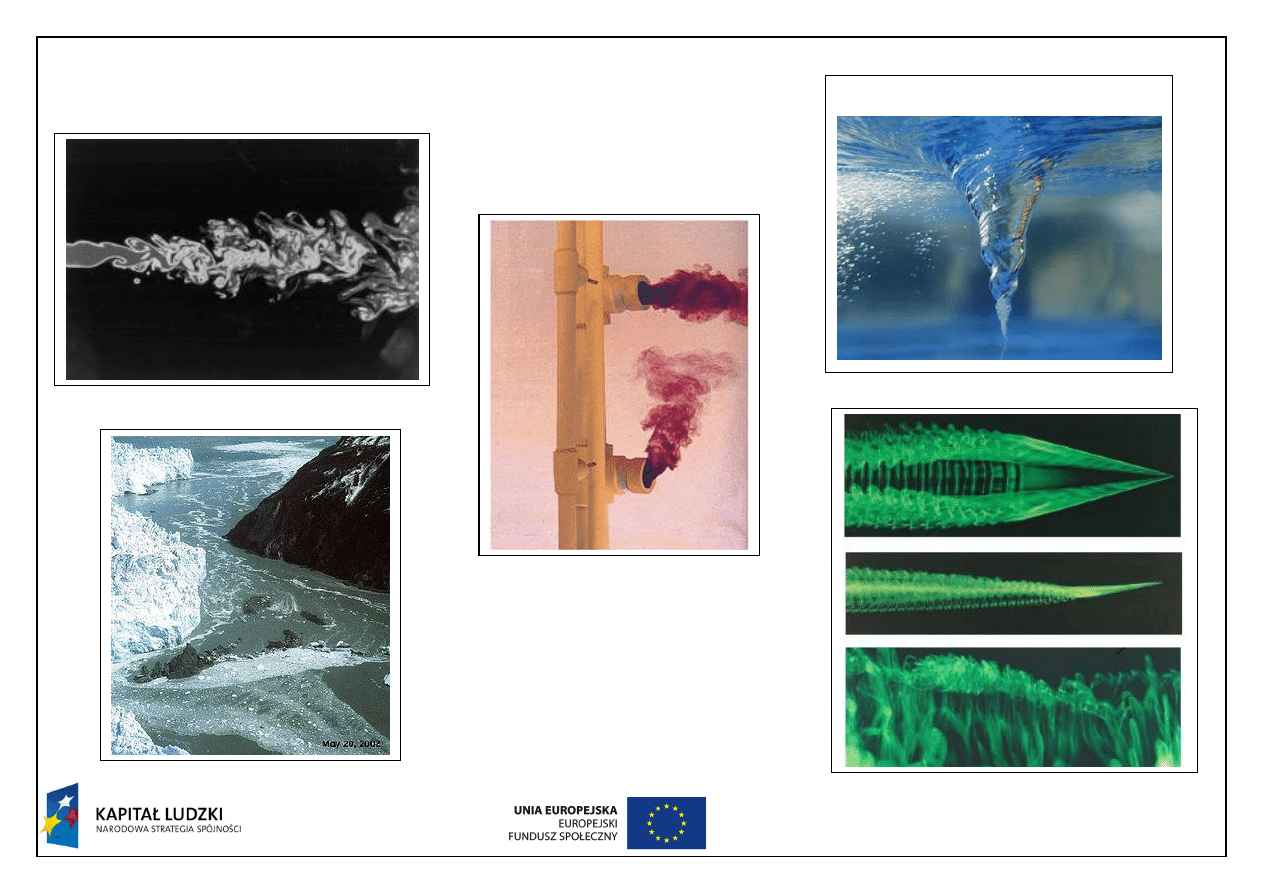
Przykłady przepływów turbulentnych 

 
 

 

 

 

 

 

 

http://en.wikipedia.org/wiki/File:Hubbard_Glacier_May_20.2000.jpg 

http://encyclopedia2.thefreedictionary.com/Turbulent+Flow 

http://knol.google.com/k/flow-separation-and-divorce-cost# 

http://www.ratiotherm.pl/pl/pytania-i-odpowiedzi/jak-wygladaja-dobre-

zasobniki-ciepla/

 

“Gallery of Fluid Motion”-M. Samimy, K.S. Breuer