Biostatystyka,

# 1

/Weterynaria I/

dr n. mat. Zdzisław Otachel

Uniwersytet Przyrodniczy w Lublinie

Katedra Zastosowań Matematyki i Informatyki

ul. Akademicka 15, p.317 bud. Agro II,

e-mail: [e-mail]

materiały: http://kzmi.up.lublin.pl/˜zotachel/Wet

Lublin, 2013

dr n. mat. Zdzisław Otachel

Biostatystyka, # 1 /Weterynaria I/

Zakres materiału

•

Statystyka opisowa - analiza struktury zjawisk
masowych

•

Podstawowe pojęcia rachunku prawdopodobieństwa

•

Zmienne losowe i ich rozkłady

•

Estymacja punktowa i przedziałowa

•

Testowanie hipotez statystycznych

dr n. mat. Zdzisław Otachel

Biostatystyka, # 1 /Weterynaria I/

Literatura

Hanusz Z., Tarasińska J. Statystyka matematyczna, Wyd. AR
Lublin 2006.

Kala R. Statystyka dla przyrodników, Wyd. AR, Poznań, 2002.

Koronacki J., Mielniczuk J. Statystyka dla studentów
kierunków technicznych i przyrodniczych, WNT, 2001.

Łomnicki A. Wprowadzenie do statystyki dla przyrodników,
PWN, W-wa 2002.

Parlińska M., Parliński J. Badania statystyczne z Excelem,
Wyd. SGGW W-wa 2003.

Smolik S. Zadania z rachunku prawdopodobieństwa i
statystyki matematycznej dla Akademii Rolniczych. Wyd.
SGGW W-wa 1994.

Stanisz A. Biostatystyka. Wyd. UJ, 2006.

Cezary Watała, Biostatystyka - wykorzystanie metod
statystycznych w pracy badawczej w naukach biomedycznych.
Wyd. Alfa Medica Press, Bielsko-Biała 2002.

dr n. mat. Zdzisław Otachel

Biostatystyka, # 1 /Weterynaria I/

Przedmiot statystyki

Termin statystyka wywodzi się od włoskiego słowa stato, czyli
państwo. Został on użyty po raz pierwszy przez niemieckiego
politologa Gotfrieda Achenwalla (1719-1772) profesora
uniwersytetów w Magdeburgu i Getyndze, na oznaczenie szeroko
rozumianych wiadomości o państwie. Dla uporządkowania
wywodów ujmowano opisy w tabele, dlatego kierunek ten
ochrzczono mianem statystyki tabelarycznej. Za twórców
współczesnej statystyki uznaje się Anglików Johna Grunta
(1620-1674) i Williama Petty’ego (1623-1687), arytmetyków
politycznych. Na podstawie danych liczbowych szukali oni
prawidłowości wśród pozornie chaotycznych zjawisk masowych.

dr n. mat. Zdzisław Otachel

Biostatystyka, # 1 /Weterynaria I/

Przedmiot statystyki

Dalszy rozwój statystyki stymulowała teoria rachunku
prawdopodobieństwa, zapoczątkowana w drugiej połowie XVII w.
przez francuskich matematyków: Blaise Pascala (1623-1662) i
Pierra Fermata (1601-1665). Podwaliny pod metody współczesnej
statystyki położył Carl Friedrich Gauss (1777-1855) tworząc teorię
za pomocą, której na podstawie szeregu pomiarów jakiegoś obiektu
można oszacować jego rzeczywisty wymiar. Najwybitniejsi twórcy
współczesnych metod statystycznych to: Karl Pearson
(1857-1936), Ronald Aylmer Fisher (1890-1962), Jerzy
Spława-Neyman (1894-1981), E.S. Pearson (1895-1980), Abraham
Wald (1902-1950).

dr n. mat. Zdzisław Otachel

Biostatystyka, # 1 /Weterynaria I/

Statystyka opisowa

dr n. mat. Zdzisław Otachel

Biostatystyka, # 1 /Weterynaria I/

Podstawowe pojęcia statystyczne

Przedmiotem badań statystycznych są populacje - określone zbiory
istot, rzeczy lub zjawisk. Będą one badane pod kątem określonych
cech tj. funkcji, które przyporządkowują każdemu elementowi
populacji wartość liczbową, będącą wynikiem pomiaru.
Cechy podzielimy na:

Skokowe - przyjmujące skończoną lub przeliczalną liczbę
wartości np. liczba szczeniąt w miocie, czas oczekiwania na
zadziałanie podanego leku mierzony np. w godzinach,

Ciągłe - przyjmujące dowolne wartości z pewnego przedziału,
np. masa, średnica, długość, itp. określonego obiektu
biologicznego (np. zwierzęcia), poziom przeciwciał we krwi
zwierzęcia po podaniu szczepionki.

dr n. mat. Zdzisław Otachel

Biostatystyka, # 1 /Weterynaria I/

Całkowite i częściowe badanie populacji

Wnioskując o cechach pewnej populacji można wykonać
następujące rodzaje badań statystycznych:

Badanie całkowite - mierząc wartości interesujących cech dla
każdego elementu populacji,

Badanie częściowe - oznaczając wartości cech dla
wytypowanych na drodze losowania niektórych elementów
populacji i uogólniając wyniki, za pomocą technik
statystycznych, na całą populację.

Ze statystycznego punktu widzenia interesujący jest tylko ten drugi
rodzaj badania.
Część populacji podlegającą badaniu częściowemu nazywamy
próbą.

dr n. mat. Zdzisław Otachel

Biostatystyka, # 1 /Weterynaria I/

Szereg statystyczny

Badanie częściowe określonej cechy prowadzi do uzyskania szeregu
statystycznego (pierwotnego). Jest to ciąg pomiarów tej samej
cechy x na N obiektach populacji, wybranych do badania w sposób
losowy, mianowicie:

x

1

, x

2

, . . . , x

N

,

gdzie x

i

jest wartością (obserwacją lub pomiarem) cechy x dla

i -tego elementu wytypowanego z populacji do badania, a N ilością
przebadanych obiektów (rozmiarem, liczebnością, długością szeregu
statystycznego).
Ciąg pomiarów tej samej cechy nazywa się też próbą liczbową.

dr n. mat. Zdzisław Otachel

Biostatystyka, # 1 /Weterynaria I/

Statystyczne szeregi rozdzielcze

Rozstęp szeregu statystycznego (R) to różnica:

R = x

max

− x

min

,

gdzie x

max

i x

min

oznacza odpowiednio największy i najmniejszy

zaobserwowany pomiar.
Pierwotny szereg statystyczny zawiera nieistotne informacje,
dlatego podlega obróbce mającej na celu pominięcie tychże, a
przez to zyskanie na przejrzystości. Takie zabiegi prowadzą do
otrzymania następujących, przetworzonych danych statystycznych:

Szereg szczegółowy - pomiary uporządkowane w kolejności
rosnącej lub malejącej,
Szereg rozdzielczy - zestawienie uporządkowanych
zaobserwowanych wartości lub zakresów (przedziałów
klasowych) z odpowiadającymi im liczebnościami.

Szeregi rozdzielcze tworzy się z licznych (zawierających więcej niż
30 obserwacji) szeregów statystycznych lub, gdy w szeregu
występują powtarzające się wartości.

dr n. mat. Zdzisław Otachel

Biostatystyka, # 1 /Weterynaria I/

Rodzaje szeregów rozdzielczych

Punktowy szereg rozdzielczy - dla cech skokowych
przyjmujących skończoną liczbę wartości; ma on postać
zestawienia:

(x

i

, l

i

),

gdzie x

i

- i -ta w kolejności wzrostu zaobserwowana wartość, l

i

- ilość powtórzeń w szeregu statystycznym,
Klasowy szereg rozdzielczy - dla cech ciągłych lub skokowych
o licznych różnych wartościach (w praktyce, więcej niż 30) i
ma on postać zestawienia:

(π

i

, l

i

),

gdzie π

i

- i -ty przedział klasowy, l

i

- ilość obserwacji

należących do tego przedziału.

Przedziały klasowe na ogół są jednakowej długości, muszą być
rozłączne i ich suma ma pokrywać wszystkie wartości szeregu
rozdzielczego. Suma liczebności jest zawsze równa długości szeregu
statystycznego: l

1

+ l

2

+ · · · + l

r

= N.

dr n. mat. Zdzisław Otachel

Biostatystyka, # 1 /Weterynaria I/

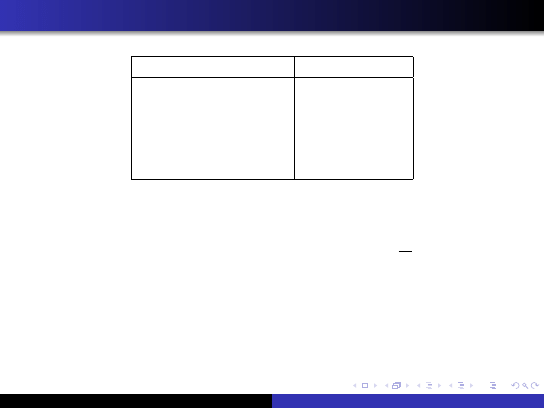
Zależność liczby klas od ilości pomiarów

Liczba pomiarów (N)

Liczba klas (k)

30-60

6-8

60-100

7-10

100-200

9-12

200-500

11-17

500-1500

16-25

Liczbę klas można wyznaczyć także na podstawie jednej z
zależności:

k ¬ 5 ln N, k ≈ 1 + 3, 332 ln N, k ≈

√

N.

Nie stosuje się większej ilości klas niż 30. Długość przedziału
klasowego obliczamy dzieląc rozstęp R przez liczbę klas k.
Graficzne przedstawienie szeregu rozdzielczego to histogram (dla
szeregów klasowych) lub diagram liczebności (dla szeregów
punktowych).

dr n. mat. Zdzisław Otachel

Biostatystyka, # 1 /Weterynaria I/

Charakterystyki używane do opisu danych statystycznych

Zbiór danych statystycznych – szereg statystyczny – zawiera
informację o cesze trudną do przetwarzania.
Łatwiej operować częścią tej informacji, którą zawierają
charakterystyki (miary) danych liczbowych. Są to funkcje
zdefiniowane na elementach szeregu statystycznego.
Do takich charakterystyk (miar) najczęściej wykorzystywanych przy
opisie struktury zbiorowości liczbowych należą:

miary średnie (przeciętne, położenia) – podają one tą wartość
wokół której skupiają się pozostałe liczby (obserwacje), jeżeli
x jest taką miarą, to zawsze

x

min

¬ x ¬ x

max

;

miary zmienności (rozproszenia, zróżnicowania, dyspersji) –
określają stopień zróżnicowania wartości w analizowanej
zbiorowości, jeżeli d jest taką miarą, to

d ­ 0,

dr n. mat. Zdzisław Otachel

Biostatystyka, # 1 /Weterynaria I/

Charakterystyki używane do opisu danych statystycznych-
cd.

przypadek d = 0 oznacza brak zmienności, wszystkie wartości są
równe swojej średniej;

miary asymetrii (skośności) – określają kierunek zróżnicowania
wartości;

miary koncentracji – określają stopień skupienia wartości
wokół średniej.

dr n. mat. Zdzisław Otachel

Biostatystyka, # 1 /Weterynaria I/

Miary średnie (przeciętne)

Dzielą się na:

1

średnie klasyczne:

średnia arytmetyczna (A),
średnia geometryczna (G),
średnia harmoniczna (H),

2

średnie pozycyjne:

dominanta (moda, wartość modalna, najczęstsza),
kwantyle

kwartyle – dzielące zbiorowość na cztery części,
decyle – dzielące zbiorowość na dziesięć części,
percentyle – dzielące zbiorowość na sto części.

Średnie klasyczne są obliczane na podstawie wszystkich wartości
szeregu statystycznego, średnie pozycyjne są wartościami
konkretnych wyrazów szeregu wyróżniających się pod pewnym
względem.

dr n. mat. Zdzisław Otachel

Biostatystyka, # 1 /Weterynaria I/

Średnia arytmetyczna

Średnią x cechy x na podstawie szeregu statystycznego
x

1

, x

2

, . . . , x

N

najczęściej policzymy posługując się średnią

arytmetyczną:

x =

x

1

+ x

2

+ · · · + x

N

N

=

P

N
i =1

x

i

N

.

Ale ta sama średnia dla szeregu rozdzielczego będzie liczona wg
wzoru na średnią ważoną, gdzie wagami są liczebności:

x =

x

1

l

1

+ x

2

l

2

+ · · · + x

r

l

r

l

1

+ l

2

+ · · · + l

r

=

P

r
i =1

x

i

l

i

P

r
i =1

l

i

,

gdzie x

1

, x

2

, . . . , x

r

oznaczają tu wartości zaoobserwowane dla

szeregu punktowego lub środki przedziałów klasowych dla szeregu
klasowego. Średnia arytmetyczna jest miarą wiarygodną tylko dla
zbiorowości o niewielkim stopniu zróżnicowania obserwacji. Gdy
rośnie asymetria (histogram nie ma osi symetrii) lub zbiorowość
jest wielomodalna (histogram ma więcej niż jedno maksimum)
stosowalność wzoru traci sens.

dr n. mat. Zdzisław Otachel

Biostatystyka, # 1 /Weterynaria I/

Średnia harmoniczna

Jeżeli obserwowane wartości są określone w jednostkach
względnych (tzn. wielkość/jednostka miary) to wartość przeciętną
szeregu x

1

, x

2

, . . . , x

N

możemy policzyć wg średniej harmonicznej:

H =

N

P

N
i =1

1

x

i

.

Dla szeregów rozdzielczych należałoby stosować wzór z
liczebnościami l

i

:

H =

l

1

+ l

2

+ · · · + l

r

P

r
i =1

1

x

i

.

dr n. mat. Zdzisław Otachel

Biostatystyka, # 1 /Weterynaria I/

Średnia geometryczna

W przypadku, gdy chcemy policzyć przeciętną wartość przyrostu
lub spadku badanej cechy użyjemy średniej geometrycznej,
dokładniej: niech x

0

, x

1

, x

2

, . . . , x

N

będzie szeregiem statystycznym

związanym z cechą x , cecha y to względna zmiana cechy x , a
y

1

, y

2

, . . . , y

N

to szereg z nią związany, gdzie

y

i

= x

i

/x

i −1

, i = 1, 2, . . . N. Wtedy

y =

N

√

y

1

· y

2

· · · · · y

N

.

Dla szeregu rozdzielczego, z wagami l

i

użyjemy wzoru:

y =

N

q

y

l

1

1

· y

l

2

2

· · · · · y

l

r

r

,

gdzie N = l

1

+ l

2

+ · · · + l

r

.

dr n. mat. Zdzisław Otachel

Biostatystyka, # 1 /Weterynaria I/

Średnie pozycyjne

Dominanta (moda) D – to taka wartość obserwacji, która w
szeregu statystycznym występuje najczęściej, ma sens tylko dla
zbiorowości jednomodalnych (o jednej wartości maksymalnej).
Kwartyle: Q

1

(dolny),Q

2

(środkowy – mediana), Q

3

(górny) dzielą

szereg na 4 części, równe pod względem liczebności (po 25%
obserwacji). Mediana (M

e

) – wartość znajdująca się dokładnie w

środku szeregu uporządkowanego. Liczba obserwacji mniejszych od
mediany jest równa ilości obserwacji większych o mediany. Mediana
to środkowy kwartyl.

dr n. mat. Zdzisław Otachel

Biostatystyka, # 1 /Weterynaria I/

Miary zmienności (dyspersji) – wariancja

Wariancja pomiarów cechy x (ozn.: S

2

x

:= S

2

) – średnia

arytmetyczna z kwadratów różnic poszczególnych,
zaobserwowanych wartości cechy x od średniej arytmetycznej x
wszystkich obserwacji.
Dla szeregu surowego lub szczegółowego liczymy ją wg wzoru:

S

2

=

1

N

N

X

i =1

(x

i

− x)

2

,

Dla szeregów rozdzielczych użyjemy wzoru z wagami:

S

2

=

1

N

r

X

i =1

l

i

(x

i

− x)

2

, N =

r

X

i =1

l

i

.

gdzie tutaj x

i

są wartościami zaobserwowanymi lub środkami

przedziałów klasowych, natomiast l

i

- liczebnościami związanymi z

zaobserwowanymi wartościami x

i

lub ilościami obserwacji

należących do kolejnych przedziałów klasowych.

dr n. mat. Zdzisław Otachel

Biostatystyka, # 1 /Weterynaria I/

Wariancja - cd.

W każdej sytuacji słuszny jest wzór:

S

2

= x

2

− (x)

2

,

gdzie x

2

oznacza średnią arytmetyczną kwadratów obserwacji (tzw.

średni kwadrat), tj.:

x

2

==

x

2

1

+ x

2

2

+ · · · + x

2

N

N

=

P

N
i =1

x

2

i

N

dla szeregu nieuporządkowanego, lub

x

2

=

x

2

1

l

1

+ x

2

2

l

2

+ · · · + x

2

r

l

r

l

1

+ l

2

+ · · · + l

r

=

P

r
i =1

x

2

i

l

i

P

r
i =1

l

i

,

dla szeregów rozdzielczych, gdzie x

1

, x

2

, . . . , x

r

oznaczają tu

wartości obserwowane (szeregi punktowe) lub środki przedziałów
klasowych (szeregi klasowe) związane z liczebnościami l

1

, l

2

, . . . , l

r

.

Wariancja jest zawsze liczbą nieujemną, wyrażoną w kwadracie
jednostki fizycznej użytej do pomiaru cechy x . Duża jej wartość
świadczy o dużym zróżnicowaniu (zmienności) obserwacji.

dr n. mat. Zdzisław Otachel

Biostatystyka, # 1 /Weterynaria I/

Poprawka Shepparda

Wariancja liczona dla szeregu nieuporządkowanego i klasowego
różnią się. Gdy histogram badanej cechy ma jedno maksimum (jest
jednomodalny) i liczności klas maleją do 0 w obu kierunkach, to od
wariancji S

2

liczonej dla szeregu klasowego odejmujemy poprawkę

Shepparda równą 1/12 kwadratu długości klasy d . Wariancja S

2

∗

uwzględniajaca poprawkę jest określona wzorem:

S

2

∗

= S

2

−

1

12

d

2

.

Poprawkę Shepparda stosuje sie w praktyce, gdy liczebność szeregu
N ­ 1000 zaś liczba klas k ­ 20.

dr n. mat. Zdzisław Otachel

Biostatystyka, # 1 /Weterynaria I/

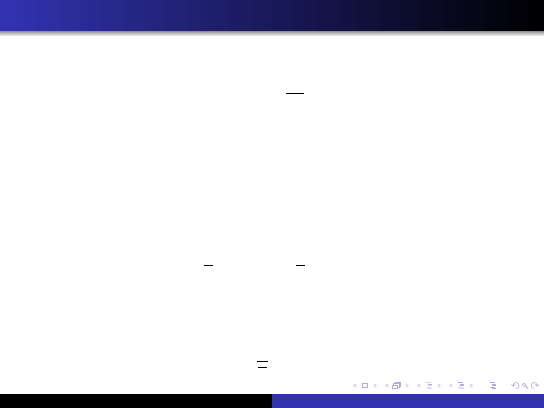
Odchylenie standardowe

Odchylenie standardowe pomiarów cechy x (ozn.: S

x

:= S ) jest

pierwiastkiem kwadratowym z wariancji:

S =

√

S

2

i określa o ile średnio obserwacje różnią się od średniej
arytmetycznej pomiarów badanej cechy. Odchylenie standardowe
służy do do konstrukcji typowego przedziału zmienności dla
badanej cechy. W tym obszarze mieści się około 2/3 wszystkich
wartości obserwowanych dla tej cechy. Typowy przedział
zmienności określa wzór:

x − S ¬ x ¬ x + S .

By porównywać zmienność dwóch zbiorowości użyjemy
niemianowanego współczynnika zmienności (ozn. V ):

V =

S

x

· 100%.

dr n. mat. Zdzisław Otachel

Biostatystyka, # 1 /Weterynaria I/

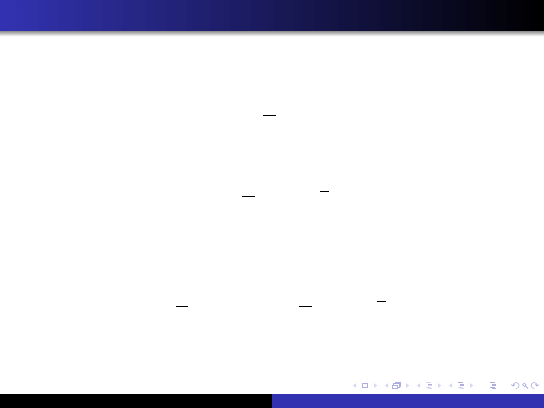
Momenty

Niech r będzie liczbą naturalną.
Moment zwykły m

r

rzędu r dla szeregu x

1

, . . . , x

N

to

m

r

=

1

N

N

X

i =1

x

r

i

.

Moment centralny M

r

rzędu r dla szeregu x

1

, . . . , x

N

to

M

r

=

1

N

N

X

i =1

(x

i

− x)

r

.

Dla szeregów rozdzielczych

(x

i

, l

i

), i = 1, . . . , n, l

1

+ l

2

+ · · · + l

n

= N :

m

r

=

1

N

N

X

i =1

x

r

i

l

i

, M

r

=

1

N

N

X

i =1

(x

i

− x)

r

l

i

.

Pierwszy moment zwykły m

1

jest średnią arytmetyczną. Pierwszy

moment centralny M

1

jest zawsze równy 0. Drugi moment

centralny M

2

jest wariancją.

dr n. mat. Zdzisław Otachel

Biostatystyka, # 1 /Weterynaria I/

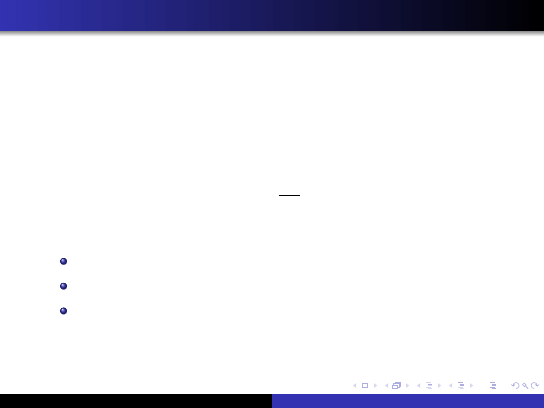
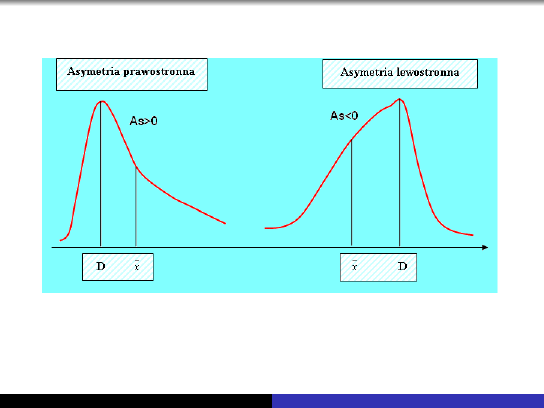
Miary asymetrii

Dla rozkładów symetrycznych - histogram ma oś symetrii
przechodzacą przez wspólną wartość średniej arytmetycznej,
dominanty i mediany - momenty centralne rzedów nieparzystych są
równe 0. Stąd trzeci moment centralny wykorzystano do
konstrukcji współczynnika asymetrii (skośności)

A

s

=

M

3

S

3

.

Wartość A

S

jest:

równa zero, dla zbiorowości symetrycznej,

dodatnia, dla zbiorowości o asymetrii prawostronnej,

ujemna, dla zbiorowości o asymetrii lewostronnej.

Im większa wartość bezwzględna współczynnika skośności tym
większa asymetria badanej zbiorowości.

dr n. mat. Zdzisław Otachel

Biostatystyka, # 1 /Weterynaria I/

dr n. mat. Zdzisław Otachel

Biostatystyka, # 1 /Weterynaria I/

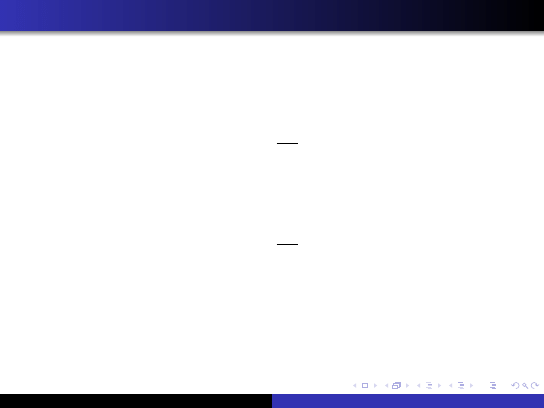
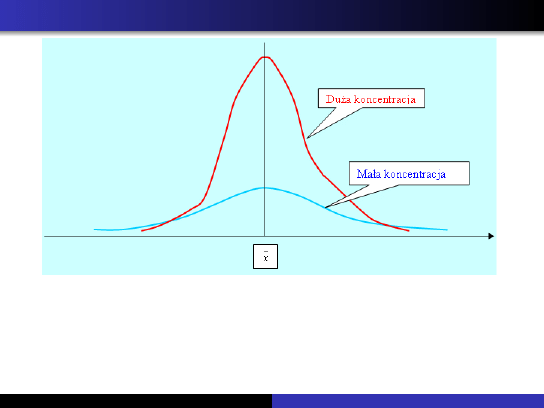
Miary koncetracji

Czwarty moment centralny służy do pomiaru koncentracji
(skupienia)

K =

M

4

S

4

.

Współczynnik ten nazywa sie też kurtozą. Inny współczynnik tego
rodzaju to eksces (współczynnik spłaszczenia), obliczamy go
następujaco:

K − 3 =

M

4

S

4

− 3.

Zachodzi ścisły związek między koncentracją wartości cechy wokół
średniej (smukłość histogramu) a ich dyspersją. Im większa jest
dyspersja tym mniejsza jest koncentracja i vice versa.

dr n. mat. Zdzisław Otachel

Biostatystyka, # 1 /Weterynaria I/

Koncetracja a dyspersja

dr n. mat. Zdzisław Otachel

Biostatystyka, # 1 /Weterynaria I/

Statystyczna analiza danych w Excelu

Excel jest wygodnym narzędziem do podstawowej analizy danych
statystycznych. Arkusz kalkulacyjny powinien mieć załadowany
pakiet ANALYSIS TOOLPAK – w menu NARZĘDZIA powinna się
wyświetlać opcja ANALIZA DANYCH. Jeżeli polecenie jest
niedostępne, to należy pakiet załadować: W menu NARZĘDZIA
kliknąć polecenie DODATKI, Na liście DOSTĘPNE DODATKI
zaznaczyć pole ANALYSIS TOOLPAK i potwierdzić.

Tworzenie szeregów rozdzielczych i ich graficzna prezentacja:
NARZĘDZIA>ANALIZA DANYCH>HISTOGRAM.

Obliczanie liczebności l

i

dla szeregów rozdzielczych: funkcja

CZĘSTOŚĆ.

Obliczanie średnich z szeregów pierwotnych – funkcje
ŚREDNIA, ŚREDNIA.GEOMETRYCZNA,
ŚREDNIA.HARMONICZNA (kategoria STATYSTYCZNE).

dr n. mat. Zdzisław Otachel

Biostatystyka, # 1 /Weterynaria I/

Statystyczna analiza danych w Excelu - cd.

Obliczanie podstawowych charakterystyk:
NARZĘDZIA>ANALIZA DANYCH>STATYSTYKA
OPISOWA

Obliczanie kwartyli: Funkcja KWARTYL (kategoria
STATYSTYCZNE)

Mediana i moda (dominanta) – funkcje MEDIANA (lub
KWARTYL(·;2)) i WYST.NAJCZĘŚCIEJ

dr n. mat. Zdzisław Otachel

Biostatystyka, # 1 /Weterynaria I/