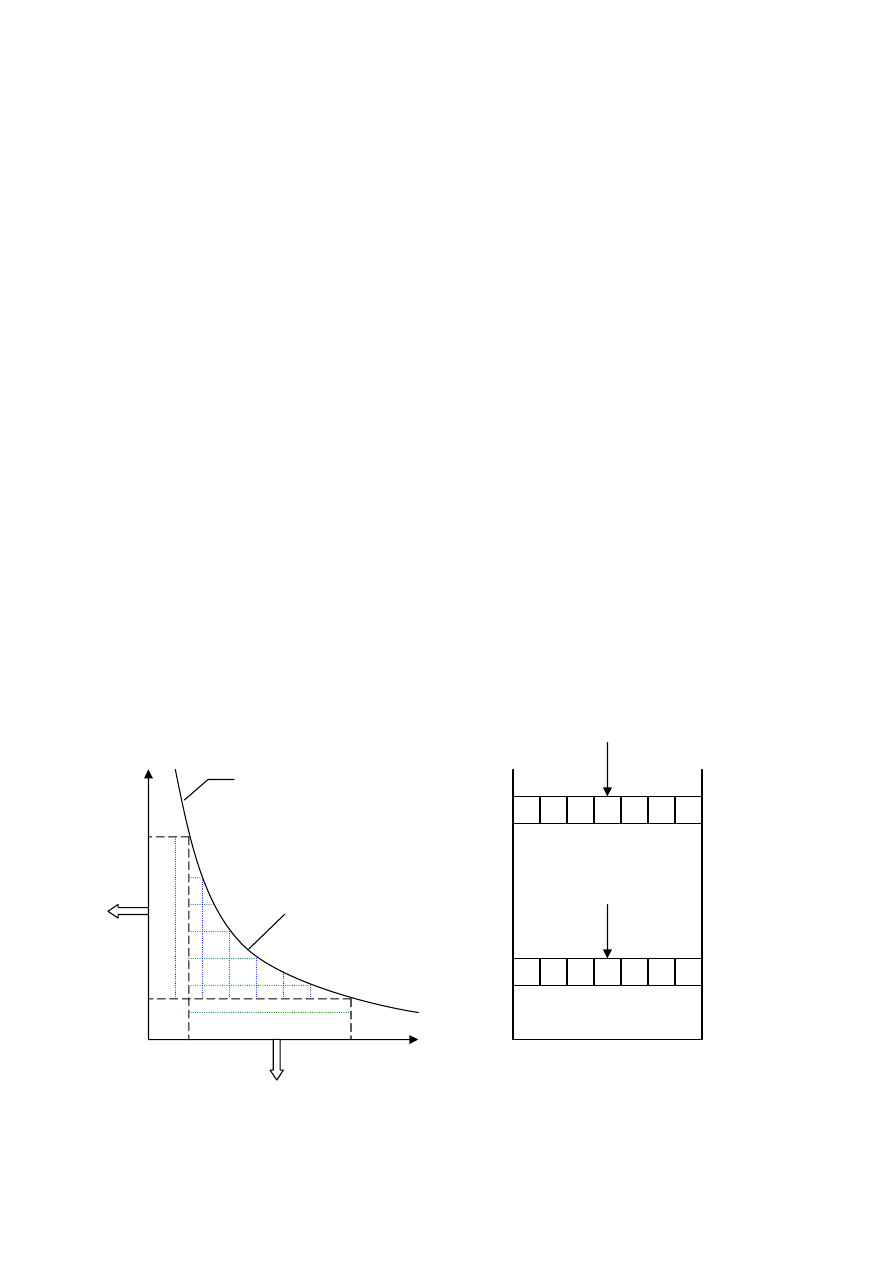
p
1
L
t
V
p
V
2
V
1
p
2
L
V
1
T
2
F
S1
p
2
V
2
T
2
F
S2
p
0
p
S2
=F
S2
/A
ΔQ
p
2
=p
S2
+p
0
p=p
S1
+p
0
p
S1
=F
S1
/A
Michał Murawski WM-32
Zadanie 1.36.
Powietrze traktowane jak gaz doskonały zajmuje zasób objętości V
1
=5[m
3
] i
osiąga następujące parametry stanu, ciśnienie p
1
=1,2[MPa] i temperature
t
1
=27[
o
C]. Następnie w przemianie izotermicznej odwracalnej powietrze zostaje
rozgęszczone osiągając ciśnienie p
2
=0,1[MPa] . Obliczyć przyrosty zasobów
energii wewnętrznej E
I
, antalpii H, entropii S oraz prace bezwzględną
objętościową L, pracę techniczną L
t
i przyrost ilości ciepła przemiany
izotermicznej odwracalnej Q .
Dane:
Szukane:
3
1
1
1
2
5
1, 2
27
0,1
V
m
p
at
t
C
T
const
p
MPa
?
?
?
?
?
?
I
t
E
H
S
L
L
Q
1. Wykres izotermy odwracalnej rozgęszczenia powietrza.
T=const
Hiperbola
równoosiowa
2. Bilans energii dla przemiany odwracalnej.
- 1 postać I zasady termodynamiki:
I
dE
Q
L
L
pdV
- 2 postać I zasady termodynamiki:
t
t
dH
Q
L
L
Vdp
3. Bilans energii wewnętrznej dla odwracalnej przemiany izotermicznej.
I
dE
Q
L
Zasób energii wewnętrznej gazu doskonałego w układzie substancjalnym:
I
E
c mT
Gaz doskonały:
c
const
Bilans energii wewnętrznej przyjmie postać:
Układ substancjalny:
m
const
0
I
dE
Q
L
Przemiana izotermiczna:
T
const
4. Bilans entarpii dla odwracalnej przemiany izotermicznej.
t
dH
Q
L
Zasób entarpii gazu doskonałego w układzie substancjalnym:
p
H
c mT
Gaz doskonały:
p
c
const
Układ substancjalny:
Bilans entarpii przyjmie postać:
m
const
t
Q
L
Przemiana izotermiczna:
T
const
5. Relacja między przyrostem ilości ciepła pracy bezwzględnej objętościowej i
pracy technicznej w przemianie izotermicznej odwracalnej.
t
Q
L
L
6. Obliczam pracę bezwzględną objętościową.
2
1
2
1
1 1
1 1
1 1
0
1 1
2
1
1 1
1 1
1
2
1
ln
ln
ln
|
V
L
V
V
V
L
pdV
pV
const
T
const
pV
p V
V
dV
L
p V
V
dV
L
p V
V
L
p V
V
V
p
p V
p V
V
p
rozwiązanie izotermy:
2
1
1
2
V
p
V
p
7. Obliczam przyrost objętościowej energii wewnętrznej.
2
2
1
1
0
0
0
I
I
I
E
T
I
E
T
I
dE
dE
dT
E
8. Obliczam przyrost zasobu entrapii.
2
2
1
1
0
0
0
H
T
H
T
dH
dH
dT
H
9. Obliczam przyrost ilości ciepła i pracy technicznej w przemianie
izotermicznej odwracalnej.
2
1
1 1
1
2
ln
ln
t
t
Q
L
L
V
p
Q
L
L
p V
pV
V
p
10. Obliczam przyrost zasobu entrapii w przemianie izotermicznej odwracalnej.
2
1
1
0
1 1
1
1
1
2
1
ln
S
Q
S
dQ
dS
dT
dS
dQ
T
p V
p
Q
S
T
T
p
11. Obliczam wartość pracy bezwzględnej objętościowej.
117720
117720 5 ln
96, 0234
100000
L
kJ
12. Obliczam wartość przyrostu ilości ciepła i pracy technicznej.
117720
117720 5 ln
96, 0234
100000
Q
kJ
13. Obliczam przyrost zasobu entrapii.
117720 5
117720
ln
319,92
300,15
100000
J
S
K