1

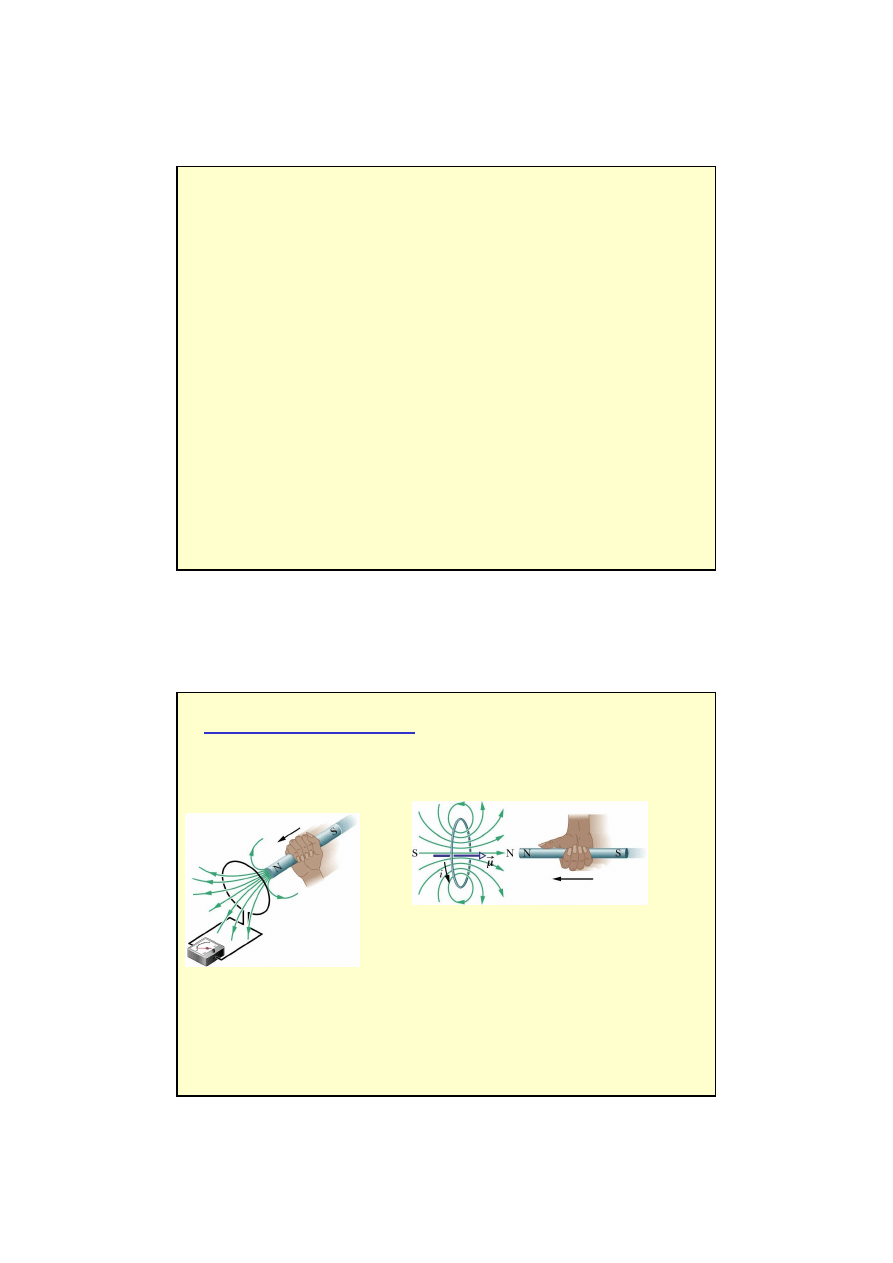
Indukcja elektromagnetyczna

Zjawisko indukcji elektromagnetycznej polega na powstawaniu siły elektromotorycznej
SEM w obwodzie podczas przemieszczania si

ę

wzgl

ę

dem siebie

ź

ródła pola

magnetycznego i tego obwodu.

W obwodzie zamkni

ę

tym SEM indukcji wywołuje

przepływ pr

ą

du indukcyjnego i w konsekwencji

powstanie wytwarzanego przez ten pr

ą

d

indukowanego pola magnetycznego.

Indukowane: siła elektromotoryczna, pr

ą

d i pole magnetyczne powstaj

ą

w obwodzie

tylko podczas ruchu magnesu.

Dla powstania pr

ą

du indukcyjnego potrzebny jest wzgl

ę

dny ruch

ź

ródła

pola magnetycznego i przewodnika.

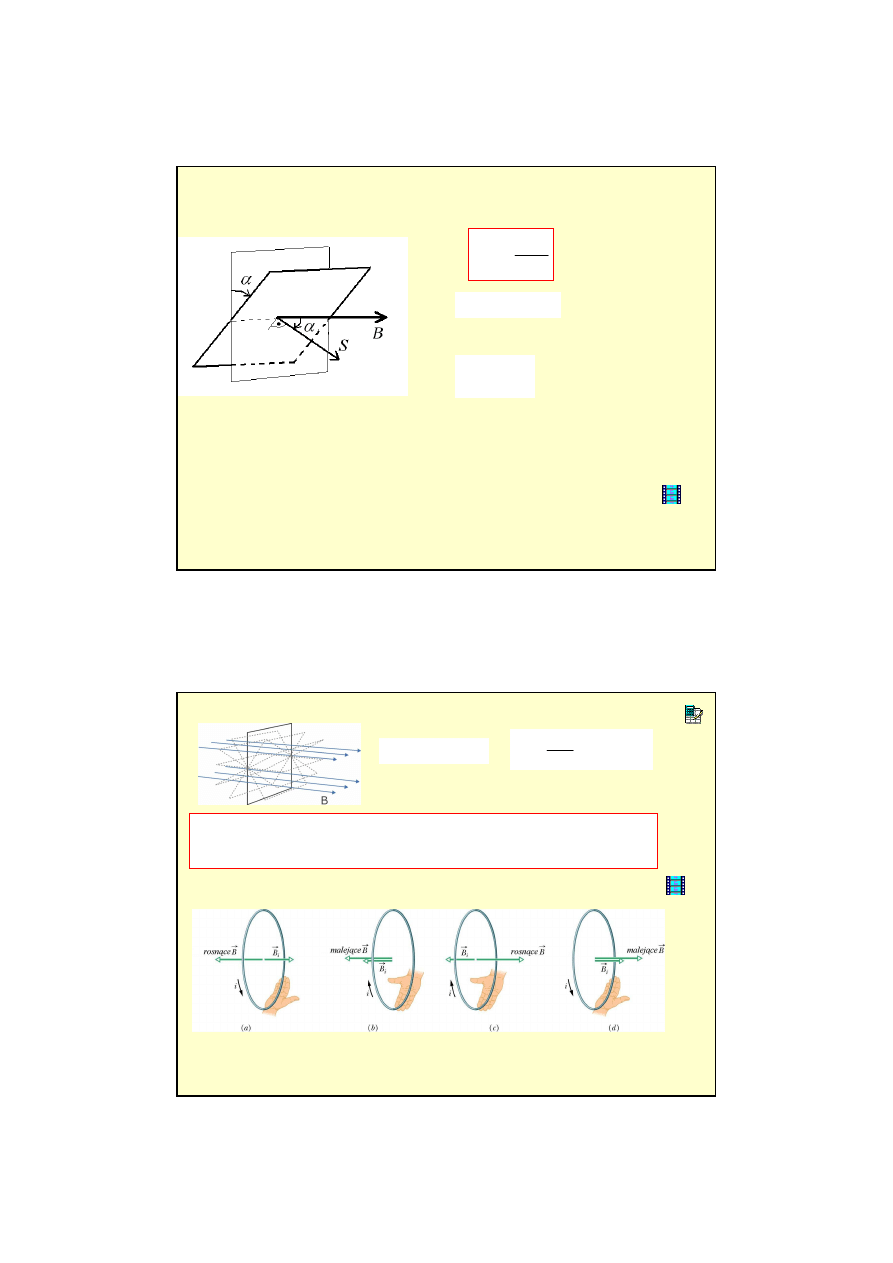
Prawo indukcji Faradaya

2

Na podstawie do

ś

wiadcze

ń

Faraday doszedł do wniosku,

ż

e o powstawaniu siły

elektromotorycznej indukcji decyduje szybko

ść

zmian strumienia magnetycznego

φ

B

dt

dφ

ε

B

−

=

strumie

ń

pola

magnetycznego

B

przez

powierzchni

ę

S

∫

=

S

B

dS

B

φ

α

φ

cos

BS

B

=

ogólnie

Strumie

ń

magnetyczny mo

ż

na zmieni

ć

:

1. zmieniaj

ą

c warto

ść

pola magnetycznego w obszarze, w którym

znajduje si

ę

przewodnik,

2. zmieniaj

ą

c wielko

ś

ci powierzchni S obwodu,

3. poprzez obrót obwodu w polu magnetycznym.

t

BS

B

ω

φ

cos

=

t

ω

ω

B

dt

dφ

ε

B

sin

=

−

=

W równaniu przedstawiaj

ą

cym prawo Faradaya wyst

ę

puje znak minus.

Kierunek pr

ą

du indukowanego w p

ę

tli i wytwarzanego przez niego pola

magnetycznego zale

ż

y od tego czy strumie

ń

pola magnetycznego ro

ś

nie czy maleje.

Reguła Lenza

Pr

ą

d indukowany ma taki kierunek,

ż

e wytwarzany przez niego własny

strumie

ń

magnetyczny przeciwdziała pierwotnym zmianom strumienia, które

go wywołały.

3

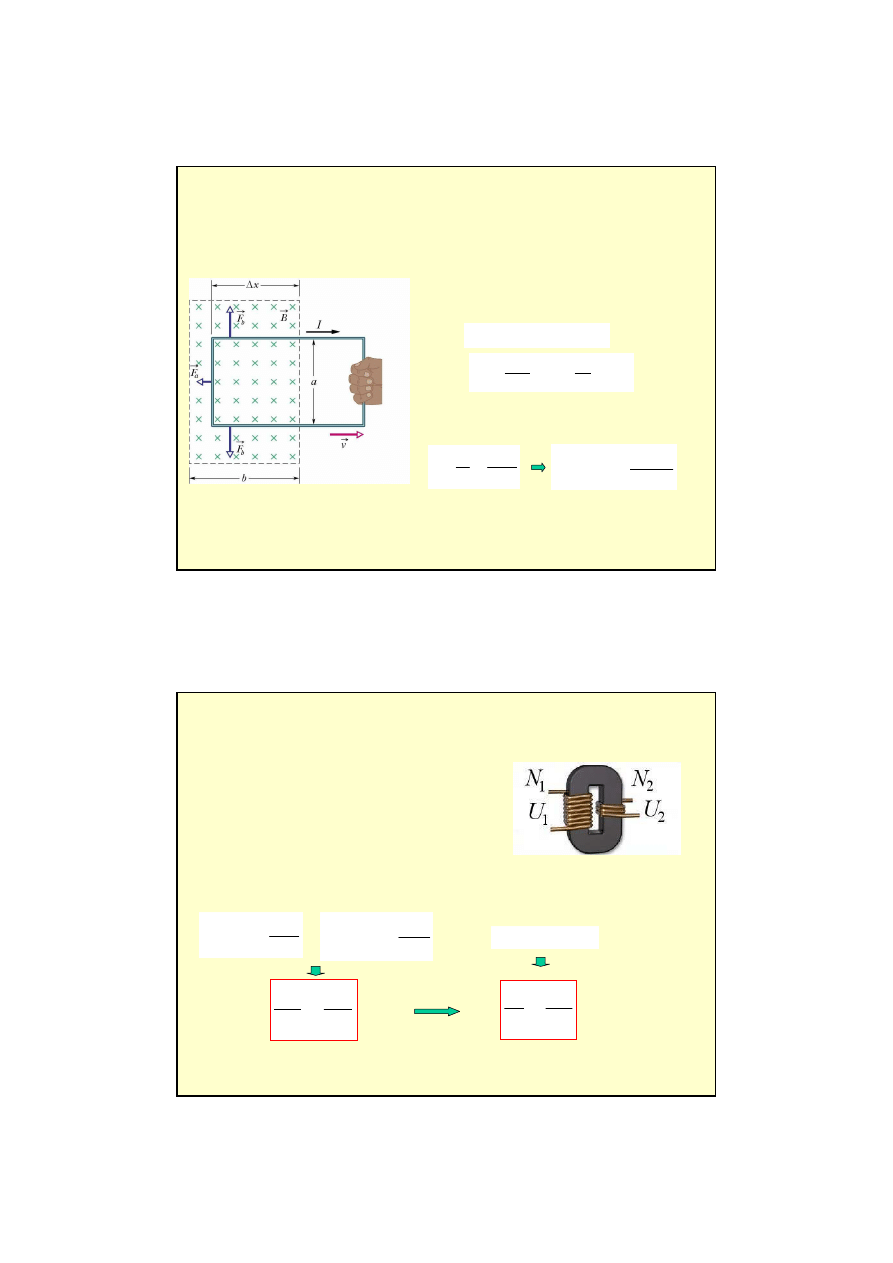
Przykład

Obwód w kształcie prostok

ą

tnej p

ę

tli jest wyci

ą

gany z obszaru stałego pola

magnetycznego (prostopadłego do p

ę

tli) ze stał

ą

pr

ę

dko

ś

ci

ą

v.

Je

ż

eli ramka przesuwa si

ę

o odcinek

∆x

to

obszar ramki o powierzchni

∆S

wysuwa si

ę

z

pola B i strumie

ń

przenikaj

ą

cy przez ramk

ę

maleje.

x

Ba

S

B

∆

=

∆

=

∆

φ

Bav

dt

dx

Ba

dt

dφ

ε

B

=

−

=

−

=

R

Bav

R

ε

I

=

=

ramka jest wykonana z przewodnika o oporze R

Siły (

F

b

) działaj

ą

ce na dłu

ż

sze boki ramki znosz

ą

si

ę

i pozostaje nieskompensowana

siła

F

a

, która działa przeciwnie do kierunku ruchu ramki i zgodnie z reguł

ą

Lenza,

przeciwdziała zmianom strumienia magnetycznego.

R

v

a

B

BIa

F

a

2

2

=

=

Indukcja elektromagnetyczna –przykład
zastosowania

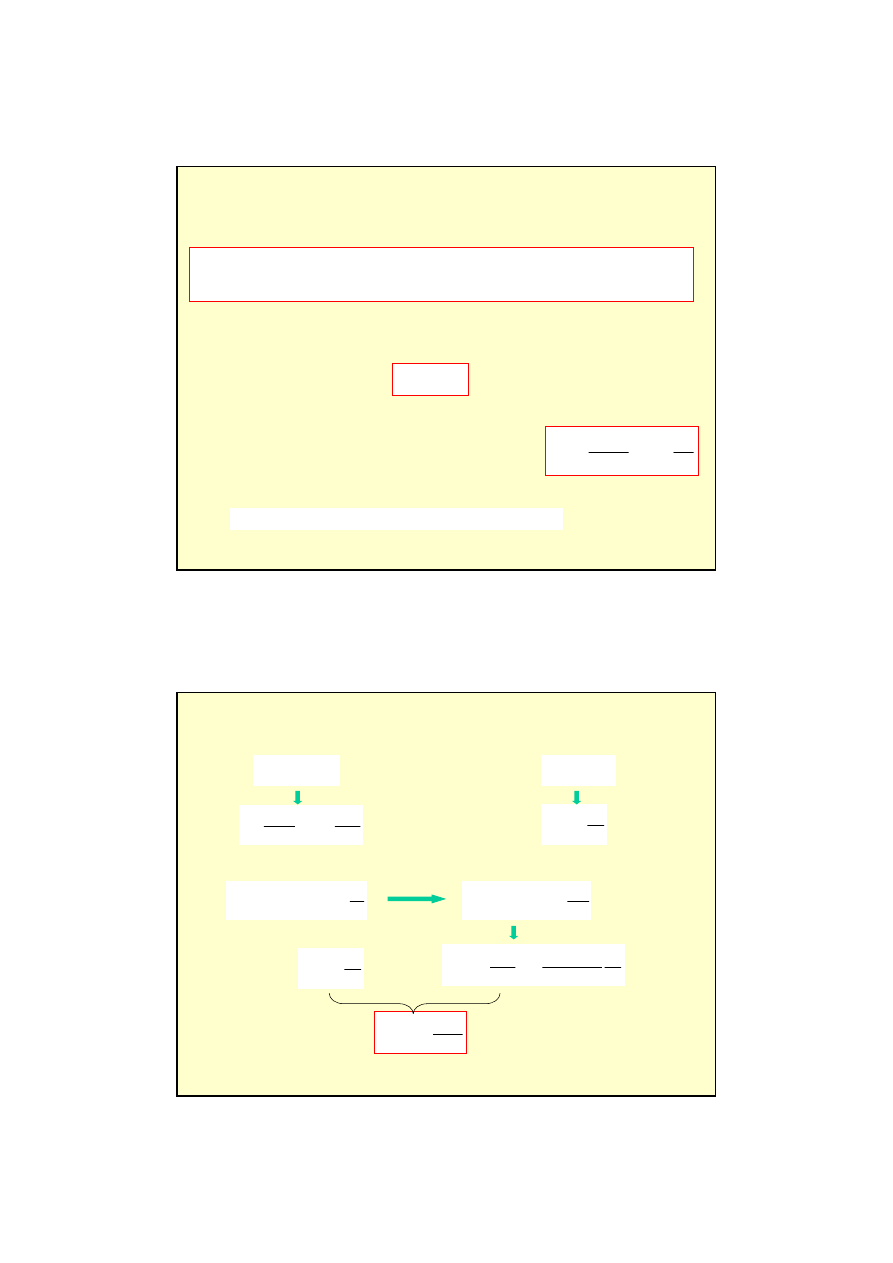
Transformator

Dwie cewki s

ą

nawini

ę

te na tym samym rdzeniu.

Jedna z cewek jest zasilana pr

ą

dem przemiennym

wytwarzaj

ą

cym w niej zmienne pole magnetyczne,

które z kolei wywołuje SEM indukcji w drugiej cewce.

Reguluj

ą

c ilo

ść

zwojów w cewkach mo

ż

emy zamienia

ć

małe napi

ę

cia na du

ż

e i

odwrotnie

Poniewa

ż

obie cewki obejmuj

ą

te same linie pola B to zmiana strumienia

magnetycznego jest w nich jednakowa.

dt

dφ

N

U

B

1

1

−

=

dt

dφ

N

U

B

2

2

−

=

1

2

1

2

N

N

U

U

=

2

2

1

1

I

U

I

U

=

1

2

2

1

N

N

I

I

=

4

Pr

ą

d płyn

ą

cy w obwodzie wytwarza strumie

ń

magnetyczny, który przenika przez ten

obwód.

LI

cał

=

φ

Całkowitym strumie

ń

jest proporcjonalny do nat

ęż

enia pr

ą

du pyn

ą

cego

przez obwód

L

- indukcyjno

ść

(współczynnik samoindukcji).

Indukcyjno

ść

własna

Gdy nat

ęż

enie pr

ą

du przepływaj

ą

cego przez obwód zmienia si

ę

to zmienia si

ę

te

ż

, wytworzony przez ten pr

ą

d, strumie

ń

pola magnetycznego przenikaj

ą

cy

obwód, wi

ę

c zgodnie z prawem indukcji Faradaya indukuje si

ę

w obwodzie SEM.

SEM wyindukowan

ą

przez zmienny pr

ą

d płyn

ą

cy przez

obwód nazywamy sił

ą

elektromotoryczn

ą

samoindukcji,

a samo zjawisko zjawiskiem indukcji własnej.

dt

dI

L

dt

d

ε

cał

−

=

−

=

ϕ

Jednostk

ą

indukcyjno

ś

ci L jest henr (H); 1 H = 1 Vs/A.

Obliczamy indukcyjno

ść

cewki o długo

ś

ci

l

, przekroju poprzecznym

S

i

N

zwojach,

przez któr

ą

płynie pr

ą

d o nat

ęż

eniu

I

.

Indukcyjno

ść

mo

ż

na zwi

ę

kszy

ć

wprowadzaj

ą

c do cewki rdze

ń

z materiału

o du

ż

ej wzgl

ę

dnej przenikalno

ś

ci magnetycznej

µ

r

(np. z

ż

elaza)

dla cewki o N zwojach strumie

ń

jest N razy wi

ę

kszy ni

ż

dla pojedynczego zwoju !

Strumie

ń

magnetyczny przez ka

ż

dy zwój cewki wynosi:

l

N

I

nI

B

r

r

0

0

µ

µ

µ

µ

=

=

l

NS

I

BS

r

B

0

µ

µ

ϕ

=

=

dt

dI

l

S

N

dt

dφ

N

ε

r

B

2

0

µ

µ

−

=

−

=

Indukcyjno

ść

L

(podobnie jak pojemno

ść

C

)

zale

ż

y tylko od geometrii układu

l

S

N

L

r

2

0

µ

µ

=

dt

dI

L

−

=

ε

dt

dI

L

−

=

ε

LI

cał

=

φ

dt

dφ

N

dt

dφ

ε

B

cał

−

=

=

B

cał

N

φ

φ

=

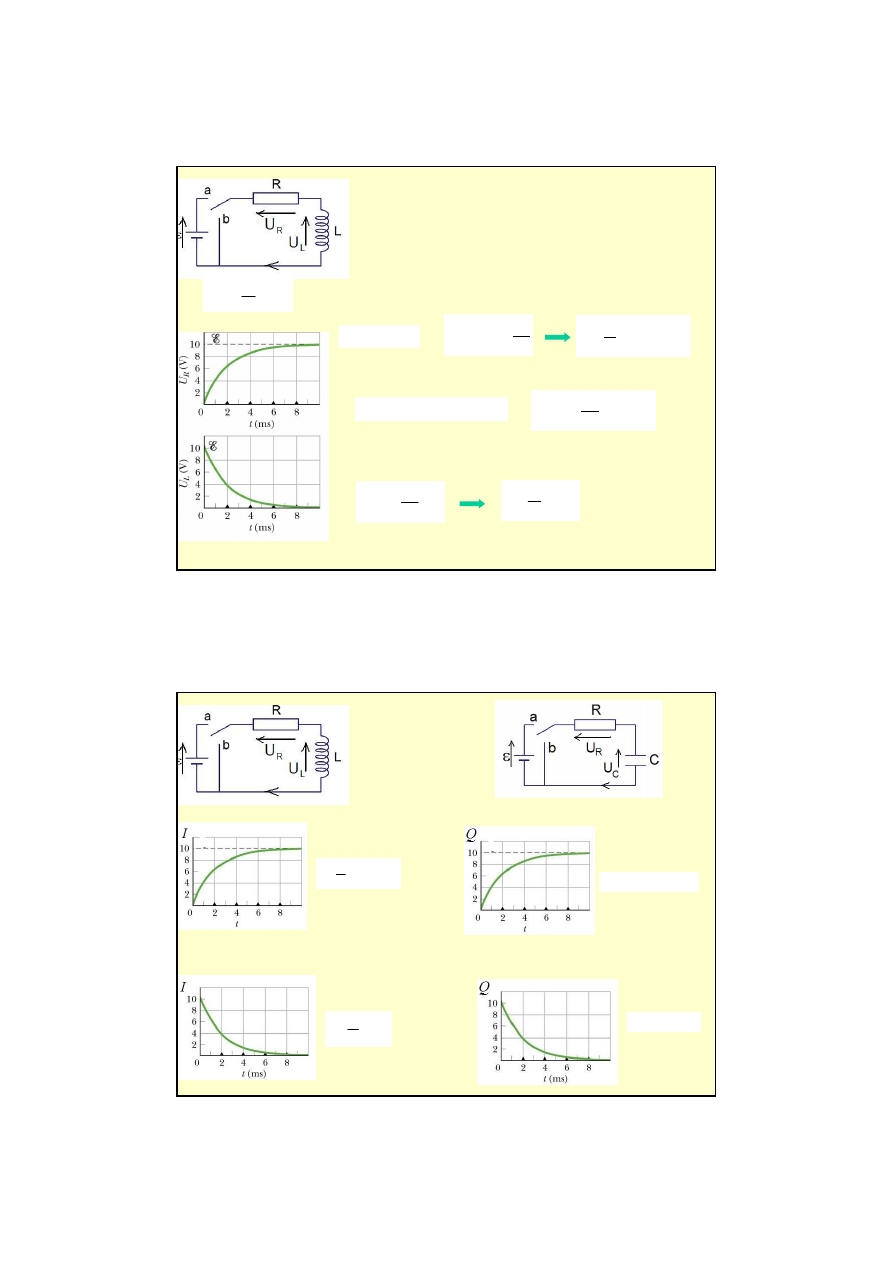
5

W obwodzie RL opó

ź

nienie w narastaniu i zanikaniu

pr

ą

du przy wł

ą

czaniu lub wył

ą

czaniu

ź

ródła SEM.

L

R

U

U

+

=

ε

przeł

ą

cznik w pozycji (a)

dt

dI

L

IR

ε

+

=

)

1

(

/ L

Rt

e

R

I

−

−

=

ε

Pr

ą

d w obwodzie narasta ze stał

ą

czasow

ą

t =R/L.

)

(

/ L

Rt

R

e

IR

U

−

−

=

=

1

ε

Rt/L

L

e

ε

dt

dI

L

U

−

=

=

przeł

ą

cznik w pozycji (b)

0

=

+

dt

dI

L

IR

L

Rt

e

R

I

/

−

= ε

Obserwujemy zanik pr

ą

du, ponownie ze stał

ą

czasow

ą

τ

=R/L

Obwód RL

L

U

dt

dI

L

ε

−

=

−

=

przeł

ą

cznik w pozycji (a)

)

1

(

/ L

Rt

e

R

I

−

−

=

ε

przeł

ą

cznik w pozycji (b)

L

Rt

e

R

I

/

−

=

ε

Obwód RL

Obwód RC

)

1

(

/ RC

t

e

C

Q

−

−

=

ε

RC

t

e

C

Q

/

−

=

ε

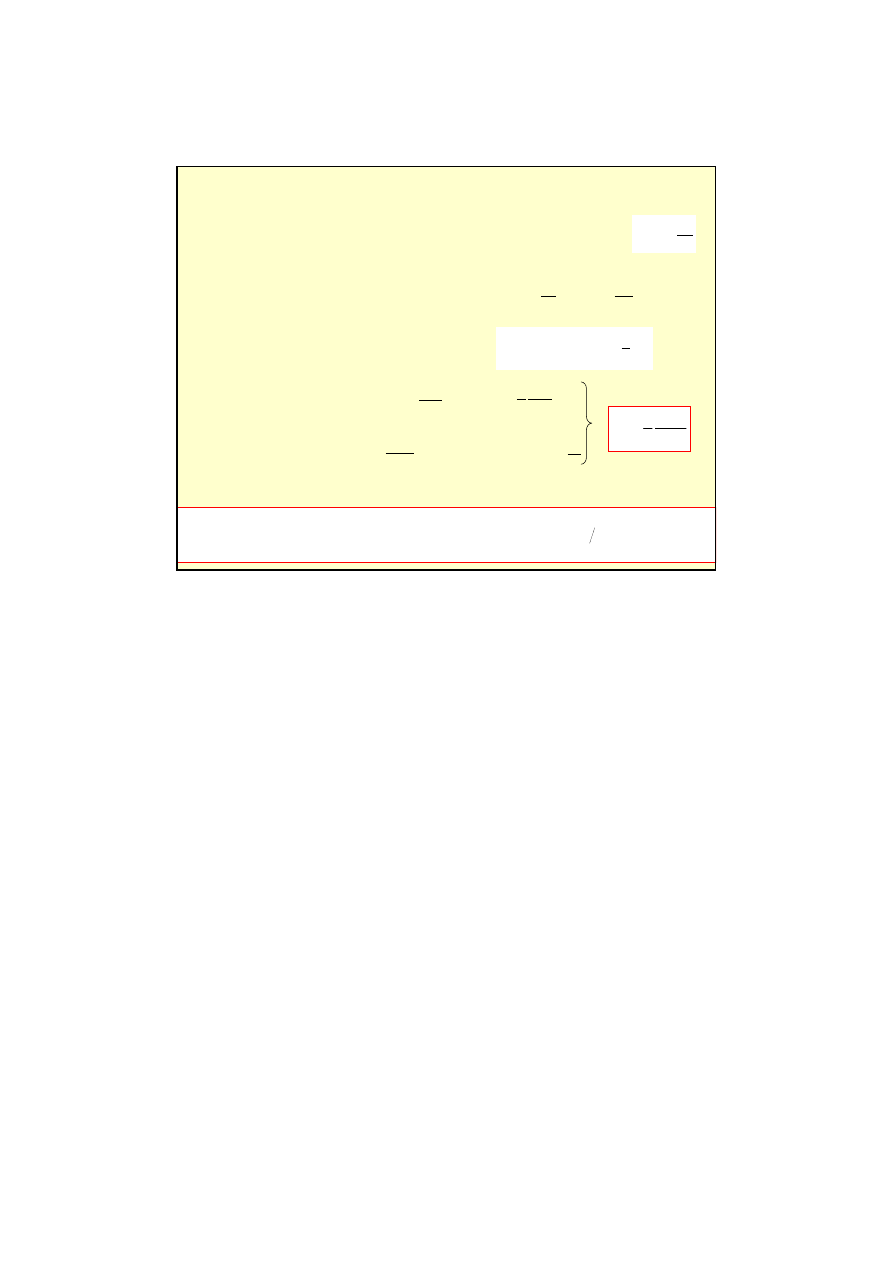
6

Zmiana pr

ą

du w obwodzie zawieraj

ą

cym cewk

ę

o indukcyjno

ś

ci L

powoduje powstanie na ko

ń

cach cewki ró

ż

nicy potencjałów U

L

.

dt

dI

L

U

L

=

dI

LI

t

d

q

d

dI

L

dq

t

d

dI

L

dq

U

dW

L

=

=

=

=

Do pokonania tej ró

ż

nicy

potencjałów przez ładunek

dq

potrzeba jest energia (praca)

dW

Całkowita energia magnetyczna zgromadzona w
cewce podczas narastania pr

ą

du od zera do

I

2

0

2

1

d

d

LI

I

LI

W

W

I

B

=

=

=

∫

∫

lS

W

w

B

B

=

lS

LI

w

B

2

2

1

=

g

ę

sto

ść

energii

l

- długo

ś

ci cewki

S

- powierzchnia

przekroju

l

S

N

L

r

2

0

µ

µ

=

l

N

I

nI

B

r

r

0

0

µ

µ

µ

µ

=

=

Energia pola magnetycznego

Je

ż

eli w jakim

ś

punkcie przestrzeni istnieje pole magnetyczne o indukcji B to mo

ż

emy

uwa

ż

a

ć

,

ż

e w tym punkcie jest zmagazynowana energia w ilo

ś

ci

na jednostk

ę

obj

ę

to

ś

ci.

0

2

2

µ

B

0

2

2

1

µ

µ

r

B

B

w

=