1
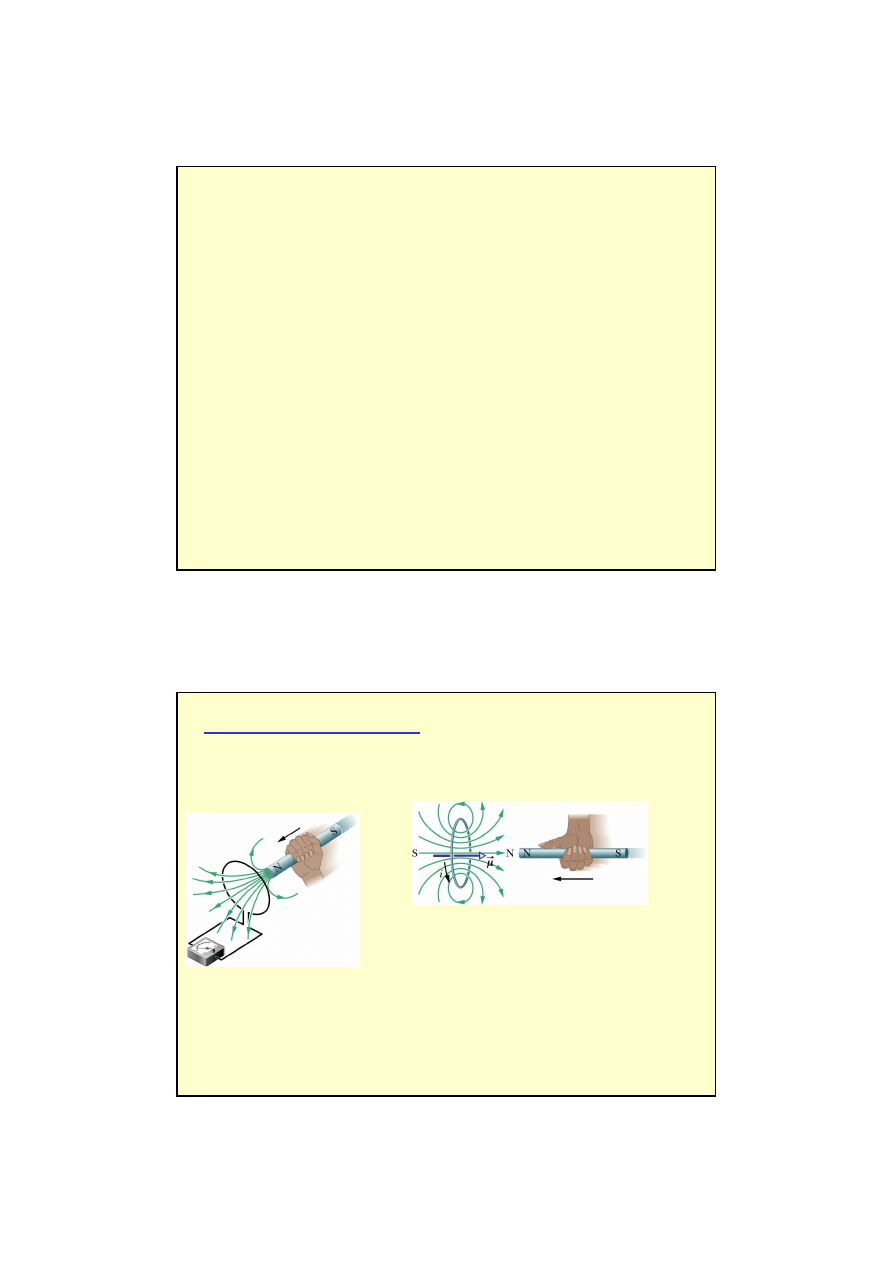
Indukcja elektromagnetyczna
Zjawisko indukcji elektromagnetycznej polega na powstawaniu siły elektromotorycznej
SEM w obwodzie podczas przemieszczania si
ę
wzgl
ę
dem siebie
ź
ródła pola
magnetycznego i tego obwodu.
W obwodzie zamkni
ę
tym SEM indukcji wywołuje
przepływ pr
ą
du indukcyjnego i w konsekwencji
powstanie wytwarzanego przez ten pr
ą
d
indukowanego pola magnetycznego.
Indukowane: siła elektromotoryczna, pr
ą
d i pole magnetyczne powstaj
ą
w obwodzie
tylko podczas ruchu magnesu.
Dla powstania pr
ą
du indukcyjnego potrzebny jest wzgl
ę
dny ruch
ź
ródła
pola magnetycznego i przewodnika.
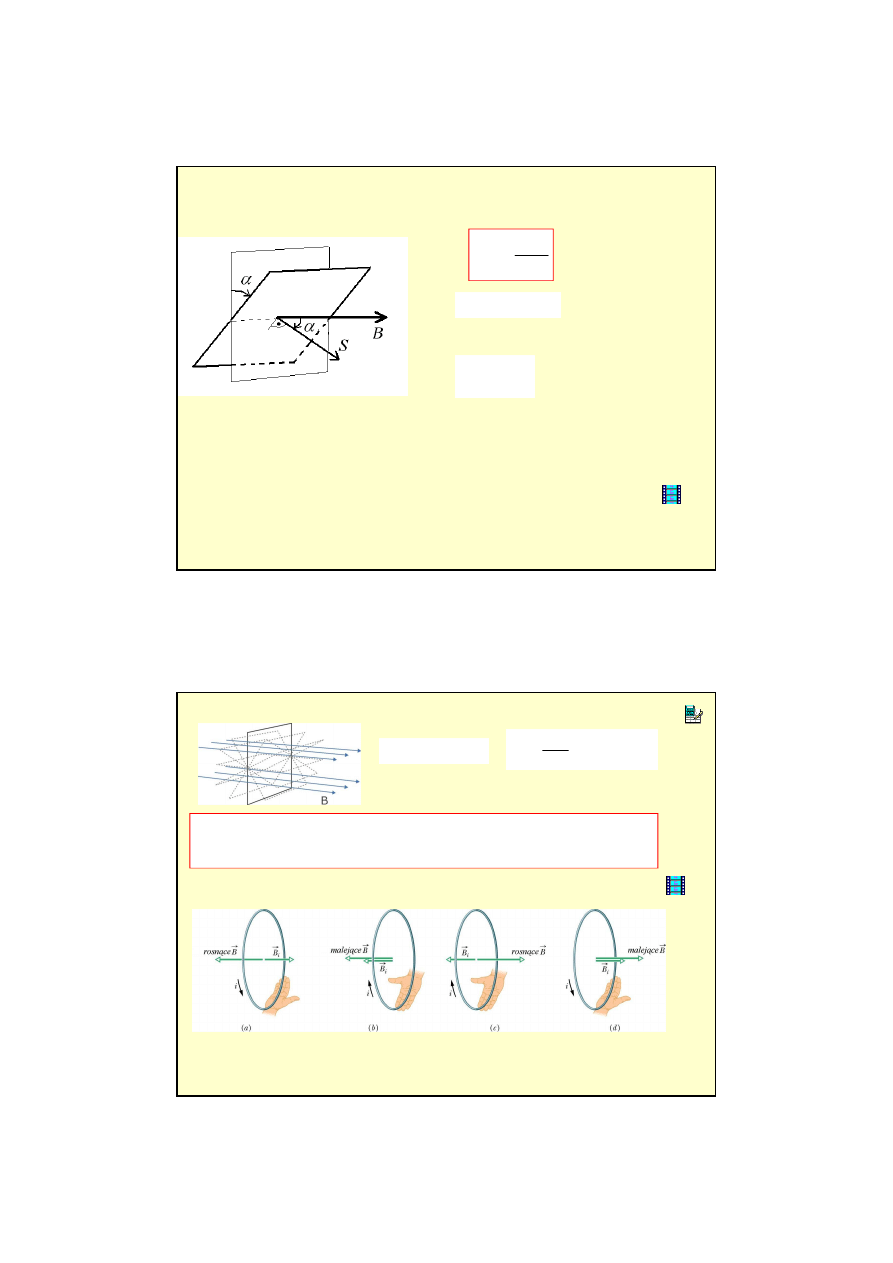
Prawo indukcji Faradaya
2
Na podstawie do
ś
wiadcze
ń
Faraday doszedł do wniosku,
ż
e o powstawaniu siły
elektromotorycznej indukcji decyduje szybko
ść
zmian strumienia magnetycznego
φ
B
dt
dφ
ε
B
−
=
strumie
ń
pola
magnetycznego
B
przez
powierzchni
ę
S
∫
=
S
B
dS
B
φ
α
φ
cos
BS
B
=
ogólnie
Strumie
ń
magnetyczny mo
ż
na zmieni
ć
:
1. zmieniaj
ą
c warto
ść
pola magnetycznego w obszarze, w którym
znajduje si
ę
przewodnik,
2. zmieniaj
ą
c wielko
ś
ci powierzchni S obwodu,
3. poprzez obrót obwodu w polu magnetycznym.
t
BS
B
ω
φ
cos
=
t
ω
ω
BS
dt
dφ
ε
B
sin
=
−
=
W równaniu przedstawiaj
ą
cym prawo Faradaya wyst
ę
puje znak minus.
Kierunek pr
ą
du indukowanego w p
ę
tli i wytwarzanego przez niego pola
magnetycznego zale
ż
y od tego czy strumie
ń
pola magnetycznego ro
ś
nie czy maleje.
Reguła Lenza
Pr
ą
d indukowany ma taki kierunek,
ż
e wytwarzany przez niego własny
strumie
ń
magnetyczny przeciwdziała pierwotnym zmianom strumienia, które
go wywołały.
3
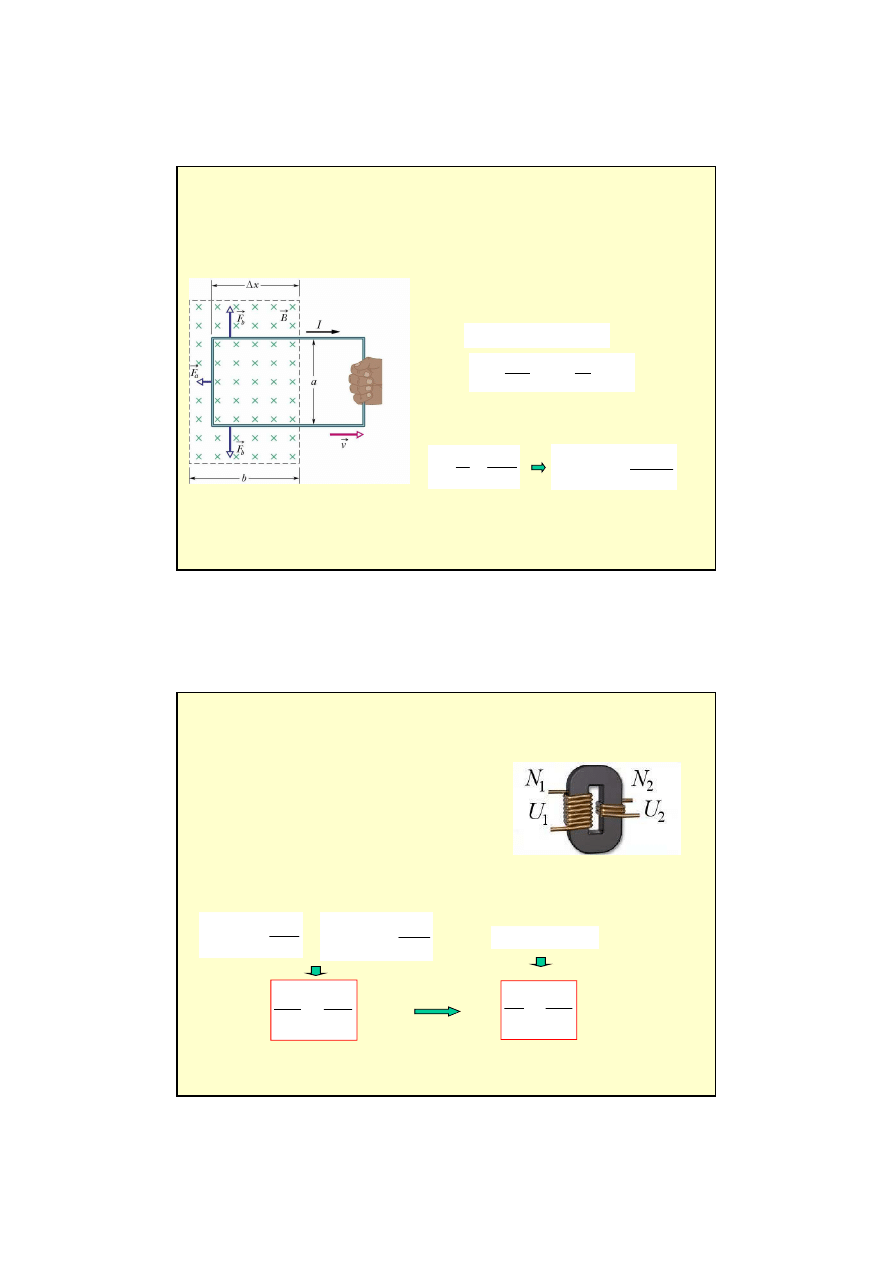
Przykład
Obwód w kształcie prostok
ą
tnej p
ę
tli jest wyci
ą
gany z obszaru stałego pola
magnetycznego (prostopadłego do p
ę
tli) ze stał
ą
pr
ę
dko
ś
ci
ą
v.
Je
ż
eli ramka przesuwa si
ę
o odcinek
∆x
to
obszar ramki o powierzchni
∆S
wysuwa si
ę
z
pola B i strumie
ń
przenikaj
ą
cy przez ramk
ę
maleje.
x
Ba
S
B
∆
=
∆
=
∆
φ
Bav
dt
dx
Ba
dt
dφ
ε
B
=
−
=
−
=
R
Bav
R
ε
I
=
=
ramka jest wykonana z przewodnika o oporze R
Siły (
F
b
) działaj
ą
ce na dłu
ż
sze boki ramki znosz
ą
si
ę
i pozostaje nieskompensowana
siła
F
a
, która działa przeciwnie do kierunku ruchu ramki i zgodnie z reguł
ą
Lenza,
przeciwdziała zmianom strumienia magnetycznego.
R
v
a
B
BIa
F
a
2
2
=
=
Indukcja elektromagnetyczna –przykład
zastosowania
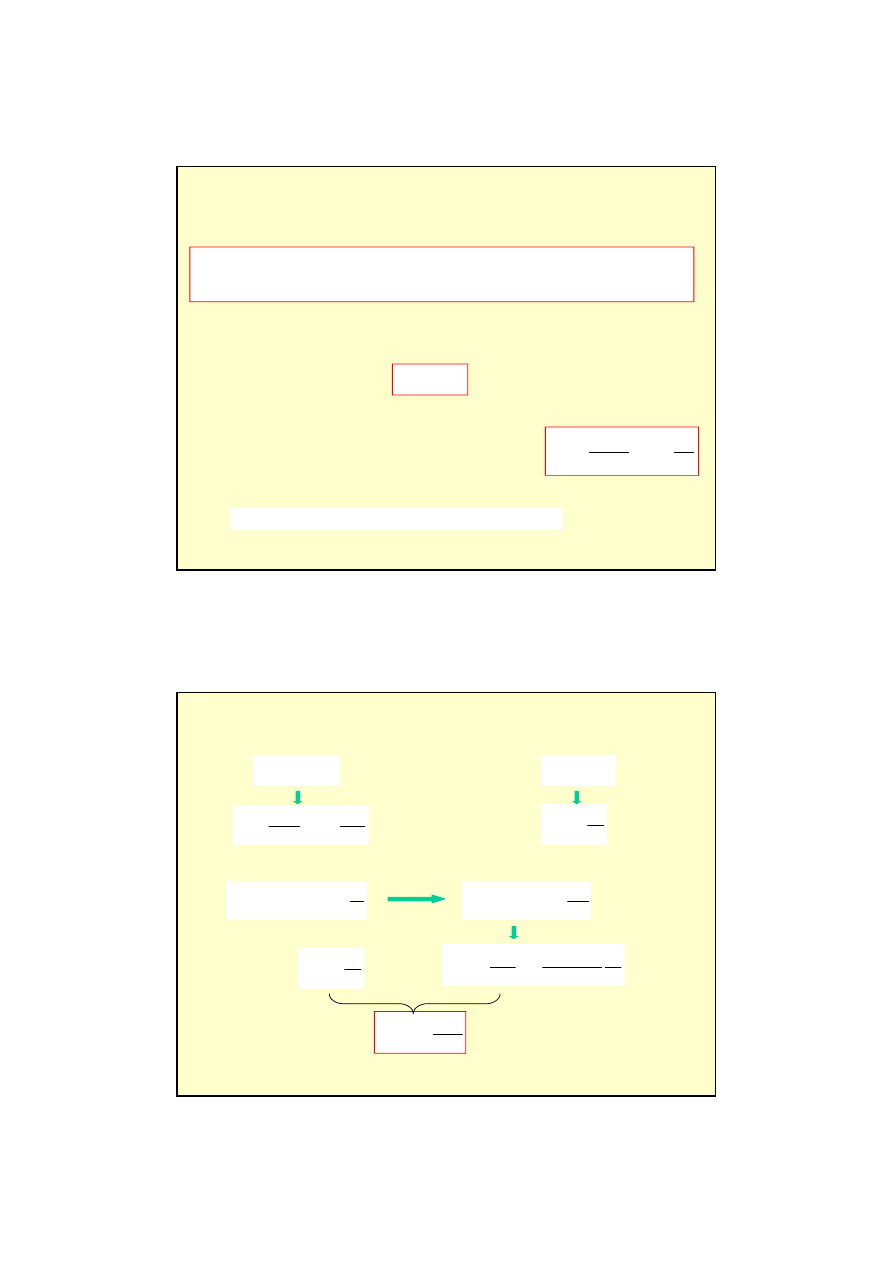
Transformator
Dwie cewki s
ą
nawini
ę
te na tym samym rdzeniu.
Jedna z cewek jest zasilana pr
ą
dem przemiennym
wytwarzaj
ą
cym w niej zmienne pole magnetyczne,
które z kolei wywołuje SEM indukcji w drugiej cewce.
Reguluj
ą
c ilo
ść
zwojów w cewkach mo
ż
emy zamienia
ć
małe napi
ę
cia na du
ż
e i
odwrotnie
Poniewa
ż
obie cewki obejmuj
ą
te same linie pola B to zmiana strumienia
magnetycznego jest w nich jednakowa.
dt
dφ
N
U
B
1
1
−
=
dt
dφ
N
U
B
2
2
−
=
1
2
1
2
N
N
U
U
=
2
2
1
1
I
U
I
U
=
1
2
2
1
N
N
I
I
=
4
Pr
ą
d płyn
ą
cy w obwodzie wytwarza strumie
ń
magnetyczny, który przenika przez ten
obwód.
LI
cał
=
φ
Całkowitym strumie
ń
jest proporcjonalny do nat
ęż
enia pr
ą
du pyn
ą
cego
przez obwód
L
- indukcyjno
ść
(współczynnik samoindukcji).
Indukcyjno
ść
własna
Gdy nat
ęż
enie pr
ą
du przepływaj
ą
cego przez obwód zmienia si
ę
to zmienia si
ę
te
ż
,
wytworzony przez ten pr
ą
d, strumie
ń
pola magnetycznego przenikaj
ą
cy obwód,
wi
ę
c zgodnie z prawem indukcji Faradaya indukuje si
ę
w obwodzie SEM.
SEM wyindukowan
ą
przez zmienny pr
ą
d płyn
ą
cy przez
obwód nazywamy sił
ą
elektromotoryczn
ą
samoindukcji,
a samo zjawisko zjawiskiem indukcji własnej.
dt
dI
L
dt
d
ε
cał
−
=
−
=
ϕ
Jednostk
ą
indukcyjno
ś
ci L jest henr (H); 1 H = 1 Vs/A.
Obliczamy indukcyjno
ść
cewki o długo
ś
ci
l
, przekroju poprzecznym
S
i
N
zwojach,
przez któr
ą
płynie pr
ą
d o nat
ęż
eniu
I
.
Indukcyjno
ść
mo
ż
na zwi
ę
kszy
ć
wprowadzaj
ą
c do cewki rdze
ń
z materiału o du
ż
ej
wzgl
ę
dnej przenikalno
ś
ci magnetycznej
µ
r
(np. z
ż
elaza).
dla cewki o N zwojach strumie
ń
jest N razy wi
ę
kszy ni
ż
dla pojedynczego zwoju !
Strumie
ń
magnetyczny przez ka
ż
dy zwój cewki wynosi:
l
N
I
nI
B
r
r
0
0
µ
µ
µ
µ
=
=
l
NS
I
BS
r
B
0
µ
µ
ϕ
=
=
dt
dI
l
S
N
dt
dφ
N
ε
r
B
2
0
µ
µ
−
=
−
=
Indukcyjno
ść
L
(podobnie jak pojemno
ść
C
)
zale
ż
y tylko od geometrii układu
przenikalno
ś
ci magnetycznej
µ
r
.
l
S
N
L
r
2
0
µ
µ
=
dt
dI
L
−
=
ε
dt
dI
L
−
=
ε
LI
cał
=
φ
dt
dφ
N
dt
dφ
ε
B
cał
−
=
−
=
B
cał
N
φ
φ
=
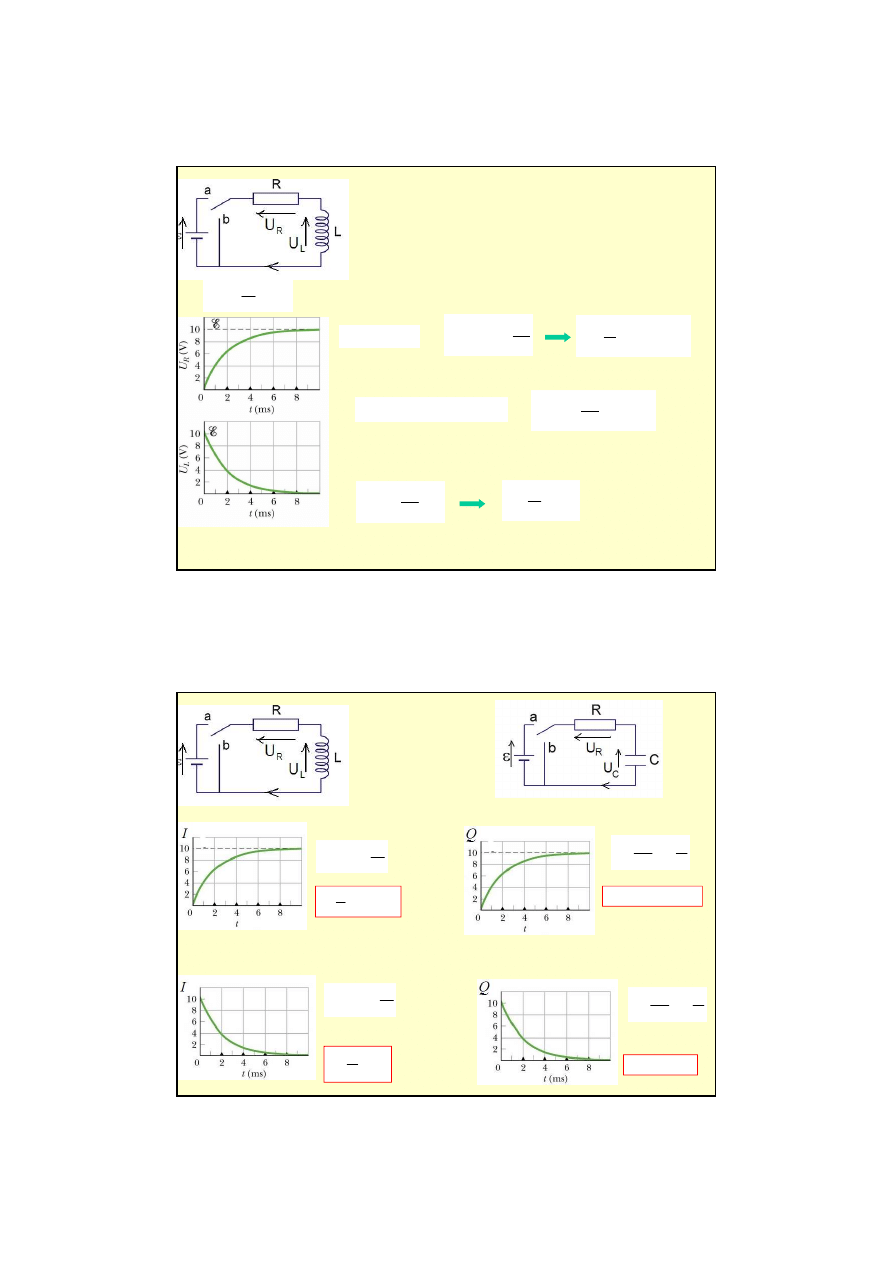
5
W obwodzie RL opó
ź
nienie w narastaniu i zanikaniu
pr
ą
du przy wł
ą
czaniu lub wył
ą
czaniu
ź
ródła SEM.
L
R
U
U
+
=
ε
przeł
ą
cznik w pozycji (a)
dt
dI
L
IR
ε
+
=
)
1
(
/ L
Rt
e
R
I
−
−
=
ε
Pr
ą
d w obwodzie narasta ze stał
ą
czasow
ą
t =R/L.
)
(
/ L
Rt
R
e
IR
U
−
−
=
=
1
ε
Rt/L
L
e
ε
dt
dI
L
U
−
=
=
przeł
ą
cznik w pozycji (b)
0
=
+
dt
dI
L
IR
L
Rt
e
R
I
/
−
= ε
Obserwujemy zanik pr
ą
du, ponownie ze stał
ą
czasow
ą
τ
=R/L
Obwód RL
L
U
dt
dI
L
ε
−
=
−
=
przeł
ą
cznik w pozycji (a)
)
1
(
/ L
Rt
e
R
I
−
−
=
ε
Obwód RL
Obwód RC
)
1
(
/ RC
t
e
C
Q
−
−
=
ε
C
Q
R
dt
dQ
+
=
ε
dt
dI
L
IR
ε
+
=
przeł
ą
cznik w pozycji (b)
L
Rt
e
R
I
/
−
=
ε
RC
t
e
C
Q
/
−
=
ε
dt
dI
L
IR
+
=
0
C
Q
R
dt
dQ
+
=
0
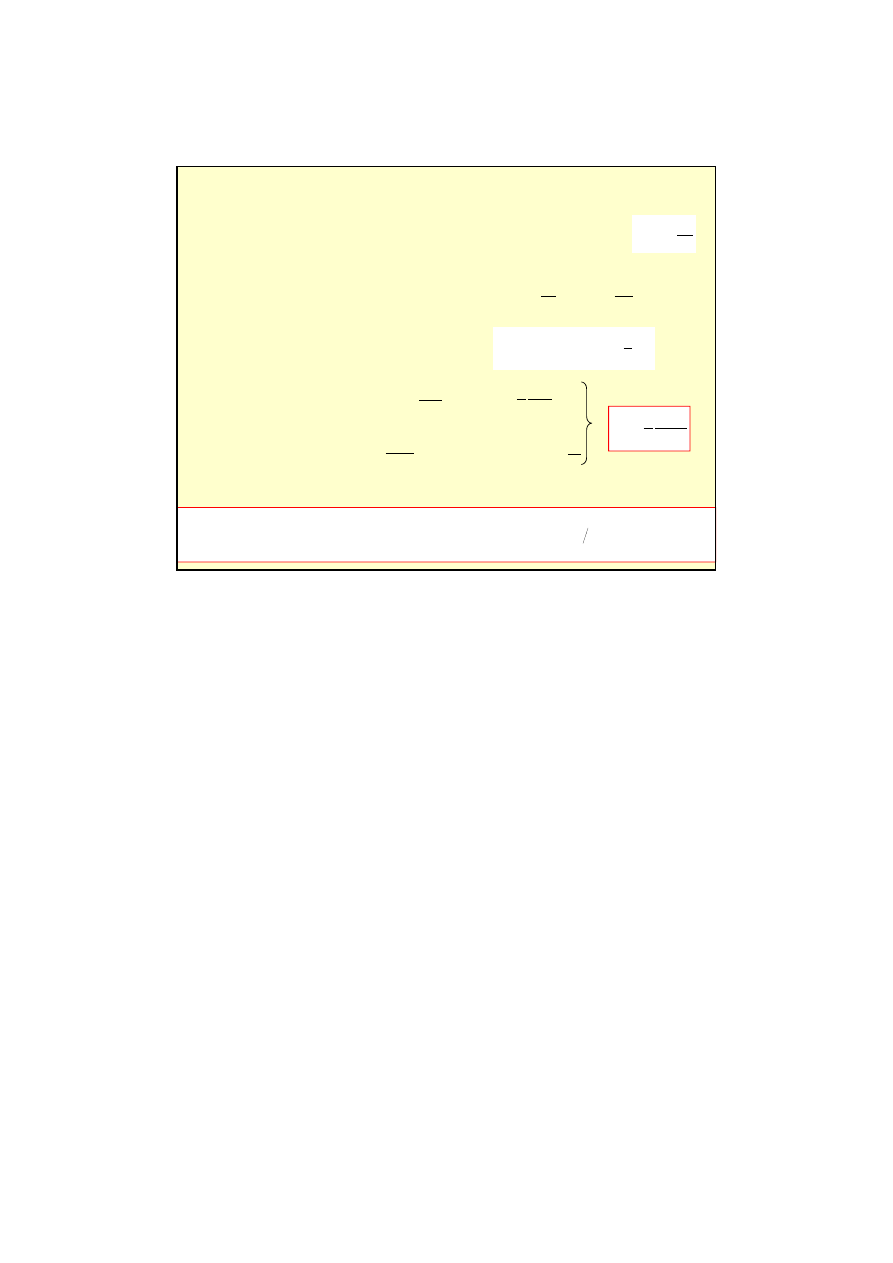
6
Zmiana pr
ą
du w obwodzie zawieraj
ą
cym cewk
ę
o indukcyjno
ś
ci L
powoduje powstanie na ko
ń
cach cewki ró
ż
nicy potencjałów U
L
.
dt
dI
L
U
L
=
dI
LI
t
d
q
d
dI
L
dq
t
d
dI
L
dq
U
dW
L
=
=
=
=
Do pokonania tej ró
ż
nicy
potencjałów przez ładunek
dq
potrzeba jest energia (praca)
dW
Całkowita energia magnetyczna zgromadzona w
cewce podczas narastania pr
ą
du od zera do
I
2
0
2
1
'
d
'
d
LI
I
LI
W
W
I
B
=
=
=
∫
∫
lS
W
w
B
B
=
lS
LI
w
B
2
2
1
=
g
ę
sto
ść
energii
l
- długo
ś
ci cewki
S
- powierzchnia
przekroju
l
S
N
L
r
2
0
µ
µ
=
l
N
I
nI
B
r
r
0
0
µ
µ
µ
µ
=
=
Energia pola magnetycznego
Je
ż
eli w jakim
ś
punkcie przestrzeni istnieje pole magnetyczne o indukcji B to mo
ż
emy
uwa
ż
a
ć
,
ż
e w tym punkcie jest zmagazynowana energia w ilo
ś
ci
na jednostk
ę
obj
ę
to
ś
ci.
r
B
µ
µ
0
2
2
0
2
2
1
µ
µ
r
B
B
w
=
Wyszukiwarka
Podobne podstrony:
14 indukcja elektromagnetycznai Nieznany (2)
14 indukcja elektromagnetyczna (2)
22 Pole magnetyczne, indukcja elektromagnetyczna
14?le elektromagnetyczne
4 indukcja elektromagnetyczna
Cw 11 Zjawisko Indukcji Elektromagnetycznej
22 pole magnetyczne, indukcja elektromagnetyczna
fizyka.org, indukcja elektromagnetyczna, Fizyka - Zadania - Indukcja elektromagnetyczna
Indukcja elektromagnetyczna id Nieznany
II 4 Indukcja elektromagnetyczna
3 2 Indukcja elektromagnetyczna 22 (2)
Zjawisko indukcji elektromagnetycznej, Studia
Egzamin - sciagi, 17. Zjawisko indukcji elektromagnetycznej, 17
więcej podobnych podstron