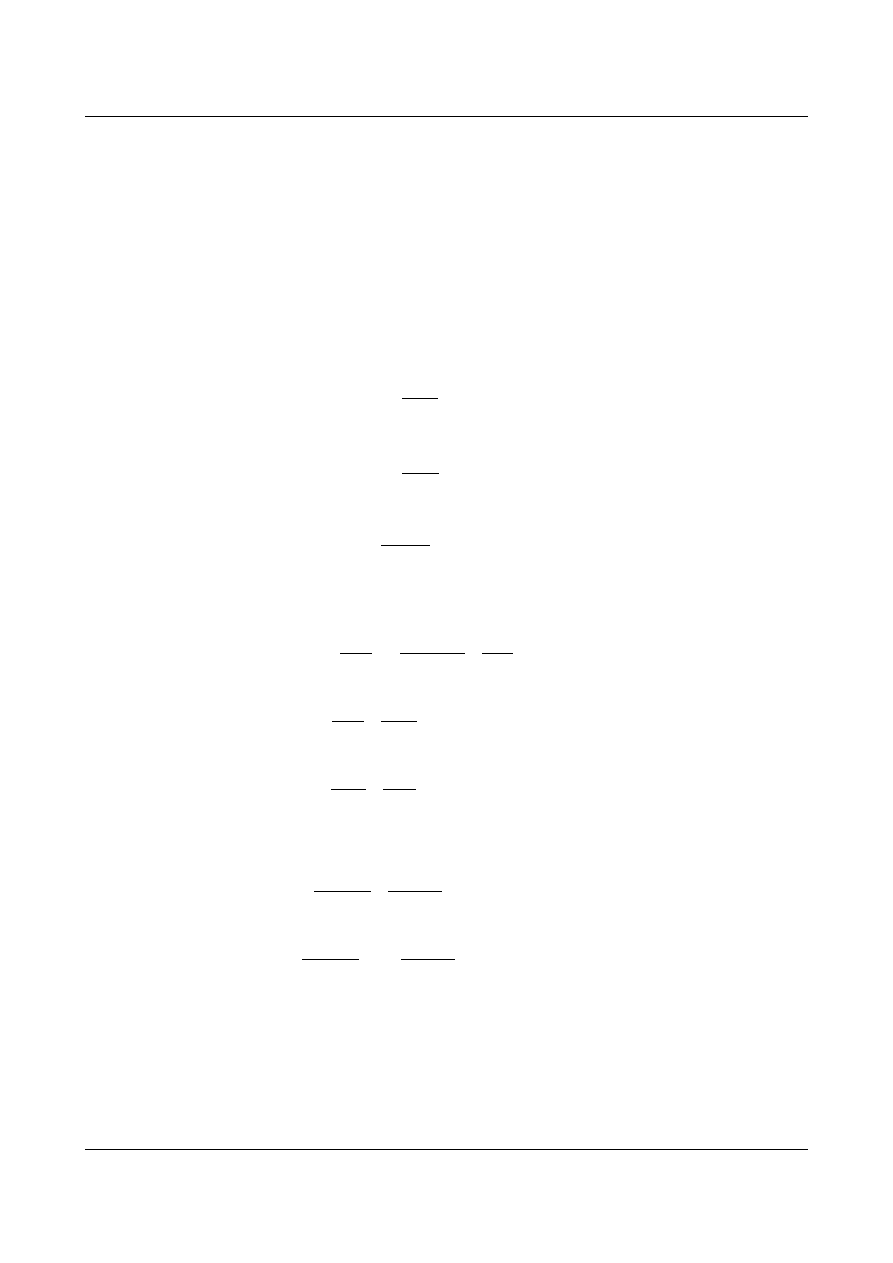
10. ROZWIĄZYWANIE ZADAŃ Z TEORII SPRĘŻYSTOŚCI

1

10.



10. ROZWIĄZYWANIE ZADAŃ Z TEORII SPRĘŻYSTOŚCI

10.1. Zastosowanie funkcji Airy'ego

∇

2





x



y



=0

(10.1)

Zakładamy, że istnieje funkcja F(x,y) spełniająca następujące warunki (przy założeniu p

x

=0 oraz

istnienia siły masowej skierowanej przeciwnie do osi Y):



x

= ∂

2

F

∂ y

2

(10.2)



y

= ∂

2

F

∂ x

2

(10.3)



xy

= ∂

2

F

∂ x ∂ y

qx

(10.4)

∇

4

F



x , y



=0

(10.5)

∇

4

≡ ∂

4

∂ x

4

2

∂

4

∂ x

2

∂ y

2

 ∂

4

∂ y

4

(10.6)

∂

x

∂

x



∂

xy

∂ y

 p

x

=0

(10.7)

∂

xy

∂ x



∂

y

∂ y

 p

y

=0

(10.8)

Sprawdzamy czy funkcja Airy'ego spełnia te warunki.

∂

3

F

∂ y

2

∂ x

− ∂

3

F

∂ x ∂ y

2

−q=0

(10.9)

−∂

3

F

∂ x

2

∂ y

q ∂

3

F

∂ x ∂ y

2

−q=0

(10.10)

Aściukiewicz P., Baron P., Gawron U., Krzysztoń A., Ratajczak D., Wojciechowski M.

AlmaMater

10. ROZWIĄZYWANIE ZADAŃ Z TEORII SPRĘŻYSTOŚCI

2

Zadanie 1.

Znaleźć stan naprężeń w dowolnym punkcie tarczy.

Rys.10.1. Rysunek do zadania 1.

Przyjmujemy taką funkcję by spełniała równania biharmoniczne – warunek konieczny.

F



x , y



=ax

2

bxycy

2

(10.11)

Warunek dostateczny:



x

= ∂

2

F

∂ y

2

=2 c

(10.12)



y

= ∂

2

F

∂ x

2

=2 a

(10.13)



xy

=−b

(10.14)

Warunki brzegowe:

1

x

=l

−h  yh

(10.15)



x

= p

x



xy

= p

(10.16)

2 c

= p

−b= p

(10.17)

Aściukiewicz P., Baron P., Gawron U., Krzysztoń A., Ratajczak D., Wojciechowski M.

AlmaMater

p

x

p

y

p

y

p

x

x

y

h

1

l

l

h

10. ROZWIĄZYWANIE ZADAŃ Z TEORII SPRĘŻYSTOŚCI

3

c

=

p

x

2

b

=− p

(10.18)

2

x

=−l

−h ∢ y∢h

(10.19)



x

= p

x



xy

= p

(10.20)

Warunki zgodne.

3

y

=−l

−h∢x∢h

(10.21)



y

= p

y



xy

= p

(10.22)

a

=

p

y

2

b

=− p

(10.23)

F

=

1
2

p

y

x

2

− p xy p

x

y

2

(10.24)

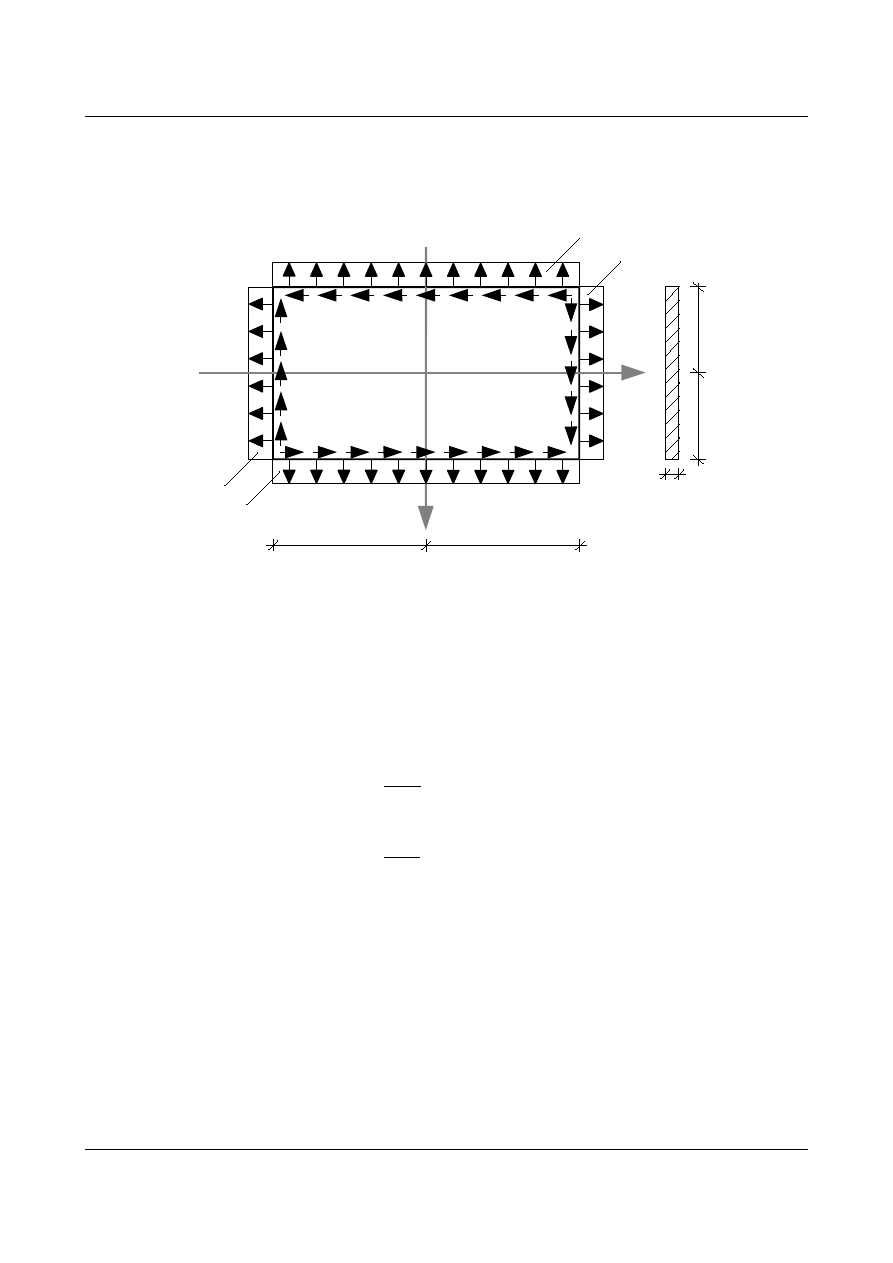
Zadanie 2.

Zginanie belki

Rys.10.2. Rysunek do zadania 2.

przyjmujemy funkcję F(x,y)

Aściukiewicz P., Baron P., Gawron U., Krzysztoń A., Ratajczak D., Wojciechowski M.

AlmaMater

l

l

b

=1

h
2

h
2

x

ql

ql

y

q

ql

ql

l

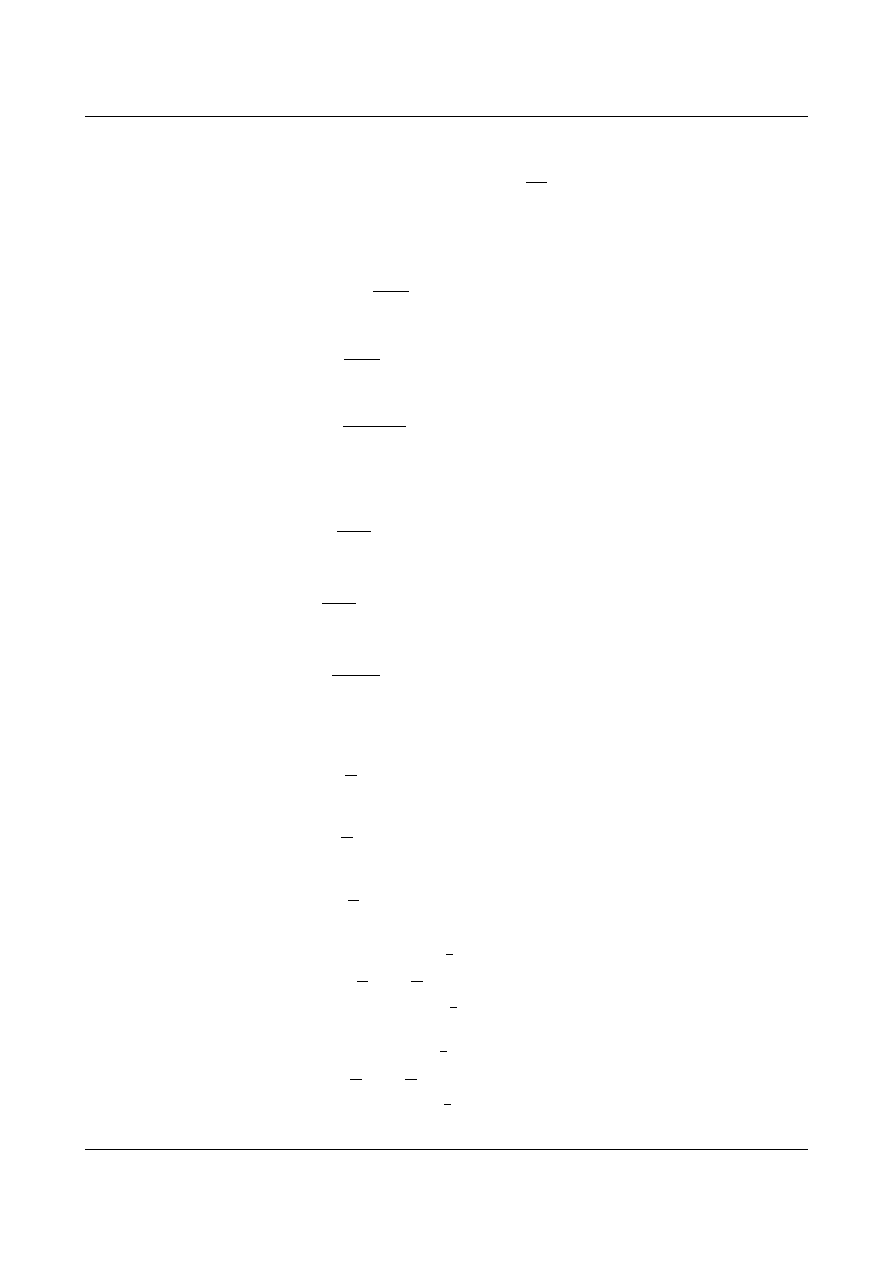
10. ROZWIĄZYWANIE ZADAŃ Z TEORII SPRĘŻYSTOŚCI

4

F



x , y



=a

2

x

2

b

3

x

2

y

d

5



x

2

y

3

−

y

5

5



(10.23)

∇

2

F

=0

(10.24)

∂

4

F

∂ x

4

=0

(10.25)

∂

4

F

∂ y

4

=−24 d

5

y

(10.26)

2 ∂

4

F

∂ x

2

∂ y

2

=24 d

5

y

(10.27)

Warunek jest spełniony.

1



x

= ∂

2

F

∂ y

2

=d

5



6 x

2

y

−4 y

3



(10.28)

2



y

= ∂

2

F

∂ x

2

=2 a

2

2 b

3

y

2 d

5

xy

3

(10.29)

3



xy

= ∂

2

F

∂ y ∂ x

=−2 b

3

x

−6 d

5

xy

2

(10.30)

Warunki brzegowe (wyrażone w naprężeniach).

1

y

=±

h
2

−lxl 

xy

=0

(10.31)

2

y

=

h
2

−lxl 

y

=−q

(10.32)

3

y

=−

h
2

−lxl 

y

=0

(10.33)

4a

x

=l −

h
2

 y

h
2

∫

−

h
2

h
2



xy

dy1

=ql

(10.34)

4b

x

=−l −

h
2

 y

h
2

∫

−

h
2

h
2



xy

dy1

=−ql

(10.35)

Aściukiewicz P., Baron P., Gawron U., Krzysztoń A., Ratajczak D., Wojciechowski M.

AlmaMater

10. ROZWIĄZYWANIE ZADAŃ Z TEORII SPRĘŻYSTOŚCI

5

5

x

=±l

∫

−

h
2

h
2



x

dy1

=0

(10.36)

6

x

=±l

∫

−

h
2

h
2



x

ydy1

=0

(10.37)



y

∣

y

=

h
2

=−q

(10.38)



y

∣

y

=−

h
2

=0

(10.39)

Po podstawieniu do wzoru (10.29) otrzymamy:

{

2 a

2

2 b

3

h
2

2 d

5

h

3

8

=−q

2 a

2

−2 b

3

h
2

−2 d

5

h

3

8

=0

(10.40)

Z układu otrzymamy:

a

2

=−

q
4

(10.41)



xy

∣

y

=

h
2

=0

(10.42)

Po podstawieniu do wzoru (10.30) otrzymamy:

x



−2 b

3

−6 d

5

−

h

2

4



=0

(10.43)

Z równań (10.40) i (10.43) otrzymujemy:

d

5

=

q

h

3

10.44)

b

3

=−

3
4

q
4

(10.45)

Zatem

Aściukiewicz P., Baron P., Gawron U., Krzysztoń A., Ratajczak D., Wojciechowski M.

AlmaMater

10. ROZWIĄZYWANIE ZADAŃ Z TEORII SPRĘŻYSTOŚCI

6



x

=

q

h

3



6 x

2

y

−4 y

3



(10.46)



y

=−

q
2

−

3
2

q
h

y



2 q

h

3

y

3

(10.47)



xy

=

3
2

q
h

x

−

6 q

h

3

x y

2

(10.48)

I

z

=I =

1 h

3

12

(10.49)

Zatem



x

=

1

I

q
2



x

2

−

2
3

y

2



y

(10.50)



y

=

1

I

q
2



y

3

3

−

h

2

4

y

−

h

3

12



(10.51)



xy

=

1

I

q
2



h

2

4

− y

2



x

(10.52)

Sprawdźmy warunki brzegowe (10.34)-10.37):

∫



xy

dy

=±ql

(10.53)

Warunek spełniony.

∫



x

dy

=0

(10.54)

Warunek spełniony.

∫

−h

2

h
2



x

ydy

=

1

I

q
2



l

2

h

3

12

−

h

2

10



≠0

(10.55)

Warunek nie jest spełniony czyli źle przyjęto funkcję F do przyjętej funkcji dodajemy F

1

F

=F F

1

(10.56)

gdzie

F

1

=d

3

y

3

(10.57)

Zatem

Aściukiewicz P., Baron P., Gawron U., Krzysztoń A., Ratajczak D., Wojciechowski M.

AlmaMater

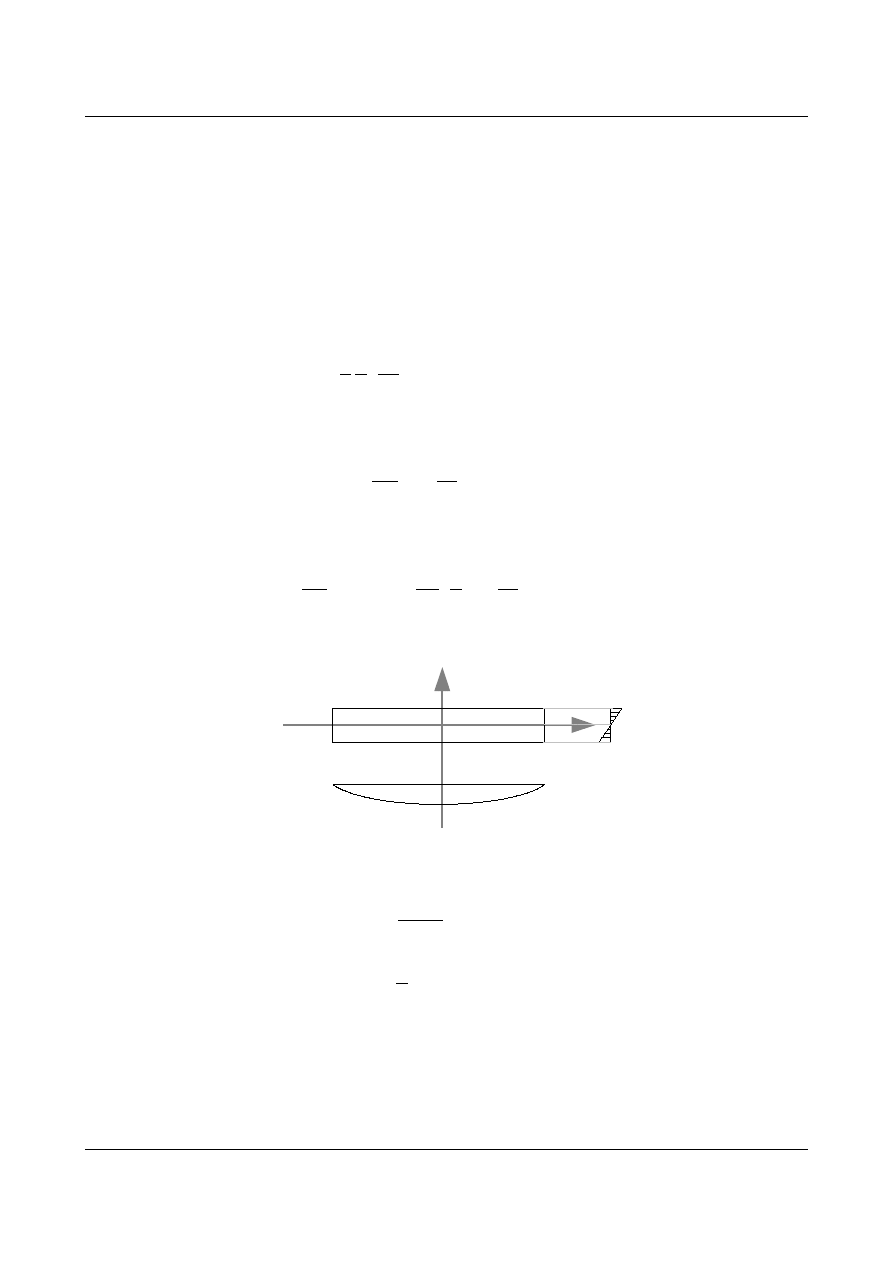
10. ROZWIĄZYWANIE ZADAŃ Z TEORII SPRĘŻYSTOŚCI

7



x

1

=6 d

3

y

(10.58)



y

1

=0

(10.59)



xy

1

=0

(10.60)

Po zmodyfikowaniu σ

x

wszystkie dotychczasowo spełnione warunki brzegowe są spełnione.

Wprowadźmy zmienione σ

x



x

=

1

I

q
2



x

2

2

3

y

2



y

6 d

3

y

(10.61)

do ostatniego warunku brzegowego, którego spełnienie prowadzi do relacji:

d

3

=−

q

2 I



l

2

−

h

2

10



(10.62)

Ostatecznie σ

x

ma postać:



x

=−

q

2 I



l

2

−x

2



y

−

q

2 I



2
3

y

2

−

h

2

10



y

(10.63)

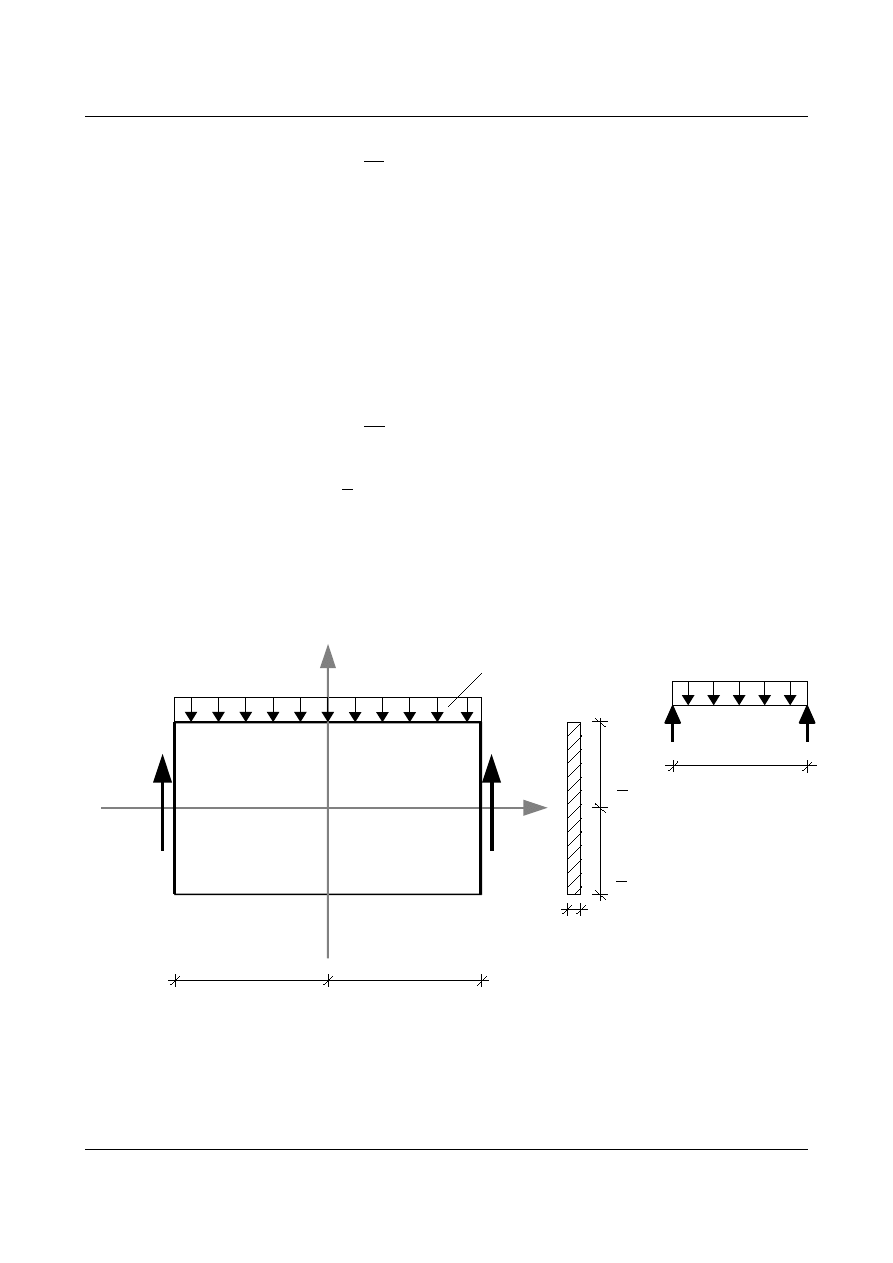
Rys. 10.3. Naprężenia



x

=−

M

 x

I

y

(10.64)

M

 x=

q
2



l

2

−x

2



(10.65)

σ

x

jest krzywą trzeciego stopnia.

Aściukiewicz P., Baron P., Gawron U., Krzysztoń A., Ratajczak D., Wojciechowski M.

AlmaMater

10. ROZWIĄZYWANIE ZADAŃ Z TEORII SPRĘŻYSTOŚCI

8

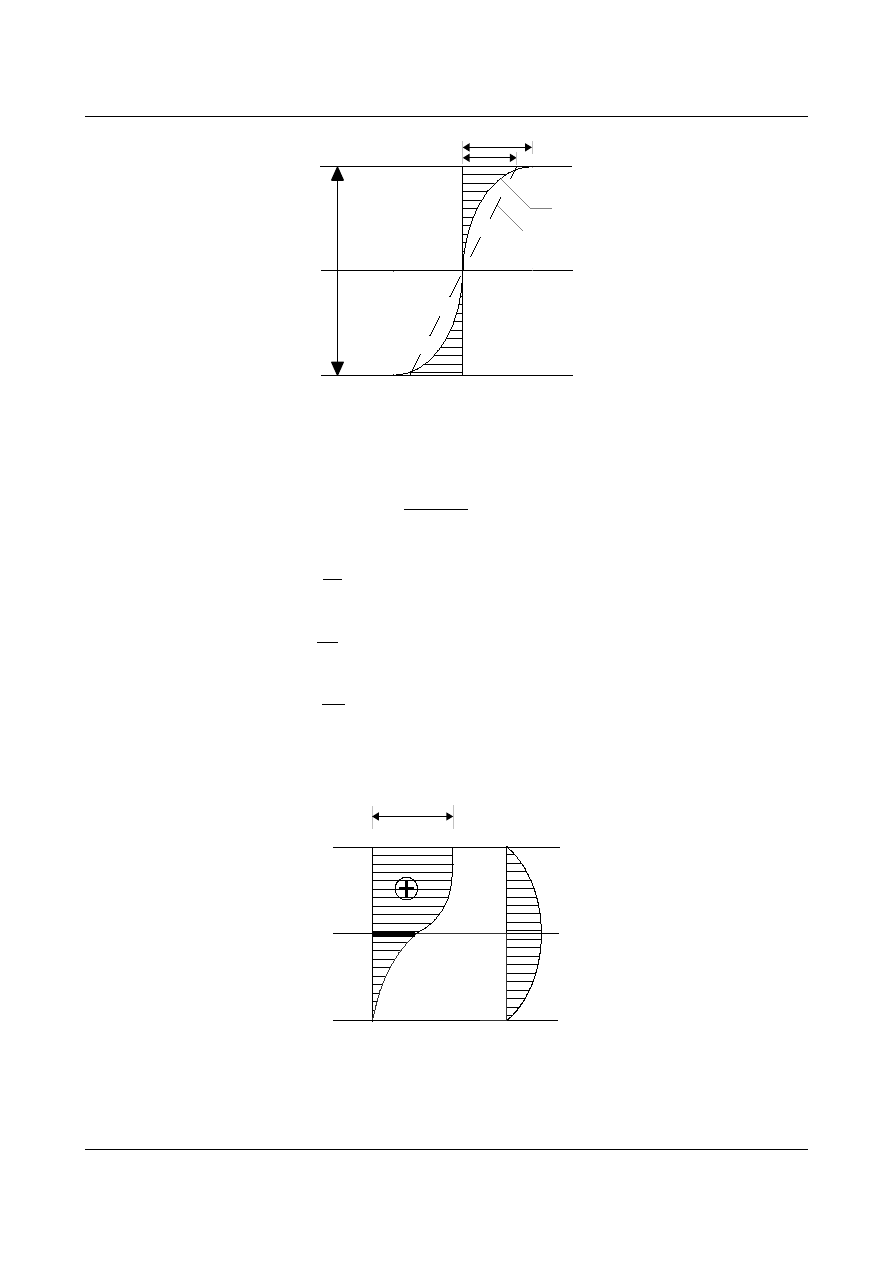
Rys. 10.4. Naprężenia σ

x

Porównajmy maksymalne naprężenia w włóknach skrajnych:

max



x

=

∣



x

d

−

x

p

∣

∣



x

d

∣

(10.67)

1

h

1 l

=0,1

0,3 promil

(10.68)

2

h

2 l

=0,25

1,7 promil

(10.69)

3

h

2 h

=0,5

6,7 promil

(10.70)

Przyjęte do rozważań wzory określające zginanie belki są wystarczająco dokładne.

Rys. 10.5. Naprężenia σ

y

, τ

xy

Aściukiewicz P., Baron P., Gawron U., Krzysztoń A., Ratajczak D., Wojciechowski M.

AlmaMater

h



x

dokł.



x

przybl.

10. ROZWIĄZYWANIE ZADAŃ Z TEORII SPRĘŻYSTOŚCI

9

Ekstremalne wartości σ

y

=q << σ

x

zatem możemy je zaniedbać w obliczeniach. τ

xy

liczymy z wzoru

znanego z wytrzymałości materiałów:

T

 x=−qx

(10.71)



xy

=

TS

Ib

(10.72)

9.2 Wyznaczenie przemieszczeń w belce.

Płaski stan naprężeń:



x

=

1

E





x

−

y





x

= ∂

u

∂ x

(10.73)



y

=

1

E





y

−

x





y

= ∂

v

∂ y

(10.74)



xy

=

1

2 G



xy



xy

=

1
2



∂ u

∂ y

 ∂

v

∂ x



(10.75)

W celu otrzymania u i v wykonujemy obustronne całkowanie nieoznaczone:



x

= ∂

u

∂ x

⇒ u x , y=

∫



x

dx

=... f

1

 y

(10.76)

Dla x w środku belki ze względu na symetrię geometryczną i obciążenia:

u

0, y=0

⇒

f

1

 y=0

(10.77)



y

= ∂

v

∂ y

⇒

v

 x , y=

∫



y

dy

=... f

1

 x

(10.78)

Wyznaczenie stałej całkowania:



xy

=

q

4 EI



h

2

4

− y

2



x

=

1
2



∂ u

∂ y

 ∂

v

∂ x





xy

= −

q

4 EI

[

l

2

x

−

x

3

3





2 q

2

−

h

2

10



x





2 y

2

−

h

2

4

x



]



1
2

df

1

 x

dx

(10.79)

df

1

 x

dx

=

q

2 EI

[



8
5





h

4

4

x

l

2

xi

x

3

3

]

(10.80)

f

1

 x=... f

0

(10.81)

Aściukiewicz P., Baron P., Gawron U., Krzysztoń A., Ratajczak D., Wojciechowski M.

AlmaMater



xy



y

d

q

q
2



y

g

10. ROZWIĄZYWANIE ZADAŃ Z TEORII SPRĘŻYSTOŚCI

10

v

 x , y=

q

2 EI

{

y

4

12

−

h

2

4

y

2

2

−

h

3

12

y



[



l

2

−x

2



y

2

2



y

4

6

−

h

2

20

y

2

]

}



q

2 EI

[

l

2

x

2

2

−

x

4

12

−

h

2

20

x

2





1





2



h

2

4

x

2

 f

0

]

(10.82)

przyjmijmy następujące warunki:

x

=±l

y

=0

}

v

=0

(10.83)

Wówczas otrzymamy:

f

0

=−

ql

2

2 EI

[

5

12



2





4
5





3



h

4

4

]

(10.84)

W wyniku podstawienia f

0

do f

1

otrzymamy wzory na ugięcie w dolnych punktach belki (tylko w

poziomie).

v

=

5 ql

4

24 EI

(10.85)

9.3 Płaskie zadania osiowo symetryczne (współrzędne biegunowe)

Zadanie osiowo symetryczne to zadanie tak skonstruowane, że funkcja miejsca i obciążenia są zależne

tylko od jednej zmiennej ( promień).

Φ=Φ(r) – funkcja naprężeń

1



r

=

1

r

d



dr

(10.86)





=

d

2



dr

2

(10.87)



r



=0

(10.88)

2

∇

2

=



d

2

d r

2



1

r

d

dr



(10.89)

∇

4

=



d

4

dr

4



2

r

d

3

dr

3

−

1

r

2

d

2

dr

2



1

r

3

d

dr



(10.90)

∇

4

r=0

(10.91)

Aściukiewicz P., Baron P., Gawron U., Krzysztoń A., Ratajczak D., Wojciechowski M.

AlmaMater

10. ROZWIĄZYWANIE ZADAŃ Z TEORII SPRĘŻYSTOŚCI

11

Istnieje tylko jedna funkcja która spełnia to równanie.

r=AlnrBr

2

ln

rCr

2

D

(10.92)

Stan naprężeń i odkształceń łatwo możemy określić z definicji.



r

=

A

r

2

B

[

1

2 lnr

]

2C

(10.93)





=−

A

r

2

B

[

3

2 lnr

]

2C

(10.94)



r



=0

(10.95)

Aściukiewicz P., Baron P., Gawron U., Krzysztoń A., Ratajczak D., Wojciechowski M.

AlmaMater