
1
Lista 4 z rozwiązaniami
Autorzy rozwiązań:
Zad.81,100 dr P.Biegański
Zad.82 -90 dr A.Kolarz.
Zad. 91 – 99,101-103 mgr. W.Magierski
Poprawione/uzupełnione rozwiązania zad. 101/103 prof. W. Salejda
Siły bezwładności
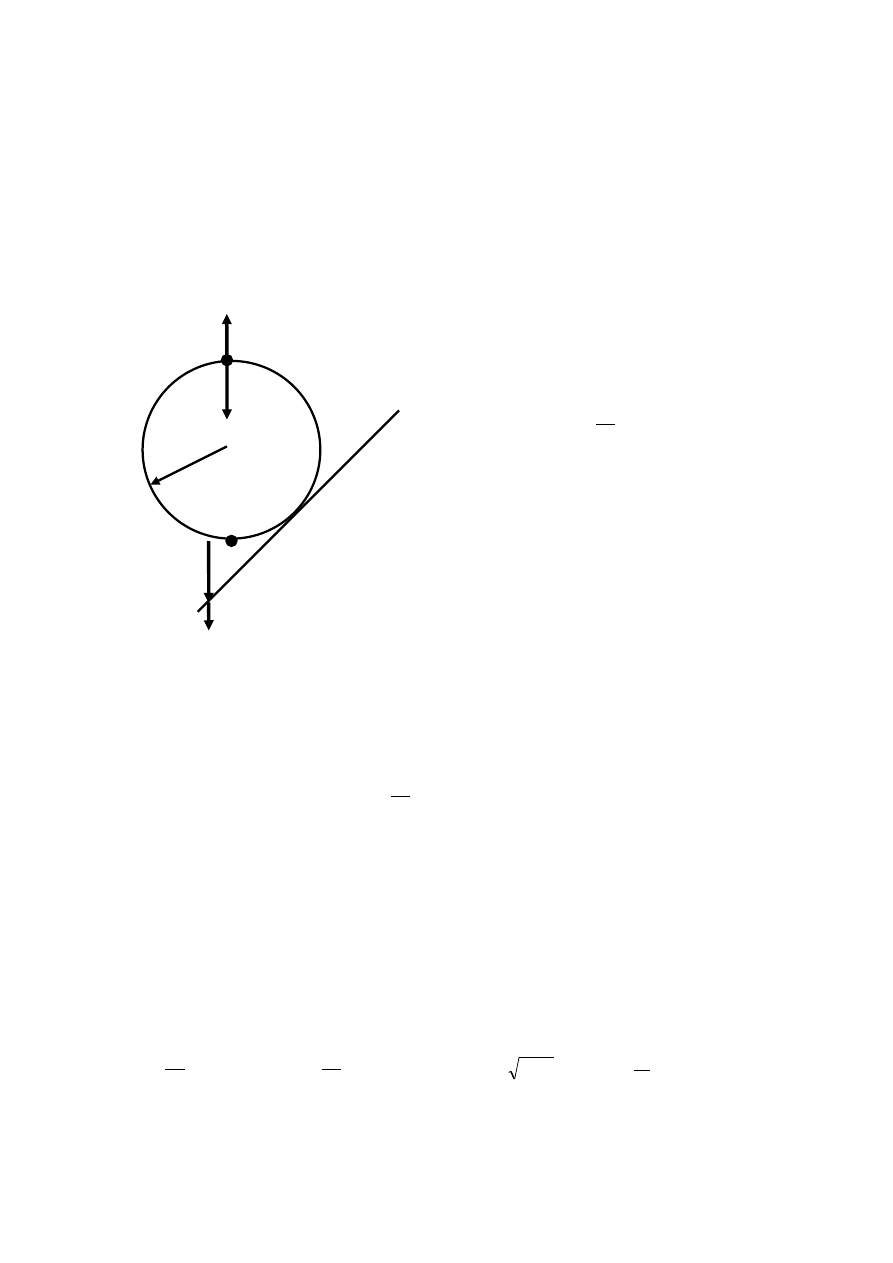
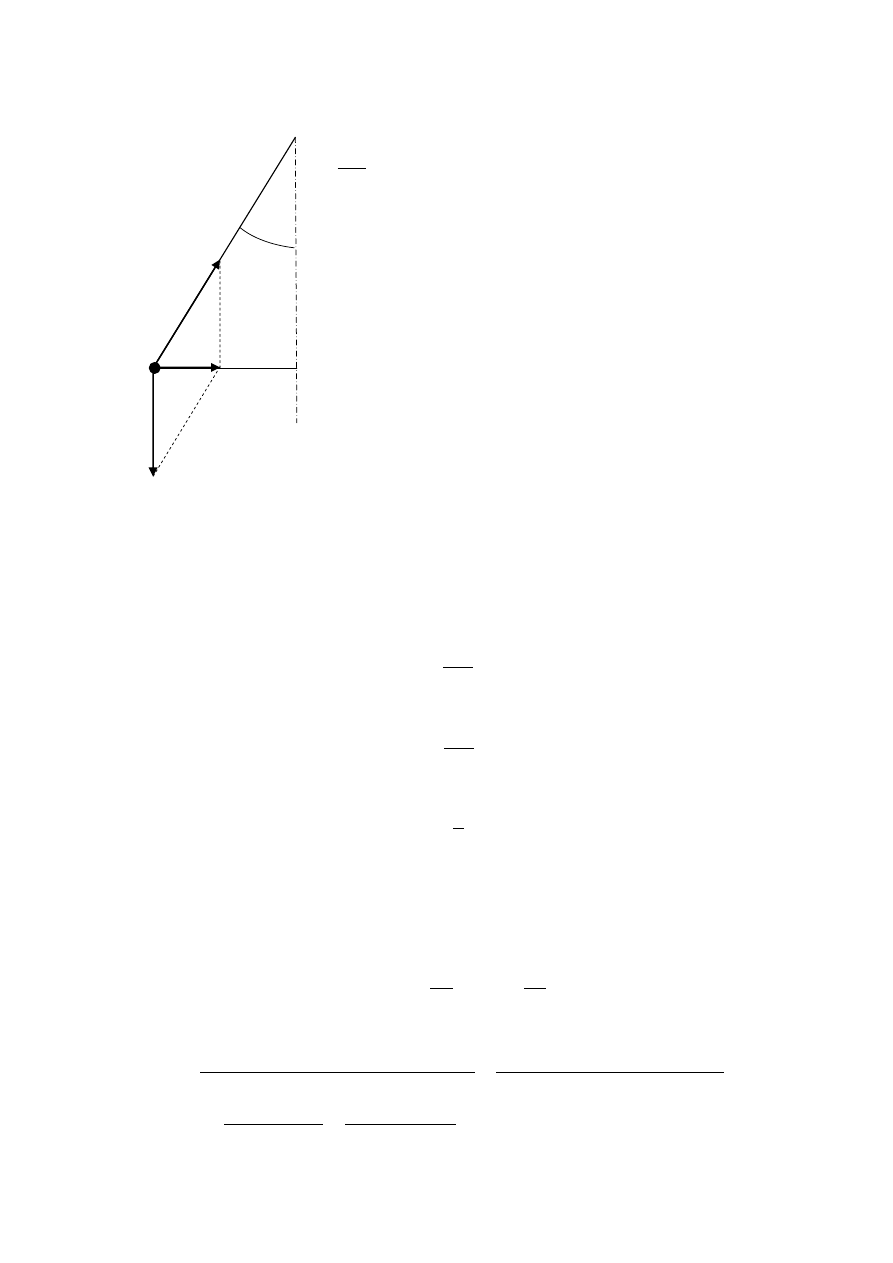
81. Jaką minimalną siłą należy działać na ciało A o masie M
A
(patrz rysunek), aby
ciało B o masie M
B
nie poruszało się względem niego (nie zsuwało się w dół),
jeśli: a) współczynnik tarcia między A i B wynosi f
AB
, gdy A porusza się po
idealnie gładkiej powierzchni? b) współczynnik tarcia między A i B wynosi f
AB
, a między A i
poziomą powierzchnią wynosi f? Obliczenia wykonać dla f
AB
= 0,6, f = 0,4, M
A
= 20 kg i M
B
= 2 kg.
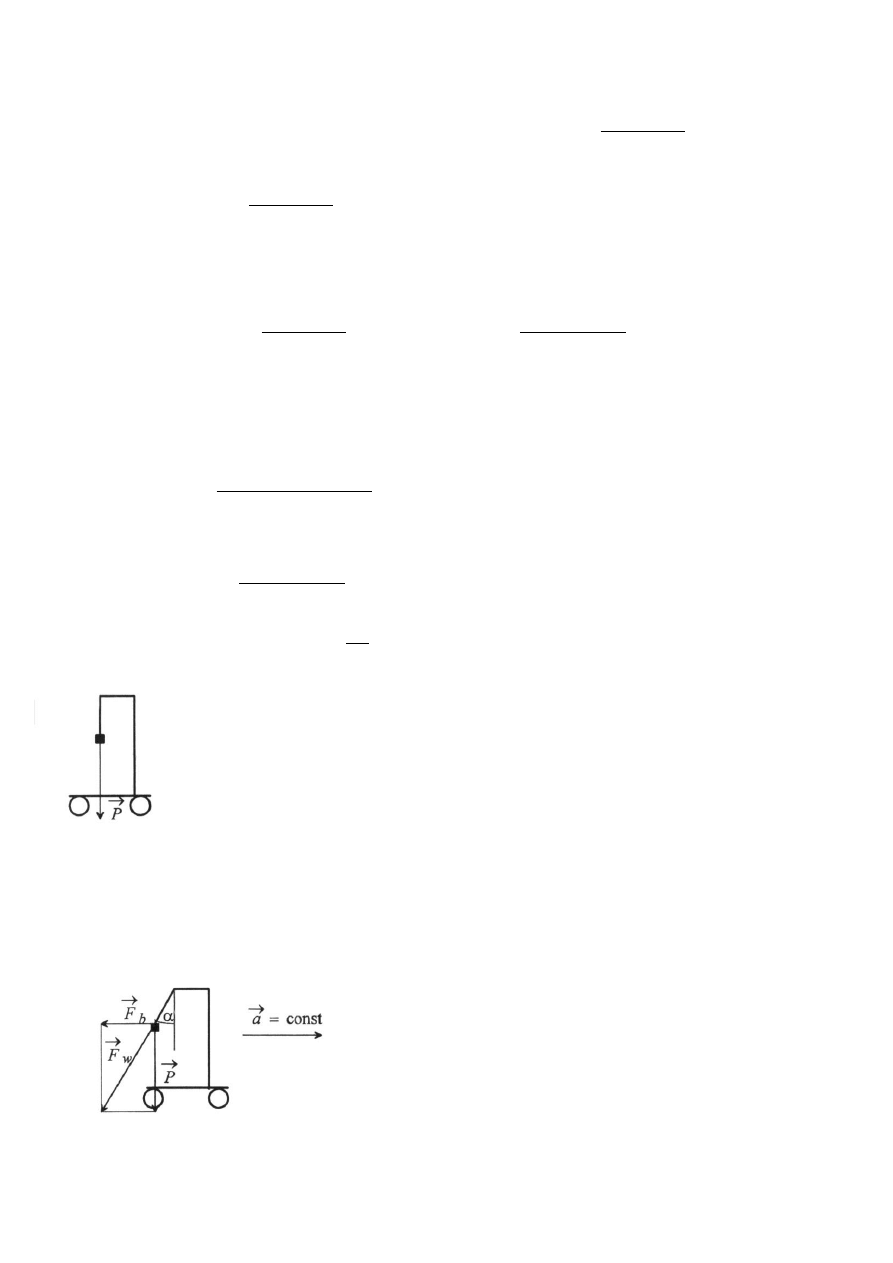
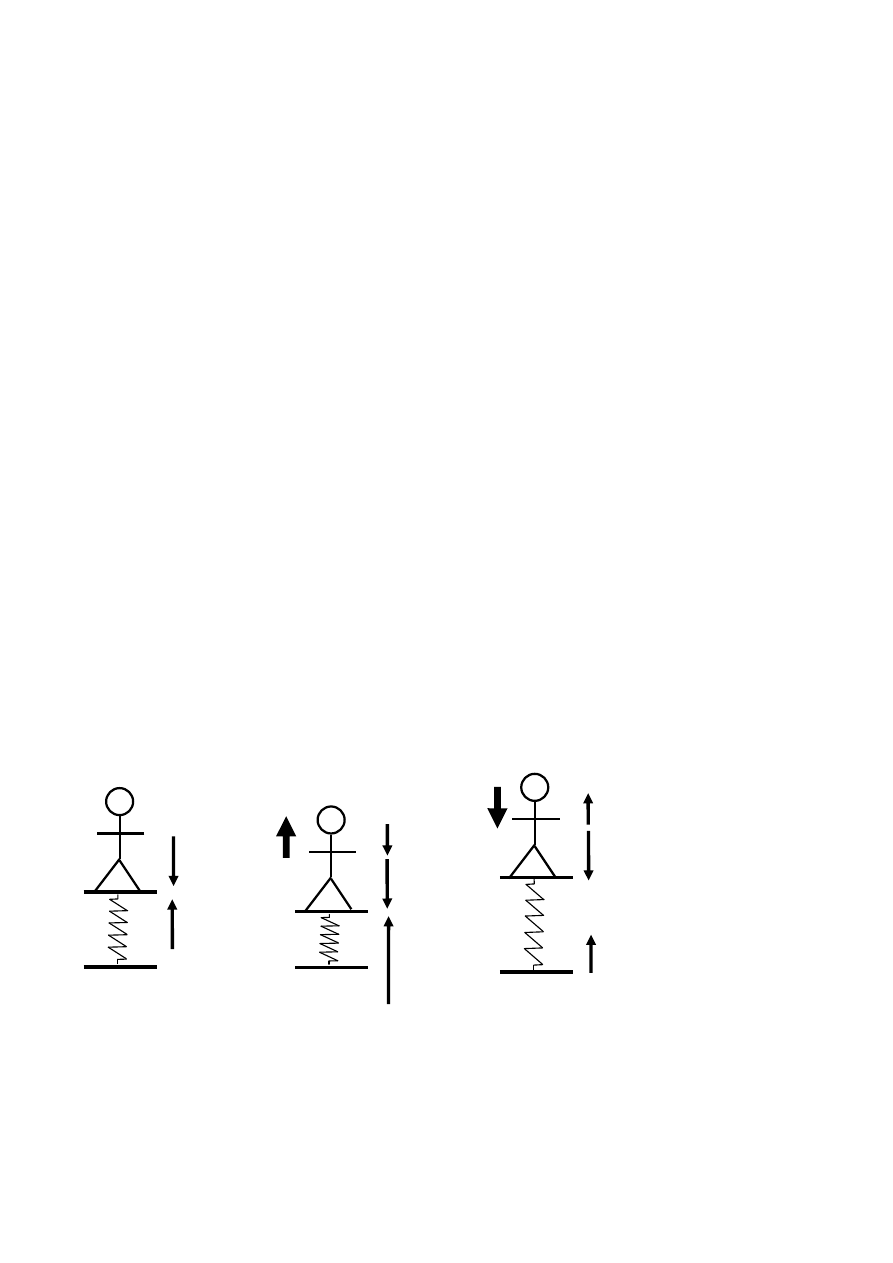
82. Wahadło o masie m wisi na podstawce umocowanej na wózku. Znaleźć kierunek nici wahadła, tj.
kąt α
nici z pionem oraz jej naprężenie T w przypadkach: a) wózek porusza się ruchem jednostajnym
po płaszczyźnie poziomej, b) wózek porusza się po płaszczyźnie poziomej z przyspieszeniem a, c)
wózek stacza się swobodnie z równi pochyłej, która tworzy kąt β z poziomem.
83. O jaki kąt odchyli się poziom cieczy przewożonej w samochodzie cysternie, gdy samochód
hamuje z opóźnieniem 5 m/s
2
(g = 10 m/s).
84. Wyznaczyć wartości sił odśrodkowych działających na człowieka znajdującego się: a) na równiku;
b) na powierzchni Ziemi poruszającej się wokół Słońca. Dane: masa człowieka 80 kg, promień Ziemi
6400 km, średnia odległość Ziemi od Słońca wynosi 150 mln. km.
85. Wyznaczyć nacisk ciała pilota o masie M na fotel samolotu wykonującą pętlę o promieniu R = 6
km leżącą w płaszczyźnie pionowej, gdy samolot jest: a) w najniższym punkcie okręgu (fotel jest pod
ciałem pilota) a prędkość samolotu wynosi 280 m/s; b) w najwyższym punkcie pętli (fotel jest nad
pilotem) a prędkość samolotu wynosi 120 m/s. Obliczenia wykonać dla M = 62 kg. W jakim punkcie
pętli i przy jakich wartościach podanych parametrów pilot przez chwilę znajdzie się w stanie
nieważkości?

2
86. Współczynnik tarcia między torem a oponami samochodu wynosi 0,8. Z jaką maksymalną
prędkością może ten samochód pokonać bez poślizgu zakręt o promieniu 40 m?
87. Na cało o masie M poruszający się w powietrzu z prędkością v nad powierzchnią Ziemi działa
oprócz siły grawitacji, siła bezwładności F
C
= 2 M v
, zwana siłą Coriolisa, gdzie
jest prędkością
kątową ruchu obrotowego Ziemi wokół osi płn-płd., przy czym wektor
jest skierowany od bieguna
płd. Ziemi do jej bieguna płn. Uzasadnić, że ciała wykonujące rzut ukośny na półkuli płn. odchylają
się od pierwotnego kierunku zawsze w prawo względem wektora prędkości v. Jaką regułę można stąd
wysnuć dla ciał wykonujących rzut ukośny na półkuli płd? Dlaczego ciała rzucone pionowo w dół,
niezależnie od półkuli, odchylają się na wschód, tj. nie spadają pionowo w dół? Wyobraź sobie
idealnie gładką rurkę o średnicy d i wysokości H ustawioną pionowo na równiku, w której spada
swobodnie i bez tarcia kulka o średnicy d. Z rurki odpompowano powietrze. Jak zależy od czasu siła
wywierana przez spadającą kulkę na boczną ściankę rurki?
88. Wiadro z wodą wprawiono w ruch po okręgu o promieniu R leżący w płaszczyźnie pionowej. Jaka
jest minimalna wartość prędkości wiadra w najwyższym punkcie toru ruchu, dla której woda nie
będzie wylewała się z niego?
89. Największy i najmniejszy pozorny ciężar ciała człowiek stojącego na wadze umieszczonej w
windzie wynosi odpowiednio 591 N i 391 N. Zakładając, że wartości przyspieszenia i opóźnienia
(przy hamowaniu) windy podczas jej ruchu w górę są takie same wyznaczyć rzeczywistą masę
człowieka oraz przyspieszenie/opóźnienie windy.
90. Samochód porusza się ze stałą prędkością v po drodze położonej na wzgórzu o promieniu
krzywizny w najwyższym punkcie równym 20 m. Wyznaczyć v, jeśli na szczycie wzgórza nacisk kół
samochodu na drogę jest zaniedbywalnie mały.
Dynamika ruchu krzywoliniowego

3
91. Jarek o masie M = 40 kg buja się na huśtawce zawieszonej na dwóch linkach o długości L = 2 m
każda. W najniższym punkcie toru P siła naprężenia każdej z linek wynosi 300 N. Wyznaczyć
prędkość i przyspieszenie dośrodkowe Jarka oraz siłę jego nacisku na deskę huśtawki w punkcie P
toru.
92. Samochód porusza się po łuku drogi o promieniu R. Powierzchnia drogi jest nachylona pod kątem
względem poziomu w kierunku do wnętrza zakrętu. Współczynnik tarcia wynosi f. Pokazać, że
maksymalna prędkość, przy której samochód nie wypadnie z zakrętu na skutek poślizgu spełnia
równość (v
max
)
2
= Rg(f+tg
)/(1-ftg
).
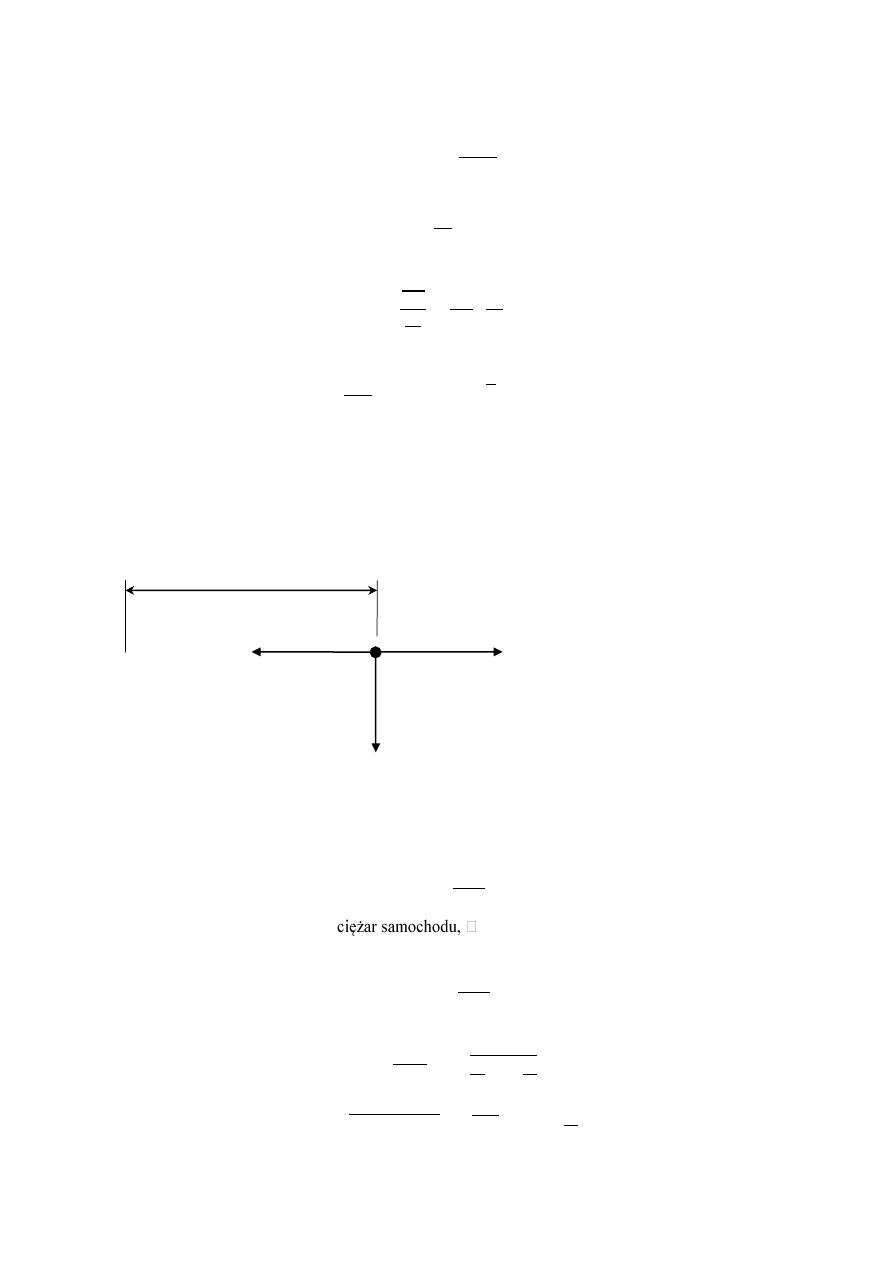
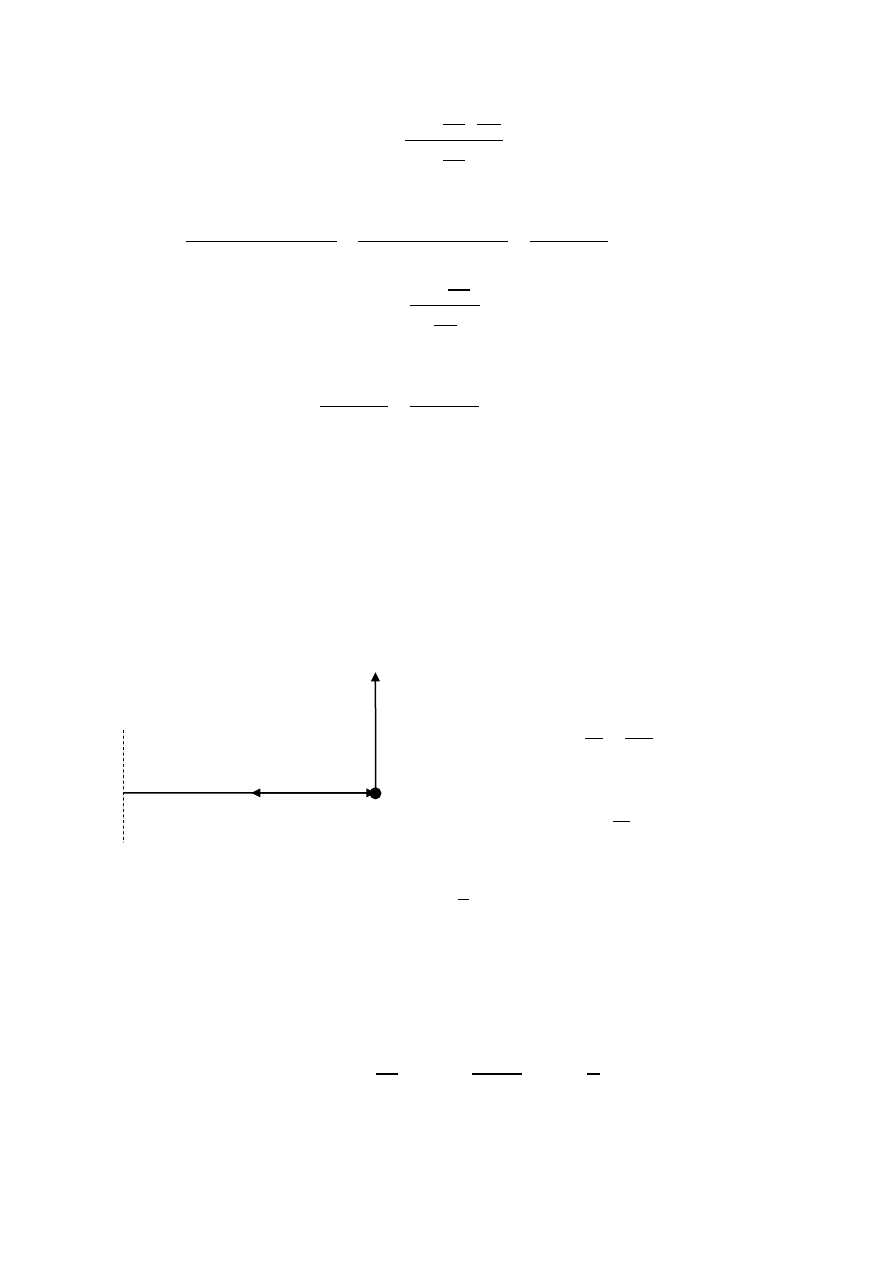
93. Samochód wpadł w poślizg na poziomym zakręcie o promieniu krzywizny 200 m, przed którym
stał znak ograniczenia prędkości do 40 km/h. O ile przekroczył kierowca dozwoloną prędkość, jeśli
współczynnik tarcia między oponami i jezdnią wynosił 4/5? Wynik podać w km/h.
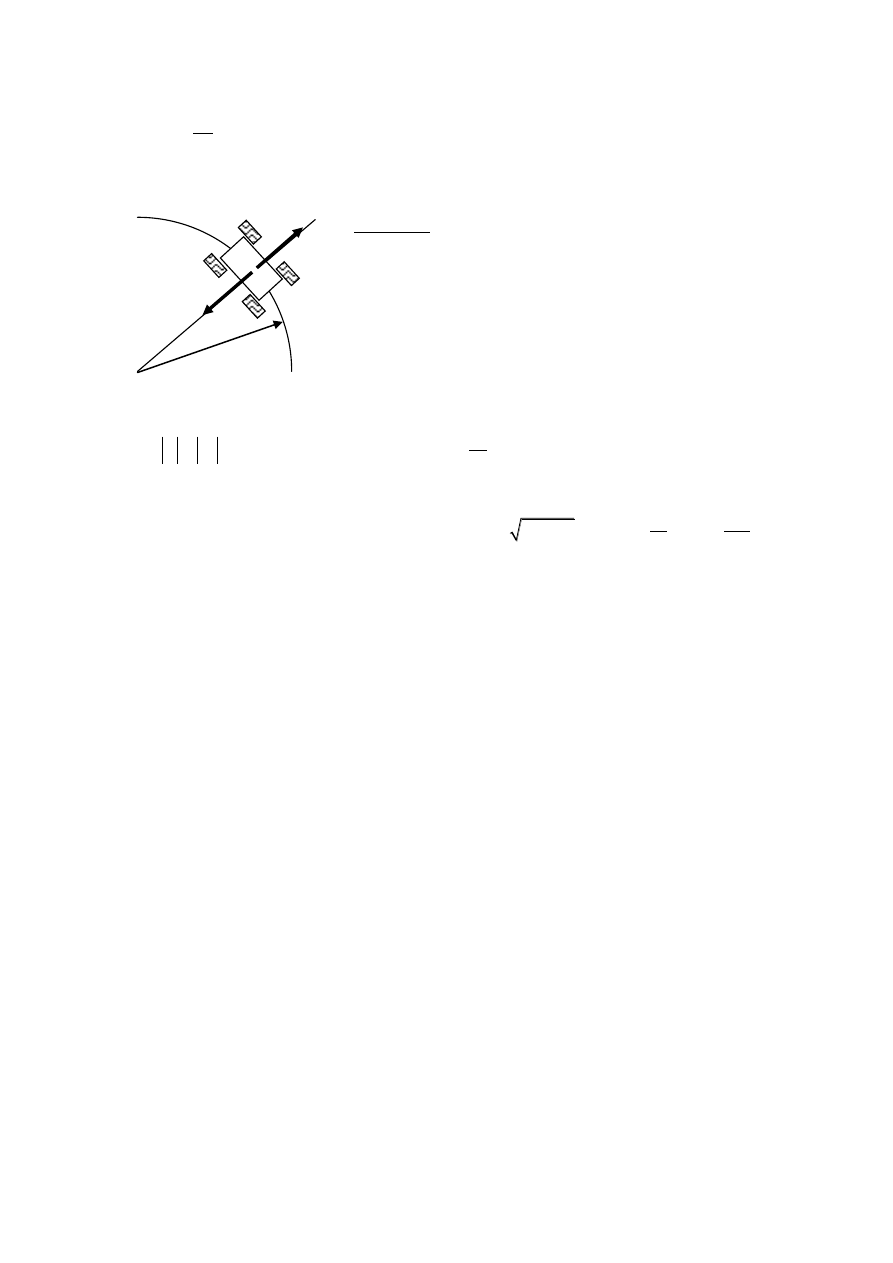
94. Rowerzysta jedzie ze stałą prędkością v = 10 m/s po torze kołowym. Kąt nachylenia płaszczyzny
roweru do poziomu wynosi α=60˚. Oblicz promień toru.
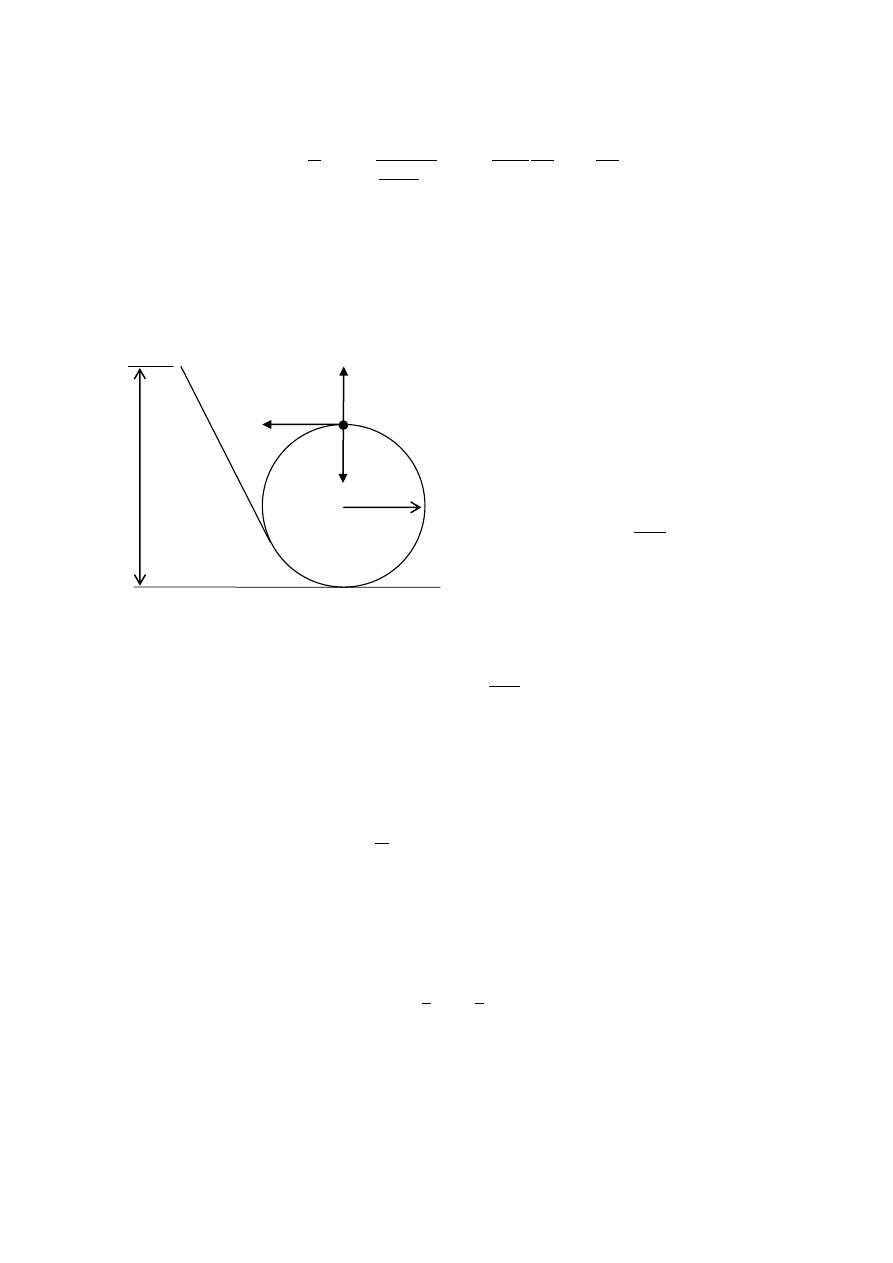
95. Droga ma łagodny płaski zakręt o promieniu R = 100 m. Jakie powinno być ograniczenie
prędkości na tym zakręcie (wyrażone w km/h) jeśli w niesprzyjających warunkach współczynnik
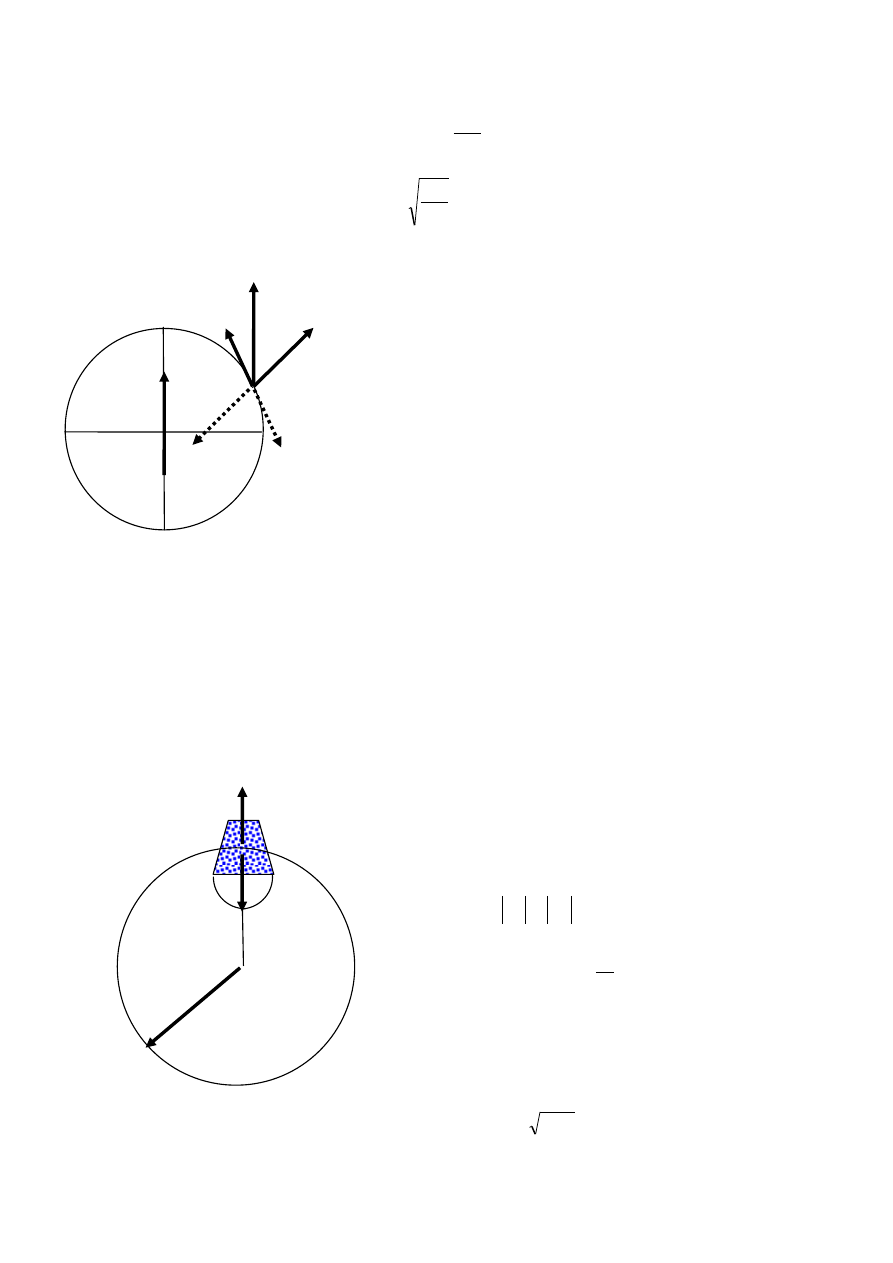
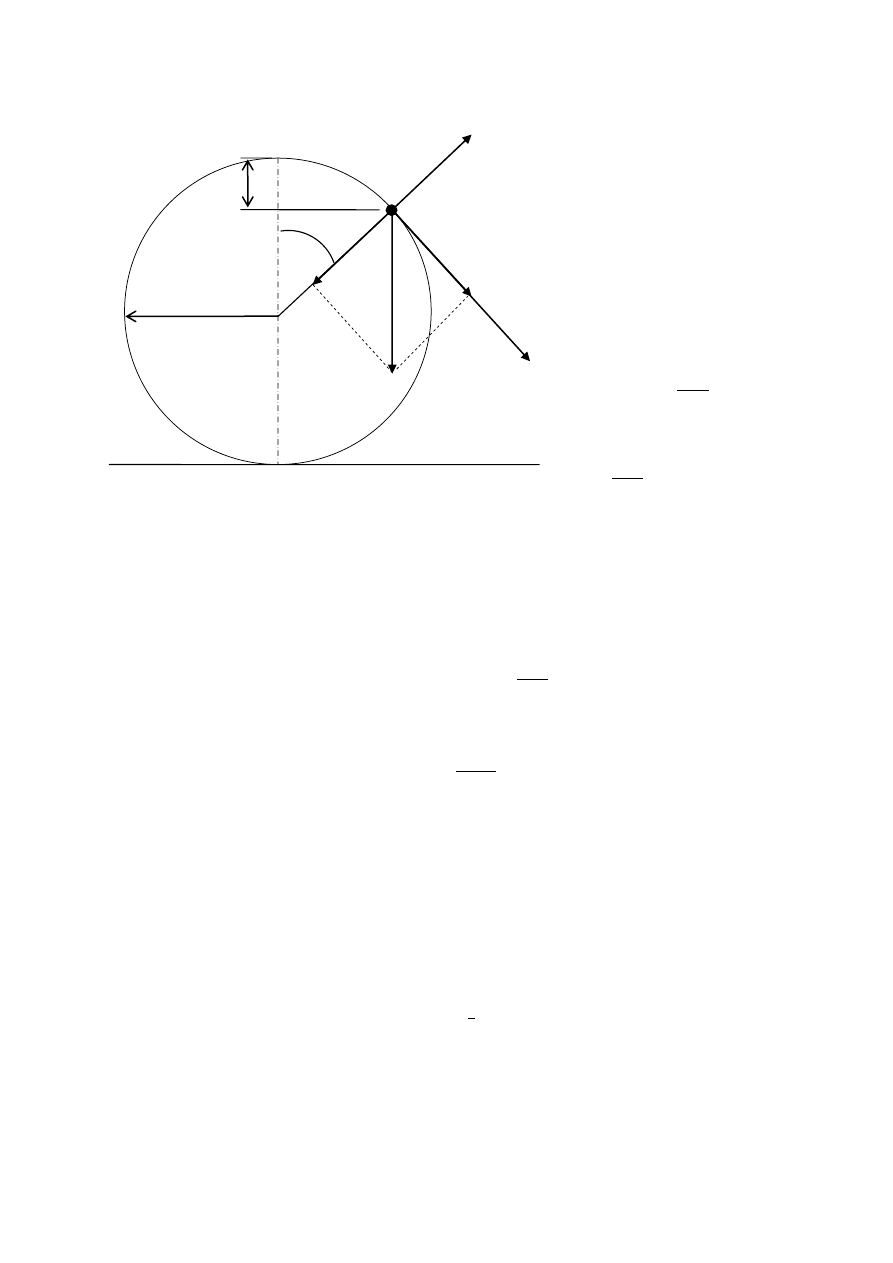
tarcia µ= 0,2 ?
96. Mała kulka stacza się po rynnie zakończonej pionową pętlą o promieniu r. Z jakiej wysokości
kulka ta powinna się stoczyć, aby nie odpaść od pętli?
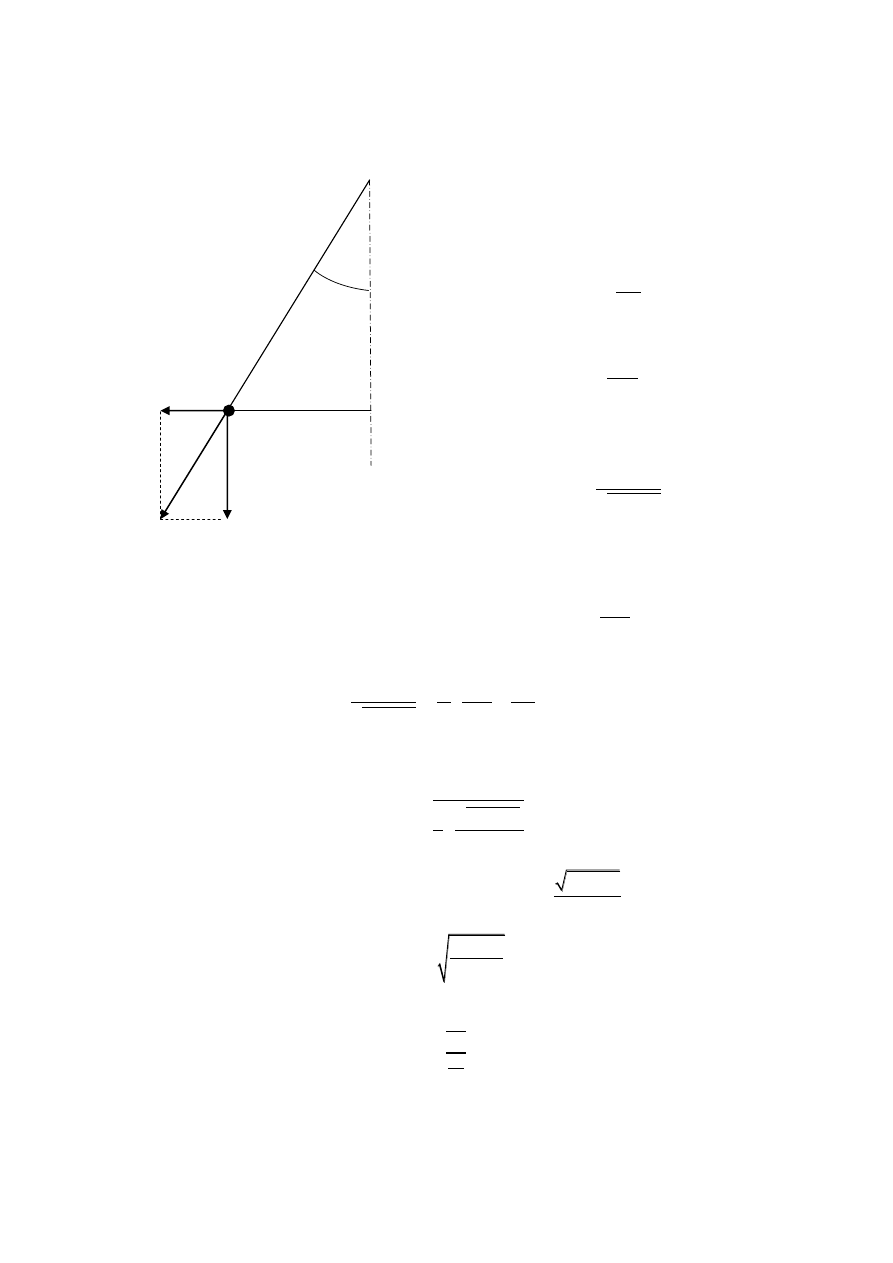
97. Z wierzchołka gładkiej kuli o promieniu R zsuwa się bez tarcia małe ciało. Wyznacz położenie
punktu, w którym wspomniane ciało oderwie się od powierzchni kuli.
98. Wahadło matematyczne można wprawić w ruch po okręgu (rysunek),
otrzymujemy wówczas wahadło stożkowe. Załóżmy, ze wychylenie takiego
wahadła wynosi
. Oblicz okres obiegu takiego wahadła.
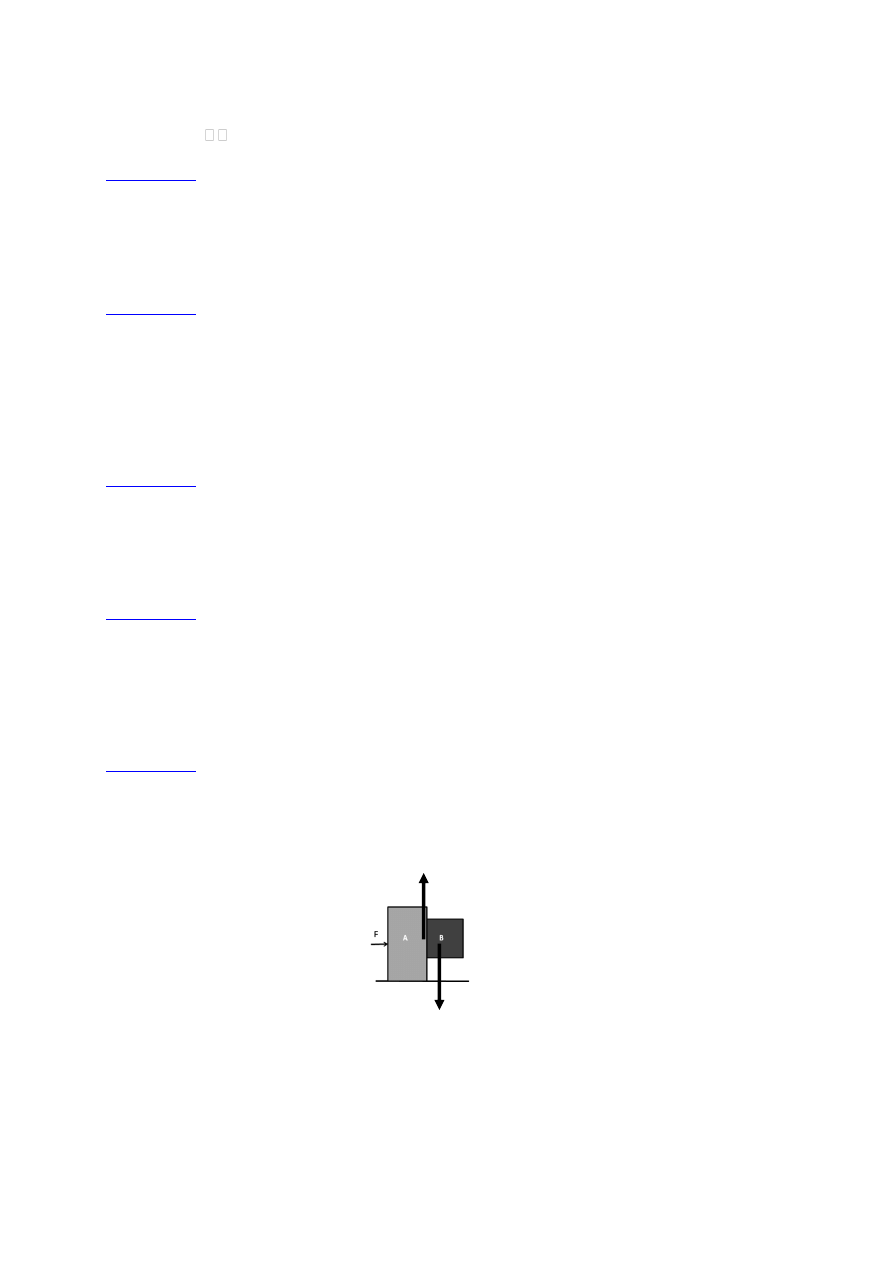
4
99. Punkt materialny rozpoczyna ruch po okręgu o promieniu R ze stałym przyspieszeniem kątowym
ε, jednostką ε
jest s
-2
.Po jakim czasie siła dośrodkowa będzie n razy większa od siły stycznej?
100. Ciężarek o masie m zawieszony na nici o długości d obraca się po okręgu ruchem jednostajnym
w płaszczyźnie poziomej. W czasie ruchu nić odchylona jest od pionu o kąt
. Oblicz siłę naprężenia
nici.
101. Słońce znajduje się w odległości 23 000 lat świetlnych od środka Drogi Mlecznej i porusza się
wokół tego środka po okręgu z prędkością 250 km/s. Ile czasu zajmuje Słońcu pełny obieg? Ile takich
obiegów wykonało Słońce, które powstało 4,5 mld lat temu. Wskazówka jeden rok świetlny do droga,
którą przebywa światło poruszające się w próżni z prędkością 300 000 km/s w czasie jednego roku,
który liczy w przybliżeniu 10
mln sekund.
102. Statek kosmiczny pokonuje w przestrzeni kosmicznej łuk okręgu o promieniu 3220 km,
poruszając się ze stałą wartością prędkości 29 000 km/h. Jaka jest wartość jego: a) prędkości kątowej?
b) przyspieszenia dośrodkowego? c) przyspieszenia stycznego?
103. Wyznaczyć zależności od czasu wartości sił: całkowitej, stycznej i dośrodkowej (składowych tej
pierwszej) działających na ciało o masie M wykonujące rzut: A) poziomy; B) ukośny. Wskazówka:
wyznaczyć najpierw wartości przyspieszeń: całkowitego, stycznego i dośrodkowego. Czy można
wyznaczyć zależność od czasu promienia krzywizny toru rzutu ukośnego i poziomego?
Rozwiązania
RZad81
a) Aby ciało się nie zsuwało:
AB
AB
AB
B
T
F
f
M
g
T
F
C
T
A
5
Siła F powiązana jest z przyspieszeniem
A
B
A
B
F
F
M
M
a
a
M
M
B
AB
B
A
B
M F
F
M
a
M
M
,
A zatem korzystając z pierwszego warunku otrzymujemy:
B
AB
AB
AB
AB
B
A
B
M F
T
F
f
f
M
g
M
M
stąd
A
B
AB
M
M
g
F
f
b) W tej części zmienia się tylko warunek na siłę całkowitą F:
A
B
A
B
A
B
A
B
A
B
F
M
M
a T
M
M
a
M
M
g f
F
M
M
g f
a
M
M
Co prowadzi do rozwiązania:
1
A
B
A
B
AB
A
B
AB
M
M
g
F
M
M
g f
f
M
M
g
f
f
RZad82
a) Ponieważ wózek porusza się ruchem jednostajnym to działa na niego jedynie
przyspieszenie ziemskie i odpowiadająca jej siła ciężkości P.
Naprężenie nici T dane jest wzorem
g
m
P
T
b) W wypadku ruchu ze stałym przyspieszeniem a pojawia się
siła bezwładności
a
m
F
b
T
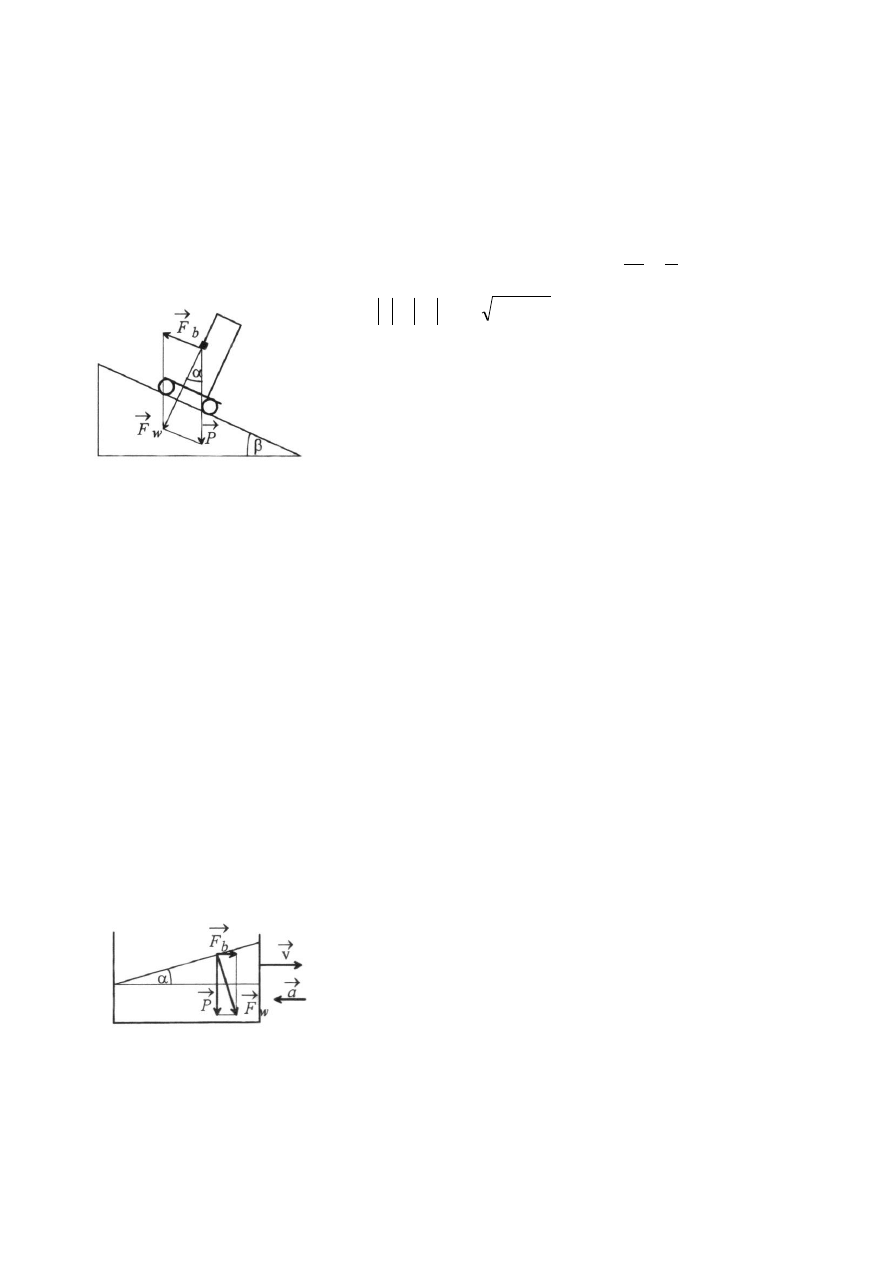
6
która powoduje odchylenie wahadła od pionu w taki sposób, że nić wahadła układa się wzdłuż siły
wypadkowej F
w
. Z rysunku wynika, że
g
a
P
F
tg
b
oraz
2
2
g
a
m
F
T
w
c) Na wózek wzdłuż równi działa składowa siły ciężkości
sin
sin
g
m
P
P
R
powodująca stałe, równoległe do równi przyspieszenie
sin
g
a
Siła bezwładności wynosi teraz
sin
g
m
F
b
Jak widać z rysunku siła wypadkowa wynosi
b
w
F
P
F
i jest prostopadła do równi czego należało się spodziewać z rozkładu siły ciężkości na składowe w
kierunku równoległym i prostopadłym do równi. W związku z powyższym muszą być spełnione
równania:
oraz
cos
g
m
F
T
w
RZad83
Wypadkowa siła F
w
działająca na dowolną elementarną masę cieczy na powierzchni jest do
powierzchni prostopadła. Gdyby tak nie było to siłę tę rozkładamy na składowe prostopadłą i
równoległą do powierzchni. Składowa prostopadła jest równoważona przez siły sprężystości cieczy
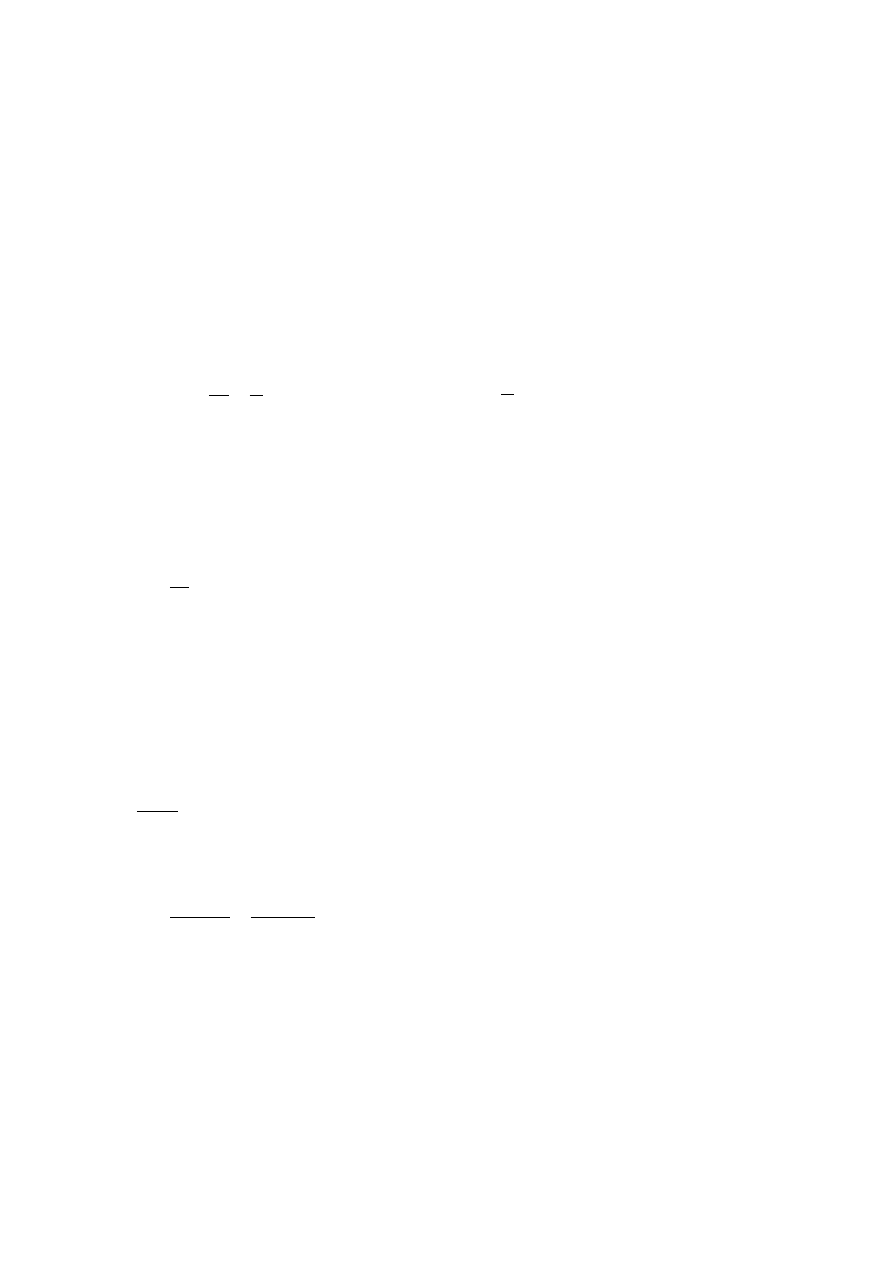
7
natomiast składowa równoległa powodowała by ruch po powierzchni czego nie obserwujemy w
stanach ustalonych.
Tak więc na element cieczy o masie Δm działa pionowo w dół siła ciężkości
g
m
P
oraz siła bezwładności
a
m
F
b
których wypadkowa jest prostopadła do powierzchni cieczy. Jak wynika z rysunku
g
a
P
F
tg
b
czyli
g
a
arctg
co po podstawieniu danych
daje
56
,
26
RZad84
Siła odśrodkowa dana jest wzorem
R
v
m
F
o
2
(1)
a) Na równiku:
W czasie t = 24godz = 86400s Ziemia wykonuje jeden obrót wokół własnej osi. W tym czasie punkt
na równiku przebywa drogę
Z
R
S
2
z prędkością
t
R
v
Z
2
co po wstawieniu do wzoru (1) daje
2
2
2
2
4
2
t
mR
R
t
R
m
F
Z
Z
Z
o
= 2,7077N
gdzie wszystkie wielkości należy sprowadzić do jednostek podstawowych układu SI.
b) W przypadku ruchu Ziemi wokół Słońca musimy założyć, że orbita jest kołowa. Wtedy po
przeliczeniu wartości R
Z-S
= 1,5·10
11
m t = 366dni·86400s/dzień=31622400s otrzymujemy wartość siły
odśrodkowej
8
F
o
= 0,4737N dla m= 80 kg
RZad85
a) W najniższym punkcie pętli siła ciężkości F
c
i siła odśrodkowa F
o
mają ten sam kierunek i zwrot –
pionowo w dół. Ich wypadkowa wynosi
o
c
N
F
F
F
co po podstawieniu danych daje siłę nacisku
N
R
v
M
g
M
F
N
1430
2
Drugi człon w powyższym wzorze jest wyrażeniem na
siłę odśrodkową.
b) W najwyższym punkcie pętli siła ciężkości F
c
jest
skierowana jak poprzednio pionowo w dół natomiast
siła odśrodkowa F
o
pionowo do góry. Ich wypadkowa
wynosi
c
o
N
F
F
F
W ostatnim wzorze od siły odśrodkowej odejmujemy siłę ciężkości gdyż fotel znajduje się nad
pilotem! Teraz, przy prędkości v
1
siła nacisku wynosi
N
g
M
R
v
M
F
N
2
,
471
2
Ujemna siła nacisku oznacza, że pilot wisi na pasach – F
N
ma kierunek F
C
!
c)
W stanie nieważkości F
N
= 0. Warunek ten może być spełniony w najwyższym położeniu na
oblatywanej pętli przy odpowiednim doborze wartości v i R:
dla R = 6000m prędkość musi wynosić
g
M
R
v
M
2
0
=>
g
R
v
2
=>
s
m
g
R
v
949
,
244
albo dla v=v
1
=120 m/s pętla musi mieć promień
R
F
c
F
o
F
c
F
o
dolot
9
m
g
v
R
1440
2
RZad86
Założenie: Ruch pojazdu odbywa się w płaszczyźnie poziomej
!!!
Na pojazd jadący z prędkością v po okręgu o promieniu
R działa siła odśrodkowa F
o
spychająca pojazd na zewnątrz łuku
oraz wypadkowa (od czterech kół) siła tarcia T przeciwdziałająca
F
o.
Aby ruch zachodził po łuku koła musi zachodzić równość
o
F
T
czyli
R
v
m
f
g
m
2
a stąd
17,888
64.4
m
km
v
f g R
s
h
RZad87
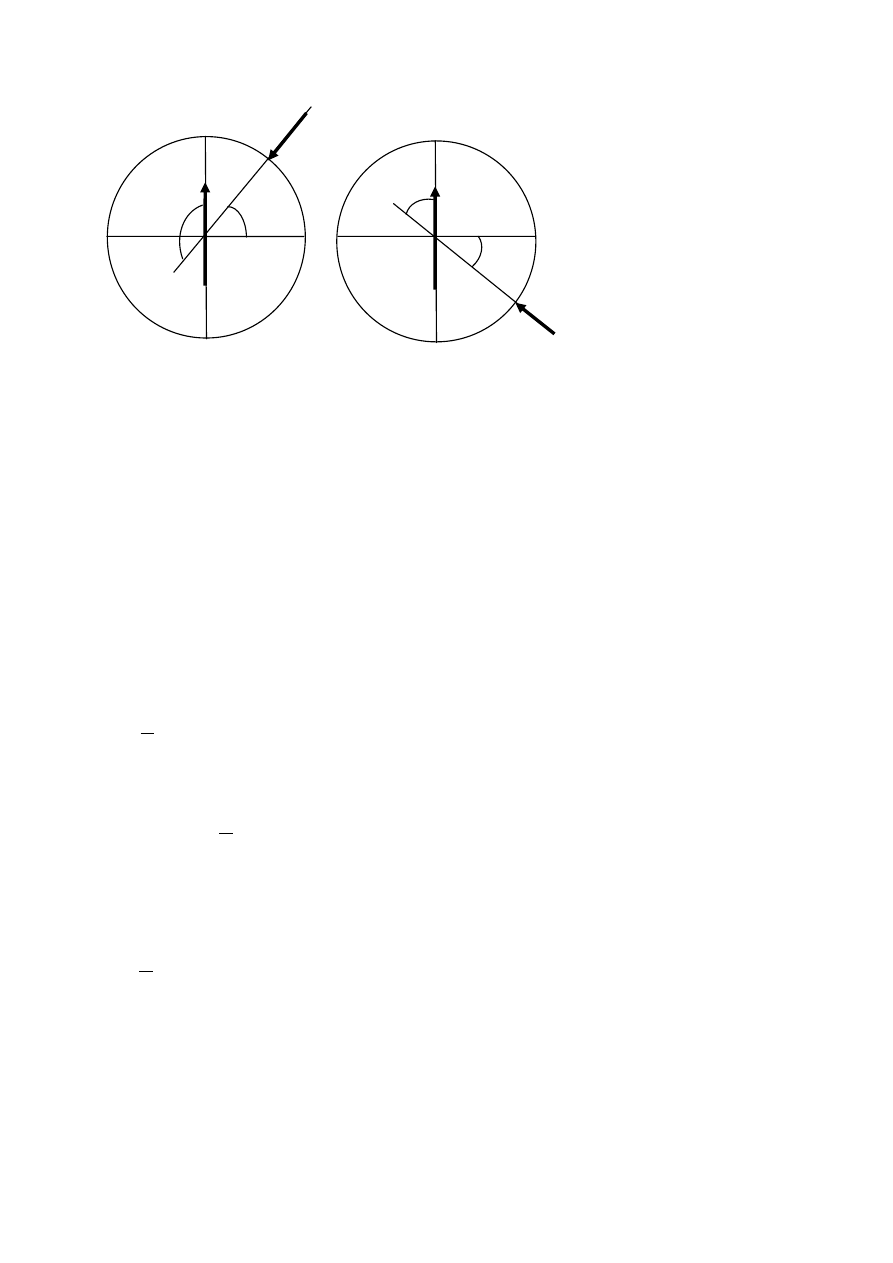
a) Dlaczego ciała rzucone pionowo w dół, niezależnie od półkuli, odchylają na wschód, tj. nie spadają
pionowo w dół?
b) Wyobraź sobie idealnie gładką rurkę o średnicy d i wysokości H ustawioną pionowo na równiku, w
której spada swobodnie i bez tarcia kulka o średnicy d. Z rurki odpompowano powietrze. Jak zależy
od czasu siła wywierana przez spadającą kulkę na boczną ściankę rurki?
c) Uzasadnić, że ciała wykonujące rzut ukośny na półkuli płn. odchylają się od pierwotnego kierunku
zawsze w prawo względem wektora prędkości v. Jaką regułę można stąd wysnuć dla ciał
wykonujących rzut ukośny na półkuli południowej?
T
R
F
o
10
a)
Siła Coriolisa jest dana wzorem
v
m
F
C
2
Z definicji iloczynu wektorowego wiemy, że wektor F
C
jest prostopadły do płaszczyzny południka
na której leżą wektory prędkości v i ω czyli do płaszczyzny rysunku. Długość tego wektora wynosi
sin
2mv
F
C
(1)
gdzie α jest kątem pomiędzy wektorami v i ω a zwrot F
C
skierowany jest za powierzchnię rysunku.
Jak widać z rys. a)
2
a więc możemy powiązać wartość siły Coriolisa z szerokością geograficzną φ
cos
2
)
2
sin(
2
mv
mv
F
C
(2)
W przypadku półkuli południowej – rys. b) – mamy
2
czyli
cos
sin
więc i tutaj wzór (1) w który przechodzi wzór (2) jest
słuszny.Na obu półkulach spadające ciało będzie odchylane przez siłę Coriolisa na wschód.
b)
Z warunków zadania wynika, że jedyną siłą działającą prostopadle do osi rurki jest
siła Coriolisa F
C
.
Prędkość kulki wynosi
t
g
v
(3)
Pn
Pd
ω
v
α
φ
Pn
α
φ
ω
v
Pd
a)
b)
11
a przebyta droga
2
2
gt
H
t
y
Po czasie
g
H
t
L
2
kulka osiągnie powierzchnię Ziemi
Wracając do zadania do wzoru (2) wstawiamy zależność (3)
co daje rozwiązanie
cos
2
cos
2
t
mg
mv
t
F
C
Widać, że F
C
zależy liniowo od czasu i można ją
zaobserwować w przedziale czasu (0,t
L
). Siła jest
skierowana na wschód.
c)
Rozważmy rzut ukośny na półkuli północnej taki,
że wektor prędkości v skierowany jest od równika ale
niekoniecznie na Pn. W tym wypadku wektor siły Coriolisa
F
C
skierowany jest za płaszczyznę rysunku czyli w prawo
od płaszczyzny rzutu. Jeśli zmienimy kierunek wektora
prędkości na -v to z definicji iloczynu wektorowego zmieni się automatycznie zwrot wektora siły
Coriolisa F
C
(strzałki przerywane) ale dalej będzie ona działać w prawo od płaszczyzny rzutu.
Na półkuli południowej rzut w stronę bieguna Pd będzie odchylany na
wschód
natomiast rzut w
stronę równika zastanie odchylony na
zachód
- znów w obu wypadkach w
lewo
od płaszczyzny
wektora v .
RZad88
Na wodę we wiadrze działa siła ciężkości F
C
skierowana
pionowo w dół oraz siła odśrodkowa F
O
skierowana
pionowo do góry. Aby woda nie wylewała się z wiadra
musi być spełniony warunek
O
C
F
F
czyli
R
v
m
f
g
m
2
gdzie m jest sumą mas wody i wiadra. Minimalna szukana
prędkość wynosi
R
g
v
Pn
Pd
ω
v
ω
F
C
-v
-F
C
F
O
R
F
C
12
F
C
F
C
F
C
F
R
a
a
F
B
F
B
F
G
F
D
a = 0
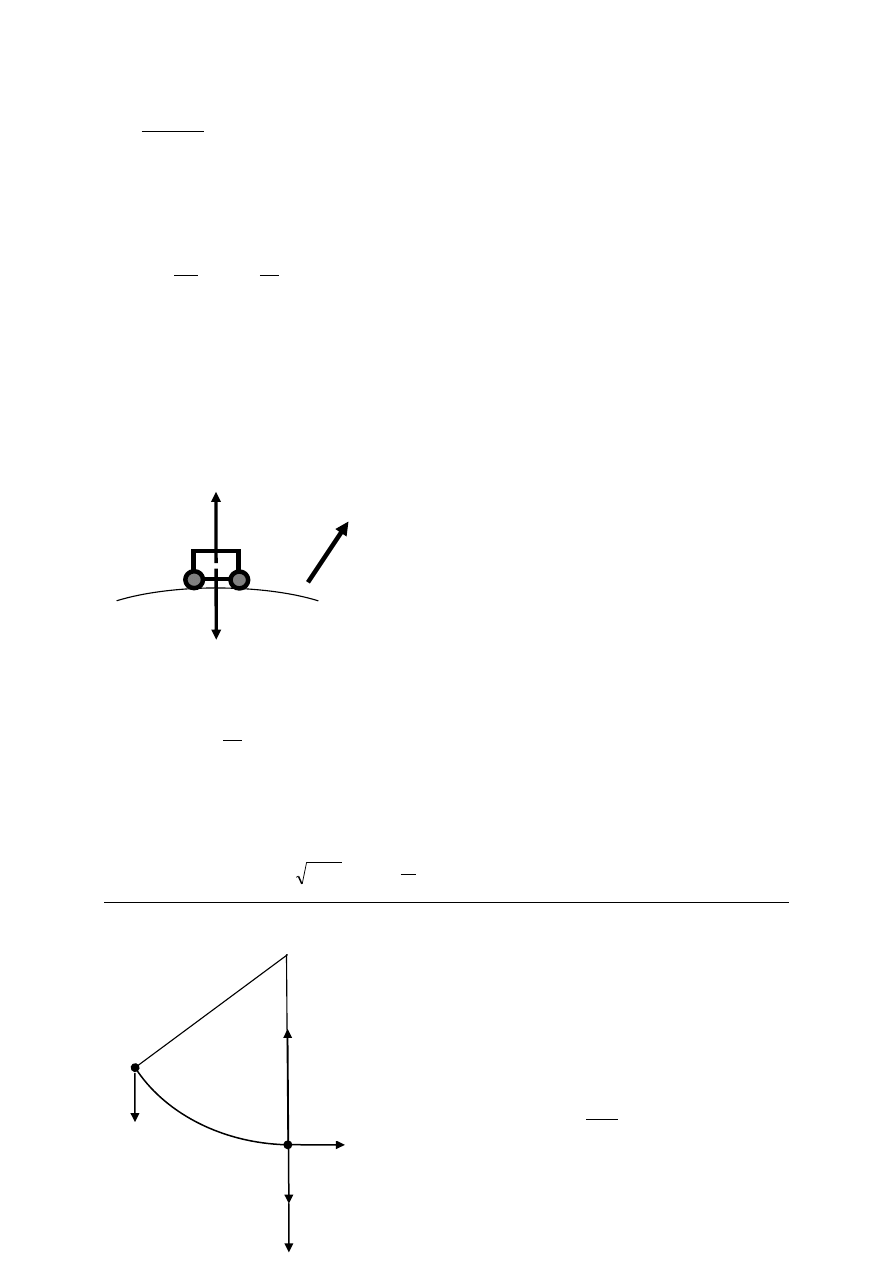
RZad89
Gdy waga pozostaje w spoczynku lub porusza się ruchem jednostajnym (rys. po lewej) wskazania
wagi F
R
odpowiadają rzeczywistemu ciężarowi F
C
człowieka
g
m
F
F
C
R
Gdy winda rusza z przyspieszeniem a do góry (rys. środkowy) pojawia się dodatkowo
siła bezwładności F
B
a
m
F
B
działająca w kierunku przeciwnym niż przyspieszenie. Teraz waga wykazuje
B
C
G
F
F
F
czyli
a
m
g
m
F
G
(1)
W
trakcie
hamowania
opóźnienie
ma
kierunek przeciwny
(rys. po prawej)
stąd
B
C
D
F
F
F
a
m
g
m
F
D
(2)
Dodając stronami wzory (1) i (2) otrzymujemy
13
kg
g
F
F
m
D
G
1
,
49
2
Z równania (2) wyliczamy teraz przyspieszenie
2
04
,
2
s
m
m
F
g
a
D
RZad90
Wypukłość mostu wymusza ruch po łuku koła co jest przyczyną powstania siły odśrodkowej F
O
skierowanej na szczycie przęsła pionowo do góry.
Na samochód działa jeszcze siła ciężkości F
C
skierowana pionowo w dół. Wypadkowa tych sił
wynosi
O
C
w
F
F
F
co prowadzi do równania skalarnego
R
v
m
g
m
F
w
2
„Zaniedbywanie mały nacisk kół...” oznacza, że siła wypadkowa
0
w
F
co prowadzi do
zależności
s
m
R
g
v
14
,
14
RZad91
Oznaczmy siłę naprężającą każdą z linek huśtawki przez N, a
prędkość Jarka w punkcie P jako v. W najniższym punkcie
toru P obie liny muszą zrównoważyć ciężar Jarka Mg oraz –
wynikającą z ruchu po okręgu – siłę odśrodkową F
od
:
𝐹
od
=
𝑀𝑣
2
𝐿
R
Mg
2N
P
Mg
F
od
v
L
F
O
F
C
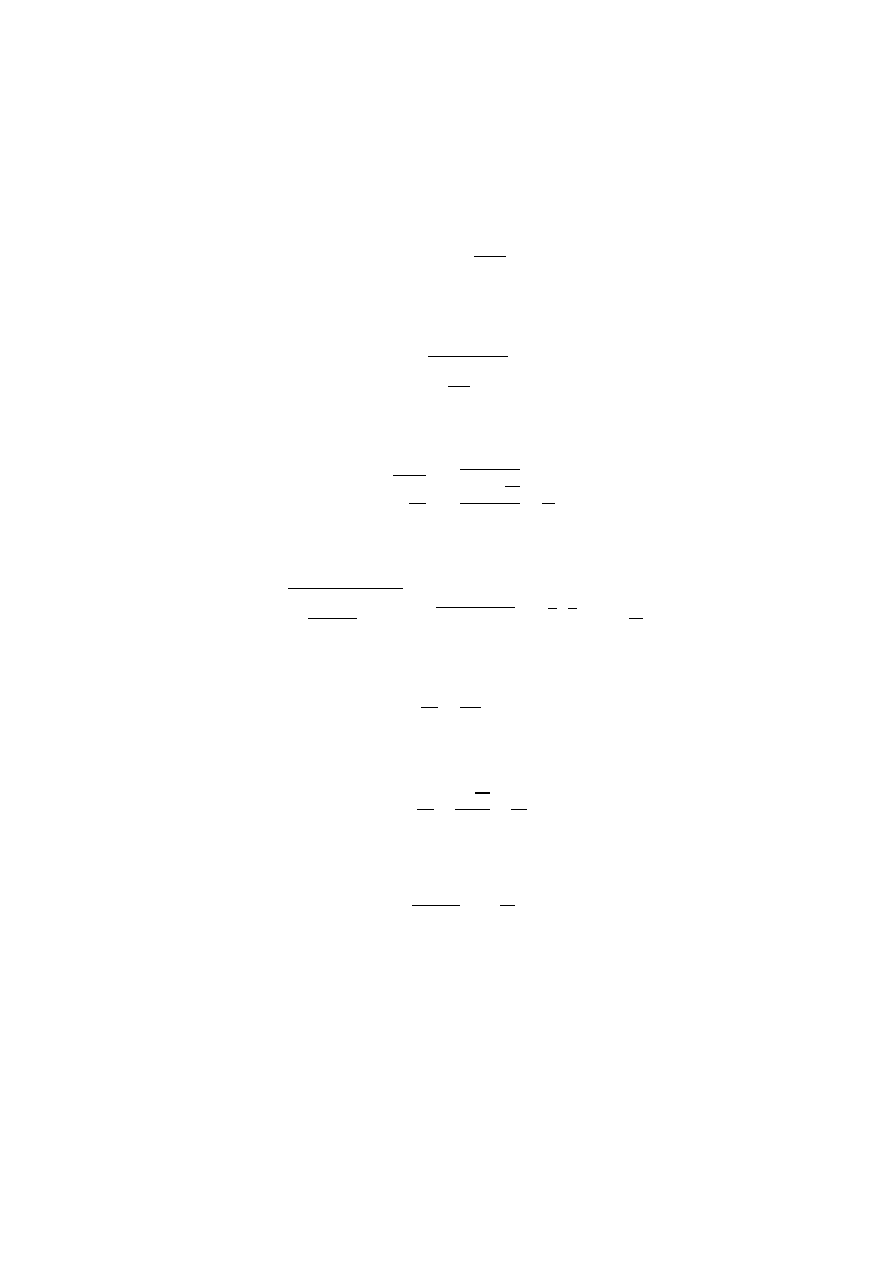
14
W punkcie P mamy równowagę sił:
2𝐍 = 𝑀𝐠 + 𝐅
𝑜𝑑
Ponieważ wszystkie siły działają w tym samym kierunku możemy rozważać długości wektorów, a
zatem:
2𝑁 = 𝑀𝑔 +
𝑀𝑣
2
𝐿
Z równania tego wyznaczymy szukaną prędkość v:
𝑀𝑣
2
= 𝐿 2𝑁 − 𝑀𝑔
𝑣 = 𝐿
2𝑁
𝑀
− 𝑔
Sprawdźmy jednostki:
𝑣 = m
N
kg
=
m ∙ kg
m
s
2
kg
=
m
s
Policzmy wartość prędkości:
𝑣 = 2
2 ∙ 300
40
− 10 = 2 15 − 10 = 2 5 ≅ 3,2
m
s
Przyspieszenie dośrodkowe wiążemy z siłą dośrodkową, która w punkcie P wynosi 2N-mg
𝑎
𝑑
=
𝐹
𝑑
𝑀
=
2𝑁
𝑀
− 𝑔
Sprawdzamy jednostki:
𝑎
𝑑
=
N
kg
=
kg
m
s
2
kg
=
m
s
2
i obliczamy:
𝑎
𝑑
=
2 ∙ 300
40
= 5
m
s
2
Siła nacisku F
n
Jarka na deskę huśtawki jest równoważona przez siły napinające liny, zatem zgodnie z
III zasadą dynamiki:
𝐹
𝑛
= 2𝑁
𝐹
𝑛
= 2 ∙ 300 = 600 N
Odp. W punkcie P toru prędkość Jarka wynosi 3,2 m/s, przyspieszenie dośrodkowe 5 m/s
2
, a siła
nacisku 600 N.
15
Q”
Q
Q’
F
od
’
F
T
R
F
od
F
od
”
RZad92
Warunek maksymalnej prędkości
poruszania się w zakręcie oznacza
równoważenie się siły tarcia F
T
i składowej
stycznej
Q’
siły
ciężkości Q = Mg samochodu ze
składową
styczną
F
od
’
siły
odśrodkowej F
od
.
𝐅
𝑇
+ 𝐐
′
= 𝐅
𝑜𝑑
′
Warunek ten może być zapisany w
postaci skalarnej:
𝐹
𝑇
+ 𝑄
′
= 𝐹
𝑜𝑑
′
Sumę składowych normalnych: siły
ciężkości i siły odśrodkowej (jest to siła nacisku samochodu na drogę) równoważy siła reakcji podłoża
– nie została uwidoczniona na rysunku. Łatwo zauważyć, że odpowiednie składowe wynoszą:
𝑄
′
= 𝑄 sin 𝛼 , 𝑄" = 𝑄 cos 𝛼
𝐹
𝑜𝑑
′
= 𝐹
𝑜𝑑
cos 𝛼 , 𝐹
𝑜𝑑
" = 𝐹
𝑜𝑑
sin 𝛼
Siła odśrodkowa wyraża się wzorem:
𝐹
od
=
𝑀 𝑣
𝑚𝑎𝑥
2
𝑅
=
𝑄 𝑣
𝑚𝑎𝑥
2
𝑔𝑅
Siła tarcia z definicji proporcjonalna jest do siły nacisku, mamy więc:
𝐹
𝑇
= 𝑓 𝑄" + 𝐹
𝑜𝑑
"
Podstawiając do warunku równowagi otrzymujemy:
𝑓 𝑄 cos 𝛼 +
𝑄 𝑣
𝑚𝑎𝑥
2
𝑔𝑅
sin 𝛼 + 𝑄 sin 𝛼 =
𝑄 𝑣
𝑚𝑎𝑥
2
𝑔𝑅
cos 𝛼
Mnożąc równanie obustronnie przez czynnik
−
𝑔𝑅
𝑄 cos 𝛼
i grupując po lewej stronie wyrazy
zawierające
𝑣
𝑚𝑎𝑥
2
otrzymamy:
𝑣
𝑚𝑎𝑥
2
1 − 𝑓 tan 𝛼 = 𝑔𝑅 𝑓 + tan 𝛼
Skąd już tylko krok:
𝑣
𝑚𝑎𝑥
2
= 𝑔𝑅
𝑓 + tan 𝛼
1 − 𝑓 tan 𝛼
RZad93

16
Poślizg samochodu oznacza, że siła tarcia F
T
została pokonana przez siłę odśrodkową F
od
. Aby nie
rozwiązywać nierówności rozważymy
graniczny przypadek:
𝐹
𝑇
= 𝐹
𝑜𝑑
Siła tarcia to oczywiście:
𝐹
𝑇
= 𝑓𝑄 = 𝑓𝑀𝑔
a siła odśrodkowa:
𝐹
od
=
𝑀𝑣
2
𝑅
gdzie: M to masa samochodu, Q – ciężar
samochodu, f – współczynnik tarcia, R –
promień zakrętu, v – prędkość graniczna. Podstawiając do warunku granicznego otrzymujemy:
𝑓𝑀𝑔 =
𝑀𝑣
2
𝑅
skąd dostajemy prędkość graniczną:
𝑣 = 𝑔𝑓𝑅 ,
m
s
2
m =
m
s
𝑣 = 10
4
5
200 = 1600 = 40
m
s
Przeliczmy otrzymaną wartość prędkości na km/h
40
m
s
= 40
10
−3
km
1
3600 h
= 40
3600
1000
km
h
= 144
km
h
Przekroczenie prędkości
∆𝑣 = 𝑣 − 𝑣
𝑑𝑜𝑧𝑤
∆𝑣 = 144 − 40 = 104
km
h
Odp. Kierowca przekroczył dozwoloną prędkość o 104 km/h, a ponieważ przekroczenie jest większe
niż 51 km/h otrzymuje mandat 500 zł i 10 pkt karnych.
RZad94
Rowerzysta pochyla rower tak, aby wypadkowa
F
w
sił: ciężkości i odśrodkowej (zaczepionych w
środku masy układu) przechodziła przez punkt
styku opon roweru z podłożem. Jest to warunek
równowagi roweru w układzie nieinercjalnym:
tan 𝛼 =
𝑀𝑔
𝐹
𝑜𝑑
Z kolei
𝐹
od
=
𝑀𝑣
2
𝑅
F
od
F
T
Q = Mg
R
F
od
F
w
Q=Mg
R
ŚM
17
Podstawiając do warunku równowagi otrzymujemy równanie:
tan 𝛼 =
𝑀𝑔𝑅
𝑀𝑣
2
skąd łatwo policzyć promień skrętu:
𝑅 =
𝑣
2
𝑔
tan 𝛼
Sprawdzamy jednostki
𝑅 =
m
2
s
2
m
s
2
=
m
2
s
2
∙
s
2
m
= m
i obliczamy szukaną wartość R
𝑅 =
10
2
10
tan 60° = 10 3 ≅ 17,3 m
Odp. Promień skrętu roweru wynosi 17,3 m.
RZad95
Niesprzyjającym
warunkom
przypisujemy
możliwość
wystą-
pienia
poślizgu
kół
pojazdu
w zakręcie.
Poślizg
samochodu
oznacza, że siła tarcia F
T
zostaje
pokonana przez siłę odśrodkową F
od
.
Aby nie rozwiązywać nierówności
rozważymy graniczny przypadek:
𝐹
𝑇
= 𝐹
𝑜𝑑
Siła tarcia to oczywiście:
𝐹
𝑇
= 𝜇𝑄 = 𝜇𝑀𝑔
a siła odśrodkowa:
𝐹
𝑜𝑑
=
𝑀𝑣
2
𝑅
gdzie: M to masa samochodu, Q –
– współczynnik tarcia, R – promień zakrętu, v
– prędkość graniczna. Podstawiając do warunku granicznego otrzymujemy:
𝑓𝑀𝑔 =
𝑀𝑣
2
𝑅
skąd dostajemy prędkość graniczną:
𝑣 = 𝑔𝑓𝑅 ,
m
s
2
m =
m
s
𝑣 = 10 ∙ 0,2 ∙ 100 = 200 = 14,1
m
s
F
od
F
T
Q = Mg
R
18
Przeliczmy otrzymaną wartość prędkości na km/h
14,1
m
s
= 14,1
10
−3
km
1
3600 h
= 14,1
3600
1000
km
h
= 51
km
h
Odp. Rozważany zakręt powinien być opatrzony znakiem drogowym ograniczającym dopuszczalną
prędkość do 50 km/h (znak B-33).
RZad96
Aby nie odpaść od pętli mała kulka musi mieć
na tyle dużą prędkość, aby siła odśrodkowa F
od
zdołała zrównoważyć siłę ciężkości mg w
najwyższym punkcie pętli
𝐹
𝑜𝑑
= 𝑚𝑔
z drugiej strony
𝐹
𝑜𝑑
=
𝑚𝑣
2
𝑟
Aby znaleźć prędkość kulki wystarczy
porównać energię potencjalną w momencie
startu z całkowitą energią w rozpatrywanym
punkcie:
𝑚𝑔 = 𝑚𝑔2𝑟 +
𝑚𝑣
2
2
skąd mamy:
𝑣
2
= 2𝑔 − 2𝑟 .
Podstawiając do warunku równowagi otrzymujemy równanie:
𝑚
𝑟
2𝑔 − 2𝑟 = 𝑚𝑔
i obliczamy
2 − 4𝑟 = 𝑟 ,
2 = 5𝑟 ,
=
5
2
𝑟 = 2
1
2
𝑟 .
Odp. Minimalna wysokość z jakiej powinna się stoczyć kulka wynosi 2,5r.
RZad97
F
od
v
mg
r
h
19
Miejsce oderwania zsuwającego
się ciała wyznacza warunek
równowagi sił: odśrodkowej F
od
i
składowej normalnej F
n
siły
ciężkości mg:
𝐹
𝑜𝑑
= 𝐹
𝑛
Łatwo zauważyć, że:
𝐹
𝑛
= 𝑚𝑔 cos 𝜑
i pamiętamy, że:
𝐹
𝑜𝑑
=
𝑚𝑣
2
𝑅
Podstawiamy i mamy:
𝑚𝑣
2
𝑅
= 𝑚𝑔 cos 𝜑
skąd
𝑣
2
= 𝑔𝑅 cos 𝜑
Zdając sobie sprawę z tego, że ze wzrostem kąta φ rośnie prędkość zsuwania v szukamy zależności
między tymi wielkościami. Skorzystamy z zasady zachowania energii porównując początkową energię
potencjalną ciała w najwyższym punkcie kuli z energią mechaniczną w momencie oderwania:
𝑚𝑔2𝑅 = 𝑚𝑔 2𝑅 − +
𝑚𝑣
2
2
Zauważmy też, że:
cos 𝜑 =
𝑅 −
𝑅
Po prostych przekształceniach otrzymujemy:
= 𝑅 1 − cos 𝜑
a po wstawieniu do bilansu energii:
𝑣
2
= 2𝑔𝑅 − 2𝑔𝑅 cos 𝜑
Porównując ten rezultat z wcześniejszym równaniem dla v
2
dostajemy:
2𝑔𝑅 − 2𝑔𝑅 cos 𝜑 = 𝑔𝑅 cos 𝜑
Skąd
cos 𝜑 =
2
3
𝜑 ≅ 48°
Odp. Zsuwające się po powierzchni kuli ciało oderwie się gdy jego promień wodzący zatoczy kąt
48°.
R
h
F
od
F
s
v
mg
F
n
20
RZad98
Wahadło będzie wykonywać obrót pod katem
dla
którego wypadkowa siła F
w
(suma wektorowa siły
ciężkości mg i siły odśrodkowej F
od
) będzie działać
wzdłuż nici. Łatwo zauważyć, że:
tan 𝛼 =
𝐹
𝑜𝑑
𝑚𝑔
.
Pamiętamy też, że:
𝐹
𝑜𝑑
=
𝑚𝑣
2
𝑅
,
gdzie v jest prędkością liniową masy m.
Z drugiej strony:
tan 𝛼 =
𝑅
𝐿
2
− 𝑅
2
.
Szukany okres T obiegu wahadła jest czasem jednego
obrotu (droga s = 2
R) wykonywanego z prędkością v,
zatem:
𝑣 =
2𝜋𝑅
𝑇
.
Porównując ze sobą wyrażenia na tan
i podstawiając otrzymane zależności dostajemy:
𝑅
𝐿
2
− 𝑅
2
=
𝑚
𝑅
2𝜋𝑅
𝑇
2
1
𝑚𝑔
,
Skąd po przekształceniach otrzymamy:
𝑇 = 2𝜋
𝐿
𝑔
∙
𝐿
2
− 𝑅
2
𝐿
Zauważmy, że pod pierwiastkiem mamy funkcję cosinus :
2
2
cos
L
R
L
zatem ostatecznie:
cos
2
L
T
g
Na koniec sprawdzamy jednostki:
𝑇 =
𝑚
𝑚
𝑠
2
= 𝑠 .
RZad99
L
F
od
mg
F
w
R

21
Zgodnie z definicją przyspieszenie styczne to:
𝑎
𝑠
=
d𝑣
d𝑡
=
d 𝐯
d𝑡
;
a przyspieszenie normalne (dośrodkowe) to:
𝑎
𝑛
=
𝑣
2
𝑅
.
Mnożąc powyższe równania przez masę m punktu materialnego otrzymamy wyrażenia na składowe
styczną i normalną (dośrodkową) siły odpowiedzialnej za ruch po okręgu:
𝐹
𝑠
= 𝑚
d𝑣
d𝑡
= 𝑚
d 𝐯
d𝑡
;
𝐹
𝑛
= 𝑚
𝑣
2
𝑅
.
Pomiędzy przyspieszeniem kątowym a liniowym istnieje związek:
𝑎
𝑠
= 𝜀𝑅 .
Skoro ruch po okręgu odbywa się ze stałym przyspieszeniem kątowym to i przyspieszenie styczne ma
stałą wartośd i jego wartośd można wyznaczyd dzieląc przyrost prędkości przez czas w którym on
nastąpił:
𝑎
𝑠
=
d𝑣
d𝑡
=
∆𝑣
∆𝑡
=
𝑣 − 𝑣
0
𝑡
=
𝑣
𝑡
.
Zatem
𝑣 = 𝑎
𝑠
𝑡 = 𝜀𝑅𝑡
Zgodnie z warunkami zadania:
𝑛 =
𝐹
𝑛
𝐹
𝑠
.
Podstawiając odpowiednie wyrażenia otrzymujemy:
𝑛 =
𝐹
𝑛
𝐹
𝑠
=
𝑚
𝑣
2
𝑅
𝑚
𝑣
𝑡
=
𝑣
2
𝑅
∙
𝑡
𝑣
=
𝑣𝑡
𝑅
=
𝜀𝑅𝑡
2
𝑅
= 𝜀𝑡
2
,
skąd
𝑡 =
𝑛
𝜀
i jednostka:
𝑡 =
1
𝑠
−2
= 𝑠
2
= 𝑠 .
RZad100
W układzie inercjalnym siła naciągu i siła ciężkości dają w sumie siłę dośrodkową
22
Jak widać z rysunku:
cos
cos
mg
N
mg
N
RZad101
Oznaczmy odległość Słońca od środka Drogi Mlecznej przez R, jego prędkość przez v, czas obiegu,
czyli okres obrotu przez T a czas życia przez t.
Prędkość Słońca otrzymamy dzieląc długość orbity 2
R przez czas jednego obrotu T:
𝑣 =
2𝜋𝑅
𝑇
,
skąd szukany czas wyraża się wzorem:
𝑇 =
2𝜋𝑅
𝑣
.
Z kolei liczba obiegów n to:
𝑛 =
𝑡
𝑇
.
Musimy jeszcze zauważyd, że odległości mierzone w latach świetlnych to droga jaką przebywa światło
– poruszające się z prędkością c – w czasie równym liczbie lat świetlnych pomnożonej przez liczbę
sekund w roku.
Prędkośd światła to oczywiście:
𝑐 = 300 000
km
s
= 3 ∙ 10
5
km
s
.
Zatem liczymy okres obrotu w sekundach:
𝑇 =
2𝜋 ∙ 23 000 ∙ 300 000 ∙ 10𝜋 ∙ 1 000 000
250
=
2𝜋 ∙ 2,3 ∙ 10
4
∙ 3 ∙ 10
5
∙ 10𝜋 ∙ 10
6
250
𝑇 =
1380𝜋
2
∙ 10
15
250
=
1380 ∙ 10 ∙ 10
15
250
= 5,45 ∙ 10
15
s = 5,45 ∙ 10
15
s ,
d
F
do
mg
m
N
R
23
𝑇 =
rok ∙
km
s ∙
s
rok
km
s
= s
lub w liczbie lat:
𝑇 =
2𝜋 ∙ 23 000 ∙ 300 000
250
=
2𝜋 ∙ 2,3 ∙ 10
4
∙ 3 ∙ 10
5
250
=
13,8𝜋 ∙ 10
9
2,5 ∙ 10
2
= 17,3 ∙ 10
7
lat .
𝑇 =
rok ∙
km
s ∙
km
s
= rok
Liczba obiegów zatem:
𝑛 =
4,5 ∙ 10
9
17,3 ∙ 10
7
=
450 ∙ 10
7
17,3 ∙ 10
7
= 26 = 26 = 26.
Odp.: Okres obiegu Słońca wokół centrum Drogi Mlecznej wynosi 173 mln lat a takich obiegów w
ciągu swojego „życia” Słońce wykonało 26. W. Salejda
RZad102
Oznaczmy promieo łuku okręgu przez R a prędkośd
statku przez v. Zgodnie z definicją przyspieszenie
styczne to:
𝑎
𝑠
=
d𝑣
d𝑡
=
d 𝐯
d𝑡
;
a przyspieszenie normalne (dośrodkowe) to:
𝑎
𝑛
=
𝑣
2
𝑅
.
Pomiędzy prędkością kątową a liniową w ruchu po okręgu istnieje związek:
𝜔 =
𝑣
𝑅
Obliczenia:
𝑎
𝑠
= 0 , 𝑏𝑜 𝑣 = const.
Aby wyznaczyd prędkośd kątową i przyspieszenie normalne trzeba przeliczyd prędkośd statku z km/h
na m/s:
𝑣 = 29 000
km
h
= 29 000
1000m
3600s
= 8 055
m
s
Wówczas:
m
F
n
v
R
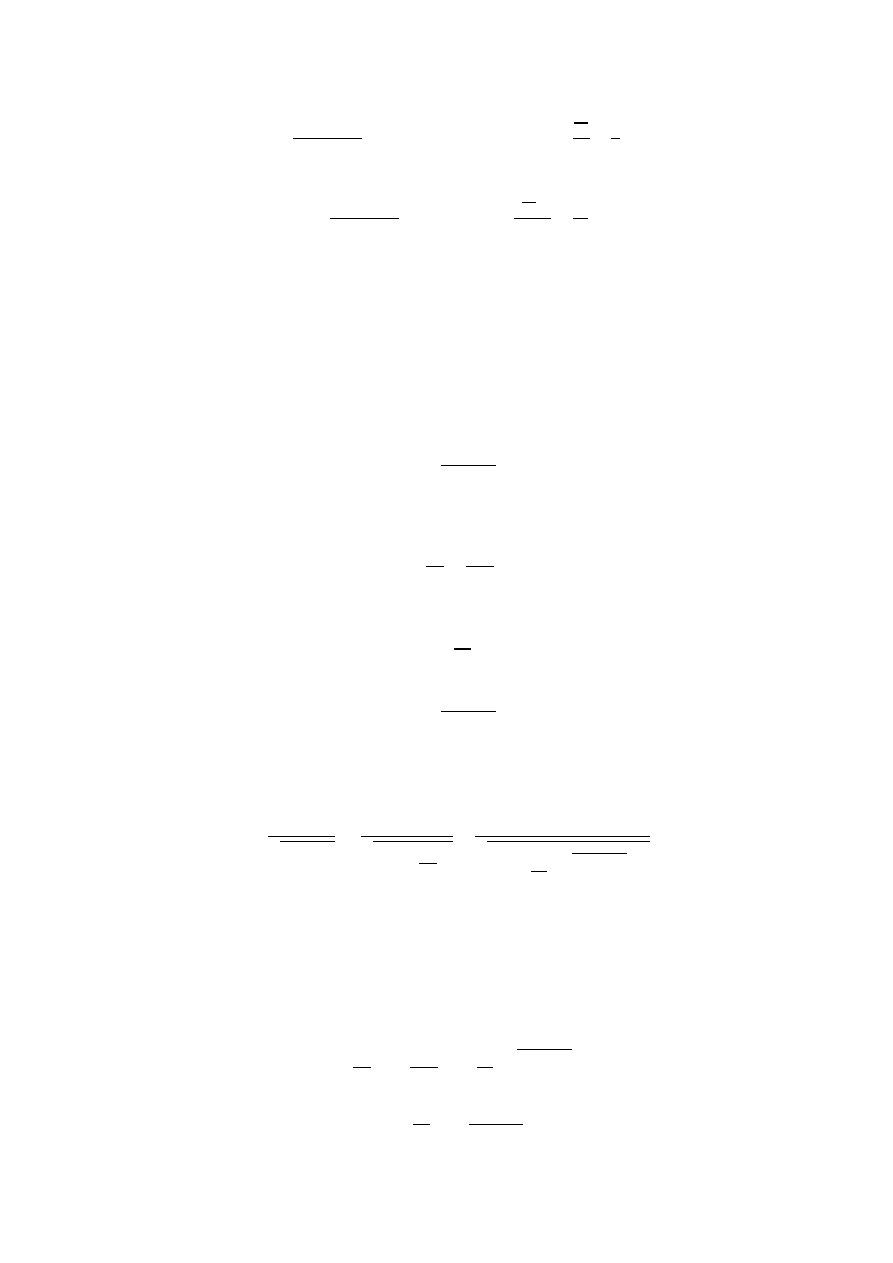
24
𝜔 =
8 055
3,22 ∙ 10
6
= 2 500 ∙ 10
−6
= 2,5 ∙ 10
−3
m
s
m
=
1
s
.
𝑎
𝑛
=
8 055
2
3,22 ∙ 10
6
= 64,88 ≅ 65
m
s
2
m
=
m
s
2
.
Odp.: Prędkośd kątowa statku wynosi 2,5 ∙ 10
−3
s
−1
, przyspieszenie dośrodkowe 65 m/s
2
,
przyspieszenie styczne równe jest zeru.
RZad103
Całkowite przyspieszenie ruchu w jednorodnym polu grawitacyjnym Ziemi to g = 9,81 m/s
2
.
Przyspieszenie to można rozłożyć na składowe: styczną a
s
i normalną a
n
, a wtedy:
𝑔 = 𝑎
𝑠
2
+ 𝑎
𝑛
2
Zgodnie z definicją przyspieszenie styczne to:
𝑎
𝑠
=
d𝑣
d𝑡
=
d 𝐯
d𝑡
;
a przyspieszenie normalne (dośrodkowe) to:
𝑎
𝑛
=
𝑣
2
𝑅
.
Z drugiej strony:
𝑎
𝑛
= 𝑔
2
− 𝑎
𝑠
2
.
Z dwóch powyższych wzorów wynika poszukiwana zależność promienia krzywizny od prędkości i jej
pochodnych, a przez to od czasu:
𝑅 =
𝑣
2
𝑔
2
− 𝑎
𝑠
2
=
𝑣
𝑥
2
+ 𝑣
𝑦
2
𝑔
2
−
d𝑣
d𝑡
2
=
𝑣
𝑥
2
+ 𝑣
𝑦
2
𝑔
2
−
d
d𝑡 𝑣
𝑥
2
+ 𝑣
𝑦
2
2
.
Zatem, aby znaleźć promień krzywizny toru rzutu w jednorodnym polu grawitacyjnym trzeba
wyznaczyć składowe: x-ową i y-ową prędkości oraz policzyć pochodną po czasie długości wektora v.
Wyrażenia opisujące siłę całkowitą i jej składowe otrzymamy mnożąc przez masę m punktu
materialnego przyspieszenie całkowite g i jego składowe styczną i normalną (dośrodkową):
𝐅 = 𝑚𝐠 lub 𝐹 = 𝑚𝑔
𝐹
𝑠
= 𝑚
d𝑣
d𝑡
= 𝑚
d 𝐯
d𝑡
= 𝑚
d
d𝑡
𝑣
𝑥
2
+ 𝑣
𝑦
2
;
𝐹
𝑛
= 𝑚
𝑣
2
𝑅
= 𝑚
𝑣
𝑥
2
+ 𝑣
𝑦
2
𝑅
,
25
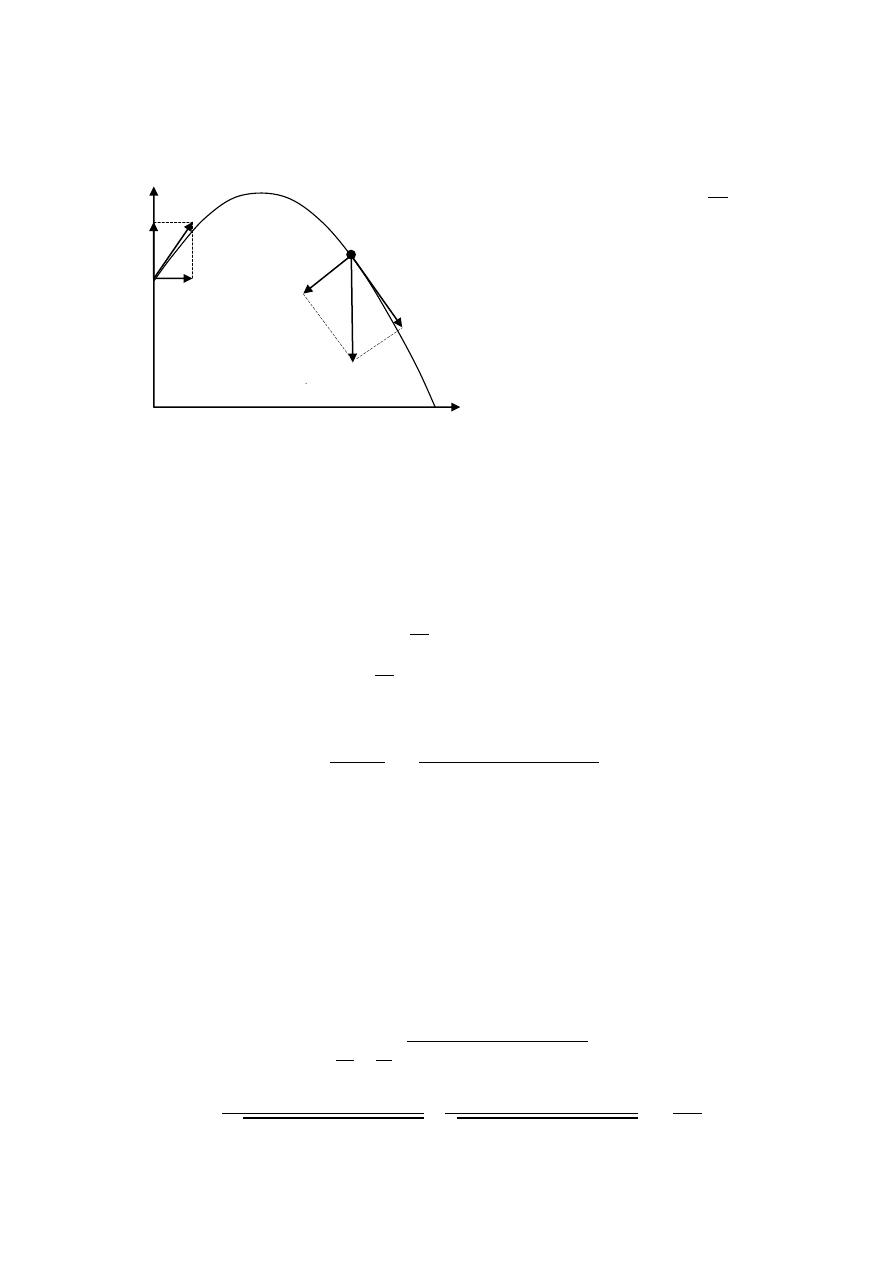
Rozważmy teraz kinematyczne równania ruchu w polu grawitacyjnym. W ogólnym przypadku można
napisać:
𝑥 𝑡 = 𝑣
0𝑥
𝑡
𝑦 𝑡 = 𝑦
0
+ 𝑣
0𝑦
𝑡 −
𝑔𝑡
2
2
gdzie
składowe wektora
prędkości
początkowej
𝐯
0
wyrażają się przez kąt 𝛼
nachylenia
wektora
prędkości
początkowej:
𝑣
0𝑥
= 𝑣
0
cos 𝛼
𝑣
0𝑦
= 𝑣
0
sin 𝛼
a y
0
oznacza początkową wysokość ciała
w chwili startu.
Przypadek A) zadania otrzymamy kładąc
= 0 (wówczas v
0y
= 0), a przypadek B) to y
0
= 0. Dzięki
takiemu podejściu możemy podad wartości sił w ogólnej postaci, a warunki początkowe uwzględnid
na koocu rozwiązania.
Wyznaczamy składowe prędkości w układzie kartezjaoskim różniczkując po czasie współrzędne:
𝑣
𝑥
𝑡 =
d𝑥
d𝑡
= 𝑣
0𝑥
= 𝑣
0
cos 𝛼
𝑣
𝑦
𝑡 =
d𝑦
d𝑡
= 𝑣
0𝑦
− 𝑔𝑡 = 𝑣
0
sin 𝛼 − 𝑔𝑡
Stąd łatwo znajdziemy długośd wektora prędkości jako pierwiastek z sumy kwadratów jego
współrzędnych:
𝑣 = 𝑣
𝑥
2
+ 𝑣
𝑦
2
= 𝑣
0
2
− 2𝑔𝑣
0
sin 𝛼 𝑡 + 𝑔
2
𝑡
2
.
Inny wariant rozwiązania polega na skorzystaniu z zależności składowych wektora prędkości od czasu
w dowolnym punkcie toru. Wektor prędkości jest styczny do toru w tym punkcie. Należy wykonad
rysunek, na którym rozłożyd należy wektor prędkości chwilowej na składowe wzdłuż osi OX i OY. W
tym samym punkcie dorysowac należy rozkład przyspieszenia całkowitego g skierowanego pionowo
w dół na kierunek styczny do toru i prostopadły. Znając funkcje trygonometryczne trójkąta
prostokątnego wektorów składowych prędkości i wektora prędkości z prostokątnego trójkąta dla
przyspieszeo całkowitego, stycznego i normalnego wyznaczamy szukane bez konieczności stosowania
rachunku różniczkowego. W. Salejda.
Możemy już policzyd przyspieszenie styczne z definicji:
𝑎
𝑠
=
d𝑣
d𝑡
=
d
d𝑡
𝑣
0
2
− 2𝑔𝑣
0
sin 𝛼 𝑡 + 𝑔
2
𝑡
2
,
𝑎
𝑠
=
−2𝑔𝑣
0
sin 𝛼 + 2𝑔
2
𝑡
2 𝑣
0
2
− 2𝑔𝑣
0
sin 𝛼 𝑡 + 𝑔
2
𝑡
2
=
𝑔 −𝑣
0
sin 𝛼 + 𝑔𝑡
𝑣
0
2
− 2𝑔𝑣
0
sin 𝛼 𝑡 + 𝑔
2
𝑡
2
= 𝑔
−𝑣
𝑦
𝑣
.
y
0
y
x
v
0x
v
0y
mg
F
n
F
s
v
0
m
26
Mnożąc to wyrażenie przez masę poruszającego się punktu otrzymamy siłę styczną:
𝐹
𝑠
= 𝑚𝑎
𝑠
=
𝑚𝑔 −𝑣
0
sin 𝛼 + 𝑔𝑡
𝑣
0
2
− 2𝑔𝑣
0
sin 𝛼 𝑡 + 𝑔
2
𝑡
2
= 𝑚𝑔
−𝑣
𝑦
𝑣
Otrzymany wzór jest słuszny w przypadku rzutu ukośnego (przypadek B). W rzucie poziomym
(przypadek A) znika czynnik zawierający sin 𝛼 = 0:
𝐹
𝑠
=
𝑚𝑔
2
𝑡
𝑣
0
2
+ 𝑔
2
𝑡
2
= 𝑚𝑔
−𝑣
𝑦
𝑣
Ponieważ całkowita siła jest znana:
𝐹 = 𝑚𝑔
to składową dośrodkową (normalną) siły znajdziemy z trójkąta sił:
𝐹
𝑛
= 𝑚𝑔
2
− 𝑚𝑔
𝑣
𝑦
𝑣
2
= 𝑚𝑔
𝑣
2
− 𝑣
𝑦
2
𝑣
2
= 𝑚𝑔
𝑣
𝑥
𝑣
Dla przypadku B) – rzut ukośny mamy
𝐹
𝑛
=
𝑚𝑔𝑣
0
cos 𝛼
𝑣
0
2
− 2𝑔𝑣
0
sin 𝛼 𝑡 + 𝑔
2
𝑡
2
= 𝑚𝑔
𝑣
0𝑥
𝑣
Dla przypadku A) – rzut poziomy mamy:
𝐹
𝑛
=
𝑚𝑔𝑣
0
𝑣
0
2
+ 𝑔
2
𝑡
2
= 𝑚𝑔
𝑣
0
𝑣
Możemy teraz wrócid do wyrażenia na promieo krzywizny i wstawid znalezione przyspieszenie
styczne:
𝑅 =
𝑣
2
𝑔
2
− 𝑎
𝑠
2
=
𝑣
2
𝑔
2
− 𝑔
−𝑣
𝑦
𝑣
2
=
𝑣
2
𝑔
2
− 𝑔
2
𝑣
𝑦
2
𝑣
2
=
𝑣
2
𝑔
𝑣
2
− 𝑣
𝑣
2
𝑣
=
𝑣
3
𝑔𝑣
𝑥
.
Dla przypadku A) – rzut poziomy otrzymamy zależnośd od czasu promienia krzywizny:
𝑅(𝑡) =
𝑣
0
2
+ 𝑔
2
𝑡
2
3
2
𝑔𝑣
0
.
Dla przypadku B) – rzut ukośny mamy
𝑅(𝑡) =
𝑣
0
2
− 2𝑔𝑣
0
sin 𝛼 𝑡 + 𝑔
2
𝑡
2
3
2
𝑔𝑣
0
cos 𝛼
.
Sprawdzamy jednostki:
𝑅 =
m
2
s
2
3
2
m
s
2
m
s
=
m
3
s
3
m
2
s
3
= m
Wyszukiwarka
Podobne podstrony:
Fizyka I Lista zadań numer 2
Fizyka I Lista zadan numer 8 id 176727
Fizyka I Lista zadań numer 7
Fizyka I Lista zadań numer 1
Fizyka I Lista zadań numer 5
Fizyka I Lista zadan numer 9 id 176728
Fizyka I Lista zadań numer 8
Fizyka I Lista zadań numer 9
Fizyka I Lista zadań numer 5
Fizyka lista zadan 1 id 176924 Nieznany
Fizyka lista zadań 1, Mechanika i Budowa Maszyn PWR MiBM, Semestr I, Fizyka
Fizyka lista zadan 1 id 176924 Nieznany
IV lista zadan z Fizyki Transport, 1 Studia PWR (Transport 1 Rok 1 Semestr), Fizyka PWR dr.Henryk Ka
więcej podobnych podstron