
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
MINISTERSTWO EDUKACJI
NARODOWEJ
Hanna Grządziel
Wykonywanie badań i pomiarów układów cyfrowych
stosowanych w telekomunikacji
725
[02].O1.04
Poradnik dla ucznia
Wydawca
Instytut Technologii Eksploatacji – Państwowy Instytut Badawczy
Radom 2006

„
Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
1
Recenzenci:
mgr inż. Anna Górska
mgr inż. Beata Miętus
Opracowanie redakcyjne:
mgr inż. Hanna Grządziel
Konsultacja:
mgr inż. Andrzej Zych
Korekta:
Poradnik stanowi obudowę dydaktyczną programu jednostki modułowej 725[02].O1.04
„Wykonywanie badań i pomiarów układów cyfrowych stosowanych w telekomunikacji”
zawartego w modułowym programie nauczania dla zawodu Monter sieci i urządzeń
telekomunikacyjnych.
Wydawca
Instytut Technologii Eksploatacji – Państwowy Instytut Badawczy, Radom 2006

„
Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
2
SPIS TREŚCI
1. Wprowadzenie
3
2. Wymagania wstępne
5
3. Cele kształcenia
6
4. Materiał nauczania
7
4.1. Sygnał cyfrowy i pozycyjne systemy liczbowe
7
4.1.1. Materiał nauczania
7
4.1.2. Pytania sprawdzające
14
4.1.3. Ćwiczenia
14
4.1.4. Sprawdzian postępów
16
4.2. Synteza układów kombinacyjnych
17
4.2.1. Materiał nauczania
17
4.2.2. Pytania sprawdzające
23
4.2.3. Ćwiczenia
23
4.2.4. Sprawdzian postępów
26
4.3. Komutacyjne i arytmetyczne układy cyfrowe
27
4.3.1. Materiał nauczania
27
4.3.2. Pytania sprawdzające
33
4.3.3. Ćwiczenia
33
4.3.4. Sprawdzian postępów
35
4.4. Układy sekwencyjne - liczniki, rejestry
36
4.4.1. Materiał nauczania
36
4.4.2. Pytania sprawdzające
41
4.4.3. Ćwiczenia
41
4.4.4. Sprawdzian postępów
43
4.5. Pamięci i układy mikroprocesorowe
44
4.5.1. Materiał nauczania
44
4.5.2. Pytania sprawdzające
47
4.5.3. Ćwiczenia
48
4.5.4. Sprawdzian postępów
49
5. Sprawdzian osiągnięć
50
6. Literatura
56

„
Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
3
1. WPROWADZENIE
Poradnik stanowi pomoc w przyswajaniu wiedzy o układach cyfrowych technologii TTL
i CMOS, a także ułatwia wykonywanie badań, lokalizację usterek i uruchamianie prostych
układów cyfrowych.
Poradnik ten zawiera:
1. Wymagania wstępne, czyli wykaz niezbędnych umiejętności i wiedzy, które powinieneś
mieć opanowane, aby przystąpić do realizacji tej jednostki modułowej.
2. Cele kształcenia tej jednostki modułowej.
3. Materiał nauczania (rozdział 4) podzielony na 5 tematów. Umożliwia on samodzielne
przygotowanie się do odpowiedzi na pytania sprawdzające, wykonania ćwiczeń i
sprawdzianów postępów. Wykonując sprawdzian postępów powinieneś odpowiadać na
pytanie „tak”–, jeśli opanowałeś materiał lub „nie”, co oznacza, że powinieneś jeszcze
nad tym popracować. Do poszerzenia wiedzy wykorzystaj wskazaną literaturę oraz inne
źródła informacji.
Ćwiczenia znajdujące się w każdym temacie zawierają treść poleceń, wskazówki
dotyczące sposobu wykonania oraz opis wyposażenia stanowiska potrzebnego do
realizacji ćwiczenia. Jeżeli masz trudności ze zrozumieniem tematu lub ćwiczenia, to
poproś nauczyciela lub instruktora o wyjaśnienie i ewentualne sprawdzenie, czy dobrze
wykonujesz daną czynność.
4. W rozdziale 5 poradnika zamieszczony jest zestaw zadań sprawdzających Twoje
opanowanie wiedzy i umiejętności z zakresu całej jednostki modułowej. Prawidłowe
wykonanie tego sprawdzianu jest dowodem osiągnięcia umiejętności określonych
w tej jednostce modułowej. Przykładowe testy sprawdzające znajdziesz także
w literaturze [1].
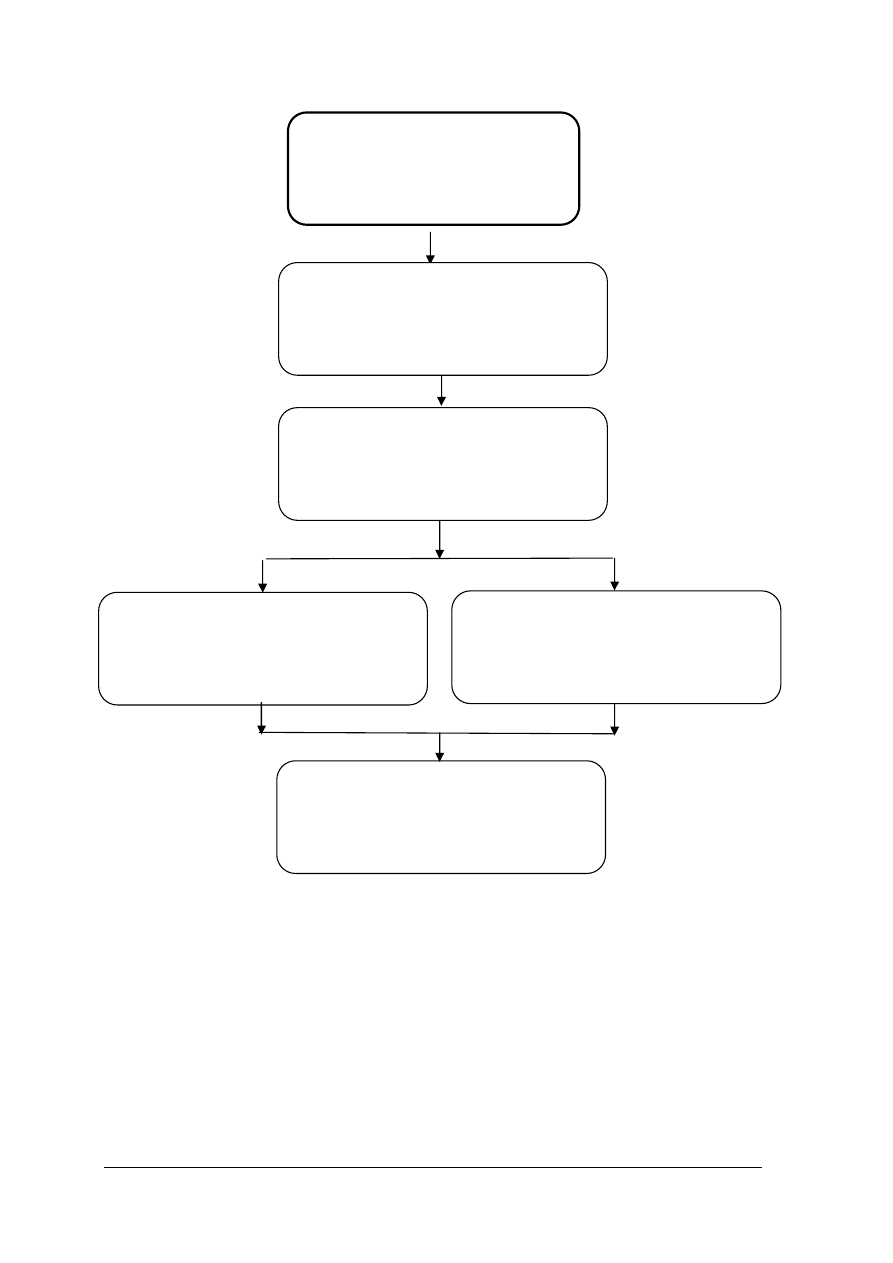
Jednostka modułowa: Wykonywanie badań i pomiarów układów cyfrowych stosowanych
w telekomunikacji, której treści teraz poznasz jest konieczna do zapoznania się z procesem
analizy działania i lokalizacji usterek w układach cyfrowych i stanowi jedną z pięciu
jednostek
w
module
725[02].O1
–
Pomiary
parametrów
elementów
i układów elektronicznych – schemat 1. Ten ogólnozawodowy moduł przygotowuje Cię do
realizacji modułów zawodowych programu nauczania dla zawodu monter sieci
i urządzeń telekomunikacyjnych.
Bezpieczeństwo i higiena pracy
W czasie pobytu w pracowni musisz przestrzegać regulaminów, przepisów bhp oraz
instrukcji przeciwpożarowych, wynikających z rodzaju wykonywanych prac. Przepisy te
poznasz
podczas
przeszkolenia
wstępnego
rozpoczynającego
Twoja
pracę
w laboratorium.
„
Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
4
725(02).O1
Pomiary parametrów elementów
i układów elektronicznych
725(02).O1.05
Analiza działania oraz zastosowania
podstawowych maszyn i urządzeń
elektrycznych
725(02).O1.03
Wykonywanie badań i pomiarów układów
analogowych stosowanych
w telekomunikacji
725(02).O1.01
Wykonywanie badań i pomiarów obwodów
prądu stałego
725(02).O1.02
Wykonywanie badań i pomiarów obwodów
prądu przemiennego
725(02).O1.04
Wykonywanie badań i pomiarów
układów cyfrowych stosowanych
w telekomunikacji
Schemat układu jednostek modułowych w module 725[02].O1

„
Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
5
2. WYMAGANIA WSTĘPNE
Przystępując do realizacji programu jednostki modułowej „Wykonywanie badań
i pomiarów układów cyfrowych stosowanych w telekomunikacji” powinieneś umieć:
–
stosować podstawowe prawa elektrotechniki,
–
interpretować
podstawowe
zjawiska
z
zakresu
elektrotechniki
występujące
w obwodach prądu stałego i zmiennego,
–
rozpoznawać na podstawie wyglądu oraz symbolu elementy elektroniczne,
–
analizować proste układy prądu stałego i zmiennego,
–
obliczać i oszacować podstawowe wielkości elektryczne w układach prądu stałego
i zmiennego,
–
dobierać przyrządy pomiarowe do pomiarów w układach prądu stałego i zmiennego,
–
rysować prosty układ pomiarowy,
–
planować pomiary w obwodach prądu stałego i zmiennego,
–
organizować stanowisko pomiarowe,
–
łączyć układy zgodnie ze schematem,
–
dokonywać pomiarów podstawowych wielkości elektrycznych w układach prądu stałego
i zmiennego,
–
analizować i interpretować wyniki pomiarów oraz wyciągać wnioski praktyczne,
–
przedstawiać wyniki w formie tabeli i wykresu,
–
czytać informację z tabeli lub wykresu,
–
demonstrować efekty wykonywanych pomiarów,
–
przewidywać zagrożenia dla życia i zdrowia w czasie realizacji ćwiczeń,
–
udzielać pierwszej pomocy w przypadkach porażenia prądem elektrycznym,
–
stosować procedurę postępowania w sytuacji zagrożenia,
–
korzystać z różnych źródeł informacji.

„
Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
6
3. CELE KSZTAŁCENIA
W wyniku realizacji programu jednostki modułowej powinieneś umieć:
–
zakodować liczby w kodzie binarnym, heksagonalnym i BCD,
–
zastosować podstawowe prawa algebry Boole’a,
–
rozpoznać na podstawie symbolu graficznego i katalogowego podstawowe elementy
cyfrowe i technologie ich wykonania,
–
rozróżnić funkcje podstawowych układów cyfrowych,
–
przeanalizować działanie prostych układów cyfrowych na podstawie schematów
logicznych,
–
przeanalizować działanie układów cyfrowych na podstawie schematów blokowych,
–
wskazać podstawowe zastosowania elementów i układów cyfrowych,
–
obsłużyć urządzenia do testowania elementów układów cyfrowych,
–
zinterpretować wyniki pomiarów w układach cyfrowych oraz wyciągnąć wnioski
praktyczne,
–
skorzystać z katalogów układów cyfrowych różnych technologii,
–
połączyć proste układy do badania elementów cyfrowych i bloków funkcjonalnych,
–
wykryć usterki w układach cyfrowych,
–
przewidzieć zagrożenia dla życia i zdrowia w czasie realizacji ćwiczeń.
„
Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
7
4. MATERIAŁ NAUCZANIA
4.1. Sygnał cyfrowy i pozycyjne systemy liczbowe
4.1.1. Materiał nauczania
4.1.1.1. Pozycyjne systemy liczbowe
Wszyscy posługujemy się na codzień systemem dziesiętnym, który jest systemem
pozycyjnym, tzn. na poszczególnych pozycjach zapisywana jest liczba jednostek, dziesiątek,
setek, tysięcy,....
2856 = 2 * 1000 + 0 * 100 + 0 * 10+6 * 1= 2 * 10
3
+ 8 * 10
2
+ 5 * 10
1
+ 6 * 10
0
cyfra na 1 pozycji
cyfra na 2 pozycji
cyfra na 4 pozycji
1000
100
10
1
Waga cyfry
10
3
10
2
10
1
10
0
2
8
5
6
W każdym systemie pozycyjnym wyróżnić możemy: podstawę systemu P i zbiór cyfr C
i
.
Dla systemu dziesiętnego:
P = 10 C
i
= {0,1,2,3,4,5,6,7,8,9}
Ostatnia cyfra w systemie o podstawie P to P-1
Ponieważ liczby mogą być zapisywane w różnych systemach liczbowych –
w systemach o różnych podstawach - w nawiasie obok liczby zapiszemy podstawę systemu
liczbowego, w którym jest zapisana, przykładowo liczbę dziesiętną zapiszemy w postaci -
2856
(10)
a liczbę w systemie o podstawie 2 – 1101
(2)
(można inaczej powiedzieć, że jest to
liczba w systemie dwójkowym zwanym także binarnym) [3].
4.1.1.2. Konwersja z systemu dwójkowego na dziesiętny
Dla systemu binarnego ( dwójkowego):
P = 2 C
i
= {0,1} Pamiętaj, że ostatnia cyfra w systemie o podstawie P to P-1
Wartość liczby
1101
(2)
możemy obliczyć korzystając z tabeli wagowej dla systemu binarnego
8
4
2
1
Waga cyfry
2
3
2
2
2
1
2
0
1
1
0
1
1101
(2)
= 1*8 + 1*4 + 0*2 + 1*1 = 13
(10)
W zależności od systemu liczbowego określona liczba ma inny zapis. Proces zmiany
sposobu zapisu liczby nazywany konwersją.
„
Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
8
4.1.1.3. Konwersja z systemu szesnastkowego na dziesiętny
W praktyce do analizy działania układów cyfrowych i mikroprocesorowych stosuje się
także system o podstawie P=16 (system szesnastkowy zwany również systemem
heksadecymalnym). Korzystanie z tego systemu pozwala skrócić – zmniejszyć liczbę cyfr
w dużych liczbach. Zapis w systemie szesnastkowym stosuje się przykładowo do zapisu
adresów portów oraz adresowania komórek pamięci w systemach komputerowych.
Dla systemu szesnastkowego:
P = 16 C
i
= {0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F}
gdzie A =10, B=11, C=12, D=13, E=14, F=15
Przykład liczby w systemie szesnastkowym:
4.1.1.4. Konwersja z systemu dziesiętnego na dwójkowy
Teraz dowiesz się jak można zamienić liczbę z systemu dziesiętnego na dwójkowy.
Algorytm postępowania przedstawia poniższy przykład:
Jak zauważyłeś, liczbę dziesiętną dzielimy przez nową podstawę systemu, w tym
przypadku przez 2, z dokładnością do liczby całkowitej – bez ułamków. Powstałe reszty
zapisane w odpowiedniej kolejności tworzą zapis dwójkowy. Dzielenie kończymy, gdy
uzyskamy wynik równy 0. Korzystając z tego algorytmu możemy zamienić liczbę
z dziesiętnego systemu na inny – o dowolnej podstawie.
256
16
1
Waga cyfry
16
2
16
1
16
0
2
A
F
2AF
(16)
= 2*16
2 +
10*16
1
+ 15*16
0
2AF
(16)
= 2*256 + 10*16 + 15*1 = 687
(10)
37
(10)
: 2 = 18, reszta 1
18 : 2 = 9, reszta 0
9 : 2 = 4, reszta 1
4 : 2 = 2, reszta 0
2 : 2 = 1, reszta 0
1 : 2 = 0, reszta 1
1
0
0
1
0
1
37
(10)
=
2
5
2
4
2
3
2
2
2
1
2
0
(2)
„
Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
9
1 0111 1011
(2)
=
1
7
B
0001 0111 1011
(2)
=
↔ ↔ ↔
1 7 B
16
2
16
1
16
0
(16)
101111011
(2)
= 17B
(16)
4.1.1.5. Konwersja z systemu dziesiętnego na szesnastkowy
Sposób wykonania tej zamiany jest podobny jak poprzednio tylko tym razem dzielimy
liczbę dziesiętną przez 16.
4.1.1.6. Konwersja z systemu binarnego na szesnastkowy
Z systemu binarnego na system szesnastkowy można zamienić liczbę korzystając
z następującego algorytmu: zapis liczby w systemie dwójkowym zaczynając od przecinka
dzielimy na grupy składające się z 4 cyfr, w razie potrzeby przed pierwszą cyfrą można
dopisać zera. Każdą grupę 4 cyfr składających się z 0 i 1 zamieniamy na cyfrę szesnastkową.
4.1.1.7.
Działania na liczbach w różnych systemach
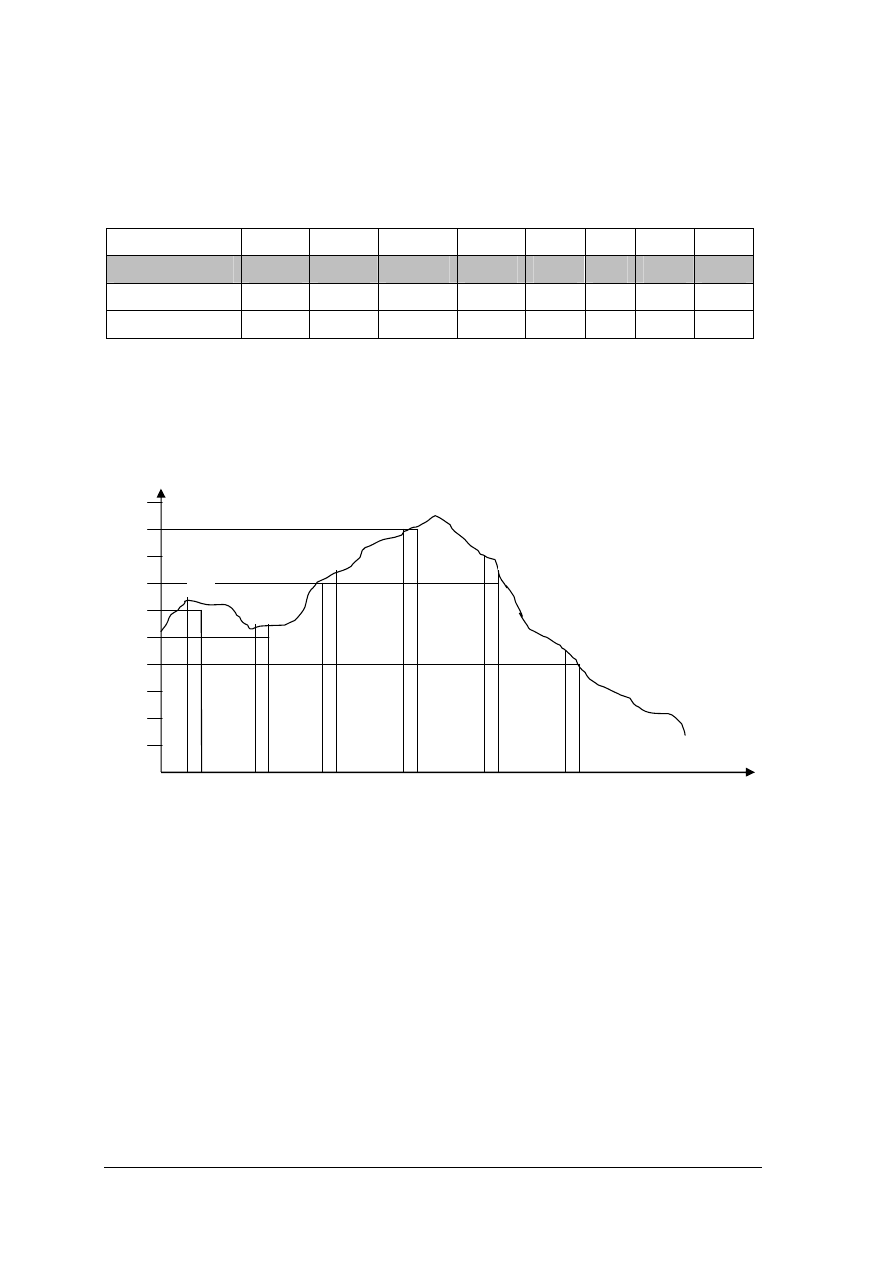
Dodawanie wykonujemy podobnie jak w systemie dziesiętnym: zaczynamy dodawać
cyfry od prawej strony i jeśli wynik jest większy od podstawy, to odejmujemy wielokrotność
podstawy, resztę zapisujemy pod kreską a wielokrotność podstawy dodajemy do sumy dwóch
kolejnych cyfr.
Odejmowanie wykonujemy podobnie: zaczynamy odejmować cyfry od prawej strony
i jeśli cyfra odjemnika jest większa niż cyfra odjemnej, to musimy wykonać pożyczkę
z pozycji wcześniejszej. Przypomnij sobie jak to się robi w systemie dziesiętnym
i przeanalizuj przykłady znajdujące się poniżej.
37
(10)
: 16 = 2 reszta 5
2 : 16 = 0 reszta 2
2
5
37
(10)
=
16
1
16
0
(16)
37
(10)
= 25
(16)
1
110001
(2)
+ 1011
111100
1
10A
(16)
+ 13F
249
1
108
(10)
+ 135
243
po pożyczce
0
1
1
2+
1 1 0 0 0 1
(2)
- 1 0 1 1
1 0 0 1 1 0
2
15+ 16+
3 0 A
(16)
- 1 3 F
1 C B
po pożyczce 2 9+ 10+
3 5 2
(10)
- 1 7 5
1 7 7
„
Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
10
4.1.1.8. Sygnał cyfrowy
System dwójkowy nazywany jest systemem binarnym od słowa „bit”. Bitem nazywamy
elementarną jednostkę informacji, która może przyjmować wartość 0 lub 1. Ciąg 8 bitów
nazywamy bajtem.
Liczba zapisana w jednym bajcie może mieć następującą postać:
waga bitu
128=2
7
64=2
6
32=2
5
16=2
4
8=2
3
4=2
2
2=2
1
1=2
0
liczba binarna
0
0
0
1
0
1
1
1
oznaczenie bitu
b
7
b
6
b
5
b
4
b
3
b
2
b
1
b
0
MSB
LSB
Bit związany z największą wagą nazywamy najstarszym lub najbardziej znaczącym –
MSB, a bit związany z najmniejszą wagą (skrajny od prawej strony) najmłodszym lub
najmniej znaczącym – LSB.
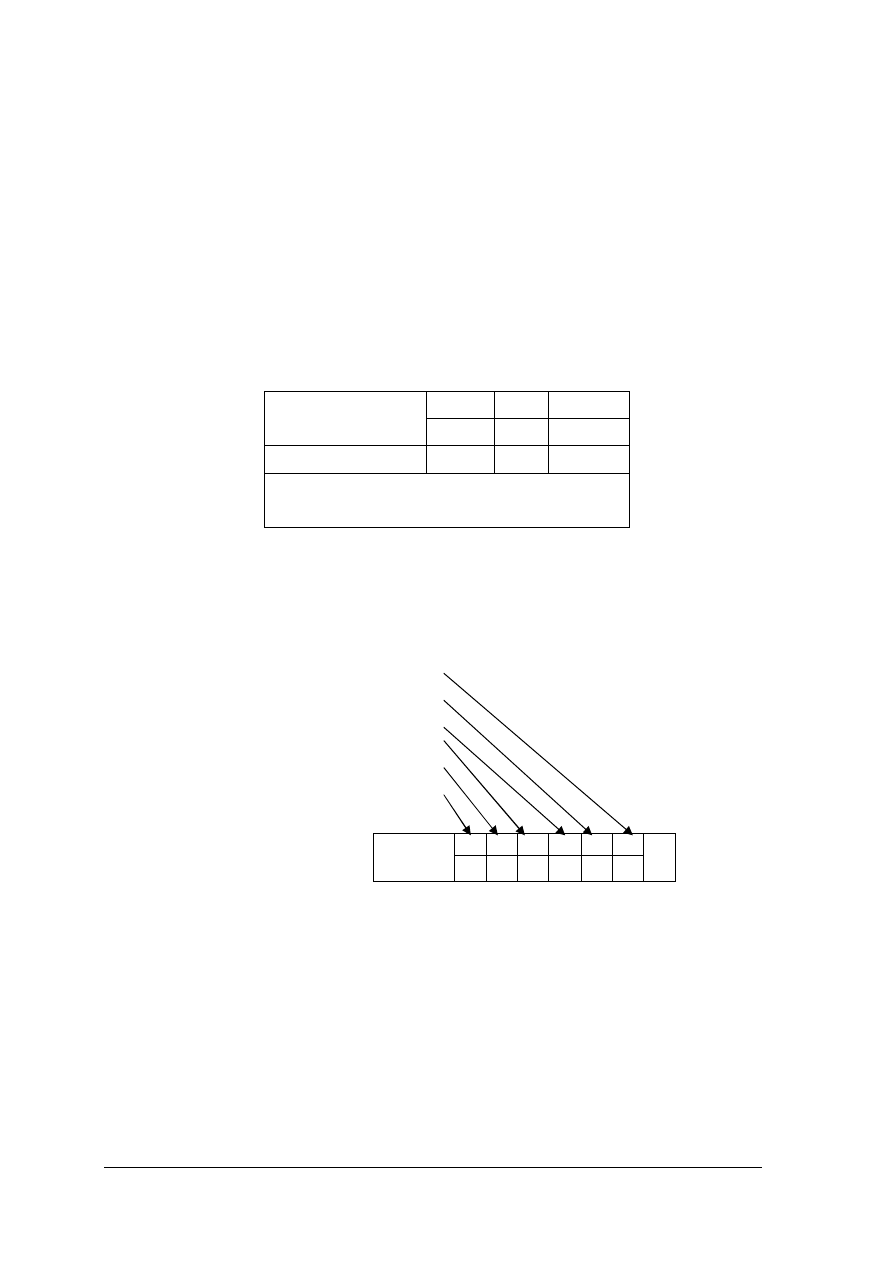
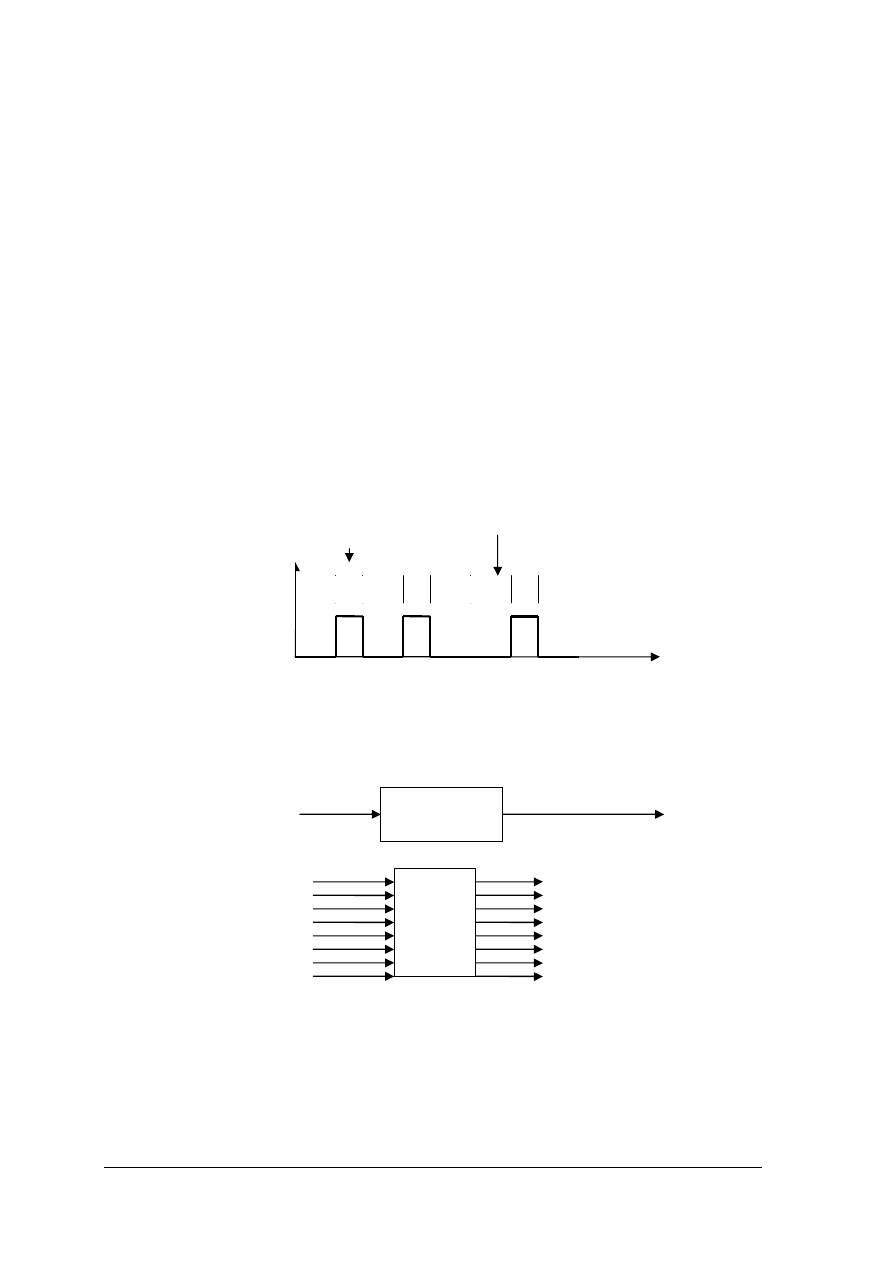
Nasze rozważania dotyczące zapisu binarnego mają na celu wyjaśnienie jak powstaje
sygnał cyfrowy. Na rys.1 przedstawiony jest przebieg amplitudy dźwięku w czasie. Jest to
sygnał analogowy – ciągły w czasie.
Rys. 1. Zmiana zapisu sygnału z analogowego na cyfrowy.
Aby zapisać „cyfrowo” dźwięk wykonuje się następujące czynności:
−
mierzy się wartość amplitudy sygnału w pewnych odcinkach czasu, przykładowo 44
tysiące razy na sekundę, jest to „próbkowanie”,
−
ustala się próg próbkowania dla określenie wartości amplitudy tak, aby można ją było
przedstawić jako całkowitą wielokrotność jednostki zwanej progiem próbkowania –
proces ten nazywamy „kwantyzacją”,
A
9
8
7
6
5
4
3
2
1
0110
0101
0111
1001
0111
0100
t
6
5
9
7
4
Binarne kody próbek
P
róg
k
w
an
to
wa
n
ia
7
„
Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
11
−
ustaloną w poprzednim kroku wartość amplitudy określoną przez liczbę wskazującą na
wielokrotność progu próbkowania zapisujemy w kodzie binarnym – proces ten
nazywamy „kodowaniem”.
Na rys. 1 pokazany jest zapis amplitudy w pewnym przedziale czasu. Załóżmy, że
dokonano w tym czasie 6 pomiarów amplitudy, a w wyniku kwantyzacji największa wartość
amplitudy wyniosła 9. Każdą, tak określoną wartość amplitudy zamieniono na postać binarną,
a do zakodowania zastosowano w tym przypadku kod binarny naturalny.
Jakość zapisu cyfrowego (jakość dźwięku) będzie zależna od tego, jaka jest częstotliwość
próbkowania – im więcej pomiarów w jednostce czasu, tym lepsza jakość oraz od progu
kwantyzacji – im mniejszy próg, tym lepiej (tym lepszy dźwięk).
Do zamiany sygnału z postaci analogowej na cyfrową wykorzystujemy układy
przetworników analogowo-cyfrowych (przetworników A/C). Sygnały cyfrowe są bardziej
odporne na zniekształcenia i można je regenerować. Dlatego też często w celu transmisji
sygnału przetwarzamy go w przetworniku A/C, aby w fazie końcowej odtworzyć sygnał
analogowy w przetworniku cyfrowo-analogowym (przetworniku C/A).
Cyfrowo zapisujemy nie tylko dźwięki, ale korzystając ze skanera można też zapisywać
cyfrowo obraz. Często korzystamy z cyfrowych aparatów fotograficznych. Wszystkie te
informacje mają postać sygnału cyfrowego, w którym rozróżniamy dwa stany stan „1” zwany
wysokim – H i stan „0” zwany niskim – L.
Przebieg sygnału cyfrowego może być następujący:
Rys. 2. Cyfrowa postać sygnału.
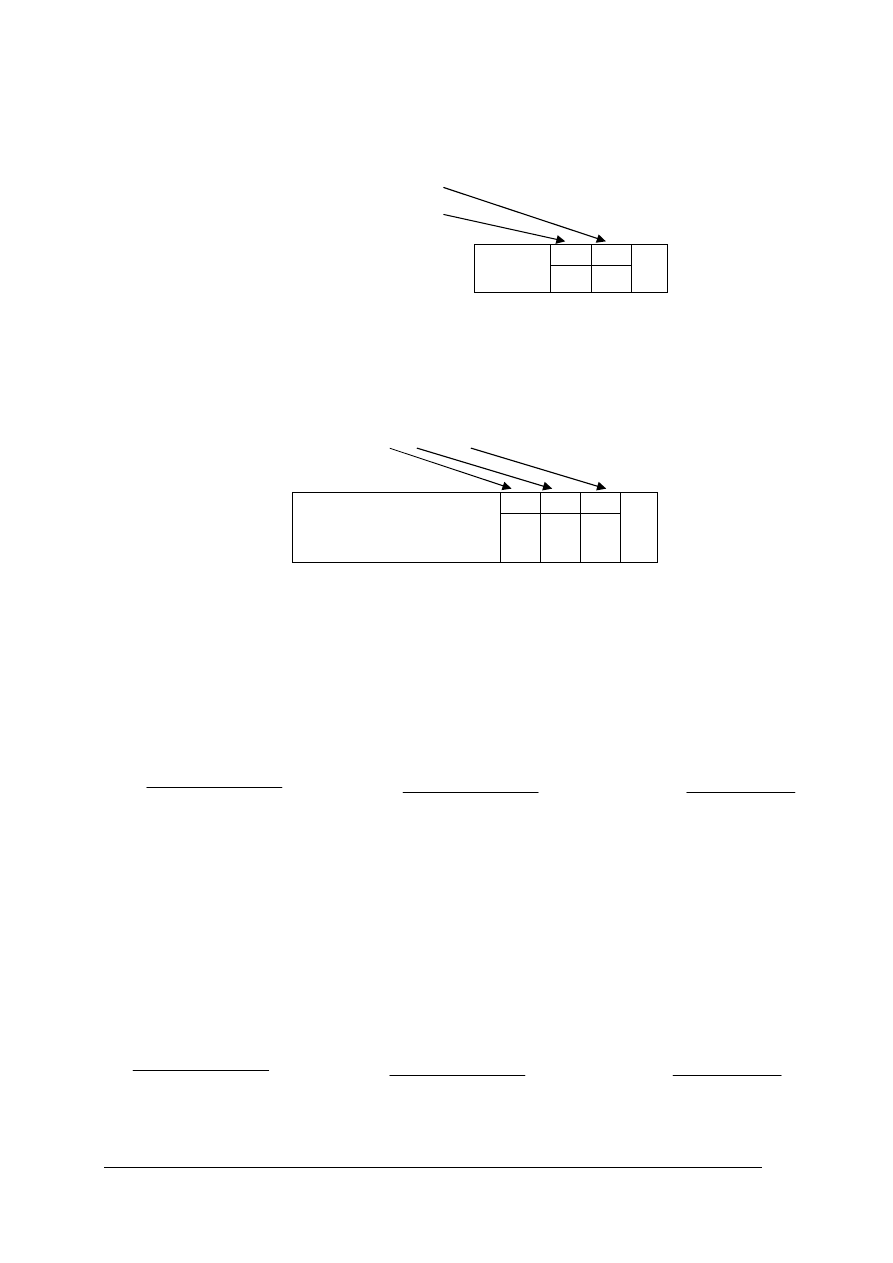
Sygnały mogą być przesyłane, wprowadzane lub wyprowadzane z układu cyfrowego
szeregowo – „bit po bicie” lub równolegle – wszystkie bity „jednocześnie”
Rys. 3. Transmisja sygnału cyfrowego: a) szeregowa, b) równoległa.
4.1.1.9. Kody binarne
Jak już wcześniej wyjaśnialiśmy, aby dokonać cyfrowego zapisu informacji analogowej
należy wykonać: próbkowanie, kwantyzację i kodowanie. Teraz zapoznasz się
z najpopularniejszymi kodami służącymi do kodowania informacji.
1
0
0
0
1
t[s]
A
[v]
0
1
0
Stan wysoki
Stan niski
01010010
01010010
0
1
0
1
0
0
1
0
1
0
1
0
0
1
a)
b)
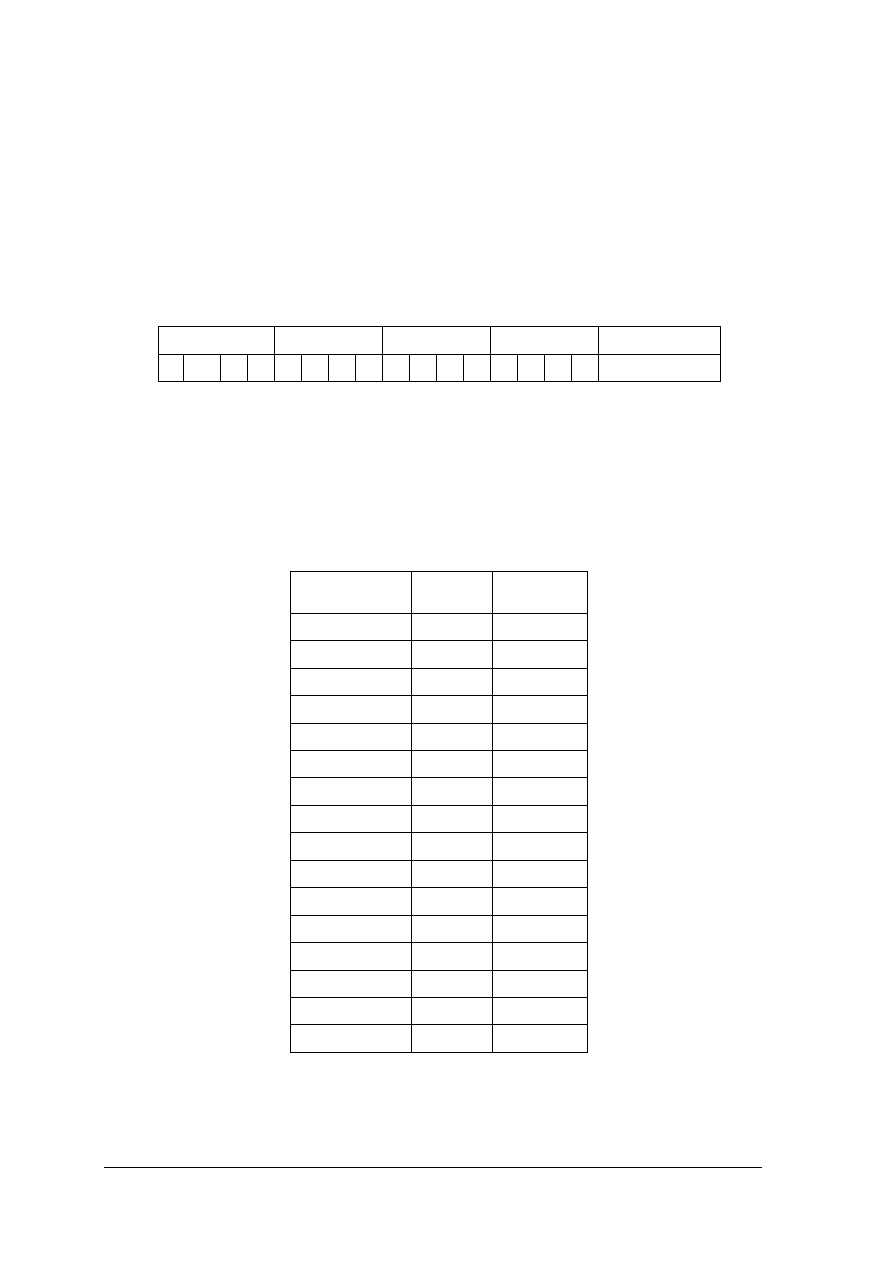
„
Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
12
Kod binarny prosty - naturalny
Zapis w postaci naturalnego systemu dwójkowego został już wcześniej opisany. Można
za jego pomocą kodować informacje, które dadzą się zapisać w postaci liczb całkowitych bez
znaku. Kodu tego używa się na przykład do kodowania rzeczywistych adresów komórek
pamięci.
Kod BCD
Kodowanie dwójkowo-dziesiętne BCD (od angielskiego Binary Coded Decimal) polega
na zastąpieniu każdej cyfry dziesiętnej odpowiadającym jej 4-cyfrowym zapisem binarnym.
5 9 0 3
(10)
= 0101 1001 0000 0011
BCD 8421
Tabela 1. Przykład liczby dziesietnej zakodowanej kodem BCD .
5
9
0
3
(10)
0 1
0 1 1 0 0 1 0 0 0 0 0 0 1 1
BCD 8421
Kod szesnastkowy
Jeżeli podzielimy bajt na dwie czterobitowe grupy - dwa półbajty, to będziemy mogli
przedstawić je za pomocą jednej cyfry szesnastkowej. Stosowanie kodu szesnastkowego
pozwala znacznie skrócić zapis adresów binarnych lub kodów instrukcji w języku
wewnętrznym procesora.
Kodowanie znacznie ułatwi Ci umieszczona poniżej tabela kodów.
Tabela 2. Tabela kodów
Cyfra
szesnastkowa
Zapis
binarny
Zapis
dziesiętny
0
0000
0
1
0001
1
2
0010
2
3
0011
3
4
0100
4
5
0101
5
6
0110
6
7
0111
7
8
1000
8
9
1001
9
A
1010
10
B
1011
11
C
1100
12
D
1101
13
E
1110
14
F
1111
15
System szesnastkowy jest bardzo zwięzły w zapisie. Bardzo proste jest przejście
z systemu binarnego na szesnastkowy i odwrotnie. W celu oznaczenia systemu można na
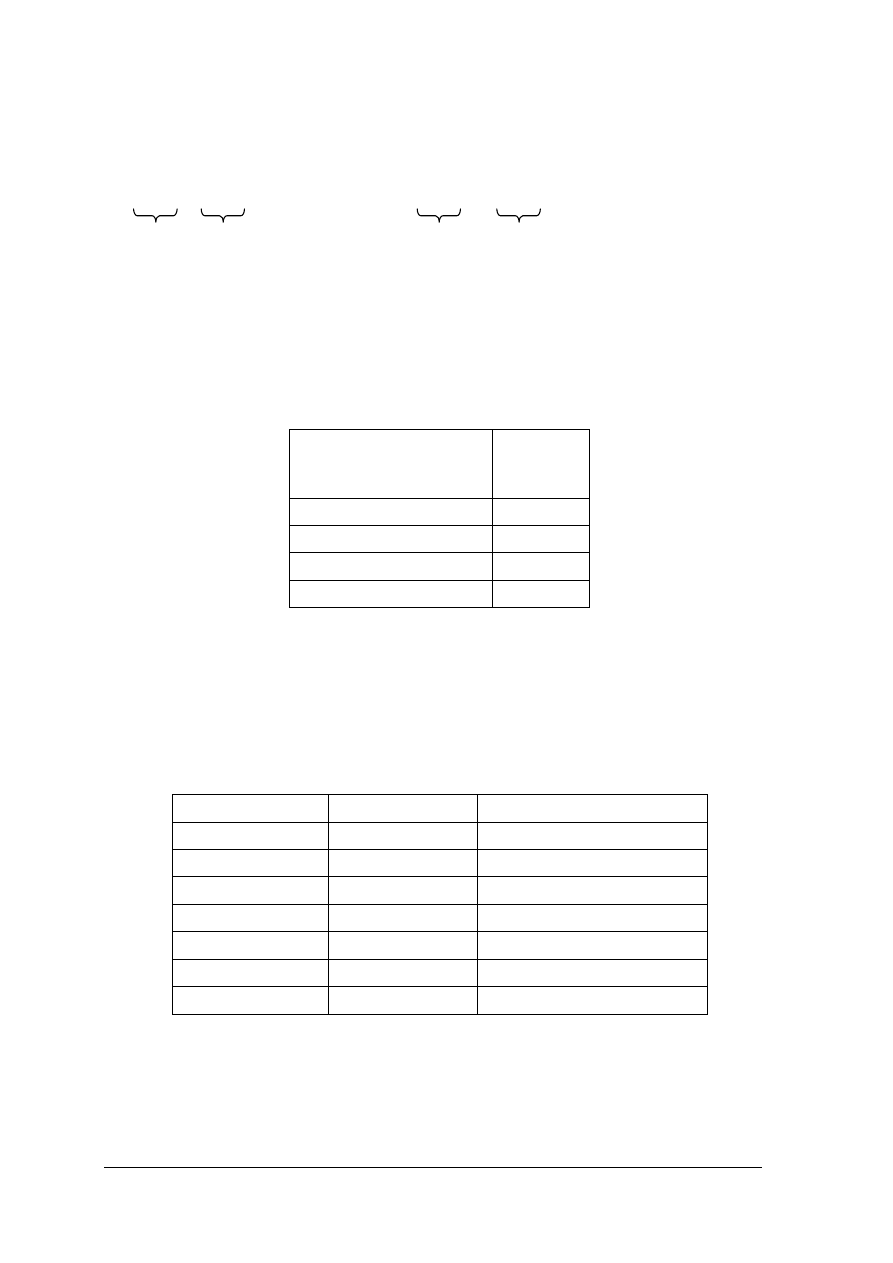
„
Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
13
końcu liczby umieścić literę B – dla kodu binarnego lub H – dla kodu szesnastkowego oraz D
– dla dziesiętnego. Ta konwersja umożliwia też zamianę odwrotną.
1110
0010
B = E2 H
3
C
H =
00111100 B
E
2
0011
1100
Kody detekcyjne
W układach cyfrowych stosowane są najczęściej dwa kody detekcyjne, kody, które
umożliwiają wykrycie błędu:
1. Kod z kontrolą parzystości – do bitów stanowiących informację dodajemy jeden bit
kontrolny, którego wartość zależy od tego czy w informacji jest parzysta liczba jedynek.
Tabela 3. Informacje uzupełnione bitem kontrolnym
Informacja
Bit
kontrolny
parzystości
1010010
1
0010001
0
1111111
1
0000000
0
W każdym słowie kodowym składającym się z informacji i bitu kontrolnego jest parzysta
liczba jedynek. Stwierdzenie nieparzystej ich liczby w informacji sygnalizuje fakt wystąpienia
błędu na drodze transmisji. Niestety przekłamanie na dwóch pozycjach pozostaje nie wykryte,
jednak zdarzenie to jest mało prawdopodobne.
2. Kod ze stałą liczbą jedynek - kod „1 z N”, gdzie N może być dowolna liczbą całkowitą.
Kod „1zN” jest najczęściej stosowanym kodem ze stałą liczbą jedynek. Znając liczbę
jedynek w słowie kodowym można łatwo wykryć błąd w transmisji.
Tabela 4. Tabela kodów „1 z 10”
Kod „1 z 10”
Zanegowany kod „1z 10”
Cyfra/ waga kodu
9 8 7 6 5 4 3 2 1 0
9 8 7 6 5 4 3 2 1 0
0
0 0 0 0 0 0 0 0 0 1
1 1 1 1 1 1 1 1 1 0
1
0 0 0 0 0 0 0 0 1 0
1 1 1 1 1 1 1 1 0 1
2
0 0 0 0 0 0 0 1 0 0
1 1 1 1 1 1 1 0 1 1
....
..........................
8
0 1 0 0 0 0 0 0 0 0
1 0 1 1 1 1 1 1 1 1
9
1 0 0 0 0 0 0 0 0 0
0 1 1 1 1 1 1 1 1 1
Kod ASCII
W postaci binarnej można zapisywać nie tylko liczby, ale i dowolne znaki. Wystarczy
ustawić je w kolejności i każdemu przypisać numer - kod znaku. Litery ustawiono
w porządku alfabetycznym, kolejność innych znaków ustalono tworząc w ten sposób

„
Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
14
standard. Najbardziej znany jest standard w skrócie określany ASCII. Kod znaku jest
zapisywany w jednym bajcie. Tabelę tego kodu znajdziesz w literaturze [3, s. 325].
4.1.2. Pytania sprawdzające
Odpowiadając na pytania sprawdzisz, czy jesteś przygotowany do wykonania ćwiczeń.
1. Czym się charakteryzują pozycyjne systemy liczbowe?
2. Jaka jest podstawa systemu binarnego i jakie cyfry mogą występować w binarnym
zapisie liczby?
3. Jaka jest podstawa systemu szesnastkowego i jakie cyfry mogą występować
w zapisie liczby w tym systemie?
4. Jak dokonać konwersji liczby z sytemu binarnego na system dziesiętny i odwrotnie?
5. Jak wykonać dodawanie liczb zapisanych w systemie binarnym?
6. Jak dokonać konwersji liczby z sytemu dziesiętnego na system szesnastkowy
i odwrotnie?
7. Jak dokonać konwersji liczby z sytemu binarnego na system szesnastkowy
i odwrotnie?
8. Jakie procesy pozwalają przekształcić sygnał analogowy na postać cyfrową?
9. Jakie czynniki wpływają na jakość sygnału cyfrowego?
10. Gdzie znajduje zastosowanie kod binarny i heksadecymalny?
11. Do czego służą kody detekcyjne?
12. Do czego służy kod ASCII?
13. Jakie korzyści wynikają ze stosowania przetworników A/C i C/A?
14. W jakich urządzeniach stosuje się przetwarzanie informacji z postaci analogowej na
cyfrową i odwrotnie?
15. Od czego zależy jakość przetwarzanego sygnału, uzasadnij to na przykładach?
4.1.3. Ćwiczenia
Ćwiczenie 1
Wykonaj konwersję:
- z systemu dwójkowego na dziesiętny następujących liczb:
a) 1010
(2)
b) 10101
(2)
c) 1110101
(2)
- z systemu dziesiętnego na dwójkowy następujących liczb:
d) 33
(10)
e) 10
(10)
f) 121
(10)
- z systemu dziesiętnego na szesnastkowy następujących liczb:
g) 33
(10)
h) 13
(10)
i) 121
(10)
-
z systemu szesnastkowego na dziesiętny następujących liczb:
j) 21
(16)
k) E1
(16)
- z systemu szesnastkowego na binarny następujących liczb:
l) 91
(16)
m) E1
(16)
-
z systemu dwójkowego na dziesiętny następujących liczb:
n) 10101
(2)
o) 11101011
(2)
„
Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
15
Sposób wykonania ćwiczenia
Aby wykonać ćwiczenie, powinieneś:
1) zapoznać się z algorytmem wykonania konwersji liczb zapisanych w różnych systemach
(Materiał nauczania pkt.4.1.1),
2) dokonać konwersji krok po kroku,
3) sprawdzić poprawność wykonanych działań poprzez wykonanie konwersji odwrotnej.
Jeśli masz trudności zwróć się o pomoc do nauczyciela.
Wyposażenie stanowiska pracy:
−
przybory do pisania,
−
poradnik ucznia,
−
literatura[3].
Ćwiczenie 2
Wykonaj następujące działania arytmetyczne:
Sposób wykonania ćwiczenia
Aby wykonać ćwiczenie, powinieneś:
1) zapoznać się z algorytmem wykonania działań na liczbach w różnych systemach
(Materiał nauczania pkt.4.1.1),
2) wykonać działanie krok po kroku zwracając szczególną uwagę na nową podstawę
systemu, w którym wykonywane jest działanie,
3) sprawdzić poprawność wykonanych działań poprzez wykonanie działania odwrotnego, –
jeśli masz trudności zwróć się o pomoc do nauczyciela.
Wyposażenie stanowiska pracy:
−
przybory do pisania, kalkulator,
−
poradnik dla ucznia,
−
literatura [3].
Ćwiczenie 3
Zakoduj liczbę dziesiętną 53 w następujących kodach:
a) w kodzie binarnym,
b) w kodzie BCD
8421,
c) w kodzie heksadecymalnym.
Sposób wykonania ćwiczenia
Aby wykonać te ćwiczenie, powinieneś:
1) zapoznać się z tabelami odpowiednich kodów (Materiał nauczania pkt.4.1.1),
2) wykonać kodowanie,
3) sprawdzić poprawność kodowania, – jeśli masz trudności zwróć się o pomoc do
nauczyciela.
b) 1 1 1 1 0 1
(2)
- 1 0 1 1
a) 1 1 0 0 0 1
(2)
+ 1 0 1 1

„
Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
16
Wyposażenie stanowiska pracy:
−
przybory do pisania,
−
poradnik ucznia,
−
literatura [3].
Ćwiczenie 4
Zakoduj swoje imię korzystając z tabeli kodów ASCII zapisując kod binarny każdej litery
i jej odpowiednik w kodzie heksadecymalnym.
Kod binarny każdej litery uzupełnij o bit parzystości.
Sposób wykonania ćwiczenia
Aby wykonać te ćwiczenie, powinieneś:
4) zapoznać się z tabelami odpowiednich kodów (Materiał nauczania pkt.4.1.1),
5) wykonać kodowanie,
6) sprawdzić poprawność kodowania, – jeśli masz trudności zwróć się o pomoc do
nauczyciela.
Wyposażenie stanowiska pracy:
−
przybory do pisania,
−
poradnik ucznia,
−
literatura [3].
4.1.4. Sprawdzian postępów
Tak Nie
Czy potrafisz:
1) zapisać liczbę w systemie dwójkowym i szesnastkowym?
¨
¨
2) dokonać konwersji z systemu dwójkowego na dziesiętny?
¨
¨
3) dokonać konwersji z systemu szesnastkowego na dziesiętny?
¨
¨
4) dokonać konwersji z systemu dziesiętnego na dwójkowy?
¨
¨
5) dokonać konwersji z systemu dziesiętnego na szesnastkowy?
¨
¨
6) dokonać konwersji z systemu dwójkowego na szesnastkowy?
¨
¨
7) dokonać konwersji z systemu szesnastkowego na dwójkowy?
¨
¨
8) zapisać liczbę w kodzie binarnym, heksadecymalnym, BCD
8421
?
¨
¨
9) wykonać kodowanie informacji w kodzie ASCII?
¨
¨
10) wykonać dodawanie i odejmowanie liczb w systemie binarnym?
¨
¨
11) określić procesy umożliwiające zamianę sygnału analogowego
na postać cyfrową?
¨
¨
12) ocenić wpływ parametrów przetwarzania A/C na jakość
odtwarzanego sygnału analogowego?
¨
¨
13) wskazać przykłady praktycznego zastosowania przetworników
A/C i C/A
¨
¨
„
Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
17
4.2. Synteza układów kombinacyjnych
4.2.1. Materiał nauczania
4.2.1.1. Algebra Boole’a
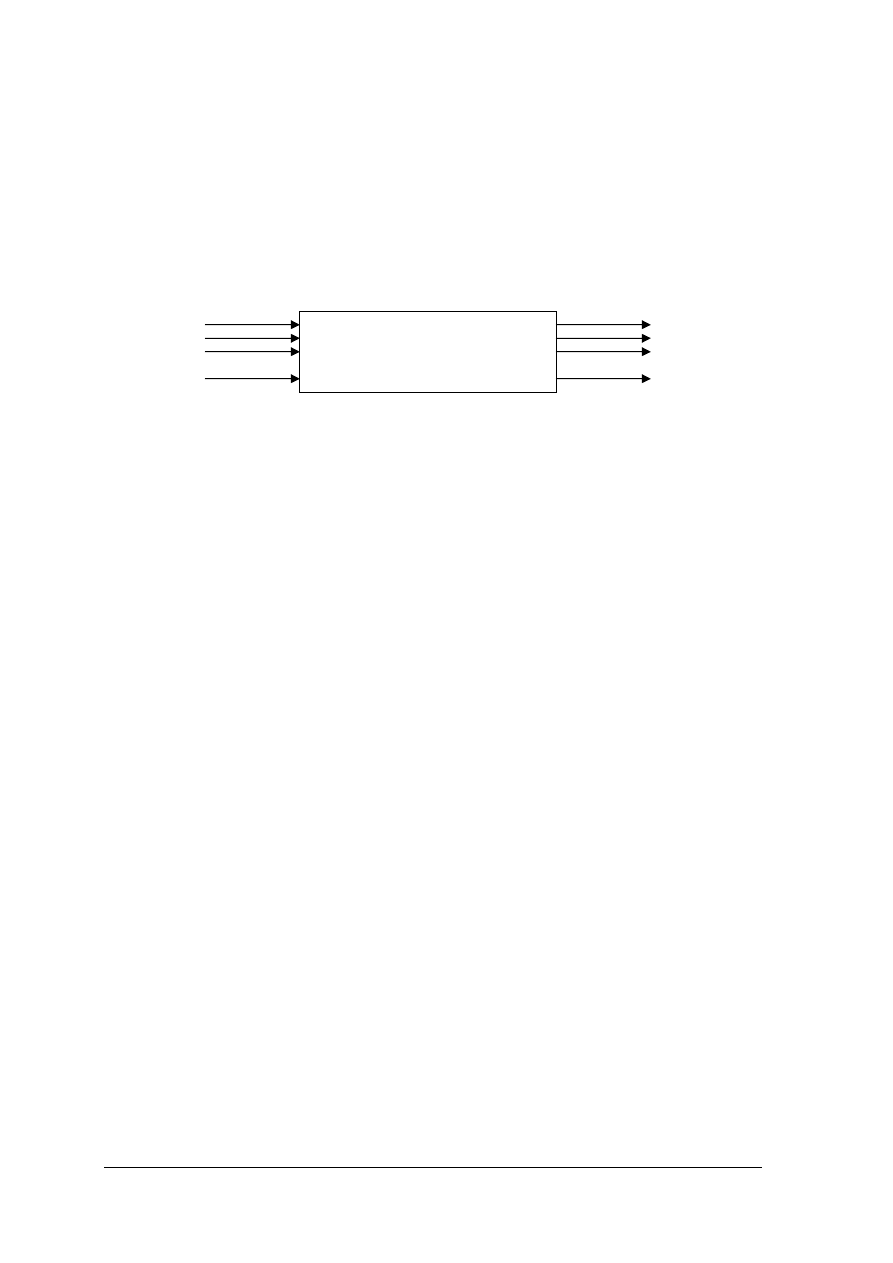
Układem kombinacyjnym nazywamy układ logiczny, w którym stan na wyjściach zależy
wyłącznie od stanu na wejściach – od kombinacji stanów na wejściach.
Rys. 4. Układ kombinacyjny.
Układy logiczne działają zgodnie z aksjomatami algebry Boole’a. Aksjomat to
twierdzenie, które przyjmujemy za prawdziwe bez udowadniania. Algebra ta posługuje się
tylko dwoma wielkościami: „1” logiczna - prawda i „0” logiczne – fałsz. Na dowolnych
zmiennych logicznych, które mogą mieć wartość 1 lub 0 można wykonać następujące
działania logiczne: dodawanie logiczne, mnożenie logiczne i negację. Dla ułatwienia
działania te będziemy oznaczać podobnie jak w algebrze, którą posługujesz się dotychczas:
dodawanie logiczne – znak „+”, mnożenie logiczne – znak „ ∙ ”. Negację zmiennej A
zaznaczamy A’ lub Ā. Pamiętaj, że dodawanie arytmetyczne to inne działanie niż dodawanie
logiczne i wyniki tych działań też mogą być różne. Zapoznaj się z podstawowymi
twierdzeniami algebry Boole’a:
A + A + A + ∙∙∙ + A = A
A ∙ A ∙ A ∙∙∙ A = A
A + 1 = 1
A ∙ 1 = A
A + 0 = A
A ∙ 0 = 0
A + A’= 1
A ∙ A’ = 0
Prawo podwójnej negacji A’’ = A
Prawa de Morgana:
(A + B )’ = A’∙ B’
(A ∙ B )’ = A’+ B’
Pozostałe prawa znajdziesz w literaturze [3, 6]. Korzystając z tych aksjomatów będziesz mógł
w sposób uproszczony opisywać działanie układów cyfrowych.
4.2.1.2. Bramki logiczne – funktory
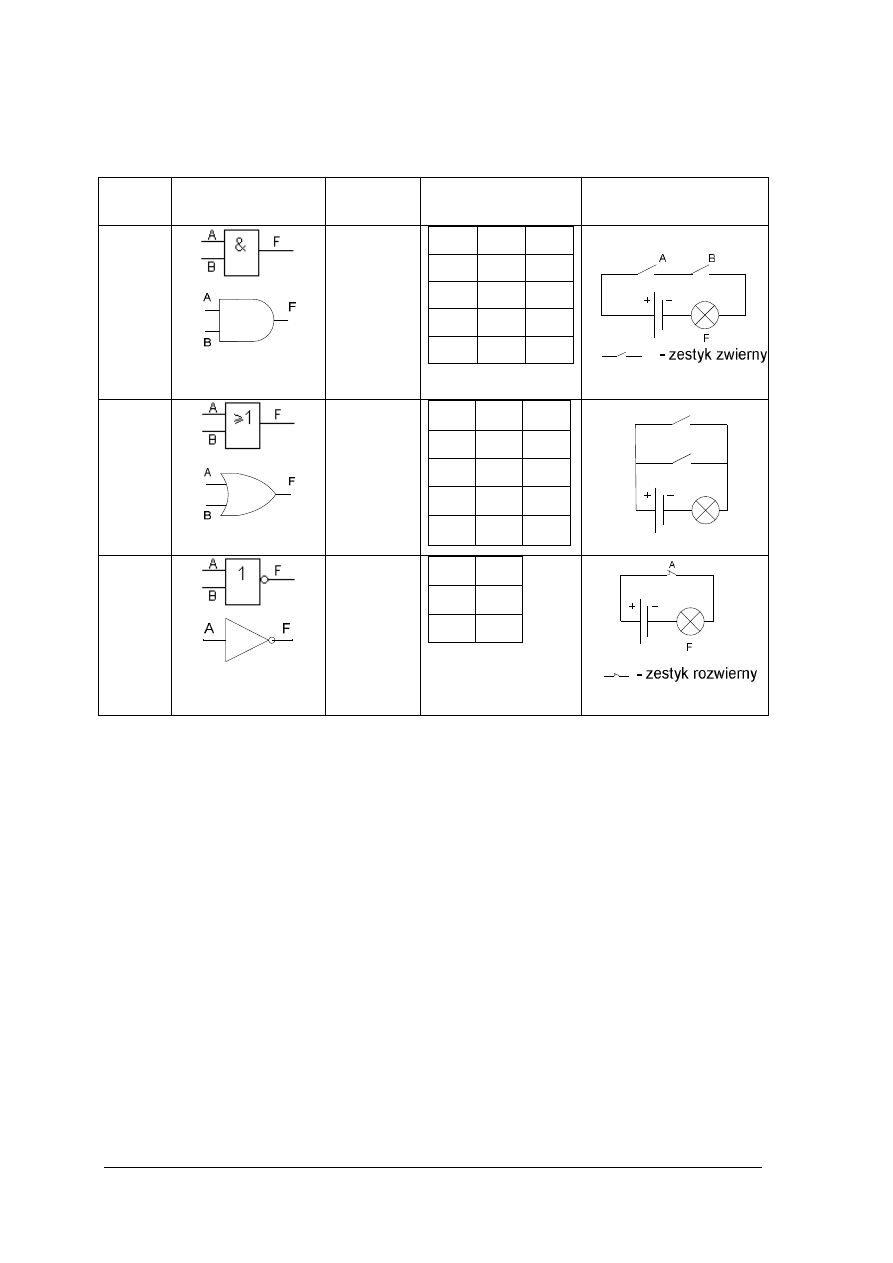
Układy, które realizują funkcje logiczne nazywamy popularnie bramkami. Tabela 6
przedstawia informacje o trzech podstawowych bramkach logicznych: AND, OR, NOT. A i B
są wejściami, na które podawane są sygnały logiczne „0” lub „1”. Jaki sygnał będzie na
wyjściu bramki, przy każdej z czterech możliwych kombinacji sygnałów wejściowych,
przedstawia tabela działania.. Ostania kolumna tabeli 6 zawiera obwody zastępcze na
przełącznikach, które ułatwią Ci zrozumienie działania odpowiednich bramek. Przeanalizuj te
układy zakładając, że jeśli żarówka się świeci to odpowiada to F=1, dla zestyków zwiernych
przyjmujemy, że zestyk w stanie otwartym odpowiada stanowi logicznemu „0”, zestyk
Układ kombinacyjny
Wej
śc
ia
W
yj
śc
ia
„
Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
18
w stanie zamkniętym odpowiada stanowi logicznemu „1”. Dla zestyków rozwiernych
przyjmujemy odwrotnie.
Tabela 6. Podstawowe bramki logiczne
Nazwa
bramki
Symbol graficzny
Funkcja
Tabela działania
Realizacja
na
przełącznikach
AND
F = A ∙ B
mnożenie
logiczne
(iloczyn
logiczny)
A
B
F
0
0
0
0
1
0
1
0
0
1
1
1
OR
F = A + B
dodawanie
logiczne
(suma
logiczna)
A
B
F
0
0
0
0
1
1
1
0
1
1
1
1
A
B
F
NOT
F = A’
negacja
A
F
0
1
1
0
Za pomocą bramek AND, OR, NOT można zrealizować dowolny układ logiczny. Tworzą
one układ funkcjonalnie pełny.
W praktycznym zastosowaniu znajdują się jeszcze inne bramki logiczne. Bramki NAND
i NOR są bramkami uniwersalnymi, co oznacza, że za pomocą wyłącznie jednego typu tych
bramek, można zrealizować każdy układ. Każda z tych bramek też tworzy układ
funkcjonalnie pełny.
Bramki wykonujące tę samą funkcję logiczną mogą różnić się dodatkowymi
parametrami. Bardzo powszechne w zastosowaniu są bramki NAND z otwartym kolektorem,
posiadające możliwość regulacji prądu na wyjściu a poprzez to posiadające większą
obciążalność. Bramki NAND z przerzutnikiem Schmidta charakteryzują się różnymi
napięciami przełączania w zależności od tego czy napięcie wejściowe wzrasta czy maleje [3].
Kolejną grupą są bramki trójstanowe, w których obok stanów „1” i „0” pojawia się stan
wysokiej impedancji HZ – stan, w którym rezystancja bramki > 10
9
Ω. Bramki transmisyjne
obok pracy trójstanowej mają możliwość transmisji dwukierunkowej zarówno sygnałów
cyfrowych jak i analogowych. Więcej informacji na temat tych bramek znajdziesz
w literaturze [3].
Dodatkowe bramki to ExOR i ExNOR, także bardzo często stosowane w praktyce.
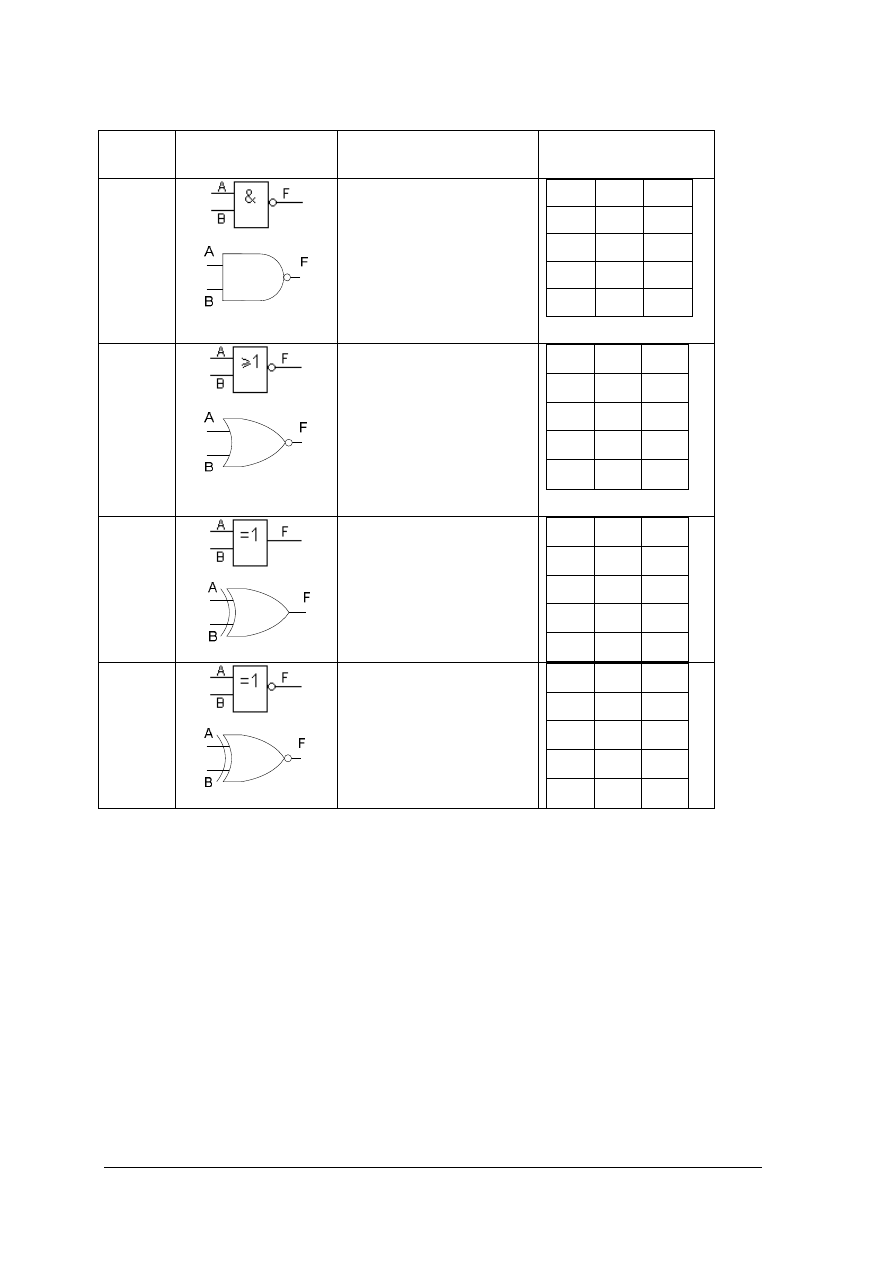
„
Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
19
Tabela 7.
Nazwa
bramki
Symbol graficzny
Funkcja
Tabela działania
NAND
F=(A ∙ B)’
Negacja iloczynu
A
B
F
0
0
0
0
1
0
1
0
0
1
1
1
NOR
F=(A+B)’
Negacja sumy
A
B
F
0
0
0
0
1
1
1
0
1
1
1
1
ExOR
F = A’B + AB’
A
B
F
0
0
0
0
1
1
1
0
1
1
1
0
ExNOR
F = A’B’ + AB
A
B
F
0
0
1
0
1
0
1
0
0
1
1
1
Uwaga: W tabeli przedstawiono dwa symbole graficzne każdej bramki – górny, według
normy PN-IEC 617-12 :1995, - dolny, według norm amerykańskich. Oba rodzaje symboli
stosowane są w Polsce.
4.2.1.3. Opis działania układów logicznych
Działanie układu logicznego można opisać za pomocą: opisu słownego, tabeli działania
zwanej też tabelą prawdy, funkcji logicznej i schematu logicznego.
Opis słowny zawiera informacje o ilości wejść i wyjść, znaczeniu „0” i „1” na wejściu
i wyjściu układu oraz jak ma się zachować układ we wszystkich możliwych sytuacjach.
Komentarz słowny możemy zapisać symbolicznie w postaci tabeli działania (tabeli prawdy).
Rozważymy to na przykładzie dwuwejściowej bramki AND – jej działanie opisuje
stwierdzenie: bramka AND ma na wyjściu sygnał logiczny o wartości „1” tylko wtedy, gdy na
obu wejściach jest stan „1”. W tabeli 6 znajdziesz zapis tego komentarza w postaci tabeli
działania oraz funkcji logicznej.
„
Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
20
Układ kombinacyjny zwykle jest bardziej złożony i składa się z wielu bramek logicznych
– zapis graficzny sposobu powiązań pomiędzy tymi bramkami nazywamy schematem
logicznym. Analiza działania układów logicznych będzie łatwiejsza, gdy spróbujesz sam
zaprojektować prosty układ.
4.2.1.4. Projektowanie układów logicznych można podzielić na następujące kroki:
1. Wyobraź sobie działanie projektowanego układu. Określ liczbę wejść i wyjść.
2. Zapisz działanie układu w postaci „tabeli prawdy”, sprawdź czy uwzględniłeś wszystkie
możliwe kombinacje sygnałów wejściowych. Liczba kombinacji (K) zależy od liczby
wejść (N) w układzie i wynosi K = 2
N
. Dla układu, który ma dwa wejścia można
utworzyć 4 kombinacje – zobacz tabele działania dla dwuwejściowych bramek
logicznych [Tabela 6 i 7].
3. Na podstawie tabeli wypisz funkcję logiczną, która opisuje działanie projektowanego
układu,
a) pokreśl w tabeli wszystkie wiersze, dla których wartość funkcji na wyjściu jest
równa „1”,
b) każdy podkreślony wiersz zapisz jako iloczyn zmiennych wejściowych (A, B, C, ..)
w taki sposób, że jeśli zmienna jest równa 0 to zapisujemy ją z negacją –
przykładowo A’ a jeśli jest równa 1 to bez negacji – A,
c) zapisz funkcji jest sumą tych iloczynów.
4. Zapisz funkcję w najprostszej postaci. Możesz zastosować w tym celu prawa algebry
Boole’a lub inną metodę minimalizacji. Jedną z metod minimalizacji jest metoda
Karnaugh’a. Aby uprościć funkcję metodą Karnaugh’a:
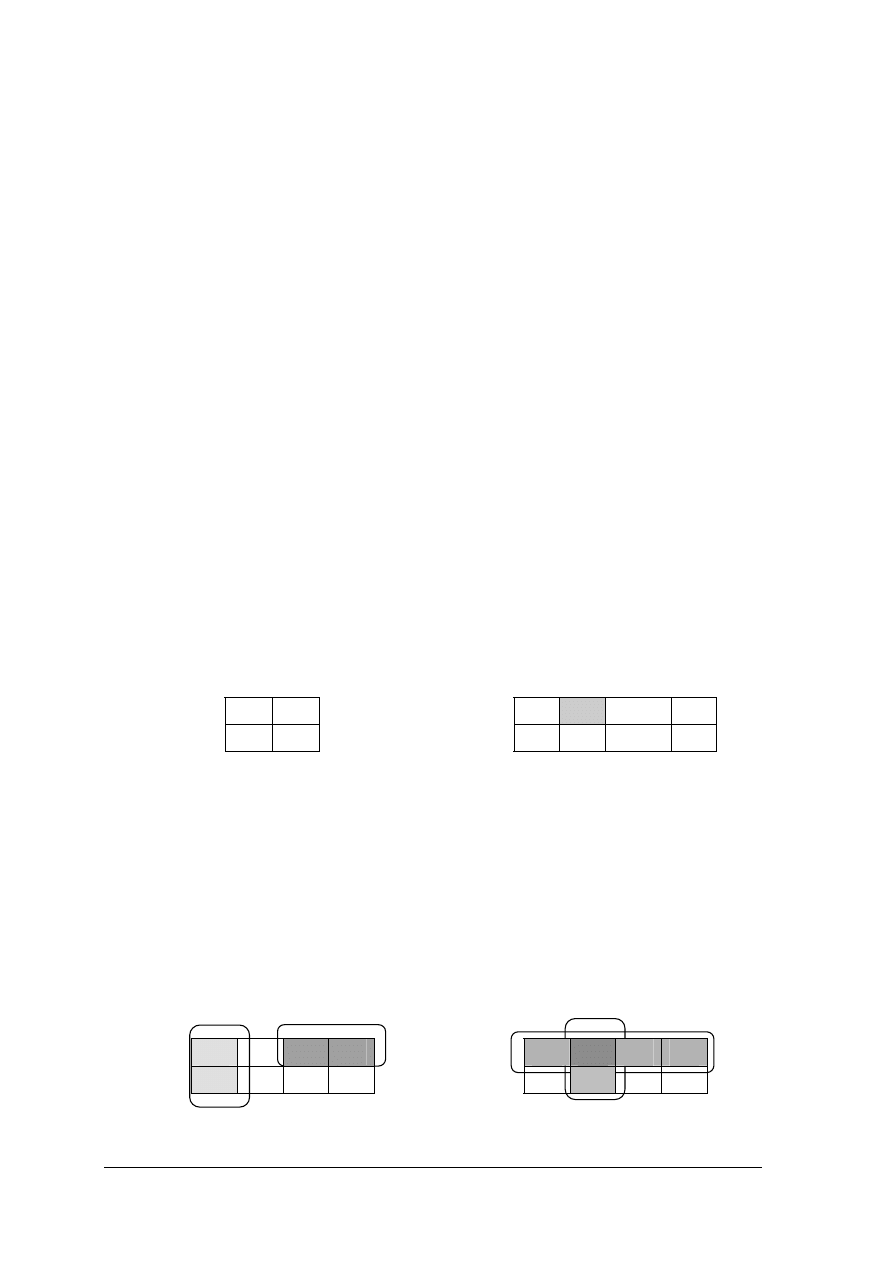
a) wybierz odpowiednią tablicę minimalizacyjną – dla dwóch, trzech lub więcej
zmiennych wejściowych - tyle ile zmiennych ma funkcja, którą chcesz uprościć.
Rys. 5.Tablice minimalizacyjne a) dla funkcji dwóch zmiennych b) dla funkcji trzech zmiennych.
Tablice minimalizacyjne dla większej liczby zmiennych znajdziesz w literaturze [3,6]
b) wpisz do wybranej tablicy wartości funkcji na wyjściu,
Przykład: w zacieniowane pole tablicy (Rys.5b) należy wpisać wartość funkcji
trzywejściowej F(A,B,C) dla następującej kombinacji sygnałów wejściowych A=0,
B=0 i C=1
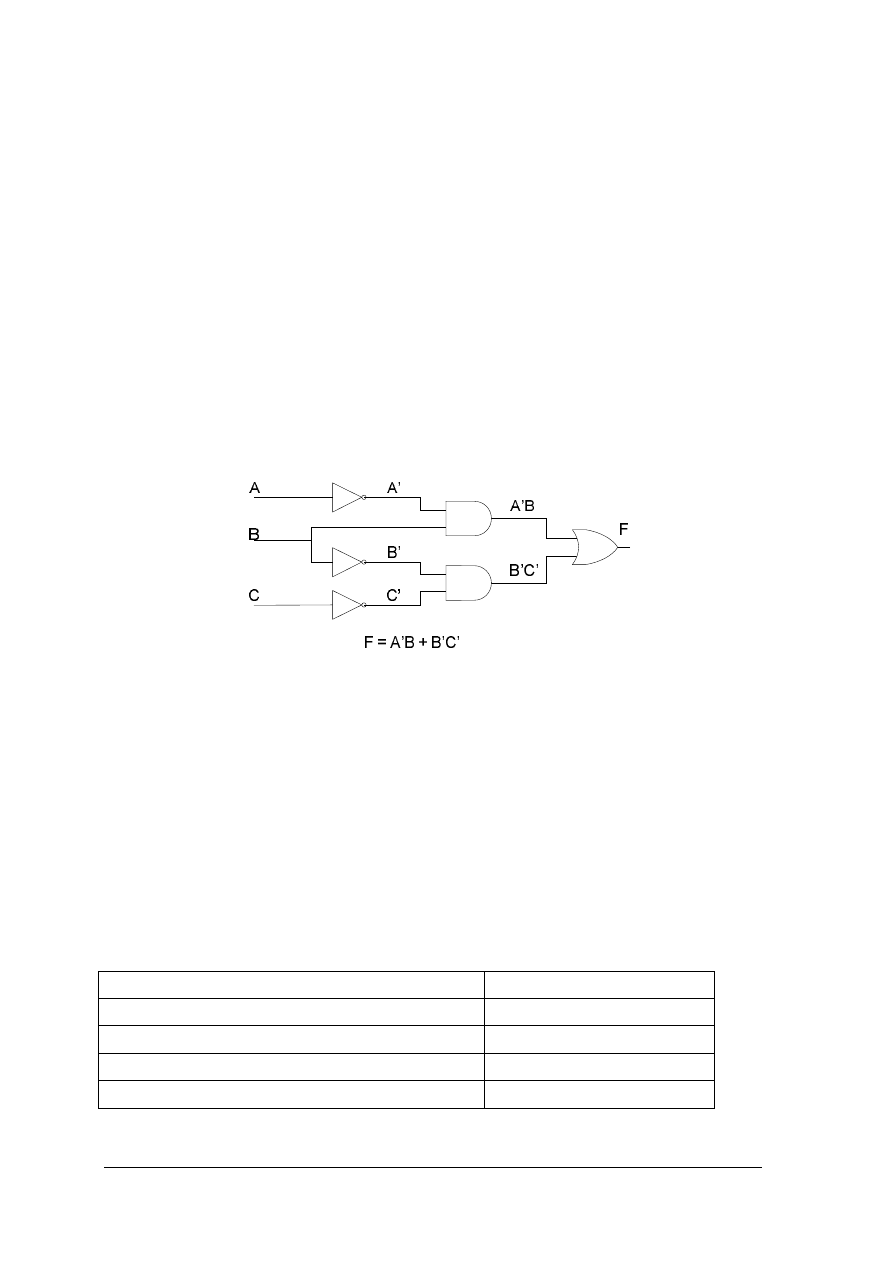
c) zaznacz obszary w tablicach składające się z sąsiadujących jedynek, których liczba
jest potęgą dwójki: 2
0
=1, 2
1
=2, 2
2
=4, ... staraj się utworzyć jak największe obszary,
Popatrz na przykłady zaznaczonych obszarów w tablicach poniżej (Rys.6).
A/BC 00
01
11
10
b)
A/BC 00
01
11
10
0
1
0
1
1
0
1
1
1
1
1
1
0
1
1
1
0
1
0
0
Rys. 6. Tablice minimalizacyjne z zaznaczonymi obszarami do minimalizacji.
a) dla funkcji dwóch zmiennych, b) dla funkcji trzech zmiennych.
B=0
B=1
b)
BC
BC
BC
BC
A\B 0
1
A\BC 00
01
11
10
A=0
0
A=1
1
F(111)
Tablica dla F (AB)
Tablica dla F(ABC)
a
)
a)
„
Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
21
Jedynka wyróżniona najciemniejszym wypełnieniem w prawej tablicy należy
jednocześnie do dwóch obszarów: poziomego, składającego się z czterech jedynek
i pionowego, składającego się z dwóch jedynek. Więcej informacji na temat zaznaczania
obszarów minimalizacyjnych znajdziesz w literaturze [3].
d)
z każdego zaznaczonego obszaru zapisz iloczyn zmiennych wejściowych (ABC),
które w całym obszarze nie zmieniają wartości;
W lewej tablicy (Rys.5) z obszaru składającego się z dwóch jedynek otrzymalibyśmy
B’C’, – ponieważ dla całego obszaru B=0 i C=0. Dla obszaru składającego się z
czterech jedynek w prawej tablicy (Rys.5) otrzymamy A’, ponieważ A w całym
obszarze nie zmienia wartości i jest równe „0”. Dodatkowe przykłady znajdziesz w
literaturze [3, str.49].
e) uproszczony zapis funkcji jest sumą iloczynów otrzymanych z wszystkich
zaznaczonych obszarów. Dla lewej tablicy z rys.5 otrzymamy F = B’C’ + A’B.
5. Na koniec na podstawie uproszczonej funkcji rysujemy schemat logiczny układu,
zastępując zapis działania logicznego odpowiednią bramką logiczną: negację - bramką
NOT, iloczyn - bramką AND, sumę - bramką OR.
Schemat logiczny dla funkcji F = B’C’ + A’B jest następujący:
Rys. 6. Schemat logiczny układu opisanego funkcją F= A’B + B’C’
W praktyce często potrzebna jest umiejętność zrozumienia działania układu na podstawie
schematu logicznego. Jest to szczególnie ważne w przypadku konieczności wykrywania
usterek w pracy układów. Aby określić przyczynę błędnego działania układu należy:
−
określić na podstawie schematu prawidłowe działanie układu jako całości i każdego
elementu – bramki wchodzącej w jego skład,
−
na podstawie pomiarów stwierdzić sposób działania układu z usterką,
−
porównać otrzymane wyniki z prawidłowymi i dokonać identyfikacji elementu
działającego niepoprawnie.
4.2.1.5. Technologia TTL i CMOS produkcji układów scalonych
Układy cyfrowe mogą być wykonane w różnej technologii i różnym stopniu scalenia.
Tabela 8.
Stopień scalenia
Liczba bramek w układzie
SSI – mały stopień scalenia
Do 10 bramek
MSI – średni stopień scalenia
Od 10 do 100 bramek
LSI - duży stopień scalenia
Od 100 do 1000 bramek
VLSI – bardzo duży stopień scalenia
Od 1000 do 10 000
Duży asortyment układów w technologii TTL i CMOS zdecydował o ich dość
powszechnym zastosowaniu. W każdej z tych technologii można wyróżnić szereg serii
„
Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
22
układów. Układy TTL – LS (UCY74LSxx), 4000B (MCY 74xxx) oraz układy ACT, które są
układami CMOS kompatybilnymi z układami TTL to układy najbardziej reprezentatywne
w swoich grupach.
Sposób oznaczania układów przy pomocy symboli katalogowych znajdziesz w literaturze
[3, 8].
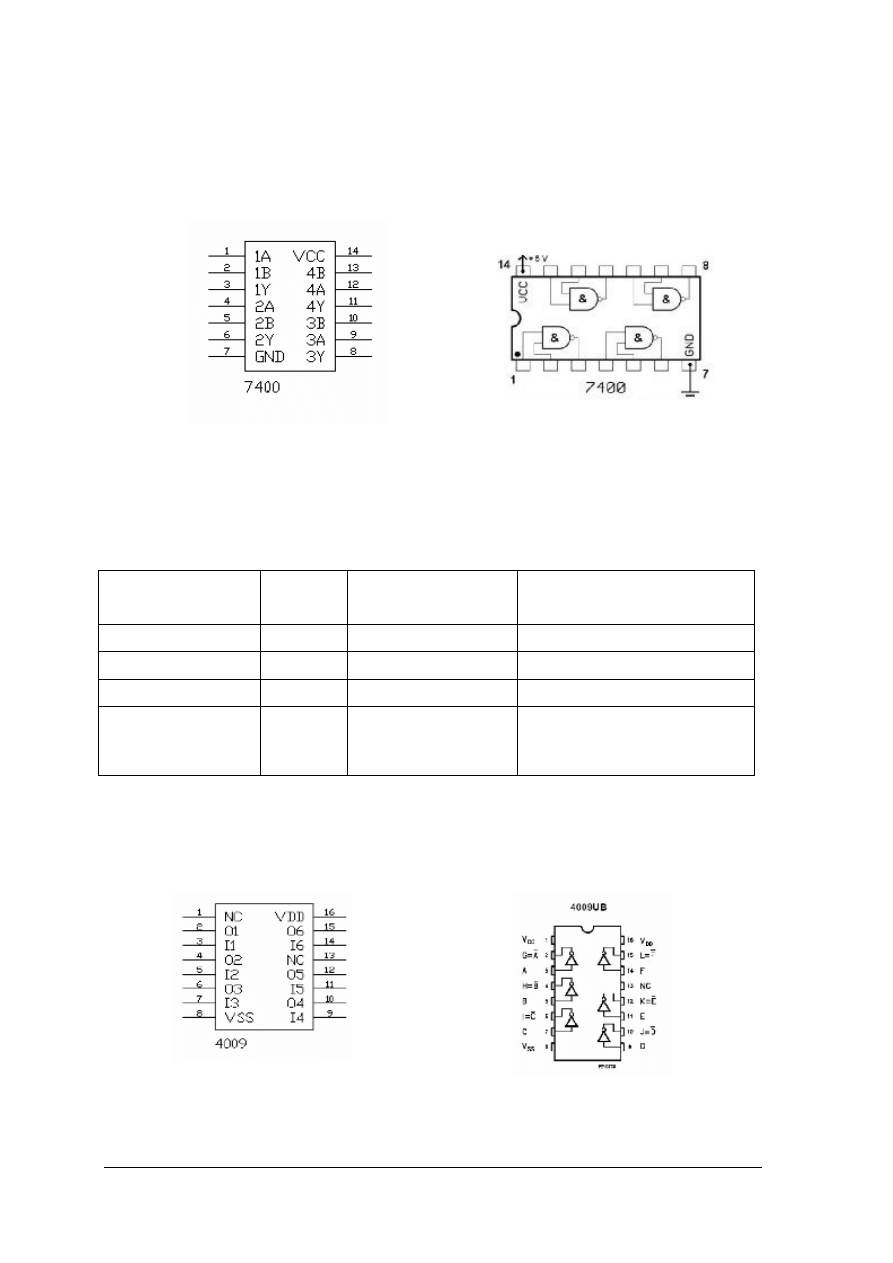
Rys. 7. Układ scalony w technologii TTL - UCY 7400N: a) opis wyprowadzeń, b) rozmieszczenie bramek.
Układy scalone TTL i CMOS różnią się przede wszystkim parametrami. Tabela 9
przedstawia porównanie podstawowych parametrów obu technologii. Więcej danych na temat
tych układów szukaj w katalogach i literaturze [3, 8].
Tabela 9.
Parametr
Jednostka
Technologia CMOS
Seria 4000B
Technologia TTL
Seria LS
Napięcie zasilania
V
3 – 18
4,75 – 5, 25
Moc statyczna
nW
10
2 000 000
Czas propagacji
ns
90
10
Margines zakłóceń
%
napięcia
zasilania
30
Około 10
Z porównania tych parametrów wynika, że układy CMOS serii 4000B są wolniejsze ale
pobierają znacznie mniej mocy, mają szeroki zakres napięć zasilających i są bardziej odporne
na zakłócenia.
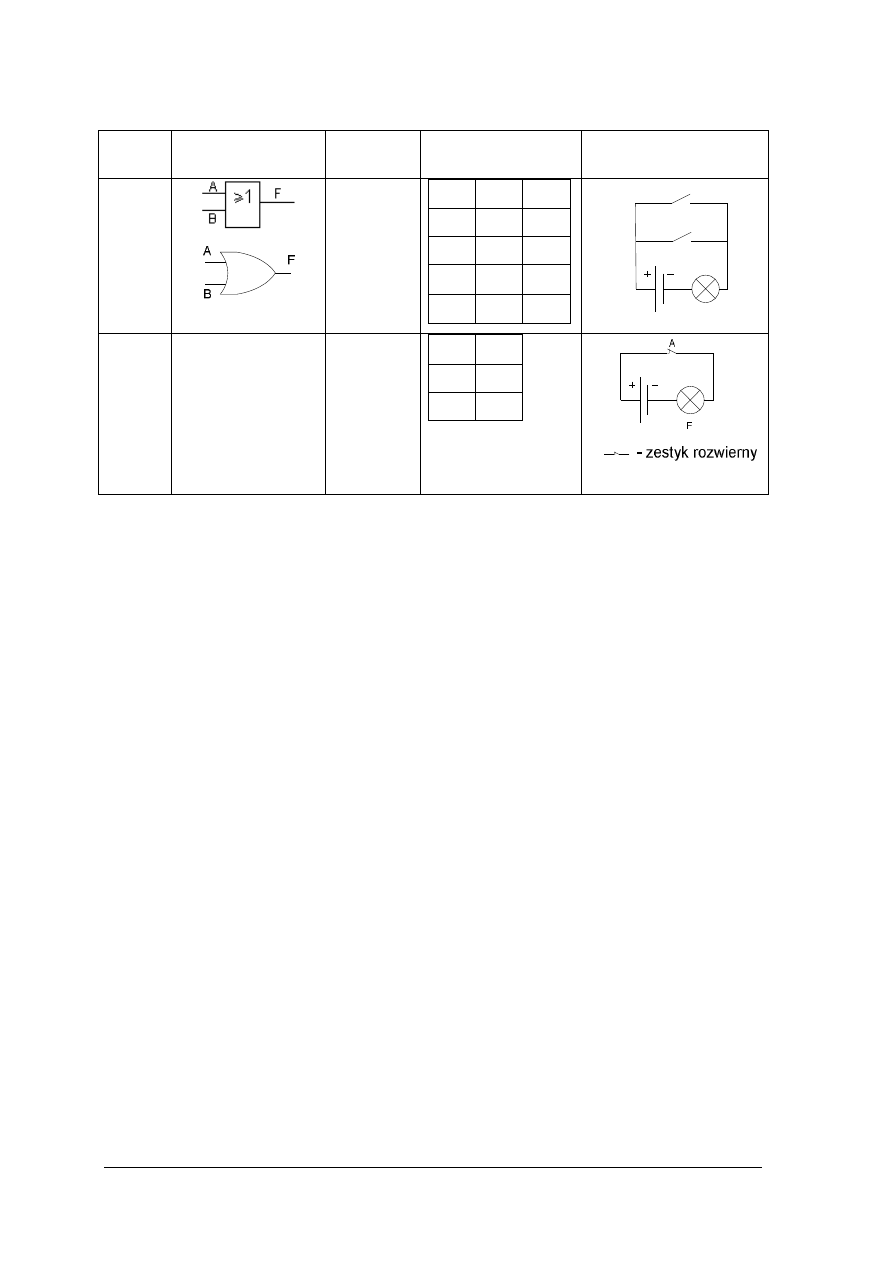
a)
b)
Rys. 8. Układ scalony w technologii CMOS – 4009: a) opis wyprowadzeń, b) rozmieszczenie bramek.
a)
b)

„
Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
23
4.2.2. Pytania sprawdzające
Odpowiadając na pytania, sprawdzisz, czy jesteś przygotowany do wykonania ćwiczeń.
1. Jaki układ nazywamy układem kombinacyjnym?
2. Na jakich wartościach operuje algebra Boole’a?
3. W jakim celu stosujemy aksjomaty algebry Boole’a?
4. Jakie funkcje realizują bramki AND, OR, NOT?
5. Co to znaczy, że bramki tworzą układ funkcjonalnie pełny?
6. Czym się charakteryzują bramki z otwartym kolektorem?
7. Czym się charakteryzują bramki z przerzutnikiem Schmidta?
8. Jakie są sposoby opisu działania układów logicznych?
9. Jak opisać działanie układu logicznego za pomocą tabeli prawdy?
10. W jaki sposób z tabeli prawdy otrzymać funkcje logiczną opisującą działanie układu?
11. Jak uprościć funkcję z zastosowaniem aksjomatów algebry Boole’a?
12. Jak uprościć funkcję metodą Karnaugha?
13. Jak na podstawie funkcji narysować schemat logiczny układu?
14. Jakie podstawowe własności posiadają układy cyfrowe technologii TTL i CMOS?
15. Jak zinterpretować oznaczenie katalogowe układu w technologii TTL i CMOS?
4.2.3. Ćwiczenia
Ćwiczenie 1
Korzystając z praw algebry Boole’a oblicz wartość logiczną wyrażenia:
a) (1 + 1) ∙ (1 + 0) =
b) (A + A’) ∙ B =
c) AA’ + ( B + 1) =
d) (A + B)’ + A’’ =
Aby wykonać ćwiczenie, powinieneś:
1) zapoznać się z prawami algebry Boole’a ( materiał nauczania pkt.4.2.1),
2) wykonać działanie krok po kroku zwracając szczególną uwagę na poprawne zastosowanie
odpowiednich aksjomatów,
3) sprawdzić poprawność wykonanych działań – jeśli masz trudności zwróć się
o pomoc do nauczyciela.
Wyposażenie stanowiska pracy:
−
przybory do pisania,
−
poradnik ucznia,
−
literatura [3].
Ćwiczenie 2
Uzupełnij brakujące informacje w następującej tabeli:
„
Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
24
Tabela 10. Bramki logiczne
Nazwa
bramki
Symbol graficzny
Funkcja
Tabela działania
Realizacja
na
przełącznikach
OR
F =
A
B
F
0
0
0
1
1
0
1
1
A
B
F
A
F
0
1
1
0
Sposób wykonania ćwiczenia
Aby wykonać ćwiczenie, powinieneś:
1) zapoznać się z opisem działania poszczególnych bramek logicznych (Materiał nauczania
pkt.4.2.1),
2) wpisać w odpowiednie miejsca tabeli brakujące informacje,
3) sprawdzić poprawność wykonanych działań.
Wyposażenie stanowiska pracy:
−
przybory do pisania,
−
poradnik ucznia,
−
literatura [3, 4, 8].
Ćwiczenie 3
Wykonaj badanie bramek NOT, NAND, NOR, EXOR - układów scalonych technologii
TTL i CMOS oraz sprawdź działanie układu zmontowanego zgodnie ze schematem
przedstawionym na rys. 6.
a) wyznacz charakterystykę przełączania bramki NOT w technologii TTL Uwy=f (Uwe)
i określ na jej podstawie napięcie przełączania,
b) zmierz wartość napięcia na wyjściu bramki NOT w stanie niskim U
OL
i wysokim U
OH
i porównaj otrzymane wyniki z danymi katalogowymi tego układu,
c) zbadaj poprawność działania pojedynczej bramki układu UCY 7400, UCY 7402, UCY
7486 i 4009 – wyznacz jej tabelę działania i porównaj otrzymane wyniki
z informacjami zawartymi w materiale nauczania i literaturze [8],
d) połącz układ korzystając ze schematu przedstawionego w materiale nauczania rys.6. s.
21. W razie konieczności dokonaj modyfikacji schematu dostosowując go do
dostępnych układów scalonych, na podstawie pomiarów wyznacz jego tabelę
działania, otrzymany wynik porównaj z tabelą prawdy zapisaną na podstawie funkcji –
oblicz wartość logiczną wstawiając do wzoru odpowiednie wartości logiczne A,B,C
tak jak w ćwiczeniu 1a.

„
Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
25
Sposób wykonania ćwiczenia
Aby wykonać ćwiczenie, powinieneś:
1) zapoznać się z danymi katalogowymi badanych bramek (Materiał nauczania pkt.4.2.1.4 i
literatura [3,8]),
2) narysować schemat układu do pomiaru charakterystyki przełączania. Odszukaj układ
pomiarowy w literaturze [8] i sprawdź jego poprawność,
3) wykonać pomiary krok po kroku zmieniając napięcie wejściowe i odczytując napięcie na
wyjściu, zapisując jednocześnie w tabeli otrzymane wyniki pomiarów,
4) narysować charakterystykę w odpowiednio dobranym układzie współrzędnych, jeśli masz
z tym problemy poszukaj tej charakterystyki w literaturze [8],
5) wykonać pomiar napięcia w stanie niskim U
OL
i wysokim U
OH
za pomocą woltomierza
lub oscyloskopu,
6) skorzystać z próbnika stanów logicznych, woltomierza lub oscyloskopu do określania
stanu na wyjściu badanej bramki czy układu przy określonej kombinacji stanów
wejściowych,
7) jeśli to możliwe – przećwicz poszczególne kroki, korzystając z programu do symulacji
pracy układów logicznych.
Wyposażenie stanowiska pracy:
−
przybory do pisania,
−
poradnik dla ucznia,
−
stanowisko
laboratoryjne
do
badania
układów
cyfrowych
wyposażone
w podstawowe przyrządy pomiarowe i zestawy układów do badań,
−
stanowisko komputerowe z programem do symulacji pracy układów cyfrowych,
−
literatura [3, 4, 5, 8].
Ćwiczenie 4
Wykonaj badanie działania układu opisanego następującą tabelą prawdy.
Tabela 11. Tabela prawdy
a) zapisz funkcję F(ABC) opisującą działanie układu na podstawie
jego tabeli prawdy,
b) uprość wypisaną funkcję metodą Karnaugh’a.,
c) narysuj schemat tego układu,
d) korzystając z katalogu układów scalonych TTL [2] określ jakie
układy scalone i ile tych układów należy zastosować, aby wykonać
ten układ w praktyce,
e) określ jakim napięciem należy zasilać zaprojektowany układ,
f) wykonaj symulację komputerową działania tego układu, zmontuj
układ rzeczywisty i porównaj działanie układu
z założeniami.
Sposób wykonania ćwiczenia
Aby wykonać ćwiczenie, powinieneś:
1) zapoznać się z instrukcją dotyczącą wypisywania funkcji z tabeli działania (Materiał
nauczania pkt.4.2.1.4),
A B C
F
0 0
0
1
0
0
1
1
0
1
0
0
0
1
1
1
1
0
0
0
1
0
1
0
1
1
0
0
1
1
1
1

„
Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
26
2) wykonać działanie krok po kroku zwracając szczególną uwagę na poprawny zapis
zmiennych z negacją i bez negacji,
3) sprawdzić poprawność przed rozpoczęciem minimalizacji,
4) wykonać minimalizację zgodnie z instrukcją (Materiał nauczania pkt.4.2.1.4),
5) narysować schemat logiczny tego układu,
6) dobrać układy scalone technologii TTL do jego praktycznej realizacji i określić ich
liczbę,
7) wykonać symulację komputerową działania układu,
8) zmontować układ zgodnie ze schematem.
Wyposażenie stanowiska pracy:
−
stanowisko laboratoryjne do badania układów cyfrowych wyposażone w podstawowe
przyrządy pomiarowe i zestawy układów do badań,
−
stanowisko komputerowe z programem do symulacji pracy układów cyfrowych,
−
przybory do pisania,
−
poradnik ucznia,
−
literatura [3, 4, 6, 8].
4.2.4. Sprawdzian postępów
Tak Nie
Czy potrafisz:
1) opisać działanie układów logicznych różnymi metodami?
¨
¨
2) zastosować aksjomaty algebry Boole’a do upraszczania funkcji
logicznych?
¨
¨
3) uprościć funkcję logiczną metodą tablic Karnaugh’a ?
¨
¨
4) wyjaśnić działanie podstawowych bramek logicznych?
¨
¨
5) dokonać interpretacji podstawowych parametrów układów
scalonych technologii TTL i CMOS?
¨
¨
6) narysować schemat logiczny układu na podstawie funkcji?
¨
¨
7) określić działanie układu na podstawie schematu logicznego?
¨
¨
8) dobrać układy scalone do realizacji wybranej funkcji logicznej?
¨
¨
9) sprawdzić poprawność działania układu logicznego?
¨
¨
10) połączyć układ logiczny zgodnie ze schematem?
¨
¨
„
Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
27
4.3. Komutacyjne i arytmetyczne układy cyfrowe
4.3.1. Materiał nauczania
4.3.1.1. Układy zmiany kodu
Układem komutacyjnym nazywamy układ umożliwiający przełączanie sygnałów,
w naszym przypadku będzie chodziło o przełączanie sygnałów cyfrowych. Do grupy tych
układów zaliczamy:
−
kodery/ transkodery, dekodery, enkodery,
−
multipleksery, demultipleksery.
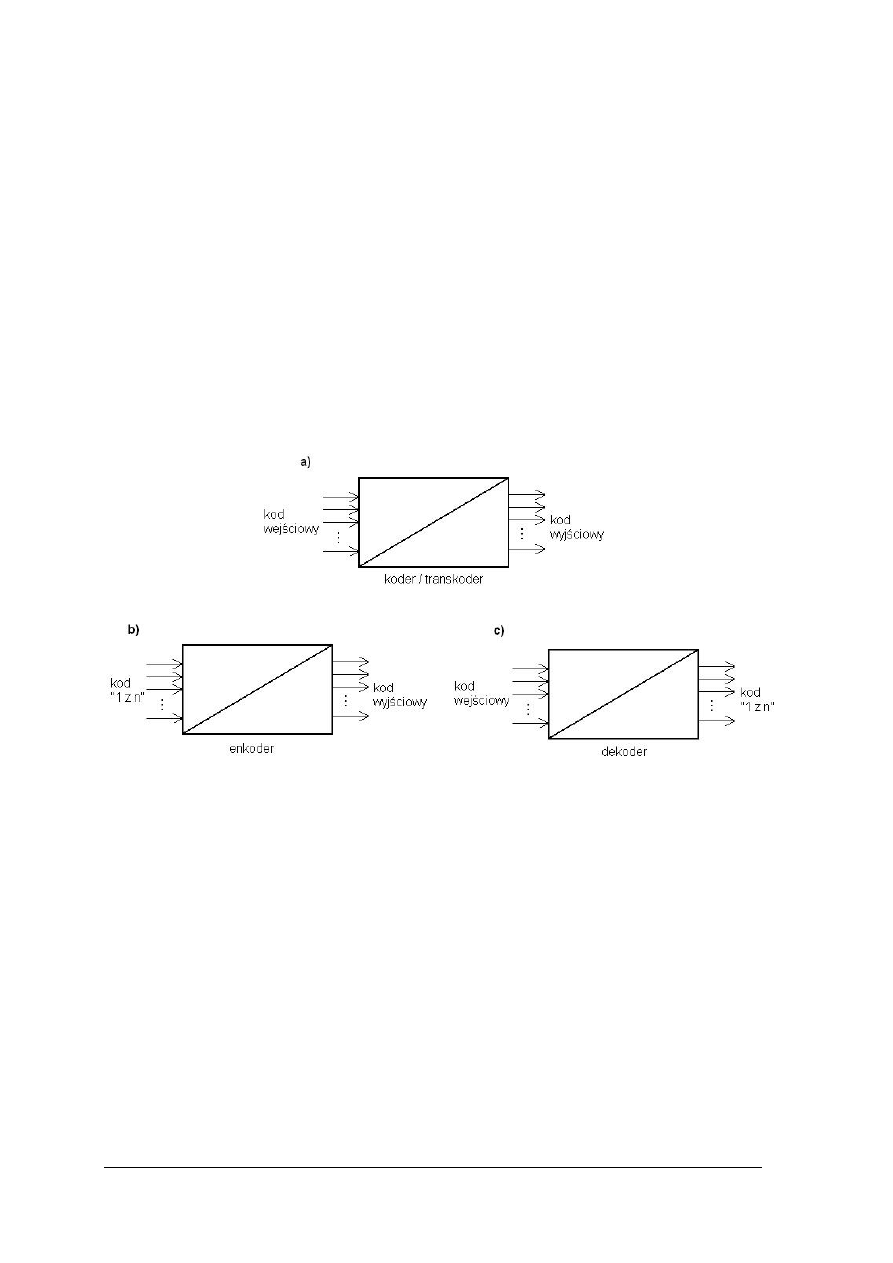
Kodery lub transkodery to układy realizujące proces zamiany kodu wejściowego na inny
zwany wyjściowym, przy czym żaden z tych kodów nie jest kodem „1z n”.
Enkoder to koder, w którym kod wejściowy jest kodem „1z n”, dekoder to koder,
w którym kod wyjściowy jest kodem „1z n”
Rys. 9. Symbole graficzne a) koder, b) enkoder, c) dekoder.
Działanie układów wielowyjściowych opisuje tyle funkcji, ile wyjść posiada układ.
Projektując takie układy postępujemy z każdą funkcją tak, jak to przestawiono
w materiale nauczania w pkt. 4.2.1.4.
Kodery, dekodery, multipleksery i demultipleksery należą do grupy układów średniej
skali integracji. Mogą być one wykonane w technologii TTL lub CMOS. Wraz ze
zwiększeniem skali integracji układów scalonych coraz większy mamy asortyment szybkich
układów CMOS, które ponadto charakteryzują się dużymi obciążeniami i są w pełni zgodne
końcówkowo i oznaczeniowo z układami TTL. Można więc przykładowo, układ TTL 74LS00
zastąpić układem 74 HCT00 lub 74ACT00 z grupy układów CMOS, jednak decyzję tę należy
dodatkowo uzależnić od wyniku analizy parametrów wejściowych i wyjściowych
współpracujących ze sobą bezpośrednio układów. W celu uniknięcia tych problemów
wygodniej jest projektując układ stosować układy jednej technologii.
Więcej informacji na temat parametrów szybkich układów CMOS znajdziesz
w katalogach w wersji drukowanej lub, coraz popularniejszych przez swoją dostępność,
wersjach elektronicznych.
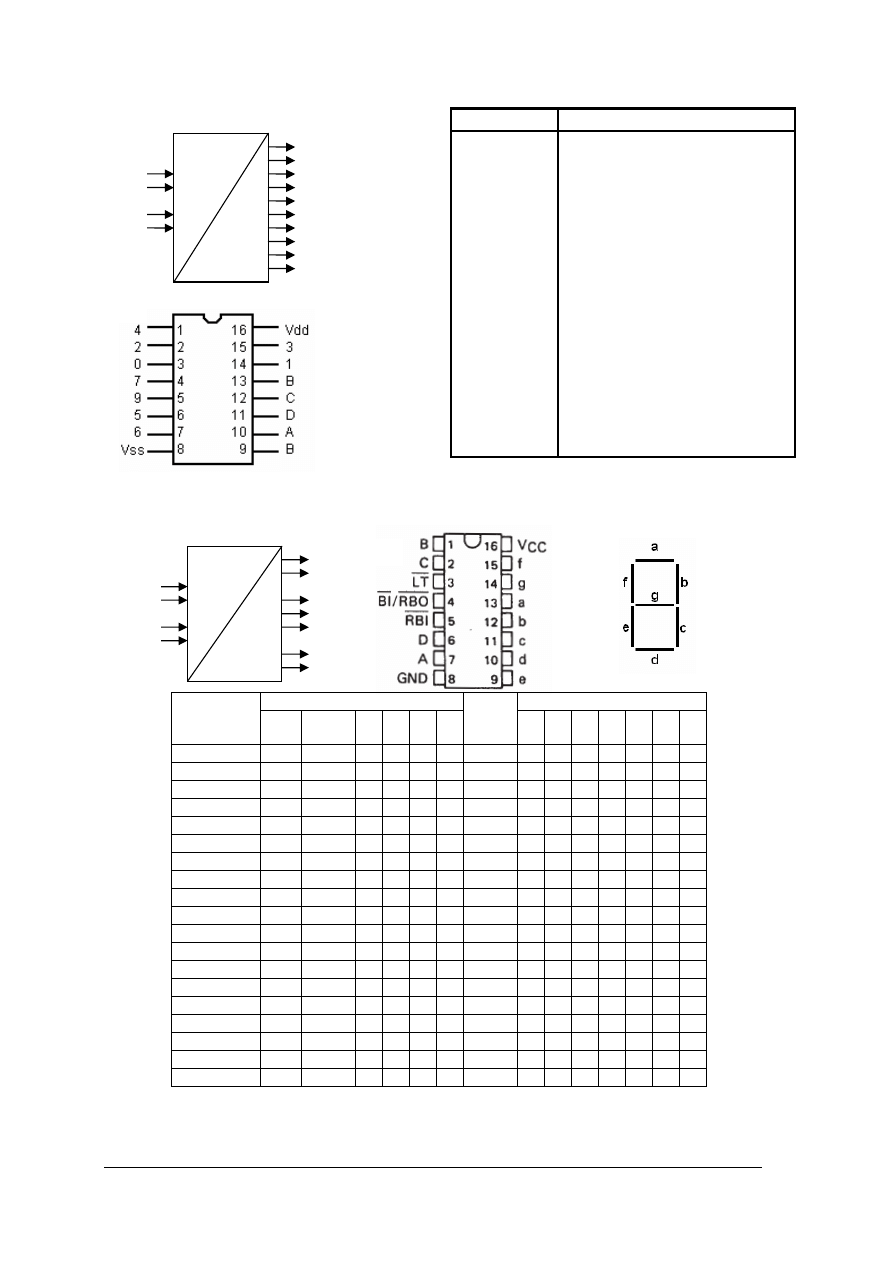
Przykłady układów zmiany kodu: Układ CMOS 4028 - dekoder z kodu BCD na kod „1
z 10”
„
Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
28
A
B
C
D
a
b
c
d
e
f
g
d)
Rys. 10. Dekoder a) symbol graficzny, b) tabela działania, c) rozkład wyprowadzeń.
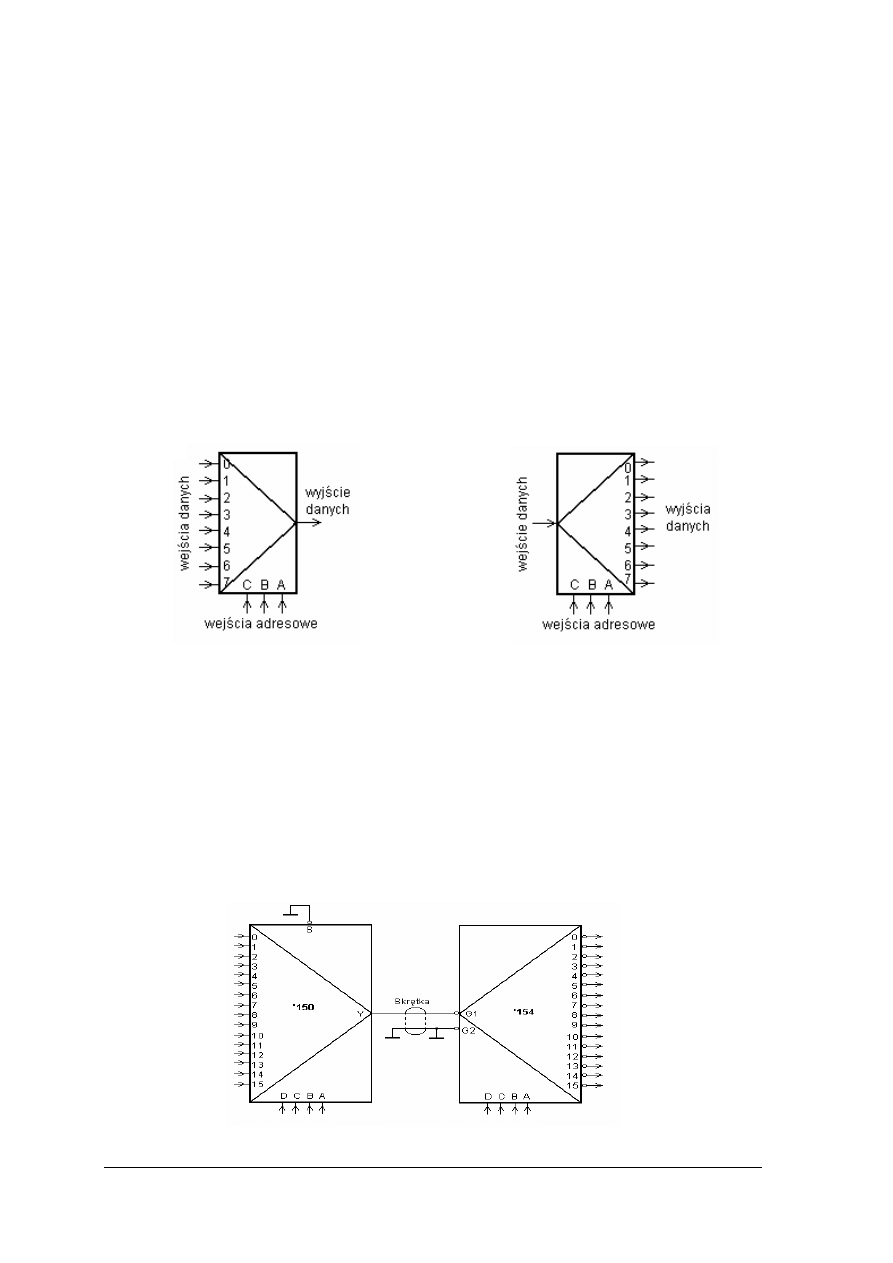
Układ TTL - 74LS47 – transkoder z kodu BCD na kod wskaźnika siedmiosegmentowego
Wejścia
Wyjścia
Liczba
dziesiętna
lub funkcja
LT
RBI
D C B A
BI /
RBO
a
b
c
d
e
f
g
0
H
H
L
L
L
L
H
L
L
L
L
L
L
H
1
H
X
L
L
L
H H
H L
L
H H H H
2
H
X
L
L
H L
H
L
L
H L
L
H L
3
H
X
L
L
H H H
L
L
L
L
H H L
4
H
X
L
H L
L
H
H L
L
H H L
L
5
H
X
L
H L
H H
L
H L
L
H L
L
6
H
X
L
H H L
H
H H L
L
L
L
L
7
H
X
L
H H H H
L
L
L
H H H H
8
H
X
H L
L
L
H
L
L
L
L
L
L
L
9
H
X
H L
L
H H
L
L
L
H H L
L
10
H
X
H L
H L
H
H H H L
L
H L
11
H
X
H L
H H H
H H L
L
H H L
12
H
X
H H L
L
H
H L
H H H L
L
13
H
X
H H L
H H
L
H H L
H L
L
14
H
X
H H H L
H
H H H L
L
L
L
15
H
X
H H H H H
H H H H H H H
BI
H
L
X X X X L
H H H H H H H
RBI
H
L
L
L
L
L
L
H H H H H H H
LT
L
X
X X X X H
L
L
L
L
L
L
L
Rys. 11. Transkoder z kodu BCD na kod wskaźnika siedmiosegmentowego a)symbol graficzny, b) rozkład
wyprowadzeń, c) segmenty wskaźnika, d) tabela działania.
D C B A 0 1 2 3 4 5 6 7 8 9
0
0
0
0
1 0 0 0 0 0 0 0 0 0
0
0
0
1
0 1 0 0 0 0 0 0 0 0
0
0
1
0
0 0 1 0 0 0 0 0 0 0
0
0
1
1
0 0 0 1 0 0 0 0 0 0
0
1
0
0
0 0 0 0 1 0 0 0 0 0
0
1
0
1
0 0 0 0 0 1 0 0 0 0
0
1
1
0
0 0 0 0 0 0 1 0 0 0
0
1
1
1
0 0 0 0 0 0 0 1 0 0
1
0
0
0
0 0 0 0 0 0 0 0 1 0
1
0
0
1
0 0 0 0 0 0 0 0 0 1
1
0
1
0
0 0 0 0 0 0 0 0 0 0
1
0
1
1
0 0 0 0 0 0 0 0 0 0
1
1
0
0
0 0 0 0 0 0 0 0 0 0
1
1
0
1
0 0 0 0 0 0 0 0 0 0
1
1
1
0
0 0 0 0 0 0 0 0 0 0
1
1
1
1
0 0 0 0 0 0 0 0 0 0
A
B
C
D
0
1
2
3
4
5
6
8
9
a)
b)
c)
c)
a)
b)
„
Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
29
Układ ten posiada dodatkowe wejścia sterujące LT’- wejście testujące, BI’/RBO’ –
wejście wygaszania wskaźnika i RBI’ – wejście wygaszania zera. W przypadku łączenia
kaskadowego układów sygnał z wyjścia BI’/RBO’ układu sterującego cyfrą mniej znaczącą
łączymy
z
wejściem
RBI’
układu
sterującego
cyfrą
bardziej
znaczącą
(o większej wadze) [8].
Prosty układ dekodera możemy zaprojektować z bramek logicznych korzystając
z procedury zamieszczonej w materiale nauczania 4.2.1.
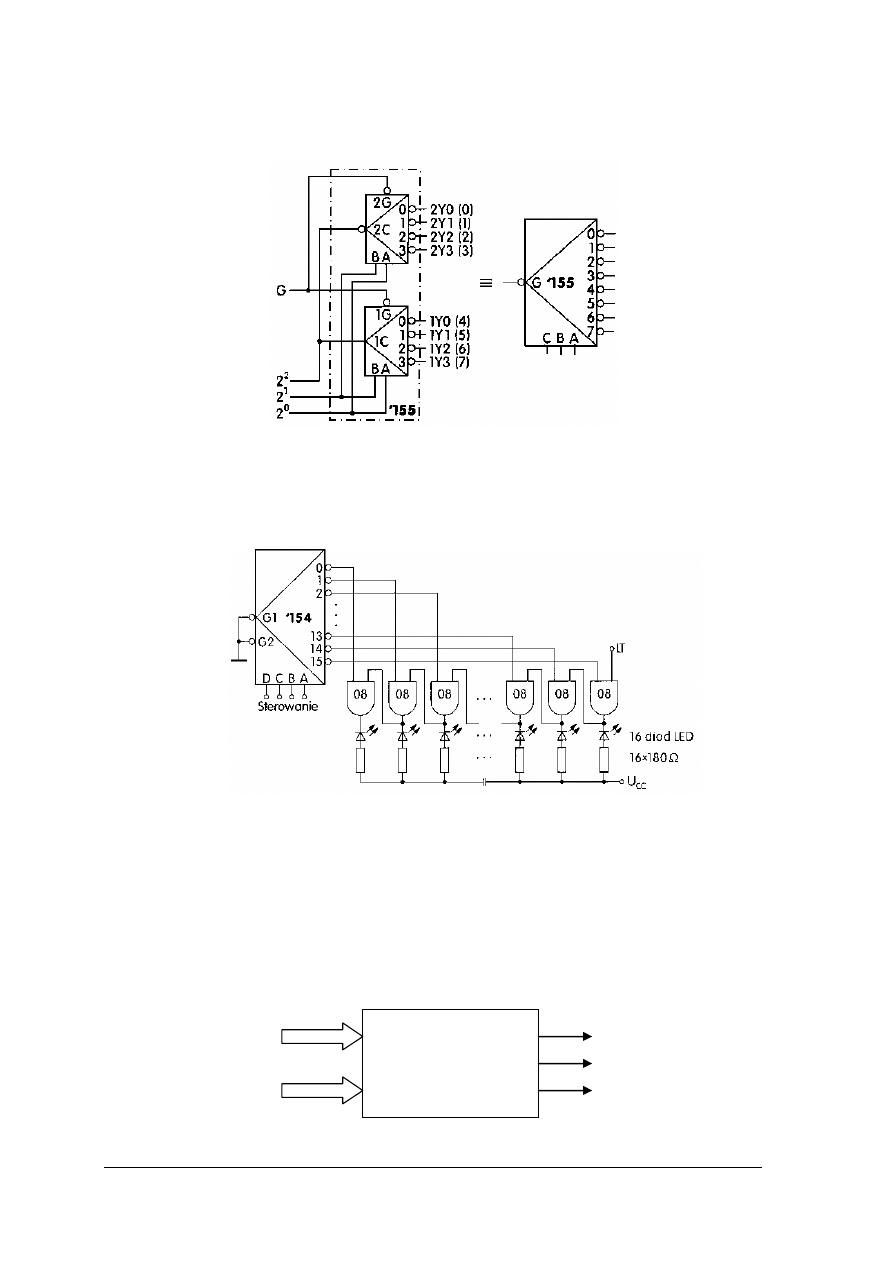
4.3.1.2. Multipleksery i demultipleksery
Multiplekser pozwala na przekazanie sygnału z wybranego wejścia danych (na podstawie
adresu)
na
wyjście.
Adres
wejścia
danych
(informacyjnego)
podawany
jest
w kodzie binarnym na specjalne wejścia zwane adresowymi.
Demultiplekser pełni funkcję odwrotną niż multiplekser, to znaczy pozwala na
przekazanie sygnału wejściowego do jednego z wielu wyjść, wskazanego przez informacje
adresową.
Rys. 12. Symbole graficzne a)multiplekser, b) demultiplekser.
Więcej danych o multiplekserze‘151 „z 8 linii na 1” znajdziesz w literaturze
[3, s. 202] lub w katalogu układów scalonych.[8]. Zwróć uwagę na zadanie, jakie spełnia
w tym układzie wejście strobujące oznaczone S. Wejście to umożliwia blokadę pracy całego
układu.
W transmisji danych cyfrowych stosuje się multipleksowy system przesyłania danych, co
umożliwia przesyłanie jedną linią zamiast wieloma – wielobitowych sygnałów binarnych.
W tym przypadku 16 bitowa informacja podana na wejścia multipleksera zostaje „bit po
bicie” nadawana w linię transmisyjną i odbierana przez demultiplekser. Ponieważ na wejścia
adresowe obu układów podaje się te same adresy, to na wyjściu demultipleksera otrzymuje się
ponownie tę sama 16 bitową informację.
Rys. 13. Multipleksowy system transmisji danych.
a)
b)
„
Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
30
Multipleksery i demultipleksery można łączyć ze sobą tworząc układy o większej liczbie
wejść lub wyjść.
Rys. 14. Demultiplekser 8 wyjściowy zbudowany z dwóch demultiplekserów 4 wyjściowych [3,s. 204].
Multipleksery mają bardzo szerokie zastosowanie. Przykłady zastosowań znajdziesz
w literaturze [3,4]. Poniżej przedstawiony jest przykład sterowania za pomocą
demultipleksera linijką świetlną.
Rys.15. Układ sterujący linijką świetlną [3, s.207].
4.3.1.3. Komparatory
Komparatory służą do porównywania wartości binarnych. Najprostszy komparator
pozwala stwierdzić czy dwie wielkości binarne są sobie równe.
Komparator uniwersalny porównuje liczby i pozwala na uzyskanie odpowiedzi, czy
porównywane liczby binarne są sobie równe lub, która z nich większa czy mniejsza.
Wynikiem porównania jest pojawienie się stanu wysokiego na jednym z wyjść, co wskazuje
na relację jaka jest pomiędzy argumentami A i B
Rys.16. Symbol graficzny komparatora uniwersalnego.
A>B
A=B
A<B
A
B
„
Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
31
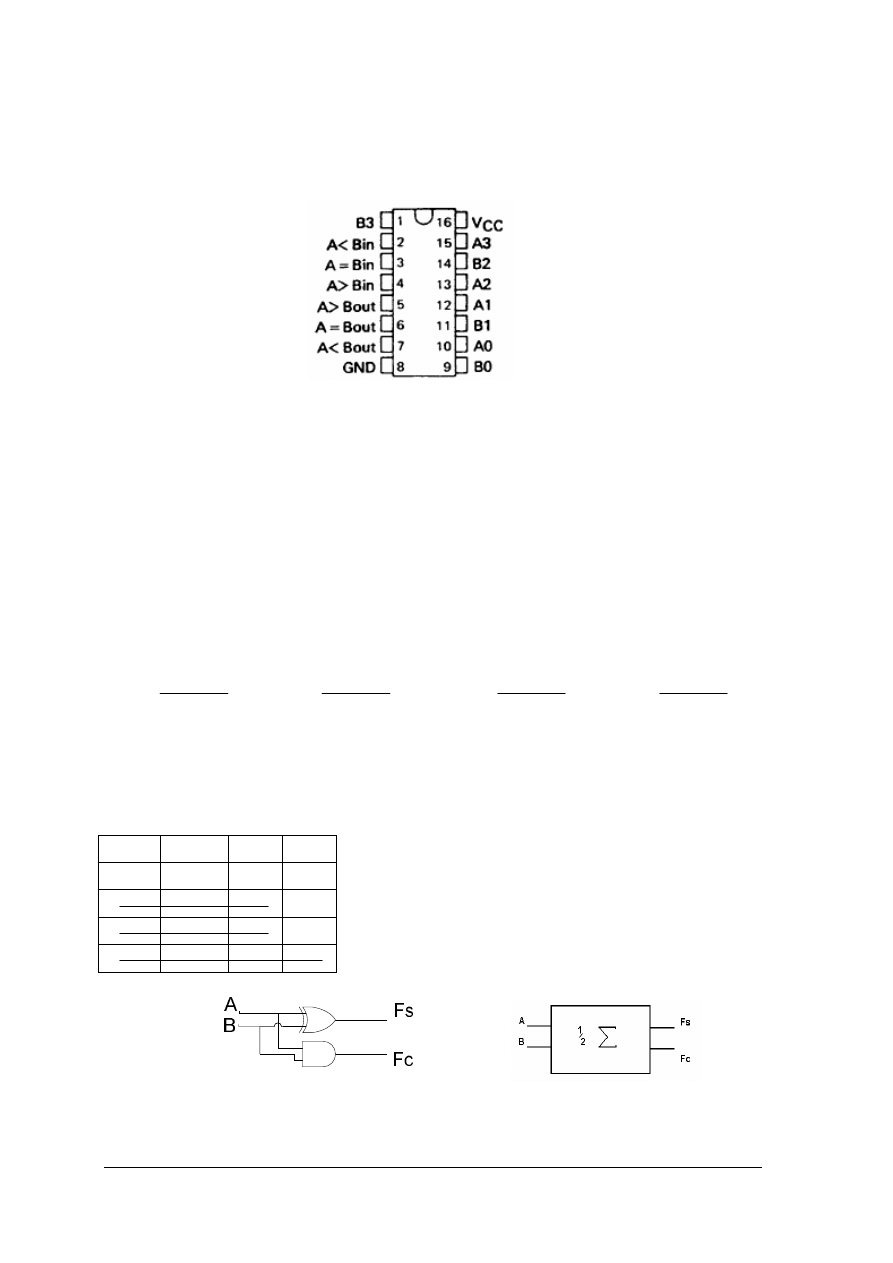
Układem komparatora jest układ TTL 7485 – jest to komparator czterobitowy.
W tym układzie porównywane są czterobitowe argumenty A i B. Zwróć uwagę na dodatkowe
wejścia kaskadowe (wyprowadzenia 2,3,4), które umożliwiają łączenie tych układów w celu
uzyskania możliwości porównywania argumentów o większej liczbie bitów.
Rys. 17. Rozkład wyprowadzeń komparatora uniwersalnego 7485N.
4.3.1.4. Sumatory
Sumatory są układami umożliwiającymi dodawanie wielkości binarnych. Sam proces
dodawania liczb binarnych jest przedstawiony w materiale nauczania 4.1.1. Sumator
umożliwia także wykonywanie odejmowania pod warunkiem, że odjemnik zostanie wcześniej
zakodowany kodem U2. Opis tego kodu znajduje się w literaturze [3, s. 226].
Najprostszym układem sumującym jest półsumator – układ, który umożliwia dodawanie
dwóch liczb jednobitowych.
Aby zaprojektować ten układ musimy wyobrazić sobie jego działanie.
Dodając dwie liczby możemy mieć następujące przypadki:
S – bit sumy, C – bit przeniesienia
Możemy to zapisać w postaci tabeli działania i postępując zgodnie z procedurą wypisać
funkcje opisujące działanie tego układu. F
S
- funkcja sumy, F
C
– funkcja przeniesienia
.
Tabela 12.
Bit A
Bit B
F
S
F
C
0
0
0
0
0
1
1
0
1
0
1
0
1
1
0
1
Rys. 18. Półsumator: a) schemat logiczny, b) symbol graficzny.
Dwa połączone półsumatory tworzą układ sumatora umożliwiającego sumowanie dwóch
bitów liczb wielobitowych.
0
(2)
+ 0
S = 0
0
(2)
+ 1
S = 1
1
(2)
+ 0
S = 1
1
(2)
+ 1
S = 0
C =1
F
S
= A’B + AB’ F
C
= AB
Uwaga: odszukaj w tabeli 6 i 7 bramki
logiczne, które realizują funkcje F
S
i F
C.
a)
b)
„
Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
32
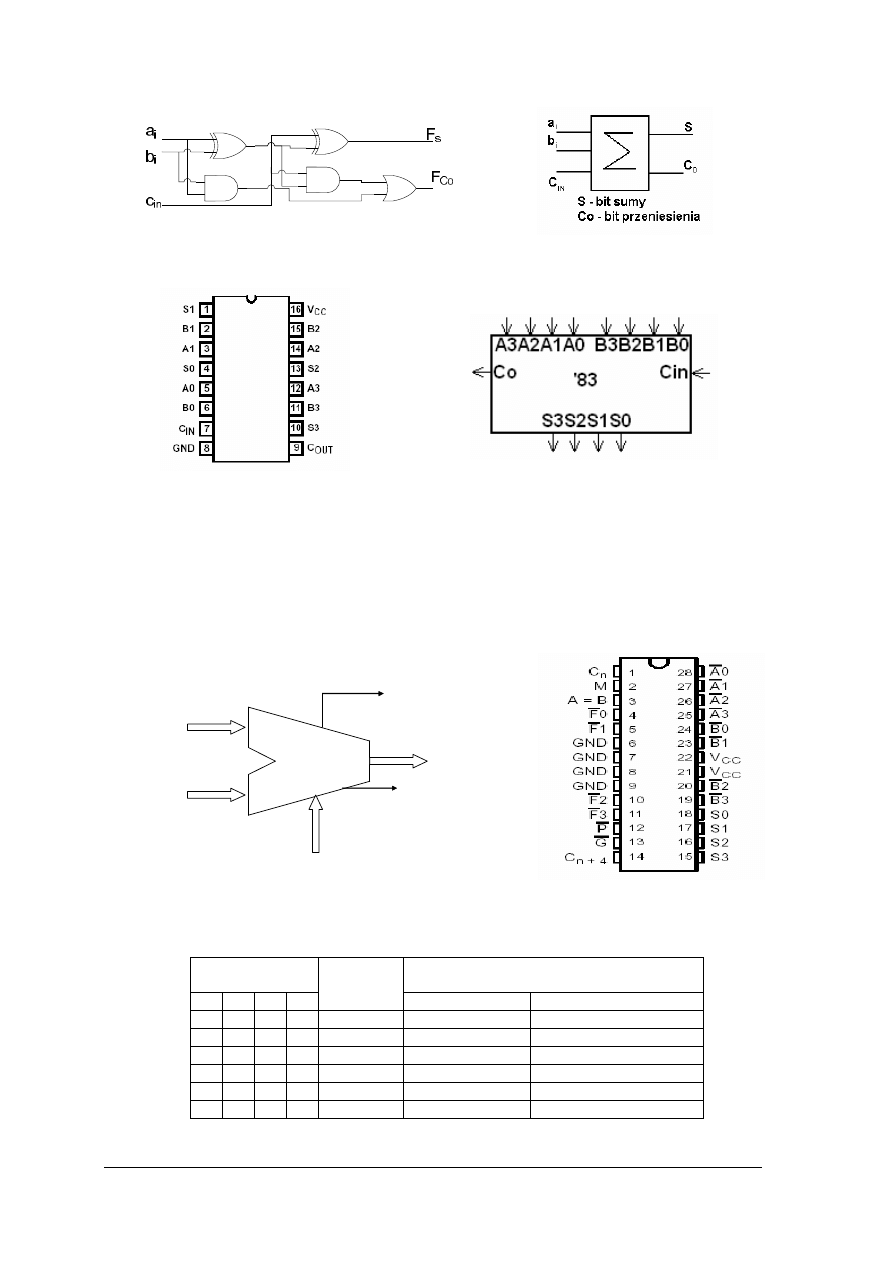
Rys.19. Sumator: a) schemat logiczny, b) symbol graficzny.
Rys. 20. Sumator czterobitowy ’83: a) rozkład wyprowadzeń, b) symbol graficzny
4.3.1.5. Jednostka arytmetyczno – logiczna ALU
Układem, który umożliwia wykonywanie operacji arytmetycznych i logicznych na
argumentach binarnych jest jednostka arytmetyczno – logiczna, zwana w skrócie ALU.
Najprostszy układ tego typu ‘181 umożliwia wykonywanie 16 operacji arytmetycznych
i 16 logicznych na argumentach czterobitowych. Wyboru wykonywanej operacji dokonuje się
poprzez dobór odpowiedniego pięciobitowego sygnału sterującego [3,4,8].
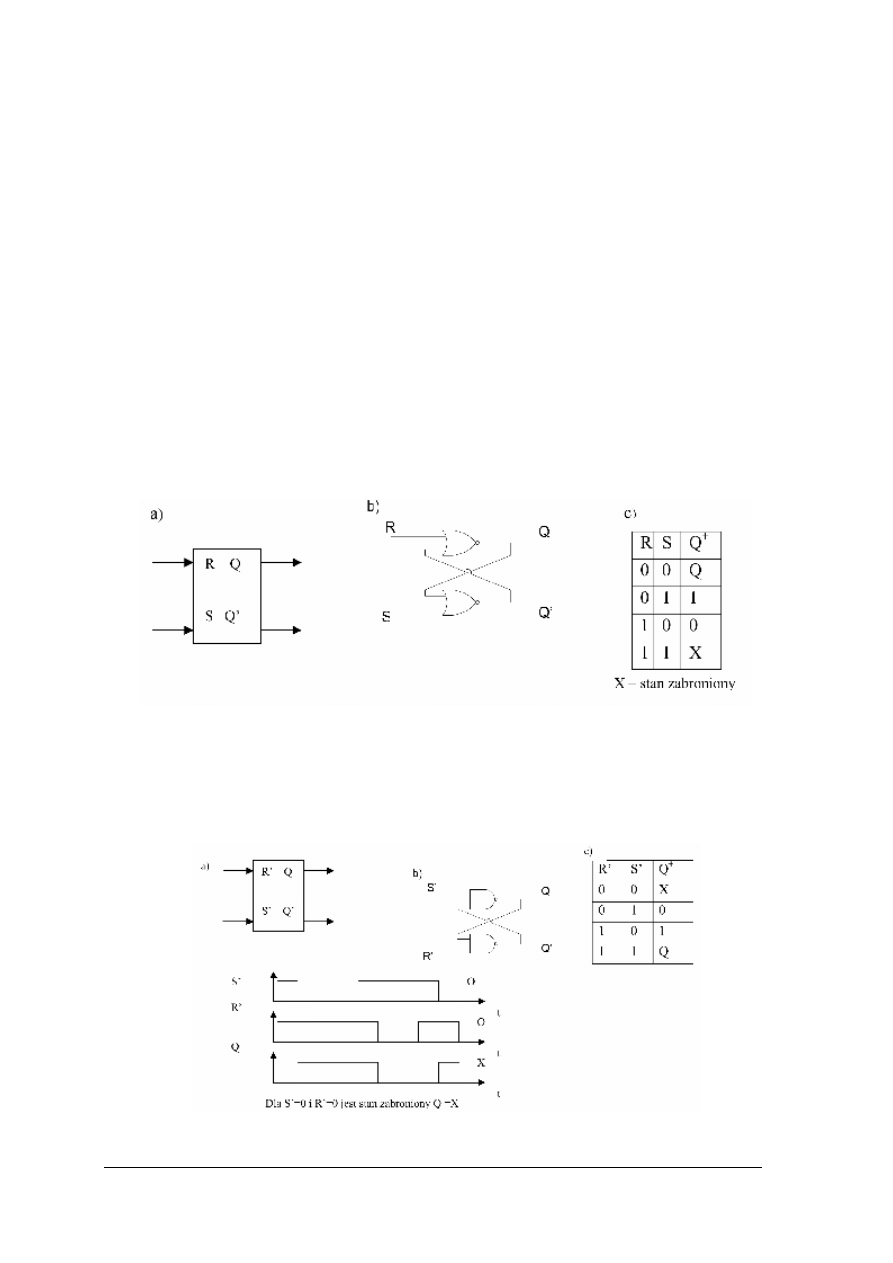
Rys. 21. a) symbol graficzny, b) rozkład wyprowadzeń ALU 74ACT1181 c) fragment tabeli działania.
Wejścia wyboru
funkcji
Operacje arytmetyczne M = 0
S3 S2 S1 S0
Funkcje
logiczne
M =1
C
n
= 0
C
n
= 1
L
L
L
L
F =A’
F = A
F = A PLUS 1
L
L
L
H
F = (A+B)’ F = A + B
F = (A + B) PLUS 1
L
L
H
L
F = A’B
F = A + B’
F = (A + B’) PLUS 1
L
L
H
H
F = 0
F = MINUS 1
F = ZERO
L
H
L
L
F = (AB)’
F = A’ PLUS AB’ F = A PLUS AB’ PLUS 1
.
…..
…..
…….
a)
b)
A
0
– A
3
B
0
– B
3
F
0
– F
3
S
0
– S
3
M
C
n
A = B
C
n +4
a)
b)
a)
b)
c)

„
Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
33
4.3.2. Pytania sprawdzające
Odpowiadając na pytania sprawdzisz, czy jesteś przygotowany do wykonania ćwiczeń.
1. Czym się charakteryzują układy komutacyjne?
2. Do czego służą dekodery?
3. Jaki jest symbol graficzny kodera?
4. Jaka jest tabela działania dekodera z kodu binarnego na kod „1z4”?
5. Czym się różni dekoder od enkodera?
6. Jak zaprojektować dekoder?
7. Jak na podstawie tabeli działania zinterpretować funkcjonowanie układu?
8. Jaka jest zasada działania multipleksera i demultipleksera?
9. Jak rozszerzyć liczbę wejść w multiplekserze?
10. Na czym polega multipleksowy system transmisji danych?
11. Do czego służą komparatory?
12. Jak zinterpretować oznaczenia wyprowadzeń wybranych układów scalonych?
13. Do czego służy sumator?
14. Jak rozszerzyć liczbę bitów argumentów w układach komparatorów i sumatorów?
15. Jaki jest symbol graficzny jednostki arytmetyczno-logicznej?
16. Jakie funkcje realizuje ALU?
4.3.3. Ćwiczenia
Ćwiczenie 1
Zaprojektuj układ dekodera z kodu binarnego na kod „1z 4”.
Sposób wykonania ćwiczenia
Aby wykonać ćwiczenie, powinieneś:
1) zapoznać się z instrukcją dotyczącą projektowania układów kombinacyjnych (Materiał
nauczania pkt. 4.2.1.4) oraz tabelami kodów binarnych (Materiał nauczania pkt. 4.1.1.9),
2) wykonać zaplanowane czynności krok po kroku,
3) narysować schemat logiczny projektowanego układu,
4) zbudować układ zgodnie ze schematem w programie symulacyjnym i zaplanować
wysterowanie wejść zgodnie z jego tabelą działania,
5) porównać otrzymane sygnały wyjściowe z zakładanymi – obserwować sygnały
wyjściowe możesz za pomocą wskaźników stanów logicznych lub za pomocą
oscyloskopu wielokanałowego.
Jeśli masz trudności poproś o pomoc nauczyciela.
Wyposażenie stanowiska pracy:
−
przybory do pisania,
−
poradnik ucznia,
−
stanowisko komputerowe z programem do symulacji pracy układów cyfrowych,
−
literatura [3, 4, 6, 8].

„
Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
34
Ćwiczenie 2
Mając do dyspozycji układ ’47 zaproponuj schemat połączeń umożliwiający
wysterowanie wyświetlacza siedmiosegmentowego
Sposób wykonania ćwiczenia
Aby wykonać ćwiczenie, powinieneś:
1) zapoznać się z zasadą dotyczącą sterowania tym układem wyświetlacza, tabelami kodu
BCD i kodu wskaźnika siedmiosegmentowego oraz tabelą działanie tego układu
(Materiał nauczania pkt. 4.3.1.1 oraz pkt. 4.1.1.9),
2) opracować plan pracy umożliwiający wykonanie ćwiczenia,
3) wykonać zaplanowane czynności krok po kroku,
4) narysować schemat sterowania badanym układem,
5) zbudować schemat w programie symulacyjnym i zaplanować wysterowanie wejść
zgodnie z jego tabelą działania,
6) porównać otrzymane sygnały wyjściowe z zakładanymi – obserwować sygnały
wyjściowe możesz za pomocą przyłączonego wskaźnika siedmiosegmentowego oraz za
pomocą oscyloskopu wielokanałowego,
7) wykonać odpowiednie połączenia w układzie ćwiczeniowym. Sygnały wejściowe możesz
podawać na wejścia za pomocą zadajników stanów logicznych.
Jeśli masz trudności poproś o pomoc nauczyciela.
Wyposażenie stanowiska pracy:
−
przybory do pisania,
−
poradnik ucznia,
−
stanowisko komputerowe z programem do symulacji pracy układów cyfrowych,
−
stanowisko
laboratoryjne
do
badania
układów
cyfrowych
wyposażone
w podstawowe przyrządy pomiarowe i zestawy układów do badań,
−
literatura [3, 4, 6, 8].
Ćwiczenie 3
Sprawdź poprawność działania półsumatora zbudowanego zgodnie ze schematem
zawartym w materiale nauczania pkt.4.3.1.4.
Sposób wykonania ćwiczenia
Aby wykonać ćwiczenie, powinieneś:
1) zapoznać się z zasadą działania tego układu (Materiał nauczania pkt. 4.3.1.4),
2) opracować wykaz czynności umożliwiający wykonanie ćwiczenia,
3) wykonać zaplanowane czynności krok po kroku,
4) wykorzystać program symulacyjny do sprawdzenia poprawności działania półsumatora
poprzez porównanie otrzymanych sygnałów wyjściowych z tabelą działania tego układu,
5) wykorzystać wyposażenie stanowiska laboratoryjnego do sprawdzenia poprawności
działania półsumatora poprzez porównanie otrzymanych sygnałów wyjściowych
z tabelą działania tego układu.
Jeśli masz trudności poproś o pomoc nauczyciela.
Wyposażenie stanowiska pracy:
−
przybory do pisania,
−
poradnik ucznia,

„
Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
35
−
stanowisko komputerowe z programem do symulacji pracy układów cyfrowych,
−
stanowisko
laboratoryjne
do
badania
układów
cyfrowych
wyposażone
w podstawowe przyrządy pomiarowe i zestawy układów do badań,
−
literatura [3, 4, 6, 8].
Ćwiczenie 4
Mając do dyspozycji katalog układów scalonych określ na podstawie tabeli działania, jaki
kod sterujący należy podać na wejścia sterujące układu ‘181, aby wykonać dodawanie
czterobitowych argumentów wejściowych.
Sposób wykonania ćwiczenia
Aby wykonać ćwiczenie, powinieneś:
1) zapoznać się z zasadą sterowania tym układem, (Materiał nauczania pkt.4.3.1.5 oraz [8]),
2) przeanalizować dokładnie tabelę działania zawartą w katalogu,
3) określić żądaną operację i z tabeli wypisać odpowiadający jej stan wejść sterujących,
4) sprawdzić poprawność odpowiedzi poprzez przygotowanie symulacji dla dowolnych
wartości argumentów lub poprzez wykonanie zadania na stanowisku badaniowym.
Wyposażenie stanowiska pracy:
−
przybory do pisania,
−
poradnik ucznia,
−
stanowisko komputerowe z programem do symulacji pracy układów cyfrowych,
−
stanowisko
laboratoryjne
do
badania
układów
cyfrowych
wyposażone
w podstawowe przyrządy pomiarowe i zestawy układów do badań,
−
literatura [3, 4, 6, 8].
4.3.4. Sprawdzian postępów
Tak Nie
Czy potrafisz:
1) opisać różnymi metodami działanie układów zmiany kodu?
¨
¨
2) zaprojektować układ dekodera z kodu binarnego na kod „1z n” ?
¨
¨
3) wyjaśnić działanie multiplekserów i demultiplekserów?
¨
¨
4) połączyć układy multiplekserów w celu zwiększenia liczby wejść ?
¨
¨
5) zinterpretować funkcje poszczególnych wejść i wyjść komparatorów?
¨
¨
6) rozróżnić symbole graficzne sumatorów, dekoderów, multiplekserów
i demultiplekserów?
¨
¨
7) określić działanie wybranego układu na podstawie opisu
wyprowadzeń?
¨
¨
8) wysterować układ logiczny zgodnie z jego tabelą działania?
¨
¨
9) opracować symulacje złożonego układu logicznego?
¨
¨
10) zinterpretować wykresy prezentujące pracę poznanego układu ?
¨
¨
„
Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
36
4.4. Układy sekwencyjne - liczniki, rejestry
4.4.1. Materiał nauczania
4.4.1.1. Przerzutniki bistabilne
Przerzutniki należą do grupy układów sekwencyjnych. Układem sekwencyjnym
nazywamy układ, w którym stan na wyjściu zależy nie tylko od stanów na wejściach tego
układu (tak było w przypadku układów kombinacyjnych), ale także od stanu wcześniejszego
na wyjściu (stanem wcześniejszym – poprzednim nazywamy stan układu, jaki istniał przed
podaniem aktualnych sygnałów na wejścia). Przyjmiemy następujące oznaczenia: Q – stan
poprzedni na wyjściu układu, Q
+
- stan
następny na wyjściu układu, Q’ – negacja Q[3,4,6].
Przerzutnik RS
Najprostszy układ przerzutnika RS można zrealizować z bramek NAND lub NOR.
Nazwa przerzutników pochodzi od nazw wejść – przerzutnik RS ma dwa wejścia
informacyjne S(set) – wejście ustawiające stan wysoki (H, „1”) na wyjściu Q i wejście
R(reset) – ustawiające stan niski (L, „0”) na wyjściu Q.
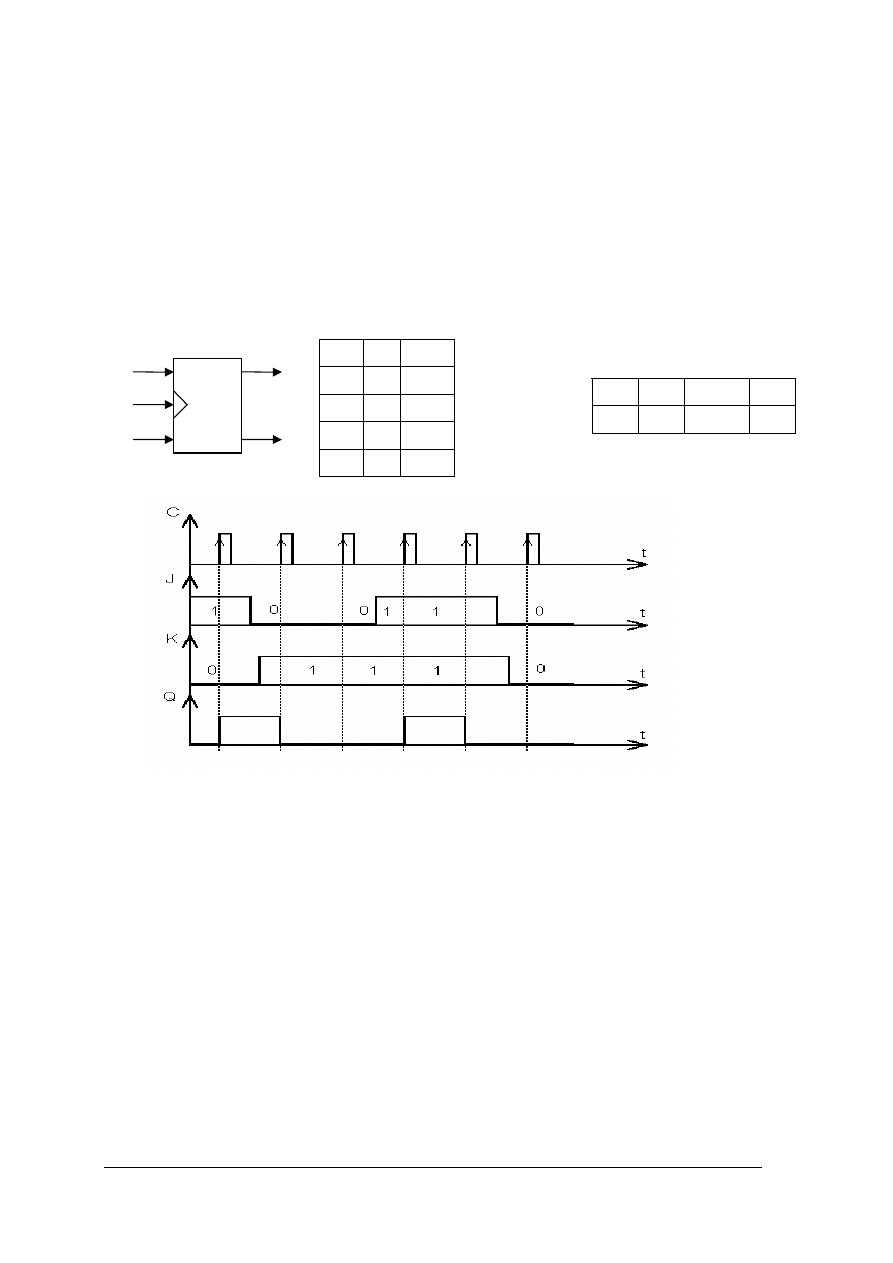
Rys. 22. Przerzutnik RS na bramkach NOR: a) symbol graficzny, b)schemat logiczny, c) tabela działania.
Przerzutnik może być wykonany z ramek NAND. Jego działanie różni się od
przerzutnika RS wykonanego na bramkach NOR. Wejście ustawiające S powoduje ustawienie
stanu wysokiego na wyjściu Q wtedy, gdy jego stan jest równy zero – mówimy, że w tym
przerzutniku „0” jest stanem aktywnym. Ustawienie Q=0 tez następuje, gdy wejście R = 0.
W symbolu graficznym i w tabeli działania zaznaczamy to pisząc z negacją - S’ i R’.
Rys. 23. Przerzutnik RS na bramkach NAND: a) symbol graficzny, b)schemat logiczny, c) tabela działania, d)
wykresy czasowe.
„
Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
37
Przerzutniki przedstawione powyżej są układami asynchronicznymi, nie posiadają wejść
zegarowych. Zastosowanie synchronizacji pracy układu poprzez wprowadzenie dodatkowego
wejścia zegarowego C (ang. clock) między innymi zwiększa odporność układu na zakłócenia,
eliminując powstawanie błędów w stanach przejściowych.
Ze względu na rodzaj zastosowanej synchronizacji rozróżniamy przerzutniki
synchronizowane zboczem impulsu zegarowego lub poziomem napięcia na wejściu
synchronizującym (są to przerzutniki typu „zatrzask” - „latch”). W przypadku przerzutników
synchronizowanych zboczem impulsu zegarowego rozróżniamy układy synchronizowane
zboczem narastającym lub opadającym. Pokażemy to na przykładach.
Przerzutnik JK
Rys. 24. Przerzutnik JK: a) symbol graficzny, b) skrócona tabela działania, c) tabela działania, d) wykresy.
Porównaj skrócone tabele działania przerzutnika RS (NOR) i JK. Jak pewnie zauważyłeś
w przerzutniku JK nie ma stanu zabronionego, a dla J=1 i K=1 układ zmienia stan na
przeciwny do tego, w jakim był przed podaniem tych sygnałów wejściowych.
W przypadku przerzutnika synchronicznego zmiana stanu może nastąpić wyłącznie
w obecności właściwego zbocza impulsu zegarowego. Przerzutnik, którego symbol jest na
rys. 23 jest synchronizowany przednim zboczem impulsu zegarowego. Taki rodzaj
synchronizacji w tabeli działania oznaczany jest symbolicznie strzałką w górę [8].
Przerzutnik oprócz wejść informacyjnych (J,K) zegarowego (C lub Clk) może posiadać
wejścia programujące S i R, które są asynchroniczne i działają bez sygnału zegarowego
a ponadto mają wyższy priorytet i blokują pracę pozostałych wejść.
Przerzutniki JK – MS są przerzutnikami typu „master – slave” i pracują w trybie
dwutaktowym. Więcej informacji na ten temat znajdziesz w literaturze [ 3, 4, 8].
J
K
Q
+
0
0
Q
0
1
0
1
0
1
1
1
Q’
Q\JK
00
01
11
10
Q=0
0
0
1
1
Q=1
1
0
0
1
J Q
C
K Q’
Q
+
= Q’J + QK’
Q
+
= 1 gdy Q=0 i J=1 lub Q=1 i K=0
a)
b)
c)
d)
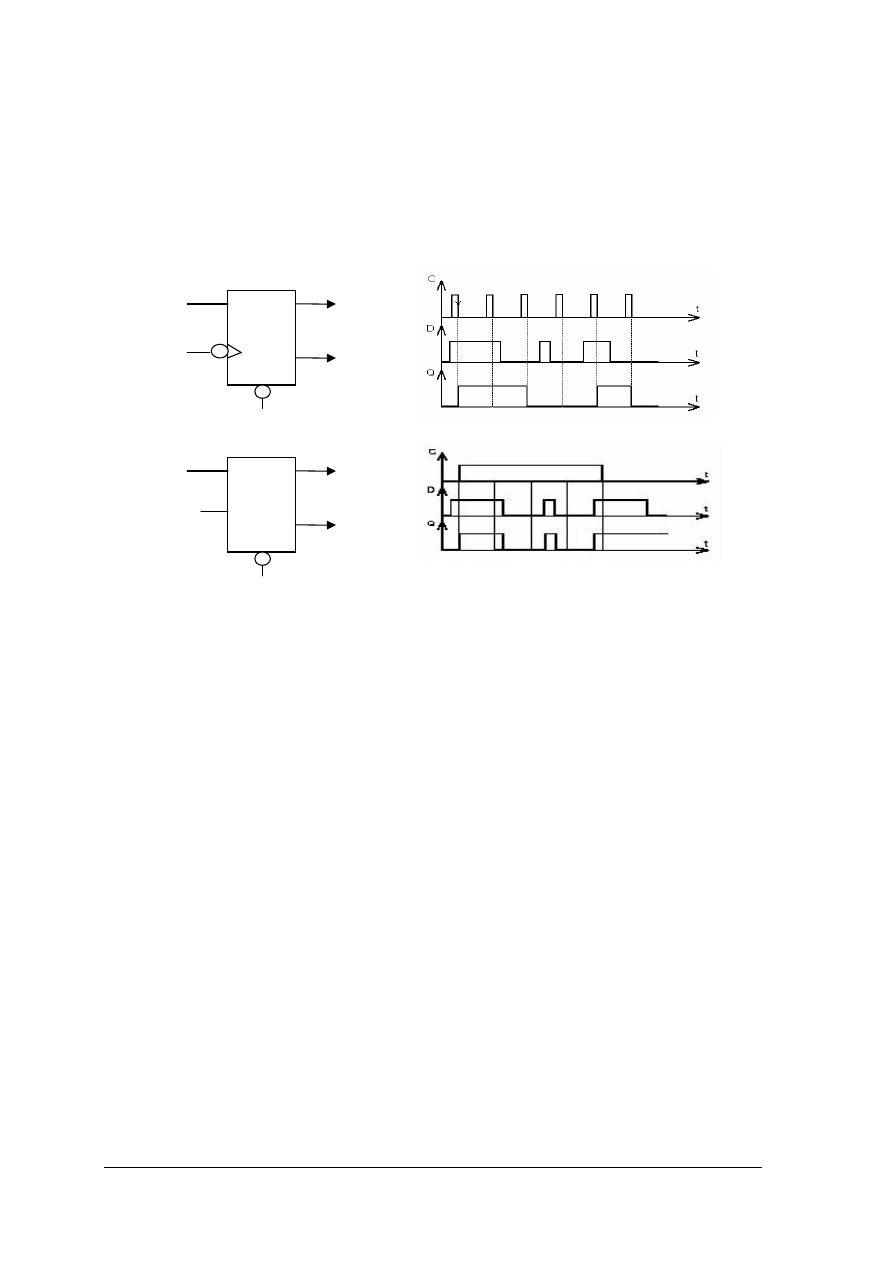
„
Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
38
Przerzutnik D
Przerzutniki D występują w dwóch wersjach: z synchronizacją zboczem impulsu
zegarowego lub typu „zatrzask” – z synchronizacją poziomem sygnału zegarowego. Oba
układy działają według tej samej tabeli, jednak wykresy prezentujące ich prace różnią się
w związku z różnym sposobem synchronizacji. Działanie przerzutnika D można opisać
stwierdzeniem, że stan na wyjściu Q przerzutnika jest równy stanowi na wejściu D jaki jest
w obecności sygnału zegarowego.
Rys.25. Przerzutniki D: a) symbol graficzny przerzutnika D synchronizowanego tylnim zboczem i jego wykresy
czasowe, b) symbol graficzny przerzutnika D synchronizowanego poziomem sygnału zegarowego typu „latch”
i jego wykresy czasowe.
4.4.1.2. Liczniki
Liczniki są układami służącymi do zliczania i pamiętania liczby impulsów wejściowych
(podawanych na wejście zegarowe pierwszego przerzutnika).
Podstawowe parametry licznika to;
−
długość licznika – liczba wyjść przerzutników, z których zbudowany jest licznik –
przykładowo – układ ‘164 to 8-bitowy licznik przesuwający,
−
pojemność licznika N – maksymalna liczba stanów licznika, zależy ona od liczby
przerzutników i tak dla licznika dwubitowego N= 2
2
, dla licznika trzybitowego N=2
3
.
Stosowane jest także określenie licznik „modulo N”, co oznacza, że po przekroczeniu N
impulsów licznik zeruje się i ponownie zaczyna liczyć. Wskazanie licznika jest liczbę binarną
będącą resztą z całkowitego dzielenia liczby impulsów przez N.
Liczniki dodające (liczące w przód) po każdym impulsie zwiększają zawartość
o jeden, liczniki odejmujące (liczące do tyłu) po każdym impulsie zmniejszają stan
o jeden a liczniki rewersyjne mają możliwość pracy dwukierunkowej.
Liczniki mogą pracować jako układy asynchroniczne lub synchroniczne. Przerzutniki JK
lub inne pracujące w trybie JK są najczęściej wykorzystywane do budowy liczników [3, 6, 8].
Licznik modulo 4 zbudowany jest z dwóch przerzutników JK pracujących w trybie
przełączania (J=1 i K=1). W układzie asynchronicznym sygnał zegarowy podawany jest
wyłącznie na wejście pierwszego przerzutnika. Jeśli układ ma liczyć w trybie dodawania to
wyjście Q pierwszego przerzutnika należy połączyć z wejściem zegarowym następnego.
D Q
C
Q’
R’
D Q
C
Q’
R’
a)
b)
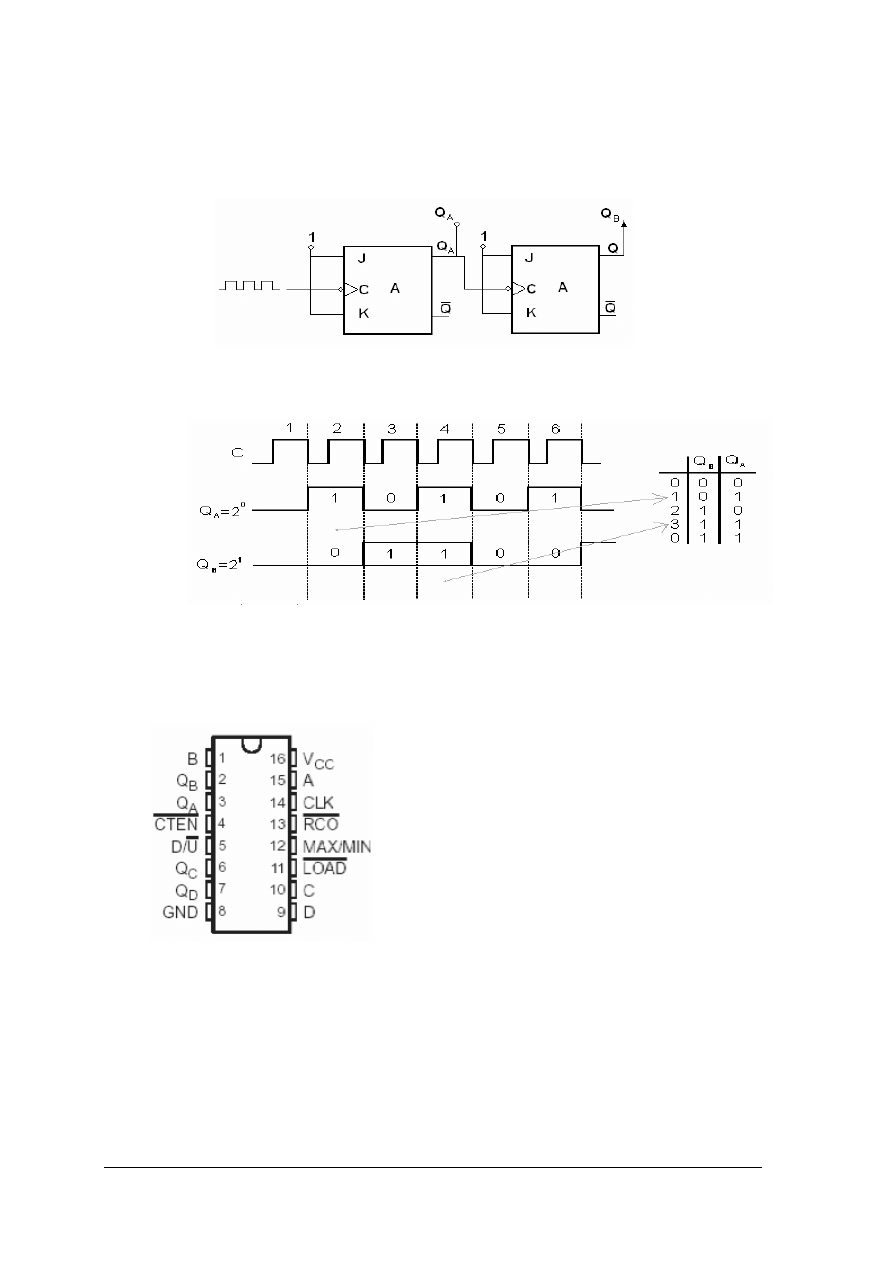
„
Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
39
Dodając kolejne przerzutniki możemy zwiększać pojemność tego licznika. Jeśli chcielibyśmy
uzyskać liczenie „do tyłu” należałoby wyjście Q’ przerzutnika połączyć z wejściem
zegarowym następnego.
Rys. 26. Licznik modulo 4 liczący „do przodu”: a)schemat logiczny, b) wykresy czasowe i tabela stanów.
W katalogach możesz znaleźć układy liczników scalonych. Dla przykładu przedstawimy
układ 4 bitowego licznika rewersyjnego – ‘191
Opis wyprowadzeń:
A, B, C, D–wejścia danych umożliwiające
równoległy zapis stanu początkowego
licznika w obecności sygnału LOAD = 0
D/U’ – określenie kierunku liczenia „w
górę” lub „w dół”
MAX/MIN – wyjście sygnalizujące przez
jeden cykl zegara przepełnienie licznika
przy liczeniu „w górę” lub wyzerowanie
przy liczeniu „w dół”
CTEN’ nieraz określane jako ENABLE –
wejście zezwalające oraz RCO’ – wyjście
używane
przy
kaskadowym
łączeniu
liczników
Rys. 27. Licznik rewersyjny 4 bitowy ‘191 z opisem wyprowadzeń.
Funkcje pozostałych wyprowadzeń nie wymagają dodatkowego komentarza.
4.4.1.3. Rejestry
Rejestr służy do przechowywania informacji.. Zbudowany jest z przerzutników, których
liczba określa ilość pamiętanych bitów informacji. Parametrami charakteryzującymi rejestry
są:
a)
b)
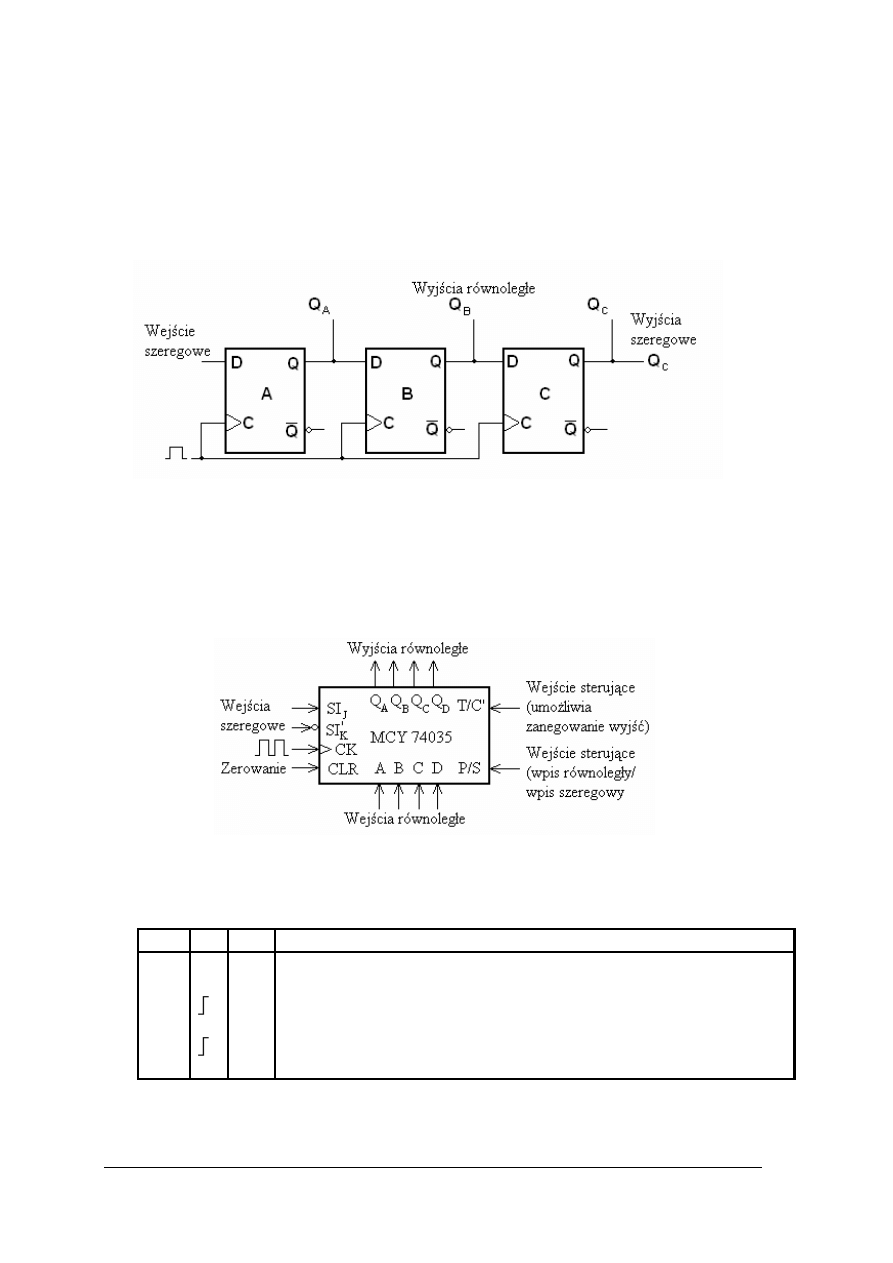
„
Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
40
−
długość rejestru – liczba bitów, które mogą być pamiętane w rejestrze,
−
tryb pracy, który określa sposób zapisu i odczytu informacji: SISO ( szeregowy zapis
i szeregowy odczyt), SIPO (szeregowy zapis i równoległy odczyt), PISO (równoległy
zapis i szeregowy odczyt), PIPO (równoległy zapis i odczyt)[3, 4, 6, 8].
Z wyjątkiem ostatniego trybu pracy wszystkie poprzednie wymagają przesuwania
informacji
w
rejestrze,
co
oznacza
konieczność
przepisywania
informacji
z przerzutnika do przerzutnika.
Rys. 28. Schemat logiczny 3-bitowego rejestru przesuwnego
Ten trzybitowy rejestr przesuwny może pracować w trybie SISO i SIPO. Jest układem
synchronicznym, ponieważ sygnał zegarowy jest podawany równolegle na wszystkie
przerzutniki.
Przeanalizujemy pracę przykładowego 4 bitowego rejestru uniwersalnego ‘035
Rys. 29. Rejestr uniwersalny ‘035
Praca układu jest opisana poniższą tabelą przy założeniu, że T/C’ = 1 oraz SI= SJ
J
= SK’
K
Tabela 13.
CLR CP P/S’ Realizowana funkcja
1
-
-
zerowanie rejestru (asynchroniczne)
0
0
przesuwanie w prawo z wpisaniem do przerzutnika A stanu wejścia
SI (Q
A
= SI)
0
1
wprowadzanie informacji z wejść równoległych (synchronizowane
zegarem)
Układ może pracować we wszystkich czterech trybach pracy: SISO, SIPO, PISO, PIPO.
Może być wykorzystywany jako licznik – wtedy SJ i SK są połączone razem, lub jako rejestr

„
Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
41
i wtedy SJ i SK połączone są poprzez negację. Po wykonaniu zewnętrznych połączeń układ
ma możliwość przesuwania informacji w lewo.
4.4.2. Pytania sprawdzające
Odpowiadając na pytania sprawdzisz, czy jesteś przygotowany do wykonania ćwiczeń.
1. Jaka jest zasada działania przerzutnika RS (NOR)?
2. Jaka jest zasada działania przerzutnika RS (NAND)?
3. Jaka jest różnica w działaniu przerzutnika JK i RS(NOR)?
4. Jakie są symbole graficzne przerzutników różnych typów?
5. Co to znaczy, że przerzutnik jest w wersji synchronicznej?
6. Jakie są sposoby synchronizacji przerzutników?
7. Jaka jest zasada działania przerzutnika D z synchronizacją zboczem?
8. Jaka jest zasada działania przerzutnika D „zatrzask’?
9. Jak rozróżnić na podstawie przebiegów czasowych rodzaj synchronizacji?
10. Do czego służą liczniki binarne?
11. Jakimi parametrami charakteryzujemy liczniki?
12. Jak narysować schemat licznika o określonej pojemności i kierunku liczenia?
13. Do czego służą rejestry?
14. Jaki parametrami charakteryzujemy rejestry?
15. Jak narysować schemat rejestru o zadanej długości i sposobie zapisu i odczytu
informacji?
16. Jak na podstawie opisu wyprowadzeń scalonego rejestru odczytać jego podstawowe
własności?
4.4.3. Ćwiczenia
Ćwiczenie 1
Zaprojektuj układ 4 bitowego asynchronicznego licznika binarnego liczącego do przodu.
Narysuj przebiegi z generatora impulsów wejściowych oraz na wyjściu każdego
z przerzutników. Zmierz okresy, porównaj częstotliwości wszystkich narysowanych
przebiegów i określ, jaka zależność występuje pomiędzy tymi sygnałami.
Na którym wyjściu licznika sygnał ma częstotliwość 4 razy mniejszą niż na wejściu?
Sposób wykonania ćwiczenia
Aby wykonać ćwiczenie, powinieneś:
1) określić, jakie przerzutniki należy zastosować i ile takich układów potrzeba do budowy
licznika (Materiał nauczania pkt.4.4.1),
2) zaplanować sposób połączeń pomiędzy przerzutnikami, aby uzyskać pracę
asynchroniczną licznika oraz odpowiedni kierunek zliczania,
3) narysować schemat logiczny projektowanego układu,
4) zbudować układ zgodnie ze schematem w programie symulacyjnym i zaplanować
wysterowanie wejść zgodnie z jego zasadą działania,
5) zbudować układ korzystając z układów będących do dyspozycji na stanowisku
laboratoryjnym,
6) porównać otrzymane sygnały wyjściowe z zakładanymi –sygnały wyjściowe obserwuj za
pomocą oscyloskopu wielokanałowego,

„
Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
42
7) narysować wszystkie przebiegi starannie pamiętając o ustawieniu podstawy czasu na
oscyloskopie,
8) zmierzyć okresy wszystkich przebiegów,
9) zastosować wzór na zależność częstotliwości od okresu przebiegu zmiennego i obliczyć
częstotliwości poszczególnych przebiegów,
10) opowiedzieć na pytania zawarte w ćwiczeniu.
Jeśli masz trudności poproś o pomoc nauczyciela.
Wyposażenie stanowiska pracy:
−
przybory do pisania,
−
poradnik ucznia,
−
stanowisko komputerowe z programem do symulacji pracy układów cyfrowych,
−
stanowisko laboratoryjne do badania układów cyfrowych wyposażone w podstawowe
przyrządy pomiarowe i zestawy układów do badań,
−
literatura [3, 4, 6, 8].
Ćwiczenie 2
Zaprojektuj układ: 4 bitowy rejestr przesuwny SISO. Narysuj przebiegi prezentujące
pracę tego układu przy zapisie i odczycie informacji 1101. Określ ile impulsów zegarowych
potrzeba, aby zapisać i odczytać tę informację? Jaki tryb pracy rejestru zapewnia najkrótszy
czas zapisu i odczytu wielobitowej informacji?
Sposób wykonania ćwiczenia
Aby wykonać ćwiczenie, powinieneś:
1) określić jakie przerzutniki należy zastosować i ile takich układów potrzeba do budowy
licznika (Materiał nauczania pkt.4.4.1),
2) zaplanować sposób połączeń pomiędzy przerzutnikami, aby uzyskać pracę rejestru
w trybie SISO,
3) narysować schemat logiczny projektowanego układu,
4) zbudować układ zgodnie ze schematem w programie symulacyjnym i zaplanować
wysterowanie wejść umożliwiające zapis i odczyt informacji 1101,
5) zbudować układ korzystając z układów będących do dyspozycji na stanowisku
laboratoryjnym,
6) porównać otrzymane sygnały wyjściowe z zakładanymi (sygnały wyjściowe obserwuj za
pomocą oscyloskopu wielokanałowego),
7) narysować wszystkie przebiegi,
8) odpowiedzieć na pytania zawarte w ćwiczeniu.
Jeśli masz trudności poproś o pomoc nauczyciela.
Wyposażenie stanowiska pracy:
−
przybory do pisania,
−
poradnik ucznia,
−
stanowisko komputerowe z programem do symulacji pracy układów cyfrowych,
−
stanowisko
laboratoryjne
do
badania
układów
cyfrowych
wyposażone
w podstawowe przyrządy pomiarowe i zestawy układów do badań,
−
literatura [3, 4, 6, 8].

„
Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
43
4.4.4. Sprawdzian postępów
Tak Nie
Czy potrafisz:
1) wyjaśnić działanie przerzutników RS, JK i D?
¨
¨
2) zapisać tabele działania tych przerzutników ?
¨
¨
3) narysować przebiegi czasowe prezentujące pracę tych układów?
¨
¨
4) wyjaśnić znaczenie podstawowych parametrów licznika?
¨
¨
5) zastosować przerzutniki do zbudowania liczników binarnych?
¨
¨
6) wyjaśnić znaczenie podstawowych parametrów rejestru?
¨
¨
7) zastosować przerzutniki do zbudowania rejestrów?
¨
¨
8) wyjaśnić działanie licznika i rejestru na podstawie schematu?
¨
¨
9) wymienić przykłady zastosowania liczników i rejestrów?
¨
¨
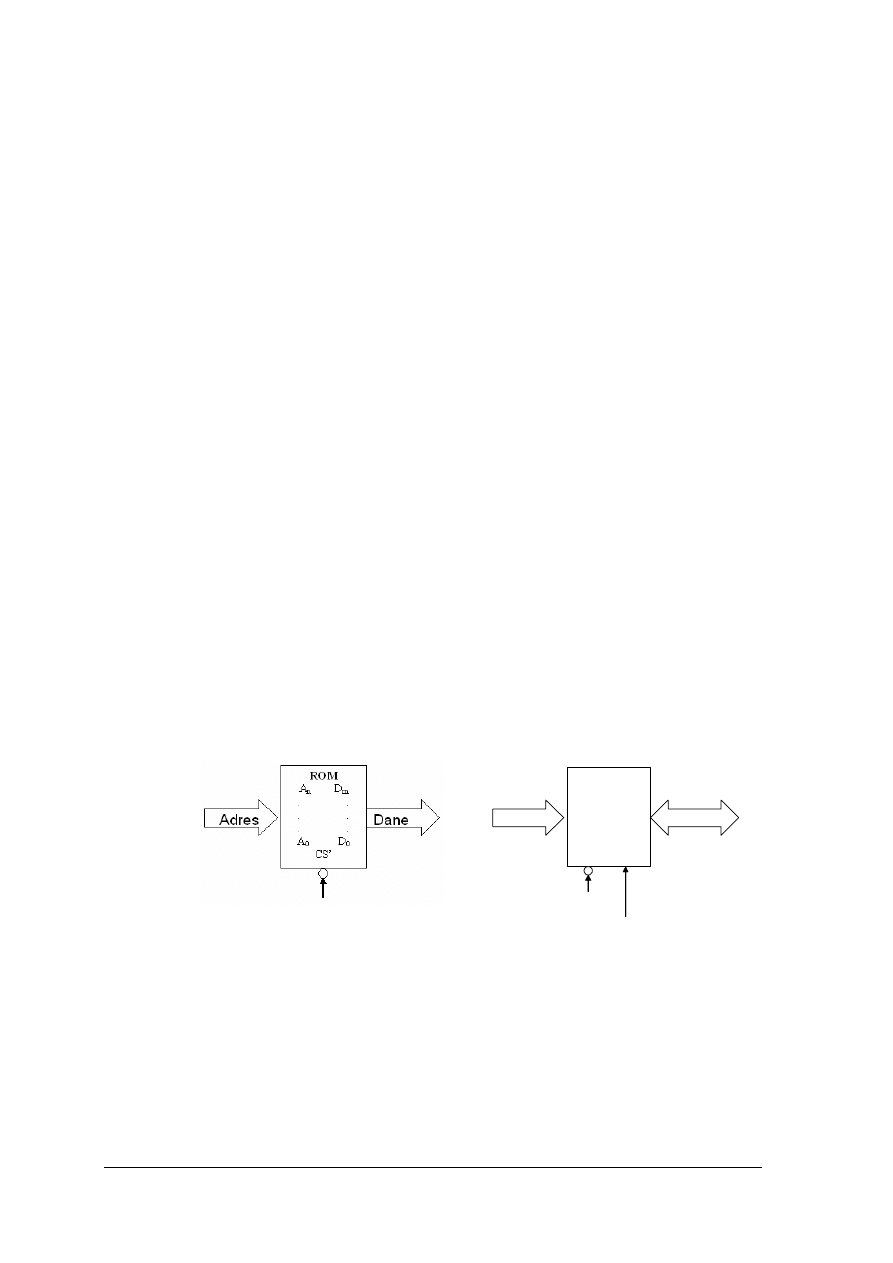
„
Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
44
4.5. Pamięci i układy mikroprocesorowe
4.5.1. Materiał nauczania
4.5.1.1. Pamięci
Pamięci charakteryzują następujące parametry:
−
pojemność pamięci – ilość bitów informacji, które może zapamiętać. Często pojemność
pamięci podaje się określając liczbę słów i ilość bitów w słowie przykładowo 64 x 8
bitów. Pojemność pamięci podaje się stosując następujące przedrostki:
1Kb = 2
10
bitów = 1024 bitów, gdzie K (kilo), b – bit
1MB = 2
10
KB = 2
10 x
2
10
bajtów = 2
20 x
8 bitów, gdzie M (mega), B – bajt = 8 bitów
1GB = 2
10
MB = 2
10 x
2
10
KB = 2
10 x
2
10 x
2
10
x 8 bitów =
2
30
x 8 bitów, , gdzie G (giga)
−
czas dostępu do pamięci lub czas cyklu pamięci – jest to parametr dynamiczny
określający szybkość pracy pamięci.
Pamięć zawiera dwa podstawowe bloki funkcjonalne: matrycę komórek pamiętających i
dekoder adresów umożliwiający wybranie/zaadresowanie dowolnej komórki [3,4].
Pamięci dzielimy na pamięci typu ROM (wyłącznie do odczytu) oraz pamięci typu RAM
(pamięci o dostępie swobodnym). Zwróć uwagę na strzałki obrazujące dane i ich zwrot
(rys.30). Pamięci RAM nazywamy pamięciami ulotnymi, ponieważ po zaniku napięcia
zasilającego pamiętana informacja ulega utracie. Pamięci RAM dzielą się na pamięci
statyczne – SRAM często używane jako pamięci typu „cache” oraz pamięci dynamiczne –
DRAM, które są wolniejsze ze względu na konieczność odświeżania pamiętanej informacji.
Specjalnym typem pamięci wielowejściowej jest pamięć VideoRAM. Pamięci ROM należą
do pamięci nieulotnych, co oznacza, że informacja po zaniku napięcia zasilającego nie ulega
utracie. W tej grupie pamięci możemy wyróżnić bardzo popularne pamięci EPROM,
EEPROM, Flash-ROM oraz powszechnie stosowane CD-ROMy. Wszystkie te pamięci
umożliwiają zapis informacji. W pamięci EPROM kasowanie informacji odbywa się pod
wpływem promieniowania ultrafioletowego – stąd konieczność umieszczenia specjalnego
układu optycznego w obudowie.
Rys.30. Pamięci: RAM i ROM.
Pamięci przedstawione na rysunku oprócz wejść adresowych, które określają adres
komórki pamięci, z której ma się odbywać odczyt informacji, lub do której informacja ma
zostać zapisana posiadają wejścia lub wyjścia danych oraz wejścia sterujące: CS’ – wybór
układu i R/W” – wejście odczyt/zapis. Odczyt informacji z pamięci ROM odbywa się
następująco: na wejścia adresowe podawany jest binarny adres komórki pamięci, wejście CS’
jest w stanie niskim i wtedy na wyjściach danych pojawi się odczytana informacja. Liczba
wyjść danych określa liczbę bitów informacji, które można odczytać w jednym cyklu pracy
pamięci. Liczba wejść adresowych określa w przypadku adresowania bezpośredniego liczbę
komórek pamięci.
RAM
A
n
D
m
. .
. .
. .
A
0
D
0
CS’ R/W’
Adres
Dane
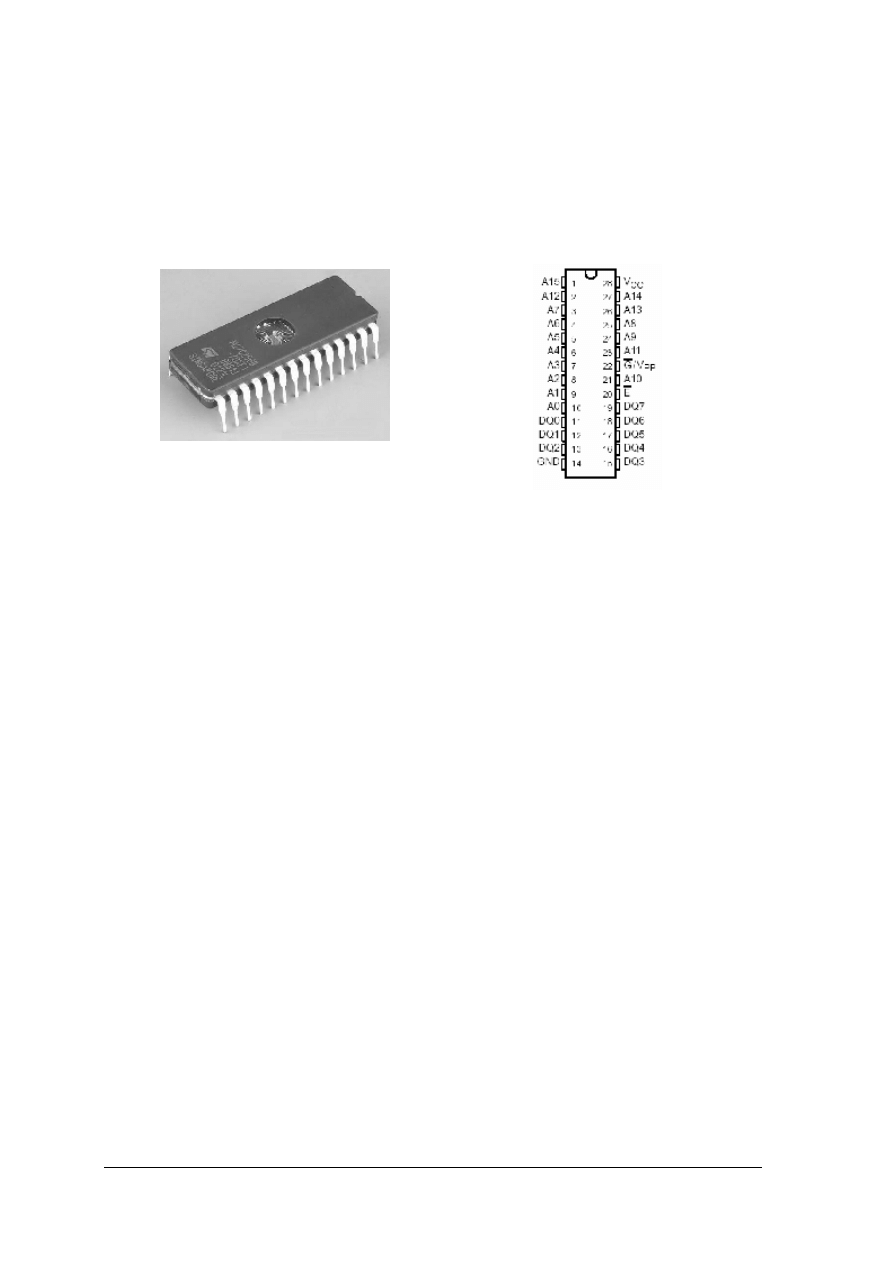
„
Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
45
Wobec konieczności projektowania pamięci o coraz większych pojemnościach stosuje się
specjalne tryby adresowania, co zapobiega zwiększaniu liczby wyprowadzeń. Zauważ, że aby
w sposób bezpośredni zaadresować pamięć o pojemności 1MB = 2
20
bajtów, należałoby
utworzyć 20 bitowy adres. Aby lepiej zrozumieć to zagadnienie przeanalizujemy dane
przykładowej pamięci EPROM - 27C256. Na zdjęciu przedstawiającym układ scalony
pamięci widoczny jest układ optyczny umożliwiający kasowanie informacji za pomocą
promieniowania ultrafioletowego.
Rys. 31. Pamięć EPROM 27C256 a)wygląd układu, b)rozkład wyprowadzeń.
Dane:
−
organizacja pamięci 64K * 8bit = 2
6
2
10
* 8bit = 2
16
* 8bit – układ może zapamiętać
−
2
16
= 65 536 słów/komórek po 8 bitów w każdym słowie/komórce,
−
układ posiada 16 wejść adresowych A
0
- A
15
oraz 8 wyjść danych D
0
- D
7
, wejścia
wykorzystywane do zasilania i do elektrycznego programowania,
−
napięcie zasilania 5V,
−
rozkład wyprowadzeń kompatybilny z istniejącymi 512K MOS ROM, PROM i EPROM,
−
max czas dostępu / min czas cyklu : 100-250 ns.
Pojemność pamięci można rozbudowywać łącząc ze sobą układy scalone o mniejszej
pojemności. Rozszerzając pojemność pamięci możemy zwiększać liczbę pamiętanych słów
oraz liczbę pamiętanych bitów w jednym słowie. Przykłady sposobu połączeń znajdziesz
w literaturze [3, s. 272 i 273].
4.5.1.2. Programowalne układy logiczne PLD
Programowalne układy logiczne zastępują coraz bardziej tradycyjne rodziny układów
logicznych w nowych konstrukcjach. Umożliwiają one skonfigurowanie potrzebnego układu
w gotowym, uniwersalnym układzie scalonym za pomocą odpowiednich narzędzi
programowych ( kompilator, program syntezy, fitter) i sprzętowych (programator). Możliwe
jest dokonywanie zmian i poprawianie funkcjonowania układu poprzez ponowne
zaprogramowanie. Najważniejszą cechą tych układów jest możliwość nadawania przez
użytkownika cech funkcjonalnych. Układy te umożliwiają budowanie systemów cyfrowych
szybko i tanio. Jednymi z pierwszych były układy PAL składające się z programowalnej
matrycy bramek AND oraz dołączonej do niej stałej matrycy bramek OR [7].
Układy EPLD zbudowane są z niewielkiej ilości dużych makrokomórek, których sposób
połączeń może być dowolnie wybierany. Większość tych układów kasowana jest
promieniowaniem ultrafioletowym.
Układy FPGA są matrycami składającymi się z dużej ilości małych makrokomórek.
Programowanie odbywa się w komórkach SRAM, które ładowane są z zewnętrznej pamięci
przy starcie systemu.
a)
b)
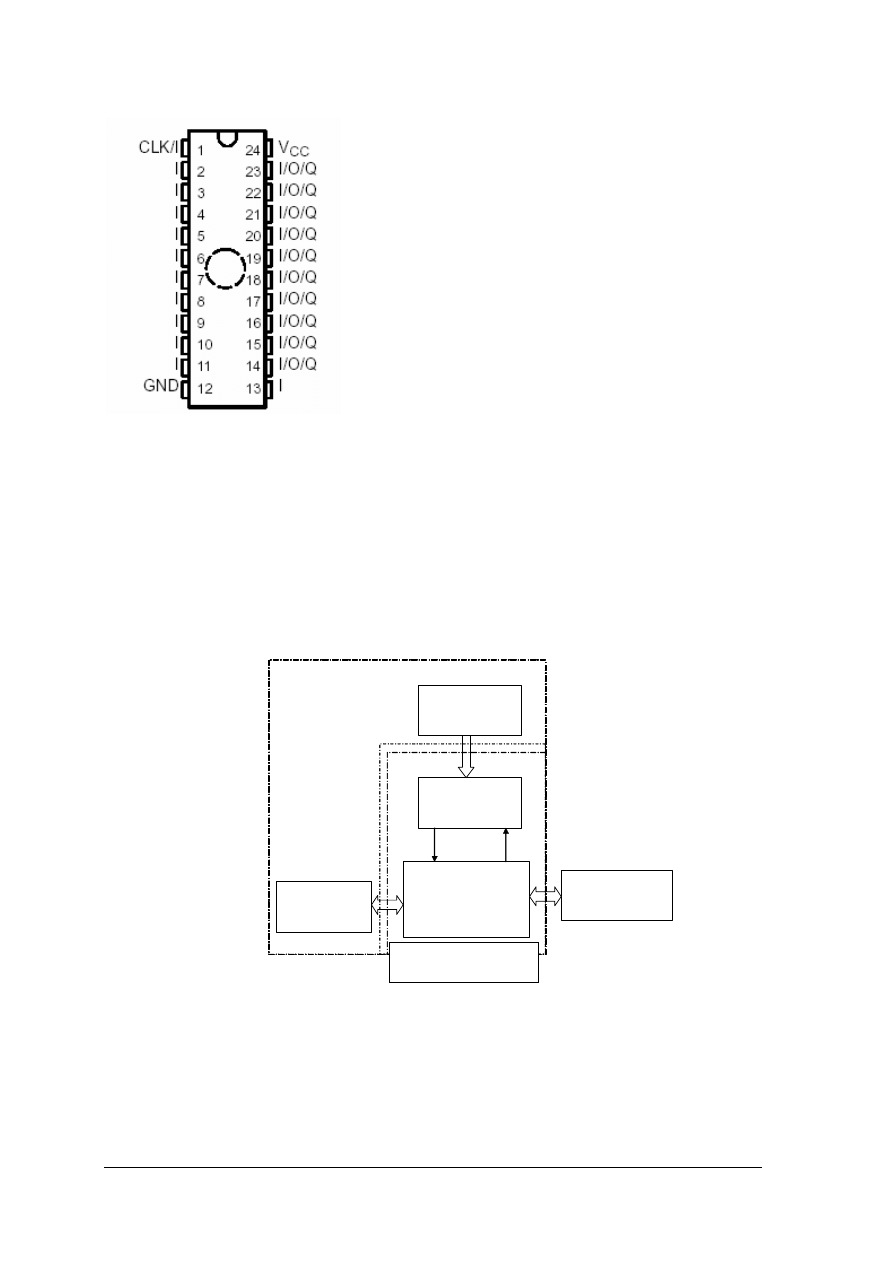
„
Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
46
Rys. 32. Układ PLD TICPAL22V10Z: rozkład wyprowadzeń i podstawowe parametry.
Więcej informacji na temat układów logicznych znajdziesz w literaturze [7] . Znajdziesz
tam informacje umożliwiające poznanie tajników oprogramowania projektowego oraz na
dołączonej płycie narzędzia, umożliwiające wykonywanie własnych projektów.
4.5.1.3. Mikroprocesory i mikrokontrolery
Każdy system komputerowy składa się z procesora, pamięci, w której zapisywany jest
wykonywany program i dane oraz z układów wejściowych i wyjściowych, które pozwalają na
komunikację z otoczeniem zewnętrznym [3,4].
Rys. 33. Uproszczony schemat blokowy systemu procesorowego [3].
Podstawowym układem systemu jest procesor. Listę możliwych do wykonania operacji
przez dany procesor nazywamy listą rozkazów tego procesora. Ciąg rozkazów określający
sekwencję wykonywanych operacji nazywamy programem.
Podstawowym układem wykonawczym procesora jest jednostka arytmetyczno-logiczna -
ALU. Procesor komunikuje się z układami wewnętrznymi za pomocą wewnętrznych
magistral.
- obudowa 24-pinowa
- kasowalny promieniami UV, co umożliwia
·rekonfigurowanie logiki i reprogramowanie
komórek
- matryca AND o rozmiarze 44 x132
- możliwość doboru liczby wejść i wyjść
(od 21 wejść i 1 wyjścia do 12 wejść i 10 wyjść)
- praktycznie zerowy prąd podtrzymania
- I/O/Q wyprowadzenia, które mogą być
wejściami, wyjściami lub dwukierunkowe
- CLK/I wejście informacyjne lub zegarowe
Pami
ęć
programu
Uk
ład
sterowania
Jednostka
arytmetyczno-
logiczna
Uk
łady
We/Wy
Pami
ęć
danych
PAMI
ĘĆ
PROCESOR
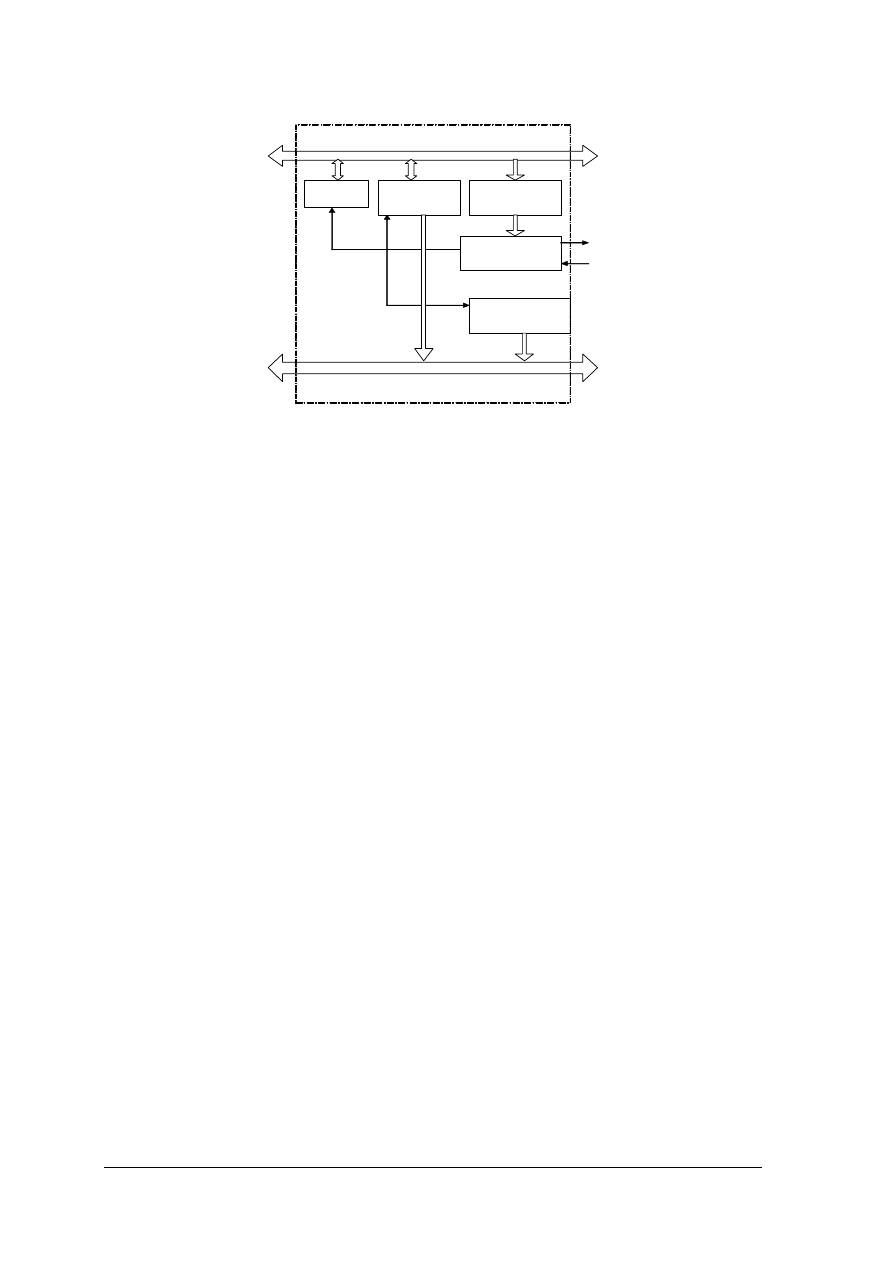
„
Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
47
Rys. 34. Uproszczony schemat funkcjonalny procesora.
Nową generacją układów procesorowych są mikrokontrolery zwane także komputerami
jednoukładowymi, które w swojej strukturze zawierają w wszystkie podstawowe bloki tylko
w znacznie mniejszym rozmiarze [2].
Przykładowo mikrokomputer jednoukładowy 89C51 jest wyposażony w pamięć EPROM
o pojemności 2K x 8 bitów, pamięć RAM o pojemności 64 x 8 bitów, port szeregowy
z interfejsem I
2
C, 16-bitowy timer. Posiada także możliwość zewnętrznego rozszerzania
pamięci.
4.5.2. Pytania sprawdzające
Odpowiadając na pytania, sprawdzisz, czy jesteś przygotowany do wykonania ćwiczeń.
1. Jaka jest zasada działania pamięci ROM?
2. Co znaczy, że pamięć jest ulotna?
3. Jakie znasz rodzaje pamięci ROM i czym się one charakteryzują?
4. Jak można poznać, że pamięć jest kasowalna przy pomocy promieniowania
ultrafioletowego?
6. Jaka jest zasada działania pamięci RAM?
7. Jakie znasz rodzaje pamięci RAM?
8. Ile wyjść danych ma pamięć o pojemności 64KB?
9. Ilu bitowy adres posiada ta pamięć przy adresowaniu bezpośrednim?
10. Jakie są cechy charakterystyczne układów PLD?
11. Co jest niezbędne do wykonania układu cyfrowego z wykorzystaniem struktury PLD?
12. Z jakich bloków funkcjonalnych zbudowany jest system komputerowy?
13. Która z magistral wewnętrznych procesora jest jednokierunkowa?
14. Jak zbudowany jest mikrokontroler?
15. Jaka jest różnica pomiędzy listą rozkazów a programem?
A L U
Z e s p ó
ł
r e je s t r ó w
R e je s t r
r o z k a z ó w
U k
ła d
s t e r o w a n ia
L ic z n ik
r o z k a z ó w
M a g is t r a la d a n y c h
M a g is t r a la a d r e s o w a
U k ł a d y
W e / W y
A d r e s o w a n ie
U k ła d ó w
W e / W y
Z e w n ę tr z n e
S y g n a ł y
S te r u j ą c e
A d r e s o w a n ie
p a m ię c i
P a m i ę ć

„
Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
48
4.5.3. Ćwiczenia
Ćwiczenie 1
Na podstawie danych katalogowych wskazanego układu pamięci określ rodzaj pamięci,
jej organizację oraz parametry dynamiczne.
Sposób wykonania ćwiczenia
Aby wykonać ćwiczenie, powinieneś:
1) określić rodzaj pamięci, liczbę wejść adresowych i liczbę wyjść danych (Materiał
nauczania pkt.4.5.1),
2) zapisać ustaloną organizację pamięci,
3) zapisać wartości parametrów dynamicznych,
4) porównać własności dwóch układów pamięci i określ ich zastosowanie.
Jeśli masz trudności poproś o pomoc nauczyciela.
Wyposażenie stanowiska pracy:
−
przybory do pisania,
−
poradnik ucznia,
−
literatura [3,8].
Ćwiczenie 2
Mając do dyspozycji 2 układy pamięci o pojemności 1 MB narysuj schemat połączeń
umożliwiający zwiększenie pojemności do 2 MB?
Sposób wykonania ćwiczenia
Aby wykonać ćwiczenie, powinieneś:
1) określić liczbę wejść adresowych i liczbę wyjść danych pamięci o pojemności 1MB
(Materiał nauczania pkt.4.5.1),
2) narysować schemat połączeń,
3) wykonać połączenie w programie symulacyjnym,
4) sprawdzić poprawność działania.
Jeśli masz trudności poproś o pomoc nauczyciela.
Wyposażenie stanowiska pracy:
−
przybory do pisania,
−
poradnik ucznia,
−
stanowisko komputerowe z programem do symulacji pracy układów cyfrowych,
−
literatura [2,5,7].
Ćwiczenie 3
Odszukaj w literaturze dwa przykłady praktycznego zastosowania mikrokontrolerów
i układów PLD
Sposób wykonania ćwiczenia
Aby wykonać ćwiczenie, powinieneś:
1) zapoznać się z informacjami zawartymi w literaturze [2,5,7],

„
Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
49
2) dokonać wyboru przykładu zastosowania mikrokontrolera i układu PLD,
3) opisać każdy z przykładów,
4) zaprezentować opracowane informacje.
Jeśli masz trudności poproś o pomoc nauczyciela.
Wyposażenie stanowiska pracy:
−
przybory do pisania,
−
poradnik ucznia,
−
stanowisko komputerowe z dostępem do Internetu,
−
literatura [2, 5, 7].
4.5.4. Sprawdzian postępów
Tak Nie
Czy potrafisz:
1) wyjaśnić działanie pamięci RAM?
¨
¨
2) wyjaśnić działanie pamięci ROM??
¨
¨
3) scharakteryzować pamięci ROM?
¨
¨
4) zinterpretować podstawowe parametry pamięci?
¨
¨
5) narysować schemat połączeń dla rozszerzenia pojemności pamięci?
¨
¨
6) wskazać podstawowe cechy i zastosowanie układów PLD?
¨
¨
7) wyjaśnić blokową budowę systemu komputerowego?
¨
¨
8) wyjaśnić blokową budowę procesora?
¨
¨
9) wymienić przykłady zastosowania komputerów jednoukładowych?
¨
¨
10) wymienić przykłady zastosowania mikrokontrolerów i układów PLD?
¨
¨

„
Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
50
5. SPRAWDZIAN OSIĄGNIĘĆ
INSTRUKCJA DLA UCZNIA
1. Przeczytaj uważnie instrukcję.
2. Podpisz imieniem i nazwiskiem kartę odpowiedzi.
3. Zapoznaj się z zestawem pytań testowych.
4. Test zawiera 20 pytań dotyczących układów cyfrowych. Pytania: od 1 do 14 są to pytania
wielokrotnego
wyboru
i
tylko
jedna
odpowiedź
jest
prawidłowa;
w pytaniach: od 15 do 20 należy udzielić krótkiej odpowiedzi.
5. Udzielaj odpowiedzi tylko na załączonej karcie odpowiedzi:
−
w pytaniach wielokrotnego wyboru zaznacz prawidłową odpowiedź X (w przypadku
pomyłki należy błędną odpowiedź zaznaczyć kółkiem, a następnie ponownie
zakreślić odpowiedź prawidłową),
−
w pytaniach z krótką odpowiedzią wpisz odpowiedź w wyznaczone pole,
6. Pracuj samodzielnie, bo tylko wtedy będziesz miał satysfakcję z wykonanego zadania.
7. Kiedy udzielenie odpowiedzi będzie Ci sprawiało trudność, wtedy odłóż jego
rozwiązanie na później i wróć do niego, gdy zostanie Ci wolny czas. Trudności mogą
przysporzyć Ci pytania: 6, 11, 15, 18, gdyż są one na poziomie trudniejszym niż
pozostałe.
8. Na rozwiązanie testu masz 90 min.
Powodzenia
ZESTAW ZADAŃ TESTOWYCH
1. Jaką liczbę otrzymamy w wyniku konwersji z systemu szesnastkowego liczby 81AF
(16)
na system binarny?
a) 1011111100101111
(2),
b) 1000000110101111
(2),
c) 1000100110101111
(2),
d) 1011100110101111
(2),
2. Wskaż prawidłowy aksjomat algebry Boole'a ?
Uwaga: zapis x' oznacza - negację x
a) x' +y' = (x + y)'
b) x + y + 1 = x + y
c) x + yz = (x + y) (x + z)
d) xx' = 1
3. Wskaż tabelę działania opisującą bramkę logiczną, której symbol graficzny przedstawia
poniższy rysunek.
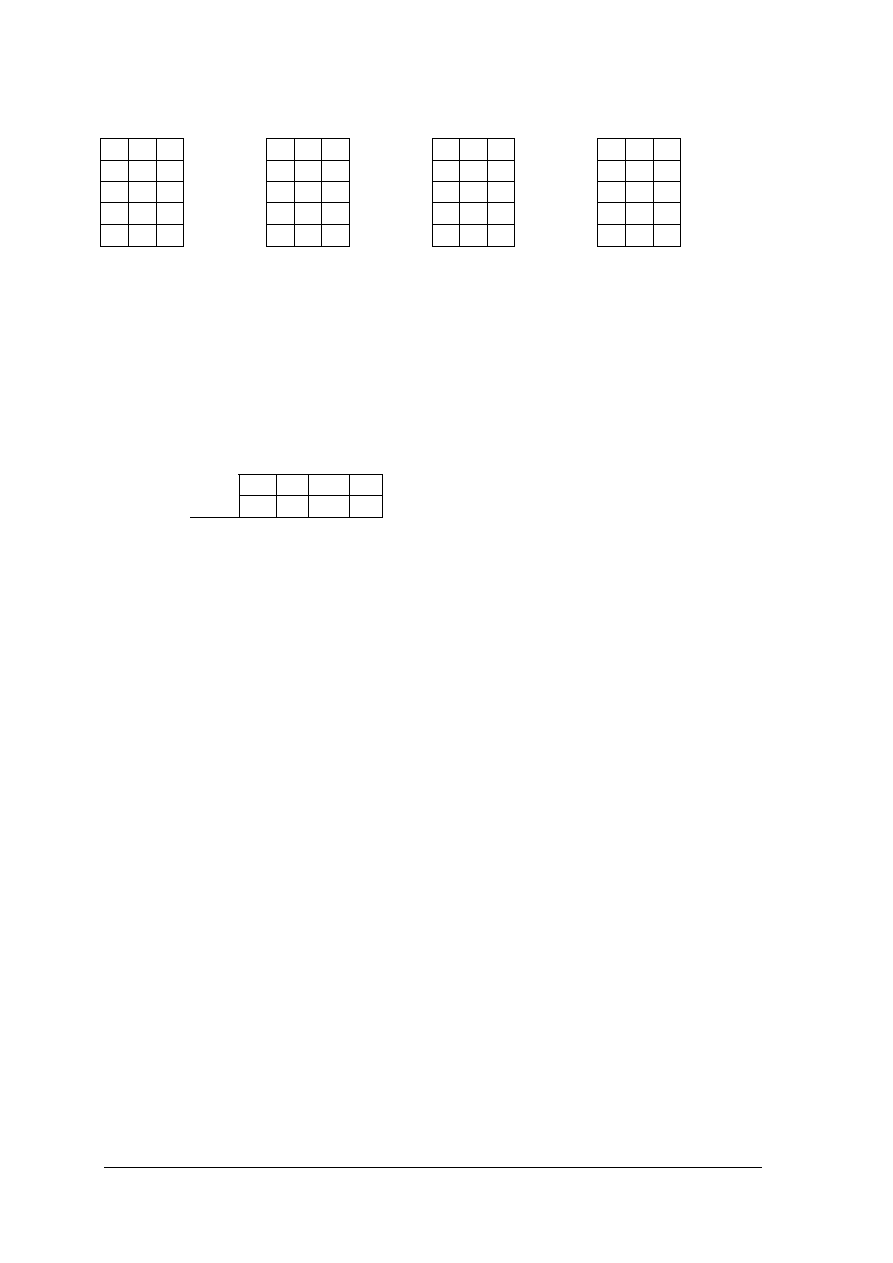
„
Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
51
a) b) c) d)
4. Jaką wartość logiczną przyjmuje funkcja F(abc) = (ac + a'b + c)a po uproszczeniu?
Uwaga: zapis a' oznacza - negację „a”
a) F = a + b + c,
b) F = a'b + c,
c) F = 1,
d) F = ac
5. Dana jest funkcja logiczna F(abc) opisana następującą tablicą Karnaugh'a
a\bc 00 10 11
01
0 0
0
1
1
1 0
1
1
1
Jaka jest postać zminimalizowana tej funkcji?
a) F(abc) = a'c + b
b) F(abc) = ab + c
c) F(abc) = a + bc
d) F(abc) = ab + bc
6. Zamek do sejfu można otworzyć w dni robocze (R) kluczem dyrektora (D) i jednego
z trzech kierowników firmy (K1, K2, K3). W pozostałe dni zamek otworzy się za pomocą
kluczy wszystkich trzech kierowników i dyrektora. Wskaż funkcję, którą realizuje układ
sterujący pracą zamka tego sejfu.
a) R’{D + K
1
K
2
K
3
} + R D {K
1
+K
2
+K
3
}
b) R’{D K
1
K
2
K
3
} + R D {K
1
+K
2
+K
3
}
c) R’{D + K
1
K
2
K
3
} + R D + {K
1
+K
2
+K
3
}
d) R’{D + K
1
K
2
K
3
} + R D { K
2
K
1
+ K
2
K
3 +
K
1
K
3
}
7. Jeżeli jedno wejście bramki dwuwejściowej NAND podłączymy do stanu wysokiego „1”
a na drugie podamy sygnał logiczny A to wyjście tej bramki jest w stanie:
a) F= A
b) F= A’
c) F= 0
d) F= 1
8. Jaką funkcję realizuje bramka ExOR
a) A’B’
b) (A+B)’
c) A’B + AB’
d) A’B’ + AB
A B F
A B F
A B F
A B F
0 0 0
0 0 0
0 0 1
0 0 0
0 1 1
0 1 0
0 1 1
0 1 1
1 0 1
1 0 0
1 0 1
1 0 1
1 1 1
1 1 1
1 1 0
1 1 0
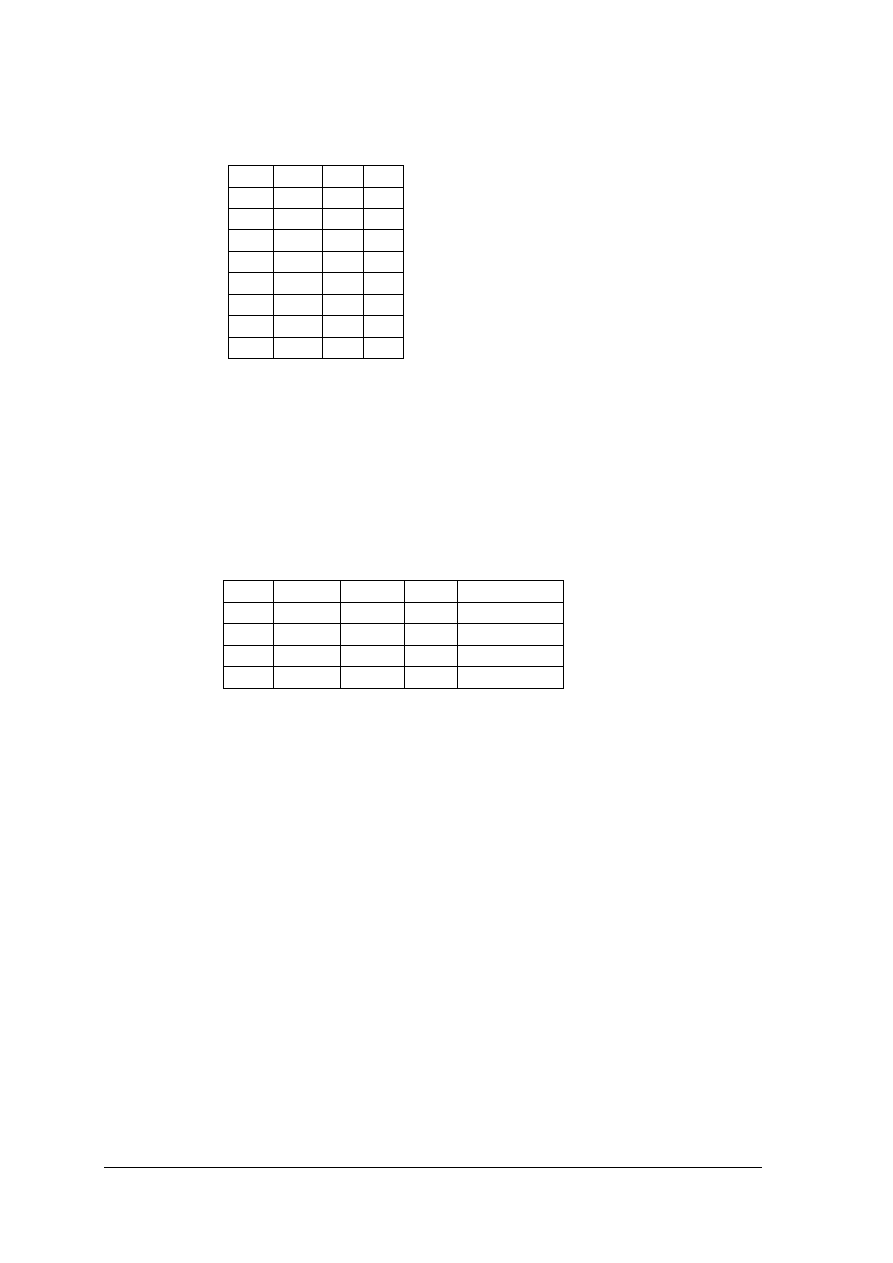
„
Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
52
9. Jaką funkcję realizuje układ, którego działanie opisuje następująca tabela?
Tabela 1.
A
B
C
F
0
0
0
1
0
0
1
1
0
1
0
1
0
1
1
1
1
0
0
0
1
0
1
1
1
1
0
0
1
1
1
0
10. Stan logiczny "1" na wyjściu układów TTL odpowiada napięciu:
a) 0 [V] - 0,8 [V]
b) 2 [V] - 5 [V]
c) 2,4 [V] - 5 [V]
d) - 0,5 [V] - 2 [V]
11. Pracę jakiego układu opisuje następująca tabela działania :
Tabela 2.
A
B
F1
F2
F3
0
0
0
0
1
0
1
0
1
0
1
0
1
0
0
1
1
0
0
1
a) sumator,
b) półsumator,
c) komparator A>B, A<B, A=B,
d) dekoder.
12. Ile wejśc i wyjść posiada układ umożliwiajacy mnożenie dwóch liczb dwubitowych
zapisanych w kodzie binarnym prostym przy założeniu, że wynik jest zapisany
w tym samym kodzie?
a) 2 wejścia i 4 wyjścia,
b) 4 wejścia i 4 wyjścia,
c) 2 wejścia i 5 wyjść,
d) 4 wejścia i 5 wyjść.
13. W kodzie binarnym wykonano dodawanie dwóch liczb A = 11010
(2)
i B = 111110
(2)
i otrzymano wynik C:
a) C = 1101000
(2)
b) C = 1001000
(2)
c) C = 1101001
(2)
d) C = 1011000
(2)
a)
F = AB + AC
b)
F = A + B’C
c)
F = A’ + B’C
d)
F = A’ B + C
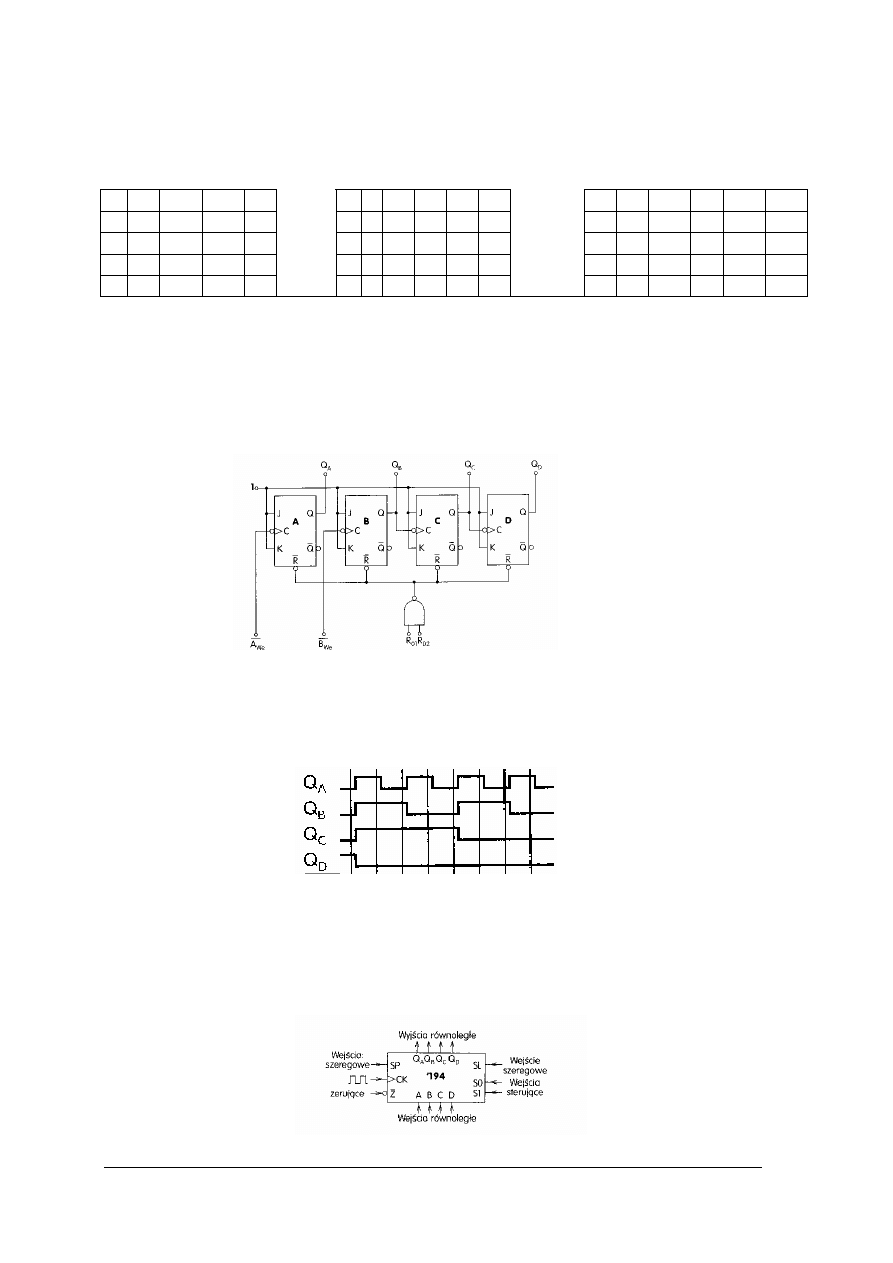
„
Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
53
14. Która tabela działania przedstawia pracę układu podnoszącego do kwadratu cyfry
dziesiętne 1,2,3 zapisane w kodzie binarnym?
a)
b)
c)
A B F
1
F
2
F
3
A B F
1
F
2
F
3
F
4
A B F
1
F
2
F
3
F
4
0 0
0
0
0
0 0 0
0
0
0
0
0
0
0
0
0
0 1
0
0
1
0 1 0
0
1
0
0
1
0
0
0
1
1 0
1
0
0
1 0 1
0
0
1
1
0
0
1
0
0
1 1
1
1
1
1 1 1
1
1
1
1
1
1
0
0
1
d) wszystkie tabele są nieprawidłowe.
15. Rysunek 1 przedstawia licznik scalony ‘93. Na które wejście należy podać impulsy
zegarowe, aby otrzymać licznik modulo 8 i które wyjścia będą wtedy wykorzystane? Jaką
pojemność będzie posiadał ten licznik jeśli wyjście Q
A
połączymy z wejściem B. Określ
kierunek liczenia tego licznika.
Rys. 1.
16. Wykresy poniżej przedstawiają pracę czterobitowego licznika. Określ kierunek liczenia
oraz stan na wyjściach w chwili oznaczonej na wykresach cyfrą 1i 2? Stan na wyjściach
zapisz w kodzie binarnym i dziesiętnym. Uwaga: wyjście Q
A
ma wagę 2
0
.
Rys. 2.
17. Rysunek 3 przedstawia rejestr uniwersalny. Ilu bitowy jest to rejestr i w jakich trybach
może pracować? Jaki rodzaj synchronizacji posiada ten układ? Jaki sygnał logiczny
należy podać na wejście zerujące, aby wyzerować ten rejestr?
Rys. 3.
1
2
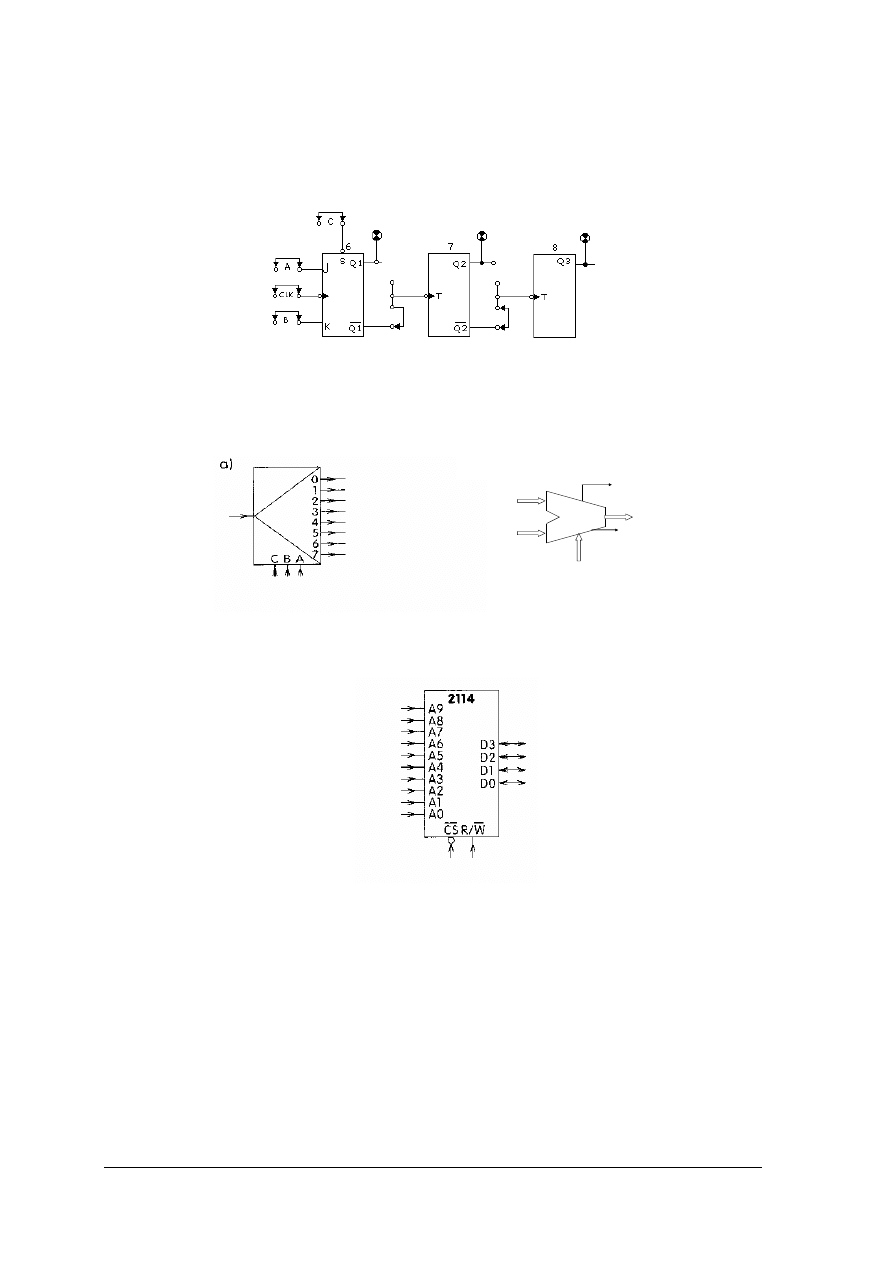
„
Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
54
18. Jaki stan musi być na wejściach J,K,S aby licznik przedstawiony na rysunku 4 mógł
zliczać impulsy zegarowe podane na wejście CLK. Zakładając, że na początku układ jest
wyzerowany określ jaki będzie stan na wyjściach Q
1,
Q
2,
Q
3
po pierwszym impulsie
zegarowym.
Rys. 4.
19. Jakie układy przedstawiają poniższe symbole graficzne - podaj pełną nazwę tych
układów i zastosowanie.
Rys. 5.
20. Określ rodzaj i organizację pamięci.
Rys. 6.
A
0
– A
3
B
0
– B
3
F
0
– F
3
S
0
– S
3
M
C
n
A = B
C
n +4
b)

„
Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
55
KARTA ODPOWIEDZI
Imię i nazwisko ……………………………………………………..
Wykonywanie badań i pomiarów układów cyfrowych stosowanych
w telekomunikacji
Zakreśl poprawną odpowiedź lub wpisz odpowiedź .
Numer
zadania
Odpowiedź
Punkty
1.
a
b
c
d
2.
a
b
c
d
3.
a
b
c
d
4.
a
b
c
d
5.
a
b
c
d
6.
a
b
c
d
7.
a
b
c
d
8.
a
b
c
d
9.
a
b
c
d
10.
a
b
c
d
11.
a
b
c
d
12.
a
b
c
d
13.
a
b
c
d
14.
a
b
c
d
15.
16.
17.
18.
19.
20.
Razem:

„
Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
56
6. LITERATURA
1. Arasimowicz E., Bednarek M., Faron J., Idzi K., Przybyłowska-Łomnicka A.: Wybór
testów dla szkół technicznych. Wydawnictwa Szkolne PWN, Warszawa-Łódź 1999
2. Doliński J.: Mikrokontrolery AVR w praktyce. BTC, Warszawa 2003
3. Głocki W.: Układy cyfrowe. WSiP, Warszawa 2001
4. Kammerer J., Oberthur W., Zastow P:. (tłumaczenie A. Rodak): Pracownia podstaw
elektrotechniki i elektroniki. WSiP, Warszawa 2000
5. Łuba T., Jasiński K., Zbierzchski B.: Specjalizowane układy cyfrowe w strukturach PLD
i FPGA. WKiŁ, Warszawa 1997
6. Marusak A.: Urządzenia elektroniczne cz.2 Układy elektroniczne. WSiP, Warszawa 2001
r.
7. Psierbiński J., Zbysiński P.: Układy programowalne, pierwsze kroki. BTC, Warszawa
2002
8. Sasal W.: Układy scalone serii UCA64/UCY74. Parametry i zastosowania. WKiŁ
Warszawa 1995
9. Miesięcznik „Elektronika Praktyczna”
10. Katalog ELFA www.elfa.se
Wyszukiwarka
Podobne podstrony:
01 Wykonywanie badan i pomiarow Nieznany
04 Wykonywanie badań i pomiarów układów cyfrowych
04 Wykonywanie izolacji termicz Nieznany (2)
04 Wykonywanie podstawowych for Nieznany (2)
04 Wykonywanie analiz ilosciowy Nieznany (2)
06 Wykonywanie badan mikrobiolo Nieznany
04 Wykonywanie zabiegow agrotec Nieznany (2)
14 Wykonywanie prac pomiarowych Nieznany
05 Wykonywanie badan biochemicz Nieznany (2)
04 Wykonywanie obliczen w uklad Nieznany
04 Wykonywanie izolacji termicz Nieznany (2)
01 Wykonywanie badań i pomiarów obwodów prądu stałego
Wykonywanie badań i pomiarów układów cyfrowych stosowanych w telekomunikacji
04 Wykonywanie pomiarow paramet Nieznany
04 Wykonywanie pomiarow paramet Nieznany
711[04] Z2 04 Wykonywanie konse Nieznany (2)
więcej podobnych podstron