
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
MINISTERSTWO EDUKACJI
NARODOWEJ
Gabriela Poloczek
Wykonywanie
obliczeń
w
układach
statycznych,
dynamicznych i kinematycznych 311[15].O1.04
Poradnik dla ucznia
Wydawca
Instytut Technologii Eksploatacji – Państwowy Instytut Badawczy
Radom 2007

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
1
Recenzenci:
mgr inż. Piotr Chudeusz
mgr Stanisław Cyrulski
Opracowanie redakcyjne:
mgr inż. Gabriela Poloczek
Konsultacja:
mgr inż. Danuta Pawełczyk
Poradnik stanowi obudowę dydaktyczną programu jednostki modułowej 311[15].O1.04
„Wykonywanie obliczeń w układach statycznych, dynamicznych i kinematycznych”,
zawartego w modułowym programie nauczania dla zawodu technik górnictwa podziemnego.
Wydawca
Instytut Technologii Eksploatacji – Państwowy Instytut Badawczy, Radom 2007

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
2
SPIS TREŚCI
1.
Wprowadzenie
3
2.
Wymagania wstępne
5
3.
Cele kształcenia
6
4.
Materiał nauczania
7
4.1.
Układy sił
7
4.1.1. Materiał nauczania
7
4.1.2. Pytania sprawdzające
16
4.1.3. Ćwiczenia
16
4.1.4. Sprawdzian postępów
21
4.2.
Środek ciężkości
22
4.2.1. Materiał nauczania
22
4.2.2. Pytania sprawdzające
24
4.2.3. Ćwiczenia
24
4.2.4. Sprawdzian postępów
26
4.3.
Kinematyka punktu i ciała sztywnego
27
4.3.1. Materiał nauczania
27
4.3.2. Pytania sprawdzające
33
4.3.3. Ćwiczenia
33
4.3.4. Sprawdzian postępów
35
4.4.
Dynamika punktu i ciała sztywnego
36
4.4.1. Materiał nauczania
36
4.4.2. Pytania sprawdzające
40
4.4.3. Ćwiczenia
40
4.4.4. Sprawdzian postępów
42
4.5.
Wytrzymałość materiałów
43
4.5.1. Materiał nauczania
43
4.5.2. Pytania sprawdzające
53
4.5.3. Ćwiczenia
54
4.5.4. Sprawdzian postępów
56
5.
Sprawdzian osiągnięć
57
6.
Literatura
62

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
3
1. WPROWADZENIE
Poradnik ten będzie Ci pomocny w przyswajaniu wiedzy dotyczącej wykonywania
obliczeń w układach statycznych, dynamicznych i kinematycznych.
W poradniku zamieszczono:
−
wymagania wstępne – wykaz umiejętności, jakie powinieneś mieć już ukształtowane,
abyś bez problemów mógł korzystać z poradnika,
−
cele kształcenia – wykaz umiejętności, jakie ukształtujesz podczas pracy z poradnikiem,
−
materiał nauczania – wiadomości teoretyczne niezbędne do osiągnięcia założonych celów
kształcenia i opanowania umiejętności zawartych w jednostce modułowej,
−
zestaw pytań, abyś mógł sprawdzić, czy już opanowałeś określone treści,
−
ć
wiczenia, które pomogą Ci zweryfikować wiadomości teoretyczne oraz ukształtować
umiejętności praktyczne,
−
sprawdzian postępów,
−
sprawdzian osiągnięć, przykładowy zestaw zadań. Zaliczenie testu potwierdzi
opanowanie materiału całej jednostki modułowej,
−
literaturę uzupełniającą.
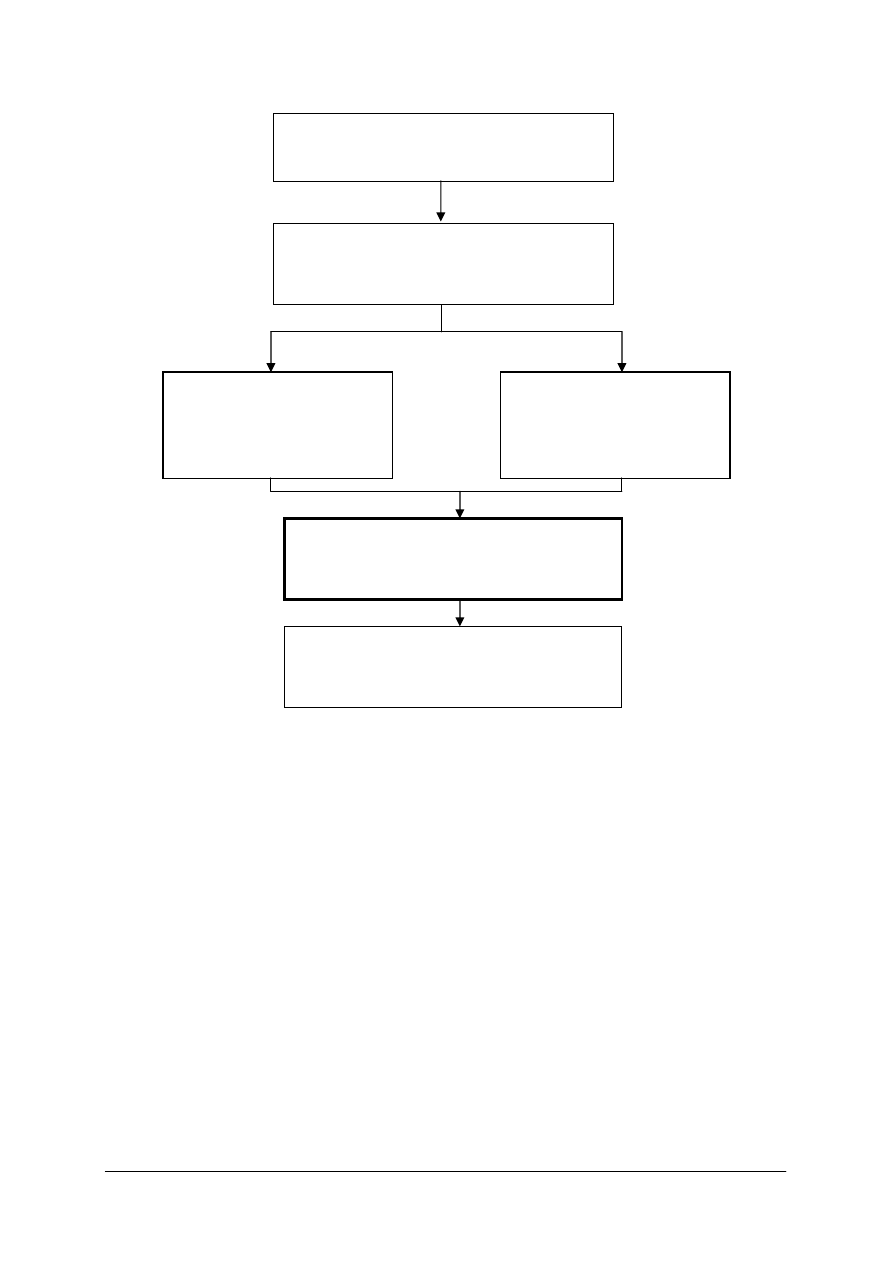
Miejsce jednostki modułowej w strukturze modułu 311[15].O1 „Podstawy konstrukcji
mechanicznych” jest wyeksponowane na schemacie zamieszczonym na stronie 4.
Bezpieczeństwo i higiena pracy
W czasie pobytu w pracowni musisz przestrzegać regulaminów, przepisów bhp
i instrukcji przeciwpożarowych, wynikających z rodzaju wykonywanych prac. Wiadomości
dotyczące przepisów bezpieczeństwa i higieny pracy, ochrony przeciwpożarowej oraz
ochrony środowiska znajdziesz w jednostce modułowej 311[15].O1.01 „Przestrzeganie
przepisów Kodeksu pracy, Prawa geologicznego i górniczego”
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
4
Schemat układu jednostek modułowych
311[15].O1
Podstawy konstrukcji mechanicznych
311[15].O1.01
Stosowanie przepisów Kodeksu pracy,
Prawa geologicznego i górniczego
311[15].O1.02
Określanie właściwości
materiałów konstrukcyjnych
311[15].O1.03
Wykonywanie rysunków
części maszyn
311[15].O1.04
Wykonywanie obliczeń w układach
statycznych, dynamicznych i kinetycznych
311[15].O1.05
Projektowanie części maszyn
i połączeń

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
5
2.
WYMAGANIA WSTĘPNE
Przystępując do realizacji programu jednostki modułowej powinieneś umieć:
−
stosować jednostki układu SI,
−
wykonywać działania na wektorach,
−
wykonywać rysunki techniczne części maszyn zgodnie z normami,
−
posługiwać się dokumentacją techniczną, Dokumentacją Techniczno-Ruchową, normami
i katalogami,
−
rozróżniać i dobierać materiały konstrukcyjne,
−
selekcjonować, porządkować i przechowywać informacje,
−
interpretować związki wyrażone za pomocą wzorów, wykresów, schematów, diagramów,
tabel,
−
obsługiwać komputer,
−
pracować w grupie,
−
organizować stanowisko pracy zgodnie z wymogami ergonomii.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
6
3. CELE KSZTAŁCENIA
W wyniku realizacji programu jednostki modułowej powinieneś umieć:
−
scharakteryzować siły i układy sił,
−
określić własności sił,
−
zastosować i przeliczyć jednostki wielkości mechanicznych w układzie SI,
−
rozróżnić modele ciał rzeczywistych,
−
rozróżnić rodzaje więzów i ich reakcje,
−
wyznaczyć warunki równowagi płaskiego i przestrzennego układu sił,
−
wykonać obliczenia w płaskim zbieżnym układzie sił,
−
wykonać obliczenia w dowolnym układzie sił,
−
zdefiniować pojęcie środka ciężkości
−
obliczyć środek ciężkości figury płaskiej,
−
obliczyć środek ciężkości figury złożonej,
−
wyznaczyć warunki równowagi sił z uwzględnieniem tarcia,
−
obliczyć siłę i moment tarcia,
−
rozróżnić układy odniesienia stosowane w mechanice technicznej,
−
zinterpretować podstawowe prawa statyki, kinematyki i dynamiki dotyczące punktu
materialnego ciała sztywnego,
−
zastosować w praktyce podstawowe prawa statyki, kinematyki i dynamiki dotyczące
punktu materialnego ciała sztywnego,
−
rozróżnić rodzaje ruchów,
−
określić parametry ruchów,
−
obliczyć prędkość obwodową, kątową i obrotową,
−
narysować wykresy prędkości i przyspieszeń punktu materialnego,
−
wykonać plany prędkości i przyspieszeń członów,
−
rozróżnić dynamiczne równania ruchu punktu materialnego,
−
obliczyć masę zredukowaną (moment bezwładności) mechanizmu,
−
obliczyć pracę, moc i sprawność,
−
rozróżnić wyważanie statyczne i dynamiczne,
−
obliczyć reakcje dynamiczne,
−
wyjaśnić pojęcie wyboczenia,
−
określić rodzaj odkształceń w elementach maszyn i urządzeń,
−
określić pojęcie sprężystości, plastyczności, kruchości, twardości i wytrzymałości
materiałów,
−
rozróżnić rodzaje obciążeń elementów konstrukcyjnych,
−
zdefiniować rodzaje naprężeń,
−
określić rodzaj odkształceń w elementach maszyn,
−
wykonać podstawowe obliczenia ze ściskania, rozciągania, ścinania i skręcania,
−
posłużyć się jednostkami wielkości mechanicznych w układzie SI,
−
wykonać podstawowe obliczenia z wytrzymałości złożonej,
−
wykonać obliczenia z wytrzymałości zmęczeniowej,
−
posłużyć się tablicami, wykresami, normami, katalogami technicznymi, czasopismami
i inną literaturą techniczną.
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
7
4. MATERIAŁ NAUCZANIA
4.1. Układy sił
4.1.1. Materiał nauczania
Własności siły
Siła to mechaniczne oddziaływanie jednego ciała na drugie. Oddziaływanie może być
bezpośrednie, gdy zachodzi przy zetknięciu ciał, lub pośrednie, gdy zachodzi na odległość.
Skutkiem oddziaływania siły na ciało może być jego ruch, zmiana ruchu czy odkształcenie.
Siłę jako wielkość wektorową określamy przez podanie trzech wielkości: wartości siły,
kierunku (prosta działania) i zwrotu. Jeżeli siła działa na punkt należy również podać jej
punkt przyłożenia, a jeżeli działa na ciało sztywne wystarczy podać jej prostą działania, gdyż
bez zmiany skutku jej działania, może być wzdłuż tej prostej przesuwana.
Jednostką siły w układzie SI jest niuton (N). Jest to siła, która ciału o masie 1 kg nadaje
przyspieszenie 1 m/s
2
.
1N = 1
2
s
m
kg
⋅
Siły dzielą się na zewnętrzne i wewnętrzne. Siły zewnętrzne mogą być czynne (dążą do
wywołania ruchu i wynikają z działania innych ciał znajdujących się na zewnątrz) oraz bierne
(przeciwdziałają ruchowi i powstają w miejscu podparcia) zwane reakcjami.
Siłami wewnętrznymi są siły międzycząsteczkowe oraz napięcia. Ostatnie są wynikiem
działania na ciało sił zewnętrznych.
W mechanice rozróżniamy dwa modele ciał:
–
punkt materialny; jest punkt geometryczny, w którym skupiona jest cała masa ciała,
–
ciało sztywne, jest to układ punktów materialnych ze sobą związanych i których to
odległości w czasie ruchu czy pod działaniem sił nie ulegają zmianie.
G ,
F
1
,
F
2
– siły czynne
R
A
,
R
B
– siły bierne
F
S
- napięcia
Rys. 1. Siły zewnętrzne i wewnętrzne [2, s. 14]
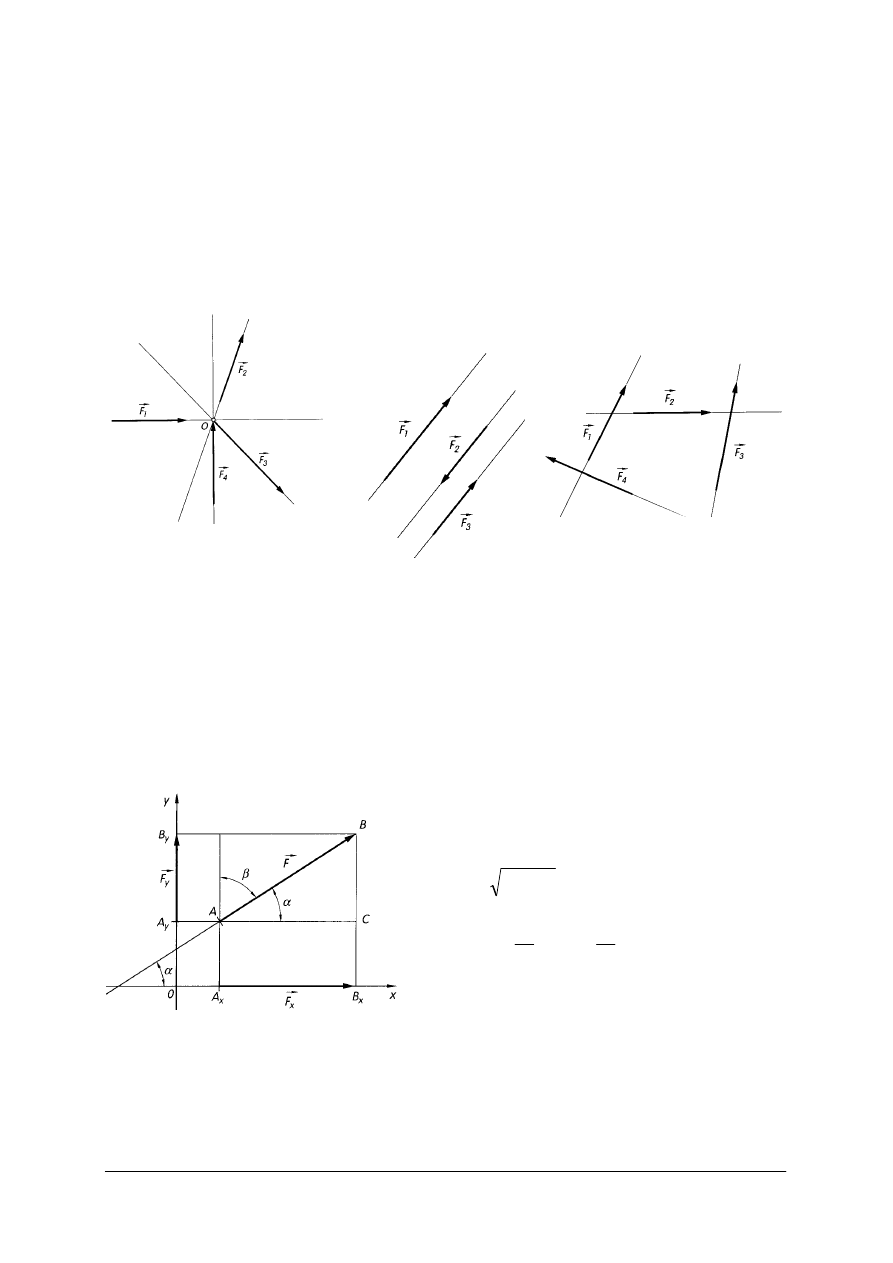
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
8
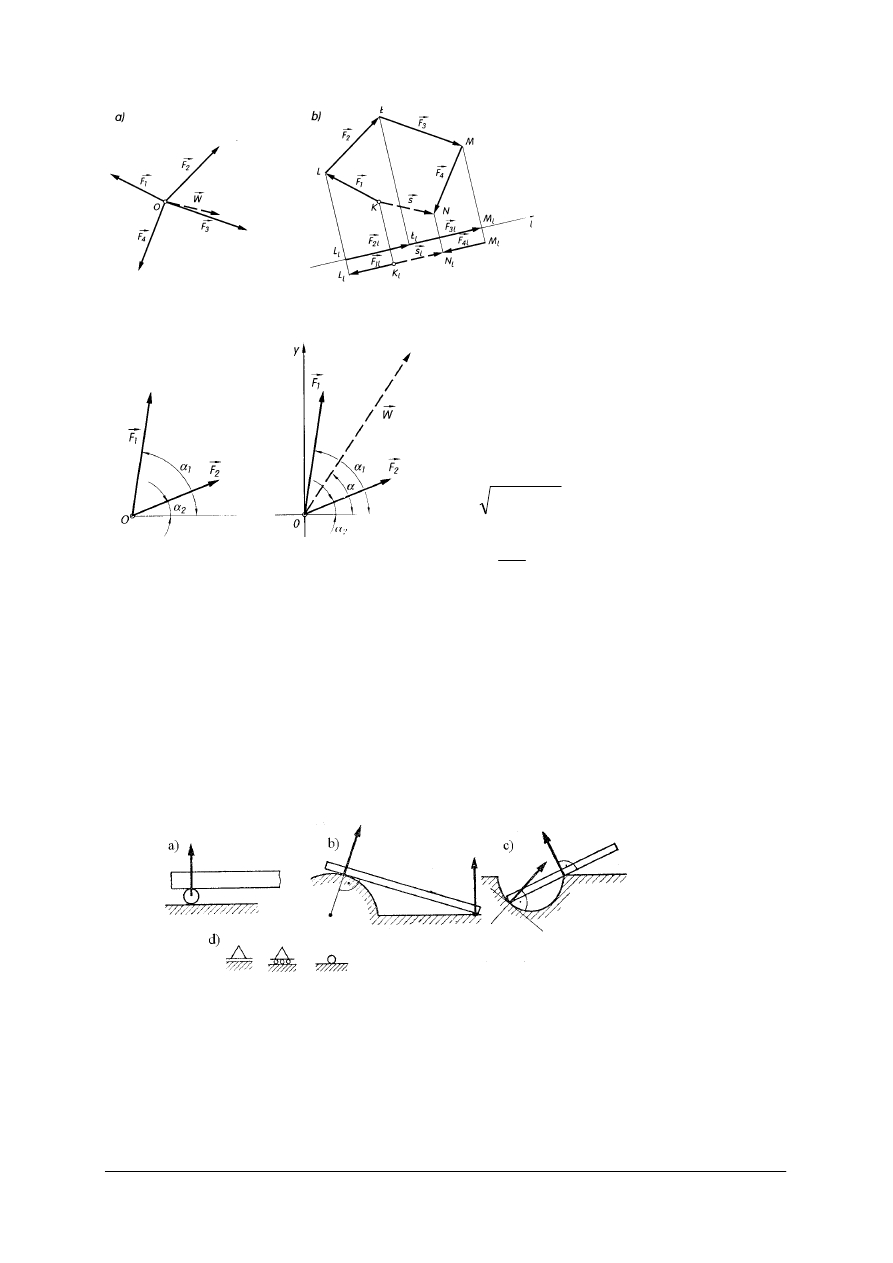
Układy sił
Układem sił nazywa się zbiór dowolnej liczby sił działających na ciało. Proste działania
sił mogą leżeć na płaszczyźnie lub w przestrzeni, tworząc układy płaskie i przestrzenne. Siły
leżące w jednej płaszczyźnie dzieli się na układy zbieżne, równoległe i dowolne.
Układem płaskim zbieżnym nazywamy zbiór sił, których proste działania przecinają się
w jednym punkcie. Układem płaskim równoległym nazywamy zbiór sił, których proste
działania są do siebie równoległe, a zwroty tych sił mogą być zgodne lub przeciwne. Płaskim
dowolnym układem sił nazywamy zbiór sił o różnych kierunkach działania.
a)
b)
c)
Rys. 2. Układy sił: a) płaski zbieżny, b) płaski równoległy, c) płaski dowolny [2, s. 17]
Składanie sił
Układy składające się z dużej ilości sił nazywamy złożonymi. Układ złożony można
zastąpić układem prostszym, którego skutek działania będzie taki sam. Czynność tę
nazywamy składaniem sił lub redukcją układu sił. Redukcję układu można wykonać
wykreślnie lub analitycznie.
W tym celu należy określić wartości rzutów na osie prostokątnego układu współrzędnych.
Rzut siły na oś jest równy iloczynowi wartości siły i cosinusa kąta zawartego między linią
działania siły a osią.
Rzuty siły F na osie x i y
F
x
= F
⋅
cos
α
F
y
= F
⋅
sin
α
Wartość siły, gdy znane są rzuty
F =
2
y
2
x
F
F
+
Kąt, który tworzy siła F z osią x i z osią y
cos
α
=
F
F
x
i cos
β
=
F
F
y
Rys. 3. Rzut prostokątny siły F na osie [2, s. 25]
W przypadku kilku sił leżących na płaszczyźnie korzystamy z twierdzenia o sumie
rzutów:
suma algebraiczna rzutów dowolnej liczby sił na dowolną oś jest równa rzutowi sumy tych sił
na tę oś.
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
9
Suma rzutów sił osie x i y:
s
x
= F
1x
+ F
2x
+ F
3x
+
....
+ F
nx
s
y
= F
1y
+ F
2y
+ F
3y
+
....
+ F
ny
lub
s
x
=
∑
ix
F
; s
y
=
∑
iy
F
Rys. 4. Rzut sumy dowolnej liczby sił na oś l [2, s. 26]
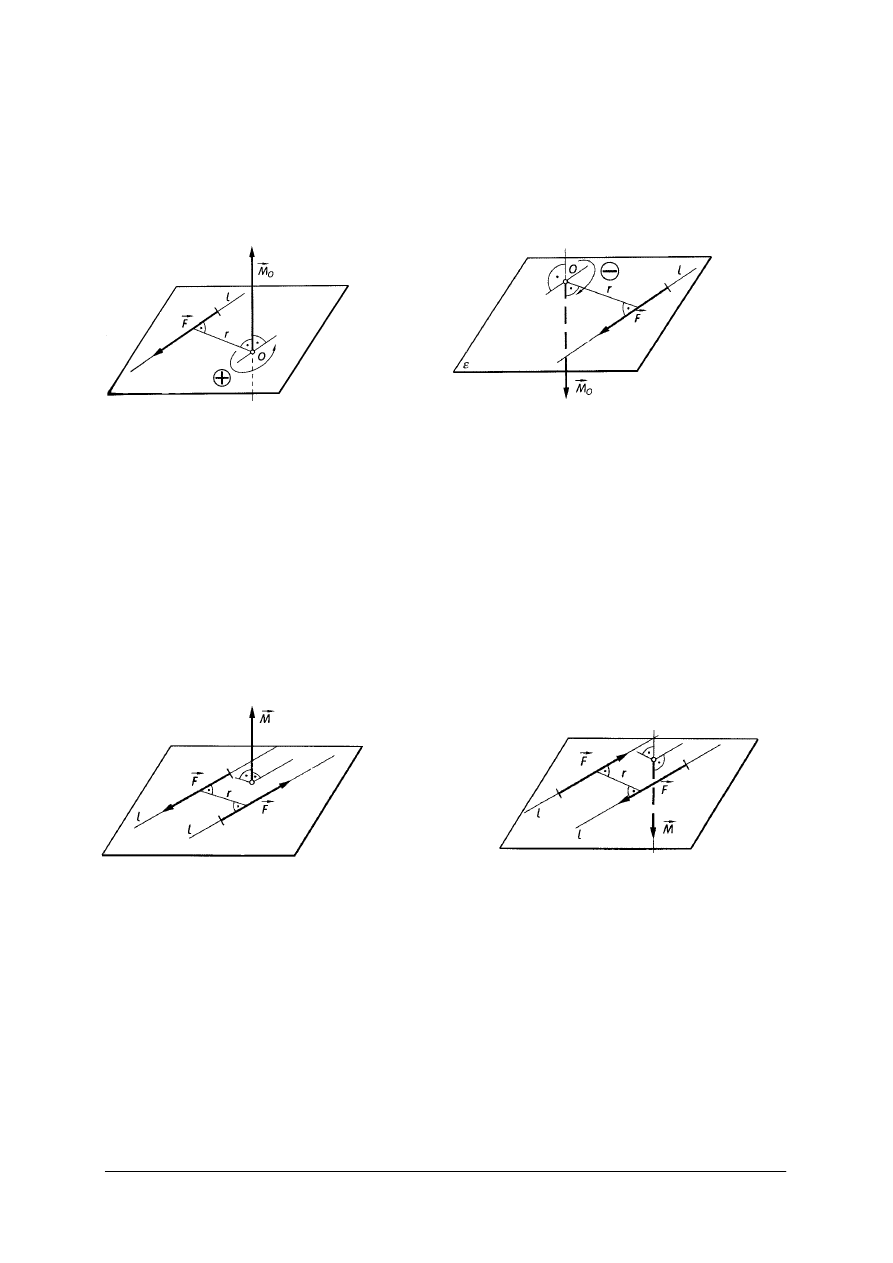
Czynności przy wyznaczaniu wypadkowej dla dwóch sił:
−−−−
w
punkcie
O
przyjęcie
początku
układu
współrzędnych,
−−−−
wyznaczenie rzutu wypadkowej na osie x i y
W
x
= s
x
=
∑
ix
F
= F
1x
+ F
2x
= F
1
⋅
cos
α
1
+ F
2
⋅
cos
α
2
W
y
= s
y
=
∑
iy
F
= F
1y
+ F
2y
= F
1
⋅
sin
α
1
+ F
2
⋅
sin
α
2
−−−−
obliczenie wartości wypadkowej
W =
2
y
2
x
W
W
+
−−−−
obliczenie cosinusa kąta
α
cos
α
=
W
W
x
−−−−
określenie zwrotu wypadkowej
Rys. 5. Wyznaczanie wypadkowej dwóch sił [2, s. 30]
Reakcje więzów
Więzami nazywamy wszystkie czynniki ograniczające swobodę ciała. Ciało swobodne
ma sześć stopni swobody, które odbieramy wprowadzając więzy. Siły oddziaływania więzów
na ciało nieswobodne nazywamy reakcjami. Kierunek reakcji zależy od grupy więzów.
Wyróżniamy następujące grupy więzów:
−−−−
podpory ruchome, w których reakcja podpory jest zaczepiona w punkcie styczności ciała
z podporą i ma kierunek prostopadły do płaszczyzny podpierającej.
Rys. 6. Podpory ruchome: a,b,c) podparcie na idealnej gładkiej powierzchni,
c) oznaczenie schematyczne podpory [1, s. 19]
−−−−
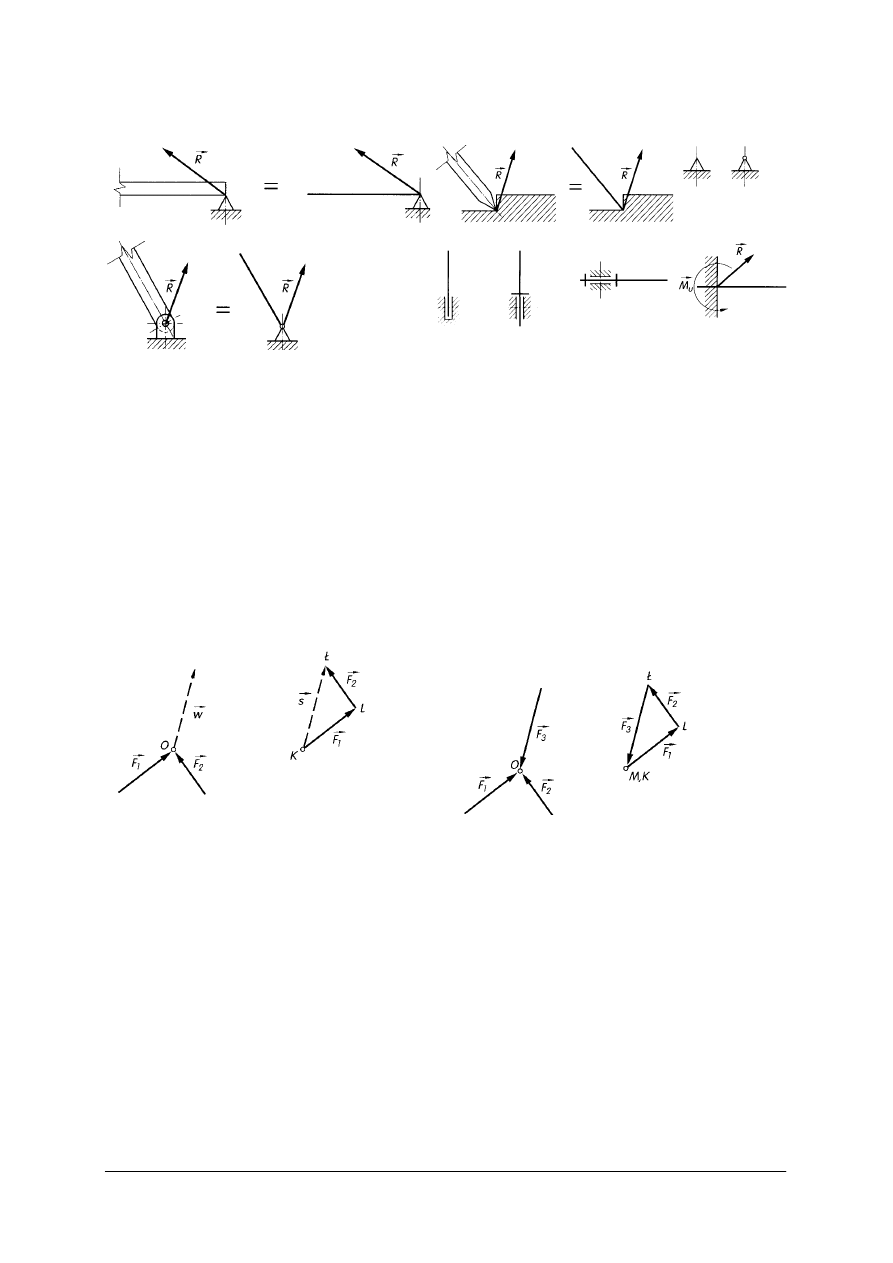
podpory stałe, w których reakcja jest zaczepiona w punkcie styczności i ma na ogół
kierunek nie prostopadły do płaszczyzny ciała podpierającego,
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
10
a)
b)
c)
d)
e)
f)
Rys. 7. Podpory stałe: a) podpora nieprzesuwna, b) podpora w kształcie „uskoku”,
c) oznaczenie schematyczne podpory stałej, d) przegub, e) łożysko oporowe, f) utwierdzenie [2, s. 20]
−−−−
więzy wiotkie, w których reakcja działa wzdłuż ich osi i należą do nich cięgna: liny,
pasy, łańcuchy.
Warunki równowagi płaskiego układu sił zbieżnych:
Płaski układ sił zbieżnych jest w równowadze, gdy działające siły się równoważą, czyli
składając taki układ sił otrzymamy wypadkową równą zero. Rozpatrujemy następujące
warunki równowagi płaskiego zbieżnego układu sił:
−−−−
wykreślne
Płaski układ sił zbieżnych jest w równowadze, jeżeli wielobok sił tego układu jest
zamknięty; początek pierwszej i koniec ostatniej siły znajduje się w tym samym punkcie.
Rys. 8. Dodawanie wykreślne sił: a) wielobok sił otwarty, b) wielobok sił zamknięty [2, s. 32]
−−−−
analityczne
Płaski układ sił zbieżnych jest w równowadze tylko wtedy, gdy spełnione są dwa
warunki:
1)
suma algebraiczna rzutów wszystkich sił na oś x jest równa zeru,
2)
suma algebraiczna rzutów wszystkich sił na oś y jest równa zeru.
Można to zapisać:
∑
ix
F
= 0;
∑
iy
F = 0
Warunki równowagi płaskiego układu sił
Siły tworzące płaski dowolny układ sił mogą dążyć do wywołania obrotu ciała względem
punktu. Wielkościami wektorowymi, które charakteryzują dowolny płaski układ sił jest
moment siły względem punktu i para sił.
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
11
Momentem siły względem punktu nazywamy wektor mający następujące cechy:
−−−−
wartość liczbową równą iloczynowi wartości siły i ramienia
⋅
r
M
O
= F
⋅
r [Nm]
−−−−
kierunek prostopadły do płaszczyzny wyznaczonej przez linię działania siły i biegun,
−−−−
zwrot zgodny z regułą śruby o gwincie prawozwojowym.
a)
b)
Rys. 9. Moment siły względem punktu: a) dodatni, b) ujemny [2, s. 33]
Jeżeli na płaszczyźnie leży układ sił oblicza się sumę momentów względem przyjętego
bieguna. Moment sumy momentów nazywa się momentem głównym lub wypadkowym.
Para sił to dwie siły o równej wartości, równoległych liniach działania i przeciwnych
zwrotach. Odległość linii działania obu sił jest r ramieniem pary. Moment pary sił równa się
iloczynowi wartości liczbowej jednej z sił pary przez ramię pary.
M = F
⋅
r [Nm]
Moment pary oznaczamy literą bez indeksu, gdyż wartość ta nie zależy od obranego
bieguna. Moment jest dodatni, gdy para dąży do obrócenia swego ramienia w stronę
przeciwną do ruchu wskazówek zegara.
Parę sił można zastąpić momentem, a moment pary sił parą sił. Pary sił można składać
wyznaczając moment pary wypadkowej.
a)
b)
M = F
⋅
r
M =
−
F
⋅
r
Rys. 10. Moment pary sił: a) dodatni, b) ujemny [2, s. 38]
Analityczne warunki równowagi dowolnego płaskiego układu sił.
Istnieją trzy analityczne warunki równowagi dowolnego płaskiego układu sił:
1)
suma algebraiczna rzutów wszystkich sił na oś x musi się równać zeru,
2)
suma algebraiczna rzutów wszystkich sił na oś y musi się równać zeru,
3)
suma algebraiczna momentów wszystkich sił, czyli moment główny układu względem
dowolnego bieguna musi się równać zeru.
Warunki powyższe można zapisać w postaci trzech równań:
W
x
= F
1x
+ F
2x
+ F
3x
+
⋅
⋅
⋅
+ F
nx
=
∑
ix
F
= 0
W
y
= F
1y
+ F
2y
+ F
3y
+
⋅
⋅
⋅
+ F
ny
= ∑
iy
F = 0
Mo = M
1O
+ M
2O
+ M
3O
+
⋅
⋅
⋅
+ M
nO
= ∑
iO
M
= 0
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
12
Wykreślne warunki równowagi dowolnego płaskiego układu sił.
Przy składaniu dowolnej liczby sił o różnych punktach zaczepienia korzystamy
z konstrukcji wieloboku sznurowego.
Dowolny płaski układ sił jest w równowadze, gdy spełnione są dwa wykreślne warunki:
−
wielobok sił musi być zamknięty.
−
wielobok sznurowy musi być zamknięty.
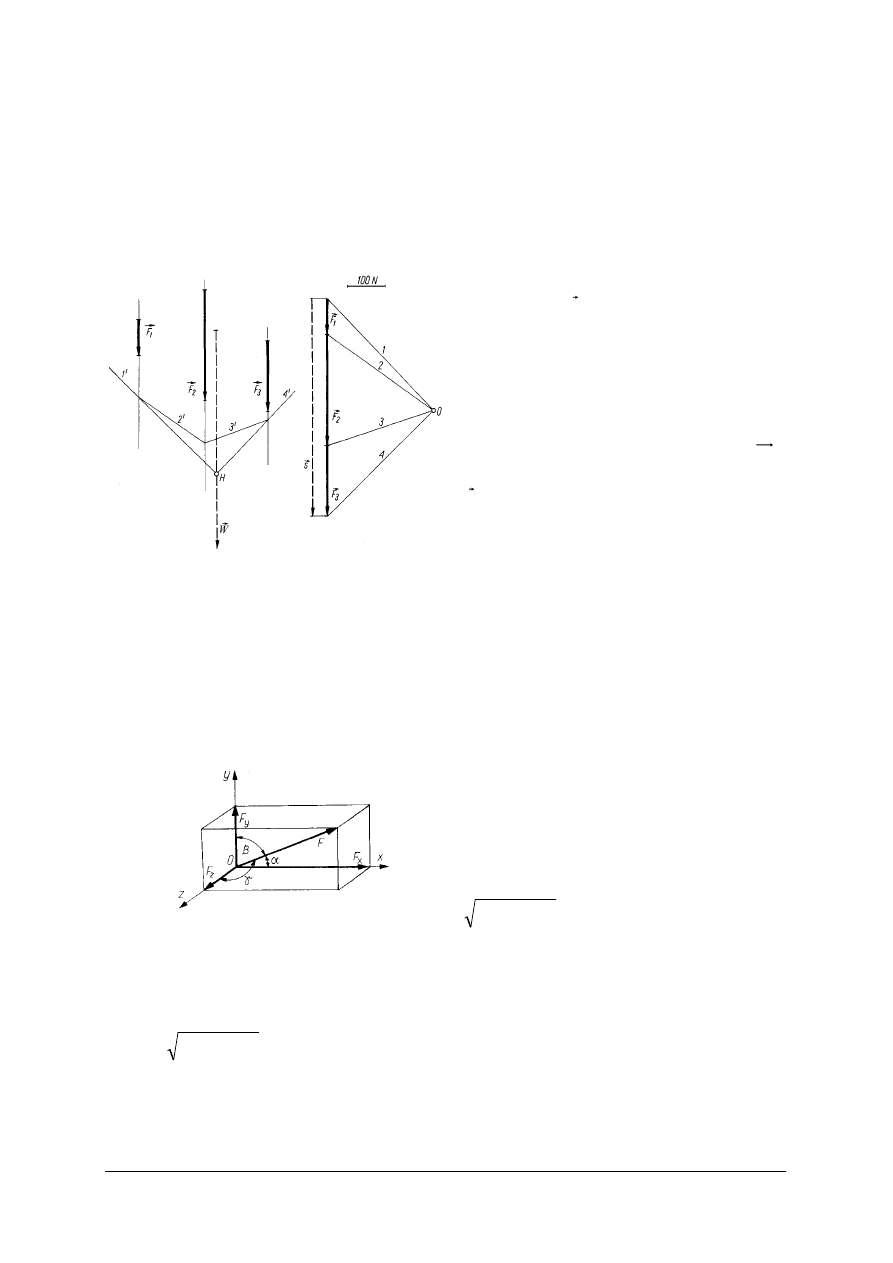
Algorytm składania dowolnego układu sił:
1. wyznaczyć sumę
s
dla sił układu,
2. obrać dowolny punkt 0 (biegun) i połączyć go
z początkiem i końcem każdej siły promieniami 1,
2, 3 i 4 otrzymując plan sił (liczba promieni o jeden
większa od liczby składanych sił),
3. wykreślić na układzie sił równolegle do
poszczególnych promieni wielobok sznurowy,
4. przedłużyć skrajne promienie do przecięcia się,
5. narysować przez otrzymany punkt wypadkową
W
,
równą co do wartości, kierunku i zwrotu sumie
s
z planu
sił
Rys. 11. Wyznaczanie wypadkowej za pomocą wieloboku sznurowego [5, s. 69]
Warunki równowagi przestrzennego układu sił
Układem przestrzennym nazywamy zbiór sił, których linie działania są dowolnie
rozmieszczone w przestrzeni i nie leżą w jednej płaszczyźnie. Układy sił dzieli się na zbieżne,
równoległe i dowolne. Układy te rozwiązuje się najczęściej metodą analityczną przy
zastosowaniu przestrzennych prostokątnych układów współrzędnych.
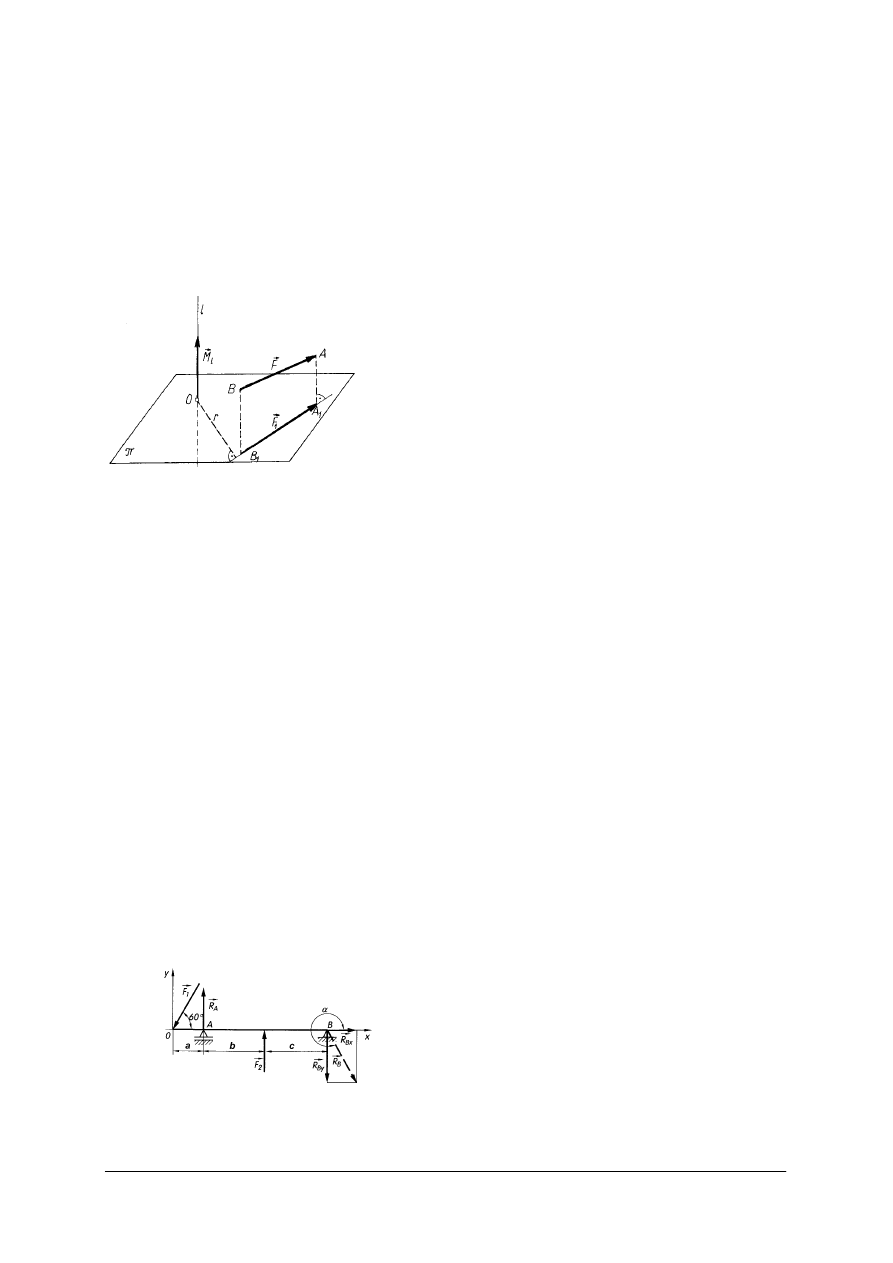
Rzut siły na osie układu XYZ:
F
x
= F
⋅
cos
α
Fy = F
⋅
cos
β
F
z
= F
⋅
cos
γ
Dla kilku sił rzuty wynoszą:
s
x
= F
1
⋅
cos
α
1
+ F
2
⋅
cos
α
2
+
⋅
⋅
⋅
+ F
n
⋅
cos
α
n
s
y
= F
1
⋅
cos
β
1
+ F
2
⋅
cos
β
2
+
⋅
⋅
⋅
+ F
n
⋅
cos
β
n
s
x
= F
1
⋅
cos
γ
1
+ F
2
⋅
cos
γ
2
+
⋅
⋅
⋅
+ F
n
⋅
cos
γ
n
Wartość siły (wypadkowej), gdy znane są rzuty wynosi:
s =
2
z
2
y
2
x
s
s
s
+
+
Rys. 12. Rzuty sił na osie przestrzennego prostokątnego układu współrzędnych [5, s. 105]
Przestrzenny układ sił zbieżnych jest w równowadze wtedy, gdy wypadkowa jest równa
zeru
s =
2
z
2
y
2
x
s
s
s
+
+
= 0
czyli muszą być spełnione trzy warunki:
s
x
=
∑
ix
F
=0, s
y
= ∑
iy
F =0, s
z
=
∑
iz
F
=0,
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
13
−
algebraiczna suma rzutów wszystkich sił na oś x jest równa zeru,
−
algebraiczna suma rzutów wszystkich sił na oś y jest równa zeru,
−
algebraiczna suma rzutów wszystkich sił na oś z jest równa zeru.
Warunki równowagi dowolnego przestrzennego układu sił
Przy wyznaczaniu równowagi tego układu uwzględnić należy moment siły względem osi.
Jest to wielkość mechaniczna, która stara się wprawić ciało w ruch obrotowy dookoła osi.
Momentem siły względem osi nazywamy moment rzutu tej siły na płaszczyznę prostopadłą
do osi – względem punktu przecięcia się osi z płaszczyzną.
Cechy wektora momentu siły względem osi:
−−−−
wartość M
l
= F
1
⋅
r
−−−−
kierunek pokrywa się z kierunkiem osi
−−−−
zwrot zgodny z regułą śruby o gwincie
prawozwojowym
.
Moment siły względem osi jest równy zeru gdy:
−−−−
siła F jest równoległa do osi,
−−−−
linia działania siły przecina się z osią
Rys. 13. Moment siły względem osi [5, s. 109]
Ciało obciążone dowolnym przestrzennym układem sił będzie w równowadze, gdy
będzie spełnionych następujących sześć warunków równowagi:
−
suma algebraiczna rzutów wszystkich sił na oś x musi być równa zeru, czyli
∑
ix
F
= 0
−
suma algebraiczna rzutów wszystkich sił na oś y musi być równa zeru, czyli ∑
iy
F = 0
−
suma algebraiczna rzutów wszystkich sił na oś z musi być równa zeru, czyli
∑
iz
F
= 0
−
suma algebraiczna momentów wszystkich sił względem osi x musi być równa zeru, czyli
∑
ix
M
=
0
−
suma algebraiczna momentów wszystkich sił względem osi y musi być równa zeru, czyli
∑
iy
M =
0
−
suma algebraiczna momentów wszystkich sił względem osi z musi być równa zeru,
−
czyli
∑
iz
M
=
0
Warunki równowagi ciała sztywnego
Dla ciała sztywnego stosujemy warunki równowagi tak jak dla płaskiego dowolnego
układu sił. Przykładem takich układów jest element konstrukcyjny przenoszący obciążenie
zginające zwany belką lub osią. Belki ze względu na sposób podparcia mogą być podparte
jedną podporą stałą i jedną ruchomą oraz jednostronnie utwierdzone. Reakcje w podporach
wyznaczyć można analitycznie lub wykreślnie.
∑
ix
F
= 0
∑
iy
F
= 0
∑
iB
M
=
0
−
F
1
⋅
cos60
0
+ R
Bx
= 0
−
F
1
⋅
sin60
0
+ R
A
+ F
2
−
R
By
= 0
F
1
⋅
sin60
0
(a + b + c)
−
R
A
(b + c)
−
F
2
⋅
c = 0
Rys. 14. Warunki równowagi dowolnego płaskiego układu sił [2, s. 51]
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
14
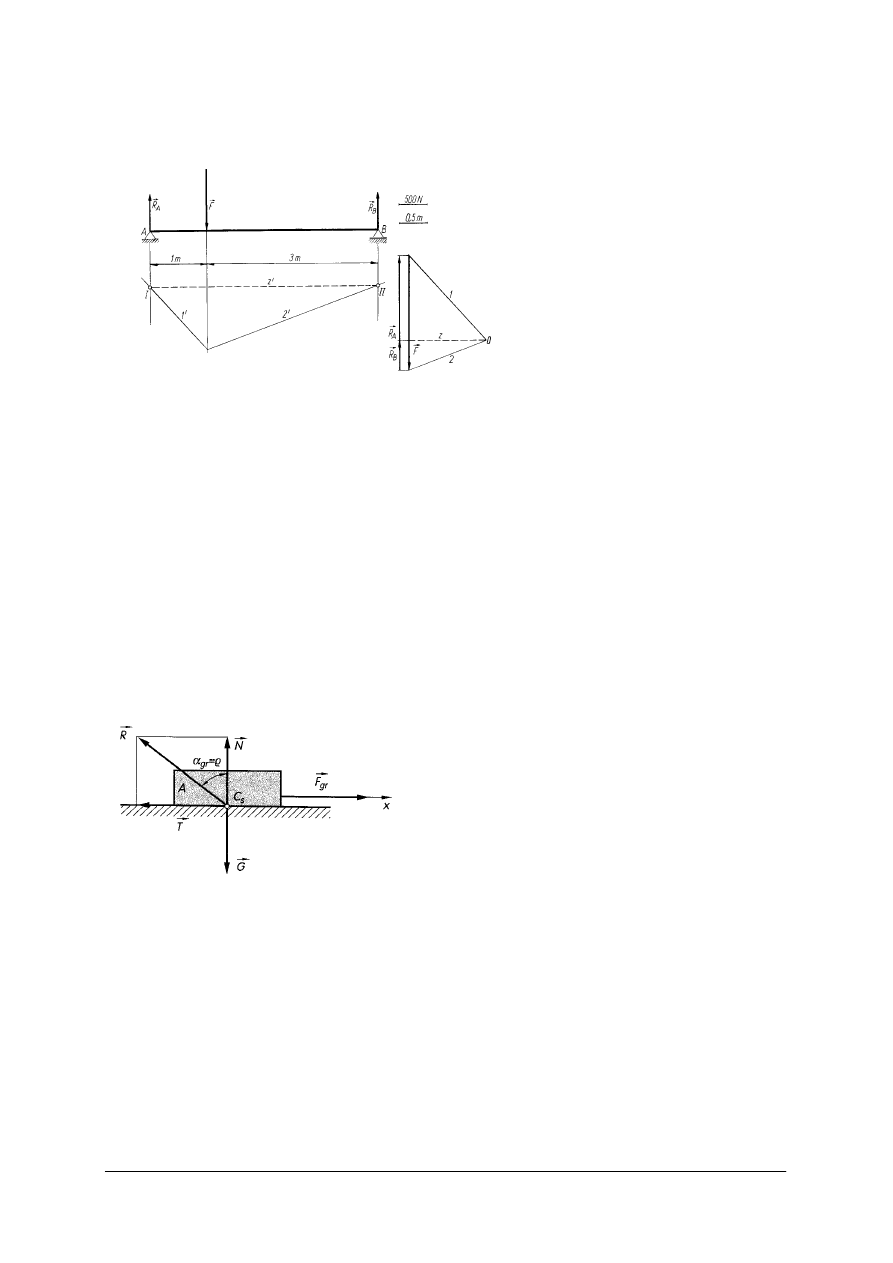
Wykreślne wyznaczanie reakcji belek polega na zastosowaniu wykreślnych warunków
równowagi układu płaskiego (wielobok sił i wielobok sznurowy muszą być zamknięte).
Algorytm wyznaczania reakcji belek:
1.
Narysować w przyjętej podziałce długości
belkę i w przyjętej podziałce siłę.
2.
Wykreślić wielobok sznurowy na siłach
zewnętrznych czynnych.
3.
Przedłużyć skrajne promienie wieloboku
sznurowego do przecięcia z kierunkami
reakcji i narysować zamykającą z
′
.
4.
Przez
biegun
0
narysować
promień
z równoległy do zamykającej.
5.
Określić reakcje i ich zwroty na wieloboku
sił.
Rys. 15. Wyznaczanie reakcji belek wykreślnie [5, s. 82]
Warunki równowagi ciała sztywnego z uwzględnieniem sił tarcia
Tarcie jako zjawisko występujące w przyrodzie i technice, powstaje zawsze podczas
ruchu ciała. Jest zjawiskiem pożądanym w hamulcach, przekładniach ciernych, sprzęgłach lub
niepożądanym w łożyskach, prowadnicach obrabiarek, w których to urządzeniach staramy się
je zmniejszyć do minimum.
Rozróżniamy tarcie ślizgowe, występujące podczas przesuwania się jednego ciała po
drugim, oraz tarcie toczne, występujące podczas toczenia.
Siła tarcia T jest zawsze przeciwnie zwrócona do siły wywołującej ruch ciała i zależy od
obciążenia G, chropowatości stykających się ciał, rodzaju materiałów użytych na materiały
trące, rodzaju ruchu oraz obecności środków smarnych itp.
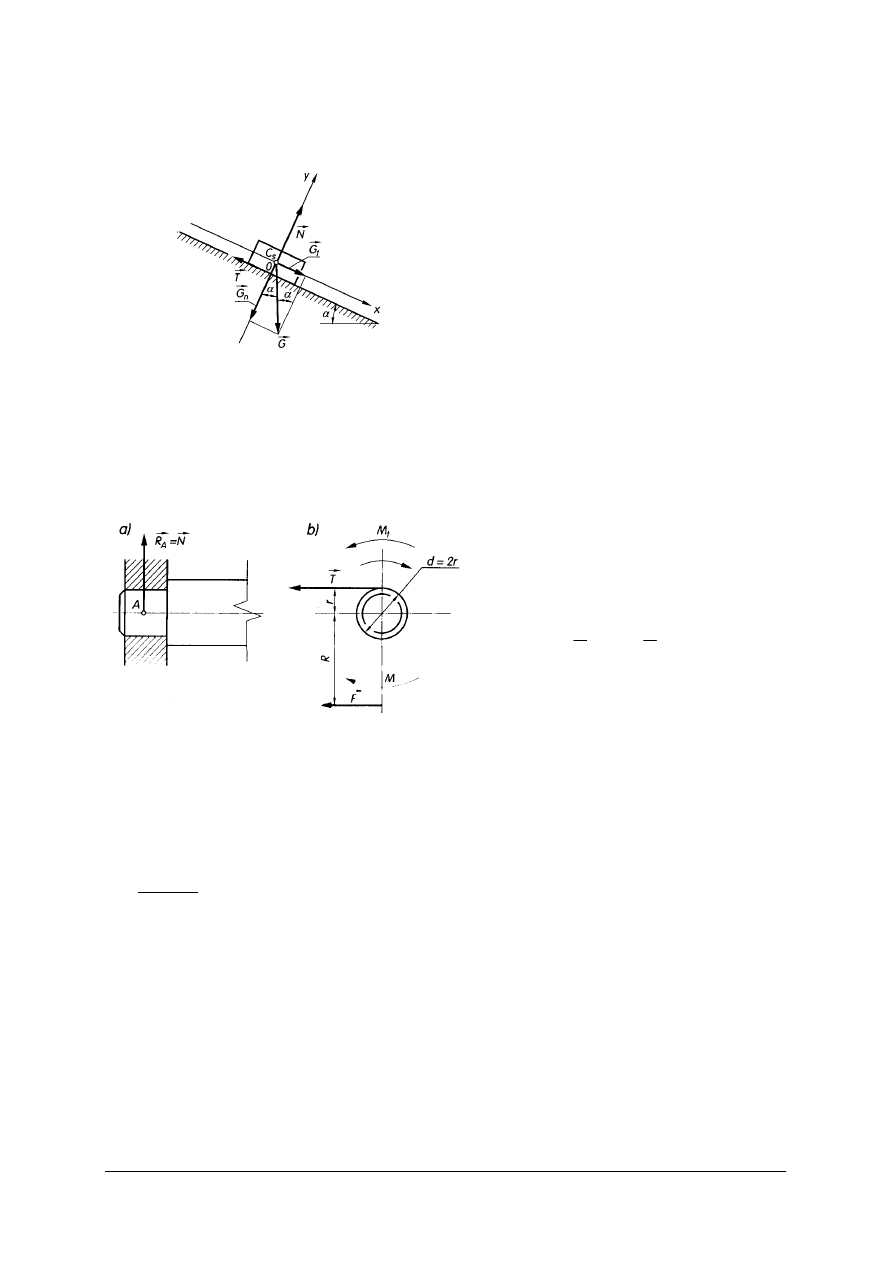
Tarcie ślizgowe wywołane jest działaniem siły normalnej G dociskającej ciała i siły
stycznej F przemieszczającej je względem siebie.
Siła tarcia w chwili równowagi granicznej:
T = N
⋅µ
µ
= tg
ρ
,
µ
−
współczynnik statycznego tarcia
ś
lizgowego
Siła tarcia w czasie ruchu:
T
k
= N
⋅µ
k
µ
k
−
współczynnik kinetycznego tarcia
ś
lizgowego
µ
>
µ
k
Rys. 16. Tarcie ślizgowe w chwili równowagi granicznej [2, s. 73]
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
15
Tarcie na równi pochyłej
Siła tarcia w chwili równowagi granicznej
(
α
gr
=
ρ
):
T = G
⋅
sin
α
gr
= G
⋅
sin
ρ
µ
= tg
ρ
µ
−
współczynnik tarcia
Rys. 17. Rozkład sił na równi pochyłej [2, s. 76]
Równię nazywamy samohamowną, gdy ciało umieszczone na równi pochyłej będzie
w spoczynku bez żadnej siły utrzymującej (
α
≤
ρ
).
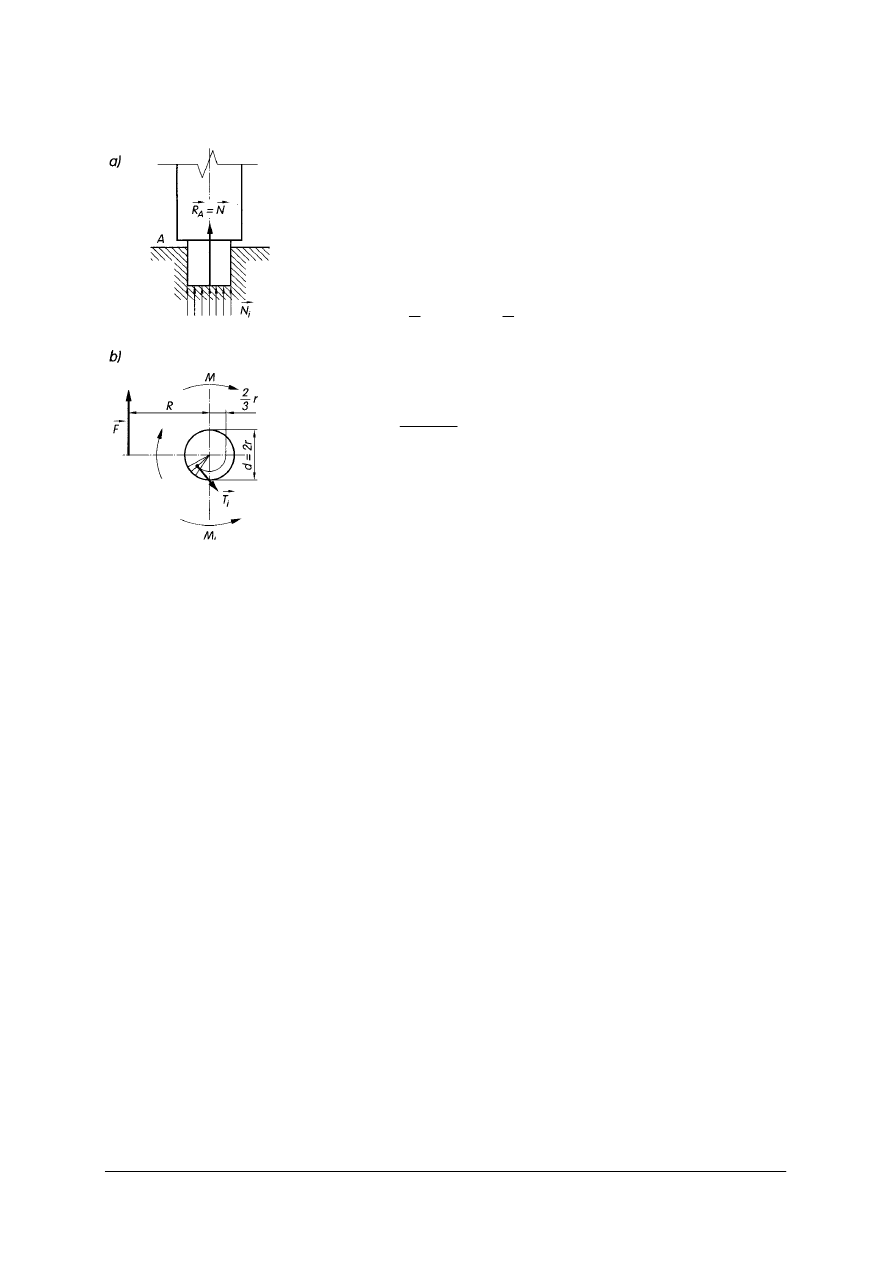
Tarcie w łożyskach poprzecznych
Siła tarcia na powierzchni styku czopa
z panwią:
T = R
A
⋅
µ
= N
⋅
µ
µ
−
współczynnik tarcia ślizgowego
Moment tarcia czopowego M
t
j
M
t
= T
⋅
2
d
= N
⋅
µ⋅
2
d
gdzie d
−
średnica czopa
Rys. 18. Moment tarcia czopowego w łożysku poprzecznym:
a) reakcja czopa, b) moment tarcia czopowego M
t
[2, s. 77]
Ruch obrotowy wałka wystąpi, gdy przyłożymy czynny moment obrotowy M o zwrocie
przeciwnym do momentu tarcia czopowego M
t.
:
M > M
t
Siła zewnętrzna na ramieniu r, która spowoduje obrót łożyska w czopie będzie miała wartość:
F >
2
d
N
⋅
⋅
µ
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
16
Tarcie w łożyskach wzdłużnych
Moment tarcia czopowego
M
t
=
2
1
N
⋅µ
⋅
r =
4
1
N
⋅
µ⋅
d
gdzie d
−
średnica czopa
Ruch obrotowy wałka występuje wtedy, gdy M > M
t
,
a siła czynna wynosi
F >
R
d
N
4
⋅
⋅
µ
Rys. 19. Moment tarcia czopowego w łożysku wzdłużnym: a) reakcja czopa,
b) moment tarcia czopowego M
t
[2, s. 78]
4.1.2. Pytania sprawdzające
Odpowiadając na pytania, sprawdzisz, czy jesteś przygotowany do wykonania ćwiczeń.
1.
Jakie cechy określają wektor siły?
2.
Jakie znasz rodzaje sił i ich układy?
3.
Na czym polega redukcja układu sił?
4.
Jakie znasz rodzaje więzów i jakie występują w nich reakcje?
5.
Jakie są wykreślne i analityczne warunki równowagi płaskiego zbieżnego układu sił?
6.
Jakie są cechy wektora momentu siły względem punktu?
7.
Co to jest para sił?
8.
Jakie są wykreślne i analityczne warunki równowagi płaskiego dowolnego układu sił?
9.
Do czego służy konstrukcja wieloboku sznurowego?
10.
Co nazywamy przestrzennym układem sił i kiedy jest on w równowadze?
11.
Jakie znasz rodzaje tarcia i od czego zależy siła tarcia?
12.
Co jest samohamowność równi pochyłej?
13.
Jaki musi być spełniony warunek w łożysku poprzecznym, aby nastąpił obrót wału?
14.
Jaki moment czynny należy przyłożyć do łożyska wzdłużnego, aby nastąpił ruch
obrotowy wału?
4.1.3. Ćwiczenia
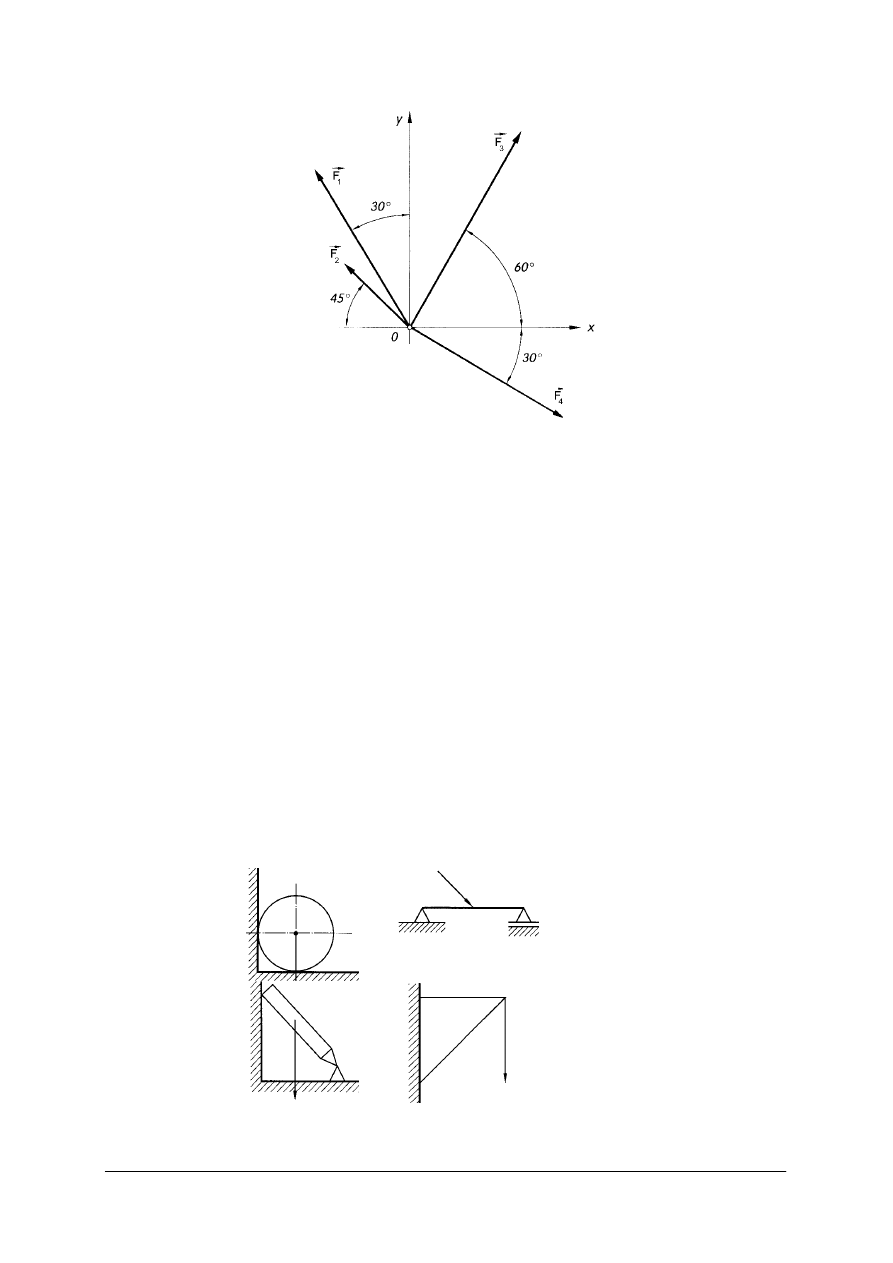
Ćwiczenie 1
Dla układu sił zbieżnych: F
1
= F
4
= 500 N, F
2
= 400 N, F
3
=1000 N wyznacz wypadkową
układu metodą wykreślną i analityczną.
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
17
Rysunek do ćwiczenia 3
Sposób wykonania ćwiczenia
Aby wykonać ćwiczenie, powinieneś:
1)
przygotować stanowisko do wykonywania ćwiczenia,
2)
narysować siły w podziałce,
3)
wyznaczyć wypadkową sił metodą wieloboku lub równoległoboku,
4)
określić cechy wektora wypadkowej,
5)
obliczyć sumę rzutów na osie układu XOY,
6)
obliczyć wypadkową i kąt, który tworzy z osią x,
7)
porównać wyniki otrzymane z obu metod wyznaczania wypadkowej,
8)
zaprezentować wykonane ćwiczenie.
Wyposażenie stanowiska pracy:
–
papier formatu A4, tablice trygonometryczne, kalkulator,
–
poradnik dla ucznia.
Ćwiczenie 2
Wyznacz kierunki i zwroty reakcji więzów przedstawionych na rysunkach.
Rysunki do ćwiczenia 1
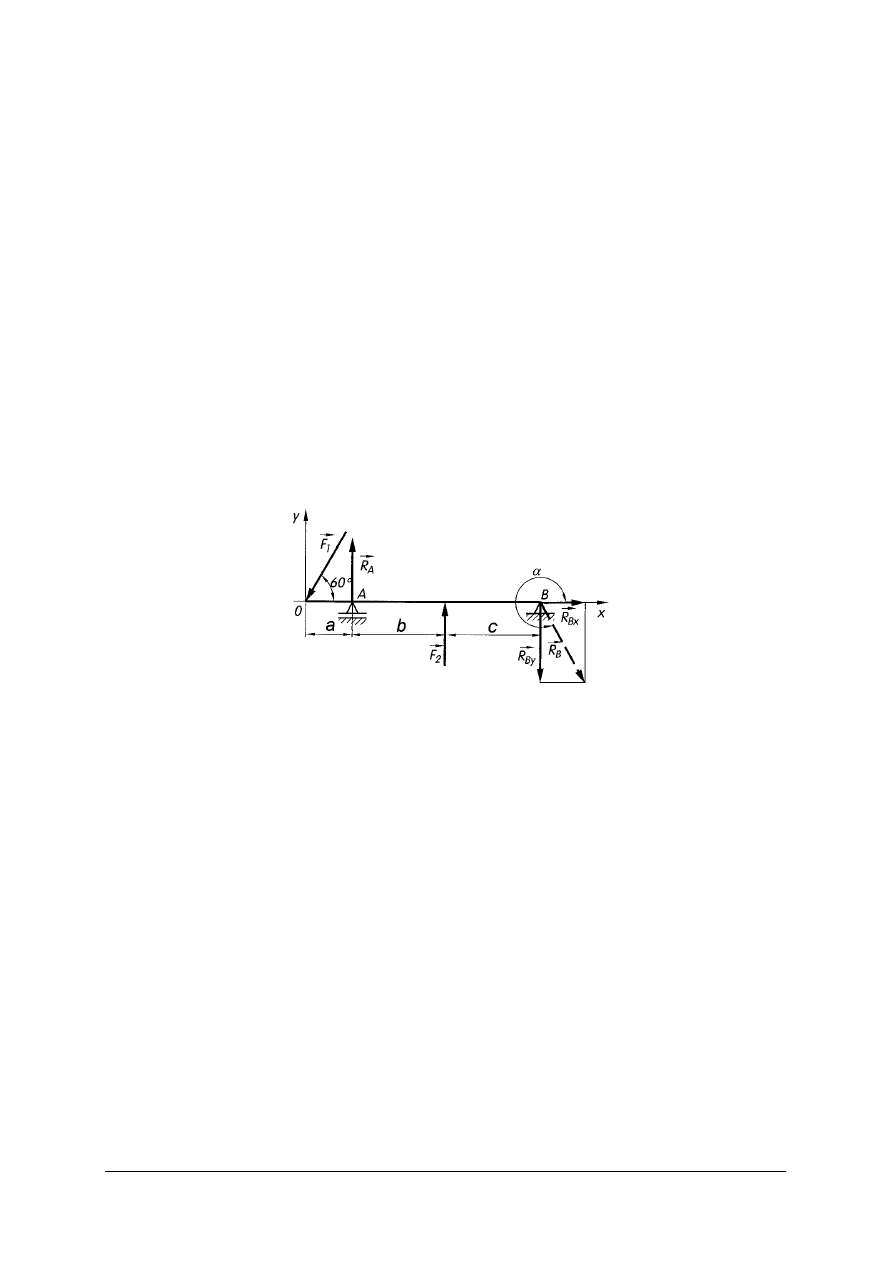
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
18
Sposób wykonania ćwiczenia
Aby wykonać ćwiczenie, powinieneś:
1)
przygotować stanowisko do wykonywania ćwiczenia,
2)
dokonać analizy przedstawionych schematów,
3)
rozróżnić rodzaje podpór,
4)
określić kierunki reakcji,
5)
naszkicować schematy i zaznaczyć reakcje w podporach i więzach,
6)
zaprezentować wykonane ćwiczenie.
Wyposażenie stanowiska pracy:
−−−−
papier formatu A4, przybory kreślarskie,
−−−−
modele podpór,
−−−−
poradnik dla ucznia,
−−−−
literatura zgodna z punktem 6 poradnika.
Ćwiczenie 3
Ułóż warunki równowagi dla przedstawionego układu płaskiego.
Rysunek do ćwiczenia 3
Sposób wykonania ćwiczenia
Aby wykonać ćwiczenie, powinieneś:
1)
przygotować stanowisko do wykonywania ćwiczenia,
2)
dokonać analizy układu sił i określić reakcje podpór,
3)
przyjąć wygodny układ współrzędnych,
4)
rozłożyć nieznany kierunek reakcji w podporze B na składowe: poziomą i pionową,
5)
założyć reakcjom zwroty wynikające z analizy obciążenia,
6)
zastosować równania równowagi (np. warunek rzutów wszystkich sił na oś x i równania
momentów sił względem punktu A i B lub warunki rzutów wszystkich sił na osie x i y
oraz równania momentów sił względem punktu A lub B).
7)
zaprezentować wykonane ćwiczenie.
Wyposażenie stanowiska pracy:
−−−−
papier formatu A4, komplet przyborów kreślarskich,
−−−−
poradnik dla ucznia.
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
19
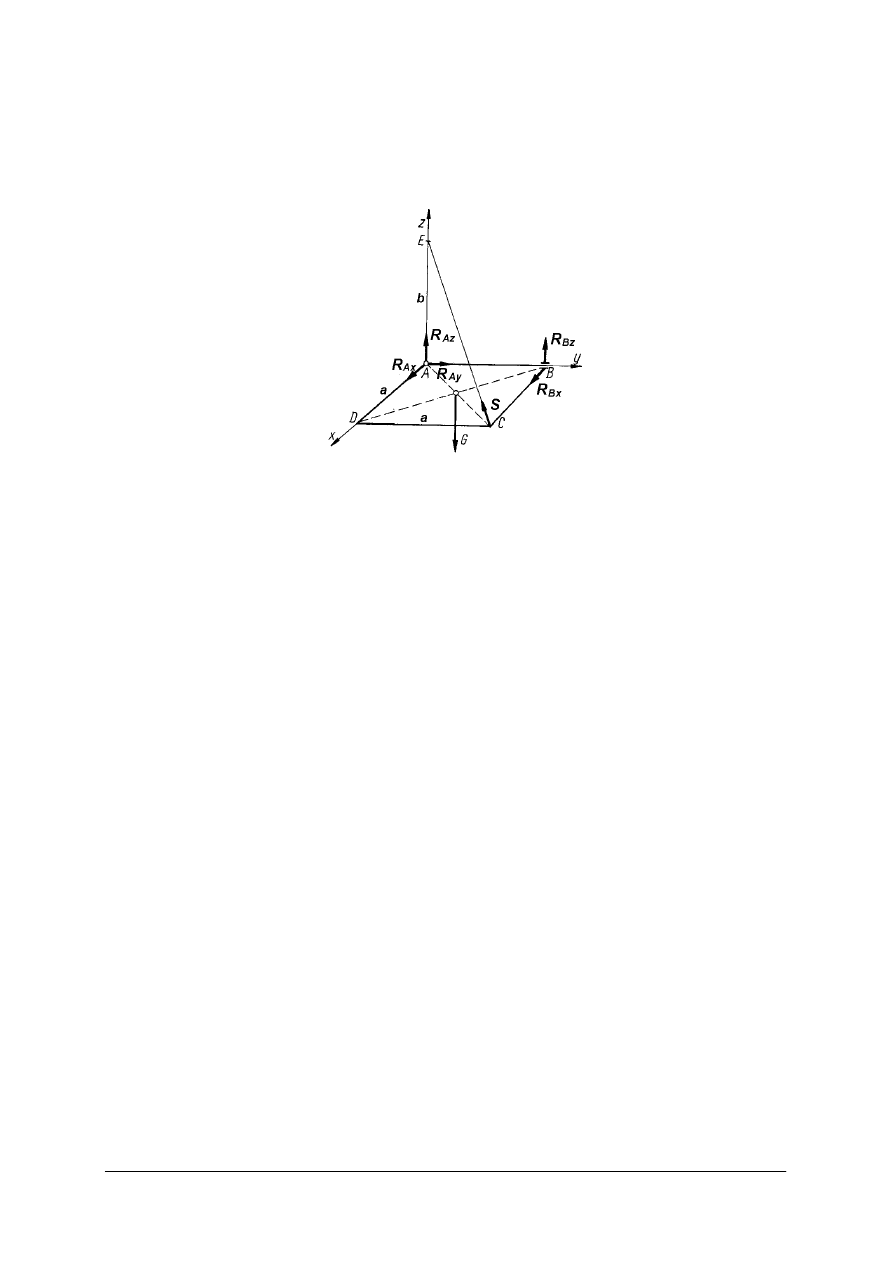
Ćwiczenie 4
Ułóż warunki równowagi dla płyty kwadratowej o ciężarze G, która w pozycji poziomej
jest utrzymywana za pomocą trzech podpór: podpory stałej w punkcie A, ruchomej w punkcie
B i liny wiotkiej w punkcie C.
Rysunek do ćwiczenia 4
Sposób wykonania ćwiczenia
Aby wykonać ćwiczenie, powinieneś:
1)
przygotować stanowisko do wykonywania ćwiczenia,
2)
dokonać analizy układu sił,
3)
określić reakcje w podporach stałych i ruchomych w układzie przestrzennym,
4)
przyjąć układ współrzędnych,
5)
rozłożyć nieznany kierunek reakcji w podporze stałej na trzy składowe, ruchomej na dwie
składowe, a w linie wzdłuż jej osi,
6)
założyć reakcjom zwroty,
7)
zastosować równania równowagi dla przestrzennego układu sił dowolnych (sześć równań
równowagi),
8)
zaprezentować wykonane ćwiczenie.
Wyposażenie stanowiska pracy:
−−−−
papier formatu A4, komplet przyborów kreślarskich,
−−−−
poradnik dla ucznia.
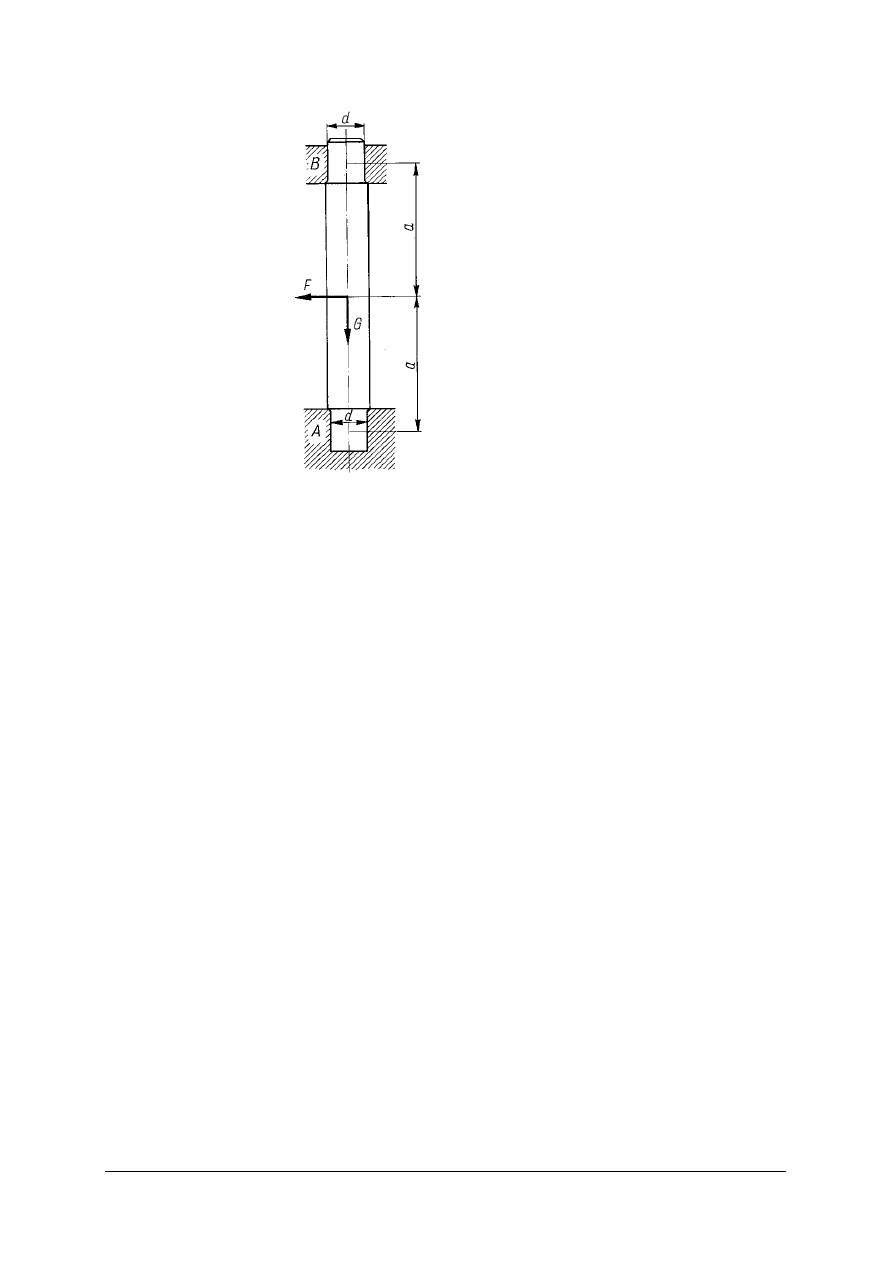
Ćwiczenie 5
Określ jaki należy przyłożyć moment obrotowy, aby pokonać poziome obciążenie wału
mieszadła i siłę tarcia w łożyskach dla danych jak na rysunku.
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
20
Dane:
F = 400 N
G = 2,5 kN
d = 50
µ = 0,07
µ – współczynnik tarcia
ś
lizgowego
Rysunek do ćwiczenia 5
Sposób wykonania ćwiczenia
Aby wykonać ćwiczenie, powinieneś:
1)
przygotować stanowisko do wykonywania ćwiczenia,
2)
dokonać analizy układu sił,
3)
określić reakcje w łożyskach,
4)
z warunków równowagi płaskiego układu sił dowolnych wyznaczyć reakcje w łożyskach,
5)
wyznaczyć moment tarcia jako sumę tarcia czopowego w łożyskach wzdłużnym
i poprzecznym,
6)
zaprezentować wyniki ćwiczenia.
Wyposażenie stanowiska pracy:
−−−−
papier formatu A4, komplet przyborów kreślarskich,
−−−−
poradnik dla ucznia.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
21
4.1.4. Sprawdzian postępów
Czy potrafisz:
Tak
Nie
1)
określić cechy wektora siły i sklasyfikować układy sił?
2)
zredukować układ sił?
3)
podać tok postępowania przy wyznaczaniu wypadkowej sił zbieżnych
metodą analityczną?
4)
podać warunki równowagi płaskiego układu sił zbieżnych?
5)
podać wykreślne i analityczne warunki równowagi płaskiego
dowolnego układu sił?
6)
wyznaczyć reakcje belek metodą wykreślną?
7)
podać analityczne warunki równowagi przestrzennego dowolnego
układu sił?
8)
wyznaczyć moment tarcia czopowego w łożysku poprzecznym
i wzdłużnym?
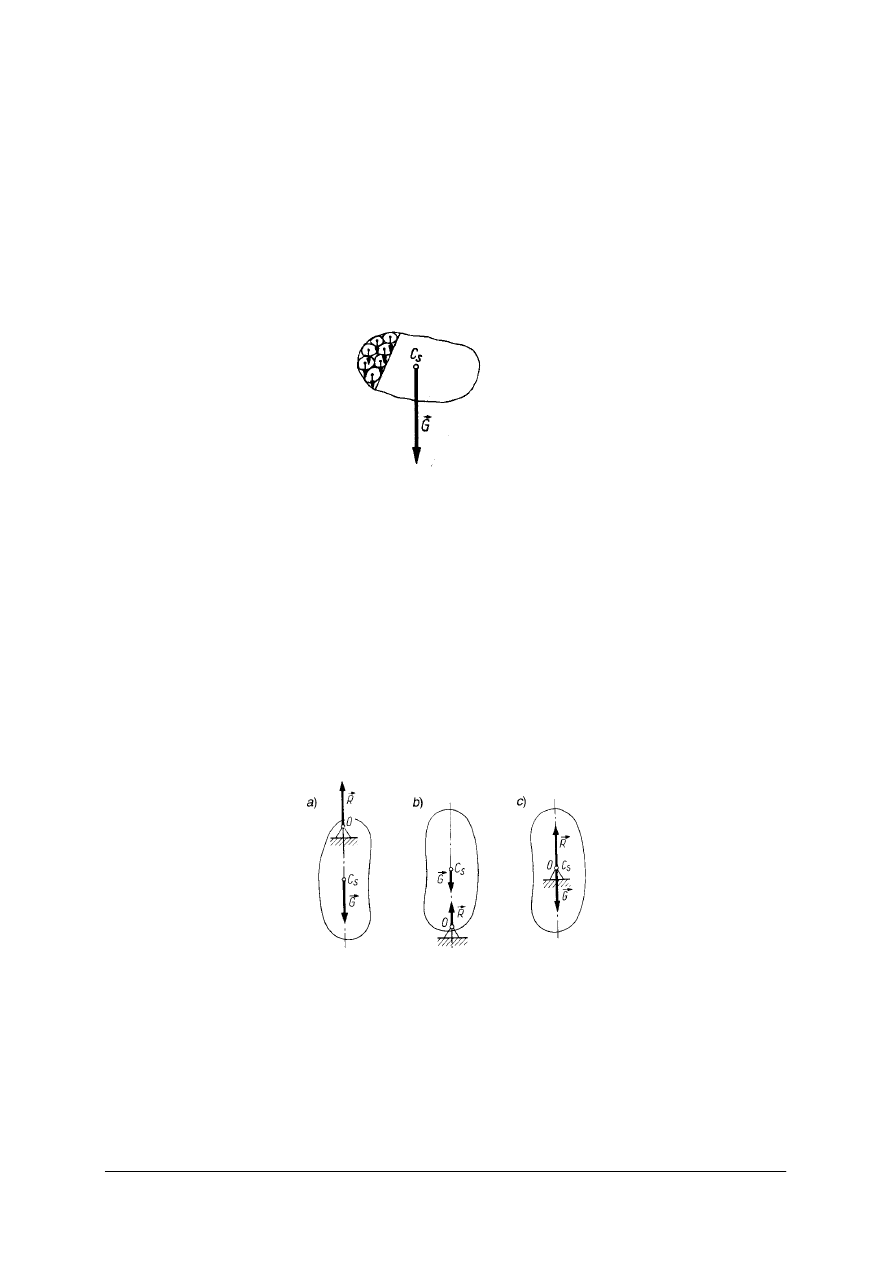
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
22
4.2. Środek ciężkości ciała
4.2.1. Materiał nauczania
Każde ciało materialne podlega działaniu sił ciężkości, które wynikają z przyciągania
ziemi. Siły te są skierowane do środka ziemi. Każde ciało można potraktować jako zbiór
cząstek elementarnych, z których każda podlega sile przyciągania. Siły wszystkich cząstek
tworzą układ sił równoległych, a wypadkowa tych sił jest ciężarem ciała i zaczepiona jest
w punkcie zwanym środkiem ciężkości C
s
(x
0
, y
0
).
Rys. 20. Ciało o ciężarze G [5, s. 119]
Dla ciał jednorodnych o prostej budowie przy wyznaczaniu środka ciężkości korzysta się
z następujących zależności :
−−−−
jeżeli ciało ma jedną oś symetrii – środek ciężkości leży na tej osi,
−−−−
jeżeli ciało ma dwie lub więcej osi symetrii – środek ciężkości leży w punkcie ich
przecięcia,
−−−−
jeżeli ciało ma środek symetrii, to jest to zarazem jego środek ciężkości,
−−−−
ś
rodek ciężkości ciała złożonego z kilku ciał pokrywa się ze środkiem ciężkości punktów
materialnych leżących w środkach poszczególnych ciał składowych.
Wyznaczanie środka ciężkości ma duże znaczenie dla określenia rodzaju równowagi ciała
sztywnego. W zależności od położenia środka ciężkości w stosunku do punktu podparcia
mogą zachodzić trzy przypadki równowagi: stała, chwiejna i obojętna.
Rys. 21. Rodzaje równowagi: a) stała, b) chwiejna, c) obojętna [5, s. 120]
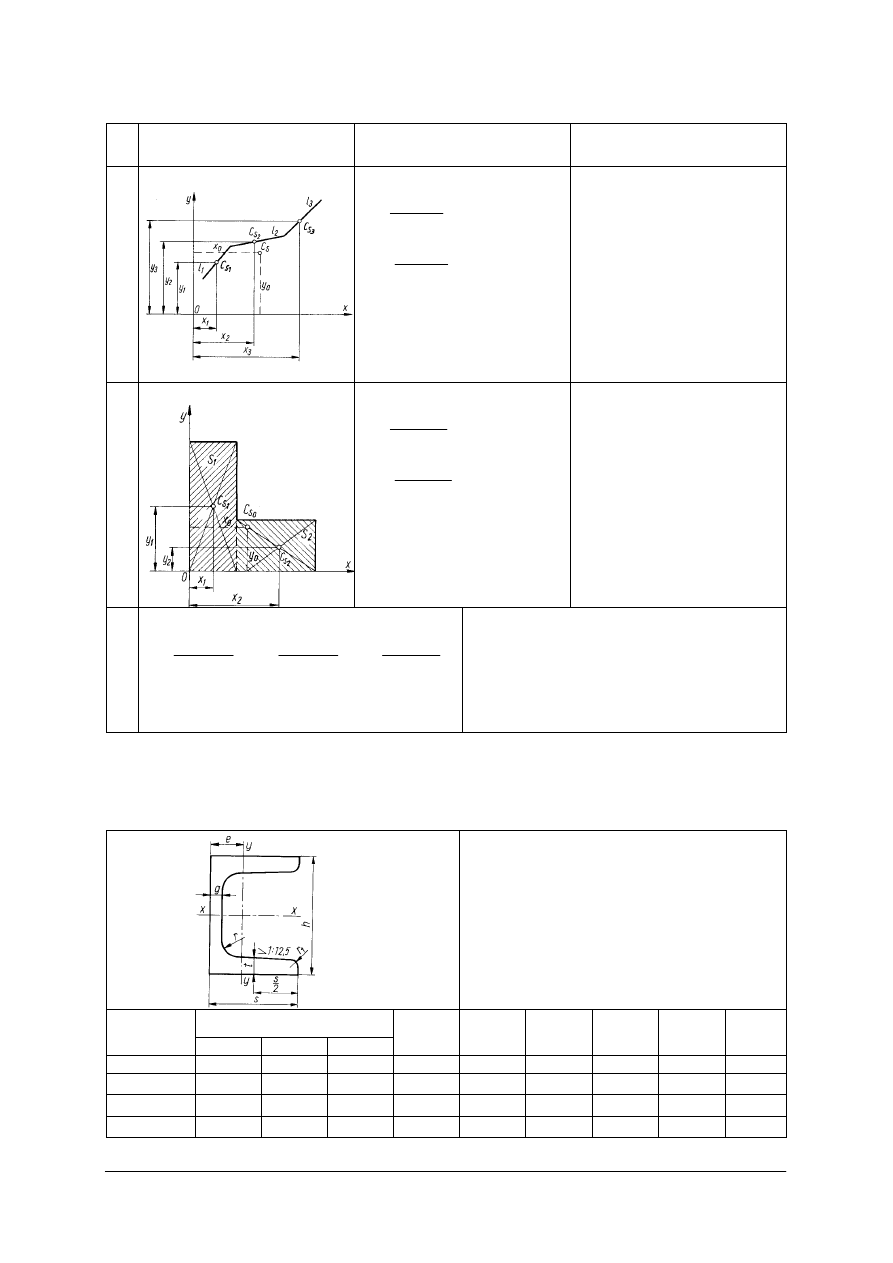
Przy wyznaczaniu środków ciężkości różnych figur korzystamy z właściwości momentu
statycznego względem dowolnej osi:
Moment statyczny odcinka, figury, objętości lub masy względem dowolnej osi jest równy
iloczynowi długości odcinka, pola figury, objętości lub masy i współrzędnej środka ciężkości
tego odcinka, pola, objętości lub masy względem danej osi.
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
23
Tabela 1. Współrzędne środka ciężkości figur [5, s. 121–124]
Lp
Rodzaj figury
Współrzędne środka
ciężkości
Momenty statyczne
1. Linia łamana
x
0 =
∑
∑
⋅
i
i
i
l
x
l
y
0
=
∑
∑
⋅
i
i
i
l
y
l
gdzie
l = l
1
+ l
2
+
⋅⋅⋅
+ l
n
=
∑
i
l
względem osi y:
x
0
⋅
∑
i
l
=
∑
i
l
⋅
x
i
[m
2
]
względem osi x:
y
0
⋅
∑
i
l
=
∑
i
l
⋅
y
i
[m
2
]
2. Figura płaska
x
0 =
∑
∑
⋅
i
i
i
S
x
S
y
0
=
∑
∑
⋅
i
i
i
S
y
S
gdzie:
S = S
1
+ S
2
+
⋅⋅⋅
+ S
n
=
∑
i
S
względem osi y:
x
0
⋅
∑
i
S
=
∑
i
S
⋅
x
i
[m
3
]
względem osi x:
y
0
⋅
∑
i
S
=
∑
i
S
⋅
y
i
[m
3
]
3. Bryła
x
0 =
∑
∑
⋅
i
i
i
V
x
V
,
y
0
=
∑
∑
⋅
i
i
i
V
y
V
,
z
0
=
∑
∑
⋅
i
i
i
V
z
V
gdzie:
V = V
1
+ V
2
+ V
3
+
⋅⋅⋅
+ V
n
=
∑
i
V
względem osi y:
x
0
⋅
∑
i
V
=
∑
i
V
⋅
x
i
[m
4
]
względem osi x:
y
0
⋅
∑
i
V
=
∑
i
V
⋅
y
i
[m
4
]
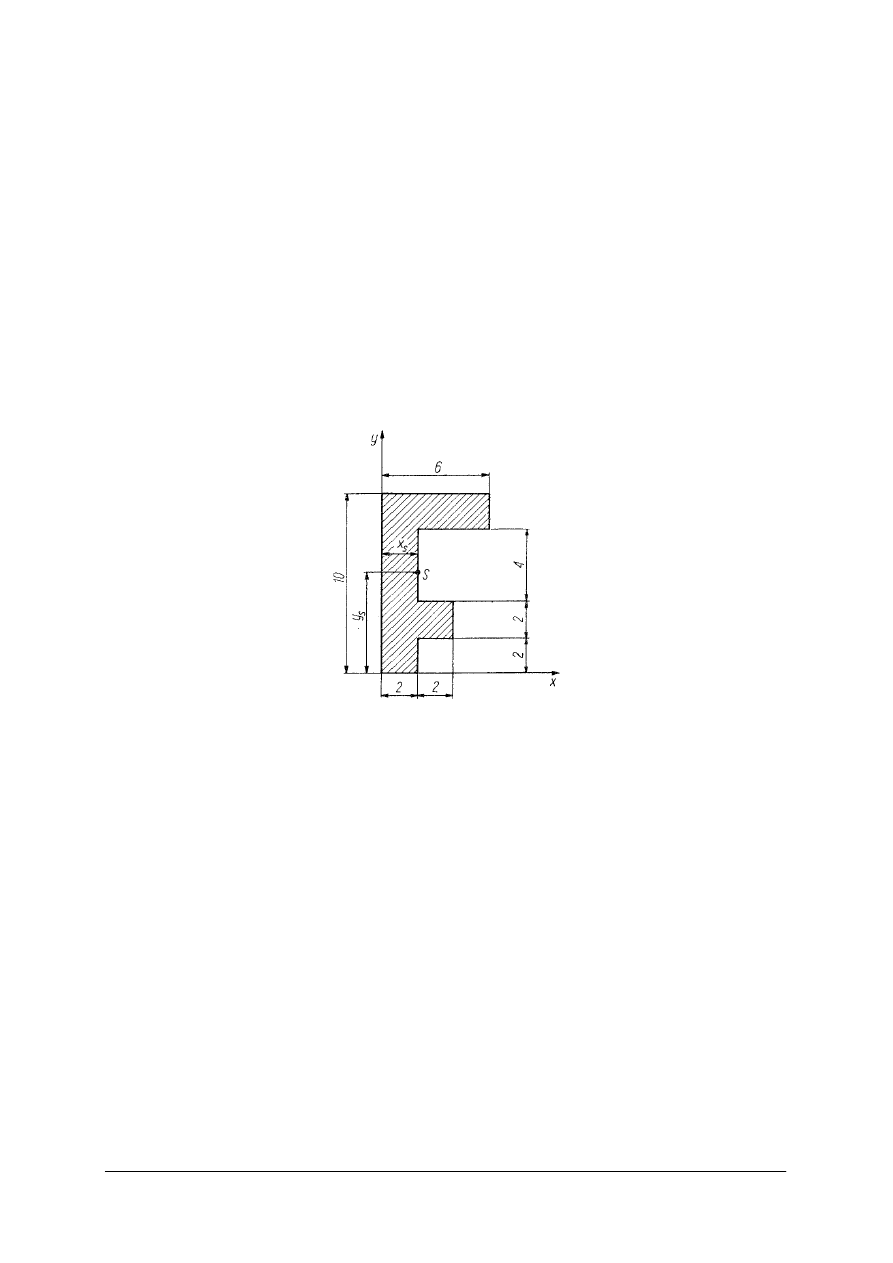
Współrzędne środka przekroju dla profili walcowanych typu: ceownik, kątownik,
dwuteownik, itp. odczytujemy z norm.
Tabela 2. Ceowniki – wymiary wybrane z normy PN-86/H-93403 [4, s. 356]
J
x
, J
y
, – moment bezwładności
i
x
, i
y
, – promień bezwładności
e – odległość od środka ciężkości
Przykład oznaczenia:
CEOWNIK 300 – St3S PN/H-93403
Wymiary
Oznaczenie
h
s
g
t
Przekrój
S
e
J
x
J
y
i
x
i
x
mm
mm
mm
mm
cm
2
cm
cm
4
cm
4
cm
cm
50
38
5
7,5
7,12
1,37
26,4
9,12
1,92
1,13
100
50
6
8,5
13,5
1,55
206
29,3
3,91
1,47
200
75
8,5
11,5
32,2
2,01
1910
148
7,70
2,14
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
24
4.2.2. Pytania sprawdzające
Odpowiadając na pytania, sprawdzisz, czy jesteś przygotowany do wykonania ćwiczeń.
1.
Co nazywa się środkiem ciężkości ciała?
2.
Ile środków ciężkości może mieć ciało sztywne?
3.
Jak zachowa się ciało, gdy punkt podparcia przyłożymy poniżej środka ciężkości?
4.
Jak wyznaczamy współrzędne środka ciężkości linii łamanej, figury płaskiej?
5.
Jakie wartości może przyjmować moment statyczny i od czego zależy?
6.
Jak wyznaczamy współrzędne środka ciężkości profili walcowanych?
4.2.3. Ćwiczenia
Ćwiczenie 1
Wyznacz położenie środka ciężkości figury płaskiej.
Rysunek do ćwiczenia 1
Sposób wykonania ćwiczenia
Aby wykonać ćwiczenie, powinieneś:
1)
dokonać analizy przedstawionej figury,
2)
sporządzić rysunek powierzchni,
3)
przyjąć układ współrzędnych,
4)
obliczyć współrzędne środka ciężkości,
5)
zwymiarować położenie środka ciężkości figury,
6) zaprezentować wykonane ćwiczenie.
Wyposażenie stanowiska pracy:
−−−−
papier milimetrowy,
−−−−
komplet przyborów kreślarskich,
−−−−
poradnik dla ucznia.
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
25
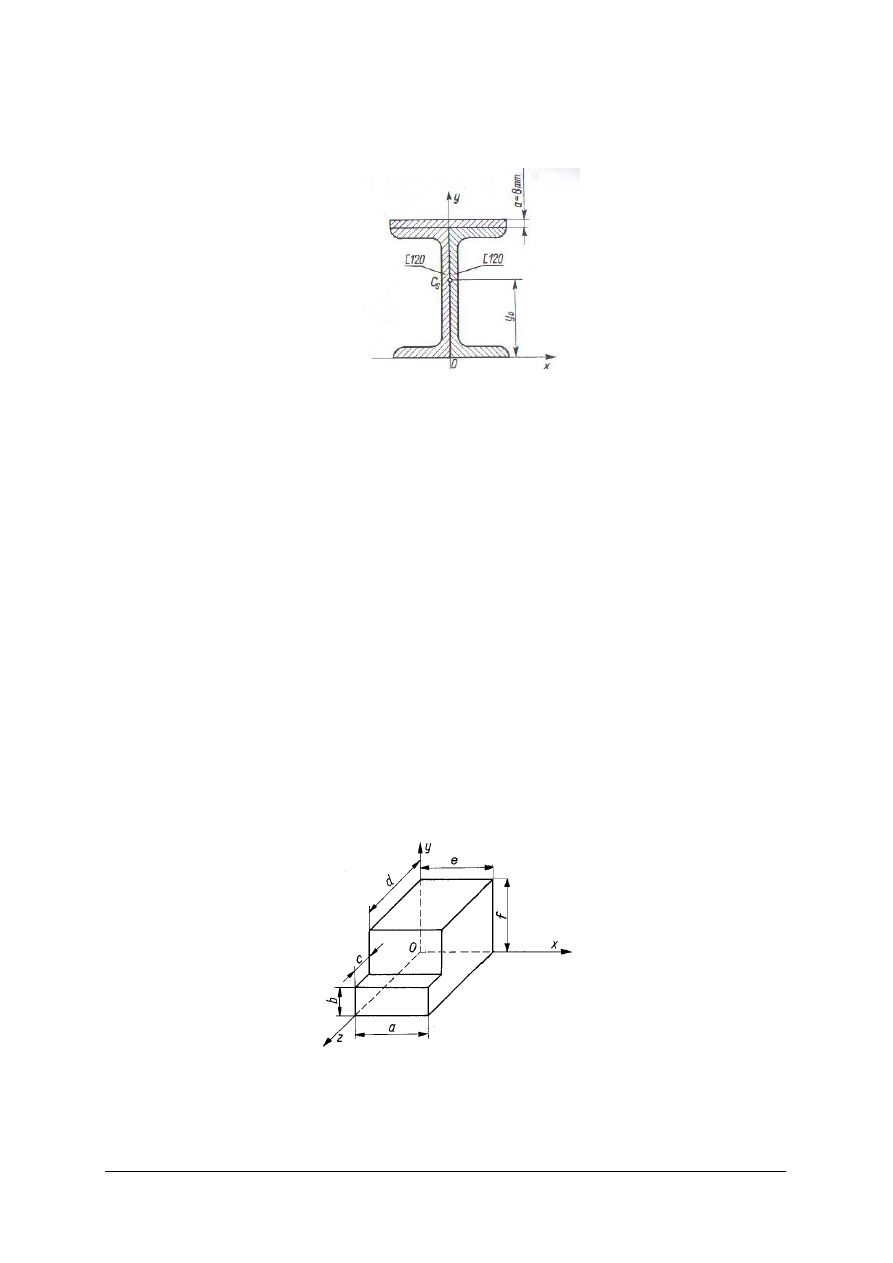
Ćwiczenie 2
Wyznacz środek ciężkości przekroju blachownicy złożonej z dwóch ceowników i jednego
płaskownika.
Rysunek do ćwiczenia 2
Sposób wykonania ćwiczenia
Aby wykonać ćwiczenie, powinieneś:
1)
dokonać analizy przedstawionej figury płaskiej,
2)
naszkicować przekrój blachownicy,
3)
przyjąć układ współrzędnych,
4)
określić współrzędne środka ciężkości dla przekroju ceownika,
5)
obliczyć współrzędne środka ciężkości,
6)
zwymiarować położenie środka ciężkości figury,
9)
zaprezentować wykonane ćwiczenie.
Wyposażenie stanowiska pracy:
−−−−
papier formatu A4,
−−−−
komplet przyborów kreślarskich,
−−−−
poradnik mechanika,
−−−−
poradnik dla ucznia.
Ćwiczenie 3
Wyznacz środek ciężkości fundamentu względem osi x, y, z.
Rysunek do ćwiczenia 3

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
26
Sposób wykonania ćwiczenia
Aby wykonać ćwiczenie, powinieneś:
1)
dokonać analizy przedstawionej figury przestrzennej,
2)
naszkicować figurę,
3)
przyjąć układ współrzędnych,
4)
określić współrzędne środka ciężkości figur prostych,
5)
obliczyć współrzędne środka ciężkości figury,
6)
zwymiarować położenie środka ciężkości figury,
7)
zaprezentować wykonane ćwiczenie.
Wyposażenie stanowiska pracy:
−−−−
papier formatu A4,
−−−−
komplet przyborów kreślarskich,
−−−−
poradnik dla ucznia.
4.2.4. Sprawdzian postępów
Czy potrafisz:
Tak
Nie
1)
wyznaczyć współrzędne środka ciężkości linii?
2)
wyznaczyć współrzędne środka ciężkości figur płaskich złożonych?
3)
wyznaczyć współrzędne środka ciężkości bryly?
4)
podać jednostkę momentu statycznego pola przekroju względem osi?
5)
odszukać współrzędne środka ciężkości dla przekroju profili
walcowanych?

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
27
4.3. Kinematyka punktu i ciała sztywnego
4.3.1. Materiał nauczania
Kinematyka jest działem mechaniki zajmującym się badaniem ruchu ciał bez
uwzględniania przyczyn, które ten ruch wywołują. Ruchem nazywamy zmianę położenia
ciała względem innego ciała, które traktowane jest jako układ odniesienia.
Ze względu na układ odniesienia ruch dzielimy na:
−
ruch bezwzględny; jest to ruch określony w ruchomym układzie odniesienia,
−
ruch względny; jest to ruch określony względem ruchomego układu odniesienia.
Ruch punktu możemy określić równaniem prędkości:
v
=
( )
t
f
i równaniem ruchu:
s
=
( )
t
f
Jednym z kryteriów podziału ruchu jest rodzaj toru punktu materialnego. Torem punktu
nazywamy linię utworzoną przez kolejne położenia poruszającego się punktu.
Ze względu na kształt toru ruch można podzielić na:
−
prostoliniowy
−
torem jest linia prosta,
−
krzywoliniowy
−
torem jest dowolna linia geometryczna na płaszczyźnie (ruch płaski)
lub w przestrzeni (ruch przestrzenny).
Ruch prostoliniowy jednostajny
W ruchu prostoliniowym jednostajnym stosunek drogi do czasu, w którym ta droga
została przebyta, nazywamy prędkością. Prędkość ma wartość stałą
v
=
t
s
=const [m/s]
Droga w ruchu jest proporcjonalna do czasu trwania ruchu.
s
=
t
v
⋅
równanie ruchu prostoliniowego jednostajnego
Wykresem prędkości w ruchu jednostajnym jest odcinek równoległy do osi czasu, a pole
zawarte pod wykresem prędkości przedstawia w odpowiedniej podziałce drogę. Graficznym
odwzorowaniem drogi jest linia prosta nachylona do osi t pod kątem
α
. Wartość kąta
α
przedstawia zależność
tg
α
=
v
=const
Jeżeli czas jest liczony od chwili, w której punkt przebył już drogę
o
s , to całkowita droga
wynosi:
s
=
o
s +
t
v
⋅
a)
b)
Rys. 22. Wykresy: a) prędkości, b) drogi [1, s. 220]
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
28
Ruch prostoliniowy zmienny
Prędkość punktu zmienia się. Jeżeli prędkość rośnie, to mamy do czynienia z ruchem
przyspieszonym, a gdy maleje z ruchem opóźnionym.
Stosunek przyrostu drogi do przyrostu czasu nazywamy prędkością średnią punktu.
v
=
t
s
∆
∆
=
1
2
1
2
t
t
s
s
−
−
Prędkością chwilową nazywamy granicę wyrażenia
t
s
∆
∆
, jeżeli przyrost t
∆
dąży do zera.
v
=lim
t
s
∆
∆
, gdy t
∆
→
0
Dla określenia przyspieszenia wyznaczamy przyrosty prędkości.
Przyspieszeniem średnim nazywamy stosunek przyrostu prędkości do czasu, w którym ten
przyrost nastąpił.
a
=
t
v
∆
∆
=
1
2
1
2
t
t
v
v
−
−
[m/s
2
]
Przyspieszenie chwilowe określa zależność
a
=lim
t
v
∆
∆
, gdy t
∆
→
0
Wielkości charakteryzujące ruch zmienny
Równania
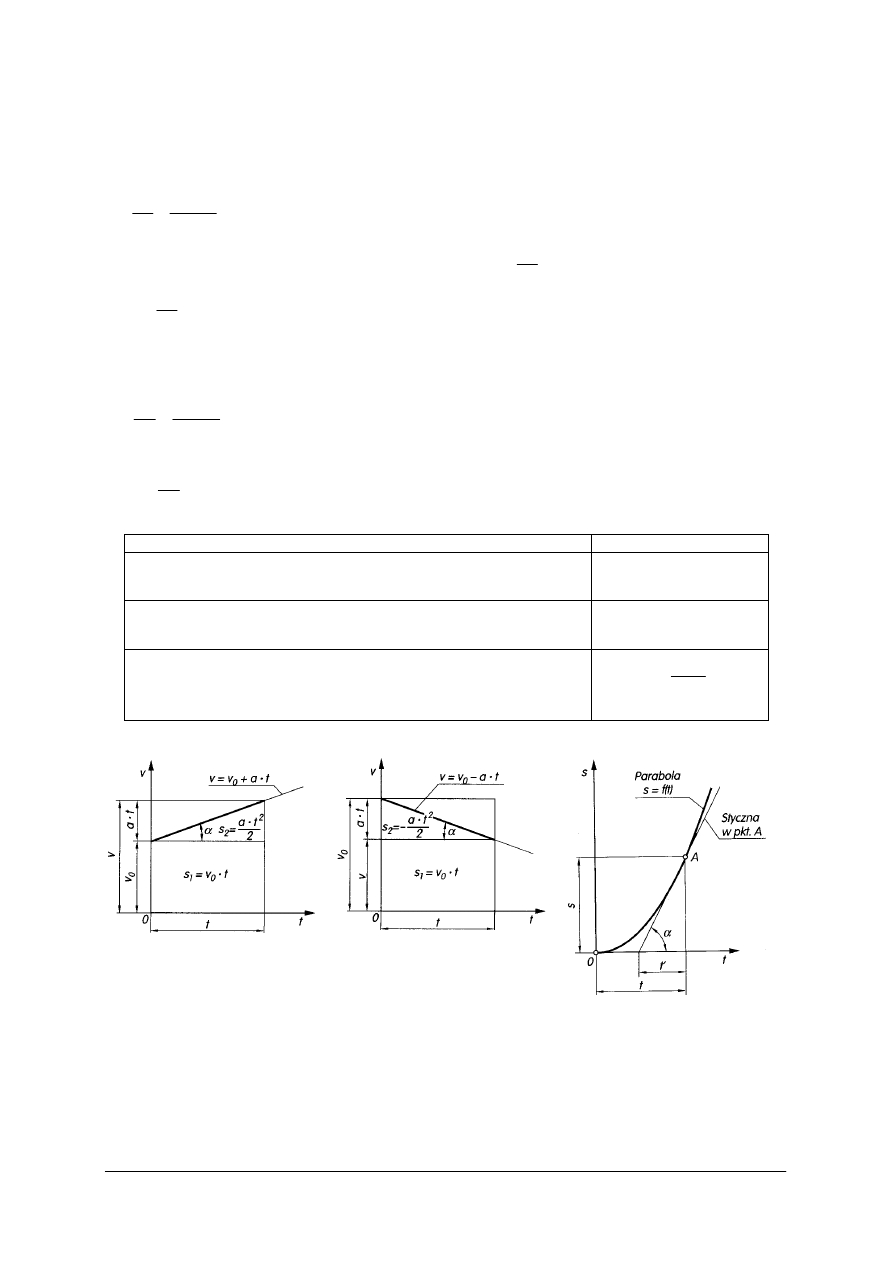
Prędkość w ruchu jednostajnie zmiennym przyspieszonym
t
a
v
v
o
⋅
+
=
Prędkość w ruchu jednostajnie zmiennym opóźnionym
t
a
v
v
o
⋅
−
=
Równanie drogi
2
2
t
a
t
v
s
o
⋅
±
⋅
=
a)
b)
Rys. 23.. Wykresy: a) prędkości, b) drogi [1, s. 224]
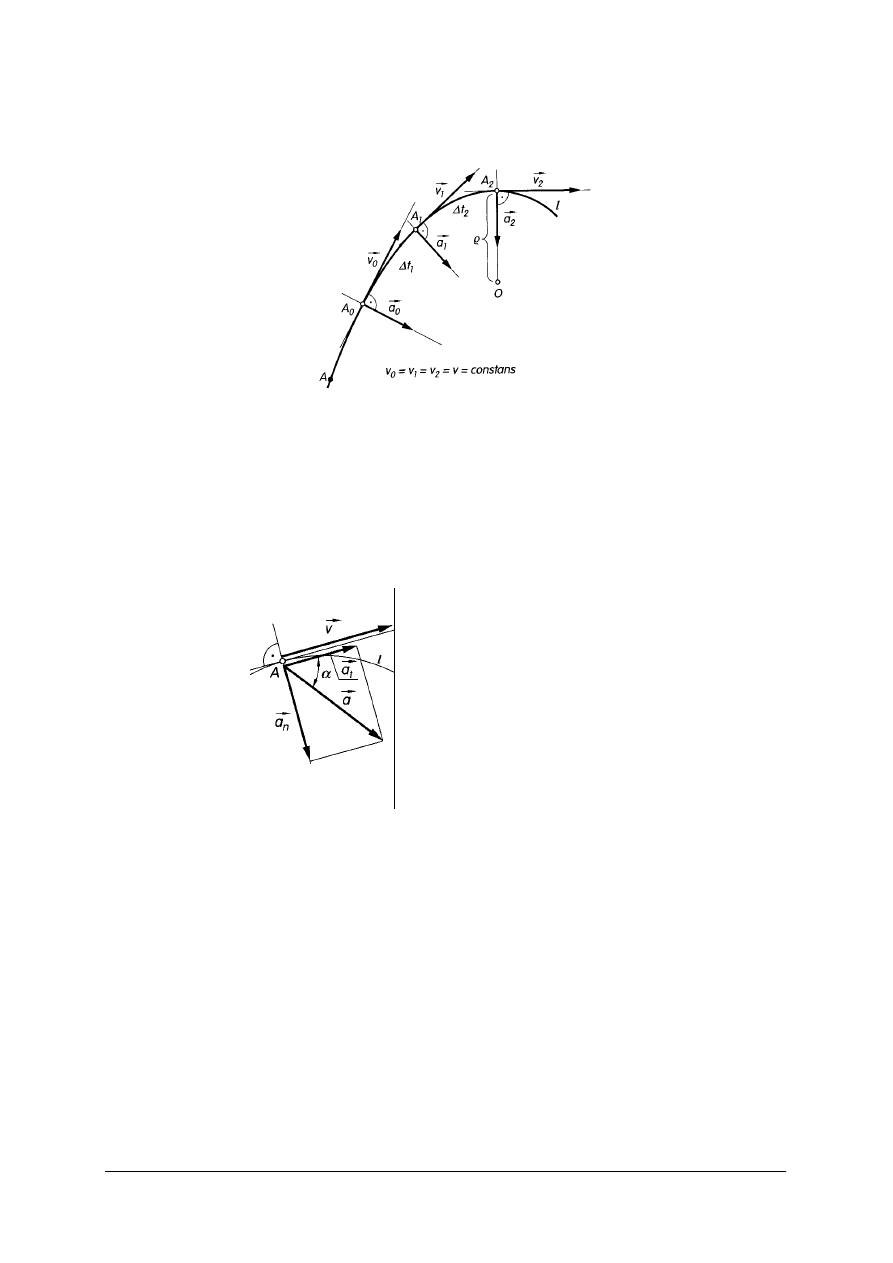
Ruch krzywoliniowy jednostajny
Torem takiego ruchu jest linia krzywa, do której styczne są wektory prędkości o równych
wartościach.
Miejsce geometryczne wektorów prędkości wykreślonych ze wspólnego punktu
nazywamy hodografem prędkości.
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
29
Hodograf w ruchu krzywoliniowym jednostajnym jest łukiem okręgu o promieniu
równym wartości prędkości poruszającego się punktu.
Rys. 24. Ruch krzywoliniowy jednostajny [2, s. 226]
Przyspieszenie chwilowe ma kierunek prostopadły (normalny) do prędkości
poruszającego się punktu. Przyspieszenie związane ze zmianą kierunku wektora prędkości
nazywa się przyspieszeniem normalnym.
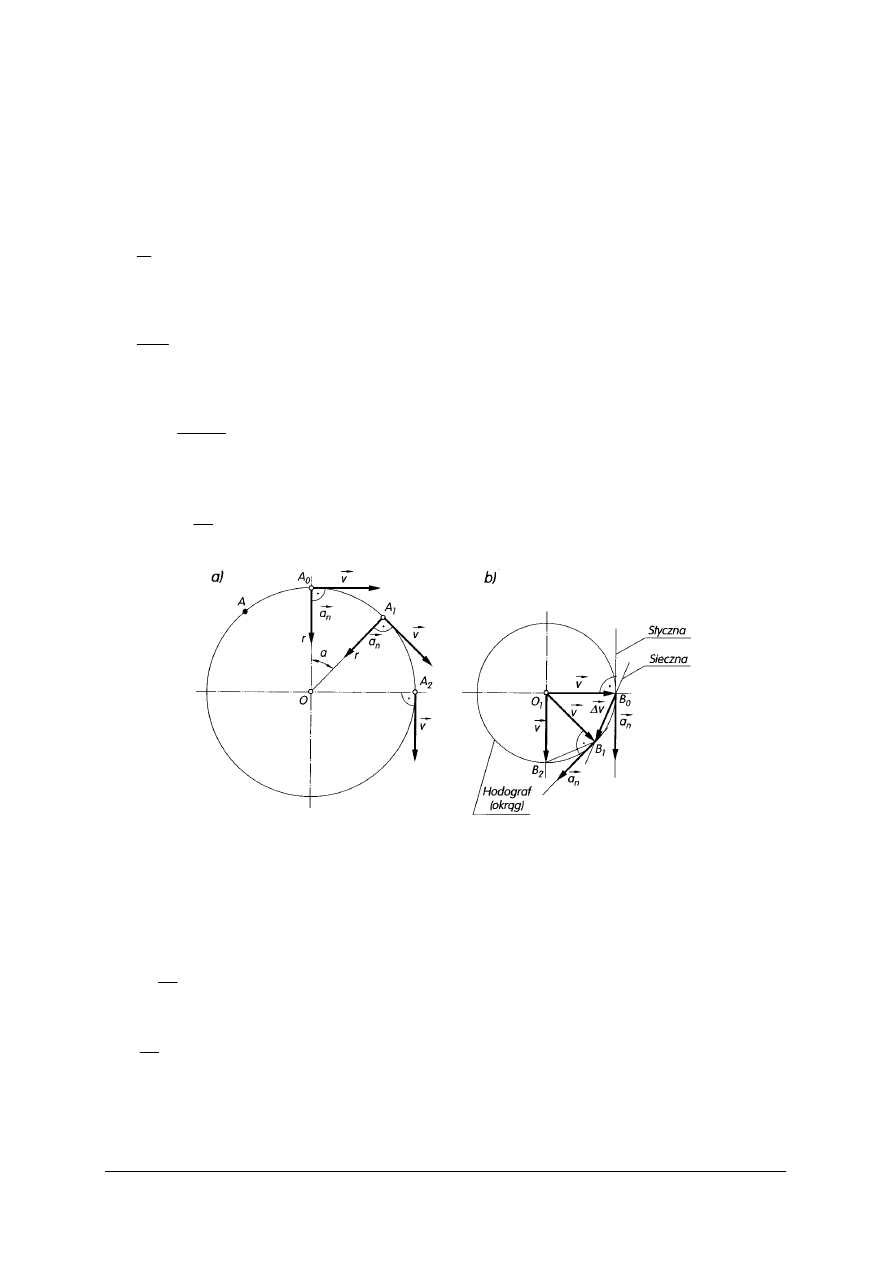
Ruch krzywoliniowy zmienny
Wektory prędkości w tym ruchu zmieniają kierunek i wartość.
Przyspieszenie:
−−−−
normalne :
n
a
=
α
sin
⋅
a
,
−−−−
styczne:
t
a
=
α
cos
⋅
a
.
Rys. 25. Przyspieszenie w ruchu krzywoliniowym zmiennym [2, s. 227]
Przyspieszenie w ruchu krzywoliniowym zmiennym tworzy z wektorem prędkości kąt
α
.
Po rozłożeniu przyspieszenia na dwa kierunki otrzymujemy przyspieszenie:
−
normalne (dośrodkowe)
n
a , o kierunku prostopadłym do toru,
−
styczne
t
a , o kierunku prędkości.
Na podstawie kierunków i wartości składowych przyspieszeń
n
a i
t
a klasyfikuje się ruchy.
Rodzaj ruchu
Wartości przyspieszeń
Ruch krzywoliniowy zmienny
n
a
≠
0
−−−−
t
a
≠
0
Ruch prostoliniowy zmienny
n
a =0
−−−−
t
a
≠
0
Ruch krzywoliniowy jednostajny
n
a
≠
0
−−−−
t
a =0
Ruch prostoliniowy jednostajny
n
a =0
−−−−
t
a =0
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
30
Ruch jednostajny po okręgu
W czasie ruchu po okręgu o promieniu r punkt materialny przebywa w równych
odstępach czasu równe drogi oraz zatacza równe kąty
α
. Prędkość punktu poruszającego się
po okręgu nazywamy prędkością liniową lub obwodową.
Stosunek drogi kątowej
α
do czasu, w którym ta droga została przebyta, nazywamy
prędkością kątową
ω
.
ω
=
t
α
[rad/s]
W mechanizmach ruchu obrotowego często prędkość kątową uzależniamy od ilości obrotów
na minutę, wielkość tę nazywamy prędkością obrotową.
ω
=
30
n
⋅
π
Prędkość liniowa
v
w ruchu jednostajnym po okręgu jest stała, równa iloczynowi prędkości
kątowej
ω
i promienia r .
v
=
r
⋅
ω
=
30
r
n
⋅
⋅
π
W ruchu jednostajnym po okręgu wartość przyspieszenia stycznego jest równa zeru,
a przyspieszenie normalne obliczamy ze wzorów
n
a =
r
⋅
2
ω
=
r
v
2
Rys. 26. Ruch punktu po okręgu: a) prędkość i przyspieszenie, b) hodograf prędkości [2, s. 231]
Ruch zmienny po okręgu koła
W ruchu zmiennym po okręgu koła występuje przyspieszenie normalne i styczne do toru.
Wielkością charakteryzującą ten ruch jest przyspieszenie kątowe, które jest stosunkiem
przyrostu prędkości kątowej do przedziału czasu, gdy ten dąży do zera.
ε
=lim
t
∆
ω
, gdy
0
→
∆
t
[rad/s
2
]
Przyspieszenie normalne
n
a =
r
v
2
Przyspieszenie styczne
t
a =
ε
⋅
r
,
gdzie r
−
promień koła.
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
31
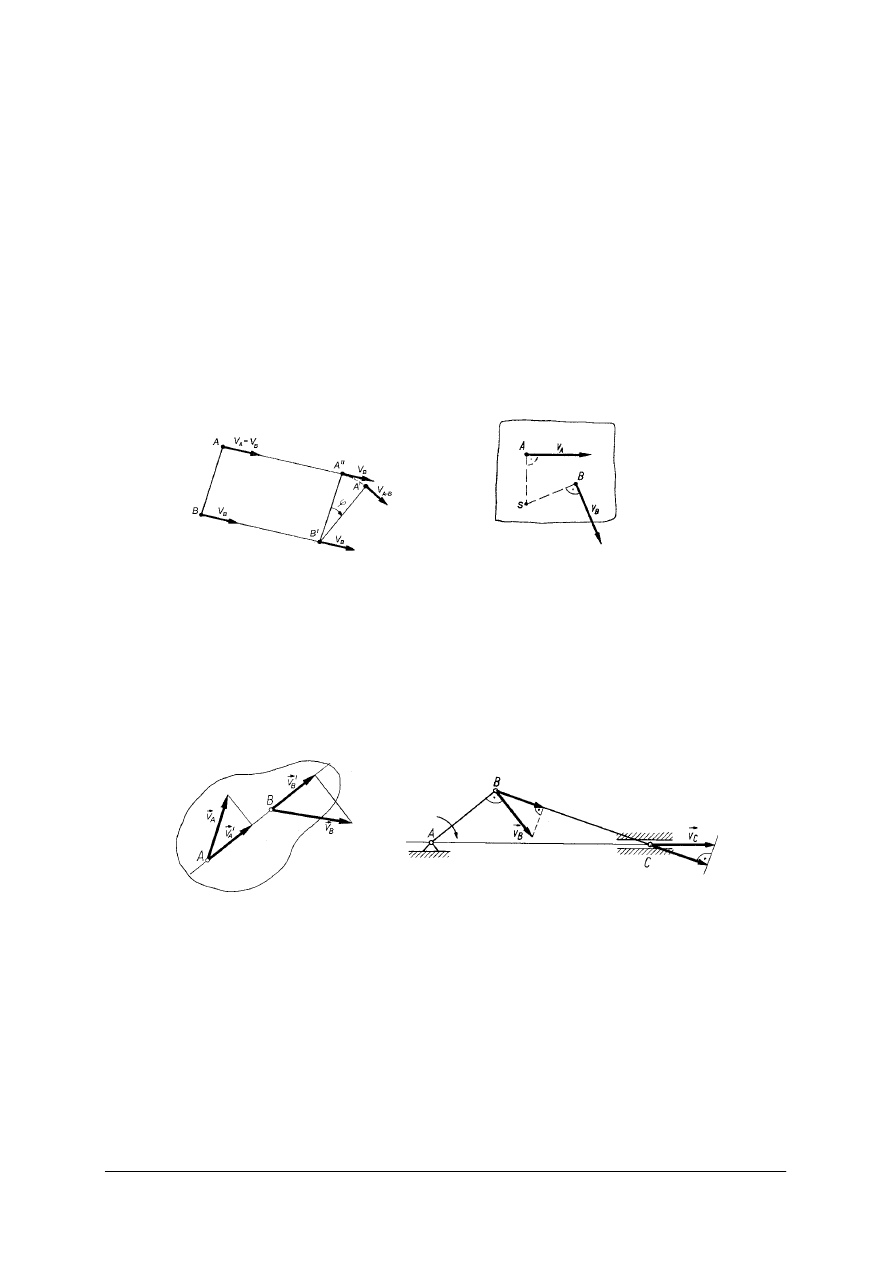
Kinematyka ciała sztywnego
Ciała sztywne mogą poruszać się ruchem:
–
postępowym, punkty ciała sztywnego zakreślają jednakowe tory, na których wszystkie
punkty mają jednakową prędkość i przyspieszenie.
–
obrotowym, punkty wykonują ruch dookoła prostej, zwanej osią obrotu. Jeżeli prędkość
kątowa jest wielkością stałą ruch nazywa się ruchem obrotowym jednostajnym, a jeżeli
zmienną ruchem obrotowym zmiennym.
−−−−
płaskim.
Ruch płaski ciała sztywnego może być rozpatrywany jako suma dwóch ruchów:
postępowego z prędkością dowolnego punktu ciała i obrotowego dookoła tego punktu
z prędkością kątową lub może być w każdej chwili ruchem obrotowym dookoła chwilowego
ś
rodka obrotu (S
−
środek chwilowego obrotu jest punktem przecięcia normalnych do
wektorów prędkości).
a)
b)
A
B
B
A
V
V
V
−
+
=
r
r
r
Rys. 27. Ruch płaski bryły: a) suma ruchu postępowego i obrotowego,
b) ruch obrotowy względem środka chwilowego obrotu [1, s. 267]
Prędkość punktów w ruchu płaskim możemy wyznaczyć kilkoma metodami:
−
z wykorzystaniem twierdzenia o rzutach prędkości.
Rzuty prędkości dwu punktów ciała sztywnego, poruszającego się ruchem płaskim, na
prostą łączącą te punkty są sobie równe.
Rys. 28. Rzuty prędkości i zastosowanie twierdzenia o rzutach prędkości [5, s. 359]
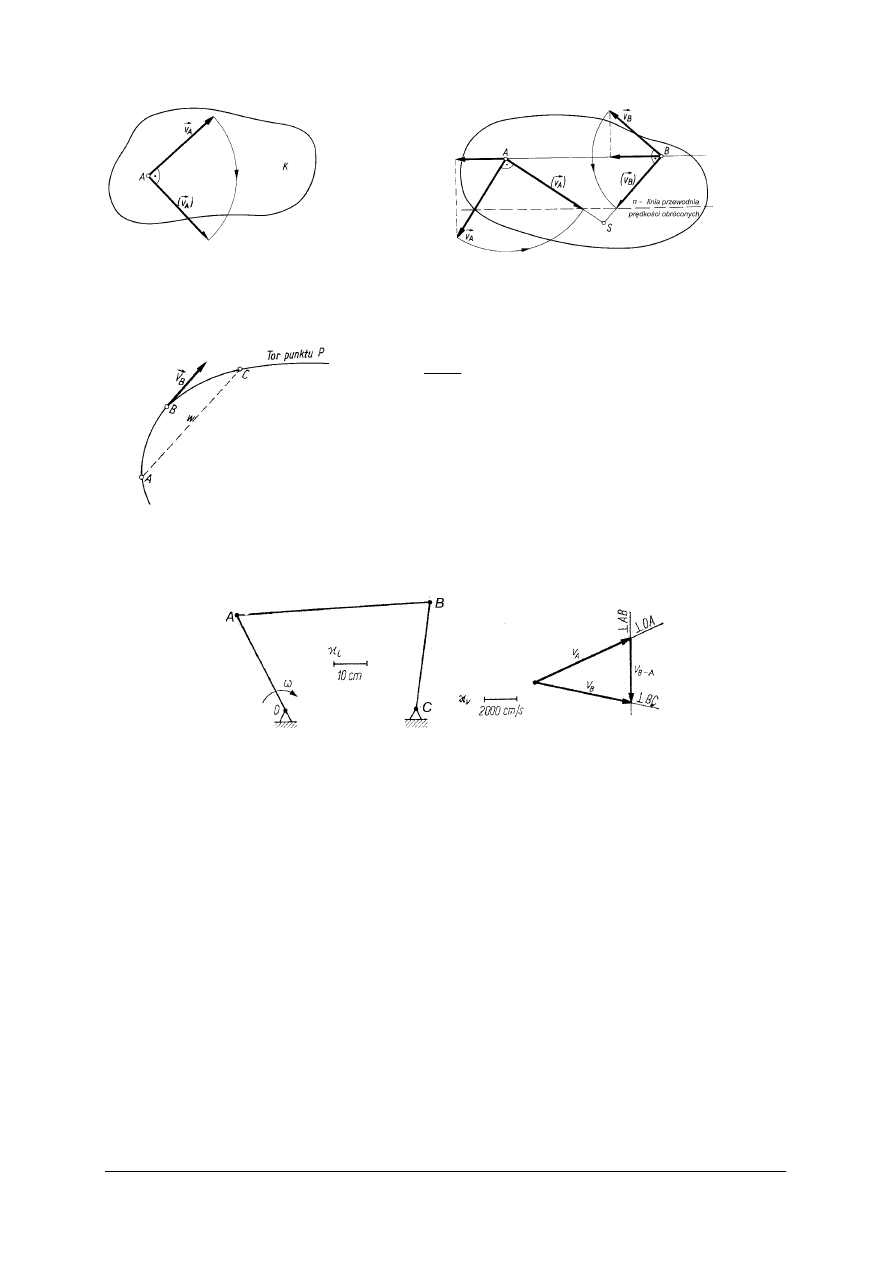
−
metodą prędkości obróconych
Linie działania prędkości obróconych wszystkich punktów poruszającego się przekroju
przecinają się w chwilowym środku obrotu S. Końce wektorów prędkości obróconych leżą na
prostej równoległej do prostej łączącej te punkty zwaną linią przewodnią prędkości
obróconych.
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
32
Rys. 29.. Prędkość obrócona i linia przewodnia prędkości obróconych [5, s. 352]
−
metodą toru ocechowanego
Prędkość w punkcie B:
t
w
k
v
B
∆
⋅
⋅
=
2
gdzie:
B
v
−
Prędkość w punkcie B w cm/s
w
−
długość siecznej, w cm
t
∆
−
czas, w jakim punkt przebywa drogę między sąsiednimi
punktami, w s,
k
−
podziałka długości
Rys. 30. Wyznaczanie prędkości metodą toru ocechowanego [5, s. 349]
−
metodą planu prędkości
Rys. 31. Wyznaczanie prędkości w czworoboku przegubowym metodą planu [1, s. 280]
W metodzie tej na podstawie równania wektorowego
A
B
A
B
v
v
v
−
+
=
r
r
r
wyznacza się wykreślnie wartości i kierunki prędkości
B
v
i prędkości względnej
A
B
v
−
.
Przyspieszenie w ruchu płaskim wyznacza się metodą planu korzystając z wyników
uzyskanych przy wyznaczeniu prędkości metodą planu.
Przy wyznaczaniu przyspieszeń członów mechanizmów w ruchu złożonym
wykorzystujemy równanie wektorowe przyspieszeń do wykreślenia jego składowych.
Dla mechanizmu korbowo-wodzikowego równanie przyspieszeń ma postać:
At
B
An
B
At
An
B
a
a
a
a
a
−
−
+
+
+
=
r
r
r
r
r
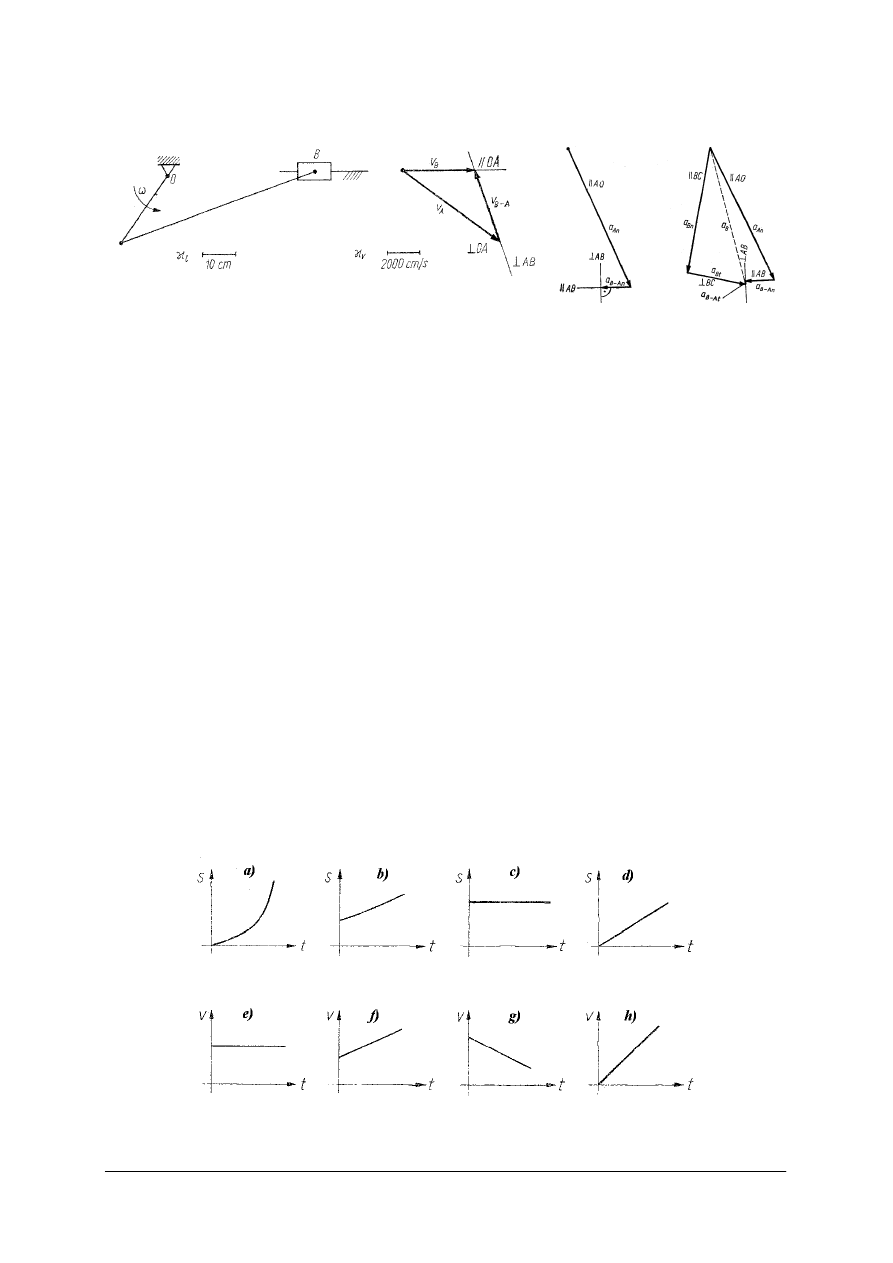
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
33
a)
b)
Rys. 32. Mechanizmu korbowo-wodzikowego: a) wyznaczanie prędkości metodą planu
b) wyznaczanie przyspieszeń metodą planu [1, s. 285]
4.3.2. Pytania sprawdzające
Odpowiadając na pytania, sprawdzisz, czy jesteś przygotowany do wykonania ćwiczeń.
1.
Co to jest tor punktu?
2.
Jakie wielkości charakteryzują ruch punktu?
3.
Co przedstawia pole pod wykresem prędkości?
4.
Od czego zależy droga w ruchu jednostajnie przyspieszonym?
5.
Co jest wykresem drogi w ruchu jednostajnie przyspieszonym?
6.
W jaki sposób na wykresie drogi określimy prędkość w dowolnym punkcie?
7.
Jakie znasz przyspieszenia w ruchu punktu?
8.
W jakim ruchu występuje przyspieszenie normalne?
9.
Jak dzielimy ruchy ze względu na wartości przyspieszeń: normalnego i stycznego?
10.
Jakie wielkości charakteryzują ruch jednostajny punktu po okręgu?
11.
Co to jest środek chwilowego obrotu i jak go wyznaczamy?
12.
Jakie znasz metody wyznaczania prędkości w ruchu płaskim?
13.
Jak wyznaczamy przyspieszenie w ruchu płaskim?
4.3.3. Ćwiczenia
Ćwiczenie 1
Napisz równania drogi i prędkości dla przedstawionych wykresów.
Rysunek do ćwiczenia 1
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
34
Sposób wykonania ćwiczenia
Aby wykonać ćwiczenie, powinieneś:
1)
przygotować stanowisko do wykonywania ćwiczenia,
2)
zapoznać się wykresami drogi i prędkości,
3)
przyporządkować wykresom wzory na drogę i prędkość,
4)
określić rodzaj ruchu ze względu na tor,
5)
określić rodzaje przyspieszeń w tych ruchach,
6)
zaprezentować wykonane ćwiczenie.
Wyposażenie stanowiska pracy:
−
przybory kreślarskie,
−
poradnik dla ucznia.
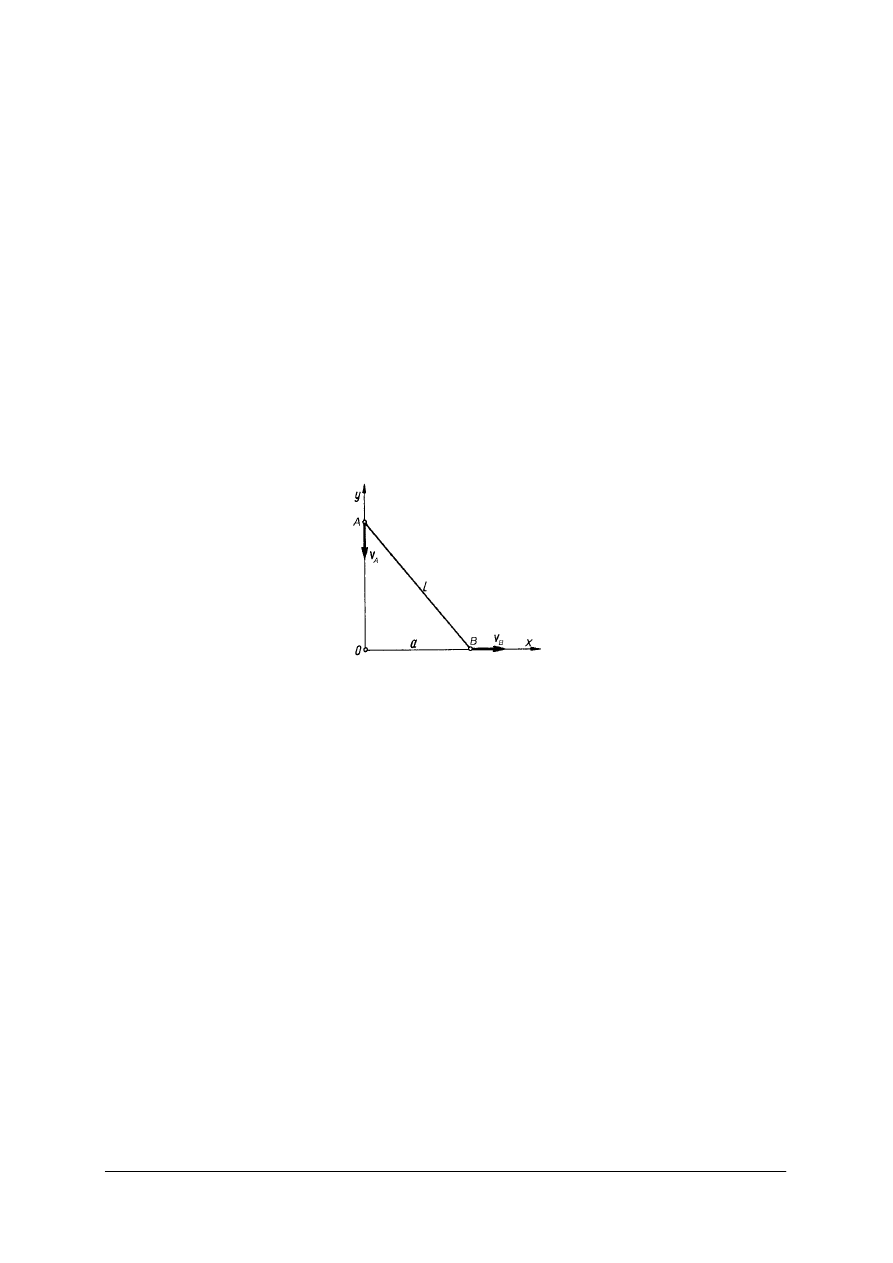
Ćwiczenie 2
Wyznacz prędkość chwilową w punkcie B dla pręta o długości l , który przesuwa się
końcami wzdłuż osi, jeżeli znana jest prędkość punktu A.
Rysunek do ćwiczenia 3
Sposób wykonania ćwiczenia
Aby wykonać ćwiczenie, powinieneś:
1)
przygotować stanowisko do wykonywania ćwiczenia,
2)
określić rodzaj ruchu, jaki wykonuje punkt,
3)
wyznaczyć środek chwilowego obrotu,
4)
obliczyć prędkość kątową dla punktu A względem środka chwilowego obrotu,
5)
obliczyć prędkość punktu B.
Wyposażenie stanowiska pracy:
−−−−
przybory kreślarskie,
−−−−
poradnik dla ucznia.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
35
4.3.4. Sprawdzian postępów
Czy potrafisz:
Tak
Nie
1)
dokonać podziału ruchów punktu ze względu na tor i prędkość?
2)
napisać równanie drogi w ruchu prostoliniowym zmiennym?
3)
określić cechy wektora przyspieszenia normalnego?
4)
napisać
równanie
ruchu
prostoliniowego
jednostajnie
przyspieszonego?
5)
narysować i wyznaczyć prędkość w ruchu jednostajnym po okręgu?
6)
scharakteryzować przyspieszenie w ruchu jednostajnym po okręgu?
7)
dokonać klasyfikacji ruchów ze względu na przyspieszenie?
8)
scharakteryzować parametry w ruchu zmiennym po okręgu?
9)
wyznaczyć prędkość w ruchu płaskim?
10)
wyznaczyć przyspieszenie w ruchu płaskim?
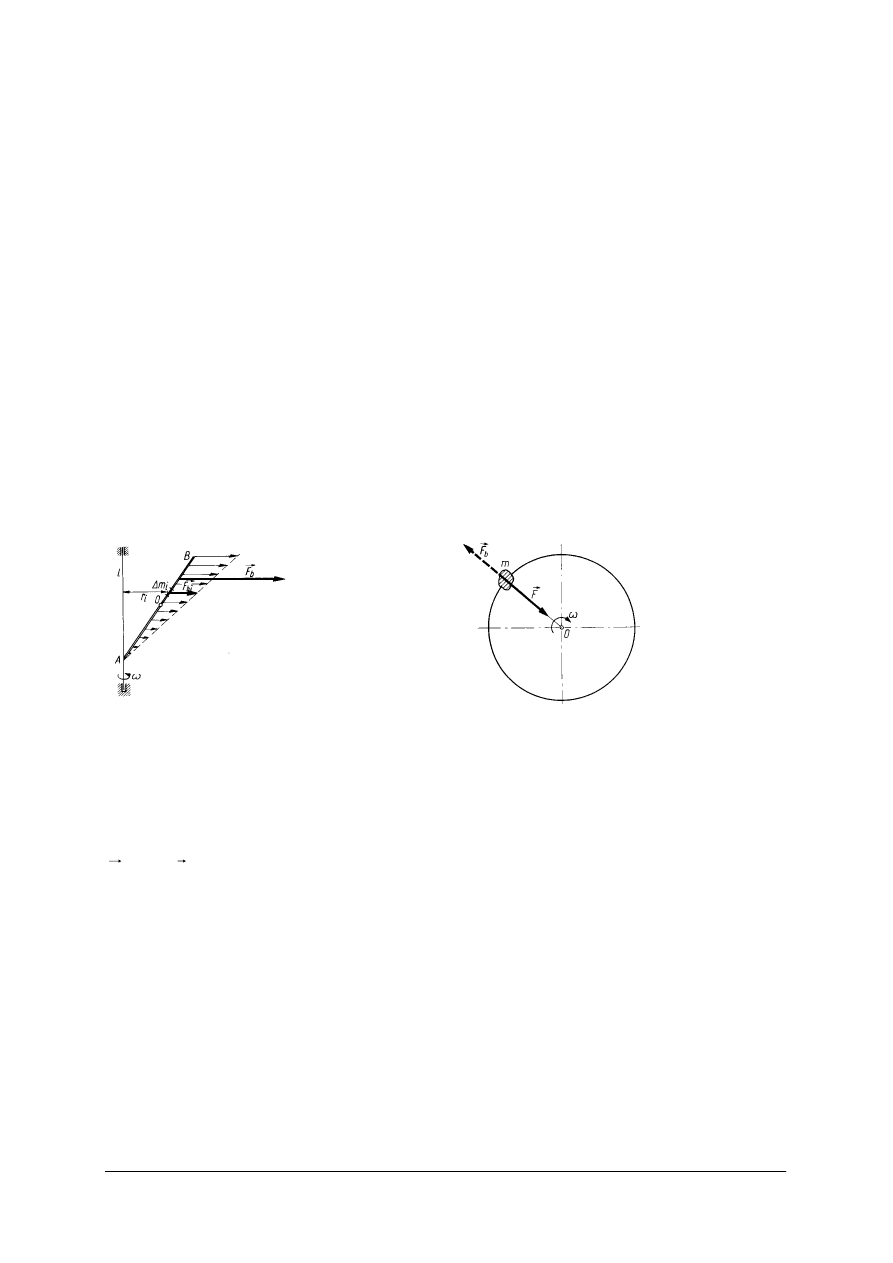
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
36
4.4. Dynamika punktu i ciała sztywnego
4.4.1. Materiał nauczania
Dynamika jest działem mechaniki, która bada związki między ruchem ciała
i przyczynami, który ten ruch wywołują. Zasady dynamiki oparte są na trzech prawach
Newtona.
Pierwsze prawo ( prawo bezwładności): Punkt materialny lub ciało sztywne, na który nie
działa żadna siła, lub działają siły równoważące się, pozostaje w spoczynku lub w ruchu
jednostajnym prostoliniowym.
Drugie prawo: Przyspieszenie punktu materialnego lub ciała sztywnego jest
proporcjonalne do wartości siły działającej na ten punkt i ma kierunek oraz zwrot zgodnie
z działającą siłą
F
=
a
m
⋅
(dynamiczne równanie ruchu punktu)
Trzecie prawo: Każdemu działaniu towarzyszy równe, lecz przeciwnie zwrócone
przeciwdziałanie.
Z drugim prawem związana jest siła bezładności, która jest zwrócona przeciwnie niż
przyspieszenie ruchu.
a)
b)
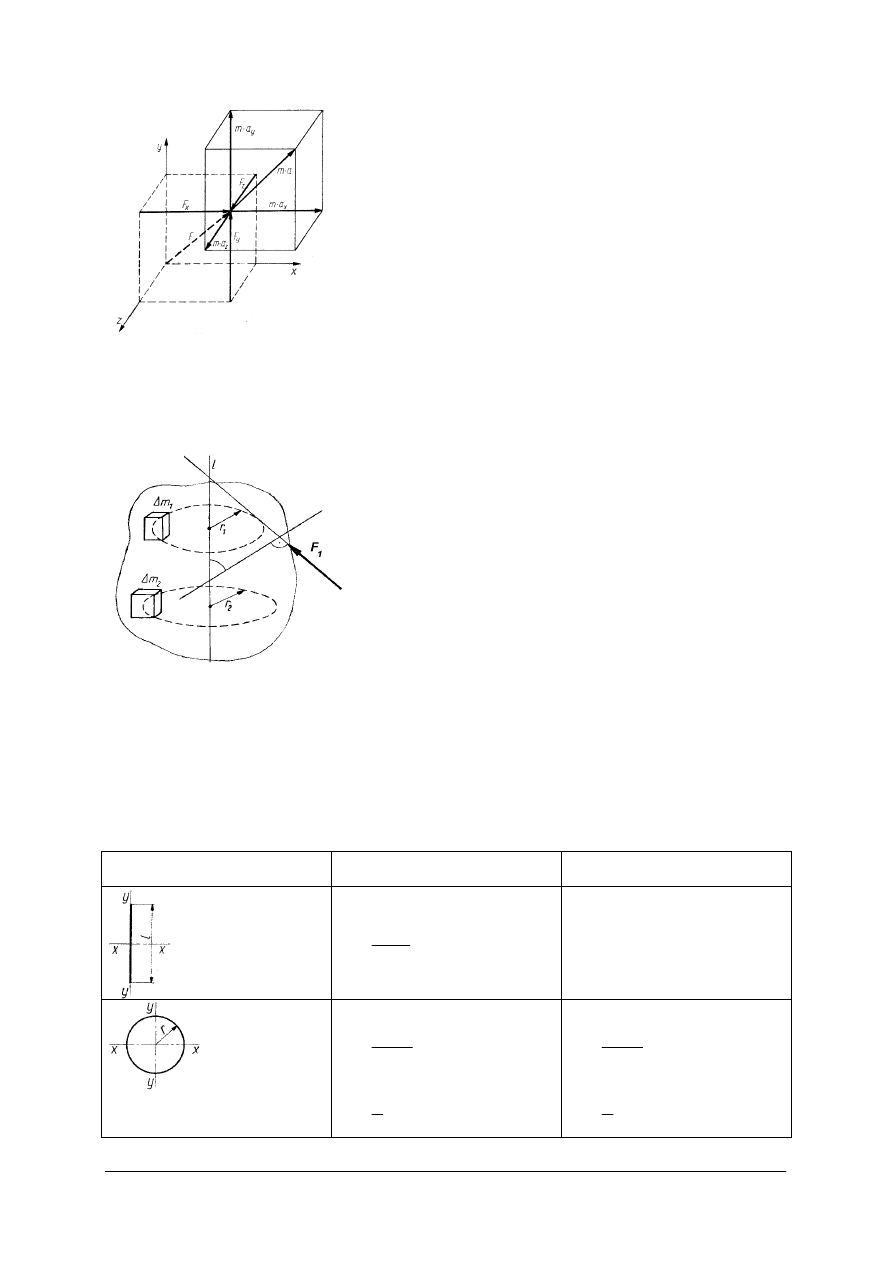
Rys. 33. Siły bezwładności w ruchu obrotowym: a) pręta, b) punktu [5, s.377]
Siła bezwładności jest równa iloczynowi masy poruszającego się ciała i przyspieszenia
tego ruchu.
Suma wszystkich sił zewnętrznych działających na punkt materialny znajdujący się
w ruchu równoważy się w każdej chwili z siłą bezwładności tego punktu.
F
+
( )
a
m
⋅
−
=0 zasada D
′
Alemberta
W ruchu postępowym badanie ruchu sprowadza się do badania jednego punktu, przy
czym najczęściej punkt ten jest środkiem masy ciała. Siła F działająca na środek masy ciała
w przestrzennym prostokątnym układzie osi współrzędnych ,
x y
, z rozłożona może być na
trzy składowe, które wywołują ruch wzdłuż tych osi.
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
37
Dynamiczne równania ruchu postępowego
x
x
a
m
F
⋅
=
y
y
a
m
F
⋅
=
z
z
a
m
F
⋅
=
Rys. 34. Ruch postępowy i równanie dynamiczne ruchu [1, s. 302]
W ruchu obrotowym ciała sztywnego dookoła nieruchomej osi wyznaczamy dynamiczne
równanie ruchu dla każdej elementarnej masy z uwzględnieniem elementarnego momentu
obrotowego.
Dynamiczne
równania
ruchu
obrotowego
dla
elementarnej masy
i
i
i
a
m
F
⋅
∆
=
Elementarny moment obrotowy
⋅
∆
=
⋅
i
i
i
m
r
F
2
i
r
ε
⋅
Dynamiczne
równanie
ruchu
obrotowego
ciała
sztywnego
ε
⋅
=
J
M
M
−
moment bezwładności ciała
J
−
masowy moment bezwładności ciała
ε
−
przyspieszenie kątowe
Rys. 35. Ruch obrotowy i równanie dynamiczne ruchu obrotowego [1, s. 303]
Masowe momenty bezwładności pól o prostych figurach i brył geometrycznych
wyznacza się najczęściej względem osi przechodzącej przez środek masy (osie główne lub
ś
rodkowe) korzystając ze wzorów z tabel.
Tabela 3. Masowe momenty bezwładności prostych figur i brył geometrycznych
Rysunek figury
(bryły)
x
J
y
J
x
J
=
12
2
l
m
⋅
y
J
=0
koło
x
J
=
4
2
r
m
⋅
kula
x
J
=
2
5
2
r
m
⋅
⋅
y
J =
4
2
r
m
⋅
y
J =
2
5
2
r
m
⋅
⋅
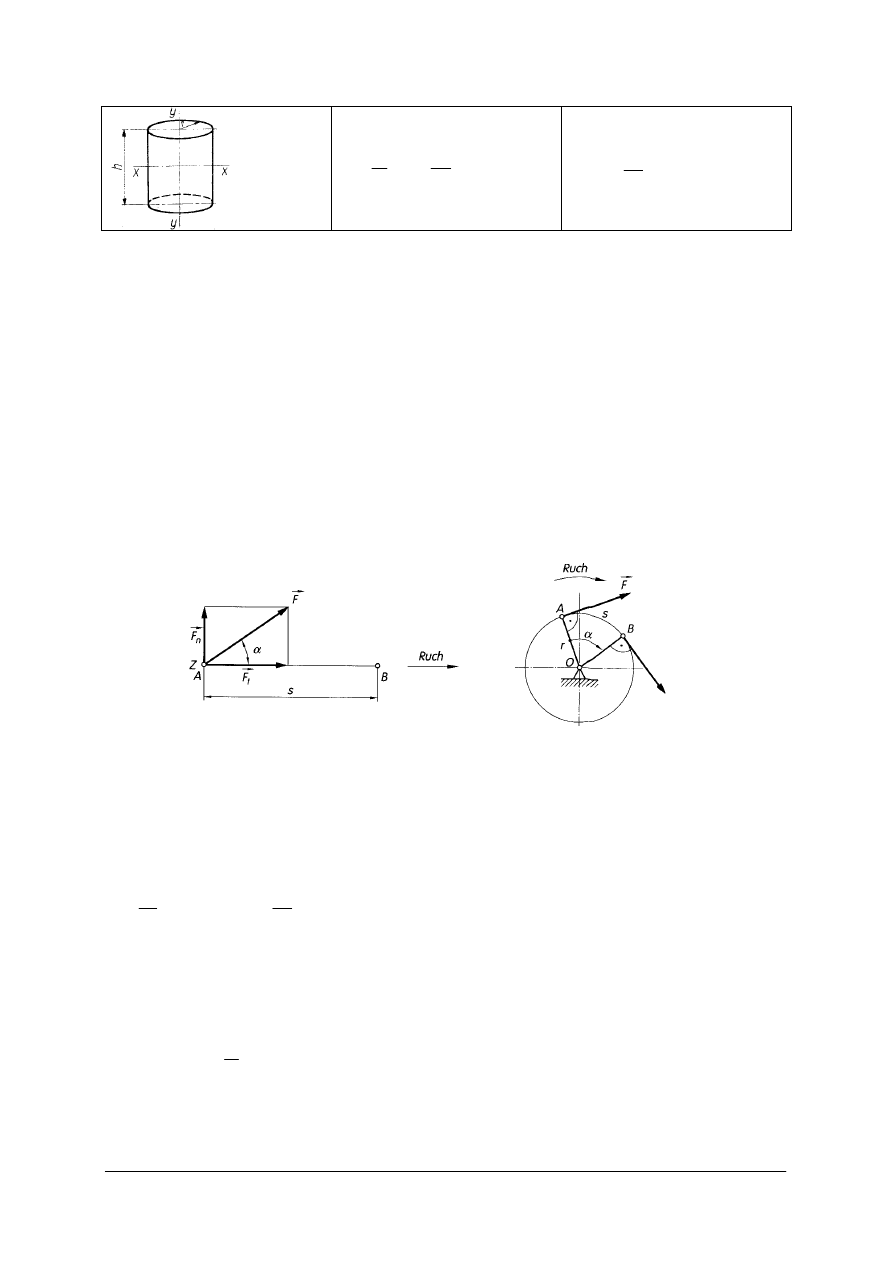
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
38
x
J =
+
3
4
2
2
h
r
m
y
J
=
2
2
r
m
⋅
Gdy oś obrotu jest przesunięta równolegle do osi głównej masowy moment bezwładności
oblicza się korzystając z twierdzenia Steinera.
2
z
m
J
J
o
l
⋅
+
=
Moment bezwładności ciała sztywnego względem dowolnej osi jest równy sumie
momentu bezwładności
o
J
względem osi równoległej do prostej l i przechodzącej przez
ś
rodek masy oraz iloczynu masy i ciała i kwadratu odległości między nimi.
Z ruchomym punktem, który pod działaniem siły może się przesuwać wzdłuż określonego
toru, związana jest praca.
Praca mechaniczna w ruchu prostoliniowym jest równa iloczynowi siły działającej
wzdłuż kierunku ruchu i drogi, jaką przebył punkt zaczepienia tej siły.
Praca w ruchu obrotowym wyraża się iloczynem momentu obrotowego M oraz kąta obrotu
α
wyrażonego w radianach.
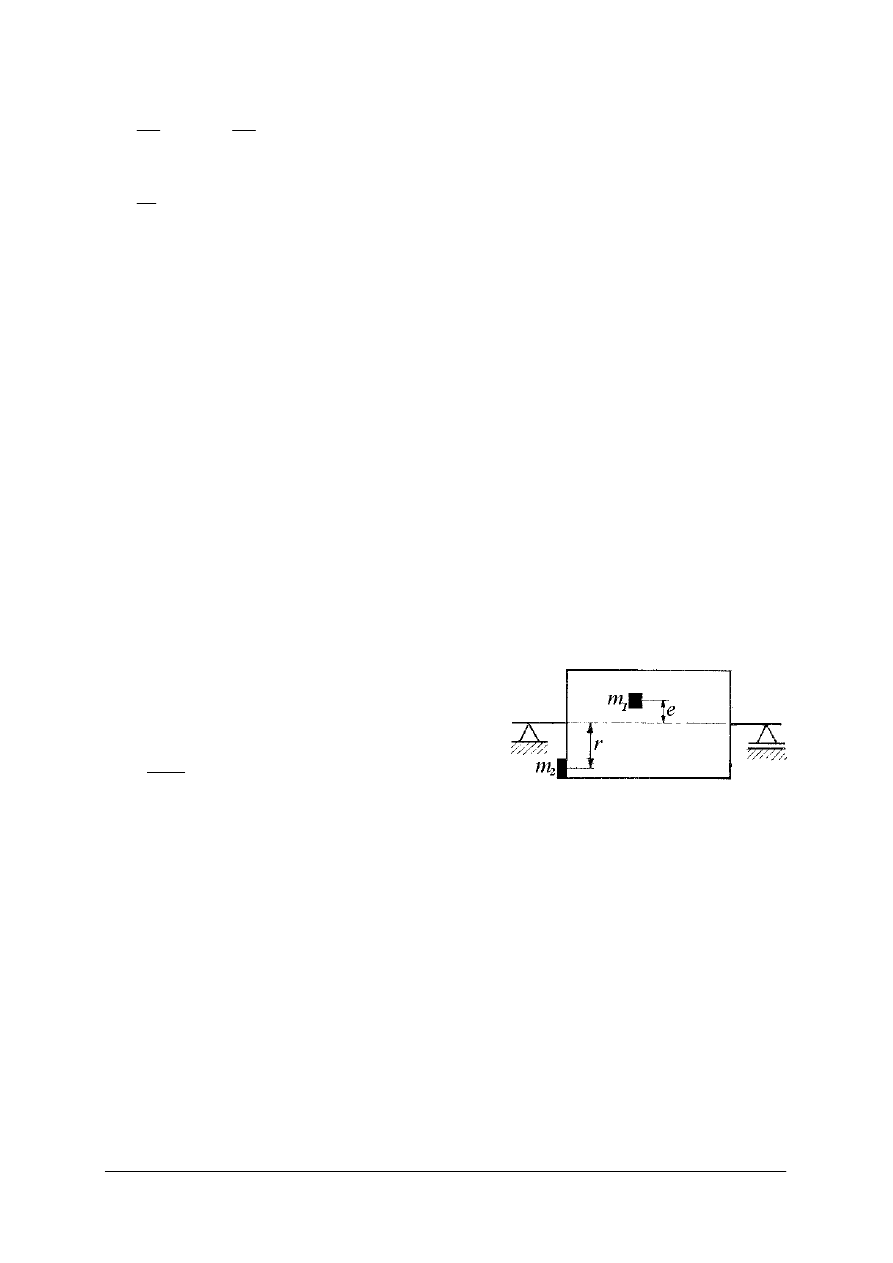
a)
b)
s
F
W
⋅
=
α
cos
⋅
[1J = N
⋅
1m]
α
⋅
=
M
W
Rys. 36. Praca w ruchu: a) prostoliniowym, b) obrotowym [2, s. 264]
Jednostką pracy w układzie jednostek SI jest dżul (J). Jest to praca wykonana siłą jednego
niutona na drodze jednego metra.
Moc jest pojęciem służącym do oceny pracy.
Moc P jest to iloraz pracy i czasu, w którym ta praca została wykonana.
t
W
P
=
[W],
1W=
s
J
1
v
F
P
⋅
=
w ruchu prostoliniowym
α
⋅
=
M
P
w ruchu obrotowym.
Jednostką mocy w układzie jednostek SI jest wat (W), czyli praca jednego dżula wykonana
w czasie jednej sekundy.
W urządzeniach mechanicznych moment obrotowy (skręcający) oblicza się ze wzoru:
=
M
95514, 14
n
P
⋅
[N
⋅
m]
P
−
moc w kW
n
−
prędkość obrotowa w obr/min.
Sprawnością maszyny
η
nazywamy stosunek pracy użytecznej
u
W do pracy włożonej W .
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
39
W
W
u
=
η
lub
W
W
u
=
η
⋅
100%
Sprawność można również określić stosunkiem mocy użytecznej
u
P do mocy włożonej P .
p
P
u
=
η
Jeżeli maszyna składa się z kilku mechanizmów, to sprawność ogólna jest iloczynem
sprawności poszczególnych mechanizmów.
n
η
η
η
η
η
⋅
⋅
⋅
⋅
=
K
3
2
1
Sprawność jest liczbą niemianowaną zawartą w przedziale
1
0
<
<
η
.
Wyrównoważanie
W obracających się elementach maszyn środek masy powinien leżeć na osi obrotu.
W przypadku, gdy jest on przesunięty, wówczas w czasie obrotu na elementy maszyn działa
siła odśrodkowa. Siła ta powoduje zmienne reakcje (dynamiczne) w podporach (łożyskach),
a to z kolei wywołuje drgania korpusów maszyn, niszczenie łożysk. Reakcje dynamiczne
wywołane siłą odśrodkową znacznie przekraczają reakcje statyczne. W celu usunięcia reakcji
dynamicznych, zmniejszenia ich, każdy element wirujący powinien być wyrównoważony
(wyważony).
Rozróżniamy wyrównoważanie:
–
statyczne,
–
dynamiczne,
–
statyczno–dynamiczne.
Wyrównoważanie statyczne polega na dodaniu do wirującego elementu dodatkowej masy
do „lekkiej” strony krążka, doprowadzając do tego, aby środek masy całego elementu leżał na
osi obrotu. Masę korekcyjną obliczamy porównując siły odśrodkowe.
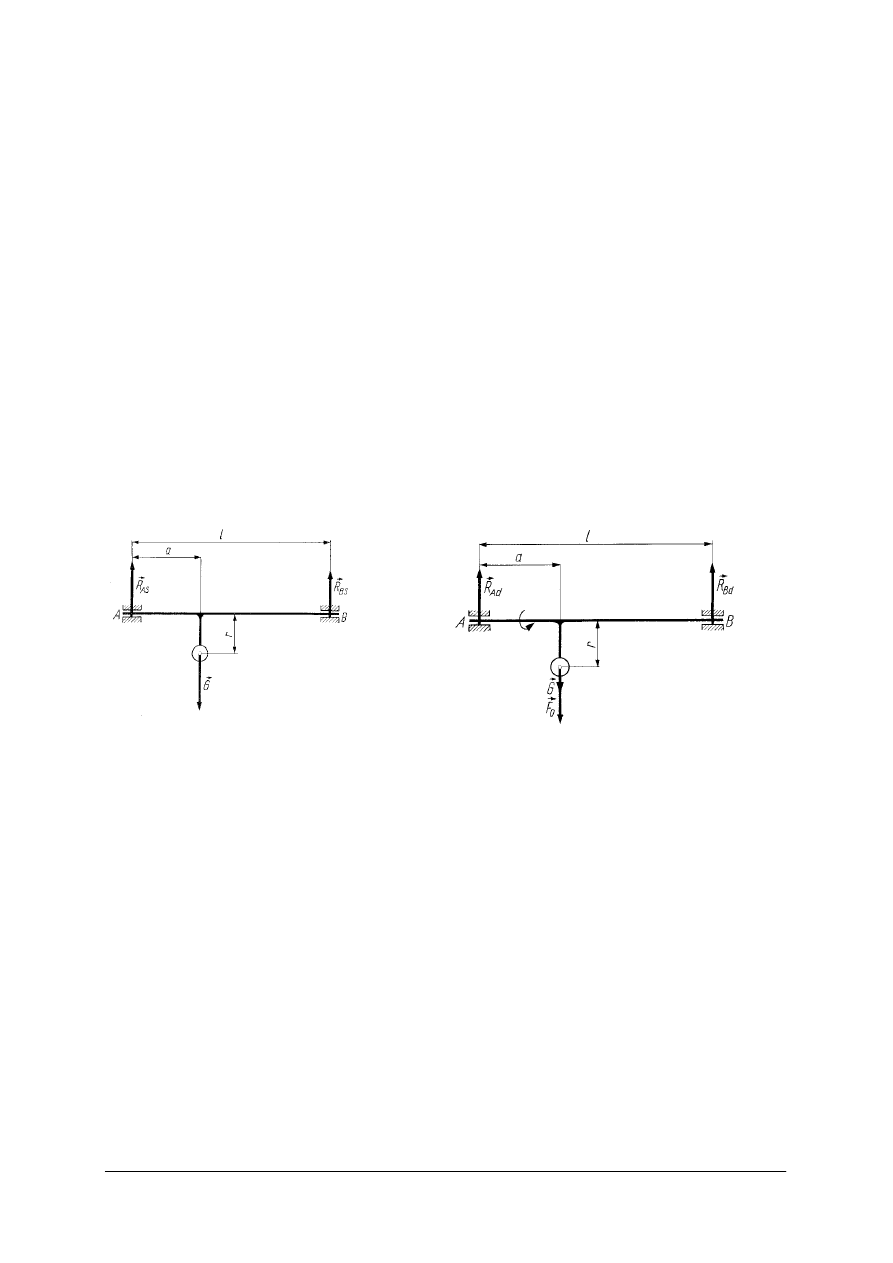
Rys. 37. Wirujący element maszyny [1, s. 317]
Siła odśrodkowa wirującego walca o masie m
1
2
1
ω
⋅
⋅
=
e
m
F
Siła odśrodkowa dla masy korekcyjnej m
2
⋅
=
2
m
F
2
ω
⋅
r
r
e
m
m
⋅
=
1
2
gdzie:
1
m
– masa wirującego elementu,
2
m
– masa, którą należy dodać,
e
– przesunięcie środka masy od osi obrotu,
r
– odległość masy dodatkowej od osi obrotu,
ω
– prędkość kątowa
Wyrównoważanie statyczne daje dobre wyniki dla krążków o małej grubości, które leżą
w płaszczyźnie prostopadłej do osi obrotu.
Wyrównoważanie dynamiczne stosuje się do elementów maszyn, których środki masy
leżą na osi obrotu, ale nie pokrywają się z główną środkową osią bezwładności. W czasie
ruchu siły bezwładności tworzą parę sił, która wywołuje reakcje dynamiczne.
Wyrównoważenie dynamiczne polega na dołożeniu dwóch mas korekcyjnych leżących po
przeciwnych stronach osi obrotu i dobranych tak, aby siły działające na te masy tworzyły parę
sił o momencie równym momentowi reakcji dynamicznych.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
40
4.4.2. Pytania sprawdzające
Odpowiadając na pytania, sprawdzisz, czy jesteś przygotowany do wykonania ćwiczeń.
1.
Które prawo dynamiki nazywane jest prawem bezwładności?
2.
Od czego zależy siła bezwładności?
3.
Od czego zależy wartość masowych momentów bezwładności dla pól i brył?
4.
Co nazywamy pracą mechaniczną?
5.
Od czego zależy moc?
6.
Jaka jest zależność między mocą, prędkością obrotową i momentem obrotowym?
7.
Od czego zależy sprawność maszyny składającej się z kilku mechanizmów?
8.
Jakie wielkości może przyjmować sprawność?
9.
Kiedy powstają reakcje dynamiczne?
10.
Na czym polega wyrównoważanie statyczne i dynamiczne?
4.4.3. Ćwiczenia
Ćwiczenie 1
Oblicz masowy moment bezwładności dla koła zamachowego o masie 100 kg
i średnicy 1 m.
Sposób wykonania ćwiczenia
Aby wykonać ćwiczenie, powinieneś:
1)
zorganizować stanowisko do wykonania ćwiczenia,
2)
określić wzór na moment dla odpowiedniego rodzaju bryły,
3)
określić oś obrotu,
4)
na podstawie danych obliczyć masowy moment obrotowy,
5)
zaprezentować wyniki ćwiczenia.
Wyposażenie stanowiska pracy:
−−−−
przybory kreślarskie,
−−−−
poradnik dla ucznia.
Ćwiczenie 2
Oblicz pracę potrzebną do podniesienia ciężaru G = 3000 N za pomocą wciągarki
suwnicy na wysokość 5 m.
Sposób wykonania ćwiczenia
Aby wykonać ćwiczenie, powinieneś:
1)
zapisać dane do obliczenia z ćwiczenia,
2)
obliczyć pracę,
3)
zaprezentować wyniki ćwiczenia.
Wyposażenie stanowiska pracy:
−−−−
przybory kreślarskie,
−−−−
poradnik dla ucznia.
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
41
Ćwiczenie 3
Określ minimalną moc silnika windy towarowej o maksymalnym udźwigu 1000 kg, która
porusza się z prędkością 2 m/s. Sprawność urządzenia wynosi 75%.
Sposób wykonania ćwiczenia
Aby wykonać ćwiczenie, powinieneś:
1)
zorganizować stanowisko do wykonania ćwiczenia,
2)
obliczyć moc użyteczną windy,
3)
obliczyć całkowitą moc z uwzględnieniem sprawności urządzenia,
4)
zaprezentować wyniki ćwiczenia.
Wyposażenie stanowiska pracy:
−−−−
przybory kreślarskie,
−−−−
poradnik dla ucznia.
Ćwiczenie 4
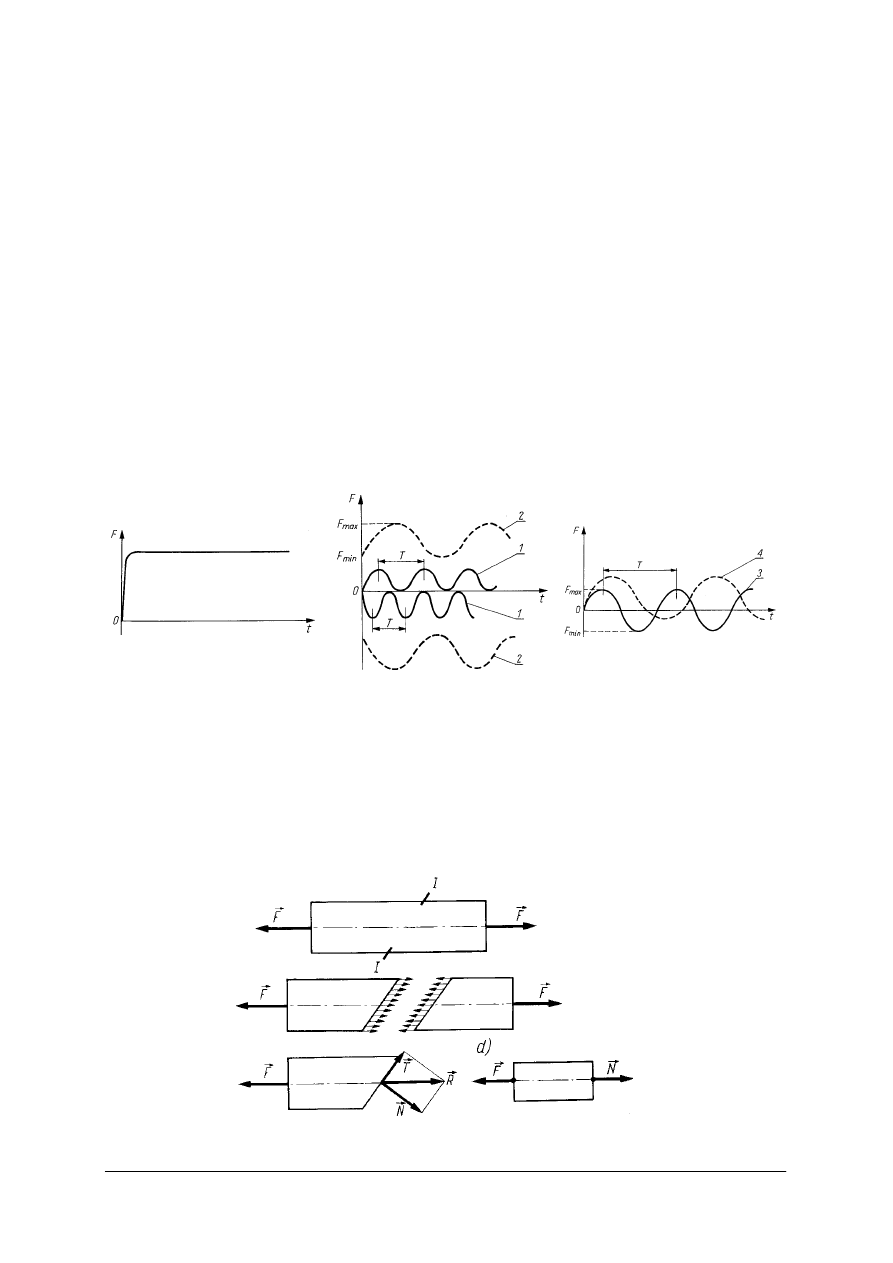
Oblicz reakcje dynamiczne dla wału do którego przyspawano pręt o długości r z ciężarem
G. Wał obraca się z prędkością kątową ω.
Rysunki do ćwiczenia 4
Sposób wykonania ćwiczenia
Aby wykonać ćwiczenie, powinieneś:
1)
zorganizować stanowisko do wykonania ćwiczenia,
2)
obliczyć reakcje statyczne uwzględniając ciężar,
3)
obliczyć siłę odśrodkową wirującego ciężaru,
4)
obliczyć reakcje dynamiczne z uwzględnieniem siły odśrodkowej,
5)
określić sumę reakcji statycznej i dynamicznej w podporach w skrajnych położeniach
ciężarka,
6)
zaprezentować wyniki ćwiczenia.
Wyposażenie stanowiska pracy:
−−−−
przybory kreślarskie,
−−−−
poradnik dla ucznia.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
42
4.4.4. Sprawdzian postępów
Czy potrafisz:
Tak
Nie
1)
scharakteryzować siłę bezwładności?
2)
napisać zasadę D
′
Alemberta?
3)
wyjaśnić dynamiczne równanie ruchu postępowego?
4)
wyjaśnić dynamiczne równanie ruchu obrotowego?
5)
wyjaśnić zastosowanie twierdzenia Steinera?
6)
zinterpretować jednostki pracy i mocy?
7)
obliczyć pracę urządzenia?
8)
określić minimalną moc urządzenia?
9)
obliczyć sprawność urządzenia?
10)
obliczyć reakcje dynamiczne w łożyskach?
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
43
4.5. Wytrzymałość materiałów
4.5.1. Materiał nauczania
Elementy konstrukcyjne oraz części maszyn podczas pracy są obciążone siłami
zewnętrznymi, które powodują odkształcenia. Graniczną wartość obciążenia, przy którym
element konstrukcyjny ulega zniszczeniu nazywamy wytrzymałością. Przy projektowaniu
elementów konstrukcyjnych należy określić ich wymiary, postać i materiał, z którego będą
wykonane. W zależności od sposobu działania obciążenia na elementy konstrukcyjne
wyróżniamy następujące rodzaje odkształceń: rozciąganie, ściskanie, ścinanie, skręcanie
i zginanie, które nazywamy odkształceniami prostymi. Elementy maszyn przenoszące
jednocześnie co najmniej dwa obciążenia proste podlegają obciążeniom złożonym (zginanie
ze skręcaniem, ściskanie ze zginaniem).
Ze względu na charakter obciążeń mechanicznych, obciążenia dzielimy na:
−
stałe(statyczne, niezmienne, trwałe),
−
zmienne.
a)
b)
c)
Rys. 38. Rodzaje cykli obciążeń i naprężeń: a) stały, b) jednostronnie zmienny (1 – tętniący odzerowo,
2 – tętniący jednostronny), c) obustronnie zmienny (3 – wahadłowy symetryczny,
4 – dwustronny niesymetryczny), T okres ( cykl zmiany obciążeń i naprężeń) [3, s. 15]
Siły zewnętrzne powodują pojawienie się sił wewnętrznych zwanych naprężeniami lub
napięciami.
Wypadkową sił wewnętrznych R równą co do wartości sile zewnętrznej F można
rozłożyć na dwa kierunki: siłę prostopadłą do przekroju N i styczną do przekroju T.
Rys. 39. Siły: normalna i styczna w dowolnym przekroju pręta rozciąganego [3, s.156]
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
44
Stosunek wartości siły normalnej N do pola przekroju S nazywamy naprężeniem normalnym.
σ
=
S
N
[Pa]
1 Pa =1
2
m
N
Stosunek wartości siły stycznej T do pola przekroju S nazywamy naprężeniem stycznym.
τ
=
S
T
[Pa]
Naprężenia dopuszczalne
W elementach konstrukcyjnych obciążonych siłami powstają naprężenia normalne
i styczne. Podczas obliczeń wytrzymałościowych należy uwzględnić dwa warunki:
−−−−
wytrzymałości, element konstrukcyjny nie może ulec zniszczeniu,
−−−−
sztywności, odkształcenia muszą być małe i sprężyste.
Naprężenia, które mogą wystąpić w materiale bez naruszenia powyższych warunków,
nazywamy dopuszczalnymi. Indeks charakteryzuje rodzaj odkształcenia:
−−−−
k
r
(k
rj
, k
rc
)
−
naprężenia dopuszczalne na rozciąganie,
−−−−
k
c
(k
cj
, k
rc
)
−
naprężenia dopuszczalne na ściskanie,
−−−−
k
t
(k
tj
, k
to
)
−
naprężenia dopuszczalne na ścinanie,
−−−−
k
g
(k
gj
, k
go
)
−
naprężenia dopuszczalne na zginanie,
−−−−
k
s
(k
sj
, k
so
)
−
naprężenia dopuszczalne na skręcanie,
−−−−
k
o
(k
oj
, k
oo
)
−
naprężenia na nacisk powierzchniowy.
Naprężenia dopuszczalne wyznaczamy doświadczalnie dla różnych gatunków materiałów.
W przypadku rozciągania materiałów kruchych (beton, szkło) wynoszą:
k
r
=
n
R
m
[MPa],
dla materiałów plastycznych (stal)
k
r
=
n
R
e
[MPa]
gdzie:
m
R
−
granica wytrzymałości na rozciąganie w MPa
e
R
−
granica plastyczności w MPa,
n
−
obliczeniowy współczynnik bezpieczeństwa, (
n
= 1,3
÷
12)
Granice wytrzymałości i plastyczności wyznaczamy dla każdego materiału w próbach
wytrzymałościowych.
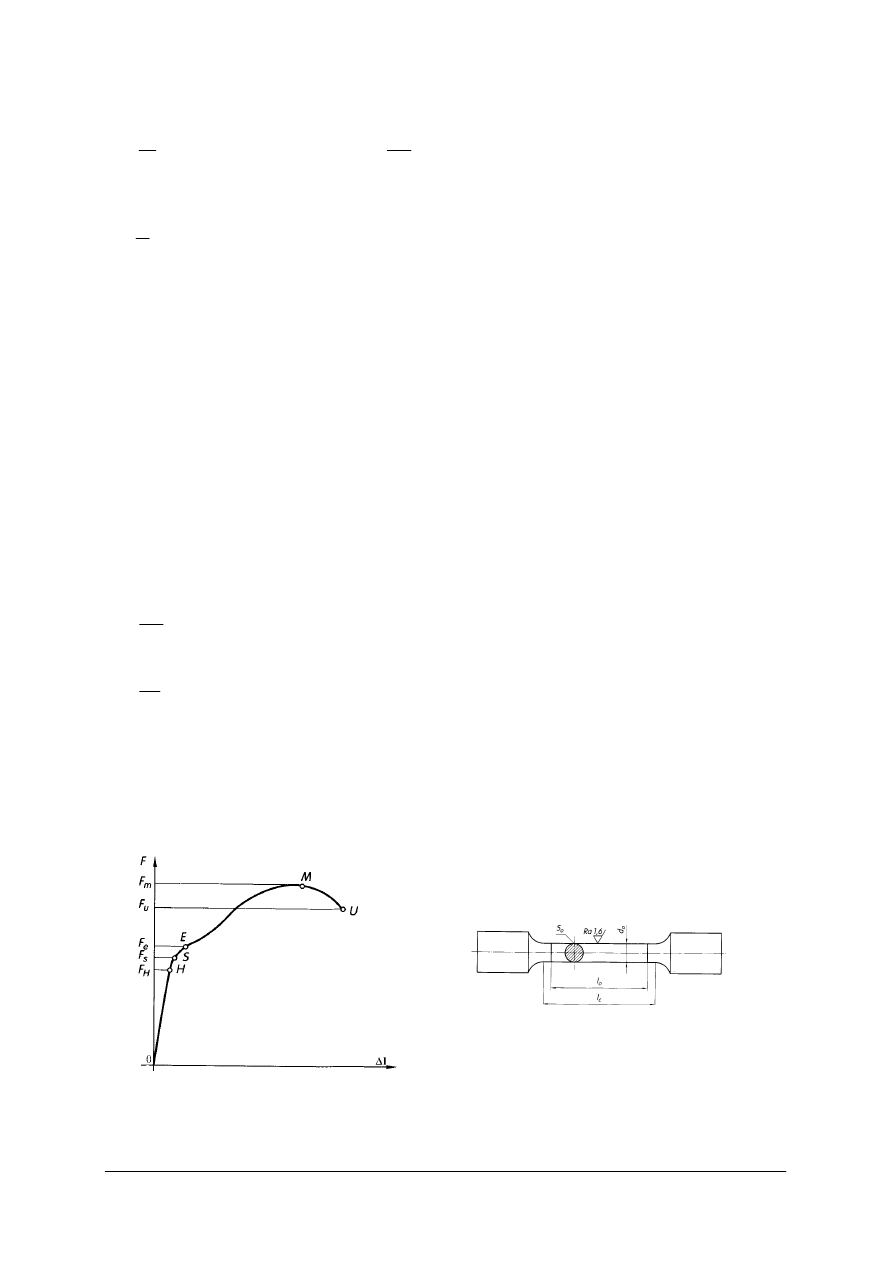
Rys.
40.
Wykres rozciągania stali i znormalizowany kształt próbki do próby rozciągania [2, s. 99]
W czasie próby rozciągania wyznacza się granicę plastyczności i wytrzymałości materiałów.
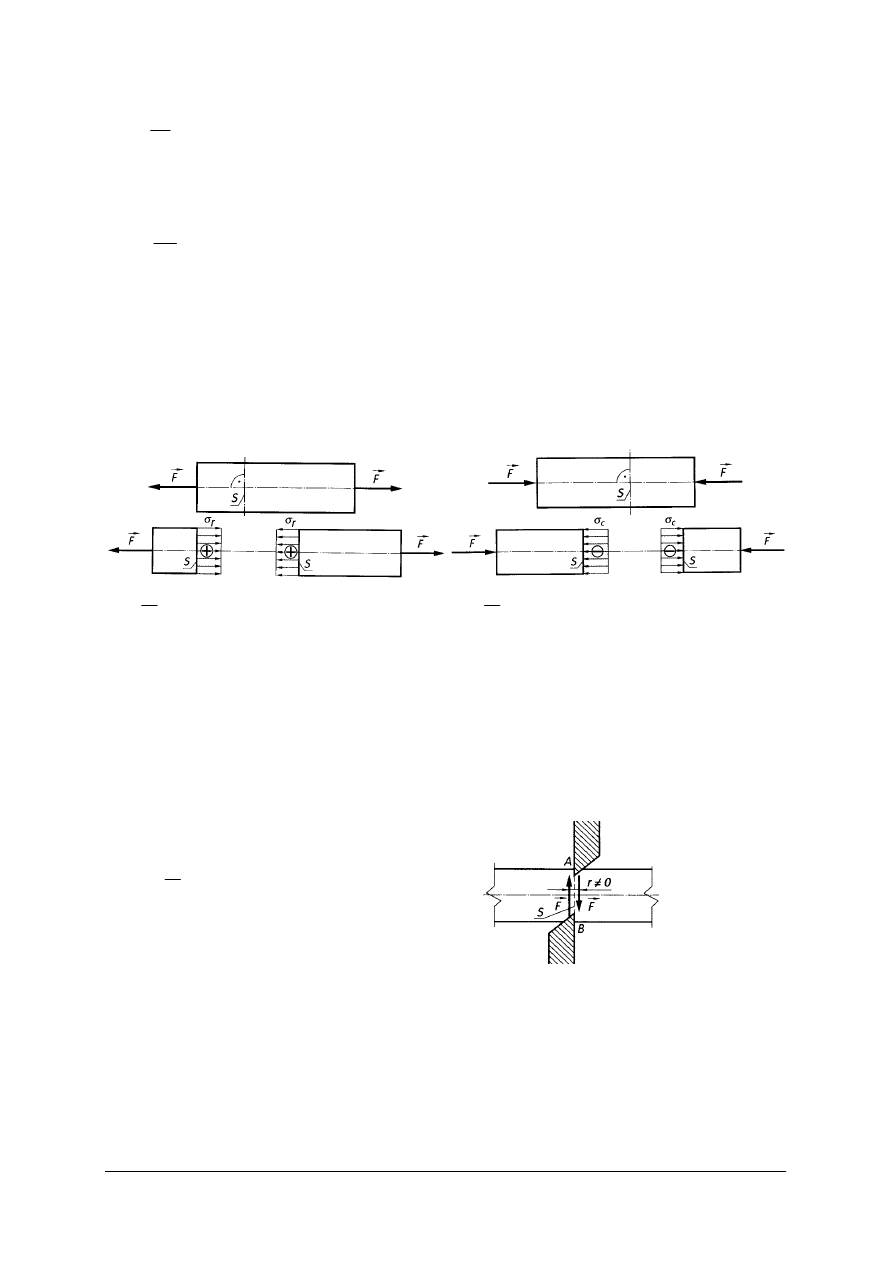
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
45
e
R =
0
S
F
e
[MPa]
Granica plastyczności to naprężenie, po osiągnięciu którego występuje wyrażny wzrost
wydłużenia rozciąganej próbki bez wzrostu lub nawet spadku obciążenia.
m
R
=
0
S
F
m
[MPa]
Wytrzymałość materiału na rozciąganie
m
R
jest to stosunek największej siły
m
F
przenoszonej
przez próbkę do pierwotnego pola
0
S
przekroju poprzecznego próbki.
Obliczanie elementów konstrukcyjnych
−−−−
na rozciąganie i ściskanie
Naprężenia normalne panujące w przekrojach rozciąganych i ściskanych mogą być co
najwyżej równe naprężeniom dopuszczalnym.
a)
b)
r
σ
=
r
k
S
F
≤
(
)
rj
rj
k
k ,
c
σ
=
c
k
S
F
≤
(
)
rc
cj
k
k ,
Rys. 41. Naprężenia normalne w prętach: a) rozciąganych, b) ściskanych [2, s. 95]
−−−−
na ścinanie
W praktyce mamy do czynienia ze ścinaniem technologicznym, w którym materiał jest
niszczony naciskami wywieranymi przez np. ostrza nożyc, czyli przez siły tworzące parę.
Rzeczywiste naprężenia styczne
τ
w przekroju ścinanym S nie mogą być większe od
naprężenia dopuszczalnego
t
k
.
τ
=
t
k
S
F
≤
(
)
to
tj
k
k
,
Rys. 42. Ścinanie technologiczne [5, s. 198]
−−−−
na zginanie
Zginaniu podlegają elementy zwane belkami lub osiami. Odkształcenie to powodują
obciążenia działające na belkę w postaci sił skupionych, obciążenia ciągłego lub momentów.
Obciążenia te wywołują w przekrojach belek momenty zginające i siły tnące.
Momentem zginającym w dowolnym przekroju belki nazywamy sumę algebraiczną
momentów wszystkich sił zewnętrznych działających na belkę po jednej stronie
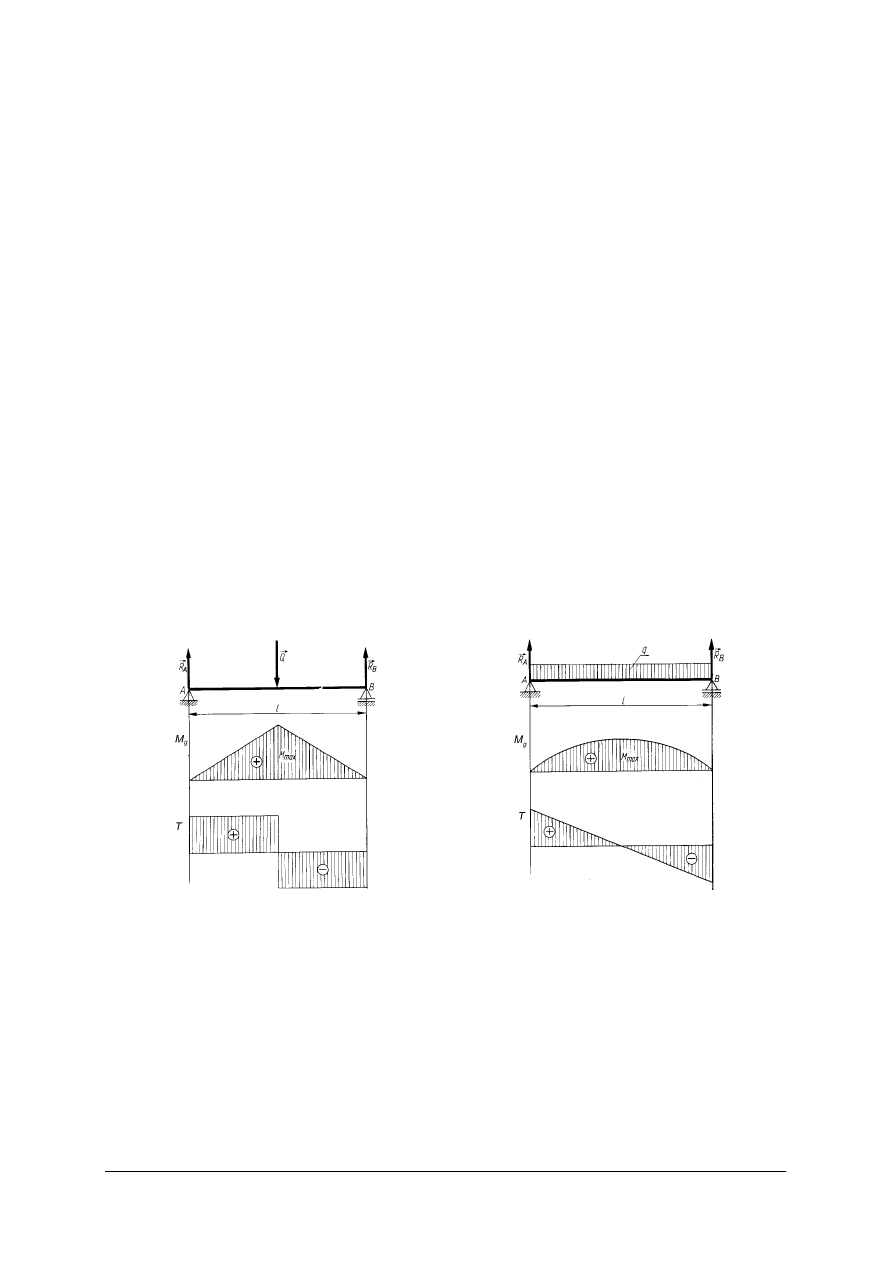
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
46
rozpatrywanego przekroju, obliczonych względem środka ciężkości tego przekroju. Moment
zginający od sił prostopadłych zwróconych do góry uważa się za dodatni, a od sił zwróconych
w dół
−
za ujemny. Z przekroje niebezpieczne uważamy miejsca, w których momenty
zginające osiągają wartości maksymalne.
Siła tnąca w dowolnym przekroju belki jest algebraiczną sumą wszystkich sił
zewnętrznych działających prostopadle do osi belki po jednej stronie belki.
Siła tnąca od sił zewnętrznych po lewej stronie przekroju jest dodatnia, gdy siły są zwrócone
do góry, a ujemna, gdy siły zwrócone są w dół. Natomiast od sił po prawej stronie przekroju
jest ujemna, gdy siły zewnętrzne są zwrócone do góry, a dodatnia, gdy zwrócone w dół.
Przebieg zmian obciążenia belki wzdłuż jej osi można zilustrować za pomocą wykresów
momentów zginających
gi
M
i sił tnących
i
T .
Analityczne wyznaczanie momentów zginających sił tnących belek obciążonych siłami
skupionymi sprowadza się do:
−−−−
analitycznego wyznaczania reakcji za pomocą równań równowagi,
−−−−
wyznaczenia momentów zginających w miejscach przyłożenia sił skupionych,
−−−−
sporządzenia wykresów momentów zginających w podziałce,
−−−−
obliczenia sił tnących w poszczególnych przedziałach belki,
−−−−
sporządzenia wykresu sił tnących w podziałce,
−−−−
lokalizacji przekroju niebezpiecznego ( T = 0 i
max
g
M
).
Moment zginający belkę obciążoną siłami skupionymi jest liniową funkcją odległości wzdłuż
osi belki, a wykres sił tnących składa się z odcinków równoległych do osi belki.
Dla obciążenia ciągłego wykresem momentów zginających jest część paraboli, a sił tnących
linia nachylona pod kątem do osi belki.
a)
b)
Rys. 43. Wykresy momentów zginających i sił tnących dla: a) siły skupionej, b) obciążenia ciągłego [5, s. 219]
Naprężenia normalne przy zginaniu zmieniają się proporcjonalnie do odległości warstwy
obojętnej.
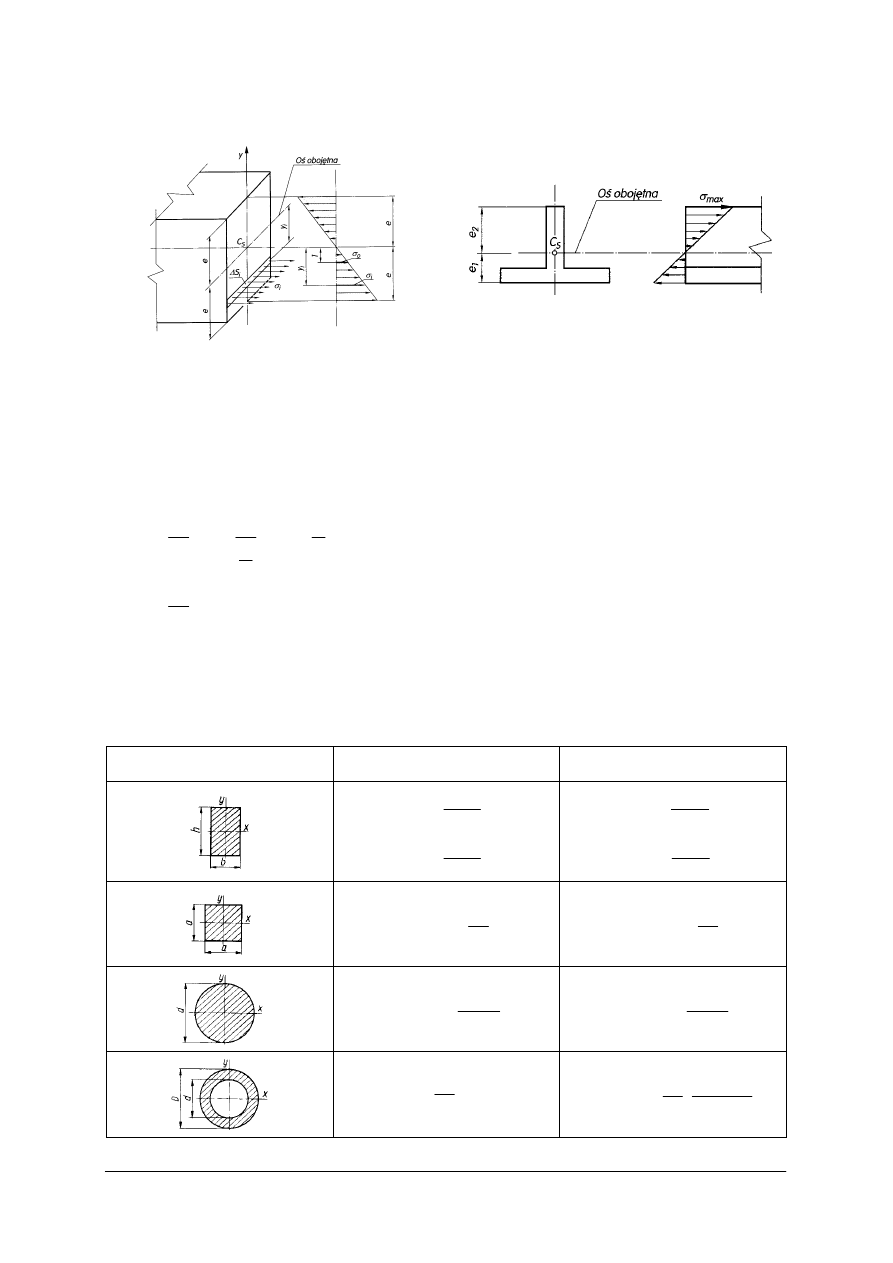
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
47
a)
b)
Rys. 44. Wykresy naprężeń dla przekrojów: a) prostokąta, b) teownika [2, s. 146]
M
−
moment zginający przekroju belki
J
−
moment bezwładności przekroju belki względem osi obojętnej
y
=
e
−
odległość od osi obojętnej dla warstw skrajnych
Znak plus odnosi się do warstw rozciąganych, minus do warstw ściskanych.
Największe naprężenia występują w warstwach skrajnych dla y =
max
y
=
e
max
σ
=
e
J
M
⋅
±
=
e
J
M
±
gdzie
e
J
=W
−
wskaźnik wytrzymałości przekroju na zginanie
max
σ
=
W
M
±
Największe naprężenia normalne występują w warstwach skrajnych belki i są równe
stosunkowi momentu zginającego w rozważanym przekroju belki do wskaźnika
wytrzymałości tego przekroju na zginanie.
Tabela 4. Osiowe momenty bezwładności i wskaźniki wytrzymałości przekroju na zginanie dla figur płaskich
[5, s. 240]
Przekrój
Moment bezwładności
Wskaźnik wytrzymałości
przekroju na zginanie
x
J
=
12
3
h
b
⋅
y
J
=
12
3
b
h
⋅
x
W
=
6
2
h
b
⋅
y
W
=
6
2
b
h
⋅
x
J
=
y
J
=
12
4
a
x
W
=
y
W
=
6
3
a
x
J
=
y
J
=
64
4
d
⋅
π
x
W
=
y
W
=
32
3
d
⋅
π
x
J
=
y
J
=
(
)
4
4
64
d
D
−
π
x
W
=
y
W
=
D
d
D
4
4
32
−
⋅
π

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
48
Dla elementów konstrukcyjnych o złożonych przekrojach momenty bezwładności oblicza
się korzystając z twierdzenia Steinera:
l
J =
x
J +
2
a
S
⋅
l
J
−
osiowy moment bezwładności względem osi l
x
J
−
osiowy moment bezwładności względem osi x,
przechodzącej przez środek ciężkości przekroju
S
−
pole figury
a
−
odległość między osiami
Rys. 44.Twierdzenie Steinera [5, s. 242]
Moment bezwładności figury płaskiej względem osi równoległej do osi środkowej jest
równy momentowi bezwładności tej figury względem osi środkowej, powiększonemu o
iloczyn pola figury i kwadratu odległości między osiami.
Obliczanie belek na zginanie
W belkach zginanych w przekrojach poprzecznych występują jednocześnie momenty
zginające i siły tnące, które wywołują w przekrojach naprężenia normalne od momentów
zginających i naprężenia styczne od sił stycznych. Wartość naprężeń normalnych zależy od
momentu zginającego, wymiarów, kształtu i usytuowania przekroju belki i nie może
przekraczać naprężenia dopuszczalnego dla zginania.
σ
=
g
k
W
M
≤
(
)
go
gj
k
k ,
Obliczanie elementów skręcanych
Skręcanie zachodzi wtedy, gdy element jest obciążony dwoma momentami równymi,
przeciwnie zwróconymi, działającymi w dwóch płaszczyznach prostopadłych do osi
elementu. Przykładami elementów skręcanych są wałki w skrzyniach biegów, wały odbioru
i przyjęcia mocy itd.
Moment skręcający
s
M w danym przekroju poprzecznym pręta jest sumą algebraiczną
momentów wszystkich par sił zewnętrznych działających po dowolnej stronie
rozpatrywanego przekroju i leżących w płaszczyźnie prostopadłej do osi pręta.
Wartość momentu w każdym przekroju przedstawia się za pomocą wykresu momentów
skręcających
s
M . Momenty skręcające przekazywane przez wał obliczamy ze wzoru:
s
M =9554,14
n
P
s
M
−
moment skręcający w Nm,
P
−
moc w kW,
n
−
prędkość obrotowa wału w obr/min.
Moment obrotowy powoduje w przekrojach poprzecznych powstanie naprężeń
stycznych, które są równe stosunkowi momentu skręcającego do wskaźnika przekroju na
skręcanie.
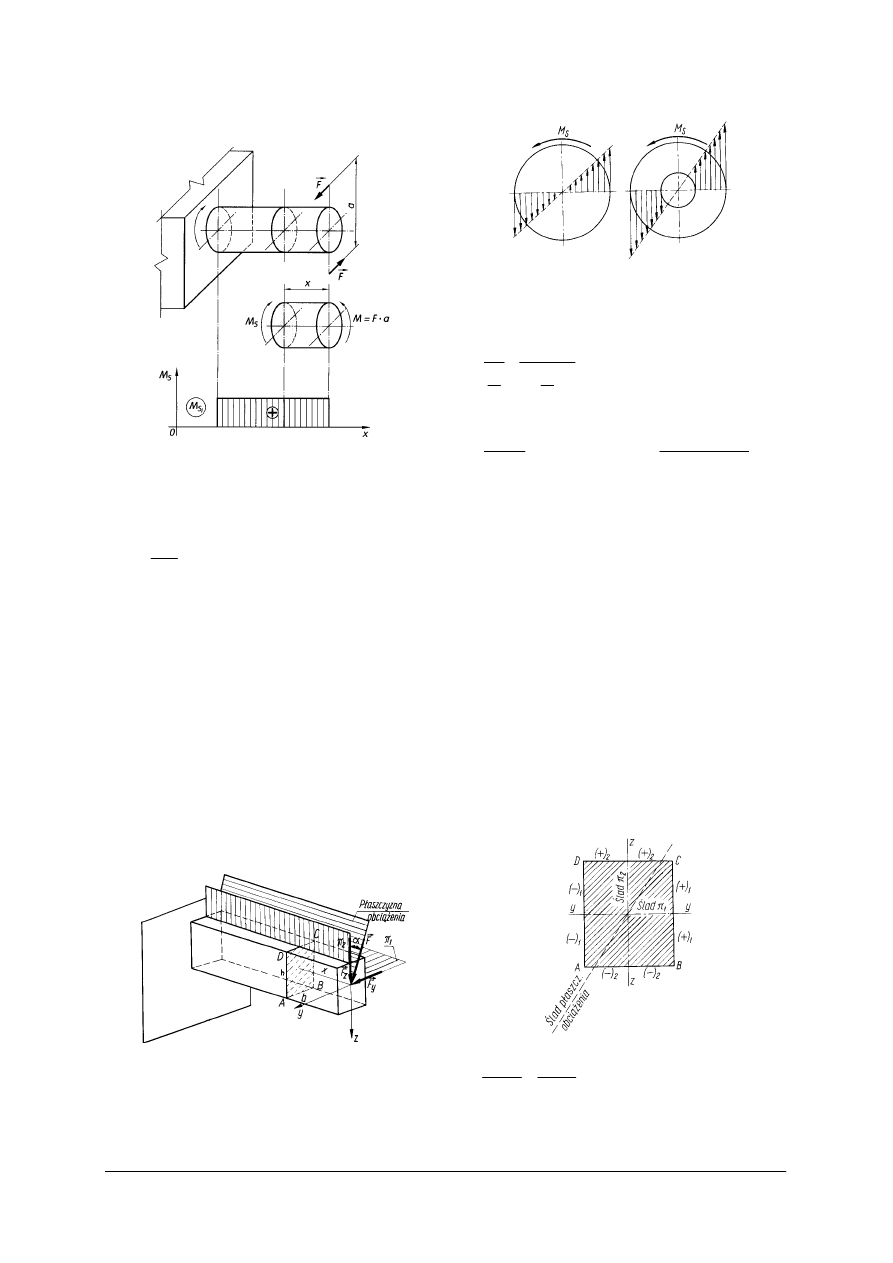
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
49
Wskaźnik przekroju na skręcanie
0
W
0
W
=
2
0
d
J
=
2
d
J
J
y
x
+
Dla pełnego wału
o
W
=
16
3
d
⋅
π
Dla wału drążonego
0
W
=
(
)
D
d
D
16
4
4
−
⋅
π
Rys. 45. Moment skręcający i naprężenia styczne [2, s. 164]
Warunek wytrzymałości wałów na skręcanie
τ
=
s
o
s
k
W
M
≤
(
)
so
sj
k
k ,
:
Wytrzymałość złożona
W elementach maszyn i urządzeniach w większości przypadków występują jednocześnie
dwa lub więcej stanów naprężeń. Mówimy wtedy o wytrzymałości złożonej i należą do niej:
ukośne zginanie, zginanie ze ściskaniem lub rozciąganiem, nieosiowe ściskanie, zginanie ze
skręcaniem. Naprężenia występujące w tych przypadkach mogą mieć jednakowe kierunki,
wówczas naprężenia sumuje się i porównuje z naprężeniami dopuszczalnymi lub występują
naprężenia normalne i styczne, wtedy wyznacza się naprężenia zastępcze.
Zginanie ukośne
Zginanie to występuje wówczas, gdy siła leży w płaszczyźnie prostopadłej do osi belki.
Największe naprężenia rozciągające w punkcie C:
σ
=
z
y
W
x
F
⋅
+
y
z
W
x
F
⋅
;
1
M
=
x
F
y
⋅
;
2
M
=
x
F
z
⋅
Rys. 46. Zginanie ukośne i rozkład naprężeń [5, s. 276, 277]
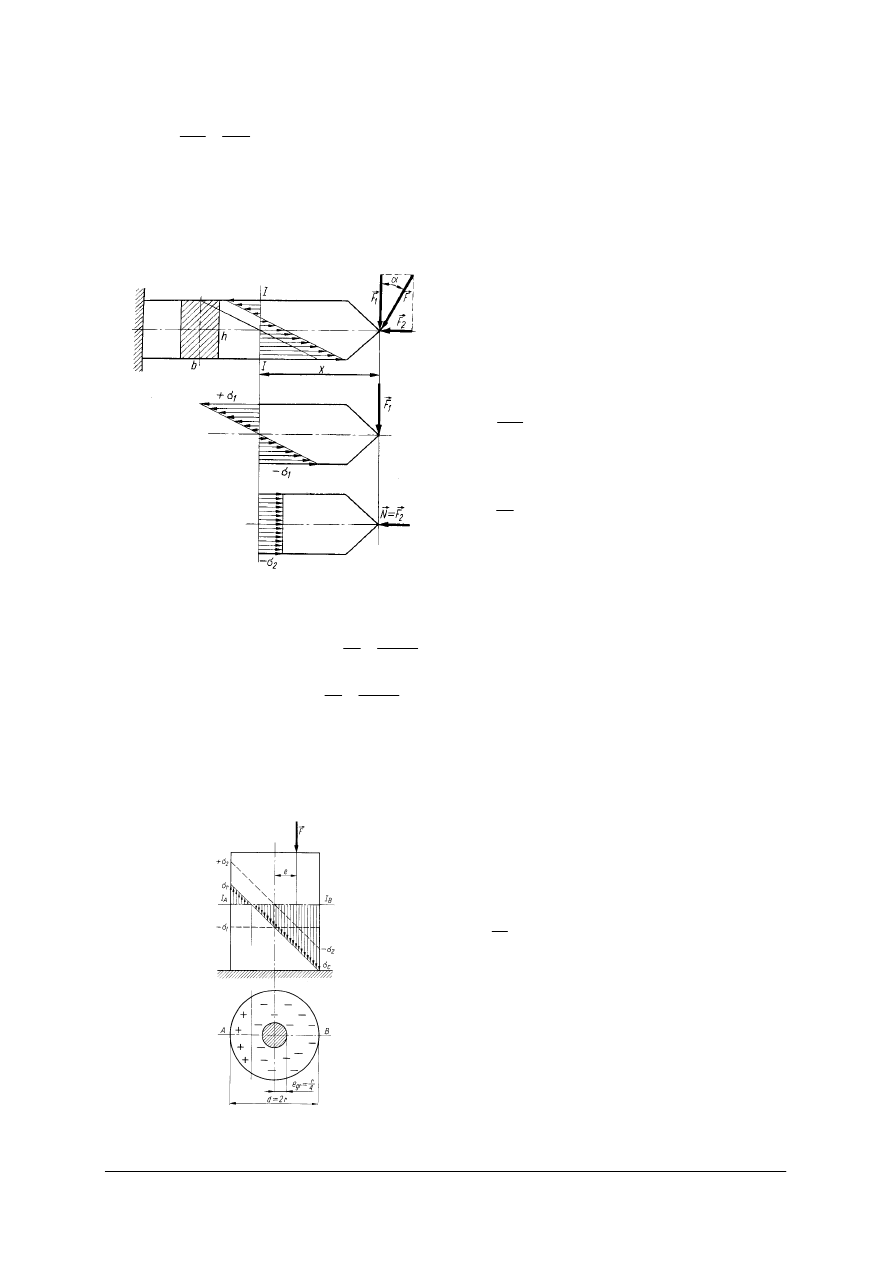
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
50
max
σ
=
±
g
y
z
k
W
M
W
M
≤
+
2
1
warunek wytrzymałości dla największych naprężeń w przekroju
Zginanie z osiowym rozciąganiem lub ściskaniem
Ten rodzaj złożonego obciążenia występuje między innymi w korpusach wiertarek
w hakach urządzeń transportowych.
Naprężenia normalne od zginania w skrajnych
włóknach
σ
=
±
W
M
1
;
1
M
=
x
F
⋅
1
−
moment zginający
Naprężenia ściskające
σ
=
−
S
N
Rys. 47. Zginanie z osiowym ściskaniem [5, s. 280]
Warunki wytrzymałości przy jednoczesnym:
−
zginaniu i rozciąganiu
σ
=+
r
k
W
M
S
N
≤
±
max
,
−
zginaniu i ściskaniu
σ
=
−
c
k
W
M
S
N
≤
±
max
.
Szczególnym przypadkiem jednoczesnego zginania i ściskania jest ściskanie
mimośrodowe. Występuje ono wówczas, gdy słup jest ściskany siłą, która nie leży w osi, lecz
jest przesunięta o wartość
e
, zwaną mimośrodem. Naprężenia są sumą naprężeń ściskających
w całym przekroju słupa i naprężeń zginających wywołanych momentem.
Naprężenia ściskające
1
σ
=
−
S
F
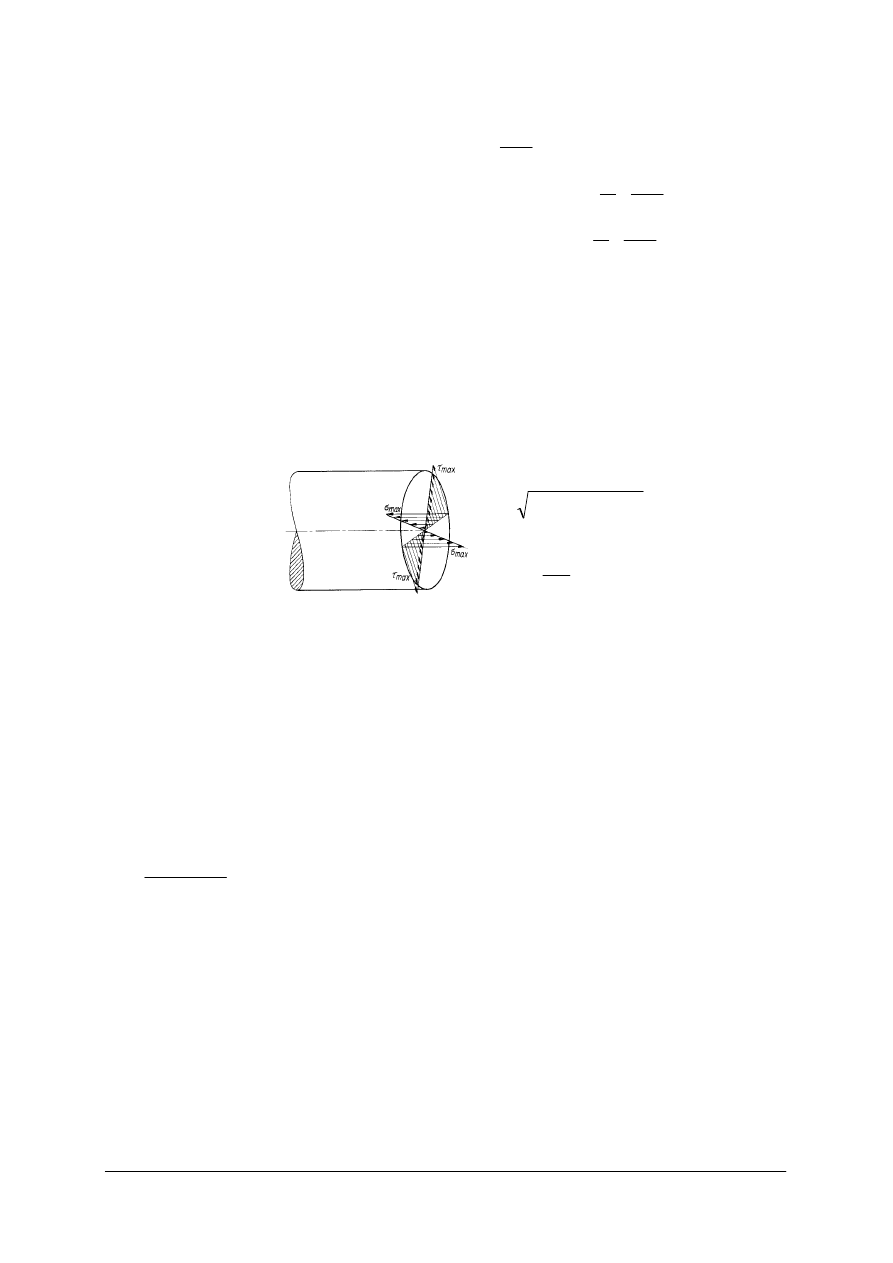
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
51
Naprężenia zginające
g
σ
=
W
e
F
⋅
±
dla punktu A:
r
σ
=
−
S
F
+
W
e
F
⋅
r
k
≤
dla punktu B:
c
σ
=
−
S
F
−
W
e
F
⋅
c
k
≤
Rys. 48. Ściskanie mimośrodowe [5, s. 282]
Skręcanie z równoczesnym zginaniem
Skręcanie ze zginaniem najczęściej występuje w przypadku wałów z osadzonymi na nich
kołami zębatymi, pasowymi, tarczami hamulcowymi. Występują wówczas jednocześnie
naprężenia styczne pochodzące od skręcania oraz naprężenia normalne od zginania.
Moment zredukowany wg hipotezy Hubera
z
M
=
2
2
75
,
0
s
M
M
⋅
+
Warunek wytrzymałości
z
σ
=
g
z
k
W
M
≤
Rys. 49. Skręcanie ze zginaniem [5, s. 285]
Stan obciążenia wynikający z jednoczesnego działania momentu skręcającego i zginającego
zastępuje się momentem zredukowanym (zastępczym)
z
M
, obliczanym z hipotez.
Wyboczenie
Zjawisko wyboczenia występuje przy osiowym ściskaniu prętów o małych wymiarach
poprzecznych w stosunku do ich długości. Zjawisko wyboczenia polega na utracie
stateczności elementów pod wpływem ściskania (następuje wygięcie). Siłę krytyczną
kr
F , po
przekroczeniu której następuje wyboczenie, wylicza się ze wzoru Eulera.
kr
F =
2
min
2
r
l
J
E
⋅
⋅
π
gdzie: E
−−−−
moduł sprężystości wzdłużnej materiału pręta w Pa,
min
J
−
najmniejsza wartość osiowego momentu bezwładności przekroju poprzecznego
pręta w m
4
,
r
l
−
długość zredukowana pręta, zależna od sposobu jego zamocowania, w m.
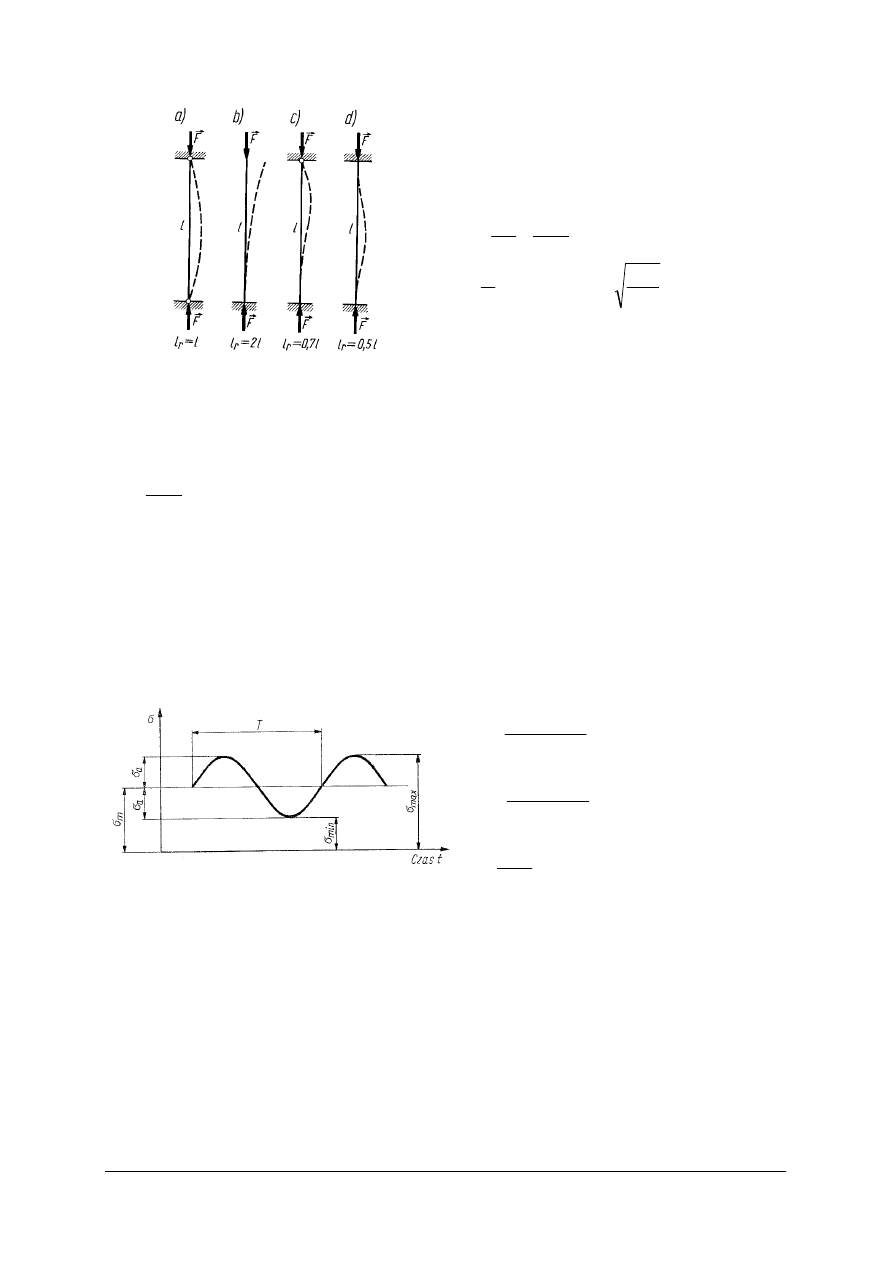
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
52
a)
pręt zamocowany na obu końcach przegubowo,
b)
pręt utwierdzony jednym końcem,
c)
pręt jednym końcem utwierdzony, a drugim
zamocowany przegubowo,
d)
pręt na obu końcach utwierdzony.
kr
σ
=
S
F
kr
=
2
2
λ
π
E
⋅
naprężenie krytyczne
λ
=
i
l
r
,
i
=
S
J
min
gdzie:
λ
−
smukłość pręta,
i
−
promień bezwładności
.
Rys. 50. Sposoby zamocowania [5, s. 294]
Dla wyboczenia w granicach sprężystości i proporcjonalności materiału naprężenia krytyczne
wynoszą
kr
σ
=
2
2
λ
π
E
⋅
H
R
≤
,
H
R
−
granica proporcjonalności.
Wytrzymałość zmęczeniowa
W elementach maszyn, które poddano zmiennym obciążeniom, powstają naprężenia
zmieniające się w czasie użytkowania, które nazywamy naprężeniami zmęczeniowymi.
Naprężenia zmieniają się w czasie jednego okresu drgań T między skrajnymi wartościami:
naprężeniem maksymalnym
max
σ
i minimalnym
min
σ
.
Cykl naprężeń charakteryzują wielkości:
–
amplituda naprężenia
2
min
max
σ
σ
σ
−
=
a
–
naprężenie średnie
2
min
max
σ
σ
σ
+
=
m
–
współczynnik asymetrii cyklu
min
max
σ
σ
=
R
Rys. 51. Zmienność naprężeń w czasie [1, s. 201]
Wartość największego naprężenia Z, które materiał może przenieść nieograniczoną liczbę
razy, nazywa się wytrzymałością zmęczeniową. Parametry: naprężenie i liczbę cykli
przedstawia się na wykresie Wıhlera. W próbach zmęczeniowych określa się umowną liczbę
cykli naprężeń; dla stali wynosi 10
7
cykli lub przyjmuje szacunkowo w odniesieniu do
wytrzymałości na rozciąganie R
m
.
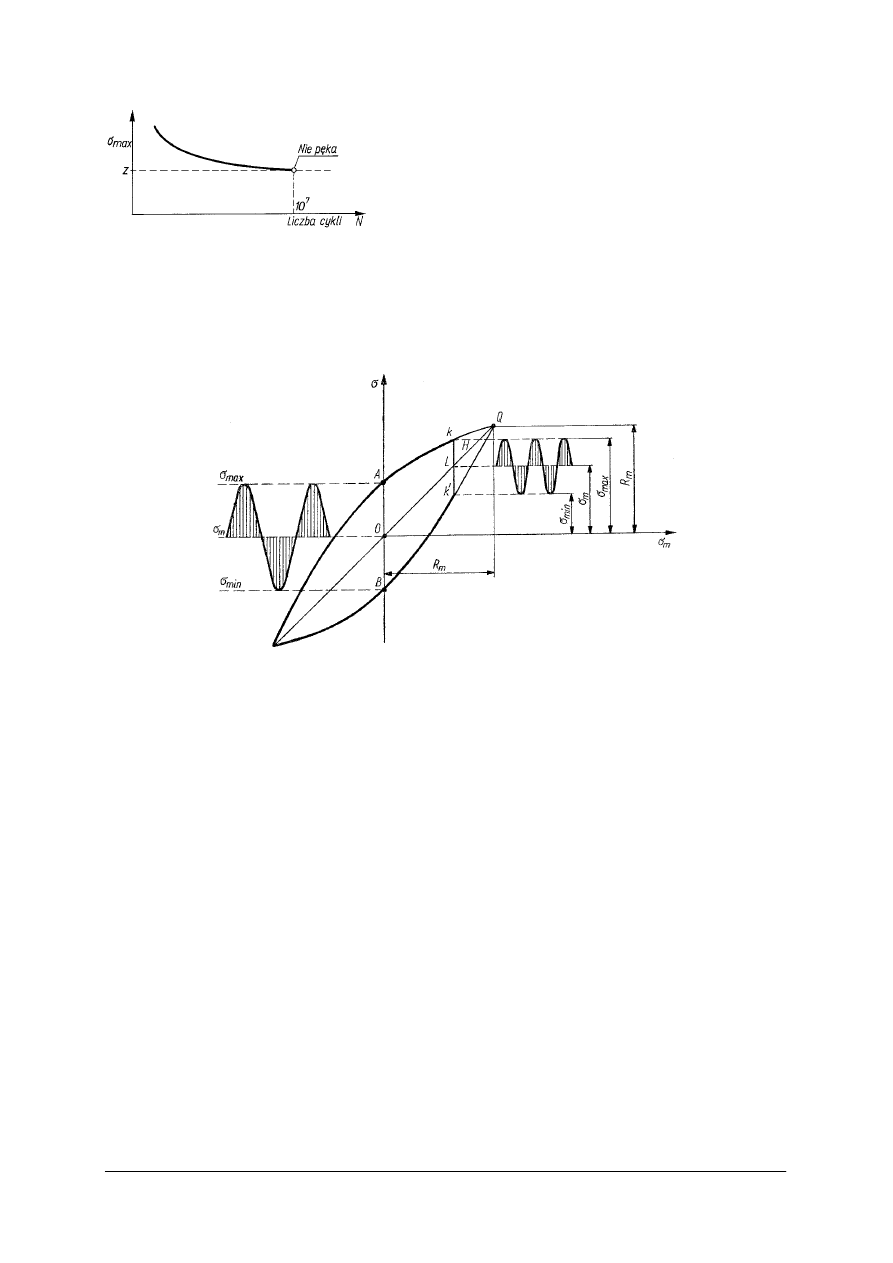
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
53
Przykładowe zależności dla stali:
Wytrzymałość na zginanie obustronne
m
go
R
Z
)
6
,
0
4
,
0
(
−
=
Wytrzymałość na skręcanie obustronne
go
so
Z
Z
⋅
=
6
,
0
Wytrzymałość na rozciąganie i ściskanie wahadłowe
go
rc
Z
Z
⋅
=
7
,
0
Rys. 52. Krzywa Wıhlera [5, s. 311]
Zależność wytrzymałości zmęczeniowej od naprężenia maksymalnego oraz średniego
i amplitudy naprężeń dla różnych materiałów przedstawia się za pomocą różnych wykresów.
z których najczęściej spotykany jest wykres Smitha.
Rys. 53. Wykres Smitha [1, s. 206]
4.5.2. Pytania sprawdzające
Odpowiadając na pytania, sprawdzisz, czy jesteś przygotowany do wykonania ćwiczeń.
1.
Jakie znasz rodzaje odkształceń w elementach maszyn?
2.
Jaki rodzaje naprężeń występują podczas odkształceń?
3.
Od czego zależy naprężenie dopuszczalne?
4.
Co nazywamy ścinaniem technologicznym?
5.
Co to jest siła tnąca i moment zginający?
6.
Jaka jest zależność między wykresami momentów zginających i sił tnących?
7.
Jak obliczamy wskaźnik wytrzymałości przekroju na zginanie?
8.
Gdzie w obliczeniach wytrzymałościowych stosujemy twierdzenie Steinera?
9.
Jaki jest warunek wytrzymałościowy przy zginaniu?
10.
Jak obliczamy wskaźnik przekroju na zginanie?
11.
Jakie naprężenia występują przy skręcaniu?
12.
Jak obliczamy naprężenia przy jednoczesnym skręcaniu i zginaniu?
13.
Co to jest wyboczenie?
14.
Od czego zależy naprężenie krytyczne przy wyboczeniu?
15.
Co nazywamy wytrzymałością zmęczeniową?

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
54
4.5.3. Ćwiczenia
Ćwiczenie 1
Oblicz naprężenie normalne w przekroju poprzecznym pręta o średnicy d = 20 mm
rozciąganego siłami osiowymi F = 10 kN. Dobierz gatunek materiału dla pręta.
Sposób wykonania ćwiczenia
Aby wykonać ćwiczenie, powinieneś:
2)
zorganizować stanowisko do wykonania ćwiczenia,
3)
określić siły działające na pręt,
4)
naszkicować obciążenie pręta,
5)
wyznaczyć naprężenia normalne w pręcie,
6)
dobrać gatunek materiału,
7)
zaprezentować wyniki ćwiczenia.
Wyposażenie stanowiska pracy:
−−−−
normy własności wytrzymałościowych stali,
−−−−
poradnik mechanika,
−−−−
poradnik dla ucznia.
Ćwiczenie 2
Dobierz profil dwuteownika wykonanego ze stali St3S ściskanego siłą F = 400 kN.
Sposób wykonania ćwiczenia
Aby wykonać ćwiczenie, powinieneś:
1)
zorganizować stanowisko do wykonania ćwiczenia,
2)
odszukać w normach naprężenie dopuszczalne na ściskanie dla materiału dwuteownika,
3)
obliczyć z warunku wytrzymałościowego minimalny przekrój dwuteownika,
4)
dobrać dwuteownik z norm,
5)
zaprezentować wyniki ćwiczenia.
Wyposażenie stanowiska pracy:
−−−−
normy własności wytrzymałościowych stali,
−−−−
tablice wyrobów hutniczych,
−−−−
poradnik mechanika,
−−−−
poradnik dla ucznia.
Ćwiczenie 3
Wyznacz średnicę znormalizowaną wału skręcanego wykonanego ze stali „20”, który
przenosi moc P = 30 kW przy prędkości obrotowej 120 obr/min.
Sposób wykonania ćwiczenia
Aby wykonać ćwiczenie, powinieneś:
1)
obliczyć moment skręcający wał,
2)
napisać warunek wytrzymałościowy dla wałów skręcanych,
3)
przeanalizować wielkości występujące we wzorze,
4)
w tablicach wytrzymałościowych odszukać naprężenie dopuszczalne dla materiału wału,
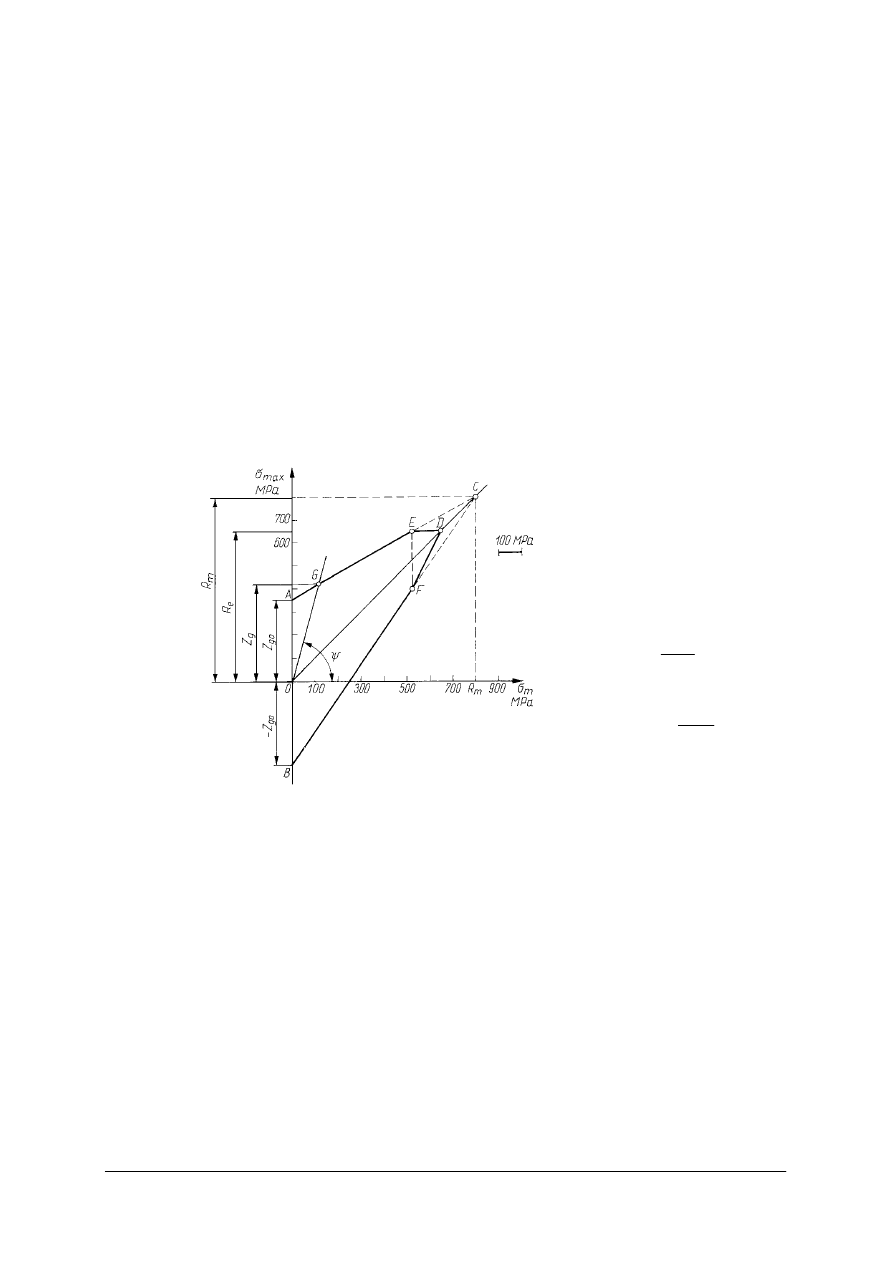
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
55
5)
określić współczynnik wytrzymałości przekroju kołowego na skręcanie,
6)
obliczyć minimalną średnicę wału skręcanego,
7)
przyjąć średnicę znormalizowaną z norm,
8)
zaprezentować wyniki ćwiczenia.
Wyposażenie stanowiska pracy:
−−−−
normy własności wytrzymałościowych stali,
−−−−
tablice wyrobów hutniczych,
−−−−
poradnik mechanika,
−−−−
poradnik dla ucznia.
Ćwiczenie 4
Określ wytrzymałość zmęczeniową Z
g
dla pręta wykonanego ze stali 20H, który jest
obciążony siłą w cyklu dwustronnym niesymetrycznym w granicach 15±40 kN. Naprężenia
wywołane obciążeniem, wynoszą:
275
max
≈
σ
MPa oraz
125
min
−
≈
σ
MPa.
max
min
F
F
R
=
R
tg
+
=
1
2
ψ
Rysunek do ćwiczenia 4 [4, s. 28]
Sposób wykonania ćwiczenia
Aby wykonać ćwiczenie, powinieneś:
1)
zorganizować stanowisko do wykonania ćwiczenia,
2)
odczytać z tablic wytrzymałościowych
m
R ,
e
R dla materiału pręta,
3)
obliczyć szacunkową wartość wytrzymałości na zginanie obustronne,
4)
obliczyć
min
F
i
max
F
oraz
ψ
dla obciążenia niesymetrycznego,
5)
narysować układ współrzędnych
m
σ
,
max
σ
i oznaczyć charakterystyczne punkty na
wykresie zgodnie z rysunkiem,
6)
wykreślić prostą pod kątem
ψ
i odczytać wartość wytrzymałości zmęczeniowej
g
Z
,
7)
obliczyć moment skręcający wał,
8)
zaprezentować wyniki ćwiczenia.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
56
Wyposażenie stanowiska pracy:
−−−−
normy własności wytrzymałościowych stali,
−−−−
poradnik mechanika,
−−−−
literatura wskazana przez nauczyciela,
−−−−
poradnik dla ucznia.
4.5.4. Sprawdzian postępów
Czy potrafisz:
Tak
Nie
1)
określić warunki wytrzymałościowe dla prętów rozciąganych
i ściskanych?
2)
rozróżnić naprężenia normalne i styczne?
3)
wyznaczyć wskaźnik przekroju na zginanie dla różnych profili?
4)
wyznaczyć naprężenia w pręcie zginanym?
5)
wyznaczyć moment skręcający?
6)
wyznaczyć naprężenia w pręcie skręcanym?
7)
dobrać gatunek materiału dla różnych obciążeń?
8)
wyznaczyć
naprężenia
w
pręcie
jednocześnie
zginanym
i rozciąganym?
9)
określić warunek wytrzymałości dla przypadku jednoczesnego
skręcania i zginania?
10)
określić, od czego zależy siła krytyczna przy wyboczeniu?
11)
wyznaczyć wytrzymałość zmęczeniową?
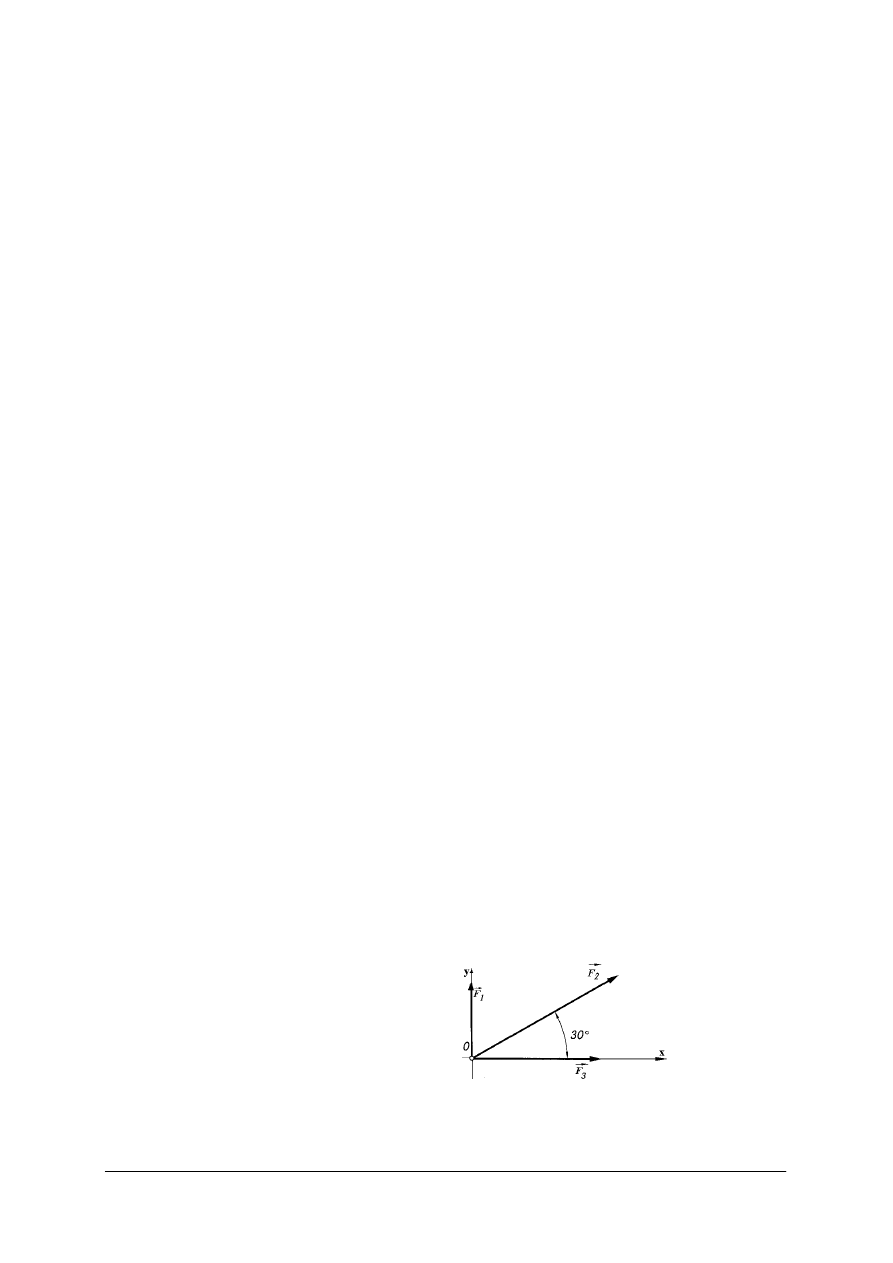
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
57
5. SPRAWDZIAN OSIĄGNIĘĆ
INSTRUKCJA DLA UCZNIA
1.
Przeczytaj uważnie instrukcję.
2.
Podpisz imieniem i nazwiskiem kartę odpowiedzi.
3.
Zapoznaj się z zestawem zadań testowych.
4.
Test zawiera 20 zadań. Do każdego zadania dołączone są 4 możliwości odpowiedzi.
Tylko jedna jest prawidłowa.
5.
Udzielaj odpowiedzi na załączonej karcie odpowiedzi, stawiając w odpowiedniej rubryce
znak X. W przypadku pomyłki należy błędną odpowiedź zaznaczyć kółkiem, a następnie
ponownie zakreślić odpowiedź prawidłową.
6.
Zadania wymagają prostych obliczeń, które powinieneś wykonać przed wskazaniem
poprawnego wyniku.
7.
Pracuj samodzielnie, bo tylko wtedy będziesz miał satysfakcję z wykonanego zadania.
8.
Jeśli udzielenie odpowiedzi będzie Ci sprawiało trudność, wtedy odłóż jego rozwiązanie
na później i wróć do niego, gdy zostanie Ci wolny czas.
9.
Na rozwiązanie testu masz 30 min.
Powodzenia!
ZESTAW ZADAŃ TESTOWYCH
1.
Do wielkości wektorowych zaliczamy
a)
pracę, naprężenie.
b)
masę, moc.
c)
prędkość, przyspieszenie.
d)
ciśnienie, temperaturę.
2.
Naprężenie 10 MPa jest równe
a)
1000 N/mm
2
.
b)
100 kN/mm
2
.
c)
10 MN/mm
2
.
d)
10 N/mm
2
.
3.
Kierunek siły reakcji więzów jest znany w przypadku
a)
utwierdzenia,
b)
łożysk poprzecznych,
c)
przegubów,
d)
więzów wiotkich.
4.
Suma rzutów trzech sił na oś x wynosi
a)
F
x
= F
2
· cos 30
0
+F
3
b)
F
x
= F
1
· cos 30
0
+ F
2
+F
3
c)
F
x
= F
1
· cos 30
0
+ F
2
– F
3
d)
F
x
= F
1
+ F
2
· cos 30
0
+F
3
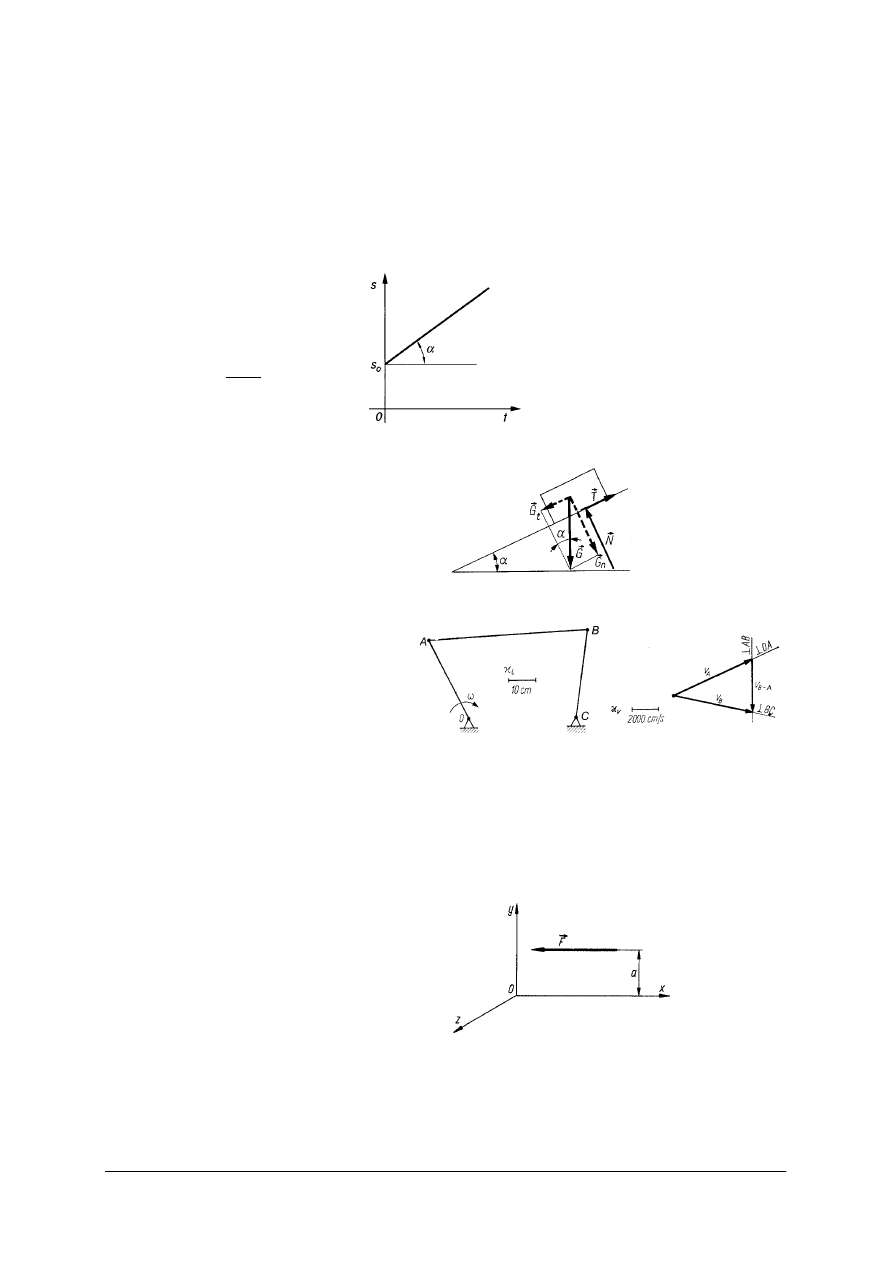
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
58
5.
Dowolny płaski układ sił jest w równowadze, gdy spełnione są następujące warunki:
wielobok sił jest
a)
zamknięty i wielobok sznurowy otwarty.
b)
otwarty i wielobok sznurowy otwarty.
c)
otwarty i wielobok sznurowy zamknięty.
d)
zamknięty i wielobok sznurowy zamknięty.
6.
Równanie drogi dla wykresu ma postać
a)
α
tg
s
=
t
⋅
.
b)
s
=
o
s +
t
v
⋅
.
c)
s
=
o
s –
t
v
⋅
.
d)
s
=
o
s +
2
2
t
a
⋅
7.
Siła tarcia dla ciała w chwili równowagi granicznej wynosi
a)
T = Gּcosαּµ.
b)
T = Gּsinα.
c)
T = Gּµ.
d)
T = Gּtgα.
8.
Przedstawiony sposób wyznaczania prędkości mechanizmów płaskich to
a)
plan przyspieszeń.
b)
hodograf prędkości.
c)
plan prędkości.
d)
metoda prędkości odwróconych.
9.
Wytrzymałość materiałów zajmuje się
a)
wyznaczaniem parametrów ruchu.
b)
wytwarzaniem elementów maszyn.
c)
projektowaniem elementów konstrukcyjnych.
d)
prawidłową eksploatacją maszyn i urządzeń.
10.
Moment siły ma wartość M = F·a
≠
0 względem osi
a)
z.
b)
z i x.
c)
x.
d)
x i y.
11.
Naprężenie w pręcie o boku 2 cm rozciąganym siłą F = 80 kN wynosi
a)
400 MPa.
b)
200 MPa.
c)
160 MPa.
d)
120 MPa.
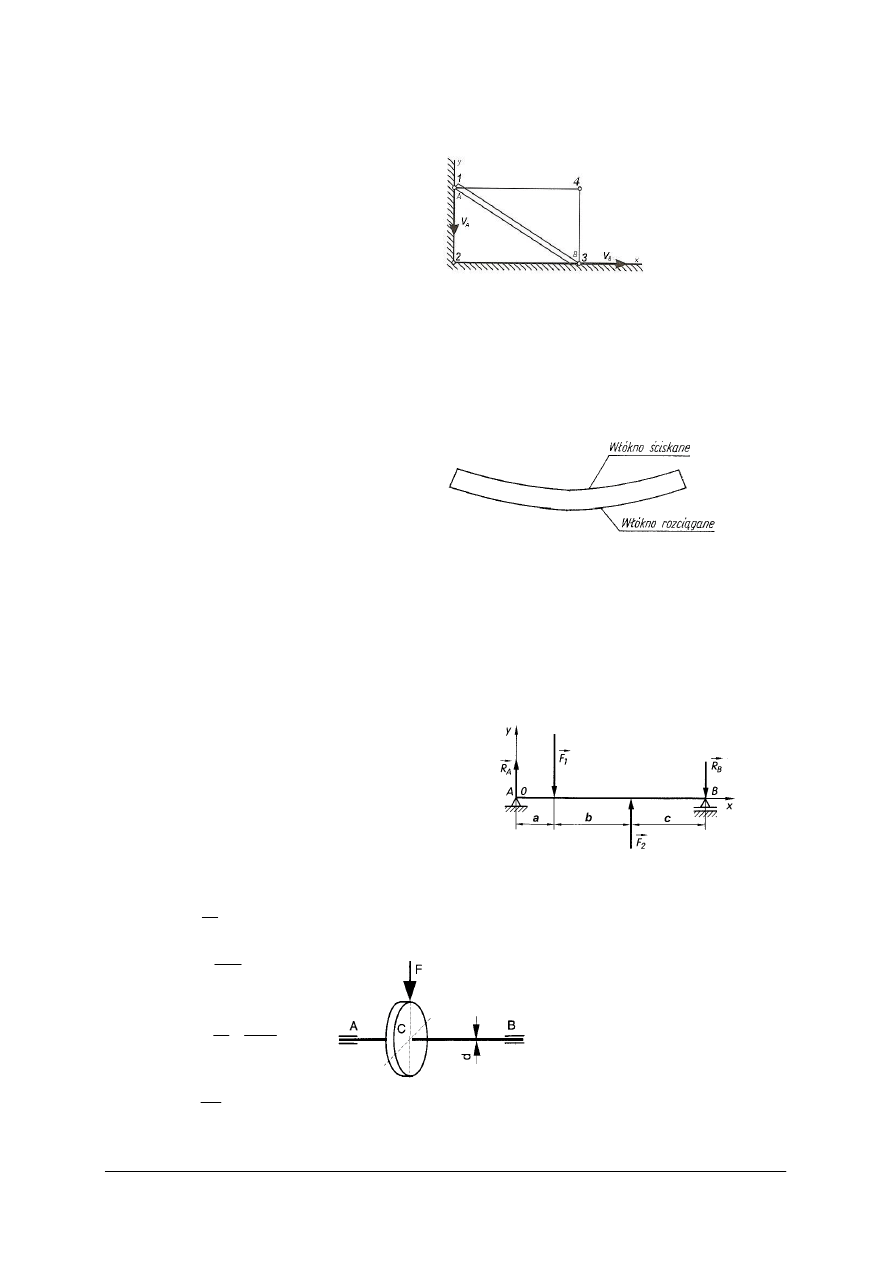
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
59
12.
Chwilowy środek obrotu pręta, który przesuwa się końcami po osiach x i y z, znajduje się
w punkcie
a)
1.
b)
2.
c)
3.
d)
4.
13.
Ś
rodek ciężkości ciała
a)
zmienia położenie wewnątrz ciała podczas ruchu ciała.
b)
musi pokrywać się z punktem materialnym ciała.
c)
nie zmienia swego położenia przy odkształceniu plastycznym ciała.
d)
pokrywa się ze środkiem ciężkości punktów materialnych ciał składowych.
14.
Odkształcenie elementu na rysunku zachodzi podczas
a)
skręcania.
b)
ś
ciskania.
c)
zginania.
d)
rozciągania.
15.
Długość zredukowana dla pręta o długości l podczas wyboczenia zamocowanego na obu
końcach przegubowo wynosi
a)
l
r
= l.
b)
l
r
= 2 l.
c)
l
r
= 0,7 l.
d)
l
r
= 0,5 l.
16.
Moment główny względem punktu B wynosi
a)
−
F
1
⋅
a+F
2
(a+b) R
B
(a+b+c) = 0.
b)
−
R
A
(a+b+c)+ F
2
(a + b)
−
F
1
⋅
a = 0.
c)
−
R
A
(a+ b+c)+F
2
(b+ c)
−
F
1
⋅
a = 0.
d)
+R
A
(a+ b+c)
−
F
1
(b+ c)+F
2
⋅
c = 0.
17.
Ś
rednicę d na przedstawionym schemacie obciążenia oblicza się wg wzoru
a)
τ
=
t
k
S
F
≤
(
)
to
tj
k
k ,
.
b)
τ
=
s
o
s
k
W
M
≤
.
c)
c
σ
=
−
S
F
−
W
e
F
⋅
c
k
≤
.
d)
σ
=
g
k
W
M
≤
(
)
go
gj
k
k ,
.
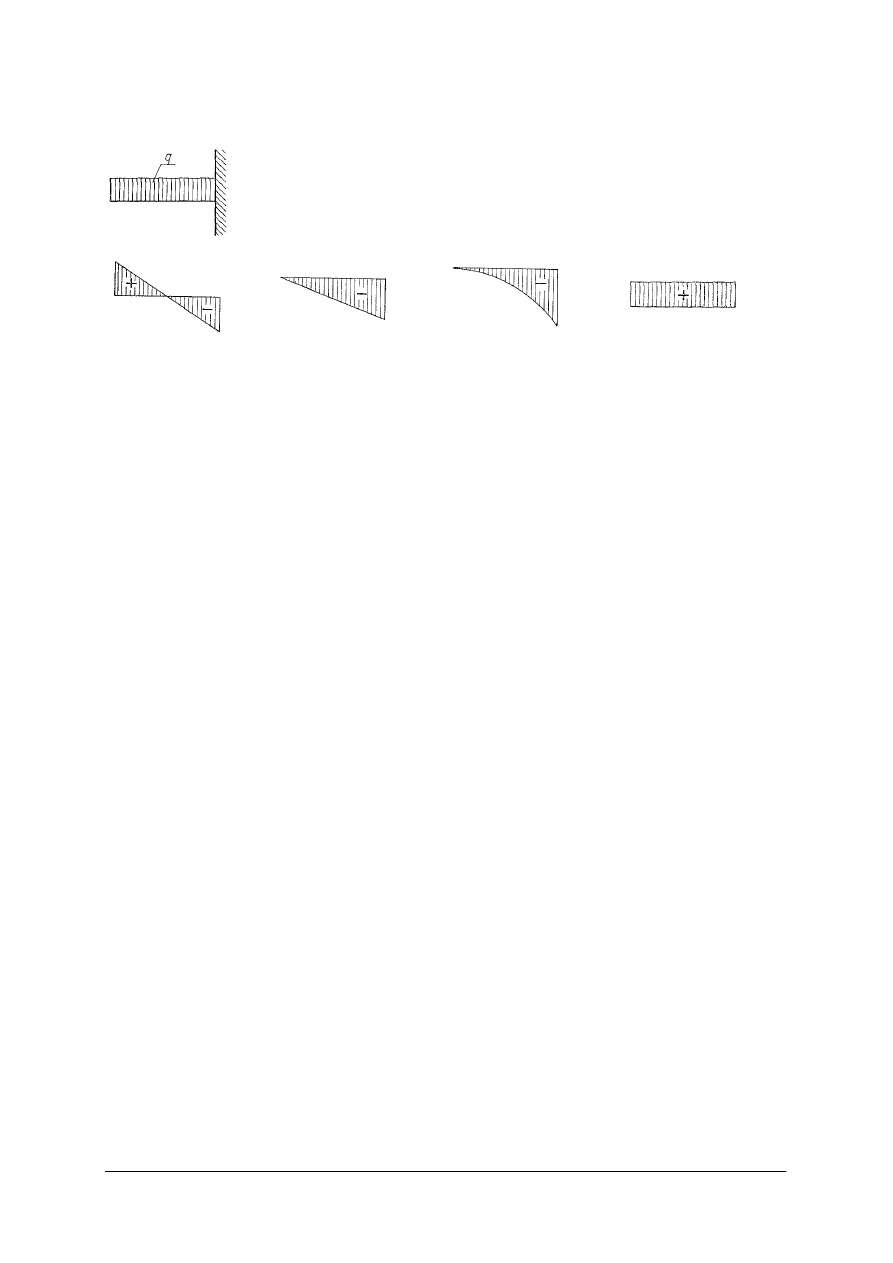
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
60
18.
Dla obciążenia belki wskaż wykres momentów zginających
a)
b)
c)
d)
19.
Profile walcowane „wyboczają” się w kierunku
a)
osi o najmniejszym momencie bezwładności.
b)
osi o największym momencie bezwładności.
c)
dowolnym.
d)
warstw o największym momencie zginającym.
20.
Moment skręcający dla pręta utwierdzonego z jednej strony, a z drugiej strony
obciążonego parą sił w płaszczyźnie prostopadłej do osi pręta przyjmuje wartość
a)
maksymalną w połowie pręta.
b)
jednakową na całej długości pręta.
c)
maksymalną w miejscu utwierdzenia pręta.
d)
maksymalną w miejscu przyłożenia pary sił.
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
61
KARTA ODPOWIEDZI
Imię i nazwisko................................................................................................
Wykonywanie
obliczeń
w
układach
statycznych,
dynamicznych
i kinematycznych
Zakreśl poprawną odpowiedź
Nr
zadania
Odpowiedź
Punkty
1.
a
b
c
d
2.
a
b
c
d
3.
a
b
c
d
4.
a
b
c
d
5.
a
b
c
d
6.
a
b
c
d
7.
a
b
c
d
8.
a
b
c
d
9.
a
b
c
d
10.
a
b
c
d
11.
a
b
c
d
12.
a
b
c
d
13.
a
b
c
d
14.
a
b
c
d
15.
a
b
c
d
16.
a
b
c
d
17.
a
b
c
d
18.
a
b
c
d
19.
a
b
c
d
20.
a
b
c
d
Razem:

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
62
6. LITERATURA
1.
Janicki L.: Mechanika techniczna. Wydawnictwo Szkolne i Pedagogiczne, Warszawa
1986
2.
Kozak B.: Mechanika techniczna. Wydawnictwo Szkolne i Pedagogiczne, Warszawa
2004
3.
Rutkowski A., Stępniewska A.: Zbiór zadań z części maszyn. Wydawnictwo Szkolne
i Pedagogiczne, Warszawa 1998
4.
Rutkowski A.: Części maszyn. Wydawnictwo Szkolne i Pedagogiczne, Warszawa 1998
5.
Siuta W.: Mechanika techniczna. Wydawnictwo Szkolne i Pedagogiczne, Warszawa
1997
Wyszukiwarka
Podobne podstrony:
04 Wykonywanie pomiarow paramet Nieznany
04 Wykonywanie izolacji termicz Nieznany (2)
04 Wykonywanie podstawowych for Nieznany (2)
04 Wykonywanie analiz ilosciowy Nieznany (2)
04 Wykonywanie zabiegow agrotec Nieznany (2)
04 Wykonywanie badan i pomiarow Nieznany (2)
04 Wykonywanie pomiarow paramet Nieznany
04 Wykonywanie izolacji termicz Nieznany (2)
04 Wykonywanie obliczeń w układach statycznych
711[04] Z2 04 Wykonywanie konse Nieznany (2)
713[05] Z2 04 Wykonywanie oklad Nieznany
714[01] Z2 04 Wykonywanie robot Nieznany (2)
311[15] O1 04 Wykonywanie oblic Nieznany
711[04] Z2 04 Wykonywanie konse Nieznany (2)
2014 Matura 05 04 2014 odpid 28 Nieznany (2)
04 les sonsid 5067 Nieznany (2)
więcej podobnych podstron