Ewa Dziuban, Mykhaylo Dorozhovets,
Adam Kowalczyk, Andrzej Rylski, Anna Szlachta,
Roman Tabisz, Barbara Wilk, Jakub Wojturski
Praca zbiorowa pod redakcją
ADAMA KOWALCZYKA
CD
CD
E
METROLOGIA
ELEKTRYCZNA ELEKTRONICZNA
Laboratorium
Część
Rzeszów 2005
Wydano za zgodą Rektora
Materiały pomocnicze do zajęć
z przedmiotu "metrologia I"
nie recenzowane
Druk wykonano z makiet dostarczonych przez Autorów
wielkość mierzona, jednostka miary,
wzorzec jednostki miary, metoda pomiaru, układ pomiarowy,
wynik pomiaru, niepewność pomiaru, błąd pomiaru,
elektroniczny przyrząd pomiarowy, wzorcowanie
ISBN 83-7199-368-4
Oficyna Wydawnicza Politechniki Rzeszowskiej
ul. W. Pola 2, 35-959 Rzeszów
Nakład 350 + 35 egz. Ark. wyd. 7,63. Ark. druk. 7,75. Papier
III 70g
Oddano do druku w październiku 2005 r. Wydrukowano w październiku 2005 r.
Drukarnia Oficyny Wydawniczej, ul. W. Pola 2, 35-959 Rzeszów
nr 61/05
nr
Ćwiczenie nr 2.
Ćwiczenie nr 3.
Ćwiczenie nr
Ćwiczenie nr 5.
Ćwiczenie nr 6.
Ćwiczenie nr 7.
Ćwiczenie nr 8.
Ćwiczenie nr 9.
Ćwiczenie nr 10.
Ćwiczenie nr
Ćwiczenie nr 12.
TREŚCI
ELEKTRONICZNA APARATURA w LABORATORIUM
METROLOGII cz. (Ewa Dziuban) 5
ELEKTRONICZNA APARATURA w LABORATORIUM
METROLOGII
II (Jakub Wojturski) 12
OCENA DOKŁADNOŚCI PRZYRZĄDÓW
POMIAROWYCH (Roman Tabisz) 21
OPRACOWANIE SERII WYNIKÓW POMIARU
(Mykhaylo Dorozhovets)
POMIARY NAPIĘĆ PRĄDÓW STAŁYCH
(Ewa Dziuban) 49
POMIARY REZYSTANCJI
(Ewa Dziuban)
POMIARY CZĘSTOTLIWOŚCI
CZASU
(Anna Szlachta) 62
POMIARY PARAMETRÓW ZMIENNYCH
PRZEBIEGÓW NAPIĘCIOWYCH (Barbara Wilk) 70
POMIARY IMPEDANCJI
(Andrzej Rylski)
POMIARY MOCY ENERGII ELEKTRYCZNEJ
(Andrzej Rylski) 91
POMIARY PRZESUNIĘCIA FAZOWEGO
(Adam Kowalczyk) 104
MOSTKI NIEZRÓWNOWAŻONE PRĄDU STAŁEGO
(Adam Kowalczyk)

1
APARATURA w LABORATORIUM
METROLOGII cz.
ćwiczenia jest poznanie podstawowej, typowej aparatury
używanej
Laboratorium Metrologii i laboratoriach
funkcji zasilaczy, generatorów,
i przygotowanie do
Zakres ćwiczenia ograniczono do obsługi przyrządów
sygnał o zadanych parametrach amplitudowych i częstotliwości i
vnie zmierzyć te parametry. Oscyloskop wprowadzono jedynie dla
gdyż funkcjom i
oscyloskopu poświęcone jest
Parametry amplitudowe przebiegu zmiennego: amplituda, wartość skuteczna
oraz zależności miedzy nimi.
2.
matematyczny przebiegu sinusoidalnego: częstotliwość, okres,
fazowe.
3. Źródło prądowe, źródło napięciowe.
Wprowadzenie
1. Źródła sygnałów
W laboratorium studenckim źródłem prądu i napięcia stałego są zasilacze
stabilizowane o regulowanej wartości tych sygnałów. Źródłem napięć zmiennych są
generatory funkcyjne dostarczające
o przebiegach sinusoidalnych, trójkątnych
i prostokątnych w zadanym, szerokim zakresie częstotliwości.
Zasilacz stabilizowany
S
Zasilacz laboratoryjny serii NDN-DF 1700S (rys. 1.1) jest
urządzeniem dostarczającym stabilizowanego napięcia stałego w dwóch trybach pracy:
stabilizacja napięcia (CV.) i stabilizacja prądu ( C C ) . Zasilacz dysponuje
Ćwiczenie 1
ELEKRONICZNA APARATURA w LABORATORIUM
METROLOGII cz.
Cel ćwiczenia
Celem ćwiczenia jest poznanie podstawowej, typowej aparatury kontrolno-
używanej
Laboratorium Metrologii laboratoriach elektronicznych:
poznanie funkcji zasilaczy, generatorów,
i przygotowanie do ich
obsługiwania. Zakres ćwiczenia ograniczono do obsługi przyrządów pozwalających
ustawić sygnał o zadanych parametrach amplitudowych i częstotliwości i następnie
poprawnie zmierzyć te parametry. Oscyloskop wprowadzono jedynie dla obserwacji
przebiegów, gdyż funkcjom i wykorzystywaniu oscyloskopu poświęcone jest osobne
ćwiczenie.
Zagadnienia
1. Parametry amplitudowe przebiegu zmiennego: amplituda, wartość skuteczna
i średnia oraz zależności miedzy nimi.
2. Model matematyczny przebiegu sinusoidalnego: częstotliwość, okres, przesunięcie
fazowe.
3. Źródło prądowe,
napięciowe.
W p r o w a d z e n i e
1. Źródła
W laboratorium studenckim źródłem prądu i napięcia stałego są zasilacze
stabilizowane o regulowanej wartości tych
Źródłem napięć zmiennych są
generator}' funkcyjne dostarczające
o przebiegach sinusoidalnych, trójkątnych
i prostokątnych w zadanym, szerokim zakresie częstotliwości.
Zasilacz stabilizowany
S
Zasilacz laboratoryjny serii NDN-DF 1700S (rys. 1.1) jest precyzyjnym
urządzeniem dostarczającym stabilizowanego napięcia stałego w dwóch trybach pracy:
stabilizacja napięcia (CV.) i stabilizacja prądu ( C C ) . Zasilacz dysponuje jednym
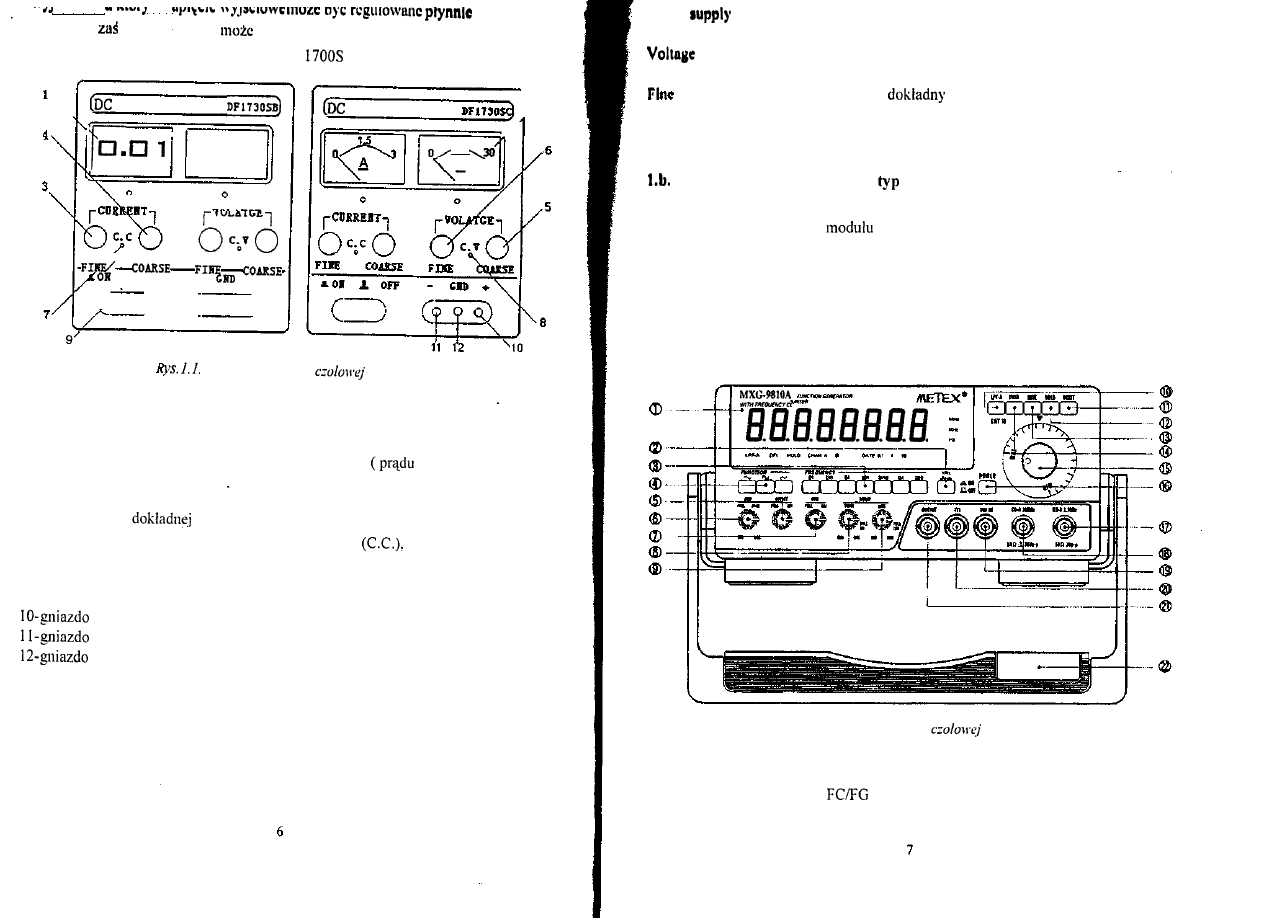
w zakresie od
0 do 20V,
prąd wyjściowy
być regulowany płynnie w zakresie od 0 do 10A
(20A). Dane techniczne zasilacza NDN-DF
zawarte są katalogu.
\
POWER SUPPLY
2 9 .
e
X OFF -
+
C ) (o o o)
POWER SUPPLY
V
V
y
Wygląd i opis płyty
zasilacza
1- wskaźnik pomiaru prądu wyjściowego,
2- wskaźnik pomiaru napięcia wyjściowego,
3- potencjometr dokładnej regulacji prądu wyjściowego
ograniczenia),
4- potencjometr zgrubnej regulacji prądu wyjściowego,
5- Potencjometr zgrubnej regulacji napięcia wyjściowego,
6- Potencjometr
regulacji napięcia wyjściowego,
7- diodowy wskaźnik pracy w trybie stabilizacji prądu
8- diodowy wskaźnik pracy w trybie stabilizacji napięcia (CV.),
9- włącznik zasilania. Włączenie zasilania sygnalizowane jest świeceniem diody CC.
lub CV.,
wyjściowe + : biegun dodatni zasilania,
wyjściowe - : biegun ujemny zasilania,
masy ( chassis) urządzenia
Słowniczek terminów angielskich
DC (direct current)
CC (constant current)
CV. (constant voltage)
sygnał stały (prąd lub napięcie)
prąd stabilizowany
napięcie stabilizowane
Power
Current
Coarsc
GND (ground)
ON / OFF
zasilacz
prąd
napięcie
zgrubny
masa
włączony /wyłączony
Generator funkcyjny METEX
MXG 9802
Generator funkcyjny MXG 9802 jest przyrządem składającym się z modułu
generatora funkcyjnego i
cyfrowego miernika częstotliwości (rys. 1.2).
Dostarcza napięcie sinusoidalne, prostokątne, trójkątne z możliwością regulacji
symetrii. Posiada oddzielne gniazdo wyjściowe prostokątnego sygnału o poziomie TTL.
Częstotliwość generowanego napięcia może być regulowana od 0,2 Hz do 2 MHz
w siedmiu podzakresach, zaś amplituda może być regulowana w zakresie do 20 V.
Dane techniczne generatora MXG 9802 zawarte są katalogu.
Rys. 1.2. Wygląd i opis płyty
generatora
1 - wyświetlacz LED
2- przełącznik rodzaju pracy
(częstotliwościomierz / generator)
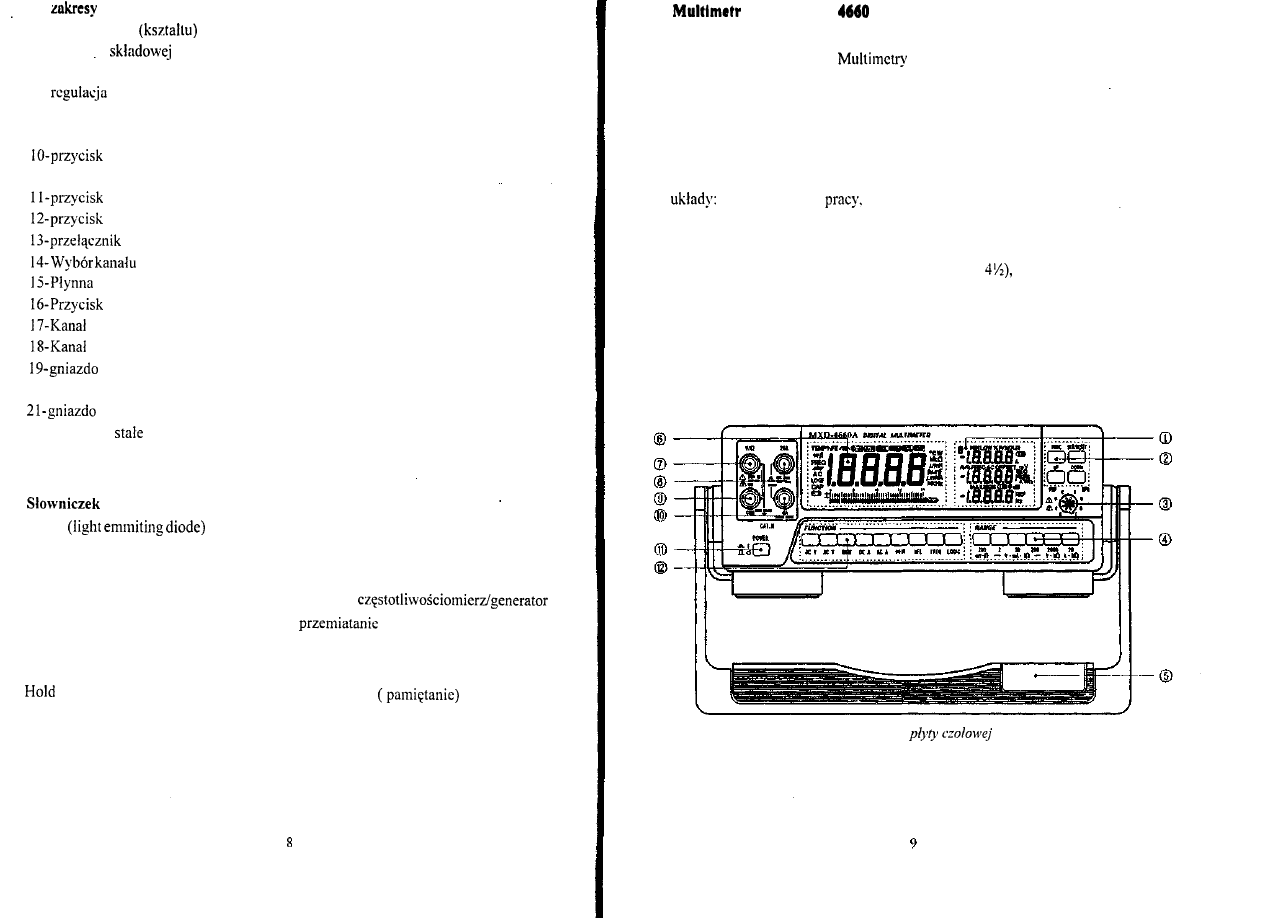
3-
częstotliwości
4- wybór funkcji
generowanego napięcia
5- regulacja
stałej
6- regulacja amplitudy generowanego napięcia
7-
symetrii generowanego napięcia
8- regulacja szerokości przemiatania częstotliwości
9- regulacja poziomu przemiatania częstotliwości
LPF (usuwanie szumów wysokoczęstotliwościowych zakłócających
pomiar częstotliwości)
RESET
zapamiętywania danych
wyboru czasu bramkowania częstotliwościomierza
(A&B)
regulacja częstotliwości generatora
zasilania
B (gniazdo wejściowe częstościomierza)
A (gniazdo wejściowe częstościomierza)
wejściowe regulacji częstotliwości generatora napięciem zewnętrznym
20-gniazdo wyjściowe sygnału TTL
wyjściowe generatora funkcyjnego
22-montaż na
terminów angielskich
LED
dioda świecąca
FREQUENCY częstotliwość
OFFSET składowa stała
FC/ FG ( Frequency Counter /Function Generator)
Sweep
częstotliwości
Gate bramka
Channel kanał
zatrzymanie
OUTPUT wyjście
Power zasilanie
2.
cyfrowy MXD
Multimctry cyfrowe typu METEX (rys. 1.3) służą do pomiaru wielkości
i parametrów elektrycznych.
mierzą: napięcie stałe i zmienne (DC V,
AC V) oraz natężenie prądu stałego i zmiennego (DC A, AC A), rezystancję, niektóre
typy mierzą częstotliwość, pozwalają sprawdzić tranzystor w układzie hFE oraz stany
logiczne [3].
Multimetr jako system pomiarowy nie będzie omawiany w niniejszym
ćwiczeniu. Dla sprawnej obsługi wystarczy wiedzieć, że w jego strukturze zawierają
się
wyboru rodzaju
przełączania zakresów, przetwornika analogowo-
cyfrowego, mikroprocesora do obróbki wyników pomiaru i sterowania, wskaźnika
cyfrowego oraz sprzężenia z interfejsem szeregowym RS232.
Cyfrowy wskaźnik pokazuje 19999 cyfr (miernik
polaryzację i przecinek
dziesiętny. Dołączony 43-segmentowy wskaźnik paskowy (linijka) wyświetla wartości
analogowe pomiaru. Przeciążenie zakresu sygnalizowane jest dźwiękiem, wskazaniem
OL (overload) i migotaniem wskaźnika paskowego.
Dane techniczne multimetru Metex MXD 4660 zawarte są katalogu.
Rys. 1.3. Wygląd i opis
multimetru
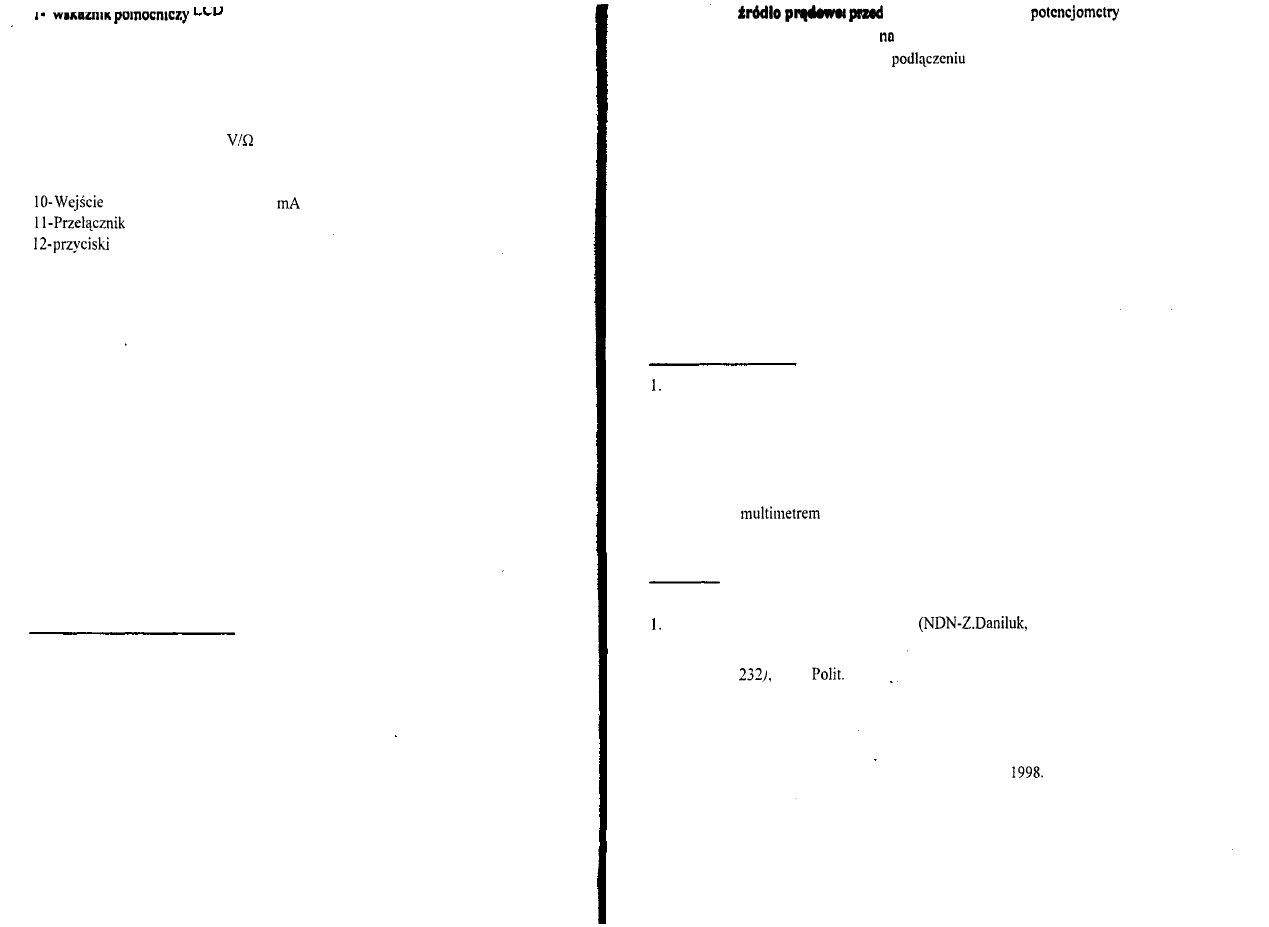
2- przycisk funkcji programowanych
3- gniazdo sprawdzania tranzystora
4- przełącznik zakresów
5- montaż na stałe
6- wskaźnik główny LCD
7- gniazdo wejściowe pomiaru
8- gniazdo wejściowe pomiaru dużych prądów 20A
9- gniazdo wejściowe wspólne
pomiaru małych prądów 20
zasilania WŁĄCZONE / WYŁĄCZONE
wyboru rodzaju pomiaru
Multimetr Metex MXD4460 wyposażony jest w dodatkowe możliwości
udostępniane za pomocą przycisku FUNKCJI PROGRAMOWANYCH (2). Symbole
wybranej funkcji pojawiają się nad wskaźnikem.
FUNKCJE PROGRAMOWANE:
• D-H pamiętanie bieżącego wyniku na wskaźniku pomocniczym
• A-H wskazywanie wartości MIN. MAX i AVG (średnia) na wskaźniku
pomocniczym
• REL mierzenie stosunku procentowego względem zadanej wartości referencyjnej,
a następnie mierzenie różnicy pomiędzy wartością bieżącą a referencyjną
• MEM wprowadzanie do wybranej pamięci w celu późniejszego wykorzystania
• RCL Pobieranie zmierzonej wartości z jednej z pamięci
• CMP porównanie wyniku pomiaru z zadanymi wartościami referencyjnymi: górną
i dolną
IV. Program ćwiczenia
1. Obsługa zasilacza i muitimetru:
UWAGA:
Przed włączeniem zasilacza potencjometry regulacji napięcia powinny być
ustawione na minimum, potencjometry regulacji prądu wyjściowego (3) i (4)
ustawione na maksimum. Po podłączeniu obciążenia i włączeniu zasilacza ustawić
żądane napięcie potencjometrami (5) i (6).
10
Zasilacz Jako
włączeniem zasilacza
regulacji
prądu (3) i (4) powinny być ustawione
minimum, potencjometry regulacji napięcia
(5) i (6) ustawione na maksimum. Po
obciążenia i włączeniu zasilacza
ustawić żądany prąd wyjściowy zgrubnie pokrętłem (4) oraz dokładnie pokrętłem (3).
Ustawić według wskazań prowadzącego: napięcie stałe U DC o zadanych
wartościach (kilka wartości odrębnych dla każdego ćwiczącego).
Ustawić według wskazań prowadzącego: źródło prądowe o zadanym natężeniu prądu
(kilka wartości odrębnych dla każdego ćwiczącego).
2. Obsługa generatora:
Ustawić napięcie zmienne: sinusoidalne, trójkątne, prostokątne o parametrach
zadanych, równocześnie obserwując obraz na oscyloskopie i wskazanie muitimetru.
V. Pytania kontrolne
Jaką wartość sygnału zmiennego wskazuje multimetr?
2. Podać schemat blokowy woltomierza cyfrowego napięcia zmiennego.
3. Podać schemat blokowy woltomierza cyfrowego napięcia stałego.
4. Zastosowania oscyloskopu.
5. Podać definicję współczynnika kształtu.
6. Podać definicję współczynnika szczytu.
7. Jak można
sprawdzić, czy przebieg ma składową stałą.
Literatura
Firmowe instrukcje obsługi przyrządów
METEX Instruments).
2. Marcyniuk A. Podstawy miernictwa elektrycznego dla kierunku elektronika
(str. 215-
Wyd.
Śląskiej. Gliwice, 2002.
3. Szadkowski B. (red) Laboratorium metrologii elektrycznej i elektronicznej.
Wyd. Polit. Śląskiej, Gliwice. 1998.
4. Zielonko R., Bartosiński B., Hoja J., Rydzkowski W., Toczek W., Laboratorium
z podstaw miernictwa Wyd. Polit. Gdańskiej, Gdańsk.
11
Ćwiczenie 2
ELEKRONICZNA APARATURA w LABORATORIUM
METROLOGII cz. II
I. Cel ćwiczenia
Celem ćwiczenia jest poznanie zasady działania, sposobu obsługi
i podstawowych zastosowań pomiarowych
cyfrowego oraz
elektronicznego oscyloskopu analogowego.
II. Zagadnienia
Budowa i zasada działania częstościomierza cyfrowego.
2. Zasada cyfrowego pomiaru częstotliwości sygnału okresowego.
3. Budowa i zasada działania oscyloskopu analogowego.
4. Zasada pomiaru amplitudy napięcia i okresu przebiegu periodycznego.
Wprowadzenie
1. Częstościomierz cyfrowy
Częstościomierz cyfrowy służy do bezpośredniego cyfrowego pomiaru
częstotliwości lub okresu przebiegu periodycznego oraz pośredniego pomiaru np.
stosunku częstotliwości lub kąta przesunięcia fazowego dwóch przebiegów.
Za pomocą częstościomierza cyfrowego możliwy jest także pomiar niektórych
parametrów jednorazowych przebiegów impulsowych (np. czasu trwania impulsu)
a także cyfrowy pomiar odstępu czasu.
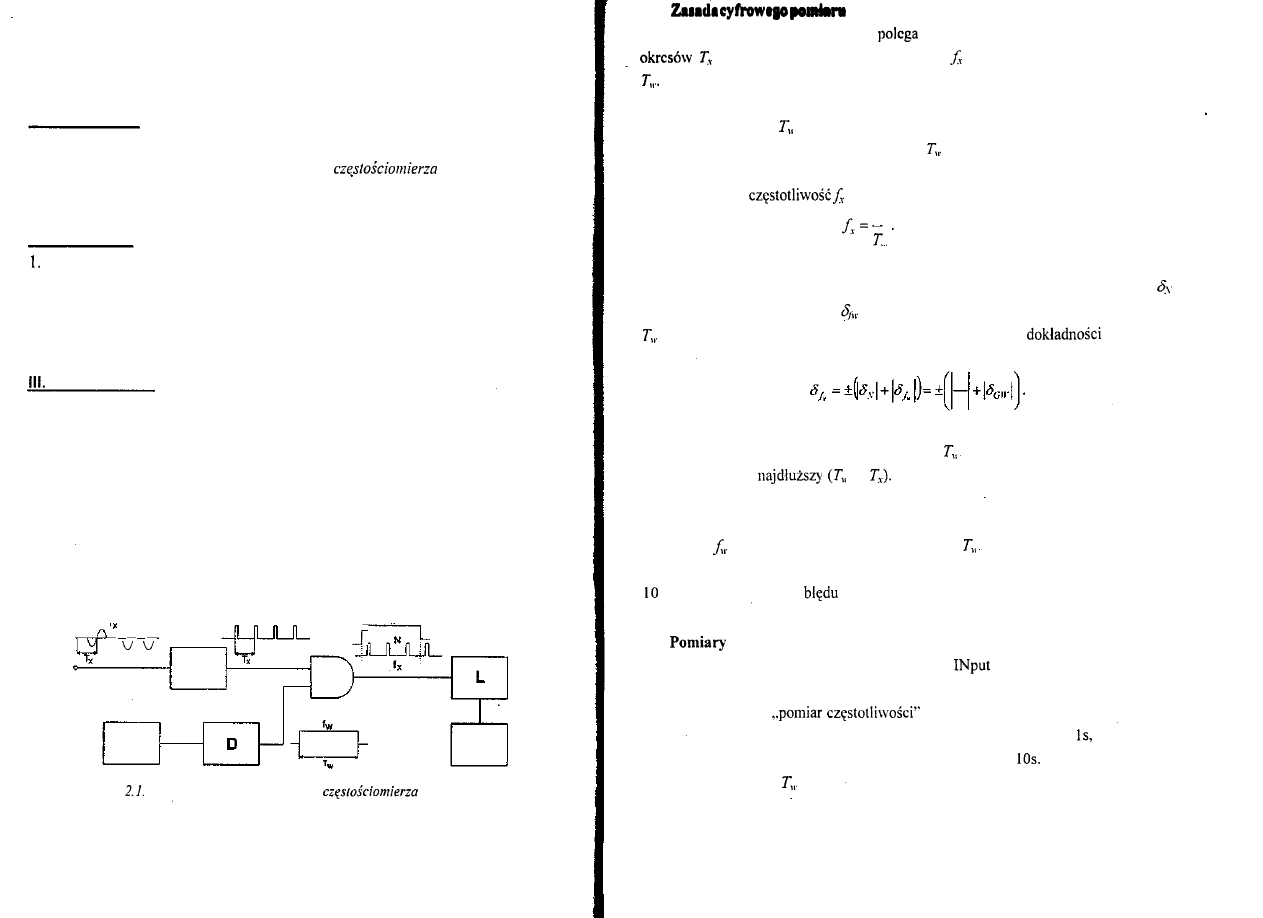
Uproszczony schemat blokowy częstościomierza cyfrowego przedstawiony jest
na rysunku 2.1.
A
A A
V
UF
GW
B
N
Rys.
Uproszczony schemat blokowy
cyfrowego
12
1.1.
częstotliwości
Cyfrowy pomiar częstotliwości
na zliczaniu (przez licznik L) liczby
przebiegu o częstotliwości mierzonej we wzorcowym przedziale czasu
Przebieg mierzony, po przejściu przez układ formowania impulsów, podawany jest
na jedno z wejść bramki B. Na wejście drugie podawany jest sygnał otwierający
bramkę - jeden okres
przebiegu z generatora wzorcowego GW i ew. dekadowego
dzielnika częstotliwości D. Jeżeli w czasie
otwarcia bramki liczba zliczonych
impulsów wynosi N to, zgodnie z definicją częstotliwości (ilość zdarzeń na jednostkę
czasu), mierzona
wynosi:
N_
(2.1)
Błąd pomiaru częstotliwości związany jest z błędem 4v zliczania impulsów
(bezwzględny błąd zliczania wynosi ±1 impuls, zatem względny błąd zliczania
równy jest ±1/N) oraz z błędem
wyznaczenia odcinka czasu trwania jednego okresu
przebiegu z generatora wzorcowego (błąd ten zależy od
generatora
wzorcowego). Tak więc względny błąd cyfrowego pomiaru częstotliwości wynosi:
1
N
(2.2)
Jak widać, błąd pomiaru jest tym mniejszy im większa jest liczba N zliczonych
impulsów. Wynika z tego wniosek, iż czas
otwarcia bramki powinien być
nastawiany na jak
»
W niektórych modelach częstościomierzy cyfrowych istnieje możliwość prostej
kontroli poprawności działania poprzez zliczanie impulsów o częstotliwości
wzorcowej
we wzorcowym przedziale czasu
(obie wielkości z własnego
generatora GW). Wynik pomiaru powinien być liczbą równą całkowitej potędze liczby
(z uwzględnieniem ew.
zliczania ±1 impuls).
1.2.
za pomocą częstościomierza cyfrowego
Mierzony przebieg podłączamy do wejścia
częstościomierza za pomocą
kabla koncentrycznego zakończonego wtykami BNC. Przyciskiem wyboru funkcji
pomiaru wybieramy
a następnie nastawiamy ,.czas otwarcia
bramki". Typowo, czas otwarcia bramki powinien wynosić 0,1 lub
w skrajnych
przypadkach (np. bezpośredni pomiar małej częstotliwości)
Należy zauważyć, iż
czas otwarcia bramki
wpływa nie tylko na dokładność pomiaru, ale również na
13
Wynik pomiaru
jest zawsze wraz z przecinkiem
i aktualną jednostką pomiaru (Hz,
Za pomocą
cyfrowego możliwy jest również
pomiar okresu
sygnału periodycznego. Zamienione są wówczas funkcje
mierzonego i otwierającego bramkę - bramka otwierana jest na jeden okres
przebiegu mierzonego natomiast licznik zlicza impulsy o częstotliwości wzorcowej
Dokładność pomiaru obliczana jest analogicznie jak dla pomiaru częstotliwości (wzór
2.2).
2. Oscyloskop analogowy
Oscyloskop elektroniczny
uniwersalnym przyrządem pomiarowym
wykorzystywanym w laboratorium. Zasadniczą zaletą oscyloskopu jest możliwość
zarówno obserwacji kształtu sygnału w funkcji czasu
mierzonego napięcia
kreślony jest na ekranie lampy w czasie rzeczywistym) jak i pomiaru niektórych
parametrów sygnałów napięciowych (amplituda, okres, przesunięcie czasowe dwóch
lub więcej przebiegów) w szerokim zakresie
(kilkadziesiąt MHz).
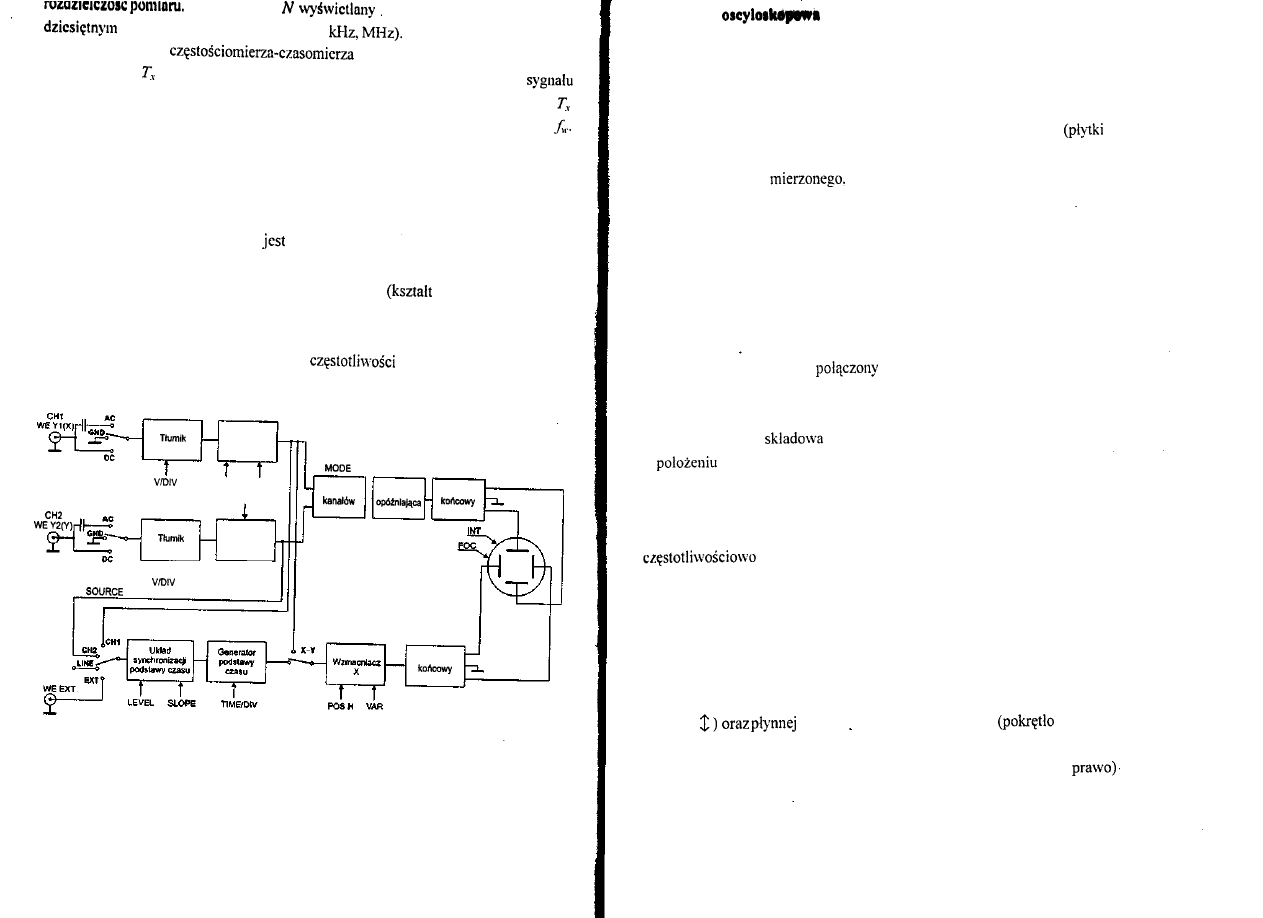
Uproszczony schemat blokowy oscyloskopu przedstawiony jest na rysunku 2.2.
Wzmacniacz
Y1
POS V VAR
Wzmacniacz
Y2
POS V VAR
Przełącznik
-
Unia
Wzmacniacz
Y
LAMPA
Wzmacniacz
X
Rys. 2.2. Uproszczony schemat blokowy oscyloskopu
2.1. Lampa
Obraz przebiegu kreślony jest na ekranie lampy oscyloskopowej. Lampa
oscyloskopowa składa się z wyrzutni elektronów (żarzona katoda i siatka sterująca tzw.
cylinder Wehnelta), układu elektrycznych soczewek ogniskujących i przyspieszających
wiązkę elektronów (anody cylindryczne), dwóch par płytek (elektrod) odchylających
strumień elektronów w osi X (płytki ustawione pionowo) i osi Y
ustawione
poziomo) oraz ekranu pokrytego luminoforem. Elektrony, odchylane zgodnie ze
zmianami napięcia
uderzają w luminofor wywołując jego świecenie.
Od strony obserwatora na ekranie umieszczona jest siatka z podziałką. umożliwiająca
odczytanie wymiarów i dokonanie pomiarów. Dodatkowe układy lampy umożliwiają
regulację jasności (INTensivity) i ostrości (FOCus) kreślonej na ekranie linii.
2.2. Blok odchylania pionowego
Blok odchylania pionowego steruje ruchem plamki na ekranie w kierunku osi Y.
Z gniazda wejściowego BNC kanału Y (najczęściej niesymetrycznego, czyli
posiadającego jeden biegun
elektrycznie z masą oscyloskopu i przewodem
uziemiającym) sygnał mierzony doprowadzony jest do trójpozycyjnego przełącznika
rodzaju sprzężenia kanału (AC/GND/DC). W pozycji AC z badanego sygnału
eliminowana jest
stała (blokowana na szeregowym kondensatorze),
w
GND sygnał wejściowy jest odłączony a wejście zwarte do masy (służy do
ustawiania położenia linii na ekranie) a w pozycji DC na ekranie widoczny jest sygnał
wraz ze składową stałą.
Następnie sygnał badany doprowadzany jest do tłumika (skompensowany
dzielnik RC), który umożliwia wybranie odpowiedniego zakresu
pomiarowego i dopasowanie wysokości przebiegu do wymiaru pionowego ekranu
(najczęściej 8 działek). Z uwagi na dokładność pomiaru najkorzystniej jest, aby
wysokość obrazu była jak największa. Nastawianie odbywa się za pomocą
przełącznika skokowej regulacji wzmocnienia (Volts/DlVision).
W dalszej kolejności sygnał podawany jest do wzmacniacza wstępnego,
w którym realizowana jest funkcja przesuwania pionowego obrazu (pokrętło POSition
Vertical
regulacji wzmocnienia kanału
VARiable). Wybór
kalibrowanego (CALibrated) współczynnika wzmocnienia (zwykle poprzez
przekręcenie pokrętła płynnej regulacji wzmocnienia skrajnie w
oznacza
14
15

wzmocnienie kanału Y i
pomiaru, np.
wartości amplitudy napięcia.
W oscyloskopach dwukanałowych z lampą
za
wzmacniaczami wstępnymi znajduje się przełącznik elektroniczny
sterujący
wizualizacją obu przebiegów na ekranie. Możliwe jest wyświetlanie tylko jednego
1 lub CHannel 2) albo wyświetlanie sumy obu kanałów (ADDing).
Przy jednoczesnym wyświetlaniu (DUAL) możliwa jest praca naprzemienna
(ALTernating) - ten tryb pracy polega na naprzemiennym kreśleniu pełnego obrazu raz
z jednego, raz z drugiego kanału oraz praca „siekana" (CHOPPed) - polega na
wielokrotnym szybkim
obu kanałów i tworzeniu obrazów z nałożenia
kolejnych fragmentów przebiegów. Praca „siekana" używana jest do
przebiegów o malej częstotliwości (zapobiega migotaniu oglądanego obrazu).
Drugi kanał odchylania pionowego wyposażony jest zwykle w przełącznik
odwracający polaryzację sygnału (lNVert), który zastosowany wraz z przełącznikiem
ADDing umożliwia wizualizację różnicy obu sygnałów (jest to tzw. praca różnicowa
oscyloskopu).
Po przejściu sygnału
linię opóźniającą (stosowaną w celu uwzględnienia
czasu przetwarzania sygnałów w torze odchylania poziomego, ok. 200ns) sygnał
mierzony trafia na wzmacniacz końcowy odchylania pionowego, który steruje
elektrodami odchylania pionowego lampy oscyloskopowej.
2.3.
odchylania poziomego
Blok odchylania
steruje ruchem plamki w poziomie (w kierunku osi
X). Składa się on z generatora
czasu (wytwarzającego napięcie narastające
liniowo, tzw. napięcie
układu synchronizacji podstawy czasu (źródło
wyzwalania wewnętrzne CH1 lub CH2, zewnętrzne EXTernal lub wyzwalanie
z częstotliwością sieci 50Hz
i układu wyzwalania (wybór poziomu wyzwalania -
pokrętło LEVEL oraz wybór zbocza wyzwalania - pokrętło SLOPE). Dodatkowo w
torze odchylania poziomego znajduje się wzmacniacz napięciowy (w którym
realizowana jest funkcja przesuwania obrazu w poziomie - pokrętło POSition
i wzmacniacz końcowy, który steruje pracą elektrod odchylania
poziomego lampy.
Napięcie piłokształtne doprowadzone do płytek odchylania poziomego umożliwia
odwzorowanie badanego przebiegu w funkcji czasu. Prędkość przemieszczania się
16
plamki w
pomocą przełącznika skokowej regulacji
podstawy
względu na dokładność pomiaru najkorzystniej
jest. gdy
nus
przebiegu (np. okres sygnału) przyjmuje jak
największą długość (typowa szerokość ekranu wynosi 10 działek). Jeżeli współczynnik
podstawy czasu jest
(czyli zgodny z wartościami opisanymi na
to możliwe jest wykonanie
np. okresu badanego przebiegu.
Kalibrowaną
podstawę czasu nastawia się skręcając pokrętło płynnej
regulacji
czasu
w pozycję skrajnie w prawo.
jeżeli do
odchylania poziomego (poprzez wejście X)
doprowadzone zostanie napięcie o innym kształcie niż
to wówczas
odwzorowanie przebiegu nic będzie liniową funkcją czasu. W przypadku
doprowadzenia do wejścia X oraz do wejścia Y napięć okresowych i przestawieniu
oscyloskopu w tryb pracy X-Y otrzymujemy obraz będący złożeniem geometrycznym
obu
tzw
7
. figury Lissajous. Kształt figury zależy od kształtu
ich amplitudy i
oraz wzajemnego przesunięcia fazowego.
Aby obraz badanego
być
musi pojawiać się
w
w tym samym miejscu ekranu. Zgodność (synchronizację) miejsca i czasu
rozpoczęcia kreślenia zapewniają układ wyzwalania i układ synchronizacji podstawy
czasu. Układ synchronizacji (sterowany
mierzonym) powoduje rozpoczęcie
narastania napięcia
zawsze od tego samego poziomu (pokrętło
i tego samego zbocza (narastającego: SLOPE + lub opadającego: SLOPE -)
napięcia mierzonego.
2.4. Pomiary za pomocą oscyloskopu
Przed rozpoczęciem pomiarów należy:
Nastawić odpowiednie parametry kreślonej linii - pokrętłami regulacji
jaskrawości i ostrości linii regulować tak, aby linia była cienka, dobrze
zogniskowana i niezbyt jasna.
2. Pokrętła
regulacji
Y oraz podstawy czasu nastawić
w pozycji
3. Przycisk ekspansji podstawy czasu (MAGnitude) ustawić w położeniu
1".
4. Zidentyfikować przewody: sygnałowy i masowy (przypadkowa zamiana tych
przewodów podczas pomiarów może spowodować zwarcie i uszkodzenie
badanego
elektronicznego). W tym celu dotykamy palcem końcówki
17
%
r
„reakcję" na
widać wyraźne
linii. Problem identyfikacji przewodów nie
dotyczy oczywiście kabli koncentrycznych BNC bez przejściówki.
Jeżeli do pomiarów napięć o wartościach rzędu miliwoltów używane są przewody
zakończone końcówkami banankowymi, należy zwrócić uwagę, aby
przewody
jak najkrótsze. W przeciwnym przypadku pomiar może być utrudniony
wskutek indukowania się zakłóceń o częstotliwości sieci i przenikania ich do
oscyloskopu.
Pomiar odpowiednich wartości napięcia oraz czasu polega na wyznaczeniu
wysokości lub długości odcinków proporcjonalnych do mierzonej wielkości
i przemnożeniu ich przez odpowiednie
opisane na pokrętłach skokowej
regulacji czułości kanałów Y (gdy mierzymy amplitudę napięcia lub inne
napięciowe) lub skokowej regulacji podstawy czasu (gdy mierzymy okres lub inne
czasowe przebiegu). Ponieważ rezystancja wejściowa oscyloskopu jest duża
(zwykle
więc bezpośrednie
oscyloskopu do obwodu pomiarowego
nie powoduje istotnego błędu systematycznego pomiaru. Należy pamiętać, aby
wymiary odpowiednich odcinków odczytywać bez błędu paralaksy i zawsze przy tej
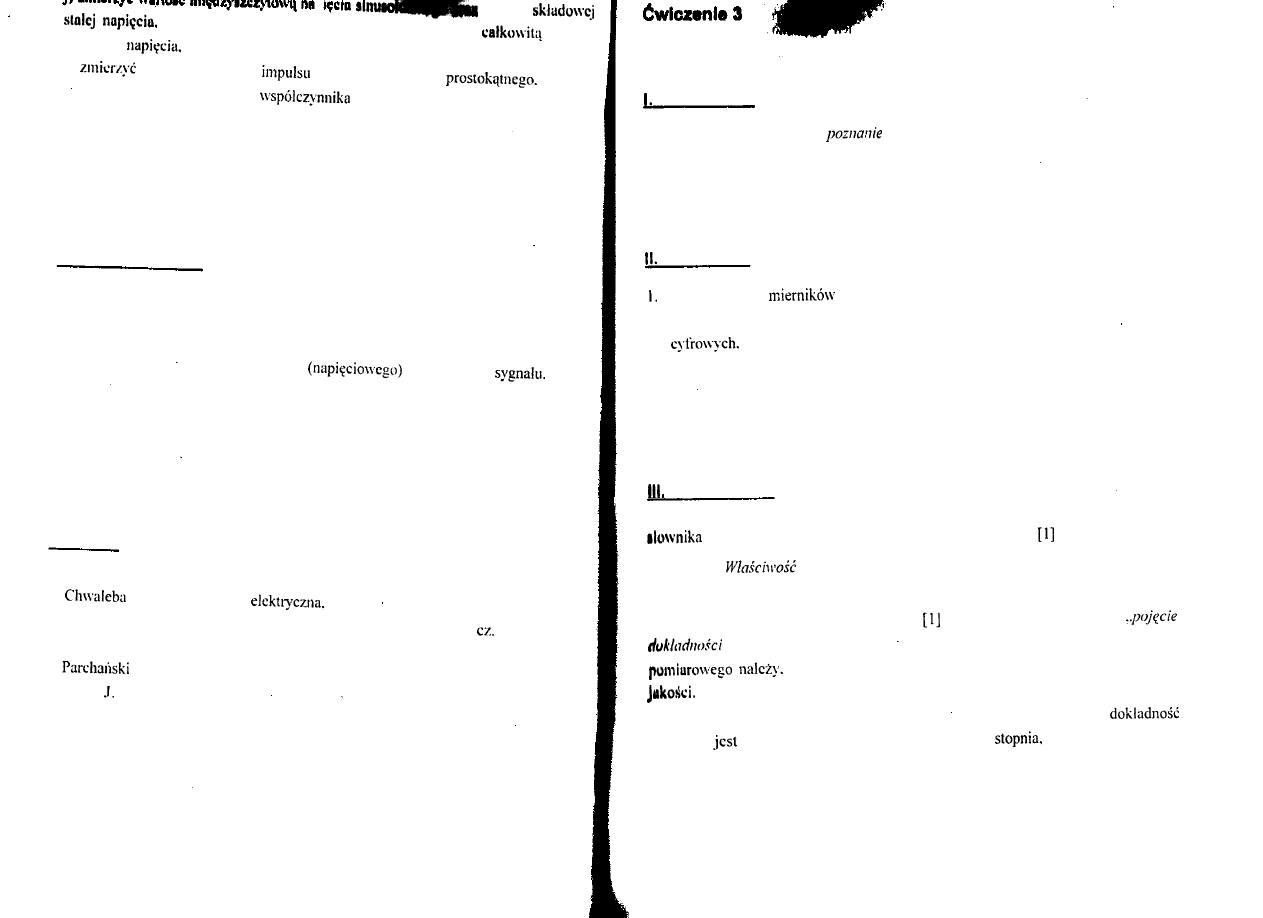
samej stronie krawędzi linii. Przykładowy widok ekranu oscyloskopu podczas pomiaru
napięcia sinusoidalnego (z zaznaczonym poziomem i zboczem wyzwalania)
przedstawiony jest na rysunku 2.3.
SLOPE
\
•
'•
/
T7
i !
\ : /
\
\
i
j
"I
Rys. 2.3. Pomiary parametrów napięcia sinusoidalnego
wartość napięcia obliczana
ze wzoru:
(2.3)
18
natomiast okres przebiegu wyznaczony na podstawie wzoru:
(2.4)
gdzie:
[V/dz] - nastawiony współczynnik odchylania w torze Y, C, [czas/dz] -
nastawiona podstawa czasu.
Należy pamiętać, iż znamienną zaletą oscyloskopu jest możliwość obserwacji
kształtu sygnałów i ich wzajemnego położenia względem siebie. Dokładność pomiaru
za pomocą oscyloskopu jest niewielka (rzędu kilku procent) i określona głównie
błędami granicznymi toru odchylania pionowego i podstawy czasu oraz nieliniowością
odchylania lampy oscyloskopowej.
IV. Program ćwiczenia
1. Zapoznać się z
i
cyfrowego:
a) sprawdzić poprawność
częstościomierza, zapisać wynik kontroli,
stwierdzić, czy przyrząd działa poprawnie czy nie,
b) zmierzyć częstotliwość sygnału prostokątnego dołączonego z generatora
wynik zapisać w sprawozdaniu,
c) zmierzyć wartość okresu sygnału, zapisać wynik pomiaru.
2. Zapoznać się z działaniem i podstawową obsługą oscyloskopu analogowego:
u) sprawdzić nastawienia parametrów kreślonej na ekranie linii,
b) sprawdzić
i pokręteł bloku odchylania pionowego,
c) sprawdzić
przełączników i pokręteł bloku odchylania poziomego,
cl) sprawdzić działanie przełączników i pokręteł bloku wyzwalania,
c) zidentyfikować przewód sygnałowy i przewód masowy na kablu koncentrycznym
z przejściówką
0 zaobserwować pracę oscyloskopu w trybie
oraz w trybie
sprawdzić działanie przełącznika pracy naprzemiennej i pracy siekanej,
nastawić sumacyjny i różnicowy tryb pracy oscyloskopu,
i) zaobsenvo\vać powstawanie figur
19
p
wartość
obliczyć wartość skuteczną składowej zmiennej i
wartość
skuteczną
k)
wartość szerokości
oraz okresu napięcia
obliczyć
wartość częstotliwości i wartość
wypełnienia sygnału.
3. Zapisać wnioski i spostrzeżenia z pomiarów.
V. Pytania kontrolne
1. Jakie wielkości fizyczne można zmierzyć za pomocą częstościomierza cyfrowego?
2. Omówić ogólną zasadę cyfrowego pomiaru częstotliwości.
3. Jakie są zasadnicze zalety oscyloskopu?
4. Omówić podstawowe elementy toru Y
przetwarzania
5. Omówić podstawowe elementy toru X (czasowego) przetwarzania sygnału.
6. Jaka jest zasada pomiaru za pomocą oscyloskopu amplitudy napięcia i okresu
przebiegu periodycznego?
7. Na co należ}' zwrócić uwagę, aby prawidłowo zmierzyć parametry napięciowe
i czasowe badanego sygnału?
Literatura
1. Rydzewski J.: Pomiary oscyloskopowe, Warszawa: WNT, 1995.
2.
A. i in.: Metrologia
Warszawa: WNT, 1998.
3. Dyszyński J.: Metrologia elektryczna i elektroniczna - laboratorium
I, Rzeszów:
OWPRz. 1997.
4.
J.: Miernictwo elektryczne i elektroniczne, Warszawa: WSiP, 1997.
5. Dusza i in.: Podstawy miernictwa. Warszawa: OWPW. 1998.
OCENA
DOKŁADNOŚCI PRZYRZĄDÓW POMIAROWYCH
Cel ćwiczenia
Celem ćwiczenia jest
zasad sprawdzania dokładności wskazań
użytkowych przyrządów pomiarowych analogowych i cyfrowych oraz praktyczne
wykonanie oceny dokładności analogowego (wskazówkowego) miliamperomierza
oraz cyfrowego woltomierza tablicowego na wybranych zakresach.
Zagadnienia
Zasada działania
analogowych i cyfrowych (porównanie).
2. Określanie maksymalnych błędów dopuszczalnych mierników analogowych
i
deklarowanych przez ich producentów.
.1. Zasady doboru mierników i przyrządów kontrolnych przeznaczonych do
sprawdzania poprawności wskazań mierników użytkowych.
4. Praktyczne sprawdzenie dokładności wskazań jednozakresowych tablicowych
przyrządów pomiarowych oraz uniwersalnych cyfrowych przyrządów pomiarowych.
Wprowadzenie
Dokładność przyrządu pomiarowego, zgodnie z definicją międzynarodowego
podstawowych i ogólnych terminów metrologicznych
jest to:
,.
przyrządu pomiarowego dawania odpowiedzi
(wskazań) bliskich wartości prawdziwej ".
Definicja ta opatrzona jest w słowniku
następującym komentarzem:
jest pojęciem jakościowym". Zagadnienie oceny dokładności przyrządu
więc potraktować jako zadanie należące do dziedziny oceny
Chcąc oceniać jakość przyrządu pomiarowego ze względu na jego
konieczne
zgodnie z definicją jakości [2], ustalenie
w jakim spełnione są
odpowiednie wymagania dotyczące dokładności przyrządu pomiarowego.
20
21
wymagania
stawiane przyrządom pomiarowym
względu na ich dokładność mogą być bardzo
różne. Dlatego też dla tego
przyrządu pomiarowego możliwe jest uzyskanie
ocen jego dokładności. W zależności od przyjętego kryterium wynikiem
oceny dokładności przyrządu pomiarowego mogą być różne stwierdzenia. Na przykład
takie:
A-
B-
C-
dokładność przyrządu pomiarowego jest wystarczająca do
realizacji zamierzonego celu, wymagającego wykonywania
pomiarów tym przyrządem.
dokładność przyrządu pomiarowego jest lepsza od
wymaganej tylko
zakresu pomiarowego.
dokładność przyrządu pomiarowego nie jest gorsza od
dokładności deklarowanej przez jego producenta
Najbardziej podstawowym i powszechnym wymaganiem stawianym przyrządom
pomiarowym jest wymaganie dokładności nie gorszej od dokładności deklarowanej
przez ich producentów. Wymaganie to oznacza że maksymalny błąd wskazań
przyrządu pomiarowego nie powinien w danym punkcie sprawdzeń, przekraczać
wartości Maksymalnego Błędu Dopuszczalnego - MBD. [ang: Maximum
Error- MPEJ w całym zakresie pomiarowym. Ponieważ maksymalny błąd
dopuszczalny nie jest tym samym błędem co błąd maksymalny
należy dla
podkreślenia tego faktu oznaczać go inaczej na przykład jako -
•
Wartości maksymalnych dopuszczalnych błędów
przyrządów
pomiarowych producenci deklarują dla całej serii danego typu przyrządów i określają
na podstawie statystycznych danych zbieranych podczas wzorcowania wykonywanego
w czasie ich produkcji.
Deklaracje te podawane są w każdej instrukcji obsługi, najczęściej odrębnie dla
każdego zakresu pomiarowego. W zależności od rodzaju przyrządów pomiarowych
deklaracja
podawana przez ich producentów jest zróżnicowana.
producenci formułują deklarację dokładności dla przyrządów analogowych
wskazówkowych a inaczej dla przyrządów lub multimetrów cyfrowych wyposażonych
w elektroniczne wzmacniacze pomiarowe oraz przetworniki analogowo-cyfrowe
22
Dla
analogowych wskazówkowych deklaracja dokładności
jest w postaci klasy dokładności -
definiowanej wyrażeniem
=
(1)
- jest wartością nominalnego zakresu (wskazań) przyrządu pomiarowego
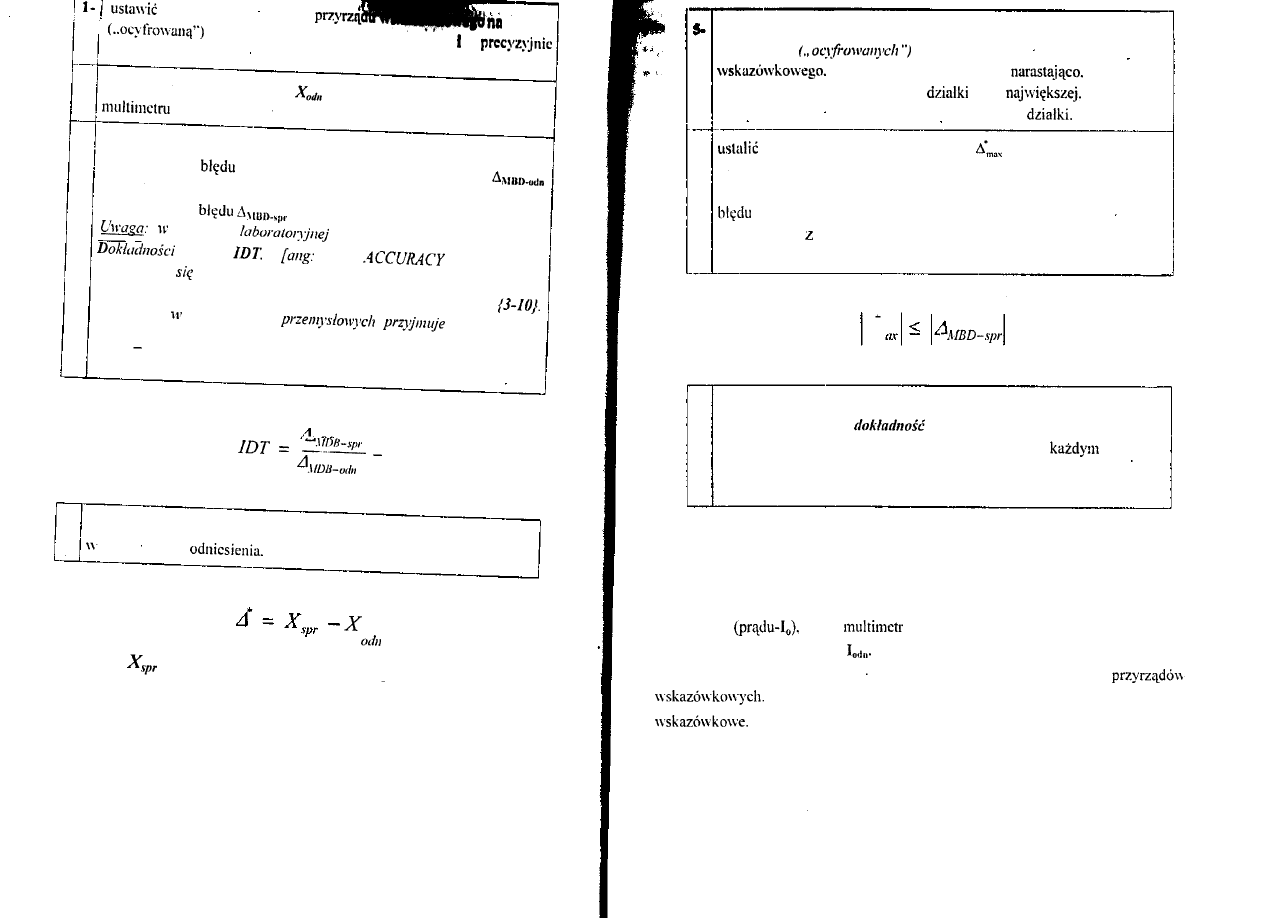
Graficzna interpretacja wyrażenia (1) definiującego klasę dokładności
przyrządu pomiarowego przedstawiona jest na rysunku
.2
-+-
50%
X-
mierzona
100%
t
Interpretacja graficzna definicji klasy
przyrządu pomiarowego
Z rysunku 3.1. jednoznacznie wynika że w każdym punkcie zakresu
pomiarowego przyrządu wskazówkowego, dla którego określono klasę dokładności,
wartość maksymalnego błędu dopuszczalnego -
jest stała !!!!!!
W celu sprawdzenia tego, czy wskazówkowy przyrząd pomiarowy posiada
nie gorszą od dokładności którą zadeklarował jego producent konieczne
wykonanie odpowiedniej procedur)' sprawdzającej. Procedur sprawdzających
można opracować wiele
i mogą one różnić się na przykład ilością punktów
sprawdzania na danym zakresie pomiarowym lub ilością powtórzeń w danym punkcie
sprawdzeń.
Najbardziej uproszczoną procedurą sprawdzania dokładności wskazówkowych
przyrządów pomiarowych może być procedura składająca się z następującej sekwencji
czynności:
23
wskazanie sprawdzanego
opisuną
i
działkę, za pomocą stabilnego
regulowanego źródła wartości odniesienia (zasilacza lub knlibratora).
odczytać wartość odniesienia -
na polu odczytowym kalibratora lub
wskazującego wartości odniesienia.
2-
3-
sprawdzić czy w danym punkcie sprawdzania wartość maksymalnego
dopuszczalnego
kalibratora lub multimetru odniesienia
jest wymaganą ilość razy mniejsza od wartości maksymalnego
dopuszczalnego
przyrządu sprawdzanego.
praktyce
oblicza się w tym celu Iloraz
Testu -
TEST
RAT10 - TAR]
i sprawdza
czy jego wartość jest większa od przyjętej wartości,
będącej liczbą wybraną z liczb należących do przedziału od
Najczęściej
laboratoriach
się kryterium
IDT > 4, i sprawdza się prawdziwość nierówności określonej
wyrażeniem (2).
> 4
(2)
4- obliczyć odchylenie wskazań przyrządu sprawdzanego od ustalonej
p. 2. wartości
korzystając z wyrażenia (3)
(3)
gdzie:
- wskazanie przyrządu sprawdzanego
powtórzyć czynności opisane w punktach od 1-4 dla wszystkich
opisanych
działek sprawdzanego przyrządu
ustawiając wartości wskazań
to znaczy od
najmniejszej wartości opisanej
do
a następnie
malejąco od największej do najmniejszej opisanej
6-
maksymalne odchylenie wskazań
na podstawie uzyskanych
wyników sprawdzeń i sprawdzić czy jego wartość bezwzględna jest
mniejsza od bezwzględnej wartości maksymalnego dopuszczalnego
deklarowanego przez producenta przyrządu sprawdzanego
i obliczanego wyrażenia (1). Inaczej ujmując, sprawdzić czy spełniona
jest nierówność (4).
4
(4)
7-
Dokonać oceny dokładności sprawdzanego przyrządu wskazówkowego
(ustalić czy jego
nie jest gorsza od dokładności
deklarowanej przez producenta)
analizując w
punkcie
sprawdzania czy jednocześnie prawdziwe są nierówności określone
wyrażeniami (2) i (4).
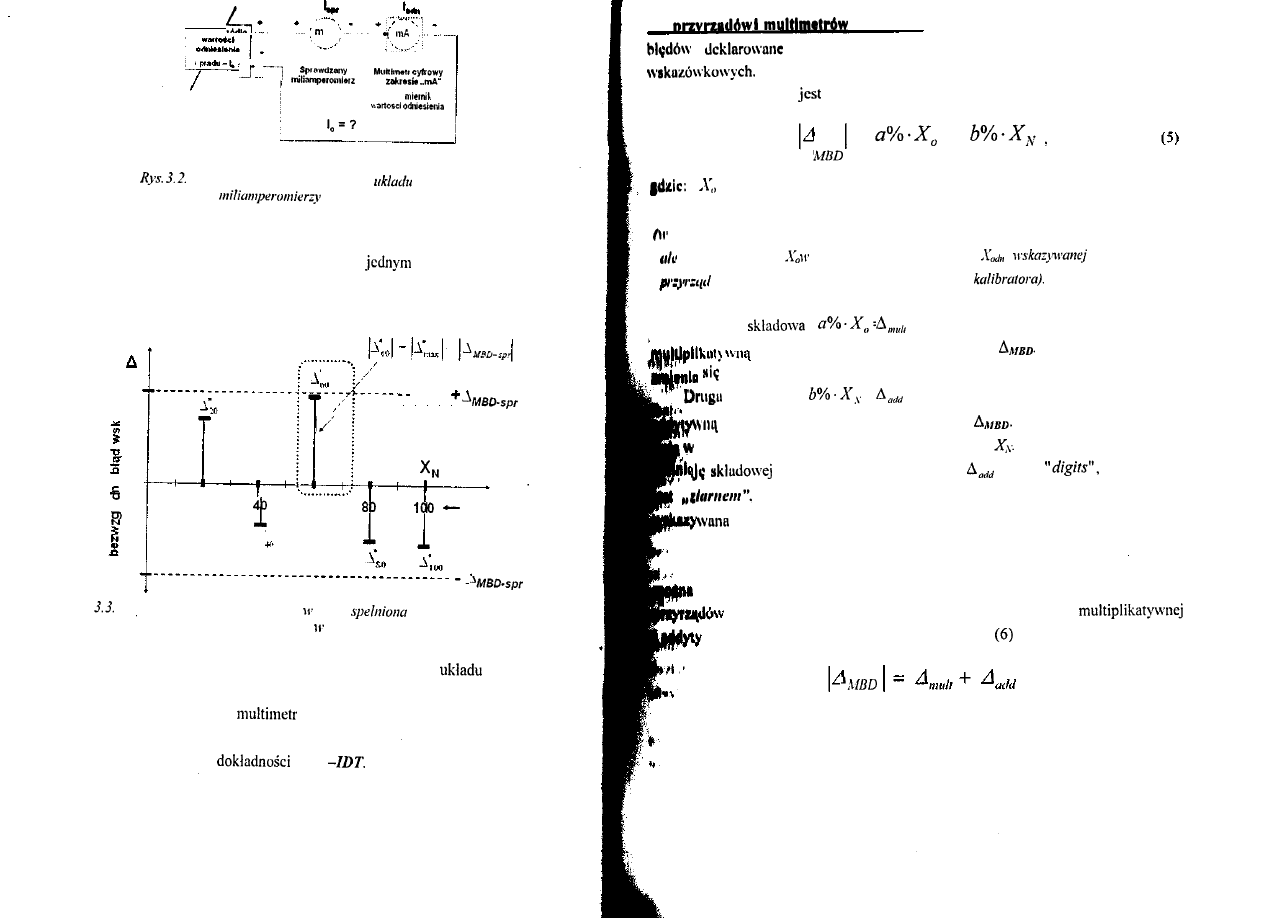
Na rysunku 3.2. przedstawiony jest schemat ideowy przykładowego układu
pomiarowego przeznaczonego do sprawdzania miliamperoniierzy wskazówkowych
w którym wykorzystane jest precyzyjnie regulowane i stabilne źródło wartości
odniesienia
oraz
cyfrowy o odpowiedniej dokładności jako
miernik wartości odniesienia -
W układzie tym można zrealizować opisaną wyżej
uproszczoną procedurę sprawdzania dokładności użytkowych
Takich na przykład jak miliamperomierze lub amperomierze
24
25
Precyzyjnie
regulowane
•
A •
wskazówkowy
na
- |alo
Schemat ideowy przykładowego
do sprawdzania
wskazówkowych.
Na rysunku 3.3. przedstawiona jest graficzna interpretacja sytuacji w której we
wszystkich punktach sprawdzania ustalanych w
kierunku zmian wielkości
mierzonej (wartość wielkości mierzonej wzrasta lub maleje) spełniona jest nierówność
(2).
•c
ra
N
-
—
20
A'
~~~
X- Wielkość mierzona
x
60
działki
Rys.
Graficzna interpretacja sytuacji której
jest nierówność (2) podczas
sprawdzania przyrządu wskazówkowego jednym kierunku zmian wartości mierzonej.
W przedstawionym na rysunku 3.2. schemacie
pomiarowego
przeznaczonego do sprawdzania dokładności wskazówkowych przyrządów
pomiarowych, zastosowano
cyfrowy wskazujący wartości odniesienia
w poszczególnych punktach sprawdzeń. Należy na to zwrócić baczną uwagę podczas
obliczania wartości ilorazu
testu
Dla
cyfrowych wartości maksymalnych dopuszczalnych
są przez ich producentów inaczej niż dla przyrządów
W tym przypadku deklaracja dokładności dla danego zakresu
pomiarowego podawana
najczęściej w postaci wyrażenia (5)
=
+
-prawdziwa wartość wielkości mierzonej.
praktyce podczas sprawdzania dokładności podaje się przybliżenie prawdziwej
nieznanej wartości
postaci wartości odniesienia -
przez
odniesienia lub odczytanej z pola odczytowego
Pierwsza
wyrażenia (5) nazywana jest składową
maksymalnego błędu dopuszczalnego -
Wartość tej składowej
wraz ze zmianą wartości wielkości mierzonej.
składowa
=
wyrażenia (5) nazywana jest składową
maksymalnego błędu dopuszczalnego -
Wartość tej składowej jest
każdym punkcie danego zakresu pomiarowego -
Bardzo często producenci
addytywnej podają w postaci
= k •
gdzie „digits"
czyli najmniejszą wartością o jaką może zmienić się wartość
przez cyfrowy przyrząd mierzący na danym zakresie pomiarowym.
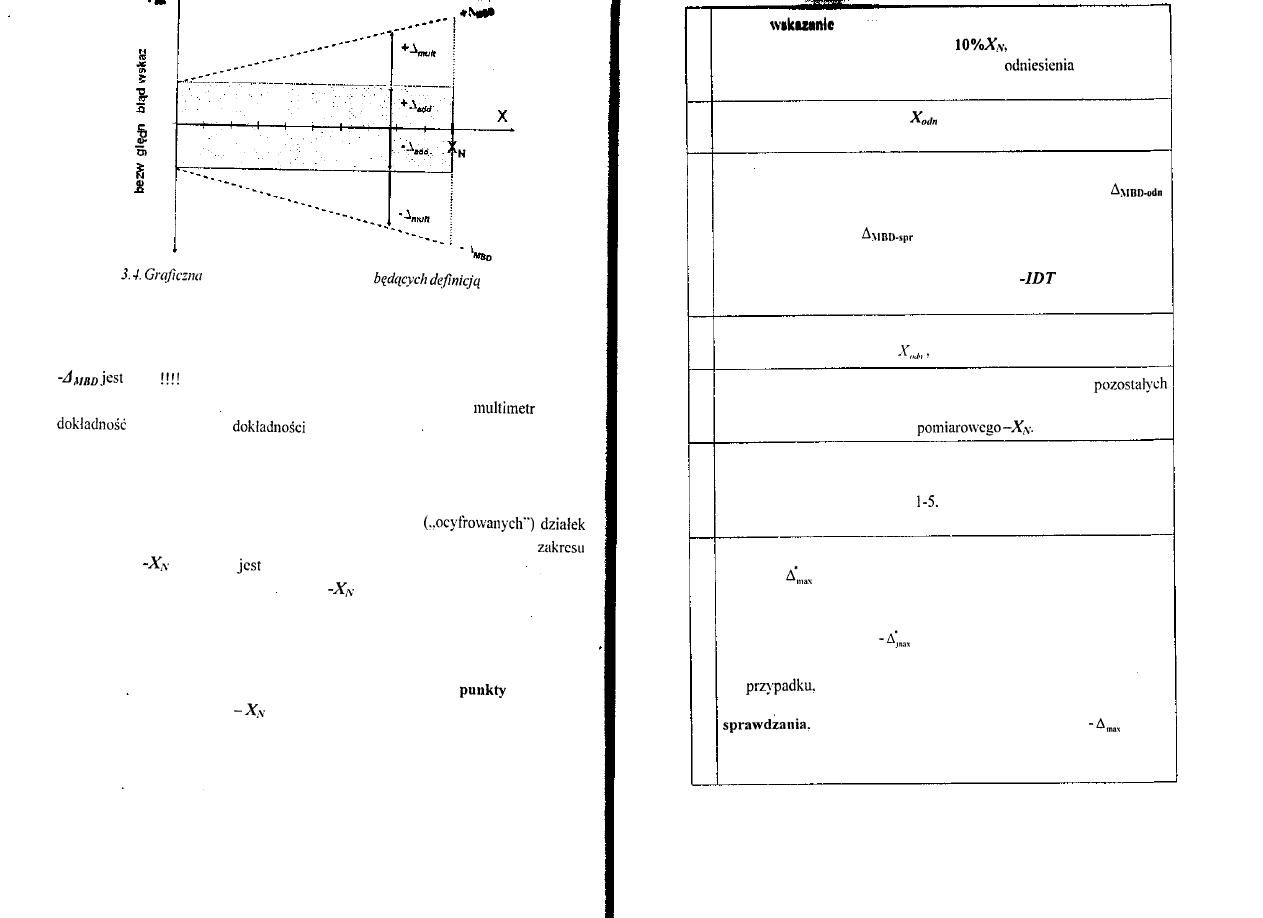
Na rysunku 3.4. przedstawiono graficzną interpretację wyrażenia (5) z którego
wyliczać wartości maksymalnych błędów dopuszczalnych dla cyfrowych
pomiarowych określanych jako suma składowej
wnej, którą można zapisać w postaci wyrażenia
(6)
26
27
•c
TO
N
-A
Rys.
interpretacja wyrażeń (5) i (6)
dokładności
deklarowanej przez producentów przyrządów lub niultimetrów cyfrowych.
Z rysunku 3.4. jasno wynika że w każdym punkcie zakresu pomiarowego
przyrządu lub multimetru cyfrowego wartość maksymalnego błędu dopuszczalnego
inna
i systematycznie wzrasta wraz ze wzrostem wartości mierzonej.
W celu sprawdzenia tego, czy cyfrowy przyrząd pomiarowy lub
posiada
nie gorszą od
którą zadeklarował jego producent można
wykonać odpowiednią procedurę sprawdzającą podobną do opisanej wcześniej
procedury sprawdzania dokładności analogowych przyrządów wskazówkowych.
Procedura ta będzie różnic się od poprzednio opisanej tylko zasadą ustalania
poszczególnych punktów sprawdzeń. Zamiast opisanych
jako punkty sprawdzeń przyjmowane są odpowiednie części nominalnego
pomiarowego
. Zalecane
przyjmowanie pięciu takich punktów stanowiących:
10%, 30%, 50%, 70% i 90% wartości
nominalnego zakresu sprawdzanego
cyfrowego przyrządu pomiarowego lub multimetru.
W przypadku sprawdzania multimetru cyfrowego można zastosować tak określone
5 punktów sprawdzeń dla zakresu podstawowego, natomiast dla pozostałych
zakresów tej samej wielkości mierzonej można zastosować 3
sprawdzeń:
10%, 50% i 90% wartości
Po uwzględnieniu wyżej opisanych uwag najbardziej uproszczona procedura
sprawdzania dokładności cyfrowych przyrządów pomiarowych lub niultimetrów może
być następująca:
1-
2-
3-
4-
5-
6-
7-
ustawlć
sprawdzanego przyrządu cyfrowego mierzącego na
danym zukresic na wartość równą
za pomocą stabilnego
i precyzyjnie regulowanego źródła wartości
(zasilacza lub
kalibratora)
odczytać wartość odniesienia -
na polu odczytowym kalibratora lub
multimetru wskazującego wartości odniesienia.
sprawdzić czy w danym punkcie sprawdzania wartość maksymalnego
dopuszczalnego błędu kalibratora lub multimetru odniesienia
jest wymaganą ilość razy mniejsza od wartości maksymalnego
dopuszczalnego błędu
sprawdzanego przyrządu lub multimetru
cyfrowego.
Obliczyć w tym celu iloraz dokładności testu
i sprawdzić czy
prawdziwa jest nierówność określona wyrażeniem (2)
obliczyć odchylenie wskazań - A', przyrządu sprawdzanego od ustalonej
w p. 2. wartości odniesienia
korzystając z wyrażenia (3).
powtórzyć czynności opisane w punktach od 1-4 dla
punktów sprawdzeń ustalonych jako 30%, 50%, 70%, 90%, nominalnej
wartości sprawdzanego zakresu
w przypadku zakresów na których przyrząd lub multimetr cyfrowy
mierzy wartość prądu lub napięcia stałego należy powtórzyć czynności
opisane w punktach od
także dla odwrotnej (ujemnej)
polaryzacji.
w każdym punkcie sprawdzania ustalić maksymalną wartość odchylenia
wskazań
korzystając z wyrażenia (3) i sprawdzić czy prawdziwa
jest nierówność (4). Należy przyjąć że w uproszczonej procedurze w
której wykonywane jest jedno sprawdzenie w danym punkcie sprawdzeń
maksymalne odchylenie
równe jest wyznaczonemu w punkcie 4.
odchyleniu -A*.
W
gdy zastosowana będzie bardziej złożona procedura
wymagająca wielokrotnych powtórzeń w tym samym punkcie
maksymalną wartość odchylenia wskazań
należy
ustalić analizując wartości odchyleń wyznaczone podczas wszystkich
powtórzeń wykonanych w tym samym punkcie sprawdzeń.
28
29
8-
oceny dokładności sprawdzanego przyrządu lub
(ustalić czy jego dokładność nie jest gorsza od dokładności
deklarowanej przez producenta)
analizując w każdym punkcie
sprawdzania czy jednocześnie prawdziwe są nierówności określone
(2) i (4).
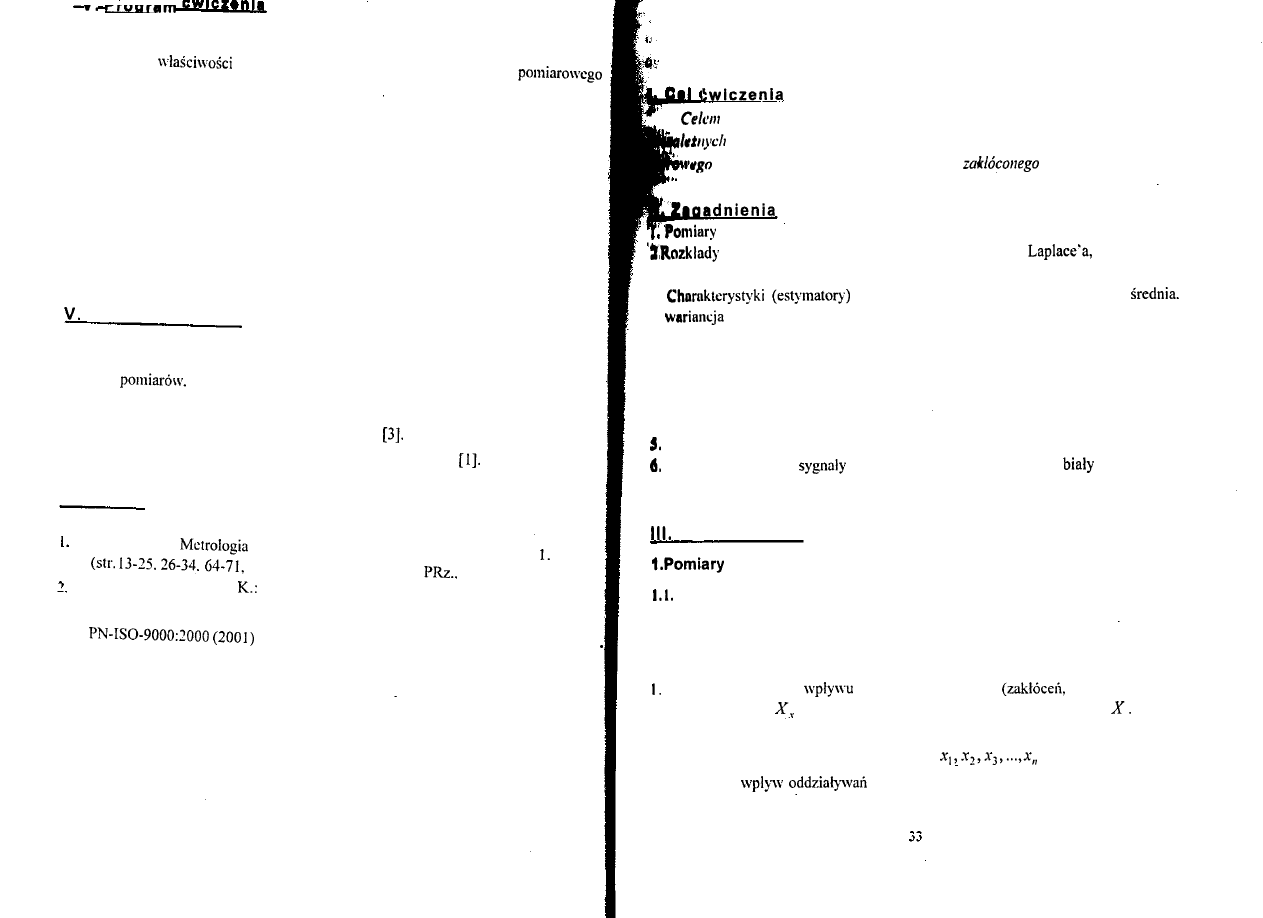
Na rysunku 3.5. przedstawiony jest schemat ideowy przykładowego układu
pomiarowego przeznaczonego do sprawdzania woltomierzy lub
cyfrowych w którym wykorzystane jest precyzyjnie regulowane i stabilne źródło
wartości odniesienia
oraz multimetr cyfrowy o odpowiedniej
dokładności jako miernik wartości odniesienia -
W układzie tym można
zrealizować opisaną wyżej uproszczoną procedurę sprawdzania dokładności
przyrządów lub
cyfrowych. Takich na
jak cyfrowe
woltomierze tablicowe.
Stabilna
wartości
odniesienia
Precyzyjnie
regulowane
Multimetr cyfrowy
na zakresie ..V"
cyfrowy
użytkowy
- jako
odniesienia
Rys. 3.5.
ideowy
układu pomiarowego przeznaczonego do
sprawdzania dokładności
cyfrowych.
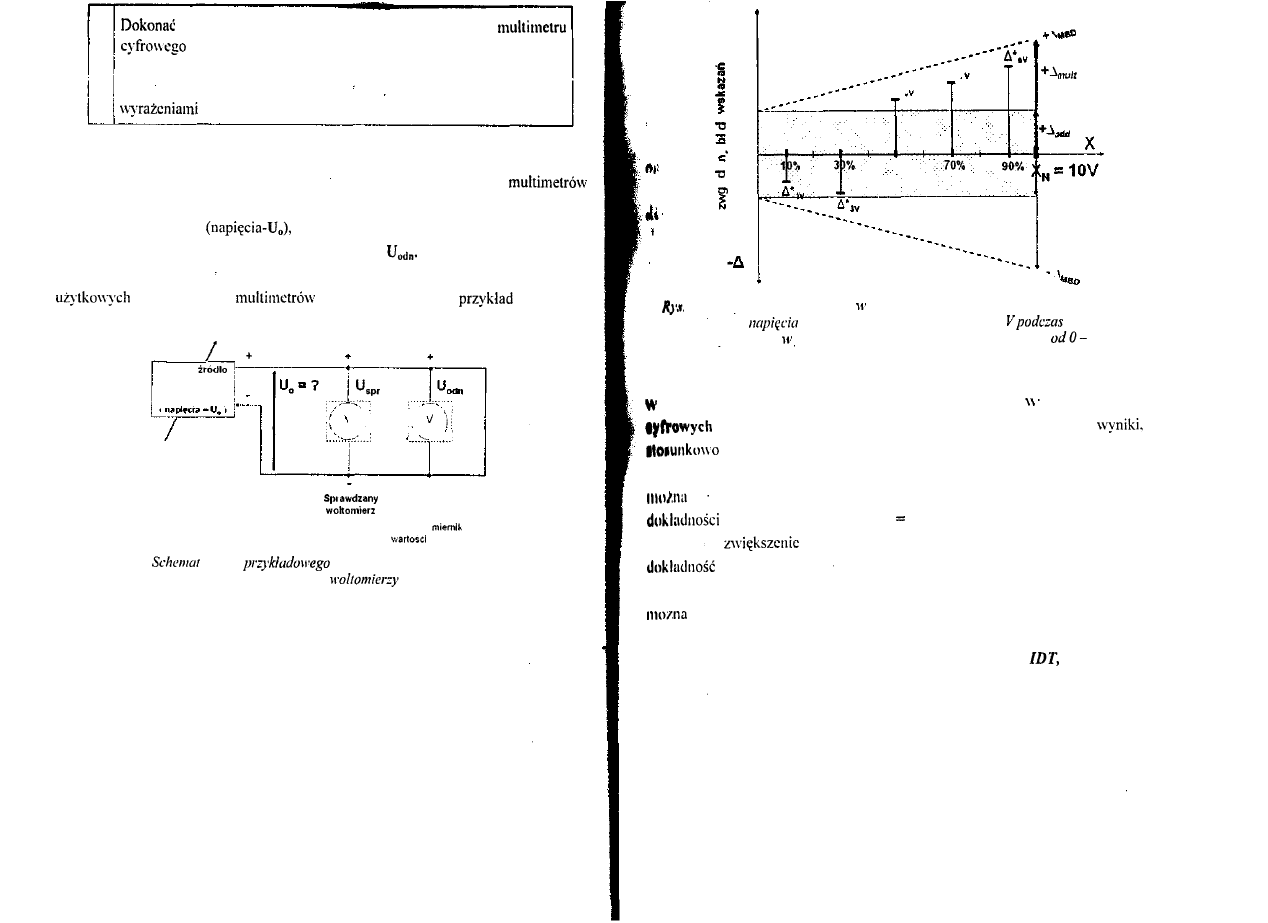
Na rysunku 3.6. przedstawiono graficzną interpretację sytuacji w której spełniona
jest nierówność (2) podczas sprawdzania dokładności cyfrowego woltomierza napięcia
stałego mierzącego na zakresie 10V. Rysunek wykonano dla sprawdzania dokładności
w jednym (dodatnim) kierunku zmian polaryzacji napięcia od 0 do +10V.
+A
>
£1
AS
A*.
50%
,:.:.
3.6. Graficzna interpretacja której spełniona jest nierówność (2) dla woltomierza
cyfrowego
stałego mierzącego na zakresie 10
sprawdzania
wykonanego
jednym kierunku zmian wartości odniesienia
10V
Starannie wykonana uproszczona procedura sprawdzania przedstawiona
punktach od 1-7 dla przyrządów wskazówkowych oraz punktach od 1-8 dla
przyrządów pomiarowych, daje wystarczająco pewne
jest
szybka do wykonania i nie generuje wysokich kosztów sprawdzenia.
Pewność ocen dokładności dokonywanych na podstawie tej uproszczonej procedury
zwiększać przyjmując jako jedno z kryterium oceny, wyższe wartości ilorazu
testu. Na przykład: 1DT 5, 6, 7, 8, 9 lub 10. Będzie to jednak
powodować
wymagań na stabilność źródła wartości odniesienia oraz na
multimetru cyfrowego wskazującego wartości odniesienia.
W konsekwencji zwiększy to koszty sprawdzania. Zamiast multimetru cyfrowego
zastosować odpowiednio dokładny kalibrator posiadający wbudowany
wskaźnik wartości odniesienia. Należy jednak starannie sprawdzić czy przy założonej
w danym laboratorium wartości ilorazu dokładności testu -
kalibrator posiada
wystarczającą dokładność. Należy także ocenić koszty zakupu kalibratora i wybrać to
rozwiązanie tylko w przypadku gdy gwarantuje on wymaganą dokładność wskazań,
II jego koszt zakupu jest niższy od kosztu zakupu stabilnego źródła wartości
odniesienia i multimetru cyfrowego o odpowiedniej dokładności.
30
31
•
1. Zapisanie danych ogólnych przyrządów pomiarowych używanych w ćwiczeniu.
2. Zapisanie
metrologicznych oraz zestawienie układu
przedstawionego na rysunku 3.1.
3. Wykonanie sprawdzenia dokładności wskazań tablicowego miliamperomierza
wskazówkowego.
4. Zapisanie właściwości metrologicznych oraz zestawienie układu pomiarowego
przedstawionego na rysunku 3.2.
5. Wykonanie sprawdzenie poprawności wskazań tablicowego woltomierza
cyfrowego na wybranym zakresie.
6. Opracowanie wyników sprawdzania dokładności obydwu przyrządów oraz
wniosków końcowych.
Pytania kontrolne
1. Spójność pomiarowa, wzorce miar, wzorce użytkowe [3].
2. Błędy
odchylenia i błędy graniczne przyrządów pomiarowych [3].
3. Definicja klasy dokładności mierników analogowych - wskazówkowych [1].
4. Definicja błędu granicznego miernika cyfrowego
5. Zasady doboru mierników wskazujących wartości odniesienia
Literatura
Dyszyński J. :
Elektryczna i Elektroniczna - Laboratorium cz.
87-90) Rzeszów: Ofic. Wyd.
1989,1996.
Piotrowski J.. Kostyrko
Wzorcowanie aparatury pomiarowej WNT
Warszawa.
Systemy Zarządzania Jakością. Podstawy
i terminologia.
Międzynarodowy Słownik Podstawowych i Ogólnych Terminów Metrologii.
Wydanie polskie. Warszawa: Główny Urząd Miar, 1996 r.
3.
4.
32
ĆWICZENIE 4
OPRACOWANIE SERII WYNIKÓW POMIARU
.V.
ćwiczenia jest poznanie zasad statystycznego opracowywania serii
wyników obserwacji i oceny niepewności wyniku pomiaru na przykładzie
pomiaru okresu napięcia sinusoidalnego
szumem normalnym.
ze statystycznym opracowaniem serii wyników obserwacji.
prawdopodobieństwa: normalny (Gaussa),
jednostajny,
Studenta.
3,
opisujące wielkości przypadkowe: wartość
eksperymentalna oraz odchylenie standardowe eksperymentalne
wyników obserwacji, wariancja eksperymentalna oraz odchylenie standardowe
eksperymentalne średniej arytmetycznej - wyniku pomiaru.
4. Niepewność wyniku pomiaru typu A, standardowa i rozszerzona niepewność typu
A. Obliczanie niepewności typu A podczas statystycznego opracowania serii
wyników obserwacji, współczynnik rozszerzenia, poziom ufności.
Cyfrowa zasada pomiaru okresu.
Parametry opisujące
napięciowe: sinusoidalny i szum
w dziedzinie
amplitudowej.
Wprowadzenie
ze statystycznym opracowaniem serii wyników obserwacji
Cele wykonywania pomiarów ze statystycznym opracowaniem serii
obserwacji
Pomiary ze statystycznym opracowaniem serii wyników obserwacji wykonuje
się w dwóch podstawowych przypadkach:
w celu zmniejszenia
oddziaływań losowych
szumów) podczas
pomiaru stałej
(jednak nieznanej) wartości wielkości mierzonej
W tym
przypadku mierzony jest ten sam parametr tego samego obiektu badania,
a zmienne w czasie kolejne wartości
n wyników obserwacji
odwzorują
losowych;
2. w
wyznaczania parametrów
który
charakteryzuje się pewnym
wartości wielkości badanej. Przykładowo
takim obiektem może być linia produkcyjna, na przykład rezystorów pewnego
typu o zadanej wartości nominalnej rezystancji
Wartości
rezystancji produkowanych poszczególnych rezystorów różnią się pomiędzy
i zadaniem statystycznego opracowania tych wartości może być wyznaczanie
wartości oczekiwanej rezystancji, wariancji oraz standardowego
tolerancji wartości rezystancji serii rezystorów na zadanym poziomie
a nawet i rozkładu prawdopodobieństwa wartości rezystancji. Te parametry
charakteryzują jakość (dokładność) linii produkcyjnej, analizowane wartości
rezystancji i?,,
w takim zagadnieniu występują jako losowe
wartości w przestrzeni zbioru wartości.
W danym ćwiczeniu badane jest pierwsze zagadnienie. Z punktu widzenia
obiektywnego podczas pomiaru wartości wielkości stałej w wyniku wpływu losowych
oddziaływań
kolejne wyniki pomiaru
tej wielkości zmieniają się chaotycznie,
nieregularnie i są równe
X + (1)
gdzie
2,
n jest liczbą zaobserwowanych wyników.
Jednak z punku widzenia eksperymentatora w podanym wyżej modelu (1) są
dwie nieznane wartości: X - co jest celem pomiaru oraz
- co jest celem redukcji
(zmniejszania)
Otóż eksperymentatorowi dostępne są tylko wartości
...
1.2. Ocena wielkości mierzonej uzyskiwana na podstawie opracowania
statystycznego serii obserwacji
W procesie statystycznego opracowania serii wyników obserwacji należy
wyznaczyć najlepszą ocenę wartości wielkości mierzonej oraz oszacować parametry
(charakterystyki) niepewności wyniku na zadanym poziomie ufności.
Najlepsza ocena wartości wielkości mierzonej zależy nie tylko od samych
wartości zaobserwowanych i ich liczby a także od ich rozkładu
tzn. od sposobu wzajemnego ich usytuowania. Za najlepszą ocenę wartości wielkości
mierzonej przyjmuje się parametr rozkładu prawdopodobieństwa, który ma
najmniejszą wariancję (rozproszenie lub fluktuacje) przy opracowaniu kilku kolejnych
serii wyników obserwacji z tą
liczbą wyników. Dla niektórych szeroko
34
najlepszą oceną wartości wielkości
mierzonej są:
Dla
normalnego
którego
są opisane poniżej,
najlepszą oceną jest wartość średnia wyników obserwacji
1
= - x
n n
,
Laplace'a
a, b). który opisuje się zależnością
(2)
(3)
- jest punktem środkowym rozkładu - oczekiwaniem matematycznym
oraz medianą
A- jest parametrem, który wyznacza wariancję
= 2 •
najlepszą oceną jest mediana wyników obserwacji, która dla
liczby wyników obserwacji
zdefiniowana jako wynik obserwacji ze
Średnim numerem uporządkowanej serii wyników
a w razie parzystej liczby wyników obserwacji medianą jest wartość średnia
dwóch środkowych wyników uporządkowanej serii wyników
'
(5)
3) Dla rozkładu jednostajnego (rys.2,c,d) najlepszą oceną jest wartość średnia ze
(minimalnego oraz maksymalnego) wyników obserwacji, a przy
uporządkowanej serii - średnia z pierwszego
oraz ostatniego
wyników
rozstępu serii wyników)
5.1 s.n
Normalny rozkład (rozkład Gaussa) (a) oraz przykładowe usytuowanie 25
obserwacji przy normalnym rozkładzie (b)
35
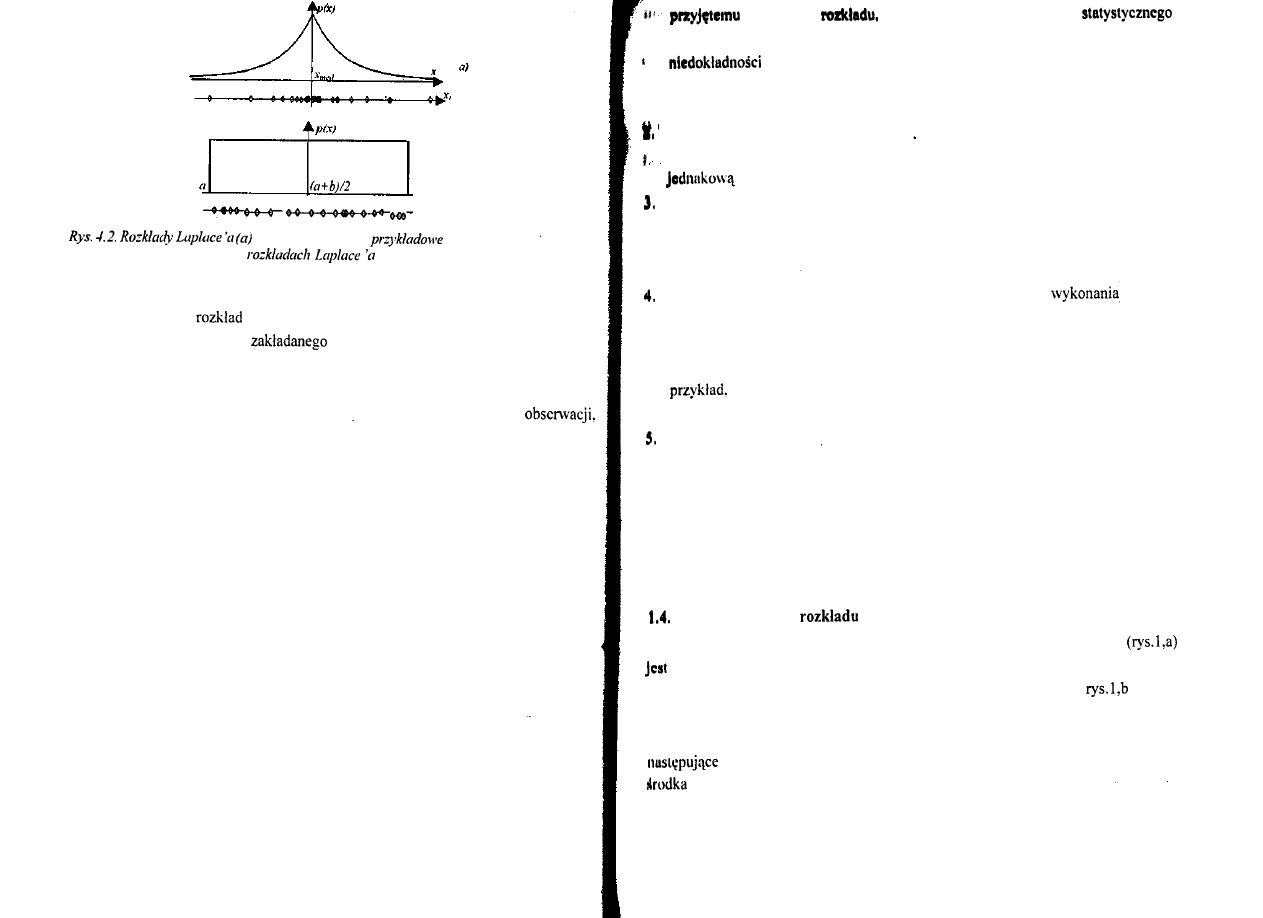
b)
c)
V
i jednostajny (c) oraz
usytuowanie 25 wyników
obserwacji przy
(b) i jednostajnym (d).
Należy zauważyć, że parametry te będą najlepszymi tylko w tych przypadkach,
kiedy rzeczywisty
prawdopodobieństwa eksperymentalnej próbki jest
w dużym stopniu zbliżony do
modelu. Niektóre parametry rozkładów są
w mniejszym stopniu czułe na nieodpowiedniość rozkładów, a niektóre - w większym
stopniu. Taka nieodpowiedniość może występować na przykład wskutek
oddziaływania zakłóceń impulsowych, powodujących powstanie wyników
których wartości w dużym stopniu różnią się od wartości pozostałych wyników.
Z pośród różnych parametrów rozkładów mediana charakteryzuje się bardzo małą
czułością na takie zakłócenia, a średnia z rozstępu, na odwrót, charakteryzuje się
bardzo dużą czułością na takie zakłócenia.
W danym ćwiczeniu są badane serii wyników obserwacji z założeniem a priori
normalnego rozkładu prawdopodobieństwa. Założenie to zostało przyjęte na podstawie
dokładnej analizy większych serii wyników obserwacji (kilkuset i więcej).
1.3. Wymagania do pomiarów z wielokrotnymi obserwacjami
Ogólnie niezależnie od rozkładu prawdopodobieństwa, jakość uzyskiwanego
wyniku pomiaru zwiększa się ze zwiększeniem liczby wyników obserwacji. Jednak
należy uwzględniać przynajmniej pięć zastrzeżeń:
1. Rzeczywisty rozkład prawdopodobieństwa efektów (oddziaływań) losowych
powinien odpowiadać modelowi rozkładu (przyjętemu a priori). Jeżeli
rzeczywisty rozkład prawdopodobieństwa efektów losowych nie odpowiada
36
modelowi
wtedy uzyskiwany podczas
opracowania wyników obserwacji wynik pomiaru oraz jego parametry
będą w dużym stopniu różnić się od najlepszych, które będą mieć
miejsce w razie zbliżenia rozkładu prawdopodobieństwa eksperymentalnego
Z rozkładem modelowym.
Podczas zbierania wartości obserwacji oddziaływania losowe powinny być
Mobilne w czasie, tzn., że poszczególne wyniki powinny charakteryzować się
zmiennością losową -wariancją.
Oddzielne wyniki obserwacji powinny być wzajemnie nieskorelowanymi -
statystycznie niezależnymi. Obecność korelacji (statystycznej zależności)
wzajemnej pomiędzy wynikami obserwacji powoduje pogorszenie jakości
uzyskiwanej oceny wartości wielkości mierzonej.
Wartość wielkości mierzonej powinna być stała podczas
serii jej
obserwacji (przeprowadzenia eksperymentu pomiarowego). Zmienność (dryft)
wartości mierzonej podczas wykonania eksperymentu powoduje wzrost wpływu
efektów dynamicznych, tym większe im większy czas trwania eksperymentu (na
dla zwiększenia liczby obserwacji w celu zmniejszenia niepewności
wyniku pomiaru).
Każdy wynik obserwacji nie powinien być obciążony wpływem oddziaływań
systematycznych, powinny one być skorygowane. Nie skorygowane resztki
systematycznych oddziaływań powodują zmniejszenie efektywności
statystycznego opracowania wyników obserwacji. Na przykład, zwiększenie
liczby obserwacji ponad pewną wartość może nie powodować zmniejszenia
złożonej niepewności wyniku, ponieważ dominującą pozostaje składowa
niepewności od innego, nie statystycznego wpływu.
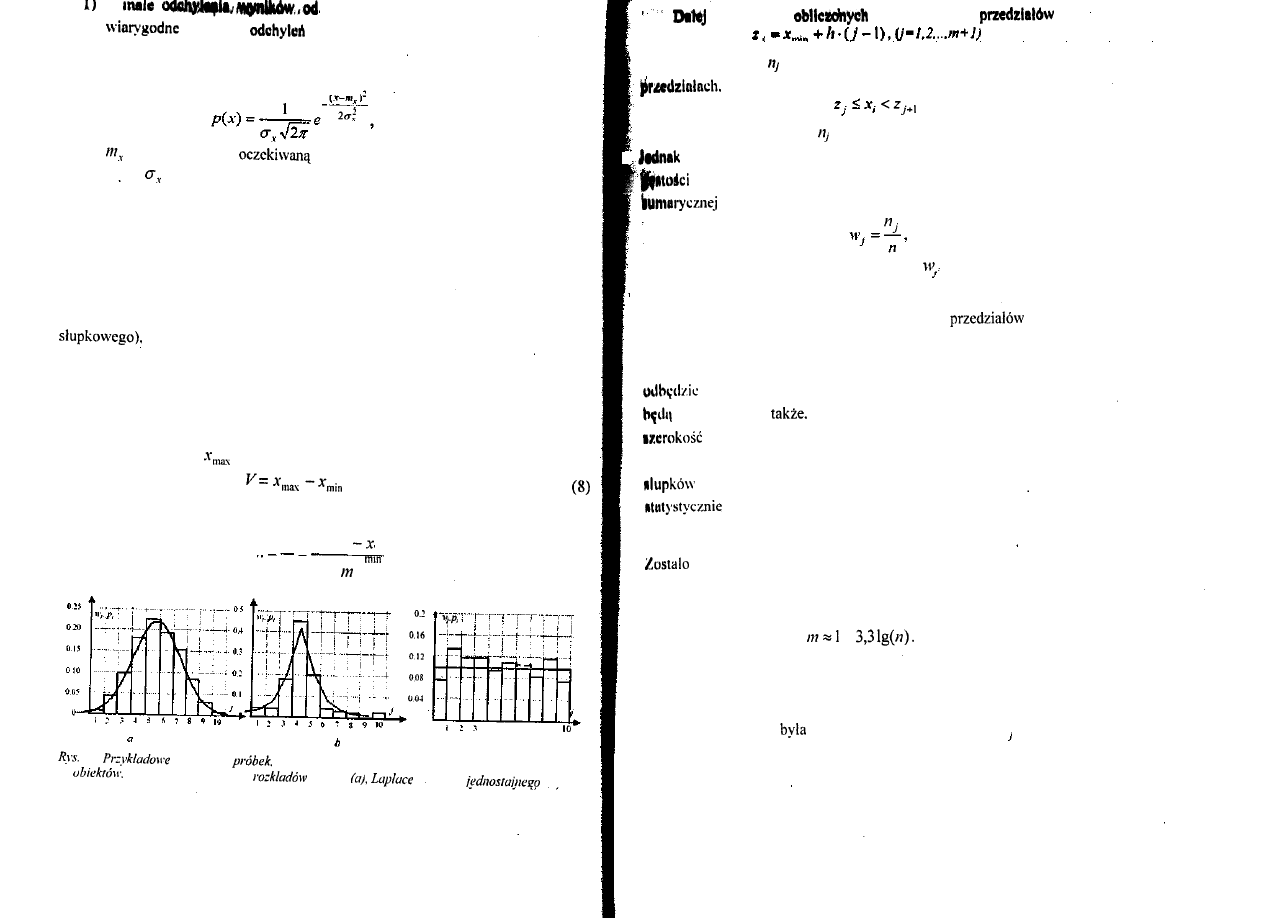
Model normalnego
(Gaussa)
Model rozkładu prawdopodobieństwa normalnego (rozkładu Gaussa)
szeroko wykorzystywany tak w teoretycznych badaniach jak i podczas
praktycznego opracowania serii wyników obserwacji. Przykładowo na
została
pokazana jedna z realizacji o 25 wynikach obserwacji wielkości mierzonej
z normalnym rozkładem prawdopodobieństwa. Przy takim modelu mają miejsce
właściwości wyników obserwacji (rozkład jest symetryczny względem
o charakterystycznym dzwono podobnym kształcie):
37
-
wartości średniej są w większym stopniu
od dużych
od wartości średniej;
2) - dodatnie i ujemne odchylenia wyników od wartości średniej są jednakowo
wiarygodne. Analitycznie rozkład ten opisuje się zależnością
na podstawie
granic sąsiednich
- oo < x < oo (7)
gdzie
- jest wartością
- punkt wokół którego grupują się wyniki
obserwacji,
- jest odchyleniem standardowym - miara rozrzutu wartości
obserwacji wokół wartości oczekiwanej.
1.5. Histogram i zasada jego tworzenia
Kształt rozkładu gęstości prawdopodobieństwa można oszacować w różny
sposób. Jednym z najstarszych i zarazem bardzo skutecznym sposobem jest graficzny
sposób prezentacji danych statystycznych w postaci histogramu (wykresu
który jest analogiem gęstości i jest wynikiem uśredniania rozkładu
statystycznego próbki.
Histogramem nazywa się zbiór prostokątów stykających się pomiędzy sobą
bokami o jednakowej szerokości h i o różnych wysokościach (rys.3). Dla budowy
histogramu najpierw cały interwał wartości wyników obserwacji (próbki) jako różnica
pomiędzy maksymalną
oraz minimalną wartościami
jest dzielony na m jednakowych przedziałów (klas) o szerokości (słupków)
V x
fa
_ ' _ max
m
,
0 -
'
,,
4 5 6 7 g 9
C
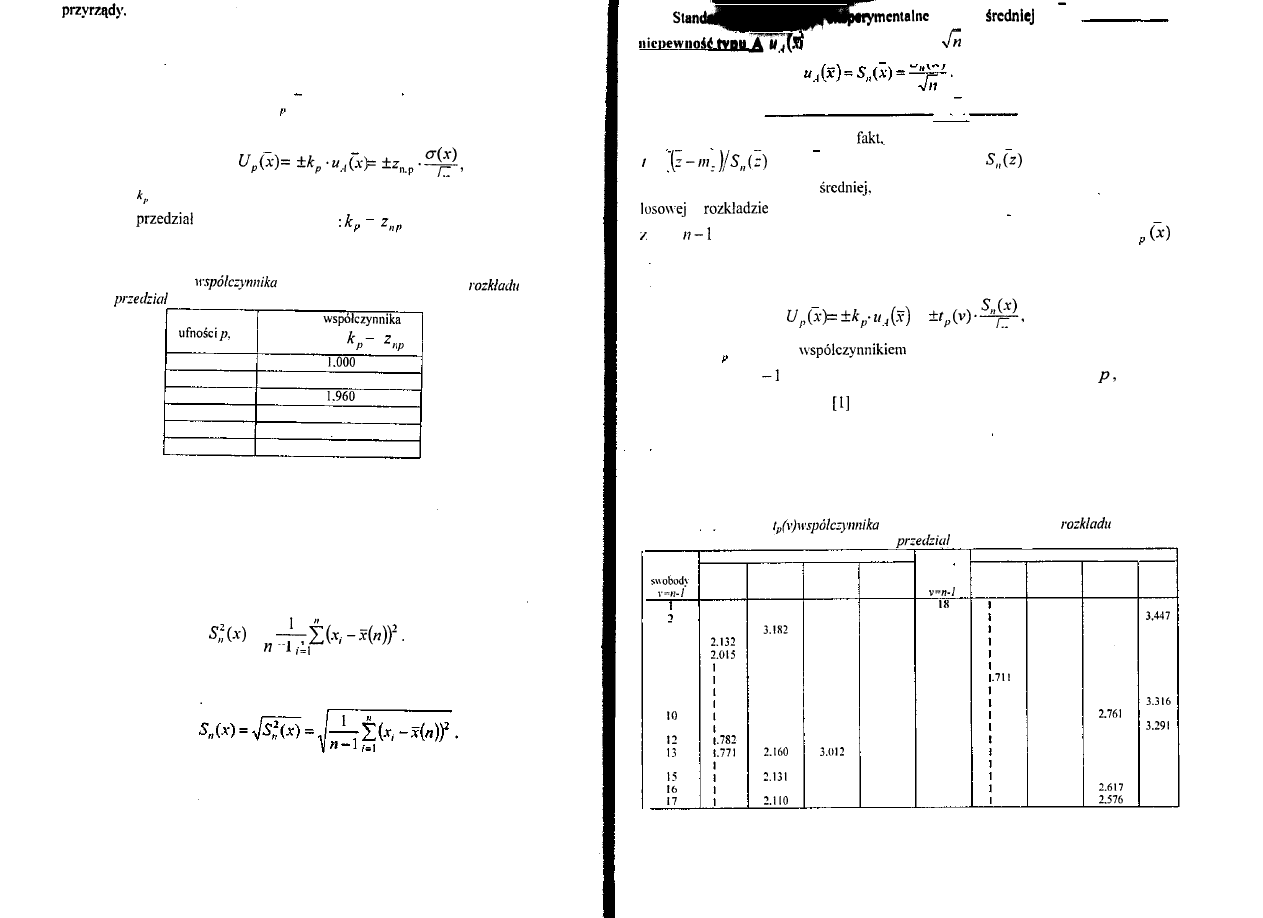
4.3.
histogramy
uzyskiwanych podczas opracowania wyników obserwacji
z
opisywanych modelami
Gaussa
'a (b) oraz
(ci.
, (9)
Oblicza się liczby
wyników obserwacji, które mieszczą się w odpowiednich
tzn. odpowiadają warunkowi
(10)
Często wartości liczb
są wysokościami odpowiednich słupków histogramu.
1
w celu uzyskania skali wykresu histogramu odpowiadającej skali rozkładu
prawdopodobieństwa wykorzystuje się normowanie tych liczb do
liczby obserwacji n:
(11)
Tak obliczone unormowane wartości
są empirycznymi częstotliwościami
trafiania wyników obserwacji w zadane przedziały.
Dla wyznaczania wartości liczby tych
nie ma dokładnego
teoretycznego uzasadnienia. Z jednej strony liczba przedziałów nie może być mała,
ponieważ w tym przypadku szerokość przedziałów będzie duża, wskutek czego
się za duże uśrednianie liczb empirycznego rozkładu (szczegóły rozkładu
utracone). Ale
liczba przedziałów nie może być za duża, ponieważ wtedy
przedziałów będzie za mała, wskutek czego wartości liczb wyników
W odpowiednich przedziałach będą małe, co powoduje dużą zmienność wysokości
dla różnych próbek (serii wyników obserwacji), histogram będzie
niestabilny.
Dla wyznaczania liczby przedziałów (klas) wykorzystuje się wzory empiryczne.
zaproponowanych wiele zasad dla wyboru liczb przedziałów w zależności od
liczby obserwacji, przykładowo szeroko jest wykorzystywany empiryczny wzór
Slurgesa:
+
(12)
Przy budowie histogramu ważne jest to, żeby liczba wyników obserwacji była
dostatecznie duża (minimalnie od kilkudziesięciu, a lepiej od kilkuset) z której
pierwiastek wyznacza możliwy rozrzut wysokości słupków od serii do serii, żeby
w każdym przedziale
wystarczająca liczba wyników n .
38
39

2. Niepewność wyniku
opracowaniu
wyników obserwacji
Niepewność wyniku pomiaru oznacza wątpliwość, co do wartości wyniku
pomiaru i ten termin odnosi się zarówno do pojęcia ogólnego jak i do konkretnych
ilościowych miar: niepewności standardowej, złożonej oraz rozszerzonej.
Niepewność standardowa
— jest niepewnością wyrażoną w formie
odchylenia standardowego wyniku.
Złożona niepewność standardowa wyniku jest określana, gdy wynik pomiaru jest
zależny od innych wielkości bezpośrednio mierzonych, równa pierwiastkowi
kwadratowemu z sumy wyrazów, będących wariancjami lub kowariancjami tych
wielkości z wagami zależnymi od tego jak wynik pomiaru zmienia się wraz z ich
zmianami.
Niepewność rozszerzona U (x) określa przedział wokół wyniku pomiaru, od
którego oczekuje się, że obejmuje dużą część rozkładu wartości wielkości, które
można uzasadniony sposób przyporządkować wielkości mierzonej.
Z niepewnością rozszerzoną jest powiązany współczynnik rozszerzenia -jest to
współczynnik liczbowy zastosowany jako mnożnik standardowej niepewności w
celu otrzymania niepewności rozszerzonej
( ) ' ( )
Współczynnik rozszerzenia i niepewność rozszerzona są zależne od rozkładu
prawdopodobieństwa wyniku pomiaru oraz od poziomu ufności który odwzoruje tą
część rozkładu wielkości, którą można w uzasadniony sposób przyporządkować
wielkości mierzonej.
Poziom ufności p przyjmuje zwykle wartości z przedziału od 90% do 99%,
rozszerzenia - wartości od 1,65 do około 3.
Niepewność typu A
jest niepewnością obliczaną drogą analizy
statystycznej serii obserwacji.
Niepewność typu B
jest niepewnością obliczaną sposobami innymi niż
analiza statystyczna serii obserwacji.
Rozszerzoną niepewnością typu A jest przedział, w którym mieści się część p
możliwych wartości wielkości mierzonej i jest on obliczany jako iloczyn standardowej
niepewności i współczynnika rozszerzenia, którego wartość na ogól zależy od
rozkładu
poziomu ufności p oraz liczby obserwacji
40
opracowania
wyników przy normalnym rozkładzie
obserwacji
oltjność
opracowania wyników obserwacji z normalnym
zmniejszenia
na wynik pomiaru efektów losowych z normalnym
prawdopodobieństwa wykorzystuje się uśrednianie wyników
tzn. za najlepsza ocenę wyników pomiaru jest przyjmowana ich
wnrlość średnia
X
=
= -
(14)
n
Kreska nad
oznacza wartość
a indeks (n) podkreśla, że wartość
obliczona z n wyników obserwacji.
W
statystyki matematycznej
że dzięki uśrednianiu n wyników
obserwacji standardowe odchylenie cr(x) wartości średniej zmniejsza się 4n
porównaniu od wartości
standardowego odchylenia wyników obserwacji
(15)
Otóż w celu zmniejszenia wpływu oddziaływań losowych z normalnym
prawdopodobieństwa na wynik pomiaru (wartość średnią) n razy podczas
należy zaobserwować n
2
nieskorelowanych wyników. Przykładowo dla
wpływu oddziaływań losowych 10 razy należy zaobserwować i uśrednić
100 wyników. Jeżeli chcemy zmniejszyć wpływ oddziaływań 100 razy wtedy
uśrednianych wyników powinna równać się
(10
Zwiększenie
liczby wyników obserwacji pociąga za sobą proporcjonalne zwiększenie czasu
co może powodować zwiększenie wpływu innych oddziaływań
zmiennych a także i zmiany wartości samej wielkości mierzonej.
3) Metoda oceny niepewności rozszerzonej wartości średniej zależy od danych a priori
o parametrach rozkładu prawdopodobieństwa wyników obserwacji.
3.2. Obliczanie niepewności wyniku pomiaru dla zadanej wartości odchylenia
standardowego wyników obserwacji
Wartość odchylenia standardowego wyników obserwacji może być znana na
podstawie opracowania poprzednich wyników eksperymentu. Przy tym uzasadnione
jest
że w ramach danego stanowiska pomiarowego (układ pomiarowy,
41
warunki itp.) wartość standardowego odchylenia wyników obserwacji jest
stała i można ją wyznaczyć jeden raz na podstawie eksperymentu o dostatecznie dużej
liczbie obserwacji i dalej wykorzystywać przy opracowaniu wyników w następnych
eksperymentach.
Niepewność rozszerzona U (x) wyniku (wartości średniej) na zadanym
poziomie ufności jest obliczana według wzoru
(16)
gdzie
- jest współczynnikiem rozszerzenia, określającego dla rozkładu
normalnego
o poziomie ufności p
— , wartość, którego wybiera się
z tablicy 1 [1].
Tablica 4.1. Wartość
rozszerzenia, określającego dla
normalnego
o poziomie ufności p.
Poziom
%
68.28
90
95
95.45
99
99,73
Wartość
rozszerzenia
—
1,645
2,000
2.576
3.000
3.3. Obliczanie niepewności wyniku pomiaru przy nieznanej wartości
standardowego odchylenia wyników obserwacji.
Jeżeli wartość odchylenia standardowego wyników obserwacji nie jest znana, to
należy ją oszacować. W tym celu najpierw wyznacza się wariancję eksperymentalną
wyników obserwacji na podstawie n wyników obserwacji według wzoru
=
(17)
—
Wtedy standardowe odchylenie eksperymentalne wyników obserwacji równa się
pierwiastkowi z wariancji standardowej
(18)
42
wartości
5(x) (standardowa
)
także zmniejsza się
razy
(19)
Dla obliczenia niepewności rozszerzonej U(x) typu A wyniku pomiaru, w tym
przypadku wykorzystuje się ten
że rozkład prawdopodobieństwa zmiennej
=
(gdzie z jest wartością średnią a
jest eksperymentalnym
standardowym odchyleniem
obliczonymi z n wartości obserwacji zmiennej
o
normalnym z wartością oczekiwaną w.) jest rozkładem Studenta
v =
stopniami swobody [ ]. W takim razie niepewność rozszerzona U
wartości średniej (wyniku pomiaru) na zadanym poziomie ufności jest obliczana
według wzoru
=
(20)
gdzie t (v) - jest
rozszerzenia, określającego dla rozkładu
Studenta o v = n stopni swobody przedział o poziomie ufności
wartość,
którego wybiera się z tablicy 2
Jeżeli liczba wyników obserwacji wynosi kilkadziesiąt (praktycznie ponad 30),
wtedy rozkład Studenta praktycznie transformuje się w rozkład normalny i wtedy
niepewność rozszerzoną można obliczać na podstawie współczynnika rozszerzenia dla
rozkładu normalnego.
Tablica4
Liczba
stopni
3
4
5
6
7
8
9
II
14
2 Wartość
rozszerzenia, określającego dla
Studenta
o
90
6.314
2.920
2.353
.943
.895
.860
.833
.812
.796
.761
.753
.746
.740
v=n-l stopniach swobody
o poziomie ufności p.
Poziom ufności p. %
95
12.706
4.303
2.776
2.571
2.447
2.365
2.306
2.262
2.228
2.201
2.179
2.145
2.120
99
63.657
9.925
5.841
4.604
4.032
3.707
3.499
3.355
3.250
3.169
3.106
3.055
2.977
2.947
2.921
2.898
99.73
235.784
19.206
9.219
6.620
5.507
4.904
4.530
4.277
4.094
3.957
3.850
3.764
3.694
3.636
3.586
3.544
3.507
Liczba
stopni
swobody
19
20
21
22
23
24
25
26
27
28
29
30
40
60
120
oo
Poziom ufności p. %
90
.734
.729
.725
.721
.717
.714
.708
.706
.703
.701
.699
.697
.684
.671
.658
.645
95
2.101
2.093
2.086
2.080
2.074
2.069
2.064
2.060
2.056
2.052
2.048
2.045
2.042
2.021
2.000
1.980
1.960
99
2.878
2.861
2.845
2.831
2.819
2.807
2.797
2.787
2.779
2.763
2.756
2.750
2.704
2.660
99.73
3.475
3.422
3.400
3.380
3.361
3.345
3.330
3.303
3.280
3.270
3.199
3.130
3.064
3.000
43

3.4.
wyniku pomiaru
Końcowy wynik pomiaru powinien zawierać:
wartość poszukiwaną (średnią),
2) niepewność rozszerzoną.
3) poziom ufności,
4) niepewność standardowa,
5) współczynnik
6) liczbę
(stopni swobody),
7) rozkład prawdopodobieństwa
i rekomenduje się przedstawiać w następującej formie
X = x(n) ±U-,
= , = , n = , rozkład .
(21)
4. Przykład:
W celu zmniejszenia wpływu oddziaływań losowych podczas pomiaru wartości
natężenia prądu elektrycznego przeprowadzono n=25 pomiarów, w wyniku których
zaobserwowano następujące wartości (w
Ij=:
5.048;
5.019; 4,912; 4,985; 4,951:
5,017; 4,963;
5,027;
5,056; 4.958; 4,997; 4,962: 5,055; 4,950; 5,038;
4,953:5.090.
Na podstawie poprzednich badań wiadomo jest, że rozkład oddziaływań podczas
pomiarów jest normalny jednak wartość standardowego odchylenia w różnych
eksperymentach nie jest
tzn. może się zmieniać.
Należy oszacować wartość natężenia prądu mierzonego oraz jego rozszerzoną
niepewność na poziomie ufności p=95 %.
Rozwiązanie
1. Obliczamy wartość średnią wyników obserwacji
mA.
2. Ponieważ standardowe odchylenie poszczególnych wyników obserwacji nie jest
obliczamy jego wartość eksperymentalną
S„
(/) =
=
3. Standardowe odchylenie eksperymentalne wartości średniej natężenia prądu
(niepewność standardowa typu A
(/)) stanowi
4. Dla obliczania niepewności rozszerzonej typu A wartości średniej natężenia prądu
z tablicy 2 wyznaczamy współczynnik rozszerzenia
(25
= 2,060. Wtedy
niepewność rozszerzona wartości średniej (wyniku pomiaru) na zadanym
poziomie ufności 95% stanowi
=
=
5. Wynik pomiaru (po zaokrągleniu najpierw niepewności rozszerzonej
0,020 mA i następnie wartości średniej 4,9992
4,999
)
przedstawiamy w postaci
/ = (4,999 ± 0,020) mA, p = 95%,n 25, (I)
= 2,060, rozkład Studenta.
5. Cyfrowy pomiar okresu sygnału sinusoidalnego
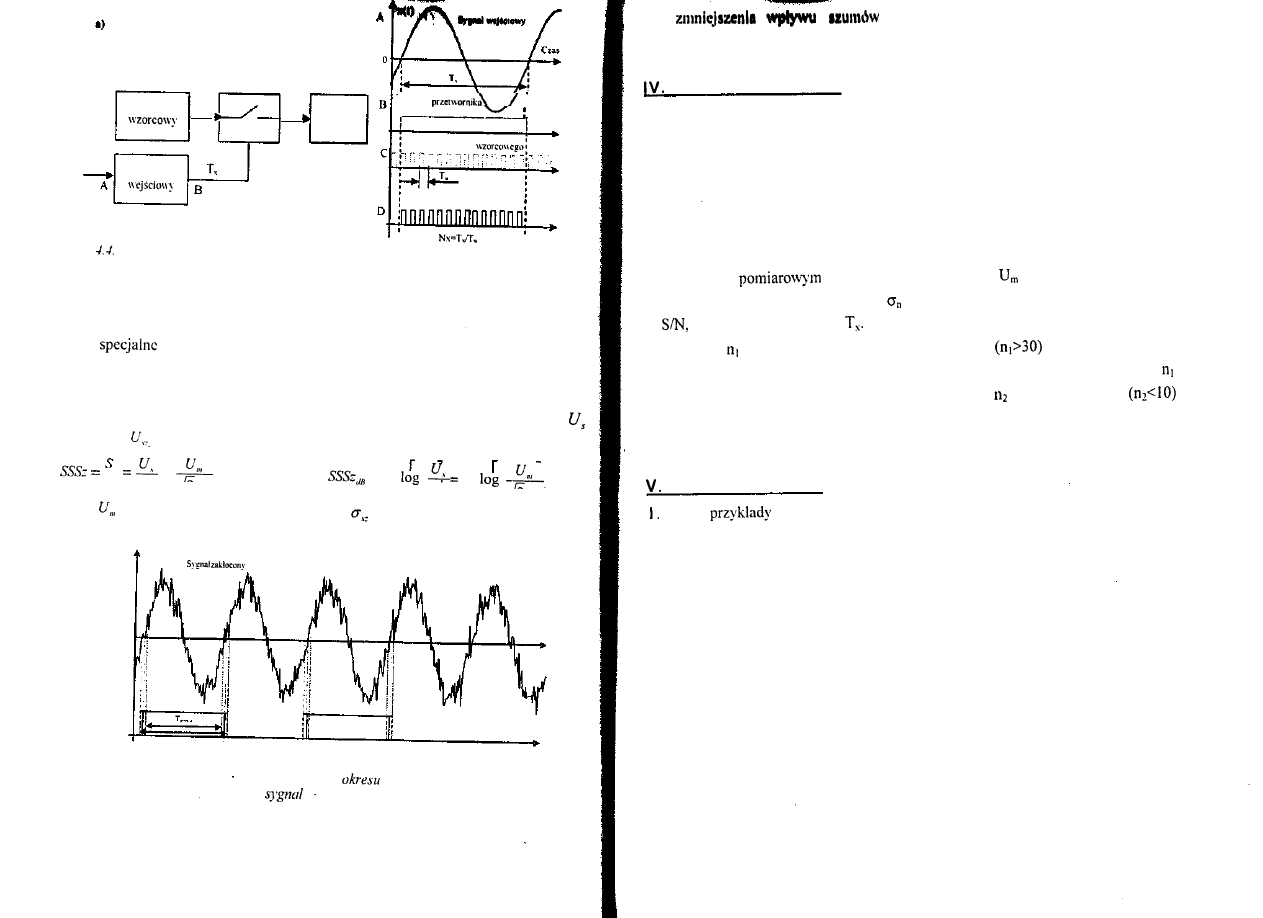
5.1. Zasada cyfrowego pomiaru okresu
Cyfrowy pomiar okresu (rys.4) polega na zliczaniu (przez licznik) liczby
okresów
impulsów o częstotliwości wzorcowej
= 1 /
z generatora
wzorcowego w przedziale czasu, równym okresowi
wejściowego sygnału
pomiarowego. Przebieg wejściowy x(t) (punkt A na rys.4), po przejściu przez
przetwornik wejściowy jest przetworzony w impuls, którego czas trwania równa się
okresowi
sygnału (punkt B na rys.4). i podawany jest na wejście otwierające
bramkę. Na wejście drugie bramki podawane są impulsy o okresie
z wyjścia
generatora wzorcowego (punkt C na rys.4). Licznik zlicza tylko te impulsy generatora,
które zmieszczą się w przedziale okresu sygnału wejściowego (w czasie otwarcia
bramki) (punkt D na rys.4). Liczba zliczonych impulsów wynosi:
(22)
i jest proporcjonalna do wartości okresu
44
45
b)
Bramka
x(t)
Generator
Przetwornik
C
i
i
D
Licznik
Wyjście
!
! wejściowego
Czas
Impulsy generatora
Czas
Impulsy zliczone przez licznik
Czas
Rys.
Uproszczony schemat blokowy cyfrowego miernika okresu (a) oraz czasowe przebiegi przy
pomiarze okresu (b).
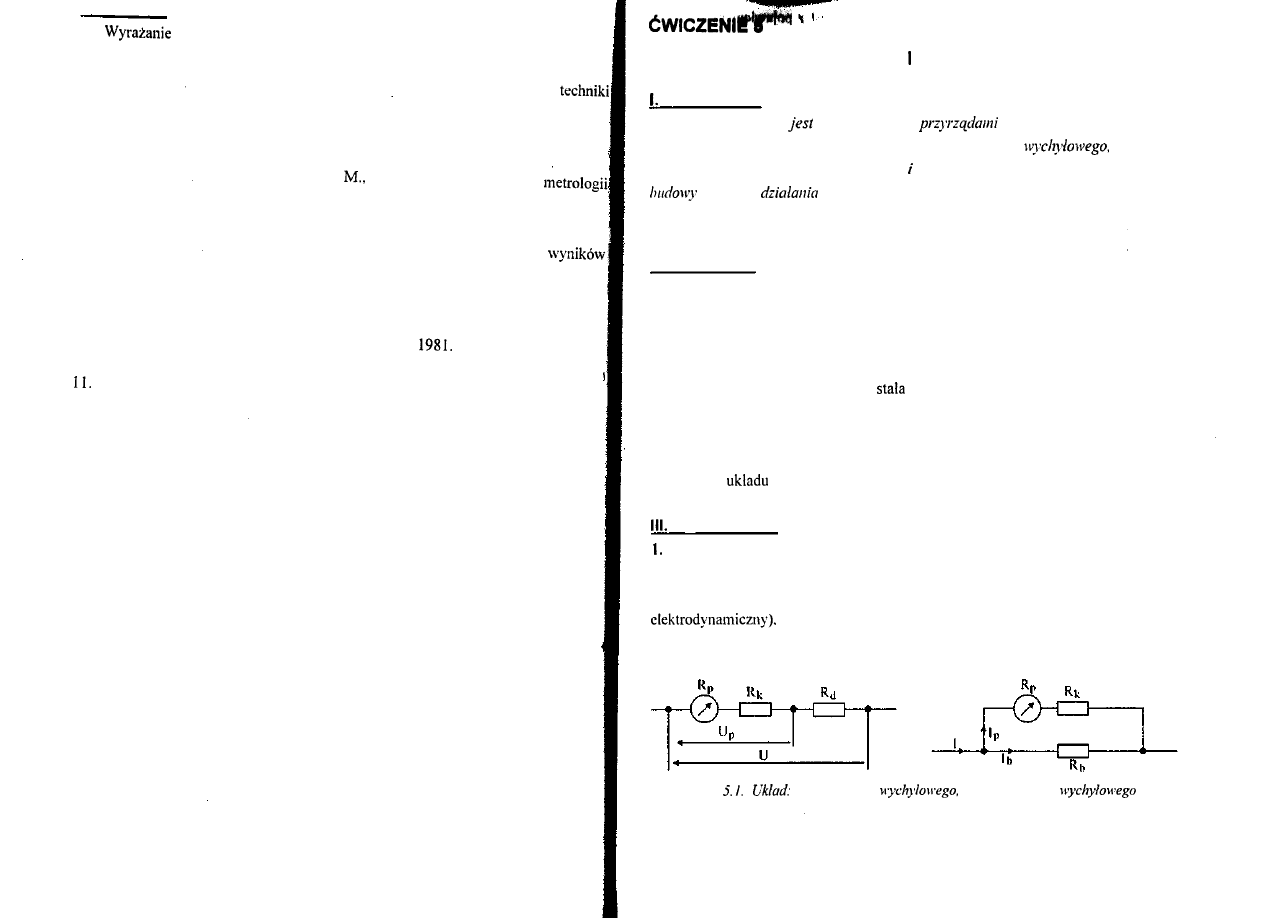
5.2. Wpływ szumów podczas cyfrowego pomiaru okresu
Jeżeli sygnał wejściowy jest zakłócony szumem (rys. 5) wtedy, jeżeli nie będą
użyte
środki ich eliminacji, mogą powstać losowe błędy pomiaru okresu,
które przejawiają się w losowych zmianach wyników pomiaru kolejnych okresów tego
samego sygnału (rys.5). Wpływ zakłóceń jest tym większy, im mniejszy jest stosunek
sygnał szum, który jest zdefiniowany jako stosunek wartości skutecznych sygnału
oraz szumu
—
=
lub w decybelach
= 20
20
\. (23)
gdzie
- jest wartością szczytową sygnału,
- jest standardowym odchyleniem
szumu.
szumem
Zmiany czasu trwania impulsu
otwierającego bramkę
Rys.4.5. Powstanie rozrzutu wartości mierzonych
wskutek oddziaływania szumu na
wejściowy.
Dla
wykorzystuje się uśrednianie n wyników
pomiarów oraz inne metody.
Program ćwiczenia:
1. Zestawić układ wg rys. 6.1 do cyfrowego pomiaru okresu napięcia sinusoidalnego
zakłóconego szumem. Zanotować w tabeli podstawowe dane używanych w układzie
przyrządów.
2. Zaobserwować przebiegi na oscyloskopie i odpowiednie wskazania czasomierza
cyfrowego przy różnych poziomach zakłóceń napięcia sinusoidalnego szumem
(różnych stosunkach sygnał/szum).
3. Wyniki obserwacji przedstawić we wnioskach.
4. W układzie
dobrać: wartość amplitudy
napięcia sinusoidalnego,
wartość odchylenia standardowego
szumu normalnego, stosunek sygnał/szum
nastawę wartości okresu
5. Dokonać
odczytów wartości mierzonego okresu
i opracować wyniki
pomiaru stosując model rozkładu błędów Gaussa. Na podstawie zebranych
wyników sporządzić histogram. Opracować pierwsze wyników pomiaru
stosując model rozkładu Studenta. Porównać otrzymane wyniki.
Pytania kontrolne
Podać
typowych sytuacji pomiarowych, w których występuje dyspersja
wyników.
2. Przy założeniu rozkładu normalnego serii wyników obserwacji, jaka wartość jest
najlepszym oszacowaniem wyniku pomiaru?
3. Określić pojęcie standardowej niepewności typu A wyniku pomiaru.
4. Podać wzór dla obliczania niepewności standardowej - metoda typu A.
5. Jak zależy wartość standardowej niepewności typu A od liczby obserwacji?
6. Określić pojęcie rozszerzonej niepewności wyniku pomiaru.
7. W jakich sytuacjach uzasadnione jest stosowanie rozkładu Studenta przy obliczaniu
rozszerzonej niepewności wyniku pomiaru?
8. Jakie dane należy podać przy przedstawieniu wyniku pomiaru?
46
47
Literatura
1.
niepewności pomiaru. Przewodnik. Główny Urząd Miar. 1999.
2. Jaworski J.: Matematyczne podstawy metrologii. Warszawa: WNT, 1979.
3. Jaworski, J.. Morawski R., Olędzki J.: Wstęp do metrologii i
eksperymentu. Warszawa: WNT, 1992.
4. Marcyniuk A.: Teoria pomiarów. Gliwice: Wydawnictwo Politechniki Śląskiej,
1981.
5. Marcyniuk A.. Pasecki E. Pluciński
Szadkowski B.: Podstawy
elektrycznej. Warszawa: WNT, 1984.
6. Piotrowski J.: Podstawy metrologii. Warszawa: PWN, 1976.
7. Strzałkowski A., Śliżyński A.: Matematyczne metody opracowywania
pomiarów. Warszawa: PWN. 1973.
8. Sydenham P.H.: Podręcznik metrologii. Tom 1. Podstawy teoretyczne. Warszawa:!
WKiŁ, 1988.
9. Szydłowski H.: Teoria pomiarów. Warszawa: PWN,
10. Taylor J.R.: Wstęp do analizy błędu pomiarowego. Warszawa: PWN, 1995.
Turzeniecka D.: Ocena niepewności wyniku pomiarów. Poznań: Wydawnictwo]
Politechniki Poznańskiej. 1997.
POMIARY NAPIĘĆ PRĄDÓW STAŁYCH
Cel ćwiczenia
Celem ćwiczenia
zaznajomienie z
do pomiaru napięcia i prądu
stałego: poznanie budowy woltomierza i amperomierza
schematu
blokowego woltomierza elektronicznego struktury kompensatora oraz wpływu ich
i zasady
na wyniki pomiarów. Zakres ćwiczenia obejmuje pomiary
napięcia stałego, prądu stałego i rezystancji wewnętrznej źródła napięcia.
II. Zagadnienia
1. Zasada i dokładność pomiaru napięcia stałego za pomocą woltomierza
magnetoeleklrycznego.
2. Zasada i dokładność pomiaru napięcia stałego za pomocą woltomierza cyfrowego.
3. Błąd systematyczny występujący podczas pomiaru napięcia stałego.
4. Znajomość pojęć i zależności:
przyrządu, czułość przyrządu, rezystancja
wewnętrzna, rezystancja jednostkowa woltomierza magnetoelektrycznego, poprawka.
5. Na czym polega podwójna kompensacja i w którym z kompensatorów się ją
stosuje.
6. Schemat
i zasada pomiaru kompensatorem technicznym.
Wprowadzenie
Mierniki wychylowe
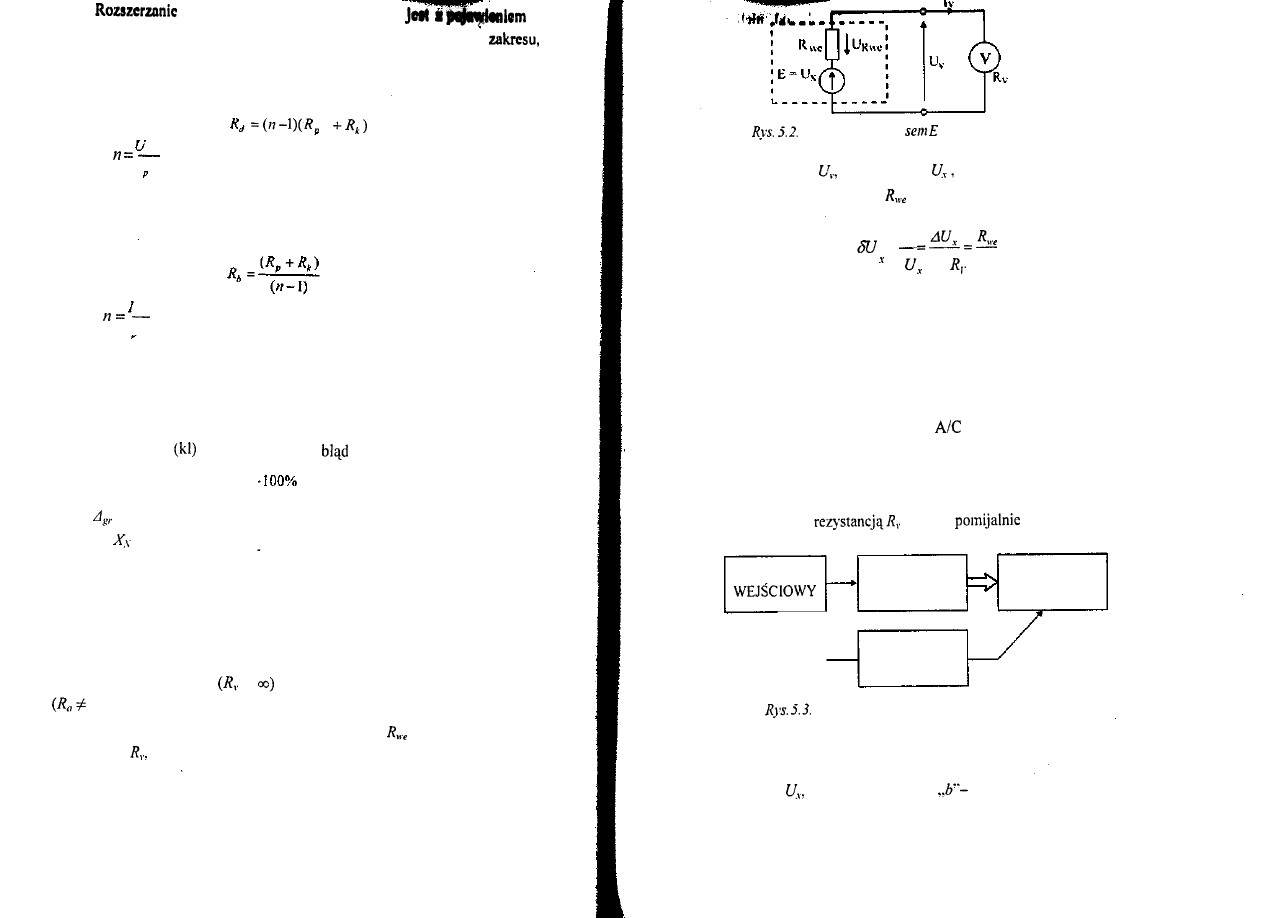
Mierniki wychyłowe do pomiarów napięcia i prądu stałego zbudowane są
/. przetwornika elektromechanicznego (np. magnetoelektryczny, elektromagnetyczny,
rezystora kompensującego zmiany temperatury oraz rezystorów
rozszerzających zakres pomiarowy. Układy
wychyłowego przedstawiono na rysunku 5.1.
woltomierza i amperomierza
Rys.
a) woltomierza
b) amperomierza
48
49
zakresu tych przyrządów związane
się w ich
układach dodatkowych rezystorów, co powoduje przy przełączaniu
zmianę
wartości rezystancji przyrządu.
Rezystory szeregowe (posobniki) poszerzające zakres woltomierza dobiera się według
wzoru:
gdzie:
U
(5.1)
Rezystory równoległe (boczniki) poszerzające zakres prądowy amperomierza dobiera
się według wzoru:
(5.2)
gdzie:
Niedokładność przyrządów elektromechanicznych określana jest przez producenta w
czasie kalibracji przez podanie klasy, którą definiuje się jako największy dopuszczalny
błąd pomiaru w odniesieniu do zakresu pomiarowego przyrządu.
Klasa dokładności
wyrażana jest przez
względny, procentowy:
gdzie:
to graniczny, dopuszczalny błąd bezwzględny pomiaru
zaś
to zakres nominalny
(5.3)
Włączenie woltomierza lub amperomierza do układu, w którym ma zostać
zmierzone napięcie (prąd) powoduje powstanie dodatkowego błędu, będącego
skutkiem niedoskonałości energetycznej przyrządu mierzącego. Ten dodatkowy błąd
jest częścią błędu systematycznego wynikającą ze skończonej wartości rezystancji
wewnętrznej woltomierza
<
oraz większą od zera rezystancją amperomierza
0). Na rys. 5.2. przedstawiony został, dla przykładu, schemat wyjaśniający
wzajemny wpływ rezystancji wewnętrznej źródła
i rezystancji wewnętrznej
woltomierza
którego skutkiem może być wspomniany błąd dodatkowy.
Schemat pomiaru
za pomocą woltomierza
Woltomierz wskazuje
czyli nie E =
ale wartość pomniejszoną o spadek
napięcia na rezystancji wewnętrznej
źródła. Wartość błędu względnego z tym
związanego wynosi:
Ogólnie błąd systematyczny można wyeliminować z wyniku pomiaru stosując
odpowiednią poprawkę.
2. Woltomierze cyfrowe
Woltomierze cyfrowe do pomiaru napięcia stałego zbudowane są najogólniej
z układów (rys. 5.3): wejściowych (dopasowujących sygnał mierzony do wejścia
woltomierza), wzmacniacza, przetwornika
i wskaźnika. Układ wejściowy
realizowany jest jako dzielnik rezystancyjny lub wtórnik napięciowy (często na
tranzystorze polowym MOSFET). Ponieważ woltomierz cyfrowy wprowadza do
układu mierzonego rezystancję o dużej wartości (rzędu kilku MD), to błąd
systematyczny związany z
staje się
mały.
UKŁAD
\
PRZETWORNIK
A/C
UKŁAD
STERUJĄCY
WYŚWIETLACZ
Schemat blokowy cyfrowego woltomierza DC
Dopuszczalny błąd graniczny woltomierza podawany jest przez producenta jako
suma dwóch elementów, z których jeden z czynnikiem ,.a" zależy od wartości
wielkości mierzonej
drugi z czynnikiem
od użytego zakresu pomiarowego
50
51
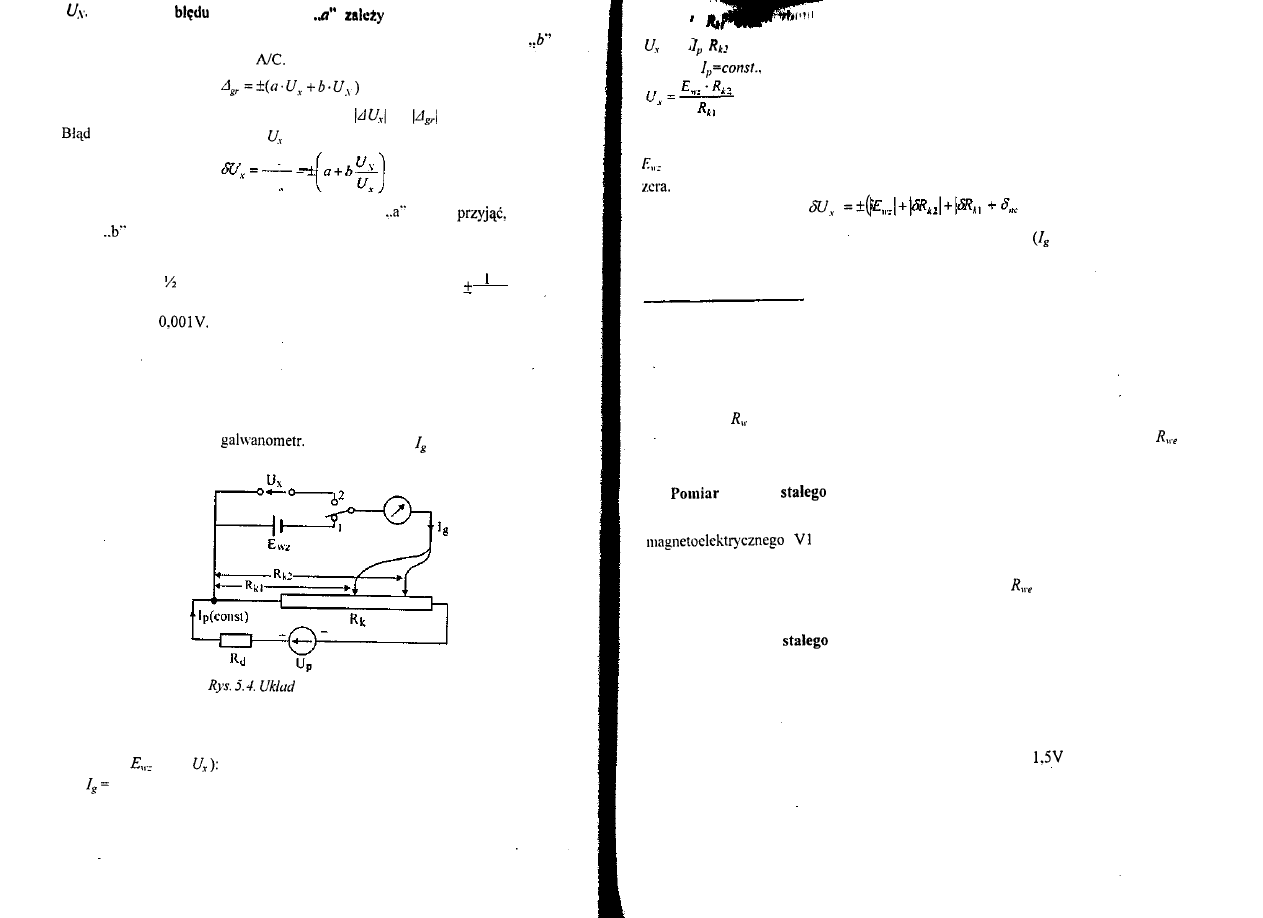
Składowa
z czynnikiem
głównie od nieliniowości toru
analogowego woltomierza i błędu wzorca napięcia, składowa z czynnikiem
zależy
od rozdzielczości przetwornika
. (5.4)
W najgorszym przypadku błąd pomiaru napięcia
=
względny pomiaru napięcia
z definicji dany jest wzorem:
AU.
U..
X
(5.5)
Gdy producent podaje tylko składową błędu
należy
że składowa
błędu
jest równa błędowi rozdzielczości czyli wartości odpowiadającej jednej
cyfrze ostatniej pozycji wskaźnika. Na przykład na zakresie 20V miernika o
rozdzielczości 4
cyfry (19999) błąd rozdzielczości jest równy 100%. to jest
±0,005%, czyli
3.Kompensatory napięcia.
Zasada działania kompensatora bazuje na metodzie zerowej: napięcie mierzone
kompensowane jest przez napięcie z układu kompensatora, a wskaźnikiem zrównania
wartości obu napięć jest
Gdy jego prąd = 0, to kompensowane
napięcia są sobie równe.
G
kompensatora napięcia
Pomiar kompensatorem wyposażonym we wzorcowe źródło napięcia odbywa się
w dwóch etapach (na rysunku 5.4. pozycje 1 i 2 odpowiadające kompensacji źródła
wzorcowego
oraz
Gdy
0
otrzymuje się dwa wyniki:
=
ponieważ
to
=
(5.6)
Dokładność pomiaru kompensatorem zależy od dokładności źródła wzorcowego
i rezystora kompensacyjnego (rezystor wzorcowy) oraz od czułości wskaźnika
Błąd graniczny kompensatora wynosi:
i \
\\)
(5.7)
W momencie skompensowania przyrząd nie pobiera prądu = 0), zatem pomiar
kompensatorem jest wolny od błędu systematycznego.
IV. Program ćwiczenia
1. Wyznaczanie rezystancji wewnętrznej źródła napięcia
W podanym układzie pomiarowym, przy otwartym wyłączniku W odczytać
wartość napięcia z woltomierza cyfrowego V3. Zamknąć wyłącznik i odczytać
wskazania amperomierza cyfrowego i woltomierza cyfrowego. Wartość rezystora
dekadowego
należy nastawić tak, aby uzyskać widoczną różnicę wskazań
woltomierza w obu przypadkach. Obliczyć wartość rezystancji wewnętrznej źródła
według podanego wzoru.
2.
napięcia
woltomierzem magnetoelektrycznym
Uwzględniając biegunowość źródła U i oznaczenia na zaciskach woltomierza
zmierzyć napięcie wybierając najbardziej odpowiedni
zakres pomiarowy woltomierza. Obliczyć poprawkę eliminującą błąd systematyczny
pomiaru spowodowany rezystancją wewnętrzną źródła
oraz błąd graniczny
pomiaru. Podać końcowy wynik pomiaru.
3. Pomiar napięcia
woltomierzem cyfrowym
Dobrać najkorzystniejszy zakres pomiarowy woltomierza cyfrowego V3 i zmierzyć
badane napięcie. Obliczyć błąd graniczny pomiaru oraz podać wynik końcowy.
4. Pomiar napięcia kompensatorem
Połączyć układ pomiarowy według podanego schematu i ustawić napięcie
zasilające dla kompensatora technicznego na poziomie
(istotne), zakres
pomiarowy Z kompensatora ustawić w położeniu xl (0..200mV).
52
53
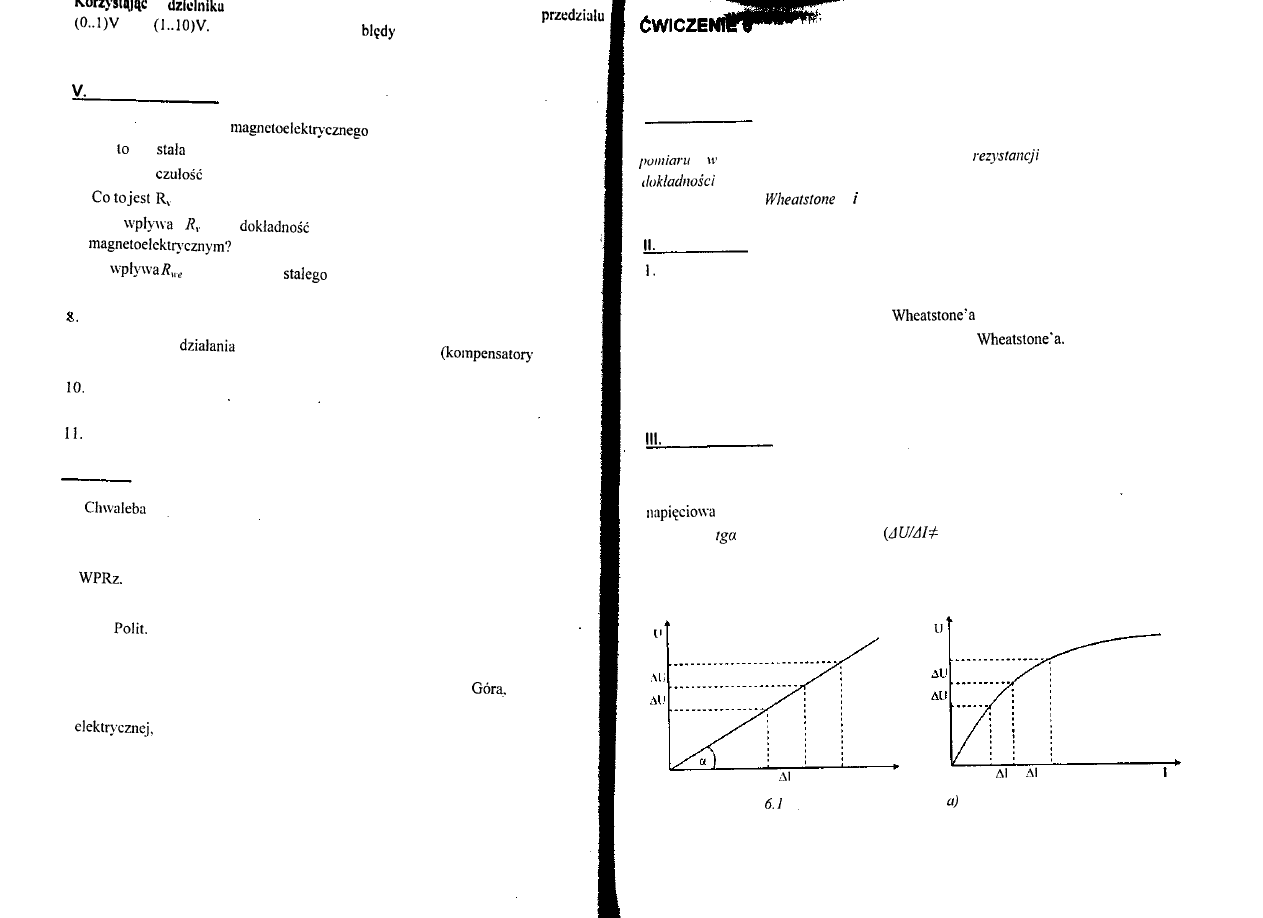
7.
z
napięcia dokonać pomiaru amplitudy napięcia z
oraz
Podać wartości napięć,
graniczne pomiarów oraz zapisać
końcowe wyniki pomiarów.
Pytania kontrolne
1. Budowa woltomierza
wielozakresowego.
2. Co jest
woltomierza magnetoelektrycznego?
3. Co to jest
woltomierza magnetoelektrycznego?
4.
woltomierza magnetoelektrycznego?
5. Jak
na
pomiaru napięcia stałego woltomierzem
6. Jak
źródła napięcia
na dokładność pomiaru?
Jak wyznaczamy i eliminujemy błąd systematyczny przy pomiarze napięcia stałego?
Błąd graniczny pomiaru napięcia stałego woltomierzem cyfrowym.
9. Ogólna zasada
kompensatorów napięcia stałego
ze stałym
i zmiennym prądem pomocniczym).
Na czym polega podwójna kompensacja i w którym z rodzajów kompensatorów się
ją stosuje?
Definicja i sposób wyznaczania względnego granicznego błędu pobudliwości.
Literatura
1.
A.. Poniński M. Siedlecki A.: Metrologia elektryczna, Warszawa:
WNT, 1997.
2. Dyszyński J.: Metrologia elektryczna i elektroniczna - laboratorium cz. I. Rzeszów:
1997.
3. Szadkowski B. (red.) Laboratorium metrologii elektrycznej i elektronicznej,
Wyd.
Śląskiej, Gliwice, 1998
4. Furmankiewicz L. (red.) Laboratorium metrologii elektrycznej (materiały
pomocnicze cz. III) Wyd. Politechniki Zielonogórskiej , Zielona
2000
5. Marcyniuk A., Pasecki E., Pluciński M., Szadkowski B.: Podstawy metrologii
Warszawa: WNT, 1984.
POMIARY REZYSTANCJI
|. Cel ćwiczenia
Celem ćwiczenia jest wdrożenie umiejętności poprawnego wyboru metody
zależności od wartości mierzonej
oraz postulowanej
wyniku pomiaru. Wybór dotyczy: omomierza cyfrowego, metody
technicznej, mostka
'a mostka Thomsona.
Zagadnienia
Zasada pomiaru rezystancji omomierzem cyfrowym.
2. Metoda techniczna pomiaru rezystancji.
3. Zasada pomiaru rezystancji mostkiem
i Thomsona.
4. Konstrukcja technicznego i laboratoryjnego mostka
5. Układ technicznego i laboratoryjnego mostka Thomsona.
6. Warunek równowagi mostka Wheatstone'a i Thomsona.
Wprowadzenie
Wybór metody pomiaru rezystancji zależy od jej wartości, charakterystyki
prądowo-mapięciowej oraz zakładanej dokładności wyniku. Charakterystyka prądowo-
U= f(I), rys. 6.1. decyduje o podziale rezystancji na liniowe
(AU/AI =
= const) i nieliniowe
const). Wartość R rezystancji liniowej
nie zależy od wartości prądu. By ją poznać, wystarczy wykonać pomiar przy jednej
wartości prądu. Pomiar taki zapewniają: omomierze wychyleniowe i cyfrowe, mostki
oraz metoda techniczna i jej liczne modyfikacje [1, 2, 3].
Al
1
Rys.
Charakterystyki rezystancji: liniowej, b) nieliniowej
54
55
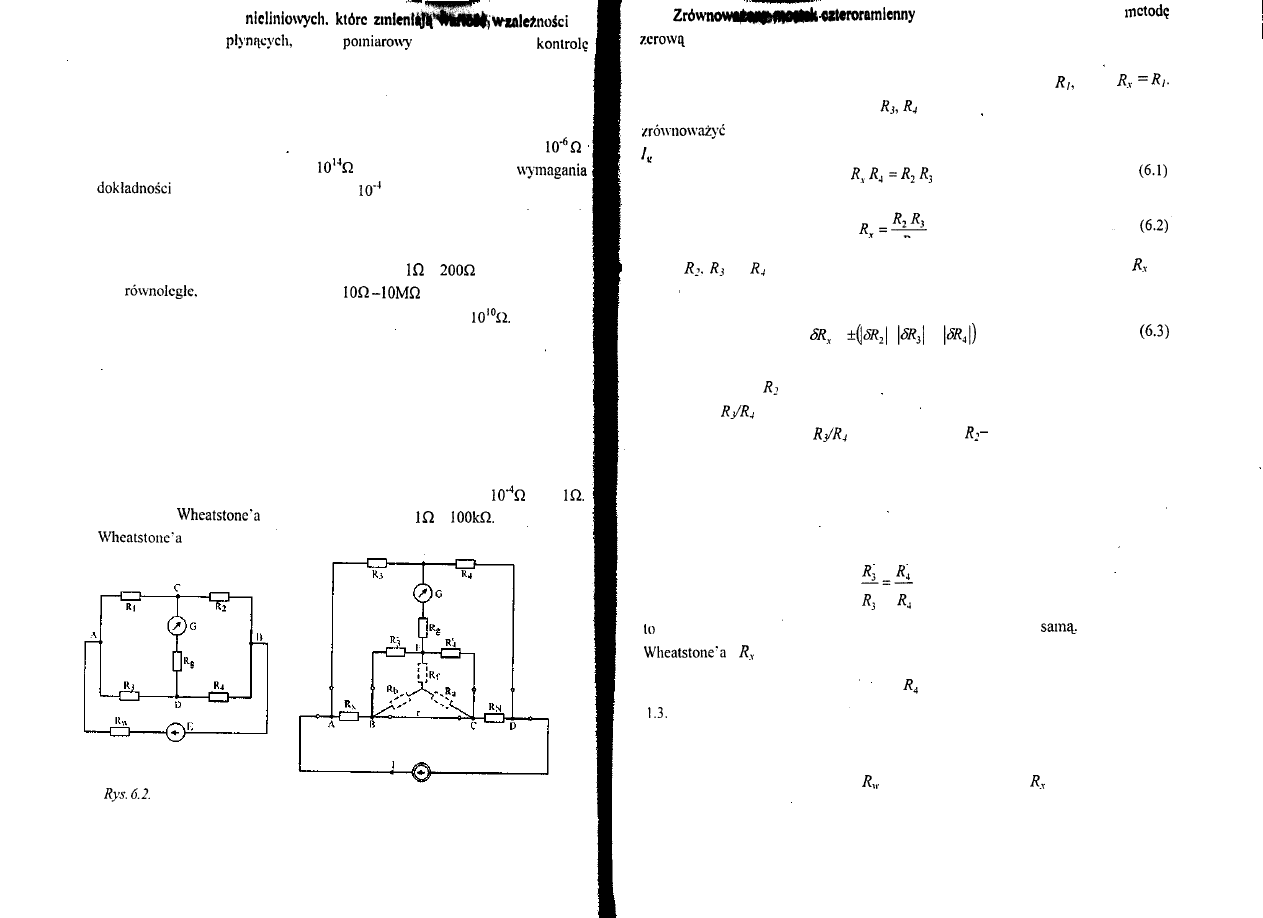
Do pomiaru rezystancji
od
wartości prądu przez nie
układ
powinien zapewnić
wartości prądu i napięcia na rezystancji mierzonej. Wymaganie takie spełnia metoda
pośrednia zwana techniczną.
1. Pomiary rezystancji liniowych
Praktyczne pomiary rezystancji obejmują wartości w zakresie od
(rezystancja przewodów, boczników) do
(rezystancja izolacji), zaś
co do
zmieniają się w granicach od
% (pomiary wzorców rezystancji)
do kilku procent (pomiary techniczne).
1.1. Omomierze
Do pomiarów rezystancji o wartościach z zakresu
-
służą omomierze
analogowe
dla wartości z zakresu
omomierze szeregowe, zaś
omomierze elektroniczne o różnych zakresach mierzą do wartości
Omomierze
elektroniczne cyfrowe działają wykorzystując przetworzenie rezystancji na
proporcjonalne do niej napięcie i następnie cyfrowy pomiar napięcia. Często stanowią
jedną z funkcji multimetru cyfrowego (DMM - Digital MultiMeter). Omomierze
cyfrowe o dużej rozdzielczości zapewniają dokładność pomiaru rzędu 0,05%
1.2. Metoda zerowa
Do pomiarów o średniej dokładności (około 1%) służą mostki techniczne.
Techniczne mostki Thomsona mierzą rezystancje w zakresie od
do
Techniczne mostki
mają zakres pomiarowy
-
Laboratoryjne
mostki
zapewniają pomiar dokładny, rzędu 0,05 %.
1:
Schemat laboratoryjnych mostków a) Wheatstone 'a b) Thomsona
Wheatstone'a (rys. 6.2.) realizuje
pomiaru rezystancji. W mostku rozróżnić można przekątną zasilania AB
i przekątną wskaźnika zera (galwanometru) CD. Zazwyczaj przyjmuje się, że
rezystancja mierzona wpinana jest do gałęzi mostka w miejsce
czyli
Regulując odpowiednio rezystancje R;,
(rezystancje w ramionach mostka) należy
mostek, czyli doprowadzić do wartości zerowej prąd galwanometru:
= 0. W stanie równowagi obowiązuje zależność zwana warunkiem równowagi:
Mierzoną rezystancję można wyznaczyć z wyrażenia:
Jeżeli
i
są rezystorami wzorcowymi, to mierzona rezystancja
jest
porównywana bezpośrednio z wzorcami i dokładność pomiaru zależy od ich
dokładności:
=
+
+
Praktycznie równoważenie mostka odbywa się na dwa sposoby:
- przez zmianę
(tzw. rezystancji porównawczej) przy dobranym wcześniej
stosunku
= const, ten sposób stosowany jest w mostkach laboratoryjnych,
- przez zmianę stosunku
przy utrzymaniu - const, ten sposób stosowany
w mostkach technicznych.
Mostek Thomsona (sześcioramienny) służy do pomiaru rezystancji o małych
wartościach, ponieważ jego konstrukcja umożliwia eliminację wpływu rezystancji
przewodów łączących i styków na wynik pomiaru. Jeżeli dla mostka Thomsona
spełniony zostanie dodatkowy warunek:
(6.4)
równanie na jego warunek równowagi przyjmuje postać taką
jak dla mostka
i można wyznaczyć ze wzoru:
tf
v
=^ (6.5)
Metoda porównawcza i podstawienia
Metoda porównawcza należy do dokładnych metod pomiaru rezystancji a polega
na porównaniu za pomocą kompensatora spadków napięcia na połączonych szeregowo
(rys. 6.3.) rezystorze wzorcowym
i rezystorze badanym
(zakres stosowania:
56
57
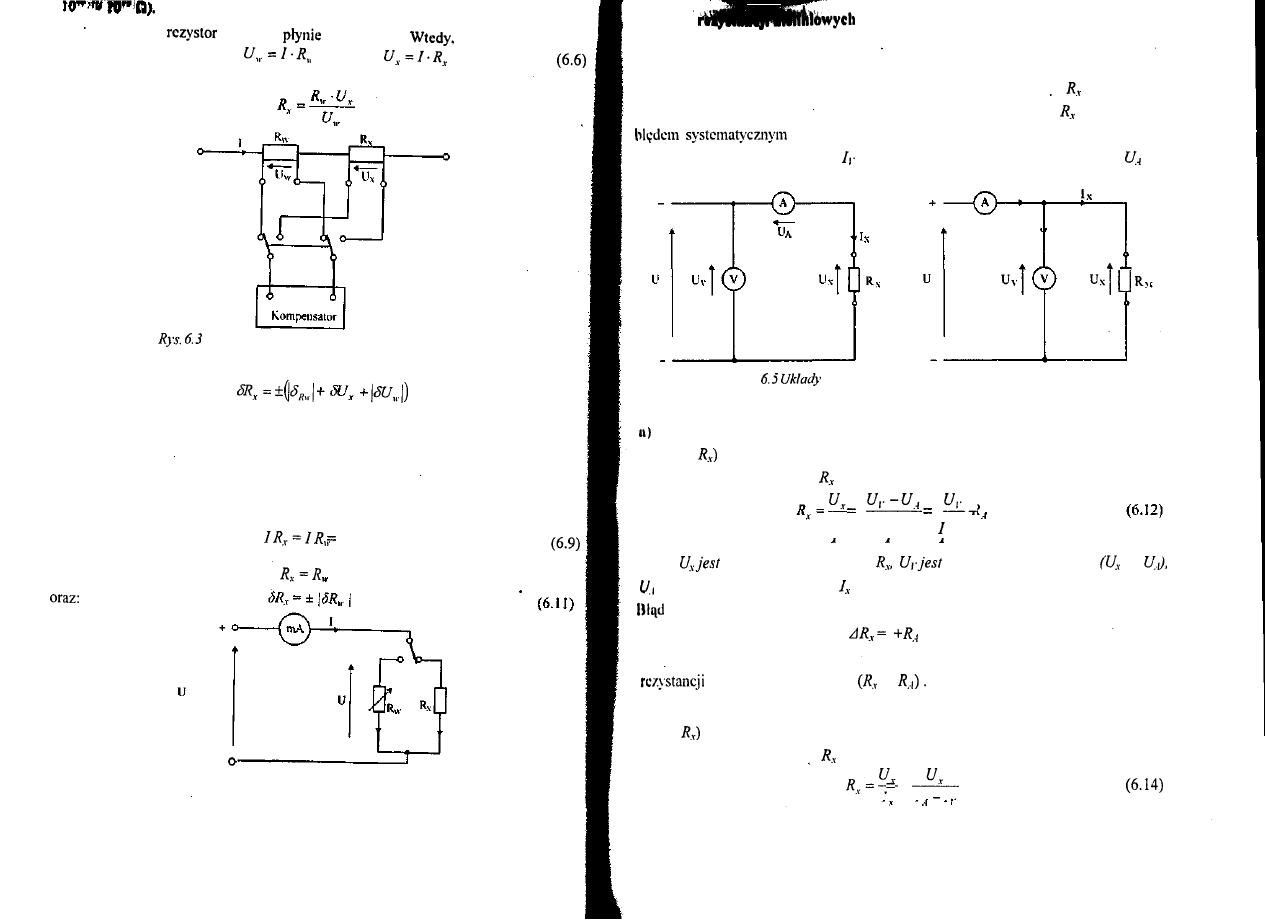
Dzięki zastosowaniu kompensatora napięcia można przyjąć, że przez
rezystor badany i
wzorcowy
ten sam prąd.
z pomiarów:
oraz
można otrzymać:
(6.7)
Zasada pomiaru rezystancji metodą porównania
Dokładność metody porównawczej określa wzór:
\\
\ \
(6.8)
Metoda podstawienia (rys. 6.4.) zapewnia dokładny pomiar rezystancji o dużej
wartości (zakres stosowania: 10
4
- 10" fi). Polega ona na podstawieniu w obwodzie
z czułym wskaźnikiem prądu w miejsce mierzonej rezystancji - rezystancji wzorcowej
o regulowanej wartości. Należy tak nastawić tę rezystancję, by po jej podstawieniu
wskaźnik prądu nie zmienił swego wskazania. Wtedy:
U
Zatem: '
(6.10)
= const
-
2. Pomiar
(metoda techniczna)
Do pomiaru rezystancji nieliniowej (ale można nią mierzyć również rezystancje
liniowe) służy metoda techniczna, pośrednia, polegająca na wykorzystaniu
woltomierza i amperomierza (rys. 6.5). Wartość mierzonej rezystancji wylicza się na
podstawie prawa Ohma ze wskazań przyrządów. Obliczona wartość obarczona jest
wynikającym z niedoskonałości energetycznej woltomierza
lub amperomierza (pobór prądu
przez woltomierz, albo spadek napięcia
na
umperomierzu).
1A
Iv
Rys. 6.4 Zasada pomiaru rezystancji metodą podstawienia
Rys.
do pomiaru rezystancji metodą techniczną:
a) poprawnie mierzonego prądu, b) poprawnie mierzonego napięcia
Układ poprawnie mierzonego prądu (amperomierz wskazuje prąd płynący
przez
Poprawną wartość rezystancji
określa wzór:
/ /
x
x
x
gdzie:
napięciem na rezystancji
wskazaniem woltomierza
+
napięciem na amperomierzu,
wskazaniem amperomierza
metody wynosi:
(6.13)
Wynika stąd wniosek, by układ poprawnie mierzonego prądu stosować do. pomiaru
o dużych wartościach
»
b) Układ poprawnie mierzonego napięcia (woltomierz wskazuje spadek napięcia
na
Poprawną wartość rezystancji określa wzór:
/ / /
58
59
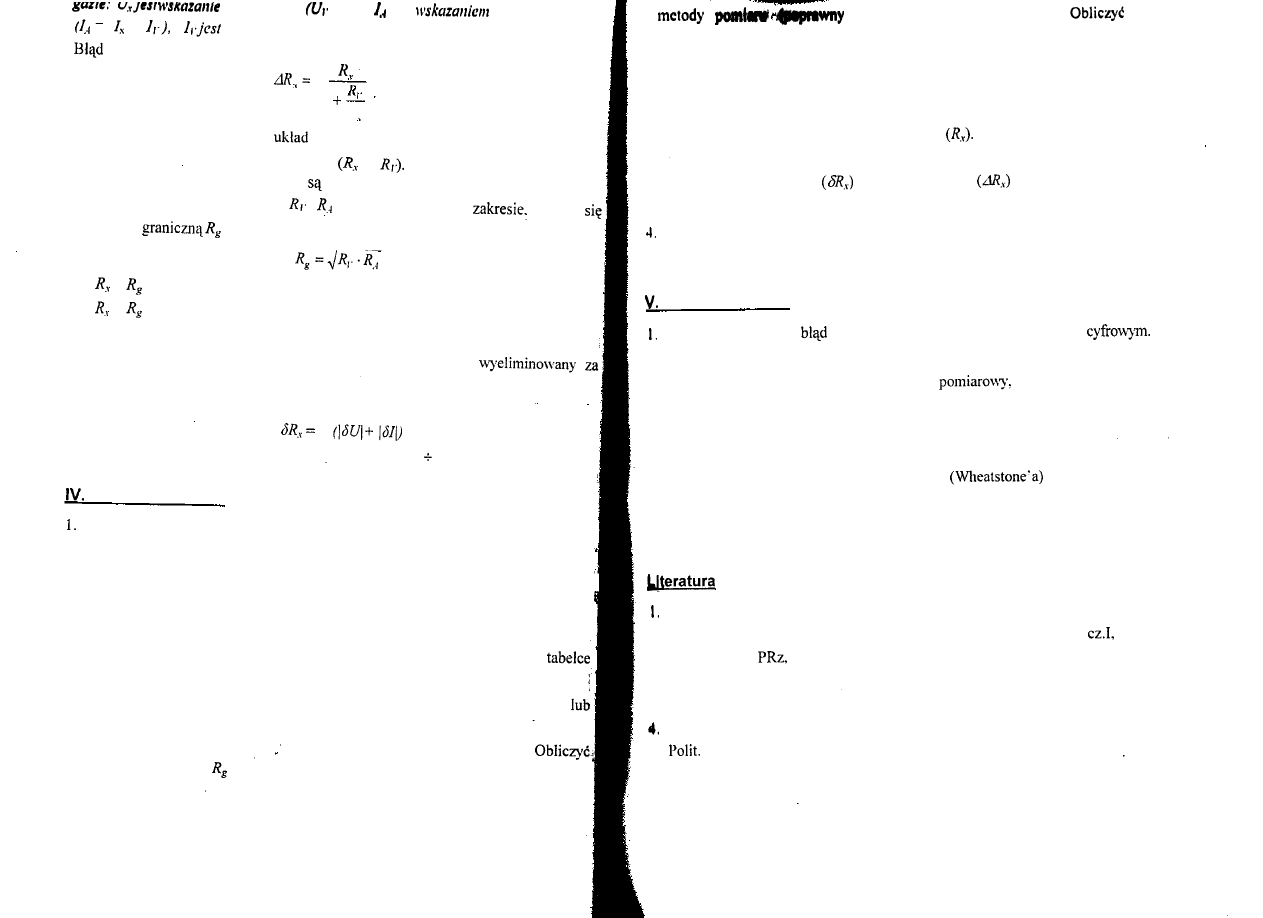
woltomierza
• UJ, Jest
amperomierza
- +
a
to prąd pobierany przez woltomierz
metody wynosi:
—
1
(6.15)
R..
Wynika stąd wniosek, by
poprawnie mierzonego napięcia stosować do
pomiaru rezystancji o małych wartościach
«
Dla ułatwienia decyzji, jeżeli dostępne dane techniczne woltomierza i amperomierza
i można z nich uzyskać wartości
i
na wykorzystywanym
oblicza
rezystancję
ze wzoru:
(6.16)
Dla < stosuje się układ poprawnie mierzonego napięcia.
Dla > stosuje się układ poprawnie mierzonego prądu.
Określenie dokładności metody technicznej powinno uwzględniać błąd metody
wybranego układu (który jako błąd systematyczny może być
pomocą poprawki) oraz błędy graniczne wnoszone przez woltomierz i amperomierz
a zależne od ich klasy. Dla metody pośredniej błąd względny graniczny wynosi:
±
(6.17)
Praktycznie dokładność metody technicznej wynosi ok. ±1 5%.
Program ćwiczenia
Wybrać rezystor z zestawu, zapisać jego dane do tabelki. Dobrać zakres pomiarowy i
omomierza na podstawie przewidywanej wartości rezystancji rezystora wynikającej'
z jego danych. Zweryfikować zakres, by błąd rozdzielczości pomiaru był]
najmniejszy. Zanotować wynik i obliczyć bezwzględną wartość błędu granicznego j
pomiaru.
2. Zmierzyć rezystancję tego samego rezystora metodą techniczną. Zapisać w
j
dane zastosowanych przyrządów. Obliczyć przewidywane wartości napięcia i prądu
(należy założyć jedną z nich np. równą zakresowi woltomierza ale niniejszą
równą napięciu osiąganemu z zasilacza). Zestawić w tabelce dobrane zakresy i
pomiarowe oraz podać charaktenstyczne dla nich rezystancje wewnętrzne.
rezystancję graniczną dla dobranych zakresów pomiarowych i dokonać wyboru
pomiar napięcia albo prądu).
błędy
systematyczne metody. Zmontować wybrany układ pomiarowy, zapisać wyniki
i dokonać potrzebnych obliczeń.
3. Wybrać rezystor z zestawu i podłączyć do mostka. Ustawić na technicznym mostku
Wheatstone'a przewidywany zakres pomiarowy. Zrównoważyć mostek. Odczytać
i zapisać wartość mierzonej rezystancji
Powtórzyć pomiary w celu
wyeliminowania powstania błędu grubego. Określić i obliczyć wartość błędu
granicznego względnego
i bezwzględnego
pomiaru. Zapisać wynik
pomiaru.
Za pomocą technicznego mostka Thomsona zmierzyć wybraną rezystancję. W celu
eliminacji błędu grubego powtórzyć dodatkowo pomiar.
Pytania kontrolne
Podaj i omów wzór na
graniczny pomiaru rezystancji omomierzem
2. Narysuj układ do pomiaru rezystancji metodą techniczną.
3. Podaj zasadę pozwalającą wybrać układ
wprowadzający mniejszy
błąd systematyczny w technicznej metodzie pomiaru rezystancji.
4. W jakim celu zmieniamy kierunek prądu w obwodzie mostka (tzw. komutacja)?
5. Co ogranicza zakres pomiarowy mostka Wheatstone'a od dołu a co od góry?
7. Różnice budowy mostka czteroramiennego
i sześcioramiennego
(Thomsona). W jakim celu skonstruowano mostek sześcioramienny.
8. Schemat i rozwiązania konstrukcyjne mostka technicznego Thomsona.
Chwaleba A.: Metrologia elektryczna, Warszawa: WNT, 1997.
2. Dyszyński J.: Metrologia elektryczna i elektroniczna - laboratorium
Rzeszów:
Wydawnictwo
1997.
3. Marcyniuk A., Pasecki E..Pluciński M., Szadkowski B, Podstawy metrologii
elektrycznej, WNT, Warszawa 1984
Szadkowski B. (red) Laboratorium metrologii elektrycznej i elektronicznej, Wyd.
Śląskiej, Gliwice, 1998
60
61
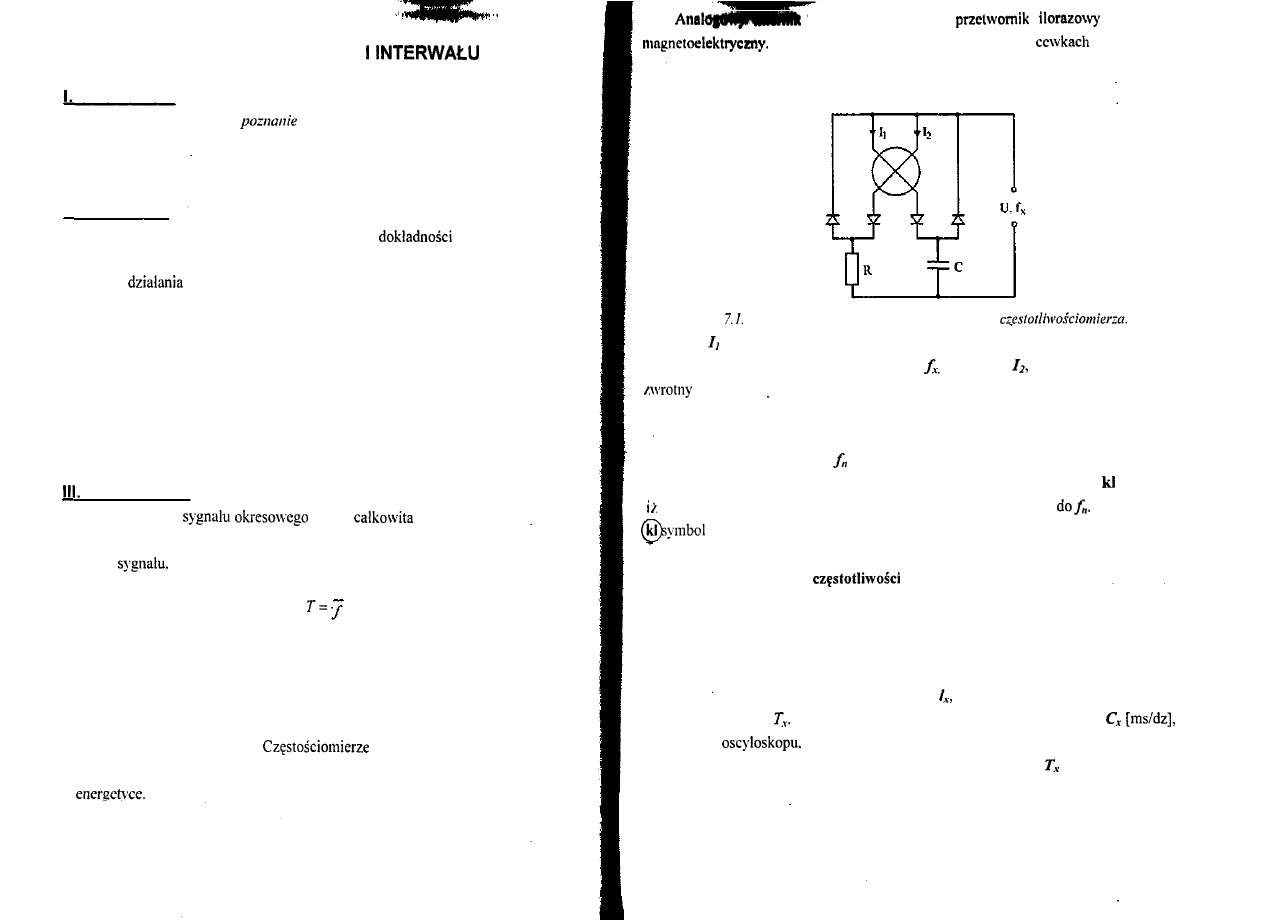
Ćwiczenia 7
POMIARY CZĘSTOTLIWOŚCI
CZASU
Cel ćwiczenia
Celem ćwiczenia jest
podstawowych metod pomiaru częstotliwości.
Metody analogowe, zasada cyfrowego pomiaru częstotliwości i interwalu czasu,
pomiary częstotliwości z wykorzystaniem oscyloskopu elektronicznego.
II. Zagadnienia
1. Symbole dotyczące dokładności i definicje klasy
mierników.
2. Budowa i zasada działania ilorazowego miernika częstotliwości.
3. Zasada
miernika z przetwarzaniem częstotliwość/prąd.
4. Bezpośredni i pośredni cyfrowy pomiar częstotliwości.
5. Cyfrowy pomiar interwalu czasu i okresu.
6. Pomiar częstotliwości za pomocą oscyloskopu.
7. Pomiar częstotliwości metodą porównania z wzorcem.
8. Błąd zliczania.
9. Schemat blokowy układu pomiarowego uniwersalnego miernika częstotliwości
i okresu sygnałów periodycznych (ogólnie interwału czasu).
Wprowadzenie
Częstotliwość
jest to
liczba cykli sygnału w jednej
sekundzie, wyrażana jest w hercach [Hz]. Czas trwania pełnego cyklu nazywamy
okresem
zależność pomiędzy okresem a częstotliwością wyraża zależność:
1
(7.1)
gdzie:
T- okres sygnału,
/- częstotliwość sygnału.
Metody pomiaru częstotliwości dzielą się na metody analogowe i cyfrowe.
Do metod analogowych należy między innymi pomiar częstotliwości za pomocą
przetwornika ilorazowego.
ilorazowe elektromagnetyczne
i elektrodynamiczne są wykorzystywane do pomiaru częstotliwości sieciowej
w
częstotliwości posiada
najczęściej
Układ jest tak zbudowany, że prądy w obu
przetwornika
0 wartości proporcjonalnej do napięcia, są w różny sposób zależne od częstotliwości.
Na rys. 7.1 przedstawiono układ takiego miernika.
Rys.
Schemat ilorazowego elektromagnetycznego
Prąd wytwarzający w przetworniku moment napędowy, jest proporcjonalny do
napięcia zasilającego U i do częstotliwości natomiast
wytwarzający moment
jest proporcjonalny do napięcia, ale nie zależy od jego częstotliwości [1].
W pomiarach częstotliwości sieci energetycznej stosowane są mierniki
wskazówkowe lub cyfrowe o zawężonym zakresie pomiarowym, np. od 45 do 65 Hz,
czyli zakres takiego miernika = 65 - 45 = 20 Hz W miernikach częstotliwości
sieciowej spotyka się dwa sposoby określenia klasy dokładności. Symbol
oznacza,
następuje odniesienie do zakresu pomiarowego przyrządu, czyli
W przypadku
oznacza odniesienie do wartości mierzonej [1,2].
7.1. Bezpośredni pomiar
oscyloskopem elektronicznym
Przyrządem używanym często do pomiaru częstotliwości jest oscyloskop
elektroniczny. Pomiar częstotliwości oscyloskopem elektronicznym może odbywać się
bezpośrednio z wykorzystaniem kalibrowanej podstawy czasu, lub też pośrednio
poprzez porównanie z wzorcem. Metoda bezpośrednia pomiaru częstotliwości polega
na odczytaniu z ekranu oscyloskopu wartości
odpowiadającej jednemu okresowi
przebiegu badanego
Znając współczynnik odchylania podstawy czasu
odczytany z
który oznacza ile jednostek czasu przypada na jedną działkę
odchylania poziomego można obliczyć okres sygnału badanego
(7.2). Ważne jest,
aby tor odchylania poziomego był skalibrowany.
62
63
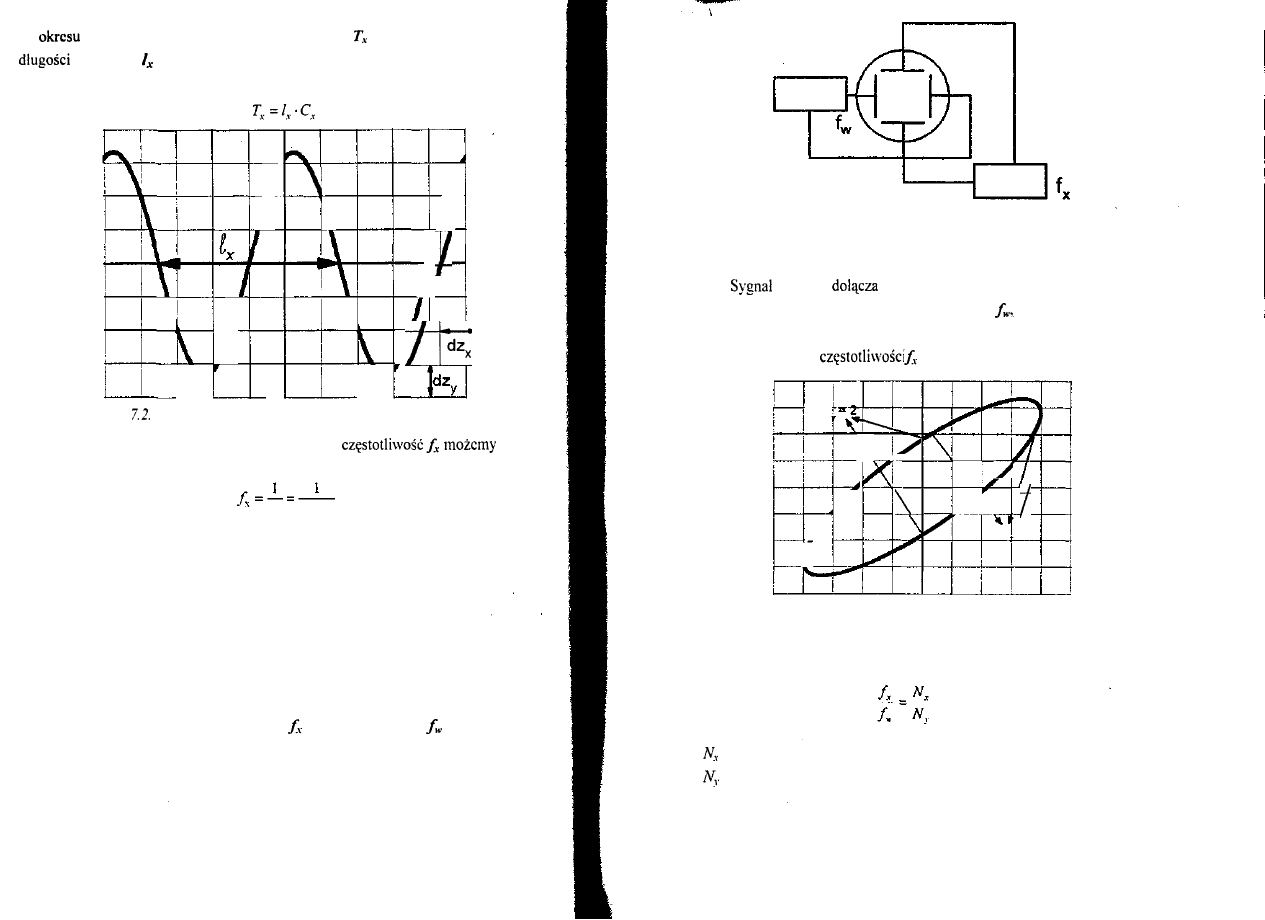
Na rys. 7.2. przedstawiono sposób odczytania długości odcinka proporcjonalnego
do
sygnału badanego. Okres badanego sygnału
można obliczyć jako iloczyn
odcinka
oraz wartości współczynnika odchylania podstawy czasu.
Wyrażenie to przyjmuje postać:
(7.2)
\
r
i
/
/
//
—
\
\
r
//
i
Rys.
Sposób obliczania częstotliwości oscyloskopem elektronicznym
Przekształcając równanie (7.1) i (7.2) badaną
obliczyć
ze wzoru:
(7.3)
Pomiar częstotliwości oscyloskopem z wykorzystaniem generatora podstawy
czasu cechuje mała dokładność, większe dokładności tego pomiaru uzyskuje się
w metodzie pośredniej - porównania z wzorcem częstotliwości.
7.2. Porównawczy pomiar częstotliwości - metoda krzywych Lissajous
Metoda porównania z wzorcem za pomocą oscyloskopu elektronicznego
nazywana jest często metodą elipsy lub krzywych Lissajous. W metodzie tej
oscyloskop powinien pracować w trybie X-Y, czyli przy wyłączonej podstawie czasu.
Schemat podłączenia sygnału badanego oraz wzorcowego
do oscyloskopu
przedstawia rys. 7.3.
64
Generator
wzorcowy
Generator
badany
Rys. 7.3. Pomiar częstotliwości metodą porównania z wzorcem
Sygnał z generatora wzorcowego dołączany jest do gniazda wejściowego X
oscyloskopu.
badany
się do gniazda wejściowego Y oscyloskopu.
Należy tak zmieniać wartość częstotliwości wzorcowej
aby uzyskać na ekranie
obraz elipsy lub innej nieskomplikowanej krzywej. Gdy obraz będzie nieruchomy
możemy wyznaczyć wartość
ze wzoru (7.4).
—N
/
r
\ .
/
V
/ \
N = 2
Rys. 7.4. Sposób obliczania stosunku częstotliwości na podstawie figury Lissajous
Liczba przecięć figury na ekranie oscyloskopu z prostą równoległą do osi X i do
osi Y wyznacza stosunek częstotliwości badanej do wzorcowej:
(7.4)
gdzie:
- liczba przecięć z prostą równoległą do osi X,
- liczba przecięć z prostą równoległą do osi Y.
65
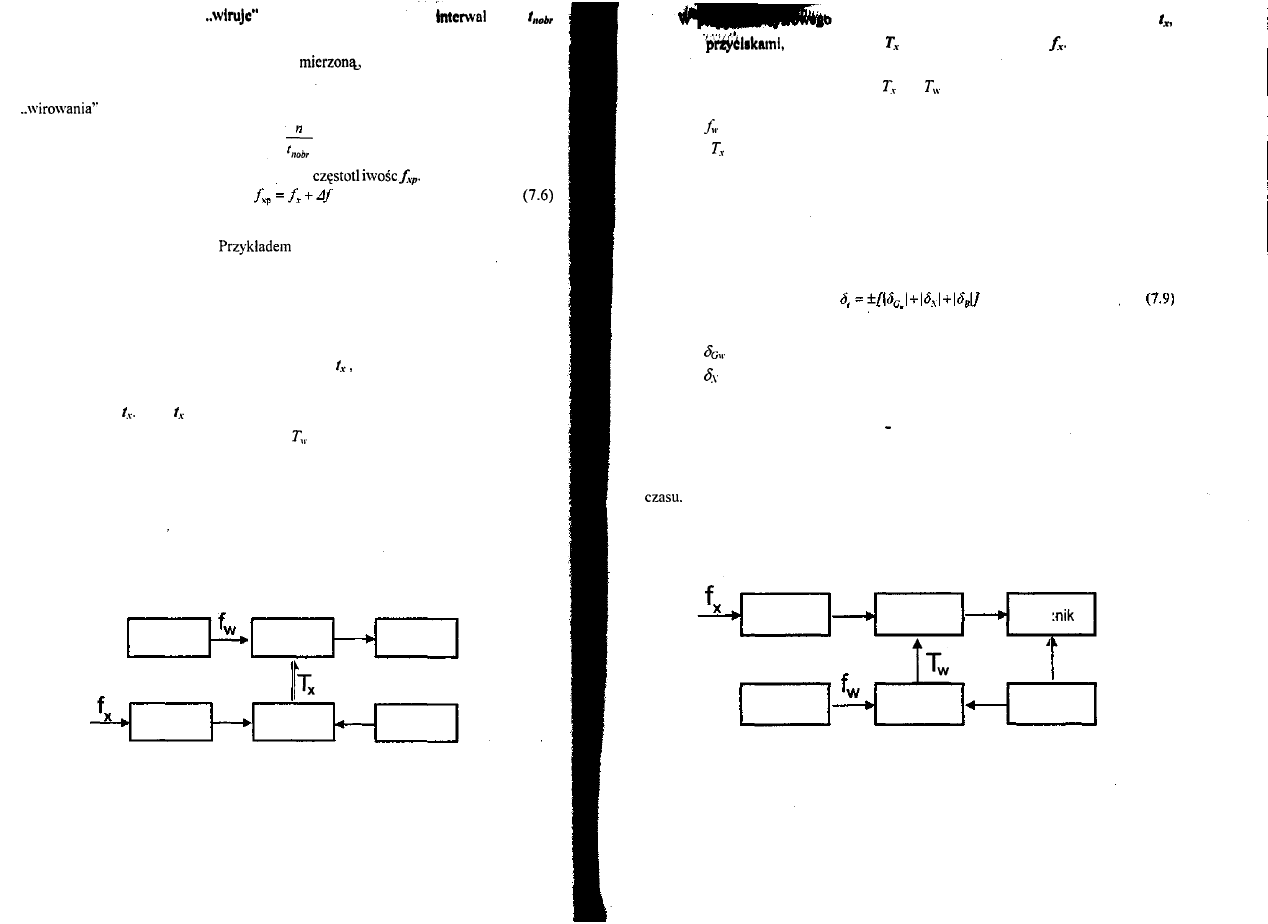
W przypadku, gdy obraz
na ekranie, należy zmierzyć
czasu
potrzebny na wykonanie kilku n pełnych „obrotów" figury. Następnie należy obliczyć
wartość różnicy Af pomiędzy częstotliwością
a wzorcową. Zwiększając (lub
zmniejszając) płynnie częstotliwość wzorcową, zaobserwować zmianę prędkości
elipsy, aby określić znak różnicy częstotliwości.
Af = (7.5)
Następnie należy obliczyć poprawioną wartość
Inną z metod analogowych pomiaru częstotliwości jest zastosowanie układu
mostka zmiennoprądowego.
takiego mostka może być mostek
Robinsona - Wiena, a także mostek rezonansowy' [2, 3].
7.3. Cyfrowy miernik czasu - okresu
Cyfrowy pomiar czasu polega na odpowiednim wysterowaniu bramki tak, aby licznik
zliczył impulsy generatora wzorcowego w czasie
zadanym przyciskami START
oraz STOP. Liczba impulsów n zliczona przez licznik jest proporcjonalna do czasu
otwarcia bramki Czas możemy wyznaczyć z zależności:
t,= n (7.7)
Schemat blokowy cyfrowego miernika okresu jest to szczególny przypadek miernika
interwału czasu, został on przedstawiony na rys. 7.5. Głównymi blokami tego układu
jest generator częstotliwości wzorcowej, układ sterowania, układ formujący oraz
bramka. Układ sterowania otwiera bramkę oraz zeruje licznik przed każdym
pomiarem. Układ formujący (inaczej układ dyskryminatora) nadaje sygnałowi
wejściowemu żądaną amplitudę i kształt.
Generator
wzorcowy
Układ
formujący
Bramka
i
Licznik
\
Układ
sterowania
Układ
automatyki
Rys. 7.5. Schemat blokowy cyfrowego miernika okresu.
66
miernika okresu bramka otwierana jest nic na czas
zadawany
ale na okres
częstotliwości badanej Zależność (7.7)
przyjmuje postać:
= n
(7.8)
gdzie:
- częstotliwość wzorcowa,
- okres częstotliwości badanej (czas otwarcia bramki),
n - liczba zliczanych impulsów.
Maksymalny błąd pomiaru cyfrowym miernikiem czasu (okresu) wynika z błędu
zliczania, błędu generatora wzorcowego i błędu bramkowania, spowodowanego
występowaniem czasu opóźnienia bramki i układu sterowania [1,2]. Wartość tego
błędu można obliczyć z zależności:
gdzie:
- błąd generatora wzorcowego,
- błąd zliczania,
Sg - błąd bramkowania.
7.4. Cyfrowy miernik częstotliwości metoda bezpośrednia
Schemat blokowy toru pomiarowego cyfrowego miernika częstotliwości
przedstawia rys. 7.6. Składa się on z identycznych bloków, jak w cyfrowym mierniku
a różni jedynie się sposobem ich połączenia. Sygnał wejściowy podawany jest
na układ formujący, gdyż liczniki muszą być sterowane impulsami o określonej
amplitudzie i kształcie [5].
Układ
formujący
Generator
wzorcowy
Bramka
Układ
sterowania
Licz
Układ
automatyki
Rys. 7.6. Schemat blokowy cyfrowego miernika częstotliwości
67
automatyki kasuje licznik przed każdym pomiarem oraz odblokowujc
sterowania.
sterowania otwiera i zamyka bramkę. Czas otwarcia bramki
jest równy okresowi częstotliwości
7V. W czasie otwarcia bramki 7V
licznik zlicza n impulsów sygnału
zatem:
(7.10)
Częstotliwość sygnału wejściowego możemy wyznaczyć z zależności
(7.11)
Na błąd pomiaru częstotliwości metodą cyfrową ma wpływ dokładność generatora
wzorcowego oraz błąd zliczania. W celu zmniejszenia błędu dyskretyzacji (zliczania)
należy odpowiednio dobrać częstotliwość wzorcową. Stosunek częstotliwości
wzorcowej do częstotliwości badanej powinien być nie mniejszy niż
aby zapewnić
wystarczający czas otwarcia bramki.
Program ćwiczenia
1. Przed przystąpieniem do wykonywania ćwiczenia należy włączyć generator
funkcyjny, generator wzorcowy i
cyfrowy w celu ustabilizowania
się warunków termicznych pracy przyrządów.
2. Sprawdzić działanie kasety dydaktycznej jako układu stopera o zmiennej
(wybranej) rozdzielczości zależności od
3. Połączyć układ według schematu do pomiaru częstotliwości sieci
a kasetę
jako cyfrowy miernik częstotliwości.
4. Dobrać częstotliwość wzorcową tak, aby na wyświetlaczu była maksymalna liczba
cyfr. Zapisać wartość częstotliwości wzorcowej.
5. Zanotować wartości częstotliwości, zmierzone za pomocą miernika analogowego
i częstościomierza PFL.
6. Obliczyć wartość częstotliwości na podstawie wskazania kasety i porównać
z wynikami otrzymanymi z pozostałych przyrządów.
7. Wyznaczyć częstotliwość graniczną kasety dydaktycznej.
1. Omówić podstawowe bloki funkcjonalne układu do cyfrowego
i interwalu czasu.
2. Omówić pojęcia: błąd operacji zliczania, błąd operacji bramkowania, błąd wzorca
częstotliwości i interwału czasu, łączny błąd pomiaru.
3. Podać definicję częstotliwości i okresu stanowiące podstawę cyfrowych pomiarów
tych parametrów.
4. Jak osiągnąć dużą dokładność pomiaru częstotliwości w przypadku małych
częstotliwości np. 50 Hz?
5. Co decyduje o niedokładności cyfrowego pomiaru częstotliwości?
6. Jak zminimalizować błąd zliczania dla cyfrowego pomiaru małej częstotliwości?
7. Co
na niedokładność pomiaru częstotliwości oscyloskopem?
8. Co decyduje o niedokładności pomiaru w metodzie porównania do wzorca?
Literatura
1.
J.: Metrologia Elektryczna i Elektroniczna. Laboratorium
Rzeszów:
Wyd.PRz, 1997.
2. Marcyniuk A., Piasecki E.,
M., Szadkowski B.: Podstawy metrologii
elektrycznej. Warszawa: WNT, 1984.
3. Ratyńska J.: Laboratorium techniki pomiarowej. Radom Zakład Poligraficzny
Politechniki Radomskiej, 1997.
4. Rydzewski J.:
oscyloskopowe. Warszawa: WNT, 1994.
5. Sahner G.: Wstęp do miernictwa cyfrowego. Warszawa: WKL, 1982.
68
69
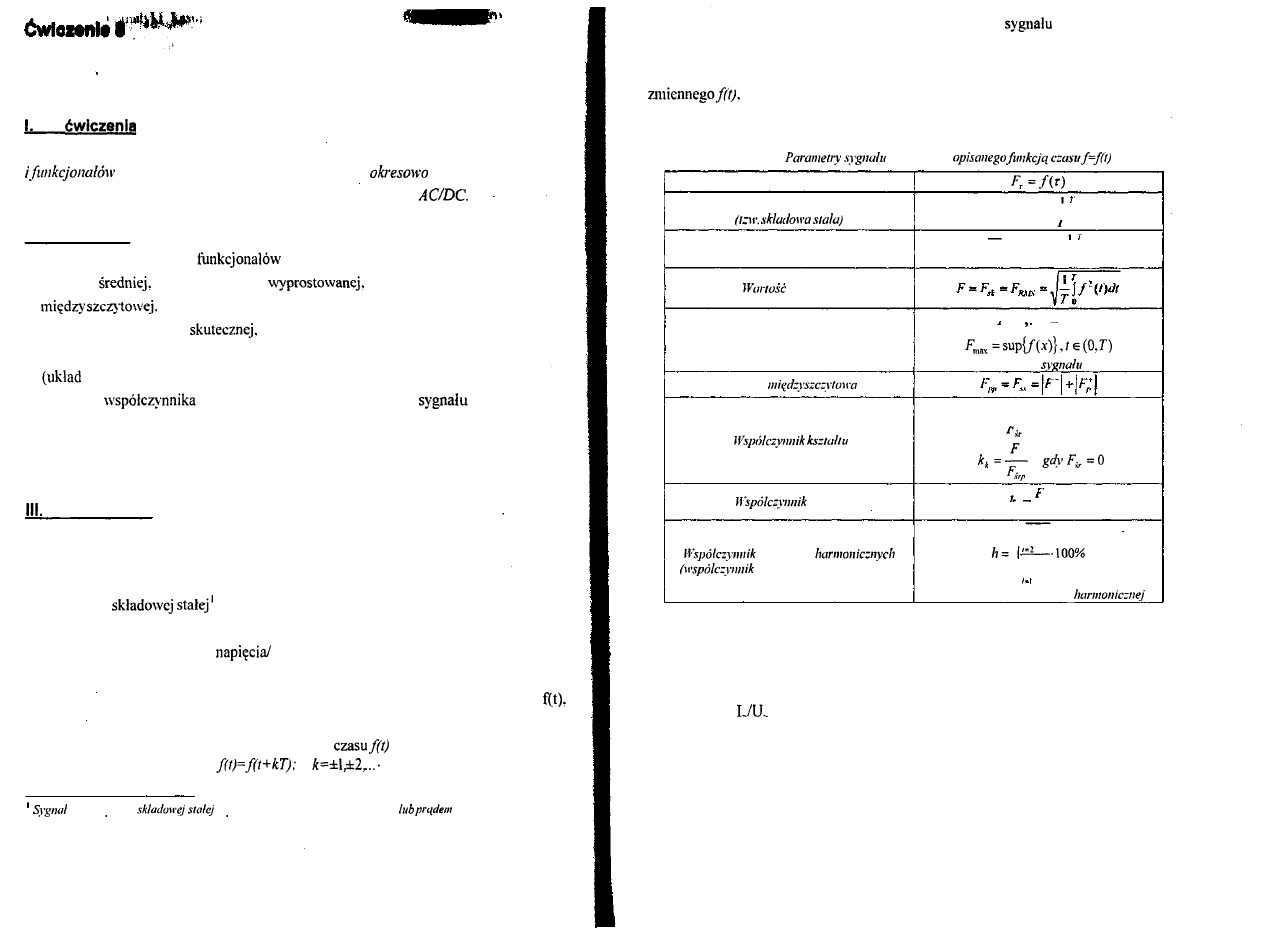
POMIARY PARAMETRÓW ZMIENNYCH
PRZEBIEGÓW NAPIĘCIOWYCH
Cel
Celem ćwiczenia jest poznanie metod stosowanych do wyznaczania parametrów
sygnałów pomiarowych na przykładzie
zmiennego sygnału
napięciowego oraz zwrócenie szczególnej uwagi na przetworniki
II. Zagadnienia
1. Definicje parametrów i
sygnałów okresowych: wartości skutecznej,
wartości
wartości średniej
wartości szczytowej, wartości
2. Przetworniki wartości
przetworniki wartości średniej wyprostowanej
(prostownik jednopołówkowy/ dwupołówkowy), przetworniki wartości szczytowej,
szeregowy/ równoległy), przetwornik wartości międzyszczytowej.
3. Definicje
kształtu i współczynnika szczytu
napięciowego
oraz układy pomiarowe do ich wyznaczania.
4. Woltomierze napięcia zmiennego (analogowe i cyfrowe).
5. Pomiary parametrów napięć zmiennych za pomocą oscyloskopu elektronicznego.
Wprowadzenie
Sposób wykonania pomiaru napięcia lub prądu zmiennego zależy przede
wszystkim od:
- charakteru zmienności tych wielkości w funkcji czasu
- obecności
- częstotliwości mierzonego sygnału
- przyjętej miary mierzonego
prądu.
Zdeterminowane sygnały napięciowe lub prądowe występujące w układach
pomiarowych są najczęściej modelowane za pomocą funkcji czasu
przedstawianych analitycznie, graficznie lub tabelarycznie. Szczególne znaczenie
posiadają sygnały okresowe opisane przez funkcję
spełniające warunek:
(8.1)
gdzie T oznacza okres sygnału. Wszystkie właściwości
okresowego można
wyznaczyć na podstawie badania sygnału w czasie jednego okresu.
W tabeli 8.1 zestawiono wzory definicyjne miar stosowanych dla przebiegu okresowo
reprezentującego zarówno napięcie, jak i prąd. Podane oznaczenia miar
są najczęściej używane w języku polskim i angielskim.
Tabela S.J.
okresowego
Wartość chwilowa
Wartość średnia
Wartość średnia wyprostowana
skuteczna
Wartość szczytowa
Wartość
szczytu
zawartości
zniekształceń nieliniowych)
0
1
0
p
ma\
p *
max
T- okres
p
F
max
' F
A, - wartość skuteczna i - tej
Układy pomiarowe do wyznaczania wymienionych parametrów i funkcjonałów zostaną
omówione na przykładzie pomiaru napięcia zmiennego. Układy te można również
wykorzystać do pomiaru prądu zmiennego, dzięki zastosowaniu dodatkowego
przetwornika
. Rolę takiego przetwornika w zakresie niskich częstotliwości
(np. w obwodach sieciowych) zazwyczaj pełni rezystor wzorcowy o malej wartości
rezystancji, który należy umieścić w badanym obwodzie prądowym.
okresowy bez
nazwany jest odpowiednio napięciem
przemiennym.
70
71
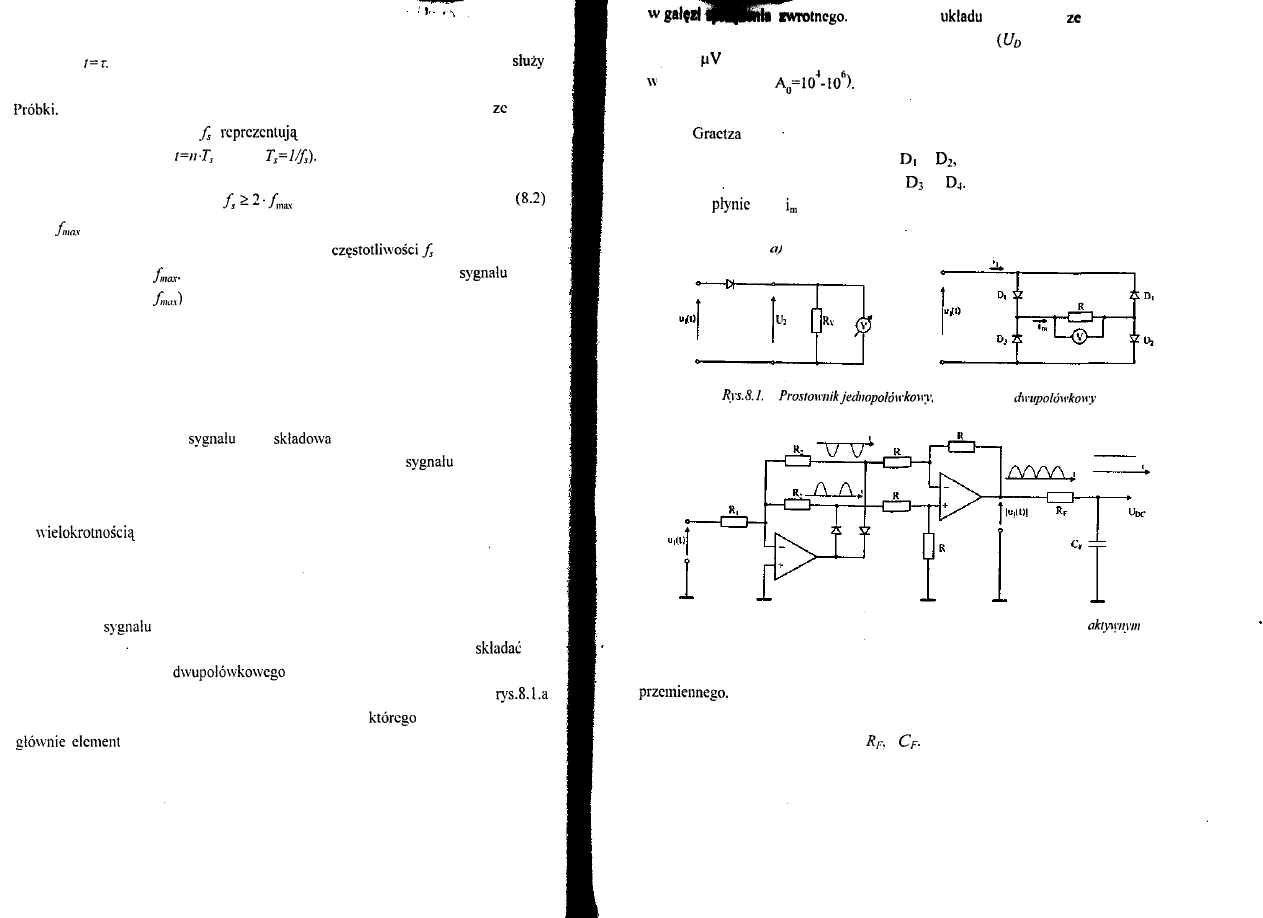
Pomiar wartości chwilowej
Wartość chwilowa napięcia zmiennego jest to wartość, którą funkcja u(t) osiąga
w chwili
Do obserwacji przebiegu czasowego napięcia zmiennego
oscyloskop elektroniczny lub cyfrowy.
uzyskane w wyniku operacji próbkowania sygnału pomiarowego
stałą
częstotliwością próbkowania
wartości chwilowe sygnału pobrane
w chwilach próbkowania
(gdzie
Wartość częstotliwości próbkowania
równomiernego powinna być dobrana zgodnie z warunkiem Shannona-Kotielnikowa
gdzie
oznacza największą częstotliwość występującą w widmie sygnału
próbkowanego. W praktyce przyjmuje się wartość
od 5 do 10 razy
większą od wartości
Do ograniczenia widma próbkowanego
(tzn.
ograniczenia wartości
stosuje się analogowy filtr dolnoprzepustowy, tzw. filtr
antyaliasingowy. Na podstawie zbioru próbek pobranych zgodnie z warunkiem (8.2)
można odtworzyć sygnał oryginalny.
Pomiar wartości średniej
Wartość średnia jest miarą powszechnie stosowaną do wyrażenia wydajności procesu
elektrolizy. Wartość średnia
(tzw.
stała) jest mierzona:
- przyrządami magnetoelektrycznych, jeżeli częstotliwość
jest znacznie
większa od częstotliwości drgań własnych ustroju pomiarowego;
- cyfrowymi przyrządami całkującymi, przy czym czas całkowania powinien być
okresu mierzonego sygnału.
Pomiar wartości średniej wyprostowanej
Wartość średnią wyprostowaną otrzymuje się w wyniku operacji wyznaczania wartości
bezwzględnej
(tzw. operacji prostowania), a następnie uśredniania w czasie
równym okresowi mierzonego sygnału. Układ pomiarowy powinien
się
z prostownika jedno lub
o liniowej charakterystyce statycznej oraz
woltomierza napięcia stałego (lub amperomierza prądu stałego). Na
przedstawiono układ prostownika jednopołówkowego,
właściwości określa
prostowniczy - dioda. W praktyce najczęściej stosuje się układy ze
wzmacniaczami operacyjnymi - rys.8.2. Dzięki silnemu ujemnemu sprzężeniu
zwrotnemu układ ma charakterystykę liniową niezależną od charakterystyki diod
72
Zastosowanie
prostownika wzmacniaczem
operacyjnym zapewnia spadek napięcia progowego diody
= 0,2-0,6V) do poziomu
(0.2-60)
w zależności od wartości wzmocnienia wzmacniacza pracującego
otwartej pętli (np.
Rolę prostownika dwupołówkowego często pełni tzw. układ Gractza (rys.8.1.b) lub
układ
ze wzmacniaczem operacyjnym. W czasie dodatniego półokresu
napięcia wejściowego przewodzą diody
i
zaś w czasie ujemnego półokresu
napięcia wejściowego przewodzą diody
i
Podczas obu półokresów przez
rezystor R
prąd w tym samym kierunku (efekt prostowania dupołówkowego).
b)
a)
b) Prostownik
Rys.8.2. Przetwornik wartości średniej wyprostowanej bazujący na prostowniku
Na rys.8.2 zaprezentowano układ do pomiaru wartości średniej wyprostowanej sygnału
w którym zastosowano liniowy prostownik aktywny. Wynik operacji
uśredniania za pomocą filtru dolnoprzepustowego w dużym stopniu zależy od doboru
wartości rezystancji i pojemności
Nieodpowiedni wybór wspomnianych
wartości jest przyczyną niepożądanych tętnień o niewielkiej amplitudzie nakładających
się na napięcie stałe na wyjściu przetwornika.
73
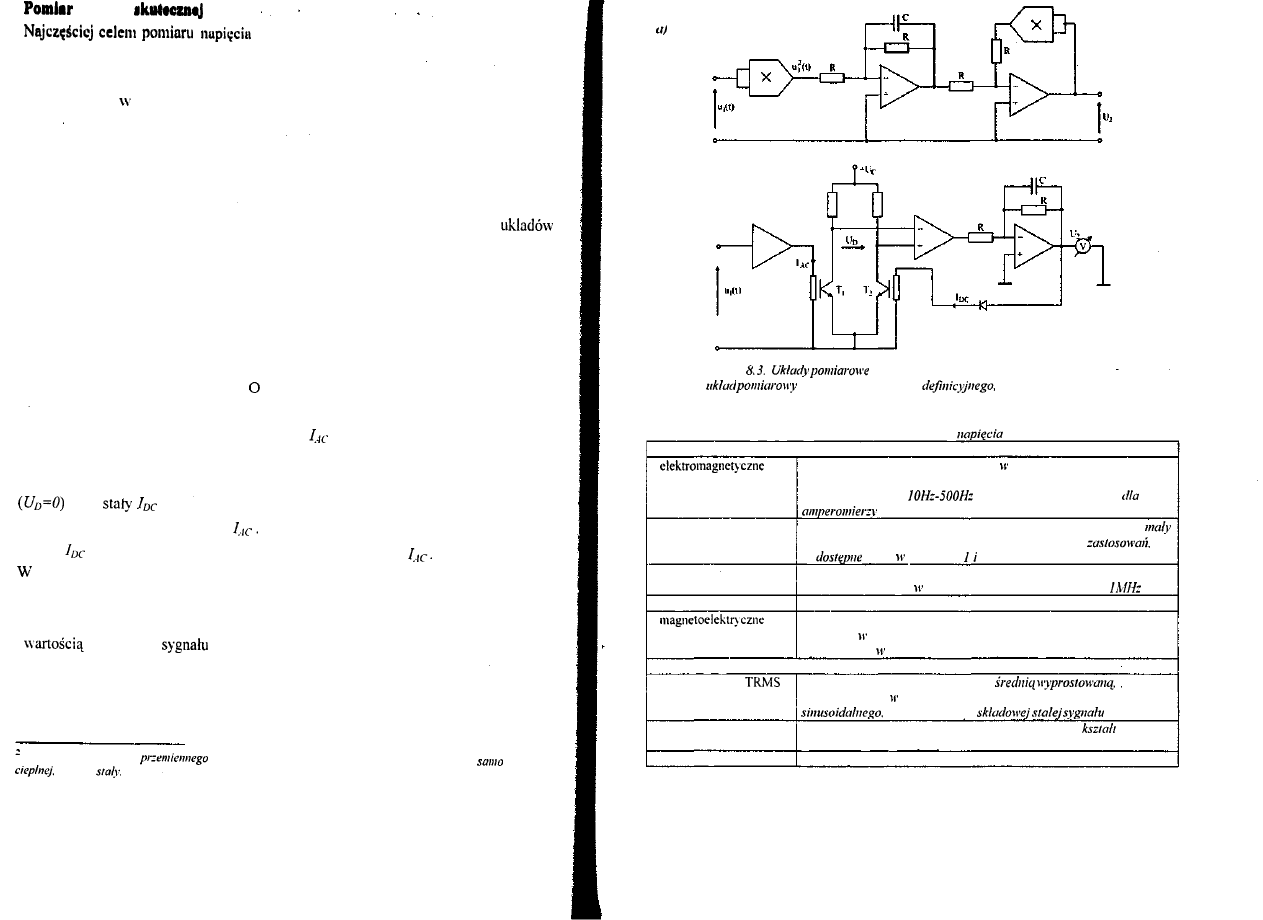
wartości
lub prądu zmiennego jest określenie wartości
skutecznej. Układy pomiarowe przeznaczone do wyznaczania wartości skutecznej
buduje się na bazie przetwornika pomiarowego AC/DC o charakterystyce
przetwarzania
kształcie paraboli oraz woltomierza napięcia stałego. Stała
przemarzania takiego przetwornika nie powinna zależeć od częstotliwości w zakresie
odpowiadającym częstotliwościom wszystkich składowych harmonicznych mierzonego
sygnału. W celu uzyskania parabolicznej charakterystyki przetwornika wykorzystuje
się różne rozwiązania, m.in.:
- aproksymację charakterystyki kwadratowej odcinkami za pomocą
diodowo - rezystancyjnych (tzw. kwadrator diodowy),
- analogowe przetwarzanie sygnału wg wzoru definicyjnego - rys.8.3.a,
- metodę termiczną bazującą na definicji wartości skutecznej
2
- rys.8.3.b.
Układ pomiarowy zbudowany na podstawie wzoru definicyjnego jest często
realizowany w scalonych przetwornikach wartości skutecznej. Wykonuje on trzy
operacje: podnoszenie napięcia wejściowego do kwadratu, wyznaczanie wartości
średniej oraz obliczenie pierwiastka. wyniku operacji uśredniania decyduje przyjęcie
wartości stałej czasowej RC, odpowiedniej do częstotliwości mierzonego przebiegu.
W przetwornikach termicznych mierzony prąd
przepływa przez cienki drut grzejny,
a termopara lub tranzystor pełniące rolę czujnika temperatury T, wytwarza napięcie
stałe, proporcjonalne do wzrostu temperatur}' złącza. W stanie równowagi termicznej
prąd
płynący przez drugi drut grzejny wydziela w jednostce czasu
taką samą ilość ciepła, jak prąd
W takim przypadku wartość natężenia prądu
stałego
jest równa wartości skutecznej prądu przemiennego
tabeli 8.2 podano przyrządy analogowe i cyfrowe stosowane do pomiaru wartości
skutecznej w obwodach prądu przemiennego. Przy wyborze odpowiedniego przyrządu
pomiarowego należy kierować się żądaną dokładnością pomiaru, częstotliwością
i
mierzonego
oraz stopniem jego odkształcenia.
Wartość skuteczna prądu
to taka wartość prądu, która wydziela na rezystorze tyle
energii
co prąd
74
b)
Rys.
do wyznaczania wartości skutecznej napięcia
a)
zrealizowany wg wzoru
b) przetwornik termiczny
Tabela 8.2. Przyrządy do pomiaru wartości skutecznej
i prądu okresowo zmiennego
Przyrządy analogowe
-
- elektrodynamiczne
- elektrostatyczne
- cieplne
-
z przetwornikami
poprawny pomiar wartości skutecznej przypadku sygnału
przemiennego o małym stopniu odkształcenia,
pasmo częstotliwości
dla woltomierzy i do 3kHz
woltomierze elektrodynamiczne cechuje bardzo duży pobór mocy,
zakres częstotliwości, co znacznie ogranicza ich zakres
są
tylko klasach 0, 0,2
woltomierze elektrostatyczne mierzą napięcia przemienne o dużej
wartości (kilka kV) i szerokim zakresie częstotliwości do
rzadko stosowane
poprawnie mierzą wartość średnią wyprostowaną lub wartość
szczytową zależności od zastosowanego przetwornika oraz są
wyskalowane wartościach skutecznych dla przebiegu sinusoidalnego
Przyrządy cyfrowe
bez przetwornika
z przetwornikiem TRMS
oznaczone jako AC & DC
zazwyczaj poprawnie mierzą wartość
ale
wyskalowane są wartościach skutecznych dla przebiegu
nie uwzględniają
poprawny pomiar wartości skutecznej bez względu na
sygnału
przemiennego, wykorzystują przetwornik True RMS
poprawny pomiar wartości skutecznej sygnału ze składową stalą
75
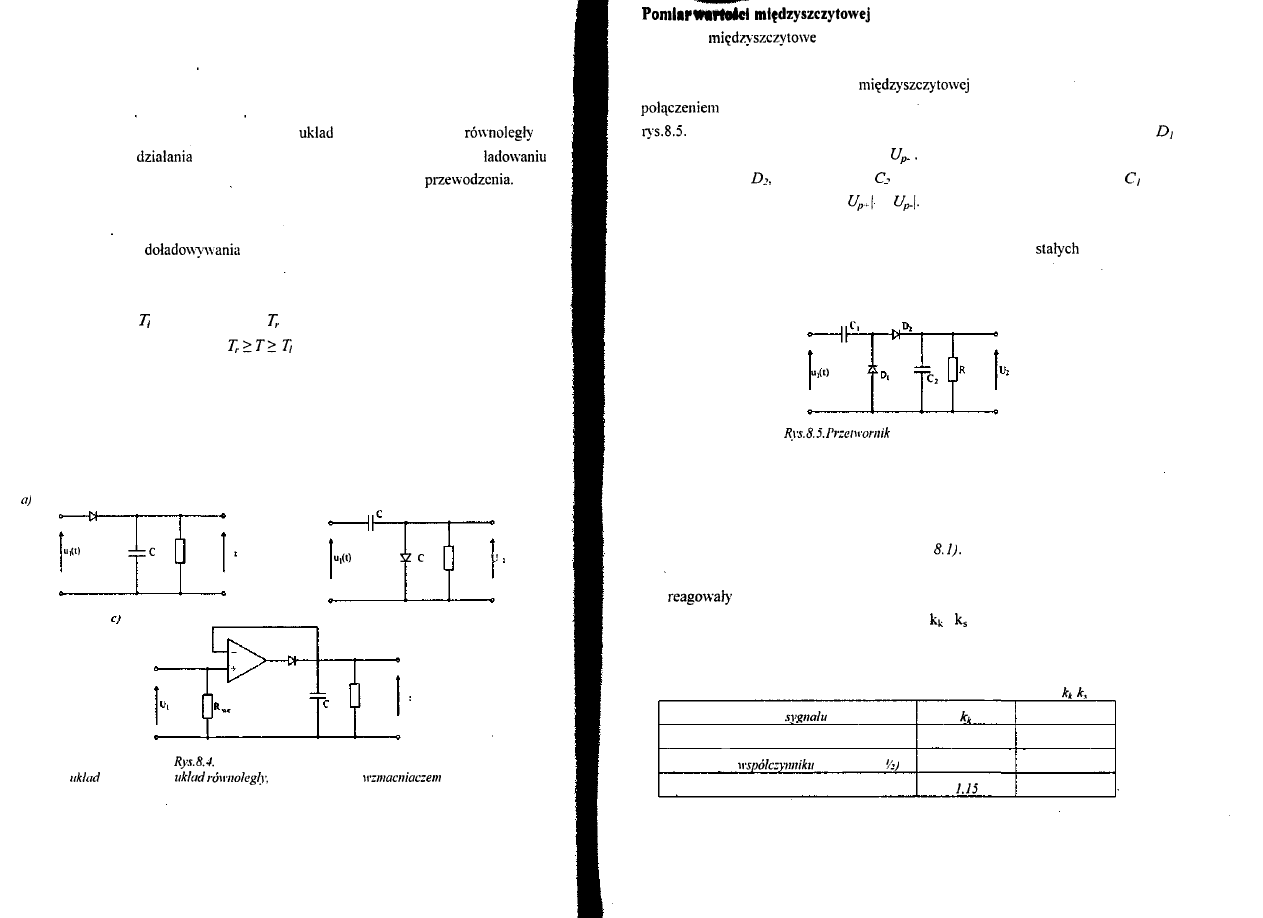
Pomiar wartości szczytowej (maksymalnej)
Pomiar wartości szczytowej napięcia zmiennego jest realizowany za pomocą
przetwornika przetwarzającego mierzone napięcie na sygnał proporcjonalny do
wartości szczytowej (dodatniej lub ujemnej) mierzonego napięcia. Wyróżnia się dwa
rodzaje przetworników wartości szczytowej:
szeregowy i układ
-
rys.8.4.a.b. Zasada
obu przetworników jest podobna i polega na
kondensatora w czasie, gdy dioda jest spolaryzowana w kierunku
Gdy
dioda jest spolaryzowana w kierunku zaporowym kondensator rozładowywuje się
przez rezystancję diody i rezystancję wewnętrzną źródła. W stanie ustalonym pracy
przetwornika proces
i rozładowywania przebiega cyklicznie, a wartość
średnia napięcia na kondensatorze odpowiada w przybliżeniu wartości szczytowej
mierzonego przebiegu. W celu zapewnienia poprawnego działania układu stałe
czasowe ładowania
i rozładowywania
kondensatora powinny spełniać warunek
(8.3)
gdzie T jest okresem mierzonego sygnału. Zastosowanie przetwornika wartości
szczytowej ze wzmacniaczem operacyjnym (rys.8.4.c) umożliwia znaczne
zmniejszenie wartości napięcia progowego diody, co pozwala na zwiększenie
dokładności przetwarzania (podobnie, jak w przypadku prostownika liniowego).
b)
R U:
R
R U;
Przetworniki wartości szczytowej
a)
szeregowy, b)
c) przetwornik ze
operacyjnym
76
Napięcie
jest powszechnie stosowane w przypadku sygnałów
okresowych niesymetrycznych oraz w pomiarach przeprowadzanych za pomocą
oscyloskopu. Do pomiaru wartości
można zastosować układ będący
kaskadowym dwóch prostowników: równoległego i szeregowego -
W czasie trwania ujemnej półfali sygnału wejściowego przewodzi dioda
i kondensator C/ ładuje się do napięcia
Gdy napięcie wejściowe jest dodatnie, to
przewodzi dioda
a kondensator
przejmuje ładunek zgromadzony na
oraz
ładuje się ostatecznie do napięcia |
+|
Wartość międzyszczytową można także wyznaczyć wykorzystując dwa detektory:
szczytu dodatniego oraz szczytu ujemnego. Sumowanie napięć
uzyskanych na
wyjściu obu wspomnianych detektorów przeprowadza się za pomocą wzmacniacza
operacyjnego (tzw. układu sumującego).
wartości międzyszczytowej
Pomiar współczynników kształtu, szczytu i zawartości harmonicznych
Do scharakteryzowania przebiegu okresowo zmiennego wykorzystuje się również
współczynniki: kształtu, szczytu. Pomiar wartości tych współczynników odbywa się na
podstawie zależności definicyjnych (tabelo
Mierzony sygnał podaje się
równocześnie na wejście dwóch przyrządów lub układów pomiarowych dobranych tak.
aby
na wielkości występujące we wzorze definicyjnym.
W tabeli 8.3 podano wartości współczynników i teoretycznie wyznaczonych dla
typowych przebiegów przemiennych.
Tabela 8.3. Teoretycznie wyznaczone wartości współczynników i
Nazwa
sinusoidalny
prostokątny (o
wypełnienia
trójkątny
1,11
1.00
k,
1,41
1.00
1,73
11
Wyznaczenie zawartości współczynnika harmonicznych
zniekształceń nieliniowych) polega na pomiarze wartości skutecznej badanego sygnału
(bez składowej
oraz wartości skutecznej sygnału, z którego wyeliminowano
pierwszą harmoniczną. Zazwyczaj rolę filtrów służących do tłumienia pierwszej
harmonicznej
wzmacniacze selektywne lub
o odpowiednio dobranej
strukturze
mostek
IV. Program ćwiczenia
1. Na wejście modułu zawierającego różne przetworniki AC/DC podać z generatora
funkcyjnego sygnał sinusoidalny bez składowej stałej. Zmieniając wartość
częstotliwości sygnału wejściowego obserwować kolejno na oscyloskopie
elektronicznym
wyjściowe z poszczególnych przetworników
Zanotować wnioski dotyczące poprawności działania badanych przetworników
w paśmie częstotliwości od 40Hz do lOOkHz oraz wyjaśnić przyczyny
zaobserwowanych nieprawidłowości.
2. Wykonać pomiary napięcia przemiennego o częstotliwości
z przedziału
dla różnych przebiegów (sinusoidalnego,
trójkątnego) za pomocą dwóch różnych woltomierzy cyfrowych napięcia
zmiennego oraz wykorzystując dostępne przetworniki AC/DC. Wyznaczyć wartości
współczynników kształtu i szczytu dla wymienionych przebiegów i porównać je
z wartościami teoretycznymi. Wyjaśnić przyczynę rozbieżności wskazań
zastosowanych woltomierzy napięcia zmiennego (tj. woltomierza z przetwornikiem
TRMS i woltomierza reagującego na wartość średnią wyprostowaną) podczas
pomiaru napięcia przemiennego o tym samym kształcie.
3. Zarejestrować sygnał sinusoidalny za pomocą karty przetwornika
z komputerem klasy PC, odpowiednio dobierając częstotliwość
próbkowania do badanego sygnału. Następnie uruchomić program do analizy
który umożliwia wyznaczenie różnych parametrów i współczynników
sygnału na podstawie zbioru próbek reprezentujących sygnał pomiarowy. Porównać
uzyskane wyniki z wynikami otrzymanymi na podstawie wcześniej wykonanych
pomiarów.
78
4. Przeprowadzić pomiar wartości skutecznej napięcia sinusoidalnego
składową stałą wykorzystując woltomierz cyfrowy mierzący wartość skuteczną
wraz składową stałą. Następnie zmierzyć oddzielnie składową stałą oraz
składową zmienną badanego przebiegu i na podstawie tych
obliczyć
wartość skuteczną całego sygnału.
Pytania kontrolne
1. Narysować układ pomiarowy do wyznaczania współczynników kształtu i szczytu
sygnału napięciowego.
2. Podać definicję wartości średniej wyprostowanej napięcia zmiennego oraz
narysować układ prostownika dwupołówkowego.
3. Podać definicję wartości skutecznej napięcia zmiennego i omówić metody pomiaru
wartości skutecznej stosowane w woltomierzach cyfrowych napięcia zmiennego.
4. Podać definicję wartości
napięcia zmiennego i narysować układ
pomiarowy do jej wyznaczenia.
5. Jak wyznaczyć wartość skuteczną sygnału
znając
skuteczne
jego harmonicznych?
Literatura
P.H. : Podręcznik metrologii. Tom 2. WKiŁ Warszawa, 1988, (213-219)
Rylski A.: Metrologia prąd zmienny. Oficyna Wyd. Politechniki Rzeszowskiej
Rzeszów 2004.
Dyszyński J.: Metrologia elektryczna i elektroniczna. Laboratorium
Oficyna
Wyd. Politechniki Rzeszowskiej 1997.
79
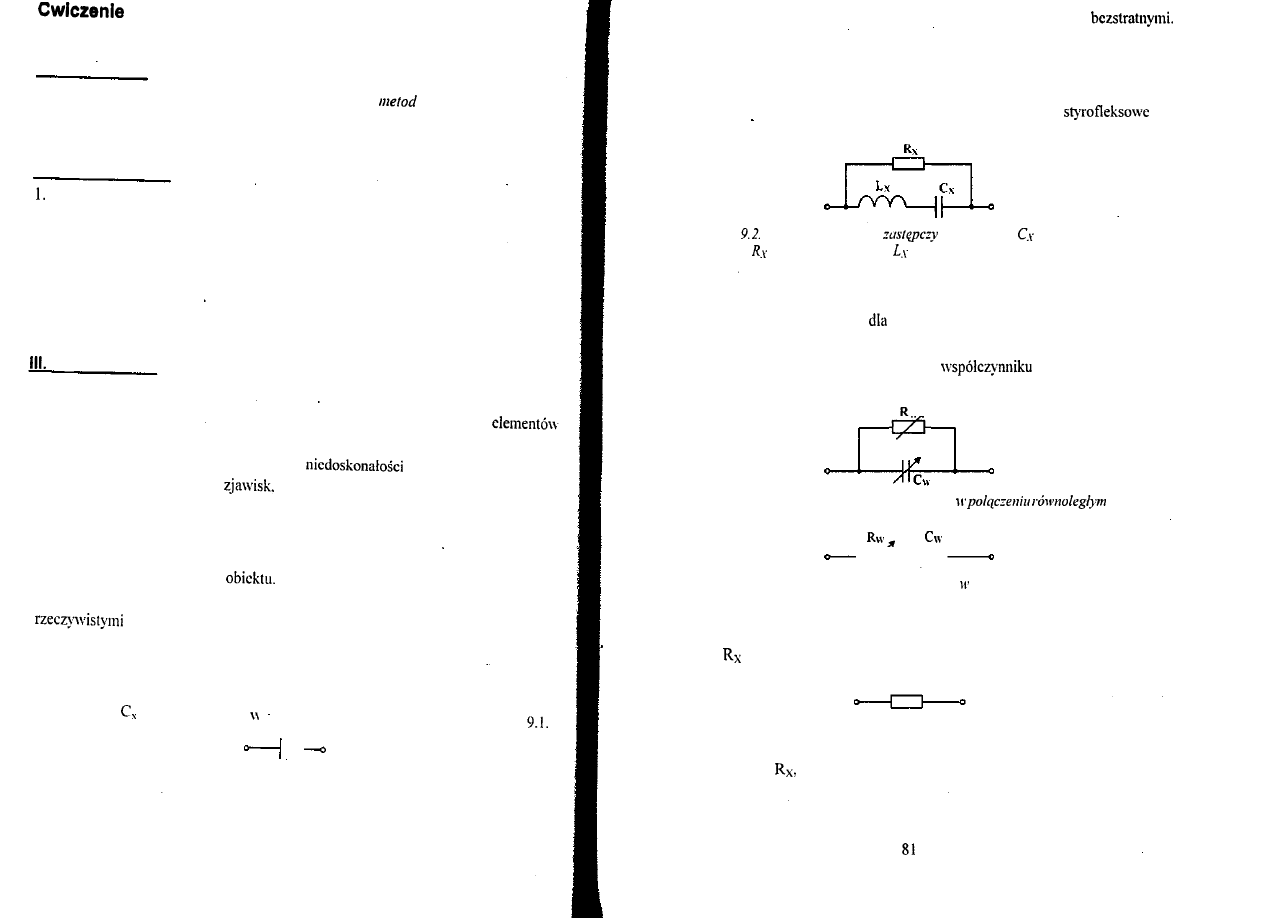
9
POMIARY IMPEDANCJI
I. Cel ćwiczenia
Celem ćwiczenia jest poznanie wybranych
pomiaru właściwości
rezystorów, kondensatorów i cewek.
II. Zagadnienia
Elektryczne schematy zastępcze rezystora, kondensatora, cewki.
2. Metoda techniczna pomiaru rezystancji.
3. Metoda pośredniego pomiaru indukcyjności
4. Obliczanie dokładności pomiaru w metodzie pośredniej.
5. Zasada pomiaru rezystancji omomierzem cyfrowym.
6. Pomiar mostkiem zmiennoprądowym i półautomatycznym.
Wprowadzenie
1. Schematy zastępcze wybranych impedancji
Mierzone impedancje. rezystorów-, kondensatorów, cewk, i innych
charakteryzują się wielkością podstawową, najczęściej dominującą co do wartości,
oraz innymi wielkościami, wynikającymi z
technologii wykonania,
z wpływu otoczenia i innych
zwane często wielkościami pasożytniczymi.
W opisie właściwości impedancji wykorzystuje się schematy zastępcze (modele
elektryczne) składające się z podstawowych wielkości R - rezystancja, C - pojemność,
L - indukcyjność, połączone w różny sposób zapewniający właściwy model,
odpowiadający warunkom pracy
W celu uproszczenia analizy obiektu stosuje
się modele uproszczone, które wynikają z przyjętych założeń związanych
z
warunkami pracy tego obiektu. Warunki te dotyczą: częstotliwości
roboczych, wpływu otoczenia.
1.1 Schematy zastępcze kondensatora
Kondensator
jest przedstawiany schematach układów ideowych jak na rys.
|Cx
W rzeczywistości nie dysponujemy kondensatorami idealnymi,
Model elektryczny kondensatora można przedstawić jak na rys. 9.2.
W zależności od technologii wykonania kondensatora, szczególnie indukcyjność
rozproszenia może być różna. Kondensatory ceramiczne lub tantalowe charakteryzują
się znacznie mniejszą indukcyjnością rozproszenia niż kondensatory
czy
elektrolityczne.
Rys.
Elektryczny schemat
kondensatora
- pojemność,
- rezystancja strat.
- indukcyjność rozproszenia
Do porównania mierzonych kondensatorów w układach mostkowych stosuje się
zestawy: kondensator wzorcowy regulowany i rezystor wzorcowy regulowany
w połączeniu równoległym rys. 9.3,
kondensatorów których współczynnik strat jest
większy niż współczynnik strat kondensatora wzorcowego, lub w połączeniu
szeregowym rys. 9.4, dla kondensatorów o
strat mniejszym niż
współczynnik strat kondensatora wzorcowego.
Rys. 9.3. Pojemnościowa gałąź wzorcowa
Rys. 9.1. Symbol kondensatora
Rys. 9.4. Pojemnościowa gałąź wzorcowa połączeniu szeregowym
1.2 Schematy zastępcze rezystora
Rezystor
rysowany jest w schematach układów ideowych jak na rys. 9.5.
Rx
Rys. 9.5. Element rezystancyjny - symbol
W układach prądu zmiennego, urządzeń wykonawczych lub w układzie pomiarowym
mierząc rezystancję
musimy uwzględnić również jej składową bierną rys. 9.6,
w rezultacie schemat układu regulowanej gałęzi wzorcowej jest uproszczony rys. 9.7.
80
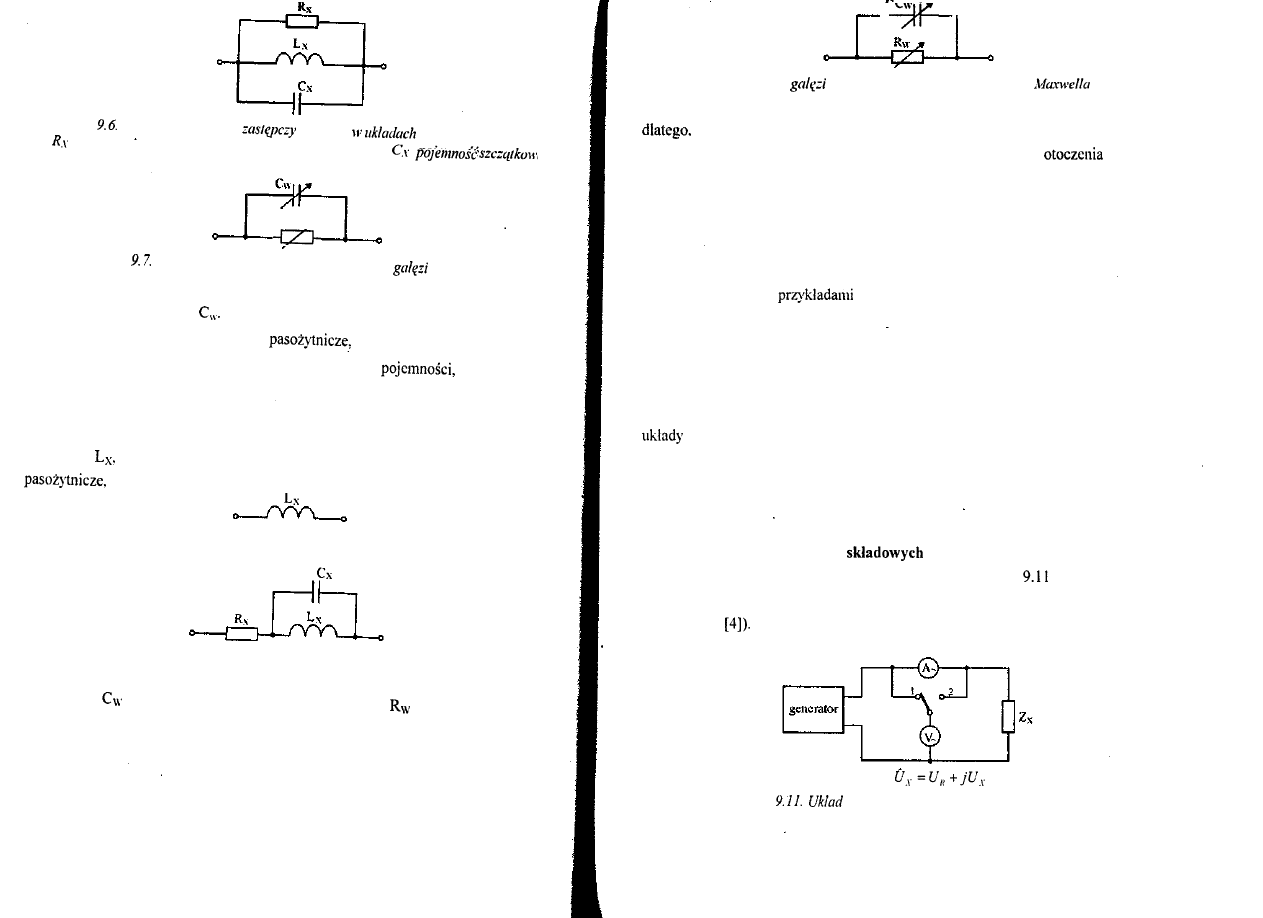
Rys.
Elektryczny schemat
rezystora
zmienno prądowych
- rezystancja podstawowa, L.\ - indukcyjność szczątkowa
-
szczątkowa
Rys.
Schemat rezystancyjnej zmiennoprądowej
wzorcowej
Rysunek ten jest podobny do rys. 9.3, różnica dotyczy jedynie wartości
pojemności kondensatora
W tym przypadku jest ona zwykle dużo mniejsza,
ponieważ ma kompensować jedynie
niewielkie wartości pojemności
mierzonego rezystora. Często, oprócz pasożytniczych
trzeba również
uwzględniać pasożytniczą indukcyjność rezystora, wówczas układy komplikują się.
1.3 Schematy zastępcze cewki
Cewka
której symbol przedstawiono na rys. 9.8. posiada również elementy
rys. 9.9.
Rys. 9.8. Symbol cewki indukcyjnej
Rys. 9.9. Elektryczny schemat zastępczy cewki
W układzie wzorcowym cewkę można odwzorować za pomocą kondensatora
wzorcowego
i wzorcowego elementu rezystancyjnego
rys. 9.10. Można tak
zrealizować model indukcyjności tylko wtedy, gdy na drodze układowej uzyska się
przesunięcie fazy przetwarzające właściwości kondensatora we właściwości cewki
(np mostek Maxwella - Wiena, rozdział 9.3 [4]).
82
Rys. 9.10. Schemat
wzorcowej do równoważenia mostka
- Wiena
W układach modelujących cewki niechętnie stosuje się wzorcowe indukcyjności
że:
- wymagają stosowania specjalnych ekranów by uniknąć wpływu
na wartość
indukcyjności.
- regulacja wartości indukcyjności jest trudna,
- duże gabaryty dla dużych indukcyjności.
Przedstawione schemat}' gałęzi mostka prądu zmiennego, wykorzystywane do
porównania z mierzoną impedancją w postaci rezystora, kondensatora, czy cewki są
jedynie najprostszymi
z możliwych rozwiązań.
Bardzo często w pomiarach rezystancji różnych podzespołów (rezystorów, cewek,
kondensatorów, transformatorów itp) stosuje się zasilanie układów pomiarowych ze
źródeł stałoprądowych ponieważ wielkości pasożytnicze takie jak pojemność lub
indukcyjność rozproszenia jest wówczas niemierzalna i nie zakłóca pomiaru. Układy
pomiarowe stają się wówczas prostsze. Najczęściej wykorzystywane w pomiarach są
z metodą techniczną pomiaru impedancji i metodą mostkową, zasilane
odpowiednio prądem zmiennym lub stałym. Poniżej metody te zostaną opisane.
W przypadku pomiarów przy zasilaniu układów prądem zmiennym występuje problem
wydzielenia informacji z sygnału o wartości składowej czynnej i składowej biernej.
2. Metoda techniczna pomiaru
impedancji
Metoda techniczna pomiaru składowych impedancji rys.
polega na pomiarze
wektorów napięcia oraz prądu za pomocą woltomierza i amperomierza wektorowego
(rozdział 2.1
Rys.
metody technicznej pomiaru impedancji
83
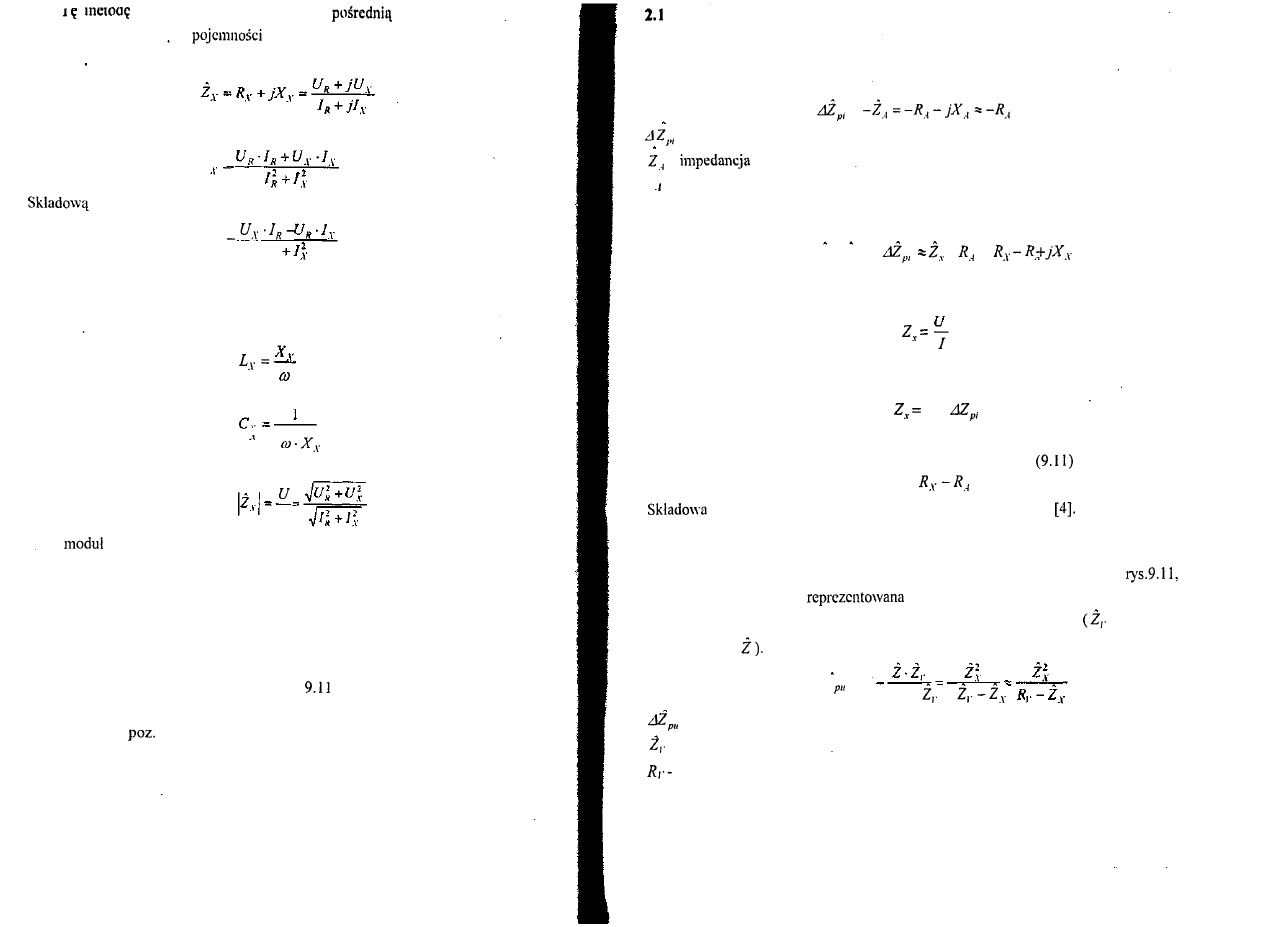
nazywa się również metodą
pomiaru danej składowej
impedancji (rezystancji,
czy indukcyjności). Obliczenie składowych
impedancji można dokonać za pomocą wzorów (9.1, 9.2. 9.3).
Wartość składowej czynnej wynosi
R
bierną można obliczyć ze wzoru
y
(9.1)
(9.2)
(9.3)
Jeżeli składowa bierna ma charakter indukcyjny wówczas ze wzoru (9.4) można
obliczyć indukcyjność, natomiast w przypadku charakteru pojemnościowego
impedancji, wartość pojemności można obliczyć ze wzoru (9.5)
(9.4)
Wartość modułu impedancji oblicza się ze wzoru (9.6):
1
(9.5)
(9.6)
U. I -
wartości skutecznych składowych wektorów napięcia i prądu lub napięcie
i prąd odczytane z przyrządów mierzących wartości skuteczne.
Tak wyznaczone składowe impedancji są obciążone niepewnością wynikającą
z błędów metody pomiarowej, niepewności instrumentalnych i zakłóceń. Przybliżoną
wartość niepewności składowej impedancji obliczonej z pomiarów pośrednich można
obliczyć metodą różniczki zupełnej.
Pomiar w metodzie technicznej rys.
może być realizowany w dwóch
układach pomiarowych, poprawny pomiar prądu (pozycja 1 przełącznika), poprawny
pomiar napięcia
2. Każda z tych metod wymaga uwzględnienia wpływu błędu
metody na wynik pomiaru.
84
Błąd systematyczny metody poprawnego pomiaru prądu
Błąd systematyczny metody uwzględnia się w wyniku pomiaru jako poprawkę,
której wartość w metodzie poprawnego pomiaru prądu jest równa rezystancji
amperomierza pomnożonej przez ,.-\" (9.7).
=
(9.7)
- wartość poprawki w metodzie poprawnego pomiaru prądu,
-
amperomierza, której wartość wystarczy często przedstawić w formie
R - rezystancja amperomierza
Wartość impedancji po uwzględnieniu poprawki oblicza się według wzoru (9.8)
Z = Z, +
- =
(9.8)
Wartość modułu impedancji można obliczyć ze wskazań przyrządów mierzących
wartości skuteczne napięcia i prądu (9.9)
(9.9)
Wartość ta jest większa od rzeczywistej o błąd wprowadzony przez układ pomiarowy
(9.10)
Z +
(9.10)
Poprawka wprowadza następującą zmianę wartości składowej czynnej mierzonej
impedancji lub rezystancji przy zasilaniu układu prądem stałym
R =
(9.11)
bierna jest obciążona pomijalnie małym błędem metody
2.2 Błąd systematyczny metody poprawnego pomiaru napięcia
W metodzie poprawnego pomiaru napięcia (poz. 2 przełącznika)
impedancja woltomierza
głównie przez rezystancję jego posobnika
jest elementem zmniejszającym mierzoną wartość impedancji
włączone
równolegle do
Wartość poprawki można obliczyć ze wzoru (9.12)
(9.12)
Ż +
- wartość poprawki w metodzie poprawnego pomiaru napięcia,
- impedancja woltomierza.
rezystancja woltomierza
Postać wzoru przybliżonego do obliczenia poprawki w tej metodzie jest złożona.
85
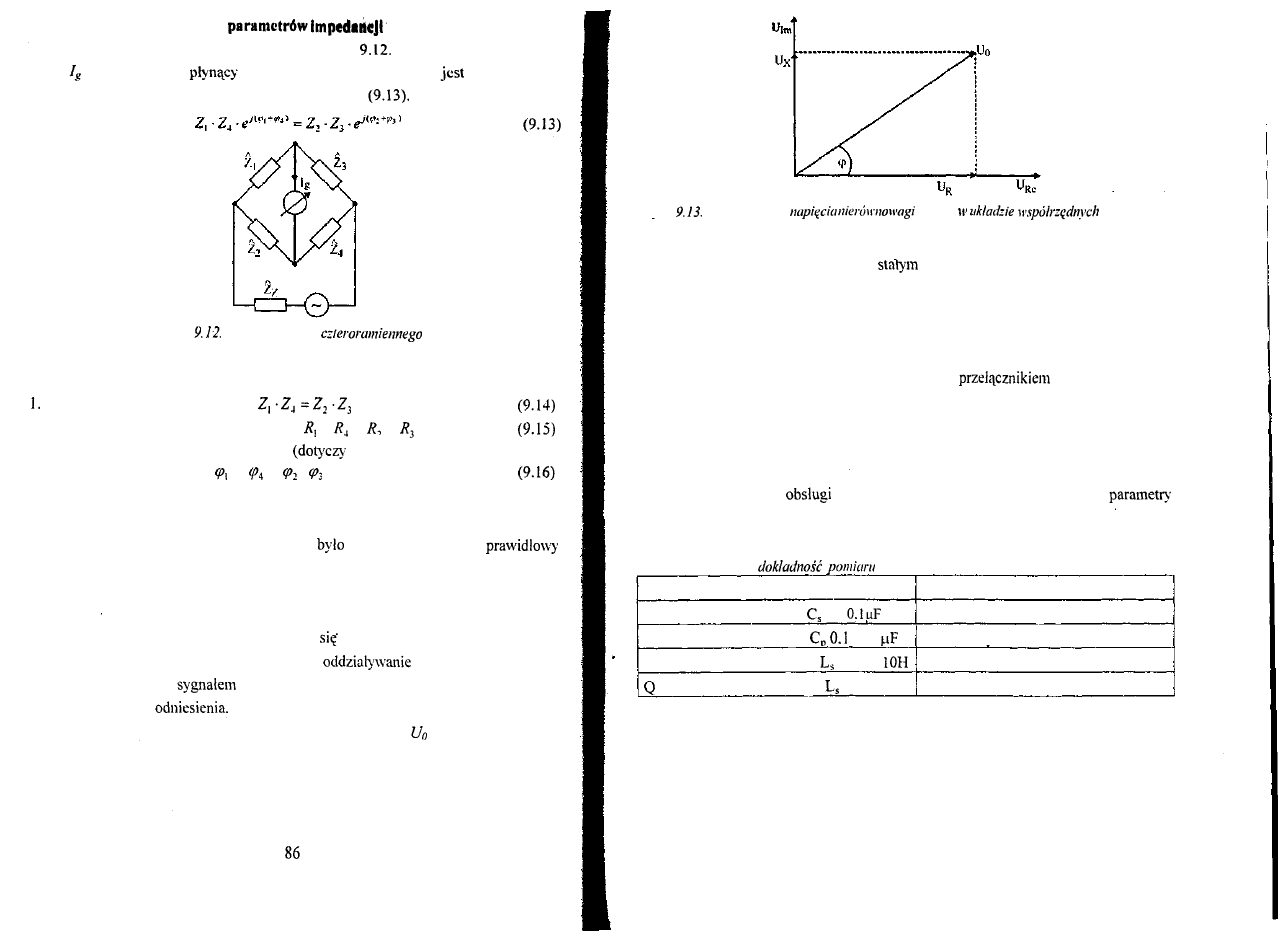
3. Metody mostkowe pomiaru
Ogólną strukturę mostka przedstawiono na rys.
Jeżeli = 0. czyli prąd
w gałęzi wskaźnika równowagi
równy zero to
możemy zapisać w momencie równowagi mostka wzór
Rys.
Schemat mostka
Jest to ogólny warunek równowagi mostka. Aby ten warunek był spełniony muszą być
spełnione szczegółowe następujące warunki
warunek równowagi modułów:
lub przy zasilaniu mostka prądem stałym
•
=
•
2. warunek równości wartości argumentów
tylko mostka zasilanego prądem
przemiennym):
+
= +
Z konieczności spełnienia jednocześnie tych dwóch warunków przy zasilaniu
mostka prądem przemiennym, wynikają trudności równoważenia układów
mostkowych. Aby układ mostkowy można
w sposób szybki i
zrównoważyć, konieczna jest informacja o równowadze np. modułów i o równowadze
faz. W celu uzyskania tej informacji występuje potrzeba stosowania odpowiednich
układów wskaźników równowagi. Wskaźniki mające wyszczególnić informacje
o module i fazie sygnału nazywają
wskaźnikami synchronicznymi.
We wskaźnikach synchronicznych następuje
sygnału z generatora
zasilającego mostek, z
nierównowagi mostka, sygnał z generatora jest
wówczas sygnałem
którego zwrot pokrywa się z osią rzeczywistą, co
ilustruje rys. 9.13. natomiast sygnał nierównowagi mostka
jest pod kątem <p
w stosunku do napięcia z generatora. W procesie równoważenia mostków stosuje się
również selektywne wskaźniki równowagi, oscyloskopy i inne.
RYS.
Obraz wektora
mostka
zespolonych
Przy zasilaniu mostków prądem
w równaniu równowagi (9.15) pozostaje
tylko składowa rezystancyjna co jest jednoznaczne z możliwością pomiaru tylko
rezystancji.
3.1 Pomiar mostkiem półautomatycznym
W mostkach półautomatycznych wybiera się
mierzoną składową
(pomiar indukcyjności, pojemności, rezystancji), która jest równoważona ręcznie
przełącznikami obrotowymi i jej odczyt jest dokonywany na podstawie wartości
uzależnionych od uzyskanego położenia przełącznika w momencie zrównoważenia
mostka, natomiast druga składowa jest równoważona automatycznie i jej wartość jest
nieznana. W instrukcji
takich mostków podawane są między innymi
mostka przedstawione w tablicy 9.1 i 9.2.
Tablica 9.1. Zakres i
stratności kondensatora i dobroci cewki
Rodzaj i zakres pomiaru
D - Pojemność szeregowa
0 -
D - Pojemność równoległa
- 50
Q - indukcyjność szeregowa
0.02 -
- indukcyjność równoległa 10 - 500H
Niedokładność pomiaru
±(0.001 + 5 % odczytu)
± 5% odczvtu
± 5% odczytu
±(0,001 + 5% odczytu) dla 1/Q
87
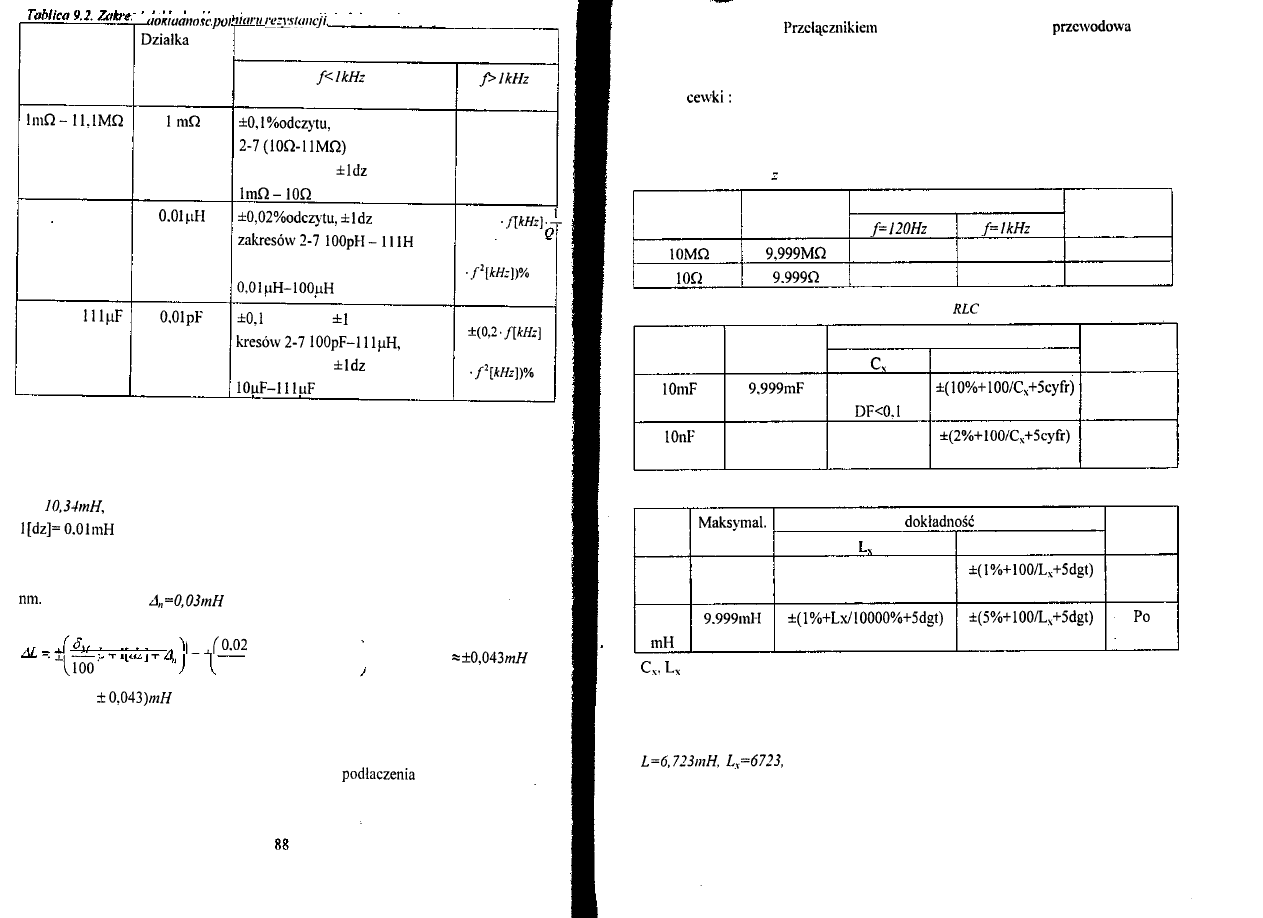
Rodzaj pomiaru
i zakres
O.OluH-lllH
O.OlpF-
?;
na
najmniejszym
zakresie
indukcyjności i pojemności
Niedokładność pomiaru
±ldz dla zakresów
±0,3%odczytu,
dla zakresu
dla
±0,3%odczytu, ±ldz dla zakresu
%odczytu,
dz dla za
±0,3%odczytu,
dla zakresu
dodatkowe
±(0,2
+ 0,002
+ 0,002
3.2 Przykład obliczenia wyniku pomiaru indukcyjności
Przykład obliczenia niedokładności i wyniku pomiaru indukcyjności czujnika.
Po zrównoważeniu mostka odczytano:
L =
nieczulość mostka (najmniejsza zmiana nastawionej wartości w czasie równowagi
mostka, powodująca zauważalne wychylenie wskaźnika równowagi - wyznacza się ją
czasie pomiaru)
obliczenia:
= ±
100
10,34 + 0,01 + 0,03 ] = ±0,042068
L = (10,34,
4. Pomiar miernikiem RLC
Mierniki RLC mogą posiadać 4 zaciski do
badanej impedancji.
Najczęściej 2 zewnętrzne zaciski są zaciskami napięciowymi i 2 wewnętrzne są
zaciskami prądowymi.
wybiera się rodzaj pracy 2
lub 4
przewodowa, kolejnym przełącznikiem ustala się wielkości mierzone np.
Pomiar rezystora : R i C lub R i L
Pomiar
L i R lub L i Q;
Pomiar kondensatora: C i R lub C i tg8.
Pierwsza wielkość często jest mierzona dokładniej niż druga.
Tablica 9.3. Wybrane instrukcji parametry miernika RLC dla pomiaru rezystancji
zakres
maksymalne
wskazanie
dokładność
±(2%+8cyfr)
±(1.2%+8cyfr)
±(2%+8cyfr)
±(1.2%+8cyfr)
kalibracja
uwagi
Po rozwarciu
Po zwarciu
Tablica 9.4. Wybrane z instrukcji parametry miernika
dla pomiaru pojemności
zakres
maksymalne
wskazanie
9,999nF
dokładność
±(5%+5cyfr)
±(l%+5cyfr)
DF<0,l
DF
DF<0.1
DF<0,l
kalibracja
uwagi
Po rozwarciu
Po rozwarciu
Tablica 9.5. Wybrane z instrukcji parametry miernika RLC dla pomiaru indukcyjności
zakres
1000H
10
wskazanie
999,9H
±(0,3%+Lx/10000%+5dgt)
DF/Q
kalibracja
uwagi
Po roz
warciu
zwarciu
- wskazanie pola odczytowego bez przecinka dziesiętnego
4.1 Przykład obliczenia wyniku pomiaru indukcyjności miernikiem RLC
Wyniki pomiaru cewki przetwonika indukcyjnościowego:
Q= 2,01
89
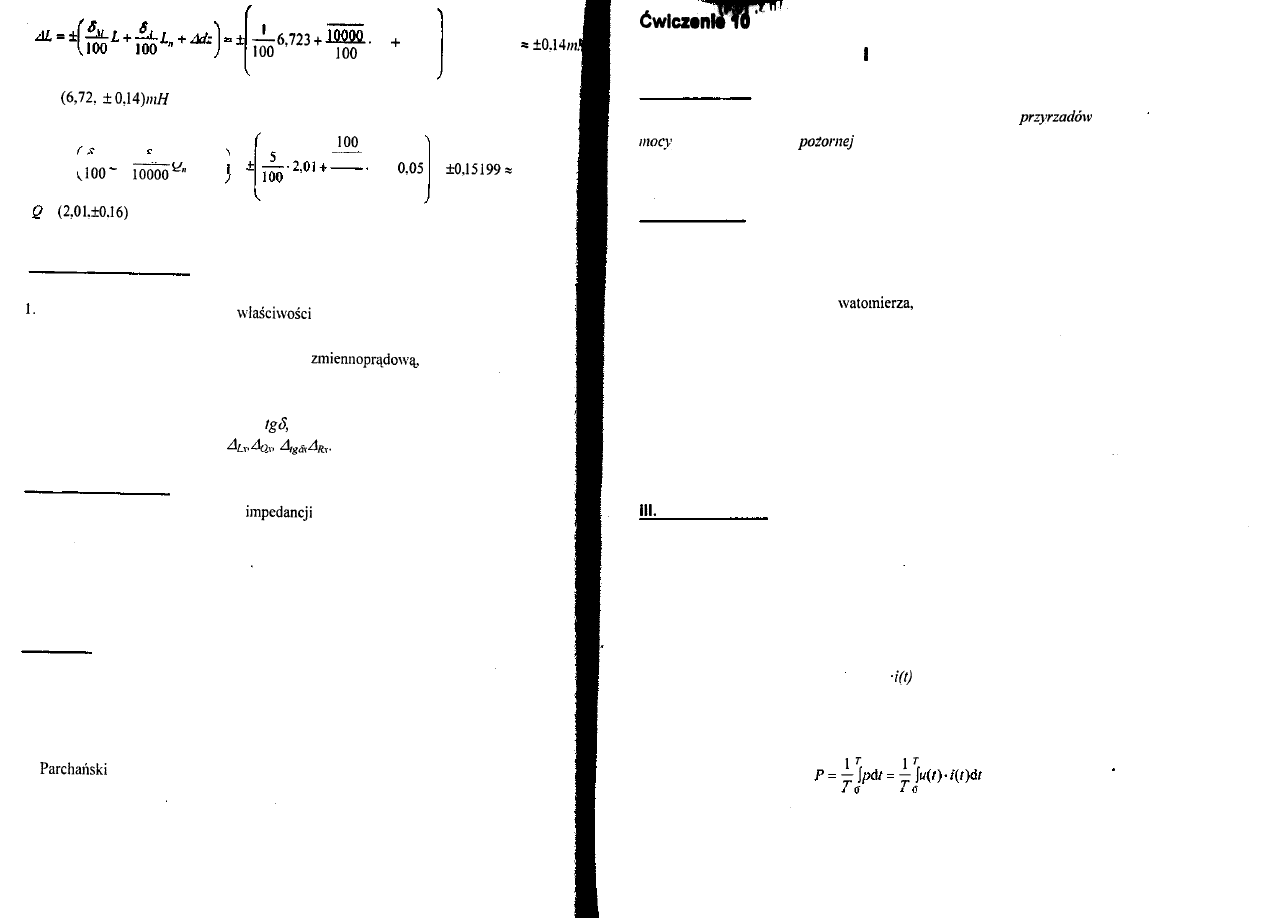
6723
10 0,005
= ±0,13946
L =
=
6723
100
•10 +
=
±0,16
IV. Program ćwiczenia
1. Zadania laboratoryjne
Zmierzyć charakterystyczne
przetwornika indukcyjnościowego :
a. rezystancję metodą techniczną staloprądową
b. indukcyjność, metodą techniczną
c. rezystancję i indukcyjność miernikiem RLC
2. Opracowanie wyników pomiarów
1. Obliczyć: dobroć Q, stratność
2. Obliczyć błąd pomiaru:
V. Pytania kontrolne
1. Przedstawić schemat do pomiaru
metodą techniczną.
2. Jak wybrać układ do pomiaru impedancji metodą techniczną, aby błąd
systematyczny metody był najmniejszy?
3. Co wpływa na dokładność pomiaru indukcyjności metodą pośrednią?
4. Co wpływa na dokładność pomiaru pojemności metodą pośrednią?
Literatura
1 Marcyniuk A., Pasecki E., Pluciński M.: Podstawy metrologii elektrycznej, WNT,
Warszawa, 1984.
2 Chwaleba A., Poniński M., Siedlecki A.: Metrologia elektryczna, WNT, Warszawa,
1996.
3
J.: Miernictwo elektryczne i elektroniczne, WSiP. Warszawa, 1997r.
4 Rylski A.: Metrologia II prąd zmienny. OWPRz. Rzeszów, 2004.
POMIARY MOCY ENERGII ELEKTRYCZNEJ
I. Cel ćwiczenia
Celem ćwiczenia jest poznanie wybranych układów i
do pomiaru
czynnej, biernej,
i do pomiaru energii elektrycznej odbiorników
jednofazowych
II. Zagadnienia
1. Budowa, działanie i właściwości pomiarowe elektromechanicznych
i elektronicznych przetworników mocy
2. Definicja stałej znamionowej licznika
3. Obliczanie: stałej podziałki
dopuszczalnej przeciążalności obwodów
napięciowego i prądowego, wyniku i dokładności pomiaru,
4. Budowa i działanie wskaźników kolejności faz w sieci trójfazowej,
5. Układy do pomiaru mocy czynnej, biernej i pozornej w sieci jednofazowej.
6. Cel i metody kompensacji mocy biernej indukcyjnej odbiornika prądu
przemiennego.
7. Budowa licznika indukcyjnego i elektronicznego energii elektrycznej.
8. Budowa i właściwości przetwornika hallotronowego.
Wprowadzenie
1. Pomiary mocy prądu elektrycznego
W praktyce pomiarowej coraz częściej spotyka się zarówno źródła napięcia, jak
i odbiorniki o nieliniowej charakterystyce prądowo-napięciowej. W obwodach prądu
przemiennego, w których napięcie i prąd są funkcjami czasu, wprowadza się pojęcie
mocy chwilowej równej iloczynowi chwilowej wartości napięcia i prądu. Moc
chwilowa jest funkcją czasu (10.1).
p(t)=u(t)
(10.1)
Stan energetyczny odbiornika zasilanego napięciem i prądem zmiennym w czasie
charakteryzuje się mocą średnią za okres T (10.2) dla iloczynu wektorów napięcia
i prądu.
(10.2)
90
91
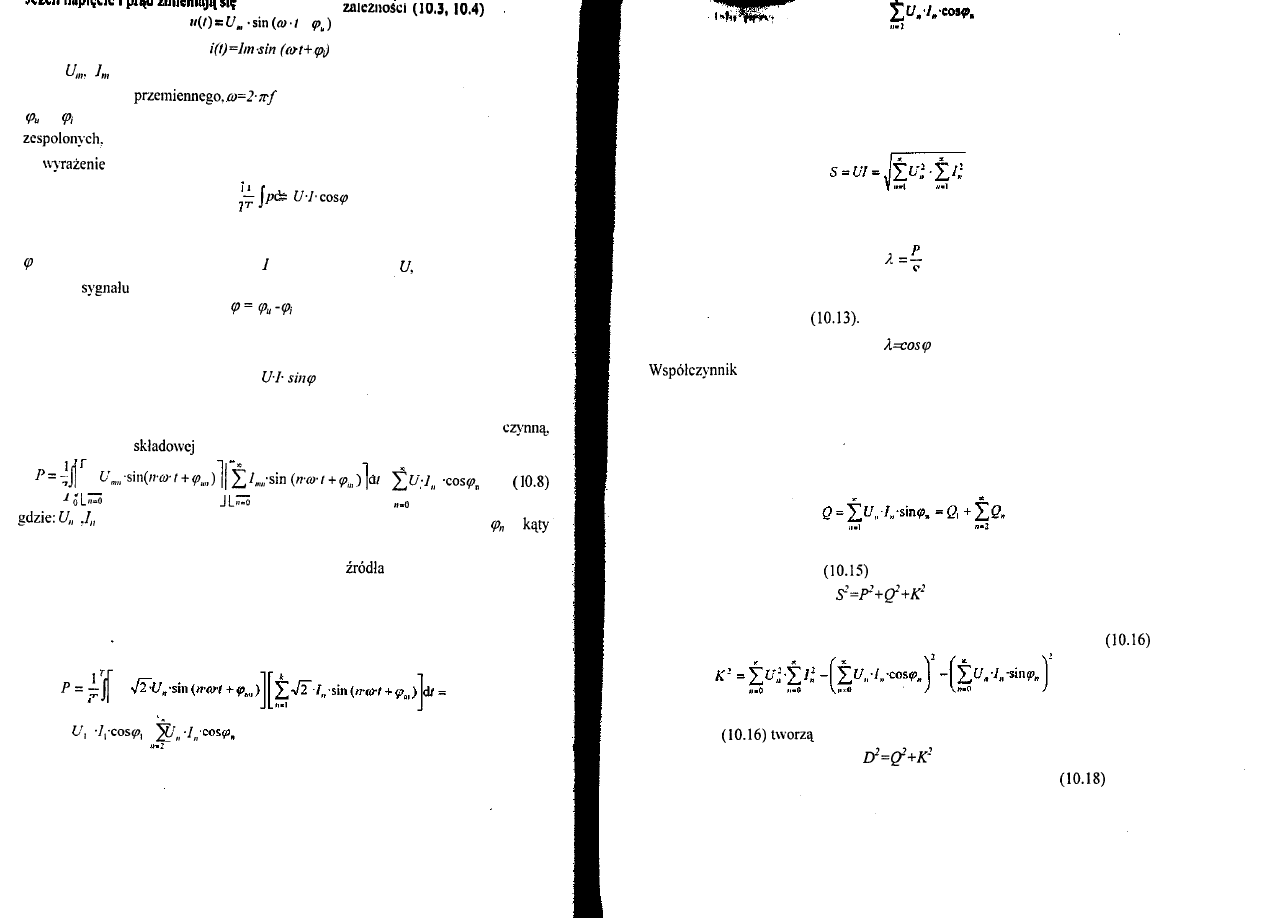
sinusoidalnie wg
+
(10.3)
(10.4)
gdzie:
-amplitudy odpowiednio napięcia i prądu;
co - pulsacja prądu
.
- kąty przesunięć fazowych wektorów napięcia i prądu dla płaszczyzny liczb
po podstawieniu do wzoru (10.2) i przeprowadzeniu obliczeń otrzymuje
się
na moc czynną (10.5).
T
P =
(10.5)
o
gdzie: U, I - wartości skuteczne odpowiednio napięcia i prądu odbiornika;
- kąt fazowy między wektorem prądu i wektorem napięcia
T- okres
(10.6)
Przez analogię do mocy czynnej dla prądu przemiennego o sinusoidalnym napięciu
i prądzie wprowadza się pojęcie mocy biernej dla iloczynu skalarnego (10.7)
Q =
(10.7)
Jeżeli prąd i napięcie są niesinusoidalne i ich wartości chwilowe są opisane za pomocą
szeregów trygonometrycznych Fouriera, to wyrażenie na moc
z uwzględnieniem
stałej opisuje wzór (10.8).
Ź
=
J
- wartości skuteczne n-tych harmonicznych napięcia i prądu;
-
fazowe między poszczególnymi harmonicznymi prądu i napięcia.
Jeżeli do obwodu elektrycznego zasilanego ze
sinusoidalnego zostanie
dołączony odbiornik o nieliniowej charakterystyce prądowo-napięciowej, to będzie on
źródłem prądowym wyższych harmonicznych. Moc czynna obwodu elektrycznego przy
braku składowej stałej i dla skończonej liczby wyższych harmonicznych jest określona
zależnością (10.9).
Ż
=
+
Wyrażenie
(10.9)
92
(10.10)
określa moc czynną wyższych harmonicznych wytworzonych w odbiorniku
nieliniowym.
W celu scharaktyzowania właściwości energetycznych układu elektrycznego podaje się
wartość mocy pozornej S równej iloczynowi wartości skutecznej napięcia i prądu
(10.11)
(10.11)
Stosunek mocy czynnej do mocy pozornej odbiornika jest nazywany współczynnikiem
mocy czynnej (10.12).
(10.12)
Dla przebiegów sinusoidalnych napięcia i prądu współczynnik mocy X jest równy
cosinusowi kąta fazowego
(10.13)
mocy czynnej obwodu elektrycznego charakteryzuje zdolność tego
obwodu do odbioru energii elektrycznej w stosunku do wydolności energetycznej
źródła zasilania.
Przez analogię do mocy czynnej obwodów zasilanych przebiegami niesinusoidalnymi
wprowadza się pojęcie mocy biernej wyrażającej się sumą mocy biernych
poszczególnych harmonicznych (10.14).
. (10.14)
Pomiędzy tak zdefiniowanymi pojęciami mocy czynnej, mocy biernej i mocy pozornej
istnieje zależność funkcyjna
(10.15)
gdzie K - moc odkształcenia.
W ogólnym przypadku moc odkształcenia może być określona zależnością
(10.16)
Moc bierna Q określona zależnością (10.14) oraz moc odkształcenia określona
zależnością
tzw. moc dystorsji (10.17).
(10.17)
W układach jednofazowych moc chwilową można zapisać wzorem
93
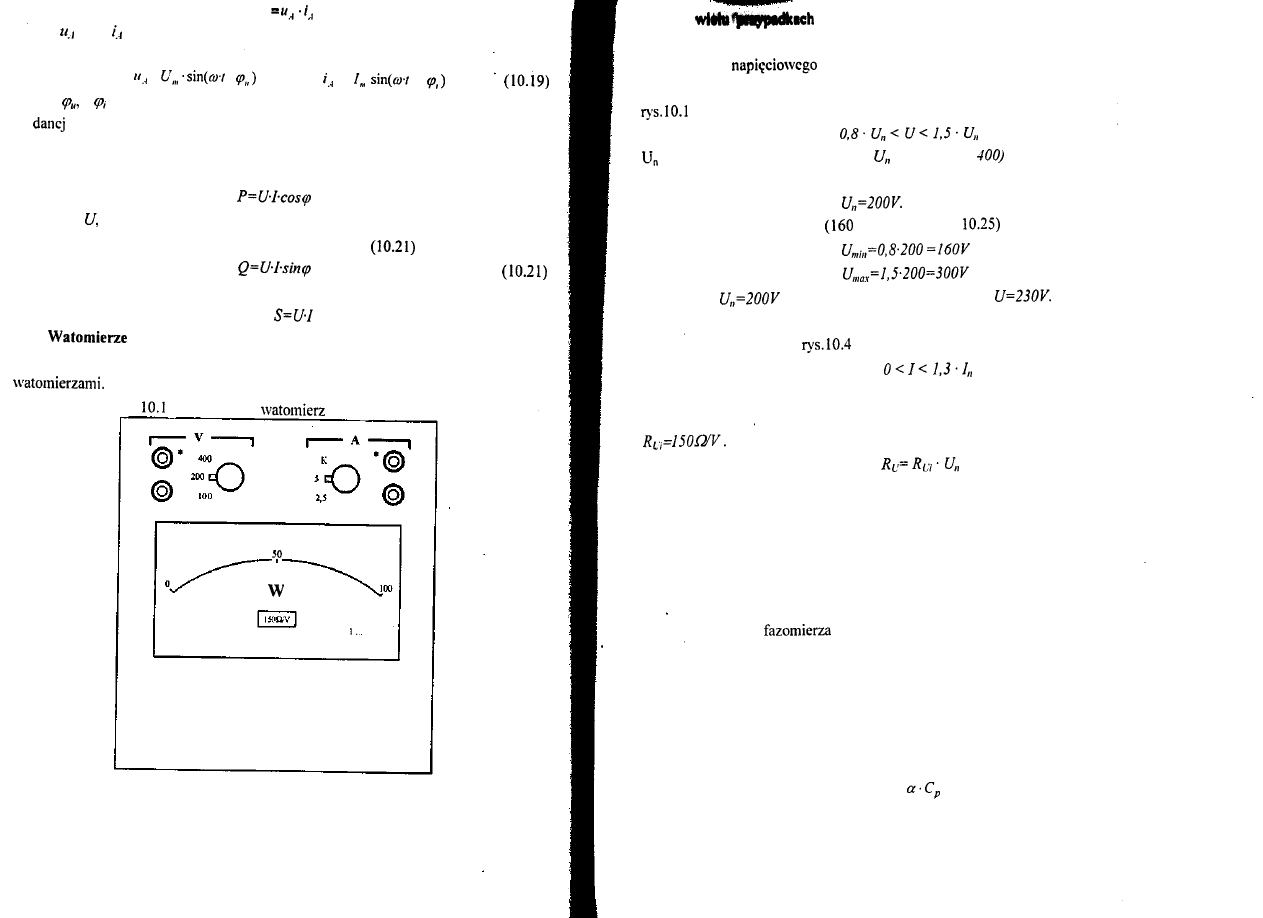
P
(10.18)
gdzie: oraz
- wartości chwilowe odpowiednio napięcia i prądu danej fazy.
W układach zasilanych napięciem sinusoidalnym (10.19)
=
+
=
+
gdzie:
- odpowiednie kąty przesunięcia fazowego wektorów napięcia i prądu
w
fazie w stosunku do przyjętego sygnału odniesienia.
Podstawiając wyrażenie na napięcia i prądy do wzoru (10.18) i dokonując
odpowiednich przekształceń, otrzymuje się wyrażenie na moc czynną (10.20)
(10.20)
przy czym: /- wartości skuteczne napięcia i prądu fazowego.
Podobnie można napisać wyrażenie na moc bierną układu
Moc pozorną wyrażamy zależnością
(10.22)
2.
Do pomiaru mocy czynnej i biernej wykorzystywane są przyrządy zwane
Przyrząd taki posiada cztery zaciski wejściowe, dwa prądowe i dwa
napięciowe. Na rys.
przedstawiono
analogowy.
0,8..
l,5Un
0... 1 ... l,3In
Rys. 10.1. Rysunek watomierza analogowego
94
W
zaciski prądowe wyróżniają się większymi gabarytami.
Gwiazdki przy zaciskach oznaczają doprowadzenia do początków uzwojeń. Zakres
pracy obwodu
watomierza jest ograniczony do przedziału napięciowego
opisanego w oknie ze skalą przyrządu, w prawym dolnym rogu. Dla watomierza na
przedział ten określony jest wzorem (10.23).
(10.23)
jest wartością ustawionego zakresu
= (100, 200,
V.
Jeżeli włączamy cewkę napięciową na napięcie fazowe U=220V to wystarczy ustawić
przełącznik zakresu na wartości
Dopuszczalny przedział zmian napięcia na
zaciskach watomierza wynosi
- 300)V, (10.24,
(10.24)
(10.25)
Na zakresie
można
mierzyć moc przy napięciu
Podobnie ustalony jest przedział zmian wartości prądu. W prawym dolnym rogu pola
odczytowego watomierza
jest podany wzór (10.26)
(10.26)
Kolejnym parametrem podanym na polu odczytowym tego przyrządu jest rezystancja
cewki napięciowej i prądowej. Rezystancja cewki napięciowej jest podana w postaci
Wartość rezystancji cewki napięciowej można obliczyć ze wzoru
(10.27)
Przy pomiarze małych mocy nabiera znaczenia sposób włączenia watomierza do
układu. Układ poprawnego pomiaru napięcia stosuje się wówczas gdy prąd cewki
napięciowej watomierza jest pomijalny w stosunku do prądu badanego odbiornika lub
z poprawnym pomiarem prądu gdy spadek napięcia na cewce prądowej jest pomijalny
w stosunku do napięcia na odbiorniku. Należy przeprowadzić analizę przy wyborze
miejsca włączenia pozostałych przyrządów: amperomierza, woltomierza,
częstościomierza,
itd. z punktu widzenia ich wpływu na mierzone
wielkości.
3. Pomiar mocy czynnej w odbiornikach jednofazowych
Moc czynną odbiornika jednofazowego można z mierzyć w układzie poprawnie
mierzonego prądu jak na rysunku 10.2. Woltomierz i amperomierz są miernikami
pomocniczymi, nie powinny wpływać na wynik pomiaru mocy, który oblicza się
z zależności (10.28)
P =
(10.28)
95
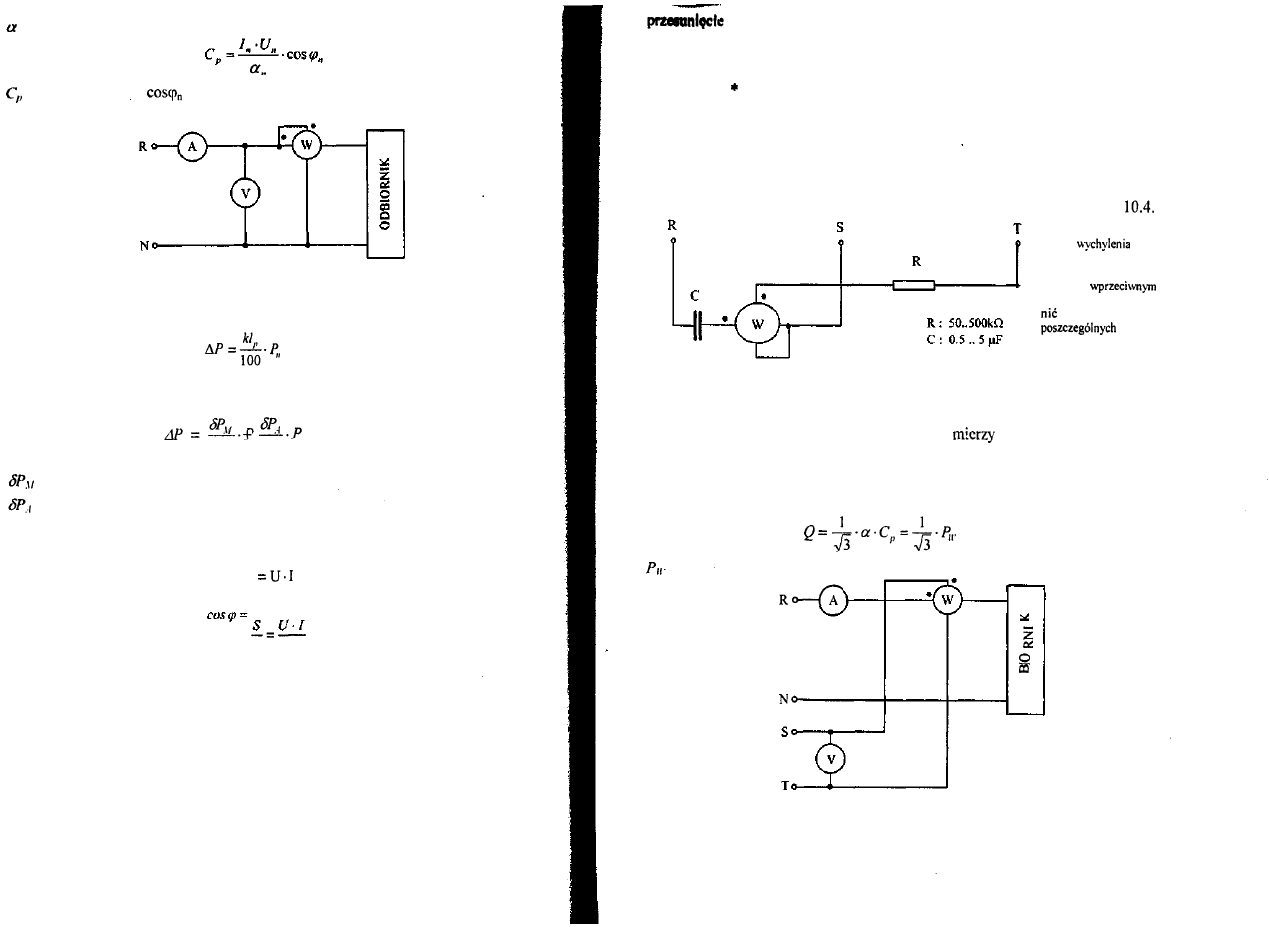
- wychylenie wskazówki [dz]
(10.29)
- stała przyrządu.
- współczynnik mocy wynikający z konstrukcji przyrządu,
najczęściej równy 1.
Rys. 10.2. Schemat układu do pomiaru mocy czynnej odbiornika jednofazowego
Dokładność bezwzględną pomiaru wykonanego w normalnych warunkach,
przyrządami analogowymi oblicza się z zależności (10.30):
(10.30)
Przy pomiarach przyrządami cyfrowymi dokładność pomiaru oblicza się według wzoru
(10.31).
(10.31)
100 100 "
- błąd multiplikatywny watomierza cyfrowego,
- błąd addytywny watomierza cyfrowego.
Jeśli woltomierz i amperomierz nie są tylko przyrządami kontrolnymi , ale mają
odpowiednią dokładność, można wyznaczyć moc pozorną odbiornika (10.32)
S
(10.32)
oraz współczynnik mocy (10.33)
P P
(10.33)
4. Pomiar mocy biernej w odbiornikach jednofazowych
Pomiar mocy biernej realizuje się najczęściej watomierzem odpowiednio
włączonym do układu pomiarowego rys. 10.4. Obwody prądowe wpinamy jak do
pomiaru mocy czynnej, obwody napięciowe zasila się napięciem opóźnionym o 90°
względem napięcia jak do pomiaru mocy czynnej. W tym celu wykorzystuje się
96
fazowe występujące między napięciami fazowymi, a przewodowymi
w trójfazowej sieci symetrycznej. Aby zbudować poprawny układ pomiarowy trzeba:
* sprawdzić czy istnieje symetria zasilania.
wyznaczyć kolejność faz
* zastosować poprawną metodę pomiaru tejże mocy.
Symetrię zasilania sprawdzamy porównując wszystkie napięcia fazowe
z przewodowymi. Do wyznaczenia kolejności faz można zastosować specjalny
przyrząd lub wykorzystując watomierz w układzie jak na rys. 10.3. Moc bierną dla
odbiornika jednofazowego mierzy się w układzie przedstawionym na rysunku
W przypadku dodat-
niego
wa-
tomierza kolejność faz
jest zgodna ze schema-
tem zaś
wypadku należy zamie-
kolejność nazw
faz.
Rys. 10.3. Schemat układu do wyznaczania kolejności faz
Jeśli watomierz wskazuje wartości dodatnie -
on moc bierną indukcyjną,
w przypadku ujemnych wyników mierzy on moc bierną pojemnościową, wówczas
w watomierzach analogowych, należy zmienić zaciski jednego z obwodów aby
uzyskać prawidłowe wychylenie wskazówki. Wynik pomiaru oblicza się jako:
(10.34)
- odczyt z watomierza cyfrowego
o
o
Rys. 10.4. Schemat układu pomiaru mocy biernej odbiornika jednofazowego
97
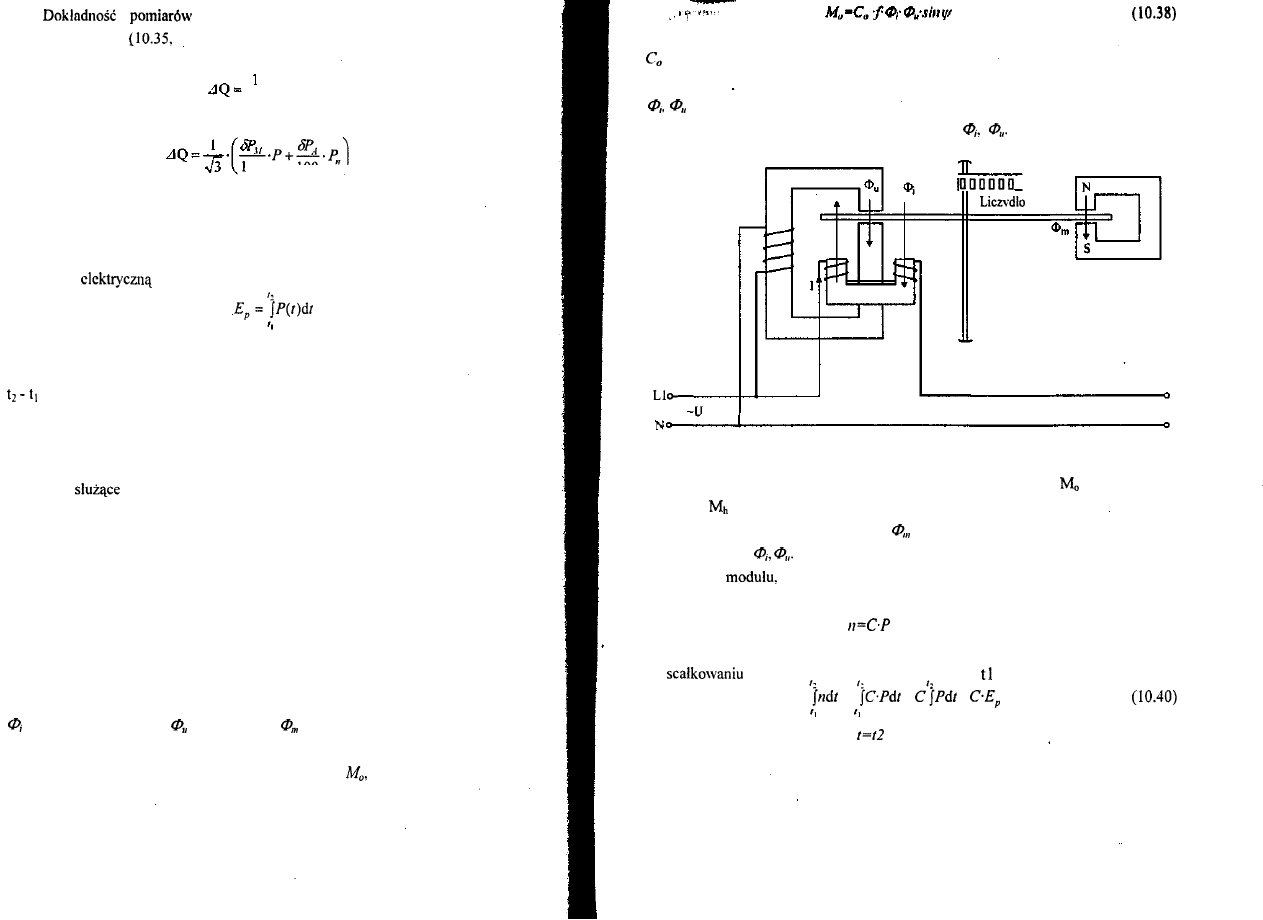
uwzględniającą tylko błędy instrumentalne można
obliczyć wzorami
10.36). Przy pomiarach przyrządami analogowymi błąd
bezwzględny wynosi:
Przy pomiarach przyrządami cyfrowymi błąd bezwzględny wynosi:
(10.36)
00 100 ")
Pomiar mocy biernej może być dokonany w innym układzie pomiarowym, wówczas
dokładność pomiaru należy obliczyć zgodnie z instrukcją obsługi przyrządu.
5. Pomiary energii prądu elektrycznego
Energię
czynną określa zależność
• (10.37)
gdzie: P(t) - moc czynna pobierana przez odbiornik, której wartość ulega zmianie
w czasie t;
- przedział czasu, w którym dokonuje się pomiaru energii.
Pomiar energii polega zatem na pomiarze mocy czynnej z jednoczesnym całkowaniem
jej w czasie. Ze względu na to, że na wskazaniach liczników oparte są rozliczenia
pieniężne, budowa i eksploatacja liczników podlega szczególnym przepisom.
Przyrządy
do pomiaru energii elektrycznej, liczniki energii są dwojakiego
rodzaju:
- liczniki elektromechaniczne,
- liczniki elektroniczne.
Do liczników elektromechanicznych zalicza się liczniki indukcyjne przeznaczone do
pomiaru energii prądu przemiennego oraz liczniki magnetoelektryczne stosowane do
pomiaru energii prądu stałego. Liczniki indukcyjne, są stosunkowo tanie
i charakteryzują się dużym współczynnikiem niezawodności. Licznik indukcyjny jest
watomierzem, wyposażonym w mechanizm zliczający liczbę obrotów tarczy.
Na ruchomą tarczę licznika (rys. 10.5) działają strumienie zmienne w czasie: prądowy
i strumień napięciowy
oraz strumień
wytworzony przez magnes trwały. Pod
wpływem strumienia napięciowego i prądowego, przesuniętych względem siebie
w czasie i przestrzeni, powstaje moment obrotowy
powodujący obrót tarczy
z prędkością n. Moment ten jest wyrażony wzorem
98
gdzie:
- stała momentu obrotowego;
/- częstotliwość;
- strumienie magnetyczne prądowy i napięciowy;
y/- kąt przesunięcia fazowego między strumieniami
(Di
|
Rys. 10.5. Uproszczona konstrukcja licznika indukcyjnego jednofazowego
Na tarczę obracającą się pod wpływem momentu obrotowego
działa moment
hamujący
proporcjonalny do prędkości obrotowej. Moment ten jest wytworzony
głównie przez strumień magnetyczny
magnesu trwałego i w niewielkiej części
przez strumienie
Jeżeli momenty napędowy i hamujący działające na tarczę są
równe co do
to tarcza obraca się ruchem jednostajnym z prędkością obrotową
n. A zatem
(10.39)
gdzie C - współczynnik proporcjonalności.
Po
zależności (10.39.) w przedziale czasu do t2 otrzymuje się
N =
=
=
=
'I
Liczba obrotów tarcz}' w czasie
- tl jest wprost proporcjonalna do pobranej
w tym czasie energii. Współczynnik proporcjonalności C nosi nazwę stałej licznika.
99
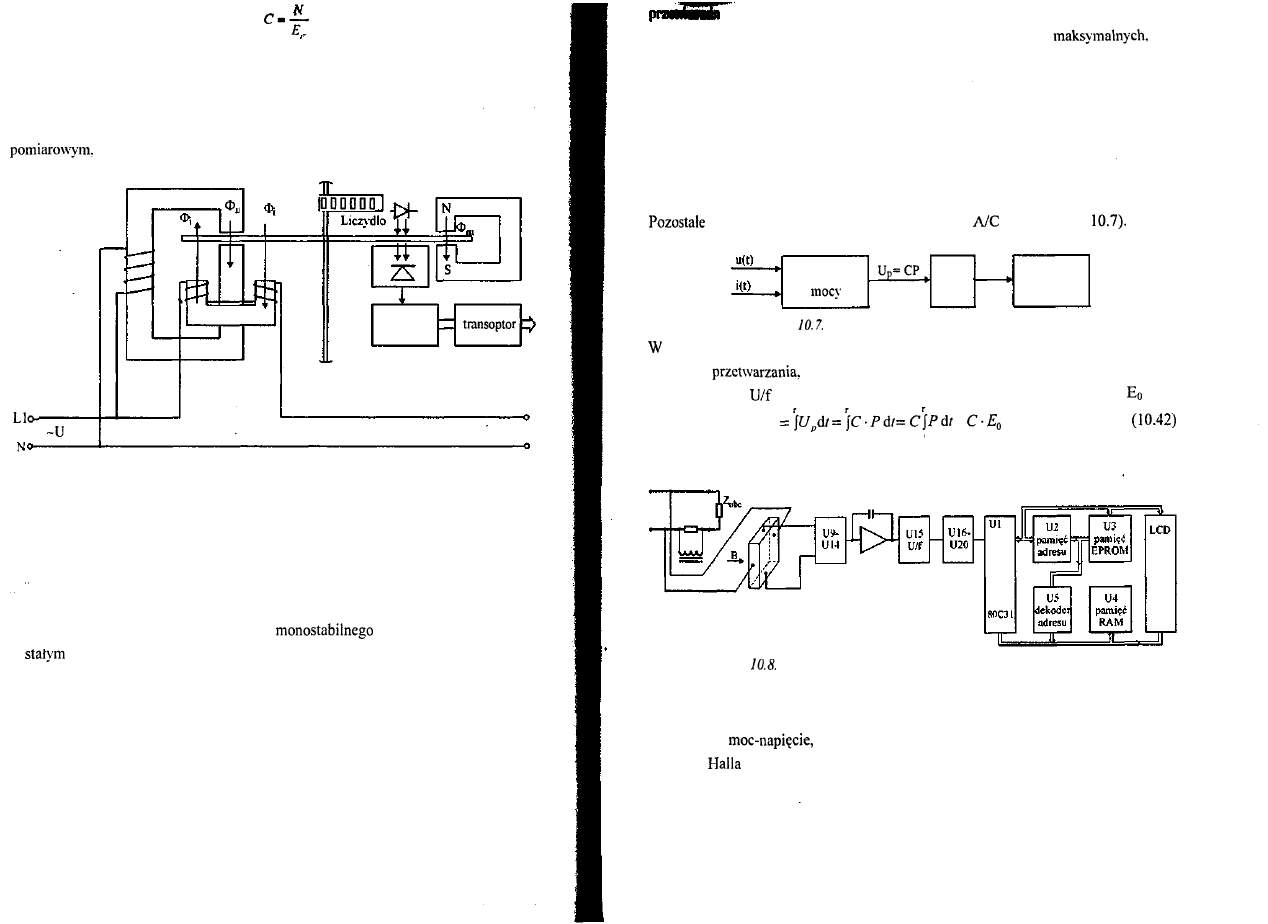
(10.41)
Wyraża ona liczbę obrotów tarczy przypadającą na jednostkę energii elektrycznej.
6. Licznik indukcyjny z nadajnikiem impulsów
W celu przystosowania licznika indukcyjnego do współpracy z systemem
a także w celu umożliwienia zdalnego odczytu energii pobranej,
wyposaża się go w nadajnik impulsów rys. 10.6.
r
przerzutnik
Rys. 10.6. Uproszczona konstrukcja licznika indukcyjnego jednofazowego
z nadajnikiem impulsów
Na tarczy znajduje się kilka otworów, przez które przechodzi strumień świetlny
z diody elektroluminescencyjnej do fototranzystora. Pojawienie się otworu w tarczy na
osi dioda i fototranzystor powoduje wpisanie do przerzutnika RS jedynki „1" lub zera
..0". Przerzutnik RS znajduje się w układzie wytwarzającym impulsy. Impulsy
następnie są podawane do układu formowania impulsów. Układ ten składa się z filtru
dolnoprzepustowego oraz przerzutnika
wytwarzającego impulsy
o
czasie trwania niezależnym od prędkości obrotowej wirnika. Przerzutnik
monostabilny jest sprzężony z układem wyjściowym poprzez transoptor stanowiący
galwaniczne oddzielenie układu przetwarzającego liczbę obrotów tarczy licznika na
liczbę generowanych impulsów układu wyjściowego. Galwaniczne oddzielenie tych
obwodów eliminuje wpływ zakłóceń układu przetwarzania indukowanych w linii
łączącej nadajnik z odbiornikiem. Licznik ten może być przystosowany do współpracy
z rejestratorem lub urządzeniem mikroprocesorowym zaprogramowanym do
100
ia Ilości impulsów odebranych z układu czujnika optoelektronicznego
obrotów wirnika, na wartość energii, np. dla uśrednionych mocy
dla
czterech niezależnie programowalnych sezonów taryfowych itp.
7. Liczniki elektroniczne
W liczniku elektronicznym są realizowane dwie operacje:
- mnożenie wartości napięcia i prądu w celu otrzymania wielkości zależnej od mocy,
- całkowanie funkcji mocy w celu uzyskania wielkości proporcjonalnej do mierzonej
energii.
człony licznika stanowi układ przetwornika
i licznik (rys.
Przetwornik
U/f
Licznik
impulsów
Rys.
Schemat blokowy licznika elektronicznego
układzie licznika jako przetwornik mocy może być użyty przetwornik o dowolnym
sposobie
lecz o określonych właściwościach metrologicznych.
W przetworniku
każdemu impulsowi odpowiada określona wartość energii
E
=
0 0
0 0 0
Zliczenie wszystkich impulsów daje wartość całkowitej energii w czasie pomiaru.
Rys.
Schemat blokowy elektronicznego licznika energii czynnej
Opisany układ licznika energii elektrycznej składa się z trzech części: przetwornika
energii na impulsy, licznika impulsów i zasilacza. Przedstawiony schemat zawiera
przetwornik
którego głównym elementem jest hallotron. Na wyjściu
czujnika
otrzymujemy napięcie zależne od wartości napięcia i prądu oraz
przesunięcia fazowego między nimi. Do wydzielenia składowej czynnej z sygnału
101

wyjściowego
metoda
W zależności od obciążenia na wyjściu lego układu otrzymujemy napięcie uśrednione
zmieniające się w granicach 0 -
Napięcie to steruje przetwornik U/f.
Częstotliwość wyjściowa przetwornika ustalona jest przez elementy układu R,C
i wyraża się zależnością
/
V
(10.43)
Dla
częstotliwość f
Zakres napięć wejściowych i częstotliwości
wyjściowych jest dobrany ze względu na najmniejszą nieliniowość przetwornika U/f,
która wynosi ±0,005%. Każdemu impulsowi na wyjściu przetwornika U/f odpowiada
określona ilość energii
= '\C • Pdt
= C\Pdt = C •
0 0 o
Zliczenie wszystkich impulsów daje wartość całkowitej energii przepływającej w sieci
czasie pomiaru. Impulsy wyjściowe podawane na 12 - stopniowy licznik binarny
U17 i układ
zerujący licznik
7 w przypadku poboru mocy mniejszej od mocy
rozruchu licznika energii. Moc rozruchu Pr jest ustawiana wartościami elementów
układu i wynosi
Została ona określona na takim poziomie ze względu na
dużą nieliniowość przetwornika U/f przy napięciu wejściowym bliskim zeru.
Z licznika
impulsy są dzielone przez 4 - bitowy licznik BCD
i
Otrzymujemy stałą licznika
Oznacza to, że na każdy impuls
wyjściowy z przetwornika energii przypada energia
10 Wh. Impulsy wyjściowe
z przetwornika są zliczane przez licznik zbudowany w oparciu o system
mikroprocesorowy. Głównymi elementami systemu są mikroprocesor 80C31 (Ul)
i zatrzask adresowy
(U2) służący do zapamiętania adresu wpisywanego
sygnałem ALE. Sygnału zegarowego dostarcza rezonator kwarcowy
MHz.
W układzie zapewniono automatyczne jego zainicjowanie (zerowanie mikroprocesora)
po włączeniu zasilania. Mikroprocesor komunikuje się z
zewnętrznymi za
pośrednictwem szyny systemowej. Do szyny tej podłączone są: pamięć programu,
pamięć danych i wyświetlacz LCD.
102
IV.
ćwiczenia
1. Zadania laboratoryjne
1. Sprawdzić
do pomiaru mocy i energii pobieranej przez jednofazowy silnik
asynchroniczny przetwornicy dwumaszynowej
z programem do
wizualizacji parametrów sieci energetycznej -
zmierzyć prąd, napięcie,
moc czynną, moc
moc
THD (THD
Harmonie
Distortion, współczynnik zawartości harmonicznych, współczynnik zniekształceń
nieliniowych) oraz pobraną energię w zadanym czasie dla biegu jałowego
i przyjętego obciążenia silnika.
2. Opracować wyniki pomiarów.
Obliczyć: dla obu stanów pracy silnika moc
bierną i pozorną, na podstawie
pomiarów napięcia, prądu i
oraz pobraną energię w czasie pomiaru przez
zliczenie ilości obrotów tarczy i pomnożenie tej liczby przez stałą licznika.
Porównać wyniki obliczeń z wynikami uzyskanymi z pomiarów przetwornikiem PP9.
Obliczyć wartość pojemności kondensatora energetycznego poprawiającego
współczynnik mocy odbiornika od wartości
do
(np.0.95), włączyć go do
układu i powtórzyć
Wyciągnąć wnioski.
V. Pytania kontrolne
1. Przedstawić zasadę pomiaru mocy czynnej za pomocą watomierza - układy
PMN i PMP.
2. Jakie mierniki powinny być stosowane dodatkowo z watomierzem w układach
pomiarowych? Wyjaśnić dlaczego.
3. Przedstawić zasadę pomiaru mocy biernej przy pomocy watomierza.
4. Przedstawić zasadę pomiaru mocy pozornej przy pomocy woltomierza
i amperomierza.
5. Omówić cel i sposoby kompensacji mocy biernej.
6. Schemat uproszczony budowy i zasada działania licznika energii elektrycznej
7. Budowa i
jednofazowego, indukcyjnego licznika energii elektrycznej
Literatura
1. Dyszyński J.: Metrologia elektryczna i elektroniczna. WPRz Rzeszów, 1989.
2. Kuśmierek Z.: Pomiary mocy i energii w układach elektroenergetycznych, WNT
1994r.
3.
A. i inni: Metrologia elektryczna, WNT, Warszawa, 1994r
4. Parchański J.: Miernictwo elektryczne i elektroniczne, WSiP, Warszawa, 1997r.
5. Rylski A.: Metrologia II prąd zmienny, OWPRz, Rzeszów, 2004.
103
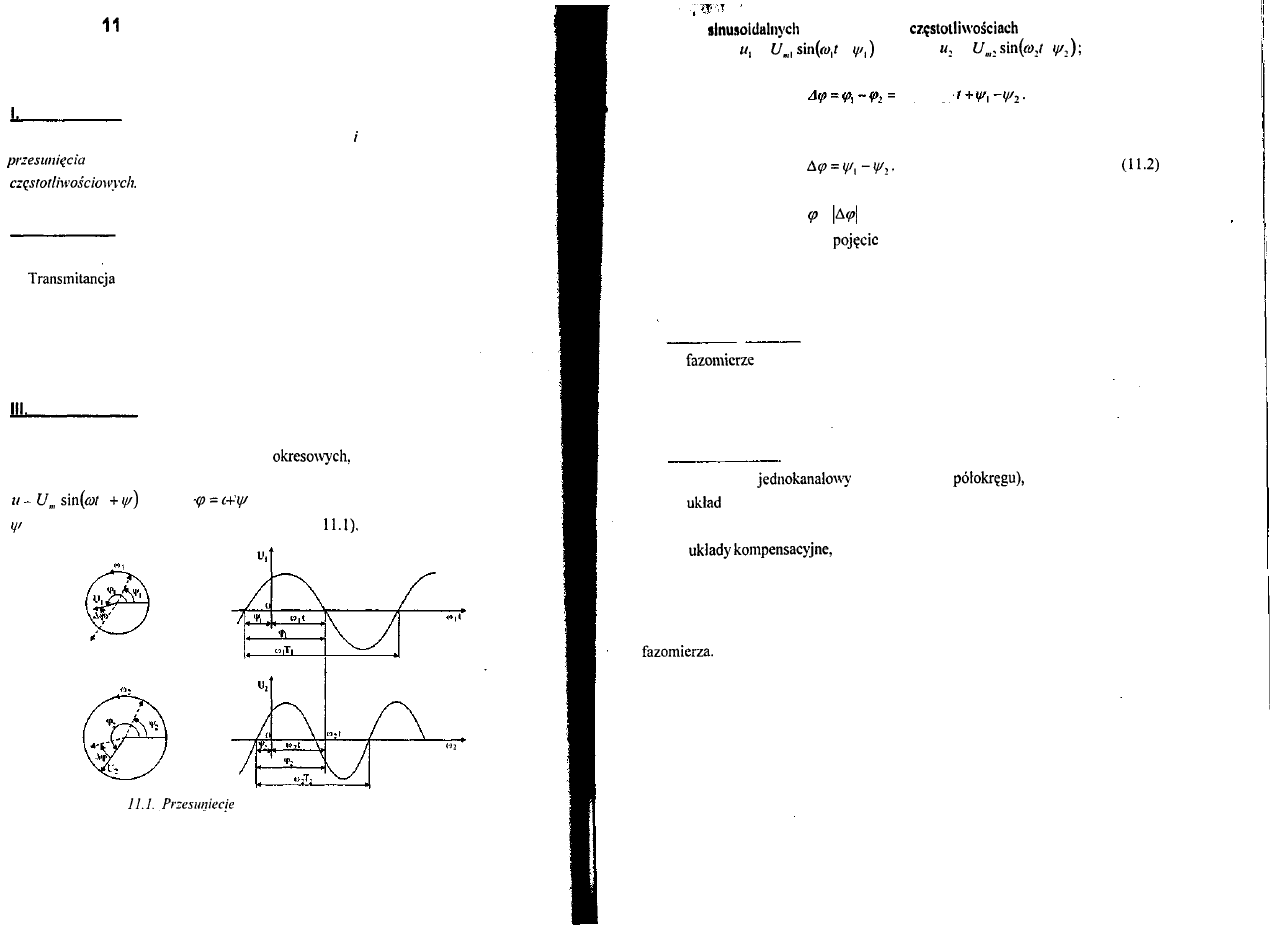
Ćwiczenie
POMIARY PRZESUNIĘCIA FAZOWEGO
Cel ćwiczenia
Celem ćwiczenia jest poznanie analogowych cyfrowych metod pomiaru
fazowego i ich zastosowanie do wyznaczania charakterystyk fazowo-
II. Zagadnienia
1. Pojęcia fazy. przesunięcia faz i przesunięcia fazowego dla sygnałów sinusoidalnych;
2.
widmowa, charakterystyki amplitudowo-częstotliwościowe i fazowo-
częstotliwościowe;
3. Oscyloskopowe metody pomiaru przesunięcia fazowego;
4. Fazomierze elektroniczne analogowe;
5. Cyfrowa metoda pomiaru przesunięcia fazowego.
Wprowadzenie
1. Pojęcia podstawowe
Pojęcie fazy odnosi się do zjawisk
najczęściej do sinusoidalnych
przebiegów występujących w postaci napięć i prądów. Fazą napięcia
-
jest kąt
(cały argument sinusoidalnej funkcji); wielkość
jest fazą początkową (fazą w chwili t = 0) (rys.
t
Rys.
fazy między przebiegami sinusoidalnymi.
104
Ula dwóch
napięć o różnych
=
+
i
=
+
przesunięciem faz nazywa się różnicę faz w chwili t
(11.1)
Przesunięcie faz dla dwóch napięć sinusoidalnych posiadających jednakowe
częstotliwości nie zależy od czasu i jest równe różnicy ich faz początkowych
Wartość bezwzględną przesunięcia faz nazywa się przesunięciem fazowym
=
= ty/
x
-i//
2
\. (11.3)
Dla napięć niesinusoidalnych
przesunięcia fazowego zastępuje się pojęciem
przesunięcia w czasie (czasem opóźnienia) napięć.
Najczęściej stosowane są następujące metody i zasady pomiaru przesunięcia fazowego:
1. metody bezpośrednie:
•
elektromechaniczne,
• fazomierze elektroniczne analogowe,
• fazomierze cyfrowe,
• oscyloskop dwukanałowy.
2. metody pośrednie:
• oscyloskop
(zasady elipsy i
•
z trzema woltomierzami,
• układy z watomierzami,
•
• pomiary algorytmiczne (w dziedzinie czasu i dziedzinie częstotliwości)
np. zasada korelacyjna.
Przyrząd służący do bezpośredniego pomiaru kąta przesunięcia fazowego nosi nazwę
W praktyce najczęściej do pomiaru kąta przesunięcia fazowego stosuje się
oscyloskopy dwu i jednokanalowe oraz fazomierze elektroniczne: analogowe
i cyfrowe.
Pomiary przesunięcia fazowego pomiędzy dwoma napięciami sinusoidalnymi
o takiej samej częstotliwości są potrzebne przy wyznaczaniu charakterystyk fazowych
różnego rodzaju czwórników (wzmacniaczy, transformatorów, dzielników, filtrów,
przesuwników fazowych), podczas synchronizacji generatorów itp.
105
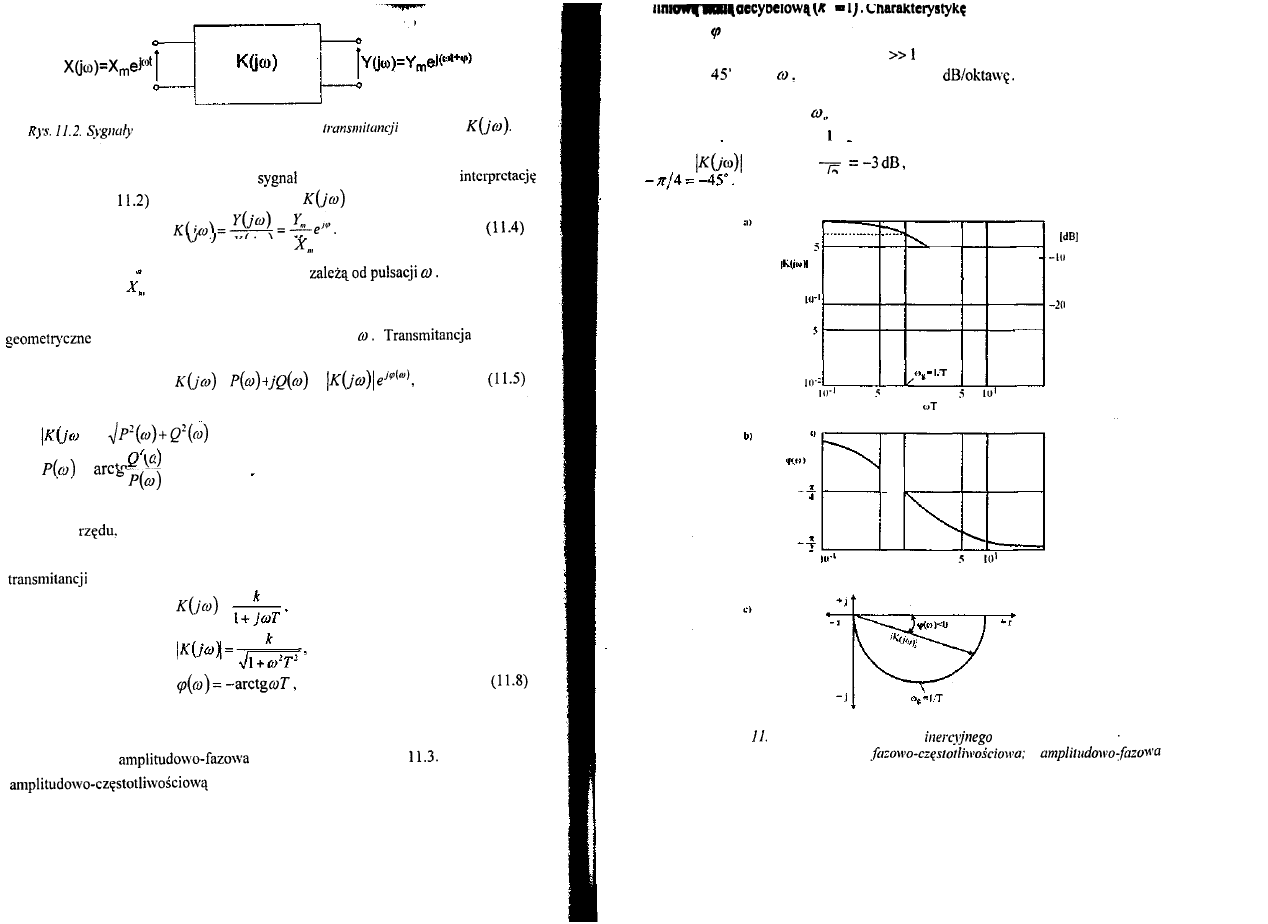
wejściowy i wyjściowy systemu o
widmowej
Podając na wejście liniowego sytemu
sinusoidalny i stosując
symboliczną (rys.
transmitancję widmową
można wyrazić wzorem:
X{jco)
Y
Stosunek amplitud —— i przesunięcie fazowe ę
Funkcję zespoloną K(jco) można przedstawić na płaszczyźnie zespolonej jako miejsce
końców wektora przy zmianie pulsacji
widmowa
może być rozdzielona na część rzeczywistą i urojoną:
=
=
przy czym
)| =
- charakterystyka amplitudowo-częstotliwościowa,
=
- charakterystyka fazowo-częstotliwościowa.
W analogowych torach pomiarowych najczęściej występują układy: inercyjne
pierwszego
drugiego i n-tego rzędu oraz oscylacyjny drugiego rzędu.
Przykładowo, dla układu inercyjnego pierwszego rzędu odpowiednie wyrażenia dla
widmowej i charakterystyk częstotliwościowych wynoszą:
=
(11.6)
(11.7)
przy czym: k - współczynnik wzmocnienia statycznego, T - stała czasowa. .
Charakterystyki: amplitudowo-częstotliwościowa, fazowo-częstotliwościowa
i charakterystyka
przedstawione są na rys.
Charakterystykę
przedstawiono w podwójnie logarytmicznej skali
106
z
razową przedstawiono w liniowej
skali na osi
i logarytmicznej na osi częstotliwości.
Charakterystyka amplitudowa dla coT przechodzi w prostą. Prosta ta przebiega
pod kątem
do osi
tzn. z tłumieniem - 20
Dla
1
= —
* T
wartość
jest równa
a charakterystyka fazowa przyjmuje wartość
10"
\
\
\
\
10"
0
- -30
-40
\
5 10"
Rys.
3. Charakterystyki układu
pierwszego rządu:
a) amplitudowo-częstotliwościowa; b)
c)
107
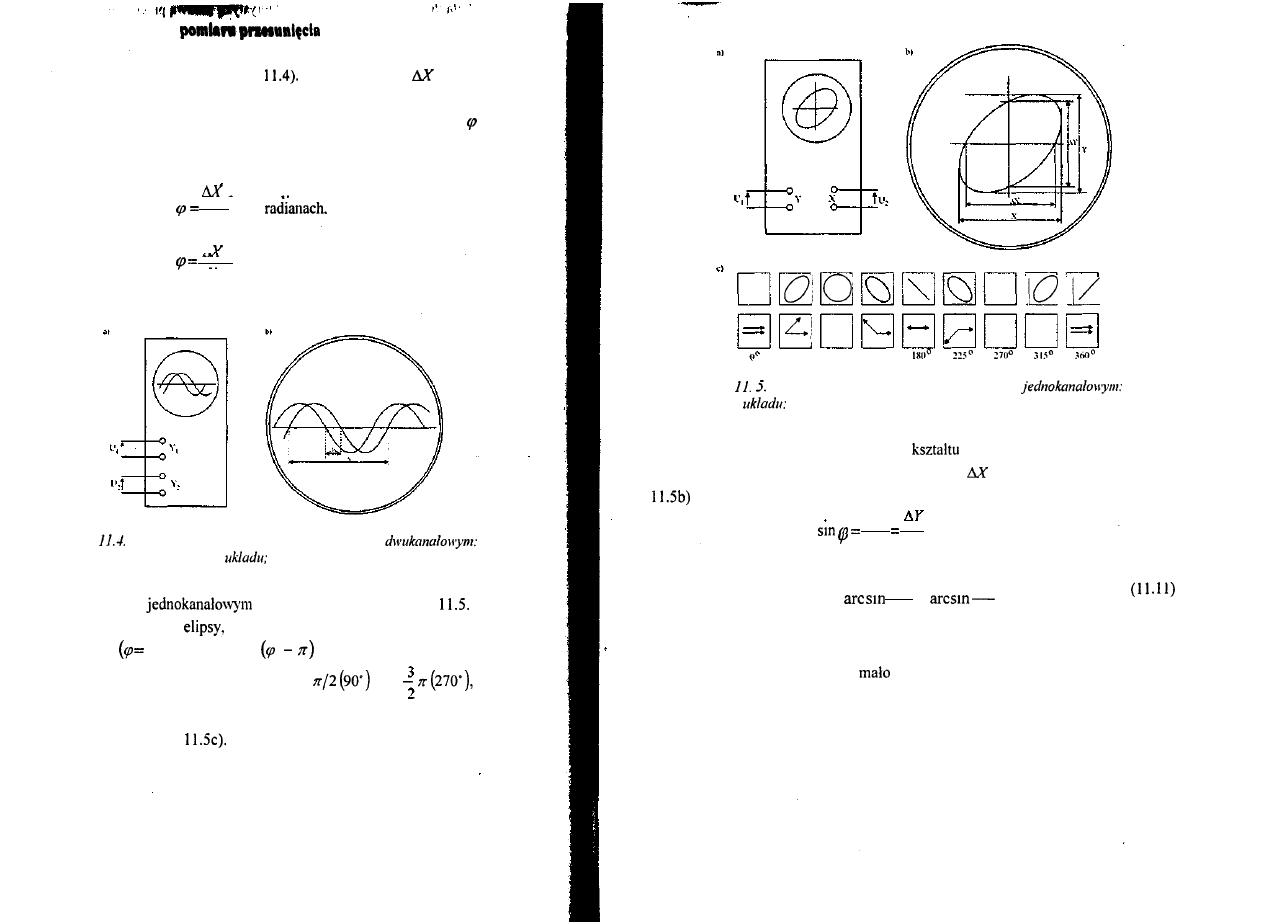
2. Oscyloskopowe metody
fazowego
Oscyloskop dwukanalowy umożliwia bezpośrednią obserwację przebiegów
czasowych napięć o przesunięciu ę (rys.
Oznaczając przez
odcinek między
przejściami przez wartość zerową obydwu przebiegów, a za pomocą X - odcinek
odpowiadający okresowi przebiegu, wzajemne przesunięcie fazowe
określa
zależność
lub
2n w
X
Ą
360° w stopniach kątowych.
(11.9)
Rys.
Pomiar przesunięcia fazowego oscyloskopem
a) schemat
b) obraz na ekranie.
W oscyloskopie
w układzie podanym na rys.
na ekranie
powstaje nieruchomy obraz
która w szczególnych przypadkach, gdy fazy obu
napięć są zgodne
0) lub przeciwnie
-
przyjmuje postać prostej nachylonej
względem osi ekranu. Gdy przesunięcie wynosi
lub
elipsa ma
osie pokrywające się z osiami ekranu i jeśli amplitudy obu napięć są jednakowe, na
ekranie powstaje okrąg (rys.
108
/
u
o
r
V
45° 90° 135°
Rys.
Pomiar przesunięcia fazowego oscyloskopem
a) schemat
b) obraz na ekranie; c) szczególne przypadki obrazu na ekranie.
W przypadkach pośrednich na podstawie
elipsy można określić przesunięcie
fazowe napięć. Po zmierzeniu długości odcinków
oraz X lub AY oraz Y (rys.
oblicza się
AA"
lub
X Y
. AX . AY
ę =
=
X Y
(11.10)
Błąd pomiaru przesunięcia fazowego za pomocą oscyloskopu jest stosunkowo duży
(osiąga wartość 10%), ponieważ
dokładny jest pomiar długości odpowiednich
odcinków a także ze względu na niepożądane przesunięcia fazowe oraz nieliniowości
w torach odchylania oscyloskopu. Korzystne jest stosowanie oscyloskopów o dużym
ekranie.
109
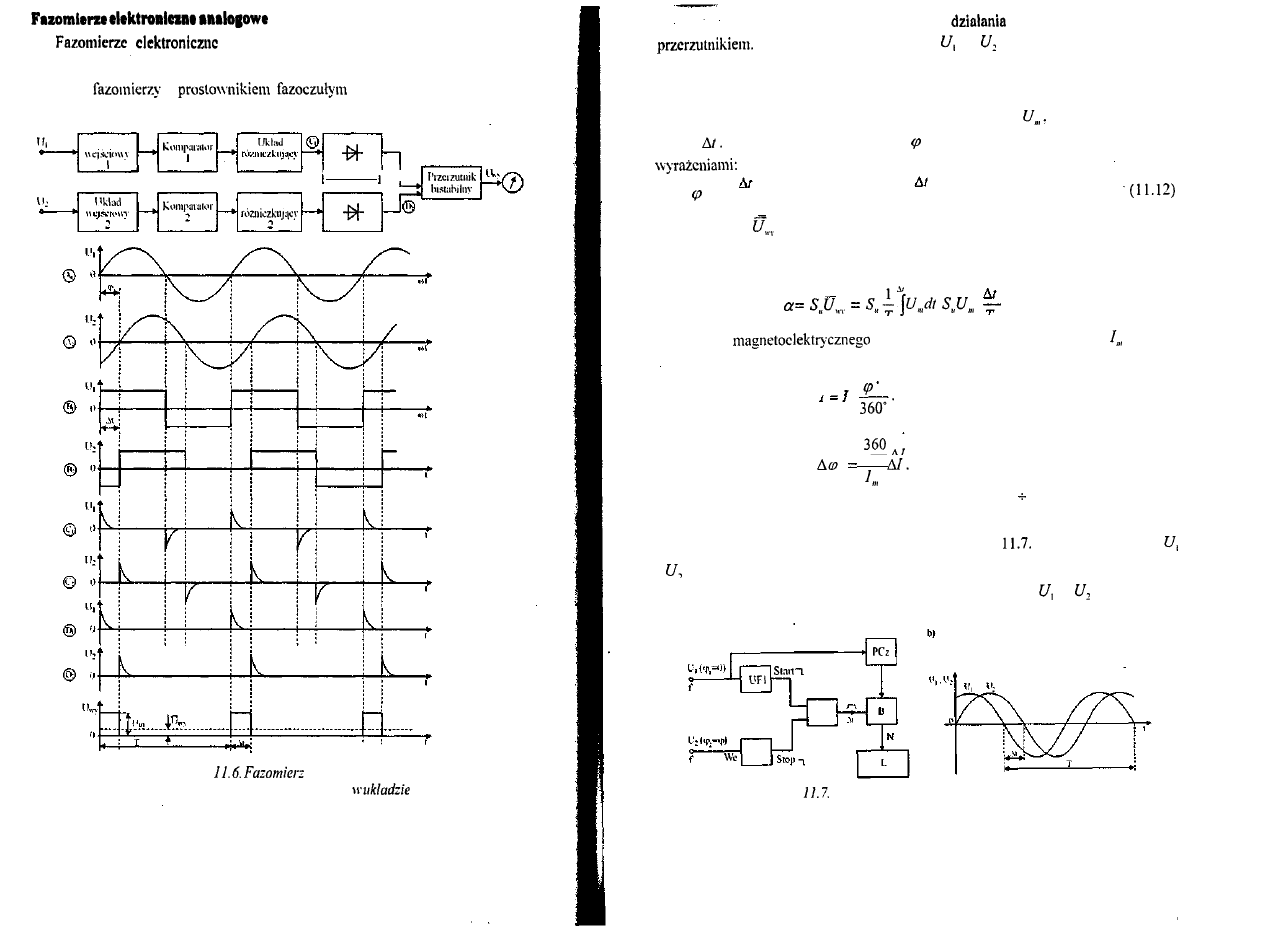
3.
analogowe są budowane przeważnie na zakresy
częstotliwościowe od 20 Hz do kilkuset kHz (granicznie do kilku MHz). Stosowane są
rozwiązania
z
i fazomierze z przetwarzaniem
przesunięcia fazowego w odstęp czasu.
©
©
1'klad
®
©
1
lJklad
©
©
M
Rys.
impulsowy:
a) schemat blokowy; b) przebiegi czasowe napiąć
fazomierza.
110
Na rysunku 11.6 przedstawiono zasadę
fazomierza impulsowego
z
W mierniku napięcia badane
i
są przetwarzane w układach
formujących w przebiegi impulsowe o takich samych okresach jak napięcia badane.
Następnie impulsy te sterują pracą przerzutnika bistabilnego. Na wyjściu przerzutnika
otrzymuje się ciąg impulsów prostokątnych o amplitudzie
okresie T i czasie
trwania
Kąt przesunięcia fazowego
może być określony stosunkiem At/T
i
= 2n—
w radianach lub ę = 360 — w stopniach kątowych.
T T
Wartość średnia
przebiegu prostokątnego na wyjściu przerzutnika jest mierzona za
pomocą przetwornika (miliamperomierza) magnetoelektrycznego. Wskazanie miernika
M
wynosi:
=
.
(11.13)
Przy użyciu
przyrządu wskazującego o zakresie
średnia
wartość prądu płynącego przez miernik wynosi
7
'"
Zdolność rozdzielcza takiego fazomierza jest równa
A •
a błąd pomiaru kąta przesunięcia fazowego nie przekracza 3 5%.
(11.14)
(11.15)
4. Fazomierz cyfrowy
Schemat blokowy miernika przedstawiono na rys.
Napięcia wejściowe
i
po uformowaniu w przebiegi prostokątne w układach formujących UF1 i UF2
posiadają stromo opadające zbocza w chwilach przejścia napięć
i
przez zero od
wartości dodatniej do ujemnej.
a)
f _
vn
PB
kf
Rys.
Cyfrowy miernik przesunięcia fazowego:
a) schemat blokowy miernika; b) wykresy czasowe przesuniętych przebiegów.
111
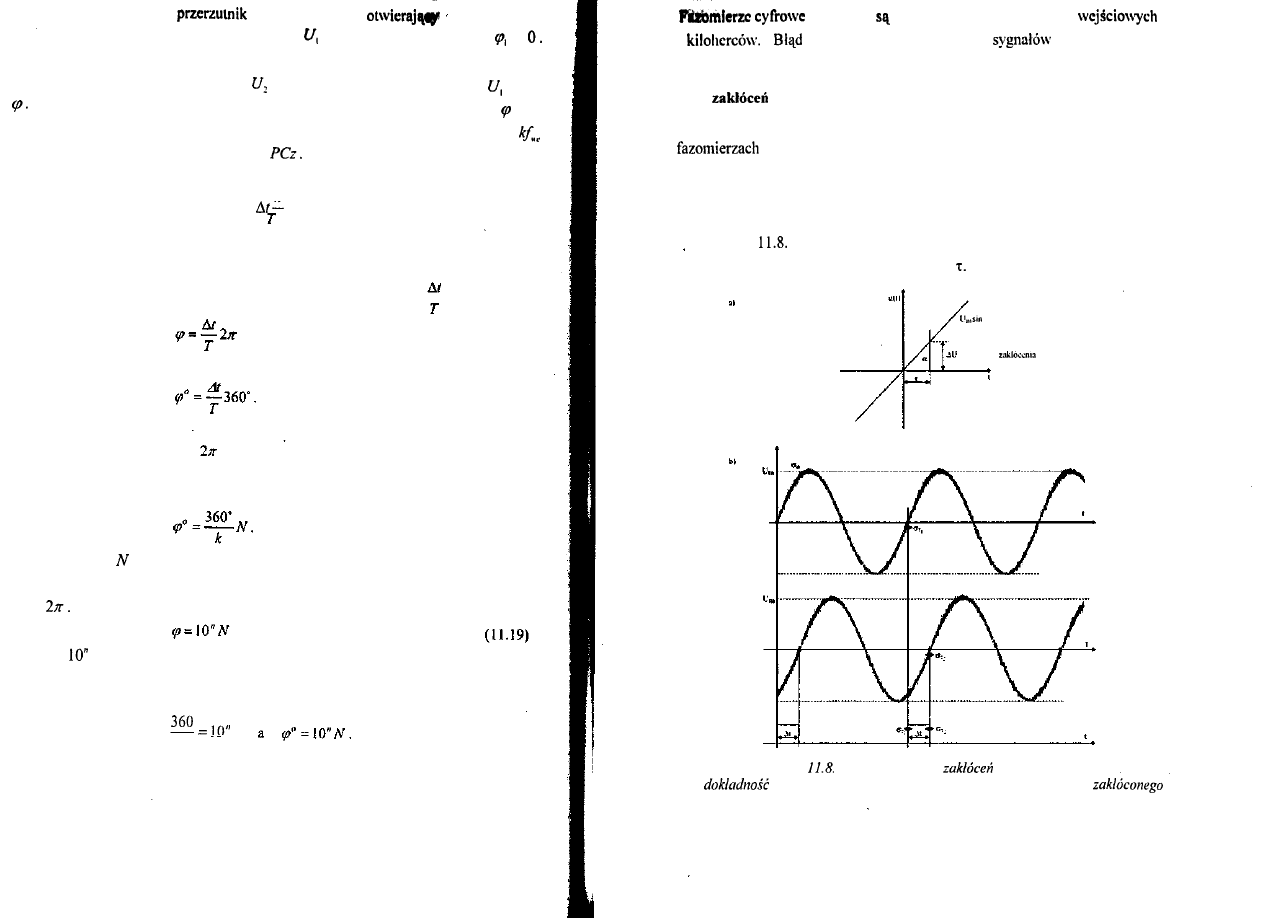
Sygnał wyzwalający
bramkujący PB i
bramkę (Start)
powstaje w chwili przejścia przez zero napięcia
w torze odniesienia o fazie
=
Sygnał kończący impuls na wyjściu przerzutnika i zamykający bramkę (Stop) powstaje
w chwili przejścia przez zero napięcia
przesuniętego względem napięcia
o kąt
Czas otwarcia bramki A/ jest proporcjonalny do przesunięcia fazowego obu
napięć i w tym czasie licznik miernika zlicza impulsy o częstotliwości
wytworzone w powielaczu częstotliwości
Liczba impulsów zliczonych
k
N = Atkf =
(11.16)
przy czym: k - mnożnik powielacza częstotliwości, / - częstotliwość napięć
wejściowych, T - okres napięć wejściowych.
Przesunięcie fazowe napięć (w rad) wyrażone przez stosunek — wynosi:
(11.17)
a mierzone w stopniach kątowych
Po przekształceniu ostatnich wzorów otrzymuje się przesunięcie fazowe w radianach
lub przesunięcie fazowe w stopniach kątowych
Aby liczba
wskazana na polu odczytowym miernika była miarą przesunięcia
fazowego w radianach, mnożnik k powielacza musi wynosić dziesiętną wielokrotność
liczby
Wówczas
a czynnik
uwzględnia się przez wyświetlenie przecinka dziesiętnego.
Aby wskazania miernika były miarą przesunięcia w stopniach kątowych,
mnożnik powielacza musi wynosić dziesiętną wielokrotność liczby 360. Wówczas
k
112
stosowane przy częstotliwościach napięć
do
kilku
fazomierzy cyfrowych dla
nie zawierających
zakłóceń mieści się w przedziale od 0,01 do 1°.
5. Wpływ
losowych
Zakłócenia losowe, najczęściej addytywne, sygnałów wejściowych są
w
elektronicznych źródłem istotnych błędów związanych
z niedokładnością określenia chwili czasowej otwarcia i zamknięcia bramki (błąd
wyzwalania).
Wpływ zakłóceń losowych na dokładność pomiaru kąta przesunięcia fazowego
ilustruje rysunek
Addytywne zakłócenie o amplitudzie AU zmienia moment
przejścia sygnału sinusoidalnego przez zero o czas
ot
- amplituda
Rys.
Ilustracja wpływu
losowych;
a) na
wyznaczania przejścia przez zero sygnału sinusoidalnego
szumem; b) na rozrzut detekcji zera przy pomiarze przesunięcia fazowego
113

Stałe nachylenie
wejściowego w punkcie wyzwalania związane jest
z amplitudą zakłócenia AU i błędem
momentu wyzwalania zależnością:
S = tga —. (11.20)
Nachylenie
sinusoidalnego w punkcie przejścia przez zero
S = — =
=
.
Z obydwu ostatnich wyrażeń wynika związek
AU
T =
(11.21)
Całkowity błąd graniczny w odniesieniu do okresu T będący sumą błędów określania
chwil wyzwalania w obydwu
wynosi
Dla równych amplitud sygnałów w obydwu kanałach
=
=
--•100%.
wyrażenia
można obliczyć wariancję momentu wyzwalania
(11.23)
(11.24)
V
J
Dla jednakowych poziomów charakterystyk widmowych nieskorelowanych zakłóceń
v obydwu kanałach fazomierza:
ostatecznie wariancja czasu otwarcia bramki
AU
(11.26)
114
IV.
ćwiczenia
Zadania laboratoryjne
Zestawienie danych przyrządów pomiarowych i pomocniczych wykorzystywanych
w ćwiczeniu.
2. Pomiar przesunięcia fazowego za pomocą oscyloskopu.
3. Badanie
zakłóceń na wyniki pomiarów przesunięcia fazowego.
4. Porównanie wyników pomiaru przesunięcia fazowego różnymi metodami.
5. Wyznaczenie charakterystyki statycznej przetwornika rezystancja/przesunięcie
fazowe.
6. Opracowanie wyników i przeprowadzenie dyskusji dotyczącej wyników
pomiarów.
V. Pytania kontrolne
1. Od czego zależy dokładność pomiaru w oscyloskopowych zasadach pomiaru
przesunięcia fazowego?
2. Omówić zasady przetwarzania sygnałów stosowane w fazomierzach
elektronicznych analogowych.
3. Jak można określić znak przesunięcia fazowego, jeżeli zasada pomiaru pozwala
wyznaczyć tylko wartość modułu?
4. Narysować schemat blokowy fazomierza cyfrowego. Omówić działanie miernika.
Jakie warunki należy spełnić aby liczba podawana na polu odczytowym była miarą
przesunięcia fazowego w stopniach kątowych i radianach?
5. Omówić wpływ
wejściowych (formujących) w
cyfrowym na
wynik pomiaru.
Literatura
1. Chwaleba A., Poniński M. Siedlecki A.: Metrologia elektryczna. WNT, Warszawa
1994.
2. Dyszyński J.: Metrologia elektryczna i elektroniczna. Laboratorium Część I.
Oficyna wydawnicza Politechniki Rzeszowskiej, Rzeszów 1997.
3. Gajda J., Sroka R.: Pomiary kąta fazowego. Modele - układy - algorytmy. Kraków
2000.
4. Marcyniuk A., Pasecki E.,
M., Szadkowski B.: Podstawy metrologii
elektrycznej. WNT. Warszawa 1984;
115
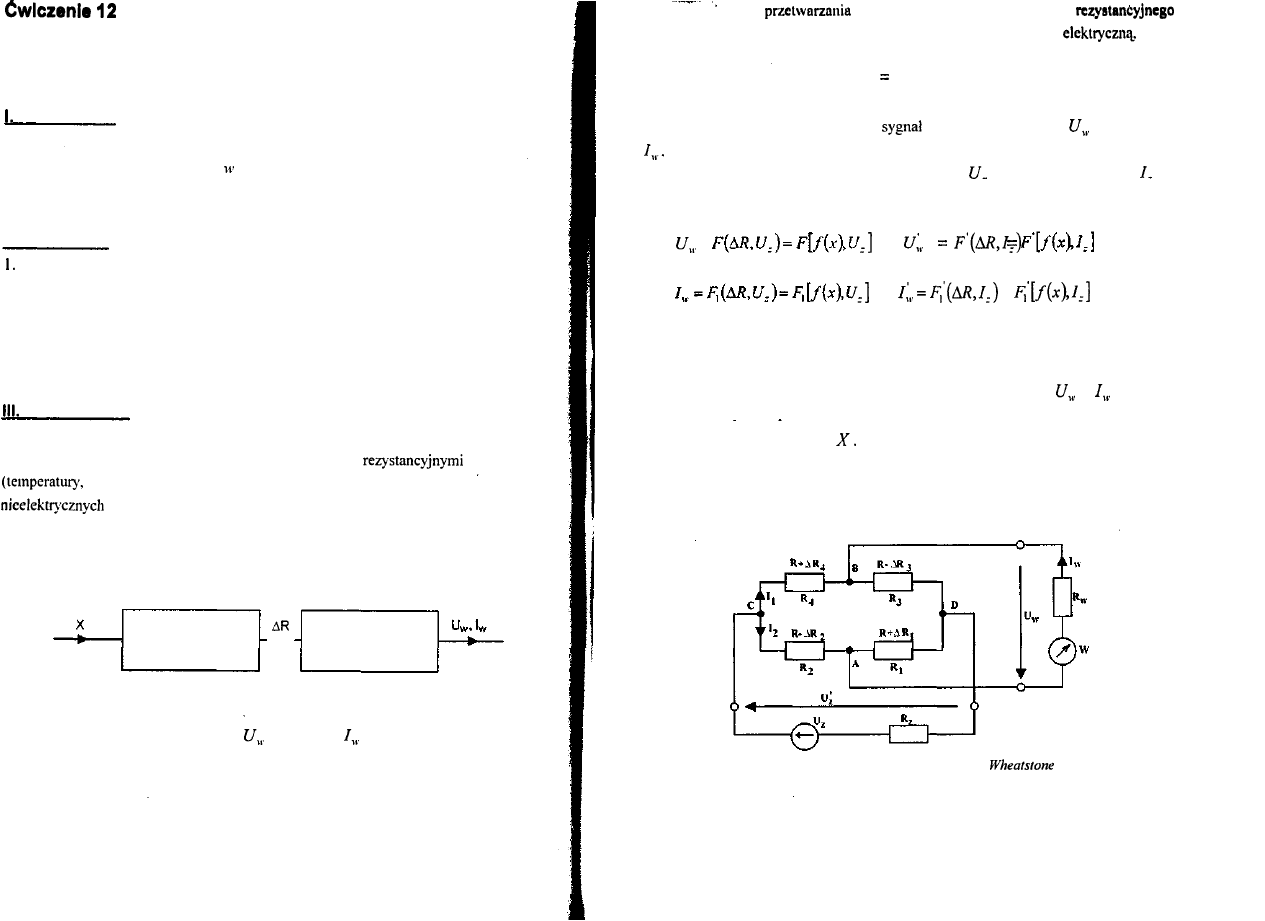
MOSTKI NIEZRÓWNOWAŻONE PRĄDU STAŁEGO
Cel ćwiczenia
Celem ćwiczenia jest badanie właściwości metrologicznych mostków
niezrównoważonych prądu stałego
układach współpracy z wybranymi modelami
czujników rezystancyjnych.
II. Zagadnienia
Mostek niezrównoważony prądu stałego o równych ramionach z jednym, dwoma
i czterema czujnikami;
2. Mostek niezrównoważony prądu stałego ze stosunkiem ramion z jednym
czujnikiem;
3. Właściwości statyczne czujników rezystancyjnych.
Wprowadzenie
3.1. Mostki niezrównoważone prądu stałego
Mostki niezrównoważone prądu stałego współpracujące z
czujnikami
siły, ciśnienia itp.) są powszechnie stosowane w pomiarach wielkości
metodami elektrycznymi.
W takim łańcuchu powtarzania wielkości nieelektrycznej można wyróżnić dwa
podstawowe elementy: czujnik rezystancyjny i niezrównoważony mostek prądu stałego
(rys. 12.1)
Wielkość
nieelektryczna
Czujnik
rezystancyjny
Niezrównoważony
mostek prądu stałego
Rys. 12.1. Schemat blokowy toru przetwarzania wielkości nieelektrycznej X na sygnał
napięciowy
lub prądowy
116
Statyczną funkcję
pierwszego elementu - czujnika
przetwarzającego mierzoną wielkość nieelektryczną X na wielkość
którą
jest zmiana rezystancji AR opisuje ogólna zależność:
AR f{x) (12.1)
Drugi element toru przetwarzania - mostek niezrównoważony prądu stałego
przetwarza zmianę rezystancji AR na
wyjściowy napięciowy
lub prądowy
które można łatwo mierzyć lub wykorzystać do dalszego przetwarzania.
Jeżeli mostek jest zasilany napięciowo napięciem
lub prądowo prądem
to
wyjściowe sygnały mostka można opisać ogólnymi zależnościami:
=
lub
(12.2)
lub
=
(12.3)
Wyrażenia te przedstawiają odpowiednio napięciowe i prądowe statyczne funkcje
przetwarzania mostka niezrównoważonego prądu stałego współpracującego
z czujnikiem rezystancyjnym. W mostku zasilanym z wysokostabilnego zasilacza
napięciowego lub prądowego można przyjąć że sygnały wyjściowe
i
nie zależą
od wartości U. lub /. i są tylko zależne od zmian rezystancji AR czujnika w funkcji
mierzonej wielkości fizycznej
Podstawowy układ niezrównoważonego mostka Wheatstone'a przy zasilaniu
napięciowym przedstawia rysunek 12.2.
Rys. 12. 2. Niezrównoważony mostek
'a
117
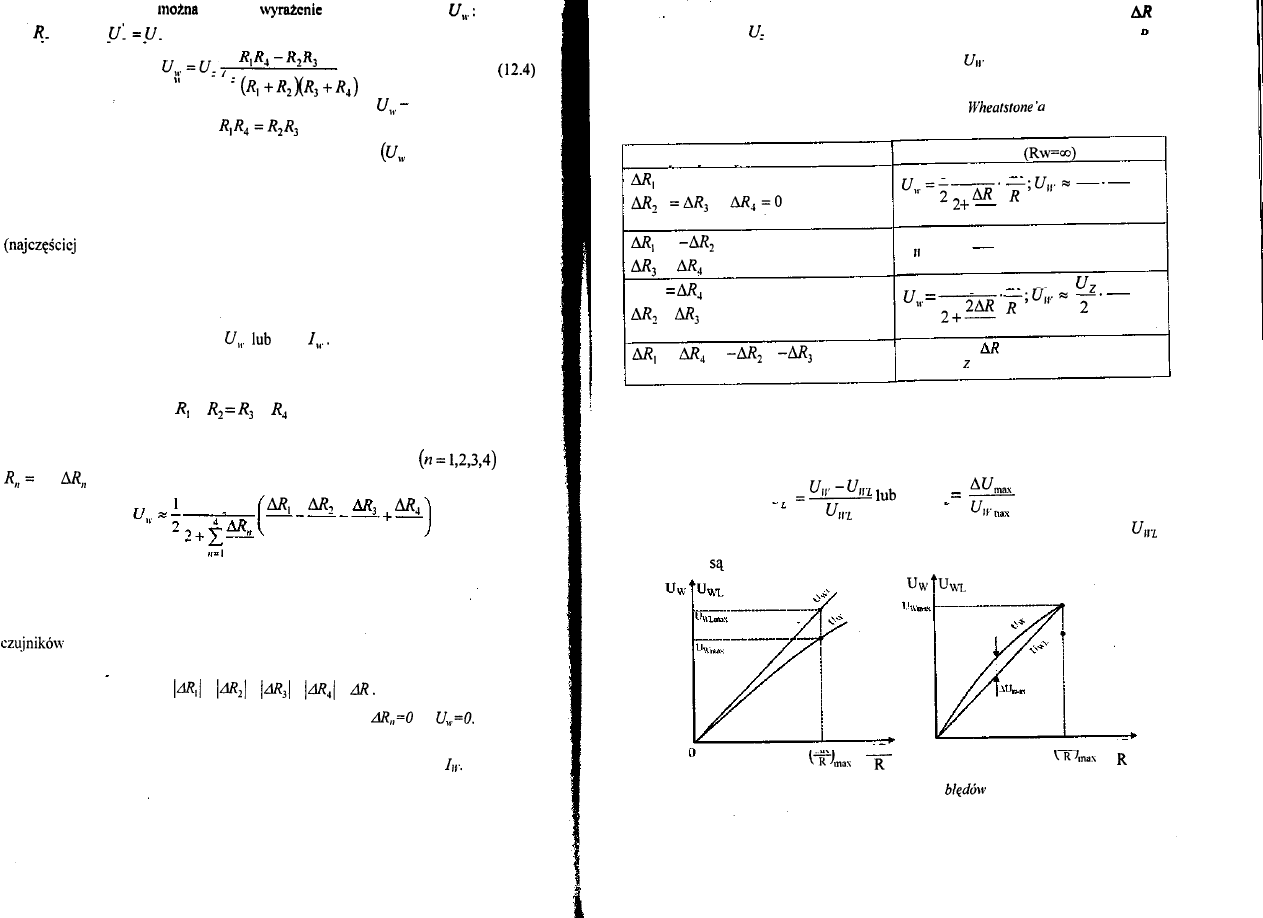
Z twierdzenie Thevenina
otrzymać
na napięcie mostka
dla
=0
oraz warunek równowagi dla mostka zrównoważonego przy
-
0
(12.5)
Z warunku tego korzysta się stosując mostki zrównoważone
=
0) do dokładnych
pomiarów rezystancji.
We współczesnych systemach pomiarowych i systemach regulacji
automatycznej istnieje potrzeba dysponowania i przetwarzania sygnałów elektrycznych
napięciowych lub prądowych) związanych określonymi zależnościami
z mierzonymi (mierzonymi i regulowanymi) wielkościami fizycznymi. W takich
sytuacjach układ mostka zrównoważonego jest mało przydatny, natomiast interesujące
jest wykorzystanie mostka niezrównoważonego pracującego jako przetwornik zmiany
rezystancji AR czujnika w napięcie
prąd
W mostku mogą występować jeden, dwa lub cztery czujniki rezystancyjne. Często
gałęzie mostka dobiera się tak że stan równowagi mostka występuje gdy
=
= = R
. (12.6)
Mostek taki nazywamy równoramiennym. W mostku równoramiennym z niewielkimi
przyrostami rezystancji w czterech gałęziach czujnikowych AR„
przy
R +
słuszna jest przybliżona zależność
U.
R R
R
R
(12.7)
R
Z ostatniego równania i rysunku 2 wynikają zasady włączania czujników pomiarowych
w gałęzie mostka niezrównoważonego: zmiany rezystancji czujników włączonych
w gałęzie sąsiednie powinny być o przeciwnych znakach, natomiast zmiany rezystancji
włączonych w przeciwległe gałęzie powinny być o takich samych znakach.
Szczególnym przypadkiem jest równość wartości bezwzględnej przyrostów
=
=
=
=
(12.8)
W stanie początkowym, gdy mostek jest zrównoważony
i
Zmiany
rezystancji w gałęziach mostka powodują wystąpienie w przekątnej pomiarowej
mostka sygnału niezrównoważenia w postaci napięcia Uw lub prądu
Dla stałej
118
.
.
.
wartości napięcia
zasilającego mostek, związek między zmianą rezystancji —
w gałęziach czujnikowych a napięciem wyjściowym
określają statyczne funkcje
przetwarzania (Tablica 12.1).
Tablica 12.1. Niezrównoważony mostek
(podstawowe zależności dla zasilania napięciowego)
Zmianv rezystancji
=AR
=
=
= AR
=
= 0
AT?,
= AR
=
= 0
=
=
=
= AR
Napięcie wyjściowe
4 R
R
2 R
U. AR
AR
R
R
"
R
Ogólnie mostki niezrównoważone mają nieliniowe funkcje przetwarzania. Jedynie dla
wybranych konfiguracji i przy ograniczeniach zakresów odstrojenia od stanu
równowagi mogą być przyjęte liniowe charakterystyki przetwarzania.
Odstępstwo od charakterystyki liniowej można ocenić za pomocą błędu liniowości:
A.
8,
(12.9)
Podane definicje ilustruje rysunek 3. Modele liniowe charakterystyki mostka
realizowane przy pomocy stycznej i siecznej.
Rys. 12.3. Ilustracja do definicji
liniowości
119
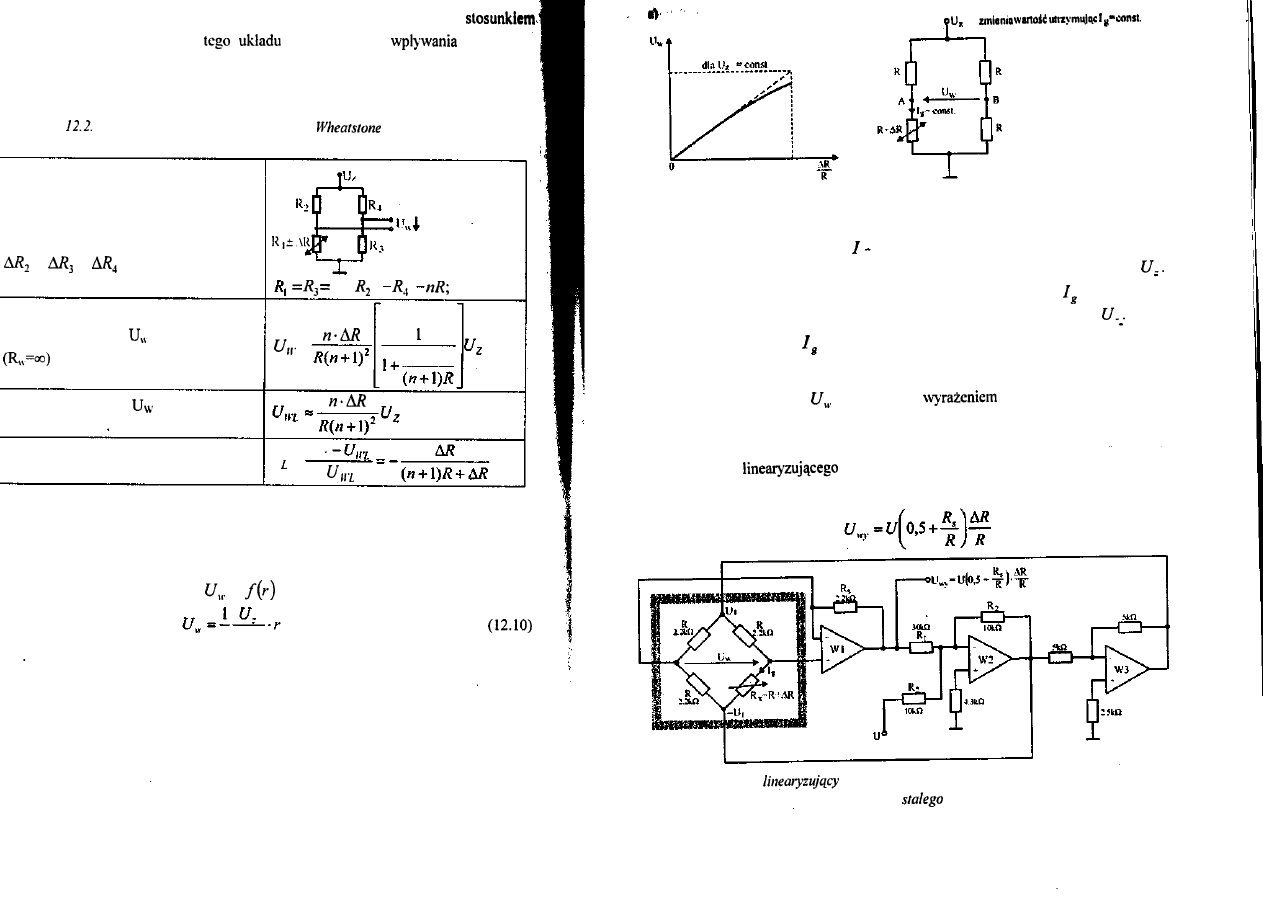
Szczególnym przypadkiem mostka niezrównoważonego jest mostek ze
ramion (tablica 12.2). Zaletą
jest możliwość
na czułość
i liniowość przetwarzania, co wykorzystuje się w różnego rodzaju układach
kompensujących niepożądane wpływy wielkości fizycznych.
Tablica
Niezrównoważony stosunkowy mostek
'a z jednym czujnikiem
(podstawowe zależności dla zasilania napięciowego)
Układ mostka
Zmiana rezystancji:
=
=
= 0
R',
— —
Napięcie wyjściowe
=
AR
Przybliżenie liniowe
dla AR « (n+l)R
Błąd liniowości mostka
3.2. Linearyzacja układów z mostkami niezrównoważonymi
Równoramienny mostek z jednym czujnikiem, wstępnie zrównoważony, posiada
nieliniową funkcję przetwarzania
=
22 + r
gdzie r = —
R
120
b)
•
Rys. 12.4. Zasada linearyzacji charakterystyki statycznej mostka prądu stałego
Linearyzację charakterystyki statycznej przedstawionej na rys. 12.4a można
uzyskać stosując stabilizacji prądu w gałęzi czujnika (rys. 12.4b). Dła uzyskania
takiego efektu potrzebne są odpowiednie zmiany napięcia zasilania mostka
Przykładowo dla wzrostu rezystancji czujnika (AR dodatnie) prąd
zmniejszy się
i dla jego stabilizacji należy odpowiednio zwiększyć napięcie zasilania
Cała
operacja stabilizacji prądu poprzez regulację napięcia zasilania może odbywać się
automatycznie w układzie stabilizatora elektronicznego.
Napięcie wyjściowe mostka
jest określone
Przykład układu
charakterystykę mostka przedstawia rysunek 12.5.
Liniowa funkcja przetwarzania w układzie jest określona zależnością:
(12.12)
(12.11)
Rys. 12.5. Układ
charakterystykę statyczną mostka niezrównoważonego
prądu
121
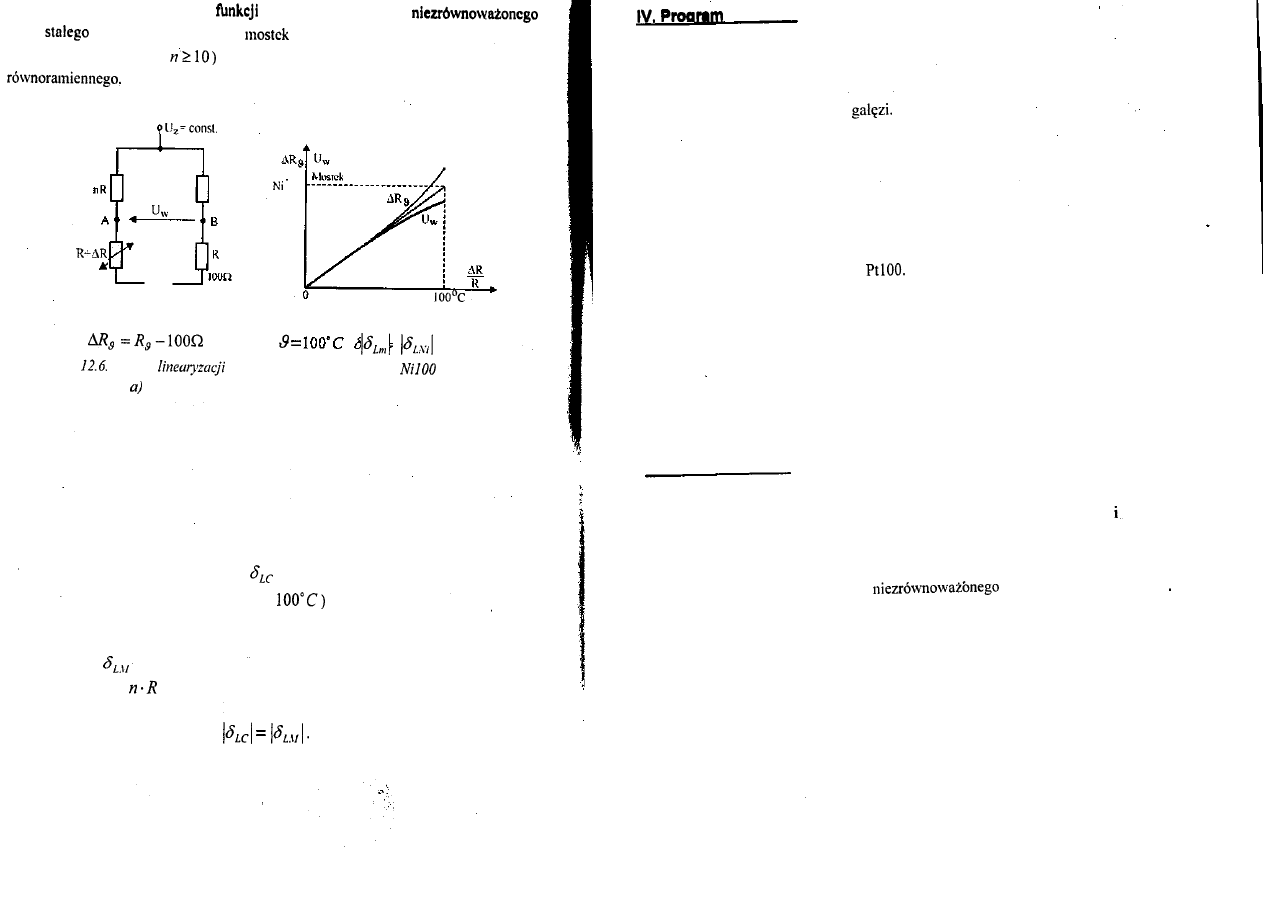
Poprawę liniowości statycznej
przetwarzania mostka
prądu
można uzyskać stosując
stosunkowy (tablica 12.2). Dla dużych
wartości n (praktycznie
błąd liniowości maleje n razy, względem mostka
ale także tak samo zmniejsza się czułość mostka.
a)
Czujnik Ni 100
T
nR
b)
Czujnik
100
9
dla
Rys.
Zasada
charakterystyki układu czujnik
- mostek
niezrównoważony: schemat ideowy układu, b) podstawowe charakterystyki statyczne
W niektórych sytuacjach nieliniowy mostek niezrównoważony może spełniać rolę
układu linearyzującego nieliniowy czujnik pomiarowy (rys. 12.6). Najlepszy skutek
linearyzacji osiąga się wtedy, gdy charakterystyka przetwarzania mostka jest odwrotna
(w znaczeniu matematycznym) względem charakterystyki czujnika.
W praktycznych sytuacjach funkcje przetwarzania czujnika i mostka nie są dokładnie
odwrotne i w celu linearyzacji (poprawy liniowości) układu czujnik-mostek należy
wyznaczyć błąd liniowości czujnika
dla górnej granicy przyjętego zakresu
pomiarowego (na rys. 12.6b jest to wartość
a następnie dla odpowiadającego
AR
tej wartości zakresowej przyrostu rezystancji czujnika — obliczyć ź wyrażenia na
R
błąd liniowości
mostka stosunkowego (tablica 12.2) wymagany stosunek ramion
n oraz rezystancji
przy założeniu równości wartości bezwzględnych błędów
liniowości czujnika i mostka
(12.13)
122
ćwiczenia
Zadania laboratoryjne
4.1. Wyznaczanie statycznej funkcji przetwarzania mostka niezrównoważonego ze
zmianą rezystancji w jednej
4.2. Badanie mostka z różnicowymi zmianami rezystancji w dwóch ramionach
mostka.
4.3. Wyznaczenie charakterystyki statycznej mostka dla zmian rezystancji
w czterech ramionach.
4.4. Linearyzacja charakterystyki mostka zawierającego liniowy model czujnika
temperatury.
4.5. Badanie mostka z czujnikiem
4.6. Wyznaczanie charakterystyki mostka równoramiennego z modelem czujnika
NilOO.
4.7. Linearyzacja charakterystyki statycznej układu: mostek stosunkowy - model
czujnika NilOO.
4.8. Opracowanie wyników i przeprowadzenie dyskusji dotyczącej wyników
pomiarów.
V. Pytania kontrolne
1. Omówić zasadę działania mostka niezrównoważonego prądu stałego. Podać
równanie mostka i narysować jego charakterystyki dla jednej, dwóch czterech
gałęzi czynnych.
2. Od czego zależy czułość mostka niezrównoważonego prądu stałego?
3. Omówić zastosowanie mostka
prądu stałego do korekcji
nieliniowości czujników rezystancyjnych.
4. Podać przykłady wykorzystania mostków niezrównoważonych prądu stałego
w pomiarach wielkości nieelektrycznych.
123
Wyszukiwarka
Podobne podstrony:
Przykłady rachunkowe do wykładu, Elektrotechnika, Metrologia, laboratorium, instrukcje
Badanie charakterystyk statycznych przetworników cyfrowych, Metrologia - laboratorium
Metrologia, laboratorium fizyczne, Laboratorium semestr 2 RÓŻNE
Przykłady rachunkowe do wykładu2, Elektrotechnika, Metrologia, laboratorium, instrukcje
Metrologia 4, Metrologia - laboratorium
Metrologia 1, Metrologia - laboratorium
Metrologia laboratorium v2003
20'', Politechnika Lubelska, Studia, semestr 5, Sem V, Sprawozdania, sprawozdania, Sprawozdania, Lab
JW Energetyka Starosta 1 rok, Regulamin laboratorium Metrologii
14'''''''''', Politechnika Lubelska, Studia, semestr 5, Sem V, Sprawozdania, sprawozdania, Sprawozda
Laboratorium Metrologii
TR 2, LABORATORIUM METROLOGII ELEKTRYCZNEJ I ELEKTRONICZNEJ
Metrologia - Pomiar współczynników tłumienia zakłóceń woltomierza cyfrowego napięcia stałego, Labora
17', LABORATORIUM METROLOGII ELEKTRYCZNEJ I ELEKTRONICZNEJ
Metrologia, odpowiedzi na pytania z laboratorium, Lab 2
MA 16, LABORATORIUM METROLOGII ELEKTRYCZNEJ I ELEKTRONICZNEJ
więcej podobnych podstron