J. Górski, M. Skowronek,

M. Gołota, K. Winkelmann • Teoria sprężystości i plastyczności – Egzamin nr 2, rok akad. 2010/2011 • KMBiM WILiŚ PG

TEORIA

SPRĘŻYSTOŚCI I PLASTYCZNOŚCI

EGZAMIN NR 2, ROK AKAD. 2010/2011

• 15. 09. 2011r. • KMBiM WILi

Ś PG

Czas trwania egzaminu: 120 minut (2 godz.)

Uwagi:

•

Każde z zadań części zadaniowej należy rozwiązać na osobnej kartce
(kartkach), natomiast wszystkie zadania

części teoretycznej należy rozwiązać na

jednej kartce!

•

Wszystkie kartki należy podpisać (imię, nazwisko, numer indeksu, grupa)!

• W

przypadku braku rozwiązania zadania (zadań) także należy oddać podpisaną

kartkę (kartki)!

C Z Ę Ś Ć Z A D A N I O W A

ZADANIE 1:

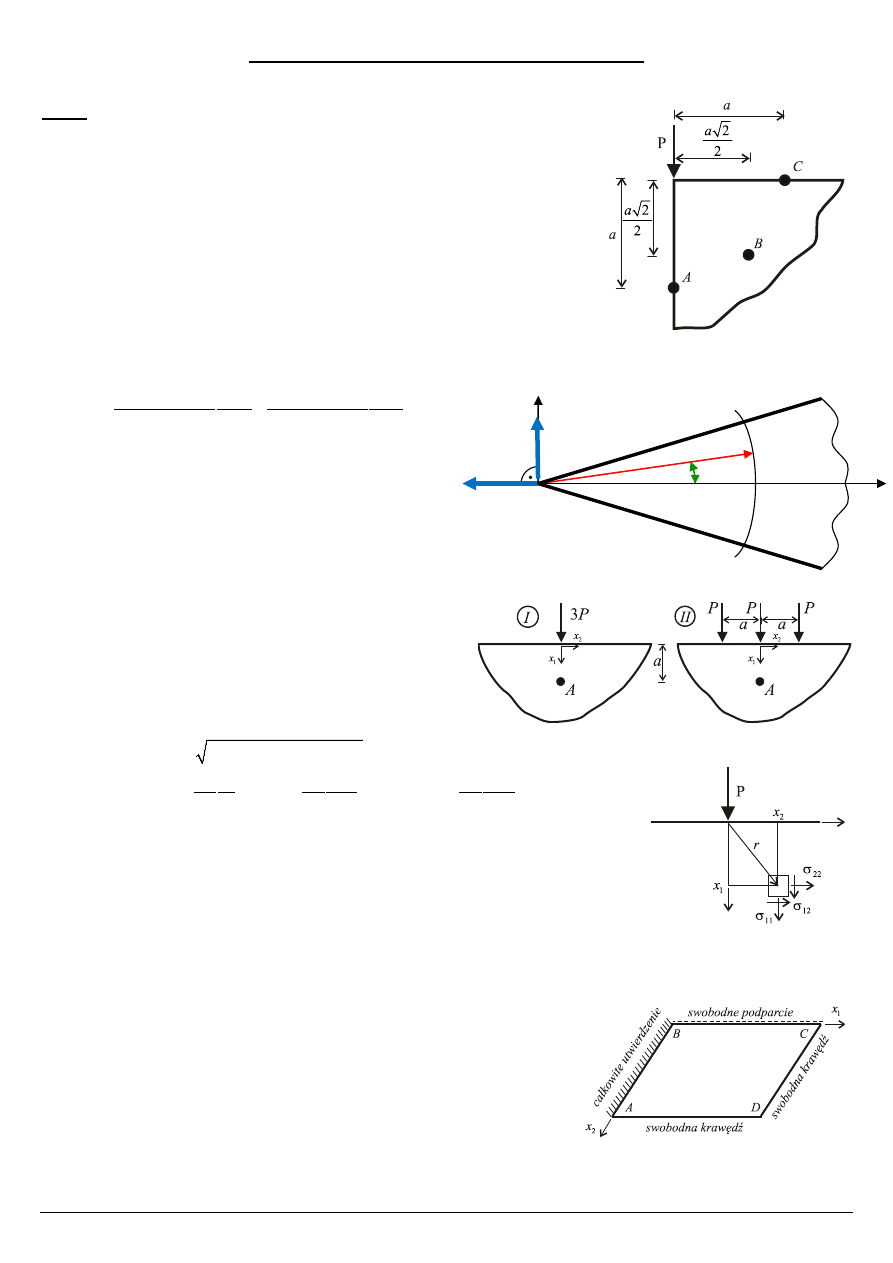
Dana jest tarcza o grubości g (Rys. 1)

a)

Określić stan naprężenia (obliczenie i rysunek) we wskazanych punktach A, B, i
C tarczy.

b)

Przyjmując, że miarą wytężenia w punkcie jest wartość bezwzględna

ekstremalnych naprężeń stycznych (hipoteza Treski) podać, w którym z punktów

wytężenie, jest największe a w którym najmniejsze.
Wzór ogólny (Rys. 2):

(

)

(

)

1

2

2

cos

2

sin

2

sin 2

2

sin 2

rr

P

P

g

r

g

r

ϕ

ϕ

σ

α

α

α

α

=

−

+

−

Rys. 1

ZADANIE 2:

Stan naprężenia w punkcie dany jest tensorem

[

]

15

0

8

0

6

0

MPa

8

0

3

σ

−









= 







−







Stosując niezależnie hipotezy Treski i H-M-H obliczyć zapas

bezpieczeństwa przyjmując, że wszystkie składowe naprężenia rosną
równomiernie.

Przyjąć

0

25MPa

σ

=

ZADANIE 3:

Dane są dwa stany naprężenia tarczy

półnieskończonej wg Rys. 3 o grubości g.

a)

Podać w układzie

1 2

Ox x

, analitycznie i graficznie, stan

naprężenia w punkcie A w obu przypadkach,

b)

Stosując hipotezę H-M-H określić, w którym ze stanów

panuje większe naprężenie

Wzór H-M-H

2

2

2

11

22

11

22

12

3

z

σ

σ

σ

σ σ

σ

=

+

−

+

Rys. 2

Rys. 3

Wzory (Rys. 4):

3

1

11

4

2P x

g r

σ

π

= −

,

2

1 2

22

4

2P x x

g r

σ

π

= −

,

2

1

2

12

21

4

2P x x

g r

σ

σ

π

=

= −

C Z Ę Ś Ć T E O R E T Y C Z N A

1. Poda

ć warunki brzegowe krawędzi AB, BC i CD płyty kwadratowej

o boku a (Rys. 5).

2.

Narysować w PSN obszary bezpieczne, odpowiednio wg hipotez: Treski i H-M-H,

przy

0

20 MPa

σ

=

Zaznaczyć na otrzymanym rysunku stany

Rys. 4

A:

[

]

18

0

0

0

10

0

MPa

0

0

0

σ









= 













, B:

[

]

10

0

0

0

12

0

MPa

0

0

0

σ









=

−















Skomentować otrzymane rezultaty.

3.

Skąd wynikają wnioski o symetrii tensorów:

–

małych odkształceń

ε



,

–

naprężeń (Cauchy)

σ



?

Rys. 5

4.

Opisać założenia: małych przemieszczeń i małych odkształceń w opisie stanu geometrycznego ciała stałego.

1

x

r

ϕ

α

α

g

×

2

x

1

P

2

P