Opis i prezentacja graficzna zmiennych.

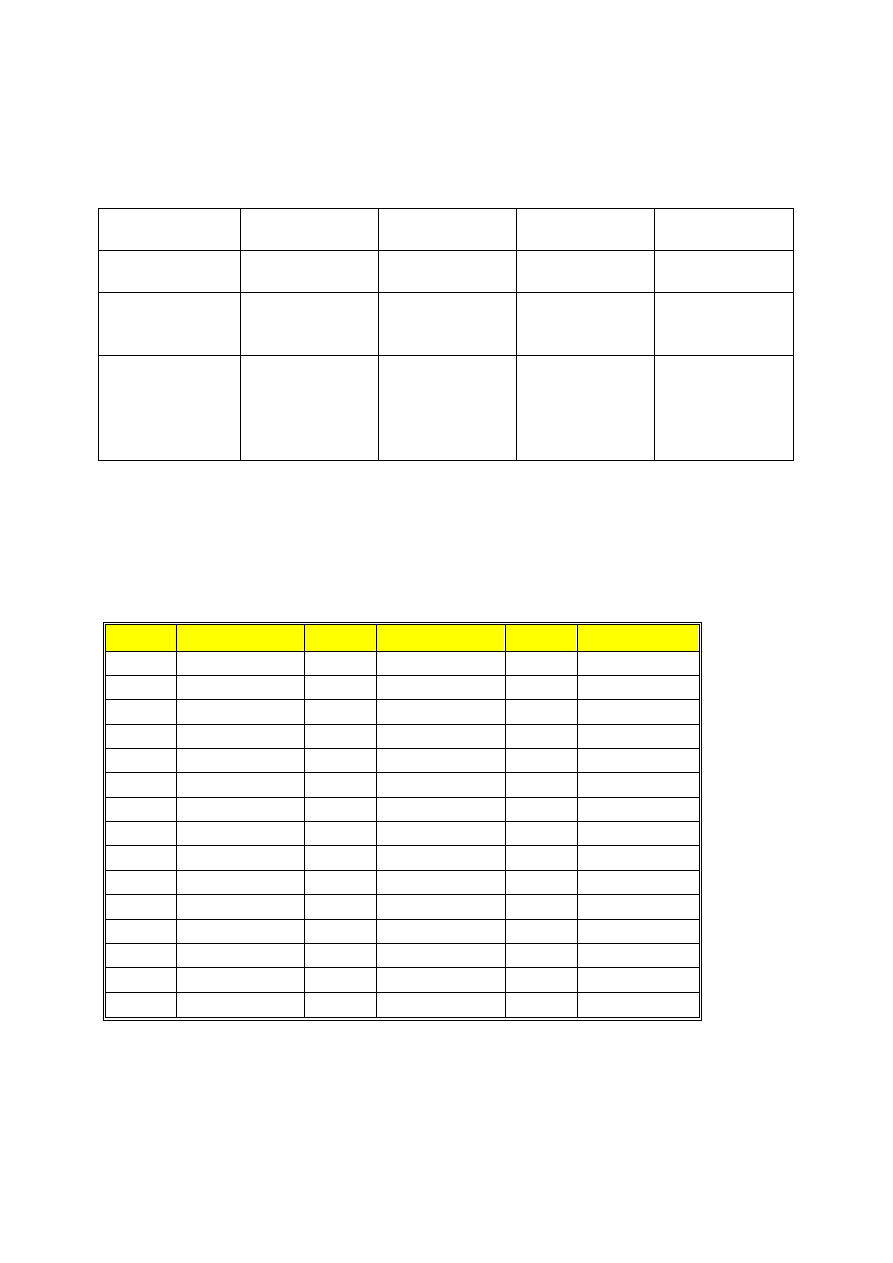
Opis zmiennych wykonujemy zgodnie ze schematem zawartym w poniższej tabeli:

zmienne

Miara tendencji

centralnej

Miara

rozproszenia

Inne

Grafika

NOMINALNE

Dominanta

Liczba kategorii

Wykres kołowy
lub słupkowy

PORZĄDKOWE Mediana

Dominanta

Kwartyle
Odchylenie
ć

wiartkowe

Wykres
słupkowy

ILOŚCIOWE
(interwałowe i
ilorazowe)

Ś

rednia

Mediana
Dominanta

Odchylenie
standardowe
Kwartyle
Odchylenie
ć

wiartkowe

Kurtoza
Skośność

Histogram

1. Zmienne nominalne.

Respondenci w ankiecie odpowiedzieli na pytanie o wykonywany zawód lub zajęcie w
następujący sposób:

osoba

zawód

osoba

zawód

osoba

zawód

1

uczeń

16

przedsiębiorca

31

tokarz

2

nauczyciel

17

tokarz

32

księgowa

3

przedsiębiorca

18

księgowa

33

student

4

tokarz

19

student

34

uczeń

5

księgowa

20

uczeń

35

nauczyciel

6

student

21

pracownik biura

36

sprzedawca

7

uczeń

22

uczeń

37

przedsiębiorca

8

nauczyciel

23

księgowa

38

pracownik biura

9

sprzedawca

24

skrawacz

39

księgowa

10

przedsiębiorca

25

spawacz

40

adwokat

11

pracownik biura

26

student

41

przedsiębiorca

12

uczeń

27

uczeń

42

student

13

księgowa

28

sprzedawca

43

uczeń

14

skrawacz

29

lekarz

44

sprzedawca

15

spawacz

30

nauczyciel

45

lekarz

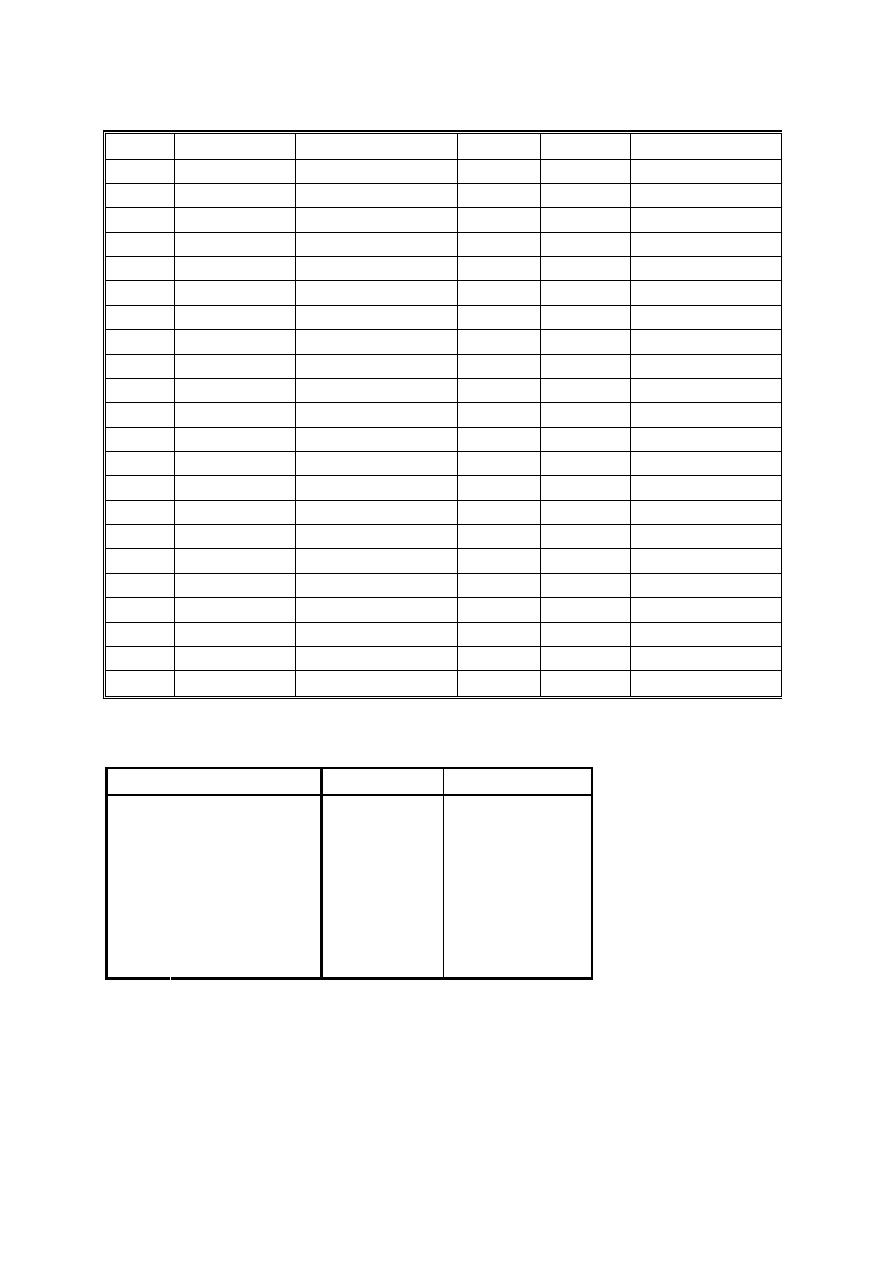
Dane powyższe należy pogrupować, a niektóre występujące pojedynczo zawody
połączyć we wspólne kategorie np. osoby uczące się, pracownicy fizyczni, pracownicy
umysłowi, przedstawiciele wolnych zawodów:

1

adwokat

wolny zawód

24

spawacz

pracownik fizyczny

2

księgowa

pracownik umysłowy

25

spawacz

pracownik fizyczny

3

księgowa

pracownik umysłowy

26

sprzedawca

pracownik fizyczny

4

księgowa

pracownik umysłowy

27

sprzedawca

pracownik fizyczny

5

księgowa

pracownik umysłowy

28

sprzedawca

pracownik fizyczny

6

księgowa

pracownik umysłowy

29

sprzedawca

pracownik fizyczny

7

księgowa

pracownik umysłowy

30

student

osoba ucz

ą

ca si

ę

8

lekarz

wolny zawód

31

student

osoba ucz

ą

ca si

ę

9

lekarz

wolny zawód

32

student

osoba ucz

ą

ca si

ę

10

nauczyciel

pracownik umysłowy

33

student

osoba ucz

ą

ca si

ę

11

nauczyciel

pracownik umysłowy

34

student

osoba ucz

ą

ca si

ę

12

nauczyciel

pracownik umysłowy

35

tokarz

pracownik fizyczny

13

nauczyciel

pracownik umysłowy

36

tokarz

pracownik fizyczny

14

pracownik biura

pracownik umysłowy

37

tokarz

pracownik fizyczny

15

pracownik biura

pracownik umysłowy

38

uczeń

osoba ucz

ą

ca si

ę

16

pracownik biura

pracownik umysłowy

39

uczeń

osoba ucz

ą

ca si

ę

17

przedsiębiorca

wolny zawód

40

uczeń

osoba ucz

ą

ca si

ę

18

przedsiębiorca

wolny zawód

41

uczeń

osoba ucz

ą

ca si

ę

19

przedsiębiorca

wolny zawód

42

uczeń

osoba ucz

ą

ca si

ę

20

przedsiębiorca

wolny zawód

43

uczeń

osoba ucz

ą

ca si

ę

21

przedsiębiorca

wolny zawód

44

uczeń

osoba ucz

ą

ca si

ę

22

skrawacz

pracownik fizyczny

45

uczeń

osoba ucz

ą

ca si

ę

23

skrawacz

pracownik fizyczny

Obliczamy ile osób należy do każdej z kategorii:

Kategoria

Cz

ę

sto

ść

Procent

wolny zawód

8

17,8

pracownik
umysłowy

13

28,9

pracownik
fizyczny

11

24,4

osoba ucz

ą

ca si

ę

13

28,9

Ogółem

45

100,0

Jak widać w naszym zestawieniu występują DWIE dominanty. Wśród respondentów
najczęściej występują pracownicy umysłowi (13 osób) i osoby uczące się (również
13). Wykres prezentujący częstości zaprezentowany jest poniżej:

2. Zmienne porządkowe.

Respondentów poproszono o określenie ich aktualnego samopoczucia na skali od 1
(bardzo złe) do 5 (doskonałe). Uzyskany w ten sposób pomiar daje się przedstawić na
skali porządkowej. Osoby ankietowane udzieliły następujących odpowiedzi:.

osoba

samopoczucie

osoba

samopoczucie

osoba

samopoczucie

1

1

16

1

31

4

2

2

17

2

32

4

3

2

18

3

33

3

4

1

19

2

34

2

5

2

20

2

35

2

6

4

21

3

36

3

7

4

22

3

37

4

8

5

23

2

38

3

9

3

24

1

39

2

10

2

25

2

40

3

11

1

26

2

41

2

12

1

27

1

42

4

13

2

28

2

43

4

14

3

29

3

44

3

15

2

30

4

45

5

Sortujemy pomiary od najniższego do najwyższego i zliczamy odpowiedzi, a
następnie obliczamy uzyskany procent i procent skumulowany. Uzyskujemy
następujące wyniki:

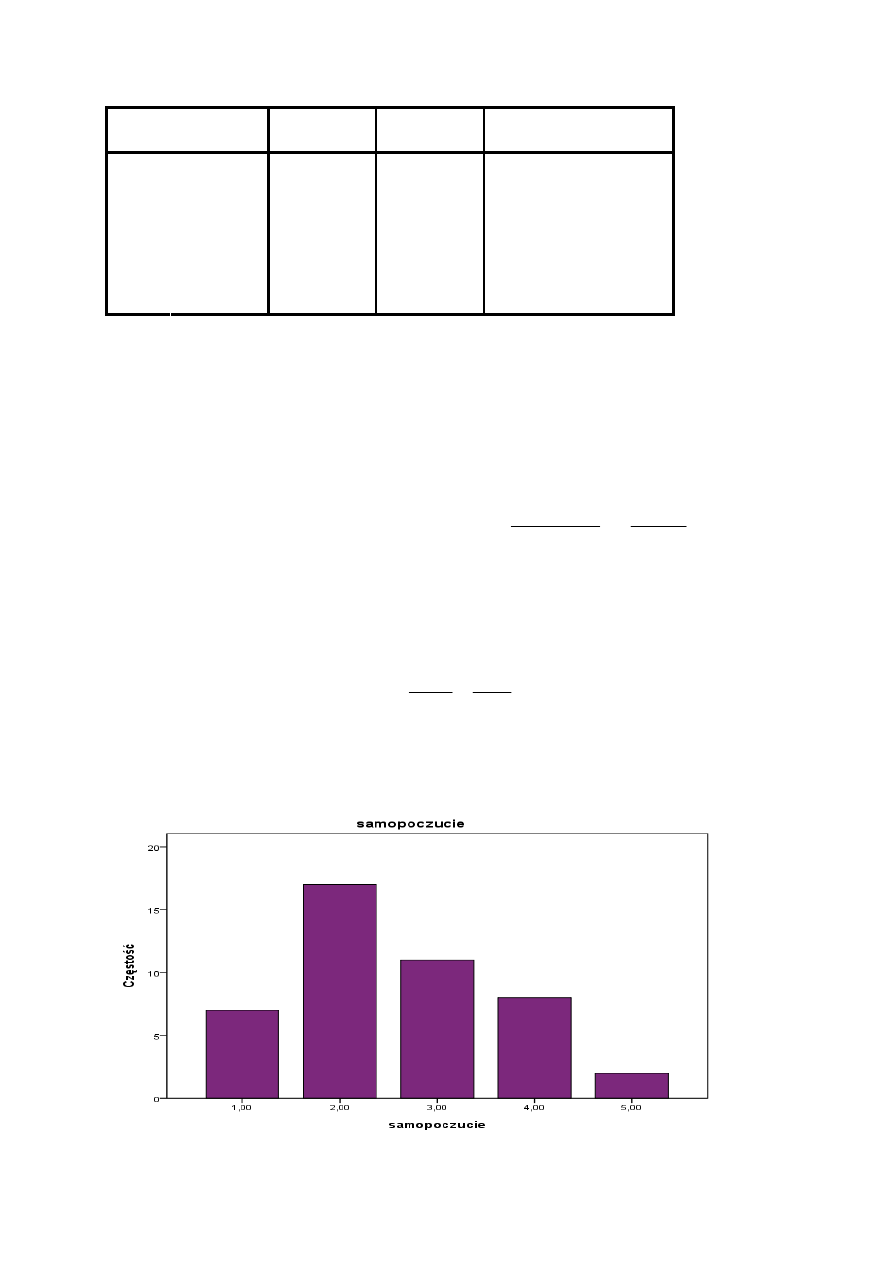
Poziom

samopoczucia

Cz

ę

sto

ść

Procent

Procent skumulowany

1

7

15,6

15,6

2

17

37,8

53,3

3

11

24,4

77,8

4

8

17,8

95,6

5

2

4,4

100,0

Ogółem

45

100,0

Z powyższej tabeli wynika, iż dominanta wynosiła 2 (tak swoje samopoczucie
określiło 37,8% badanych). Mediana – czyli pomiar środkowy również ma wartość
równą 2. Połowa badanych ma samopoczucie na poziomie 2 i niższym, a druga
połowa na poziomie 2 i wyższym.
Wartość 1 kwartyla wynosi 2. Pierwsze 25 % respondentów ma samopoczucie na
poziomie 2 i niższym. Wartość 3 kwartyla to 3. Oznacza to, iż 25% respondentów ma
samopoczucie na poziomie 3 i wyższym.

Obliczamy odchylenie ćwiartkowe:

Odchylenie wynosi 0,5, co oznacza, że wyniki połowy badanych odchylają się od
mediany o ok. ½ kategorii.

Odchylenie ćwiartkowe posłuży nam również do obliczenia pozycyjnego
współczynnika zmienności:



Współczynnik zmienności ma wartość 0,25, co świadczy o niewielkim zróżnicowaniu
zmiennej. Rozkład zmiennej graficznie przedstawimy przy pomocy wykresu
słupkowego:

5

,

0

2

2

3

2

1

3

=

−

=

−

=

Q

Q

Q

25

,

0

2

5

,

0

=

=

=

Me

Q

Q

V

3. Zmienne interwałowe i ilorazowe.

Badanych zapytano również o ich wiek. Otrzymano następujące odpowiedzi:

osoba

wiek

osoba

wiek

osoba

wiek

1

52

16

25

31

29

2

19

17

28

32

50

3

20

18

25

33

45

4

21

19

34

34

48

5

21

20

37

35

46

6

21

21

24

36

25

7

17

22

28

37

35

8

15

23

36

38

38

9

14

24

48

39

36

10

15

25

42

40

42

11

16

26

36

41

41

12

12

27

37

42

35

13

17

28

45

43

36

14

11

29

41

44

36

15

35

30

58

45

38

Podobnie, jak w przypadku danych porządkowych sortujemy pomiary od najniższego
do najwyższego i zliczamy odpowiedzi, a następnie obliczamy uzyskany procent i
procent skumulowany. Uzyskujemy następujące wyniki:

Wiek

Cz

ę

sto

ść

Procent

Procent

skumulowany

Wiek

Cz

ę

sto

ść

Procent

Procent

skumulowany

11,00

1

2,2

2,2

34,00

1

2,2

46,7

12,00

1

2,2

4,4

35,00

3

6,7

53,3

14,00

1

2,2

6,7

36,00

5

11,1

64,4

15,00

2

4,4

11,1

37,00

2

4,4

68,9

16,00

1

2,2

13,3

38,00

2

4,4

73,3

17,00

2

4,4

17,8

41,00

2

4,4

77,8

19,00

1

2,2

20,0

42,00

2

4,4

82,2

20,00

1

2,2

22,2

45,00

2

4,4

86,7

21,00

3

6,7

28,9

46,00

1

2,2

88,9

24,00

1

2,2

31,1

48,00

2

4,4

93,3

25,00

3

6,7

37,8

50,00

1

2,2

95,6

28,00

2

4,4

42,2

52,00

1

2,2

97,8

29,00

1

2,2

44,4

58,00

1

2,2

100,0

Ogółem:

45

100,0

Z powyższego zestawienia wynika, iż dominanta dla wieku wynosi 36 lat. Do takiego wieku
przyznało się 5 ankietowanych (11,1 %).

Mediana – czyli pomiar środkowy jest równa

wartości 35 lat. Połowa badanych ma 35 lat lub mniej, a druga połowa 35 lat i więcej.
Z tabeli odczytujemy również kwartale. Wynoszą one odpowiednio 21 lat (Q1) i 41
lat (Q3). Obliczamy również odchylenie ćwiartkowe i pozycyjny współczynnik
zmienności:

Dla wieku – zmiennej ilorazowej – musimy obliczyć także średnią i odchylenie
standardowe. W tym celu sumujemy wartości pomiarów i ich kwadratów:

lp

x

x

2

)

(

x

x

−

2

)

(

x

x

−

3

)

(

x

x

−

4

)

(

x

x

−

1

52

2704

20,22

408,85

8266,91

167157,01

2

19

361

-12,78

163,33

-2087,34

26676,17

3

20

400

-11,78

138,77

-1634,69

19256,67

4

21

441

-10,78

116,21

-1252,73

13504,39

5

21

441

-10,78

116,21

-1252,73

13504,39

6

21

441

-10,78

116,21

-1252,73

13504,39

7

17

289

-14,78

218,45

-3228,67

47719,70

8

15

225

-16,78

281,57

-4724,72

79280,76

9

14

196

-17,78

316,13

-5620,76

99937,17

10

15

225

-16,78

281,57

-4724,72

79280,76

11

16

256

-15,78

249,01

-3929,35

62005,18

12

12

144

-19,78

391,25

-7738,89

153075,31

13

17

289

-14,78

218,45

-3228,67

47719,70

14

11

121

-20,78

431,81

-8972,98

186458,49

15

35

1225

3,22

10,37

33,39

107,50

16

25

625

-6,78

45,97

-311,67

2113,09

17

28

784

-3,78

14,29

-54,01

204,16

18

25

625

-6,78

45,97

-311,67

2113,09

19

34

1156

2,22

4,93

10,94

24,29

20

37

1369

5,22

27,25

142,24

742,48

21

24

576

-7,78

60,53

-470,91

3663,69

22

28

784

-3,78

14,29

-54,01

204,16

23

36

1296

4,22

17,81

75,15

317,14

24

48

2304

16,22

263,09

4267,29

69215,51

25

42

1764

10,22

104,45

1067,46

10909,47

26

36

1296

4,22

17,81

75,15

317,14

27

37

1369

5,22

27,25

142,24

742,48

10

2

21

41

2

1

3

=

−

=

−

=

Q

Q

Q

29

,

0

35

10

=

=

=

Me

Q

Q

V

28

45

2025

13,22

174,77

2310,44

30543,99

29

41

1681

9,22

85,01

783,78

7226,43

30

58

3364

26,22

687,49

18025,95

472640,30

31

29

841

-2,78

7,73

-21,48

59,73

32

50

2500

18,22

331,97

6048,46

110203,02

33

45

2025

13,22

174,77

2310,44

30543,99

34

48

2304

16,22

263,09

4267,29

69215,51

35

46

2116

14,22

202,21

2875,40

40888,24

36

25

625

-6,78

45,97

-311,67

2113,09

37

35

1225

3,22

10,37

33,39

107,50

38

38

1444

6,22

38,69

240,64

1496,79

39

36

1296

4,22

17,81

75,15

317,14

40

42

1764

10,22

104,45

1067,46

10909,47

41

41

1681

9,22

85,01

783,78

7226,43

42

35

1225

3,22

10,37

33,39

107,50

43

36

1296

4,22

17,81

75,15

317,14

44

36

1296

4,22

17,81

75,15

317,14

45

38

1444

6,22

38,69

240,64

1496,79

suma:

1430

51858

0,00

6415,78

2142,91 1885484,51

ś

rednia

31,78

Wartość średnią obliczamy ze wzoru:


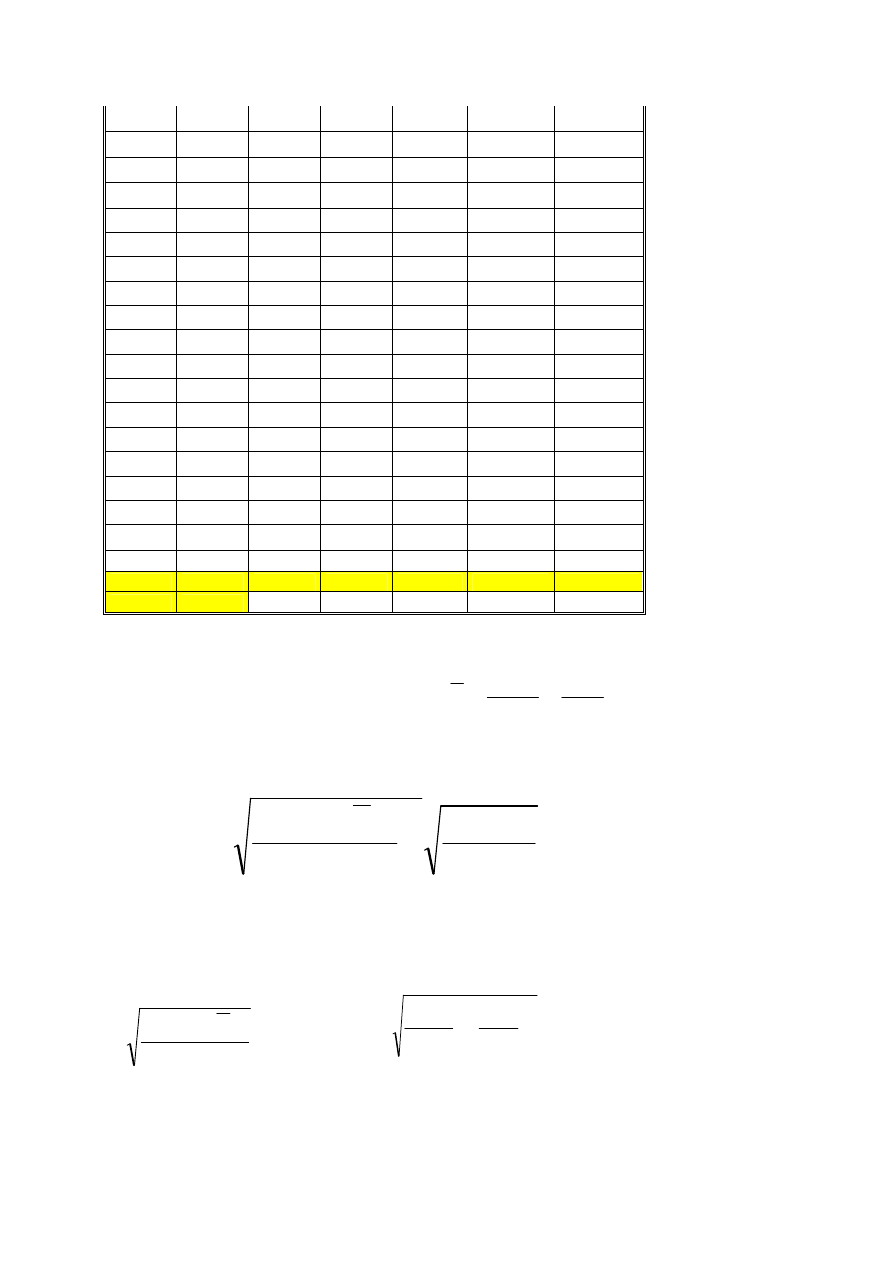
Odchylenie standardowe obliczymy natomiast w następujący sposób:





Należy zwrócić uwagę, iż podany wyżej wzór na odchylenie ma w mianowniku
wartość N-1 – jest to bowiem estymator odchylenia standardowego (estymator,
czyli statystyka służąca do szacowania wartości statystyki w populacji). Wartość ta
różni się od wartości statystyki w próbie, którą obliczalibyśmy korzystając ze wzorów:


lub


W przypadku korzystania z drugiego wzoru wykorzystalibyśmy sumę kwadratów
poszczególnych pomiarów obliczoną w trzeciej kolumnie powyższej tabeli.

78

,

31

45

1430

1

=

=

=

∑

=

N

X

X

N

i

i

08

,

12

1

45

78

,

6415

1

)

(

2

=

−

=

−

−

=

∑

N

X

X

s

N

X

X

s

∑

−

=

2

)

(

2

2















−

=

∑

∑

N

X

N

X

s

Obliczone wartości pozwolą nam na obliczenie współczynnika zmienności dla danych
interwałowych:




Obliczona wartość współczynnika pozwala ocenić zmienność cechy, którą w tym
przypadku należy określić jako niewielką.

Kolejne kolumny tabeli zawierające różnicę między pomiarem a średnią podniesione
do kolejnych potęg posłużą do obliczenia statystyk opisowych nazywanych
momentami średniej.

Pierwszy moment, to

0

)

(

1

=

−

=

∑

N

X

X

m

Jak wiadomo suma różnic poszczególnych pomiarów od średniej zawsze jest równa
zero.

Drugi moment ma wartość:

57

,

142

45

78

,

6415

)

(

2

2

=

=

−

=

∑

N

X

X

m

,

trzeci :

62

,

47

45

91

,

2142

)

(

3

3

=

=

−

=

∑

N

X

X

m

,

zaś czwarty analogicznie:

66

,

41899

45

1885484,51

)

(

4

4

=

=

−

=

∑

N

X

X

m

Trzeci i czwarty moment zostaną użyte do obliczenia skośności i kurtozy rozkładu –
niezbędnych elementów opisu statystycznego zmiennej interwałowej.

Skośność obliczamy ze wzoru:

03

,

0

57

,

142

57

,

142

62

,

47

2

2

3

1

=

=

=

m

m

m

g

Interpretując skośność należy pamiętać, iż bezwzględna wartość skośności
dwukrotnie większa od swego błędu standardowego jest wskaźnikiem odejścia od
symetrii rozkładu. Dlatego należy obliczoną wartość skośności porównać z błędem
standardowym skośności (SES), który obliczymy następująco:

38

,

0

78

,

31

08

,

12

=

=

=

x

s

v

[

]

35

,

0

48

*

46

*

43

44

*

45

*

6

)

3

)(

1

)(

2

(

)

1

(

6

=

=

+

+

−

−

=

n

n

n

n

n

SES

0,03 < 2*0,35

W naszym przykładzie bezwzględna wartość skośności nie przekracza
podwojonego błędu standardowego, zatem rozkład NIE JEST skośny.

Opierając się na wartościach czwartego i drugiego momentu obliczymy kurtozę:

94

,

0

)

57

,

142

(

66

,

41899

3

2

2

2

4

2

−

=

=

−

=

m

m

g

Podobnie jak w omawianym wyżej sposobie interpretowania skośności uzyskany
wynik kurtozy należy porównać z podwojonym błędem standardowym kurtozy (SEK).

69

,

0

50

*

42

1

2025

35

,

0

*

2

)

5

)(

3

(

1

*

2

2

=

−

=

+

−

−

=

n

n

n

SES

SEK

||||

-0,94

||||

< 2*0,69

W przypadku naszych danych bezwzględna wartość kurtozy jest mniejsza od
podwojonego błędu standardowego kurtozy, rozkład jest zatem mezokurtyczny.

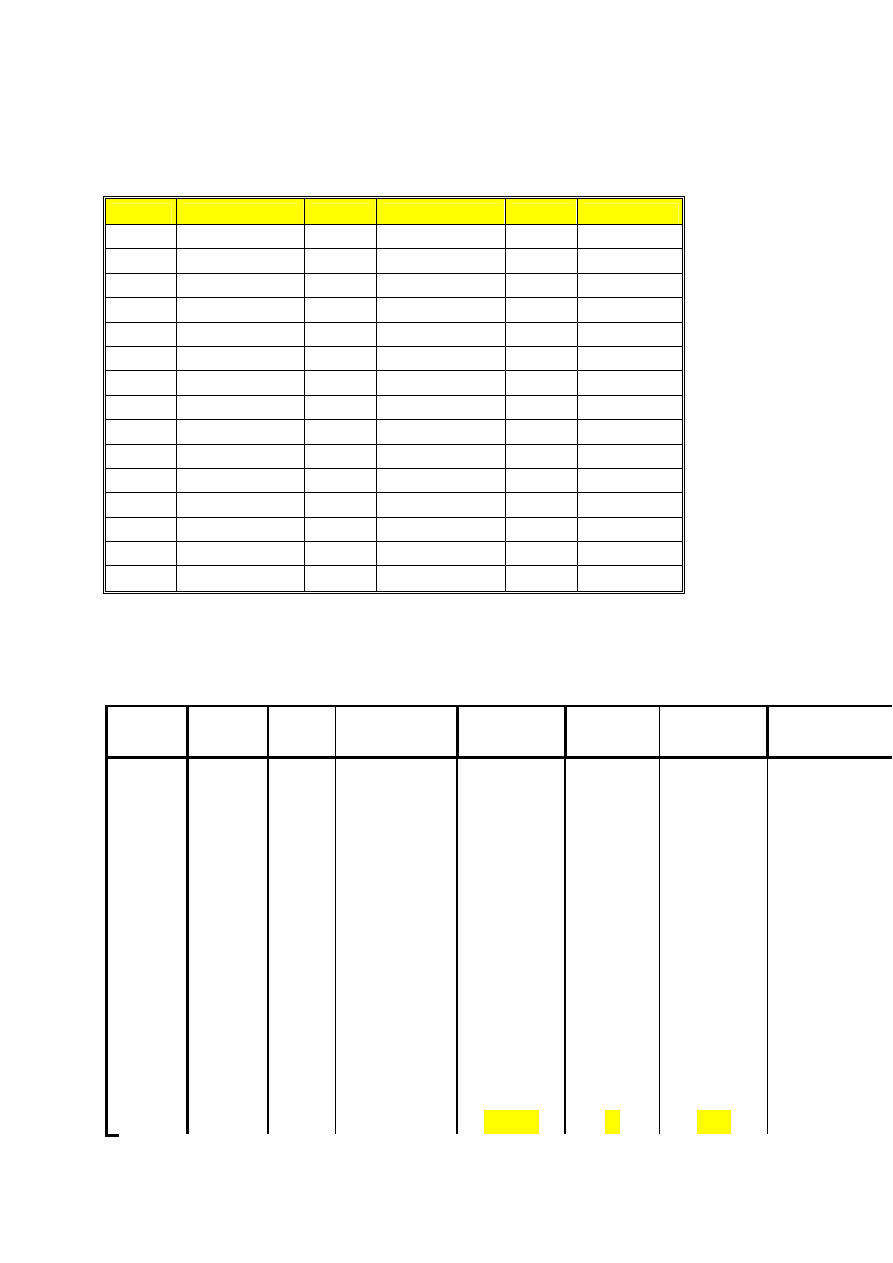
Przed rozpoczęciem wykreślania histogramu należy pogrupować dane ilościowe w
przedziały. Optymalną liczbę przedziałów klasowych dla naszych danych
wyznaczamy według następującego algorytmu:

1. Odszukujemy pomiar największy i najmniejszy

x

min

= 11

x

max

= 58

2. Wyznaczamy rozstęp (R)

R = x

max

– x

min

= 58-11 = 47

3. Wyznaczamy liczbę przedziałów (k)

k = 1 + 3,322 log n

n = 45 (liczba badanych)
log = logarytm przy podstawie 10 (liczy ten logarytm m.in. kalkulator w

„akcesoriach” w Windows)

k = 1 + 3,322 log 45 =
= 1 + 3,322 x 1,653 =
= 1 + 5,491 = 6,491

Zaokrąglamy wynik do najbliższej liczby całkowitej

: k = 6

4. Wyznaczamy szerokość przedziału (d)

d = R / k = 47/6 = 7,83

Wynik zaokrąglamy w górę:

d = 8

5. Granice przedziałów umieszcza się zwykle w połowie jednostki pomiarowej .
Tak więc w naszym przypadku dolna granica pierwszego przedziału wyniesie

10,5 (pomiar wieku został wykonany z dokładnością do 1 roku)

skumulowane

granice przedziałów

n

%

n cum % cum

10,5

18,5

8

17,78

8

17,78

18,5

26,5

9

20,00

17

37,78

26,5

34,5

4

8,89

21

46,67

34,5

42,5

16

35,56

37

82,22

42,5

50,5

6

13,33

43

95,56

50,5

58,5

2

4,44

45

100,00

suma

45

100

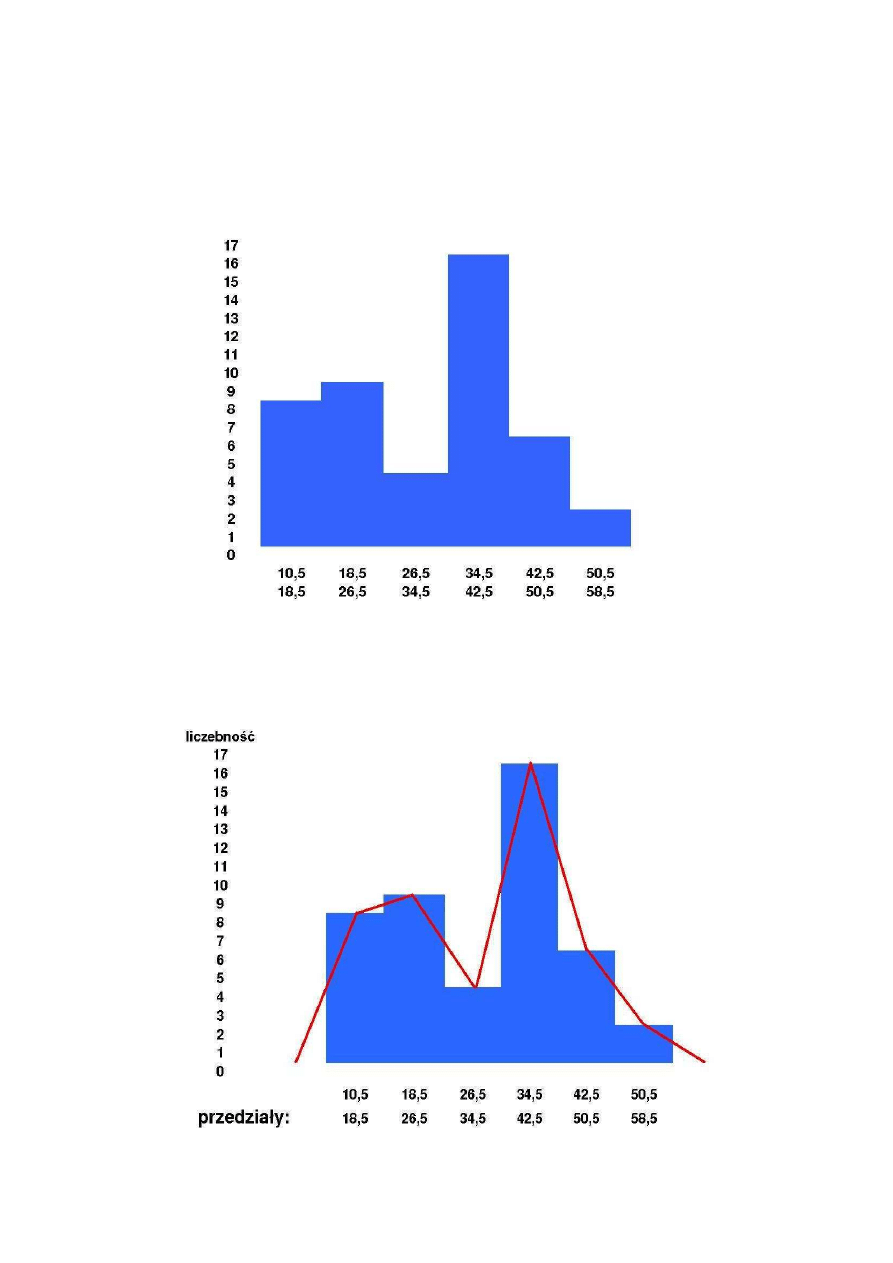
Na podstawie powyższej tabeli możemy narysować histogram ilustrujący liczebności
w poszczególnych przedziałach:

Łącząc ze sobą środki górnych boków histogramu otrzymujemy wielobok liczebności.
Pole

powierzchni

tej

figury

jest

równe

polu

powierzchni

kolumn

histogramu.