Centralne twierdzenie graniczne

Przedział ufności

Wykład V

(06.12.2010)

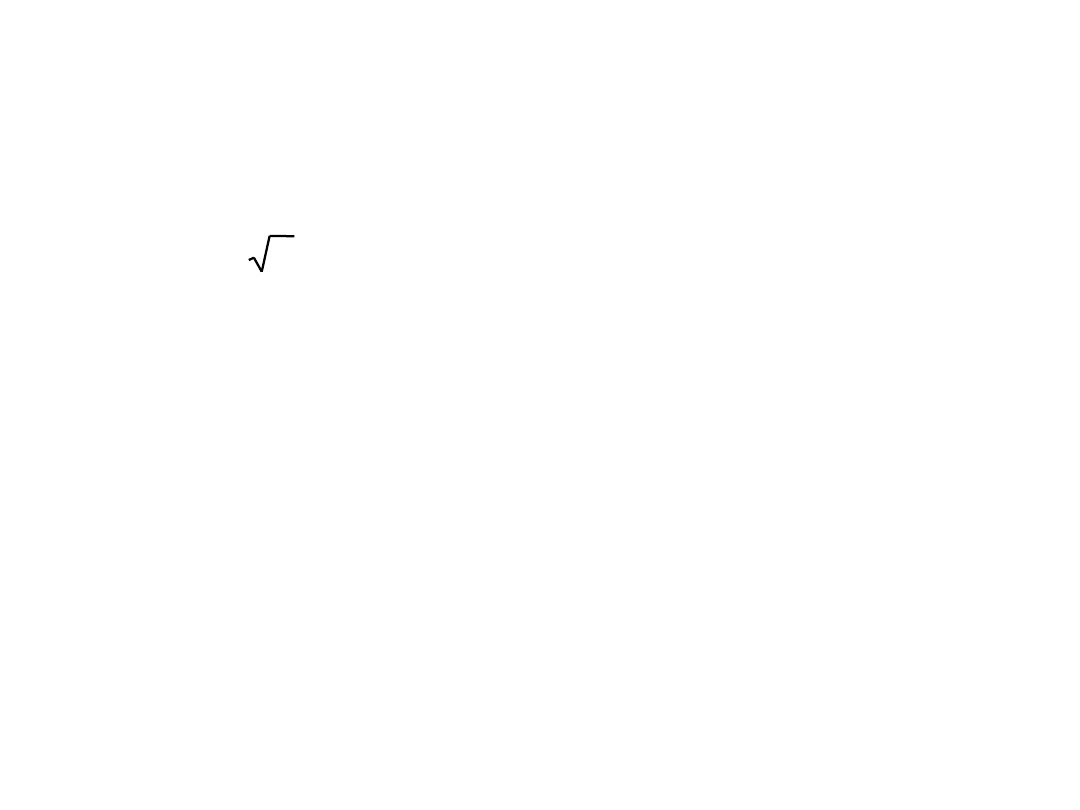
Centralne Twierdzenie Graniczne

Dla dużych prób (n>30)

m

m

=

m

s

m

=

s

/

n

Prawo wielkich liczb

Jeżeli pobieramy kolejno próby losowe o liczebności n
z populacji o dowolnym rozkładzie i o średniej

m

i wariancji

s

2

,

wtedy ze wzrostem n, rozkład statystyki dąży do rozkładu
normalnego o średniej

m

i wariancji

s

2

/n.

Co to oznacza?

Wiele zjawisk można przybliżyć rozkładem normalnym.

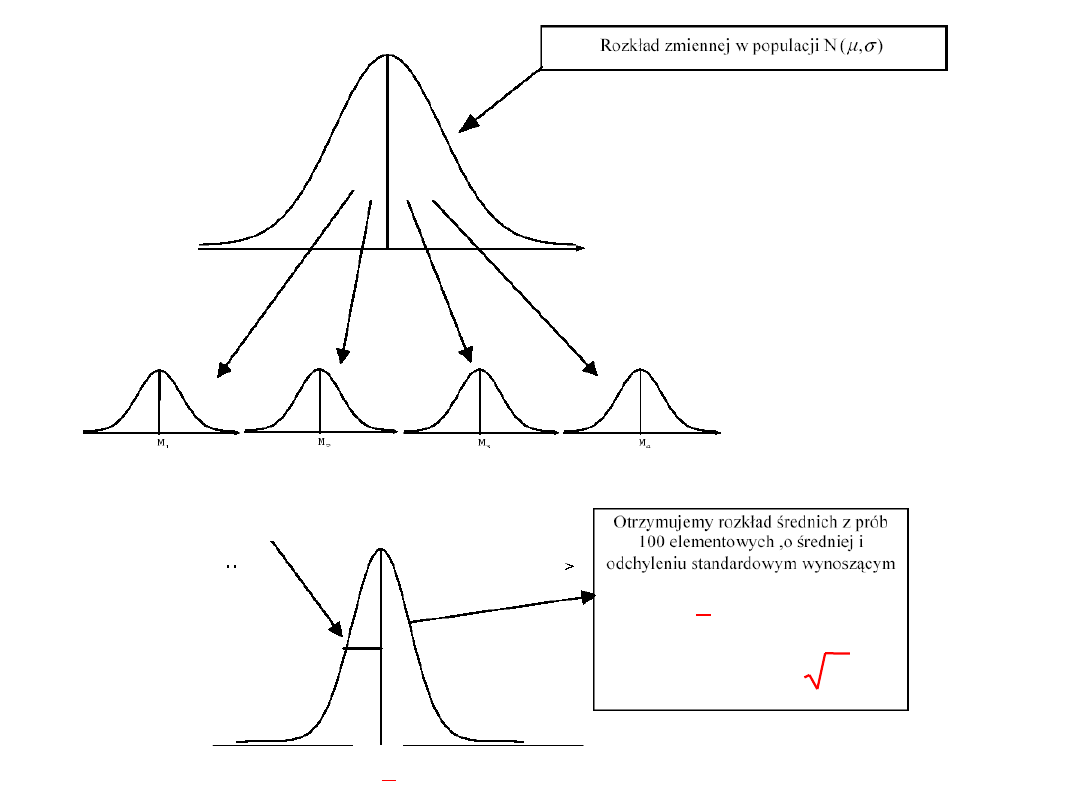
x

μ

x

s

=

s/

=m

x

μ

μ

n

Estymacja punktowa

– jest to punktowe oszacowanie

wartości szukanego parametru rozkładu.

Punktowe oszacowanie oznacza tutaj, że uzyskujemy
konkretną wartość liczbową, nie zaś przedział liczbowy,
jak dzieje się to w przypadku estymacji przedziałowej.

Metody estymacji punktowej sprowadzają się do
wyznaczenia odpowiednią metodą estymatora
szacowanego parametru.

Estymacja punktowa nie daje oceny dokładności
oszacowania nieznanego parametru



rozkładu populacji

generalnej.

Estymacja przedziałowa

– konstrukcja losowego przedziału

pokrywającego z dużym prawdopodobieństwem prawdziwą
wartość parametru populacji.

Estymator przedziałowy

jest wyznaczany przez dwie

zmienne losowe, w przeciwieństwie do estymatora
punktowego, który jest pojedynczą zmienną losową.

Przedział ufności

jest podstawowym narzędziem

estymacji przedziałowej.
Pojęcie to zostało wprowadzone do statystyki przez
amerykańskiego matematyka polskiego pochodzenia
Jerzego Spławę-Neymana.

Niech cecha X ma rozkład w populacji z

nieznanym parametrem

θ

. Z populacji wybieramy próby losowe (X

1

, X

2

, ..., X

n

), na

podstawie których wyznaczmy przedział ufności (θ - θ

1

, θ + θ

2

) o

współczynniku ufności 1-α. Przedział (θ - θ

1

, θ + θ

2

) spełnia

warunek:

P(θ

1

< θ < θ

2

) = 1 − α

gdzie θ

1

i θ

2

są funkcjami wyznaczonymi w oparciu o wyniki

otrzymane dla prób losowych.

Wzrost całej populacji studentów (

cecha X

) przybiera rozkład o

nieznanej wartości średniej (

nieznany parametr θ

).

Na podstawie pomiarów przeprowadzonych na próbach można
wyznaczyć granice przedziału ufności (

θ

1

i θ

2

).

W wyznaczonym przedziale prawdopodobieństwo występowania

nieznanego parametru θ

wynosi

1 − α

Poziom ufności - (1 – α) określa prawdopodobieństwo, że
rzeczywista wartość parametru θ w populacji znajduje się w
wyznaczonym przedziale ufności.

Im większa wartość tego współczynnika istotności α, tym
szerszy przedział ufności, a więc mniejsza dokładność
estymacji parametru. Im mniejsza wartość 1 - α, tym większa
dokładność estymacji, ale jednocześnie tym większe
prawdopodobieństwo popełnienia błędu.

Przyjmując poziom istotności 0.05, zakłada się, że w 95%
średnia z populacji mieści się w wyznaczonym na podstawie
analizy prób przedziale ufności (

θ

1

i θ

2

).

Wybór odpowiedniego współczynnika jest więc kompromisem
pomiędzy dokładnością estymacji a ryzykiem błędu.

W praktyce poziom ufności 1 - α przyjmuje zazwyczaj
wartości: 0.99; 0.95 lub 0.90, zależnie od parametru

s

.

Do wyznaczenia granic przedziału ufności przy zadanym
poziomie ufności 1- α konieczna i wystarczająca jest
znajomość rozkładu estymatora .

Zgodnie z

Centralnym Twierdzeniem Granicznym

Jeżeli pobieramy kolejno próby losowe o liczebności

n

z

populacji o wymiarze

N

i o rozkładzie normalnym, ze średnią

μ

i wariancją

s

2

, to rozkład średniej statystyki będzie

rozkładem normalnym o średniej i wariancji

s

2

/n

, pod

warunkiem, że

n/N



0.05

.

θ

x

μ

x

x

Estymacja przedziałowa średniej populacji

w przypadku dużej próby.

-

Rozmiar próby jest



30;

-

Zgodnie z centralnym twierdzeniem granicznym wartość

przyjmuje rozkład normalny niezależnie od rozkładu w populacji;

-

Na podstawie powyższego twierdzenia odchylenie standardowe

wartości wynosi

s = s

/

;

-

Jeżeli odchylenie standardowe populacji, tzn. jest wartością

nieznaną, w takiej sytuacji używa się odchylenia standardowego
próby

s = s/

.

W tym przypadku

s

jest estymatorem

punktowym

s

;

x

x

x

x

n

s

x

n

x

Przedział ufności parametru

μ

dla dużej próby

Dla (1-

a

)100% poziomu ufności przedział ufności wynosi:

jeżeli jest znane

lub

jeżeli jest nieznane

gdzie

x z

x

±

s

s

x z

x

± s

s

n

x

s

=

s/

n

x

s = s

/

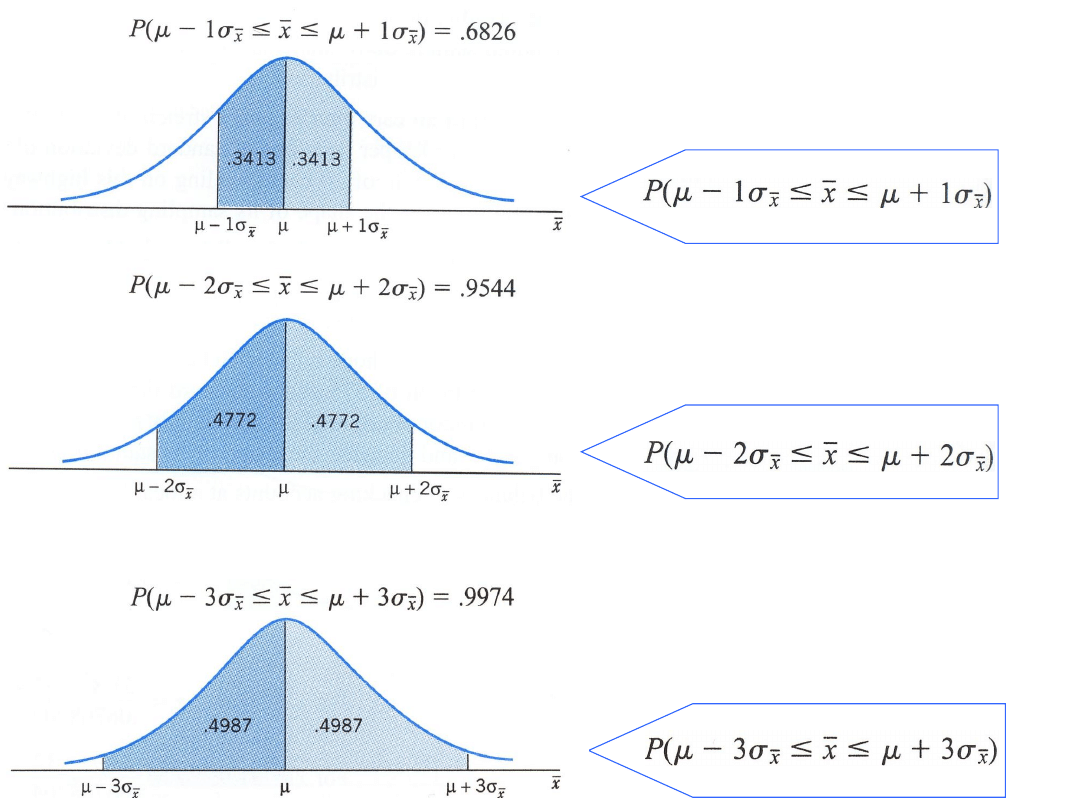
Zacieniowana powierzchnia

0.6826

Zacieniowana powierzchnia

0.9544

Zacieniowana powierzchnia

0.9974

m

x

z

.

s

x

_

x

_

=

m

x

+ z

·

s

x

_

_

x

x

x

x-

m

z=

s

Wielkość , lub jeżeli jest nieznane,
w wyrażeniu na przedział ufności nosi nazwę
maksymalnego błędu estymacji, E.

Jest to wielkość, o która jest pomniejszana i powiększana
wartość w celu uzyskania przedziału ufności dla zmiennej

Wartość

z

w wyrażeniu na przedział ufności pochodzi z tabeli

dystrybuanty rozkładu normalnego przy założonym poziomie
ufności

1-

a

.

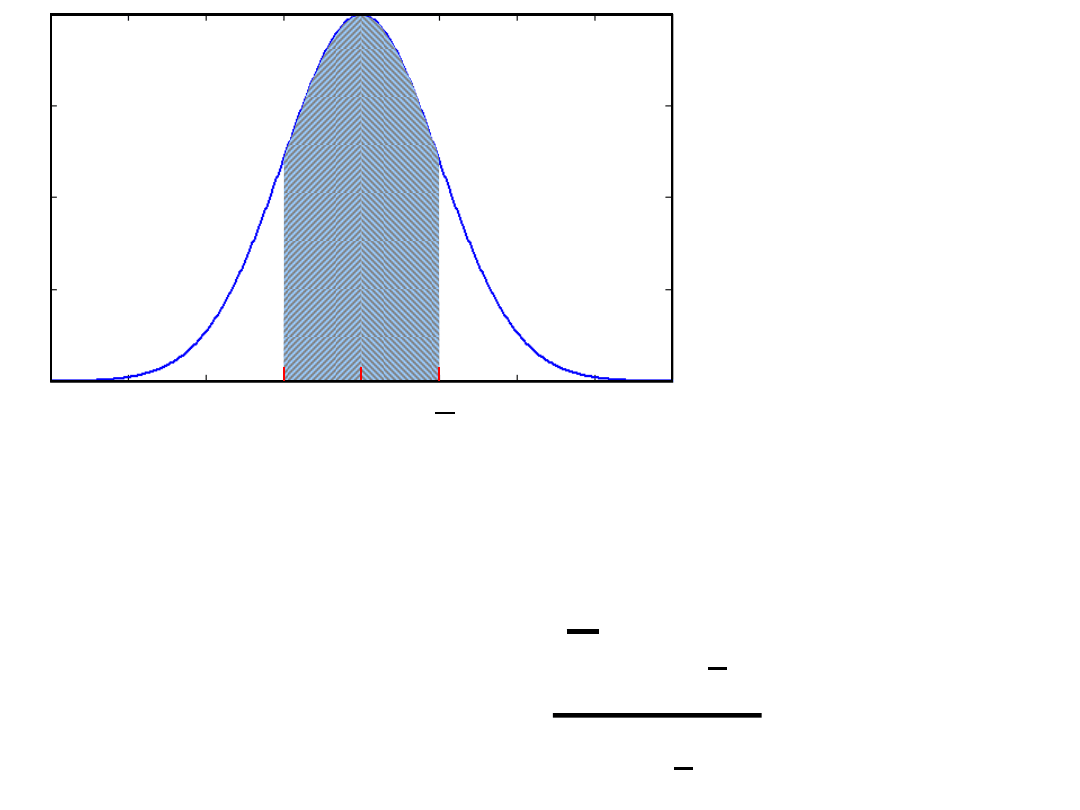
Sposób konstruowania 95% przedziału ufności dla parametru

z

x

s

z

x

s

s

x

m

.

m

.

95% przedział ufności oznacza, że całkowita powierzchnia
pod krzywa rozkładu normalnego dla estymatora
pomiędzy dwoma punktami wynosi 95%.

W celu obliczenia wartości

z

dla założonego przedział

ufności należy podzielić przez 2, tzn. 0.95/2=0.4750

x

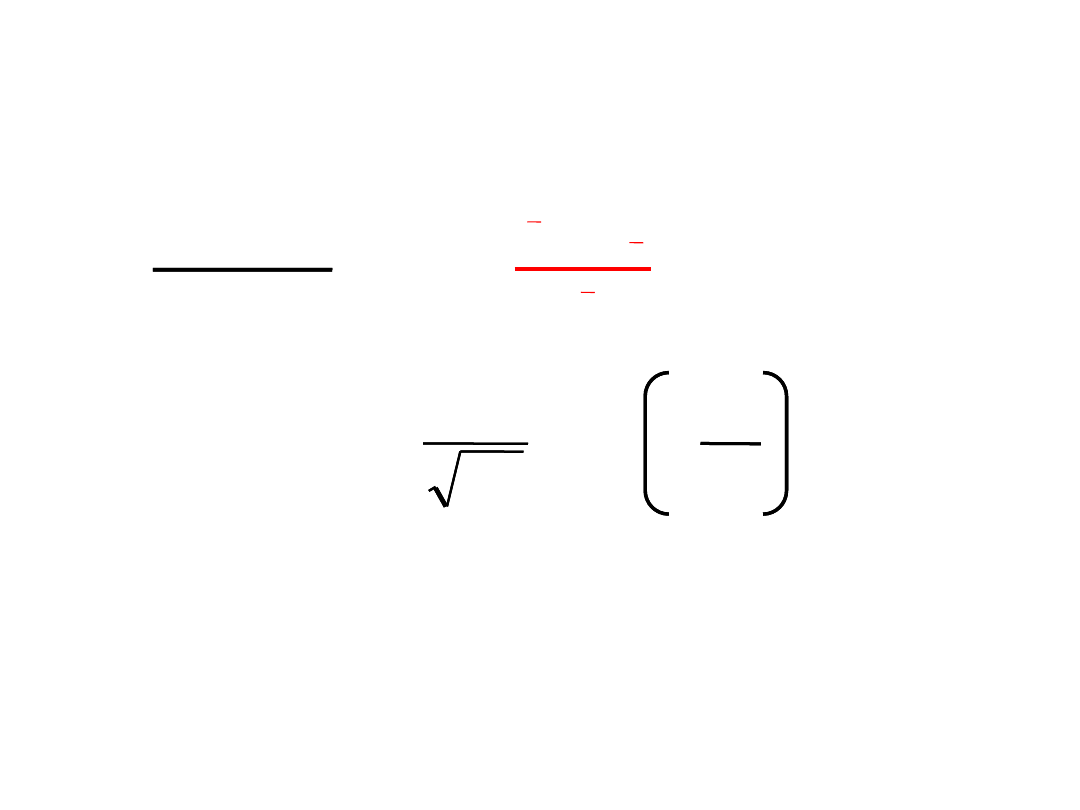
z

Zmienną losową X zastępujemy

zmienną standaryzowaną z

,

która ma

rozkład N(0,1)

z = zmienna standaryzowana

(

)

-

p

=

2

z

exp

2

1

1

,

0

;

f

2

m

-

=

z

)

-

p

=

2

exp

2

1

,

;

f

2

x

x

s

s

m

-

=

x

u

s

x

x

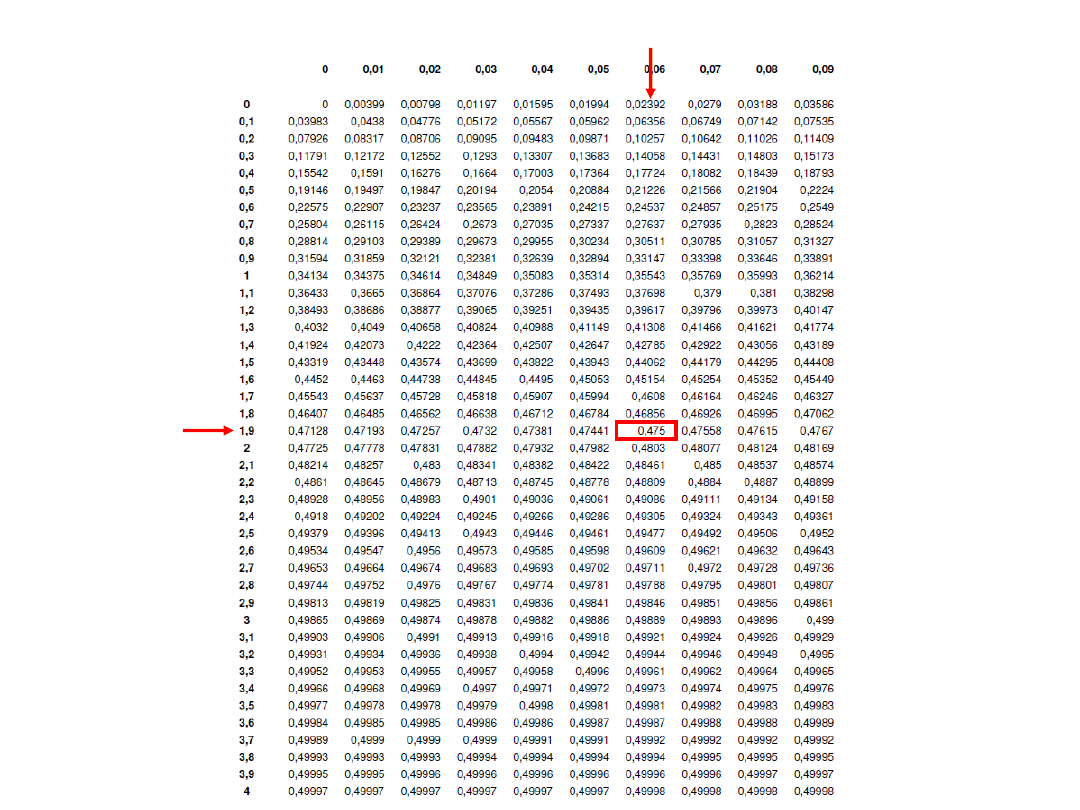
Z

z

Powierzchnia pod krzywa rozkładu normalnego N(0,1) od 0 do z

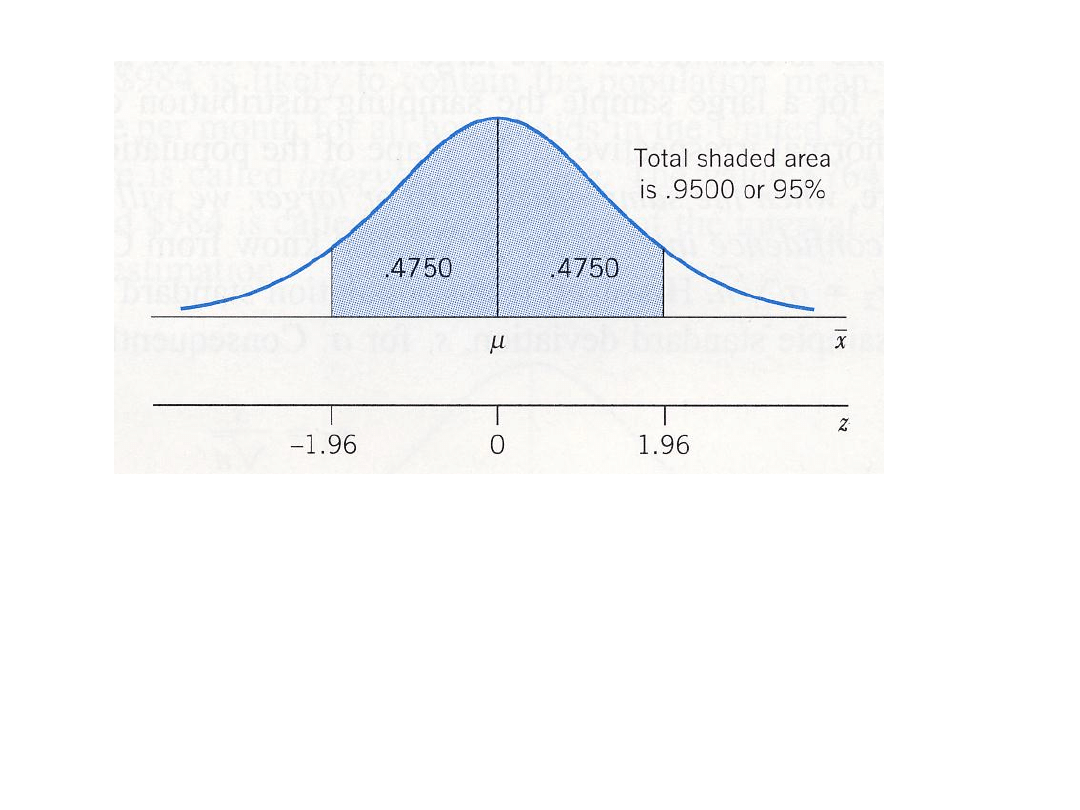
N(0,1)

Zacieniowana powierzchnia
wynosi 95% całkowitej powierzchni

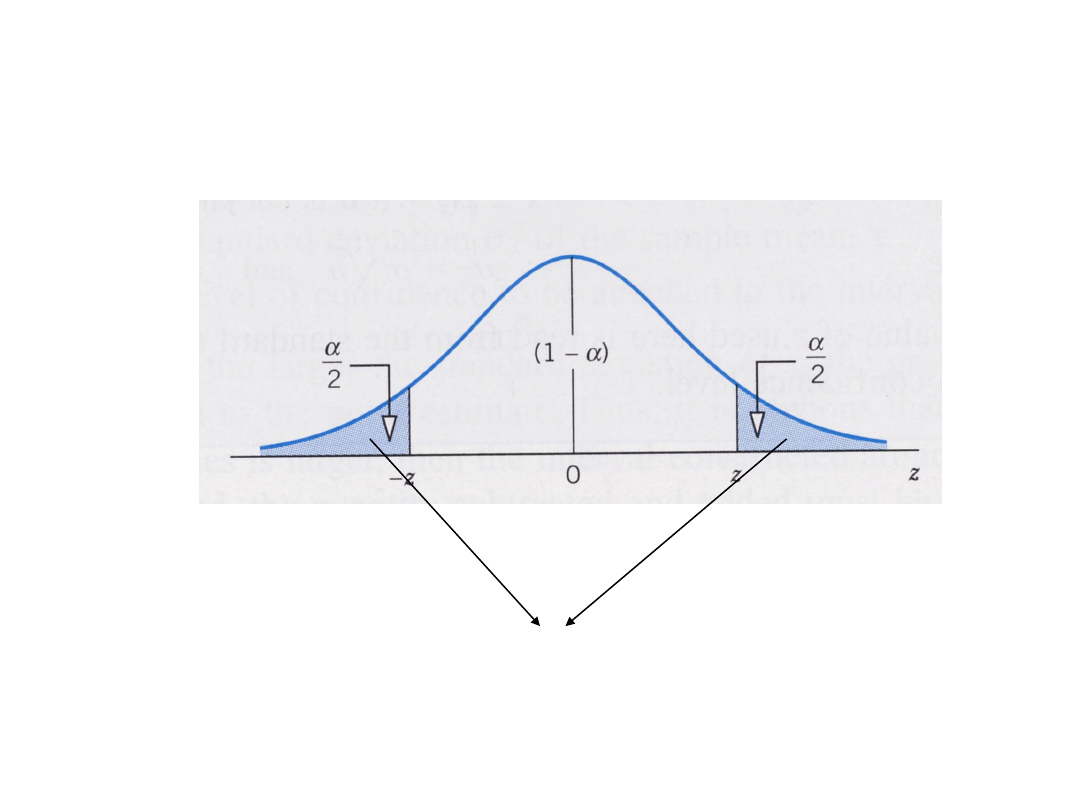
Powierzchnia na skrzydłach

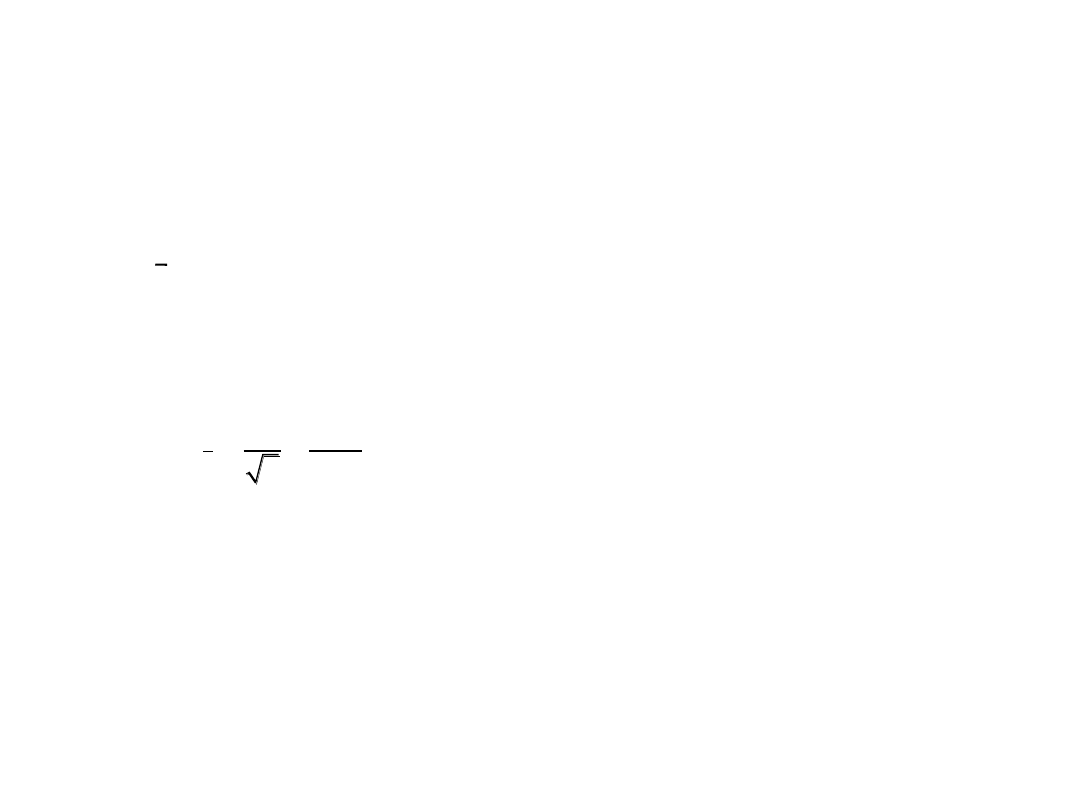
Wydawnictwo planowało wydać nowy podręcznik akademicki. Zanim podjęto

decyzję o cenie postanowiono przeanalizować rynek. W tym celu pracownicy

wydawnictwa wybrali losowo 36 podręczników i przeprowadzili analizę ich ceny.

Wartość średnia wyniosła $70.50. Ponadto dotarli do informacji, że odchylenie

standardowe dla wszystkich podręczników wynosi $4.5.

n=36;

-

Podaj estymator punktowy średniej ceny wszystkich podręczników. Ile wynosi

wartość maksymalnego błędu estymacji, przy założeniu 95% przedziale ufności?

Wynik= $70.5 i $1.47

Podaj z 90% prawdopodobieństwem granice przedziału dla wartości średniej

wszystkich książek.

Wynik= od $69.26 do $71.74

x=$70.50;

s

=$4.50

s

s

=

x

4.50

=

=

= 0.75; margines bl

ędu ±1.96 * (0.75)

6

n

Testowanie hipotez składa się z następujących etapów:

1. Przyjęcie założeń;

2. Otrzymanie rozkładu z próby;

3. Wyznaczenie poziomu istotności i obszaru krytycznego;

4. Wyliczenie statystyki testu;

5. Podjecie decyzji.