Informatyka II

Chemia biologiczna

Wykład 1 (26.09.2011)

Godz. 14

00

-15

30

Egzamin ko cowy!!!

1.

1.

Wprowadzenie do statystyki.

Wprowadzenie do statystyki.

2.

2. Statystyka opisowa – rodzaje i sposoby obliczania

parametrów statystycznych.

3.

3. Poj cie prawdopodobie stwa, generowanie zmiennych

losowych, funkcje g sto ci rozkładu prawdopodobie stwa

4.

4. Wizualizacja danych statystycznych.

5.

5. Techniki wnioskowania statystycznego – testowanie hipotez

6.

6. Analiza zale no ci zmiennych ilo ciowych – podstawy

korelacji i regresji.

7.

7. Regresja wieloraka.

1)

Marek Dobosz „Statystyczna analiza wyników bada ”

Akademicka Oficyna Wydawnicza EXIT, Warszawa 2001

2)

Andrzej Stanisz „Przyst pny kurs statystyki”

StatSoft, Kraków 2006

3)

Adam Łomnicki „Wprowadzenie do statystyki dla przyrodników”

PWN, Warszawa 2007

4)

Jacek Koronacki, Jan Mielniczuk „Statystyka dla studentów kierunków

technicznych i przyrodniczych”,

Wydawnictwo Naukowo-Techniczne, Warszawa 2006

5)

Wiesława Regiel „Statystyka matematyczna w programie Matlab”

PWN, Warszawa 2007

6)

Daniel T. Larose „Odkrywanie wiedzy z danych”

PWN, Warszawa 2006

Statystyka

Nauka zajmuj ca si :

zbieraniem,

organizacj ,

prezentacj i

analiz danych, oraz

wyci ganiem wniosków i

podejmowaniem decyzji

na ich podstawie.

Dyscyplina naukowa

Liczby opisuj ce fakty

na II r. ChB jest 67 studentów,

rednia ocen ostatniej sesji dla

II r. ChB wyniosła 3.8,

2 studentów nie uzyskało

zaliczenia z laboratorium

z podstaw chemii.

Podział statystyki jako dyscypliny naukowej na:

• statystyk teoretyczn

i

• statystyk stosowan

.

Podział

statystyki stosowanej

na:

•

statystyk opisow opart na zestawie metod

stosowanych w organizacji, prezentacji

i opisie danych poprzez tabele, wykresy

i sumaryczne miary.

•

statystyk wnioskowania indukcyjnego opart na

zestawie metod, które pozwalaj na podstawie wyników

dla próby podj

decyzj lub przewidzie wyniki

dla

populacji.

pr

pr

ó

ó

by

by

populacji

populacji

Populacja (populacja generalna)

- zbiór wszystkich

elementów b d cych przedmiotem bada statystycznych.

Przykład

: Badania demograficzne - spis powszechny.

Próba

– cz

populacji wybrana do bada statystycznych.

Przykład

: Badania opinii publicznej na przykładzie

grupy respondentów.

Próba reprezentatywna dane reprezentacyjne (ankieta).

Próba reprezentatywna - poszczególne cechy populacji s

poprawnie oszacowane na podstawie próby.

Przykładowo, po wylosowaniu próby spo ród wszystkich

osób maj cych prawo głosu (populacja), ankieter b dzie

chciał oszacowa z pewn dokładno ci poparcie dla partii

politycznych w całej populacji.

Próba

Populacja

Spis, pełne badanie statystyczne

Ankieta

Reprezentatywna

– próba, której cechy s

maksymalnie podobne do cech opisuj cych populacj .

Wybór losowy

- próba wygenerowana przy zało eniu,

e ka dy element populacji ma tak sam szans by

wylosowanym. Struktura takiej próby jest podobna do

struktury całej populacji. Wraz ze wzrostem liczebno ci

próby wzrasta jej stopie reprezentatywno ci.

Techniki losowania w wyborze losowym

Losowanie niezale ne (zwrotne)

– po ka dym

losowaniu element wraca do populacji.

Losowanie zale ne (bezzwrotne)

– po ka dym

losowaniu element nie wraca do populacji, tzn.

nie bierze udziału w dalszym losowaniu.

Metoda stosowana w przypadku małych populacji.

Wła ciwo ci próby:

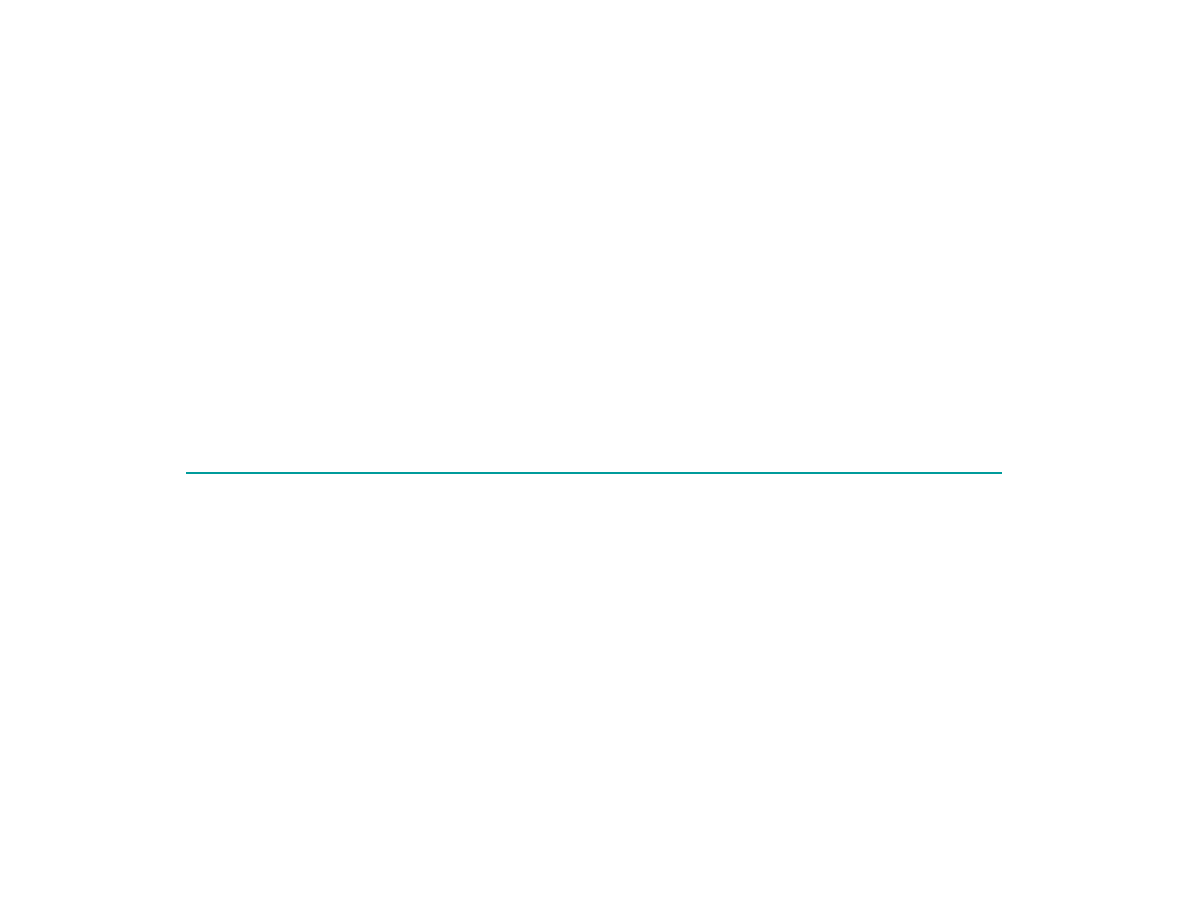
http://www.sjc.edu/rdegray/Math110F03/applets/randomsample.html

Zakład prosty polega na wytypowaniu przez graj cego

6 liczb ze zbioru liczb od 1 do 49

Na wiczenia:

Ka dy student przygotowuje,

opisuje na kartce

,

propozycj dla populacji i próby.

• W

opisie statystycznym

analizujemy badan

populacj lub prób za pomoc odpowiednich

miar.

• Wnioskowanie statystyczne

dotyczy bada

reprezentatywnych przeprowadzonych na

próbie losowej.

• Wyniki s uogólniane na cał populacj

generaln , z której pobrano prób .

Element

Specyficzny obiekt, dla którego s gromadzone informacje.

Zmienne

Ró ne warto ci posiadane przez ró ne

elementy

.

Obserwacja/opis/pomiar/

Rejestracja warto ci

zmiennych

elementów.

Zestaw danych

Zestaw danych

pomiarowych/obserwacji

dla jednej lub wielu zmiennych.

4.5

Paweł

4.1

Mirek

4.3

Zosia

3.8

Jurek

4.7

Anka

rednia

Student

5 elementów

Jedna zmienna

5 obserwacji/pomiarów

Przykład zestawu danych dla 5 elementów opisanych jedn zmienn .

Zmienne

- to wielko ci, które mierzymy, kontrolujemy

lub którymi manipulujemy w trakcie bada .

Zmienne

Ilo ciowe

Dyskretne

- liczba domów,

- liczba wypadków,

- liczba wylosowanych

oczek, itp.

Ci głe

- długo ,

- wiek,

- czas, itp.

Jako ciowe

- specjalno

na

kierunku chemia,

- kolor włosów,

- płe

Zmienne jako ciowe

(nazywane równie kategorycznymi,

czynnikowymi), to zmienne przyjmuj ce okre lon liczb

warto ci, najcz ciej nieliczbowych,

-

binarne

, np. płec (kobieta/m czyzna),

-

nominalne

, np. marka samochodu,

-

porz dkowe

, np. wykształcenie (podstawowe / rednie /

wy sze).

Zmienne ilo ciowe

, opisuj ilo . Wyró nia si skale:

-

licznikowa

(liczebno

wyst pie pewnego zjawiska,

opisywana przez liczby naturalne), np. liczba lat nauki,

-

przedziałowa

(nazywana te interwałow ), skala w której

zmienna mo e przyjmowa dowolne warto ci z okre lonego

przedziału, np. temperatura w stopniach Celsjusza,

-

ilorazowa

, to skala licznikowa, w której dodatkowo

zachowane s proporcje (a wi c skala ma zero absolutne),

np. temperatura w stopniach Kelvina, wzrost w

centymetrach itp.

Przykład zestawu danych gdzie do opisu 10 elementów wybrano 2 zmienne (m,f)

2

5

5

4

7

9

9

10

7

3

7

f

6

2

1

8

4

4

8

6

3

m

Nale y obliczy nast puj ce warto ci:

mf

2

;

(

m

)

2

; f

2

;

(

mf

)

2

f

2

m

2

m

f

2

m

f

m

2

f

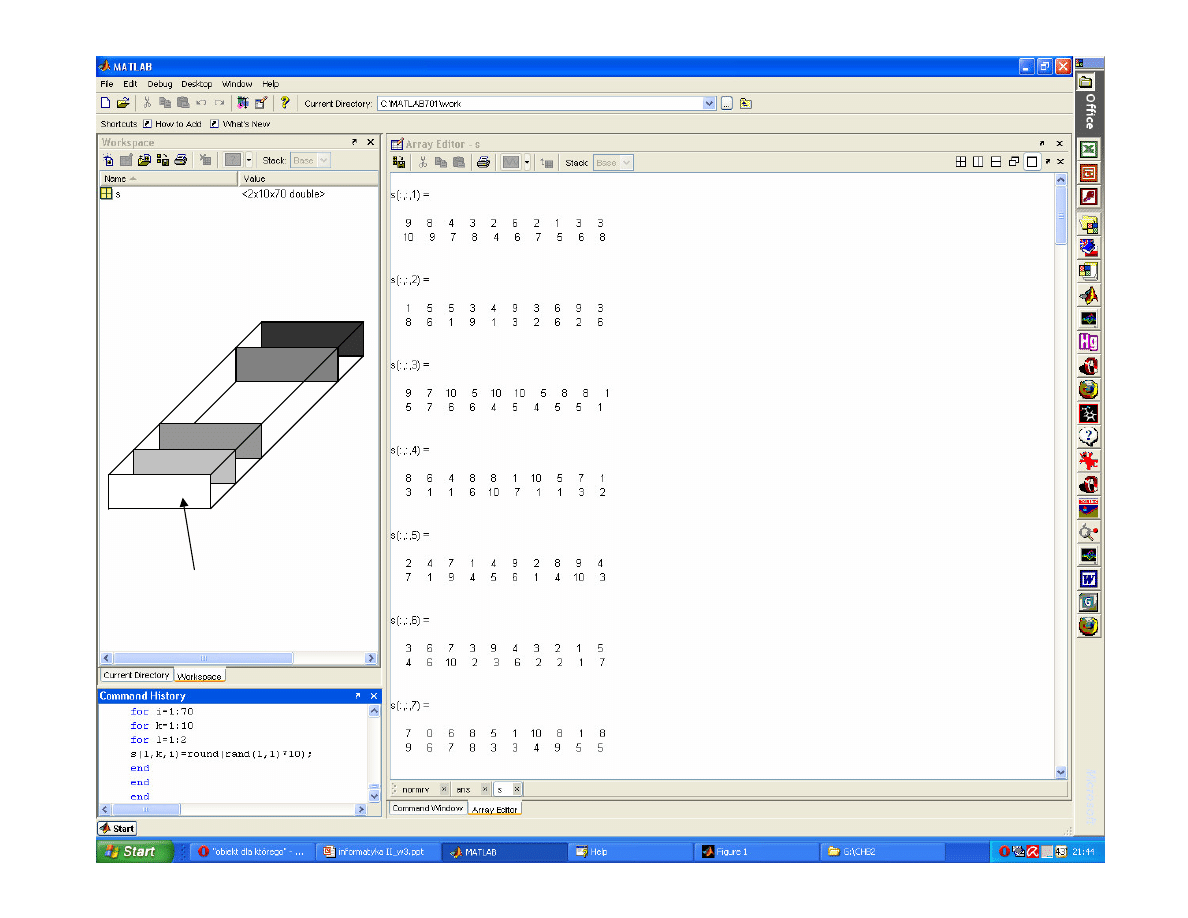
for

i=1:70

for

k=1:10

for

l=1:2

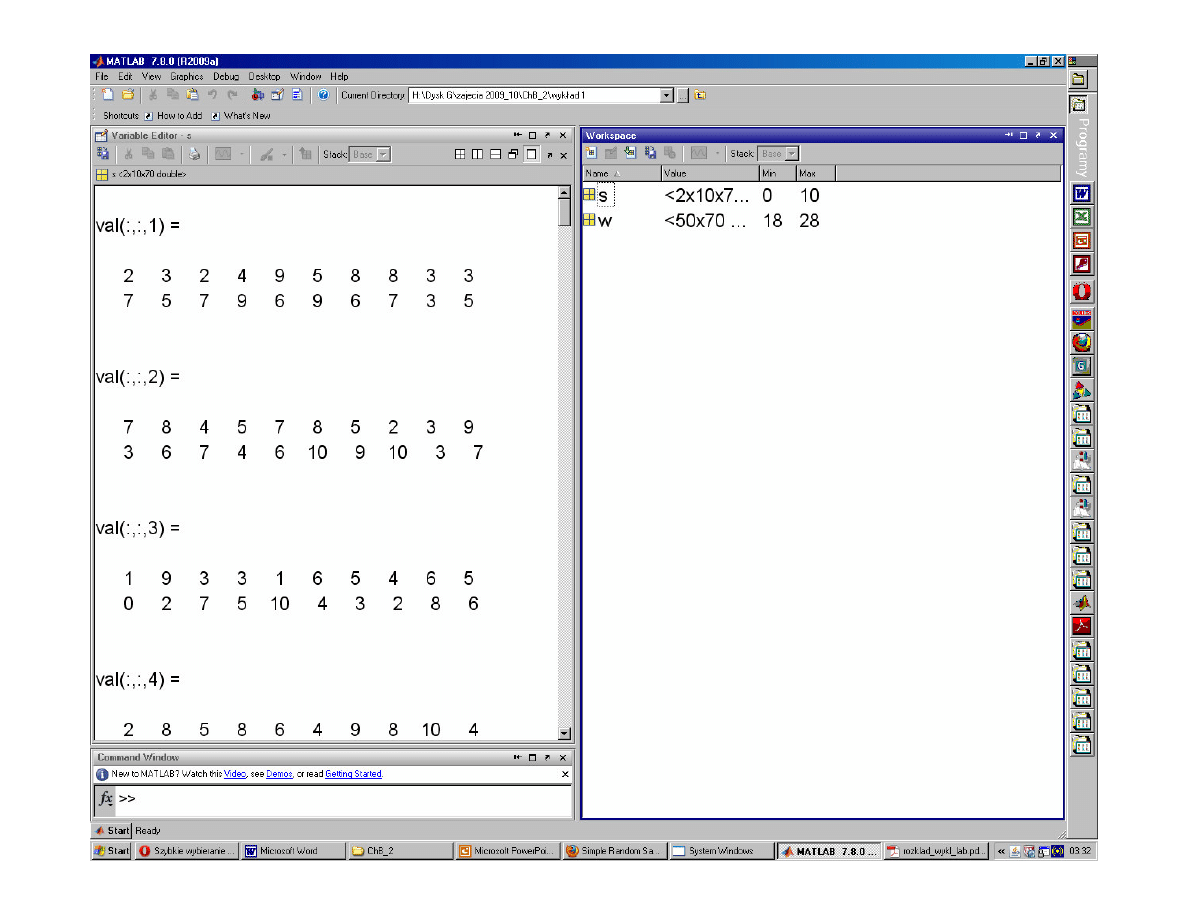
s(l,k,i)=

round

(

rand

(1,1)*10);

end

end

end

2x10x

1

2x10x

2

2x10x

3

2x10x

69

2x10x

70

Macierz

s

tensor

Numer na li cie obecno ci

na wykładzie

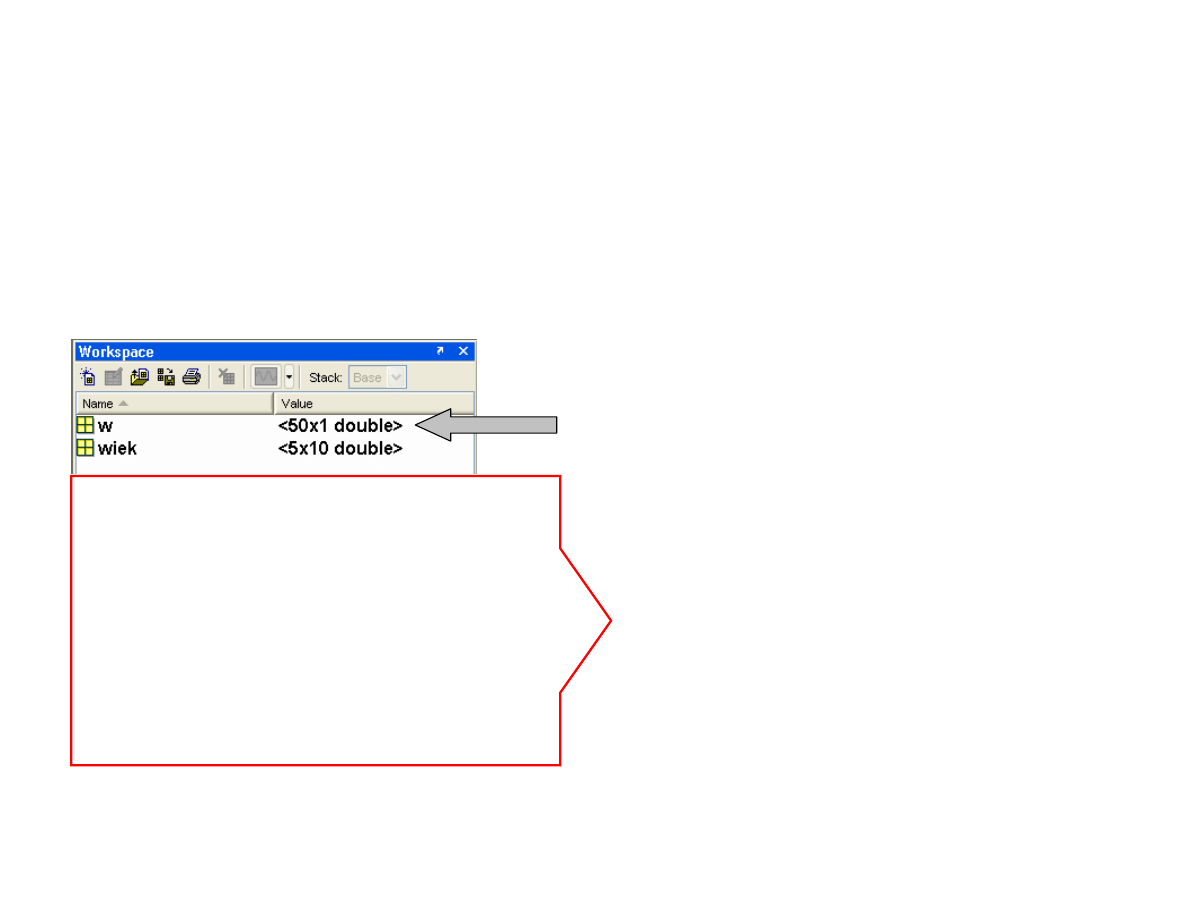
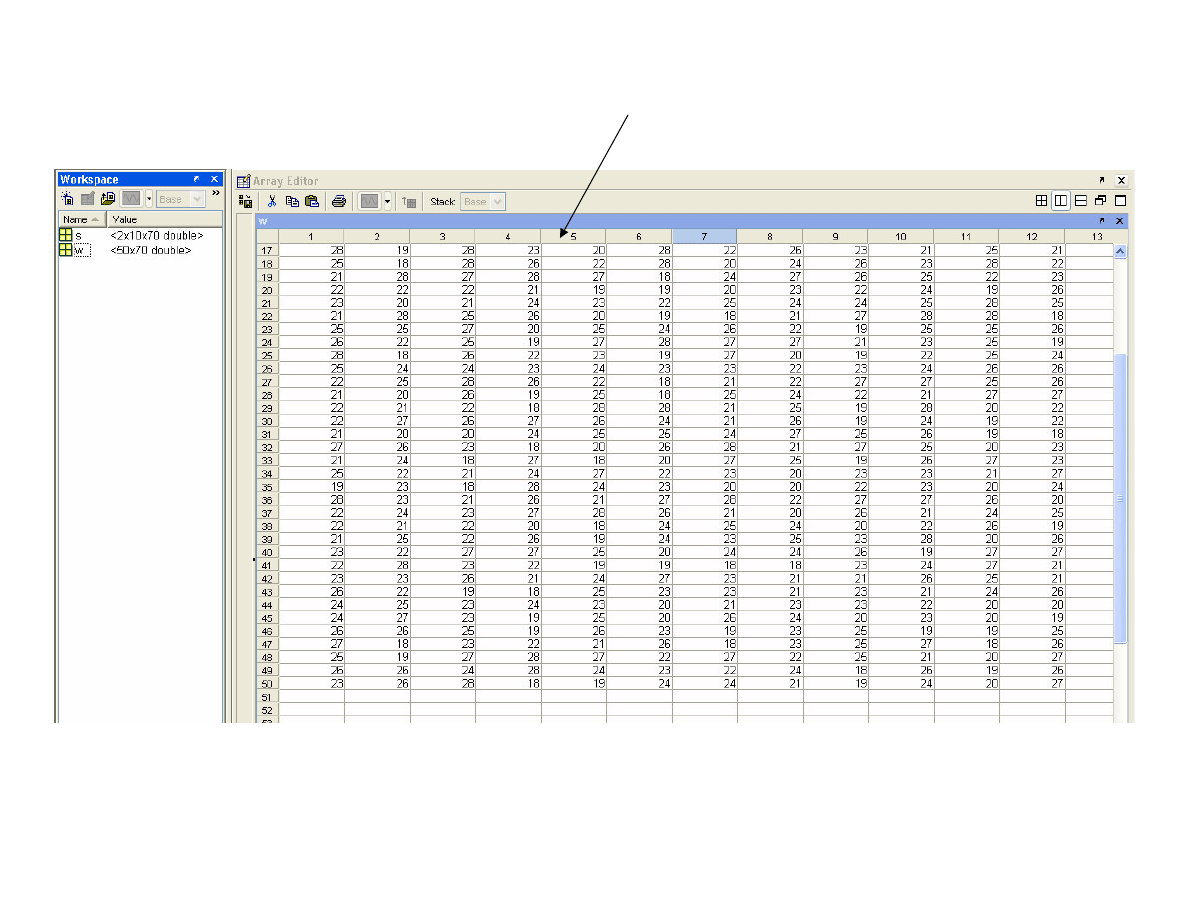
Analiza danych pierwotnych (raw data)

Dane pierwotne

– dane zapisane w kolejno ci gromadzenia

przed zastosowaniem jakiekolwiek procedury porz dkuj cej.

>> w=(round(rand(1,50)*10)+18)';

>> wiek=reshape(w,5,10)

wiek =

26 19 20 24 21 23 26 26 21 27

25 19 19 18 24 21 25 22 23 21

26 24 22 25 27 19 20 23 24 28

18 19 19 26 20 21 26 22 28 24

22 24 28 27 22 20 22 24 22 22

>> wiek=reshape((round(rand(1,50)*10)+18)',5,10)

wiek =

23 22 25 27 19 25 23 19 19 20

20 24 18 26 28 22 27 26 23 25

23 23 24 26 23 23 27 26 24 24

24 27 28 22 24 27 21 22 26 24

24 20 27 21 26 22 23 22 21 21

Zmienna ci gła, ilo ciowa

Przykład: 50 studentów spotkanych w klubie Wydziału Chemii podało swój wiek

kolumna

>> w=

reshape

(

sort

(wiek(:)),10,5)'

w =

18 18 19 19 19 19 19 19 20 20
20 20 21 21 21 21 21 22 22 22
22 22 22 22 22 23 23 23 24 24
24 24 24 24 24 25 25 25 26 26
26 26 26 26 27 27 27 28 28 28

Rozkład cz sto ci zmiennych

– liczebno

zbioru danych w poszczególnych

kategoriach/klasach.

Nale y:

- uporz dkowa rosn co warto ci zmiennej;

- zliczy liczb wyst pie warto ci według kategorii/klas;

- obliczy cz sto

wyst powania dla ka dej kategorii/klasie;

>> k=0;

>> for i=min(wiek(:)):max(wiek(:))

k=k+1;

f(k)=sum(wiek(:)==i);

end

>>

>> sum(f)

ans =

50

>> klasa=min(wiek(:)):max(wiek(:))

klasa =

18 19 20 21 22 23 24 25 26 27 28

>> rozklad=[klasa;f]

rozklad =

18 19 20 21 22 23 24 25 26 27 28

2 6 4 5 8 3 7 3 6 3

3

Liczba osób w danym wieku

Liczba wyst pie warto ci zmiennej w danej klasie

Liczba wyst pie wszystkich warto ci zmiennej

Wzgl dna cz sto

klasy

=

>> rozklad

rozklad =

18

19 20 21 22 23 24 25 26 27 28

2 6 4 5 8 3 7 3 6 3 3

0.04 0.12 0.08 0.1 0.16 0.06 0.14 0.06 0.12 0.06 0.06

4

12 8 10 16 6 14 6 12 6 6

Procentowa wzgl dna cz sto

klasy= Wzgl dna cz sto

klasy * 100

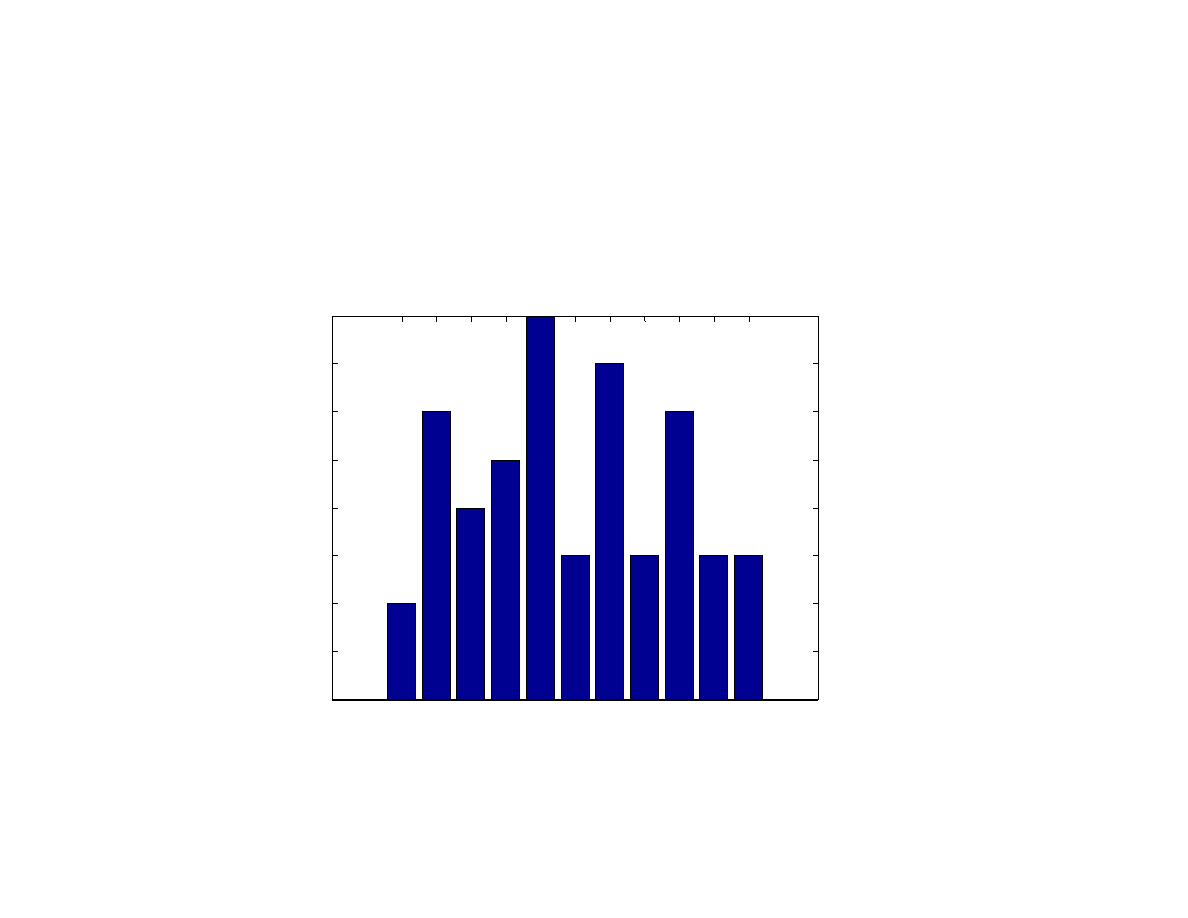
>> bar(rozklad(1,:),rozklad(3,:))

18

19

20

21

22

23

24

25

26

27

28

0

0.02

0.04

0.06

0.08

0.1

0.12

0.14

0.16

klasa (wiek)

W

zg

l

dn

a

cz

st

o

kl

as

y/

lic

ze

bn

o

kl

as

y

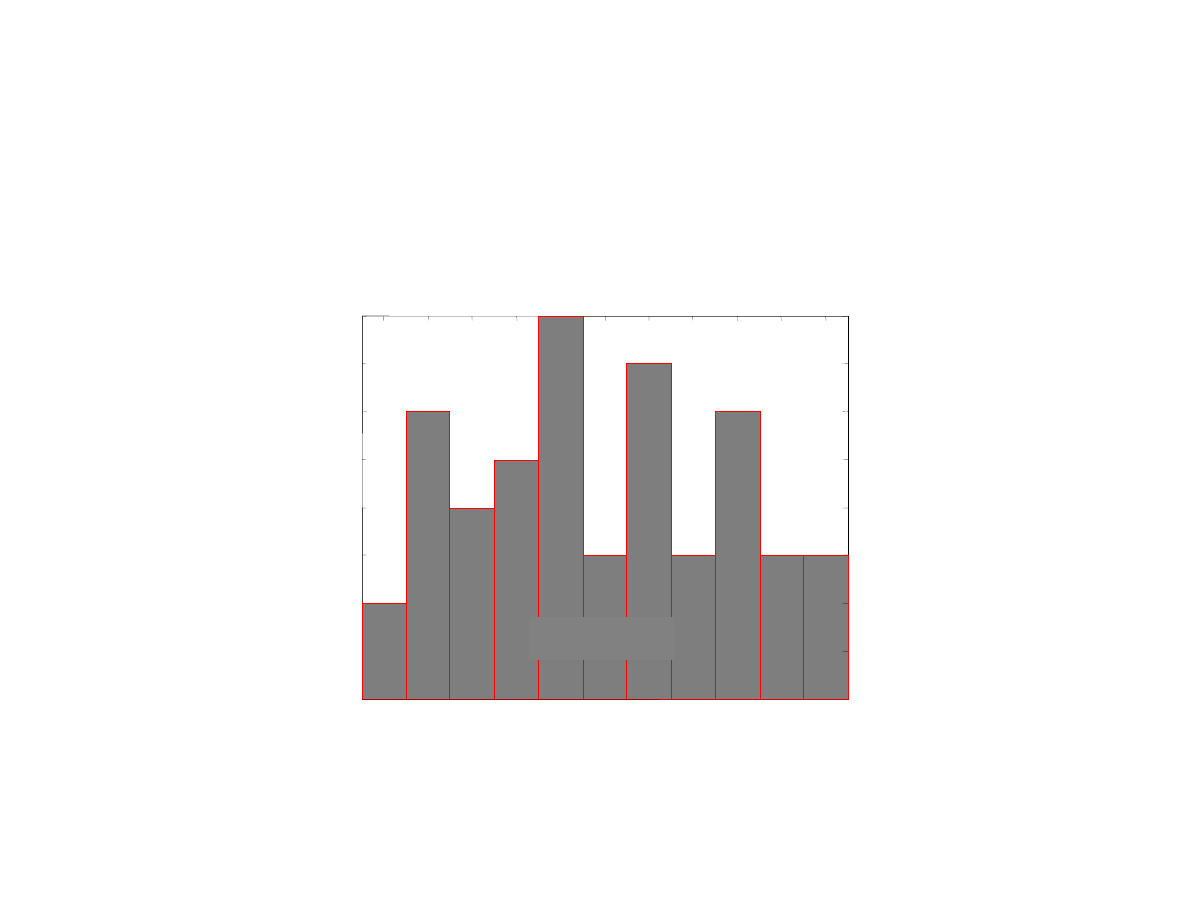
>> bar(rozklad(1,:),rozklad(4,:),

1

);axis tight

Klasa (wiek)

W

zg

l

dn

a

cz

st

o

kl

as

y/

lic

ze

bn

o

kl

as

y

18

19

20

21

22

23

24

25

26

27

28

0

2

4

6

8

10

12

14

16

Histogram

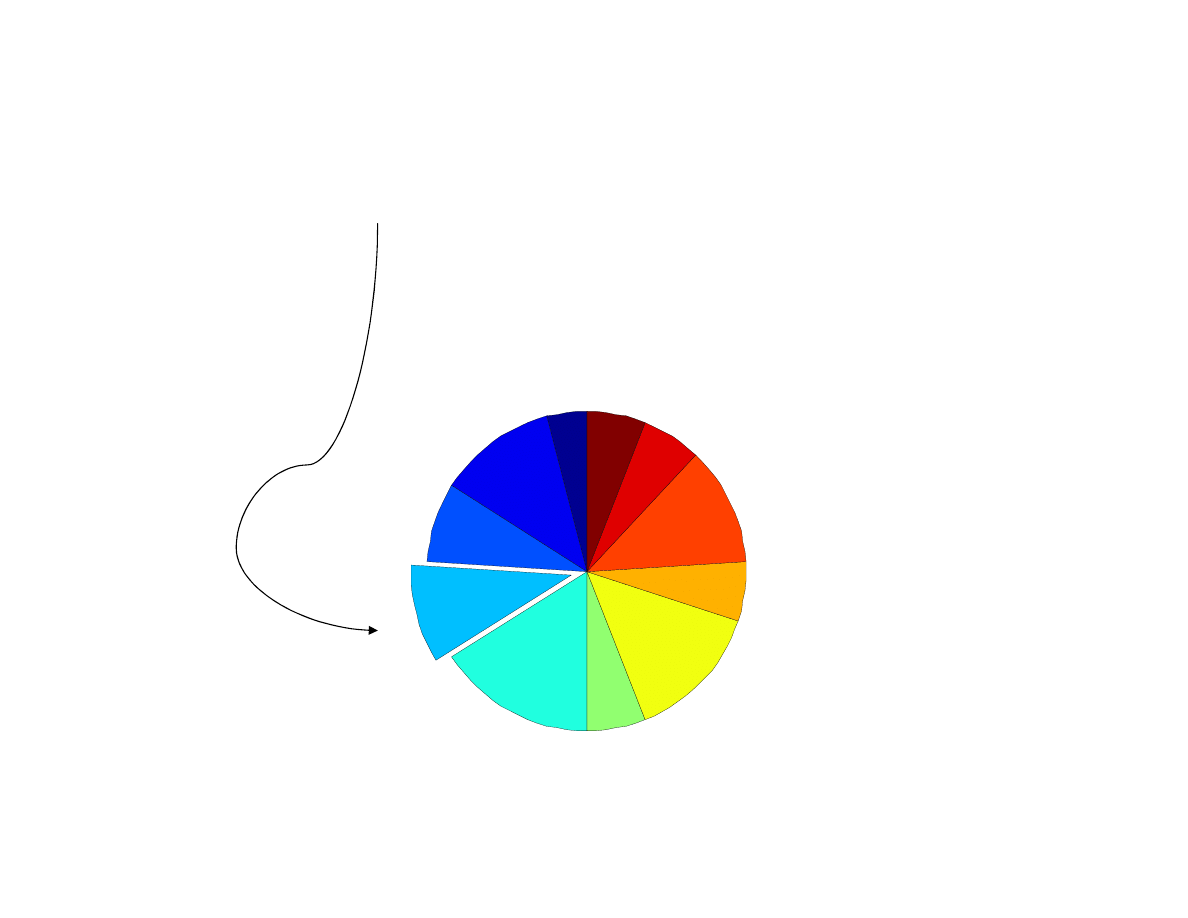
>> pie(

rozklad(3,:)

,

[0 0 0 1 0 0 0 0 0 0 0]

,

{'18' ,'19','20','21','22','23','24','25','26','27','28'}

)

18

19

20

21

22

23

24

25

26

27

28

Numer na li cie obecno ci

na wykładzie