
Autor: Martin Slota
Zdroj: http://www.zones.sk
Používanie materiálov zo ZONES.SK je povolené bez
obmedzení iba na osobné ú
č
ely a akéko
ľ
vek verejné
publikovanie je bez predchádzajúceho súhlasu zakázané.
1/3
MATURITNÉ PRÍKLADY Z MATEMATIKY
M
ATURITNÝ OKRUH
14:
D
ERIVÁCIE
1. príklad (150/Pr. 2)
Zadanie: Nájdite valec s povrchom
2
cm
100
, ktorý má najvä
č
ší objem.
Riešenie:
r
r
v
rv
r
S
π
π
π
π
2
2
100
2
2
2
2
−
=
⇒
+
=
( )
∞
∈
−
=
−
=
=
,
0
50
2
2
100
3
2
2
2
r
r
r
r
r
r
v
r
V
π
π
π
π
π
( )
2
3
50
'
r
r
V
π
−
=
( )
π
3
50
0
'
=
⇔
=
r
r
V
( )
⇒
<
−
=
0
6
''
r
r
V
π
v bode
π
3
50
=
r
je lokálne maximum. Ke
ď
že funkcia
V
rastie na intervale
π
3
50
,
0
a klesá na intervale
∞
,
3
50
π
, je v bode
π
3
50
=
r
aj globálne maximum.
r
v
2
6
20
3
50
2
3
50
2
100
=
=
−
=
π
π
π
π
π
Spomedzi všetkých valcov s povrchom
2
cm
100
má najvä
č
ší objem valec s polomerom
π
3
50
=
r
a výškou
r
v
2
=
.
2. príklad (153/8)
Zadanie: Nájdite globálne extrémy funkcie
x
x
y
f
2
:
=
na intervale
(
2
,
0
.
Riešenie:
Platí:
x
e
x
ln
=
.
( )
x
x
x
x
e
e
y
f
ln
2
2
ln
:
=
=
( )
(
)
(
)
1
ln
2
1
2
ln
2
'
ln
2
'
2
2
ln
2
+
⋅
=
+
⋅
=
⋅
=
x
x
x
x
x
x
x
x
e
x
f
x
x
x
x
Ke
ď
že
x
x
2
je pre
(
2
,
0
∈
x
vždy kladné
⇒
( )
1
1
ln
0
1
ln
0
'
−
=
⇔
−
=
⇔
=
+
⇔
=
e
x
x
x
x
f
Lokálne (na danom intervale aj globálne) minimum je v bode
e
e
e
2
1
,
1
.
Globálne maximum môže by
ť
bu
ď
v bode
( )
[
]
2
,
2 f
alebo ve
ľ
mi blízko k
0
.
e
1
+
–
0
2
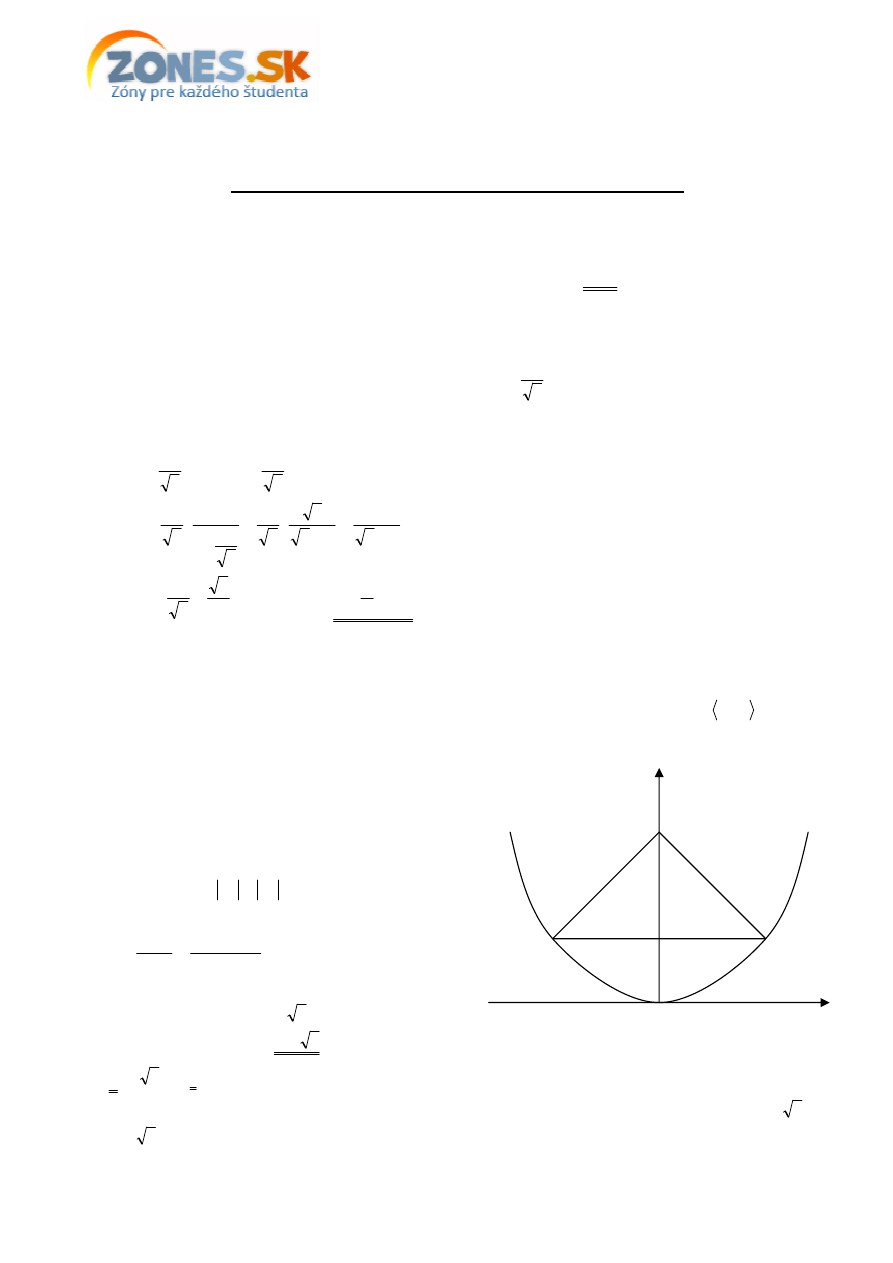
Autor: Martin Slota
Zdroj: http://www.zones.sk
Používanie materiálov zo ZONES.SK je povolené bez
obmedzení iba na osobné ú
č
ely a akéko
ľ
vek verejné
publikovanie je bez predchádzajúceho súhlasu zakázané.
2/3
MATURITNÉ PRÍKLADY Z MATEMATIKY
M
ATURITNÝ OKRUH
14:
D
ERIVÁCIE
( )
( )
⇒
=
=
=
=
=
∞
−
⋅
⋅
→
→
+
+
1
lim
lim
16
2
2
0
2
ln
2
0
2
0
4
e
e
x
f
x
x
x
x
x
globálne maximum je v bode
[ ]
16
,
2
.
3. príklad (153/11)
Zadanie: Pod akým uhlom pretína graf funkcie
+
=
3
1
ln
:
x
y
f
os x?
Riešenie:
⇒
=
⇔
=
+
⇔
=
+
0
1
3
1
0
3
1
ln
x
x
x
bod, v ktorom graf funkcie
f
pretína os x je
[ ]
0
,
0
.
( )
x
x
x
x
f
+
=
+
⋅
=
+
⋅
=
3
1
3
3
3
1
3
1
1
3
1
'
( )
°
=
=
⇒
=
=
=
=
30
6
tg
3
3
3
1
0
'
π
ϕ
ϕ
k
f
Graf funkcie
f
pretína os x pod uhlom
°
=
30
ϕ
.
4. príklad (154/13)
Zadanie: V karteziánskej súradnicovej sústave je nakreslený graf funkcie
3
,
3
:
2
−
∈
=
x
y
f
. Ozna
č
me
A
bod
[ ]
9
,
0
. Nájdite na grafe funkcie
f
body
C
B,
také, že
ABC
je rovnoramenný trojuholník so
základ
ň
ou
BC
rovnobežnou s osou x a obsah trojuholníka
ABC
je maximálny možný.
Riešenie:
[
] [
]
C
C
B
B
y
x
C
y
x
B
,
,
,
BC
je rovnobežné s osou x
y
y
y
C
B
=
=
⇒
(
ABC
∆
je rovnoramenný
)
⇒
=
∧
=
∧
0
A
C
B
x
y
y
x
x
x
x
x
C
B
C
B
=
=
⇒
−
=
⇒
2
x
y
=
(
)
(
)
3
2
9
9
2
9
2
2
x
x
x
x
y
x
v
a
S
a
−
=
−
⋅
=
−
⋅
=
⋅
=
( )
2
3
9
'
x
x
S
−
=
( )
3
3
0
'
2
=
⇔
=
⇔
=
x
x
x
S
( )
⇒
−
=
x
x
S
6
''
v bode
3
=
x
je lokálne (na danom intervale aj globálne) maximum.
( )
3
3
2
=
=
y
Súradnice bodov
C
B,
takých, že obsah trojuholníka
ABC
je maximálny možný sú
[ ]
3
,
3
B
a
[
]
3
,
3
−
C
.
y
x
A
B
C
f
a
v
a
Autor: Martin Slota
Zdroj: http://www.zones.sk
Používanie materiálov zo ZONES.SK je povolené bez
obmedzení iba na osobné ú
č
ely a akéko
ľ
vek verejné
publikovanie je bez predchádzajúceho súhlasu zakázané.
3/3
MATURITNÉ PRÍKLADY Z MATEMATIKY
M
ATURITNÝ OKRUH
14:
D
ERIVÁCIE
5. príklad (154/25)
Zadanie: Dokážte, že ak má funkcia
f
na intervale
( )
b
a
,
ohrani
č
enú deriváciu, je na tomto intervale
ohrani
č
ená.
Dôkaz (priamy):
Nech funkcia
f
má na
( )
b
a
,
ohrani
č
enú deriváciu. Potom
( ) ( )
k
x
f
b
a
x
R
k
≤
∈
∀
∈
∃
+
'
;
,
.
Platí:
b
a
b
a
+
≤
+
( ) ( )
( ) ( ) ( )
( ) ( )
( )
( ) (
)
( )
=
+
−
⋅
=
+
−
≤
+
−
=
∈
∀
0
0
v.
Lagr.
0
0
0
0
0
'
;
,
,
x
f
x
x
c
f
x
f
x
f
x
f
x
f
x
f
x
f
x
f
b
a
x
x
( ) (
)
( )
0
0
'
x
f
x
x
c
f
+
−
⋅
=
, kde
c
je medzi
0
, x
x
,
č
iže
( )
b
a
c
,
∈
.
( )
( )
(
)
( )
( ) (
)
( )
( )
⇒
∈
+
−
⋅
<
+
−
⋅
≤
⇒
∈
∧
−
<
−
∧
≤
+
+
R
x
f
b
a
k
x
f
x
x
c
f
x
f
R
x
f
b
a
x
x
k
c
f
0
0
0
0
0
'
'
⇒
funkcia
f
je ohrani
č
ená na intervale
( )
b
a,
Č
BTD.
Wyszukiwarka
Podobne podstrony:
derivation flow equation prof J Kleppe
[38]QUERCETIN AND ITS DERIVATIVES CHEMICAL STRUCTURE AND BIOACTIVITY – A REVIEW
CALC1 L 4 Derivatives
Derivational Morphology
extraction and analysis of indole derivatives from fungal biomass Journal of Basic Microbiology 34 (
DERIVAZIONE, język włoski nauka
Derivations in Minimalism (S D Epstein&T D Seely)
Methylcellulose, a Cellulose Derivative with Original Physical
Polish Weather Derivatives stro Nieznany
04 List of basic and derivative calibres
derivation flow equation prof J Kleppe
[38]QUERCETIN AND ITS DERIVATIVES CHEMICAL STRUCTURE AND BIOACTIVITY – A REVIEW
Carboxylic Acid derivatives
Global Requirements for Medical Applications of Chitin and its Derivatives
nitro alkene derivatives
Chicone C , Swanson R Linearization via the Lie derivative (EJDE monograph 02, 2000)(64s)
Black T H Derivations of applied mathematics (web draft, 2006)(246s) MCet
Derivacie
więcej podobnych podstron